Spatiotemporal Dynamics of NDVI, Soil Moisture and ENSO in Tropical South America
Abstract
1. Introduction
2. Materials and Methods
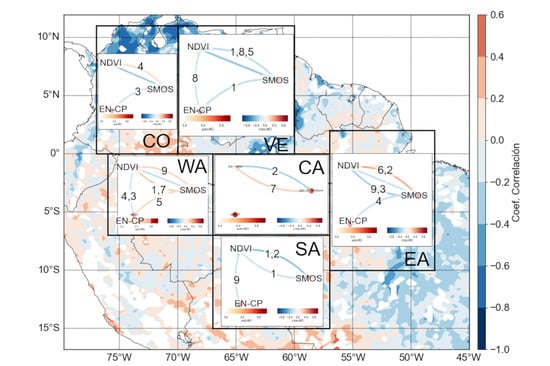
2.1. Study Area: Tropical South America
2.2. Data Sets
2.2.1. Soil Moisture (SMOS)
2.2.2. Normalized Difference Vegetation Index (NDVI)
2.2.3. El Niño–Southern Oscillation (ENSO)
2.3. Methodology
- Raw time series correspond to the observed SMOS and NDVI monthly series without any manipulation, as mentioned above.
- Standardized time series of the regionally averaged values are estimated such that the anomalies, z(t), are computed by subtracting the sample monthly mean of the raw data, x(t), and dividing by the corresponding sample monthly standard deviation [52].
2.3.1. Exploratory Analysis and Linear Correlations
- NDVI and SMOS. Temporal and spatial linear Pearson’s lagged cross-correlations are estimated between raw and standardized time series of NDVI and SMOS, for the regionally averaged values and on a pixel-by-pixel scale.
- Correlations with both ENSO types. Temporal and spatial Pearson’s lagged correlations between both variables and the EP and CP indices are estimated for both raw and standardized data sets.
2.3.2. Wavelets and Cross-Wavelets Analyses
2.3.3. Nonlinear Causality Analyses
3. Results
3.1. Raw Data
3.1.1. Exploratory Analysis
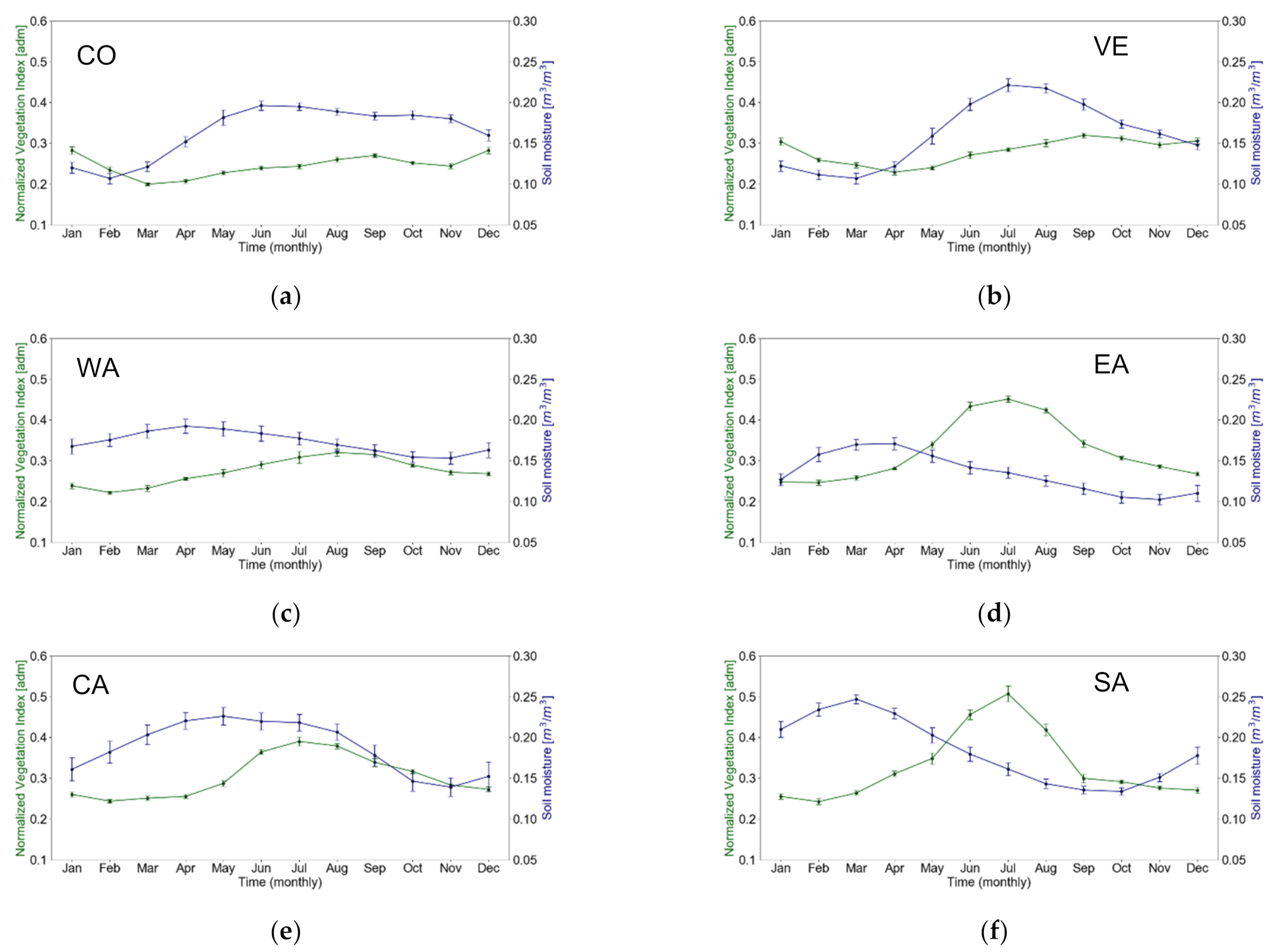
3.1.2. Long-Term Mean Annual Cycles and Time Series
3.1.3. Correlation Analysis
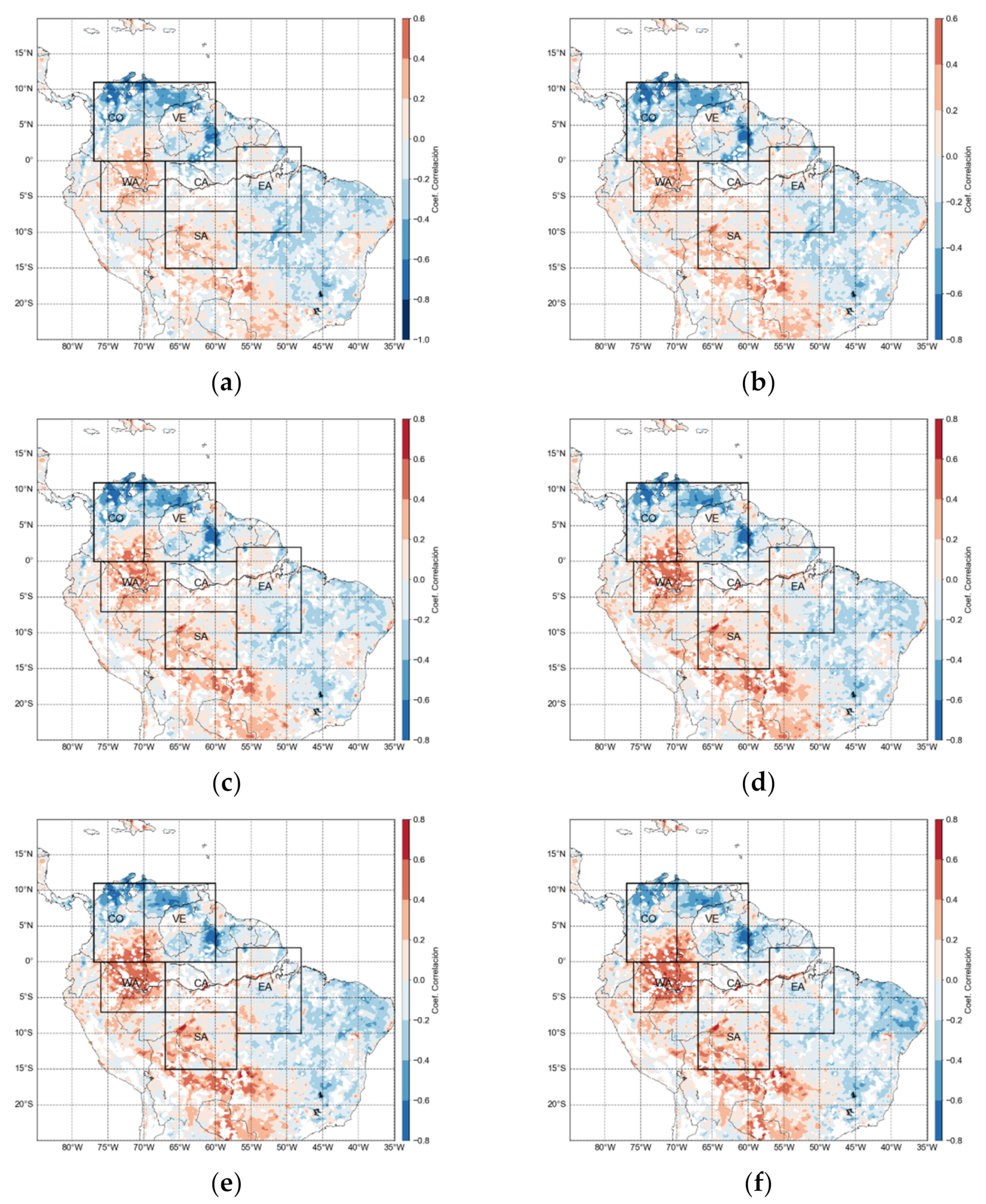
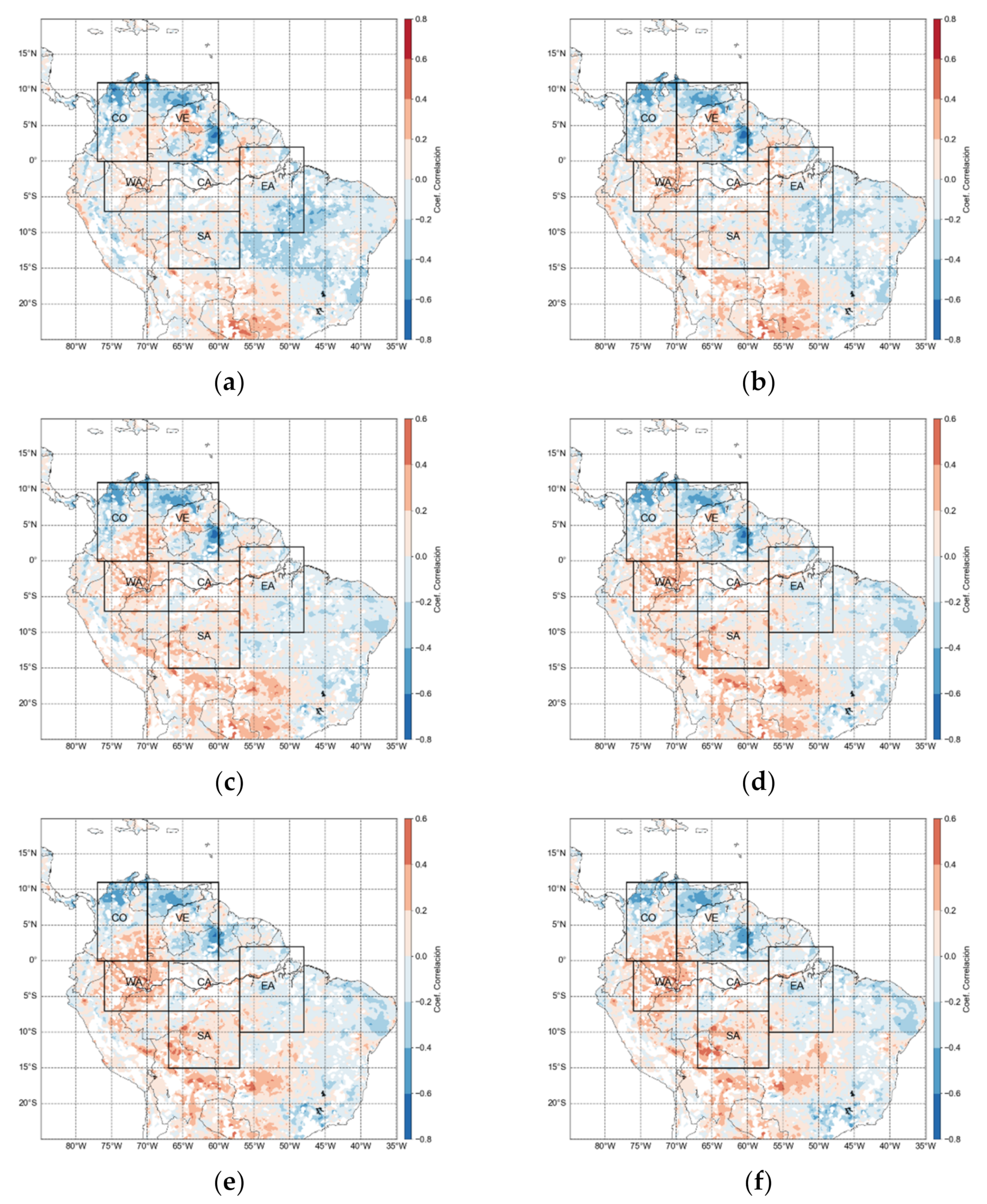
- Spatial lagged cross-correlations. Figure 4 shows maps of spatial (pixel-by-pixel) lagged cross-correlations between the monthly series of NDVI and SMOS. Results indicate significant positive correlations for most regions, especially when SMOS leads NDVI by 1, 2, and 3 months, in particular over the Colombian-Venezuelan Llanos of the Orinoco River basin, and smaller negative correlations when NDVI leads SMOS by 2 and 3 months.
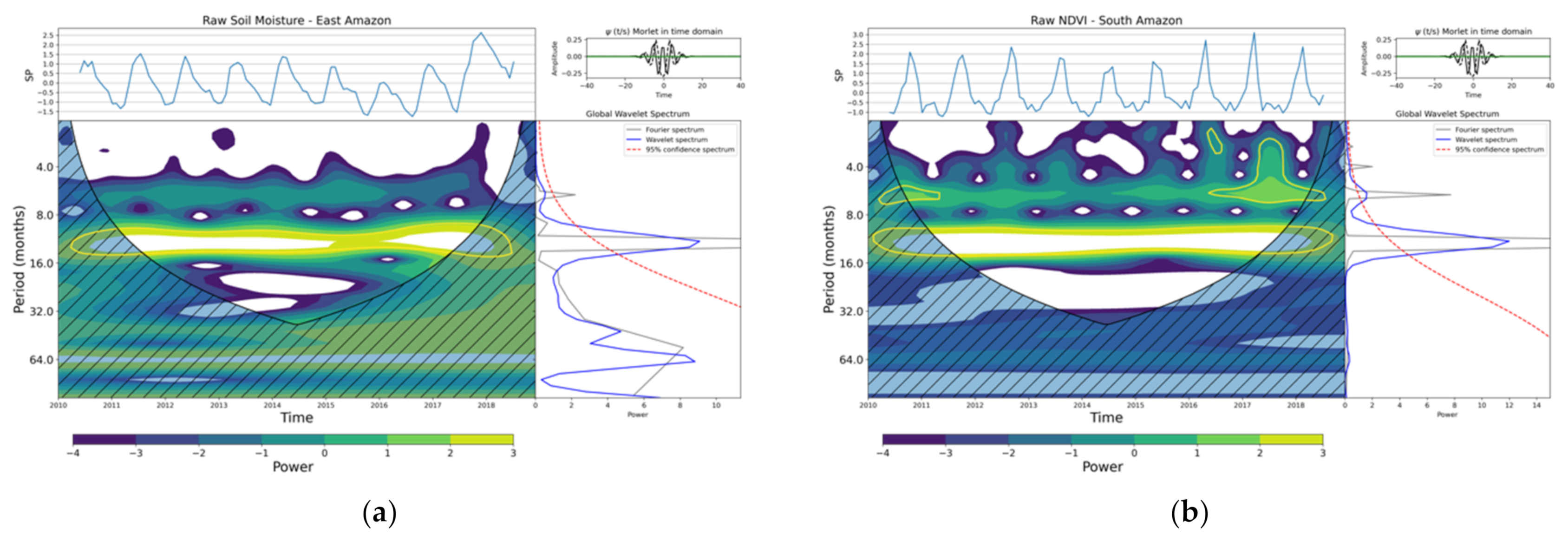
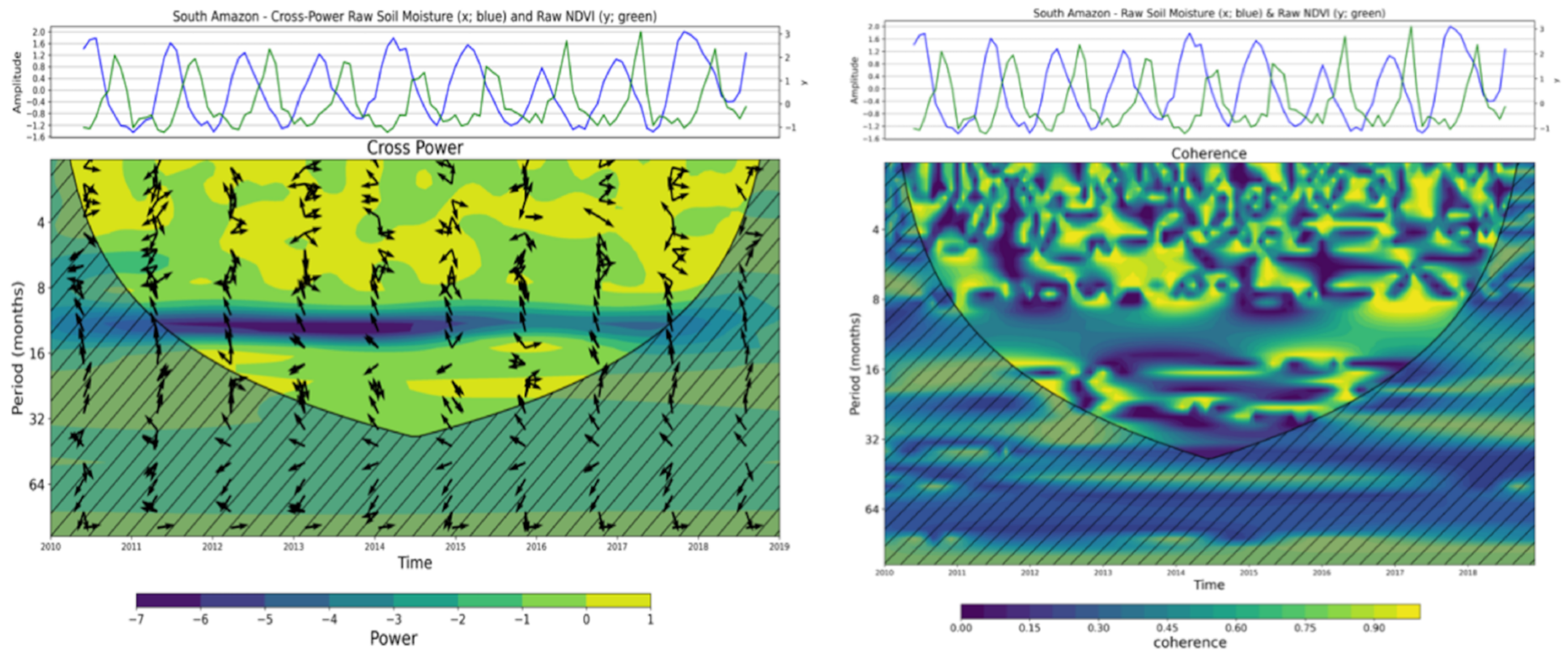
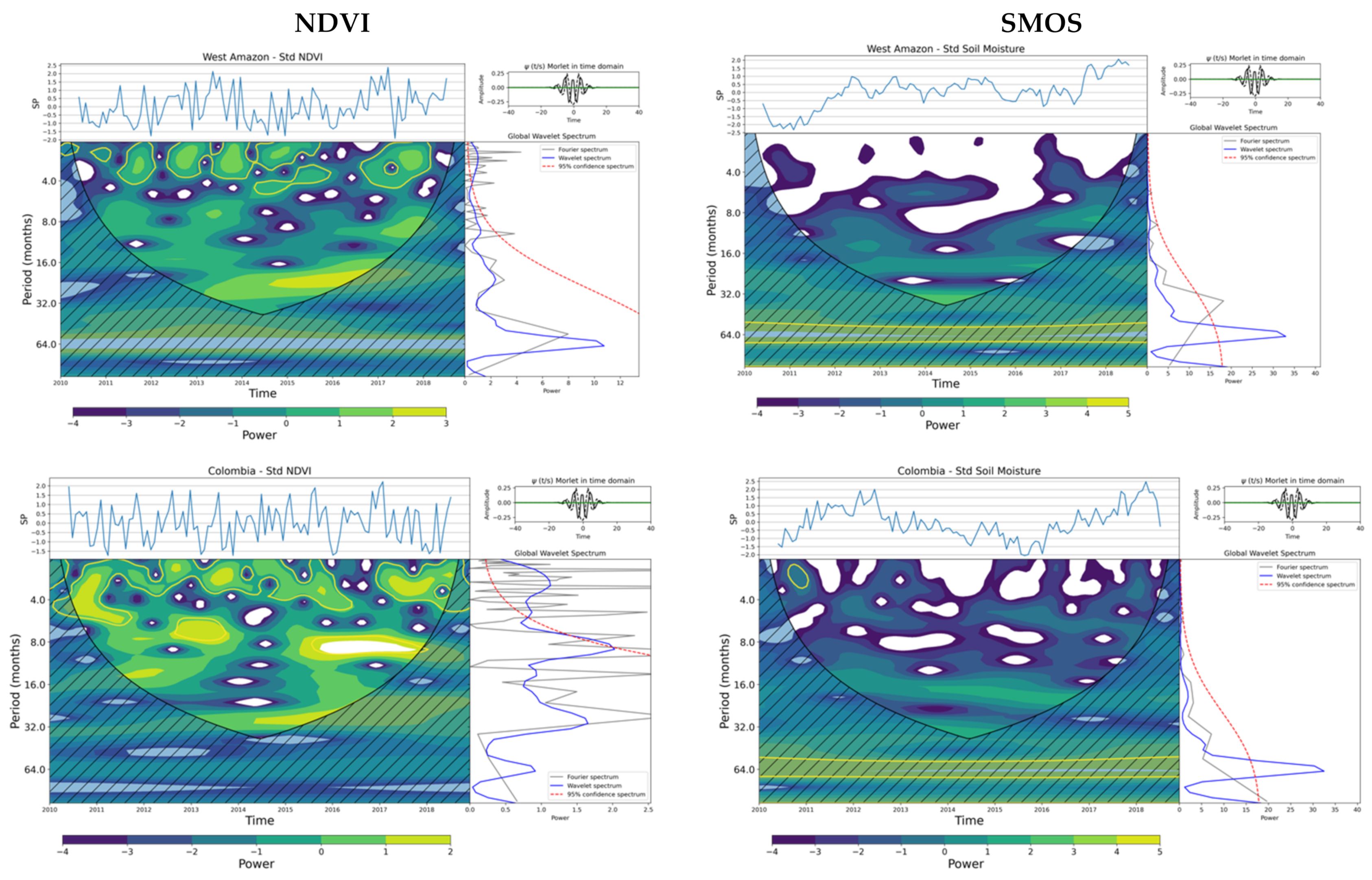
3.1.4. Wavelet Transforms, Wavelet Cross-Spectra, and Coherency Analyses
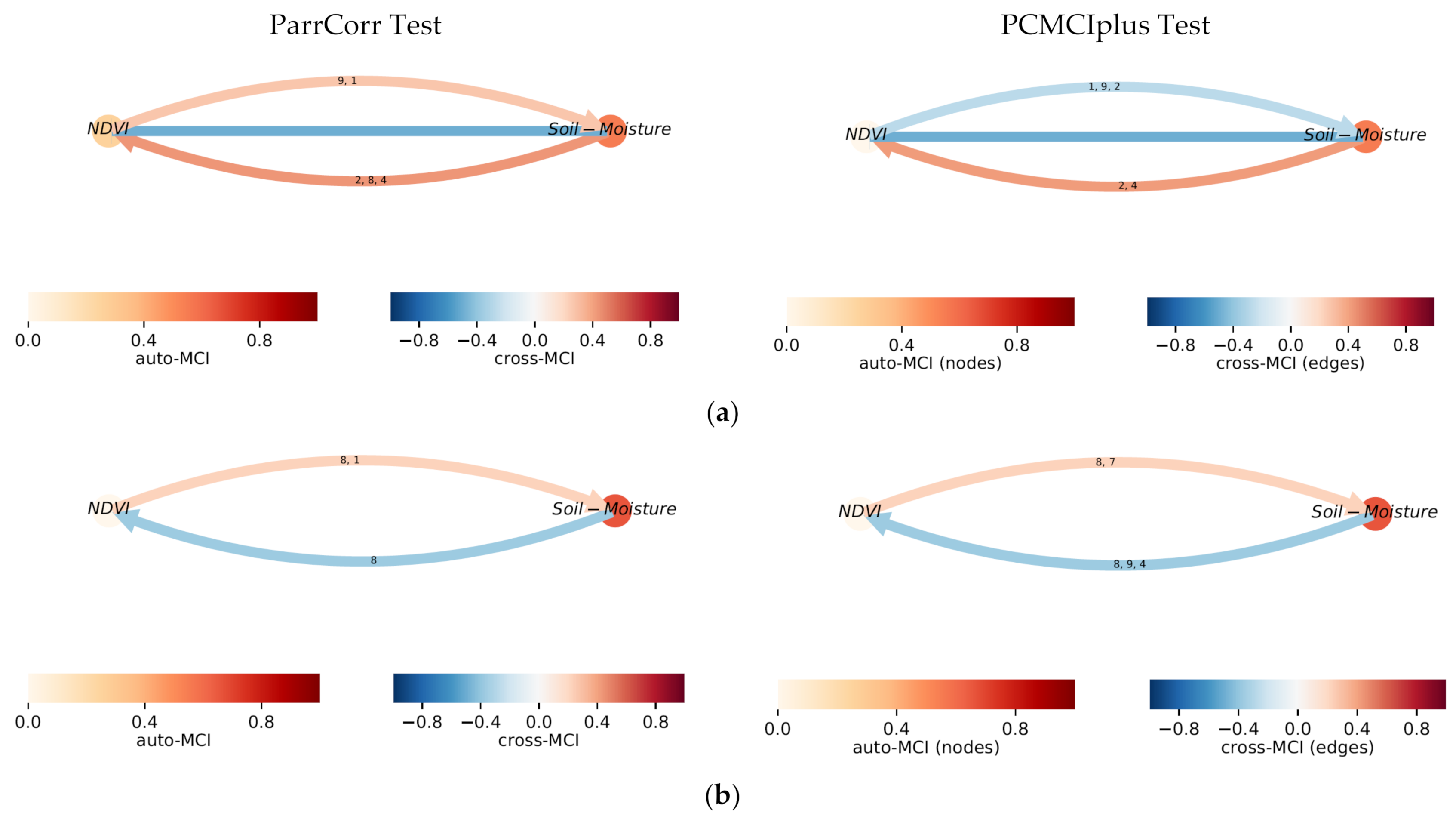
3.1.5. Nonlinear Causality Analyses
- ParrCorr test.
- PCMCIplus test.
3.2. Standardized Data—Interannual Variability Associated with ENSO
3.2.1. Correlation Analyses
- Lagged cross-correlations between time series
- Spatial lagged cross-correlations
3.2.2. Wavelet Transforms, Wavelet Cross-Spectra, and Coherency Analyses
3.2.3. Nonlinear Causality Analyses
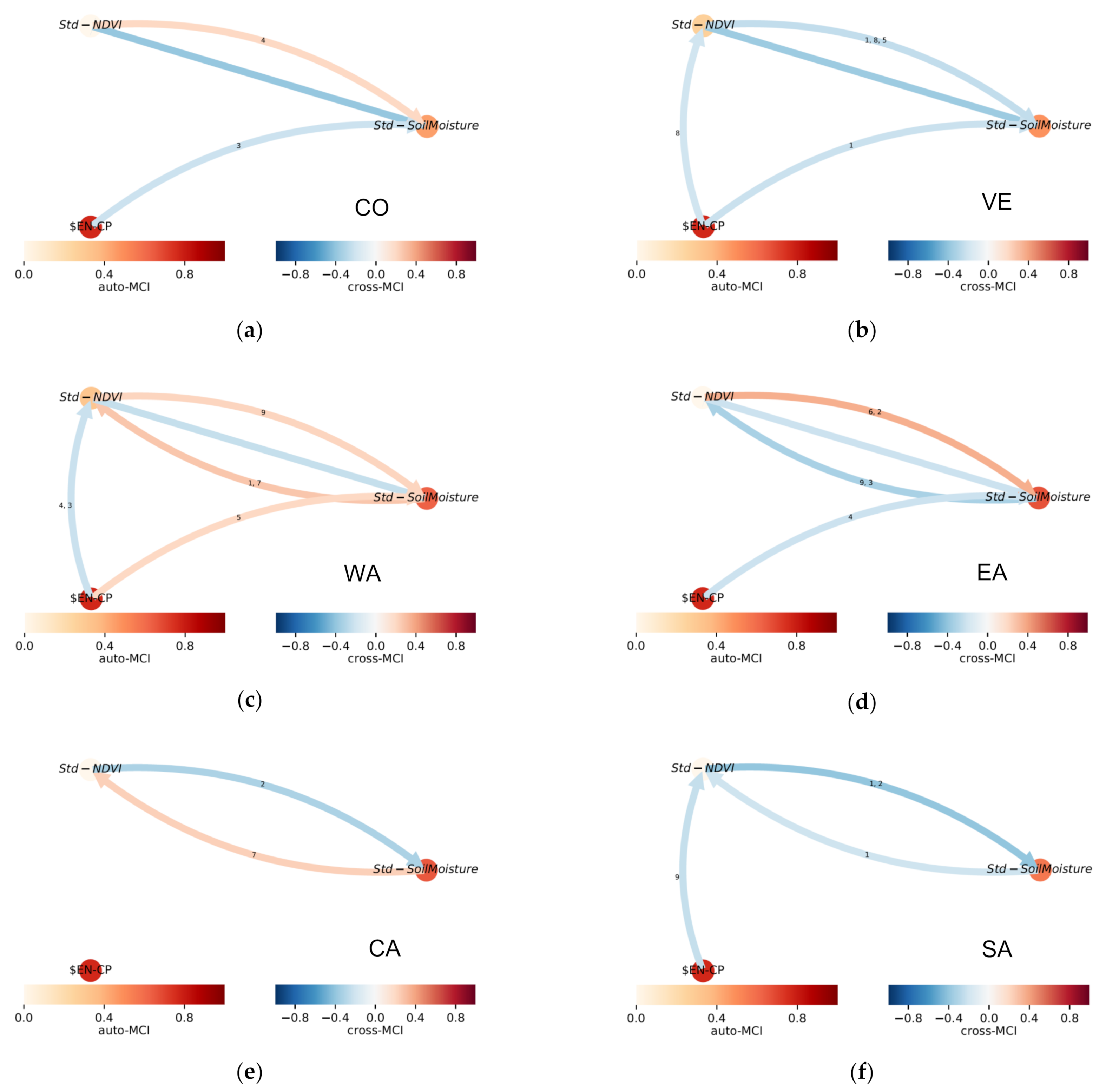
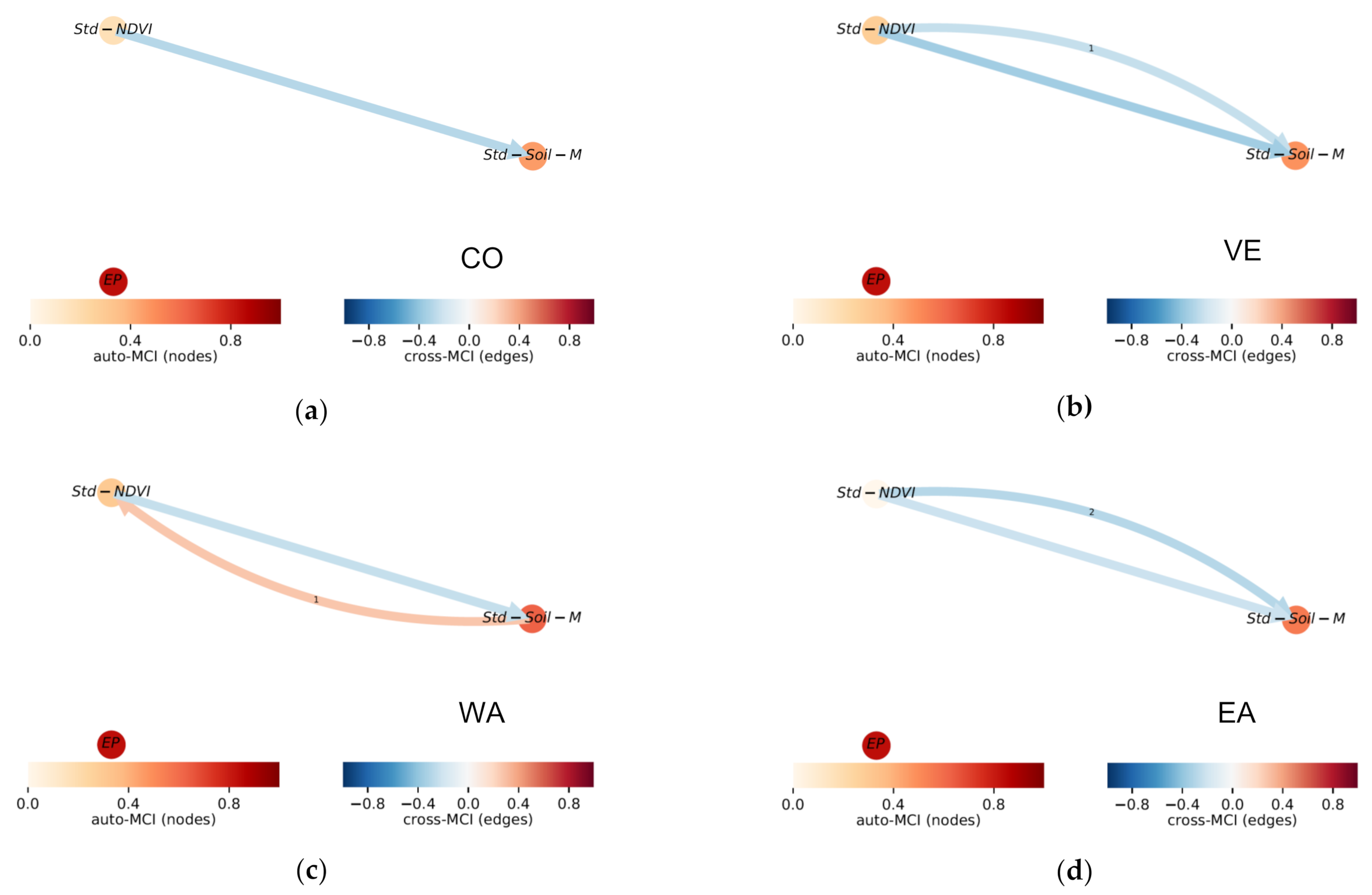
- Nonlinear auto-correlations (Auto-MCI).
- Contemporaneous nonlinear causalities.
- Lagged nonlinear causalities.
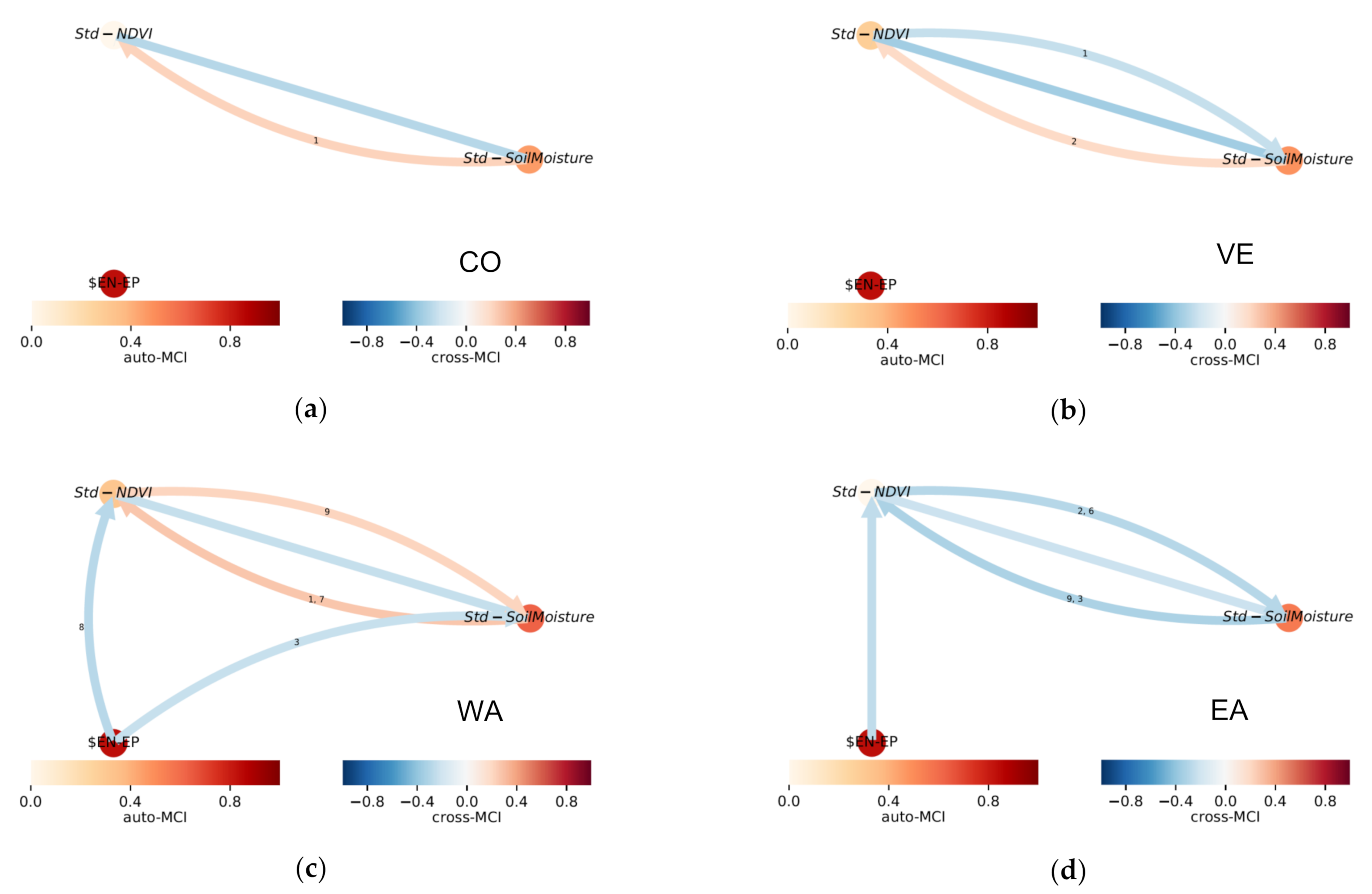
- Nonlinear autocorrelations (Auto-MCI).
- Contemporaneous nonlinear causalities.
4. Discussion
4.1. Raw Data
4.1.1. Linear Correlations
4.1.2. Wavelets and Cross-Wavelet Analyses
4.1.3. NonLinear Causality Analyses
4.2. Standardized Data—Interannual Variability Associated with ENSO
4.2.1. Correlation Analysis
4.2.2. Wavelets and Cross-Wavelet Analyses
4.2.3. Nonlinear Causality Analyses
4.3. Study Limitations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zemp, D.C.; Schleussner, C.-F.; Barbosa, H.M.J.; van der Ent, R.J.; Donges, J.F.; Heinke, J.; Sampaio, G.; Rammig, A. On the importance of cascading moisture recycling in South America. Atmos. Chem. Phys. 2014, 14, 13337–13359. [Google Scholar] [CrossRef]
- Zemp, D.C.; Schleussner, C.F.; Barbosa, H.M.; Hirota, M.; Montade, V.; Sampaio, G.; Staal, A.; Wang-Erlandsson, L.; Rammig, A. Self-amplified Amazon forest loss due to vegetation-atmosphere feedbacks. Nat. Comm. 2017, 8, 14681. [Google Scholar] [CrossRef] [PubMed]
- Coe, M.T.; Macedo, M.N.; Brando, P.M.; Lefebvre, P.; Panday, P.; Silvério, D. The Hydrology and Energy Balance of the Amazon Basin. In Interactions between Biosphere, Atmosphere and Human Land Use in the Amazon Basin, Ecological Studies; Nagy, L., Ed.; Springer: Berlin/Heidelberg, Germany, 2016; Volume 227, pp. 35–53. [Google Scholar]
- Wright, J.S.; Fu, R.; Worden, J.R.S.; Chakraborty, N.E.; Clinton, C.; Risi, Y.S.; Yin, L. Rainforest-initiated wet season onset over the southern Amazon. Proc. Natl. Acad. Sci. USA 2017, 114, 8481–8486. [Google Scholar] [CrossRef] [PubMed]
- Staal, A.; Fetzer, I.; Wang-Erlandsson, L.; Bosmans, J.H.; Dekker, S.C.; van Nes, E.H.; Rockström, J.; Tuinenburg, O.A. Hysteresis of tropical forests in the 21st century. Nat. Commun. 2020, 11, 4978. [Google Scholar] [CrossRef]
- Staal, A.; Tuinenburg, O.A.; Bosmans, J.H.; Holmgren, M.; van Nes, E.H.; Scheffer, M.; Zemp, D.C.; Dekker, S.C. Forest-rainfall cascades buffer against drought across the Amazon. Nat. Clim. Chang. 2018, 8, 539–543. [Google Scholar] [CrossRef]
- Caioni, C.; Silvério, D.V.; Macedo, M.N.; Coe, M.T.; Brando, P.M. Droughts Amplify Differences Between the Energy Balance Components of Amazon Forests and Croplands. Remote Sens. 2020, 12, 525. [Google Scholar] [CrossRef]
- Poveda, G.; Mesa, O.J. Feedbacks between hydrological processes in tropical South America and large scale oceanic atmospheric phenomena. J. Clim. 1997, 10, 2690–2702. [Google Scholar] [CrossRef]
- Poveda, G.; Jaramillo, A.; Gil, M.M.; Quiceno, N.; Mantilla, R. Seasonality in ENSO related precipitation, river discharges, soil moisture, and vegetation index (NDVI) in Colombia. Water Resour. Res. 2001, 37, 2169–2178. [Google Scholar] [CrossRef]
- Poveda, G.; Álvarez, D.M.; Rueda, O.A. Hydro-climatic variability over the Andes of Colombia associated with ENSO: A review of climatic processes and their impact on one of the Earth’s most important biodiversity hotspots. Clim. Dyn. 2010, 36, 2233. [Google Scholar] [CrossRef]
- Barreiro, M.; Díaz, N. Land–atmosphere coupling in El Niño influence over South America. Atmos. Sci. 2011, 12, 351–355. [Google Scholar] [CrossRef]
- Erfanian, A.; Wang, G.; Fomenko, L. Unprecedented drought over tropical South America in 2016: Significantly under-predicted by tropical SST. Sci. Rep. 2017, 7, 5811. [Google Scholar] [CrossRef] [PubMed]
- Builes-Jaramillo, A.; Marwan, N.; Poveda, G.; Kurths, J. Nonlinear interactions between the Amazon River basin and the Tropical North Atlantic at interannual timescales. Clim. Dyn. 2018, 50, 2951–2969. [Google Scholar] [CrossRef]
- Builes-Jaramillo, A.; Ramos, A.M.T.; Poveda, G. Atmosphere-Land Bridge between the Pacific and Tropical North Atlantic SST’s through the Amazon River basin during the 2005 and 2010 droughts. Chaos Interdiscip. J. Nonlinear Sci. 2018, 28, 085705. [Google Scholar] [CrossRef] [PubMed]
- Gentine, P.; Massmann, A.; Lintner, B.R.; Hamed Alemohammad, S.; Fu, R.; Green, J.K.; Kennedy, D.; Vilà-Guerau de Arellano, J. Land–atmosphere interactions in the tropics—A review. Hydrol. Earth Syst. Sci. 2019, 23, 4171–4197. [Google Scholar] [CrossRef]
- Levine, P.A.; Randerson, J.T.; Chen, Y.; Pritchard, M.S.; Xu, M.; Hoffman, F.M. Soil Moisture Variability Intensifies and Prolongs Eastern Amazon Temperature and Carbon Cycle Response to El Niño–Southern Oscillation. J. Clim. 2019, 32, 1273–1292. [Google Scholar] [CrossRef]
- Menéndez, C.G.; Giles, J.; Ruscica, R.; Zaninelli, P.; Coronato, T.; Falco, M.; Sörensson, A.; Fita, L.; Carril, A.; Li, L. Temperature variability and soil–atmosphere interaction in South America simulated by two regional climate models. Clim. Dyn. 2019, 53, 2919–2930. [Google Scholar] [CrossRef]
- Walter-Shea, E. Southeastern, U.S. vegetation response to ENSO events (1989–1999). Clim. Chang. 2003, 60, 1999–2000. [Google Scholar]
- Batista, G.T.; Shimabukuro, Y.E.; Lawrence, W.T. The long-term monitoring of vegetation cover in the Amazonian region of northern Brazil using NOAA-AVHRR data. Int. J. Remote Sens. 1997, 18, 3195–3210. [Google Scholar] [CrossRef]
- Koster, R.D.; Dirmeyer, P.A.; Guo, Z.; Bonan, G.; Chan, E.; Cox, P.; Yamada, T. Regions of strong coupling between soil moisture and precipitation. Science 2004, 305, 1138–1140. [Google Scholar] [CrossRef]
- Taylor, C.M.; de Jeu, R.A.; Guichard, F.; Harris, P.P.; Dorigo, W.A. Afternoon rain more likely over drier soils. Nature 2012, 489, 423–426. [Google Scholar] [CrossRef]
- Xue, Y.; De Sales, F.; Li, W.P.; Mechoso, C.R.; Nobre, C.A.; Juang, H.M. Role of land surface processes in South American monsoon development. J. Clim. 2006, 19, 741–762. [Google Scholar] [CrossRef]
- Bedoya-Soto, J.M.; Poveda, G.; Sauchyn, D. New insights on land-atmosphere feedbacks over tropical South America at interannual timescales. Water 2018, 10, 1095. [Google Scholar] [CrossRef]
- Bruno, R.D.; da Rocha, H.R.; de Freitas, H.C.; Goulden, M.L.; Miller, S.D. Soil moisture dynamics in an eastern Amazonian tropical forest. Hydrol. Processes 2006, 20, 2477–2489. [Google Scholar] [CrossRef]
- Zanin, P.R.; Satyamurty, P. Interseasonal and interbasins hydrological coupling in south America. J. Hydrometeorol. 2021, 22, 1609–1625. [Google Scholar] [CrossRef]
- Negrón-Juárez, R.; Ferreira, S.F.; Mota, M.C.; Faybishenko, B.; Monteiro, M.F.; Candido, L.A.; Ribeiro, R.P.; Oliveira, R.C.; Araujo, A.C.; Warren, J.M.; et al. Calibration, measurement, and characterization of soil moisture dynamics in a central amazonian tropical forest. Vadose Zone J. 2020, 19, 1–16. [Google Scholar] [CrossRef]
- Llopart, M.; da Rocha, R.P.; Reboita, M.; Cuadra, S. Sensitivity of simulated south america climate to the land surface schemes in RegCM4. Clim. Dyn. 2017, 49, 3975–3987. [Google Scholar] [CrossRef]
- Broedel, E.; Tomasella, J.; Cândido, L.A.; von Randow, C. Deep soil water dynamics in an undisturbed primary forest in central amazonia: Differences between normal years and the 2005 drought. Hydrol. Processes 2017, 31, 1749–1759. [Google Scholar] [CrossRef]
- Cho, J.; Ryu, J.-H.; Yeh, P.J.-F.; Lee, Y.-W.; Hong, S. Satellite-based assessment of Amazonian surface dryness due to deforestation. Remote Sens. Lett. 2016, 7, 71–80. [Google Scholar] [CrossRef]
- Hasler, N.; Avissar, R. What Controls Evapotranspiration in the Amazon Basin? J. Hydrometeorol. 2007, 8, 380–395. [Google Scholar] [CrossRef]
- Maeda, E.E.; Ma, X.; Wagner, F.H.; Kim, H.; Oki, T.; Eamus, D.; Huete, A. Evapotranspiration seasonality across the Amazon Basin. Earth Syst. Dynam. 2017, 8, 439–454. [Google Scholar] [CrossRef]
- Mu, Y.; Biggs, T.W.; De Sales, F. Forests mitigate drought in an agricultural region of the Brazilian Amazon: Atmospheric moisture tracking to identify critical source areas. Geophys. Res. Lett. 2021, 48, e2020GL091380. [Google Scholar] [CrossRef]
- Manoli, G.; Ivanov, V.Y.; Fatichi, S. Dry-season greening and water stress in Amazonia: The role of modeling leaf phenology. J. Geophys. Res. 2018, 123, 1909–1926. [Google Scholar] [CrossRef]
- Huete, A.R.; Didan, K.; Shimabukuro, Y.E.; Ratana, P.; Saleska, S.R.; Hutyra, L.R.; Yang, W.; Nemani, R.R.; Myneni, R. Amazon rainforests green-up with sunlight in dry season. Geophys. Res. Lett. 2006, 33, 06405. [Google Scholar] [CrossRef]
- Harper, A.; Baker, I.T.; Denning, A.S.; Randall, D.A.; Dazlich, D.; Branson, M. Impact of evapotranspiration on dry season climate in the Amazon forest. J. Clim. 2014, 27, 574–591. [Google Scholar] [CrossRef]
- Restrepo-Coupé, N.; da Rocha, H.R.; Hutyra, L.R.; da Araujo, A.C.; Borma, L.S.; Christoffersen, B.; Cabral, O.M.; de Camargo, P.B.; Cardoso, F.L.; da Costa, A.C.L.; et al. What drives the seasonality of photosynthesis across the Amazon basin? A cross-site analysis of eddy flux tower measurements from the Brasil flux network. Agric. For. Meteorol. 2013, 182, 128–144. [Google Scholar] [CrossRef]
- Samanta, A.; Ganguly, S.; Hashimoto, H.; Devadiga, S.; Vermote, E.; Knyazikhin, Y.; Nemani, R.R.; Myneni, R.B. Amazon forests did not green-up during the 2005 drought. Geophys. Res. Lett. 2010, 37, L05401. [Google Scholar] [CrossRef]
- Jeong, H.-I.; Ahn, J.-B. A new method to classify ENSO events into eastern and central Pacific types. Int. J. Climatol. 2017, 37, 2193–2199. [Google Scholar] [CrossRef]
- Marengo, J.A. On the hydrological cycle of the Amazon Basin: A historical review and current state-of-the-art. Rev. Bras. Meteorol. 2006, 21, 1–19. [Google Scholar]
- Gouveia, N.A.; Gherardi, D.F.M.; Aragão, L.E.O.C. The role of the Amazon River plume on the intensification of the hydrological cycle. Geophys. Res. Lett. 2019, 46, 12221–12229. [Google Scholar] [CrossRef]
- Chaudhari, S.; Pokhrel, Y.; Moran, E.; Miguez-Macho, G. Multi-decadal hydrologic change and variability in the Amazon River basin: Understanding terrestrial water storage variations and drought characteristics. Hydrol. Earth Syst. Sci. 2019, 23, 2841–2862. [Google Scholar] [CrossRef]
- Restrepo-Coupe, N.; Levine, N.M.; Christoffersen, B.O.; Albert, L.P.; Wu, J.; Costa, M.H.; Galbraith, D.; Imbuzeiro, H.; Martins, G.; da Araujo, A.C.; et al. Do dynamic global vegetation models capture the seasonality of carbon fluxes in the Amazon basin? A data-model intercomparison. Glob. Chang. Biol. 2017, 23, 191–208. [Google Scholar] [CrossRef] [PubMed]
- Da Rocha, H.R.; Manzi, A.O.; Cabral, O.M.; Miller, S.D.; Goulden, M.L.; Saleska, S.R.; Restrepo-Coupe, N.; Wofsy, S.C.; Borma, L.S.; Artaxo, P.; et al. Patterns of water and heat flux across a biome gradient from tropical forest to savanna in Brazil. J. Geophys. Res. 2009, 114, 1–8. [Google Scholar] [CrossRef]
- SMOS-BEC. Ocean and Land Products Description. Available online: http://bec.icm.csic.es/doc/BEC-SMOS-0001-PD-Ice.pdf (accessed on 21 June 2020).
- Zhuo, L.; Dai, Q.; Han, D. Evaluation of SMOS soil moisture retrievals over the central United States for hydro-meteorological application. Phys. Chem. Earth 2015, 83–84, 146–155. [Google Scholar] [CrossRef][Green Version]
- Vermote, E.; Justice, C.; Csiszar, I.; Eidenshink, J.; Myneni, R.B.; Baret, F.; Masuoka, E.; Wolfe, R.E.; Claverie, M.; NOAA CDR Program. NOAA Climate Data Record (CDR) of Normalized Difference Vegetation Index (NDVI), Version 4; NOAA National Centers for Environmental Information: Asheville, NC, USA, 2014. [Google Scholar] [CrossRef]
- Poveda, G.; Salazar, L.F. Annual and interannual (ENSO) variability of spatial scaling properties of a vegetation index (NDVI) in Amazonia. Remote Sens. Environ. 2004, 93, 391–401. [Google Scholar] [CrossRef]
- Franch, B.; Vermote, E.F.; Roger, J.C.; Murphy, E.; Becker-Reshef, I.; Justice, C.; Claverie, M.; Nagol, J.; Csiszar, I.; Meyer, D.; et al. A 30+ year AVHRR land surface reflectance climate data record and its application to wheat yield monitoring. Remote Sens. 2017, 9, 296. [Google Scholar] [CrossRef]
- Wang, C. A review of ENSO theories. Natl. Sci. Rev. 2018, 5, 813–825. [Google Scholar] [CrossRef]
- Sullivan, A.; Luo, J.; Hirst, A.C.; Bi, D.; Cai, W.; He, J. Robust contribution of decadal anomalies to the frequency of central-Pacific El Niño. Sci. Rep. 2016, 38540, 1–7. [Google Scholar] [CrossRef]
- Cai, W.; McPhaden, M.J.; Grimm, A.M.; Rodrigues, R.R.; Taschetto, A.S.; Garreaud, R.D.; Dewitte, B.; Poveda, G.; Ham, Y.-G.; Santoso, A.; et al. Climate impacts of the El Niño–Southern Oscillation on South America. Nat. Rev. Earth Environ. 2020, 1, 215–231. [Google Scholar] [CrossRef]
- Wilks, D.S. Empirical Distributions and Exploratory Data Analysis. Int. Geophys. 2011, 100, 23–70. [Google Scholar]
- Daubechies, I. The wavelet transform time-frequency localization and signal analysis. IEEE Trans. Inform. Theory 1990, 36, 961–1004. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A Practical Guide to Wavelet Analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Maraun, D.; Kurths, J. Cross wavelet analysis: Significance testing and pitfalls. Nonlinear Process. Geophys. 2004, 11, 505–514. [Google Scholar] [CrossRef]
- Yi, H.; Shu, H. The improvement of the Morlet wavelet for multi-period analysis of climate data. Comptes Rendus Geosci. 2012, 344, 483–497. [Google Scholar] [CrossRef]
- Spirtes, P.; Glymour, C. An Algorithm for Fast Recovery of Sparse Causal Graphs. Soc. Sci. Comput. 1991, 9, 62–72. [Google Scholar] [CrossRef]
- Spirtes, P.; Glymour, C.; Scheines, R. Causation, Prediction, and Search; MIT Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Runge, J.; Petoukhov, V.; Kurths, J. Quantifying the Strength and Delay of Climatic Interactions: The Ambiguities of Cross Correlation and a Novel Measure Based on Graphical Models. J. Clim. 2014, 27, 720–739. [Google Scholar] [CrossRef]
- Runge, J. Conditional independence testing based on a nearest-neighbor estimator of conditional mutual information. In Proceedings of the 21st International Conference on Artificial Intelligence and Statistics, Playa Blanca, Spain, 9 April 2018. [Google Scholar]
- Runge, J.; Bathiany, S.; Bollt, E.; Camps-Valls, G.; Coumou, D.; Deyle, E.; Glymour, C.; Kretschmer, M.; Mahecha, M.D.; Muñoz-Marí, J.; et al. Inferring causation from time series in earth system sciences. Nat. Commun. 2019, 10, 2553. [Google Scholar] [CrossRef]
- Runge, J.; Nowack, P.; Kretschmer, M.; Flaxman, S.; Sejdinovic, D. Detecting and quantifying causal associations in large nonlinear time series datasets. Sci. Adv. 2019, 5, eaau4996. [Google Scholar] [CrossRef]
- Krich, C.; Runge, J.; Miralles, D.G.; Migliavacca, M.; Perez-Priego, O.; El-Madany, T.; Carrara, A.; Mahecha, M.D. Estimating causal networks in biosphere–atmosphere interaction with the PCMCI approach. Biogeosciences 2020, 17, 1033–1061. [Google Scholar] [CrossRef]
- Poveda, G.; Waylen, P.R.; Pulwartyc, R.S. Annual and inter-annual variability of the present climate in northern South America and southern Mesoamerica. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2006, 234, 3–27. [Google Scholar] [CrossRef]
- Bedoya-Soto, J.M.; Aristizábal, E.; Carmona, A.M.; Poveda, G. Seasonal shift of the diurnal cycle of rainfall over Medellin’s valley, Central Andes of Colombia (1998–2005). Front. Earth Sci. Atmos. Sci. 2019, 7, 92. [Google Scholar] [CrossRef]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear Process. Geophys. 2004, 11, 561–566. [Google Scholar] [CrossRef]
- Mayta, V.C.; Ambrizzi, T.; Espinoza, J.C.; Silva Dias, P.L. The role of the Madden–Julian oscillation on the Amazon Basin intraseasonal rainfall variability. Int. J. Climatol. 2019, 39, 343–360. [Google Scholar] [CrossRef]
- Pulwarty, R.; Diaz, H. A study of the seasonal cycle and its perturbation by ENSO events over the Tropical Americas. In Proceedings of the Fourth International Conference on Southern Hemisphere Meteorology and Oceanography, Hobart, NSW, Australia, 29 March–2 April 1993; pp. 262–263. [Google Scholar]
- Nepstad, D.C.; de Carvalho, C.R.; Davidson, E.A.; Jipp, P.H.; Lefebvre, P.A.; Negreiros, G.H.; Da Silva, E.D.; Stone, T.H.; Trumbore, S.E.; Vieira, S. The role of deep roots in the hydrological and carbon cycles of Amazonian forests and pastures. Nature 1994, 372, 666–669. [Google Scholar] [CrossRef]
- Jipp, P.H.; Nepstad, D.C.; Cassel, D.K.; de Carvalho, C.R. Deep soil moisture storage and transpiration in forests and pastures of seasonally-dry Amazonia. Clim. Chang. 1998, 39, 395–412. [Google Scholar] [CrossRef]
- Zeng, N. Seasonal cycle and interannual variability in the Amazon hydrologic cycle. J. Geophys. Res. 1999, 104, 9097–9106. [Google Scholar] [CrossRef]
- Ramos, A.M.T.; Builes-Jaramillo, A.; Poveda, G.; Goswami, B.; Macau, E.N.; Kurths, J.; Marwan, N. Recurrence measure of conditional dependence and applications. Phys. Rev. E 2017, 95, 52206. [Google Scholar] [CrossRef]
- Bedoya-Soto, J.M.; Poveda, G.; Trenberth, K.E.; Vélez, J.J. Interannual hydro-climatic variability and the 2009–2011 extreme ENSO phases in Colombia: From Andean glaciers to Caribbean low-lands. Theor. Appl. Climatol. 2019, 135, 1531–1544. [Google Scholar] [CrossRef]
- Poveda, G.; Jaramillo, L.; Vallejo, L.F. Seasonal precipitation patterns along pathways of South American low-level jets and aerial rivers. Water Resour. Res. 2014, 50, 98–118. [Google Scholar] [CrossRef]
- Makarieva, A.M.; Gorshkov, V.G.; Li, B.-L. Revisiting forest impact on atmospheric water vapor transport and precipitation. Theor. Appl. Climatol. 2013, 111, 79–96. [Google Scholar] [CrossRef]
- Sheil, D.; Bargués-Tobella, A.; Ilsted, U.; Ibisch, P.L.; Makarieva, A.; Mcalpine, C.; Morris, C.E.; Murdiyarso, D.; Nobre, A.D.; Poveda, G.; et al. Forest restoration: Transformative trees. Science 2019, 366, 316–317. [Google Scholar] [CrossRef] [PubMed]
- Makarieva, A.M.; Nefiodov, A.V.; Nobre, A.D.; Bardi, U.; Sheil, D.; Baudena, M.; Saleska, S.R.; Rammig, A. How transpiration by forests and other vegetation determines alternate moisture regimes. arXiv 2022, arXiv:2204.07409. [Google Scholar]
- Poveda, G.; Mesa, O.J. On the existence of Lloró (the rainiest locality on Earth): Enhanced ocean-atmosphere-land interaction by a low-level jet. Geophys. Res. Lett. 2001, 27, 1675–1678. [Google Scholar] [CrossRef]
- Sakamoto, M.; Ambrizzi, T.; Poveda, G. Moisture sources and life cycle of convective systems over western Colombia. Adv. Meteorol. 2011, 2011, 1–11. [Google Scholar] [CrossRef]
- Jaramillo, L.; Poveda, G.; Mejía, J.F. Mesoscale convective systems and other precipitation features over the tropical Americas and surrounding seas as seen by TRMM. Int. J. Climatol. 2017, 37, 380–397. [Google Scholar] [CrossRef]
- Yepes, J.; Poveda, G.; Mejía, J.F.; Moreno, L.; Rueda, C. CHOCO-JEX: A Research Experiment Focused on the Chocó Low-Level Jet over the Far Eastern Pacific and Western Colombia. Bull. Am. Meteorol. Soc. 2019, 100, 779–796. [Google Scholar] [CrossRef]
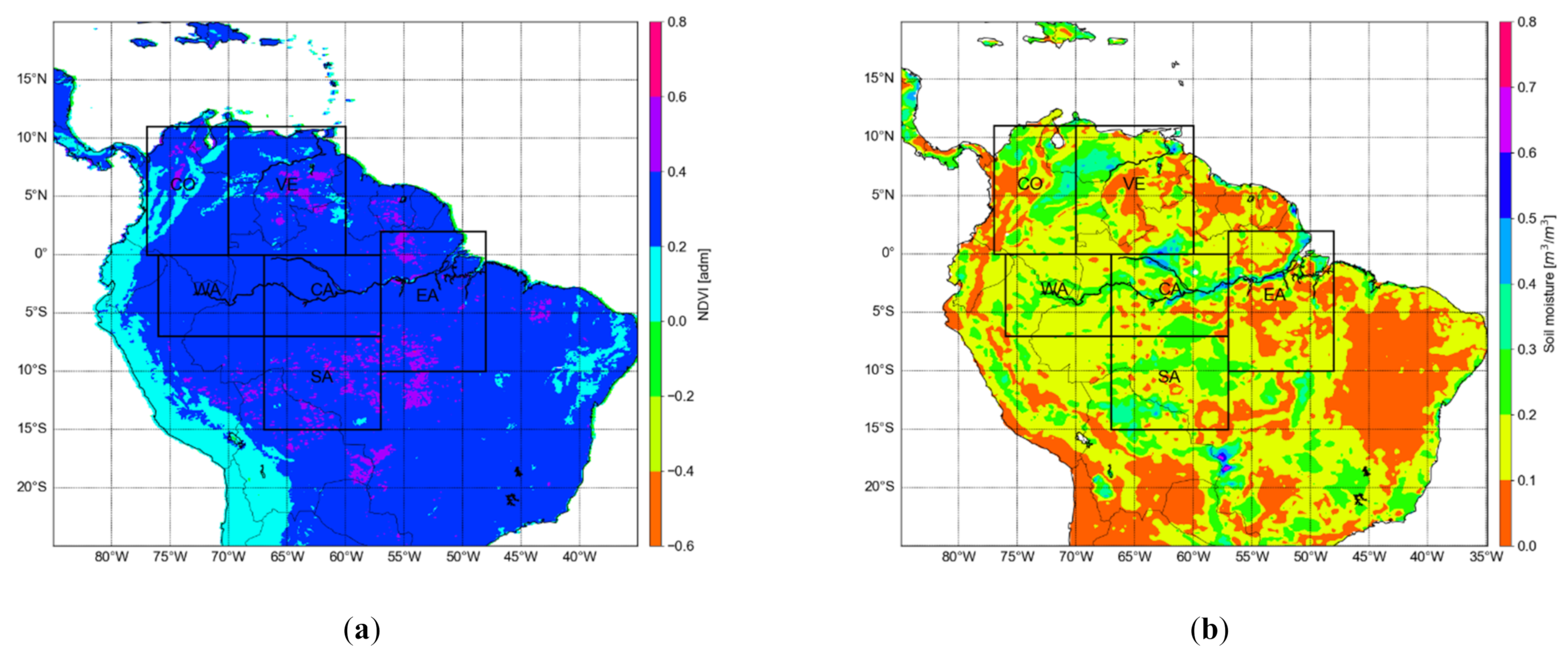




| Region | Code | Longitude | Latitude |
|---|---|---|---|
| Colombia | CO | 77°W–70°W | 0–11°N |
| Venezuela | VE | 70°W–60°W | 0–11°N |
| Western Amazonia | WA | 76°W–67°W | 7°S–0 |
| Central Amazonia | CA | 67°W–57°W | 7°S–0 |
| Eastern Amazonia | EA | 57°W–48°W | 10°S–2°N |
| Southern Amazonia | SA | 67°W–57°W | 15°S–7°S |
| Database | Variable | Resolution | Record Period | Analysis Period | Temporal Resolution | |
|---|---|---|---|---|---|---|
| Spatial | Temporal | |||||
| SMOS-BEC | Soil moisture | 25 km | Daily | Since 1 June 2010 | 1 January 2010 to 31 December 2018 | Monthly |
| NOAA | NDVI | 0.05° | Daily | Since 24 June 1981 | Monthly | |
| Index | NDVI | SMOS | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CO | WA | CA | SA | EA | VE | CO | WA | CA | SA | EA | VE | |
| Mean | 0.25 | 0.27 | 0.30 | 0.33 | 0.32 | 0.28 | 0.16 | 0.17 | 0.19 | 0.18 | 0.13 | 0.16 |
| Median | 0.25 | 0.27 | 0.29 | 0.29 | 0.30 | 0.28 | 0.18 | 0.17 | 0.19 | 0.18 | 0.13 | 0.16 |
| Std. deviation | 0.03 | 0.04 | 0.05 | 0.09 | 0.07 | 0.04 | 0.04 | 0.03 | 0.05 | 0.04 | 0.03 | 0.04 |
| IQR | 0.04 | 0.05 | 0.09 | 0.11 | 0.11 | 0.05 | 0.05 | 0.04 | 0.07 | 0.08 | 0.05 | 0.07 |
| Skewness | 0.22 | 0.43 | 0.56 | 1.09 | 0.66 | −0.13 | −0.54 | −0.15 | 0.30 | 0.31 | 0.39 | 0.12 |
| YK | −0.07 | 0.17 | 0.32 | 0.52 | 0.42 | 0.03 | −0.47 | 0.01 | −0.32 | 0.13 | 0.11 | −0.07 |
| Region | SMOS Leads NDVI | NDVI Leads SMOS | ||
|---|---|---|---|---|
| Max. Correlation | Time-Lag (Months) | Max. Correlation | Time-Lag (Months) | |
| CO | 0.62 a | −2 | 0.57 a | 10 |
| VE | 0.72 a | −2 | 0.70 a | 10 |
| WA | 0.56 a | −3 | 0.59 a | 8 |
| CA | 0.75 a | −3 | −0.78 a | 8 |
| SA | 0.78 a | −4 | 0.76 a | 9 |
| EA | 0.74 a | −3 | 0.72 a | 9 |
| Region | NDVI | Soil Moisture | ||
|---|---|---|---|---|
| Power at 12 Months | Power at 64 Months | Power at 12 Months | Power at 64 Months | |
| CO | 6 | 0 | 10 | 10 |
| VE | 10 | 0 | 12 | 7 |
| WA | 12 | 5 | 5 | 24 |
| CA | 14 | 0 | 8 | 14 |
| SA | 12 | 0 | 13 | 5 |
| EA | 15 | 0 | 9 | 9 |
| Region | NDVI | SMOS | ||||||
|---|---|---|---|---|---|---|---|---|
| CP | EP | CP | EP | |||||
| Max. Corr. | Time Lag (Months) | Max. Corr. | Time Lag (Months) | Max. Corr. | Time Lag (Months) | Max. Corr. | Time Lag (Months) | |
| CO | 0.16 | −13 | 0.21 b | 0 | −0.72 a | −3 | −0.52 a | −2 |
| WA | −0.24 b | −3 | 0.19 c | −13 | 0.38 a | 0 | 0.17 c | 0 |
| CA | −0.09 | −3 | −0.09 | −7 | −0.35 a | −9 | −0.57 a | −5 |
| SA | −0.17 c | −6 | 0.27 a | −3 | 0.22 b | 0 | −0.48 a | −4 |
| EA | −0.10 | −3 | 0.16 | −3 | −0.47 a | −9 | −0.73 a | −5 |
| VE | 0.13 | −13 | 0.18 c | −1 | −0.62 a | 0 | −0.40 a | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Álvarez, D.M.; Poveda, G. Spatiotemporal Dynamics of NDVI, Soil Moisture and ENSO in Tropical South America. Remote Sens. 2022, 14, 2521. https://doi.org/10.3390/rs14112521
Álvarez DM, Poveda G. Spatiotemporal Dynamics of NDVI, Soil Moisture and ENSO in Tropical South America. Remote Sensing. 2022; 14(11):2521. https://doi.org/10.3390/rs14112521
Chicago/Turabian StyleÁlvarez, Diana M., and Germán Poveda. 2022. "Spatiotemporal Dynamics of NDVI, Soil Moisture and ENSO in Tropical South America" Remote Sensing 14, no. 11: 2521. https://doi.org/10.3390/rs14112521
APA StyleÁlvarez, D. M., & Poveda, G. (2022). Spatiotemporal Dynamics of NDVI, Soil Moisture and ENSO in Tropical South America. Remote Sensing, 14(11), 2521. https://doi.org/10.3390/rs14112521