HDFNet: Hierarchical Dynamic Fusion Network for Change Detection in Optical Aerial Images

Abstract

Accurate change detection in optical aerial images by using deep learning techniques has been attracting lots of research efforts in recent years. Correct change-detection results usually involve both global and local deep learning features. Existing deep learning approaches have achieved good performance on this task. However, under the scenarios of containing multiscale change areas within a bi-temporal image pair, existing methods still have shortcomings in adapting these change areas, such as false detection and limited completeness in detected areas. To deal with these problems, we design a hierarchical dynamic fusion network (HDFNet) to implement the optical aerial image-change detection task. Specifically, we propose a change-detection framework with hierarchical fusion strategy to provide sufficient information encouraging for change detection and introduce dynamic convolution modules to self-adaptively learn from this information. Also, we use a multilevel supervision strategy with multiscale loss functions to supervise the training process. Comprehensive experiments are conducted on two benchmark datasets, LEBEDEV and LEVIR-CD, to verify the effectiveness of the proposed method and the experimental results show that our model achieves state-of-the-art performance.

1. Introduction

Change detection on bi-temporal optical aerial images that capture identical geographic locations in different time periods is a task which has great practical application significance with the development of satellite technology. Generally, the change area in real-world tasks can be defined as the differences covering the objects on the land surface within their attributes, positions, ranges etc. Recently, research on change detection is becoming an active topic with the rapid growth of various computer vision techniques [1,2,3,4,5].

Accurate image-change detection is usually reflected in two aspects: the ability to locate more changed areas avoiding the interference of semantic noise and to detect the located changed areas accurately. Methods based on convolution neural networks (CNNs) have been well developed recently. The CNNs features from high-level to low-level are corresponding to these two aspects. Since the change-detection tasks have double/multiple inputs, according to the input fusion strategies, convolutional networks for image-change detection can be divided into early fusion and late fusion [3]. The early fusion can capture more information of the foreground area, corresponding to the deeper features of the network; the late fusion can express more detailed information, corresponding to the shallow features of the network [1]. In other words, most of the strategies based on early fusion or late fusion are good at one aspect of the above-mentioned. When multiscale change areas appear in the bi-temporal image, various inaccurate detection phenomena may appear, such as missing detection or false alarms on disjoint multiple change areas in different scales, limited internal compactness appearing on detected change areas.

To solve the problem of multiscale features fusion of bi-temporal images, we propose a change-detection method based on hierarchical dynamic fusion network (HDFNet). Specifically, we first construct a hierarchical detection network based on a U-shape encoding-decoding framework. There is a cross fusion stream which fuse encoding features from bi-temporal images gradually and jointly. Secondly, we apply dynamic convolution modules on the decoding process to fuse features from triple streams adaptively. Thirdly, we design a multilevel supervision on multiscale hidden layer features in the decoding process to further refine the detection results.

In summary, the main contributions of this paper are three-fold:

• We propose a hierarchical network based on encoding-decoding structure for the task of image-change detection, which allows the encoding process to provide sufficient data encouraging from multiscale features for the further decoding process.
• We introduce the dynamic convolutional layers into decoding stages to self-adaptively learn the features from original encoding features and upsampled decoding features.
• We design a multilevel supervision strategy for the proposed HDFNet by supervising multilevel hidden layer features to refine the final change-detection result.

The remainder of the paper is organized as follows: Section 2 reviews the literature on image-change detection techniques. Section 3 elaborates the proposed model and the training method. Section 4 shows the experimental results and ablation studies. Section 5 discusses the proposed model. In Section 6, we draw the conclusion of the paper.

2. Related Work

There are many change-detection methods based on a variety of detection strategies, which have achieved good performance on widely ranged datasets. The existing methods can be roughly divided into traditional methods and deep learning-based methods, and each will be briefly introduced in the following sections.

2.1. Traditional Methods

The traditional methods are usually based on generating difference images from original input images. To obtain the difference images, the pixel-based approaches [6,7] mainly rely on the corresponding pixel value difference calculating and then obtain change maps based on these difference images by simply setting thresholds or clustering. Under such a simple strategy, there are often a certain number of noises within the detection results [2] due to the ignorance of context information of directly use on pixel values. By introducing improved probabilistic models into change-detection methods [8,9,10,11,12], this noise has been addressed to some extent. However, the pixel-based methods are still hard to satisfy the demand of very high-resolution images [2]. In contrast to detection of raw images [13], object-based methods [14,15,16] divide images into objects first and then analyze the relativeness within these objects to accomplish the change-detection task. These objects can provide sufficient spectral, textual, structural and geometric information and encourage the subsequent analysis for change detection.

2.2. Deep Learning-Based Methods

With the increasing maturity of deep learning technology, the change-detection field also focuses on detection frameworks based on CNNs. For change-detection task, its input is an image pair or multiple images, which involves the fusion of input. According to the strategy of fusion, these methods can be roughly categorized into late fusion and early fusion [1,3].

The late fusion can be explained as processing images separately and fuse the processed results of each image in the late phase in a framework. Following the pipelines of traditional difference images-based methods, some methods use deep neural networks as a robust feature extractor to replace the manually crafted descriptors. The networks with strong representation ability can deal with the requirements of domain knowledge, especially the pre-trained CNNs on the natural image collections with sufficient training samples. The widely used CNNs, such as VGGNets and ResNets [17,18,19], are proved with effectiveness in remote sensing tasks [20]. To adapt to a more specific domain, Zhang et al. [21] propose to train a deep brief network (DBN) from raw data to extract features in its specific field, and use cluster to analyze these features, which is similar to traditional strategies. The widely used pair-wise processing structure, Siamese, has proved effective in change-detection tasks, including multimodal images tasks, such as optical images [22] and incomplete satellite images [23].

The vanilla CNN is a stacking structure of convolution and down-sampling operations which leads to a decrease in the dimension of features. To maintain the dimension and respective field, Zhan et al. [24] proposed a Siamese structure with its branches are AlexNet cutting off pooling layers. This network generates the difference image based on the extracted features in original sizes and then obtains the change map using these difference images under the supervision of contrastive loss which is a widely used pair-wise comparing loss function. To improve the interclass discriminative ability, Zhang et al. [25] proposes an improved triplet loss to supervise a Siamese-based network. To better learn from the image pairs, some methods extract patches/superpixels instead of using raw images directly. These patches/superpixels are fed into the deep neural networks, such as zoom out CNN [26], ResNet [27], stacked contrastive AutoEncoder [10] and Sparse De-noising AutoEncoder (SDAE) [28] to learn the association within the patches/superpixels. Based on these strategies, these methods can use multiscale features in relatively narrow ranges.

Following the image-to-image strategies which are widely used in semantic segmentation, the fully convolutional network (FCN)-based methods attract research interests. The FCN [29] structure can fully take advantage of multiscale features to obtain an original size output by the encoding-decoding design. To further use the encoding features, UNet [30] introduces skip connections to improve the performance and robustness. Based on standard UNet, Lei et al. [31] and Liu et al. [32] propose image-to-image-change detection networks. Caye Daudt et al. [3] propose a series of classic image-to-image frameworks by fusing the encoding features by connecting them using skip connections in the decoding process. According to the fusion methods based on difference and concatenation, the networks are named FC-Siam-diff and FC-Siam-conc. Based on these basic frameworks, the PGA-SiamNet [4] applies a co-attention guide module onto the bridge between encoding and decoding, to further learn the correlation within the input pair. A deep image fusion network (IFN) proposed by Zhang et al. [1] introduces the spatial and channel attention modules in the fusing decoding process to improve change-detection performance from aspects of boundary completeness and internal compactness. Chen and Shi [33] extract multiscale features of each input image by ResNet and stack these features to generate features in the original size of each image. Then they fuse each feature into a compact input into a self-attention module with pyramid pooling to further adapt to multiscale information.

The early fusion means fusing input images in the very beginning of the networks. The network for street view change detection proposed by Alcantarilla et al. [34] stacks input pair as one input into the network. To tackle the error accumulation, Caye Daudt et al. [3] propose the fully convolutional early fusion (FC-EF) to process the stacked input with a UNet-based network. To further learn from multiscale features, Peng et al. [2] propose to use the Nested UNet (UNet++) [35] to detect change areas in satellite images. The UNet++ is a more powerful network based on standard UNet by equipping densely nodes and skip connections. They also design a multiple side output loss function to refine the change maps. Benefiting from the densely learning structure, this network achieves good robustness in detection precision. Zhang et al. [36] propose a coarse-to-fine change-detection framework via high-level features guided network to use context information to better locate more change areas. The final change maps are refined by a residual learning subnetwork to use the low-level features. This network achieves the robustness in detection recall. Based on UNet++, Peng et al. [37] use skip connection inside convolution unit, to emphasis the difference learning by additional skip connections. During upsampling, they use a spatial and channel attentive upsampling unit to better locate detailed information and texture features, which further improves the performance.

3. Methodology

3.1. Hierarchical Fusion Network

As shown in Figure 1, the bi-temporal images are separately fed into two image streams with standard convolutional layer blocks which are connected by max-pooling layers. Each block is composed of a convolutional layer, a batch normalization (BN) layer and a rectified linear unit (ReLU) layer. In these streams, the features from low-level to high-level are obtained by continuous convolution and down-sampling. By keeping the low-level features in each image stream are helpful to the detailed information when generating change maps. In the middle of two image streams, we place a fusion stream sharing the structure of later four convolution blocks with the image stream. To provide more representation capacity of the network, the fusion stream does not share parameters with the image streams. The input of each fusion stream convolution block is the channel-wise concatenating combination of features on the corresponding scale features in both image streams and the features from earlier fusion stream block output.

As mentioned in the previous analysis, the stacked convolutional layers and pooling layers of CNNs extract the image features from shallow to deep, corresponding to low-level detailed information and high-level context information. Although the inputs of the change-detection task are bi-temporal image pairs, the early-fusion strategy captures more context information for difference discrimination by fusing the image pair as one input into networks and extracting deep features for the image pair [1]. The design of hierarchical fusion stream fuses the information from low-level to high-level between two image streams gradually and jointly. The high-level features obtained by the fusion stream have more context information within the image pair which can provide more localization information of the change areas for the further upsampling process. At the same time, the shallow features of the individual image are kept in each image stream, which provides sufficient detailed information for the gradually upsampling on the scale of $I/8$ to I, from high-level to low-level. Thus, it is possible to improve the detection rate and accuracy of the proposed network.

3.2. Dynamic Convolution Modules

To enable the network to fully learn effective information from the encoded features and upsampled features, we introduce dynamic convolution [38] modules in the decoding process to take advantage of these features adaptively. From the perspective of perception, the traditional or static perception used in other standard convolutional layers could be presented as $y=g(W^{T}x+b)$, where parameters W and b are weight matrix and bias, respectively. Then the dynamic perception can be presented as follows,

$$y=g({\tilde{W}}^T\left(x\right)x+\tilde{b}\left(x\right))$$

(1)

$$\tilde{W}\left(x\right)=\sum _{k=1}^K{\alpha }_k\left(x\right){\tilde{W}}_k,\tilde{b}=\sum _{k=1}^K{\alpha }_k\left(x\right){\tilde{b}}_k;0\le a_k\left(x\right)\le 1,\sum _{k=1}^K{\alpha }_k\left(x\right)=1$$

(2)

where ${\alpha }_k$ is the attention weight of the K-th linear function ${\tilde{W}}_k^{T}x+{\tilde{b}}_k$, the aggregate weight $\tilde{W}\left(x\right)$ and the bias $\tilde{b}\left(x\right)$ are sharing the same attention weight. The attention weight set ${\alpha }_k\left(x\right)$ changes with the change of each input x, instead of fixed weights. They represent the optimized set $\{{\tilde{W}}_k^{T}x+{\tilde{b}}_k\}$ of linear models with given inputs. The aggregation model $\{{\tilde{W}}^T\left(x\right)x+\tilde{b}\left(x\right)\}$ is a nonlinear function, thus dynamic perception has more representation ability than static perception.

Similar to the dynamic perception, as shown in Figure 2, dynamic convolution has K convolution kernels which are sharing the same convolution kernel size and dimension on input/output. These convolution kernels use the attention weights $\left\{{\alpha }_k\right\}$ to aggregate. Specifically, global average pooling is used to compress global spatial information, and then two fully connected layers (with a ReLU layer behind for each fully connected layer) and SoftMax layer are used to obtain standardized attention weights for K convolution kernels. According to the classic design of CNN, when building dynamic convolution modules, we use the combination of a dynamic convolutional layer, a BN layer and a ReLU layer for each module.

3.3. Multilevel Supervision

As shown in Figure 3, we use the multilevel supervision (MS) strategy to supervise multiple hidden layer features. The MS strategy is to add auxiliary classifiers and loss functions to several hidden layers of a network. The proposed HDFNet uses three dynamic convolution modules in self-adaptive mechanisms which can lead to slower convergence than classical convolution modules in the training process. The introduction of MS can effectively improve the convergence speed and stability of the proposed HDFNet. It is benefiting from the auxiliary multiple loss function measuring the effectiveness of hidden layer features for change detection, and the more effective features can bring better detection results. At the same time, MS can further refine the detection on multiscale areas by involving multiscale features supervising.

Specifically, as shown in Figure 3, we process each feature of the shallower three stages as a level-output in the HDFNet decoding phase. The features on scale of I are processed into a level-output by two convolutional layers with $3\times 3$ and $1\times 1$ kernels, respectively. The features on scale $I/2$ to $I/8$ are processed by $3\times 3$ convolution and upsampled to scale of I. The upsampled features are then concatenated with the features on scale of I and fed into a $1\times 1$ convolutional layer to obtain the corresponding level-outputs. Through this pattern, the network can obtain better detection results than using only the shallowest features [39]. Since then, the level-outputs of four stages are supervised by the MS loss function $L_{ms}$ and the loss can be expressed as follows,

$$L_{ms}=\sum _{i=0}^3{w}_i{L}_{level}^{I/2^i}$$

(3)

where $L_{ms}$ is the MS loss function, $L_{level}$ is the loss function of each level-output, $w_i$ is the weight for each $L_{level}$, and the superscript $I/2^i$ is naming each loss by representing the scale of i-th $L_{level}$ that is I divided by the stride size of $2^i$, I is the input and final output image size.

HDFNet uses focal loss function [40] $L_{focal}$ to supervise the level-output with coarse stride of $2^3$, and uses $(L_1+L_2)/2$ loss functions to supervise the fine stride of $2^0$. For the middle strides of $2^1$ and $2^2$, HDFNet uses the average of $L_{focal}$ and $(L_1+L_2)/2$. The detailed calculation methods of loss functions are shown as follows,

$$L_{level}^{I/2^3}=L_{focal},L_{level}^{I/2^2}=L_{level}^{I/2^1}=(L_1+L_2)/2+L_{focal},L_{level}^{I/2^0}=(L_1+L_2)/2$$

(4)

$$L_{focal}=-\frac{1}{N}\sum _i^N({\alpha }_f{g}_i{(1-p_i)}^{\gamma }log{p}_i+(1-{\alpha }_f)(1-g_i)p_i^{\gamma }log(1-p_i))$$

(5)

$$L_1=\sum _i^N\left|y_i-{\widehat{y}}_i\right|$$

(6)

$$L_2=\sum _i^N{(y_i-{\widehat{y}}_i)}^2$$

(7)

where $p_i$ is the probability that the pixel is predicted to be true, $g_i$ is the probability that the true value of the corresponding pixel is true, ${\alpha }_f$ and $\gamma$ are the adjustment factors of focal loss function. The $y_i$ is the true value probability of a pixel while ${\widehat{y}}_i$ is the predicted probability of the corresponding pixel.

Different loss functions applied are designed according to the phenomenon that coarse stride features focus on the global context information, i.e., these features ignore some local details; while the fine stride features contain sufficient details so that they demand the loss functions focusing on the local information. The final output of HDFNet is the concatenated and $1\times 1$ convoluted combination of multiscale level-output. In this way, the HDFNet can use the global features leading to higher recall and the local features leading to higher precision, so that the obtained final change map can adapt to the multiscale change area.

4. Experiments

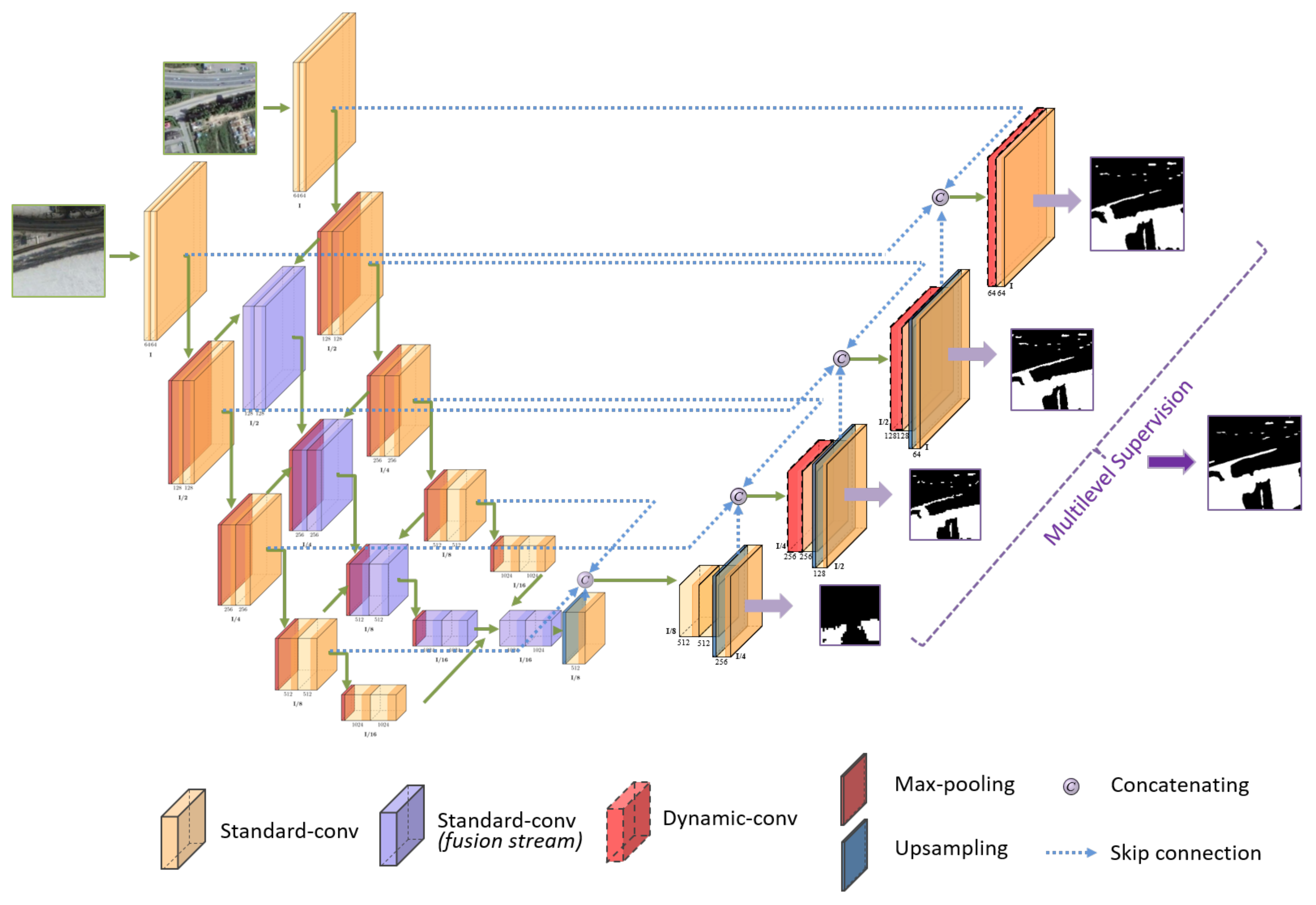
4.1. Datasets and Settings

The dataset provided by LEBEDEV [41] contains two types of images in this dataset: composite images with small target offset or not, and real optical satellite images with seasonal changes, obtained by Google Earth. The real images are 11 pairs of optical images, including seven pairs of seasonal variation images of $4725\times 2200$ pixels without additional objects and four pairs of $1900\times 1000$ pixels with additional objects, which are the data we use for experiments. The original image sets are provided as a subset consisting of 16,000 clipped images with size of $256\times 256$ from original real-temporal seasonal images, distributed with 10,000 train sets, 3000 test sets also validation sets. As shown in Figure 4, the change areas in LEBEDEV defined according to the change of cars, buildings, surface uses, etc. The visual differences caused by changing seasons are not considered to be change areas. The change areas usually appear in such as multiple scales, shapes, numbers, which leads to challenges in detection.

The LEVIR-CD [33] dataset provided by researchers from the LEarning VIsion and Remote sensing laboratory (LEVIR) of image processing center of Beijing University of Aeronautics and Astronautics, is a collection of 637 high-resolution (0.5 m/pixel) Google Earth image pairs with the size of $1024\times 1024$ pixels. These bi-temporal images come from 20 different regions of cities in Texas collected from 2002 to 2018. The change areas are mainly marked according to building change on two aspects: building growth (from soil/grass/hardened ground or building under construction to new area change) and building decay. All data is annotated by experts from artificial intelligence data service companies, who have rich experience in interpreting remote sensing images and understanding change-detection tasks. The fully annotated LEVIR-CD contains a total of 31,333 individual altered buildings. In the experiment, for the convenience of training and following other state-of-the-art methods, as shown in Figure 5, the original images are cropped into clipped images with size of $256\times 256$ without overlaps. There are 7120 clipped image pairs for training set and 2048 pairs for validation set also testing set. The challenge of this dataset is mainly reflected in the uneven distribution of positive and negative samples. In the clipped $256\times 256$ images, there are a certain number of images without change areas (that is, all pixels in a sample are negative). At the same time, the change area is mainly on architectural change.

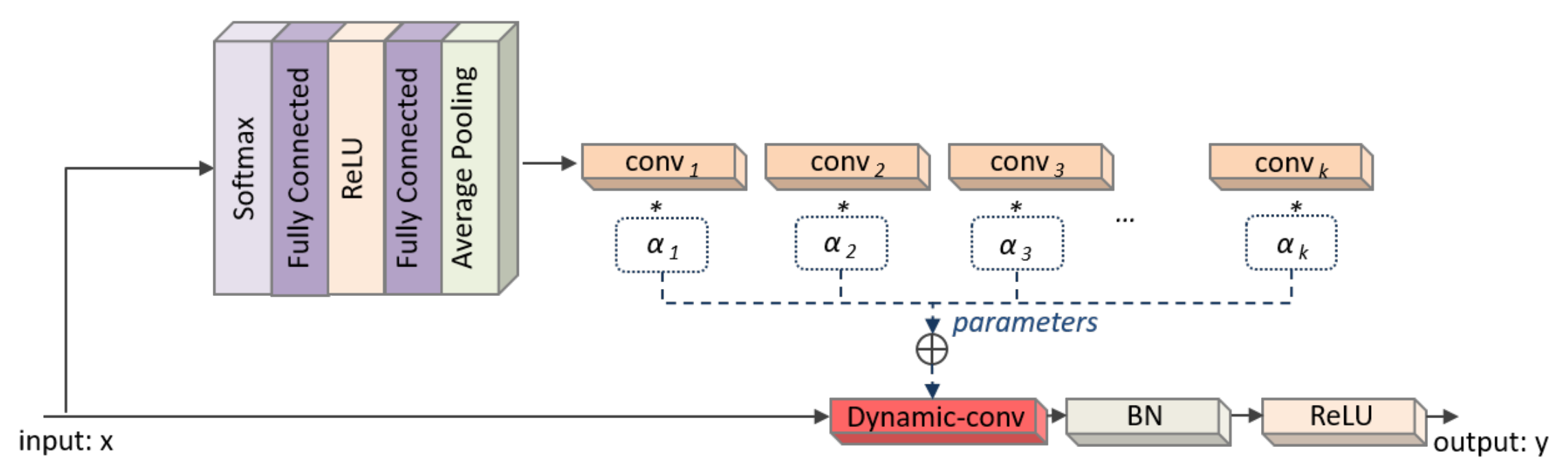
The experiments are implemented on PyTorch (version 1.0.1) platform on a 10 core Intel Xeon (R) e5-2640 V4 @ 2.40 GHz workstation with NVIDIA GTX 1080ti GPU. The batch size is 4 pairs and the learning rate is $3\times {10}^{-4}$. The number of parallel convolution kernels in dynamic convolution modules are set to $K=4$. The weight w for each $L_{level}$ is 1. The parameters in focal loss are set as ${\alpha }_f=0.75$ and $\gamma =2$. We use a random data augmentation strategy in the training process: the data loader will automatically transform the image batch according to the randomly generated augmentation probability value, including random rotation, clipping, flipping and brightness, contrast, saturation changes, etc.

4.2. Evaluation Metrics

We evaluate the predicted change map compared with groundtruth (GT) change maps, based on pixel-wise confusion matrix. Specifically, we use recall, precision and F1-score for the experiments. Thus, in the case that all datasets used are completely manually labeled, based on the predicted binary labels and GT labels, we can obtain the complete confusion matrix items, namely true positive (TP), true negative (TN), false positive (FP) and false negative (FN). Based on this, the following measurements calculate as follows,

$$Precision=\frac{TP}{TP+FP}$$

(8)

$$Recall=\frac{TP}{TP+FN}$$

(9)

$$\mathrm{F}1=2\times \frac{Precision\times Recall}{Precision+Recall}$$

(10)

where Precision refers to the proportion of the real positive to all the ’positive’ predicted by the model, while Recall refers to the proportion of the model predicted ’positive’ to all real positive samples. These two measurements are a pair of contradictory measurements, thus the F1-score is considered to be with more comprehensively measurement ability.

4.3. Result Comparison

To prove the effectiveness of our proposed HDFNet, we compare the HDFNet with other deep-learning-based change-detection methods including: (1) The deep Siamese convolutional network (DSCN) [24] is a Siamese-based network without pooling layers which can maintain the respective fields and features dimension; (2) The FC-EF, FC-Siam-conc and FC-Siam-diff [3] are based on FCN structure with early-fusion and late-fusion strategies using skip connections, which are widely used classic image-to-image baselines; (3) The fully convolutional network pyramid pooling (FCN-PP) [31] and deep Siamese multiScale fully convolutional network (DSMS-FCN) [5] involved multiscale designs based on the previous baselines, by pyramid pooling and multiscale convolutional kernels unit, respectively; (4) The change detection based on UNet++ with multiple side-outputs fusion(UNet++MSOF) design a multiple side loss supervision on features densely upsampled from multiple scales in the UNet++; (5) The IFN [1] and boundary-aware attentive network (${\mathrm{BA}}^2$Net) [36] involve attention mechanisms in the decoding process also deep supervision and refined detection to deal with features in different scales, based on late fusion and early fusion respectively; (6) The spatial–temporal attention-based network (STANet) [33] is based on late fusion and introduces pyramid pooling involved attention modules to adapt multiscale features. For quantitative comparisons, the evaluation metrics were calculated and summarized as shown in

Table 1. Result Comparison on dataset LEBEDEV.

Methods	LEBEDEV
	Precision (%)	Recall (%)	F1-Score (%)
DSCN [24]	79.18	55.74	65.07
FC-EF [3]	81.56	76.13	77.11
FC-Siam-conc [3]	84.41	82.50	83.44
FC-Siam-diff [3]	85.78	83.64	83.73
FCN-PP [31]	82.64	80.60	80.47
DSMS-FCN [5]	88.60	84.85	86.61
UNet++ MSOF [2]	89.54	87.11	87.56
IFN [1]	94.96	86.08	90.30
BA2Net [36]	88.12	95.28	91.36
STANet [33]	87.13	93.83	90.28
HDFNet	94.12	95.47	94.77

and

Table 2. Result Comparison on dataset LEVIR-CD.

Methods	LEVIR-CD
	Precision (%)	Recall (%)	F1-Score (%)
DSCN [24]	75.10	73.06	72.53
FC-EF [3]	82.55	83.68	82.31
FC-Siam-conc [3]	83.36	85.16	83.61
FC-Siam-diff [3]	82.33	86.30	83.35
FCN-PP [31]	81.85	86.19	83.30
DSMS-FCN [5]	83.55	86.25	84.49
UNet++ MSOF [2]	86.64	87.69	86.76
IFN [1]	86.08	86.80	85.95
BA2Net [36]	86.07	90.40	87.92
STANet [33]	83.80	91.10	87.30
HDFNet	87.54	89.38	88.13

, on LEBEDEV and LEVIR-CD, respectively. The best scores are highlighted by red, while green and blue indicate the second best and the third best, respectively.

From Table 1, it can be observed that on the dataset of LEBEDEV, the proposed HDFNet achieves the first in recall, F1 score and the second in precision (less than 0.9% after the first). Though the IFN achieves the highest precision, its recall is limited (at 86.08%, which is more than 9% than the proposed network). It also can be observed in Figure 6 that change maps obtained by IFN have certain unpredicted change areas. Specifically, the DSCN which does not involve design on multiscale features is the relatively lower network in all evaluation metrics. This is because of its simple structure and ignorance of the multiscale information problem within the bi-temporal images. The high-dimensional features maintained in the whole processing lead to an obvious lower recall score. By using encoding-decoding with skip connections, the baselines of FC-EF, FC-Siam-conc and FC-Siam-diff achieve greatly better performance with their brief and effective structures. Among these three baselines, late-fusion baselines show obvious advantages over the early-fusion baseline. The strategy of keeping original image encoding features for decoding can help with a higher precision and recall scores. Based on pyramid pooling which can further use multiscale information, the FCN-PP improves the F1-score by more than 3% compared with its similarly baseline FC-EF. Although the multiscale convolution kernels and pooling with in the DSMS-FCN improves F1-score about 3% compared with its similarly baseline FC-Siam-diff. It indicates that the multiscale computing operations during the encoding can effectively improve performance.

By using the densely nodes and skip connections in each encoding scale of UNet++, UNet++MSOF achieves the third precision score. However, the network gives almost equal attention to each scale, which results in limited improvement in its detection performance. Based on late-fusion strategy, by introducing spatial and channel attention mechanisms in each decoding stage and supervising on them, IFN achieves the highest precision and the third F1-score, but limited recall. Based on early-fusion strategy, ${\mathrm{BA}}^2$Net uses attention gates and coarse-to-fine strategies to use context information and local information. However, its attention gates are guided by higher level features which lead to precision is still obviously lower than that of recall. The STANet is a late-fusion-based network involving a pyramid spatial–temporal attention module achieving the third recall. It indicates that for such complex data as LEBEDEV dataset, the pattern of encoding-decoding and multiscale self-attentive learning respectively may require further design to accommodate. The proposed HDFNet reaches the highest in recall and F1-score, while precision ranks second, which is due to the fact that the network maintains the advantages of early fusion and late fusion in the process of encoding and applies self-adaptive learning by dynamic convolution modules in the process of decoding. Also, multilevel supervision can help improve performance. It is worth mentioning that HDFNet achieves a good trade-off between precision and recall.

Also, the qualitative analysis is shown in Figure 6 by showing five challenging sets of bi-temporal images, each containing disjoint multiple change areas in wide range scales. It can be observed that DSCN has obvious false detection in almost all these challenging samples. Among the three baselines based on FCN, the FC-Siam-conc and the FC-Siam-diff are more powerful than the FC-EF. The FC-EF can locate most areas of change except for some very small areas of change (sample Figure 6b,d,e). However, it does not retain each original image features, especially the shallow layer features, which makes the obvious inaccuracy of the detected change areas. The other two late-fusion baselines generally perform better than the FC-EF, which is reflected on the more complete and accurate shape of detected change areas. However, its detection rate, integrity and precision can be improved. By introducing multiscale processing modules before the decoding phase, the FCN-PP and DSMS-FCN improve the quantitative scores obviously compared with their baselines, but the improvement in the qualitative analysis is not obvious, and there is still obvious error detection in samples c, d, e.

Benefiting from the dense design on multiscale stages, the change maps obtained by UNet++MSOF are more correct than the previous methods. However, it has the problem based on the early-fusion strategy that is not accurate in the boundary and details of change areas. The IFN and STANet based on late fusion are relatively more complete in local details, benefiting from their spatial and channel attention mechanisms. However, it has false positive and false negative detection in some small areas, and appears smoother than GTs in the boundary with rich details. By introducing attention gates and refined detection, ${\mathrm{BA}}^2$Net can obtain the visually closer change maps with the GT maps, especially the boundary with complex information. The mechanism of paying more attention to higher resolution features improves the detection rate, but the neglect of the lower resolution features of each original image leads to over ranged change areas, which leads to its limited precision. The proposed HDFNet can correctly locate most of the change areas and accurately detect the shape of the areas and other information. Though there are a few errors in the very small change areas and very complex boundaries, it maintains accurate change maps in general.

It can be observed from Table 2 that on dataset LEVIR-CD, the F1-scores of most comparison methods do not show as large a gap as in LEBEDEV, except the DSCN is obviously lower than other methods. The difference in the performance of the three baselines of FCN is not obvious, and the F1-scores are about 83%, among which FC-Siam-conc is slightly higher. The FCN-PP and DSMS-FCN improve the F1-score by around 1% compared with their baselines through the multiscale pooling and convolution operations. In other words, the performance improvement of these multiscale design based on fixed kernel sizes on LEVIR-CD is not as significant as that on LEBEDEV. This may be because the multiple scale range of LEVIR-CD is not as wide as that of LEBEDEV. However, the challenge of LEVIR-CD is mainly reflected in the uneven numbers and distribution of the change areas.

The UNet++MSOF maintains its precision robustness on LEVIR-CD, reaching the second-best precision while obviously improving the F1-score to 86.76%. This is due to its adequate computation at each encoding scale and multiple outputs supervision. The IFN reaches the third precision score, while F1-score is slightly lower than UNet++MSOF, especially the recall. The ${\mathrm{BA}}^2$Net reaches the second-best recall and F1-score which benefits from its deeper features attentive guidance for network updating. By introducing attention mechanisms involving multiple scales, STANet achieves the best recall and the third F1-score, and a limited precision meanwhile. The proposed HDFNet improves the F1-score to 88.13% which is superior. At the same time, the precision rate also reaches the highest value of 87.54% in the comparison methods. Also, the HDFNet maintains the good trade-off between precision and recall among the top three networks on F1-scores.

Figure 7 also illustrates the change maps on five selected sets of bi-temporal images. The change areas in these bi-temporal image pairs range over multiple numbers, scales, shapes and distribution patterns. For multiple regular shape building change in sample (a), most of the comparing methods do not correctly detect the building change inside the highlighted boxes, while STANet is able to locate the change areas but with incompleteness detection and proposed HDFNet is more accurate than other methods. For the change areas with details in change area shape sample (b), the late-fusion-based methods FC-Siam-conc, FC-Siam-diff, IFN and STANet and proposed hierarchical fusion-based HDFNet are visually closer to the GT maps. For more densely distributed change areas within samples (c) and (d), ${\mathrm{BA}}^2$Net, STANet and HDFNet maintain the visually correctness, while HDFNet is with less errors. For sample (e), which has integrated two kinds of change areas, the HDFNET shows better adaptability, i.e., it can accurately detect and distinguish multiple dense change areas, and it can also accurately detect the change regions with complex shapes.

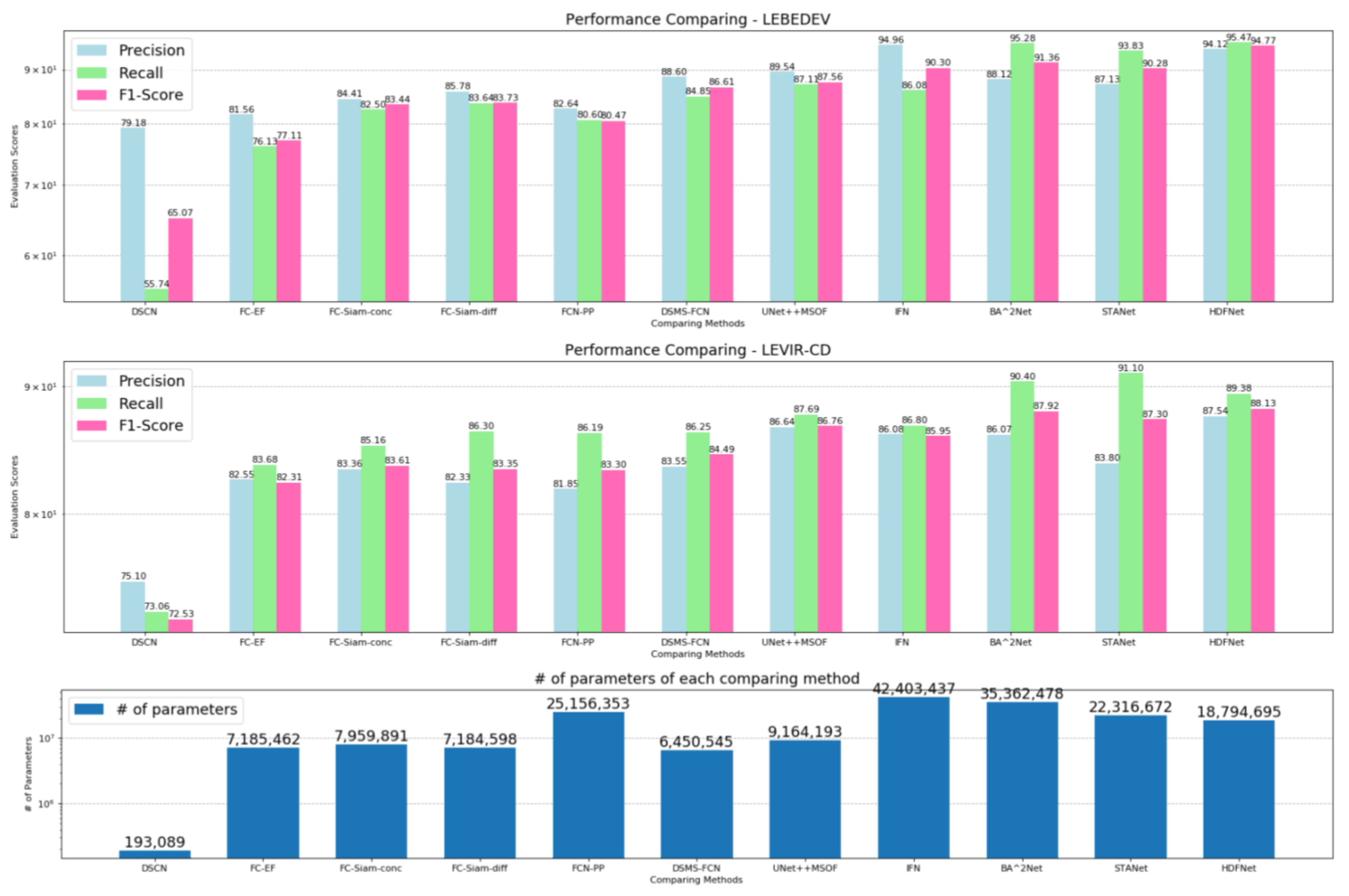
As shown in Figure 8, we summarize the performance of all comparing methods on both datasets and the numbers of their parameters in three sets of histograms. Each chart displays its evaluation scores and the number of parameters on a per-method basis, i.e., one column is for each method. It can be observed that among the methods with higher evaluation scores, the proposed method has relatively fewer parameters, which means that compared with the simple method with fewer parameters, the proposed method has greatly improved the performance. At the same time, HDFNet maintains the highest F1 score and the trade-off between precision and recall.

4.4. Ablation Study

To prove the effectiveness of proposed designs, we implement ablation studies of HDFNet on both datasets, which by quantitative analysis (recall, precision and F1 score) and qualitative analysis (by showing the selected examples) the networks with or without proposed designs.

4.4.1. Effectiveness of Cross Fusion Stream

By observing the quantitative analysis in

Table 3. Ablation study of with/without cross fusion stream.

HDFNet	LEBEDEV			LEVIR-CD
	Precision (%)	Recall (%)	F1-Score (%)	Precision (%)	Recall (%)	F1-Score (%)
HDFNet-w/o-CFS	94.59	91.89	93.18	85.44	87.79	86.23
HDFNet-w-CFS	94.12	95.47	94.77	87.54	89.38	88.13

, the introduction of cross fusion stream (CFS), bringing numbers of parameters from 13,740,781 to 18,794,605, can obviously improve the recall and the F1 score the premise of a small decrease in the precision rate (no more than 0.5%). Based on the two raw image streams, the features of each image in bi-temporal pair are kept and fused gradually and jointly encoding into deep semantic features. These features enable the network to capture more context information of bi-temporal image and improve the ability of network to detect and locate more changing regions, while keeping the local details to maintain precision. Also, the qualitative analysis in Figure 9 indicates that the fusion stream improves semantic correctness. Though the HDFNet without CFS has rich details and high precision, the recall rate is low.

Specifically, in the samples of Figure 9 (1c,1f,1h,2a,2h), there are obvious missing detection problems on small-scale change areas, which is easy to ignore when neural networks do not emphasize high-level semantic information. By using CFS to capture more high-order semantic information can better solve the problem of missing detection of these whole change regions. Also, the completeness in samples of Figure 9 (1b,1d,1e,1f,2h) is solved by the CFS. Under the circumstance of the parameters increasing about 30% by CFS, the F1 score can improve 1%–2%, also the change maps are more accurate semantically.

In addition, we conduct an ablation experiment on whether the CFS share parameters, which are presented as Sharing and Non-Sharing in

Table 4. Ablation study of fusion stream whether sharing parameters.

Fusion Stream	LEBEDEV			LEVIR-CD
	Precision (%)	Recall (%)	F1-Score (%)	Precision (%)	Recall (%)	F1-Score (%)
Sharing	91.50	96.11	93.71	87.28	87.15	86.96
Non-Sharing	94.12	95.47	94.77	87.54	89.38	88.13

. To provide more sufficient feature information for the decoding process, the encoding fusion stream uses non-sharing parameters with the image encoding streams on both sides, to provide greater representation capacity for the network. Table 4 shows that through the unshared parameters, larger network capacity improves the scores of the network, thus can improve the F1-score, especially on LEVIR-CD. The number of parameters is increased from 15,307,981 to 18,794,605 (about 20%).

4.4.2. Effectiveness of Dynamic Modules

We implement the HDFNet with/without dynamic convolution modules, with 18,207,713 and 18,794,605 parameters for each. The HDFNet without dynamic modules uses standard convolution modules instead of dynamic modules. As the analysis shown in

Table 5. Ablation study of with/without dynamic convolutional layers (presented as ‘DyConv’).

HDFNet	LEBEDEV			LEVIR-CD
	Precision (%)	Recall (%)	F1-Score (%)	Precision (%)	Recall (%)	F1-Score (%)
Standard Convolution	86.65	95.60	90.77	87.16	88.11	87.08
Dynamic Convolution	94.12	95.47	94.77	87.54	89.38	88.13

, the introduction of dynamic convolution modules can significantly improve the precision of the network, from 86.65% to 94.12%, while the recall is reduced slightly by 0.13%. It indicates that the dynamic convolutional layers can greatly improve the detection precision under the premise of small fluctuation of detection rate, to obviously improve the F1-score by 4%. This benefits from the self-adaptive learning of the dynamic convolution modules from original details and the upsampled features. Also, dynamic convolution modules can obviously balance the gap between precision and recall (from 8.95% to 1.35%). That is to say, the performance of change detection is improved by dynamic convolution modules with about 3% parameters increasing.

Figure 10 illustrates the quantitative analysis of the dynamic convolution modules ablation (presented as DyConv) experiments. It can be observed from Figure 10 that the network model without DyConv can basically detect and locate most of the change areas, except for a few tiny point change areas in sample (a), there is no obvious missing phenomenon; but there is obvious incomplete detection of the detected change areas, such as example of Figure 10 (1c,1d,1h,2h). The reason for this phenomenon may be that in the process of decoding, perception ability of static standard convolution kernel is limited, while accurate change detection needs to fully consider the feature information from three streams at the same time. Therefore, through the introduction of dynamic convolutional layers, the dynamic kernel obtained by adaptive learning provides a larger capacity for the network, making the generated change map more accurate, and the above problem has been better solved.

In the process of decoding, 1, 2 and 3 groups of dynamic convolution modules are applied respectively, which are expressed as HDFNet-1 (convolution layer with scale of I is dynamic convolution layer), HDFNet-2 (convolution layer with scale of I and $I/2$ is dynamic convolution layer), HDFNet-3 (convolution layer with scale of I, $I/2$ and $I/4$ is dynamic convolution layer), as shown in

Table 6. Ablation study of Dynamic Modules numbers.

Dynamic Modules	LEBEDEV			LEVIR-CD
	Precision (%)	Recall (%)	F1-Score (%)	Precision (%)	Recall (%)	F1-Score (%)
HDFNet-1	91.18	93.13	92.10	86.34	88.91	87.20
HDFNet-2	94.14	93.89	93.99	87.01	89.46	87.95
HDFNet-3	94.12	95.47	94.77	87.54	89.38	88.13

. Compared with HDFNet-3, HDFNet-2 (with 18,347,625 parameters) and HDFNet-1(with 18,235,749 parameters) have fewer parameters in about 2.3% and 2.9%. It can be observed that the performance gradually improves with the increase of the number of dynamic modules. Also, the dynamic convolution module has a larger improvement for quantitative evaluation of shallow features, which may be due to the shallower features containing more detailed information, and the dynamic convolution modules can automatically learn the effective information of generating accurate change maps from the rich detail information. It is worth mentioning that when there are more than three groups of dynamic modules, the network training appears the phenomenon of unstable convergence. It indicates that such an adaptive learning module has higher requirements for training data.

4.4.3. Effectiveness of Multilevel Supervision

In this section, the HDFNet ablation models with/without MS are implemented and summarized in

Table 7. Ablation study of with/without Multilevel Supervision.

HDFNet	LEBEDEV			LEVIR-CD
	Precision (%)	Recall (%)	F1-Score (%)	Precision (%)	Recall (%)	F1-Score (%)
HDFNet-w/o-MS	91.21	95.26	93.15	86.08	89.47	87.44
HDFNet-w-MS	94.12	95.47	94.77	87.54	89.38	88.13

. The ablation model without multilevel supervision only outputs the features of the shallowest I stage to generate the change map, which is then supervised by the average value of $L_1$ and $L_2$ loss function. Through the experimental comparison, it can be concluded that the multilevel supervision strategy makes further use of multiscale features, and each evaluation score has been improved in different ranges (the precision rate is more obvious, about 3%). This means that the multilevel supervision strategy can comprehensively improve each evaluation measurement with minor parameters increasing, about 1%, from 18,602,669 to 18,794,605.

The effectiveness of the MS strategy is more obvious in qualitative analysis. As shown in Figure 11, the change maps generated by HDFNet without multilevel supervision have no obvious missing detection, and some samples (such as samples 1d, 1e, 1h, 2d, 2f etc.). with incomplete change regions have no obvious large-scale incomplete phenomenon, but the change regions detected by HDFNet are slightly rough compared with the change maps with multilevel supervision. The change maps generated by HDFNet using multilevel supervision strategy are closer to the true value of change maps in shape and some details, and there is no false alarm rate. That is to say, multilevel supervision can improve the semantic correctness of change detection and the integrity of change region from recall and precision. As shown in Figure 12, we compare the training loss of the network with/without MS with the fixed epoch number and learning rate. In the early stage of training, the network using MS converges faster. In the late stage of training, the network using MS converges more smoothly, especially on Lebedev. The introduction of MS can conduct a faster and stable convergence on both datasets.

5. Discussion

In this paper, sufficient experiments are implemented on two benchmark datasets LEBEDEV and LEVIR-CD. First, through quantitative comparison, it can be observed that HDFNet is superior to other methods in F1-score, and achieves a good trade-off between recall and precision among the methods with higher F1-scores. However, the HDFNet designs without regulation terms of recall and precision in the mixed-loss function are similar to ${\mathrm{BA}}^2$Net, which means that the detection ability of HDFNet is relatively improved comprehensively. This is due to the design of HDFNet dynamic convolution, which enables the network to learn effective information from the features from three aspects. Through qualitative comparison, it can be observed that the change maps obtained by HDFNet have good adaptability to multiscale change areas, especially for large-scale change areas in bi-temporal images. It can basically and accurately locate multiple multiscale change areas and detect relatively accurate shapes. Compared with other methods, it has more accurate image-change detection compactness and boundary integrity, and has high precision and robustness in detecting changes in multiple scales. At the same time, it should be pointed out that the network also has limitations. First, when the boundary information of the change area is extremely rich, or the area of multiple change areas is extremely small, sometimes small change areas are missed and the boundary is not very accurate. Secondly, the adaptive learning mechanism of HDFNet needs sufficient and effective training data for training, while the training data of small-scale dataset is limited, and the advantage of HDFNet is not as obvious as that of the other two sufficient datasets. How to make the network model use insufficient and effective training data to effectively strengthen learning, and adjust the best possible learning based on continuous feedback, is one of the directions worthy of research.

6. Conclusions

In this paper, an HDFNet is proposed to conduct the optical aerial images change detection. First, a hierarchical fusion network based on encoding-decoding structure to implement change detection. To integrate the advantages of early-fusion and late-fusion strategies, the network is equipped with a cross fusion stream in the encoding process to fuse multiscale features from both images gradually and jointly. This hierarchical fusion strategy provides sufficient data to encourage a better decoding process. Secondly, in the decoding process, dynamic convolution modules are applied in shallow stages to improve the network complexity without increasing the network depth, which allows the network to learn the features from both bi-temporal images and upsampled features under the self-adaptive mechanism. Finally, a multilevel supervision with multiscale loss function is designed for further refining the change-detection results by supervising the hidden layer features in multiple scales. Compared with existing state-of-the-art deep learning-based networks, the proposed HDFNet achieves superior performance on benchmark datasets in the F1-score, which indicates that it achieves a more comprehensive performance. Also, HDFNet achieves a good trade-off between recall and precision without designing penalty parameters for adjusting false positives and false negatives. It can be observed from qualitative analysis that in the change maps obtained by HDFNet, more pixels are accurately detected, and the unpredicted change and false alarm are relatively fewer. The experimental results demonstrate the effectiveness and robustness of HDFNet from two aspects of difference discrimination and change area details. Further research in the future will focus on the problem of multiscale features adapting with insufficient training data and the possible directions are weakly supervised learning and so on.