Maximal Instance Algorithm for Fast Mining of Spatial Co-Location Patterns
Abstract
1. Introduction
- A maximal instance algorithm for mining co-location patterns is presented. This algorithm can generate row instances and co-locations without join operations, which can make co-location mining more efficient.
- The concept of maximal instance is introduced and used to generate all row instances of co-locations.
- Experiments show that the maximal instance algorithm is feasible and has better performance.
2. Maximal Instance Algorithm
2.1. Generation of Row Instances
2.2. RI-Tree Construction
- (1)
- Create the root of the RI-tree and label it as F.
- (2)
- Push all spatial instances into a set F in alphabetic and numerical descending order.
- (3)
- Pop an instance from and delete it in . Then create a child node of the root F for this instance.
- (4)
- Find out the instances that are neighbors of this instance, have different spatial features from this instance, and are bigger than this instance.
- If not, return to (3).
- If so, push them into a set T in alphabetic descending order and create a child node for them.
- (5)
- Find out the instances that are neighbors of the last instance in T and delete them in .
- If not, push T in M; return to (3).
- If so and if they also have a neighborhood relationship with the rest of the instances in T, put them at the end of T and create a child node for them. Return to (5).
- If so but if they are not all neighbors with other instances in T, push T in M, create another child node of the root for the last instance in T, and generate a new T by combining it with the last instance in T. Return to (5).
- (6)
- Repeat the operation above till is empty.
2.2.1. Rules of an RI-Tree
- Before building an RI-tree, all spatial instances are put into the set F. The instance will be deleted from F if a child node of the root is created for it or if it has a neighbor relationship with the child node of the root. For example, a child node of the root is created for , so will be deleted from F; and are deleted from F since they have neighbor relationships with ( is a child node of the root).
- Each node is a row instance of the co-location, and note that not all row instances are listed in the RI-tree but all neighbor relationships are contained in the RI-tree. The number of row instances is very large if there are a lot of instances in the spatial data. The aim of an RI-tree is to generate the maximal instance; there is no need to list all row instances in an RI-tree. A node in an RI-tree contains neighbor relationships between all instances in the node.
- The nodes of the n-th layer of an RI-tree are n-1-size row instances. The spatial instances in F are selected as the child node of the root, i.e., nodes in the second layer of the RI-tree. From layer 3 to layer n, there are size 2 row instances, size 3 row instances, , and n-1-size row instances. The highest size of the row instance of the example data in Figure 1 is 3 since the RI-tree constructed for this example data has only four layers.
- After creating a child node of the root, scan its neighbor relationships. The neighbor relationships are identified by the Euclidean distance metric. Two instances have a neighbor relationship if their Euclidean distance is less than the user-defined minimum distance threshold [1]. If this node has a neighbor relationship with another instance, a child node of this node will be created under this branch for these two instances; if there is no common neighbor of instances in this node, another instance will be popped from F and a child node of the root will be created for it. For example, instance is a child node of the root and the node “” is created under this branch since has a neighbor relationship with . There is no common neighbor of and , but still has relationship with , so a new child node of the root is created for , and the node has “” as a child node.
- The RI-tree is built from left to right. When a leaf node appears in one branch of the RI-tree, another branch can be established. A node is a leaf node if there is no common neighbor of instances in this node, which means the end of the branch where this node is located.
- The leaf nodes of an RI-tree are maximal instances because a leaf node is a row instance in which all instances are neighbors and no other instance can join with it to generate a high-size row instance. It is obvious that the leaf node meets the conditions of maximal instance. The number of maximal instances equals the number of branches of the RI-tree.
2.2.2. Completeness of the RI-Tree
2.3. Generation of Co-Locations
2.4. Discussions for Maximal Instance Algorithm
- The existing methods identify high-size row instances from low-size row instances, but the presented algorithm first identifies the highest-size row instances (maximal instances) based on the relationship of spatial instances and then generates all low-size row instances from highest-size row instances.
- The existing methods generate candidate patterns by joining row instances, but the presented algorithm generates candidate patterns from maximal instances without join operations.
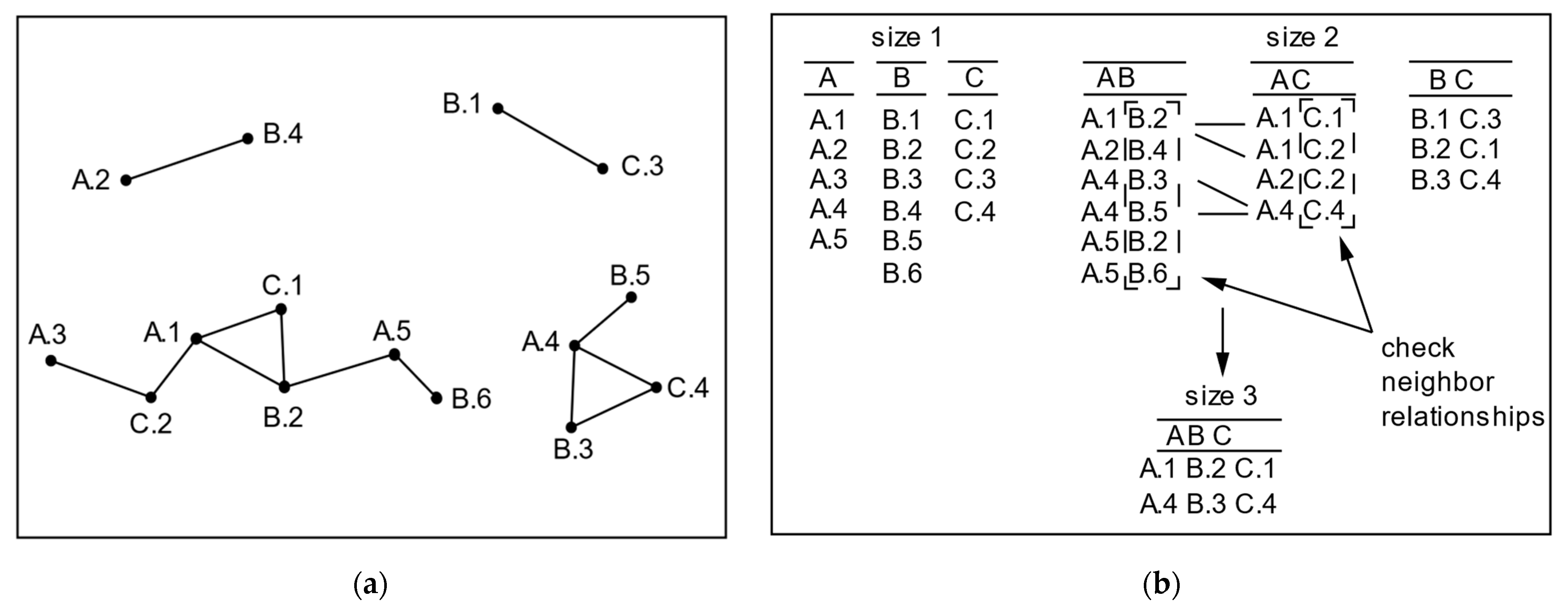
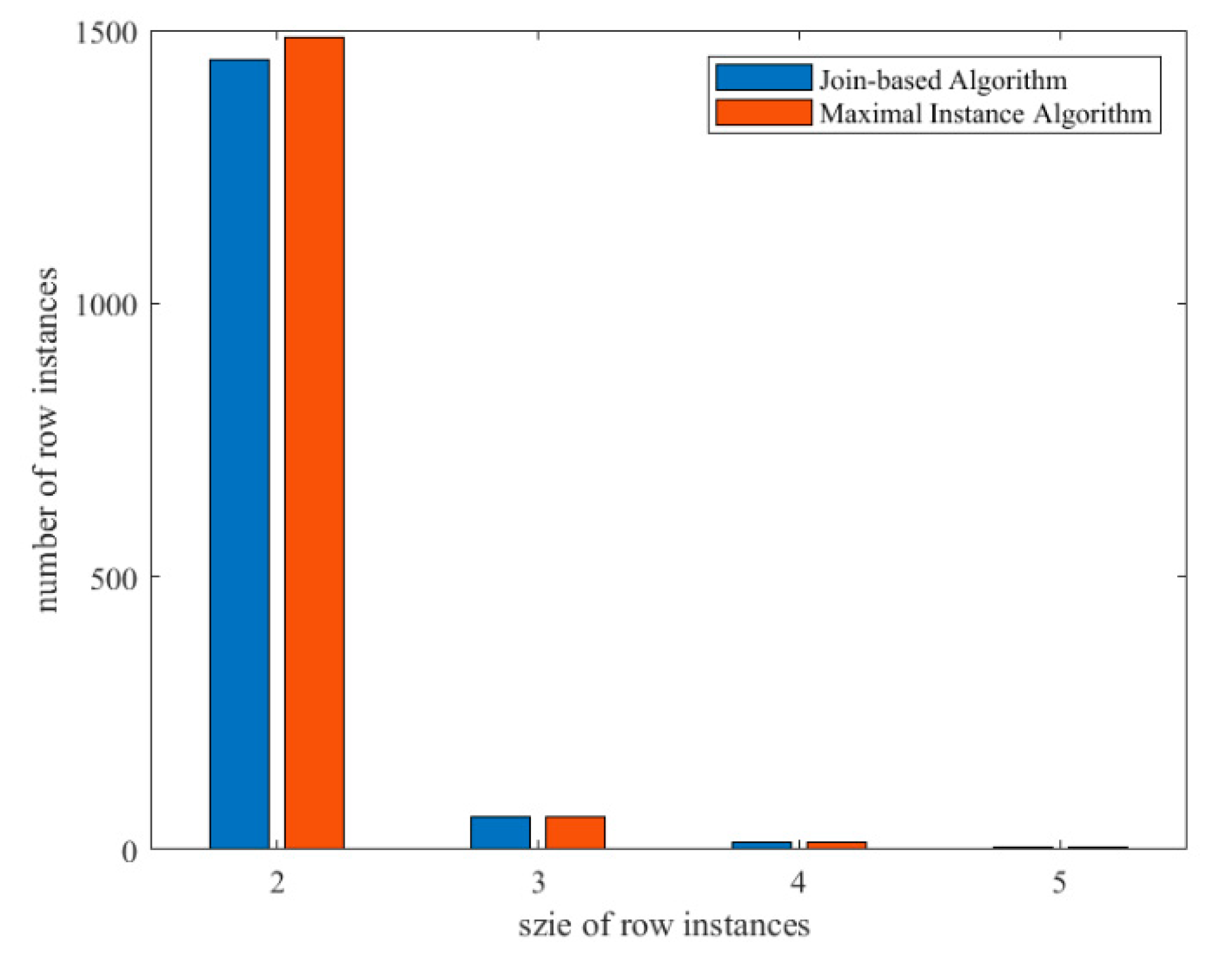
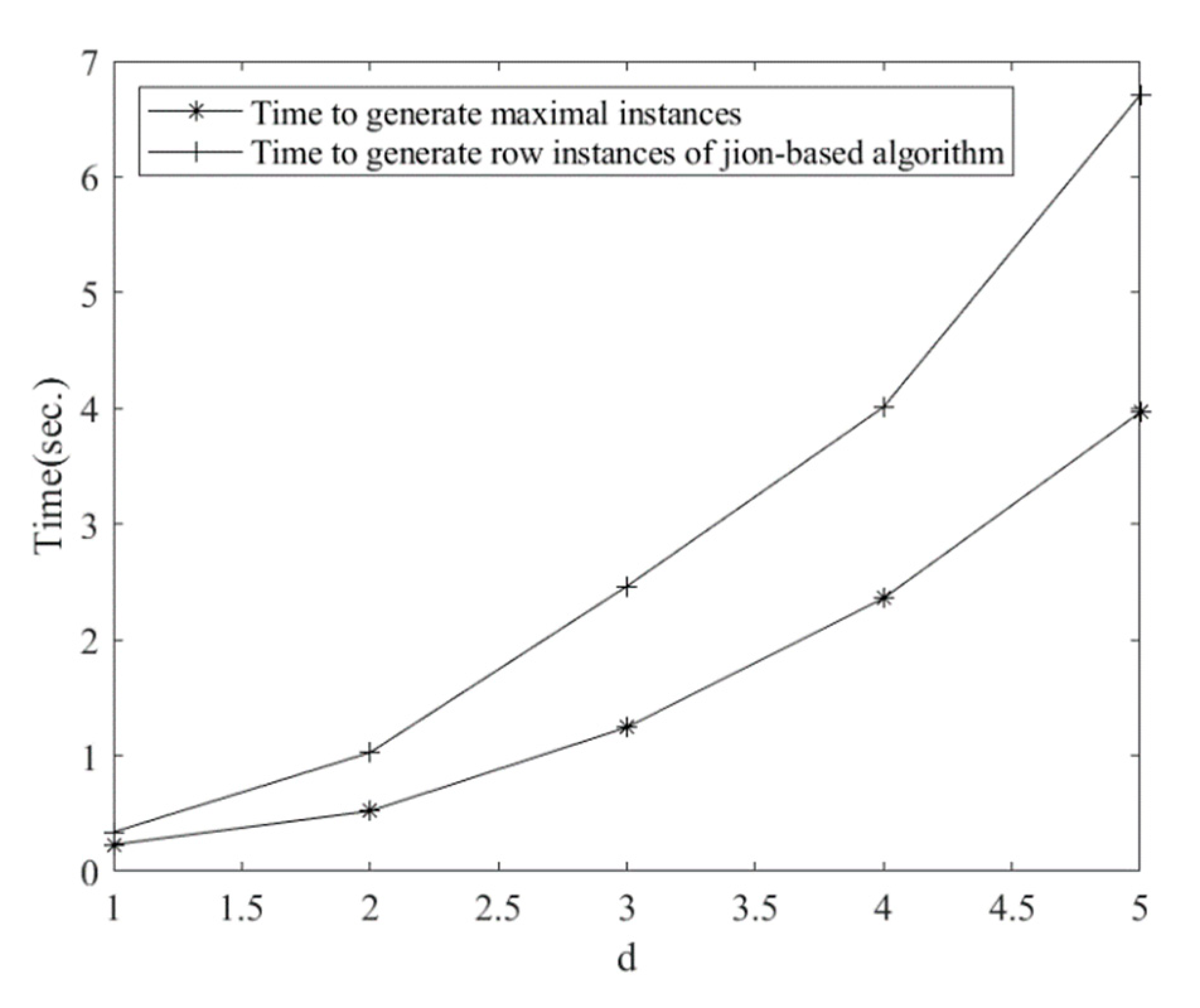
2.4.1. Comparison Analysis of Row Instance Generation
2.4.2. Comparison Analysis of Maximal Instance Algorithm
2.5. Overview of the Maximal Instance Algorithm
3. Experiments
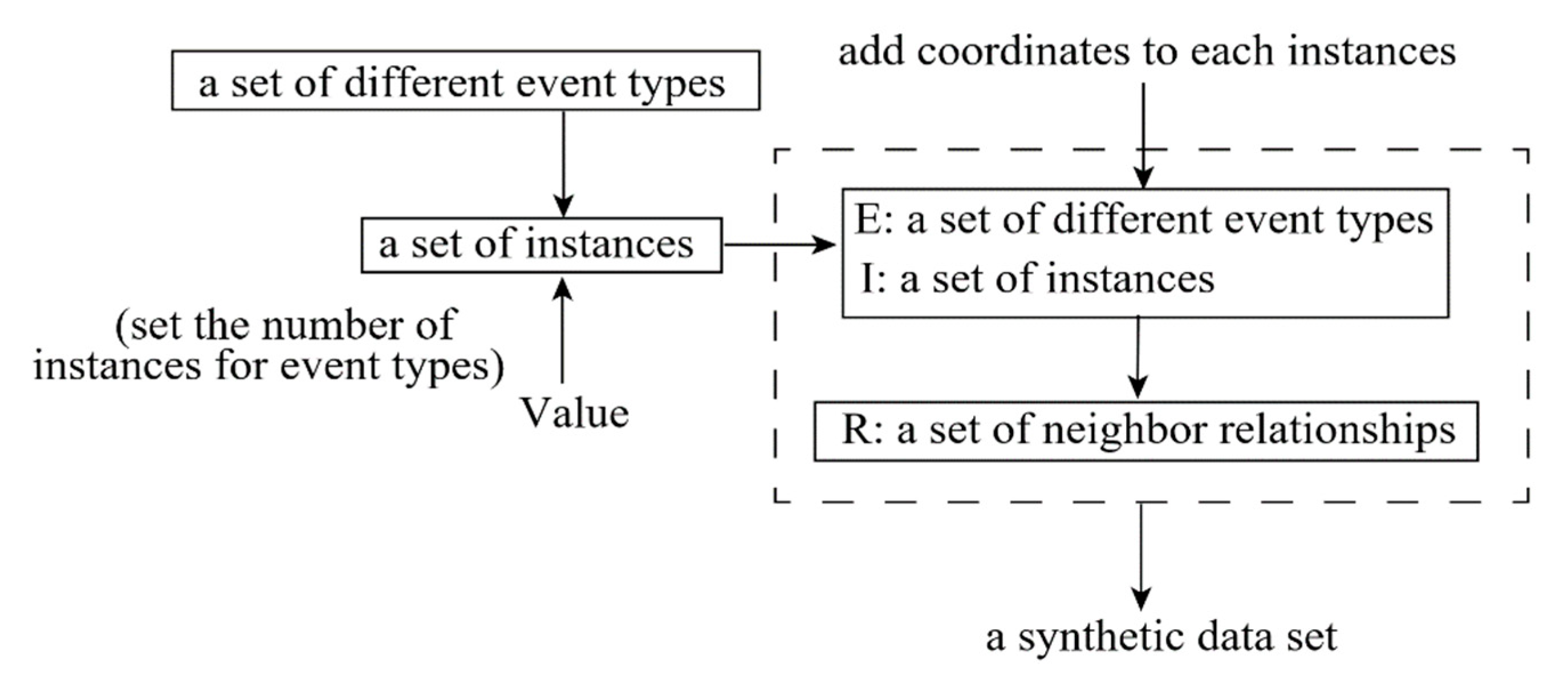
3.1. Synthetic Data Set
3.2. Real Data Set
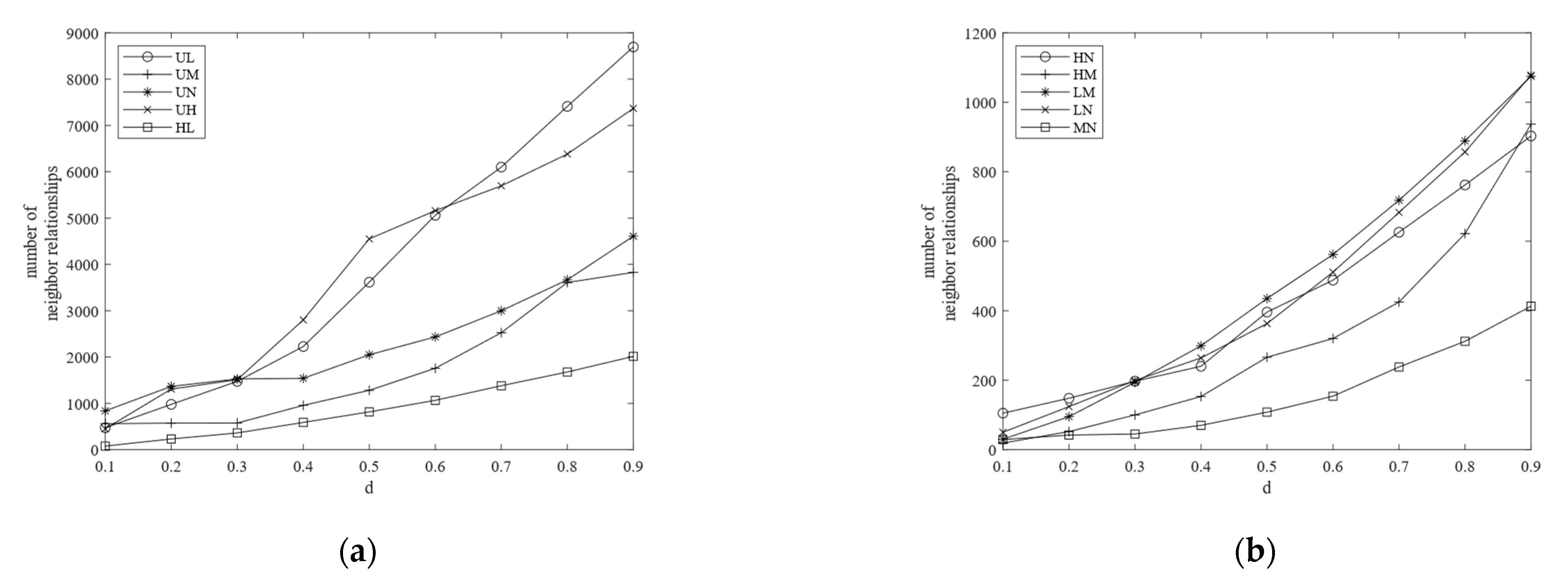
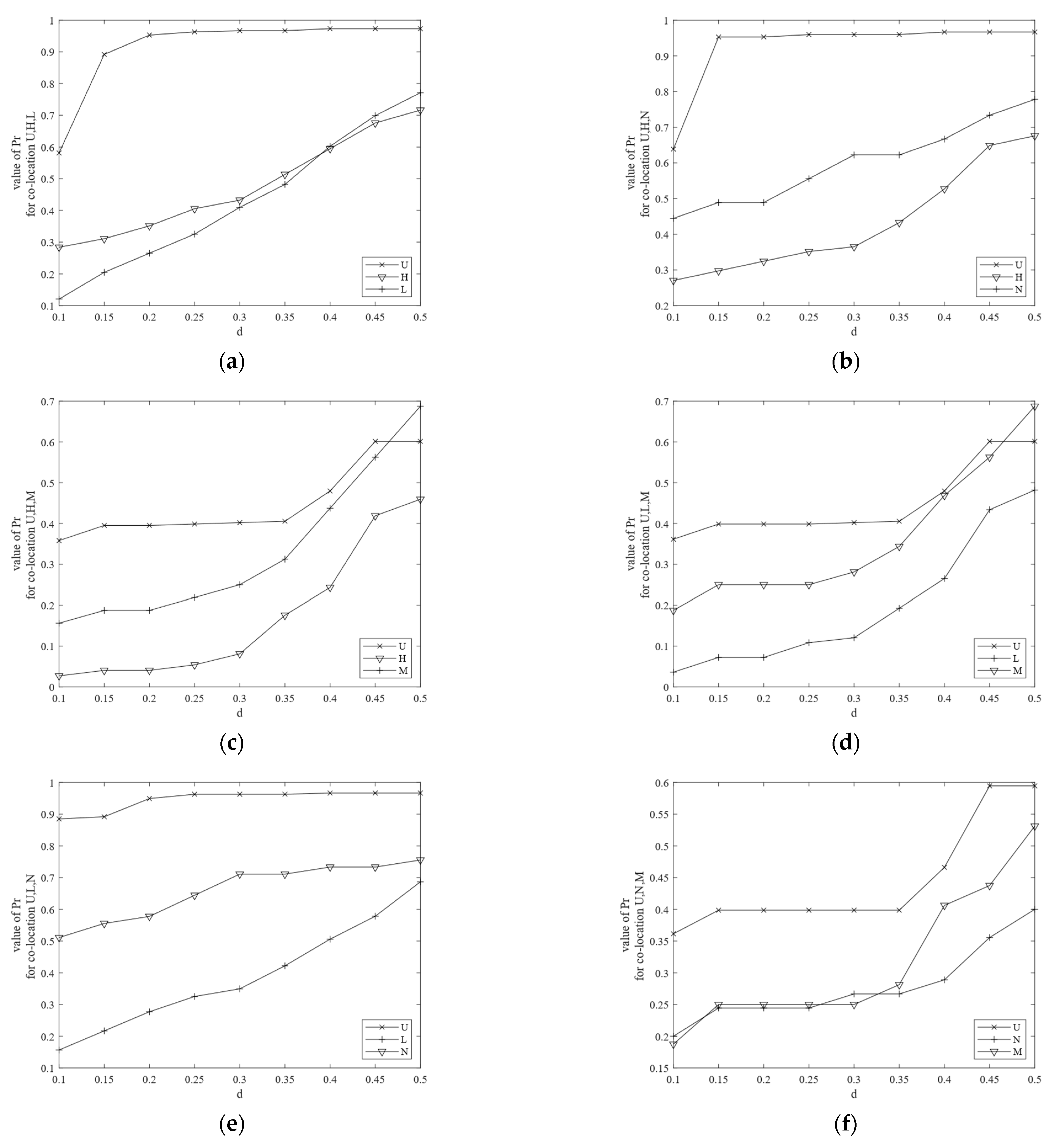
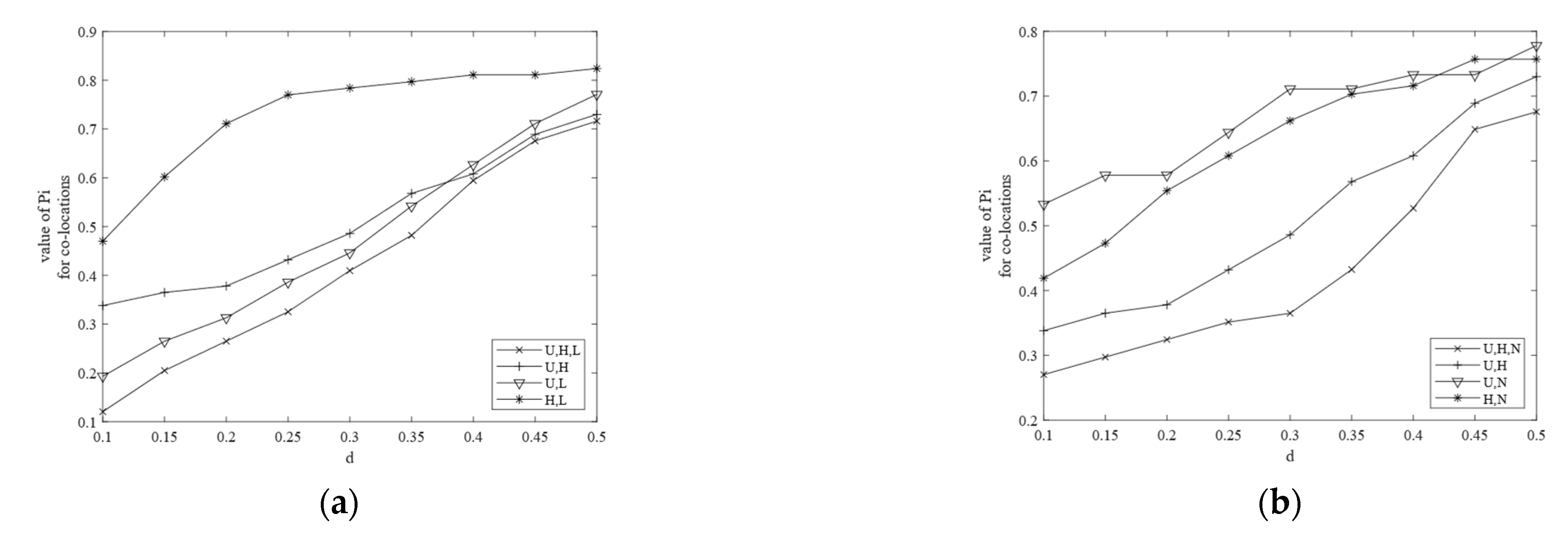
3.3. Experiment Results
- (1)
- (the value of the participation index of ) is always smaller than , , and , and the same is the case in Figure 10b, where is always smaller than , , and . This is because the participation ratio and the participation index are antimonotone (monotonically nonincreasing) as the size of the co-location increases [1] and it shows that our results are correct.
- (2)
3.4. Experimental Evaluation
4. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Huang, Y.; Shekhar, S.; Xiong, H. Discovering colocation patterns from spatial data sets: A general approach. IEEE Trans. Knowl. Data Eng. 2004, 16, 1472–1485. [Google Scholar] [CrossRef]
- Shekhar, S.; Huang, Y. Discovering Spatial co-location patterns: A summary of results. In Advances in Spatial and Temporal Databases; Jensen, C.S., Schneider, M., Seeger, B., Tsotras, V.J., Eds.; Springer: Berlin/Heidelberg, Germany, 2001; p. 2121. [Google Scholar]
- Yoo, J.S.; Shekhar, S.; Smith, J.; Kumquat, J.P. A partial join approach for mining co-location patterns. In Proceedings of the 12th annual ACM international workshop on Geographic information systems—GIS ’04, Washington, DC, USA, 12–13 November 2004; pp. 241–249. [Google Scholar] [CrossRef]
- Yoo, J.S.; Shekhar, S.; Celik, M. A Join-Less Approach for Co-Location Pattern Mining: A Summary of Results. In Proceedings of the Fifth IEEE International Conference on Data Mining (ICDM’05), Houston, TX, USA, 27–30 November 2005; p. 4. [Google Scholar]
- Yoo, J.S.; Shekhar, S. A join-less approach for mining spatial co-location pattern. IEEE Trans. Knowl. Data Eng. 2006, 18, 1323–1337. [Google Scholar]
- Djenouri, Y.; Lin, J.C.-W.; Nørvåg, K.; Ramampiaro, H. Highly Efficient Pattern Mining Based on Transaction Decomposition. In Proceedings of the 2019 IEEE 35th International Conference on Data Engineering (ICDE), Macao, China, 8–11 April 2019; pp. 1646–1649. [Google Scholar]
- Zhang, B.; Lin, J.C.-W.; Shao, Y.; Fournier-Viger, P.; Djenouri, Y. Maintenance of Discovered High Average-Utility Itemsets in Dynamic Databases. Appl. Sci. 2018, 8, 769. [Google Scholar] [CrossRef]
- Huang, Y.; Pei, J.; Xiong, H. Mining Co-Location Patterns with Rare Events from Spatial Data Sets. GeoInformatica 2006, 10, 239–260. [Google Scholar] [CrossRef]
- Verhein, F.; Al-Naymat, G. Fast Mining of Complex Spatial Co-location Patterns Using GLIMIT. In Proceedings of the Seventh IEEE International Conference on Data Mining Workshops (ICDMW 2007), Omaha, NE, USA, 28–31 October 2007; pp. 679–684. [Google Scholar]
- Al-Naymat, G. Enumeration of maximal clique for mining spatial co-location patterns. In Proceedings of the 2008 IEEE/ACS International Conference on Computer Systems and Applications, Doha, Qatar, 31 March–4 April 2008; pp. 126–133. [Google Scholar]
- Kim, S.K.; Kim, Y.; Kim, U. Maximal cliques generating algorithm for spatial colocation pattern mining. In Secure and Trust Computing, Data Management and Applications; Park, J.J., Lopez, J., Yeo, S.S., Shon, T., Taniar, D., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; Volume 186, pp. 241–250. [Google Scholar]
- Yao, X.; Wang, D.; Peng, L.; Chi, T. An adaptive maximal co-location mining algorithm. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 5551–5554. [Google Scholar] [CrossRef]
- Deng, M.; Cai, J.; Liu, Q.; He, Z.; Tang, J. Multi-level method for discovery of regional co-location patterns. Int. J. Geogr. Inf. Sci. 2017, 31, 1–25. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, P.; Zhang, C. On the Relationships between Clustering and Spatial Co-Location Pattern Mining. Int. J. Artif. Intell. Tools 2008, 17, 55–70. [Google Scholar] [CrossRef]
- Jiamthapthaksin, R.; Eick, C.F.; Vilalta, R. A framework for multi-objective clustering and its application to co-location mining. In Advanced Data Mining and Applications; Huang, R., Yang, Q., Pei, J., Gama, J., Meng, X., Li, X., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5678, pp. 188–199. [Google Scholar]
- Yu, W. Identifying and Analyzing the Prevalent Regions of a Co-Location Pattern Using Polygons Clustering Approach. ISPRS Int. J. Geo-Infor. 2017, 6, 259. [Google Scholar] [CrossRef]
- Ouyang, Z.; Wang, L.; Wu, P. Spatial Co-Location Pattern Discovery from Fuzzy Objects. Int. J. Artif. Intell. Tools 2017, 26. [Google Scholar] [CrossRef]
- Zhou, G.; Wang, L. Co-location decision tree for enhancing decision-making of pavement maintenance and rehabilitation. Transp. Res. Part C: Emerg. Technol. 2012, 21, 287–305. [Google Scholar] [CrossRef]
- Zhou, G.; Zhang, R.; Zhang, D. Manifold Learning Co-Location Decision Tree for Remotely Sensed Imagery Classification. Remote Sens. 2016, 8, 855. [Google Scholar] [CrossRef]
- Zhou, G.; Li, Q.; Deng, G.; Yue, T.; Zhou, X. Mining Co-Location Patterns with Clustering Items from Spatial Data Sets. ISPRS-Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, XLII-3, 2505–2509. [Google Scholar] [CrossRef]
- Bao, X.; Wang, L. A clique-based approach for co-location pattern mining. Inf. Sci. 2019, 490, 244–264. [Google Scholar] [CrossRef]
- Celik, M.; Kang, J.M.; Shekhar, S. Zonal co-location pattern discovery with dynamic parameters. In Proceedings of the Seventh IEEE International Conference on Data Mining, Omaha, NE, USA, 28–31 October 2007. [Google Scholar]
- Jiang, Y.; Wang, L.; Chen, H. Discovering both positive and negative co-location rules from spatial data sets. Software Engi-neering and Data Mining (SEDM). In Proceedings of the 2010 2nd International Conference on IEEE, Chengdu, China, 23–25 June 2010. [Google Scholar]
- Yu, P. FP-Tree. based Spatial Co-Location Pattern Mining; University of North Texas: Denton, TX, USA, 2005. [Google Scholar]
- Agrawal, R.; Srikant, R. Fast algorithms for mining association rules. In Readings in Database Systems, 3rd ed.; Stonebraker, M., Hellerstein, J.M., Eds.; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1998; pp. 580–592. [Google Scholar]
- ArcGIS Hub. Available online: https://hub.arcgis.com/ (accessed on 20 February 2021).





| Row Instances of All Co-Locations | |
|---|---|
| , , , , , , | |
| , , | |
| , , | |
| , , | |
| , , | |
| , , | |
| , , , , , , | |
| , , | |
| , , |
| Spatial Feature Type | Abbreviation | Number of Events |
|---|---|---|
| College and University | U | 286 |
| Hospital | H | 74 |
| Library | L | 83 |
| Nursing Home | N | 45 |
| Mineral Collecting Site | M | 32 |
| Co-Location Patterns | |
|---|---|
| 0.61 | |
| 0.63 | |
| 0.81 | |
| 0.59 | |
| 0.53 | |
| 0.44 | |
| 0.73 | |
| 0.47 | |
| 0.41 |
| Number | |
|---|---|
| Maximal Instances | 1342 |
| Size 2 Maximal Instances | 1268 |
| Size 3 Maximal Instances | 17 |
| Size 4 Maximal Instances | 5 |
| Size 5 Maximal Instances | 3 |
| False | 7 |
| Repetitive | 42 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, G.; Li, Q.; Deng, G. Maximal Instance Algorithm for Fast Mining of Spatial Co-Location Patterns. Remote Sens. 2021, 13, 960. https://doi.org/10.3390/rs13050960
Zhou G, Li Q, Deng G. Maximal Instance Algorithm for Fast Mining of Spatial Co-Location Patterns. Remote Sensing. 2021; 13(5):960. https://doi.org/10.3390/rs13050960
Chicago/Turabian StyleZhou, Guoqing, Qi Li, and Guangming Deng. 2021. "Maximal Instance Algorithm for Fast Mining of Spatial Co-Location Patterns" Remote Sensing 13, no. 5: 960. https://doi.org/10.3390/rs13050960
APA StyleZhou, G., Li, Q., & Deng, G. (2021). Maximal Instance Algorithm for Fast Mining of Spatial Co-Location Patterns. Remote Sensing, 13(5), 960. https://doi.org/10.3390/rs13050960







