A Dual-Channel Aerosol Optical Depth Retrieval Algorithm Incorporating the BRDF Effect from AVHRR over Eastern Asia
Abstract
1. Introduction
2. Datasets and Their Preprocessing
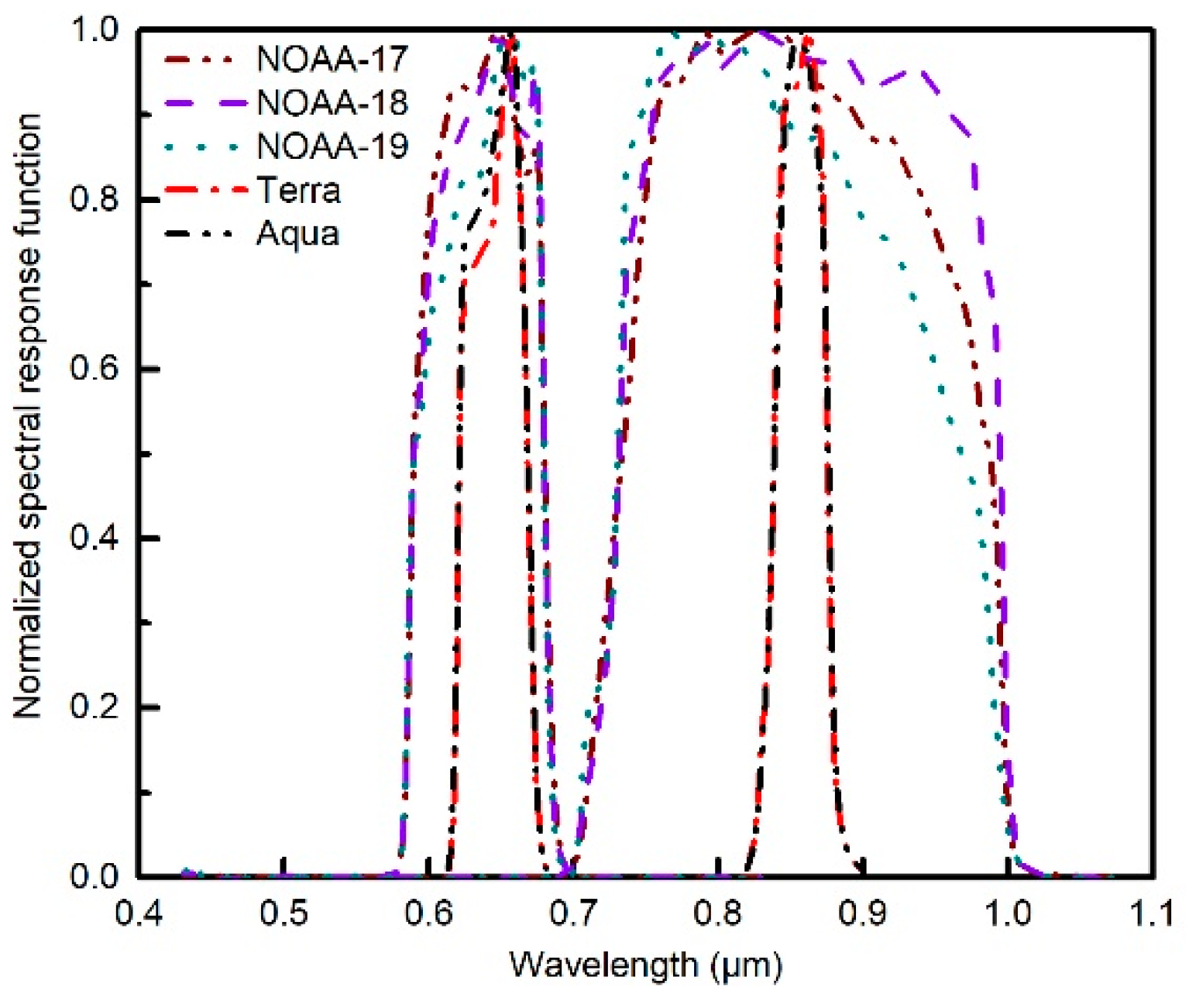
2.1. AVHRR
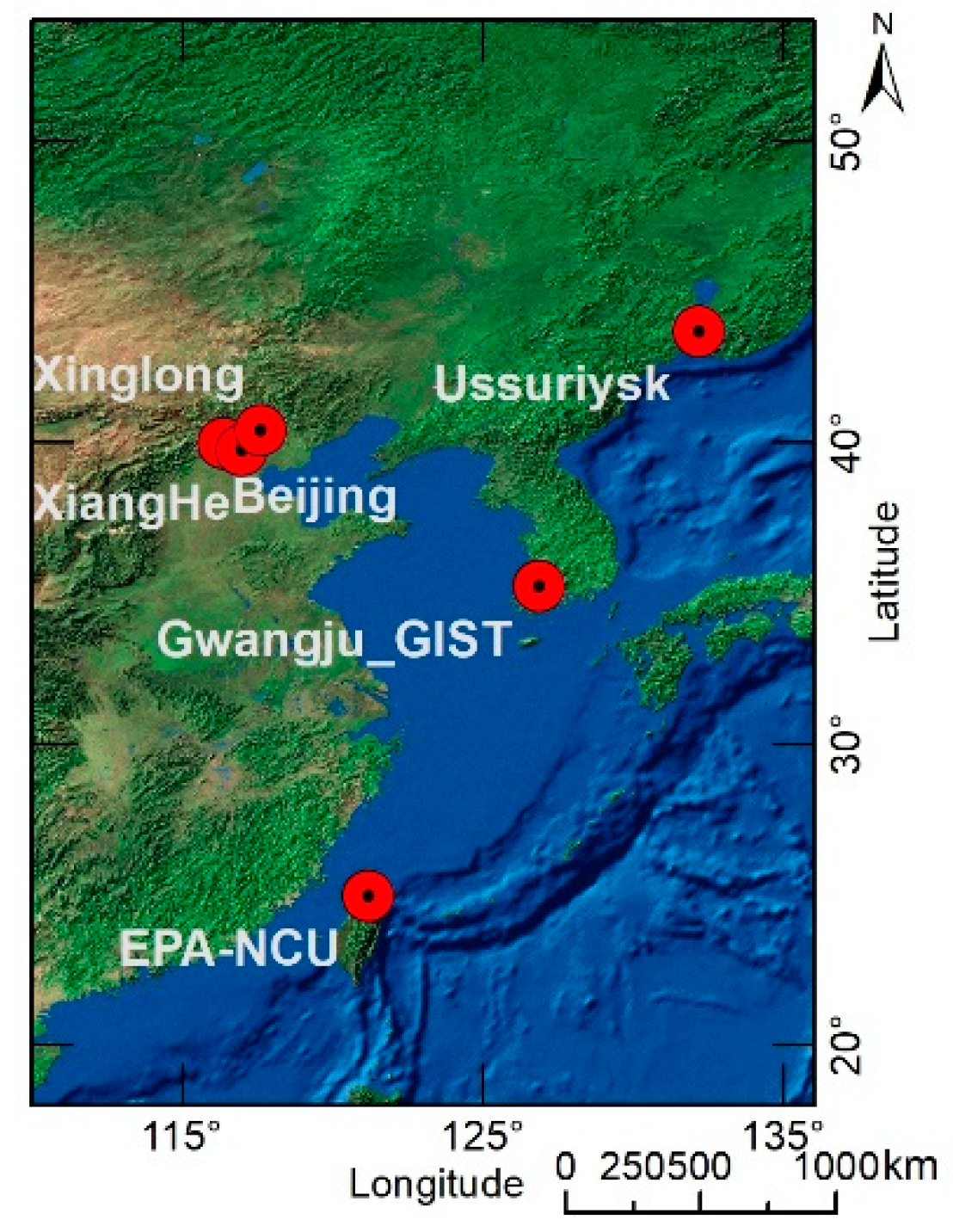
2.2. AERONET Measurements
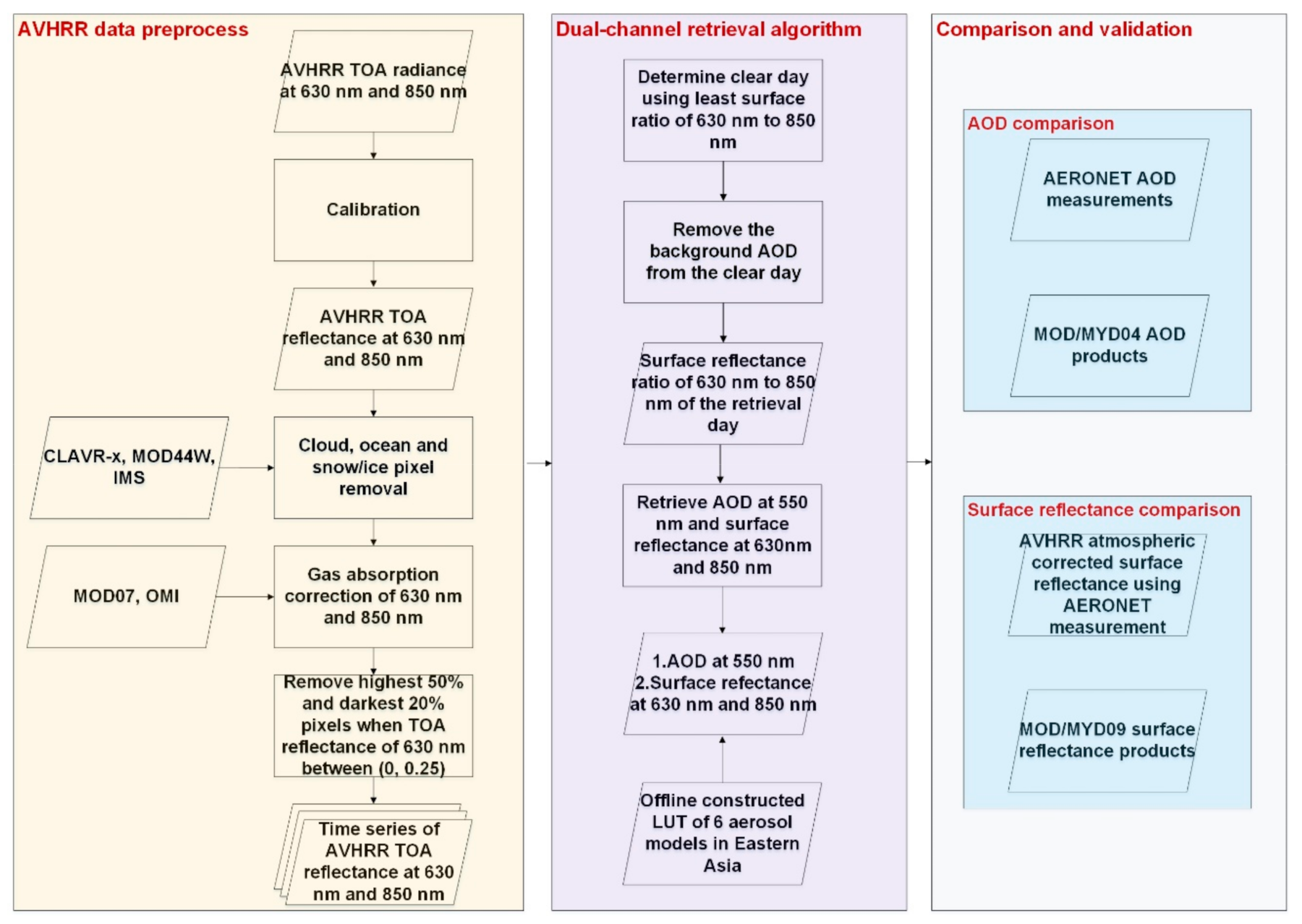
3. Retrieval Methodology
- (a)
- AVHRR data preprocess: The detailed description of calibration, the screening, and the gas absorption correction has been given in Section 2.1. Then time series of AVHRR TOA reflectance at 0.63 and 0.85 μm were prepared.
- (b)
- Dual-channel retrieval algorithm: Firstly, the clear day in 31 days was searched for each pixel according to the least TOA reflectance ratio. Secondly, the background AOD and Rayleigh scattering of the clear day was removed. Next, assuming that the surface bidirectional reflectance properties do not change during the 31 days, the surface reflectance ratio of the retrieval day was obtained. Finally, the AOD values at 0.55μm and the surface reflectance values at 0.63 and 0.85 μm were retrieved using the surface reflectance ratio of the retrieval day on the basis that the surface reflectance ratio would be monotonically decreasing as the AOD value increases. Detailed description of the algorithm is shown in Section 3.4.
- (c)
- Comparison and validation: The retrieved AOD and surface reflectance results are evaluated in terms of statistical comparisons and spatial analysis of one-day case (shown in Section 4).
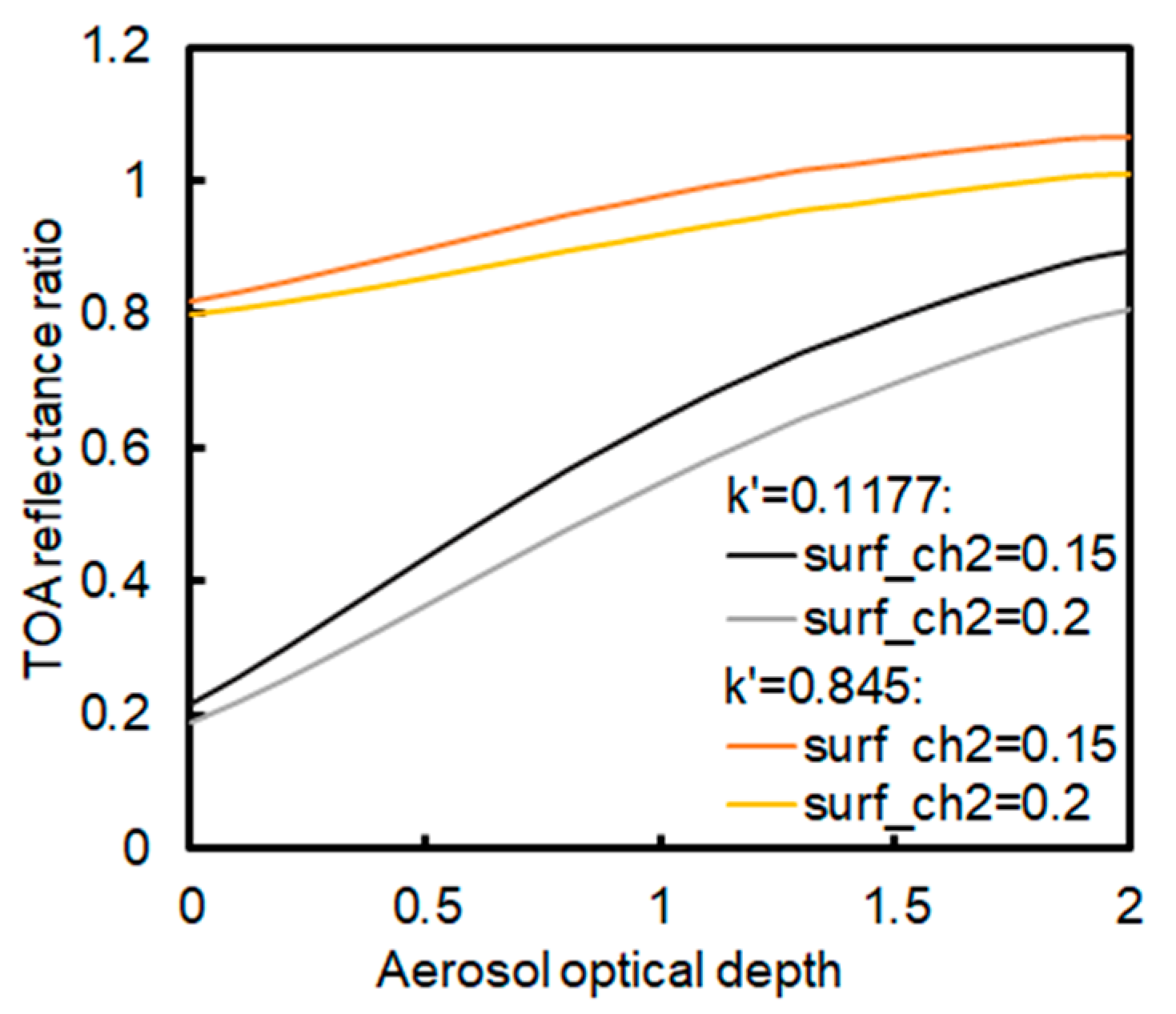
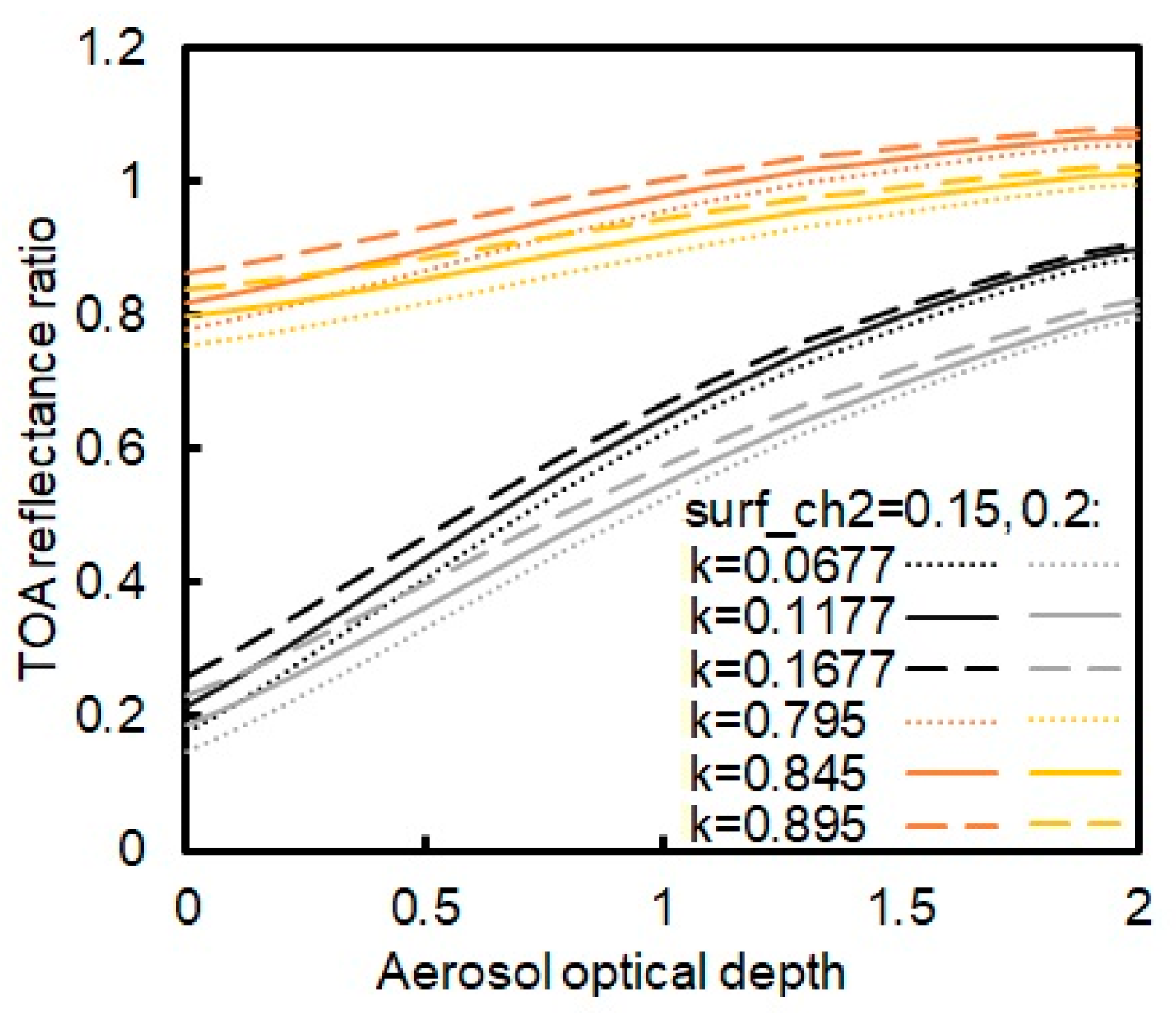
3.1. Forward Sensitivity Study and the Need for a Dual-Channel AOD Algorithm
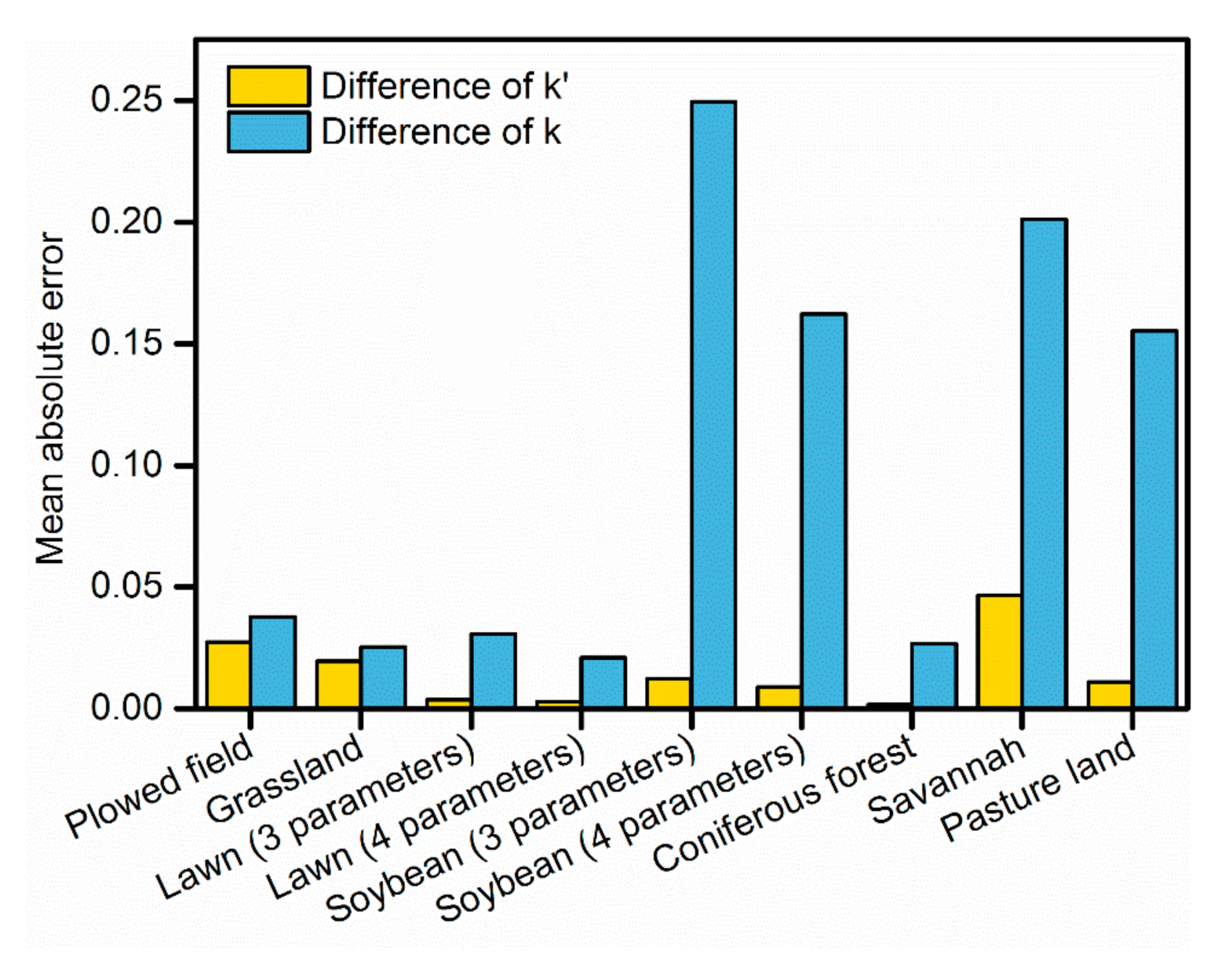
3.2. Why Choosing the Surface Reflectance Ratio to Address the BRDF Effect?
3.3. Determination of the Surface Reflectance Ratio
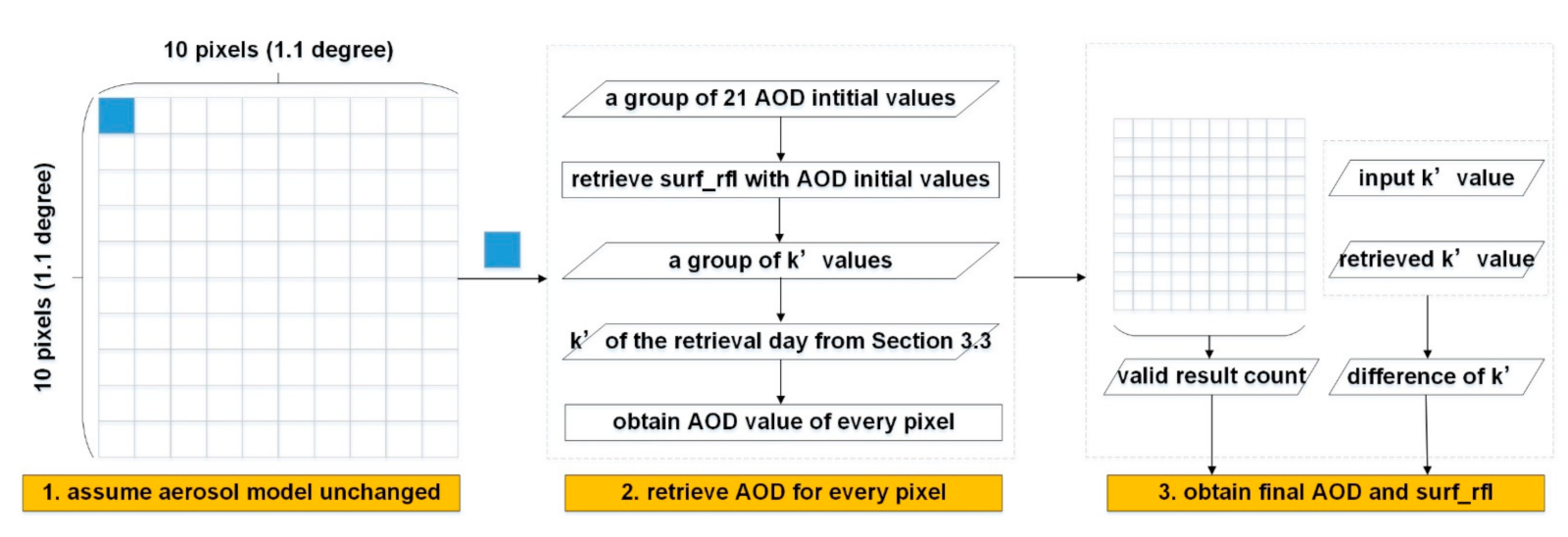
3.4. The Dual-Channel AOD Retrieval Algorithm
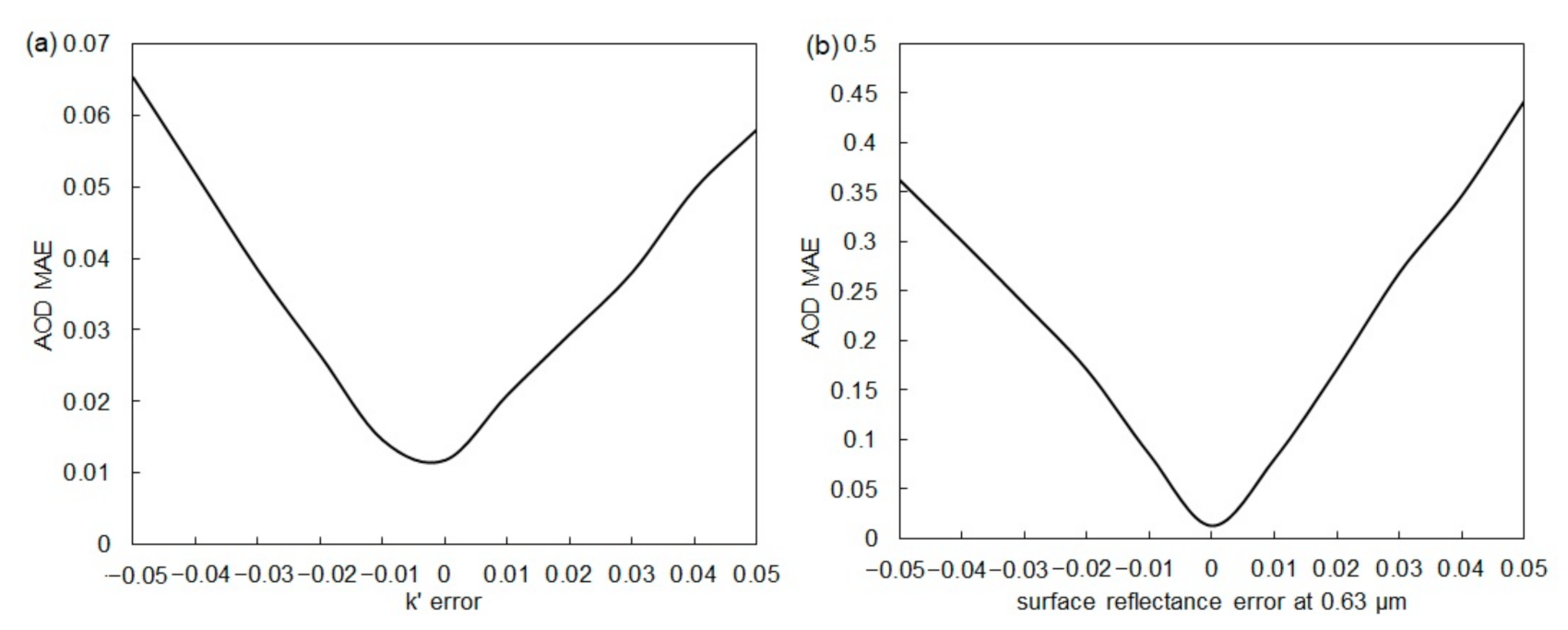
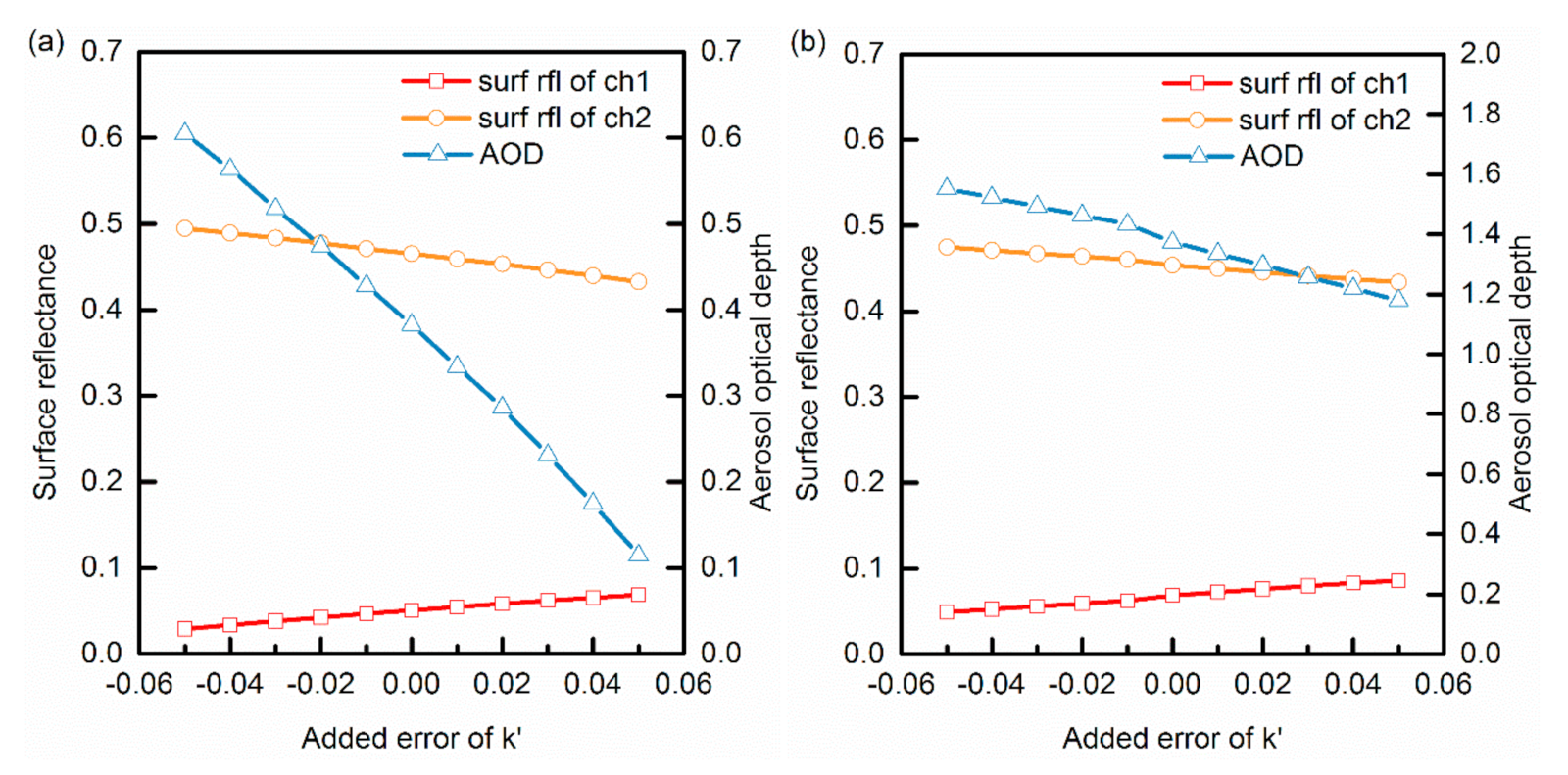
3.5. Uncertainty Study
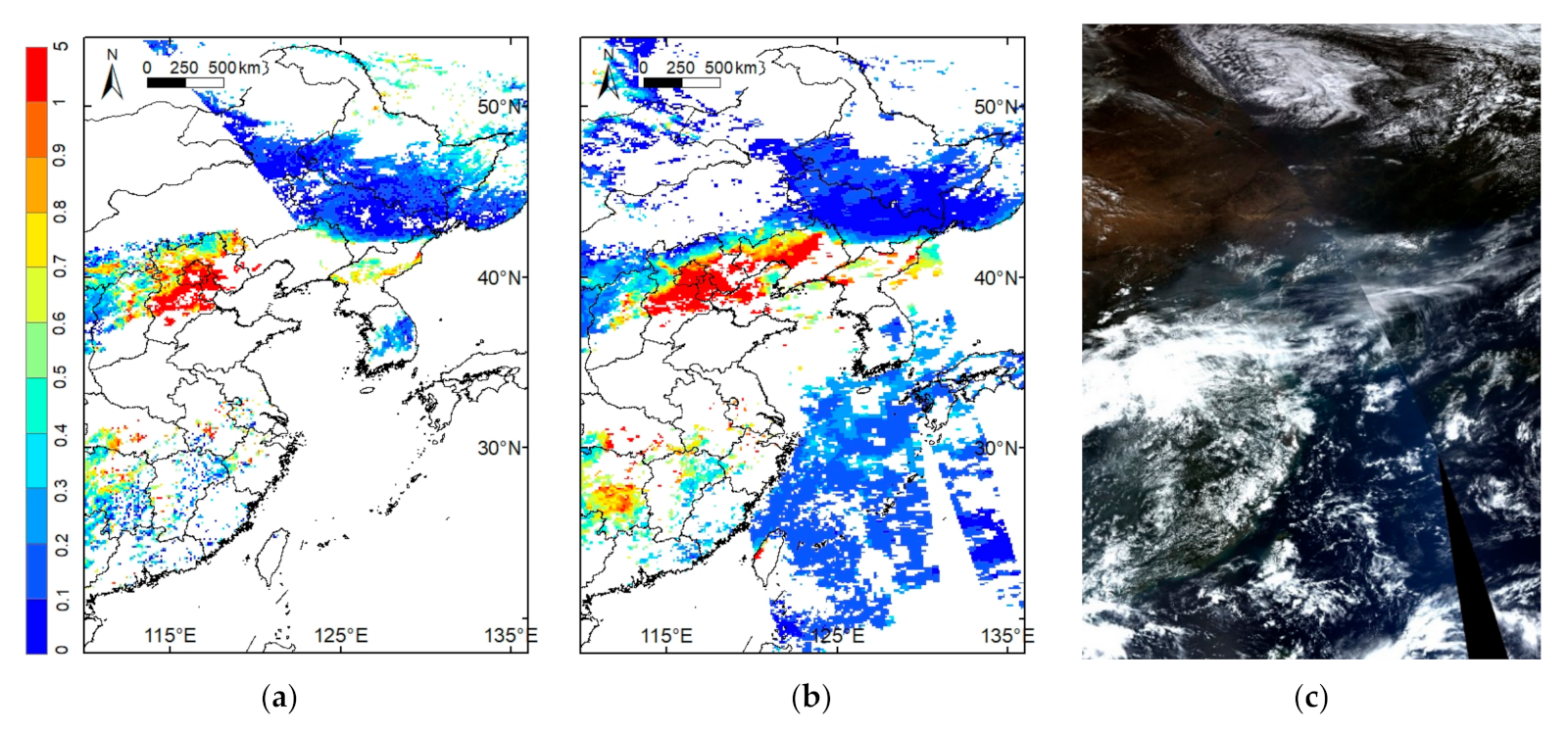
4. Results and Validation
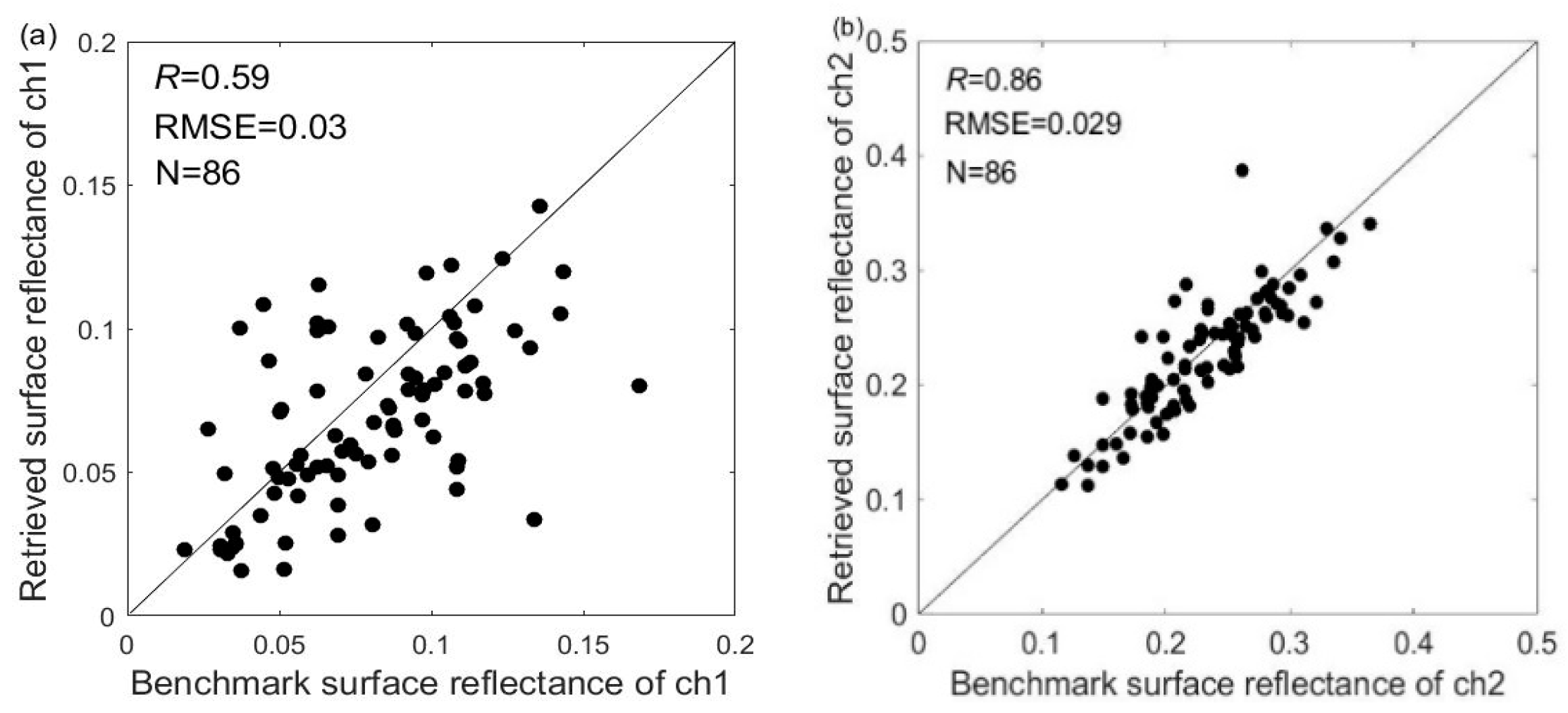
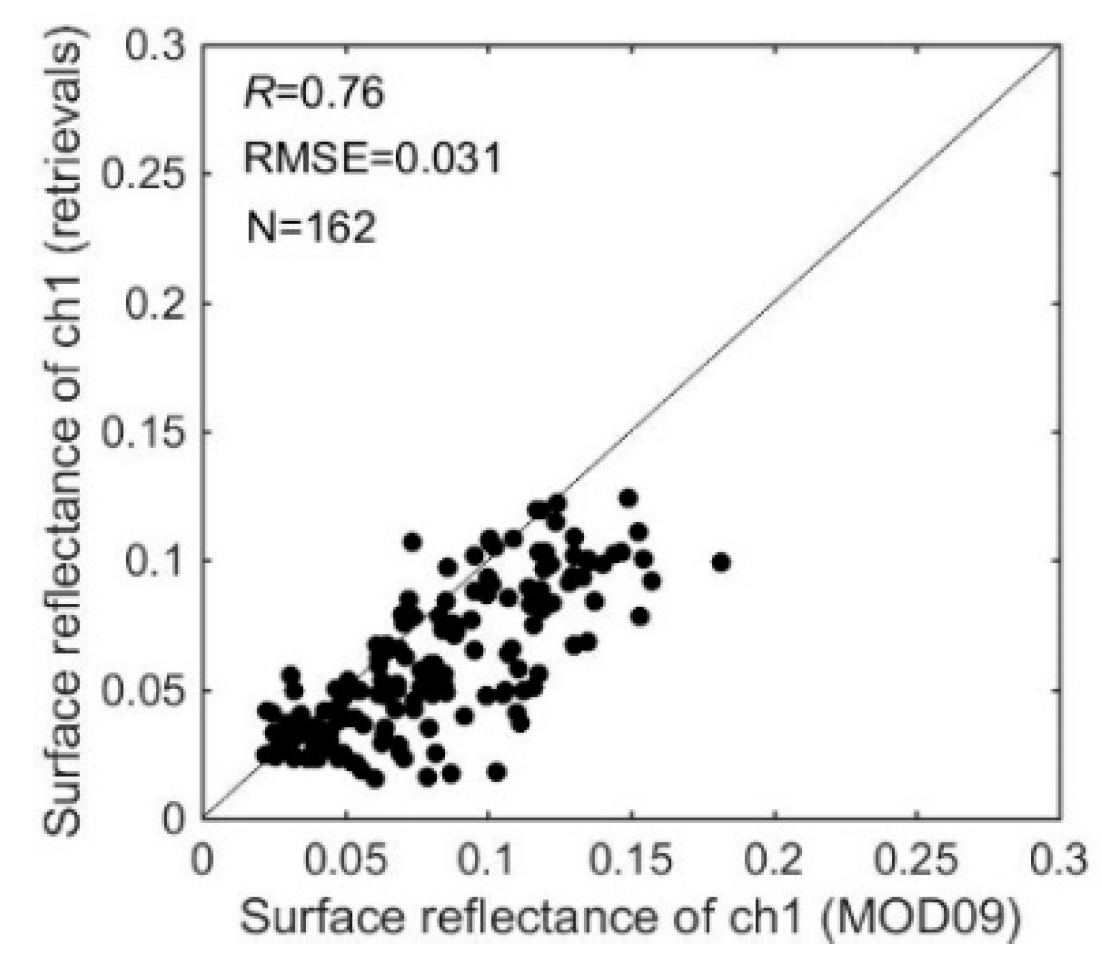
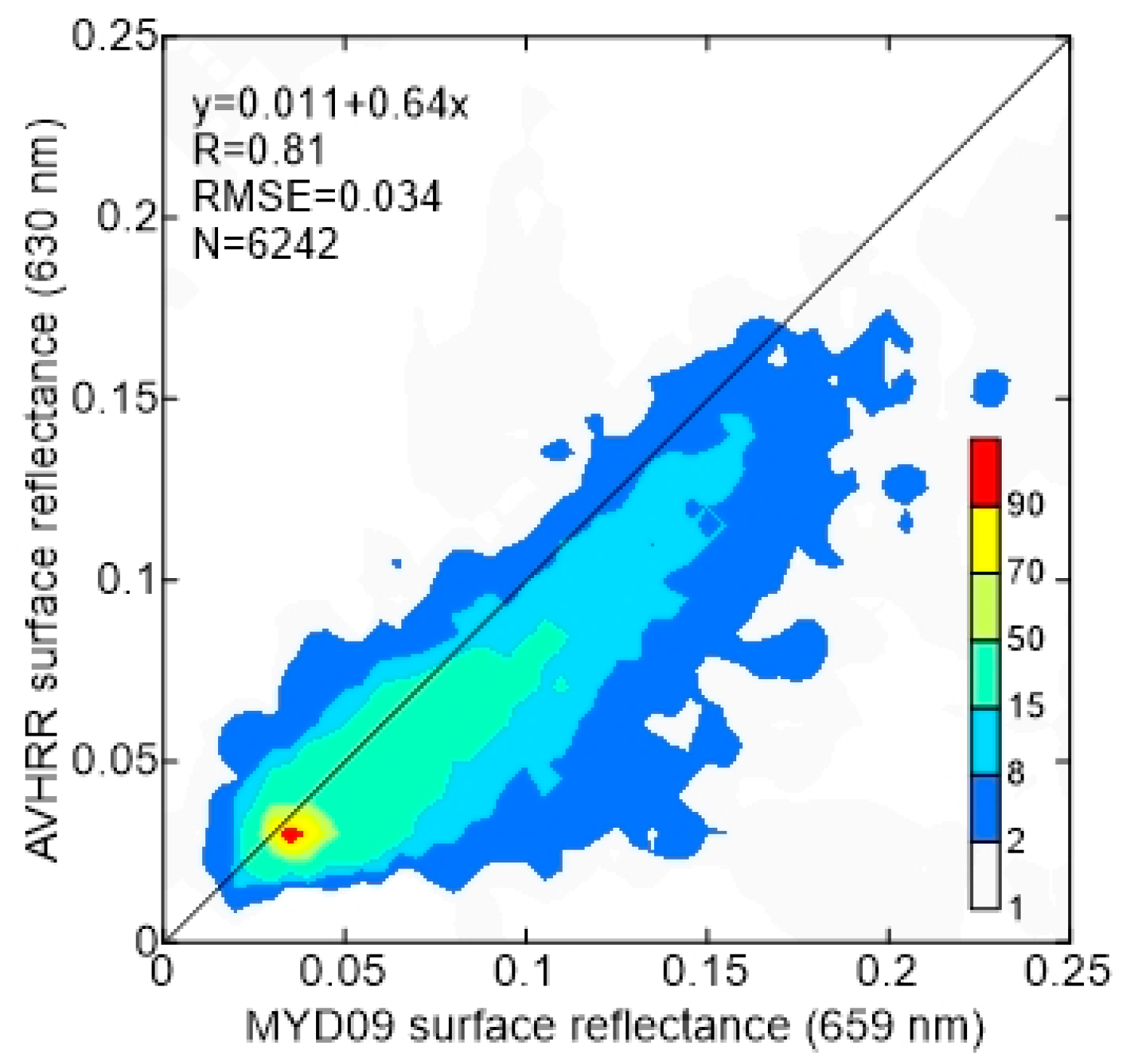
4.1. Comparison of the Retrieved Surface Reflectance against Atmospherically Corrected Surface Reflectance and MOD09 Product
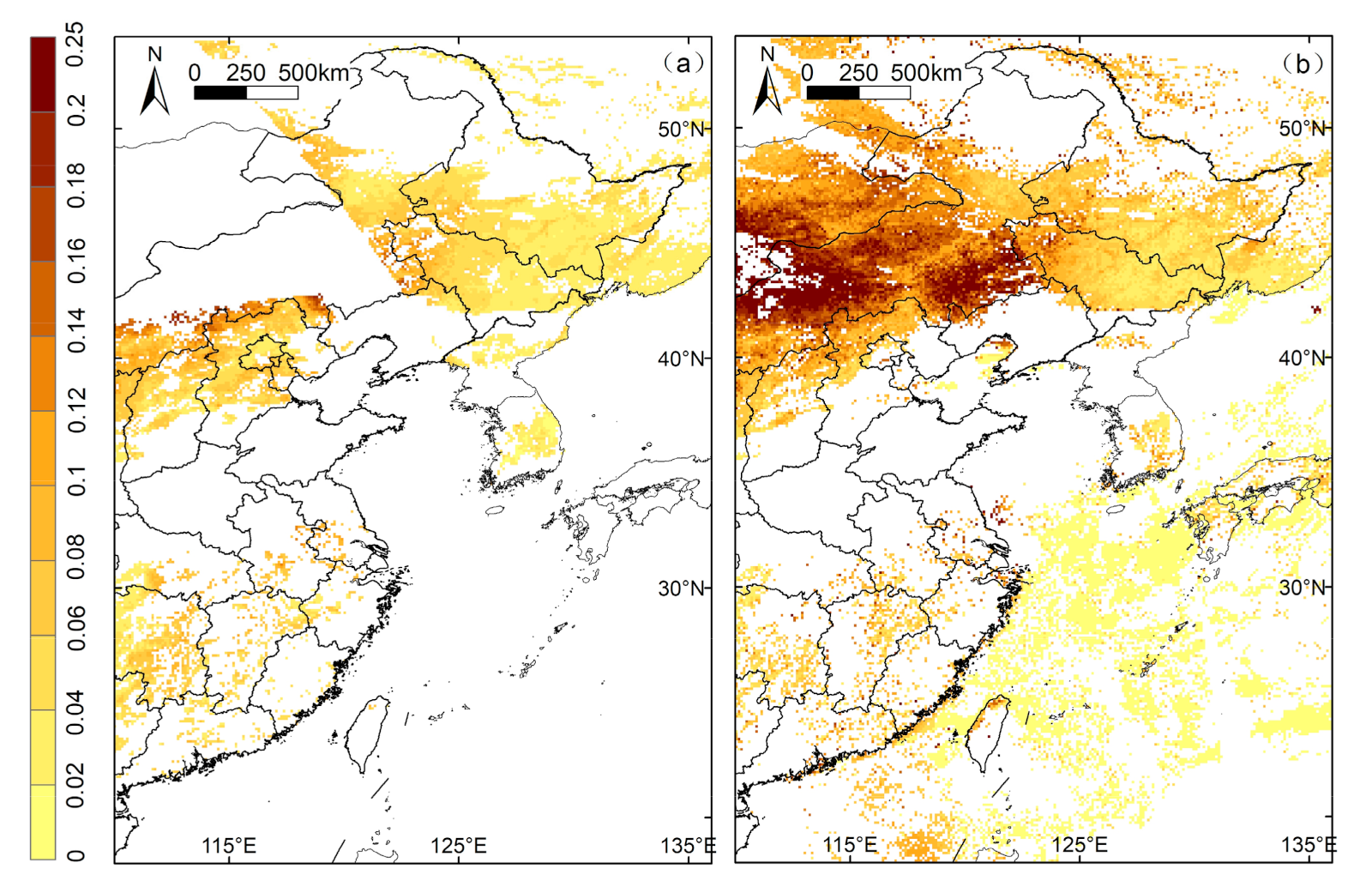
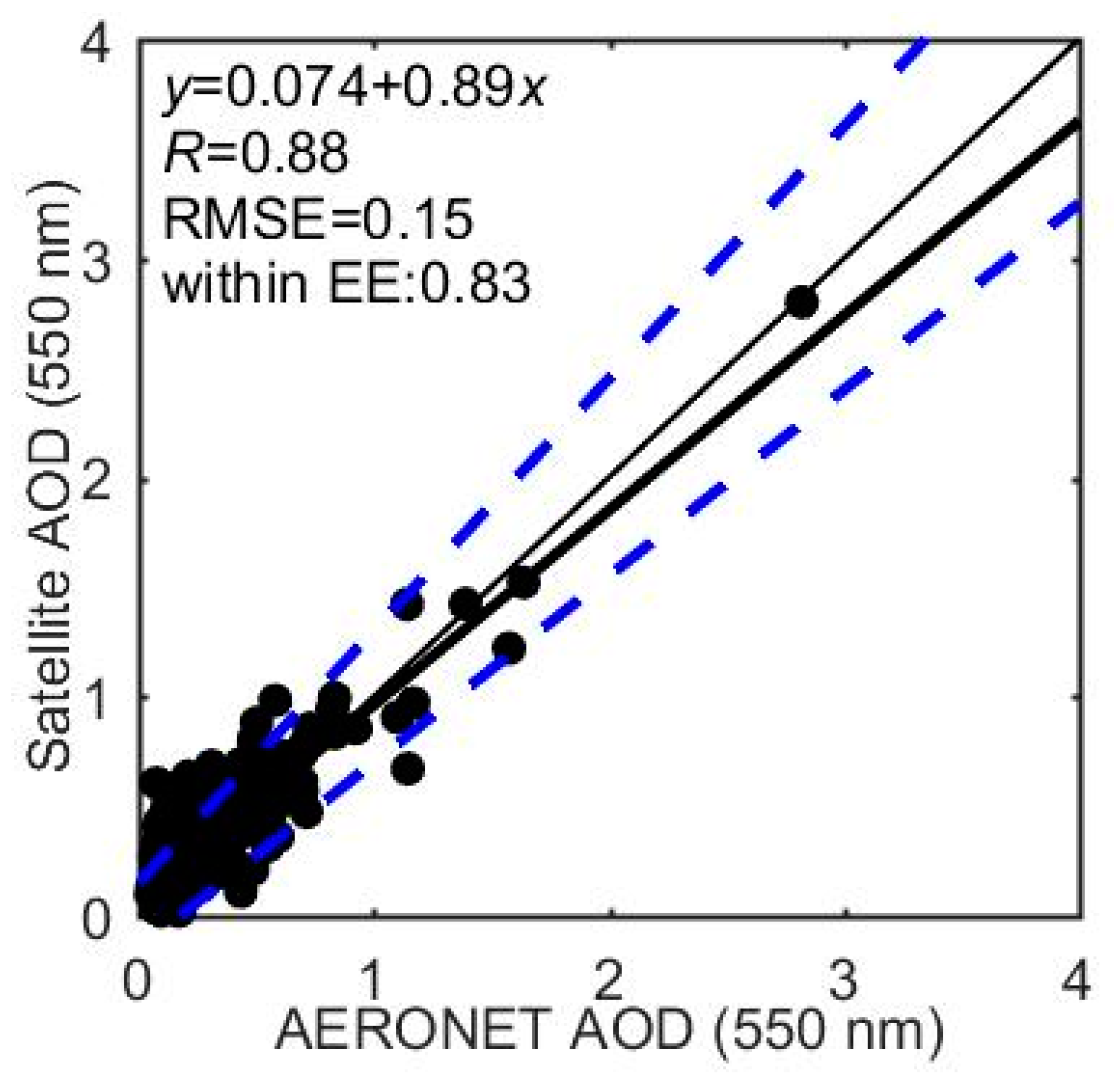
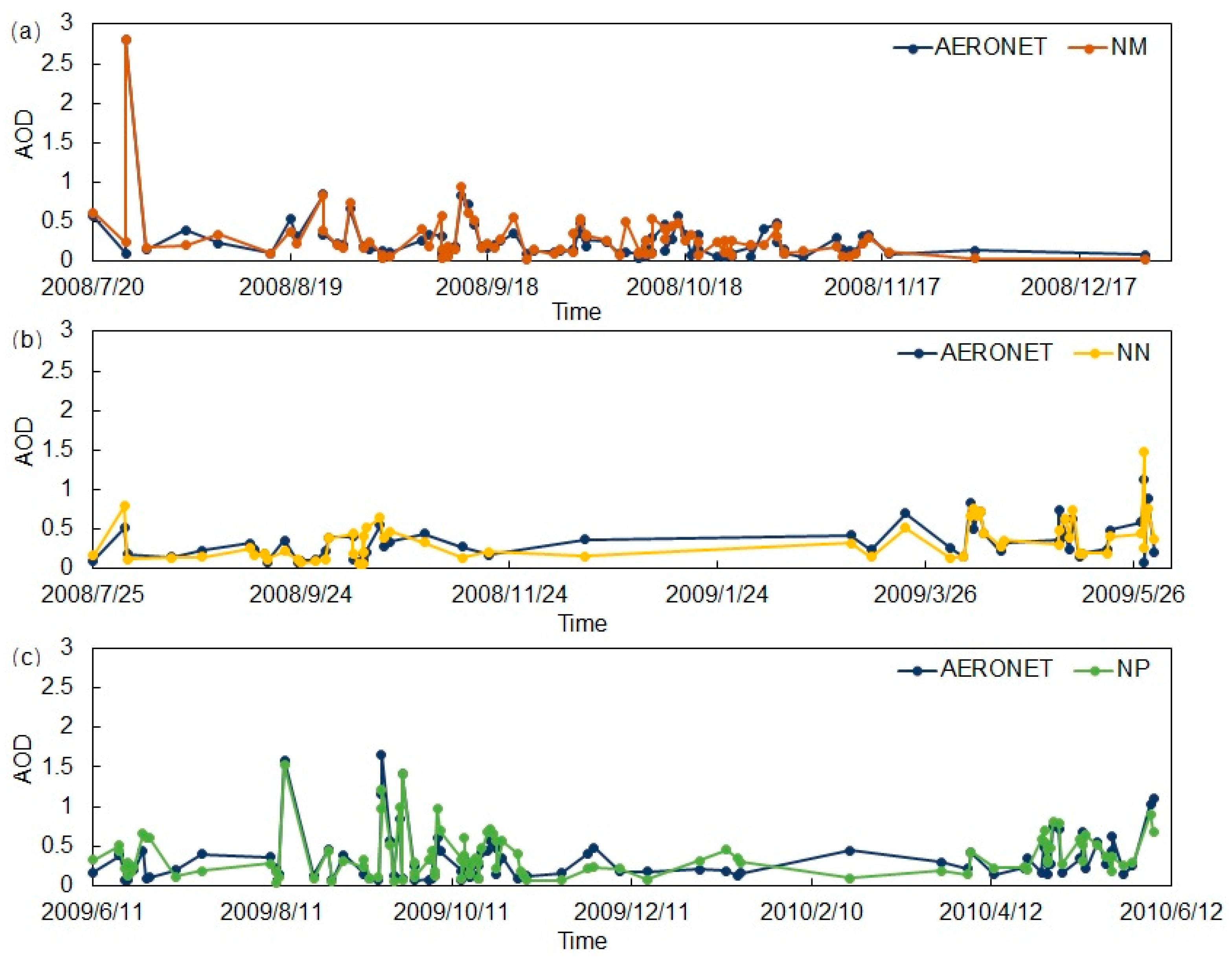
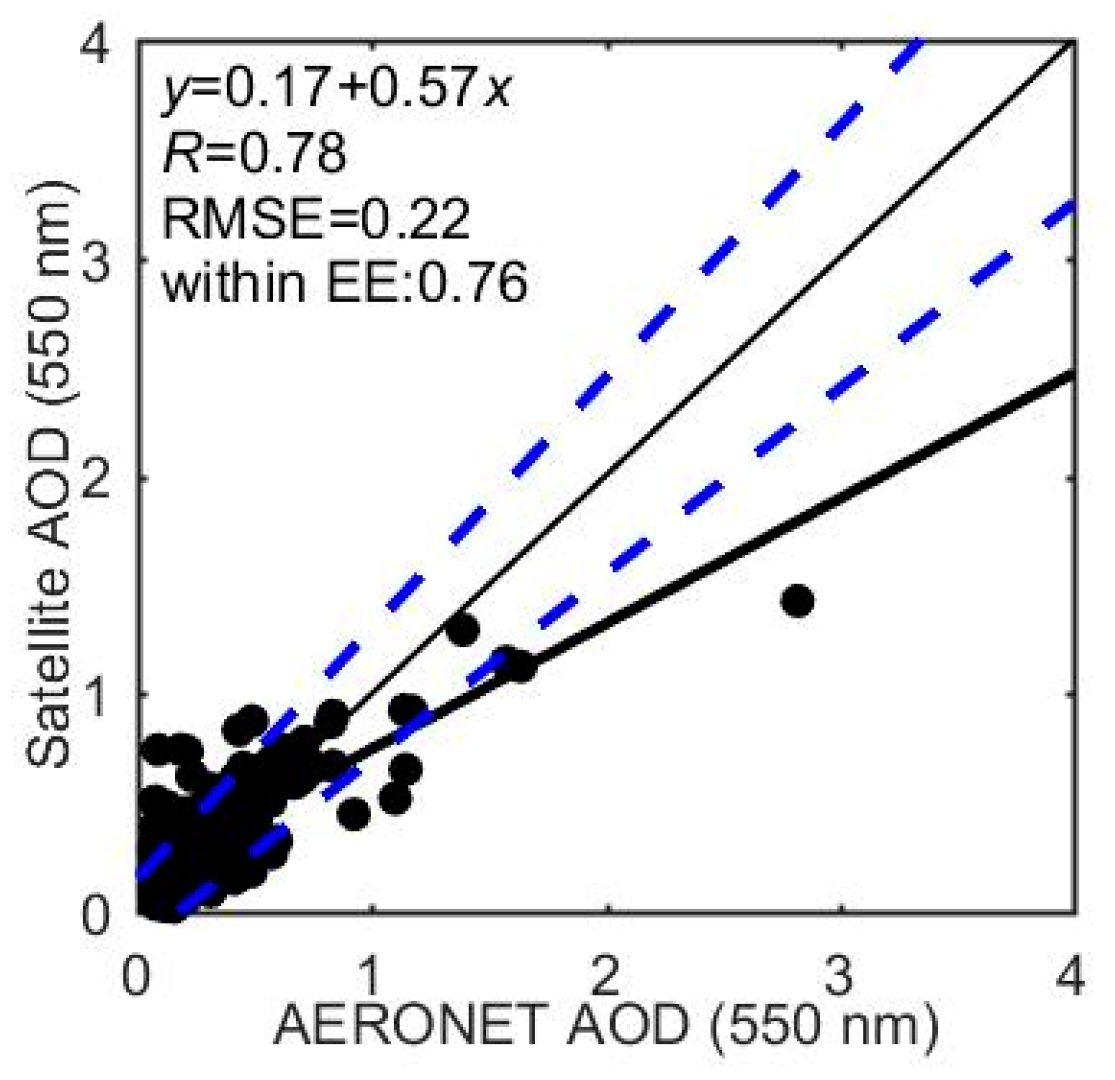
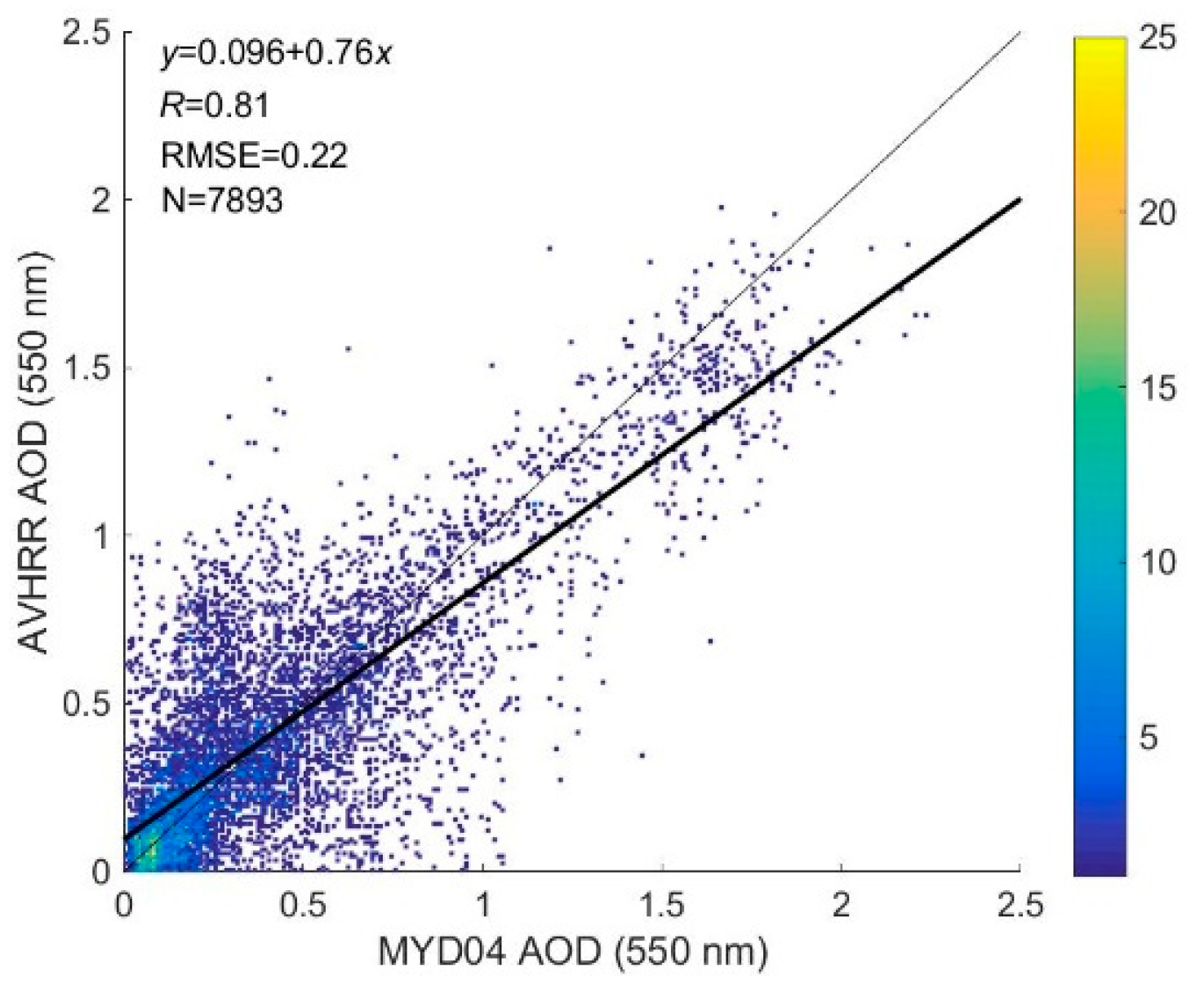
4.2. Comparison of the AOD Retrieval against the AERONET and MODIS Products
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Herman, B.M.; Browning, S.R. The effect of aerosols on the Earth-atmosphere albedo. J. Atmos. Sci. 1975, 32, 1430–1445. [Google Scholar] [CrossRef][Green Version]
- Haywood, J.M.; Ramaswamy, V.; Soden, B.J. Tropospheric aerosol climate forcing in clear-sky satellite observations over the oceans. Science 1999, 283, 1299–1303. [Google Scholar] [CrossRef]
- Hatzianastassiou, N.; Matsoukas, C.; Drakakis, E.; Stackhouse, P.W., Jr.; Koepke, P.; Fotiadi, A.; Pavlakis, K.G.; Vardavas, I. The direct effect of aerosols on solar radiation based on satellite observations, reanalysis datasets, and spectral aerosol optical properties from Global Aerosol Data Set (GADS). Atmos. Chem. Phys. 2007, 7, 2585–2599. [Google Scholar] [CrossRef]
- Xu, H.; Guo, J.P.; Ceamanos, X.; Roujean, J.L.; Min, M.; Carrer, D. On the influence of the diurnal variations of aerosol content to estimate direct aerosol radiative forcing using MODIS data. Atmos. Environ. 2016, 141, 186–196. [Google Scholar] [CrossRef]
- Kaufman, Y.J.; Tanré, D.; Boucher, O. A satellite view of aerosols in the climate system. Nature 2002, 419, 215–223. [Google Scholar] [CrossRef]
- Fan, J.; Leung, L.R.; Li, Z.; Morrison, H.; Chen, H.; Zhou, Y.; Qian, Y.; Wang, Y. Aerosol impacts on clouds and precipitation in eastern China: Results from bin and bulk microphysics. J. Geophys. Res. 2012, 117, D00K36. [Google Scholar] [CrossRef]
- Boucher, O.; Randall, D.; Artaxo, P.; Bretherton, C.; Feingold, G.; Forster, P.; Kerminen, V.-M.; Kondo, Y.; Liao, H.; Lohmann, U.; et al. IPCC AR5 (2013) Chapter 7: Clouds and Aerosols. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Wang, F.; Guo, J.; Zhang, J.; Huang, J.; Min, M.; Chen, T.; Liu, H.; Deng, M.; Li, X. Multi-sensor quantification of aerosol-induced variability in warm cloud properties over eastern China. Atmos. Environ. 2015, 113, 1–9. [Google Scholar] [CrossRef]
- Guo, J.; Deng, M.; Lee, S.S.; Wang, F.; Li, Z.; Zhai, P.; Liu, H.; Lv, W.; Yao, W.; Li, X. Delaying precipitation and lightning by air pollution over the Pearl River Delta. Part I: Observational analyses. J. Geophys. Res. Atmos. 2016, 121, 6472–6488. [Google Scholar] [CrossRef]
- Guo, J.; Liu, H.; Li, Z.; Rosenfeld, D.; Jiang, M.; Xu, W.; Jiang, J.H.; He, J.; Chen, D.; Min, M.; et al. Aerosol-induced changes in the vertical structure of precipitation: A perspective of TRMM precipitation radar. Atmos. Chem. Phys. 2018, 18, 13329–13343. [Google Scholar] [CrossRef]
- Li, Z.; Lau, W.K.-M.; Ramanathan, V.; Wu, G.; Ding, Y.; Manoj, M.G.; Liu, J.; Qian, Y.; Li, J.; Zhou, T.; et al. Aerosol and Monsoon Climate Interactions over Asia. Rev. Geophys. 2016, 54, 866–929. [Google Scholar] [CrossRef]
- Petrenko, M.; Kahn, R.; Chin, M.; Soja, A.; Kucsera, T.; Harshvardhan. The use of satellite-measured aerosol optical depth to constrain biomass burning emissions source strength in the global model GOCART. J. Geophys. Res. 2012, 117, D18212. [Google Scholar] [CrossRef]
- Guo, J.P.; Zhang, X.Y.; Wu, Y.R.; Zhaxi, Y.; Che, H.Z.; La, B.; Wang, W.; Li, X.W. Spatio-temporal variation trends of satellite-based aerosol optical depth in China during 1980–2008. Atmos. Environ. 2011, 45, 6802–6811. [Google Scholar] [CrossRef]
- De Leeuw, G.; Sogacheva, L.; Rodriguez, E.; Kourtidis, K.; Georgoulias, A.K.; Alexandri, G.; Amiridis, V.; Proestakis, E.; Marinou, E.; Xue, Y.; et al. Two decades of satellite observations of AOD over mainland China using ATSR-2, AATSR and MODIS/Terra: Data set evaluation and large-scale patterns. Atmos. Chem. Phys. 2018, 18, 1573–1592. [Google Scholar] [CrossRef]
- Holben, B.N.; Eck, T.F.; Slutsker, I.; Tanré, D.; Buis, J.P.; Setzer, A.W.; Vermote, E.F.; Reagan, J.A.; Kaufman, Y.J.; Nakajima, T.; et al. AERONET—A federated instrument network and data archive for aerosol characterization. Remote Sens. Environ. 1998, 66, 1–16. [Google Scholar] [CrossRef]
- Nakajima, T.; Higurashi, A. AVHRR remote sensing of aerosol optical properties in the Persian Gulf region, summer 1991. J. Geophys. Res. 1997, 102, 16935–16946. [Google Scholar] [CrossRef]
- Higurashi, A.; Nakajima, T. Development of a Two-Channel Aerosol Retrieval Algorithm on a Global Scale Using NOAA AVHRR. J. Atmos. Sci. 1999, 56, 924–941. [Google Scholar] [CrossRef]
- Knapp, K.R.; Stowe, L.L. Evaluating the potential for retrieving aerosol optical depth over land from AVHRR Pathfinder Atmosphere data. J. Atmos. Sci. 2002, 59, 279–293. [Google Scholar] [CrossRef]
- Hauser, A.; Oesch, D.; Foppa, N.; Wunderle, S. NOAA AVHRR derived aerosol optical depth over land. J. Geophys. Res. 2005, 110, D08204. [Google Scholar] [CrossRef]
- Riffler, M.; Popp, C.; Hauser, A.; Fontana, F.; Wunderle, S. Validation of a modified AVHRR aerosol optical depth retrieval algorithm over Central Europe. Atmos. Meas. Tech. 2010, 3, 1255–1270. [Google Scholar] [CrossRef]
- Mei, L.; Xue, Y.; Kokhanovsky, A.A.; von Hoyningen-Huene, W.; de Leeuw, G.; Burrows, J.P. Retrieval of aerosol optical depth over land surfaces from AVHRR data. Atmos. Meas. Tech. 2014, 7, 2411–2420. [Google Scholar] [CrossRef]
- Hsu, N.C.; Lee, J.; Sayer, A.M.; Carletta, N.; Chen, S.-H.; Tucker, C.J.; Holben, B.N.; Tsay, S.-C. Retrieving near-global aerosol loading over land and ocean from AVHRR. J. Geophys. Res. Atmos. 2017, 122, 9968–9989. [Google Scholar] [CrossRef]
- Husar, R.B.; Prospero, J.M.; Stowe, L.L. Characterization of tropospheric aerosols over the oceans with the NOAA advanced very high resolution radiometer optical thickness operational product. J. Geophys. Res. 1997, 102, 16889–16909. [Google Scholar] [CrossRef]
- King, M.D.; Kaufman, Y.J.; Tanré, D.; Nakajima, T. Remote sensing of tropospheric aerosols from space: Past, present and future. B. Am. Meteorol. Soc. 1999, 80, 2229–2259. [Google Scholar] [CrossRef]
- Stowe, L.L.; Carey, R.M.; Pellegrino, P.P. Monitoring the Mt. Pinatubo aerosol layer with NOAA/11 AVHRR data. Geophys. Res. Lett. 1992, 19, 159–162. [Google Scholar] [CrossRef]
- Durkee, P.A.; Pfeil, F.; Frost, E.; Shema, R. Global analysis of aerosol particle characteristics. Atmos. Environ. 1991, 25, 2457–2471. [Google Scholar] [CrossRef]
- Ignatov, A.M.; Stowe, L.L.; Sakerin, S.M.; Korotaev, G. Validation of NOAA/NESDIS satellite aerosol product over the North Atlantic in 1989. J. Geophys. Res. 1995, 100, 5123–5132. [Google Scholar] [CrossRef]
- Ignatov, A.M.; Stowe, L.L.; Singh, R.; Sakerin, S.; Kabanov, D.; Dergileva, I. Validation of NOAA/AVHRR aerosol retrievals using sunphotometer measurements from R/V Akademik Vernadsky in 1991. Adv. Space Res. 1995, 16, 95–98. [Google Scholar] [CrossRef]
- Geogdzhayev, I.V.; Mishchenko, M.I. Sensitivity analysis of aerosol retrieval algorithms using two-channel satellite radiance data. Proc. SPIE 1999, 3763, 155–168. [Google Scholar]
- Fraser, R.S.; Kaufman, Y.J.; Mahoney, R.L. Satellite measurements of aerosol mass and transport. Atmos. Environ. 1984, 18, 2577–2584. [Google Scholar] [CrossRef]
- Kaufman, Y.J.; Fraser, R.S.; Ferrare, R.A. Satellite measurements of large-scale air pollution: Method. J. Geophys. Res. 1990, 95, 9895–9909. [Google Scholar] [CrossRef]
- Price, J.C. Timing of NOAA afternoon passes. Int. J. Remote Sens. 1991, 12, 193–198. [Google Scholar] [CrossRef]
- Kaufmann, R.K.; Zhou, L.; Knyazikhin, Y.; Shabanov, V.; Myneni, R.B.; Tucker, C.J. Effect of orbital drift and sensor changes on the time series of AVHRR vegetation index data. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2584–2597. [Google Scholar]
- Devasthale, A.; Karlsson, K.-G.; Quaas, J.; Grassl, H. Correcting orbital drift signal in the time series of AVHRR derived convective cloud fraction using rotated empirical orthogonal function. Atmos. Meas. Tech. 2012, 5, 267–273. [Google Scholar] [CrossRef]
- McGregor, J.; Gorman, A.J. Some considerations for using AVHRR data in climatological studies: 1. Orbital characteristics of NOAA satellites. Int. J. Remote Sens. 1994, 15, 537–548. [Google Scholar] [CrossRef]
- Gleason, A.C.R.; Prince, S.D.; Goetz, S.J.; Small, J. Effects of orbital drift on land surface temperature measured by AVHRR thermal sensors. Remote Sens. Environ. 2002, 79, 147–165. [Google Scholar] [CrossRef]
- Heidinger, A.K.; Straka III, W.C.; Molling, C.C.; Sullivan, J.T.; Wu, X. Deriving an inter-sensor consistent calibration for the AVHRR solar reflectance data record. Int. J. Remote Sens. 2010, 31, 6493–6517. [Google Scholar] [CrossRef]
- Molling, C.C.; Heidinger, A.K.; Straka, W.C., III; Wu, X. Calibrations for AVHRR channels 1 and 2: Review and path towards consensus. Int. J. Remote Sens. 2010, 31, 6519–6540. [Google Scholar] [CrossRef]
- Stowe, L.L.; Davis, P.A.; Mcclain, E.P. Scientific Basis and Initial Evaluation of the CLAVR-1 Global Clear/Cloud Classification Algorithm for the Advanced Very High Resolution Radiometer. J. Atmos. Ocean Tech. 1999, 16, 656–681. [Google Scholar] [CrossRef]
- NOAA/NESDIS/OSDPD/SSD, IMS Daily Northern Hemisphere Snow and Ice Analysis at 4 km and 24 km Resolution, Global Snow and Ice Map Datasets; National Snow and Ice Data Center: Boulder, CO, USA, 2004.
- Vermote, E.F.; Tanré, D.; Deuzé, J.L.; Herman, M.; Morcrettte, J.-J. Second Simulation of the Satellite Signals in the Solar Spectrum, 6S: An Overview. IEEE Trans. Geosci. Remote Sens. 1997, 35, 675–686. [Google Scholar] [CrossRef]
- Dubovik, O.; King, M.D. A flexible inversion algorithm for retrieval of aerosol optical properties from Sun and sky radiance measurements. J. Geophys. Res. 2000, 105, 20673–20696. [Google Scholar] [CrossRef]
- Chu, D.A.; Kaufman, Y.J.; Ichoku, C.; Remer, L.A.; Tanré, D.; Holben, B.N. Validation of MODIS aerosol optical depth retrieval over land. Geophys. Res. Lett. 2002, 29. [Google Scholar] [CrossRef]
- Ichoku, C.; Chu, D.A.; Mattoo, S.; Kaufman, Y.J.; Remer, L.A.; Tanré, D.; Slutsker, I.; Holben, B.N. A spatio-temporal approach for global validation and analysis of MODIS aerosol products. Geophys. Res. Lett. 2002, 29. [Google Scholar] [CrossRef]
- Flowerdew, R.J.; Haigh, J.D. An approximation to improve accuracy in the derivation of surface reflectances from multi-look satellite radiometers. Geophys. Res. Lett. 1995, 22, 1693–1696. [Google Scholar] [CrossRef]
- North, P.R.J.; Briggs, S.A.; Plummer, S.E.; Settle, J.J. Retrieval of land surface bi-directional reflectance and aerosol opacity from ATSR-2 multi-angle imagery. IEEE Trans. Geosci. Remote Sens. 1999, 37, 526–537. [Google Scholar] [CrossRef]
- Vermote, E.; Justice, C.O.; Bréon, F.-M. Towards a Generalized Approach for Correction of the BRDF Effect in MODIS Directional Reflectances. IEEE Trans. Geosci. Remote Sens. 2009, 47, 898–908. [Google Scholar] [CrossRef]
- Veefkind, J.P.; de Leeuw, G.; Durkee, P.A.; Russell, P.B.; Hobbs, P.V.; Livingston, J.M. Aerosol optical depth retrieval using ATSR-2 and AVHRR data during TARFOX. J. Geophys. Res. 1999, 104, 2253–2260. [Google Scholar] [CrossRef]
- Tang, J.; Xue, Y.; Yu, T.; Guan, Y. Aerosol optical thickness determination by exploiting the synergy of TERRA and AQUA MODIS. Remote Sens. Environ. 2005, 94, 327–334. [Google Scholar] [CrossRef]
- Rahman, H.; Pinty, B.; Verstraete, M.M. Coupled Surface-Atmosphere Reflectance (CSAR) Model 2. Semiempirical Surface Model Usable with NOAA Advanced Very High Resolution Radiometer Data. J. Geophys. Res. 1993, 98, 20791–20801. [Google Scholar] [CrossRef]
- Kimes, D.; Newcomb, W.; Tucker, C.; Zonneveld, I.; Van Wijngaarden, W.; de Leeuw, J.; Epema, G. Directional reflectance factor distributions for cover types of northern Africa. Remote Sens. Environ. 1985, 18, 1–19. [Google Scholar] [CrossRef]
- Knapp, K.R.; Frouin, R.; Kondragunta, S.; Prados, A. Toward aerosol optical depth retrievals over land from GOES visible radiances: Determining surface reflectance. Int. J. Remote Sens. 2005, 26, 4097–4116. [Google Scholar] [CrossRef]
- Knapp, K.R.; Vonder Haar, T.H.; Kaufman, Y.J. Aerosol optical depth retrieval from GOES-8: Uncertainty study and retrieval validation over South America. J. Geophys. Res. 2002, 107. [Google Scholar] [CrossRef]
- Mei, L.; Xue, Y.; de Leeuw, G.; Holzer-Popp, T.; Guang, J.; Li, Y.; Yang, L.; Xu, H.; Xu, X.; Li, C.; et al. Retrieval of aerosol optical depth over land based on a time series technique using MSG/SEVIRI data. Atmos. Chem. Phys. 2012, 12, 9167–9185. [Google Scholar] [CrossRef]
- Li, Y.; Xue, Y.; de Leeuw, G.; Li, C.; Yang, L.; Hou, T.; Marir, F. Retrieval of aerosol optical depth and surface reflectance over land from NOAA AVHRR data. Remote Sens. Environ. 2013, 133, 1–20. [Google Scholar] [CrossRef]
- Lee, K.H.; Kim, Y.J. Satellite remote sensing of Asian aerosols: A case study of clean, polluted, and Asian dust storm days. Atmos. Meas. Tech. 2010, 3, 1771–1784. [Google Scholar] [CrossRef]
- Ignatov, A.; Stowe, L. Physical basis, premises, and self-consistency checks of aerosol retrievals from TRMM VIRS. J. Appl. Meteorol. 2000, 39, 2259–2277. [Google Scholar] [CrossRef]
- Zhao, T.X.-P.; Stowe, L.L.; Smirnov, A.; Crosby, D.; Sapper, J.; McClain, C.R. Development of a global validation package for satellite oceanic aerosol optical thickness retrieval based on AERONET observations and its application to NOAA/NESDIS operational aerosol retrievals. J. Atmos. Sci. 2002, 59, 294–312. [Google Scholar] [CrossRef]
- Zhao, T.X.-P.; Dubovik, O.; Smirnov, A.; Holben, B.N.; Sapper, J.; Pietras, C.; Voss, K.J.; Frouin, R. Regional evaluation of an advanced very high resolution radiometer (AVHRR) two-channel aerosol retrieval algorithm. J. Geophys. Res. 2004, 109, D02204. [Google Scholar] [CrossRef]
- Popp, C.; Hauser, A.; Foppa, N.; Wunderle, S. Remote sensing of aerosol optical depth over central Europe from MSG-SEVIRI data and accuracy assessment with ground-based AERONET measurements. J. Geophys. Res. 2007, 112, D24S11. [Google Scholar] [CrossRef]
- Li, X.; Wang, J.; Ni, W.; Strahler, A.H.; Woodcock, C. Simulation of path scattering and multiple bounces of photons between two media. Sci. China Ser. E 1996, 26, 457–466. (In Chinese) [Google Scholar]
- Yang, L.; Xue, Y.; Jie, G.; Kazemian, H.; Zhang, J.; Li, C. Improved aerosol optical depth and Ångstrom exponent retrieval over land from MODIS based on the non-lambertian forward model. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1629–1633. [Google Scholar] [CrossRef]


| Wavelength (μm) | a | b | c | |||
|---|---|---|---|---|---|---|
| AVHRR | MODIS | AVHRR | MODIS | AVHRR | MODIS | |
| 0.63 | −5.5424 | −5.7389 | 0.9083 | 0.9255 | −0.0419 | −0.0188 |
| 0.85 | −2.4187 | −5.3296 | 0.4995 | 0.8246 | −0.0248 | −0.0277 |
| Name | Longitude (°) | Latitude (°) | Elevation (m) | Characteristic |
|---|---|---|---|---|
| Beijing | 116.38 | 39.98 | 92 | urban |
| Ussuriysk | 132.16 | 43.7 | 280 | suburban, forest |
| EPA-NCU | 121.19 | 24.97 | 144 | urban, near shrubland |
| Gwangju_GIST | 126.84 | 35.23 | 52 | suburban, sparse vegetation |
| XiangHe | 116.96 | 39.75 | 36 | agricultural, rainfed croplands, suburban |
| Xinglong | 117.58 | 40.4 | 970 | forest |
| Variable Name | No. of Entries | Entries |
|---|---|---|
| Wavelength (μm) | 2 | 0.63, 0.85 |
| Solar zenith angle (°) | 8 | 0, 12, 24, 36, 48, 54, 60, 66 |
| Satellite zenith angle (°) | 11 | 0, 8, 14, 20, 24, 30, 36, 42, 48, 54, 60 |
| Relative azimuth angle (°) | 15 | 0, 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, 132, 144, 160, 180 |
| AOD | 5 | 0.0001, 0.25, 0.5, 1.0, 2.0, 3.0, 4.0 |
| Surface reflectance | 7 | 0.01, 0.12, 0.15, 0.18, 0.23, 0.34, 0.45 |
| Aerosol model | 6 | from [55] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Gu, X.; Li, J.; Mi, X. A Dual-Channel Aerosol Optical Depth Retrieval Algorithm Incorporating the BRDF Effect from AVHRR over Eastern Asia. Remote Sens. 2021, 13, 365. https://doi.org/10.3390/rs13030365
Wang Y, Gu X, Li J, Mi X. A Dual-Channel Aerosol Optical Depth Retrieval Algorithm Incorporating the BRDF Effect from AVHRR over Eastern Asia. Remote Sensing. 2021; 13(3):365. https://doi.org/10.3390/rs13030365
Chicago/Turabian StyleWang, Ying, Xingfa Gu, Jian Li, and Xiaofei Mi. 2021. "A Dual-Channel Aerosol Optical Depth Retrieval Algorithm Incorporating the BRDF Effect from AVHRR over Eastern Asia" Remote Sensing 13, no. 3: 365. https://doi.org/10.3390/rs13030365
APA StyleWang, Y., Gu, X., Li, J., & Mi, X. (2021). A Dual-Channel Aerosol Optical Depth Retrieval Algorithm Incorporating the BRDF Effect from AVHRR over Eastern Asia. Remote Sensing, 13(3), 365. https://doi.org/10.3390/rs13030365







