Identification of the Characteristic Scale of Fine Ground Objects: A Case Study of the Core Observation Area in the Middle Reaches of the Heihe River Basin
Abstract
1. Introduction
2. Materials and Preprocessing
2.1. Study Area and Data
2.2. Data Preprocessing
3. Methods
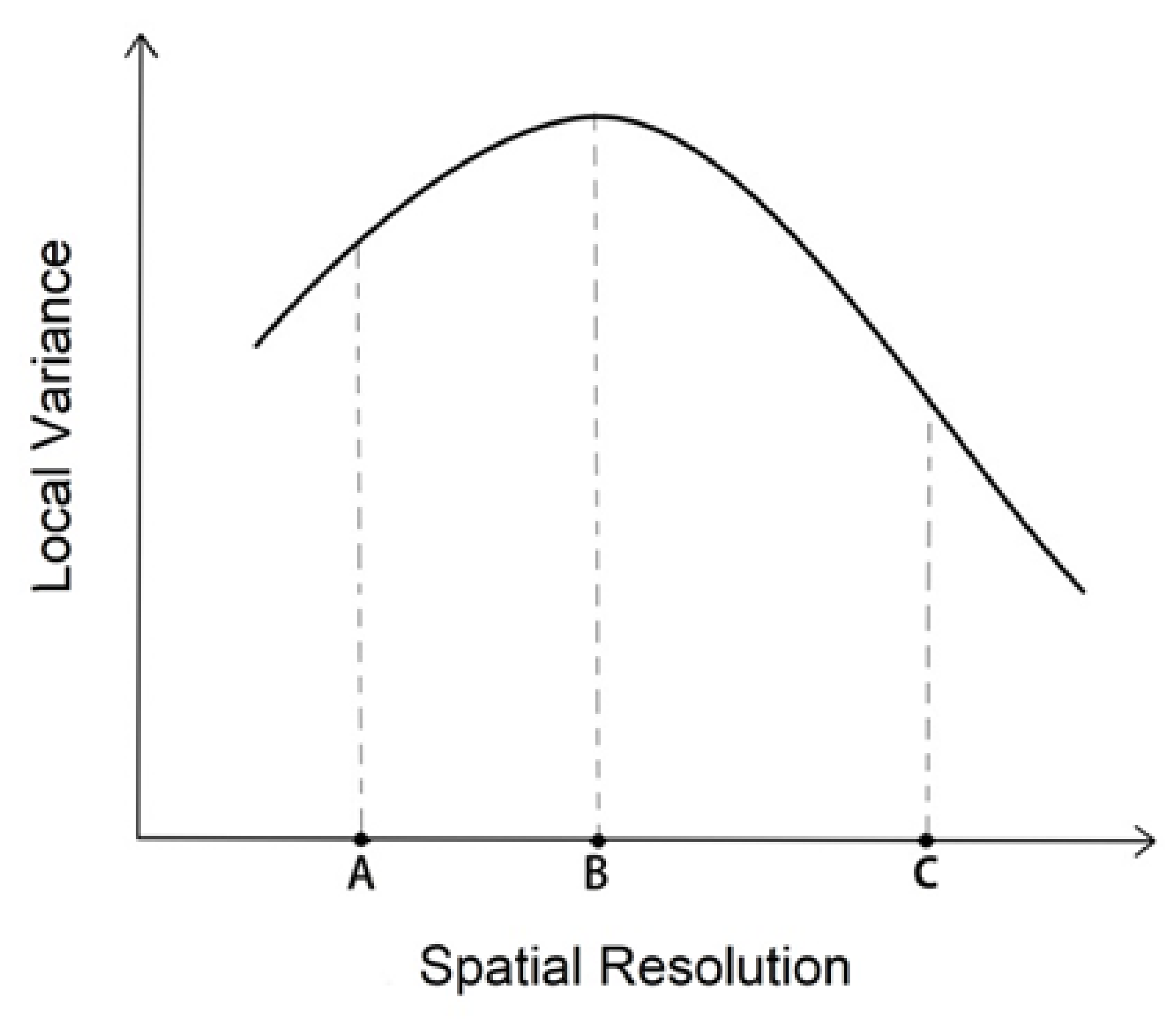
3.1. Local Variance Function
3.2. Semivariance Function
4. Results and Discussion
4.1. Analysis of the Sample Spatial Heterogeneity in a Small Research Area
- (1)
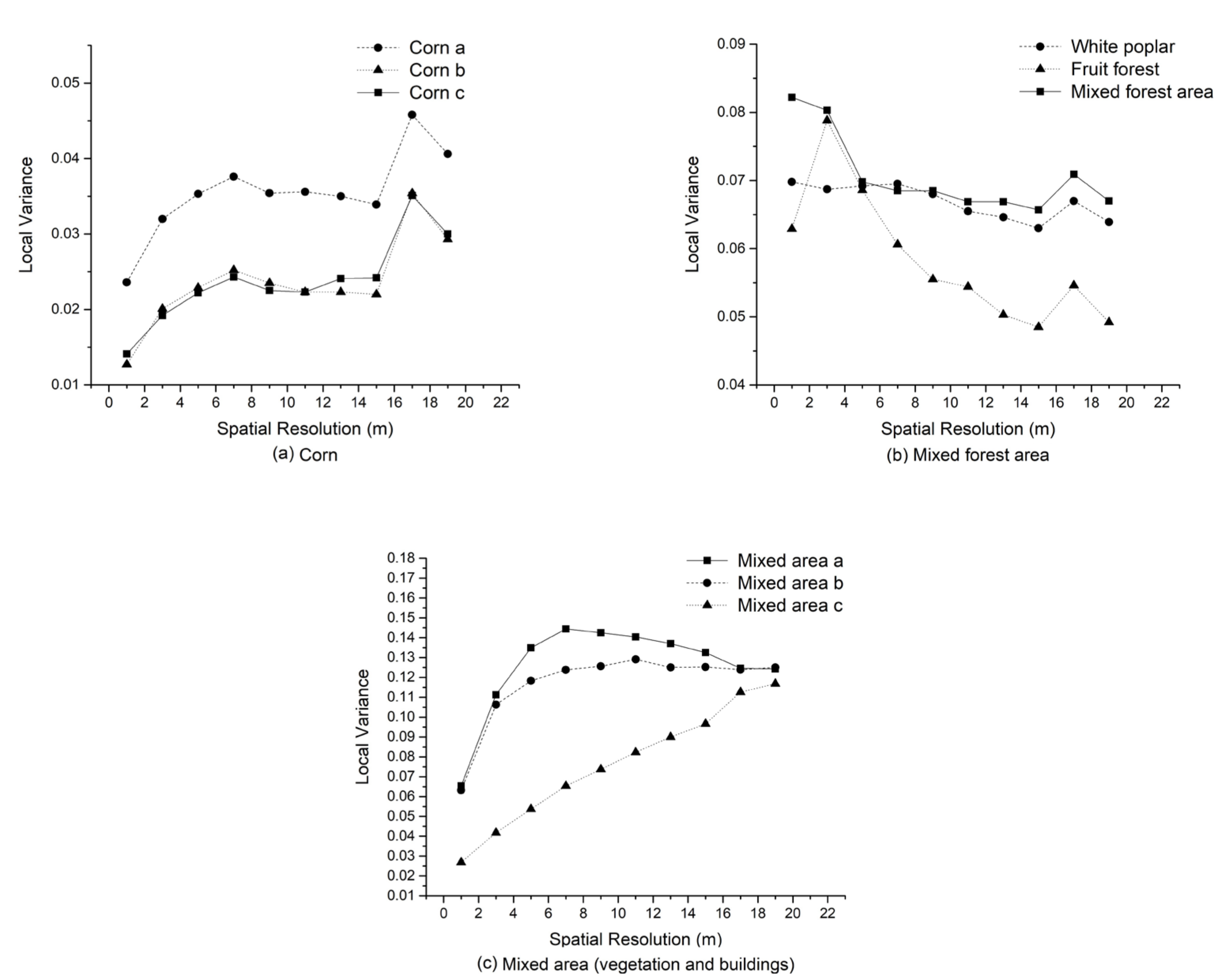
- As shown in Figure 6a, the local variances of the three samples of corn are lower (approximately 0.01–0.05) than those of the other objects. Although the local variance of corn sample a is obviously higher than that of the other two samples, the varying trends in the three local variances are consistent, which means that the overall spatial heterogeneity of this sample is much stronger, indicating that this corn field grows slightly unevenly. The local variances of the three samples are all low at the initial resolution and then increase gradually with increasing spatial resolution. This trend continues until a small peak is found at a spatial resolution of 7 m. When the spatial resolution changes from 7 m to 15 m, the local variances trend slightly downward. After this flat region, the local variances increase rapidly, and a new peak appears at a spatial resolution of 17 m. This peak is more noticeable than the first peak at 7 m. Different from the theoretical hypothesis, the local variance curve of pure corn has two peaks corresponding to two characteristic scales: 7 m and 17 m. A peak appeared in the local variance of 17 m, indicating that with the increase in the pixel size of the image, the target ground object of the study changed. The sample contains only corn class, and the fields are arranged in clumps. It maybe indicates that the feature type has changed from a small corn field to a large corn field.
- (2)
- The local variances of the forest areas are approximately 0.04–0.08. Figure 5e,f show that the spatial distribution of the white poplar, fruit forest, and mixed areas (vegetation and buildings) presents a regular row structure. However, the trends in the local variance of the three samples are distinctly different. As you can see in Figure 6b, the local variances of the white poplars decrease with the increasing resolution, and the curve changes slightly. It was originally assumed that the peak would appear when the resolution is close to the size of the objects. However, there was no obvious peak for white poplars. One possible reason is that the crown diameter of a single poplar tree is considerably smaller than the original fine resolution cells, and thus, the type of ground object studied shifted to the poplar forest rather than a single tree. Another probable cause is that this area is relatively flat, and the growth state of the forest is so homogeneous that there is not one size dominant enough to cause a peak. Thus, we can regard that the scale of the white poplars is approximately 1–7 m. The local variance of the fruit forest is lower at 1 m, but suddenly increases when the spatial resolution degrades to 3 m, resulting in a peak. As the resolution increases past the peak, the variance decreases sharply and shows no upward trend. Naturally, the scale of the fruit forest is approximately 3 m. Unlike white poplar trees, the canopy diameter of a single fruit tree is large, so the tree can be detected by a local variance graph. The mixed forest area encompasses several different sizes of vegetation. The curve starts with a high local variance at 1–3 m, and the local variance goes down rapidly between a resolution of 3 m and 5 m. Finally, the curve shows a gentle downward trend. The peak of this mixed area is considered to be 1–3 m, that is, the scale of the feature.
- (3)
- For the vegetation and building mixed area, the local variance of the three types of samples is approximately 0.02–0.16 in Figure 6c. The local variance curves of mixed areas A and B are more similar than those of a/c and b/c. With the increase in resolution, the local variances for these areas first increase and then decline. Therefore, the scales of the two samples are 7 m and 11 m, respectively. However, the local variances of mixed area C continuously increase as the resolution increases. The lack of a definite peak implies that there is not a distinct object that dominates the scene due to the limitation of the research range. The scale of the sample is not within the range of 1 m to 19 m. As mentioned earlier, image degradation will lead to a reduction in the number of pixels in the image, while local variance analysis requires a lower limit of the number. Therefore, the scope of research will be restricted to a certain extent. If the range of the study area can subsequently be extended and the pixel of the downsampled image is coarser, a peak value may be obtained.
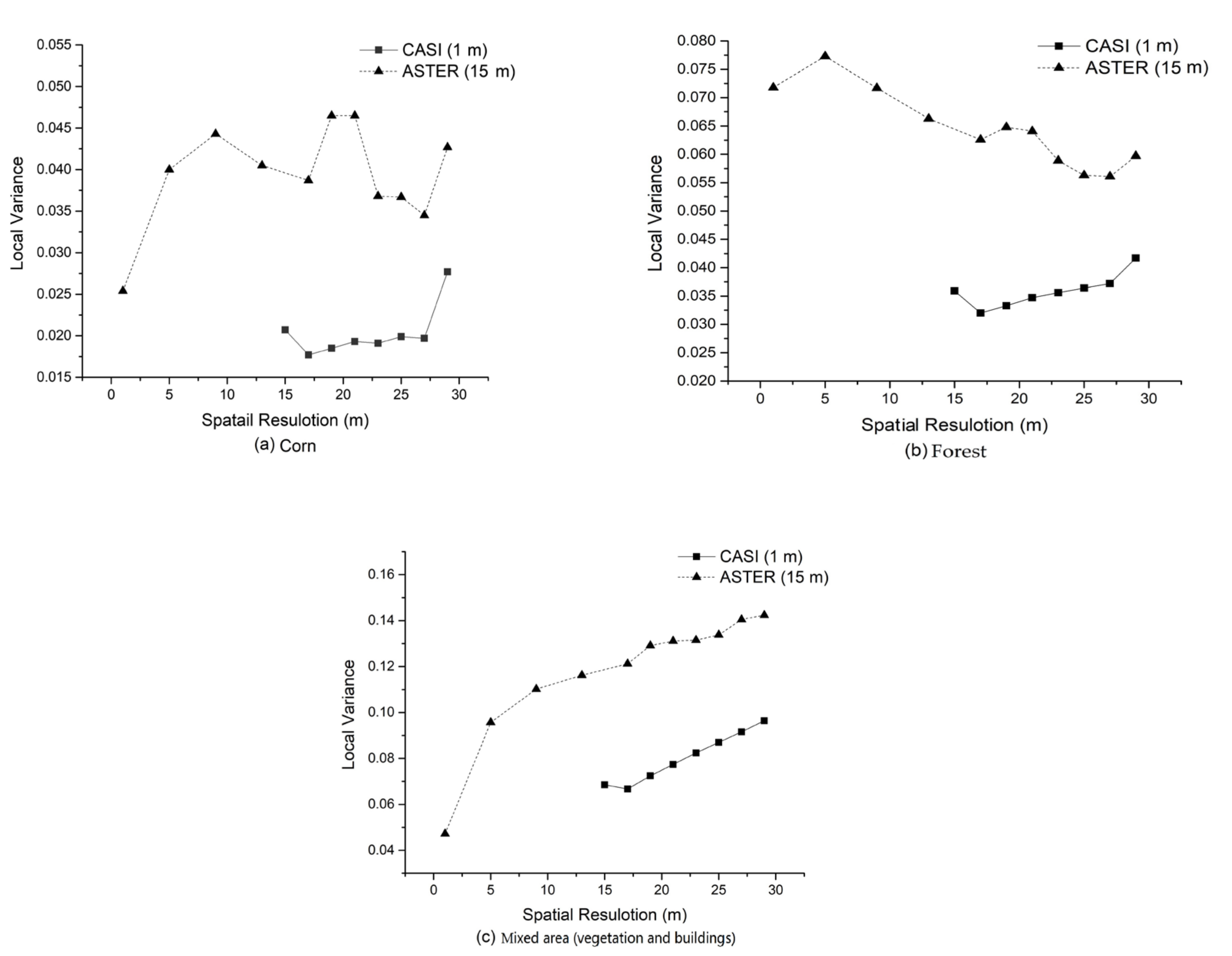
4.2. Analysis of the Heterogeneity on the Scale of Expanded Research
5. Conclusions
- (1).
- In nature, ground objects have multi-hierarchical structures. The research scale determines the type of ground objects to be detected. In this research, the spatial heterogeneity of corn is the lowest, followed by that of the forest and mixed areas (vegetation and buildings). The corn field has scales of 7 m and 20 m. A single white poplar is taken as the studied object with a scale of 1–7 m. If the studied object has shifted into blocks, its scale becomes 120–170 m. For the fruit trees, the crown diameters are relatively large. As seen from the 1 m high-resolution remote sensing image, the distance between single fruit trees also spans several pixels in the image. In our study, the studied object always corresponds to a single fruit tree, and the only scale is 3 m. For the mixed forest area, the scale of the local variance analysis is 1–5 m and that of the semivariance analysis is 25–40 m. For the mixed area (vegetation and buildings), the degree of spatial heterogeneity is the largest. Different samples have different characteristic scales, which need to be analyzed according to the specific features contained. It is also found that with the expansion of the research scope, the scales of all studied objects have increased to varying degrees. As the pixel resolution gets coarser, if the scale of some fine objects is smaller than the pixel resolution, their spatial structure cannot be detected, but the spatial distribution information of larger target features can be obtained. This is also one of the evidences of the existence of multi-scale structure of surface features, that is, the results of the research problems will change with the changes of scales.
- (2).
- Local variance analysis derived from the 15 m ASTER NDVI image barely detected the scale. This phenomenon might be caused by the fact that the scale of the ground object was not within the resolution range of the experimental image. Local variance analysis is not suitable for low or medium spatial-resolution remote sensing images as the basis image. If the scale of the research object itself is less than 15 m, the local variance method based on the original image with medium or low resolution cannot detect the scale of the object. For the semivariance analysis, regardless of the scale of the remote sensing data, a corresponding variation value will be given. Therefore, the 15 m ASTER NDVI image can be used in a semivariance analysis. However, does the range value necessarily represent the size of the sample? It is obvious that this range is meaningless for complex samples that contain more than one feature. There is no unified characteristic scale for mixed ground objects. Researchers need to determine the characteristic value according to the specific type and distribution of surface features contained in the sample. Relevant research has found that the global variation in complex images is often greater than that of individual ground object classes in the images [66].
- (3).
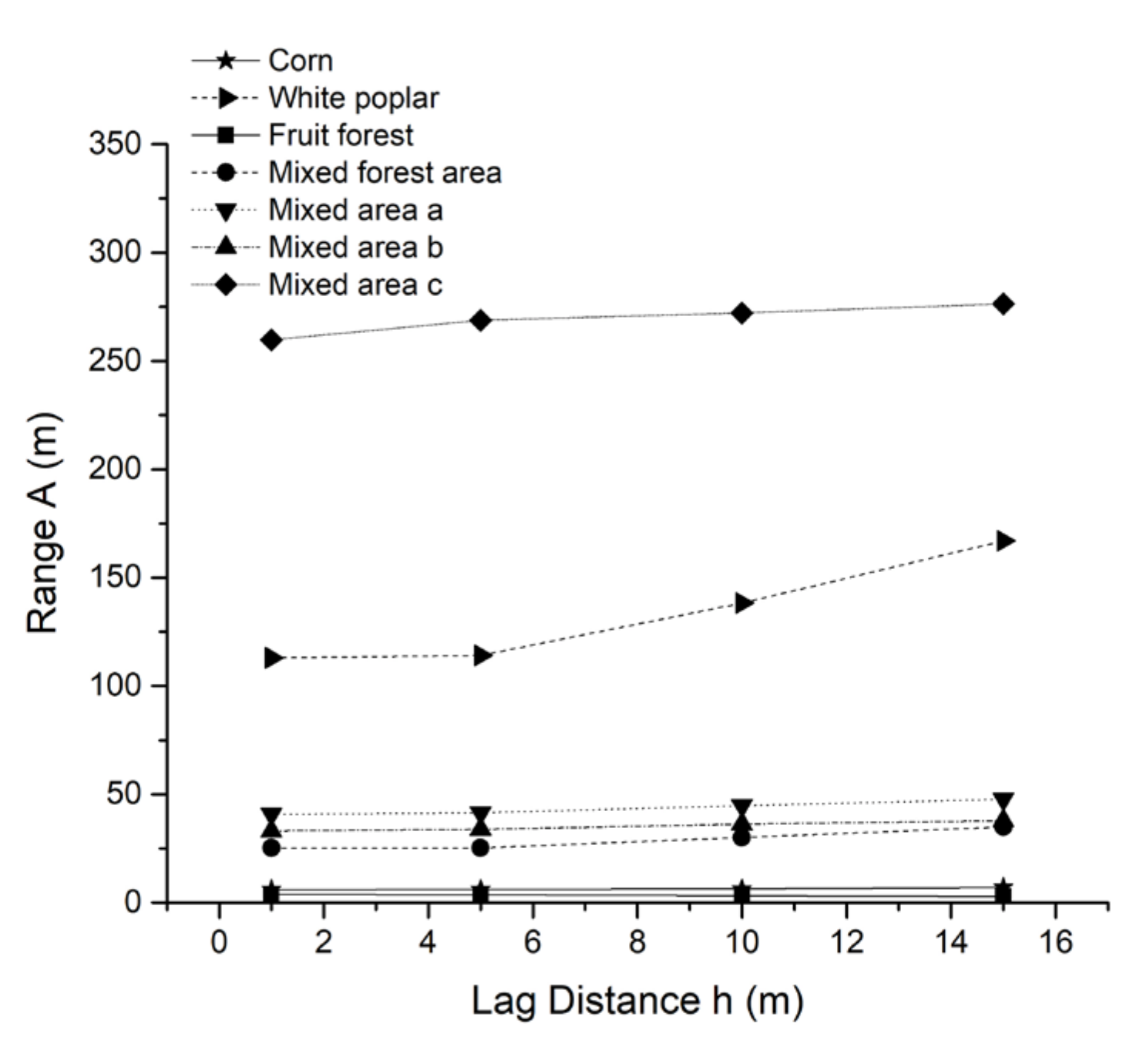
- Both local variance analysis and semivariance analysis can be used for spatial heterogeneity analysis and characteristic scale extraction. For a single object of identifiable size, the scale results obtained by the two methods are relatively consistent. The scale obtained by the local variance analysis is relatively small. It indicates that the target size identified by local variance is smaller. For example, the local variance of mixed forestland is 1–5 m, while the semivariance is 25–40 m. Nevertheless, for an object of indistinguishable size or continuous distribution, the scales obtained by the two methods are different. Local variance and semivariance are similar in mechanism and are maneuverable to facilitate researchers to quickly select the appropriate spatial resolution of remote sensing data according to the research area. However, compared with the local variance method, the semivariance method does not need to gradually reduce the resolution of the image; instead, the different values of the lag distance or separation distance of only one image need to be set. It can reduce the complexity of the experiment. In this study, the local variance analysis took 2 m as the sampling interval, so the obtained scale had an error of ±1 m. When a peak does not appear in the local variance curve, it is difficult to identify the corresponding scale. Due to the limited sample size and the limited resolution of the lower resolutions, the detection range is restricted. The semivariance analysis can obtain a corresponding range value of any image. Except for complicated samples, the obtained scale is not applicable. For pure fine features, this method is more efficient. In summary, the semivariance method has more advantages than the local variance method in the description of the overall spatial heterogeneity, the acquisition of multiscale levels, and the convenience of calculation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wu, J.; Vankat, J. A system dynamics model of island biogeography. Bull. Math. Biol. 1991, 53, 911–940. [Google Scholar] [CrossRef]
- Wu, J.; Loucks, O.L. From Balance of Nature to Hierarchical Patch Dynamics: A Paradigm Shift in Ecology. Q. Rev. Biol. 1995, 70, 439–466. [Google Scholar] [CrossRef]
- Legendre, P.; Fortin, M.J. Spatial pattern and ecological analysis. Vegetatio 1989, 80, 107–138. [Google Scholar] [CrossRef]
- Li, J.; Song, C.; Cao, L.; Zhu, F.; Meng, X.; Wu, J. Impacts of landscape structure on surface urban heat islands: A case study of Shanghai, China. Remote Sens. Environ. 2011, 115, 3249–3263. [Google Scholar] [CrossRef]
- Herold, M.; Woodcock, C.; Loveland, T.; Townshend, J.; Brady, M.; Steenmans, C.; Schmullius, C. Land-Cover Observations as Part of a Global Earth Observation System of Systems (GEOSS): Progress, Activities, and Prospects. IEEE Syst. J. 2008, 2, 414–423. [Google Scholar] [CrossRef]
- Pickett, S.T.A.; Cadenasso, M.L. Landscape Ecology: Spatial Heterogeneity in Ecological Systems. Science 1995, 269, 331–334. [Google Scholar] [CrossRef]
- Sadowski, F.G.; Malila, W.A.; Sarno, J.E.; Nalepka, R.F.J.R. The Influence of Multispectral Scanner Spatial Resolution on Forest Feature Classification. In Proceedings of the Eleventh International Symposium on Remote Sensing of Environment, Houston, TX, USA, 1 January 1977; Volume 2. [Google Scholar]
- Freek, V.D.M.; Bakker, W.; Scholte, K.; Skidmore, A.; De Jong, S.; Dorresteijn, M.; Clevers, J.; Epema, G.J.G.I. Scaling to the MERIS Resolution: Mapping Accuracy and Spatial Variability. Geocarto Int. 2000, 15, 39–50. [Google Scholar]
- Wu, J.; Shen, W.; Sun, W.; Tueller, P.T. Empirical patterns of the effects of changing scale on landscape metrics. Landsc. Ecol. 2002, 17, 761–782. [Google Scholar] [CrossRef]
- Drăgut, L.; Tiede, D.; Levick, S.R. ESP: A tool to estimate scale parameter for multiresolution image segmentation of remotely sensed data. Int. J. Geogr. Inf. Sci. 2010, 24, 859–871. [Google Scholar] [CrossRef]
- Lam, N.S.N.; Quattrochi, D.A. On the Issues of Scale, Resolution, and Fractal Analysis in the Mapping Sciences. Prof. Geogr. 1992, 44, 88–98. [Google Scholar] [CrossRef]
- Schneider, D.C. The Rise of the Concept of Scale in Ecology. BioScience 2001, 51, 545. [Google Scholar] [CrossRef]
- O’Neil, R.J.E.S. Homage to St. Michael: Or, Why Are There So Many Books on Scale? Columbia University Press: New York, NY, USA, 1998. [Google Scholar]
- McCarthy, A.J. The Irish National Electrification Scheme. Geographical Review. Geogr. Rev. 1957, 47, 539–554. [Google Scholar] [CrossRef]
- Weiss, M.; Baret, F.; Myneni, R.B.; Pragnère, A.; Knyazikhin, Y. Investigation of a model inversion technique to estimate canopy biophysical variables from spectral and directional reflectance data. Agronomie 2000, 20, 3–22. [Google Scholar] [CrossRef]
- Marceau, D.J. The Scale Issue in the Social and Natural Sciences. Can. J. Remote Sens. 1999, 25, 347–356. [Google Scholar] [CrossRef]
- Silvestri, S.; Marani, M.; Settle, J.; Benvenuto, F.; Marani, A. Salt marsh vegetation radiometry: Data analysis and scaling. Remote Sens. Environ. 2002, 80, 473–482. [Google Scholar] [CrossRef]
- Wu, J.; Jelinski, D.E.; Luck, M.; Tueller, P.T. Multiscale Analysis of Landscape Het-erogeneity: Scale Variance and Pattern Metrics. Geogr. Inf. Sci. 2000, 6, 6–19. [Google Scholar]
- Wiens, J.A. Spatial Scaling in Ecology. Funct. Ecol. 1989, 3, 385. [Google Scholar] [CrossRef]
- Li, H.; Reynolds, J.F. A Simulation Experiment to Quantify Spatial Heterogeneity in Categorical Maps. Ecology 1994, 75, 2446. [Google Scholar] [CrossRef]
- Bian, L.; Walsh, S.J. Scale Dependencies of Vegetation and Topography in a Moun-tainous Environment of Montana. Prof. Geogr. 1993, 45, 1–11. [Google Scholar] [CrossRef]
- Kotliar, N.B.; Wiens, J.A. Multiple Scales of Patchiness and Patch Structure: A Hierarchical Framework for the Study of Heterogeneity. Oikos 1990, 59, 253. [Google Scholar] [CrossRef]
- Wu, J. Hierarchy and Scaling: Extrapolating Information along a Scaling Ladder. Can. J. Remote Sens. 1999, 25, 367–380. [Google Scholar] [CrossRef]
- Seydi, S.T.; Hasanlou, M.; Amani, M. A New End-to-End Multi-Dimensional CNN Framework for Land Cover/Land Use Change Detection in Multi-Source Remote Sensing Datasets. Remote Sens. 2020, 12, 2010. [Google Scholar] [CrossRef]
- Goddijn-Murphy, L.; Williamson, B.J. On Thermal Infrared Remote Sensing of Plastic Pollution in Natural Waters. Remote Sens. 2019, 11, 2159. [Google Scholar] [CrossRef]
- Yang, X.; Xu, B.; Jin, Y.; Qin, Z.; Ma, H.; Li, J.; Zhao, F.; Chen, S.; Zhu, X. Remote sensing monitoring of grassland vegetation growth in the Beijing–Tianjin sandstorm source project area from 2000 to 2010. Ecol. Indic. 2015, 51, 244–251. [Google Scholar] [CrossRef]
- Justice, C.O.; Holben, B.N.; Gwynne, M.D. Monitoring East African vegetation using AVHRR data. Int. J. Remote Sens. 1986, 7, 1453–1474. [Google Scholar] [CrossRef]
- Costantini, M.L.; Zaccarelli, N.; Mandrone, S.; Rossi, D.; Calizza, E.; Rossi, L. NDVI spatial pattern and the potential fragility of mixed forested areas in vol-canic lake watershed. For. Ecol. Manag. 2012, 285, 133–141. [Google Scholar] [CrossRef]
- Balaguer-Beser, A.; Ruiz, L.A.; Hermosilla, T.; Recio, J.A. Using semivario-gram indices to analyse heterogeneity in spatial patterns in remotely sensed images. Comput. Geosci. 2013, 50, 115–127. [Google Scholar] [CrossRef]
- Zaccarelli, N.; Riitters, K.H.; Petrosillo, I.; Zurlini, G. Indicating disturbance content and context for preserved areas. Ecol. Indic. 2008, 8, 841–853. [Google Scholar] [CrossRef]
- Kolasa, J.; Pickett, S.T.A. Ecological Heterogeneity; Springer: New York, NY, USA, 1992; p. 86. [Google Scholar]
- Gustafson, E.J. Quantifying Landscape Spatial Pattern: What Is the State of the Art? Ecosystems 1998, 1, 143–156. [Google Scholar] [CrossRef]
- Read, J.M.; Lam, N.S.N. Spatial methods for characterising land cover and detecting land-cover changes for the tropics. Int. J. Remote Sens. 2002, 23, 2457–2474. [Google Scholar] [CrossRef]
- Sugihara, G.; May, R.M. Applications of fractals in ecology. Trends Ecol. Evol. 1990, 5, 79–86. [Google Scholar] [CrossRef]
- Atkinson, P.M.; Curran, P.J. Choosing an appropriate spatial resolution for remote sensing investigations. Photogramm. Eng. Remote Sens. 1997, 63, 1345–1351. [Google Scholar]
- Ming, D.P.; Wang, Q.; Yang, J.Y. Spatial Scale of Remote Sensing Image and Selection of Optimal Spatial Resolution. J. Remote Sens. 2008, 12, 529–537. [Google Scholar]
- Han, P.; Gong, J.Y.; Li, Z.L.; Bo, Y.C.; Cheng, L. Selection of optimal scale in re-motely sensed image classification. J. Remote Sens. 2010, 14, 507–518. [Google Scholar]
- Woodcock, C.E.; Strahler, A.H. The factor of scale in remote sensing. Remote Sens. Environ. 1987, 21, 311–332. [Google Scholar] [CrossRef]
- Webster, R. Quantitative Spatial Analysis of Soil in the Field; Springer: New York, NY, USA, 1985; pp. 1–70. [Google Scholar]
- Li, H.; Reynolds, J.F. On definition and quantification of heterogeneity. Oikos 1995, 73, 280–284. [Google Scholar] [CrossRef]
- Atkinson, P.M.; Tate, N.J. Spatial Scale Problems and Geostatistical Solutions: A Review. Prof. Geogr. 2000, 52, 607–623. [Google Scholar] [CrossRef]
- Sanderson, E.W.; Zhang, M.; Ustin, S.L.; Rejmankova, E. Geostatistical scaling of canopy water content in a California salt marsh. Landsc. Ecol. 1998, 13, 79–92. [Google Scholar] [CrossRef]
- Meisel, J.E.; Turner, M.G. Scale detection in real and artificial landscapes using semi-variance analysis. Landsc. Ecol. 1998, 13, 347–362. [Google Scholar] [CrossRef]
- Atkinson, P.M.; Curran, P. Defining an optimal size of support for remote sensing investigations. IEEE Trans. Geosci. Remote Sens. 1995, 33, 768–776. [Google Scholar] [CrossRef]
- Lathrop, R.G.; Pierce, L.L. Ground-based canopy transmittance and satellite remotely sensed measurements for estimation of coniferous forest canopy structure. Remote Sens. Environ. 1991, 36, 179–188. [Google Scholar] [CrossRef]
- Li, X.; Cheng, G.; Liu, S.; Xiao, Q.; Ma, M.; Jin, R.; Che, T.; Liu, Q.; Wang, W.; Qi, Y.; et al. Heihe Watershed Allied Telemetry Experimental Research (HiWATER): Scientific Objectives and Experimental Design. Bull. Am. Meteorol. Soc. 2013, 94, 1145–1160. [Google Scholar] [CrossRef]
- Hua, Z.; Bo, Z. Study of environment restoration after Water-distribution project in lower reaches of Heihe River. In Proceedings of the 2011 International Symposium on Water Resource and Environmental Protection, Xi’an, China, 20–22 May 2011. [Google Scholar]
- Li, X.; Liu, S.; Xiao, Q.; Ma, M.; Jin, R.; Che, T.; Wang, W.; Hu, X.; Xu, Z.; Wen, J.J.D. A multiscale dataset for understanding complex eco-hydrological processes in a heterogeneous oasis system. Sci. Data 2017, 4, 170083. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M. HiWATER: Land Cover Map in the Core Experimental Area of Flux Observation Matrix; National Tibetan Plateau Data Center: Beijing, China, 2017. [Google Scholar] [CrossRef]
- Zhihui, W.; Liangyun, L. Monitoring on Land Cover Pattern and Crops Structure of Oasis Irrigation Area of Middle Reaches in Heihe River Basin Using Remote Sensing Data. Earth Sci. 2013, 28, 948–956. [Google Scholar]
- Hu, S.S.; Zhang, L.F.; Zhang, X.; Wang, Q.; Han, B.; Zhang, N. Calculation and Reliability Analysis of Satellite Sensors Band Solar Irradiance. Remote Sens. Land Resour. 2012, 94, 97–102. [Google Scholar]
- Smith, M.S. How to Convert ASTER Radiance Values to Reflectance. An Online Guide; University Idaho: Moscow, ID, USA, 2007. [Google Scholar]
- Ricchiazzi, P.; Yang, S.; Gautier, C.; Sowle, D. SBDART: A Research and Teaching Software Tool for Plane-Parallel Radiative Transfer in the Earth’s Atmosphere. Bull. Am. Meteorol. Soc. 1998, 79, 2101–2114. [Google Scholar] [CrossRef]
- Teillet, P.M.; Barker, J.L.; Markham, B.L.; Irish, R.R.; Fedosejevs, G.; Storey, J.C. Radiometric cross-calibration of the Landsat-7 ETM+ and Landsat-5 TM sensors based on tandem data sets. Remote Sens. Environ. 2001, 78, 39–54. [Google Scholar] [CrossRef]
- Cormack, R.M.; Cressie, N.J.T.N. Statistics for Spatial Data; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2010; Volume 4, pp. 613–617. [Google Scholar] [CrossRef]
- Isaaks, E.H.; Srivastava, M.R. An Introduction to Applied Geostatistics; Oxford University Press: New York, NY, USA, 1989. [Google Scholar]
- Matheron, G. Principles of geostatistics. Econ. Geol. 1963, 58, 1246–1266. [Google Scholar] [CrossRef]
- Curran, P.J.; Atkinson, P.M. Geostatistics and remote sensing. Prog. Phys. Geogr. 1998, 22, 61–78. [Google Scholar] [CrossRef]
- Duveiller, G.; Defourny, P. A conceptual framework to define the spatial resolution requirements for agricultural monitoring using remote sensing. Remote Sens. Environ. 2010, 114, 2637–2650. [Google Scholar] [CrossRef]
- Guedes, I.C.D.L.; Mello, J.M.D.; Silveira, E.M.D.O.; Mello, C.R.D.; Reis, A.A.D.; Gomide, L.R. Continuidade espacial de características dendrométricas em povoamentos clonais de Eucalyptus sp. avaliada ao longo do tempo. Cerne 2015, 21, 527–534. [Google Scholar] [CrossRef]
- Tobler, W.R. A Computer Movie Simulating Urban Growth in the Detroit Region. Econ. Geogr. 1970, 46, 234. [Google Scholar] [CrossRef]
- Treitz, P.; Howarth, P. High Spatial Resolution Remote Sensing Data for Forest Ecosystem Classification: An Examination of Spatial Scale. Remote Sens. Environ. 2000, 72, 268–289. [Google Scholar] [CrossRef]
- Hu, X.; Hong, W.; Qiu, R.; Hong, T.; Chengzhen, W.; Wu, C. Geographic variations of ecosystem service intensity in Fuzhou City, China. Sci. Total Environ. 2015, 215–226. [Google Scholar] [CrossRef]
- Robertson, G.P. Geostatistics for the Environmental Sciences: GS+ User’s Guide; Gamma Design Software: Plainwell, MI, USA, 1998; pp. 68–94. ISBN 0-9707410-0-6. [Google Scholar]
- Davis, J.C.J.B. Statistics and Data Analysis in Geology. Biometrics 1988, 44, 526–527. [Google Scholar] [CrossRef]
- Zhu, J.X.; Wang, J.L. Appropriate Scale Extraction from Complicated Scene Model Based on Semivariogram Analysis. Geogr. Geo-Inf. Sci. 2015, 31, 33–37. [Google Scholar]
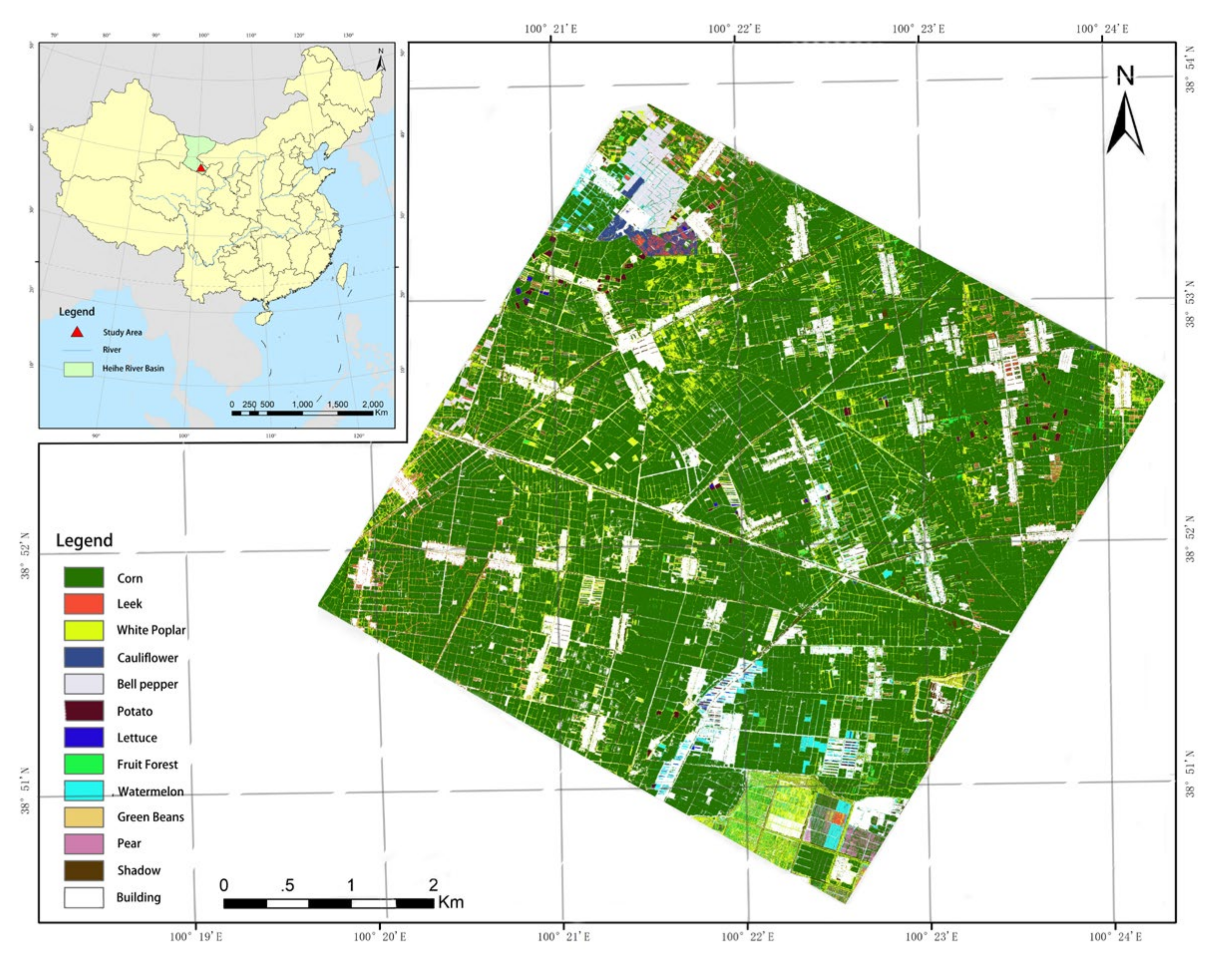



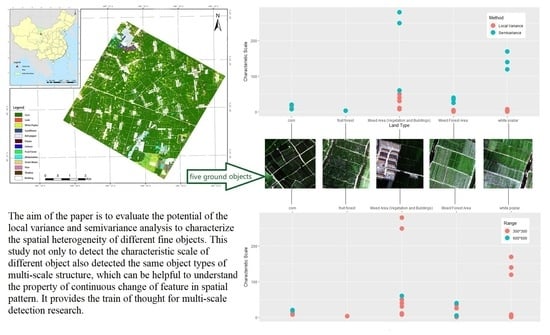
| Land Type | Area (km2) | Proportion (%) | Land Type | Area (km2) | Proportion (%) |
|---|---|---|---|---|---|
| Unclassified | 19.27 | 45.9 | Bell Pepper | 0.28 | 0.7 |
| Corn | 15.54 | 37.0 | Cauliflower | 0.16 | 0.4 |
| Building | 3.17 | 7.5 | Fruit Forest | 0.11 | 0.3 |
| White Poplar | 2.19 | 5.2 | Potato | 0.11 | 0.3 |
| Shadow | 0.46 | 1.1 | Pear | 0.07 | 0.2 |
| Leek | 0.32 | 0.8 | Green Bean | 0.02 | 0.1 |
| Watermelon | 0.30 | 0.7 | Lettuce | 0.02 | 0.1 |
| Channel | Wavelength Range (nm) | Central Wavelength (nm) | Band |
|---|---|---|---|
| ASTER-2 | 630–690 | 660 | Red |
| ASTER-3N | 720–912 | 810 | Near-infrared |
| CASI-22 | 676–690 | 680 | Red |
| CASI-28 | 762–776 | 770 | Near-infrared |
| Satellite | Band | |
|---|---|---|
| Red | Near-Infrared | |
| ASTER | 1082.73 | 1634.46 |
| CASI | 1200.24 | 1571.67 |
| CASI/ASTER | 1.109 | 0.962 |
| Model | Formula |
|---|---|
| Linear | |
| Exponential | |
| Gaussian | |
| Spherical |
| Sample | Separation Distance (h/m) | Model | R2 | Sill (C + C0) | Nugget (C0) | Range (A/m) |
|---|---|---|---|---|---|---|
| Corn a | 1 | Exponential | 0.91 | 0.00707 | 0.00108 | 6.0 |
| 5 | Exponential | 0.92 | 0.00703 | 0.00112 | 6.1 | |
| 10 | Exponential | 0.85 | 0.00706 | 0.00108 | 6.3 | |
| 15 | Exponential | 0.83 | 0.00701 | 0.00116 | 7.0 |
| Sample | Separation Distance (h/m) | Model | R2 | Sill (C + C0) | Nugget (C0) | Range (A/m) |
|---|---|---|---|---|---|---|
| White Poplar | 1 | Exponential | 0.93 | 0.02051 | 0.01622 | 113.0 |
| 5 | Exponential | 0.97 | 0.02029 | 0.01559 | 114.1 | |
| 10 | Exponential | 0.97 | 0.02104 | 0.01644 | 138.3 | |
| 15 | Exponential | 0.98 | 0.02219 | 0.01702 | 167.0 | |
| Fruit Forest | 1 | Exponential | 0.92 | 0.01687 | 0.00551 | 3.8 |
| 5 | Exponential | 0.93 | 0.01589 | 0.00527 | 3.6 | |
| 10 | Exponential | 0.95 | 0.01587 | 0.00527 | 3.2 | |
| 15 | Exponential | 0.99 | 0.01592 | 0.00528 | 2.9 | |
| Mixed Forest Area | 1 | Exponential | 0.94 | 0.01896 | 0.01256 | 25.3 |
| 5 | Exponential | 0.96 | 0.01819 | 0.01429 | 26.3 | |
| 10 | Exponential | 0.97 | 0.01681 | 0.01291 | 30.1 | |
| 15 | Exponential | 0.97 | 0.01720 | 0.01601 | 35.0 |
| Sample | Separation Distance (h/m) | Model | R2 | Sill (C + C0) | Nugget (C0) | Range (A/m) |
|---|---|---|---|---|---|---|
| Mixed area a | 1 | Exponential | 0.98 | 0.08672 | 0.02170 | 40.8 |
| 5 | Exponential | 0.99 | 0.08632 | 0.02231 | 41.5 | |
| 10 | Exponential | 0.99 | 0.08381 | 0.02589 | 44.8 | |
| 15 | Exponential | 0.99 | 0.08390 | 0.02910 | 47.7 | |
| Mixed area b | 1 | Exponential | 0.98 | 0.09420 | 0.02030 | 33.2 |
| 5 | Exponential | 0.98 | 0.09430 | 0.02130 | 33.9 | |
| 10 | Exponential | 0.98 | 0.09470 | 0.02470 | 36.2 | |
| 15 | Exponential | 0.96 | 0.09500 | 0.02680 | 37.8 | |
| Mixed area c | 1 | Exponential | 0.99 | 0.19500 | 0.00900 | 259.8 |
| 5 | Exponential | 0.99 | 0.19362 | 0.00911 | 268.8 | |
| 10 | Exponential | 0.99 | 0.19260 | 0.00910 | 272.2 | |
| 15 | Exponential | 0.99 | 0.19260 | 0.00930 | 276.3 |
| Scheme 2 | Separation Distance (h/m) | Model | R2 |
Sill (C + C0) |
Nugget (C0) |
Range (A/m) |
|---|---|---|---|---|---|---|
| Corn | 150 | Exponential | 0.98 | 0.11071 | 0.01701 | 23.1 |
| Forest | 300 | Exponential | 0.99 | 0.09512 | 0.02248 | 43.6 |
| Mixed Area | 300 | Exponential | 0.99 | 0.12330 | 0.02431 | 56.8 |
| Method | Ground Object | 300 × 300 m | 600 × 600 m |
|---|---|---|---|
| Local Variance | Corn | 7 m, 17 m | 9 m, 20 m |
| White Poplar | 1–7 m | —— | |
| Fruit Forest | 3 m | —— | |
| Mixed Forest Area | 1–3 m | 5 m | |
| Mixed Area (Vegetation and Buildings) | 7 m,11 m | —— | |
| Semivariance | Corn | 7 m | 20 m |
| White Poplar | 120–170 m | —— | |
| Fruit Forest | 3m | —— | |
| Mixed Forest Area | 25–35 m | 40 m | |
| Mixed Area (Vegetation and Buildings) | 30–50 m, 250–280 m | 60 m |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, X.; Yu, W.; Shi, J.; Ma, M.; Li, X.; Wu, W. Identification of the Characteristic Scale of Fine Ground Objects: A Case Study of the Core Observation Area in the Middle Reaches of the Heihe River Basin. Remote Sens. 2021, 13, 362. https://doi.org/10.3390/rs13030362
Wu X, Yu W, Shi J, Ma M, Li X, Wu W. Identification of the Characteristic Scale of Fine Ground Objects: A Case Study of the Core Observation Area in the Middle Reaches of the Heihe River Basin. Remote Sensing. 2021; 13(3):362. https://doi.org/10.3390/rs13030362
Chicago/Turabian StyleWu, Xiuyi, Wenping Yu, Jinan Shi, Mingguo Ma, Xiaolu Li, and Wenjian Wu. 2021. "Identification of the Characteristic Scale of Fine Ground Objects: A Case Study of the Core Observation Area in the Middle Reaches of the Heihe River Basin" Remote Sensing 13, no. 3: 362. https://doi.org/10.3390/rs13030362
APA StyleWu, X., Yu, W., Shi, J., Ma, M., Li, X., & Wu, W. (2021). Identification of the Characteristic Scale of Fine Ground Objects: A Case Study of the Core Observation Area in the Middle Reaches of the Heihe River Basin. Remote Sensing, 13(3), 362. https://doi.org/10.3390/rs13030362