Statistical Study of Ionospheric Equivalent Slab Thickness at Guam Magnetic Equatorial Location
Abstract
1. Introduction
2. Data and Methods of Analysis
3. Results
4. Discussion
5. Conclusions
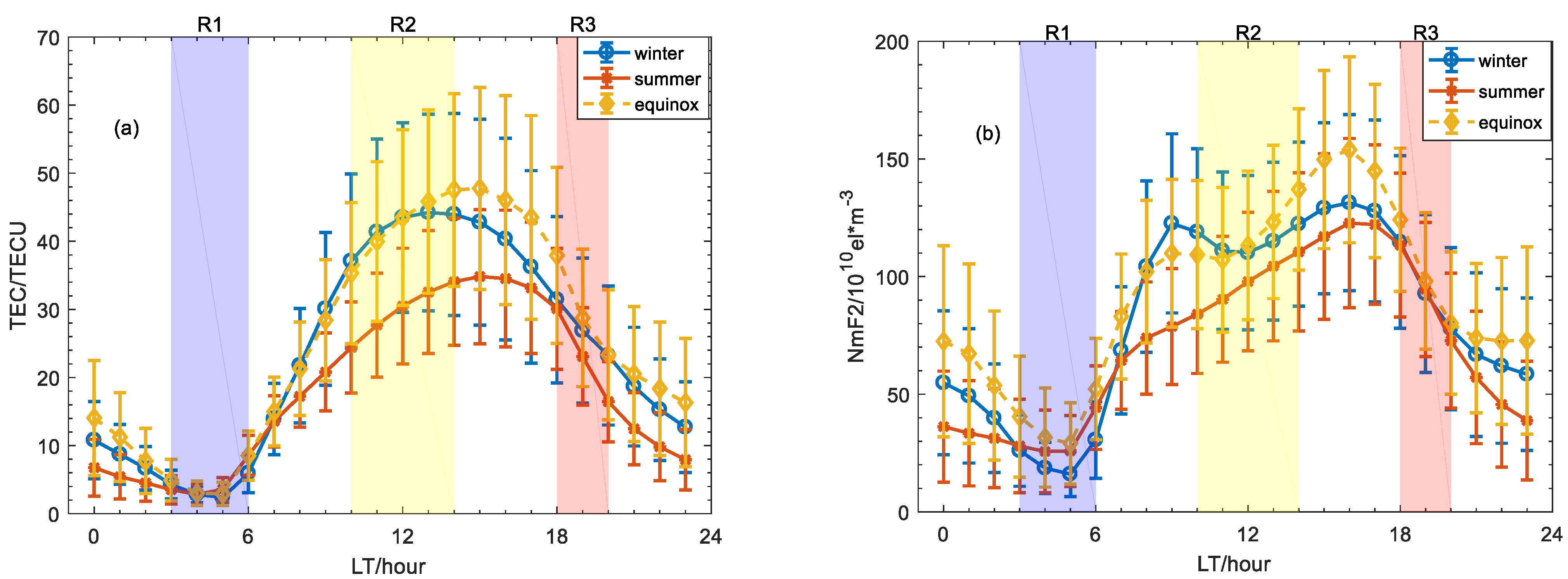
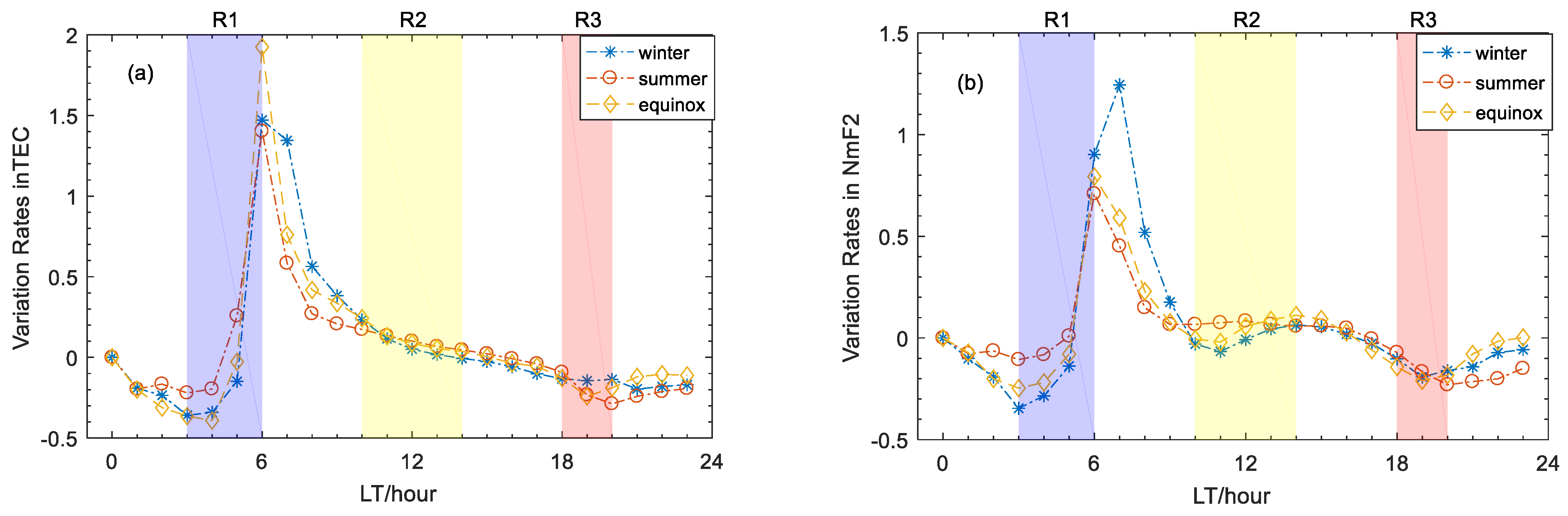
- The peak of τ appeared at noon, consistent with previous studies on equatorial latitudes.
- There is a post-sunset peak in τ observed during the winter and equinox, and it means that NmF2 is decreasing faster than TEC, which can be associated with the higher post-sunset TEC enhancement occurrence in equinox/winter, proving previous conclusions. In addition, the τ continues to decrease after post-midnight and the equinoctial one is smallest due to the largest nighttime NmF2 enhancement in equinox and the faster decrease in TEC in equinox than that in solstice.
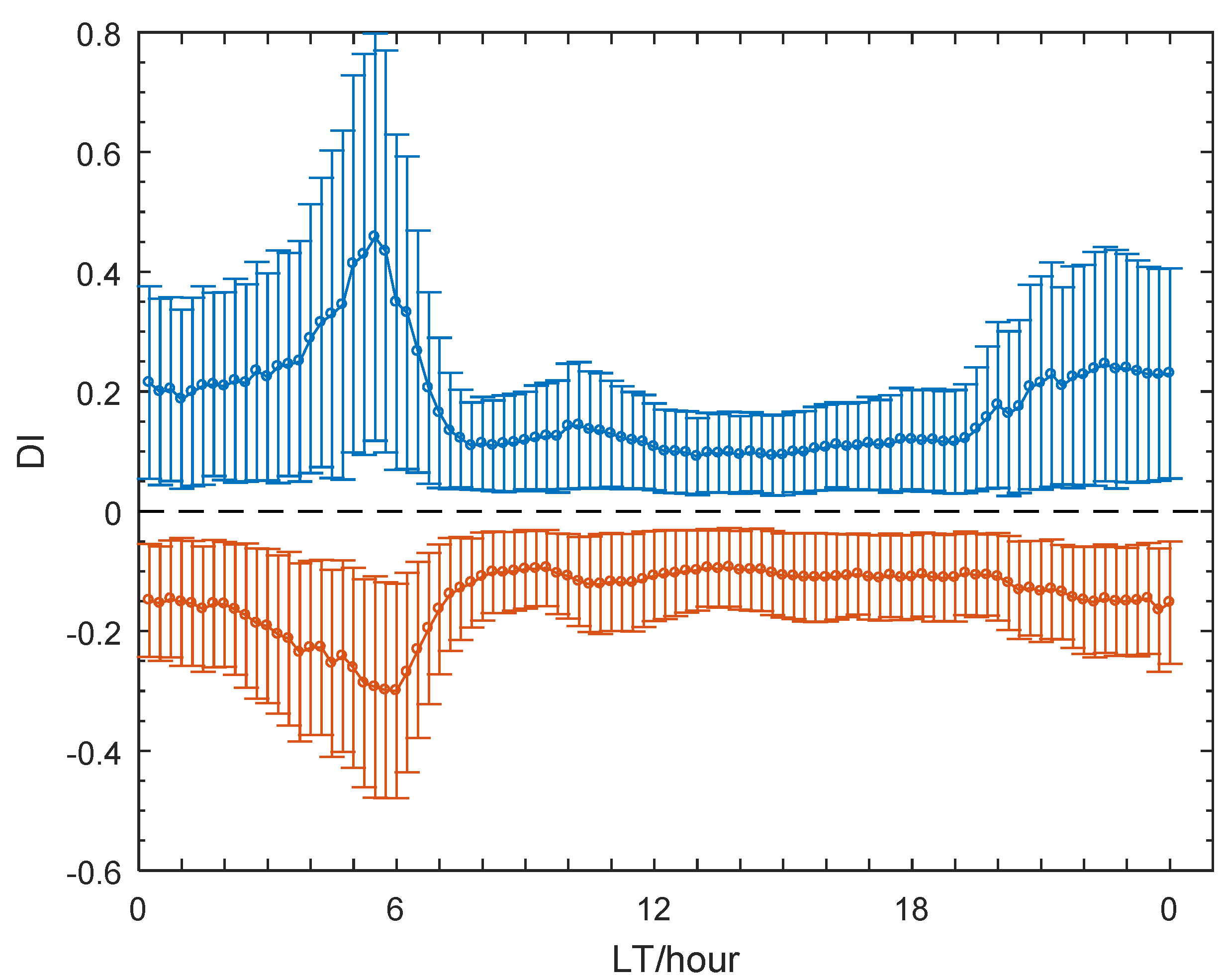
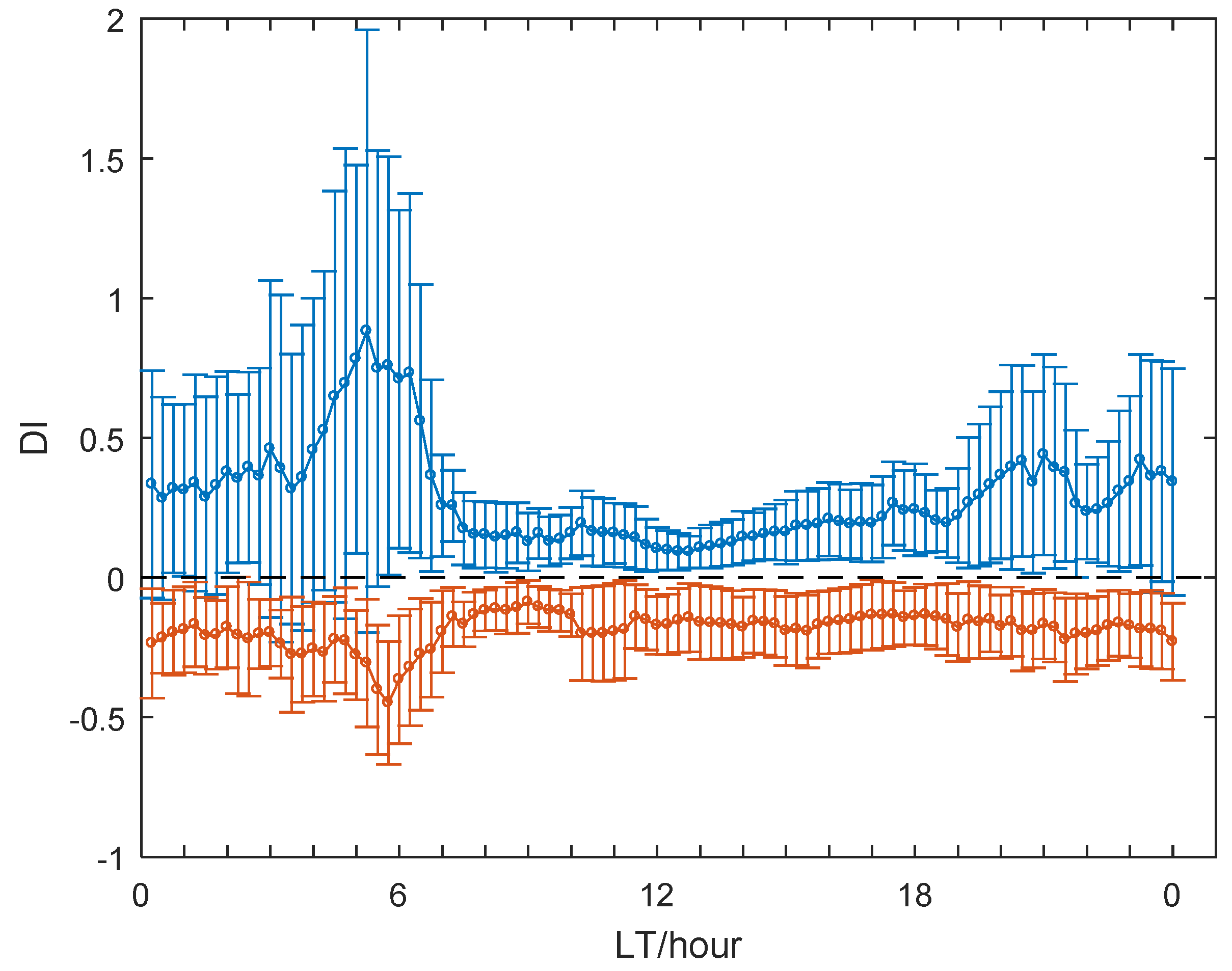
- The dependence of τ on the solar activity are different for daytime and nighttime: the daytime τ seems to increase with solar activity, as TEC is more sensitive to the solar activity than NmF2, whereas the nighttime one decreases with solar activity at night, and it should be due to the fact the H+-O+ transition height in the low solar activity is lower than that in the high solar activity at night.
- The τ has more variability during nighttime than daytime, during both the geomagnetically quiet and disturbed conditions, and the greatest variability of τ appeared at sunrise.
- The τ at noon is larger in winter and equinox than in summer. It is probably due to the absence of NmF2 noontime bite-out in summer at this region.
- There is no pre sunrise peak in τ and τ get low values during the pre-sunrise period at Guam. However, previous studies indicate that pre sunrise peak is a widely observed feature, from low to high latitude, and τ even reaches maximum at sunrise for specific seasons. The contradiction is probably due to Guam being located at equatorial latitude, as the low values in the pre sunrise period could also be seen at other longitudinal equatorial latitude station. In addition, longitudinal difference might also contribute to the difference.
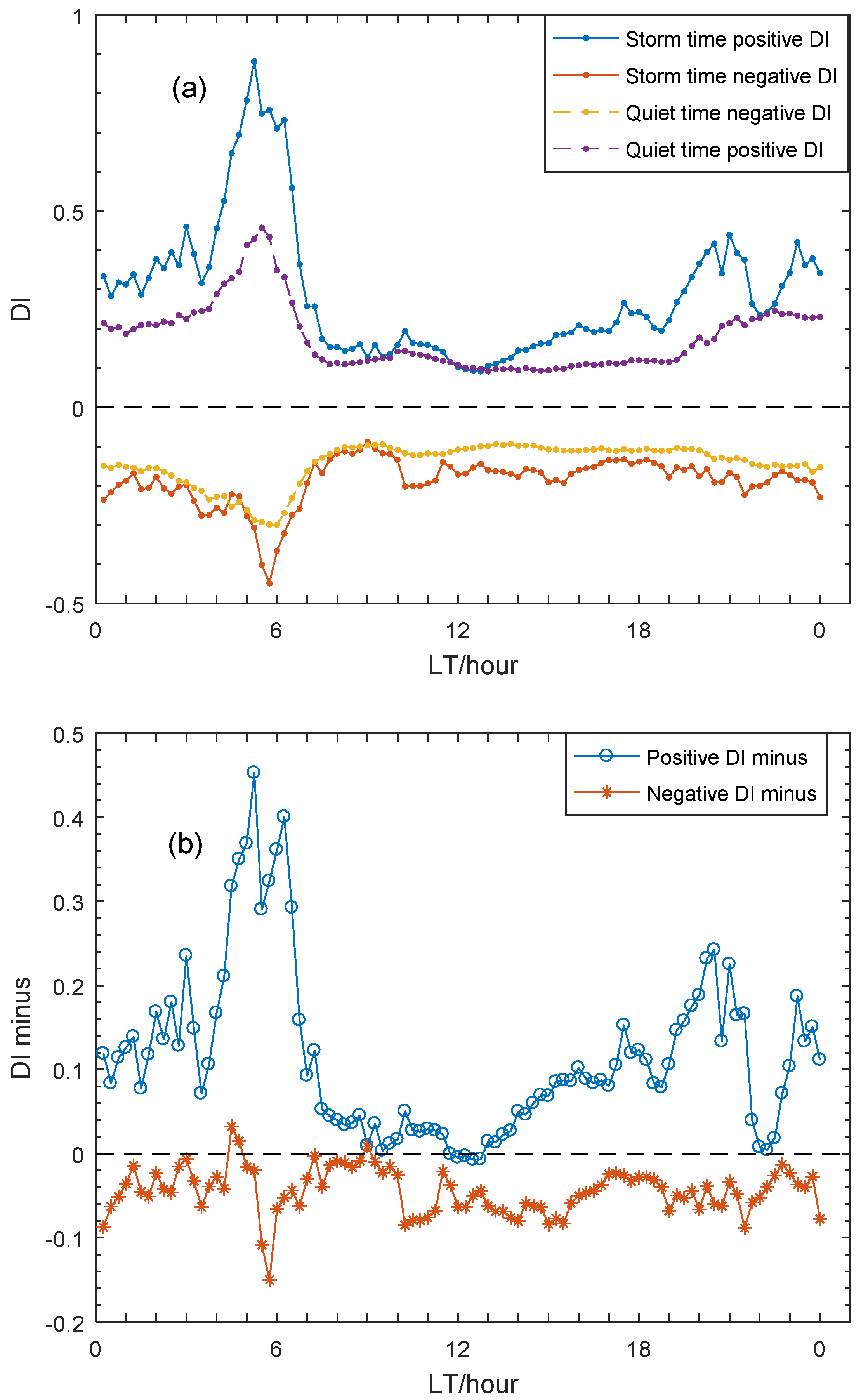
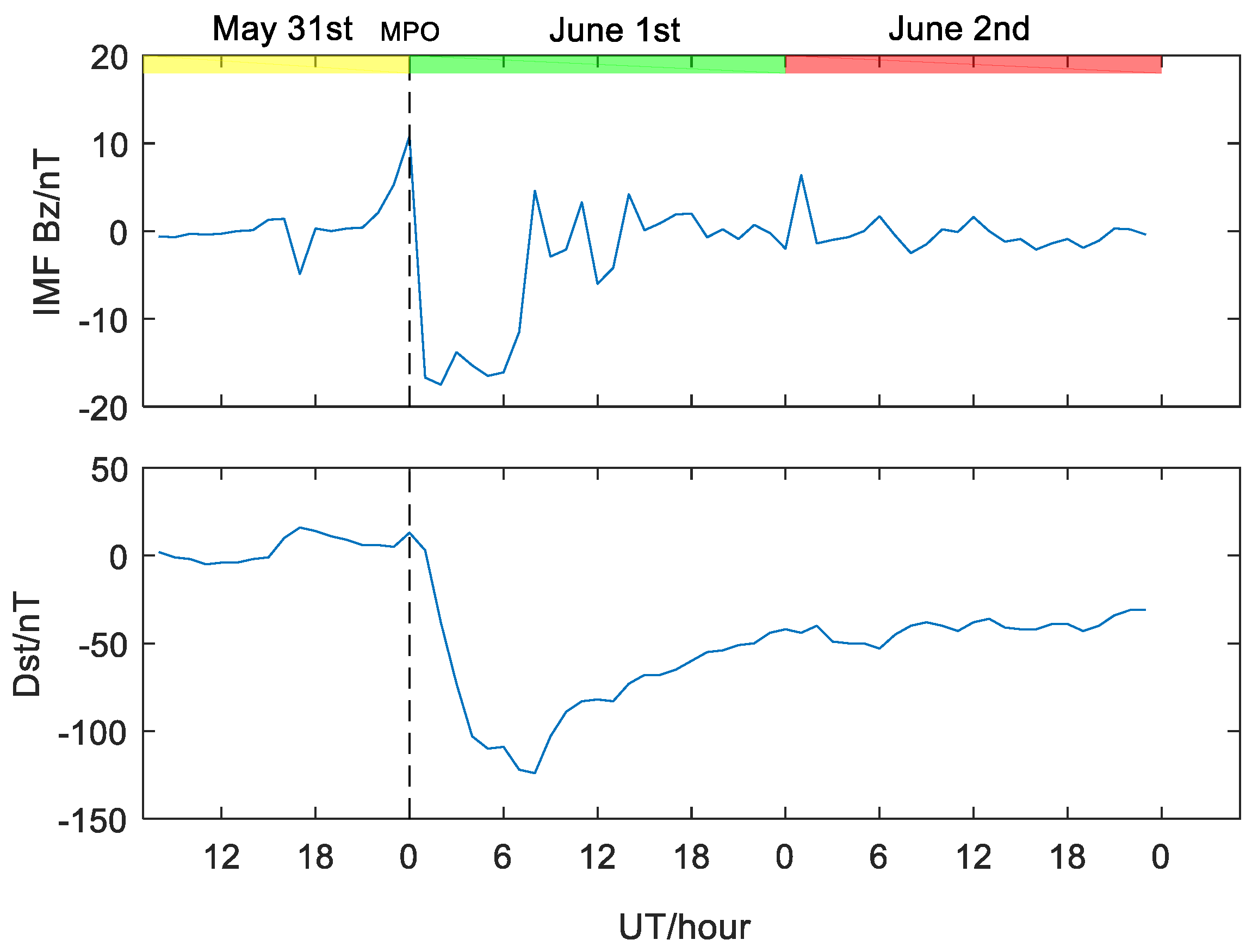
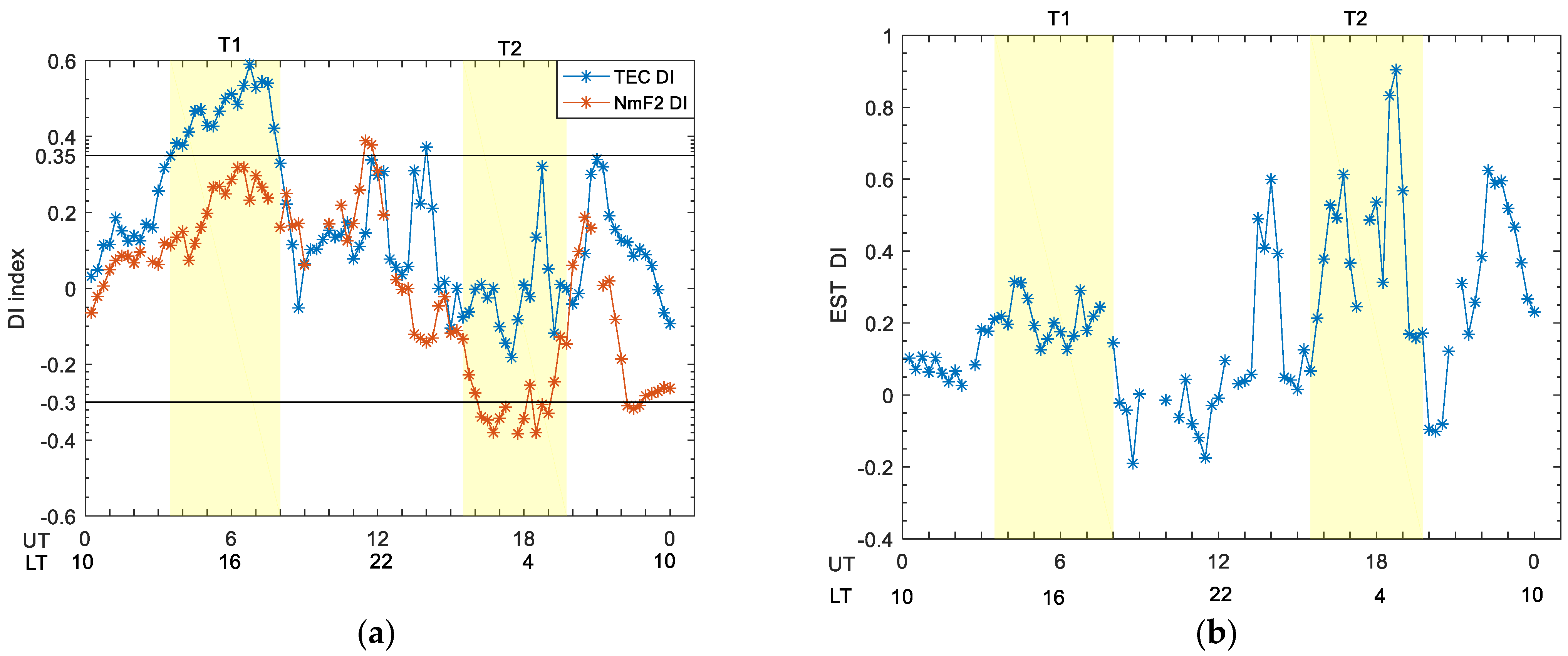
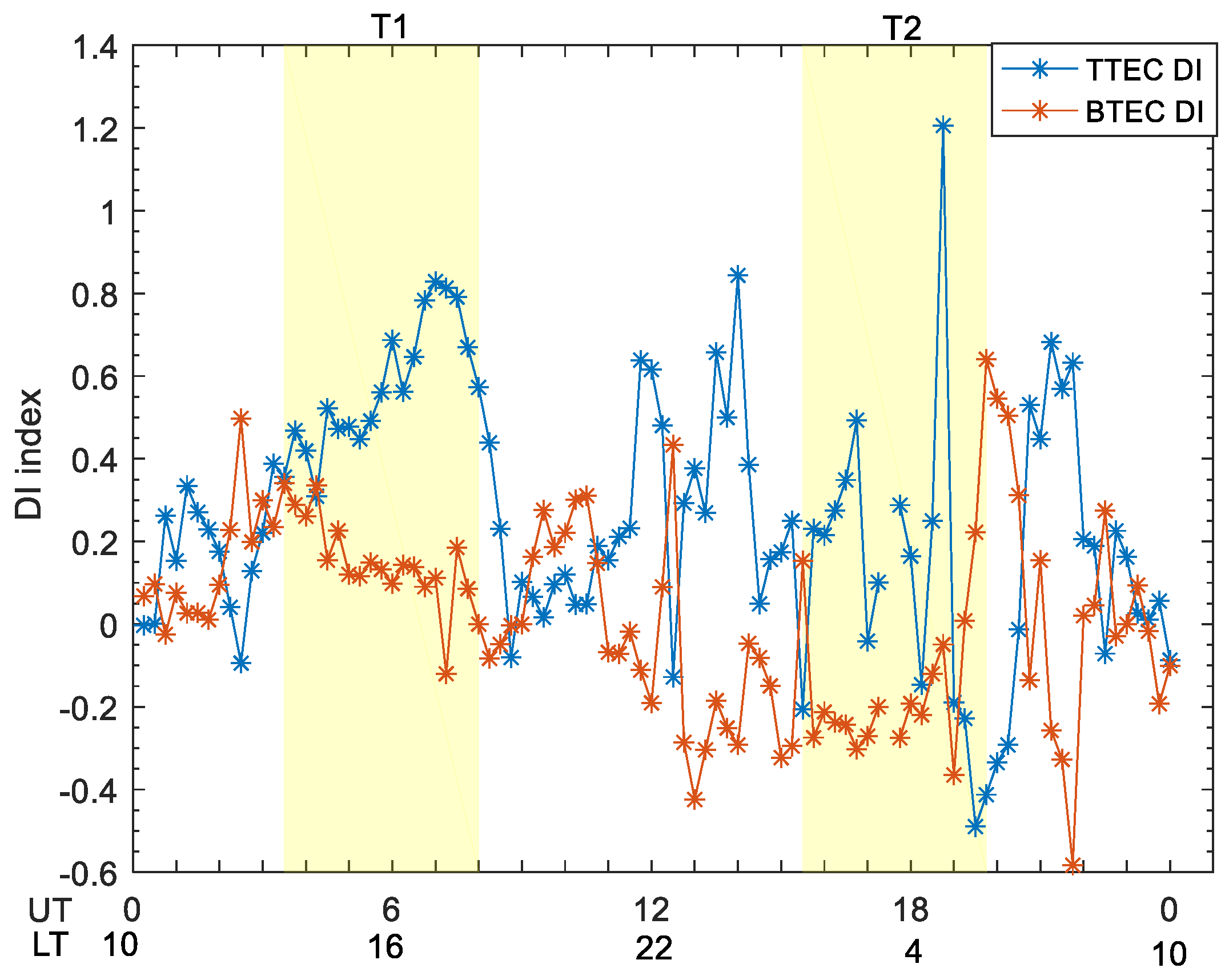
- The geomagnetic storm seems to have a positive effect on the τ during most of the storm period in Guam, except at sunrise period, when the τ attains large variability, even at the geomagnetically quiet condition. This study also provides a new physical explanation for the observed effect of geomagnetic storm on τ in Guam. During the positive storms, the penetration electric field along with storm time equator-ward neutral wind tends to increase upward drift and uplift F region, causing the large increase in TEC accompanied by relatively small increase in NmF2. On the other hand, an enhanced equatorward wind tends to push more plasma, at low latitudes, into the topside ionosphere in the equatorial region, resulting in the TEC, which does not undergo severe depletion as NmF2 does during the negative storms. Therefore, the geomagnetic storm seems to enhance τ both during the positive and negative ionospheric storms.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Breed, A.M.; Goodwin, G.L.; Vandenberg, A.-M.; Essex, E.A.; Lynn, K.J.W.; Silby, J.H. Ionospheric total electron content and ionospheric slab thickness determined in Australia. Radio Sci. 1997, 62, 1635–1643. [Google Scholar] [CrossRef]
- Wright, J.W. A model of the F-region above hmaxF2. J. Geophys. Res. 1960, 65, 185–191. [Google Scholar] [CrossRef]
- Titheridge, J.E. The ionospheric slab thickness of the mid-latitude ionosphere. Planet Space Sci. 1973, 21, 1775–1793. [Google Scholar] [CrossRef]
- Jakowski, N.; Putz, E.; Spalla, P. Ionospheric storm characteristics deduced from satellite radio beacon observations at three European stations. Ann. Geophys. 1990, 8, 343–352. [Google Scholar]
- Jakowski, N.; Mielich, J.; Hoque, M.M.; Danielides, M. Equivalent ionospheric slab thickness at the mid-latitude ionosphere during solar cycle 23. In Proceedings of the 38th COSPAR Scientific Assembly, Bremen, Germany, 18–25 July 2010. [Google Scholar]
- Jakowski, N.; Hoque, M.M.; Mielich, J.; Hall, C. Equivalent ionospheric slab thickness of the ionosphere over Europe as an indicator of long-term temperature changes in the thermosphere. J. Atmos. Terr. Phys. 2017, 163, 92–101. [Google Scholar]
- Huang, Z.; Yuan, H. Climatology of the ionospheric slab thickness along the longitude of 120° E in China and its adjacent region during the solar minimum years of 2007–2009. Ann. Geophys. 2015, 33, 1311–1319. [Google Scholar] [CrossRef]
- Maltseva, O.A.; Mozhaeva, N.S.; Nikitenko, T.V. Comparison of model and experimental ionospheric parameters at high latitudes. Adv. Space Res. 2013, 51, 599–609. [Google Scholar] [CrossRef]
- Maltseva, O.A.; Mozhaeva, N.S.; Nikitenko, T.V. Validation of the Neustrelitz Global Model according to the low latitude ionosphere. Adv. Space Res. 2014, 54, 463–472. [Google Scholar] [CrossRef]
- Maltseva, O.A.; Mozhaeva, N.S. The Use of the Total Electron Content Measured by Navigation Satellites to Estimate Ionospheric Conditions. Int. J. Nav. Obs. 2016, 2016, 7016208. [Google Scholar] [CrossRef]
- Froń, A.; Galkin, I.; Krankowski, A.; Bilitza, D.; Hernández-Pajares, M.; Reinisch, B.; Li, Z.; Kotulak, K.; Zakharenkova, I.; Cherniak, I.; et al. Towards Cooperative Global Mapping of the Ionosphere: Fusion Feasibility for IGS and IRI with Global Climate VTEC Maps. Remote Sens. 2020, 12, 3531. [Google Scholar] [CrossRef]
- Gerzen, T.; Jakowski, N.; Wilken, V.; Hoque, M.M. Reconstruction of F2 layer peak electron density based on operational vertical total electron content maps. Ann. Geophys. 2013, 31, 1241–1249. [Google Scholar] [CrossRef][Green Version]
- Krankowski, A.; Shagimuratov, I.I.; Baran, L.W. Mapping of foF2 over Europe based on GPS-derived TEC data. Adv. Space Res. 2007, 39, 651–660. [Google Scholar] [CrossRef]
- Bhonsle, R.V.; Da Rosa, A.V.; Garriott, O.K. Measurement of Total Electron Content and the Equivalent ionospheric slab thickness of the Mid latitude Ionosphere. Radio Sci. 1965, 69, 929–937. [Google Scholar]
- Kersley, L.; Hajeb-Hosseinieh, H. Dependence of ionospheric slab thickness on geomagnetic activity. J. Atmos. Terr. Phys. 1976, 38, 1357–1360. [Google Scholar] [CrossRef]
- Jin, S.; Cho, J.-H.; Park, J.-U. Ionospheric slab thickness and its seasonal variations observed by GPS. J. Atmos. Sol. Terr. Phys. 2007, 69, 1864–1870. [Google Scholar] [CrossRef]
- Huang, Y.N. Some results of ionospheric slab thickness observations at Lunping. J. Geophys. Res. 1983, 88, 5517–5522. [Google Scholar] [CrossRef]
- Davies, K.; Liu, X.M. ionospheric slab thickness in middle and low latitudes. Radio Sci. 1991, 26, 997–1005. [Google Scholar] [CrossRef]
- Minakoshi, H.; Nishimuta, I. Ionospheric electron content and equivalent ionospheric slab thickness at lower mid-latitudes in the Japanese zon. In Proc. Beacon Satellite Symposium (IBSS); University of Wales: Wales, UK, 1994; Volume 144. [Google Scholar]
- Gulyaeva, T.L.; Jayachandran, B.; Krishnankutty, T.N. Latitudinal variation of slab thickness. Adv. Space Res. 2004, 33, 862–865. [Google Scholar] [CrossRef]
- Jayachandran, B.; Krishnankutty, T.; Gulyaeva, T. Climatology of ionospheric slab thickness. Ann. Geophys. 2004, 22, 25–33. [Google Scholar] [CrossRef]
- Pignalberi, A.; Nava, B.; Pietrella, M.; Cesaroni, C.; Pezzopane, M. Midlatitude climatology of the ionospheric equivalent slab thickness over two solar cycles. J. Geod. 2021, 95, 124. [Google Scholar] [CrossRef]
- Guo, P.; Xu, X.; Zhang, G.X. Analysis of the ionospheric equivalent ionospheric slab thickness based on ground-based GPS/TEC and GPS/COSMIC RO. J. Atmos. Sol. Terr. Phys. 2011, 73, 839–846. [Google Scholar] [CrossRef]
- Odeyemi, O.O.; Adeniyi, J.O.; Oladipo, O.A.; Olawepo, A.O.; Adimu, I.A.; Oyeyemi, E.O. Ionospheric slab thickness investigation on slab-thickness and B0 over an equatorial station in Africa and comparison with IRI model. J. Atmos. Sol. Terr. Phys. 2018, 179, 293–306. [Google Scholar] [CrossRef]
- Odeyemi, O.O.; Adeniyi, J.O.; Oyeyemi, E.O.; Panda, S.K.; Jamjareegulgarn, P.J.; Olugbon, B.; Oluwadare, E.J.; Akala, A.O.; Olawepo, A.J.; Adewale, A.A. Morphologies of ionospheric-equivalent slab thickness and scale height over equatorial latitude in Africa. Adv. Space Res. 2021, in press. [Google Scholar] [CrossRef]
- Huang, H.; Liu, L.; Chen, Y.; Le, H.; Wan, W. A global picture of ionospheric slab thickness derived from GIM TEC and COSMIC radio occultation observations. J. Geophys. Res. Space Phys. 2016, 121, 867–880. [Google Scholar] [CrossRef]
- Fox, M.W.; Mendillo, M.; Klobuchar, J.A. Ionospheric equivalent ionospheric slab thickness and its modeling applications. Radio Sci. 1991, 26, 429–438. [Google Scholar] [CrossRef]
- Spalla, P.; Ciraolo, L. TEC and foF2 comparison. Ann. Geophys. 1994, 37, 929–938. [Google Scholar] [CrossRef]
- Jakowski, N.; Hoque, M.M. Global equivalent ionospheric slab thickness model of the Earth’s ionosphere. J. Space Weather Space Clim. 2021, 11, 10. [Google Scholar] [CrossRef]
- Àlàgbé, G.A. Quiet- and storm-time correlation of F2-layer ionospheric slab thickness and B0 at an equatorial station. Int. J. Res. Rev. Appl. Sci. 2012, 13, 133–138. [Google Scholar]
- Duarte-Silva, M.H.; Muella, M.T.A.H.; Silva, L.C.C.; de Abreu, A.J.; Fagundes, P.R. Ionospheric slab thickness at the equatorial anomaly region after the deep solar minimum of cycle 23/24. Adv. Space Res. 2015, 56, 1961–1972. [Google Scholar] [CrossRef]
- Gulyaeva, T.; Stanislawska, I. Night-day imprints of ionospheric slab thickness during geomagnetic storm. J. Atmos. Sol. Terr. Phys. 2005, 67, 1307–1314. [Google Scholar] [CrossRef]
- Stankov, S.M.; Warnant, R. Ionospheric slab thickness—Analysis, modelling and monitoring. Adv. Space Res. 2009, 44, 1295–1303. [Google Scholar] [CrossRef]
- Uwamahoro, J.C.; Giday, N.M.; Habarulema, J.B.; Katamzi-Joseph, Z.T.; Seemala, G.K. Reconstruction of storm-time total electron content using ionospheric tomography and artificial neural networks: A comparative study over the African region. Radio Sci. 2018, 53, 1328–1345. [Google Scholar] [CrossRef]
- Ciraolo, L.; Azpilicueta, F.; Brunini, C.; Meza, A.; Radicella, S. Calibration errors on experimental slant total electron content (TEC) determined with GPS. J. Geodesy. 2007, 81, 111–120. [Google Scholar] [CrossRef]
- Abe, O.; Villamide, X.O.; Paparini, C.; Radicella, S.; Nava, B.; Rodríguez Bouza, M. Performance evaluation of gnss-tec ionospheric slab thicknessimation techniques at the grid point in middle and low latitudes during different geomagnetic conditions. J. Geodesy 2017, 91, 409–417. [Google Scholar] [CrossRef]
- Adewale, A.; Oyeyemi, E.; Adeniyi, J.; Adeloye, A.; Oladipo, O. Comparison of total electron content predicted using the IRI-2007 model with GPS observations over Lagos, Nigeria. Indian J. Radio Space Phys. 2011, 40, 21–25. [Google Scholar]
- Seemala, G.; Valladares, C. Statistics of total electron content depletions observed over the South American continent for the year 2008. Radio Sci. 2011, 46, RS5019. [Google Scholar] [CrossRef]
- Olwendo, O.; Baki, P.; Mito, C.; Doherty, P. Characterization of ionospheric GPS Total Electron content (GPS TEC) in low latitude zone over the Kenyan region during a very low solar activity phase. J. Atmos. Sol. Terr. Phys. 2012, 84, 52–61. [Google Scholar] [CrossRef]
- Akala, A.; Seemala, G.; Doherty, P.; Valladares, C.; Carrano, C.; Espinoza, J.; Oluyo, S. Comparison of equatorial GPS-TEC observations over an African station and an American station during the minimum and ascending phases of solar cycle 24. Ann. Geophys. 2013, 31, 2085–2096. [Google Scholar] [CrossRef]
- Matamba, T.M.; Habarulema, J.B.; McKinnell, L.-A. Statistical analysis of the ionospheric response during geomagnetic storm conditions over South Africa using ionosonde and GPS data. Space Weather. 2015, 13, 536–547. [Google Scholar] [CrossRef]
- Akala, A.O.; Adewusi, E.O. Quiet-time and storm-time variations of the African equatorial and low latitude ionosphere during 2009–2015. Adv. Space Res. 2020, 66, 1441–1459. [Google Scholar] [CrossRef]
- De Dieu Nibigira, J.; Sivavaraprasad, G.; Ratnam, D.V. Performance analysis of IRI-2016 model TEC predictions over Northern and Southern Hemispheric IGS stations during descending phase of solar cycle 24. Acta Geophys. 2021, 69, 1509–1527. [Google Scholar] [CrossRef]
- Reinisch, B.W.; Galkin, T.A. Global ionospheric radio observatory (GIRO). Earth Planets Space 2011, 63, 377–381. [Google Scholar] [CrossRef]
- England, S.L.; Immel, T.J.; Huba, J.D.; Hagan, M.E.; Maute, A.; DeMajistre, R. Modeling of multiple effects of atmospheric tides on the ionosphere: An examination of possible coupling mechanisms responsible for the longitudinal structure of the equatorial ionosphere. J. Geophys. Res. Space Res. 2010, 124, A05308. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, L.; Le, H.; Wan, W.; Zhang, H. Equatorial ionization anomaly in the low-latitude topside ionosphere: Local time evolution and longitudinal difference. J. Geophys. Res. Space Res. 2016, 121, 7166–7182. [Google Scholar] [CrossRef]
- Lühr, H.; Häusler, K.; Stolle, C. Longitudinal variation of F region electron density and thermospheric zonal wind caused by atmospheric tides. Geophys. Res. Lett. 2007, 34, L16102. [Google Scholar] [CrossRef]
- Aggson, T.L.; Herrero, F.A.; Johnson, J.A.; Pfaff, R.F.; Laakso, H.; Maynard, N.C.; Moses, J.J. Satellite observations of zonal electric fields near sunrise in the equatorial ionosphere. J. Atmos. Sol. Terr. Phys. 1995, 57, 19–24. [Google Scholar] [CrossRef]
- Kelley, M.C.; Rodrigues, F.S.; Pfaff, R.F.; Klenzing, J. Observations of the generation of eastward equatorial electric fields near dawn. Ann. Geophys. 2014, 32, 1169–1175. [Google Scholar] [CrossRef]
- Zhang, R.; Liu, L.; Chen, Y.; Le, H. The dawn enhancement of the equatorial ionospheric vertical plasma drift. J. Geophy. Res: Space Phys. 2015, 120, 688–697. [Google Scholar] [CrossRef]
- Zhou, X.; Liu, H.-L.; Lu, X.; Zhang, R.; Maute, A.; Wu, H.; Yue, X.; Wan, W. Quiet-time day-to-day variability of equatorial vertical E × B drift from atmosphere perturbations at dawn. J. Geophys. Res. Space Phys. 2020, 124, e2020JA027824. [Google Scholar] [CrossRef]
- Balan, N.; Rao, P.B. Dependence of the ionospheric response on the local time of sudden commencement and the intensity of the geomagnetic storms. J. Atmos. Terr. Phys. 1990, 52, 269–275. [Google Scholar] [CrossRef]
- Kashcheyev, A.; Migoya-Orue, Y.; Amory-Mazaudier, C.; Fleury, R.; Nava, B.; Alazo-Cuartas, K.; Radicella, S.M. Multivariable comprehensive analysis of two great geomagnetic storms of 2015. J. Geophys. Res: Space Phys. 2018, 123, 5000–5018. [Google Scholar] [CrossRef]
- Buonsanto, M.J. Ionospheric storms—A review. Space Sci. Rev. 1999, 88, 563–601. [Google Scholar] [CrossRef]
- Mendillo, M. Storms in the ionosphere: Patterns and processes for total electron content. Rev. Geophys. 2006, 44, 335–360. [Google Scholar] [CrossRef]
- Immel, T.J.; Sagawa, S.L.; England, S.B.; Henderson, M.E.; Hagan, S.B.; Mende, H.U.; Frey, C.; Swenson, M.; Paxton, L.J. Control of equatorial ionospheric morphology by atmospheric tides. Geophys. Res. Lett. 2006, 33, L15108. [Google Scholar] [CrossRef]
- Rishbeth, H.; Mendillo, M. Patterns of F2-layer variability. J. Atmos. Sol. Terr. Phys. 2001, 63, 1661–1680. [Google Scholar] [CrossRef]
- Fang, T.-W.; Fuller-Rowell, T.; Yudin, V.; Matsuo, T.; Viereck, R. Quantifying the sources of ionosphere day-to-day variability. J. Geophys. Res. Space Phys. 2018, 123, 9682–9696. [Google Scholar] [CrossRef]
- Rajaram, G.; Rastogi, R.G. Equatorial Electron Densities—Seasonal and Solar Cycle Changes. J. Atmos. Terr. Phys. 1977, 39, 1175–1182. [Google Scholar] [CrossRef]
- Radicella, S.M.; Adeniyi, J.O. Equatorial ionospheric electron density below the F2 peak. Radio Sci. 1999, 34, 1153–1163. [Google Scholar] [CrossRef]
- Lee, C.C. Examination of the absence of noontime bite-out in equatorial total electron content. J. Geophys. Res. Space Res. 2012, 117, A09303. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, L.; Le, H.; Zhang, H. Equatorial North-South Difference of Noontime Electron Density Bite-out in the F2-layer. J. Geophys. Res. Space Res. 2020, 125, e2020JA028124. [Google Scholar] [CrossRef]
- Su, Y.Z.; Bailey, G.J.; Balan, N. Night-time enhancements in TEC at equatorial anomaly latitudes. J. Atmos. Terr. Phys. 1993, 56, 1619–1628. [Google Scholar] [CrossRef]
- Agrawal, A.; Maski, K.; Vijay, S.K.; MaShra, S.D. An Analytical Study of Nighttime Enhancement in foF2 during 23rd& 24th Solar Cycle at Low Latitude Station. Int. J. Eng. Trends Tech. 2018, 61, 25–30. [Google Scholar]
- Fox, M.W.; Mendillo, M.; Spalla, P. The variation of ionospheric slab thickness during geomagnetic storms. In Proceedings of the International Beacon Satellite Symposium (IBSS), Tucuman, Argentina, 27–30 March 1990. [Google Scholar]
- Bhuyan, P.K.; Lakha, S.; Tyagi, T.R. Equivalent ionospheric slab thickness of the ionosphere over 26°N through the ascending half of a solar cycle. Ann. Geophys. 1986, 4, 131–136. [Google Scholar]
- Balan, N.; Shiokawa, K.; Otsuka, Y.; Kikuchi, T.; Vijaya Lekshmi, D.; Kawamura, S.; Yamamoto, M.; Bailey, G.J. A physical mechanism of positive ionospheric storms at low latitudes and midlatitudes. J. Geophys. Res. Space Phys. 2010, 115, A02304. [Google Scholar] [CrossRef]
- Lei, J.; Zhu, Q.; Wang, W.; Burns, A.G.; Zhao, B.; Luan, X.; Zhong, J.; Dou, X. Response of the topside and bottomside ionosphere at low and middle latitudes to the October 2003 superstorms. J. Geophys. Res. Space Phys. 2015, 120, 6974–6986. [Google Scholar] [CrossRef]
- Lei, J.; Zhong, J.; Mao, T.; Hu, L.; Yu, T.; Luan, X.; Dou, X.; Sutton, E.; Yue, X.; Lin, J.; et al. Contrasting behavior of the F2 peak and the topside ionosphere in response to the 2 October 2013 geomagnetic storm. J. Geophys. Res. Space Phys. 2016, 121, 10549–10563. [Google Scholar] [CrossRef]

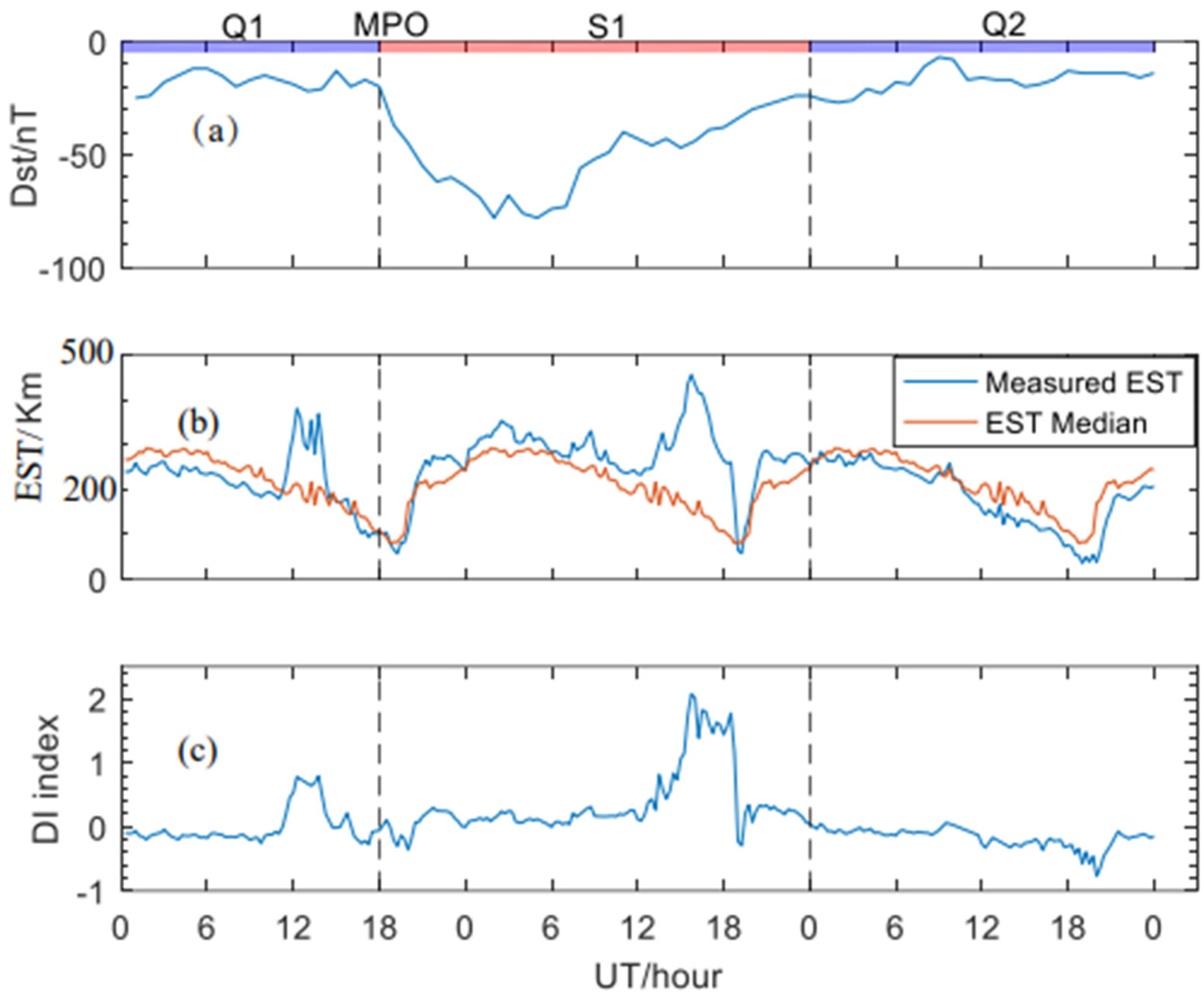

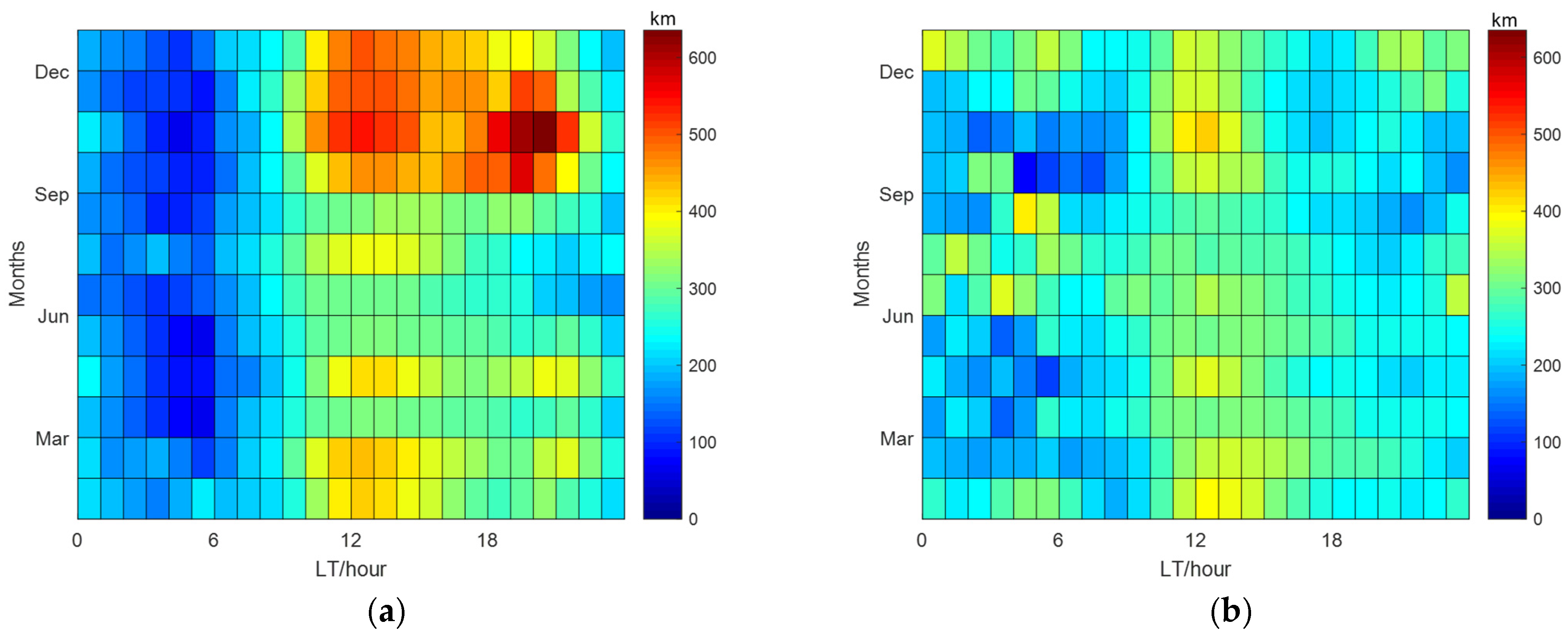
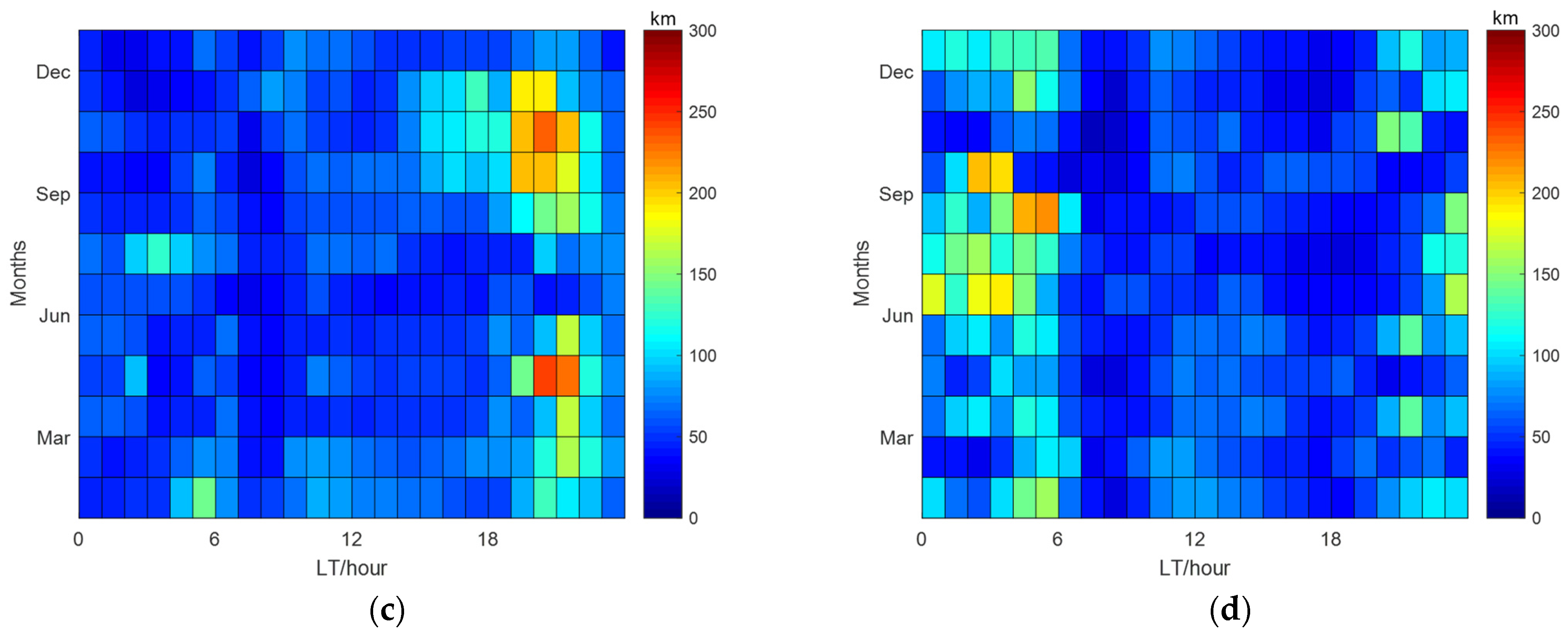
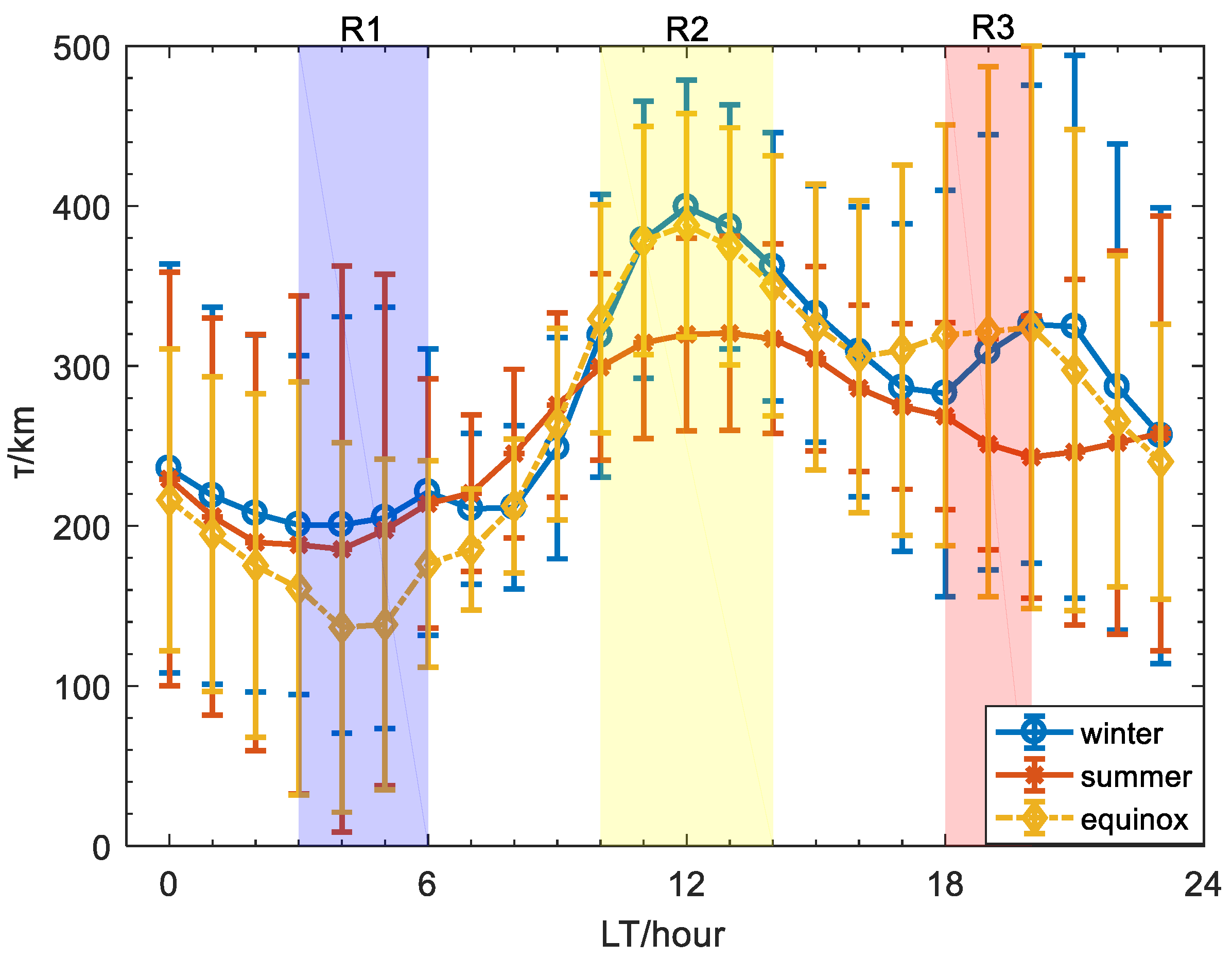
| Year | Seasons | Mean Daytime Values of τ (km) | Mean Nighttime Values of τ (km) |
|---|---|---|---|
| 2014 | Winter | 388.9 | 232.1 |
| Summer | 303.9 | 188.9 | |
| Equinox | 364.6 | 250.7 | |
| 2016 | Winter | 299.3 | 255.5 |
| Summer | 288.6 | 238.5 | |
| Equinox | 301.2 | 268.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Wu, Z.; Feng, J.; Xu, T.; Deng, Z.; Ou, M.; Xiong, W.; Zhen, W. Statistical Study of Ionospheric Equivalent Slab Thickness at Guam Magnetic Equatorial Location. Remote Sens. 2021, 13, 5175. https://doi.org/10.3390/rs13245175
Zhang Y, Wu Z, Feng J, Xu T, Deng Z, Ou M, Xiong W, Zhen W. Statistical Study of Ionospheric Equivalent Slab Thickness at Guam Magnetic Equatorial Location. Remote Sensing. 2021; 13(24):5175. https://doi.org/10.3390/rs13245175
Chicago/Turabian StyleZhang, Yuqiang, Zhensen Wu, Jian Feng, Tong Xu, Zhongxin Deng, Ming Ou, Wen Xiong, and Weimin Zhen. 2021. "Statistical Study of Ionospheric Equivalent Slab Thickness at Guam Magnetic Equatorial Location" Remote Sensing 13, no. 24: 5175. https://doi.org/10.3390/rs13245175
APA StyleZhang, Y., Wu, Z., Feng, J., Xu, T., Deng, Z., Ou, M., Xiong, W., & Zhen, W. (2021). Statistical Study of Ionospheric Equivalent Slab Thickness at Guam Magnetic Equatorial Location. Remote Sensing, 13(24), 5175. https://doi.org/10.3390/rs13245175






