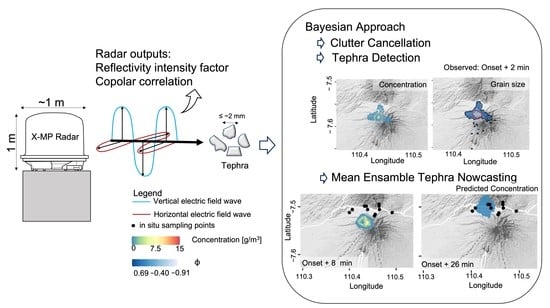
Real-Time Tephra Detection and Dispersal Forecasting by a Ground-Based Weather Radar
Abstract
:1. Introduction
2. Methods
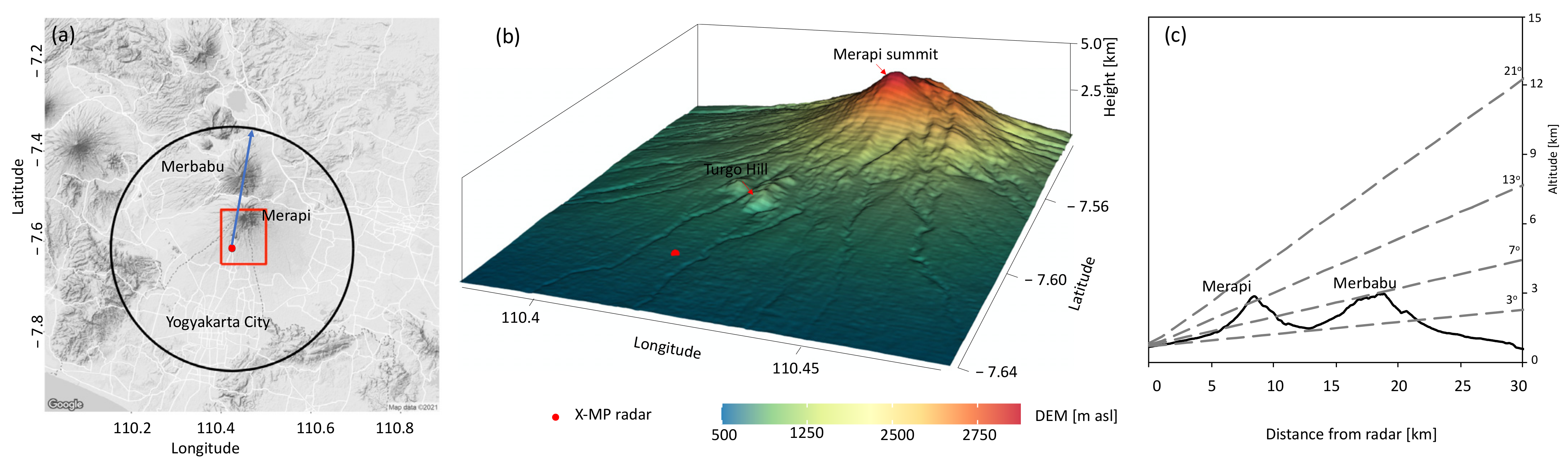
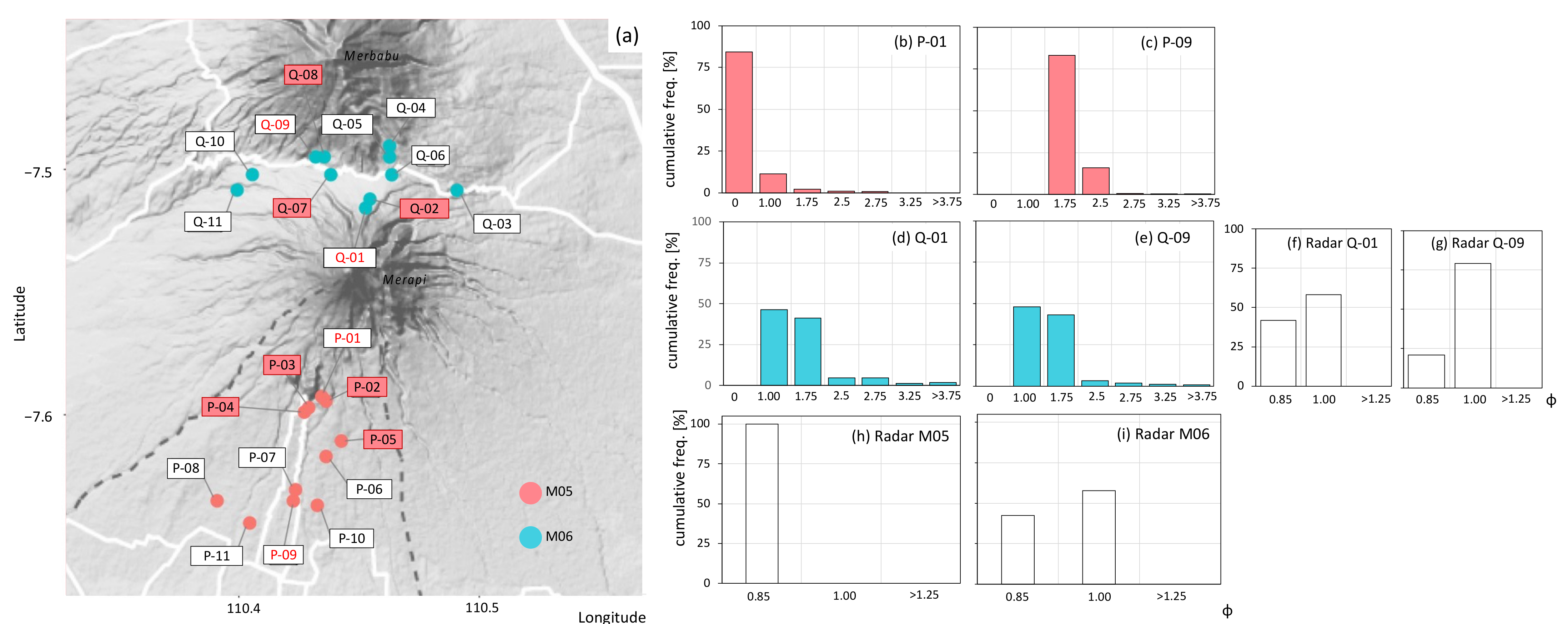
2.1. Radar Setting and Study Case
2.2. Tephra Detection
2.3. Nowcasting and Ensemble Prediction System
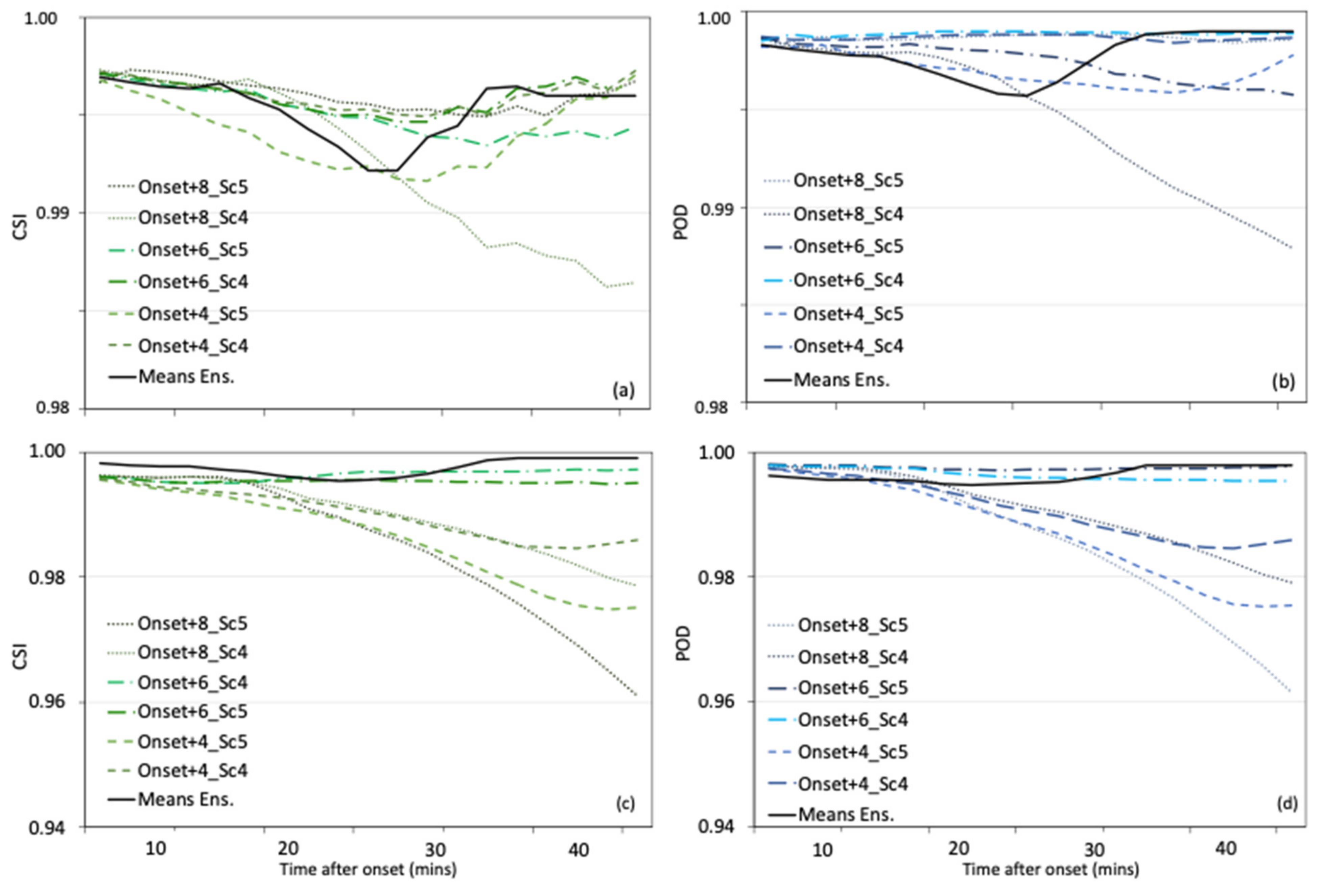
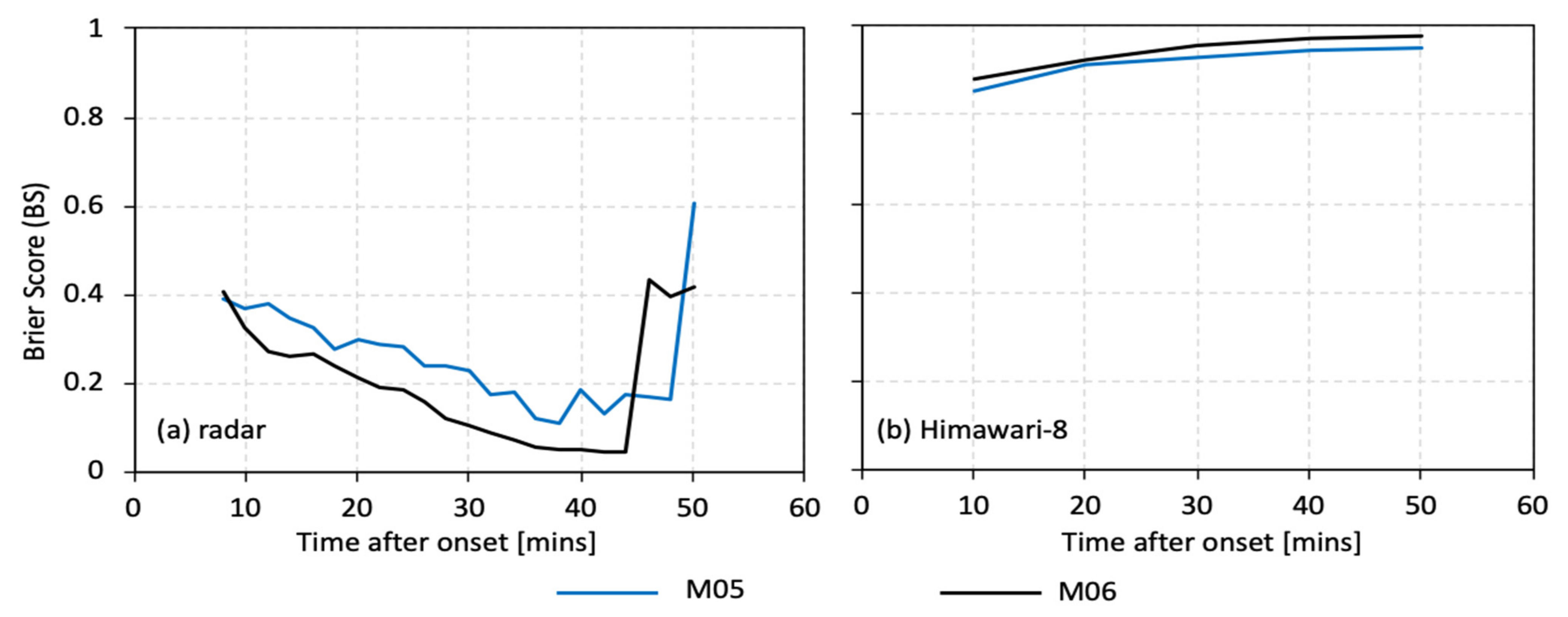
2.4. Evaluation
3. Results
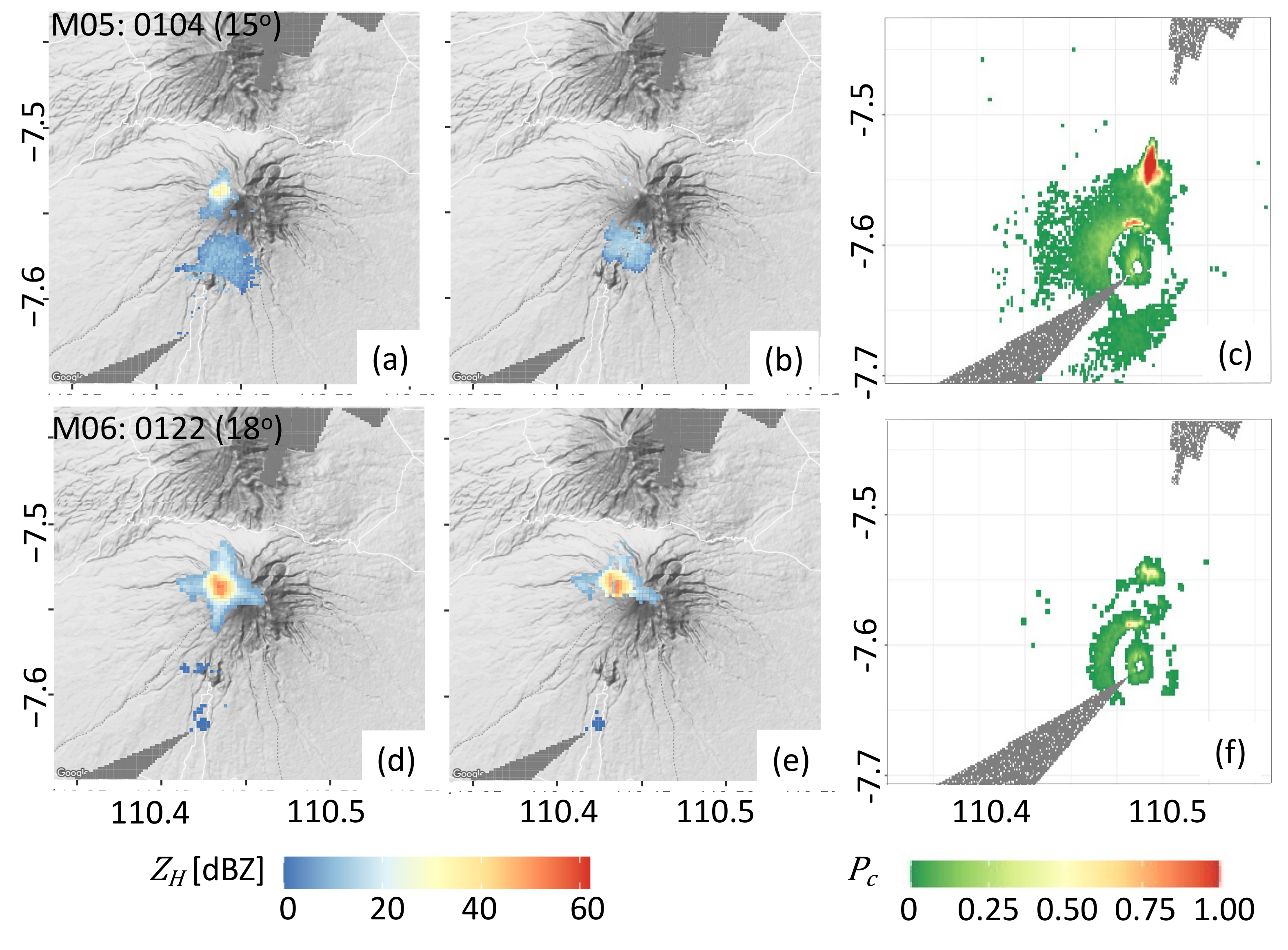
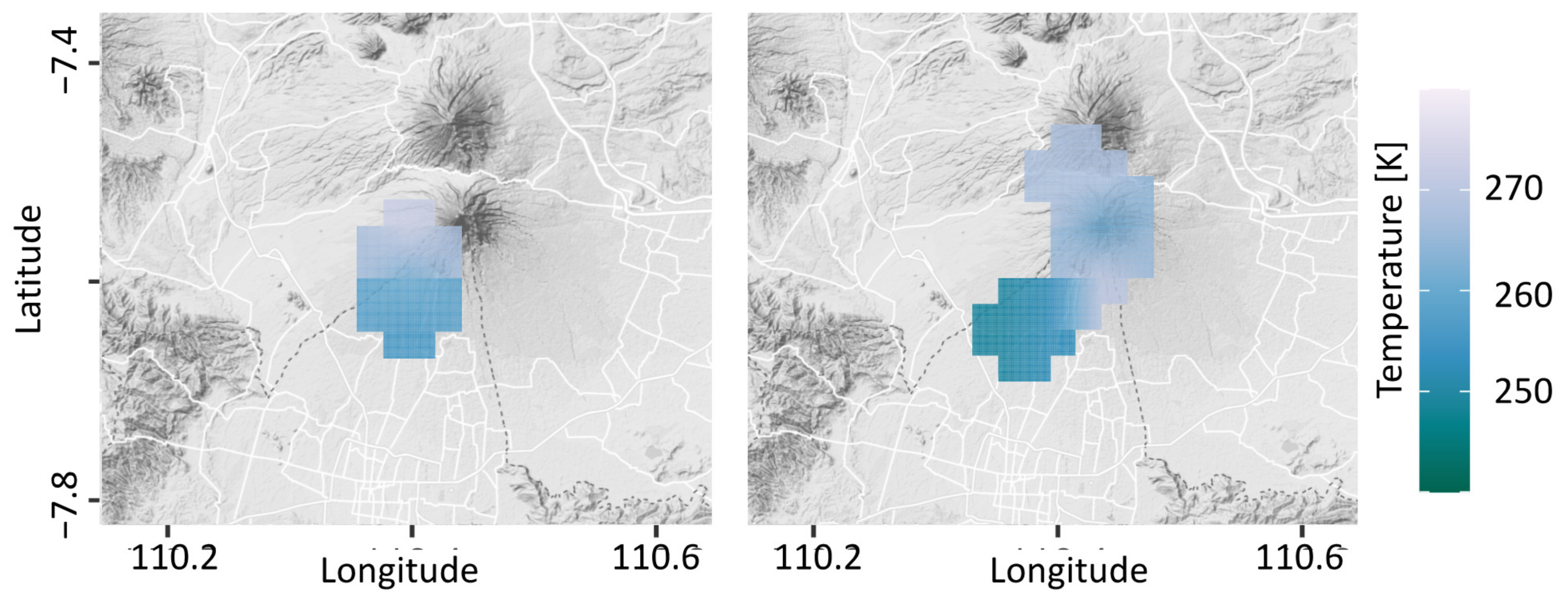
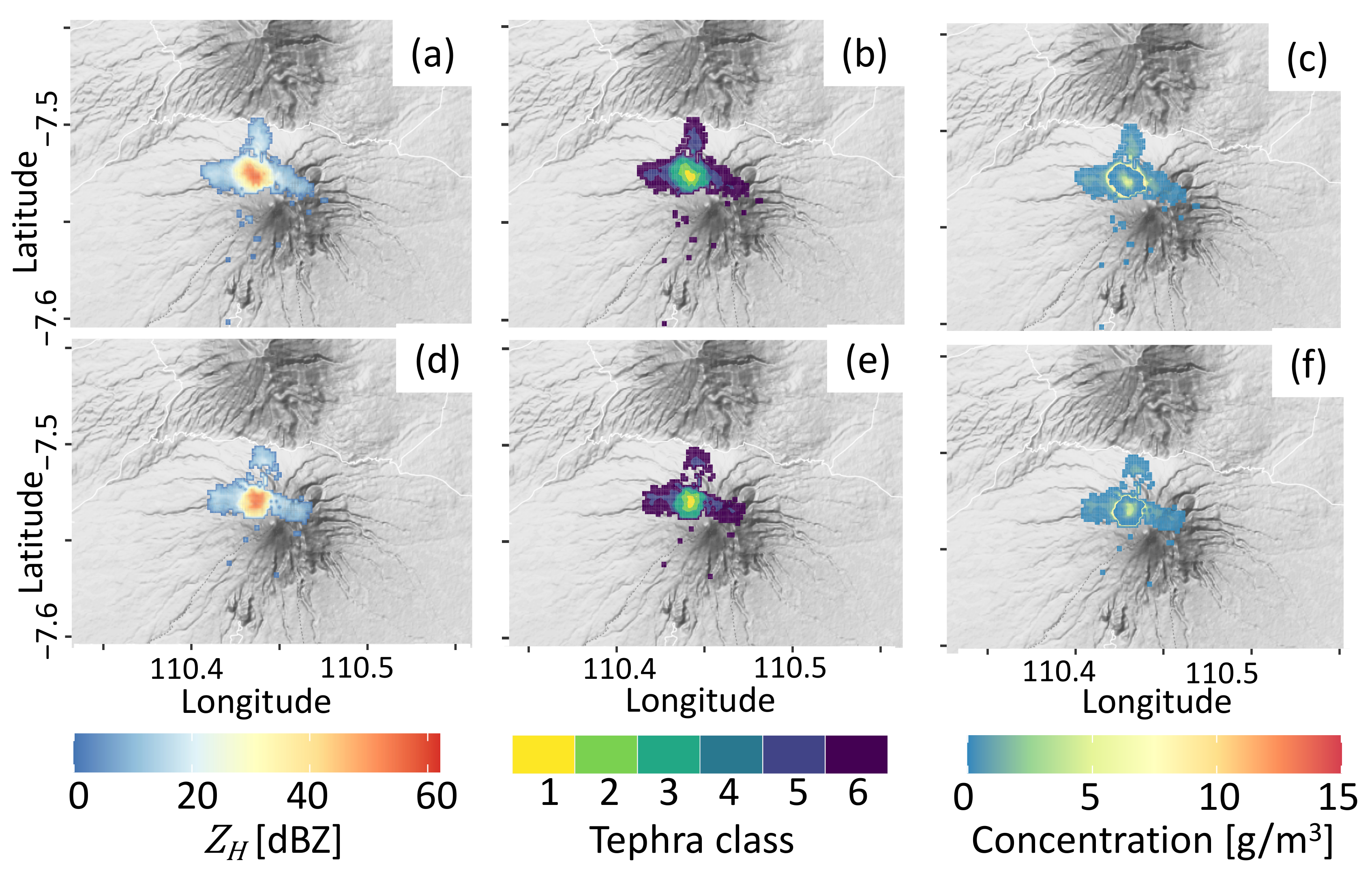
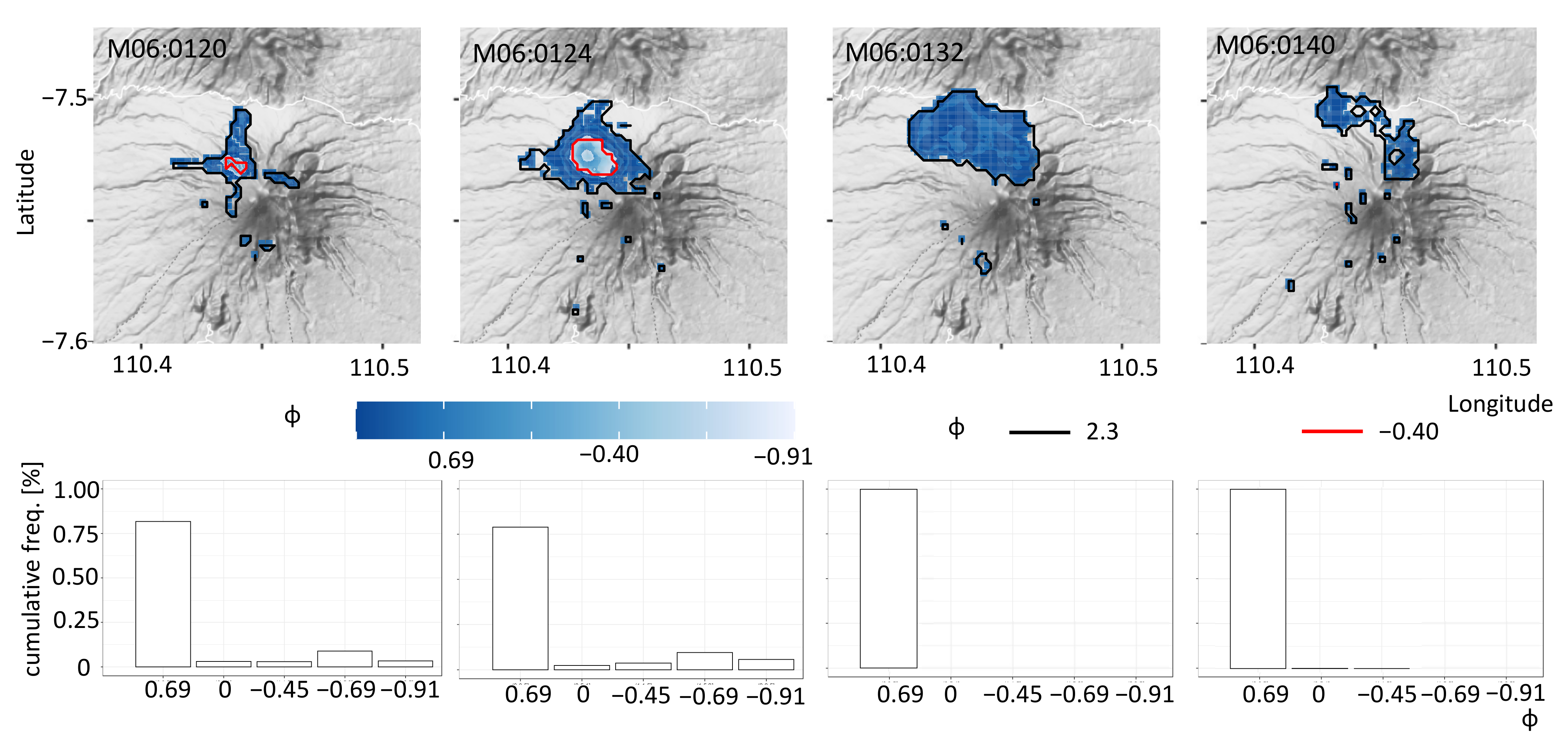
3.1. Volcanic Ash Detection
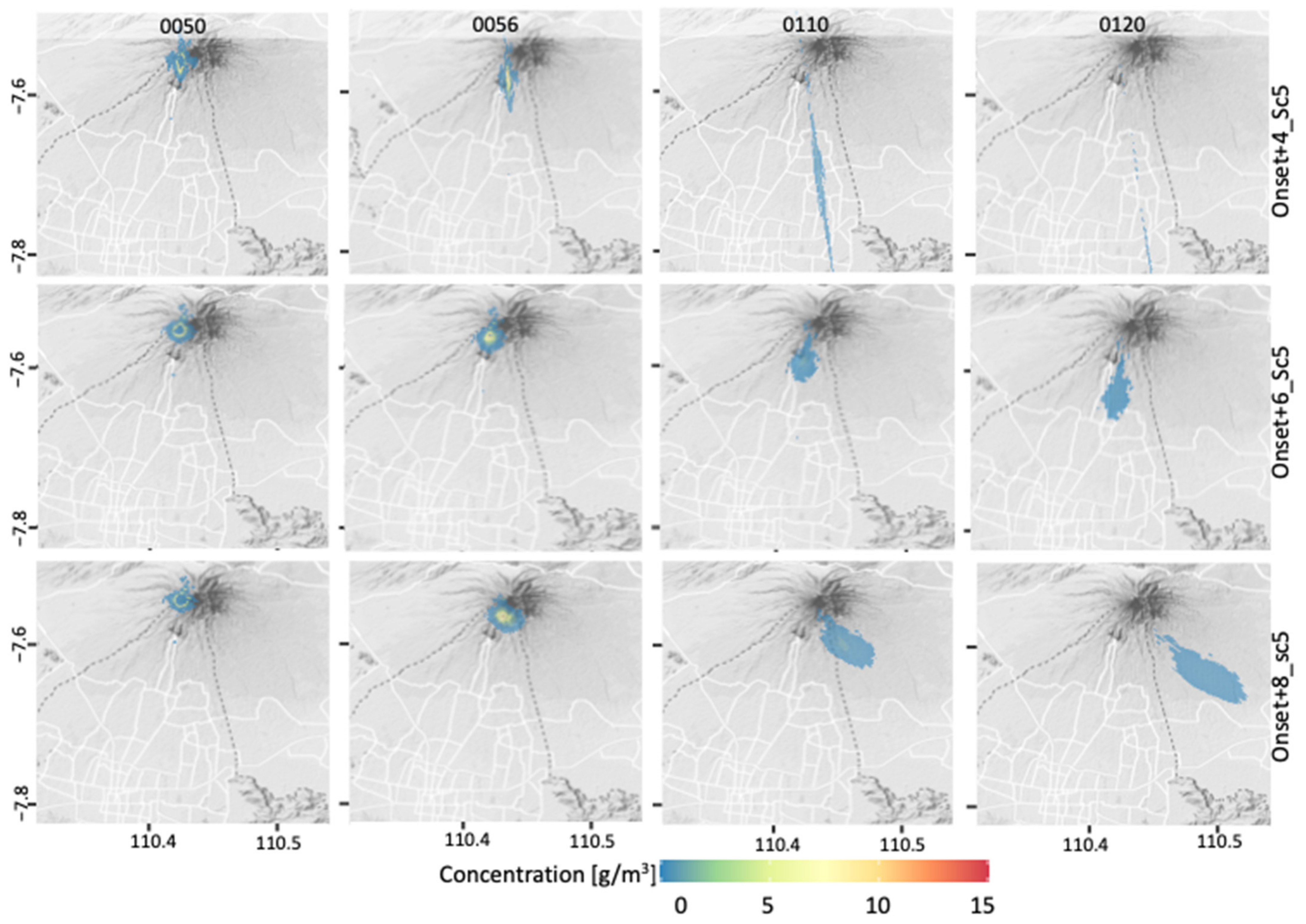
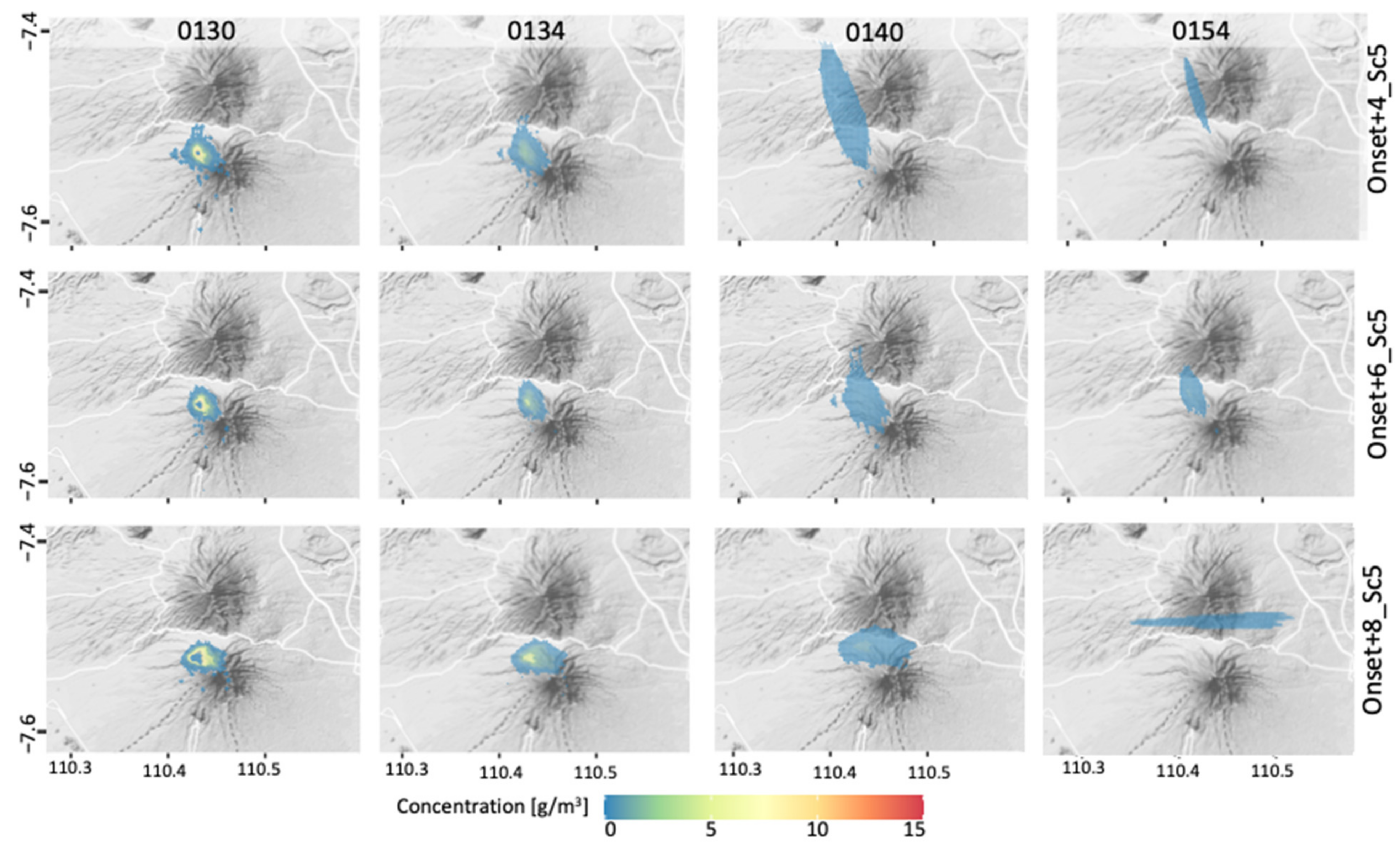
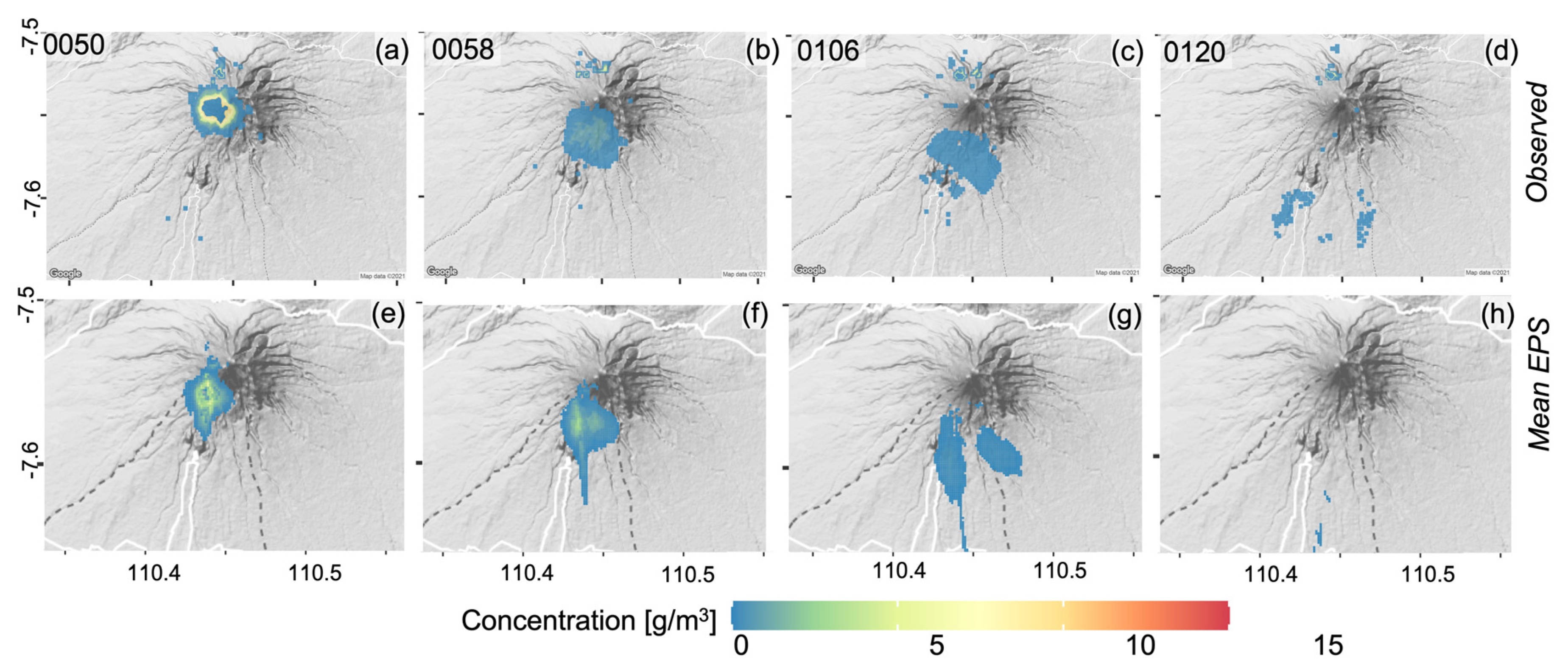
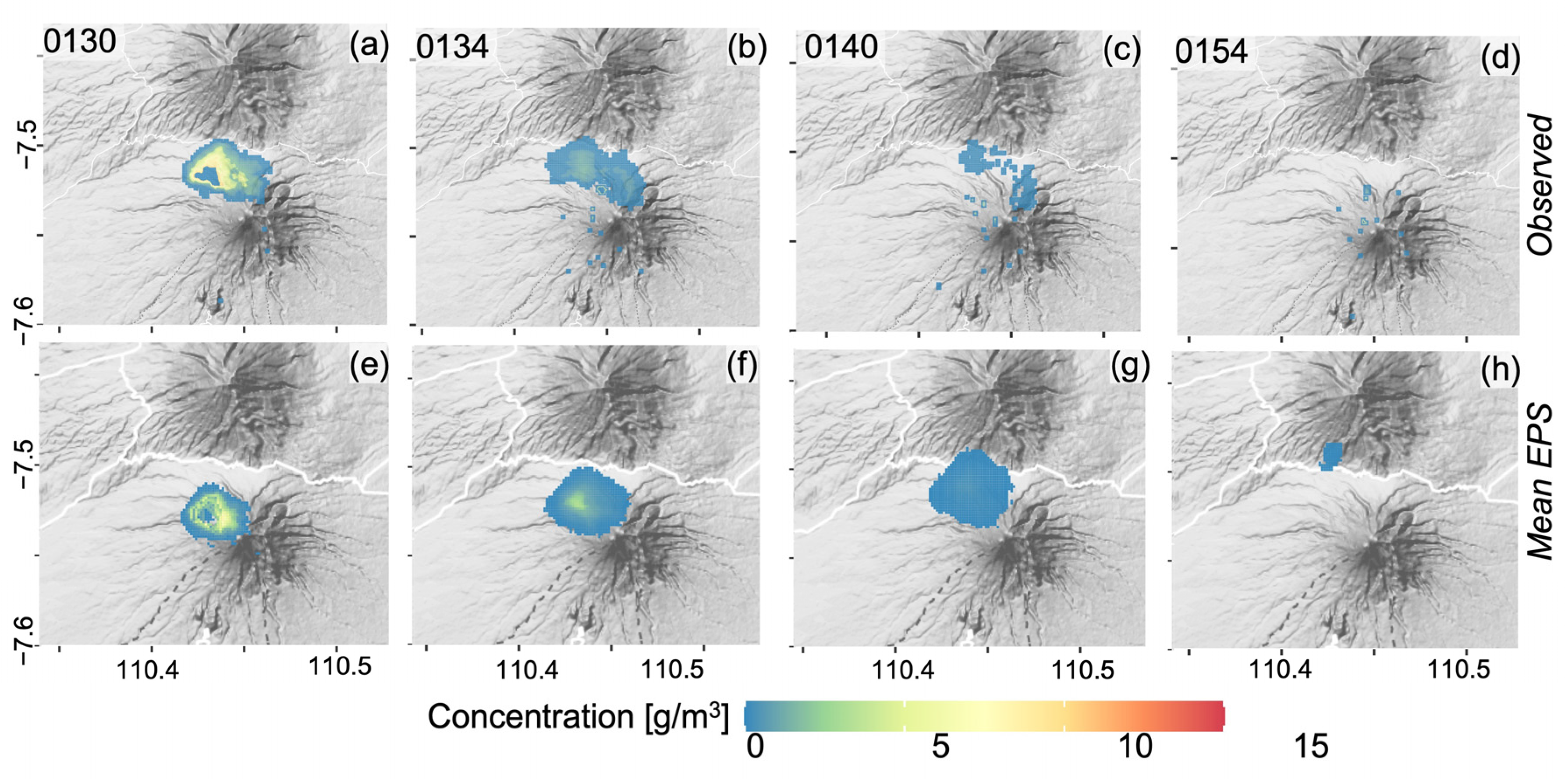
3.2. Forecasting of Plume Dispersion
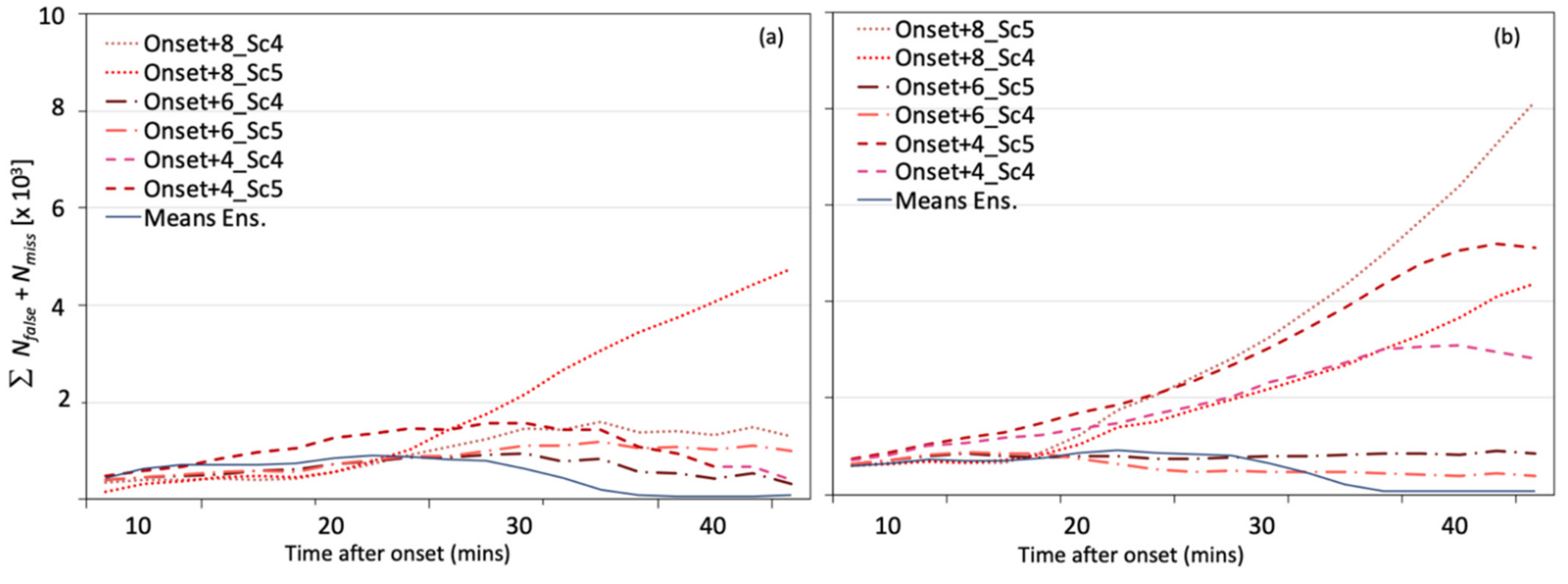
3.3. Evaluation
4. Discussion
4.1. Tephra Detection
4.2. Forecasting the Dispersal of Tephra
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Naïve Bayesian Classifier
| Concentration (g/m3) | Diameter of Particle Classes (mm) | ||||
|---|---|---|---|---|---|
| Fine Class (F) | Coarse Class (C) | ||||
| Mean | Range | Mean | Range | ||
| 0.10 | 0.015–0.35 | 1.00 | 0.35–6 | ||
| Light (L) | Mean | 0.10 | 0.10 | ||
| Range | 0.01–0.50 | 0.01–0.50 | |||
| Moderate (M) | Mean | 1.00 | 1.00 | ||
| Range | 0.50–2.00 | 0.50–2.00 | |||
| Intense (I) | Mean | 5.00 | 5.00 | ||
| Range | 2.00–10.00 | 2.00–10.00 | |||
| Class | Clutter | Non-Clutter | Invalid | |
|---|---|---|---|---|
| Elevation angle 3° | Clutter | 0.90 | 0.06 | 0.00 |
| Non-Clutter | 0.10 | 0.94 | 0.00 | |
| Invalid | 0.00 | 0.00 | 1.00 | |
| Elevation angle 5° | Clutter | 0.96 | 0.04 | 0.00 |
| Non-Clutter | 0.04 | 0.96 | 0.00 | |
| Invalid | 0.00 | 0.00 | 1.00 | |
| Elevation angle 7° | Clutter | 0.98 | 0.04 | 0.00 |
| Non-Clutter | 0.02 | 0.96 | 0.00 | |
| Invalid | 0.00 | 0.00 | 1.00 | |
| Elevation angle 9° | Clutter | 0.98 | 0.03 | 0.00 |
| Non-Clutter | 0.02 | 0.97 | 0.00 | |
| Invalid | 0.00 | 0.00 | 1.00 | |
| Elevation angle 11° | Clutter | 0.99 | 0.03 | 0.00 |
| Non-Clutter | 0.01 | 0.97 | 0.00 | |
| Invalid | 0.00 | 0.00 | 1.00 | |
| Elevation angle 13° | Clutter | 1.00 | 0.03 | 0.00 |
| Non-Clutter | 0.00 | 0.97 | 0.00 | |
| Invalid | 0.00 | 0.00 | 1.00 | |
| Elevation angle 15° | Clutter | 0.95 | 0.02 | 0.00 |
| Non-Clutter | 0.05 | 0.98 | 0.00 | |
| Invalid | 0.00 | 0.00 | 1.00 | |
| Elevation angle 18° | Clutter | 0.99 | 0.30 | 0.00 |
| Non-Clutter | 0.01 | 0.70 | 0.00 | |
| Invalid | 0.00 | 0.00 | 1.00 | |
| Elevation angle 21° | Clutter | 1.00 | 0.10 | 0.00 |
| Non-Clutter | 0.00 | 0.90 | 0.00 | |
| Invalid | 0.00 | 0.00 | 1.00 | |
| Class | F | C | |||||
|---|---|---|---|---|---|---|---|
| L | M | I | L | M | I | ||
| F (Fine class) | L | 0.94 | 0.19 | 0.04 | 0.02 | 0.00 | 0.00 |
| M | 0.06 | 0.78 | 0.18 | 0.05 | 0.01 | 0.00 | |
| I | 0.00 | 0.04 | 0.76 | 0.14 | 0.02 | 0.01 | |
| C (Coarse class) | L | 0.00 | 0.00 | 0.02 | 0.71 | 0.22 | 0.07 |
| M | 0.00 | 0.00 | 0.00 | 0.08 | 0.72 | 0.21 | |
| I | 0.00 | 0.00 | 0.00 | 0.00 | 0.04 | 0.72 | |
Appendix B. Microphysical Radar Model of Tephra Retrieval
Appendix C. Spatiotemporal Forecasting of Tephra Evolution and Cross Validation
References
- Williams, G.T.; Jenkins, S.F.; Biass, S.; Wibowo, H.E.; Harijoko, A. Remotely assessing tephra fall building damage and vulnerability: Kelud Volcano, Indonesia. J Appl. Volcanol. 2020, 9, 10. [Google Scholar] [CrossRef]
- Jenkins, S.F.; Wilson, T.M.; Magill, C.; Miller, V.; Stewart, C.; Blong, R.; Marzocchi, W.; Boulton, M.; Bonadonna, C.; Costa, A. Volcanic ash fall hazard and risk. In Global Volcanic Hazards and Risk; Loughlin, S., Sparks, S., Brown, S., Jenkins, S., Vye-Brown, C., Eds.; Cambridge University Press: Cambridge, UK, 2015; pp. 359–370. [Google Scholar] [CrossRef]
- Jenkins, S.F.; Spence, R.J.S.; Fonesca, J.F.B.D.; Solidum, R.U.; Wilson, T.M. Volcanic risk assessment: Quantifying physical vulnerability in the built environment. J Volcanol. Geotherm. Res. 2014, 276, 105–120. [Google Scholar] [CrossRef]
- Donnadieu, F.; Freville, P.; Hervier, C.; Coltelli, M.; Scollo, S.; Prestifilippo, M.; Valade, S.; Rivet, S.; Cacault, P. Near-source Doppler radar monitoring of tephra plumes at Etna. J. Volcanol. Geotherm. Res. 2016, 312, 26–39. [Google Scholar] [CrossRef]
- Donnadieu, F. Volcanological Applications of Doppler Radars: A Review and Examples from a Transportable Pulse Radar in L-Band. In Doppler Radar Observations-Weather Radar, Wind Profiler, Ionospheric Radar, and Other Advanced Applications; Bech, J., Chau, J.L., Eds.; InTech: Urbino, Italy, 2012. [Google Scholar] [CrossRef] [Green Version]
- Marzano, F.S.; Picciotti, E.; Di Fabio, S.; Montopoli, M.; Mereu, L.; Degruyter, W.; Bonadonna, C.; Ripepe, M. Near-Real-Time Detection of Tephra Eruption Onset and Mass Flow Rate Using Microwave Weather Radar and Infrasonic Arrays. IEEE Trans. Geosci. Remote Sen. 2016, 54, 6292–6306. [Google Scholar] [CrossRef] [Green Version]
- Oishi, S.; Iida, M.; Muranishi, M.; Ogawa, M.; Hapsari, R.I.; Iguchi, M. Mechanism of volcanic tephra falling detected by X-band multi parameter radar. J. Disaster Res. 2016, 11, 43–45. [Google Scholar] [CrossRef]
- Marzano, F.S.; Vulpiani, G.; Rose, W.I. Microphysical characterization of microwave radar reflectivity due to volcanic ash clouds. IEEE Trans. Geosci. Remote Sen. 2006, 44, 313–327. [Google Scholar] [CrossRef]
- Marzano, F.S.; Vulpiani, G.; Barbieri, S.; Rose, W.I. Volcanic ash cloud retrieval by ground-based microwave weather radar. IEEE Trans. Geosci. Remote Sen. 2006, 44, 3235–3246. [Google Scholar] [CrossRef]
- Montopoli, M.; Vulpiani, G.; Cimini, D.; Piccioti, E.; Marzano, F.S. Interpretation of observed microwave signatures from ground dual polarization radar and space multi-frequency radiometer for the 2011 Grímsvötn volcanic eruption. Atmos. Meas. Tech. 2014, 7, 537–552. [Google Scholar] [CrossRef] [Green Version]
- Marzano, F.S.; Picciotti, E.; Montopolli, M.; Vulpiani, G. Inside volcanic clouds–Remote sensing of ash plumes using microwave weather radars. Bull. Am. Met. Soc. 2013, 94, 1567–1586. [Google Scholar] [CrossRef]
- Shiiba, M.; Takasao, T.; Nakakita, E. Investigation of short-term rainfall prediction method by a translation model. Jpn. Conf. Hydraul. 1984, 28, 423–428. [Google Scholar]
- Hapsari, R.I.; Oishi, S.; Sunada, K.; Sano, T. Improving flood simulation in urban river basin using X-band polarimetric radar and distributed hydrological model. Ann. J. Hydra. Eng. JSCE 2010, 54, 121–126. [Google Scholar]
- Hapsari, R.I.; Oishi, S.; Sunada, K.; Nakakita, E.; Sano, T. Singular vector method on short-term rainfall prediction using radar for hydrologic ensemble prediction. Ann. J. Hydra. Eng. JSCE 2011, 67, I_109–I_114. [Google Scholar] [CrossRef]
- Hapsari, R.I. Development of Probabilistic Hydro-Meteorological Prediction for Urban Flood Disaster Prevention. Ph.D. Thesis, University of Yamanashi, Kofu, Japan, September 2011. [Google Scholar]
- Hapsari, R.I.; Oishi, S.; Syarifuddin, M.; Asmara, R.A.; Legono, D. X-MP Radar for Developing a Lahar Rainfall Threshold for the Merapi Volcano Using a Bayesian Approach. J. Disaster Res. 2019, 14, 811–828. [Google Scholar] [CrossRef]
- Zidikheri, M.J.; Lucas, C.; Potts, R.J. Quantitative verification and calibration of volcanic ash ensemble forecasts using satellite data. J. Geophys. Res.-Atmos. 2018, 123, 4135–4156. [Google Scholar] [CrossRef]
- Corradini, S.; Merucci, L.; Folch, A. Volcanic ash cloud properties: Comparison between MODIS satellite retrievals and FALL3D transport model. IEEE Geosci. Remote Sens. 2011, 8, 248–252. [Google Scholar] [CrossRef]
- Syarifuddin, M.; Oishi, S.; Hapsari, R.I.; Shiokawa, J.; Mawandha, H.G.; Iguchi, M. Estimating the Volcanic Ash Fall Rate from the Mount Sinabung Eruption on February 19, 2018 Using Weather Radar. J. Disaster Res. 2019, 14, 135–150. [Google Scholar] [CrossRef]
- Syarifuddin, M.; Oishi, S.; Nakamichi, H.; Maki, M.; Hapsari, R.I.; Mawandha, H.G.; Aisyah, N.; Basuki, A.; Loeqman, A.; Shimomura, M.; et al. A real-time tephra fallout rate model by a small-compact X-band multi-parameter radar. J Volcanol. Geotherm. Res. 2020, 405, 107040. [Google Scholar] [CrossRef]
- Syarifuddin, M.; Oishi, S.; Hapsari, R.I.; Legono, D.; Iguchi, M. Integrating X-MP Radar Data to Estimate Rainfall Induced Debris Flow in the Merapi Volcanic Area. Adv. Water Resour. 2017, 110, 249–262. [Google Scholar] [CrossRef]
- Bringi, V.N.; Chandrasekar, V. Polarimetric Doppler Weather Radar: Principles and Applications; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Zrnic, D.; Melnikov, V. Ground Clutter Recognition Using Polarimetric Spectral Parameters. Preprints, 33rd Conf. on Radar Meteorology, Cairns, Australia. Amer. Meteor. Soc. p. P11B.13. Available online: https://ams.confex.com/ams/33Radar/techprogram/paper_123205.htm (accessed on 20 November 2021).
- Setijadji, L.D.; Jesslyn, J.; Situmorang, N.G.; Wiguna, A. 2018 Eruption of Merapi: The Interpretation of Eruption Type Based on Volcanic Material Study from Explosive Eruption on May 11 and June 1, 2018 (in Bahasa Indonesia). Proceeding Seminar Nasional Kebumian 11. Yogyakarta, Indonesia, 5–6 September; 2018, pp. 908–917. Available online: https://repository.ugm.ac.id/274920/1/OVK-3_ERUPSI%20MERAPI%202018%20INTERPRETASI%20JENIS%20ERUPSI%20BERDASARKAN%20STUDI%20MATERIAL%20VULKANIK%20HASIL%20ERUPSI%20EKSPLOSIF%2011%20MEI%20DAN%201%20JUNI%20201.pdf (accessed on 15 August 2020).
- Budi-Santoso, A.; Humaida, H.; Sulistiyani; Aisyah, N.; Putra, R. The 2018 phreatic eruption, an Indication of new magmatism episodes of Merapi. In Bahasa Indonesia: Letusan Freatik 2018 Indikasi Episode Baru Aktivitas Magmatis G. Merapi. Bul. Merapi Ed. Agustus 2018, 22, 12–38. [Google Scholar]
- Centre for Volcanology and Geological Hazard Mitigation (CVGHM). Press release of Mt. Merapi on June 6, 2018, at 10:00 (in Bahasa Indonesia). 2018. Available online: http://merapi.bgl.esdm.go.id/pub/page.php?idx=321 (accessed on 28 January 2019).
- Furuno. Operator Manual: Compact X-Band Dual Polarimetric Weather Doppler Radar, Type WR-2100, Japan. 2014. Available online: https://www.furuno.com/en/systems/meteorological-monitoring/WR2120 (accessed on 20 November 2021).
- Rico-Ramirez, M.A.; Cluckie, I.D. Classification of ground clutter and anomalous propagation using dual-polarization weather radar. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1892–1904. [Google Scholar] [CrossRef]
- Lacasse, C.; Karlsdóttir, S.; Larsen, G.; Soosalu, H.; Rose, W.I.; Ernst, G.G.J. Weather radar observations of the Hekla 2000 eruption cloud, Iceland. Bull. Volcanol. 2004, 66, 457–473. [Google Scholar] [CrossRef]
- Maki, M.; Iguchi, M.; Maesaka, T.; Miwa, T.; Tanaka, T.; Kozono, T.; Momotani, T.; Yamaji, A.; Kakimoto, I. Preliminary Results of Weather Radar Observations of Sakurajima Volcanic Smoke. J. Disaster Res. 2016, 11, 15–30. [Google Scholar] [CrossRef]
- Maki, M.; Kim, Y.; Kobori, T.; Hirano, K.; Lee, D.-I.; Iguchi, M. Analyses of three-dimensional weather radar data from volcanic eruption clouds. J. Volcanol. Geotherm. Res. 2021, 412, 107178. [Google Scholar] [CrossRef]
- Marzano, F.S.; Barbieri, S.; Piccioti, E.; Karlsdottir, S. Monitoring sub-glacial volcanic eruptions using C-band radar imagery. IEEE Trans. Geosci. Remote Sens. 2009, 48, 403–414. [Google Scholar] [CrossRef]
- Corradini, S.; Montopoli, M.; Guerrieri, L.; Ricci, M.; Scollo, S.; Merucci, L.; Marzano, F.S.; Pugnaghi, S.; Prestifilippo, M.; Ventress, L.J.; et al. A Multi-Sensor Approach for Volcanic Ash Cloud Retrieval and Eruption Characterization: The 23 November 2013 Etna Lava Fountain. Remote Sens. 2016, 8, 58. [Google Scholar] [CrossRef] [Green Version]
- Vinodkumar, K.; Chandrasekar, A. Ensemble Lagged Forecasts of a Monsoon Depression over India Using a Mesoscale Model. Atmosfera 2007, 20, 25–44. [Google Scholar]
- Bivand, R.; Keitt, T.; Rowlingson, B. Rgdal: Bindings for the “Geospatial” Data Abstraction Library, R-Package Version 1.5-18. 2020. Available online: https://CRAN.R-project.org/package=rgdal (accessed on 20 November 2021).
- Kahle, D.; Wickham, H. ggmap: Spatial visualization with ggplot2. R J. 2013, 1, 144–161. [Google Scholar] [CrossRef] [Green Version]
- Bessho, K.; Date, K.; Hayashi, M.; Ikeda, A.; Imai, T.; Inoue, H.; Kumagai, Y.; Miyakawa, T.; Murata, H.; Ohno, T.; et al. An introduction to Himawari-8/9–Japan’s new-generation geostationary meteorological satellites. J. Meteor. Soc. Jpn. 2016, 94, 151–183. [Google Scholar] [CrossRef] [Green Version]
- Shimizu, A. Introduction to Himawari-8 RGB Composite Imagery. Meteorological Satellite Centre Technical Note. No.65. October 2020. Available online: https://www.data.jma.go.jp/mscweb/technotes/msctechrep65-1.pdf (accessed on 20 November 2021).
- Roebber, P.J. Visualizing multiple measures of forecast quality. Weather. Forecast. 2009, 24, 601–608. [Google Scholar] [CrossRef] [Green Version]
- Wilks, D.S. Statistical Methods in the Atmosphere; Academic Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Tournigand, P.-Y.; Taddeucci, J.; Gaudin, D.; Peña Fernández, J.J.; Del Bello, E.; Scarlato, P.; Kueppers, U.; Sesterhenn, J.; Yokoo, A. The initial development of transient volcanic plumes as a function of source conditions. J. Geophys. Res. 2019, 122, 9784–9803. [Google Scholar] [CrossRef]
- Cutler, N.A.; Streeter, R.T.; Dugmore, A.J.; Sear, E.R. How do the grain size characteristics of a tephra deposit change over time? Bull Volcanol. 2012, 83, 45. [Google Scholar] [CrossRef]
- Walker, G.P.L. Explosive Volcanic Eruptions–A New Classification Scheme. Geol. Rundsch. 1973, 62, 431–446. [Google Scholar] [CrossRef]
- Gonnermann, H.M. Magma Fragmentation. Annu. Rev. Earth 2015, 43, 431–458. [Google Scholar] [CrossRef]
- Scase, M.; Caulfield, C.; Dalsiel, S.; Hunt., J. Time-dependent plumes and jets with decreasing source strengths. J. Fluid Mech. 2006, 563, 443–461. [Google Scholar] [CrossRef] [Green Version]
- Ayzel, G.; Scheffer, T.; Heistermann, M. Rainnet v1.0: A convolutional neural network for radar-based precipitation nowcasting. Geosci. Mod. Dev. 2020, 13, 2631–2644. [Google Scholar] [CrossRef]
- Poret, M.; Corradini, S.; Merucci, L.; Costa, A.; Andronico, D.; Montopoli, M.; Vulpiani, G.; Freret-Lorgeril, V. Reconstructing volcanic plume evolution integrating satellite and ground-based data: Application to the 23 Novemberr 2013 Etna Eruption. Atmos. Chem. Phys. 2018, 18, 4695–4714. [Google Scholar] [CrossRef] [Green Version]


| Parameter | Description |
|---|---|
| Transmitter | Solid-state 200 W per channel (H, V) |
| Polarity | Dual polarimetric horizontal (H) and vertical (V) |
| Pulses | PRF 600–2500 Hz, Width 0.1–5.0 μs |
| Antenna | 0.75 m ∅, 2.7° beam width |
| Antenna gain | 33.0 dBi |
| Operating frequency | 9.47 GHz |
| Wavelength | 3.3 cm |
| Peak power | 100 W |
| Scan mode | PPI, CAPPI, RHI |
| Maximum distance display | 50 km |
| Maximum range fixed observation level | 30 km |
| Data output |
|
| No | Phenomena | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Parallel translation | X | X | |||||||
| 2 | Parallel translation and rotation | X | X | X | X | X | X | |||
| 3 | Rotation | X | X | X | X | |||||
| 4 | Parallel translation, growth-decay | X | X | X | X | X | ||||
| 5 | Parallel translation, rotation, growth-decay | X | X | X | X | X | X | X | X | X |
| 2 × 2 Confusion Matrix | Event Observed | ||
|---|---|---|---|
| YES | NO | ||
| Event Forecast | YES | Hit | Miss |
| NO | False | Hit | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Syarifuddin, M.; Jenkins, S.F.; Hapsari, R.I.; Yang, Q.; Taisne, B.; Aji, A.B.; Aisyah, N.; Mawandha, H.G.; Legono, D. Real-Time Tephra Detection and Dispersal Forecasting by a Ground-Based Weather Radar. Remote Sens. 2021, 13, 5174. https://doi.org/10.3390/rs13245174
Syarifuddin M, Jenkins SF, Hapsari RI, Yang Q, Taisne B, Aji AB, Aisyah N, Mawandha HG, Legono D. Real-Time Tephra Detection and Dispersal Forecasting by a Ground-Based Weather Radar. Remote Sensing. 2021; 13(24):5174. https://doi.org/10.3390/rs13245174
Chicago/Turabian StyleSyarifuddin, Magfira, Susanna F. Jenkins, Ratih Indri Hapsari, Qingyuan Yang, Benoit Taisne, Andika Bayu Aji, Nurnaning Aisyah, Hanggar Ganara Mawandha, and Djoko Legono. 2021. "Real-Time Tephra Detection and Dispersal Forecasting by a Ground-Based Weather Radar" Remote Sensing 13, no. 24: 5174. https://doi.org/10.3390/rs13245174
APA StyleSyarifuddin, M., Jenkins, S. F., Hapsari, R. I., Yang, Q., Taisne, B., Aji, A. B., Aisyah, N., Mawandha, H. G., & Legono, D. (2021). Real-Time Tephra Detection and Dispersal Forecasting by a Ground-Based Weather Radar. Remote Sensing, 13(24), 5174. https://doi.org/10.3390/rs13245174