Experimental Research on Evaluation of Soil Water Content Using Ground Penetrating Radar and Wavelet Packet-Based Energy Analysis
Abstract
:1. Introduction
2. Methods
2.1. Construction of Biorthogonal Wavelet Basis
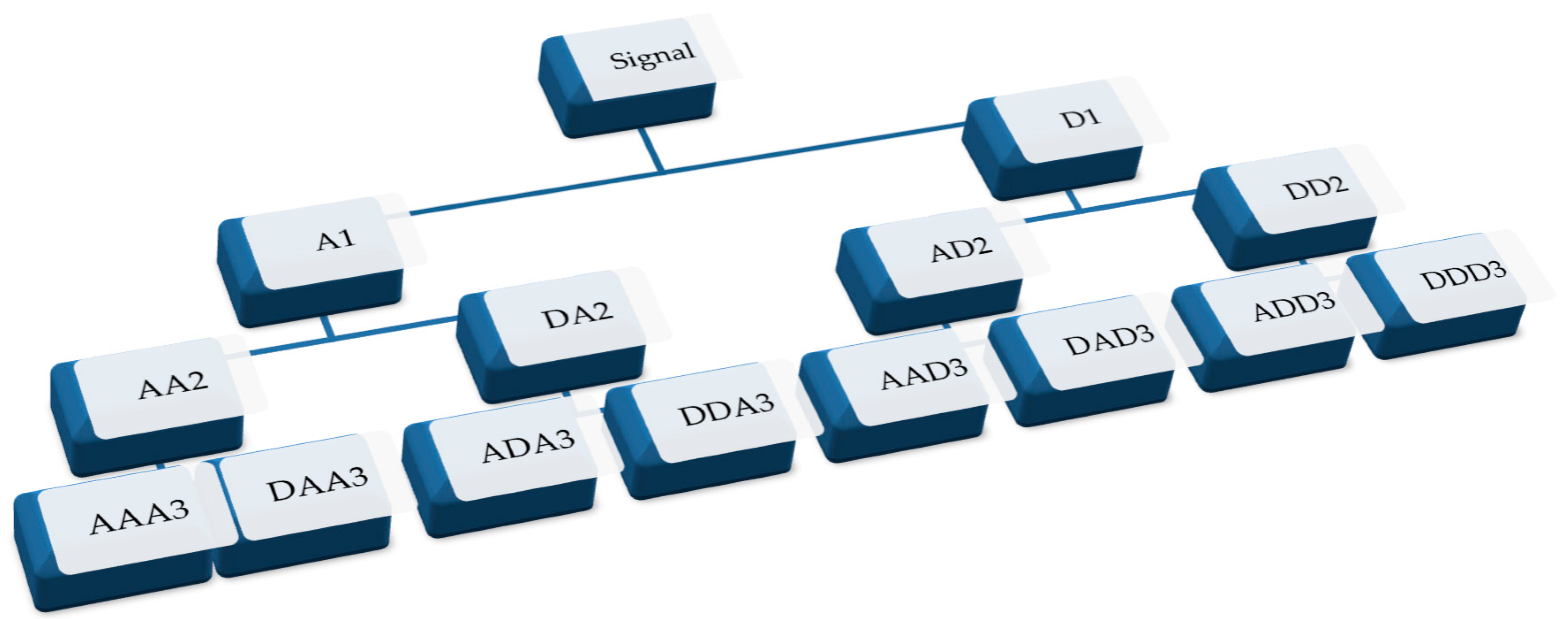
2.2. Decomposition of Wavelet Packet Transform
2.3. The WPEA Method
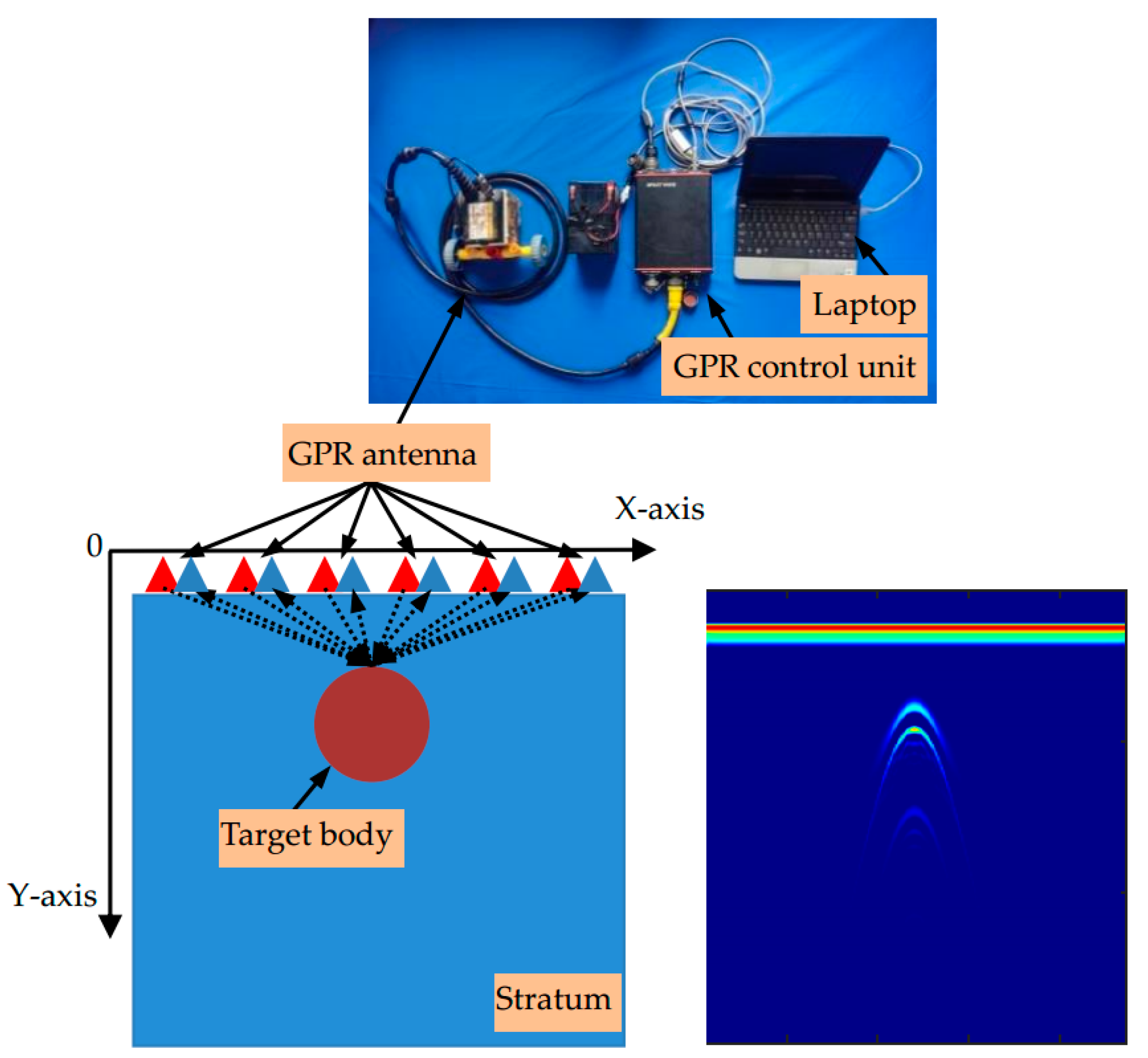
2.4. GPR Methodology
2.4.1. Detection Principle
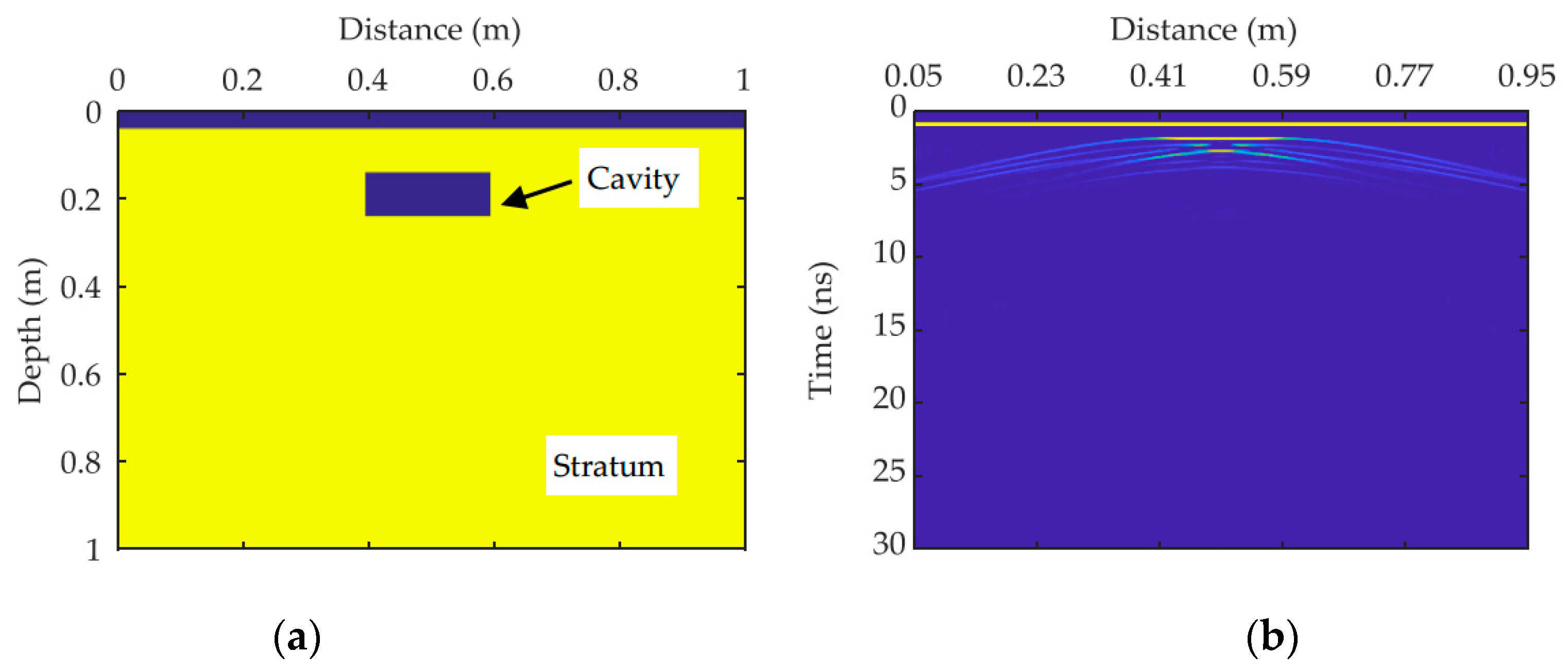
2.4.2. Forward Simulation
3. Experimental Investigation
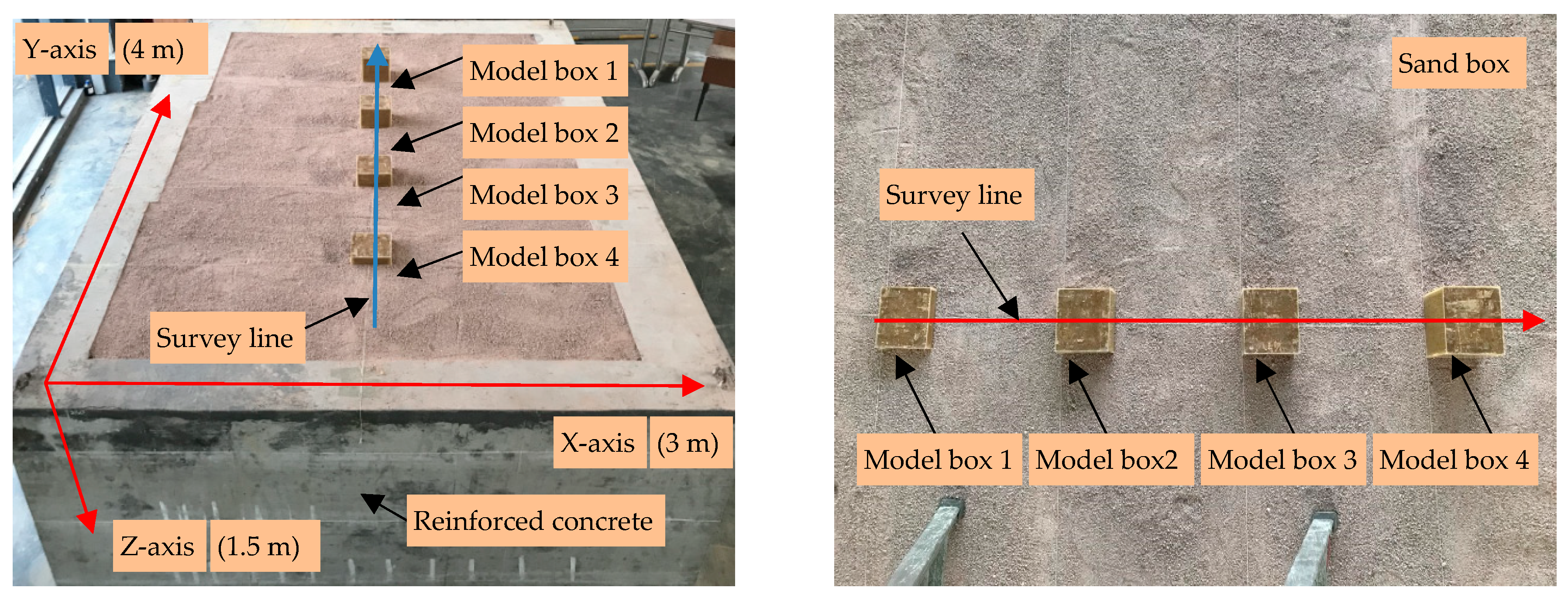
3.1. Experimental Setup
3.2. GPR Data Collection
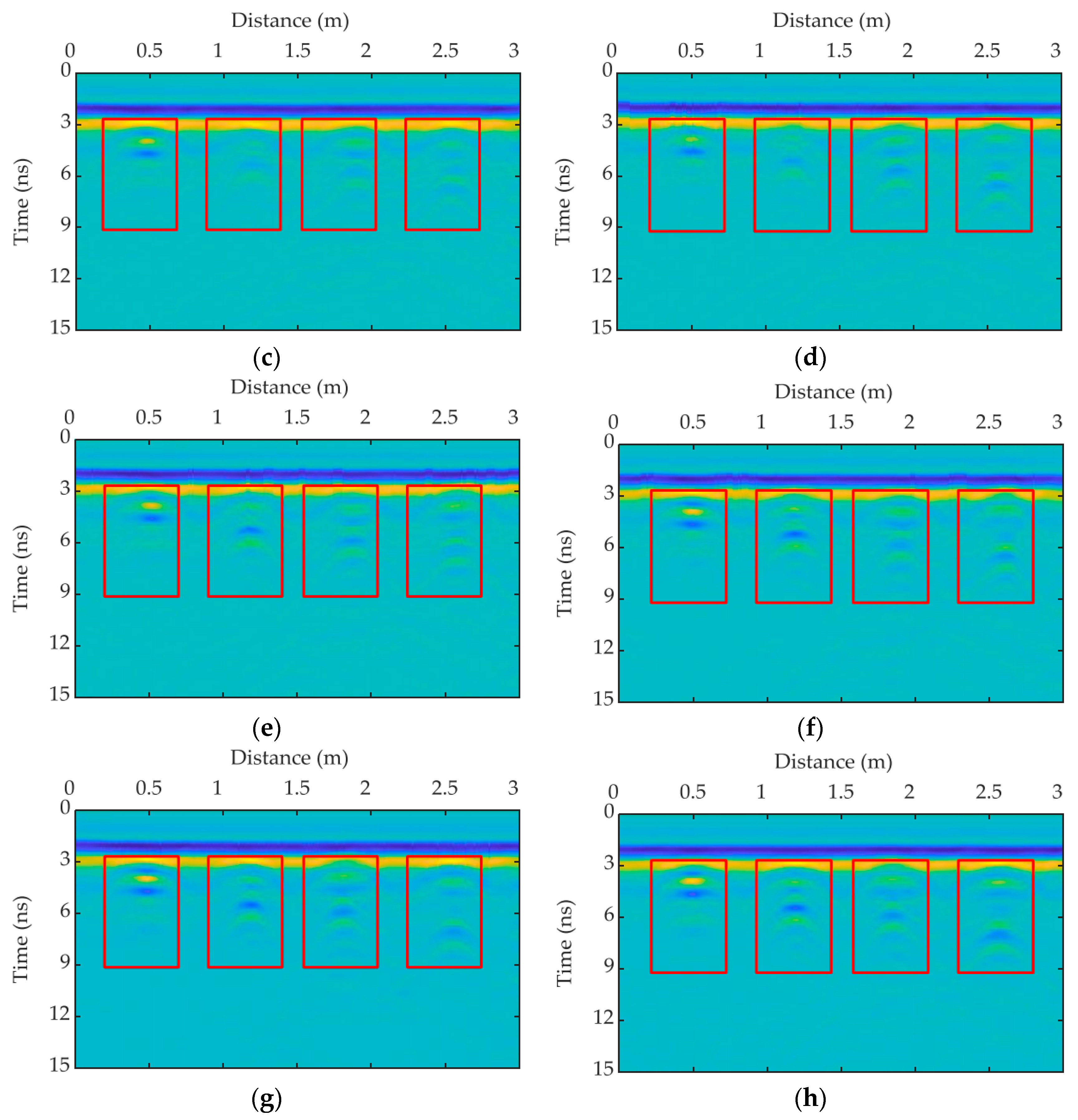
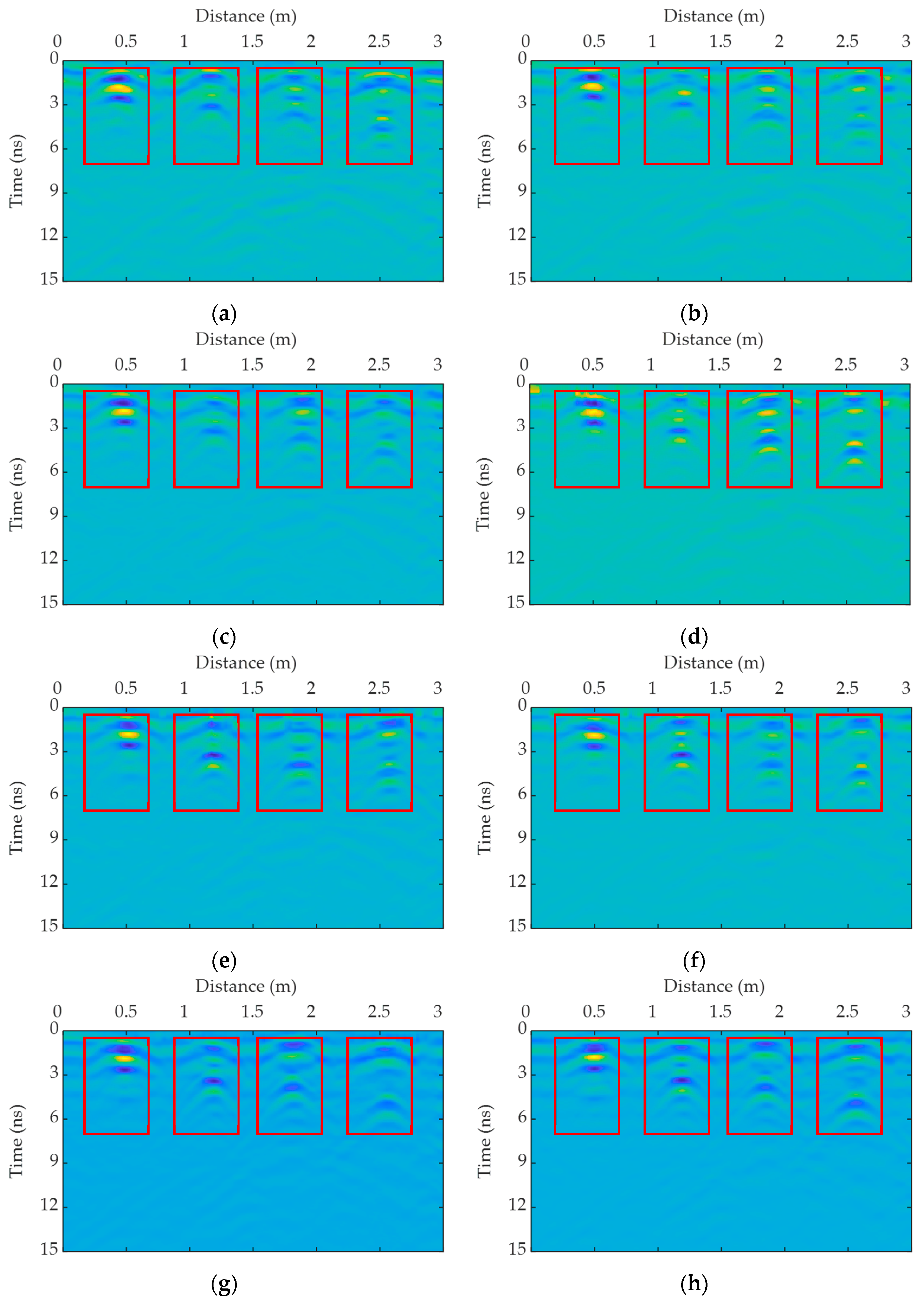
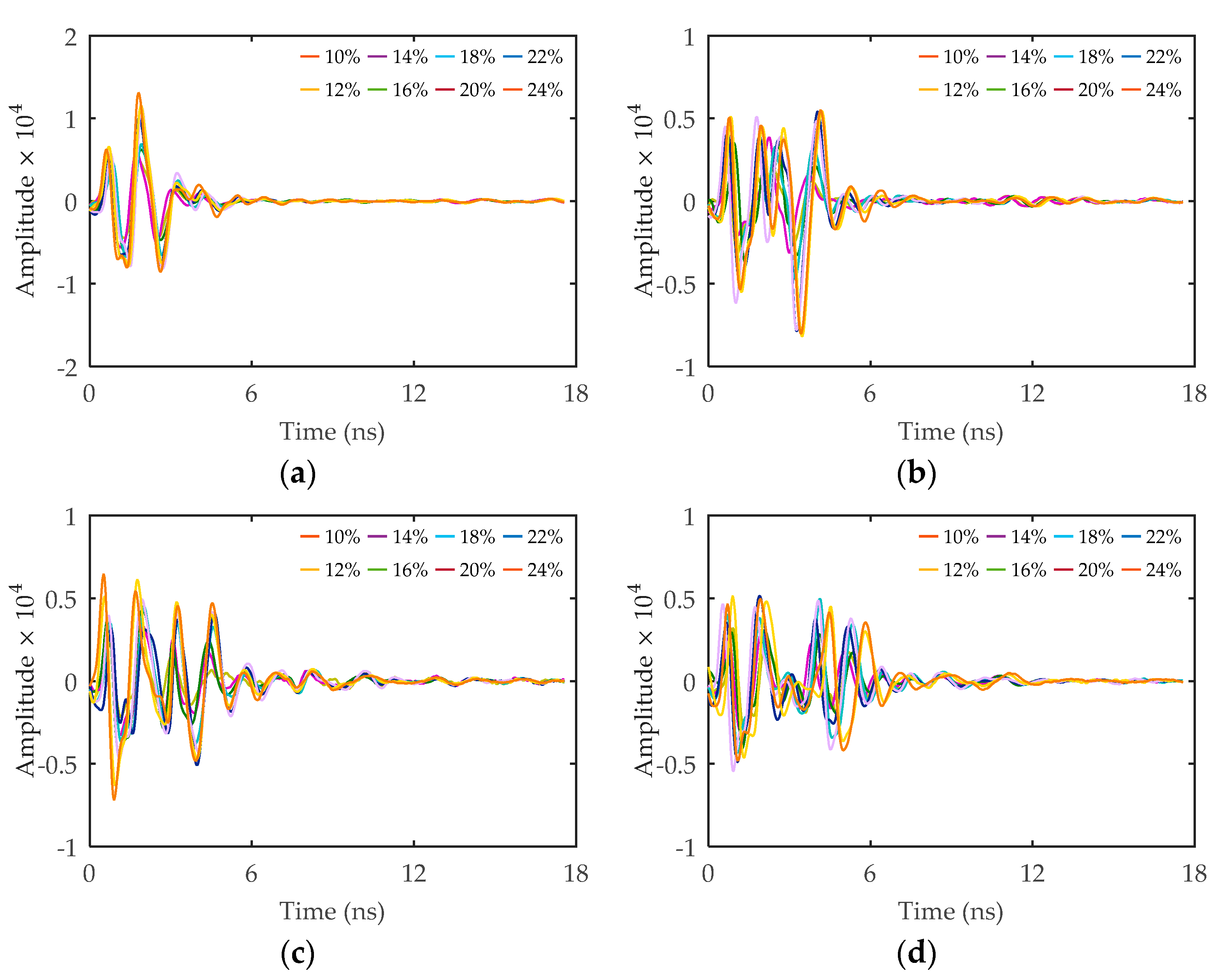
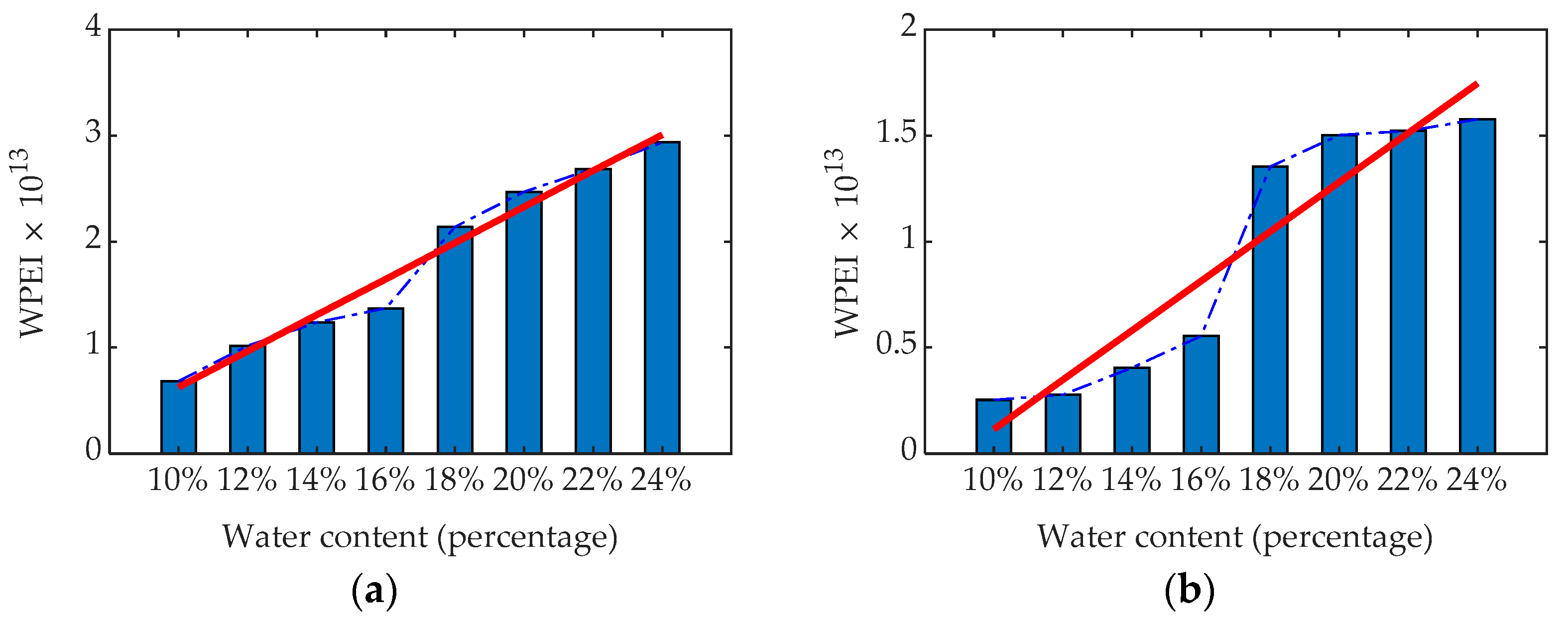
4. Results
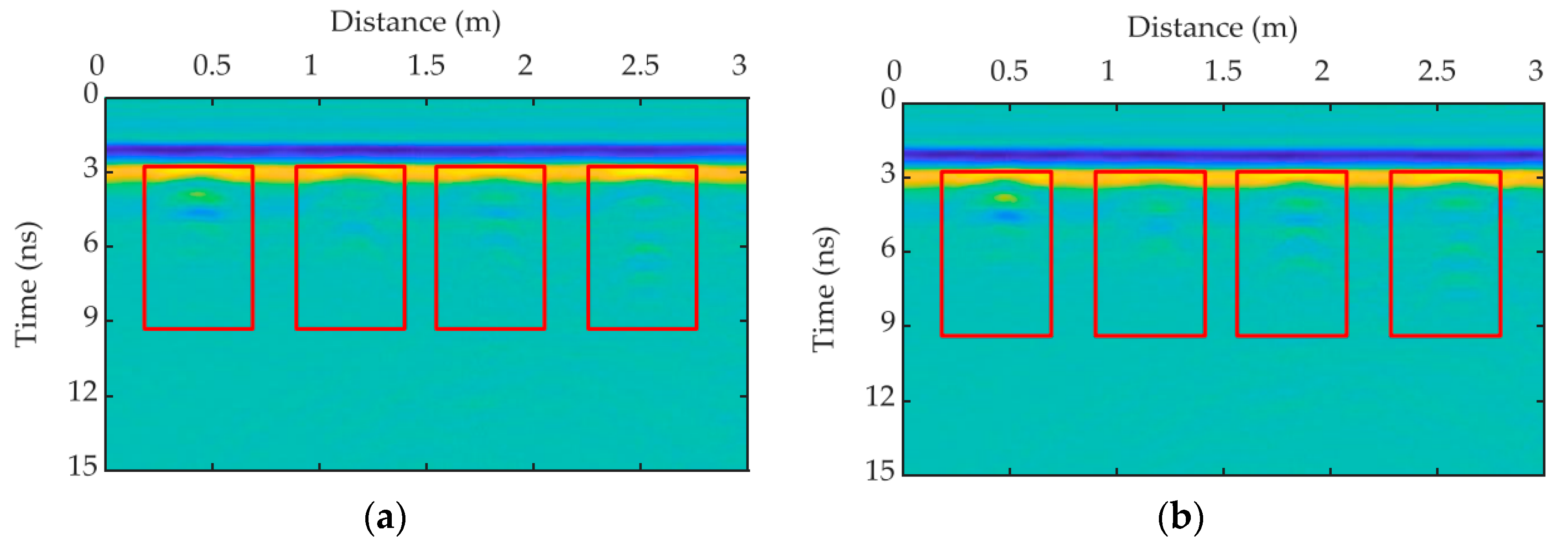
4.1. Preprocessing of GPR Signals
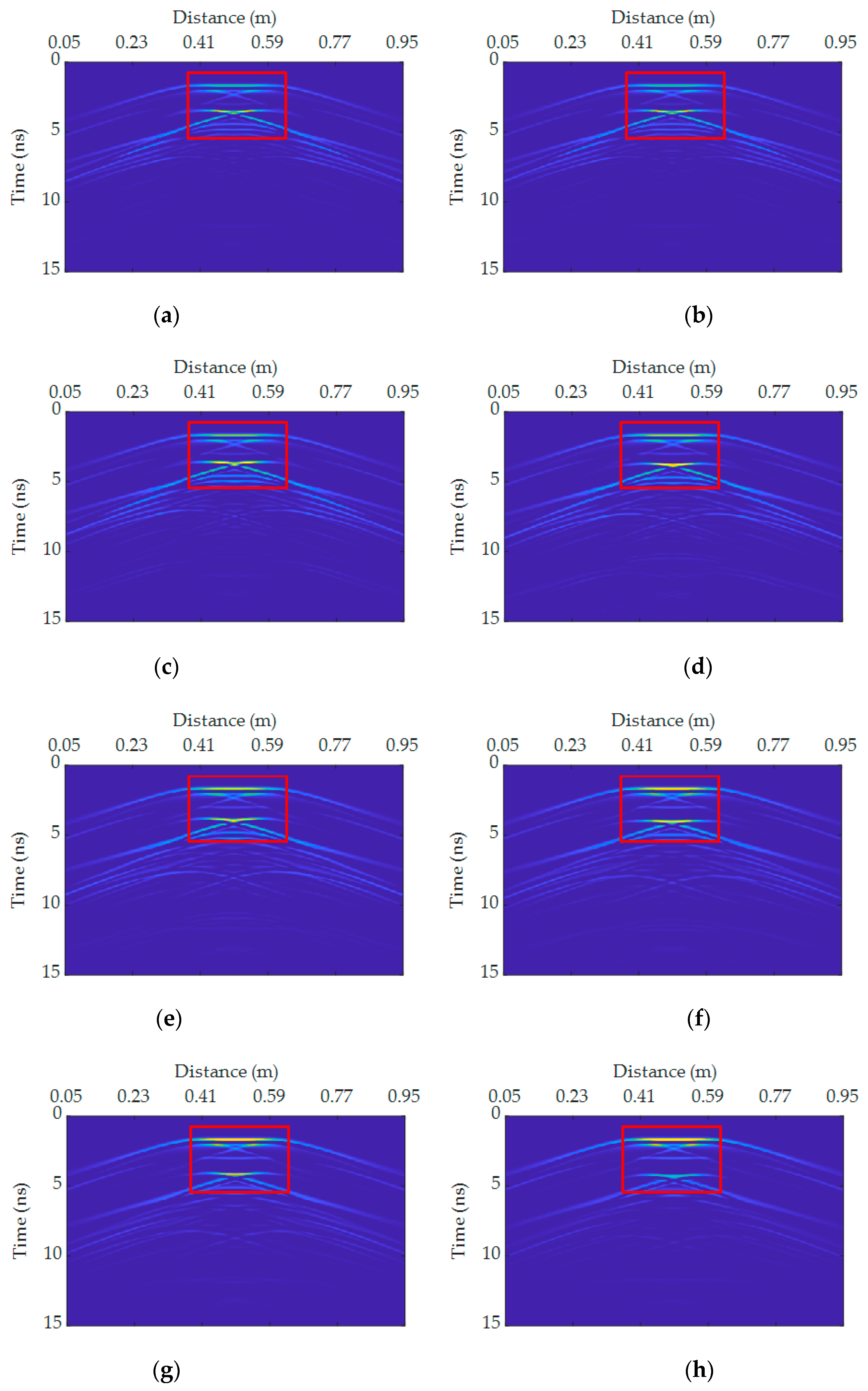
4.2. Time-Domain Signals Response
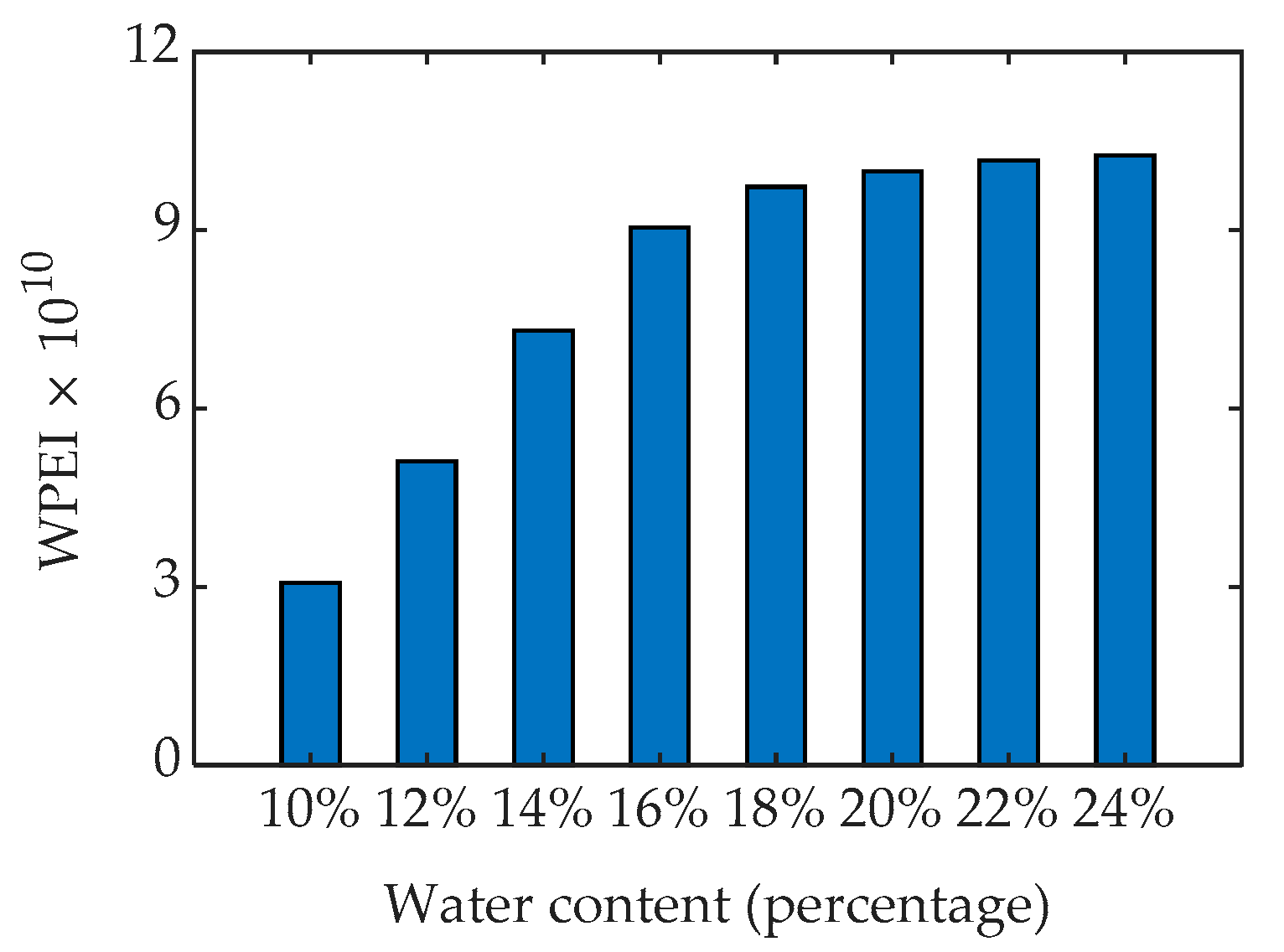
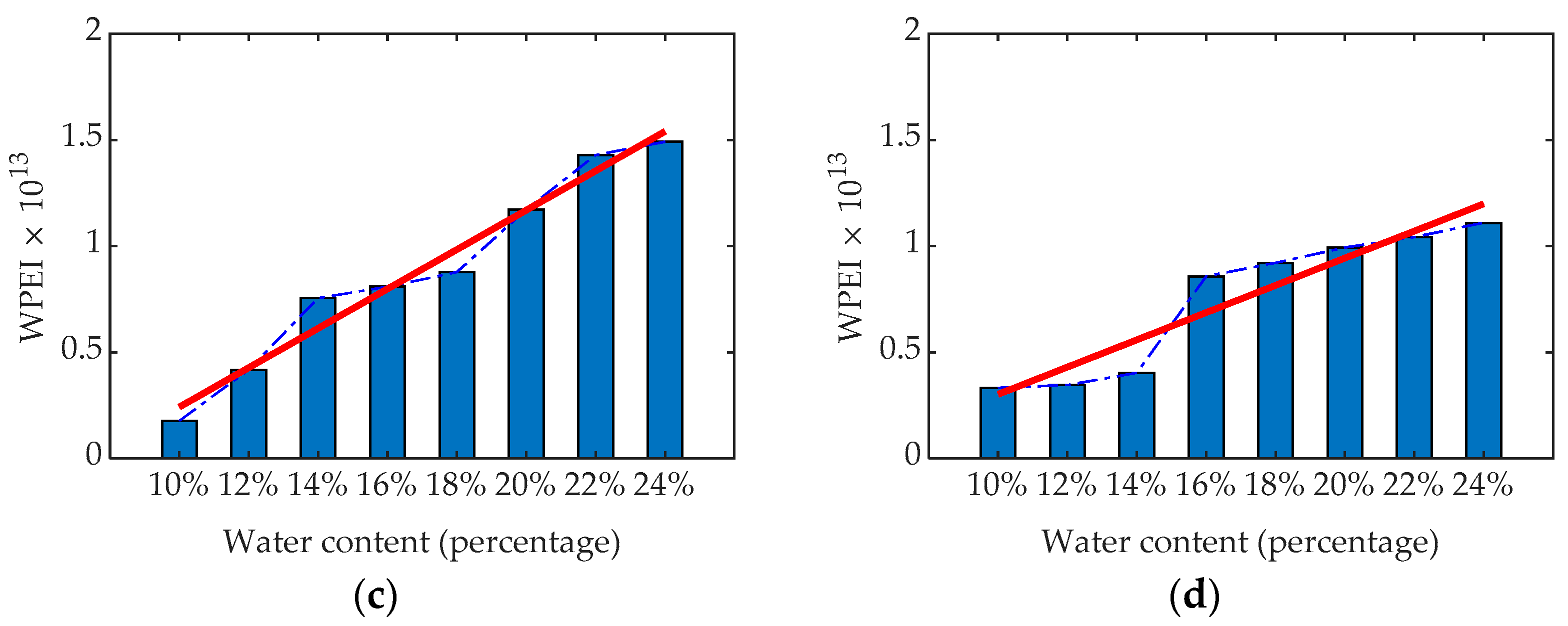
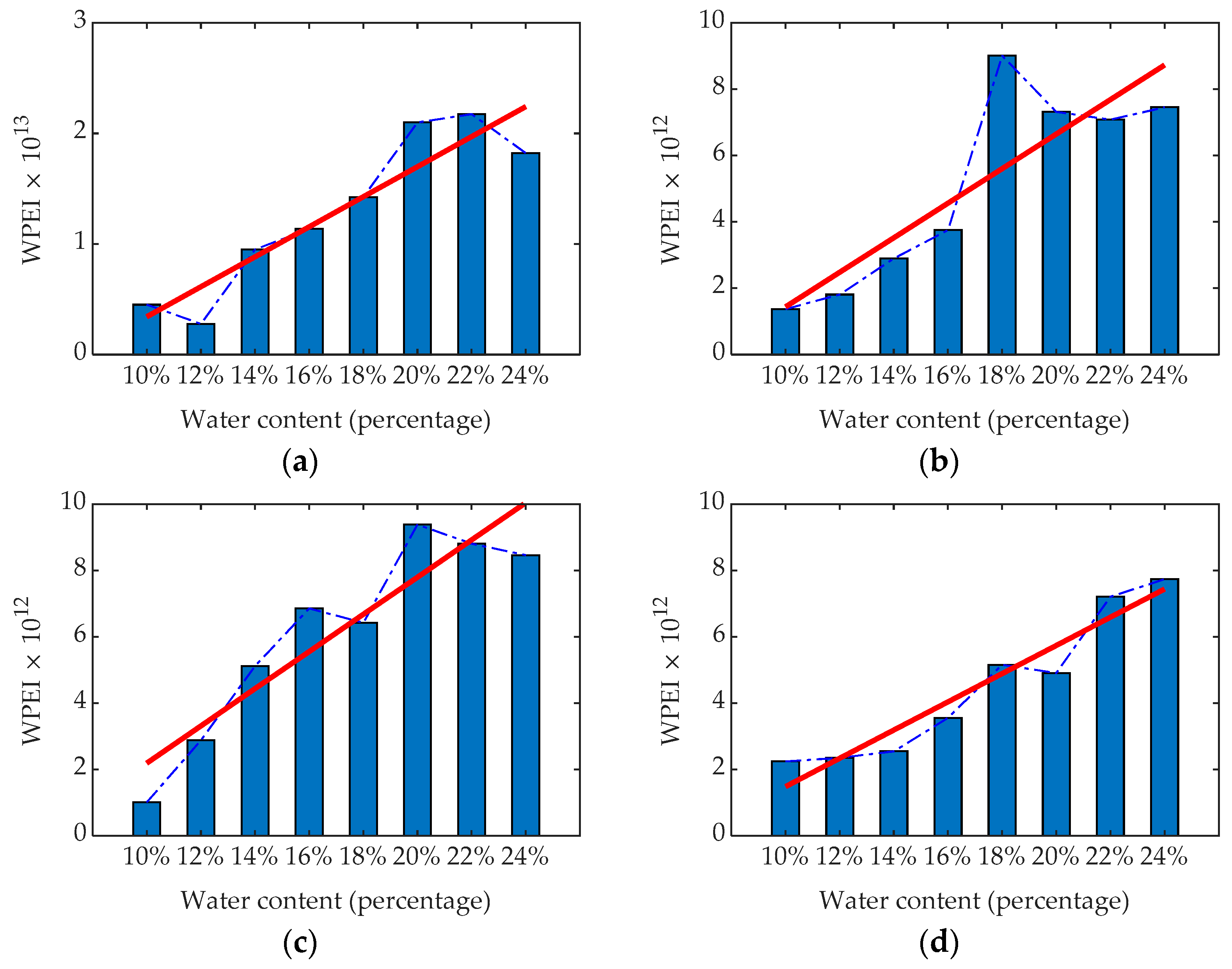
4.3. WPEI of GPR Signals
4.4. Comparative Analysis
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shen, X.; Foster, T.; Baldi, H.; Dobreva, I.; Burson, B.; Hays, D.; Tabien, R.; Jessup, R. Quantification of soil organic carbon in biochar-amended soil using ground penetrating radar (GPR). Remote Sens. 2019, 11, 2874. [Google Scholar] [CrossRef] [Green Version]
- Zajícová, K.; Chuman, T. Application of ground penetrating radar methods in soil studies: A review. Geoderma 2019, 343, 116–129. [Google Scholar] [CrossRef]
- SU, S.L.; Singh, D.N.; Shojaei Baghini, M. A critical review of soil moisture measurement. Measurement 2014, 54, 92–105. [Google Scholar] [CrossRef]
- Venmans, A.A.M.; van de Ven, R.; Kollen, J. Rapid and non-intrusive measurements of moisture in road constructions using passive microwave radiometry and GPR—Full scale test. Procedia Eng. 2016, 143, 1244–1251. [Google Scholar] [CrossRef] [Green Version]
- Klewe, T.; Strangfeld, C.; Kruschwitz, S. Review of moisture measurements in civil engineering with ground penetrating radar—Applied methods and signal features. Constr. Build. Mater. 2021, 278, 122250. [Google Scholar] [CrossRef]
- Cui, X.; Zhang, Z.; Guo, L.; Liu, X.; Quan, Z.; Cao, X.; Chen, X. The root-soil water relationship is spatially anisotropic in shrub-encroached grassland in North China: Evidence from GPR investigation. Remote Sens. 2021, 13, 1137. [Google Scholar] [CrossRef]
- Liu, J.; Cheng, Y.S. A new approach of detecting and evaluation railway by using the train-mounted ground penetrating radar in China. Adv. Mater. Res. 2011, 243–249, 4351–4355. [Google Scholar] [CrossRef]
- Cao, Q.; Song, X.; Wu, H.; Gao, L.; Liu, F.; Yang, S.; Zhang, G. Mapping the response of volumetric soil water content to an intense rainfall event at the field scale using GPR. J. Hydrol. 2020, 583, 124605. [Google Scholar] [CrossRef]
- Tong, Z.; Gao, J.; Zhang, H. Innovative method for recognizing subgrade defects based on a convolutional neural network. Constr. Build. Mater. 2018, 169, 69–82. [Google Scholar] [CrossRef]
- Barca, E.; De Benedetto, D.; Stellacci, A.M. Contribution of EMI and GPR proximal sensing data in soil water content assessment by using linear mixed effects models and geostatistical approaches. Geoderma 2019, 343, 280–293. [Google Scholar] [CrossRef]
- Shamir, O.; Goldshleger, N.; Basson, U.; Reshef, M. Laboratory measurements of subsurface spatial moisture content by ground-penetrating radar (GPR) diffraction and reflection imaging of agricultural soils. Remote Sens. 2018, 10, 1667. [Google Scholar] [CrossRef] [Green Version]
- Galagedara, L.W.; Parkin, G.W.; Redman, J.D.; von Bertoldi, P.; Endres, A.L. Field studies of the GPR ground wave method for estimating soil water content during irrigation and drainage. J. Hydrol. 2005, 301, 182–197. [Google Scholar] [CrossRef]
- Tian, J.; Yue, J.; Philpot, W.D.; Dong, X.; Tian, Q. Soil moisture content estimate with drying process segmentation using shortwave infrared bands. Remote Sens. Environ. 2021, 263, 112552. [Google Scholar] [CrossRef]
- Reynolds, S.G. The gravimetric method of soil moisture determination Part I A study of equipment, and methodological problems. J. Hydrol. 1970, 11, 258–273. [Google Scholar] [CrossRef]
- Plati, C.; Loizos, A. Estimation of in-situ density and moisture content in HMA pavements based on GPR trace reflection amplitude using different frequencies. J. Appl. Geophys. 2013, 97, 3–10. [Google Scholar] [CrossRef]
- Khakiev, Z.; Shapovalov, V.; Kruglikov, A.; Morozov, A.; Yavna, V. Investigation of long term moisture changes in trackbeds using GPR. J. Appl. Geophys. 2014, 110, 1–4. [Google Scholar] [CrossRef]
- Walker, J.P.; Willgoose, G.R.; Kalma, J.D. In situ measurement of soil moisture: A comparison of techniques. J. Hydrol. 2004, 293, 85–99. [Google Scholar] [CrossRef]
- Zhang, J.; Lin, H.; Doolittle, J. Soil layering and preferential flow impacts on seasonal changes of GPR signals in two contrasting soils. Geoderma 2014, 213, 560–569. [Google Scholar] [CrossRef]
- Zreda, M.; Desilets, D.; Ferré, T.P.A.; Scott, R.L. Measuring soil moisture content non-invasively at intermediate spatial scale using cosmic-ray neutrons. Geophys. Res. Lett. 2008, 35, L21402. [Google Scholar] [CrossRef] [Green Version]
- Bablet, A.; Vu, P.V.H.; Jacquemoud, S.; Viallefont-Robinet, F.; Fabre, S.; Briottet, X.; Sadeghi, M.; Whiting, M.L.; Baret, F.; Tian, J. MARMIT: A multilayer radiative transfer model of soil reflectance to estimate surface soil moisture content in the solar domain (400–2500 nm). Remote Sens. Environ. 2018, 217, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Verstraeten, W.W.; Veroustraete, F.; Feyen, J. Assessment of evapotranspiration and soil moisture content across different scales of observation. Sensors 2008, 8, 70–117. [Google Scholar] [CrossRef] [Green Version]
- Hu, F.; Wei, Z.; Zhang, W.; Dorjee, D.; Meng, L. A spatial downscaling method for SMAP soil moisture through visible and shortwave-infrared remote sensing data. J. Hydrol. 2020, 590, 125360. [Google Scholar] [CrossRef]
- Ferrazzoli, P.; Paloscia, S.; Pampaloni, P.; Schiavon, G.; Solimini, D.; Coppo, P. Sensitivity of microwave measurements to vegetation biomass and soil moisture content: A case study. IEEE Trans. Geosci. Remote Sens. 1992, 30, 750–756. [Google Scholar] [CrossRef]
- Qiu, J.; Crow, W.T.; Wagner, W.; Zhao, T. Effect of vegetation index choice on soil moisture retrievals via the synergistic use of synthetic aperture radar and optical remote sensing. Int. J. Appl. Earth Obs. 2019, 80, 47–57. [Google Scholar] [CrossRef]
- Kornelsen, K.C.; Coulibaly, P. Advances in soil moisture retrieval from synthetic aperture radar and hydrological applications. J. Hydrol. 2013, 476, 460–489. [Google Scholar] [CrossRef]
- Sonkamble, S.; Chandra, S. GPR for earth and environmental applications: Case studies from India. J. Appl. Geophys. 2021, 193, 104422. [Google Scholar] [CrossRef]
- Dinh, K.; Gucunski, N.; Zayed, T. Automated visualization of concrete bridge deck condition from GPR data. NDT E Int. 2019, 102, 120–128. [Google Scholar] [CrossRef]
- Fernandes, F.M.; Pais, J.C. Laboratory observation of cracks in road pavements with GPR. Constr. Build. Mater. 2017, 154, 1130–1138. [Google Scholar] [CrossRef]
- Lombardi, F.; Lualdi, M. Step-frequency ground penetrating radar for agricultural soil morphology characterisation. Remote Sens. 2019, 11, 1075. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Zhou, Z.; Wang, J.; Zhao, Y.; Dou, Z. Quantification and division of unfrozen water content during the freezing process and the influence of soil properties by low-field nuclear magnetic resonance. J. Hydrol. 2021, 602, 126719. [Google Scholar] [CrossRef]
- Wai-Lok Lai, W.; Dérobert, X.; Annan, P. A review of ground penetrating radar application in civil engineering: A 30-year journey from locating and testing to imaging and diagnosis. NDT E Int. 2018, 96, 58–78. [Google Scholar] [CrossRef]
- Roth, C.H.; Malicki, M.A.; Plagge, R. Empirical evaluation of the relationship between soil dielectric constant and volumetric water content as the basis for calibrating soil moisture measurement by TDR. J. Soil Sci. 1992, 43, 1–13. [Google Scholar] [CrossRef]
- Lunt, I.A.; Hubbard, S.S.; Rubin, Y. Soil moisture content estimation using ground-penetrating radar reflection data. J. Hydrol. 2005, 307, 254–269. [Google Scholar] [CrossRef]
- Shapovalov, V.; Yavna, V.; Kochur, A.; Khakiev, Z.; Sulavko, S.; Daniel, P.; Kruglikov, A. Application of GPR for determining electrophysical properties of structural layers and materials. J. Appl. Geophys. 2020, 172, 103913. [Google Scholar] [CrossRef]
- Benedetto, A. Water content evaluation in unsaturated soil using GPR signal analysis in the frequency domain. J. Appl. Geophys. 2010, 71, 26–35. [Google Scholar] [CrossRef]
- Bablet, A.; Viallefont-Robinet, F.; Jacquemoud, S.; Fabre, S.; Briottet, X. High-resolution mapping of in-depth soil moisture content through a laboratory experiment coupling a spectroradiometer and two hyperspectral cameras. Remote Sens. Environ. 2020, 236, 111533. [Google Scholar] [CrossRef]
- Rasol, M.A.; Pérez-Gracia, V.; Fernandes, F.M.; Pais, J.C.; Santos-Assunçao, S.; Santos, C.; Sossa, V. GPR laboratory tests and numerical models to characterize cracks in cement concrete specimens, exemplifying damage in rigid pavement. Measurement 2020, 158, 107662. [Google Scholar] [CrossRef]
- Rasol, M.A.; Pérez-Gracia, V.; Solla, M.; Pais, J.C.; Fernandes, F.M.; Santos, C. An experimental and numerical approach to combine ground penetrating radar and computational modeling for the identification of early cracking in cement concrete pavements. NDT E Int. 2020, 115, 102293. [Google Scholar] [CrossRef]
- Elshorbagy, A.; Parasuraman, K. On the relevance of using artificial neural networks for estimating soil moisture content. J. Hydrol. 2008, 362, 1–18. [Google Scholar] [CrossRef]
- Bai, H.; Sinfield, J.V. Improved background and clutter reduction for pipe detection under pavement using ground penetrating radar (GPR). J. Appl. Geophys. 2020, 172, 103918. [Google Scholar] [CrossRef]
- Szymczyk, P.; Szymczyk, M. Non-destructive building investigation through analysis of GPR signal by S-transform. Automat. Constr. 2015, 55, 35–46. [Google Scholar] [CrossRef]
- Tosti, F.; Patriarca, C.; Slob, E.; Benedetto, A.; Lambot, S. Clay content evaluation in soils through GPR signal processing. J. Appl. Geophys. 2013, 97, 69–80. [Google Scholar] [CrossRef]
- Ghasemi, F.S.A.; Abrishamian, M.S. A novel method for FDTD numerical GPR imaging of arbitrary shapes based on Fourier transform. NDT E Int. 2007, 40, 140–146. [Google Scholar] [CrossRef]
- Ling, T.; Liu, H.; Gong, S.; Huang, F. Construction and application of a new biorthogonal wavelet basis for a quantitative analysis of GPR signals. J. Appl. Geophys. 2019, 170, 103837. [Google Scholar] [CrossRef]
- Javadi, M.; Ghasemzadeh, H. Wavelet analysis for ground penetrating radar applications: A case study. J. Geophys. Eng. 2017, 14, 1189–1202. [Google Scholar] [CrossRef]
- Lu, G.; Zhao, W.; Forte, E.; Tian, G.; Li, Y.; Pipan, M. Multi-frequency and multi-attribute GPR data fusion based on 2-D wavelet transform. Measurement 2020, 166, 108243. [Google Scholar] [CrossRef]
- Baili, J.; Lahouar, S.; Hergli, M.; Al-Qadi, I.L.; Besbes, K. GPR signal de-noising by discrete wavelet transform. NDT E Int. 2009, 42, 696–703. [Google Scholar] [CrossRef]
- Artagan, S.S.; Borecky, V. Advances in the nondestructive condition assessment of railway ballast: A focus on GPR. NDT E Int. 2020, 115, 102290. [Google Scholar] [CrossRef]
- Ni, S.; Huang, Y.; Lo, K.; Lin, D. Buried pipe detection by ground penetrating radar using the discrete wavelet transform. Comput. Geotech. 2010, 37, 440–448. [Google Scholar] [CrossRef]
- Zhang, L.; Ling, T.; Yu, B.; Huang, F.; Zhang, S. Intensive interferences processing for GPR signal based on the wavelet transform and F-K filtering. J. Appl. Geophys. 2021, 186, 104273. [Google Scholar] [CrossRef]
- Verma, V.S.; Kumar Jha, R. Improved watermarking technique based on significant difference of lifting wavelet coefficients. Signal. Image Video Process. 2014, 9, 1443–1450. [Google Scholar] [CrossRef]
- Li, H.; Wang, Q.; Wu, L. A novel design of lifting scheme from general wavelet. IEEE Trans. Signal Process. 2001, 49, 1714–1717. [Google Scholar]
- Ling, T.; Zhang, L.; Liu, H.; Huang, F.; Gu, D.; Yu, B. Quantitative identification and analysis of tunnel lining defect based on the wavelet lifting scheme theory. China J. Highw. Transp. 2019, 32, 197–204. [Google Scholar]
- Daubechies, I.; Sweldens, W. Factoring wavelet transforms into lifting steps. J. Fourier Anal. Appl. 1998, 4, 247–269. [Google Scholar] [CrossRef]
- Tzanis, A. The curvelet transform in the analysis of 2-D GPR data: Signal enhancement and extraction of orientation-and-scale-dependent information. J. Appl. Geophys. 2015, 115, 145–170. [Google Scholar] [CrossRef]
- Ling, T.; Zhang, L.; Huang, F.; Gu, D.; Yu, B.; Zhang, S. OMHT method for weak signal processing of GPR and its application in identification of concrete micro-crack. J. Cent. South Univ. 2020, 26, 3057–3065. [Google Scholar] [CrossRef]
- Liao, K.; Lai, X.; Zhou, Z.; Zhu, Q. Applying fractal analysis to detect spatio-temporal variability of soil moisture content on two contrasting land use hillslopes. Catena 2017, 157, 163–172. [Google Scholar] [CrossRef]
- Kong, Q.; Chen, H.; Mo, Y.L.; Song, G. Real-time monitoring of water content in sandy soil using shear mode piezoceramic transducers and active sensing-A feasibility study. Sensors 2017, 17, 2395. [Google Scholar] [CrossRef] [Green Version]
- Xu, B.; Li, B.; Song, G. Active debonding detection for large rectangular CFSTs based on wavelet packet energy spectrum with piezoceramics. J. Struct. Eng. 2013, 139, 1435–1443. [Google Scholar] [CrossRef]
- Wang, Z.; Wei, L.; Cao, M. Damage quantification with embedded piezoelectric aggregates based on wavelet packet energy analysis. Sensors 2019, 19, 425. [Google Scholar] [CrossRef] [Green Version]
- Lu, W.; Li, P.; Chen, M.; Zhou, C.; Shu, D. Comparison of vibrations induced by excavation of deep-buried cavern and open pit with method of bench blasting. J. Cent. South Univ. 2011, 18, 1709–1718. [Google Scholar] [CrossRef]
- Chen, G.; Li, Q.; Li, D.; Wu, Z.; Liu, Y. Main frequency band of blast vibration signal based on wavelet packet transform. Appl. Math. Model. 2019, 74, 569–585. [Google Scholar] [CrossRef]
- Jiang, T.; Kong, Q.; Patil, D.; Luo, Z.; Huo, L.; Song, G. Detection of debonding between fiber reinforced polymer bar and concrete structure using piezoceramic transducers and wavelet packet analysis. IEEE Sens. J. 2017, 17, 1992–1998. [Google Scholar] [CrossRef]
- Luo, T.X.H.; Lai, W.W.L.; Giannopoulos, A. Forward modelling on GPR responses of subsurface air voids. Tunn. Undergr. Space Tech. 2020, 103, 103521. [Google Scholar] [CrossRef]
- Ercoli, M.; Di Matteo, L.; Pauselli, C.; Mancinelli, P.; Frapiccini, S.; Talegalli, L.; Cannata, A. Integrated GPR and laboratory water content measures of sandy soils: From laboratory to field scale. Constr. Build. Mater. 2018, 159, 734–744. [Google Scholar] [CrossRef]
- Warren, C.; Giannopoulos, A.; Giannakis, I. gprMax: Open source software to simulate electromagnetic wave propagation for ground penetrating radar. Comput. Phys. Commun. 2016, 209, 163–170. [Google Scholar] [CrossRef] [Green Version]
- Giannopoulos, A. Modelling ground penetrating radar by GprMax. Constr. Build. Mater. 2005, 19, 755–762. [Google Scholar] [CrossRef]
- Topp, G.C. Electromagnetic determination of soil water content: Measurements in coaxial transmission lines. Water Resour. Res. 1980, 16, 574–582. [Google Scholar] [CrossRef] [Green Version]
- Liu, J. Methods of Detection on Moisture of Railway Subgrage by Using the Ground Penetrating Radar. Ph.D. Thesis, China University of Mining and Technology, Beijing, China, 2015. [Google Scholar]
- Cao, M.; Qiao, P. Integrated wavelet transform and its application to vibration mode shapes for the damage detection of beam-type structures. Smart Mater. Struct. 2008, 17, 055014. [Google Scholar] [CrossRef]
- Yi, T.H.; Li, H.N.; Zhao, X.Y. Noise smoothing for structural vibration test signals using an improved wavelet thresholding technique. Sensors 2012, 12, 11205–11220. [Google Scholar] [CrossRef] [Green Version]

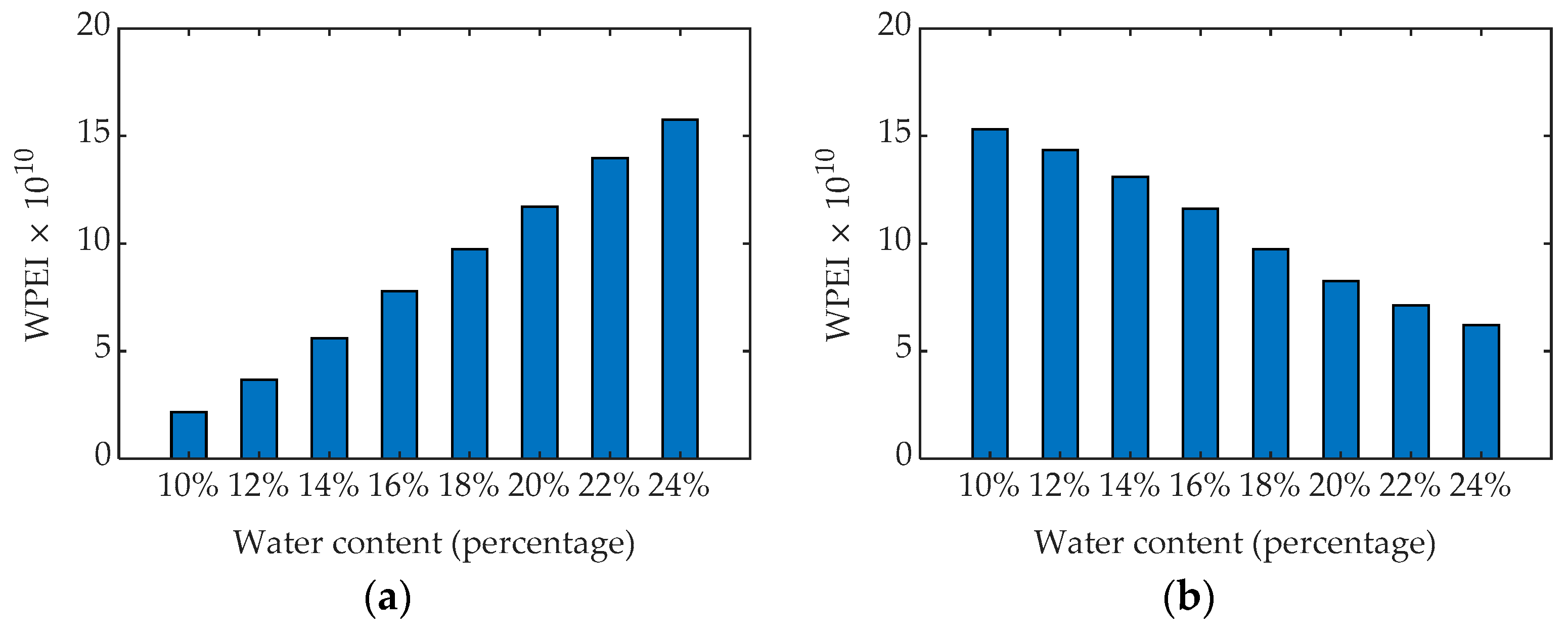

| Water Content | 10% | 12% | 14% | 16% | 18% | 20% | 22% | 24% |
|---|---|---|---|---|---|---|---|---|
| Relative dielectric constant | 5.343 | 6.115 | 6.983 | 7.941 | 8.987 | 10.116 | 11.325 | 12.611 |
| Conductivity (μS/cm) | 88.681 | 126.085 | 180.261 | 258.134 | 368.670 | 523.129 | 735.272 | 1021.533 |
| Electromagnetic wave velocity (m/ns) | 0.129 | 0.121 | 0.113 | 0.106 | 0.100 | 0.094 | 0.089 | 0.084 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Zhang, L.; Ling, T.; Fu, G.; Guo, Y. Experimental Research on Evaluation of Soil Water Content Using Ground Penetrating Radar and Wavelet Packet-Based Energy Analysis. Remote Sens. 2021, 13, 5047. https://doi.org/10.3390/rs13245047
Zhang S, Zhang L, Ling T, Fu G, Guo Y. Experimental Research on Evaluation of Soil Water Content Using Ground Penetrating Radar and Wavelet Packet-Based Energy Analysis. Remote Sensing. 2021; 13(24):5047. https://doi.org/10.3390/rs13245047
Chicago/Turabian StyleZhang, Sheng, Liang Zhang, Tonghua Ling, Guihai Fu, and Youlin Guo. 2021. "Experimental Research on Evaluation of Soil Water Content Using Ground Penetrating Radar and Wavelet Packet-Based Energy Analysis" Remote Sensing 13, no. 24: 5047. https://doi.org/10.3390/rs13245047
APA StyleZhang, S., Zhang, L., Ling, T., Fu, G., & Guo, Y. (2021). Experimental Research on Evaluation of Soil Water Content Using Ground Penetrating Radar and Wavelet Packet-Based Energy Analysis. Remote Sensing, 13(24), 5047. https://doi.org/10.3390/rs13245047






