Characterizing Rain Cells as Measured by a Ka-Band Nadir Radar Altimeter: First Results and Impact on Future Altimetry Missions
Abstract
:1. Precipitation and Atmospheric Attenuation in the Context of Altimetry Missions
2. Detection and Characterization of Rain Cells
2.1. Ka Band Atmospheric Attenuation
2.2. Description of the Datasets
2.3. Definition of the ACECAL Algorithm
2.3.1. Pre-Processing
2.3.2. Processing
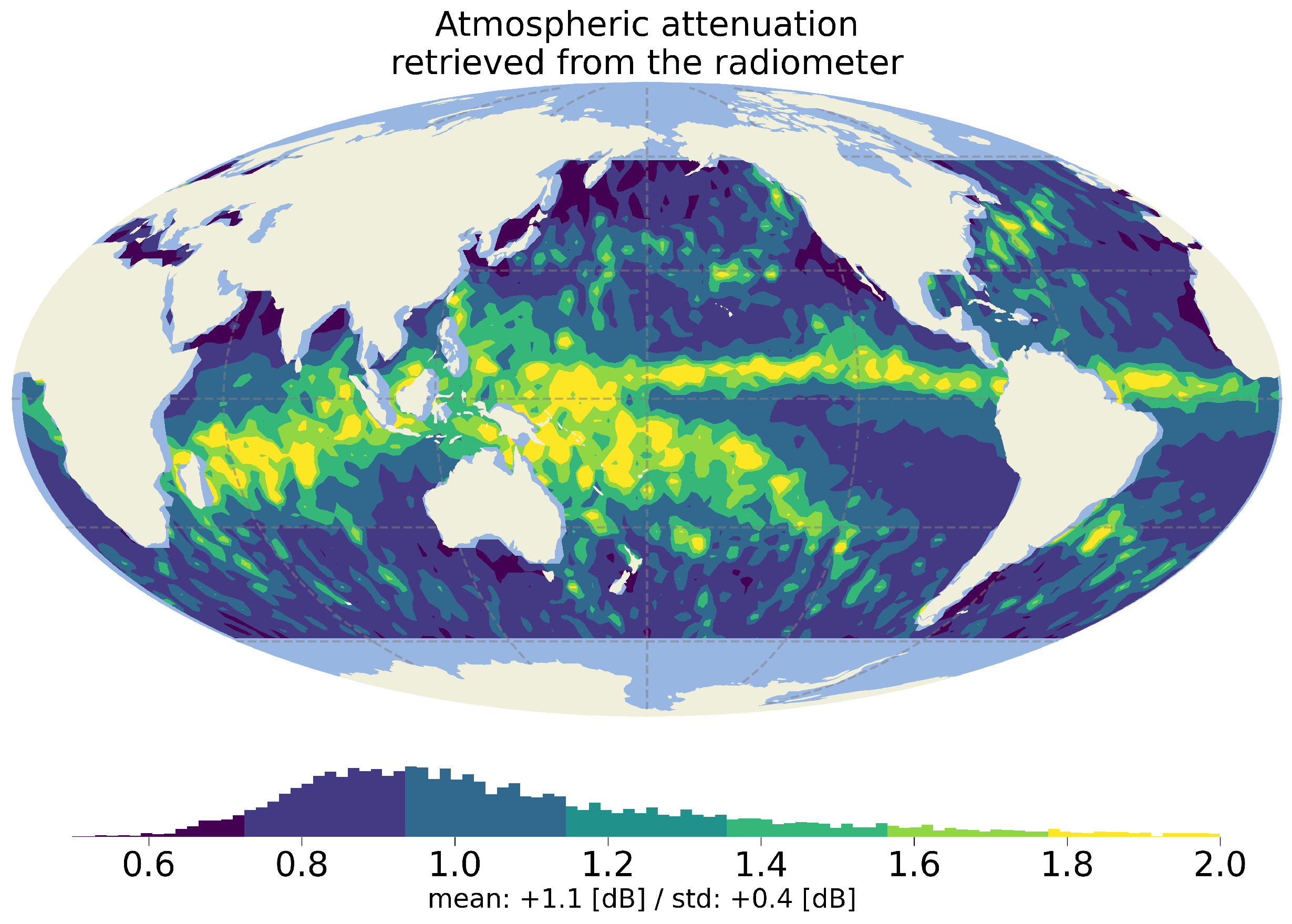
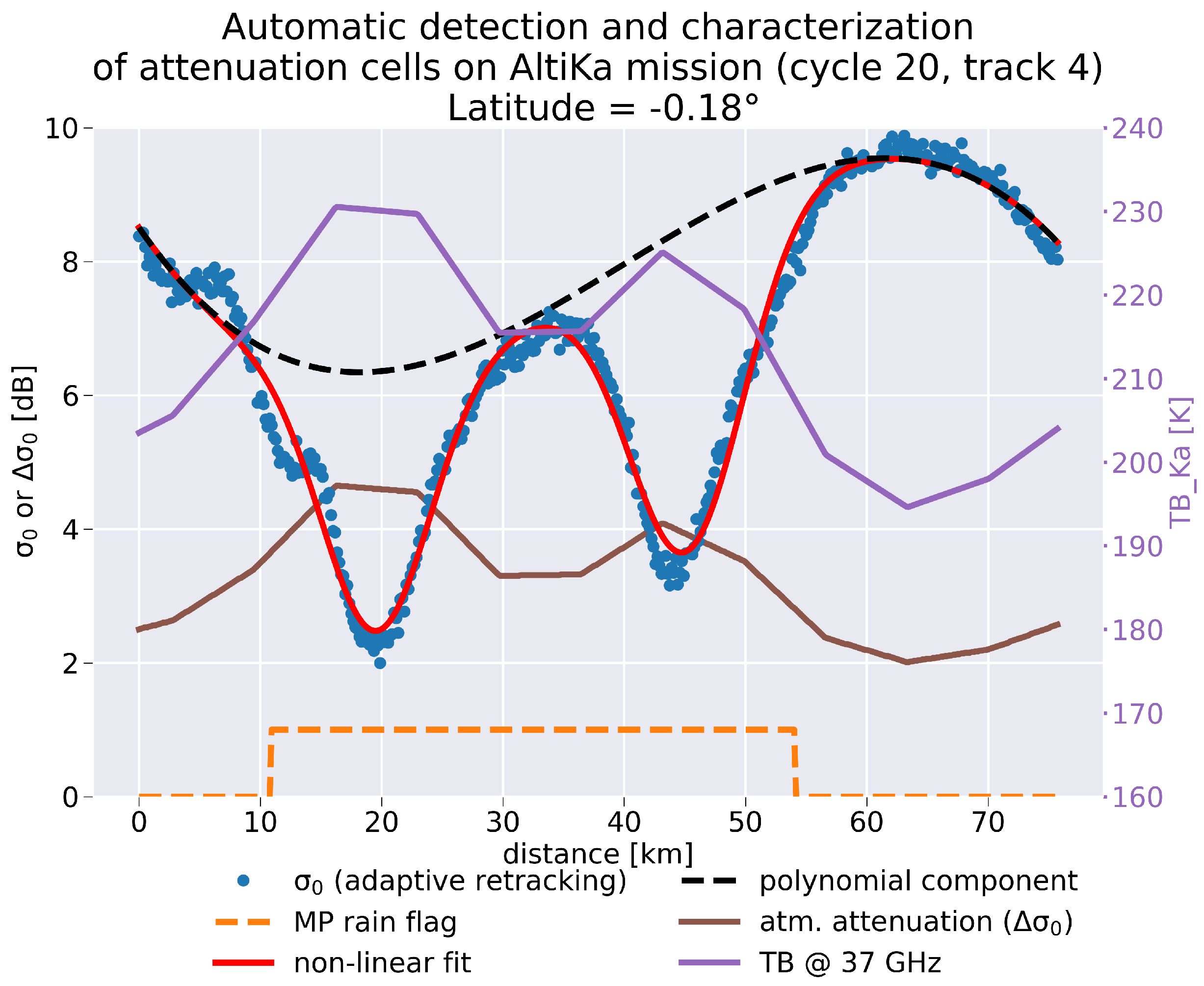
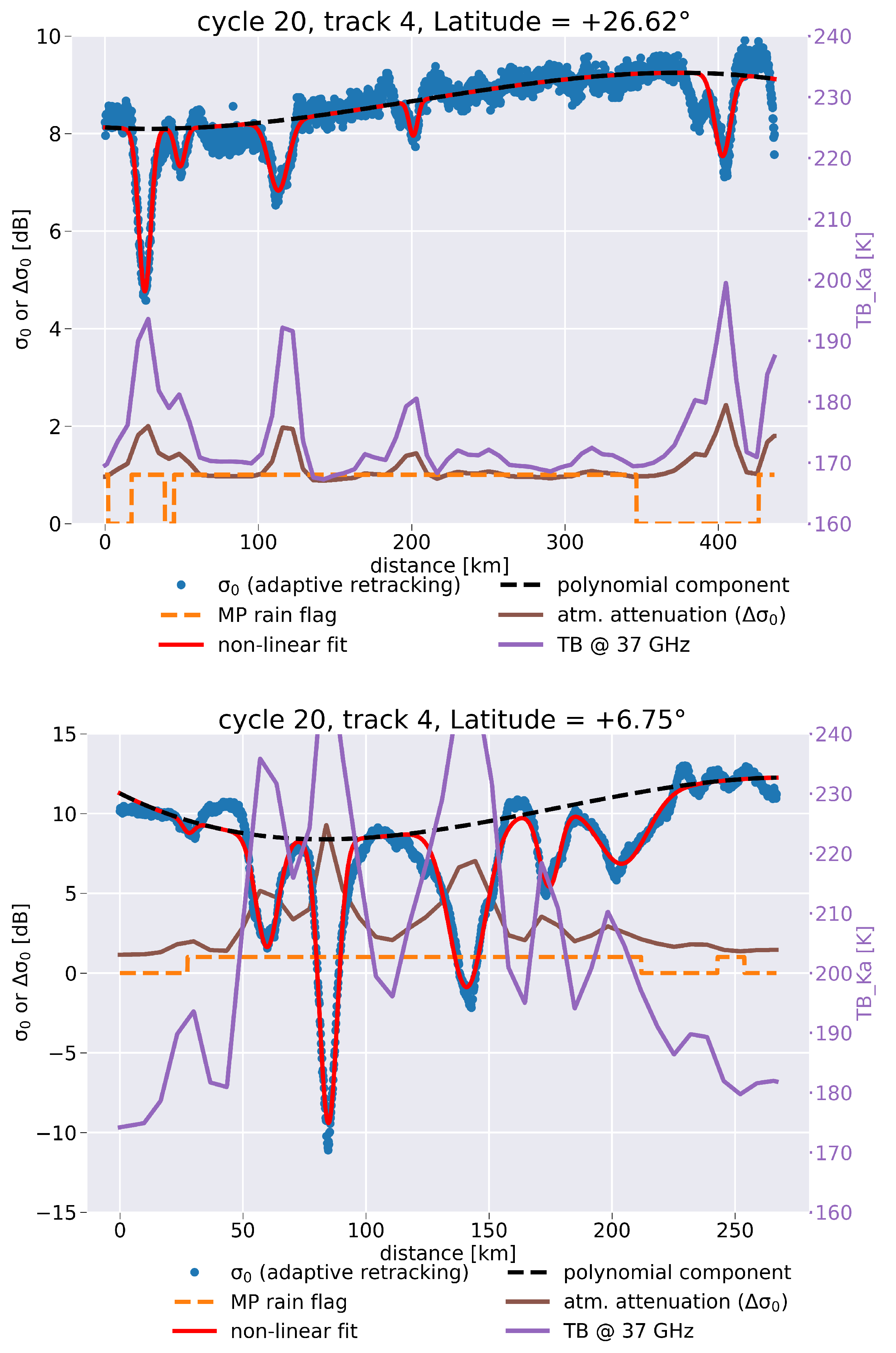
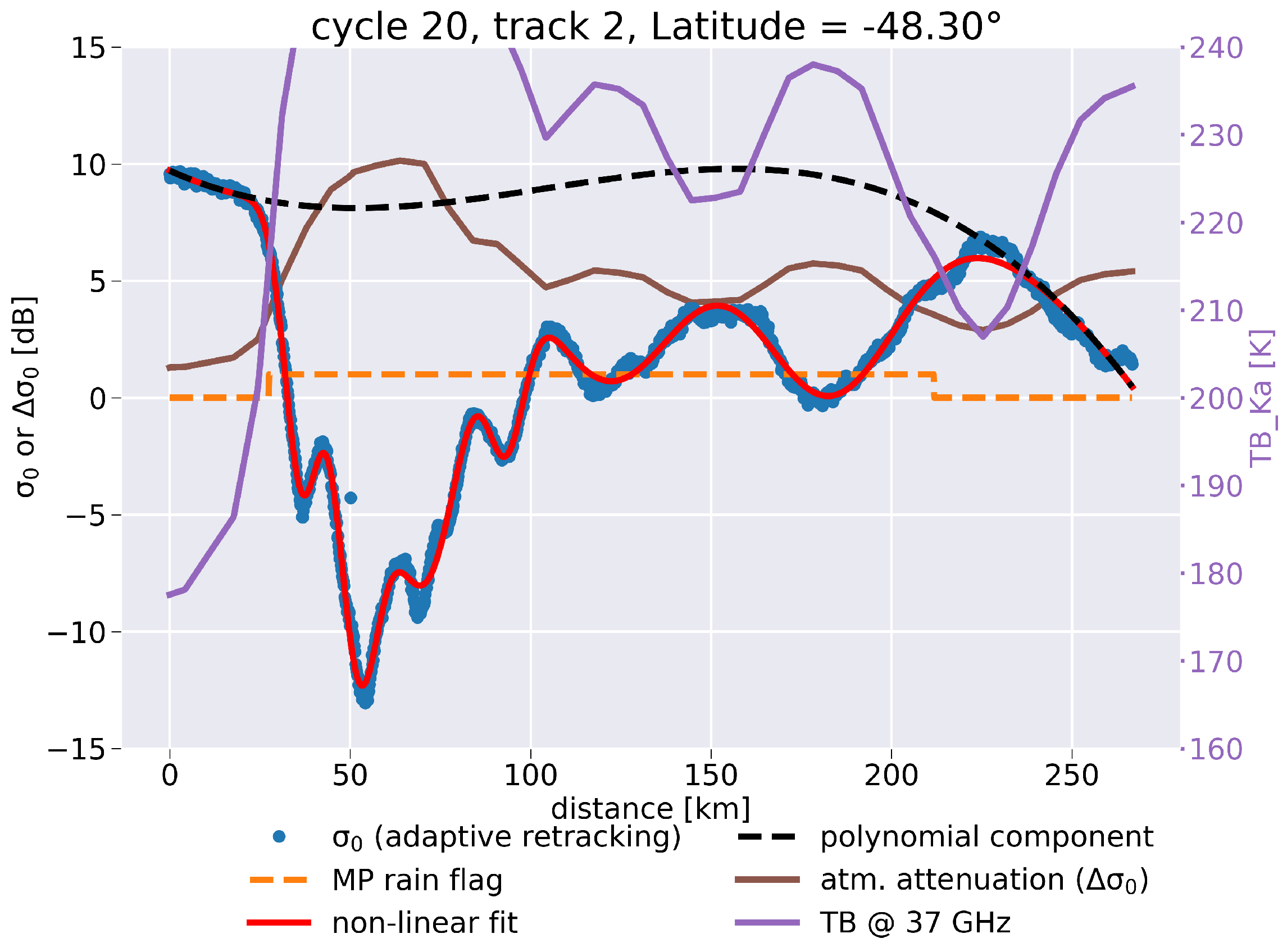
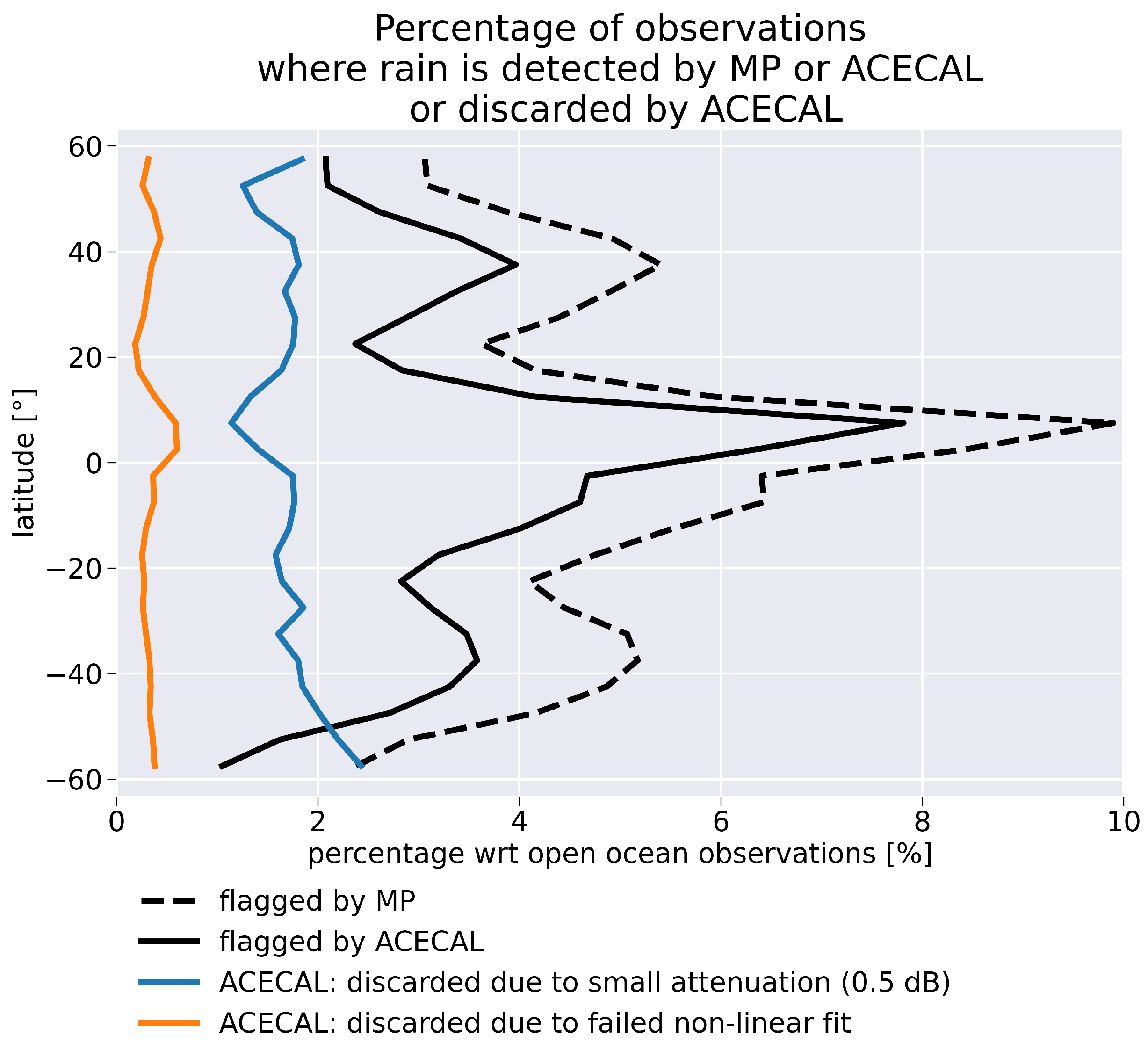
2.3.3. Illustrative Cases and Zonal Distribution of Occurrences
3. Amplitude and Size of Attenuation Cells Retrieved from SARAL/AltiKa Mission
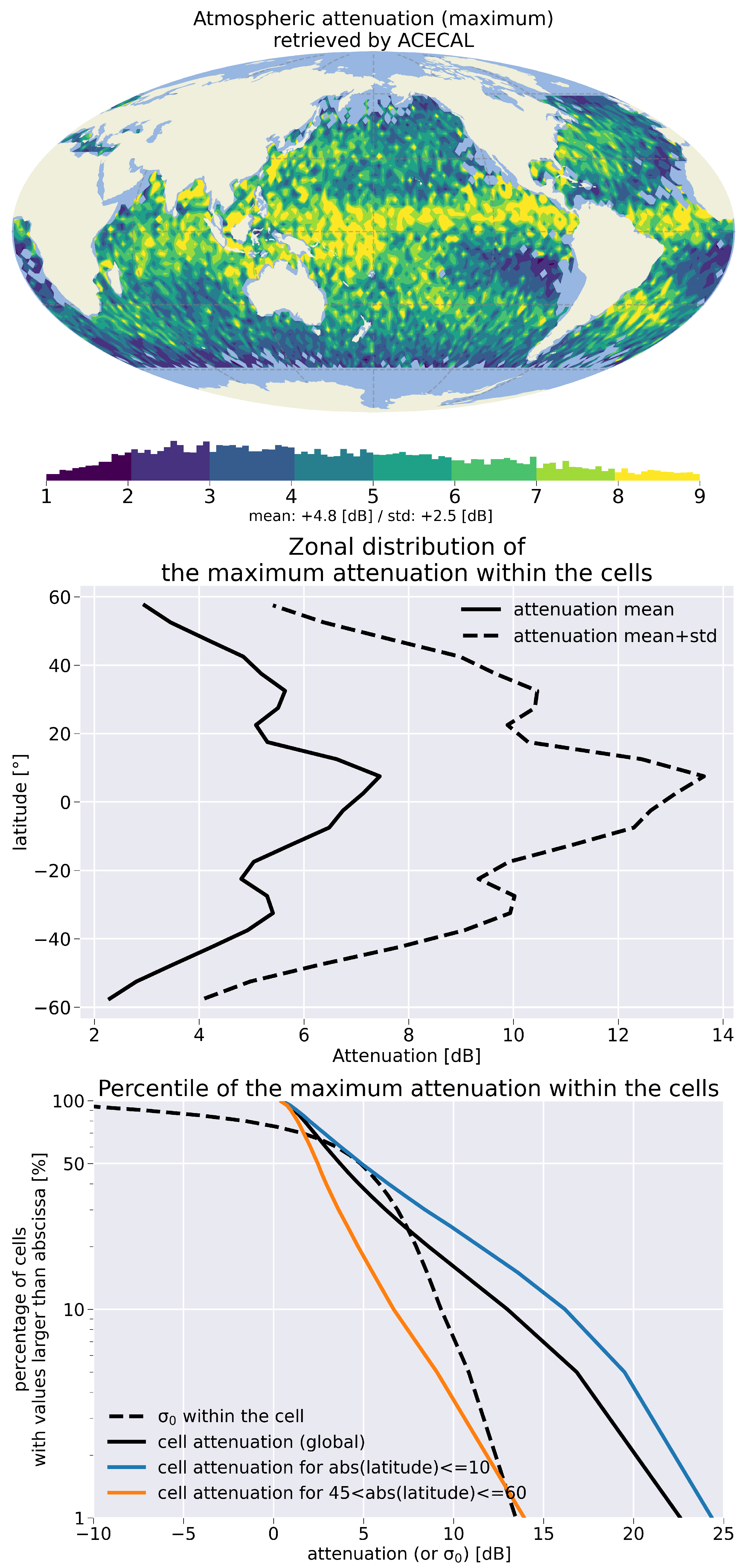
3.1. Amplitude of Attenuation Cells
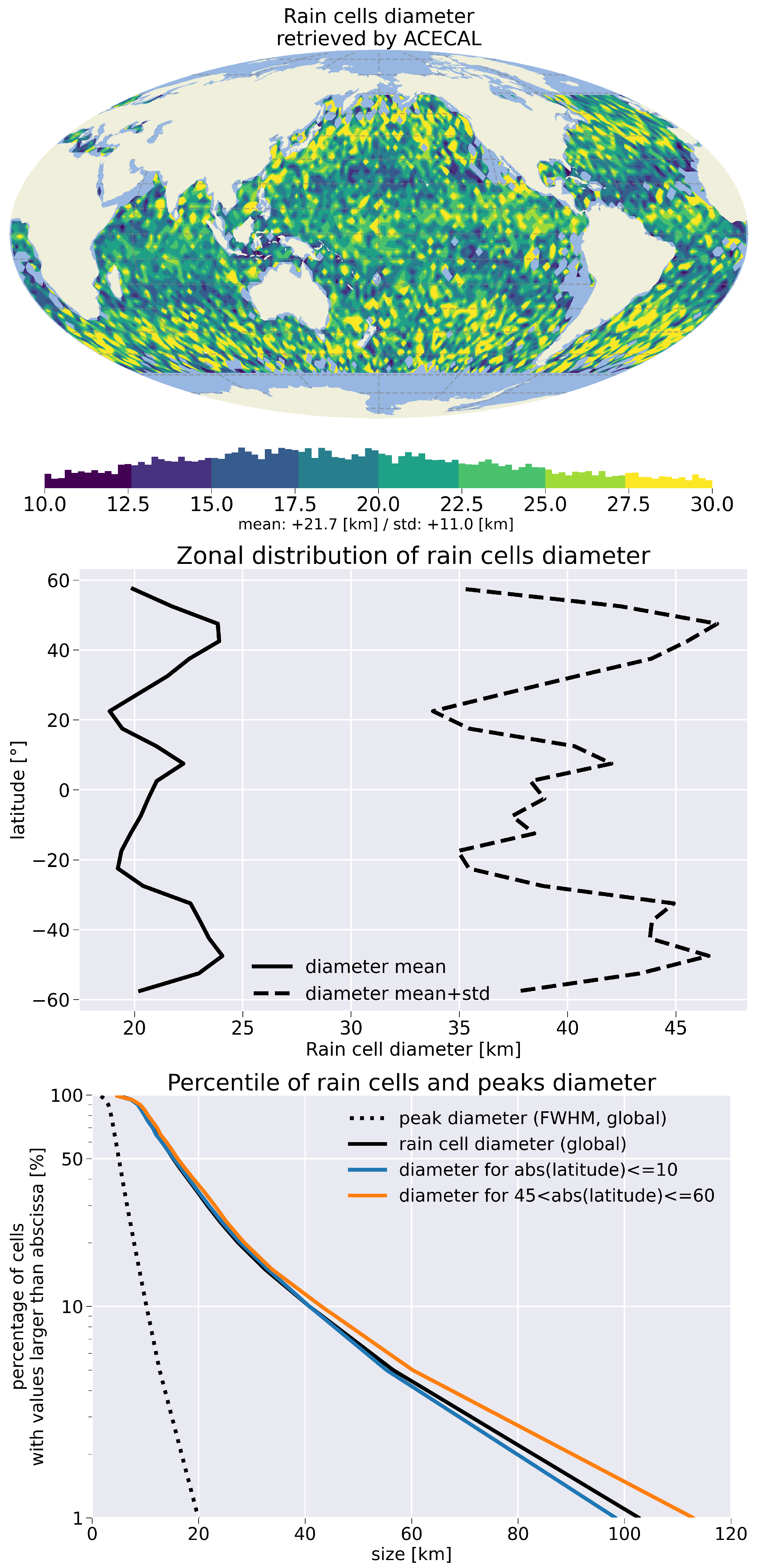
3.2. Diameter of Rain Cells
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Escudier, P.; Couhert, A.; Mercier, F.; Picard, B. Satellite radar altimetry: Principle, accuracy and precision. In Satellite Altimetry over Oceans and Land Surfaces; Stammer, D., Cazenave, A., Eds.; Taylor & Francis Inc.: Boca Raton, FL, USA, 2018; Chapter 1; pp. 1–70. [Google Scholar]
- Fu, L.L.; Christensen, E.; Yamarone, C.; Lefebvre, M.; Menard, Y.; Dorrer, M.; Escudier, P. TOPEX/Poseidon mission overview. J. Geophys. Res. Atmos. 1995, 99. [Google Scholar] [CrossRef]
- Heslop, E.E.; Sánchez-Román, A.; Pascual, A.; Rodríguez, D.; Reeve, K.A.; Faugère, Y.; Raynal, M. Sentinel-3A Views Ocean Variability More Accurately at Finer Resolution. Geophys. Res. Lett. 2017, 44, 12367–12374. [Google Scholar] [CrossRef] [Green Version]
- Quartly, G.D.; Guymer, T.H.; Srokosz, M.A. The Effects of Rain on Topex Radar Altimeter Data. J. Atmos. Ocean. Technol. 1996, 13, 1209–1229. [Google Scholar] [CrossRef] [Green Version]
- Tournadre, J.; Morland, J.C. Effects of rain on TOPEX/Poseidon altimeter data. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1117–1135. [Google Scholar] [CrossRef]
- Quartly, G.D. Sea state and rain: A second take on dual-frequency altimetry. Mar. Geod. 2004, 27, 133–152. [Google Scholar] [CrossRef] [Green Version]
- Tournadre, J. Validation of Jason and Envisat altimeter dual frequency rain flags. Mar. Geod. 2004, 27, 153–169. [Google Scholar] [CrossRef]
- Tran, N.; Obligis, E.; Ferreira, F. Comparison of two Jason-1 altimeter precipitation detection algorithms with rain estimates from the TRMM Microwave Imager. J. Atmos. Ocean. Technol. 2005, 22, 782–794. [Google Scholar] [CrossRef]
- Steunou, N.; Desjonquères, J.D.; Picot, N.; Sengenes, P.; Noubel, J.; Poisson, J.C. AltiKa Altimeter: Instrument Description and In Flight Performance. Mar. Geod. 2015, 38, 22–42. [Google Scholar] [CrossRef]
- Verron, J.; Bonnefond, P.; Aouf, L.; Birol, F.; Bhowmick, S.A.; Calmant, S.; Conchy, T.; Crétaux, J.F.; Dibarboure, G.; Dubey, A.K.; et al. The benefits of the Ka-band as evidenced from the SARAL/AltiKa altimetric mission: Scientific applications. Remote Sens. 2018, 10, 163. [Google Scholar] [CrossRef] [Green Version]
- Verron, J.; Bonnefond, P.; Andersen, O.; Ardhuin, F.; Bergé-Nguyen, M.; Bhowmick, S.; Blumstein, D.; Boy, F.; Brodeau, L.; Crétaux, J.F.; et al. The SARAL/AltiKa mission: A step forward to the future of altimetry. Adv. Space Res. 2021, 68, 808–828. [Google Scholar] [CrossRef]
- Lillibridge, J.; Scharroo, R.; Abdalla, S.; Vandemark, D. One-and two-dimensional wind speed models for ka-band altimetry. J. Atmos. Ocean. Technol. 2014, 31, 630–638. [Google Scholar] [CrossRef]
- Tournadre, J.; Lambin-artru, J.; Steunou, N. Cloud and Rain Effects on AltiKa/SARAL Ka-Band Radar Altimeter—Part I: Modeling and Mean Annual Data Availability. Science 2009, 47, 1806–1817. [Google Scholar] [CrossRef] [Green Version]
- Tournadre, J.; Lambin, J.; Steunou, N. Cloud and rain effects on ALTIKA / SARAL Ka band radar altimeter. Part II: Definition of a rain/cloud flag. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1818–1826. [Google Scholar] [CrossRef] [Green Version]
- Tournadre, J.; Poisson, J.; Steunou, N.; Picard, B. Validation of AltiKa Matching Pursuit Rain Flag. Mar. Geod. 2015, 38, 107–123. [Google Scholar] [CrossRef]
- Fu, Y.; Chen, Y.; Zhang, X.; Wang, Y.; Li, R.; Liu, Q.; Zhong, L.; Zhang, Q.; Zhang, A. Fundamental Characteristics of Tropical Rain Cell Structures as Measured by TRMM PR. J. Meteorol. Res. 2020, 34, 1129–1150. [Google Scholar] [CrossRef]
- Mesnard, F.; Sauvageot, H. Structural characteristics of rain fields. J. Geophys. Res. Atmos. 2003, 108. [Google Scholar] [CrossRef]
- Capsoni, C.; Fedi, F.; Magistroni, C.; Paraboni, A.; Pawlina, A. Data and theory for a new model of the horizontal structure of rain cells for propagation applications. Radio Sci. 1987, 22, 395–404. [Google Scholar] [CrossRef]
- Sauvageot, H.; Mesnard, F.; Tenório, R.S. The Relation between the Area-Average Rain Rate and the Rain Cell Size Distribution Parameters. J. Atmos. Sci. 1999, 56, 57–70. [Google Scholar] [CrossRef]
- Begum, S.; Otung, I.E. Rain cell size distribution inferred from rain gauge and radar data in the UK. Radio Sci. 2009, 44. [Google Scholar] [CrossRef]
- Nesbitt, S.W.; Cifelli, R.; Rutledge, S.A. Storm morphology and rainfall characteristics of TRMM precipitation features. Mon. Weather Rev. 2006, 134, 2702–2721. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.; Zipser, E. Regional variation of morphology of organized convection in the tropics and subtropics. J. Geophys. Res. Atmos. 2013, 118, 453–466. [Google Scholar] [CrossRef] [Green Version]
- Tournadre, J. Improved level-3 oceanic rainfall retrieval from dual-frequency spaceborne radar altimeter systems. J. Atmos. Ocean. Technol. 2006, 23, 1131–1149. [Google Scholar] [CrossRef]
- Ardhuin, F.; Brandt, P.; Gaultier, L.; Donlon, C.; Battaglia, A.; Boy, F.; Casal, T.; Chapron, B.; Collard, F.; Cravatte, S.E.; et al. SKIM, a candidate satellite mission exploring global ocean currents and waves. Front. Mar. Sci. 2019, 6, 209. [Google Scholar] [CrossRef] [Green Version]
- Blumstein, D.; Biancamaria, S.; Guérin, A.; Maisongrande, P. A potential constellation of small altimetry satellites dedicated to continental surface waters (SMASH mission). In AGU Fall Meeting Abstracts; American Geophysical Union: Washington, DC, USA, 2019; Volume 2019, p. H43N-2257. [Google Scholar]
- Durand, M.; Fu, L.L.; Lettenmaier, D.P.; Alsdorf, D.E.; Rodriguez, E.; Esteban-Fernandez, D. The surface water and ocean topography mission: Observing terrestrial surface water and oceanic submesoscale eddies. Proc. IEEE 2010, 98, 766–779. [Google Scholar] [CrossRef]
- Biancamaria, S.; Lettenmaier, D.P.; Pavelsky, T.M. The SWOT Mission and Its Capabilities for Land Hydrology. Surv. Geophys. 2016, 37, 307–337. [Google Scholar] [CrossRef] [Green Version]
- Picard, B.; Frery, M.L.; Obligis, E.; Eymard, L.; Steunou, N.; Picot, N. SARAL/AltiKa Wet Tropospheric Correction: In-Flight Calibration, Retrieval Strategies and Performances. Mar. Geod. 2015, 38, 277–296. [Google Scholar] [CrossRef] [Green Version]
- Valladeau, G.; Thibaut, P.; Picard, B.; Poisson, J.C.; Tran, N.; Picot, N.; Guillot, A. Using SARAL/AltiKa to Improve Ka-band Altimeter Measurements for Coastal Zones, Hydrology and Ice: The PEACHI Prototype. Mar. Geod. 2015, 38, 124–142. [Google Scholar] [CrossRef]
- Vose, R.; Becker, A.; Hilburn, K.; Huffman, G.; Kruk, M.; Yin, X. Precipitation [in “State of the Climate in 2015”]. Bull. Am. Meteorol. Soc. 2016, 97, S27–S28. [Google Scholar] [CrossRef] [Green Version]
- Poisson, J.C.; Quartly, G.D.; Kurekin, A.A.; Thibaut, P.; Hoang, D.; Nencioli, F. Development of an ENVISAT altimetry processor providing sea level continuity between open ocean and arctic leads. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5299–5319. [Google Scholar] [CrossRef]
- Obligis, E.; Rahmani, A.; Eymard, L.; Labroue, S.; Bronner, E. An Improved Retrieval Algorithm for Water Vapor Retrieval: Application to the Envisat Microwave Radiometer. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3057–3064. [Google Scholar] [CrossRef]
- Tournadre, J. Determination of rain cell characteristics from the analysis of TOPEX altimeter echo waveforms. J. Atmos. Ocean. Technol. 1998, 15, 387–406. [Google Scholar] [CrossRef]
- Newville, M.; Stensitzki, T.; Allen, D.B.; Ingargiola, A. LMFIT: Non-Linear Least-Square Minimization and Curve-Fitting for Python (Version 1.0.1). Zenodo 2014. [Google Scholar] [CrossRef]
- Goldhirsh, J. Rain Cell Size Statistics as a Function of Rain Rate for Attenuation Modeling. IEEE Trans. Antennas Propag. 1983, 31, 799–801. [Google Scholar] [CrossRef]
- Olsen, R.L.; Rogers, D.V.; Hodge, D.B. The aRb Relation in the Calculation of Rain Attenuation. IEEE Trans. Antennas Propag. 1978, 26, 318–329. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, K. Global precipitation system size. Environ. Res. Lett. 2021, 16, 054005. [Google Scholar] [CrossRef]

| Pre-Processing | ||
| Parameter | Criteria | Comment |
| surface_type | == 0 | open ocean |
| ice_flag | == 0 | no sea ice |
| distance_shoreline | ≥50 km | no land contamination on TB |
| off_nadir_angle_pf | == 0 | no platform maneuvers or depointing |
| Post-Processing | ||
| Parameter | Criteria | Comment |
| trailing_edge_variation_flag_40hz | == 1 | MP flag raised (potential rain event) |
| sig0_adaptive_40hz - atmos_corr_sig0_40hz | <15 db | no bloom |
| short-scales/large-scales windows size | 1.5 km/30 km | to select attenuation cells |
| minimum amplitude of the attenuation due to rain cells | ≥0.5 dB | to ensure the robustness of the fit |
| value of 37 GHz TB at the maximum attenuation | ≥175 K | to ensure the detection of rain event |
| Attenuation at Peak Maximum (Rain Rate [mm·h−1] @ 6 km Thickness; 3 km Thickness) | ||||
| 99th percentile | 90th percentile | median | 10th percentile | 1st percentile |
| 0.5 dB (<1; <1) | 1.0 dB (<1; <1) | 3.5 dB (1.5; 2.4) | 13 dB (6; 9) | 23 dB (10; 16) |
| Rain Cell Diameter | ||||
| 99th percentile | 90th percentile | median | 10th percentile | 1st percentile |
| 5 km | 8.5 km | 15 km | 41 km | 103 km |
| Peak Diameter (FWHM) | ||||
| 99th percentile | 90th percentile | median | 10th percentile | 1st percentile |
| 1.5 km | 3 km | 5 km | 10 km | 20 km |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Picard, B.; Picot, N.; Dibarboure, G.; Steunou, N. Characterizing Rain Cells as Measured by a Ka-Band Nadir Radar Altimeter: First Results and Impact on Future Altimetry Missions. Remote Sens. 2021, 13, 4861. https://doi.org/10.3390/rs13234861
Picard B, Picot N, Dibarboure G, Steunou N. Characterizing Rain Cells as Measured by a Ka-Band Nadir Radar Altimeter: First Results and Impact on Future Altimetry Missions. Remote Sensing. 2021; 13(23):4861. https://doi.org/10.3390/rs13234861
Chicago/Turabian StylePicard, Bruno, Nicolas Picot, Gérald Dibarboure, and Nathalie Steunou. 2021. "Characterizing Rain Cells as Measured by a Ka-Band Nadir Radar Altimeter: First Results and Impact on Future Altimetry Missions" Remote Sensing 13, no. 23: 4861. https://doi.org/10.3390/rs13234861
APA StylePicard, B., Picot, N., Dibarboure, G., & Steunou, N. (2021). Characterizing Rain Cells as Measured by a Ka-Band Nadir Radar Altimeter: First Results and Impact on Future Altimetry Missions. Remote Sensing, 13(23), 4861. https://doi.org/10.3390/rs13234861







