Study of the Boundary Layer Structure of a Landfalling Typhoon Based on the Observation from Multiple Ground-Based Doppler Wind Lidars
Abstract
:1. Introduction
2. Data and Methods
2.1. Super Typhoon Lekima
2.2. Joint Observations
2.3. Data Processing
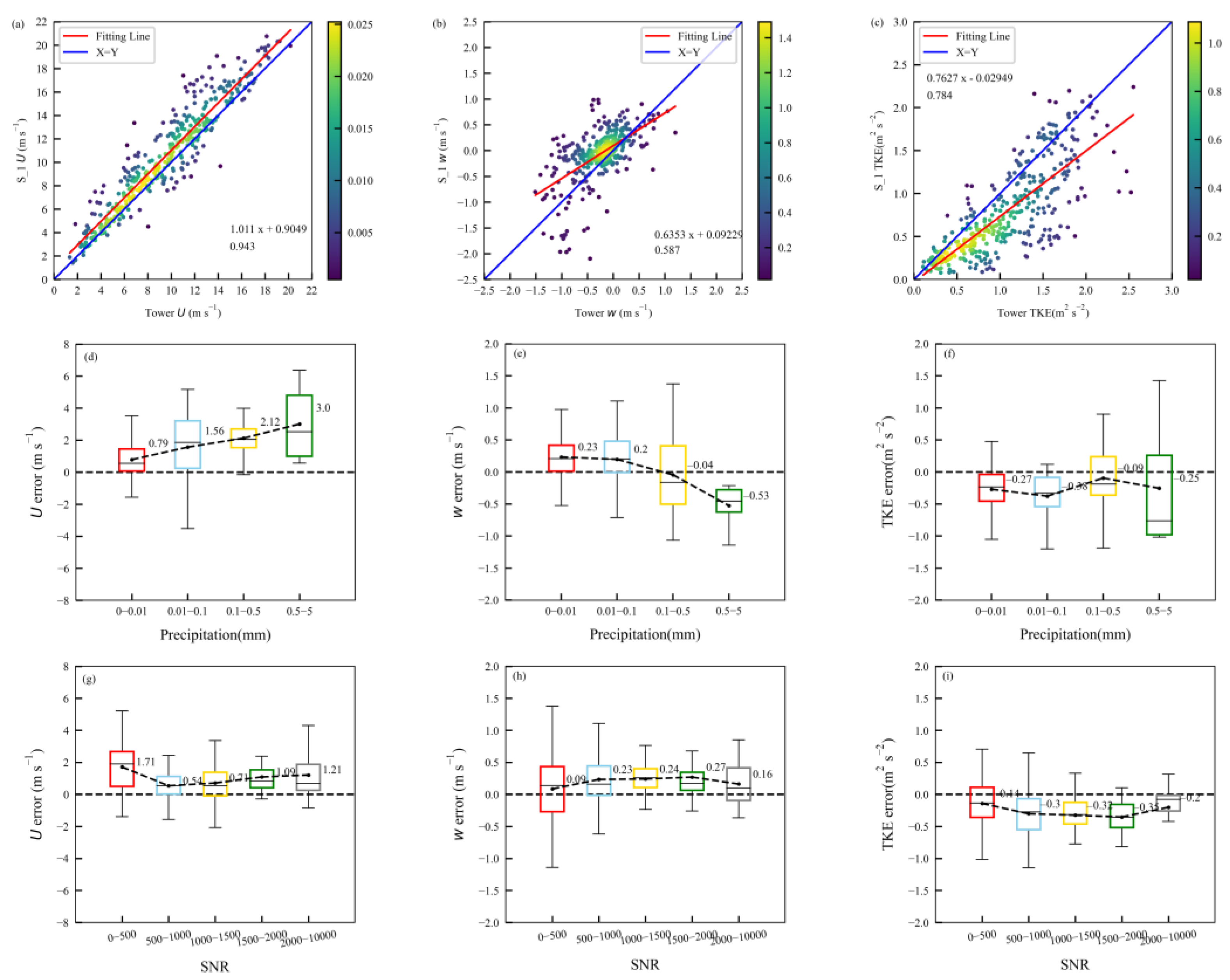
2.3.1. Data Reliability Analysis
2.3.2. Data Processing
3. Result
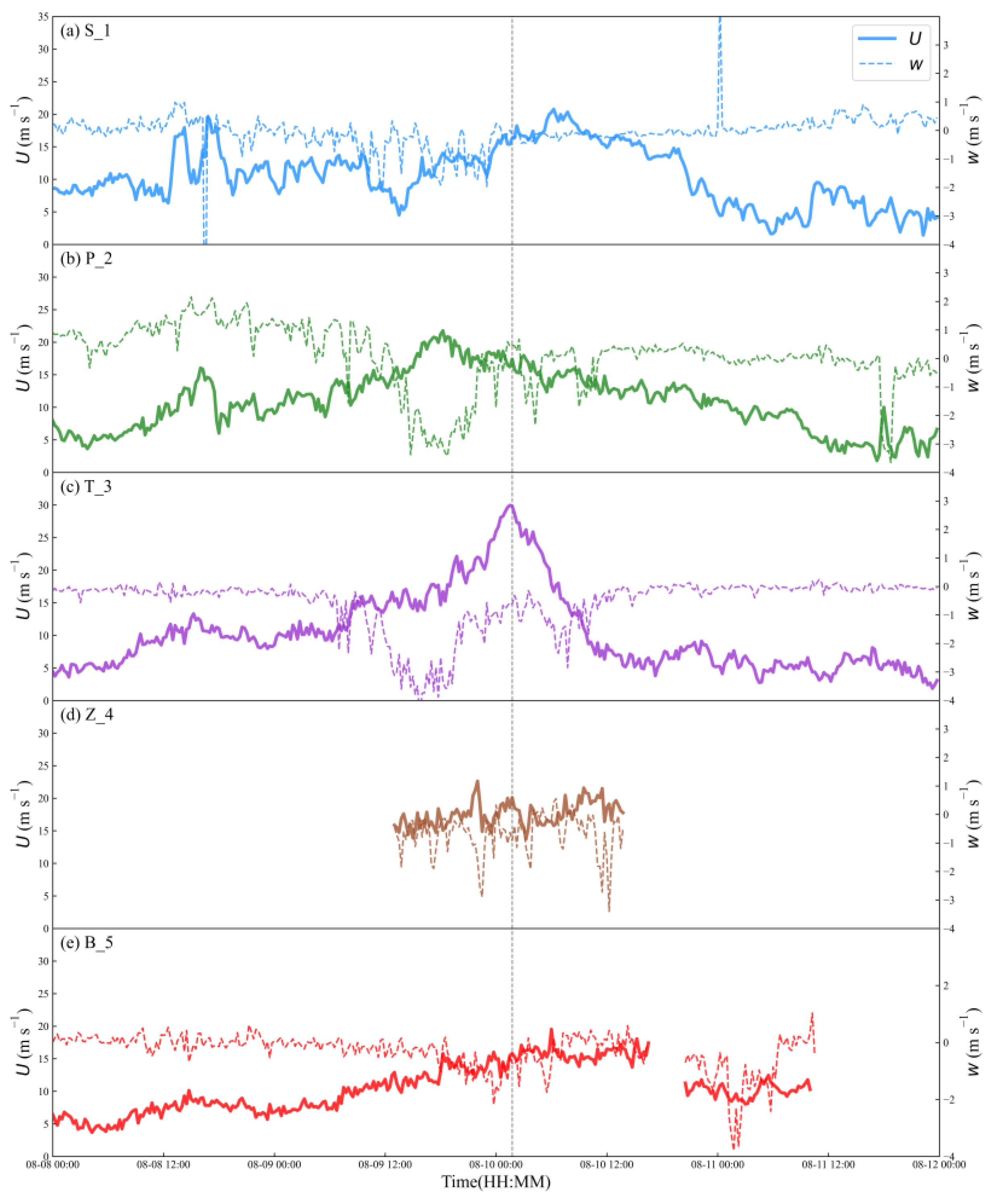
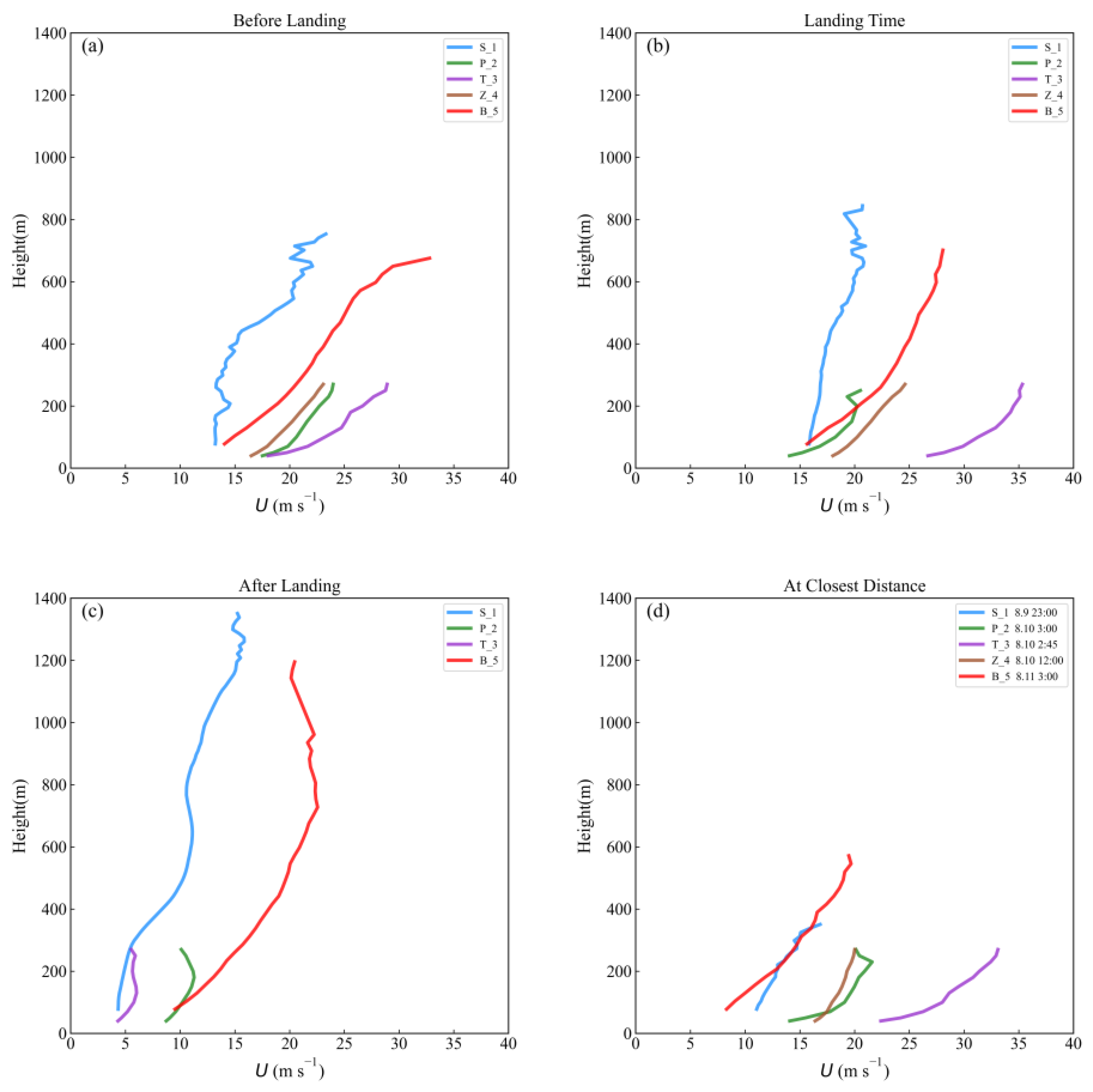
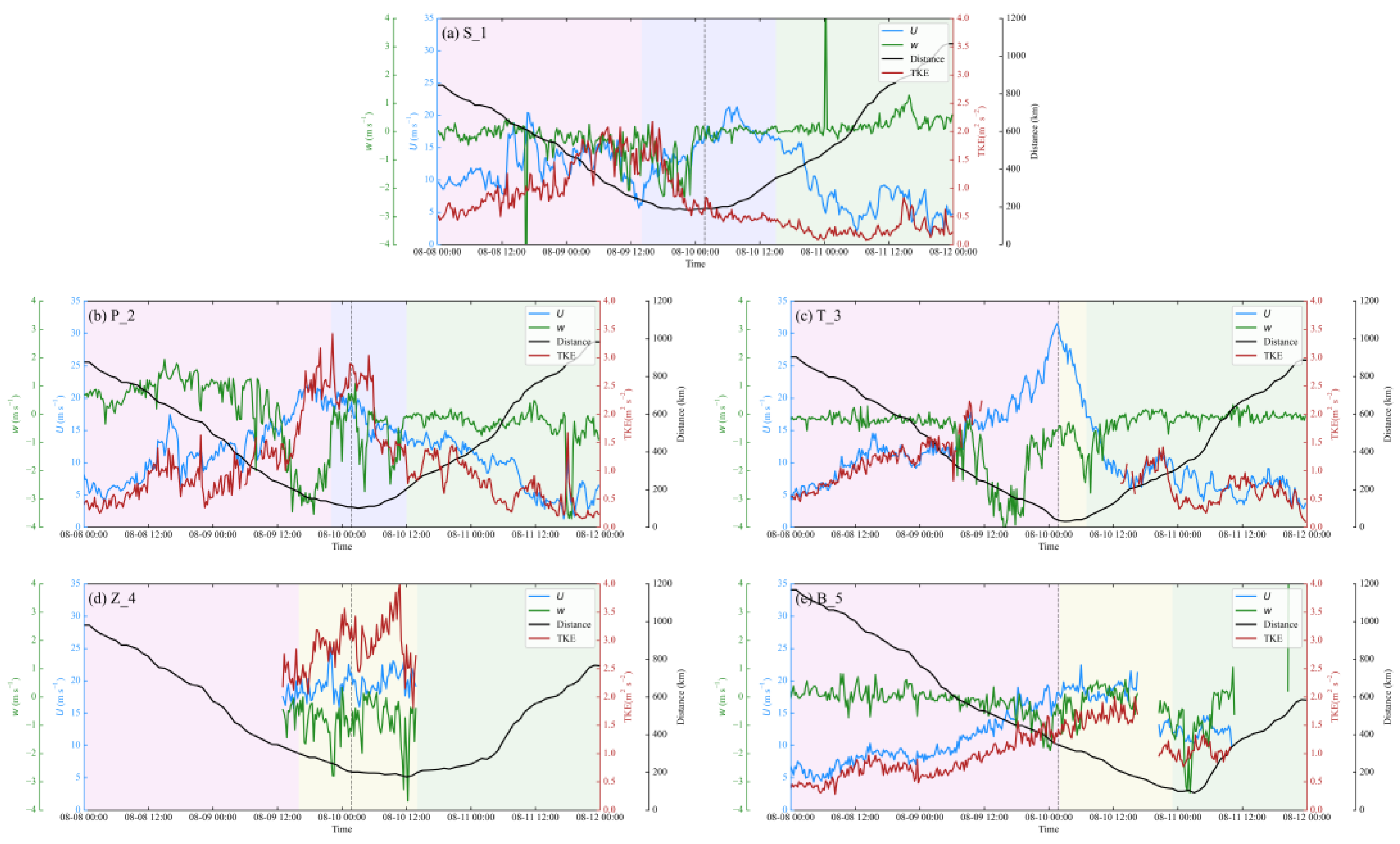
3.1. Boundary Layer Wind Field Characteristics
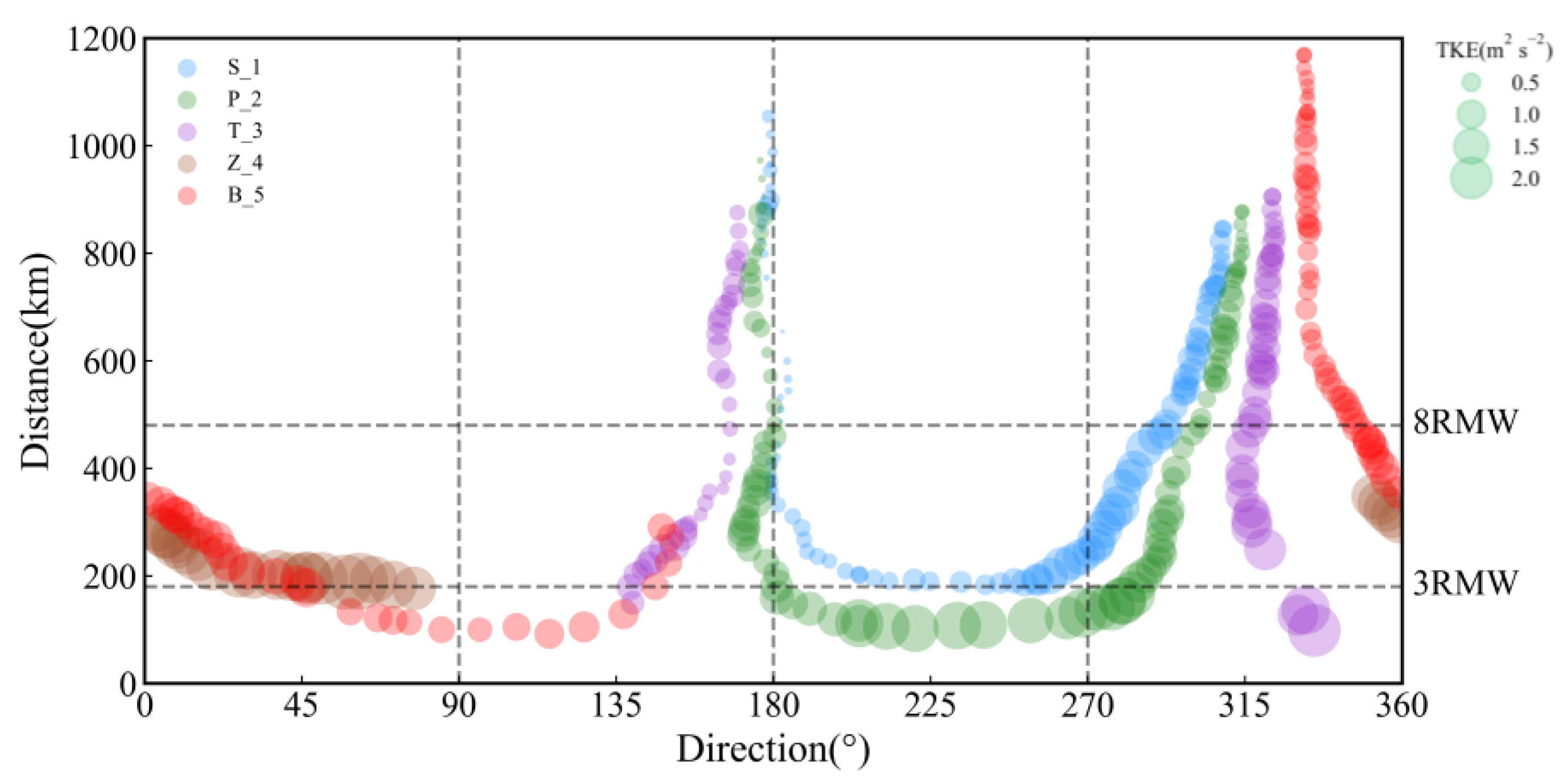
3.2. Turbulent Kinetic Energy
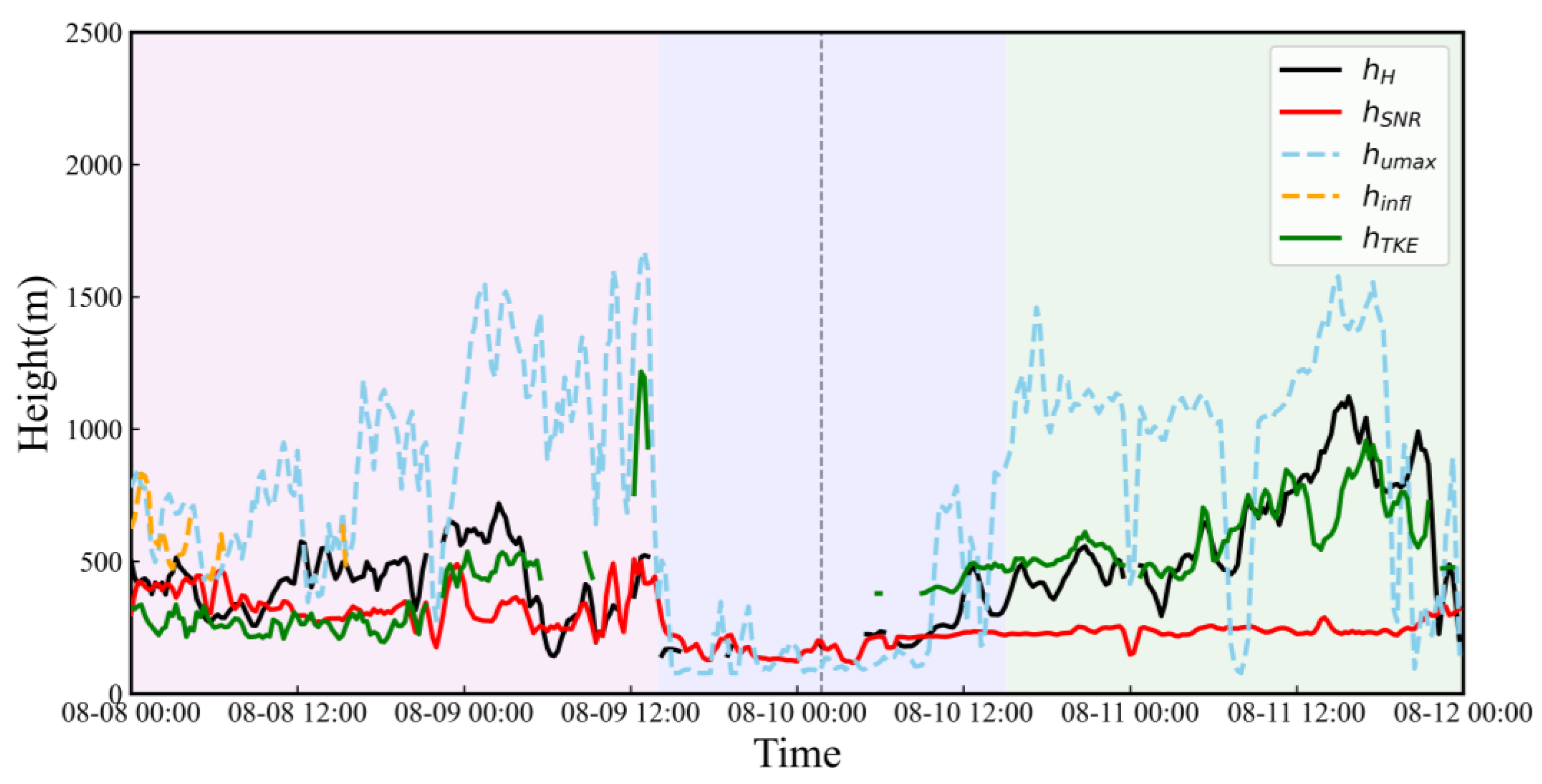
3.3. Boundary Layer Height
4. Discussion
4.1. Reliability Discussion
4.2. TKE Discussion
4.3. BLH Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Smith, R.K.; Montgomery, M.T. Hurricane boundary-layer theory. Q. J. Roy. Meteor. Soc. 2010, 136, 1665–1670. [Google Scholar] [CrossRef] [Green Version]
- Smith, R.K.; Montgomery, M.T.; Vogl, S. A critique of Emanuel’s hurricane model and potential intensity theory. Q. J. Roy. Meteor. Soc. 2008, 134, 551–561. [Google Scholar] [CrossRef] [Green Version]
- Rotunno, R.; Chen, Y.; Wang, W.; Davis, C.; Dudhia, J.; Holland, G.J. Large-Eddy Simulation of an Idealized Tropical Cyclone. B. Am. Meteorol. Soc. 2009, 90, 1783–1788. [Google Scholar] [CrossRef]
- Braun, S.A.; Tao, W.K. Sensitivity of high-resolution simulations of Hurricane Bob (1991) to planetary boundary layer parameterizations. Mon. Weather Rev. 2000, 128, 3941–3961. [Google Scholar] [CrossRef] [Green Version]
- Smith, R.K.; Thomsen, G.L. Dependence of tropical-cyclone intensification on the boundary-layer representation in a numerical model. Q. J. Roy. Meteor. Soc. 2010, 136, 1671–1685. [Google Scholar] [CrossRef]
- Zhang, J.A.; Rogers, R.F.; Tallapragada, V. Impact of Parameterized Boundary Layer Structure on Tropical Cyclone Rapid Intensification Forecasts in HWRF. Mon. Weather Rev. 2017, 145, 1413–1426. [Google Scholar] [CrossRef]
- Troen, I.; Mahrt, L. A simple model of the atmospheric boundary layer: Sensitivity to surface evaporation. Bound-lay Meteorol. 1986, 37, 129–148. [Google Scholar] [CrossRef]
- Hong, S.Y.; Pan, H.L. Nonlocal boundary layer vertical diffusion in a Medium-Range Forecast Model. Mon. Weather Rev. 1996, 124, 2322–2339. [Google Scholar] [CrossRef] [Green Version]
- Emanuel, K.A. An air–sea interaction theory for tropical cyclones. Part I: Steady-state maintenance. J. Atmos. Sci. 1986, 43, 585–605. [Google Scholar] [CrossRef]
- Powell, M.D. Boundary layer structure and dynamics in outer hurricane rainbands. Part II: Downdraft modification and mixed layer recovery. Mon. Weather Rev. 1990, 118, 918–938. [Google Scholar] [CrossRef] [Green Version]
- Anthes, R.A.; Chang, S.W. Response of the hurricane boundary layer to changes of sea surface temperature in a numerical model. J. Atmos. Sci. 1978, 35, 1240–1255. [Google Scholar] [CrossRef] [Green Version]
- Rotunno, R.; Bryan, G.H. The Maximum Intensity of Tropical Cyclones in Axisymmetric Numerical Model Simulations. Mon. Weather Rev. 2009, 137, 1770–1789. [Google Scholar] [CrossRef]
- Smith, R.K.; Montgomery, M.T.; Van Sang, N. Tropical cyclone spin-up revisited. Q. J. Roy. Meteor. Soc. 2009, 135, 1321–1335. [Google Scholar] [CrossRef] [Green Version]
- Hong, S.Y.; Noh, Y.; Dudhia, J. A new vertical diffusion package with an explicit treatment of entrainment processes. Mon. Weather Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef] [Green Version]
- Kepert, J.D. Slab- and height-resolving models of the tropical cyclone boundary layer. Part I: Comparing the simulations. Q. J. Roy. Meteor. Soc. 2010, 136, 1686–1699. [Google Scholar] [CrossRef]
- Zhang, J.A.; Rogers, R.F.; Nolan, D.S.; Marks, F.D. On the Characteristic Height Scales of the Hurricane Boundary Layer. Mon. Weather Rev. 2011, 139, 2523–2535. [Google Scholar] [CrossRef]
- Von Engeln, A.; Teixeira, J. A Planetary Boundary Layer Height Climatology Derived from ECMWF Reanalysis Data. J. Climate 2013, 26, 6575–6590. [Google Scholar] [CrossRef]
- Frisch, U.; Donnelly, R.J. Turbulence: The Legacy of A. N. Kolmogorov. Phys. Today 1996, 49, 82–84. [Google Scholar] [CrossRef] [Green Version]
- Moffatt, H.; Tsinober, A. Helicity in laminar and turbulent flow. Annu. Rev. Flud. Mech. 1992, 24, 281–312. [Google Scholar] [CrossRef]
- Bogner, P.B.; Barnes, G.M.; Franklin, J.L. Conditional instability and shear for six hurricanes over the Atlantic Ocean. Weather Forecast. 2000, 15, 192–207. [Google Scholar] [CrossRef]
- Vollaro, D.; Molinari, J. Extreme Helicity and Intense Convective Towers in Hurricane Bonnie. Mon. Weather Rev. 2008, 136, 4355–4372. [Google Scholar] [CrossRef]
- Vollaro, D.; Molinari, J. Distribution of Helicity, CAPE, and Shear in Tropical Cyclones. J. Atmos. Sci. 2010, 67, 274–284. [Google Scholar] [CrossRef] [Green Version]
- Onderlinde, M.J.; Nolan, D.S. Environmental Helicity and Its Effects on Development and Intensification of Tropical Cyclones. J. Atmos. Sci. 2014, 71, 4308–4320. [Google Scholar] [CrossRef] [Green Version]
- Chen, N.; Tang, J.; Zhang, J.A.; Ma, L.-M.; Yu, H. On the distribution of helicity in the tropical cyclone boundary layer from dropsonde composites. Atmos. Res. 2021, 249, 105298. [Google Scholar] [CrossRef]
- Ma, L.-M.; Bao, X.-W. Parametrization of Planetary Boundary-Layer Height with Helicity and Verification with Tropical Cyclone Prediction. Bound-Lay Meteorol. 2016, 160, 569–593. [Google Scholar] [CrossRef]
- Zhang, J.A. Effects of Roll Vortices on Turbulent Fluxes in the Hurricane Boundary Layer. Bound-Lay Meteorol. 2008, 128, 173–189. [Google Scholar] [CrossRef]
- Morrison, I.; Businger, S.; Marks, F.; Dodge, P.; Businger, J. An Observational Case for the Prevalence of Roll Vortices in the Hurricane Boundary Layer. J. Atmos. Sci. 2005, 62, 4121. [Google Scholar] [CrossRef]
- Zhu, P. Simulation and parameterization of the turbulent transport in the hurricane boundary layer by large eddies. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
- Zhang, J.A.; Nolan, D.S.; Rogers, R.F.; Tallapragada, V. Evaluating the Impact of Improvements in the Boundary Layer Parameterization on Hurricane Intensity and Structure Forecasts in HWRF. Mon. Weather Rev. 2015, 143, 3136–3155. [Google Scholar] [CrossRef]
- Powell, M.D.; Vickery, P.J.; Reinhold, T.A. Reduced drag coefficient for high wind speeds in tropical cyclones. Nature 2003, 422, 279–283. [Google Scholar] [CrossRef] [PubMed]
- Bucci, L.R.; O’Handley, C.; Emmitt, G.D.; Zhang, J.A.; Ryan, K.; Atlas, R. Validation of an Airborne Doppler Wind Lidar in Tropical Cyclones. Sensors 2018, 18, 4288. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Atlas, R.; Emmitt, G.; Bucci, L.; Ryan, K. Airborne Doppler Wind Lidar Observations of the Tropical Cyclone Boundary Layer. Remote Sens. 2018, 10, 825. [Google Scholar] [CrossRef] [Green Version]
- Feng, J.; Lu, X.; Yu, H.; Zhang, W.; Ying, M.; Fan, Y.; Zhu, Y.; Chen, D. An Overview of the China Meteorological Administration Tropical Cyclone Database. J. Atmos. Ocean. Tech. 2014, 31, 287–301. [Google Scholar] [CrossRef] [Green Version]
- Tang, J.; Byrne, D.; Zhang, J.A.; Wang, Y.; Lei, X.-T.; Wu, D.; Fang, P.-Z.; Zhao, B.-K. Horizontal Transition of Turbulent Cascade in the Near-Surface Layer of Tropical Cyclones. J. Atmos. Sci. 2015, 72, 4915–4925. [Google Scholar] [CrossRef]
- Fang, P.; Zhao, B.; Zeng, Z.; Yu, H.; Lei, X.; Tan, J. Effects of Wind Direction on Variations in Friction Velocity With Wind Speed Under Conditions of Strong Onshore Wind. J. Geophys. Res-Atmos. 2018, 123, 7340–7353. [Google Scholar] [CrossRef]
- Tang, S.M.; Guo, Y.; Wang, X.; Tang, J.; Li, T.T.; Zhao, B.K.; Zhang, S.; Li, Y.P. Validation of Doppler Wind Lidar during Super Typhoon Lekima (2019). Front. Earth Sci. 2020, 15. [Google Scholar] [CrossRef]
- Dai, H.; Zhao, K.; Li, Q.; Lee, W.C.; Ming, J.; Zhou, A.; Fan, X.; Yang, Z.; Zheng, F.; Duan, Y. Quasi-Periodic Intensification of Convective Asymmetries in the Outer Eyewall of Typhoon Lekima (2019). Geophys. Res. Lett. 2021, 48, e2020GL091633. [Google Scholar] [CrossRef]





| DWL | Location | Type | Longitude (°) | Latitude (°) | Altitude (m) |
|---|---|---|---|---|---|
| S_1 | SanSha | WindPrint S4000 | 120.229 | 26.919 | 40 |
| P_2 | PingYang | Windcube V2 | 120.573 | 27.669 | 254 |
| T_3 | TaiZhou | Windcube V2 | 121.417 | 28.618 | 2 |
| Z_4 | ZhouShan | Windcube V2 | 122.367 | 29.902 | 10 |
| B_5 | BaoShan | WindPrint S4000 | 121.444 | 31.391 | 9 |
| Instruments | Detection Range | Data Update | Wind Speed Range | Wind Speed Accuracy |
|---|---|---|---|---|
| WindPrint S4000 | 77.9–2450 m | 0.25 Hz | 0–75 m s−1 | 0.1 m s−1 |
| Windcube V2 | 40–290 m | 1 Hz | 0–80 m s−1 | 0.1 m s−1 |
| WindMaster Pro | 10–70 m | 20 Hz | 0–65 m s−1 | 0.1 m s−1 |
| Observations | Before Landfall >8RMW | Before Landfall 3–8RMW | Before Landfall <3RMW | After Landfall <3RMW | After Landfall 3–8RMW | After Landfall >8RMW |
|---|---|---|---|---|---|---|
| S_1 | 0.809 | 1.426 | / | / | 0.403 | 0.269 |
| P_2 | 0.688 | 1.143 | 2.506 | 2.008 | 1.057 | 0.455 |
| T_3 | 0.999 | 1.622 | 2.696 | / | 0.725 | 0.613 |
| Z_4 | / | 2.753 | / | / | 3.003 | / |
| B_5 | 0.701 | 1.292 | / | 1.111 | 1.605 0.994 | / |
| Boundary Layer Height (m) | FL | RL | RR |
|---|---|---|---|
| hH (m) | 426 | 253 | 623 |
| hTKE (m) | 352 | 433 | 613 |
| hSNR (m) | 333 | 187 | 242 |
| humax (m) | 898 | 233 | 975 |
| hinfl (m) | 629 | / | / |
| Boundary Layer Height (m) | FR | RR | FL |
|---|---|---|---|
| hH (m) | 303 | 134 | 250 |
| hTKE (m) | / | / | 287 |
| hSNR (m) | 171 | 154 | 347 |
| humax (m) | 463 | 417 | 550 |
| hinfl (m) | / | 223 | / |
| Time | TKE of S_1 (m2 s−2) | TKE of P_2 (m2 s−2) | TKE of T_3 (m2 s−2) | TKE of Z_4 (m2 s−2) | TKE of B_5 (m2 s−2) | Distance (km) |
|---|---|---|---|---|---|---|
| 8.10 5:00 | 0.45 | 2.7 | 200 | |||
| 8.10 10:00 | 0.51 | 1.9 | 250 | |||
| 8.10 12:00 | 1.13 | 2.92 | 180 | |||
| 8.10 13:00 | 0.95 | 1.55 | 200 | |||
| 8.10 13:00 | 2.48 | 1.55 | 200 | |||
| 8.10 15:00 | 0.87 | 1.6 | 190 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, W.; Tang, J.; Chen, Y.; Chen, N.; Liu, Q.; Liu, T. Study of the Boundary Layer Structure of a Landfalling Typhoon Based on the Observation from Multiple Ground-Based Doppler Wind Lidars. Remote Sens. 2021, 13, 4810. https://doi.org/10.3390/rs13234810
Shi W, Tang J, Chen Y, Chen N, Liu Q, Liu T. Study of the Boundary Layer Structure of a Landfalling Typhoon Based on the Observation from Multiple Ground-Based Doppler Wind Lidars. Remote Sensing. 2021; 13(23):4810. https://doi.org/10.3390/rs13234810
Chicago/Turabian StyleShi, Wenhao, Jie Tang, Yonghang Chen, Nuo Chen, Qiong Liu, and Tongqiang Liu. 2021. "Study of the Boundary Layer Structure of a Landfalling Typhoon Based on the Observation from Multiple Ground-Based Doppler Wind Lidars" Remote Sensing 13, no. 23: 4810. https://doi.org/10.3390/rs13234810
APA StyleShi, W., Tang, J., Chen, Y., Chen, N., Liu, Q., & Liu, T. (2021). Study of the Boundary Layer Structure of a Landfalling Typhoon Based on the Observation from Multiple Ground-Based Doppler Wind Lidars. Remote Sensing, 13(23), 4810. https://doi.org/10.3390/rs13234810







