Optimizing Matching Area for Underwater Gravity-Aided Inertial Navigation Based on the Convolution Slop Parameter-Support Vector Machine Combined Method
Abstract
:1. Introduction
2. Materials and Methods
2.1. Image Convolution
2.2. Convolution Slope Parameter
2.3. Other Characteristic Parameters
2.3.1. Difference between Convolution Rows and Columns Parameter
2.3.2. Convolution Variance
2.3.3. Pooling Difference
2.3.4. Range
2.4. Principle of Support Vector Machine Algorithm
3. Results
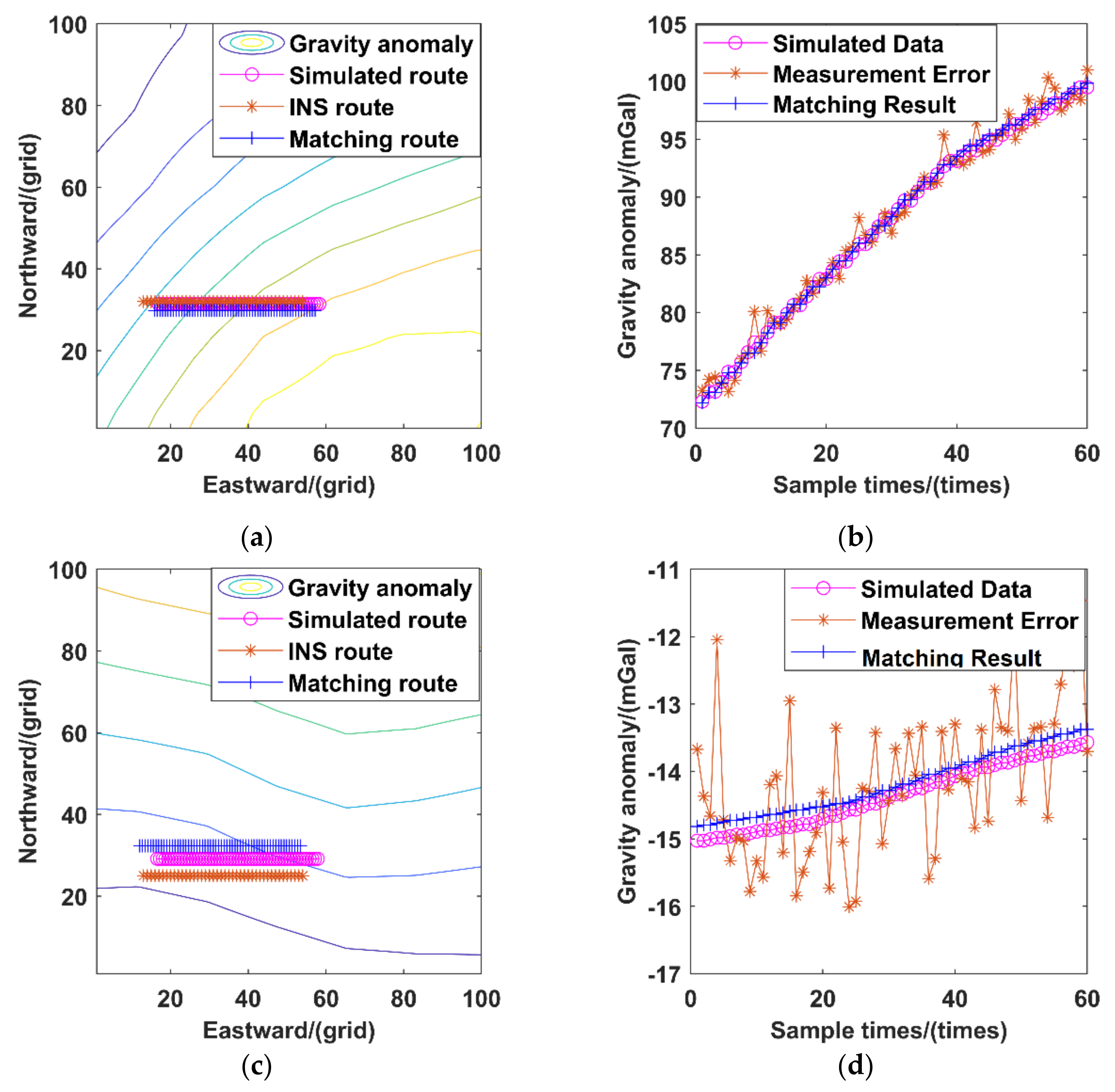
3.1. Verification
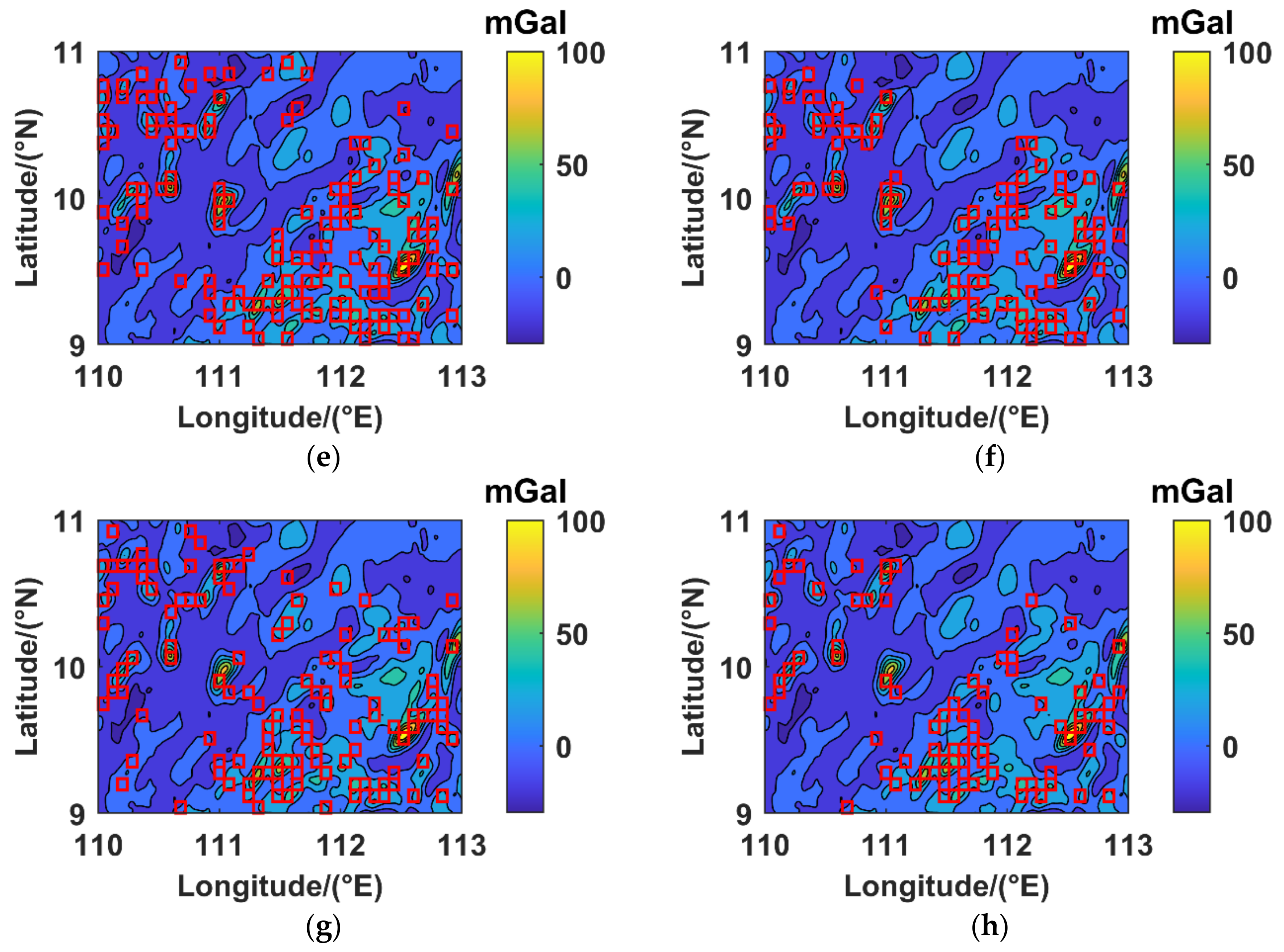
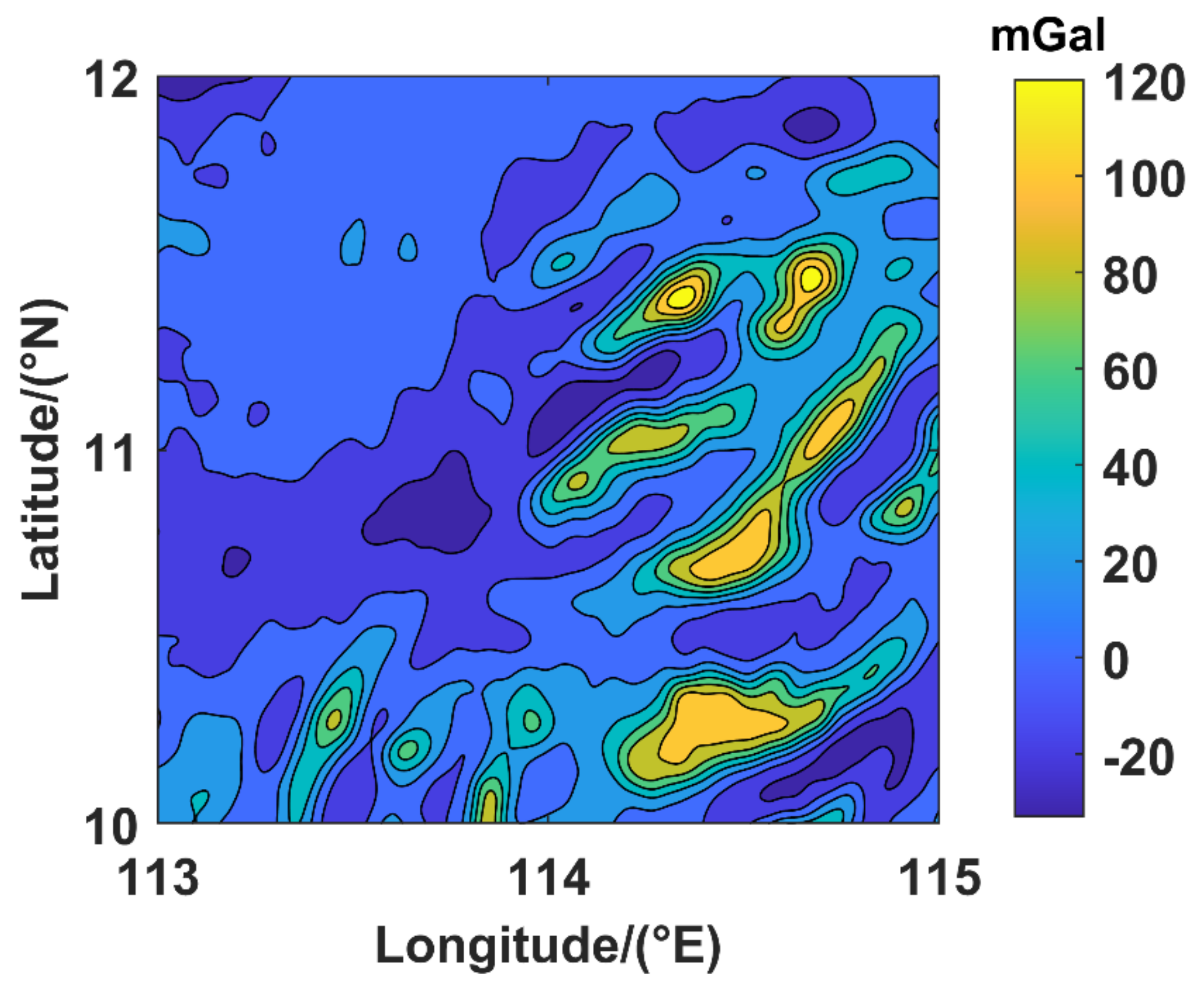
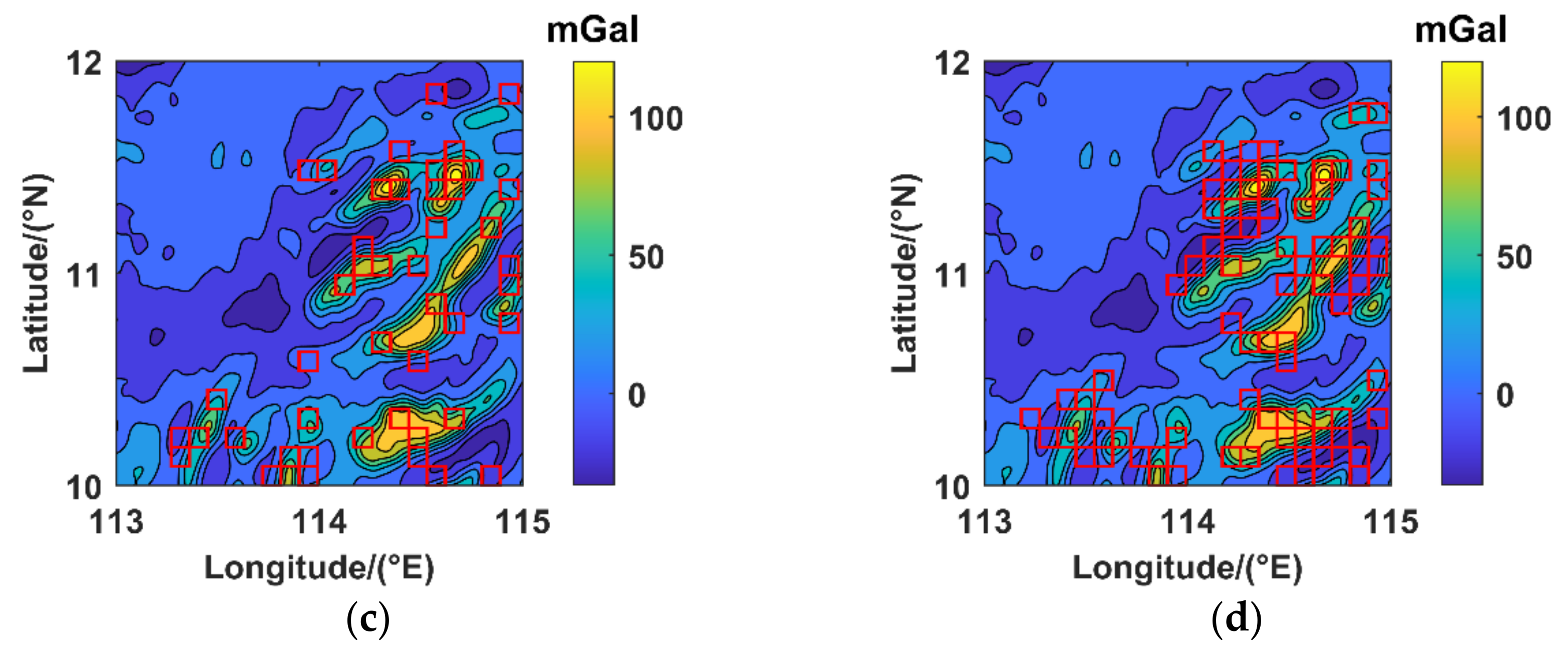
3.2. Appliction
4. Conclusions
- (1)
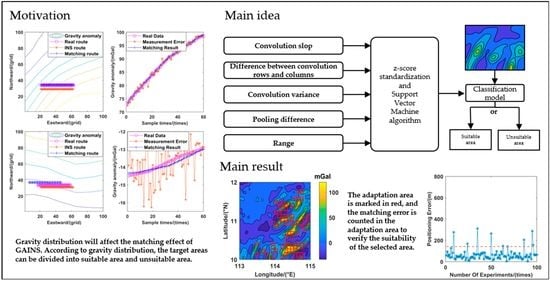
- The Sobel operator was used for convolution of the gravity anomaly map, and the convolution slope parameter was constructed. The difference between convolution rows and columns, convolution variance of the feature map, pooling difference, and range parameter of gravity anomaly map was calculated. SVM algorithm was used to fuse these five parameters, and a convolution slope parameter-support vector machine combined method is proposed.
- (2)
- The samples of the target area were divided into the training set and test set. The training set data were used to calculate the classification model, which separates the test-set samples and compares them with the pre-calibration results. In the experimental results, the classification accuracy of the test set is over 92%.
- (3)
- To verify the effectiveness of the classification results, the classification model was applied to another region, and the suitable areas and unsuitable areas were divided. The navigation experiment was carried out in the suitable areas. The results show that the positioning error is better than 100 m, and the accuracy can be more than 91%. It is proven that this method can effectively divide the matching area of GAINS.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Alamgir, M.S.M.; Sultana, M.N.; Chang, K. Link Adaptation on an Underwater Communications Network Using Machine Learning Algorithms: Boosted Regression Tree Approach. IEEE Access 2020, 8, 73957–73971. [Google Scholar] [CrossRef]
- Dai, T.; Miao, L.; Shao, H.; Shi, Y. Solving gravity anomaly matching problem under large initial errors in gravity aided navigation by using an affine transformation based artificial bee colony algorithm. Front. Neurorobot. 2019, 13, 19. [Google Scholar] [CrossRef]
- Han, Y.; Wang, B.; Deng, Z.; Fu, M. A Matching Algorithm Based on the Nonlinear Filter and Similarity Transformation for Gravity-Aided Underwater Navigation. IEEE/ASME Trans. Mechatron. 2018, 23, 646–654. [Google Scholar] [CrossRef]
- Han, Y.; Wang, B.; Deng, Z.; Wang, S.; Fu, M. A mismatch diagnostic method for TERCOM-Based underwater gravity-aided navigation. IEEE Sens. J. 2017, 17, 2880–2888. [Google Scholar] [CrossRef]
- Li, Z.; Zheng, W.; Wu, F. Improving the Reliability of Underwater Gravity Matching Navigation Based on a Priori Recursive Iterative Least Squares Mismatching Correction Method. IEEE Access 2020, 8, 8648–8657. [Google Scholar] [CrossRef]
- Wang, B.; Zhu, J.; Ma, Z.; Deng, Z.; Fu, M. Improved Particle Filter-Based Matching Method with Gravity Sample Vector for Underwater Gravity-Aided Navigation. IEEE Trans. Ind. Electron. 2021, 68, 5206–5216. [Google Scholar] [CrossRef]
- Wang, K.; Zhu, T.; Qin, Y.; Jiang, R.; Li, Y. Matching error of the iterative closest contour point algorithm for terrain-aided navigation. Aerosp. Sci. Technol. 2018, 73, 210–222. [Google Scholar] [CrossRef]
- Tang, J.; Xiong, L.; Li, K.; Ma, J. Research on matching area selection based on multiple features fusion of full tensor gravity gradient. MIPPR 2015 Autom. Target Recognit. Navig. 2015, 9812, 98120F. [Google Scholar] [CrossRef]
- Wang, B.; Zhu, Y.; Deng, Z.; Fu, M. The Gravity Matching Area Selection Criteria for Underwater Gravity-Aided Navigation Application Based on the Comprehensive Characteristic Parameter. IEEE/ASME Trans. Mechatron. 2016, 21, 2935–2943. [Google Scholar] [CrossRef]
- Wang, H.; Wu, L.; Chai, H.; Xiao, Y.; Hsu, H.; Wang, Y. Characteristics of marine gravity anomaly reference maps and accuracy analysis of gravity matching-aided navigation. Sensors 2017, 17, 1851. [Google Scholar] [CrossRef] [Green Version]
- Liu, F.; Li, F.; Jing, X. Navigability Analysis of Local Gravity Map With Projection Pursuit-Based Selection Method by Using Gravitation Field Algorithm. IEEE Access 2019, 7, 75873–75889. [Google Scholar] [CrossRef]
- Wang, B.; Zhou, M.; Deng, Z.; Fu, M. Sum vector-difference-based matching area selection method for underwater gravity-aided navigation. IEEE Access 2019, 7, 123616–123624. [Google Scholar] [CrossRef]
- Wang, C.; Wang, B.; Deng, Z.; Fu, M. A co-occurrence matrix-based matching area selection algorithm for underwater gravity-aided inertial navigation. IET Radar Sonar Navig. 2021, 15, 250–260. [Google Scholar] [CrossRef]
- Wang, C.; Wang, B.; Deng, Z.; Fu, M. A delaunay triangulation-based matching area selection algorithm for underwater gravity-aided inertial navigation. IEEE/ASME Trans. Mechatron. 2021, 26, 908–917. [Google Scholar] [CrossRef]
- Tian, R.; Sun, G.; Liu, X.; Zheng, B. Sobel edge detection based on weighted nuclear norm minimization image denoising. Electronics 2021, 10, 655. [Google Scholar] [CrossRef]
- Gonzalez, C.I.; Melin, P.; Castro, J.R.; Mendoza, O.; Castillo, O. An improved sobel edge detection method based on generalized type-2 fuzzy logic. Soft Comput. 2016, 20, 773–784. [Google Scholar] [CrossRef]
- Yildirim, O.; Baloglrf, U.B. Regp: A new pooling algorithm for deep convolutional neural networks. Neural Netw. World 2019, 29, 45–60. [Google Scholar] [CrossRef]
- Tong, Z.; Tanaka, G. Hybrid pooling for enhancement of generalization ability in deep convolutional neural networks. Neurocomputing 2019, 333, 76–85. [Google Scholar] [CrossRef]
- Zhang, C.Z.; Feng, H.J.; Xu, Z.H.; Li, Q.; Chen, Y.T. Piecewise noise variance estimation of images based on wavelet transform. J. Zhejiang Univ. Eng. Sci. 2018, 52, 1804–1810. [Google Scholar] [CrossRef]
- Li, D.G.; Zheng, S. Joint Median and Range Chart with Two-stage Sampling. Math. Pract. Theory 2010, 40, 137–140. [Google Scholar]
- Singh, D.; Singh, B. Investigating the impact of data normalization on classification performance. Appl. Soft Comput. 2020, 97, 105524. [Google Scholar] [CrossRef]
- Vapnik, V.; Golowich, S.E.; Smola, A. Support vector method for function approximation, regression estimation, and signal processing. In Advances in Neural Information Processing Systems; Neural Information Processing Systems Foundation: La Jolla, CA, USA, 1997; pp. 281–287. Available online: http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.41.3139 (accessed on 15 August 2021).
- Ju, H.; Hou, Q.; Jing, L. Fuzzy and interval-valued fuzzy nonparallel support vector machine. J. Intell. Fuzzy Syst. 2019, 36, 2677–2690. [Google Scholar] [CrossRef]
- Ding, S.; Zhu, Z.; Zhang, X. An overview on semi-supervised support vector machine. Neural Comput. Appl. 2017, 28, 969–978. [Google Scholar] [CrossRef]
- Bazi, Y.; Melgani, F. Toward an optimal SVM classification system for hyperspectral remote sensing images. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3374–3385. [Google Scholar] [CrossRef]
- Chang, C.C.; Lin, C.J. LIBSVM: A Library for support vector machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 1–27. [Google Scholar] [CrossRef]







| Area | Convolution Slop | Difference between Convolution Rows and Columns | Convolution Variance | Pooling Difference | Range |
|---|---|---|---|---|---|
| A | 1.3939 | 1.2144 | 1.2828 | 0.0212 | 1.5310 |
| B | −1.0599 | −0.9096 | −0.5548 | −0.6817 | −0.8296 |
| C | −0.4586 | −0.7998 | −0.4899 | −0.5950 | −0.6989 |
| D | 2.8311 | 3.9503 | 4.5418 | 2.8409 | 4.1681 |
| Area | Average Positioning Error/m | The Standard Deviation of Positioning Error/m |
|---|---|---|
| A | 60.98 | 36.36 |
| B | 911.34 | 617.71 |
| C | 234.42 | 141.95 |
| D | 59.67 | 49.76 |
| Direction | Number of the Suitable Area | Number of Unsuitable Areas |
|---|---|---|
| East-west | 126 | 799 |
| North-south | 136 | 789 |
| Northeast | 138 | 787 |
| Northwest | 124 | 801 |
| Direction | Classification Accuracy of the Test Set | Recall Rate of the Single Category | Classification Accuracy of All Samples | |
|---|---|---|---|---|
| Recall Rate of the Suitable Area | Recall Rate of the Unsuitable Area | |||
| East-west | 93.00% | 75.00% | 96.43% | 92.43% |
| North-south | 92.00% | 70.00% | 94.44% | 93.19% |
| Northeast | 93.00% | 72.73% | 95.51% | 94.92% |
| Northwest | 95.00% | 80.00% | 96.67% | 93.19% |
| Direction | Average Positioning Error/m | The Standard Deviation of Positioning Error/m | Correct Rate |
|---|---|---|---|
| East-west | 65.20 | 56.31 | 91% |
| North-south | 63.17 | 60.14 | 92% |
| Northeast | 71.75 | 57.26 | 91% |
| Northwest | 72.35 | 83.37 | 93% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Zheng, W.; Li, Z. Optimizing Matching Area for Underwater Gravity-Aided Inertial Navigation Based on the Convolution Slop Parameter-Support Vector Machine Combined Method. Remote Sens. 2021, 13, 3940. https://doi.org/10.3390/rs13193940
Wang S, Zheng W, Li Z. Optimizing Matching Area for Underwater Gravity-Aided Inertial Navigation Based on the Convolution Slop Parameter-Support Vector Machine Combined Method. Remote Sensing. 2021; 13(19):3940. https://doi.org/10.3390/rs13193940
Chicago/Turabian StyleWang, Shuoqi, Wei Zheng, and Zhaowei Li. 2021. "Optimizing Matching Area for Underwater Gravity-Aided Inertial Navigation Based on the Convolution Slop Parameter-Support Vector Machine Combined Method" Remote Sensing 13, no. 19: 3940. https://doi.org/10.3390/rs13193940
APA StyleWang, S., Zheng, W., & Li, Z. (2021). Optimizing Matching Area for Underwater Gravity-Aided Inertial Navigation Based on the Convolution Slop Parameter-Support Vector Machine Combined Method. Remote Sensing, 13(19), 3940. https://doi.org/10.3390/rs13193940