Global Sensitivity Analysis of a Water Cloud Model toward Soil Moisture Retrieval over Vegetated Agricultural Fields
Abstract
:1. Introduction
2. Models and Methods
2.1. Backscattering Models
2.1.1. Oh-2004 Model
2.1.2. Water Cloud Model
2.2. Global Sensitivity Analysis Methods
2.2.1. Sobol’ Method
2.2.2. FAST Method
2.2.3. DGSM Method
2.2.4. Delta Test Method
2.2.5. Morris Method
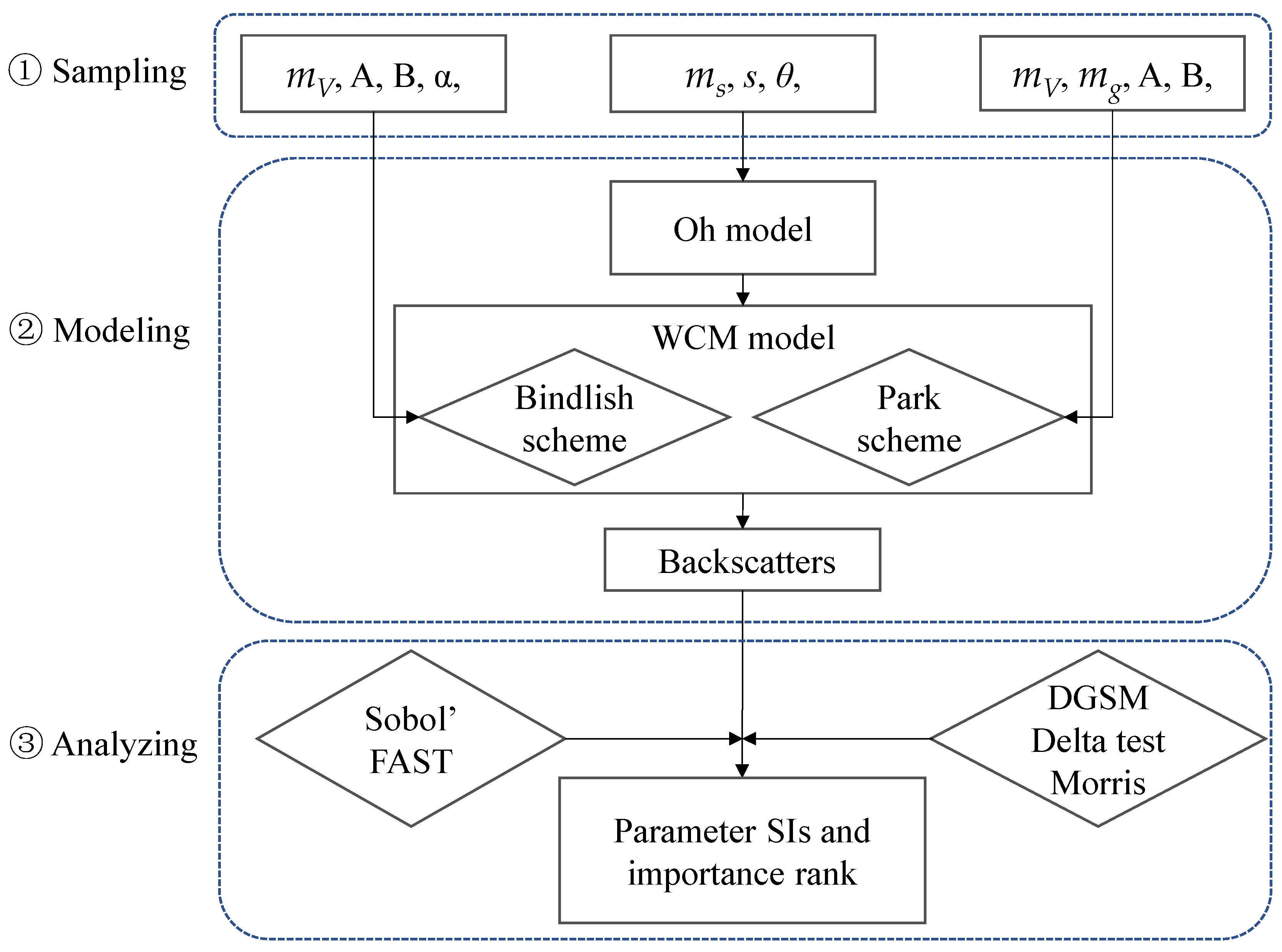
2.3. Design of Experiment
3. Results
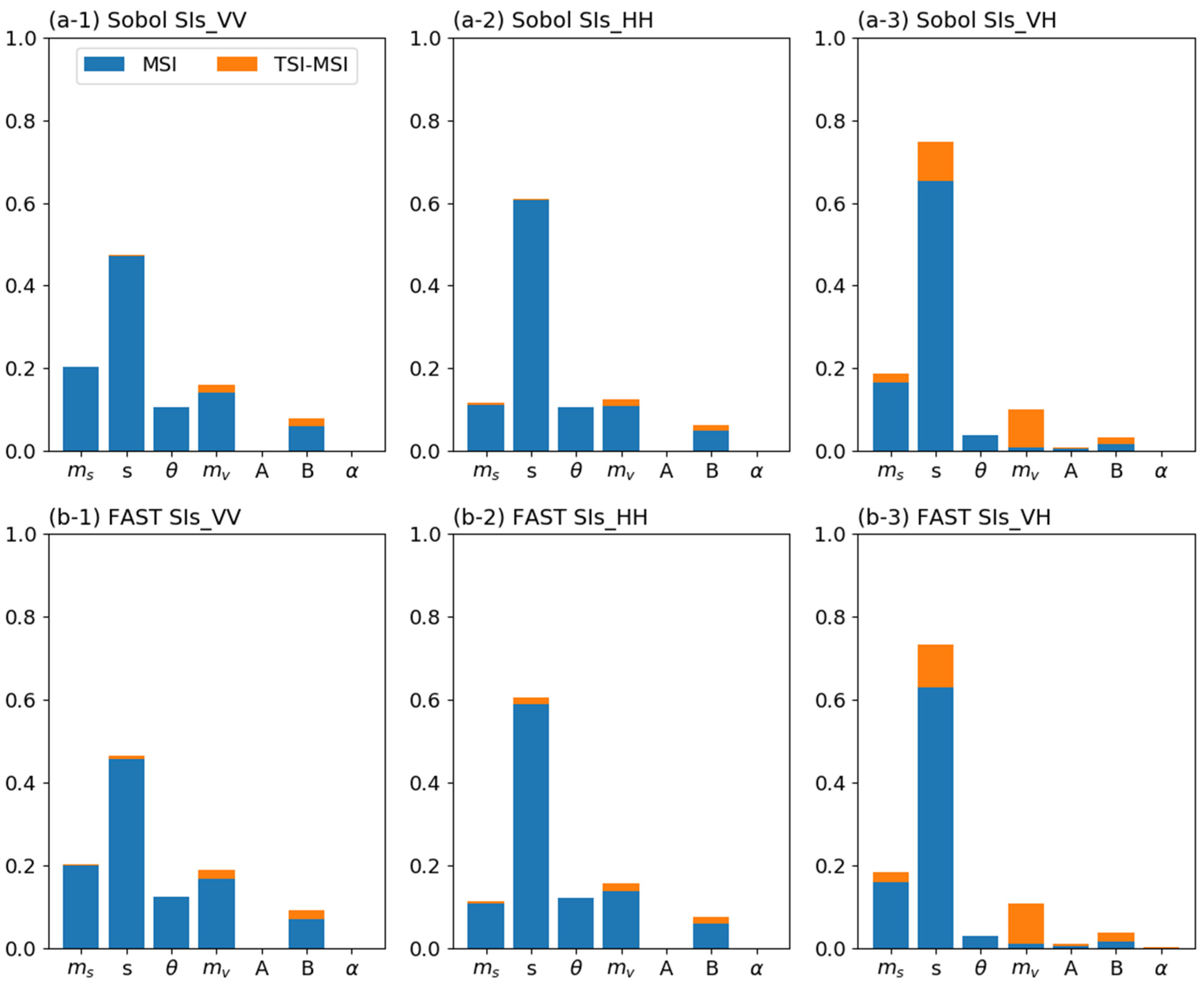
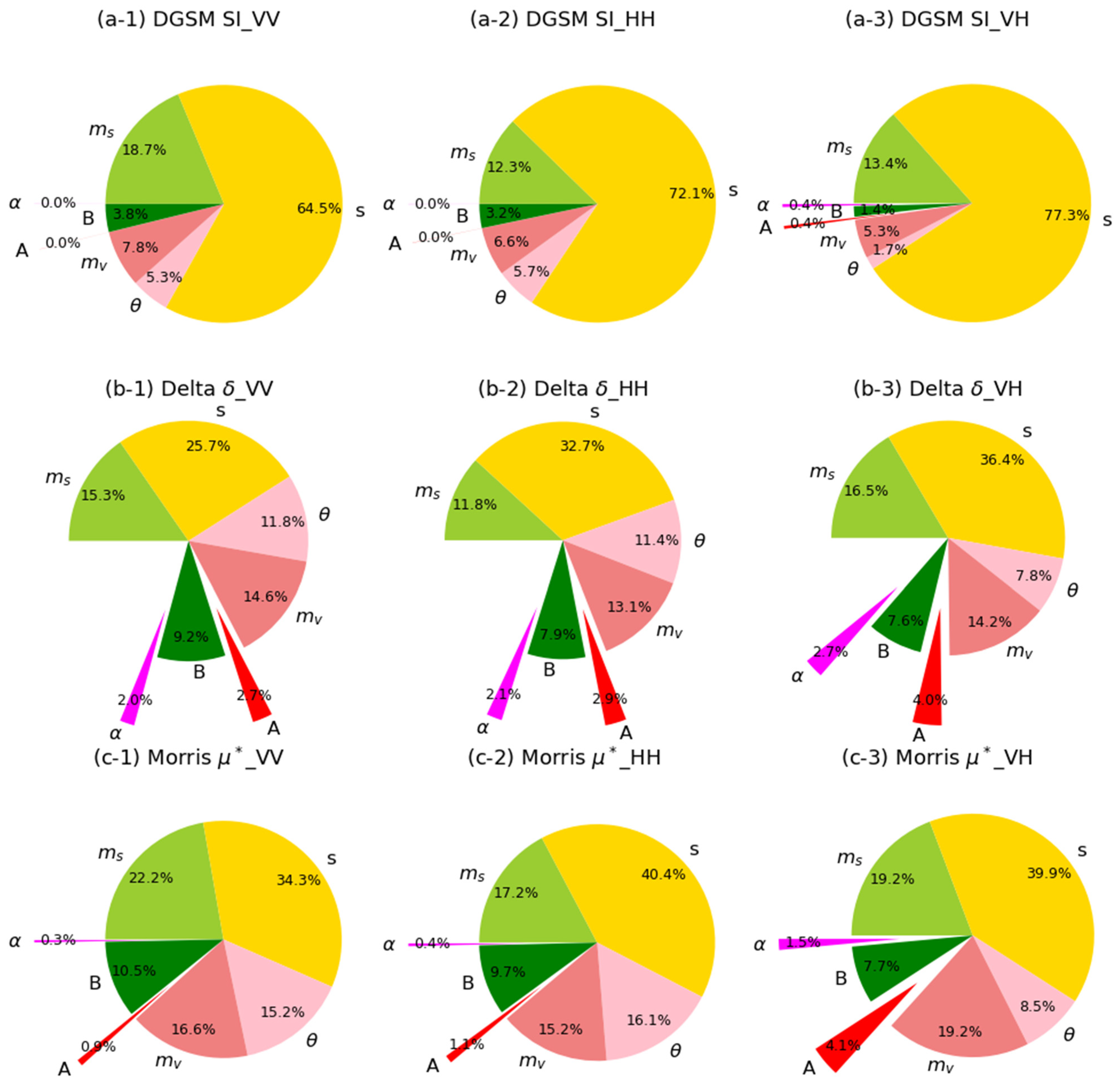
3.1. Parameter SIs under Bindlish Vegetation Description Scheme
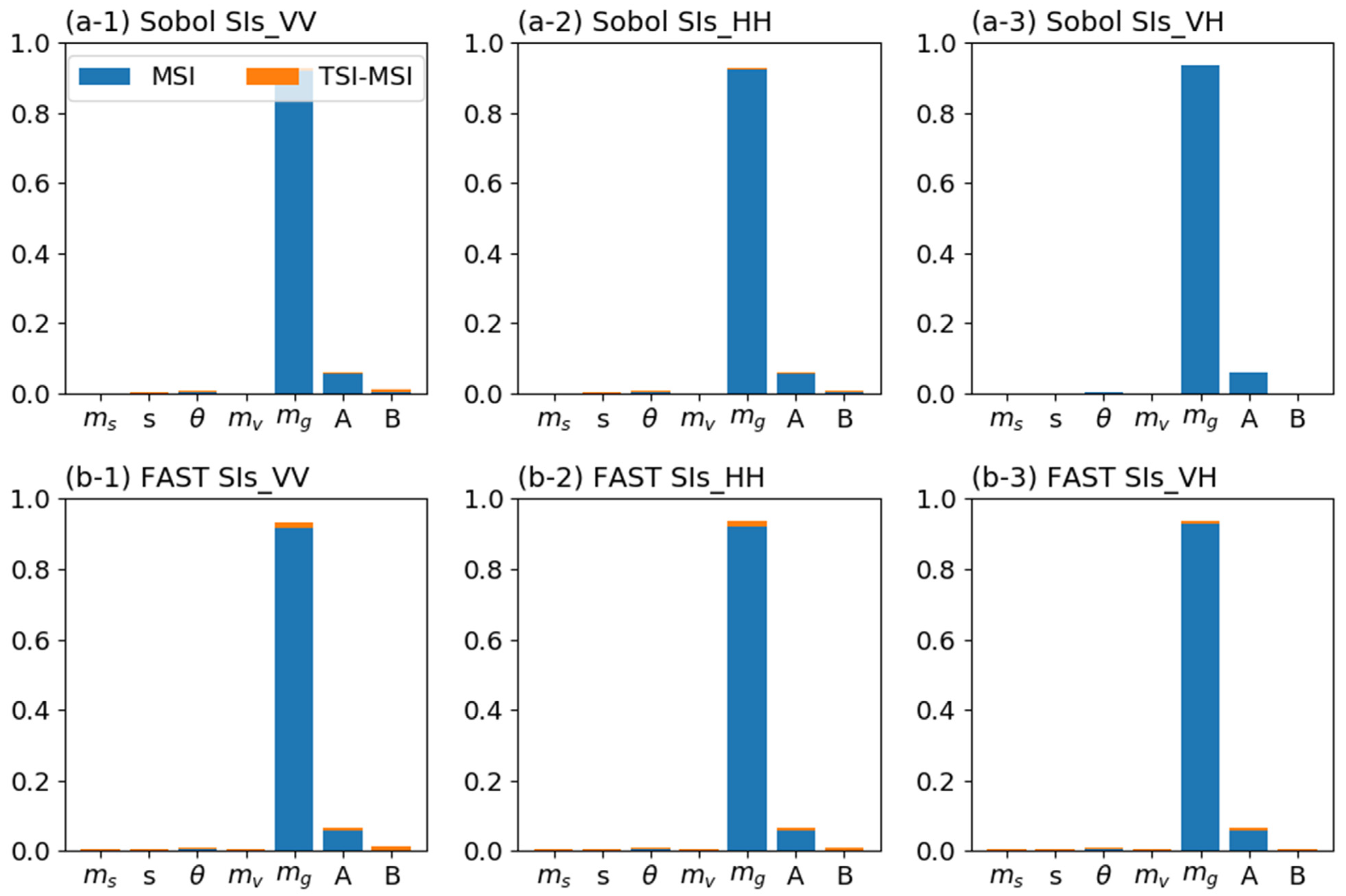
3.2. Parameter SIs under Park Vegetation Description Scheme
3.3. Parameter SIs under Varied VWC Ranges
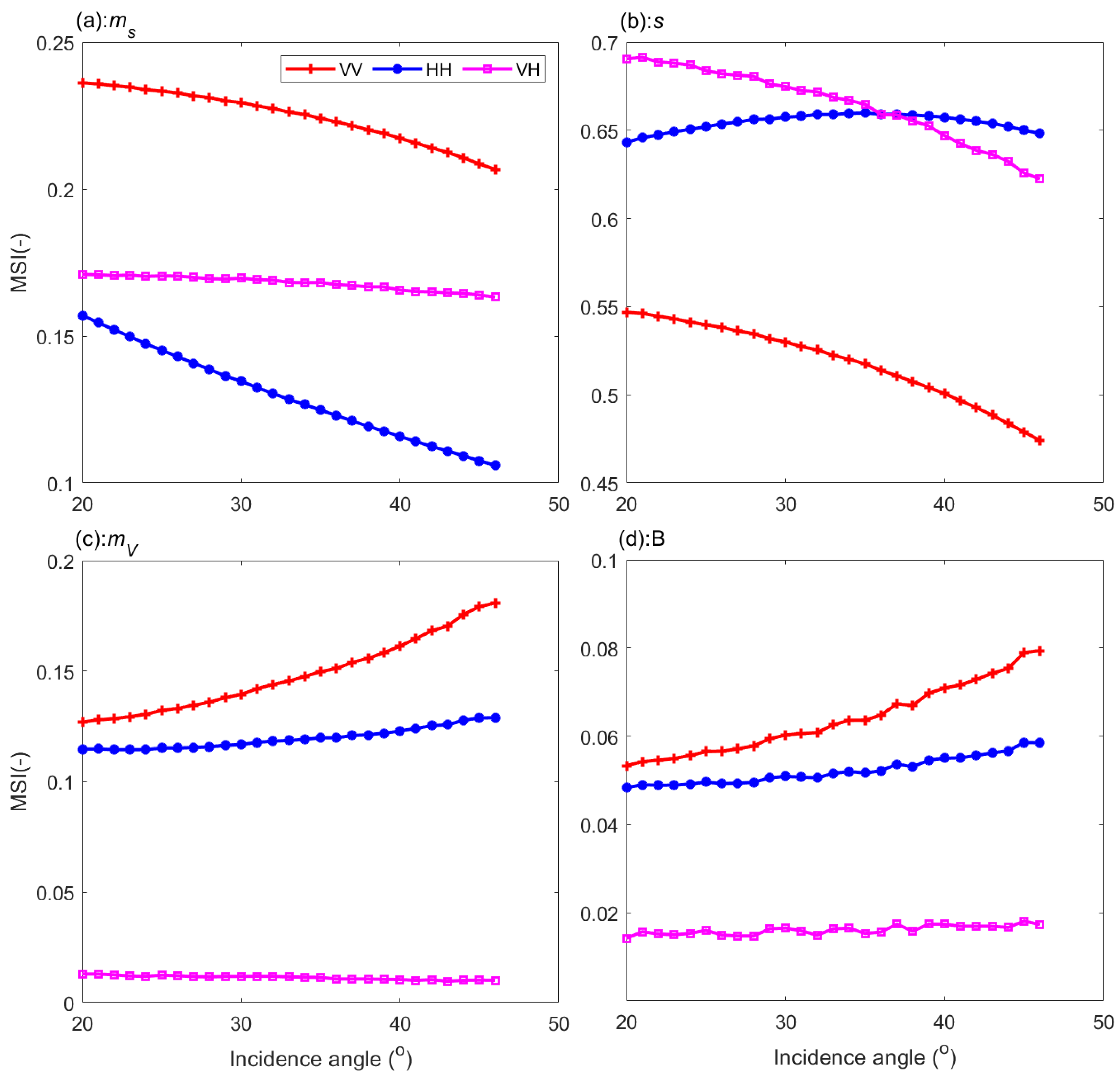
3.4. Parameter SIs on Different Incidence Angles and Polarizations
4. Discussion
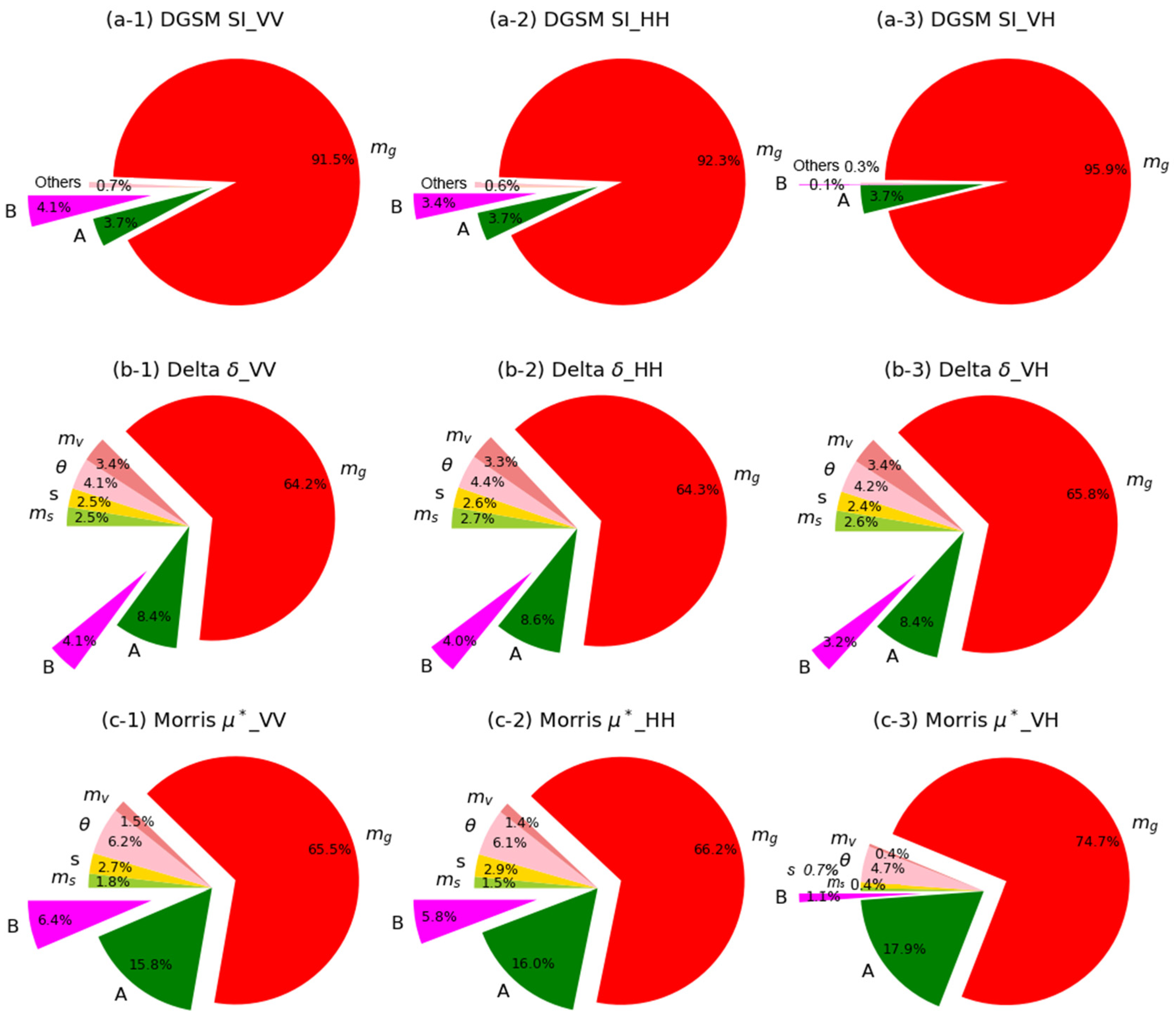
4.1. SA with Multiple Methods
4.2. Vegetation Descriptors for WCM
4.3. Optimal SAR Configuration for Parameter Estimaiton
4.4. Implication for Backscattering Modeling and Parameter Estimation
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Acronyms
| AIEM | Advanced Integral Equation Model |
| DGSM | Derivative based Global Sensitivity Measures |
| FAST | Fourier Amplitude Sensitivity Test |
| IEM | Integral Equation Model |
| LAI | Leaf Area Index |
| MSI | Main Sensitivity Index |
| NDVI | Normalized Difference Vegetation Index |
| SA | Sensitivity Analysis |
| SI | Sensitivity Index |
| SAR | Synthetic Aperture Radar |
| TSI | Total Sensitivity Index |
| WCM | Water Cloud Model |
| VWC | Vegetation Water Content |
References
- Hornacek, M.; Wagner, W.; Sabel, D.; Truong, H.L.; Snoeij, P.; Hahmann, T.; Diedrich, E.; Doubkova, M. Potential for High Resolution Systematic Global Surface Soil Moisture Retrieval via Change Detection Using Sentinel-1. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 1303–1311. [Google Scholar] [CrossRef]
- Torres, R.; Snoeij, P.; Geudtner, D.; Bibby, D.; Davidson, M.; Attema, E.; Potin, P.; Rommen, B.; Floury, N.; Brown, M.; et al. GMES Sentinel-1 mission. Remote Sens. Environ. 2012, 120, 9–24. [Google Scholar] [CrossRef]
- Ma, C.; Li, X.; Chen, K.-S. The Discrepancy Between Backscattering Model Simulations and Radar Observations Caused By Scaling Issues: An Uncertainty Analysis. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5356–5372. [Google Scholar] [CrossRef]
- Fung, A.K.; Li, Z.Q.; Chen, K.S. Backscattering from a Randomly Rough Dielectric Surface. IEEE Trans. Geosci. Remote Sens. 1992, 30, 356–369. [Google Scholar] [CrossRef]
- Chen, K.S.; Wu, T.-D.; Tsang, L.; Li, Q.; Shi, J.; Fung, A.K. Emission of Rough Surfaces Calculated by the Integral Equation Method With Comparison to Three-Dimensional Moment Method Simulations. IEEE Trans. Geosci. Remote Sens. 2003, 41, 90–101. [Google Scholar] [CrossRef]
- Oh, Y. Quantitative retrieval of soil moisture content and surface roughness from multipolarized radar observations of bare soil surfaces. IEEE Trans. Geosci. Remote Sens. 2004, 42, 596–601. [Google Scholar] [CrossRef]
- Attema, E.P.W.; Ulaby, F.T. Vegetation Modeled as a Water Cloud. Radio Sci. 1978, 13, 357–364. [Google Scholar] [CrossRef]
- Bindlish, R.; Barros, A.P. Parameterization of vegetation backscatter in radar-based, soil moisture estimation. Remote Sens. Environ. 2001, 76, 130–137. [Google Scholar] [CrossRef]
- Sikdar, M.; Cumming, I. A modified empirical model for soil moisture estimation in vegetated areas using SAR data. In Proceedings of the Igarss 2004: IEEE International Geoscience and Remote Sensing Symposium, Anchorage, AK, USA, 20–24 September 2004; Volume 1–7, pp. 803–806. [Google Scholar]
- Baghdadi, N.; El Hajj, M.; Zribi, M.; Bousbih, S. Calibration of the Water Cloud Model at C-Band for Winter Crop Fields and Grasslands. Remote Sens. 2017, 9, 969. [Google Scholar] [CrossRef] [Green Version]
- Dabrowska-Zielinska, K.; Inoue, Y.; Kowalik, W.; Gruszczynska, M. Inferring the effect of plant and soil variables on C- and L-band SAR backscatter over agricultural fields, based on model analysis. Adv. Space Res. 2007, 39, 139–148. [Google Scholar] [CrossRef]
- Kumar, K.; Rao, H.P.S.; Arora, M.K. Study of water cloud model vegetation descriptors in estimating soil moisture in Solani catchment. Hydrol. Process. 2015, 29, 2137–2148. [Google Scholar] [CrossRef]
- Hajj, M.E. Soil moisture retrieval over irrigated grassland using X-band SAR data. Remote Sens. Environ. 2016, 176, 202–218. [Google Scholar] [CrossRef] [Green Version]
- Amazirh, A.; Merlin, O.; Er-Raki, S.; Gao, Q.; Rivalland, V.; Malbeteau, Y.; Khabba, S.; Escorihuela, M.J. Retrieving surface soil moisture at high spatio-temporal resolution from a synergy between Sentinel-1 radar and Landsat thermal data: A study case over bare soil. Remote Sens. Environ. 2018, 211, 321–337. [Google Scholar] [CrossRef]
- Ma, C.; Li, X.; McCabe, M.F. Retrieval of High-Resolution Soil Moisture through Combination of Sentinel-1 and Sentinel-2 Data. Remote Sens. 2020, 12, 2303. [Google Scholar] [CrossRef]
- Attarzadeh, R.; Amini, J.; Notarnicola, C.; Greifeneder, F. Synergetic Use of Sentinel-1 and Sentinel-2 Data for Soil Moisture Mapping at Plot Scale. Remote Sens. 2018, 10, 1285. [Google Scholar] [CrossRef] [Green Version]
- Park, S.E.; Jung, Y.T.; Cho, J.H.; Moon, H.; Han, S.H. Theoretical Evaluation of Water Cloud Model Vegetation Parameters. Remote Sens. 2019, 11, 894. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.Z.; Shi, J.C. Estimation of Vegetation Parameters of Water Cloud Model for Global Soil Moisture Retrieval Using Time-Series L-Band Aquarius Observations. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 5621–5633. [Google Scholar] [CrossRef]
- Oh, Y.; Sarabandi, K.; Ulaby, F.T. Semi-empirical model of the ensemble-averaged differential Mueller matrix for microwave backscattering from bare soil surfaces. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1348–1355. [Google Scholar] [CrossRef] [Green Version]
- Gao, Y.; Walker, J.P.; Allahmoradi, M.; Monerris, A.; Ryu, D.; Jackson, T.J. Optical Sensing of Vegetation Water Content: A Synthesis Study. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 1456–1464. [Google Scholar] [CrossRef] [Green Version]
- Sobol, I.M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates. Math. Comput. Simul. 2001, 55, 271–280. [Google Scholar] [CrossRef]
- Sobol’, I.M. Sensitivity estimates for nonlinear mathematical models. Math. Model. Comput. Exp. 1993, 14, 407–414. [Google Scholar]
- Wang, Z.; Che, T.; Liou, Y.-A. Global Sensitivity Analysis of the L-MEB Model for Retrieving Soil Moisture. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2949–2962. [Google Scholar] [CrossRef]
- Wang, J.; Li, X.; Lu, L.; Fang, F. Parameter sensitivity analysis of crop growth models based on the extended Fourier Amplitude Sensitivity Test method. Environ. Model. Softw. 2013, 48, 171–182. [Google Scholar] [CrossRef]
- Ma, C.; Li, X.; Wang, J.; Wang, C.; Duan, Q.; Wang, W. A Comprehensive Evaluation of Microwave Emissivity and Brightness Temperature Sensitivities to Soil Parameters Using Qualitative and Quantitative Sensitivity Analyses. IEEE Trans. Geosci. Remote Sens. 2017, 55, 1025–1038. [Google Scholar] [CrossRef]
- Ma, C.; Li, X.; Wang, S. A Global Sensitivity Analysis of Soil Parameters Associated With Backscattering Using the Advanced Integral Equation Model. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5613–5623. [Google Scholar]
- Sobol, I.M.; Kucherenko, S. Derivative based global sensitivity measures and their link with global sensitivity indices. Math. Comput. Simul. 2009, 79, 3009–3017. [Google Scholar] [CrossRef]
- Plischke, E.; Borgonovo, E.; Smith, C.L. Global sensitivity measures from given data. Eur. J. Oper. Res. 2013, 226, 536–550. [Google Scholar] [CrossRef]
- Borgonovo, E. A new uncertainty importance measure. Reliab. Eng. Syst. Saf. 2007, 92, 771–784. [Google Scholar] [CrossRef]
- Campolongo, F.; Cariboni, J.; Saltelli, A. An effective screening design for sensitivity analysis of large models. Environ. Model. Softw. 2007, 22, 1509–1518. [Google Scholar] [CrossRef]
- Morris, M.D. Factorial Sampling Plans for Preliminary Computational Experiments. Technometrics 1991, 33, 161–174. [Google Scholar] [CrossRef]
- Saltelli, A.; Tarantola, S.; Chan, K.P.-S. A Quantitative Model-Independent Method for Global Sensitivity Analysis of Model Output. Glob. Sensit. Anal. Model Output 1999, 41, 39–56. [Google Scholar] [CrossRef]
- Cukier, R.; Fortuin, C.; Shuler, K.E.; Petschek, A.; Schaibly, J. Study of the sensitivity of coupled reaction systems to uncertainties in rate coefficients. I Theory. J. Chem. Phys. 1973, 59, 3873–3878. [Google Scholar] [CrossRef]
- Bai, X.; Zeng, J.; Chen, K.; Li, Z.; Zeng, Y.; Wen, J.; Wang, X.; Dong, X.; Su, Z. Parameter Optimization of a Discrete Scattering Model by Integration of Global Sensitivity Analysis Using SMAP Active and Passive Observations. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1084–1099. [Google Scholar] [CrossRef]
- Zeng, J.; Chen, K. Theoretical Study of Global Sensitivity Analysis of L-Band Radar Bistatic Scattering for Soil Moisture Retrieval. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1710–1714. [Google Scholar] [CrossRef]
- Baghdadi, N.; Holah, N.; Zribi, M. Soil moisture estimation using multi-incidence and multi-polarization ASAR data. Int. J. Remote Sens. 2006, 27, 1907–1920. [Google Scholar] [CrossRef]
- Holah, N.; Baghdadi, N.; Zribi, M.; Bruand, A.; King, C. Potential of ASAR/ENVISAT for the characterization of soil surface parameters over bare agricultural fields. Remote Sens. Environ. 2005, 96, 78–86. [Google Scholar] [CrossRef] [Green Version]
- Bauer-Marschallinger, B.; Freeman, V.; Cao, S.; Paulik, C.; Schaufler, S.; Stachl, T.; Modanesi, S.; Massari, C.; Ciabatta, L.; Brocca, L. Toward global soil moisture monitoring with Sentinel-1: Harnessing assets and overcoming obstacles. IEEE Trans. Geosci. Remote Sens. 2018, 57, 520–539. [Google Scholar] [CrossRef]
- Zribi, M.; Kotti, F.; Amri, R.; Wagner, W.; Shabou, M.; Lili-Chabaane, Z.; Baghdadi, N. Soil moisture mapping in a semiarid region, based on ASAR/Wide Swath satellite data. Water Resour. Res. 2014, 50, 823–835. [Google Scholar] [CrossRef] [Green Version]
| Schemes | Parameter | Meaning (Unit) | Ranges | Reference |
|---|---|---|---|---|
| Park: V1 = mg V2 = mV | ms | soil moisture (m3/m3) | 0.05–0.50 | [8] |
| s | rms of surface height (cm) | 0.2–3.1 | [8] | |
| θ | incidence angle(degree) | 29–46 | Sentinel-1 | |
| mV | vegetation water content (VWC, kg/m2) | 0.1–6.0 | [20] | |
| mg | particle moisture content (g/g) | 0.0–0.9 | [17] | |
| A | canopy type parameter | 0.05–0.13 | [17] | |
| B | canopy type parameter | 0.34–1.12 | [17] | |
| Bindlish V1 = mV V2 = mV | ms | soil moisture (m3/m3) | 0.05–0.50 | [8] |
| s | rms of surface height (cm) | 0.2–3.1 | [8] | |
| θ | incidence angle (degree) | 29–46 | Sentinel-1 | |
| mV | VWC (kg/m2) | 0.1–6.0 | [20] | |
| A | canopy type parameter | 0.0009–0.0018 | [8] | |
| B | canopy type parameter | 0.032–0.138 | [8] | |
| α | radar-shadow coefficient | 1.29–10.6 | [8] |
| Scheme | SIs (MSI/TSI) and Rank | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Range1 (0.0–1.5) | Range2 (1.5–3.0) | Range3 (3.0–4.5) | Range4 (4.5–6.0) | ||||||||||
| MSI | TSI | Rank | MSI | TSI | Rank | MSI | TSI | Rank | MSI | TSI | Rank | ||
| Park | ms | 0.153 | 0.182 | 3 | 0.012 | 0.025 | 7 | 0.001 | 0.011 | 7 | 0.000 | 0.005 | 7 |
| s | 0.205 | 0.243 | 2 | 0.020 | 0.046 | 6 | 0.002 | 0.012 | 6 | 0.000 | 0.010 | 5 | |
| θ | 0.085 | 0.094 | 6 | 0.034 | 0.048 | 4 | 0.010 | 0.019 | 4 | 0.005 | 0.010 | 3 | |
| mV | 0.254 | 0.341 | 1 | 0.026 | 0.052 | 5 | 0.001 | 0.009 | 5 | 0.000 | 0.006 | 6 | |
| mg | 0.123 | 0.207 | 5 | 0.657 | 0.753 | 1 | 0.857 | 0.893 | 1 | 0.910 | 0.925 | 1 | |
| A | 0.009 | 0.018 | 7 | 0.041 | 0.049 | 3 | 0.058 | 0.065 | 2 | 0.059 | 0.065 | 2 | |
| B | 0.132 | 0.204 | 4 | 0.103 | 0.167 | 2 | 0.022 | 0.057 | 3 | 0.004 | 0.019 | 4 | |
| Bindlish | ms | 0.256 | 0.259 | 2 | 0.250 | 0.252 | 2 | 0.227 | 0.230 | 2 | 0.204 | 0.210 | 2 |
| s | 0.600 | 0.613 | 1 | 0.574 | 0.586 | 1 | 0.514 | 0.526 | 1 | 0.457 | 0.472 | 1 | |
| θ | 0.102 | 0.103 | 3 | 0.106 | 0.107 | 3 | 0.122 | 0.123 | 3 | 0.138 | 0.140 | 3 | |
| mV | 0.010 | 0.011 | 4 | 0.015 | 0.017 | 5 | 0.009 | 0.011 | 5 | 0.008 | 0.010 | 5 | |
| A | 0.000 | 0.000 | 6 | 0.000 | 0.000 | 6 | 0.000 | 0.001 | 6 | 0.001 | 0.002 | 6 | |
| B | 0.005 | 0.007 | 5 | 0.051 | 0.053 | 4 | 0.095 | 0.097 | 4 | 0.218 | 0.224 | 4 | |
| α | 0.000 | 0.000 | 7 | 0.000 | 0.000 | 7 | 0.000 | 0.001 | 7 | 0.000 | 0.001 | 7 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, C.; Wang, S.; Zhao, Z.; Ma, H. Global Sensitivity Analysis of a Water Cloud Model toward Soil Moisture Retrieval over Vegetated Agricultural Fields. Remote Sens. 2021, 13, 3889. https://doi.org/10.3390/rs13193889
Ma C, Wang S, Zhao Z, Ma H. Global Sensitivity Analysis of a Water Cloud Model toward Soil Moisture Retrieval over Vegetated Agricultural Fields. Remote Sensing. 2021; 13(19):3889. https://doi.org/10.3390/rs13193889
Chicago/Turabian StyleMa, Chunfeng, Shuguo Wang, Zebin Zhao, and Hanqing Ma. 2021. "Global Sensitivity Analysis of a Water Cloud Model toward Soil Moisture Retrieval over Vegetated Agricultural Fields" Remote Sensing 13, no. 19: 3889. https://doi.org/10.3390/rs13193889
APA StyleMa, C., Wang, S., Zhao, Z., & Ma, H. (2021). Global Sensitivity Analysis of a Water Cloud Model toward Soil Moisture Retrieval over Vegetated Agricultural Fields. Remote Sensing, 13(19), 3889. https://doi.org/10.3390/rs13193889








