Retrieval of Secchi Disk Depth in Turbid Lakes from GOCI Based on a New Semi-Analytical Algorithm
Abstract
1. Introduction
2. Materials and Methods
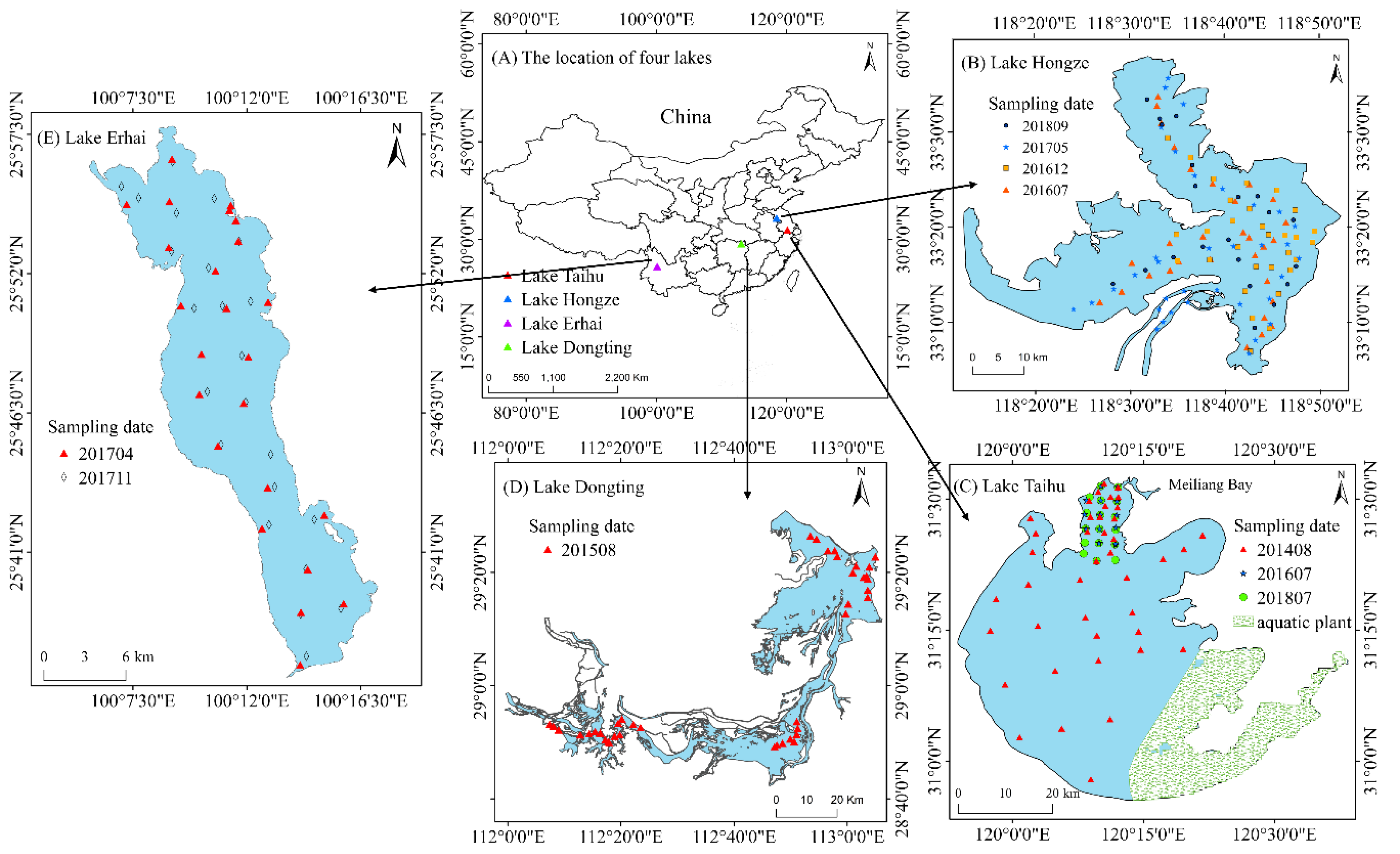
2.1. Study Area
2.2. In-Situ Water Quality Data and Spectra Data Collection
2.3. Satellite Data and Preprocessing
2.4. Wind Speed Data Collection
2.5. Data analyses and Accuracy Assessment
2.6. ZSDZ Algorithm
2.6.1. Part I
2.5.2. Part II
2.7. Noise-Equivalent ZSD
3. Results
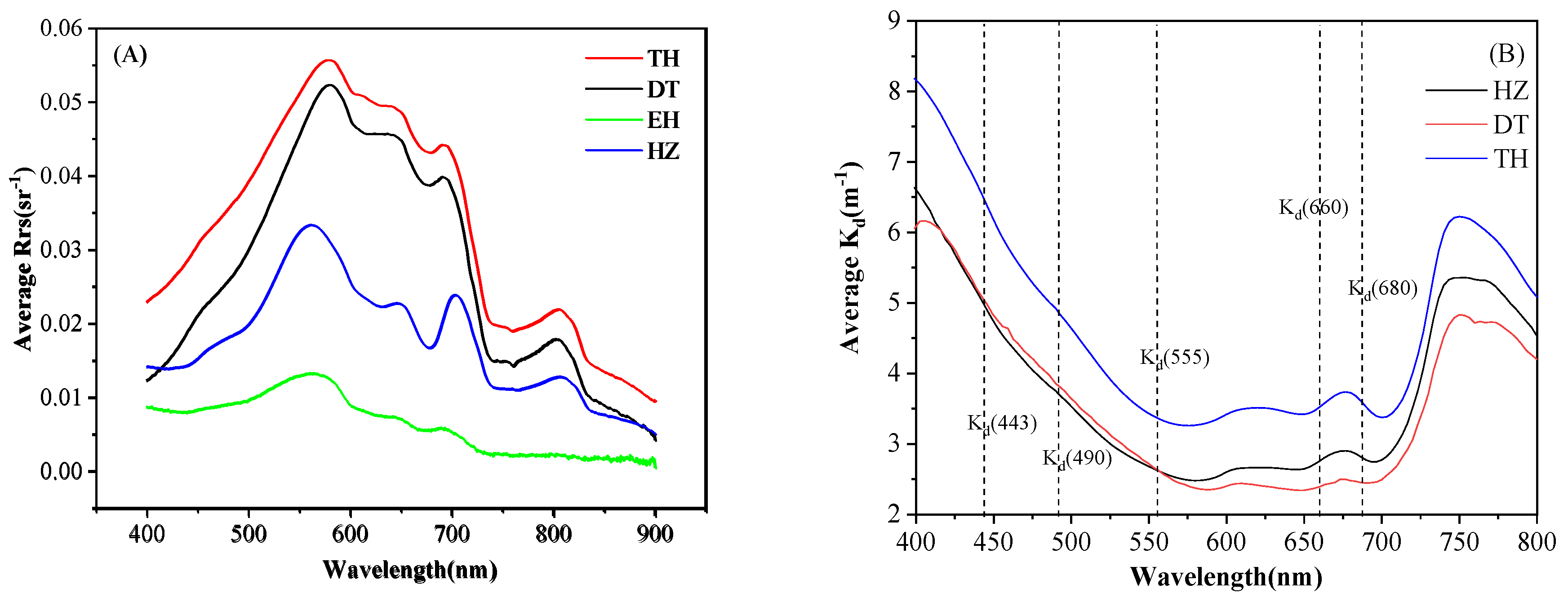
3.1. Biogeochemical and Optical Characterization
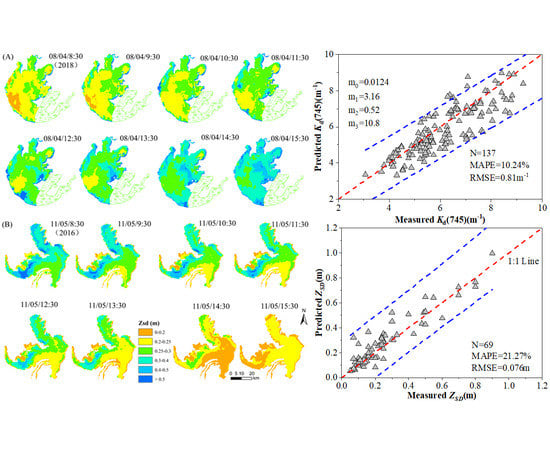
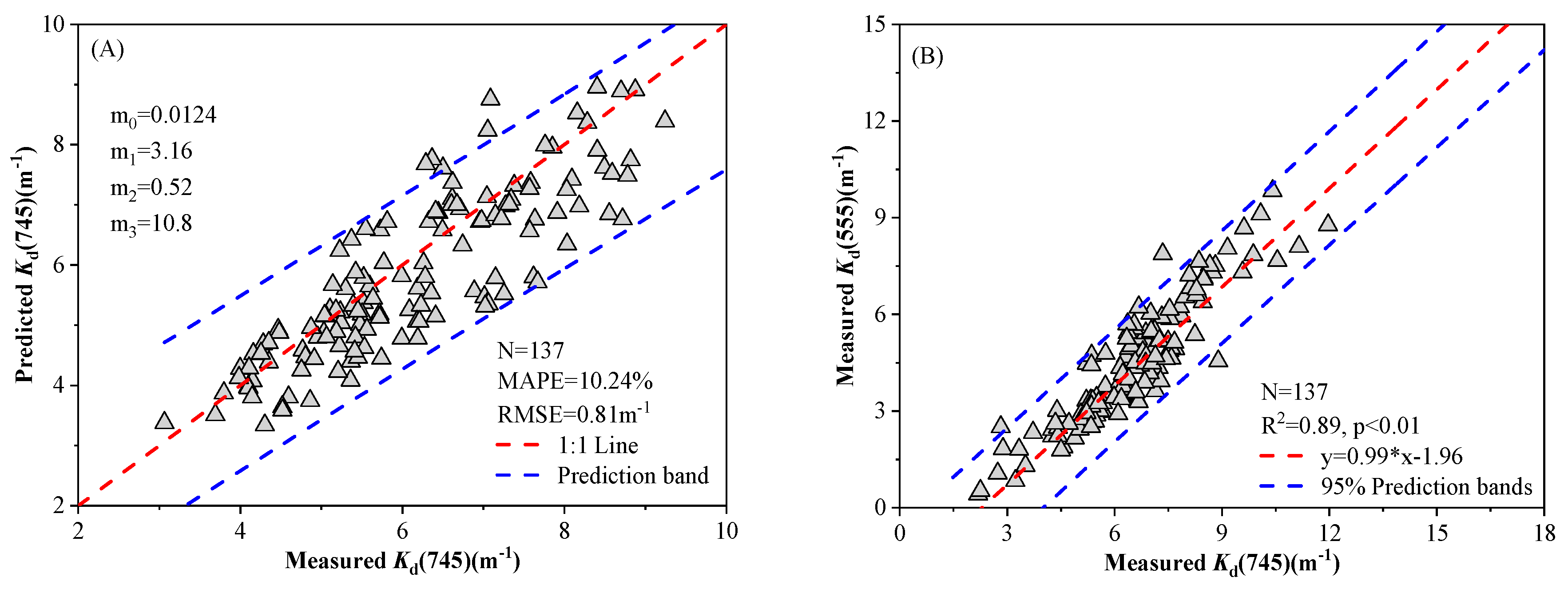
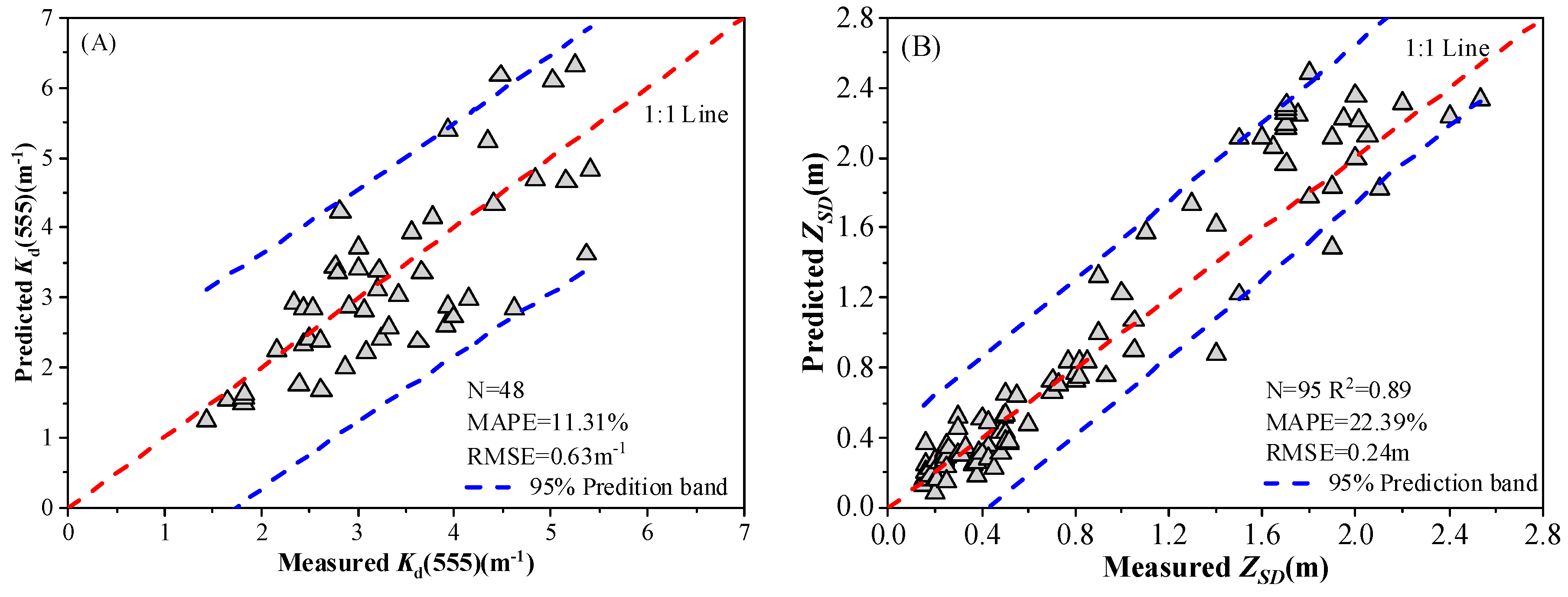
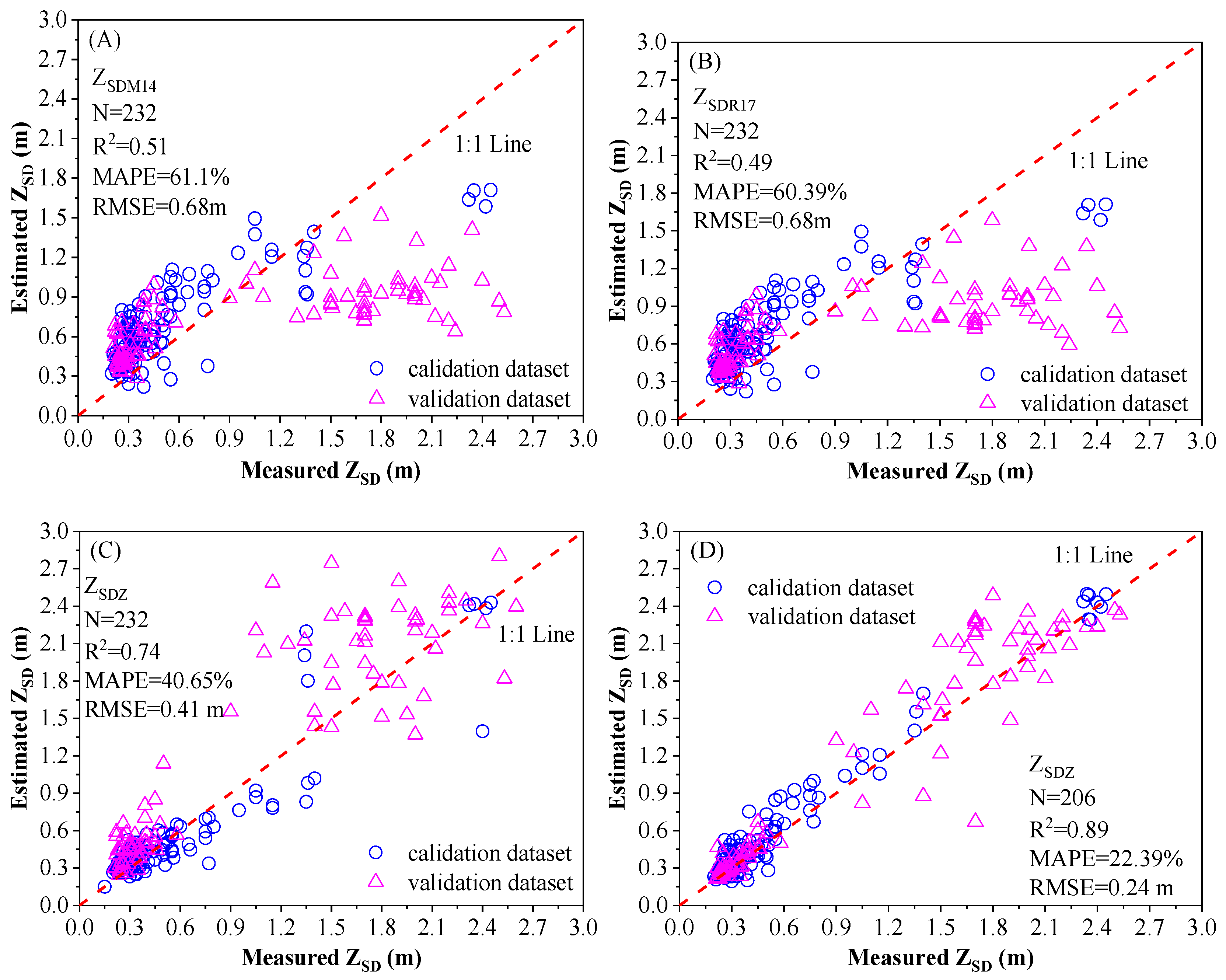
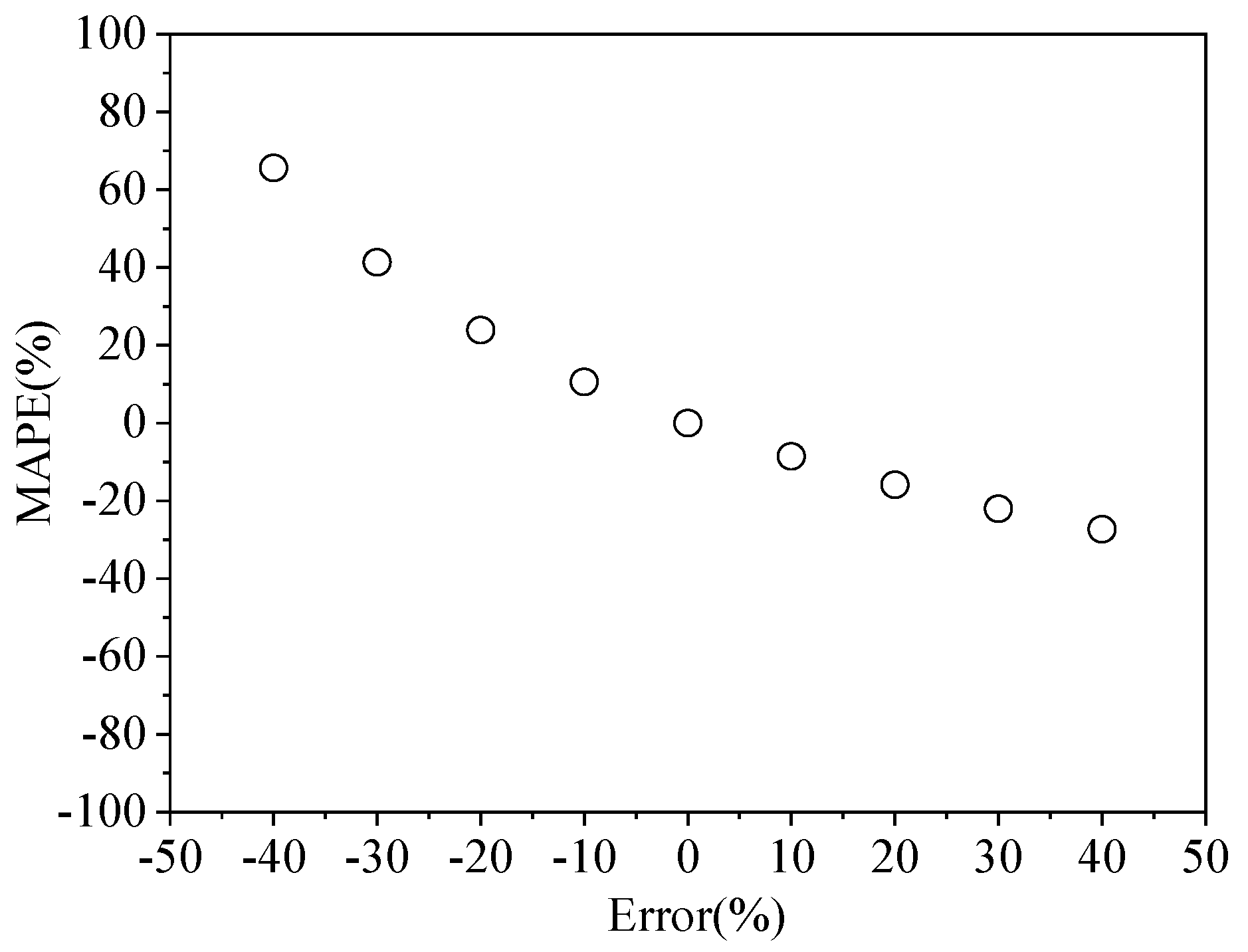
3.2. Algorithm Validation and Noise-Equivalent ZSD
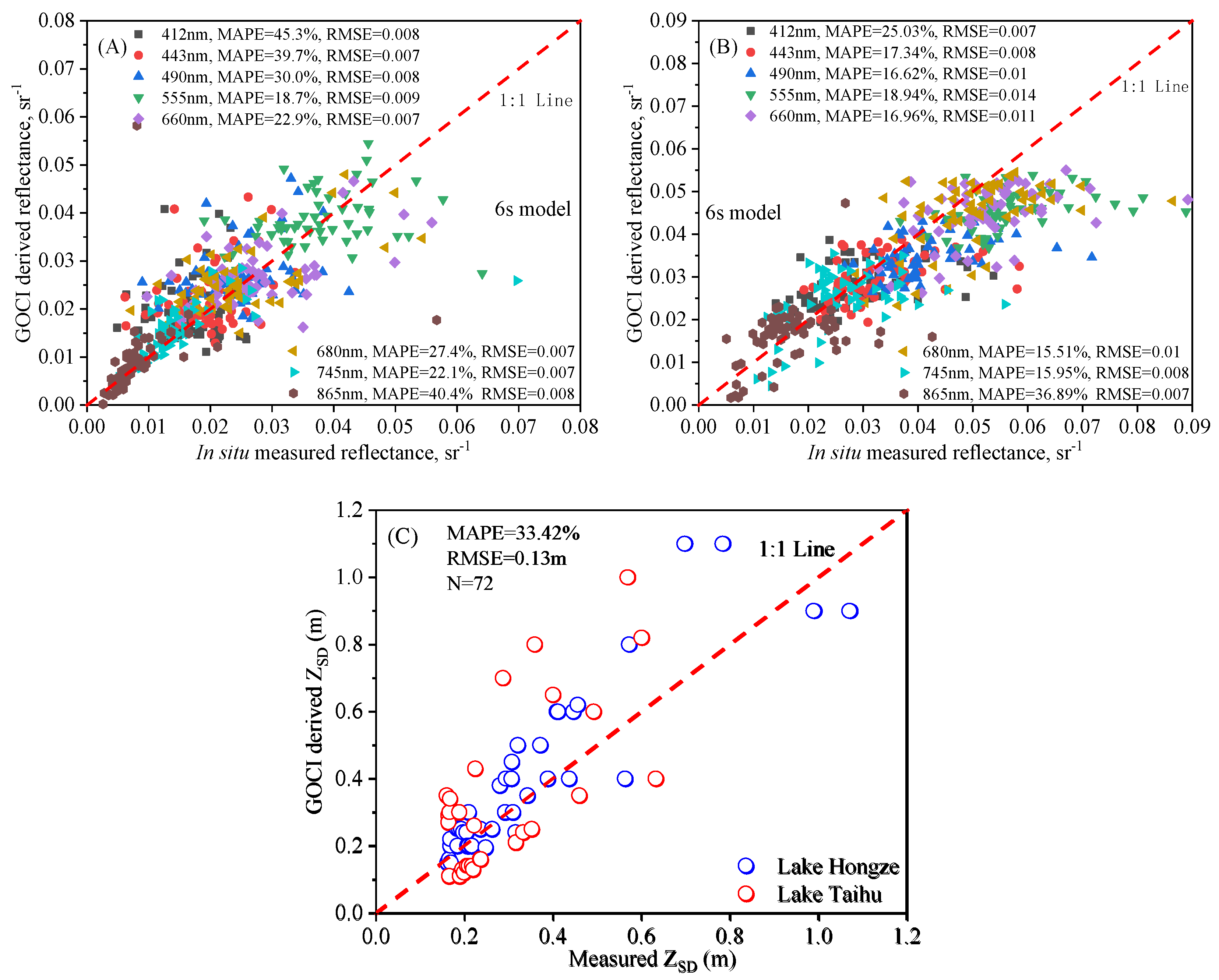
3.3. Atmospheric Correction Assessment by Synchronized Images
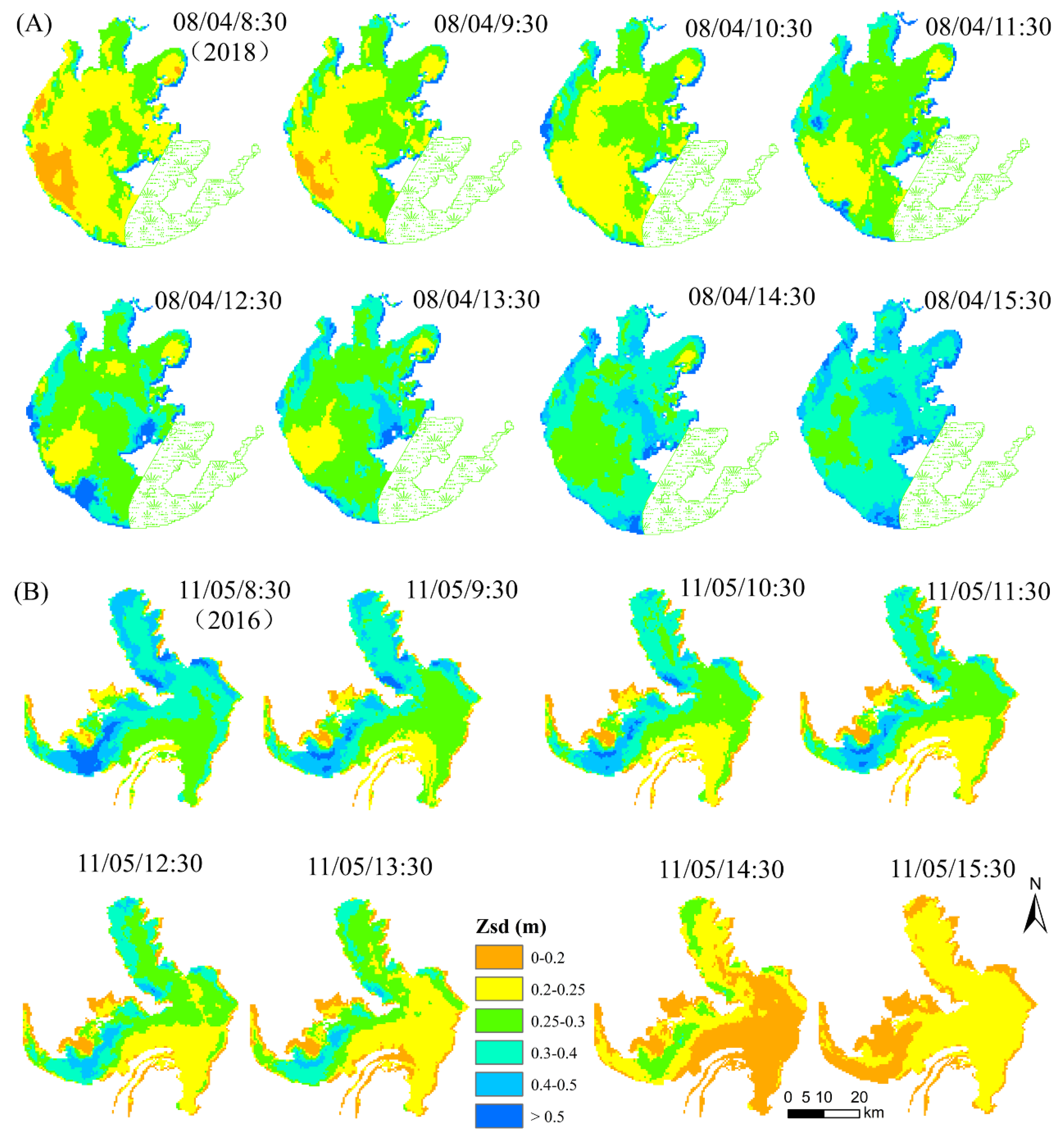
3.4. Mapping ZSD from GOCI Based on Developed Algorithm
4. Discussion
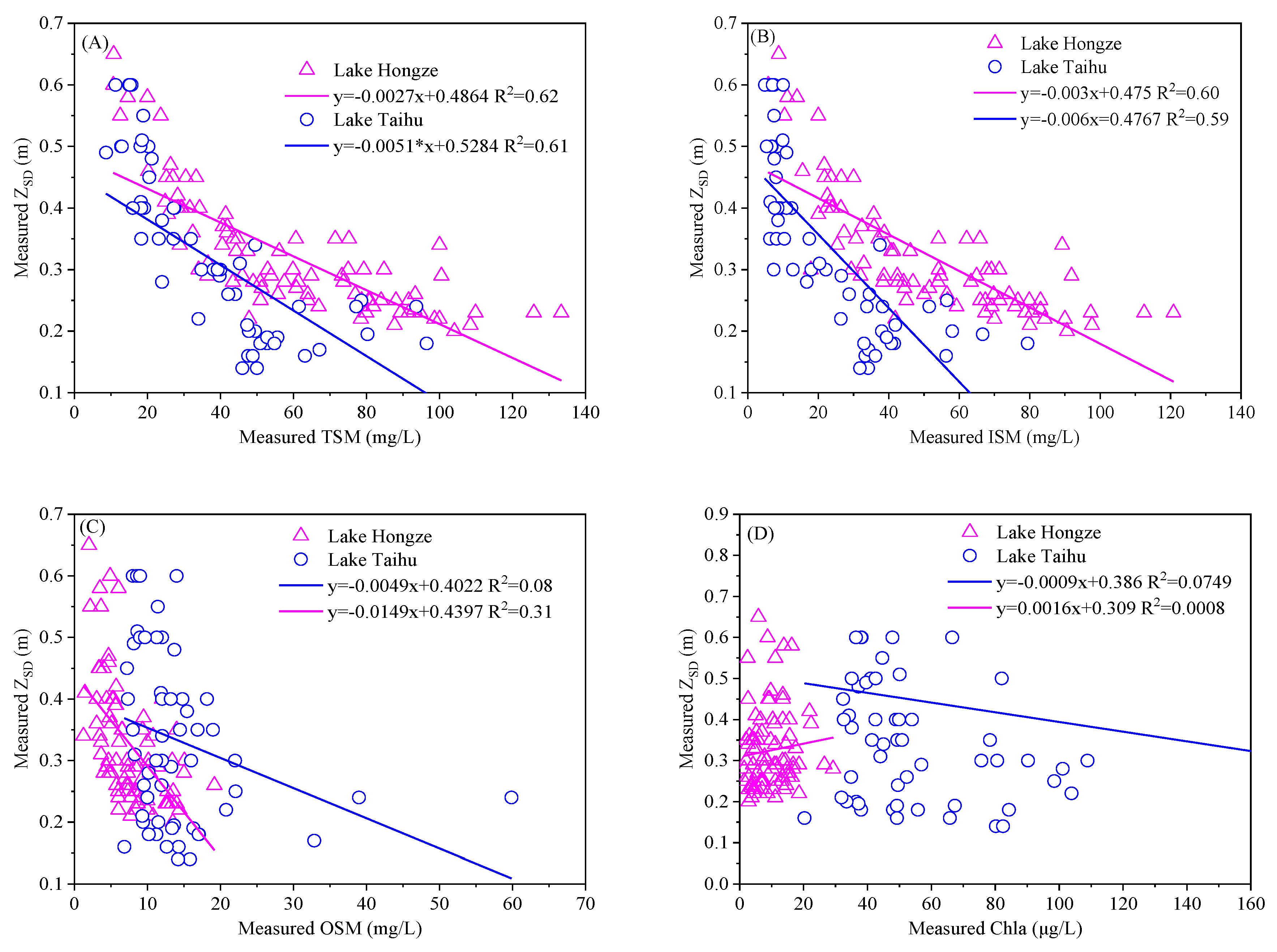
4.1. The Relationship between In-Situ ZSD and Water Constituent Concentrations
4.2. Comparison with the Exist ZSD Algorithms for GOCI
4.3. Factors in the ZSD Inversions
4.3.1. Model Parameterization
4.3.2. Measurement Uncertainties
4.3.3. Limitation of Model in Retrieving ZSD
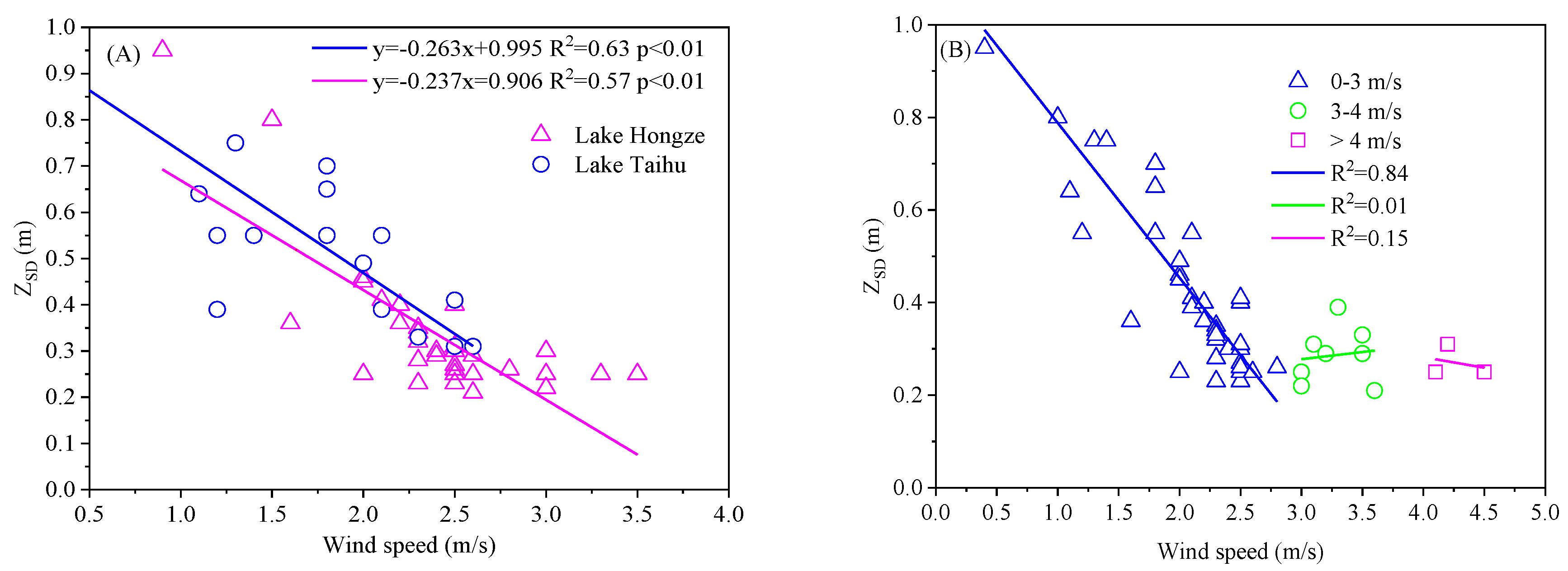
4.4. The Response of GOCI-Derived ZSD to Wind Speed
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bai, S.; Gao, J.; Sun, D.; Tian, M. Monitoring Water Transparency in Shallow and Eutrophic Lake Waters Based on GOCI Observations. Remote Sens. 2020, 12, 163. [Google Scholar] [CrossRef]
- Jiang, D.; Matsushita, B.; Setiawan, F.; Vundo, A. An improved algorithm for estimating the Secchi disk depth from remote sensing data based on the new underwater visibility theory. ISPRS J. Photogramm. Remote Sens. 2019, 152, 13–23. [Google Scholar] [CrossRef]
- Al Kaabi, M.; Zhao, J.; Ghedira, H. MODIS-Based Mapping of Secchi Disk Depth Using a Qualitative Algorithm in the Shallow Arabian Gulf. Remote Sens. 2016, 8, 423. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, Y.; Zhou, Y.; Liu, M.; Shi, K.; Yu, Z. Seasonal-Spatial Distribution and Long-Term Variation of Transparency in Xin’anjiang Reservoir: Implications for Reservoir Management. Int. J. Environ. Res. Public Health 2015, 12, 9492–9507. [Google Scholar] [CrossRef] [PubMed]
- Shi, K.; Zhang, Y.; Zhu, G.; Qin, B.; Pan, D. Deteriorating water clarity in shallow waters: Evidence from long term MODIS and in-situ observations. Int. J. Appl. Earth Obs. Geoinf. 2018, 68, 287–297. [Google Scholar] [CrossRef]
- Rodrigues, T.; Alcântara, E.; Watanabe, F.; Imai, N. Retrieval of Secchi disk depth from a reservoir using a semi-analytical scheme. Remote Sens. Environ. 2017, 198, 213–228. [Google Scholar] [CrossRef]
- Fukushima, T.; Matsushita, B.; Yang, W.; Jaelani, L.M. Semi-analytical prediction of Secchi depth transparency in Lake Kasumigaura using MERIS data. Limnology 2017, 19, 89–100. [Google Scholar] [CrossRef]
- Binding, C.E.; Greenberg, T.A.; Watson, S.B.; Rastin, S.; Gould, J. Long term water clarity changes in North America’s Great Lakes from multi-sensor satellite observations. Limnol. Oceanogr. 2015, 60, 1976–1995. [Google Scholar] [CrossRef]
- Preisendorfer, R.W. Secchi disk science: Visual optics of natural waters. Limnol. Oceanogr. 1986, 31, 909. [Google Scholar] [CrossRef]
- Lee, Z.; Shang, S.; Hu, C.; Du, K.; Weidemann, A.; Hou, W.; Lin, J.; Lin, G. Secchi disk depth: A new theory and mechanistic model for underwater visibility. Remote Sens. Environ. 2015, 169, 139–149. [Google Scholar] [CrossRef]
- Shang, S.; Lee, Z.; Shi, L.; Lin, G.; Wei, G.; Li, X. Changes in water clarity of the Bohai Sea: Observations from MODIS. Remote Sens. Environ. 2016, 186, 22–31. [Google Scholar] [CrossRef]
- Lee, Z.; Shang, S.; Qi, L.; Yan, J.; Lin, G. A semi-analytical scheme to estimate Secchi-disk depth from Landsat-8 measurements. Remote Sens. Environ. 2016, 177, 101–106. [Google Scholar] [CrossRef]
- Wang, Y.; Shen, F.; Sokoletsky, L.; Sun, X. Validation and Calibration of QAA Algorithm for CDOM Absorption Retrieval in the Changjiang (Yangtze) Estuarine and Coastal Waters. Remote Sens. 2017, 9, 1192. [Google Scholar] [CrossRef]
- Grunert, B.K.; Mouw, C.B.; Ciochetto, A.B. Deriving inherent optical properties from decomposition of hyperspectral non-water absorption. Remote Sens. Environ. 2019, 225, 193–206. [Google Scholar] [CrossRef]
- Xue, K.; Ma, R.; Duan, H.; Shen, M.; Boss, E.; Cao, Z. Inversion of inherent optical properties in optically complex waters using sentinel-3A/OLCI images: A case study using China’s three largest freshwater lakes. Remote Sens. Environ. 2019, 225, 328–346. [Google Scholar] [CrossRef]
- Watanabe, F.; Mishra, D.R.; Astuti, I.; Rodrigues, T.; Alcântara, E.; Imai, N.N.; Barbosa, C. Parametrization and calibration of a quasi-analytical algorithm for tropical eutrophic waters. ISPRS J. Photogramm. Remote Sens. 2016, 121, 28–47. [Google Scholar] [CrossRef]
- Shen, F.; Zhou, Y.; Peng, X.; Chen, Y. Satellite multi-sensor mapping of suspended particulate matter in turbid estuarine and coastal ocean, China. Int. J. Remote Sens. 2014, 35, 4173–4192. [Google Scholar] [CrossRef]
- Lou, X.; Hu, C. Diurnal changes of a harmful algal bloom in the East China Sea: Observations from GOCI. Remote Sens. Environ. 2014, 140, 562–572. [Google Scholar] [CrossRef]
- Lei, S.; Xu, J.; Li, Y.; Du, C.; Liu, G.; Zheng, Z.; Xu, Y.; Lyu, H.; Mu, M.; Miao, S.; et al. An approach for retrieval of horizontal and vertical distribution of total suspended matter concentration from GOCI data over Lake Hongze. Sci. Total Environ. 2019, 700, 134524. [Google Scholar] [CrossRef]
- Lei, S.; Xu, J.; Li, Y.; Lyu, H.; Liu, G.; Zheng, Z.; Xu, Y.; Du, C.; Zeng, S.; Wang, H.; et al. Temporal and spatial distribution of Kd(490) and its response to precipitation and wind in lake Hongze based on MODIS data. Ecol. Indic. 2020, 108, 105684. [Google Scholar] [CrossRef]
- Zheng, Z.; Ren, J.; Li, Y.; Huang, C.; Liu, G.; Du, C.; Lyu, H. Remote sensing of diffuse attenuation coefficient patterns from Landsat 8 OLI imagery of turbid inland waters: A case study of Dongting Lake. Sci. Total Environ. 2016, 573, 39–54. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Lei, S.; Bi, S.; Li, Y.; Lyu, H.; Xu, J.; Xu, X.; Mu, M.; Miao, S.; Zeng, S.; et al. Tracking spatio-temporal dynamics of POC sources in eutrophic lakes by remote sensing. Water Res. 2020, 168, 115162. [Google Scholar] [CrossRef] [PubMed]
- Lei, S.; Wu, D.; Li, Y.; Wang, Q.; Huang, C.; Liu, G.; Zheng, Z.; Du, C.; Mu, M.; Xu, J.; et al. Remote sensing monitoring of the suspended particle size in Hongze Lake based on GF-1 data. Int. J. Remote Sens. 2018, 40, 3179–3203. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, X.; Yin, Y.; Wang, M.; Qin, B. A simple optical model to estimate diffuse attenuation coefficient of photosynthetically active radiation in an extremely turbid lake from surface reflectance. Opt. Express 2012, 20, 20482–20493. [Google Scholar] [CrossRef]
- Chen, S.-L.; Zhang, G.-A.; Yang, S.-L.; Shi, J.Z. Temporal variations of fine suspended sediment concentration in the Changjiang River estuary and adjacent coastal waters, China. J. Hydrol. 2006, 331, 137–145. [Google Scholar] [CrossRef]
- Lee, Z.; Lubac, B.; Werdell, J.; Arnone, R. An update of the quasi-analytical algorithm (QAA_v5). Int. Ocean Color Group Softw. Rep. 2009, 1–9. [Google Scholar]
- Budhiman, S.; Suhyb Salama, M.; Vekerdy, Z.; Verhoef, W. Deriving optical properties of Mahakam Delta coastal waters, Indonesia using in situ measurements and ocean color model inversion. ISPRS J. Photogramm. Remote Sens. 2012, 68, 157–169. [Google Scholar] [CrossRef]
- Lee, Z.; Ahn, Y.H.; Mobley, C.; Arnone, R. Removal of surface-reflected light for the measurement of remote-sensing reflectance from an above-surface platform. Opt. Express 2010, 18, 26313–26324. [Google Scholar] [CrossRef]
- Morel, A.; Maritorena, S. Bio-optical properties of oceanic waters: A reappraisal. J. Geophys. Res. Ocean. 2001, 106, 7163–7180. [Google Scholar] [CrossRef]
- Lee, Z.; Hu, C.; Shang, S.; Du, K.; Lewis, M.; Arnone, R.; Brewin, R. Penetration of UV-visible solar radiation in the global oceans: Insights from ocean color remote sensing. J. Geophys. Res. Ocean. 2013, 118, 4241–4255. [Google Scholar] [CrossRef]
- Vanhellemont, Q.; Ruddick, K. Turbid wakes associated with offshore wind turbines observed with Landsat 8. Remote Sens. Environ. 2014, 145, 105–115. [Google Scholar] [CrossRef]
- Ryu, J.-H.; Han, H.-J.; Cho, S.; Park, Y.-J.; Ahn, Y.-H. Overview of geostationary ocean color imager (GOCI) and GOCI data processing system (GDPS). Ocean. Sci. J. 2012, 47, 223–233. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.; Shi, K.; Zha, Y.; Zhou, Y.; Liu, M. A Landsat 8 OLI-Based, Semianalytical Model for Estimating the Total Suspended Matter Concentration in the Slightly Turbid Xin’anjiang Reservoir (China). IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 398–413. [Google Scholar] [CrossRef]
- Tang, X.; Wu, M.; Li, R. Phosphorus distribution and bioavailability dynamics in the mainstream water and surface sediment of the Three Gorges Reservoir between 2003 and 2010. Water Res. 2018, 145, 321–331. [Google Scholar] [CrossRef] [PubMed]
- Volpe, V.; Silvestri, S.; Marani, M. Remote sensing retrieval of suspended sediment concentration in shallow waters. Remote Sens. Environ. 2011, 115, 44–54. [Google Scholar] [CrossRef]
- Ren, J.; Zheng, Z.; Li, Y.; Lv, G.; Wang, Q.; Lyu, H.; Huang, C.; Liu, G.; Du, C.; Mu, M.; et al. Remote observation of water clarity patterns in Three Gorges Reservoir and Dongting Lake of China and their probable linkage to the Three Gorges Dam based on Landsat 8 imagery. Sci. Total Environ. 2018, 625, 1554–1566. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.H.; Shi, W.; Jiang, L.D. Atmospheric correction using near-infrared bands for satellite ocean color data processing in the turbid western Pacific region. Opt. Express 2012, 20, 741–753. [Google Scholar] [CrossRef]
- Le, C.; Li, Y.; Zha, Y.; Sun, D.; Huang, C.; Lu, H. A four-band semi-analytical model for estimating chlorophyll a in highly turbid lakes: The case of Taihu Lake, China. Remote Sens. Environ. 2009, 113, 1175–1182. [Google Scholar] [CrossRef]
- Zhang, Y.L.; Shi, K.; Liu, J.J.; Deng, J.M.; Qin, B.Q.; Zhu, G.W.; Zhou, Y.Q. Meteorological and hydrological conditions driving the formation and disappearance of black blooms, an ecological disaster phenomena of eutrophication and algal blooms. Sci. Total Environ. 2016, 569, 1517–1529. [Google Scholar] [CrossRef]
- Arst, H.; Nõges, T.; Nõges, P.; Paavel, B. Relations of phytoplankton in situ primary production, chlorophyll concentration and underwater irradiance in turbid lakes. Hydrobiologia 2008, 599, 169–176. [Google Scholar] [CrossRef]
- Liu, J.; Sun, D.; Zhang, Y.; Li, Y. Pre-classification improves relationships between water clarity, light attenuation, and suspended particulates in turbid inland waters. Hydrobiologia 2013, 711, 71–86. [Google Scholar] [CrossRef]
- Shi, K.; Zhang, Y.; Liu, X.; Wang, M.; Qin, B. Remote sensing of diffuse attenuation coefficient of photosynthetically active radiation in Lake Taihu using MERIS data. Remote Sens. Environ. 2014, 140, 365–377. [Google Scholar] [CrossRef]
- Feng, L.; Hou, X.; Zheng, Y. Monitoring and understanding the water transparency changes of fifty large lakes on the Yangtze Plain based on long-term MODIS observations. Remote Sens. Environ. 2019, 221, 675–686. [Google Scholar] [CrossRef]
- Miao, S.; Lyu, H.; Wang, Q.; Li, Y.; Wu, Z.; Du, C.; Xu, J.; Bi, S.; Mu, M.; Lei, S. Estimation of terrestrial humic-like substances in inland lakes based on the optical and fluorescence characteristics of chromophoric dissolved organic matter (CDOM) using OLCI images. Ecol. Indic. 2019, 101, 399–409. [Google Scholar] [CrossRef]
- Wu, Y.; Li, L.; Gan, N.; Zheng, L.; Ma, H.; Shan, K.; Liu, J.; Xiao, B.; Song, L. Seasonal dynamics of water bloom-forming Microcystis morphospecies and the associated extracellular microcystin concentrations in large, shallow, eutrophic Dianchi Lake. J. Environ. Sci. (China) 2014, 26, 1921–1929. [Google Scholar] [CrossRef]
- Shi, K.; Zhang, Y.; Zhu, G.; Liu, X.; Zhou, Y.; Xu, H.; Qin, B.; Liu, G.; Li, Y. Long-term remote monitoring of total suspended matter concentration in Lake Taihu using 250m MODIS-Aqua data. Remote Sens. Environ. 2015, 164, 43–56. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, Y.; Yin, Y.; Wang, M.; Qin, B. Wind and submerged aquatic vegetation influence bio-optical properties in large shallow Lake Taihu, China. J. Geophys. Res. Biogeosciences 2013, 118, 713–727. [Google Scholar] [CrossRef]
- Mishra, S.; Mishra, D.R.; Lee, Z. Bio-Optical Inversion in Highly Turbid and Cyanobacteria-Dominated Waters. IEEE Trans. Geosci. Remote Sens. 2014, 52, 375–388. [Google Scholar] [CrossRef]
- Röttgers, R.; Dupouy, C.; Taylor, B.B.; Bracher, A.; Woźniak, S.B. Mass-specific light absorption coefficients of natural aquatic particles in the near-infrared spectral region. Limnol. Oceanogr. 2014, 59, 1449–1460. Available online: https://aslopubs.onlinelibrary.wiley.com/doi/abs/10.4319/lo.2014.59.5.1449 (accessed on 18 March 2020). [CrossRef]
- Liu, G.; Li, L.; Song, K.; Li, Y.; Lyu, H.; Wen, Z.; Fang, C.; Bi, S.; Sun, X.; Wang, Z.; et al. An OLCI-based algorithm for semi-empirically partitioning absorption coefficient and estimating chlorophyll a concentration in various turbid case-2 waters. Remote Sens. Environ. 2020, 239, 111648. [Google Scholar] [CrossRef]
- Ogashawara, I.; Mishra, D.R.; Nascimento, R.F.F.; Alcântara, E.H.; Kampel, M.; Stech, J.L. Re-parameterization of a quasi-analytical algorithm for colored dissolved organic matter dominant inland waters. Int. J. Appl. Earth Obs. Geoinf. 2016, 53, 128–145. [Google Scholar] [CrossRef]
- Lee, Z.; Carder, K.L.; Mobley, C.D.; Steward, R.G.; Patch, J.S. Hyperspectral remote sensing for shallow waters. 2. Deriving bottom depths and water properties by optimization. Appl. Opt. 1999, 38, 3831–3843. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.; Shi, K.; Yang, H.; Li, Y.; Zhu, A.X.; Sun, D.; Xu, L.; Zou, J.; Chen, X. Satellite observation of hourly dynamic characteristics of algae with Geostationary Ocean Color Imager (GOCI) data in Lake Taihu. Remote Sens. Environ. 2015, 159, 278–287. [Google Scholar] [CrossRef]
| Step | Property | Expression | Approach |
|---|---|---|---|
| 1 | Semi-analytical | ||
| 2 | Semi-analytical | ||
| 3 | Empirical | ||
| 4 | , | Analytical | |
| 5 | Semi-analytical | ||
| 6 | Empirical | ||
| 7 | Semi-analytical |
| Parameters | Statistics | HZ(N = 87) | TH(N = 58) | DT(N = 40) | EH(N = 47) |
|---|---|---|---|---|---|
| Chla (μg/L) | Min–Max | 1.39–149 | 9.23–301.93 | 2.79–52.08 | 7.27–34.34 |
| Aver ± SD | 13.67 ± 19.5 | 57.44 ± 46.3 | 16.08 ± 12.4 | 14.74 ± 5.51 | |
| CV(%) | 142.64 | 80.61 | 77.61 | 37.36 | |
| TSM (mg/L) | Min–Max | 7.18–193.33 | 8.66–96.47 | 3.75–200.53 | 1.96–7.5 |
| Aver ± SD | 58.22 ± 31.77 | 33.16 ± 22.6 | 52.44 ± 46.5 | 3.91 ± 1.01 | |
| CV(%) | 54.57 | 68.15 | 88.62 | 25.82 | |
| ISM (mg/L) | Min–Max | 5.45–174.16 | 4.22–79.41 | 1.65–182.93 | 0.15–4 |
| Aver ± SD | 50.48 ± 29.28 | 19.68 ± 17.84 | 45.36 ± 44.16 | 2.89 ± 0.82 | |
| CV(%) | 58.01 | 90.66 | 97.35 | 66.77 | |
| OSM (mg/L) | Min–Max | 1.23–35.07 | 3.44–59.85 | 2.1–19.46 | 1.83–5.3 |
| Aver ± SD | 7.73 ± 4.59 | 13.47 ± 9.15 | 7.11 ± 3.76 | 2.89 ± 0.82 | |
| CV(%) | 59.37 | 67.91 | 52.93 | 28.61 | |
| ZSD (m) | Min-Max | 0.15–0.8 | 0.15–1.0 | 0.15–1.05 | 0.9–2.48 |
| Aver ± SD | 0.28 ± 0.13 | 0.43 ± 0.24 | 0.5 ± 0.25 | 1.56 ± 0.34 | |
| CV(%) | 72.43 | 56 | 51.3 | 22.37 | |
| OSM/TSM | Min–Max | 0.03–0.47 | 0.16–0.81 | 0.05–0.61 | 0.03–0.53 |
| Aver ± SD | 0.14 ± 0.07 | 0.46 ± 0.16 | 0.19 ± 0.12 | 0.27 ± 0.13 | |
| CV(%) | 49.46 | 36.16 | 63.57 | 47.64 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, S.; Lei, S.; Li, Y.; Lyu, H.; Xu, J.; Dong, X.; Wang, R.; Yang, Z.; Li, J. Retrieval of Secchi Disk Depth in Turbid Lakes from GOCI Based on a New Semi-Analytical Algorithm. Remote Sens. 2020, 12, 1516. https://doi.org/10.3390/rs12091516
Zeng S, Lei S, Li Y, Lyu H, Xu J, Dong X, Wang R, Yang Z, Li J. Retrieval of Secchi Disk Depth in Turbid Lakes from GOCI Based on a New Semi-Analytical Algorithm. Remote Sensing. 2020; 12(9):1516. https://doi.org/10.3390/rs12091516
Chicago/Turabian StyleZeng, Shuai, Shaohua Lei, Yunmei Li, Heng Lyu, Jiafeng Xu, Xianzhang Dong, Rui Wang, Ziqian Yang, and Jianchao Li. 2020. "Retrieval of Secchi Disk Depth in Turbid Lakes from GOCI Based on a New Semi-Analytical Algorithm" Remote Sensing 12, no. 9: 1516. https://doi.org/10.3390/rs12091516
APA StyleZeng, S., Lei, S., Li, Y., Lyu, H., Xu, J., Dong, X., Wang, R., Yang, Z., & Li, J. (2020). Retrieval of Secchi Disk Depth in Turbid Lakes from GOCI Based on a New Semi-Analytical Algorithm. Remote Sensing, 12(9), 1516. https://doi.org/10.3390/rs12091516