A Lightweight Spectral–Spatial Feature Extraction and Fusion Network for Hyperspectral Image Classification
Abstract
:1. Introduction
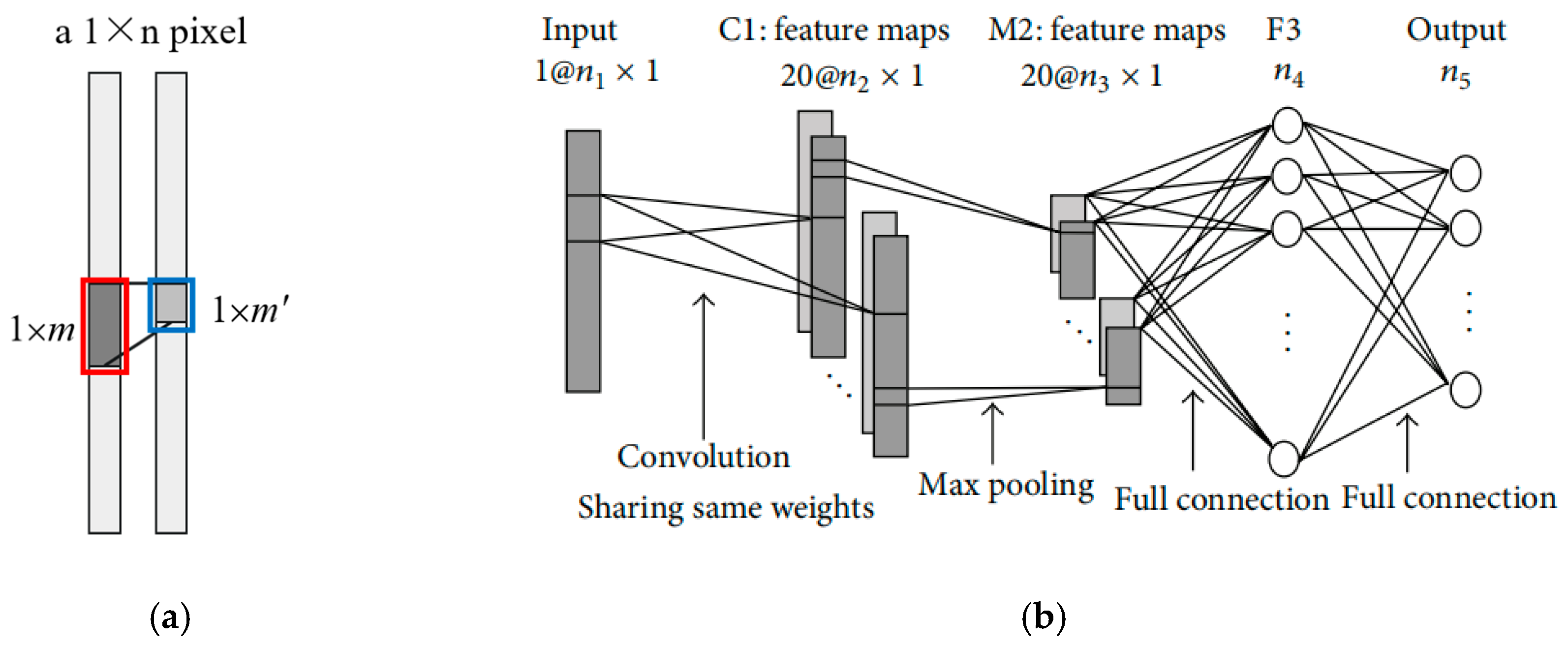
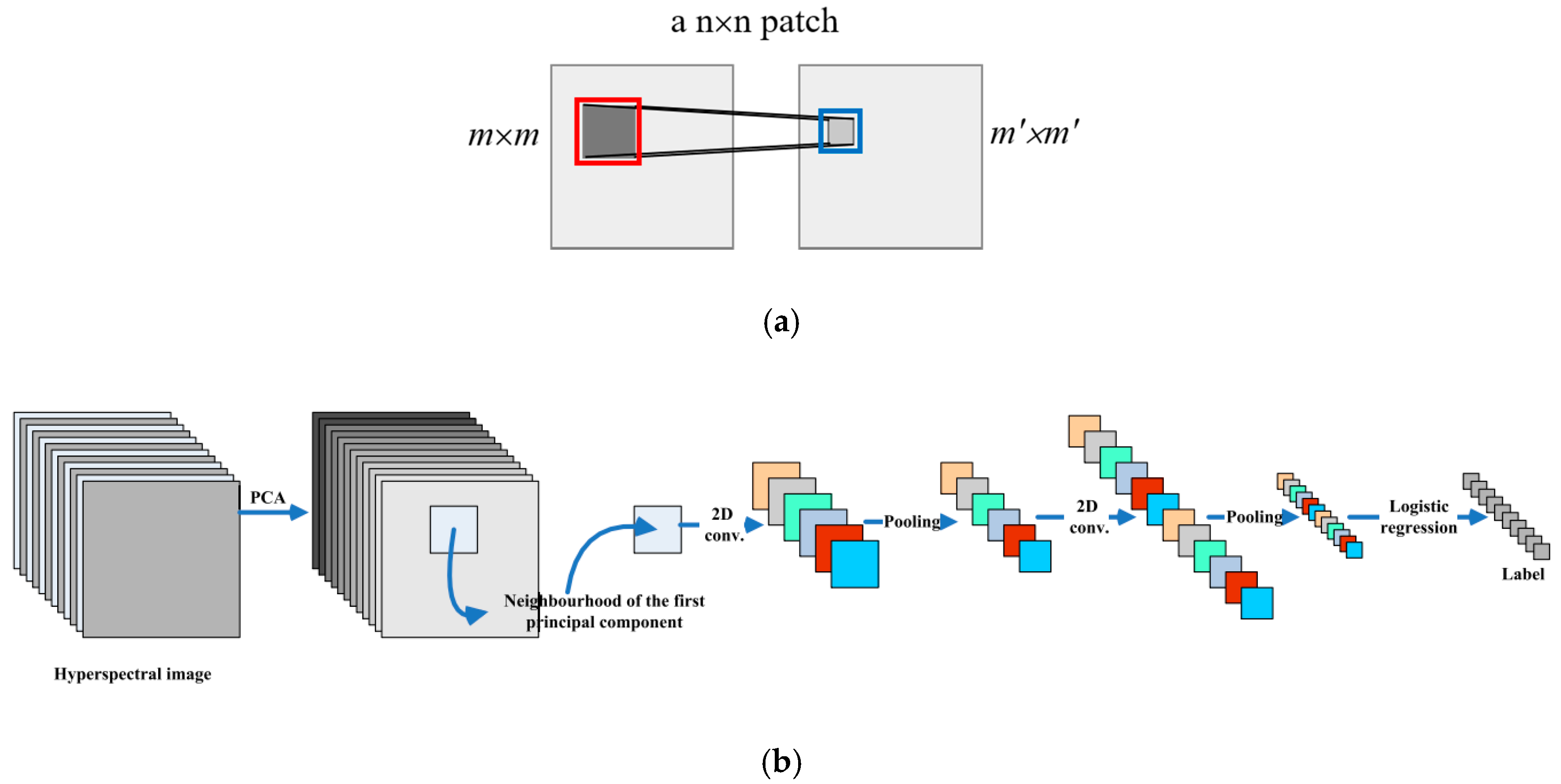
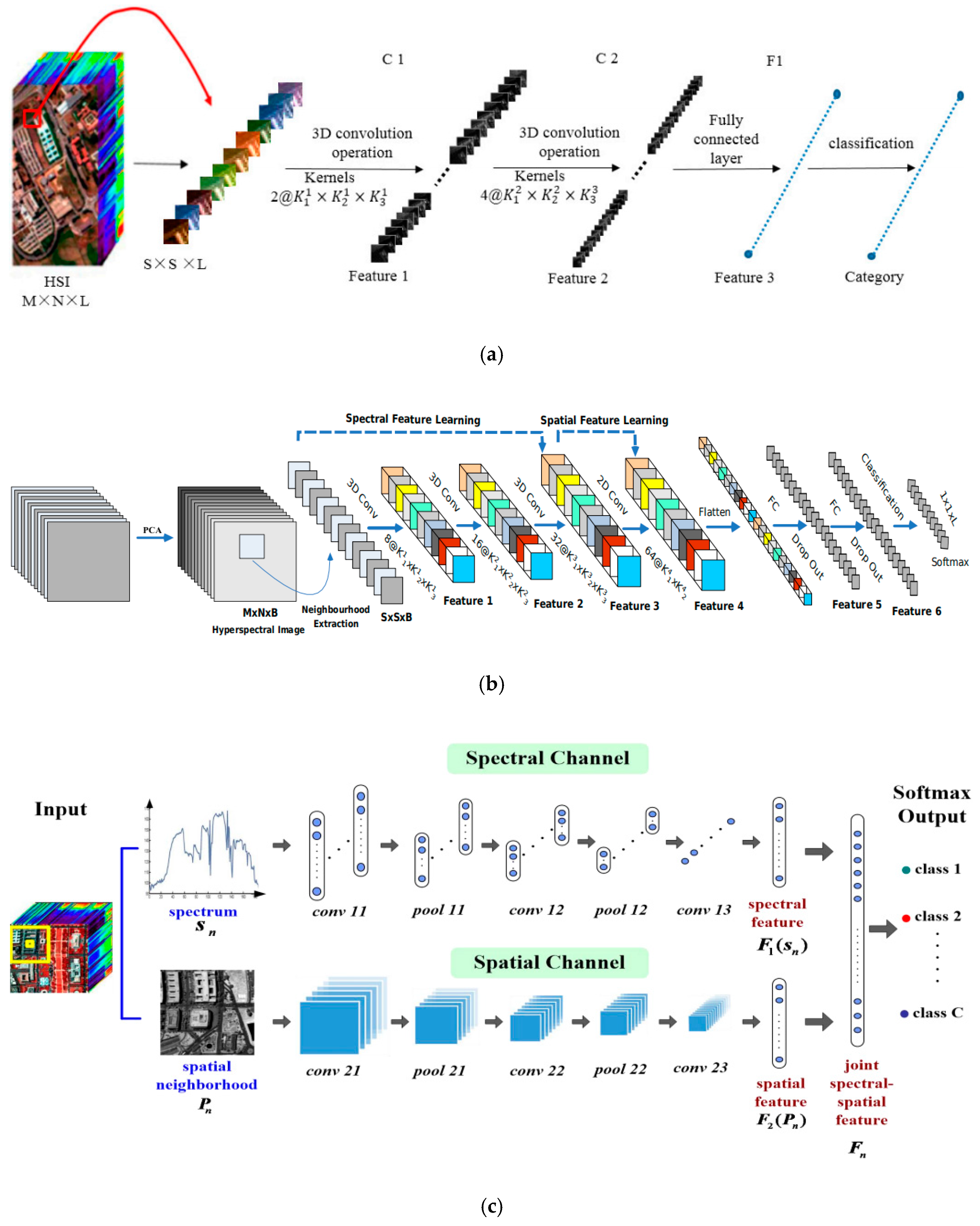
2. Related Work
3. Proposed Methodology
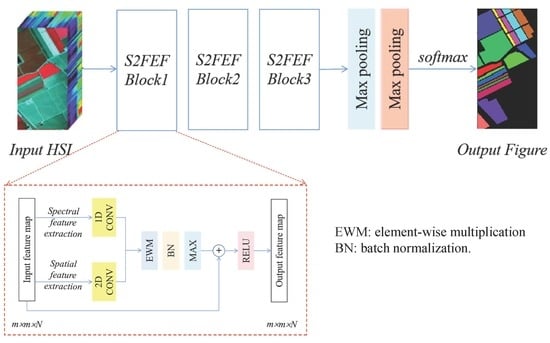
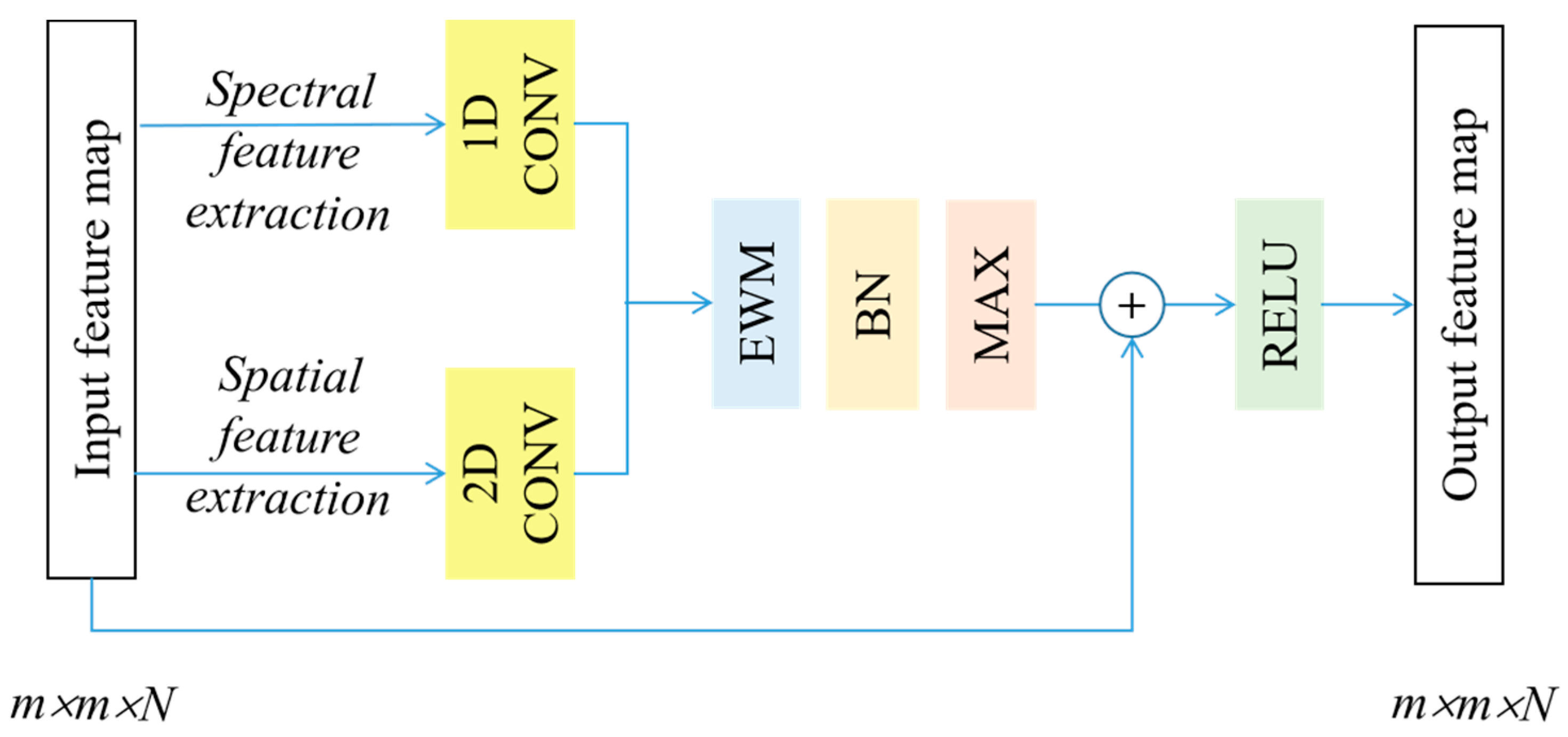
3.1. S2FEF Block
| Algorithm 1: Feature Extraction with S2FEF Block |
| Input: A joint spectral–spatial feature map F, |
| Spectral/Spatial kernel size Spe/Spa and kernel number k. |
| Output: A new joint spectral–spatial feature map F’. |
| 1. begin |
| 2. Extract spectral/spatial features fspe/fspa with k spectral/spatial kernel (size 1 × 1 × Spe/Spa × Spa × 1). |
| 3. Fuse the spectral and spatial features together by element-wise multiplication (fspe × fspa) to get the joint features fjoint. |
| 4. Select the max value from the corresponding pixel in fjoint to form a special feature F’. |
| 5. Return F’. |
| 6. end |
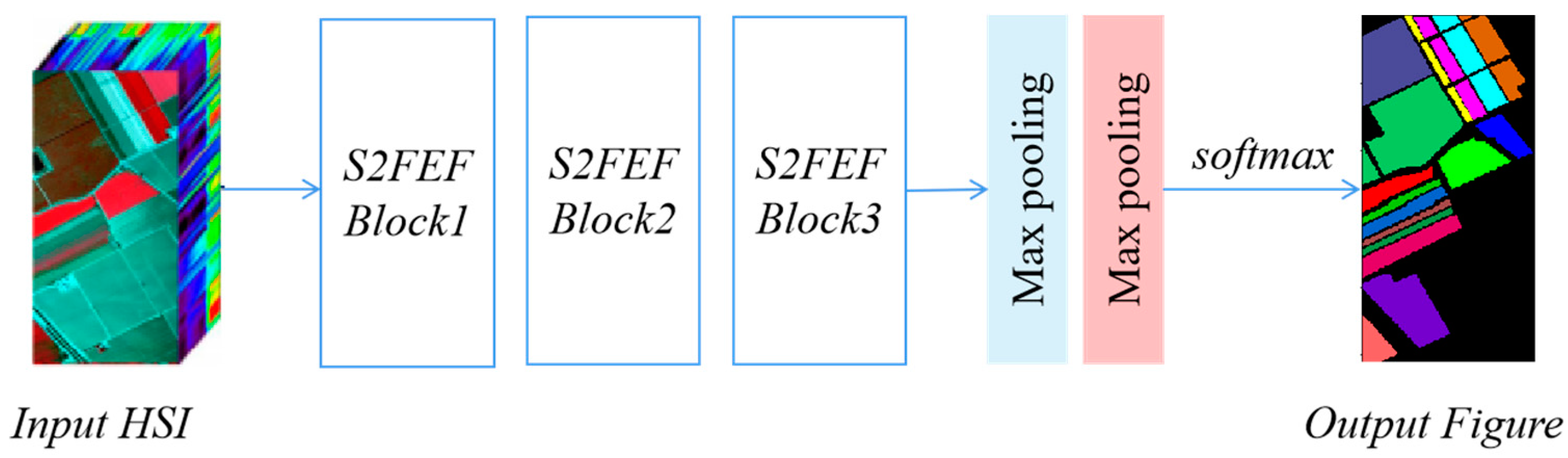
3.2. S2FEF-CNN Architecture
| Algorithm 2: S2FEF-CNN Classification |
| Input: Hyperspectral image cube size m, S2FEF block number Kk. |
| Output: The class label L of each pixel. |
| 1. begin |
| 2. Create input data set I in which each pixel input cube is size m × m × N (N is the spectrum band number). |
| 3. For each pixel in training set from I. |
| 4. Extract spectral–spatial features by Kk S2FEF blocks. |
| 5. The joint feature is pooled by two max pooling layers after which the feature size is m’ × m’ × N’. |
| 6. Flatten the feature into a vector v. |
| 7. Computing the softmax output L. |
| 8. Return L. |
| 9. end |
4. Experimental Results
4.1. Datasets
4.2. Parameters Setting
4.3. Comparison of Parameter Numbers
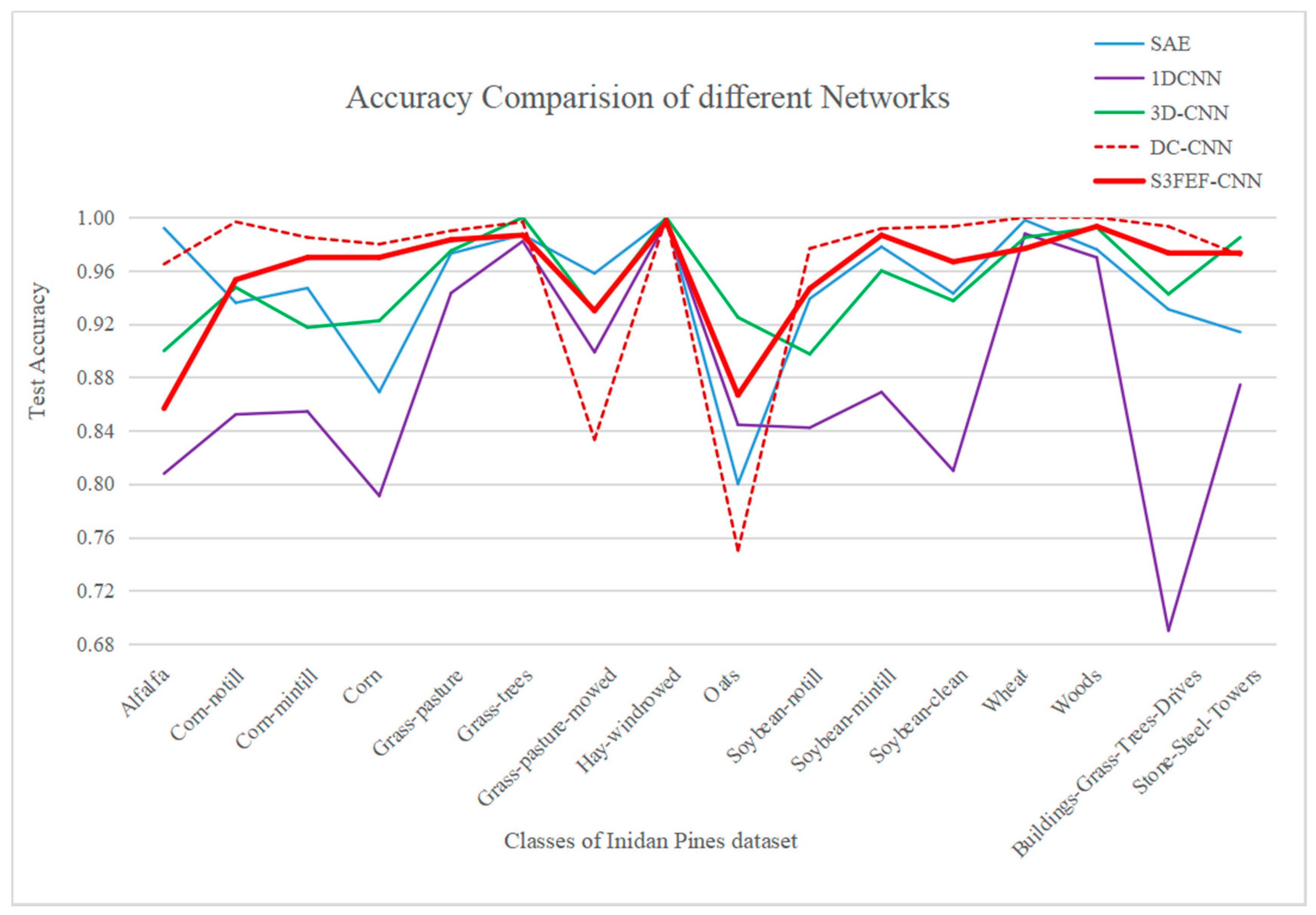
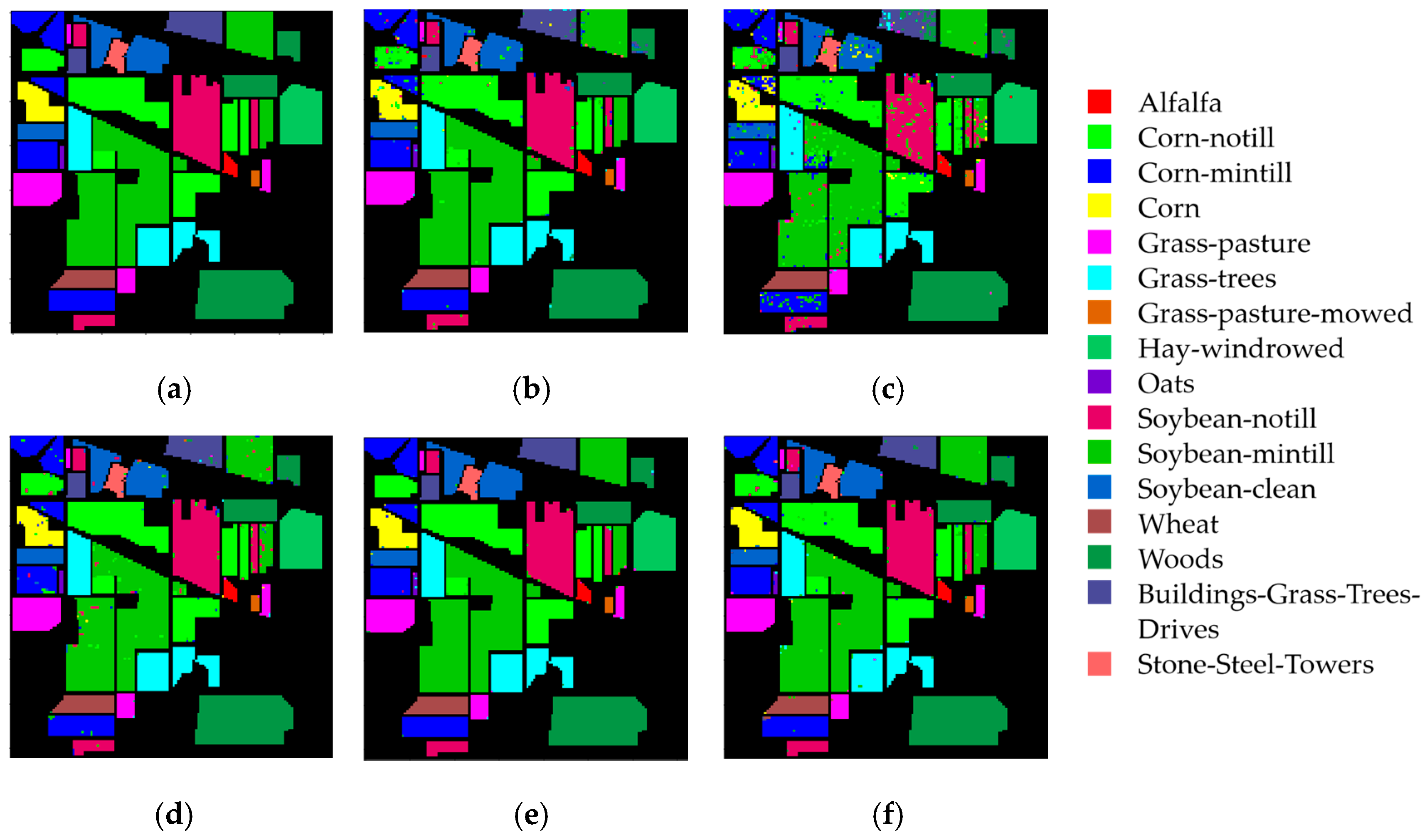
4.4. Results of the Indian Pines Dataset
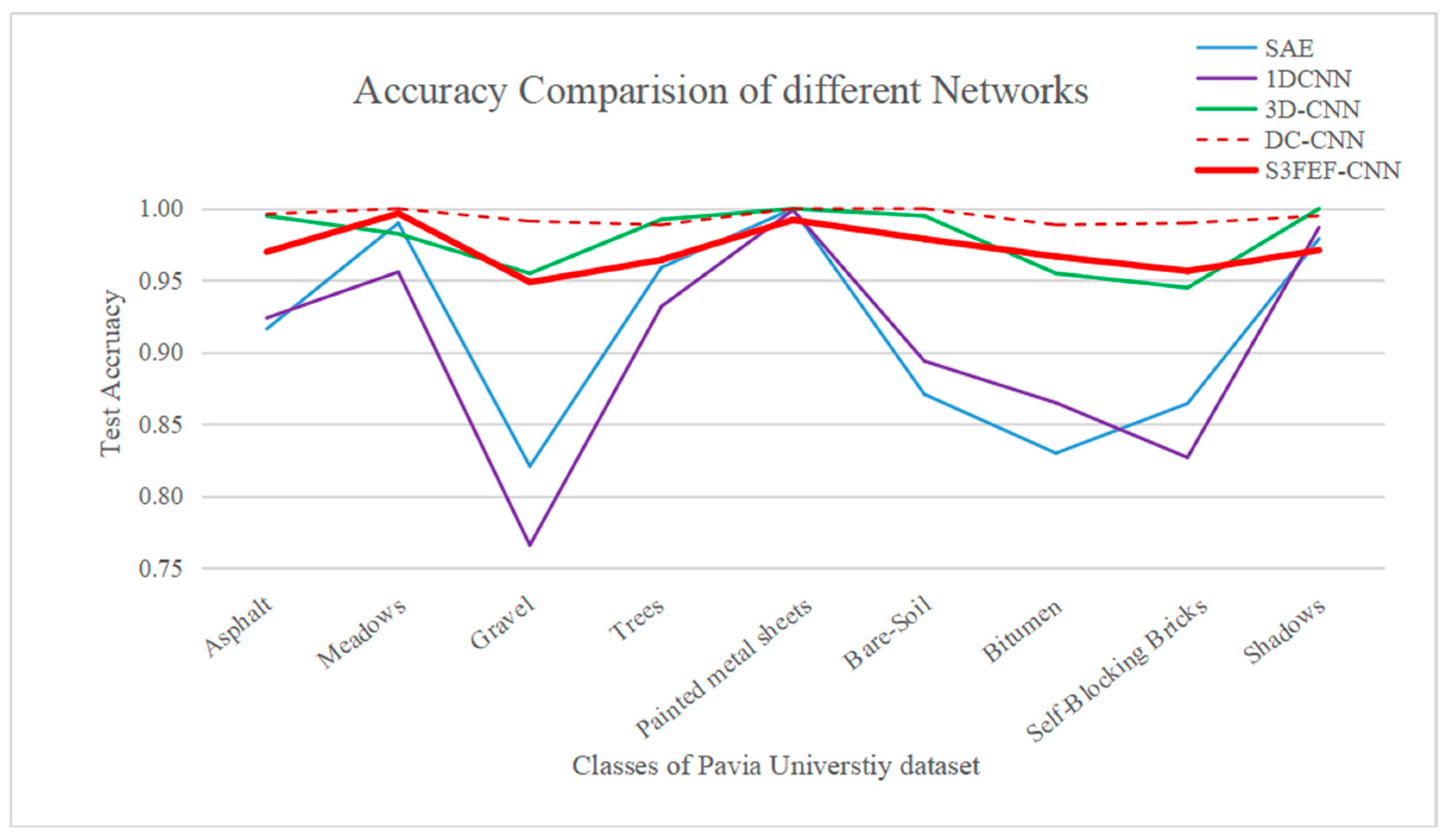
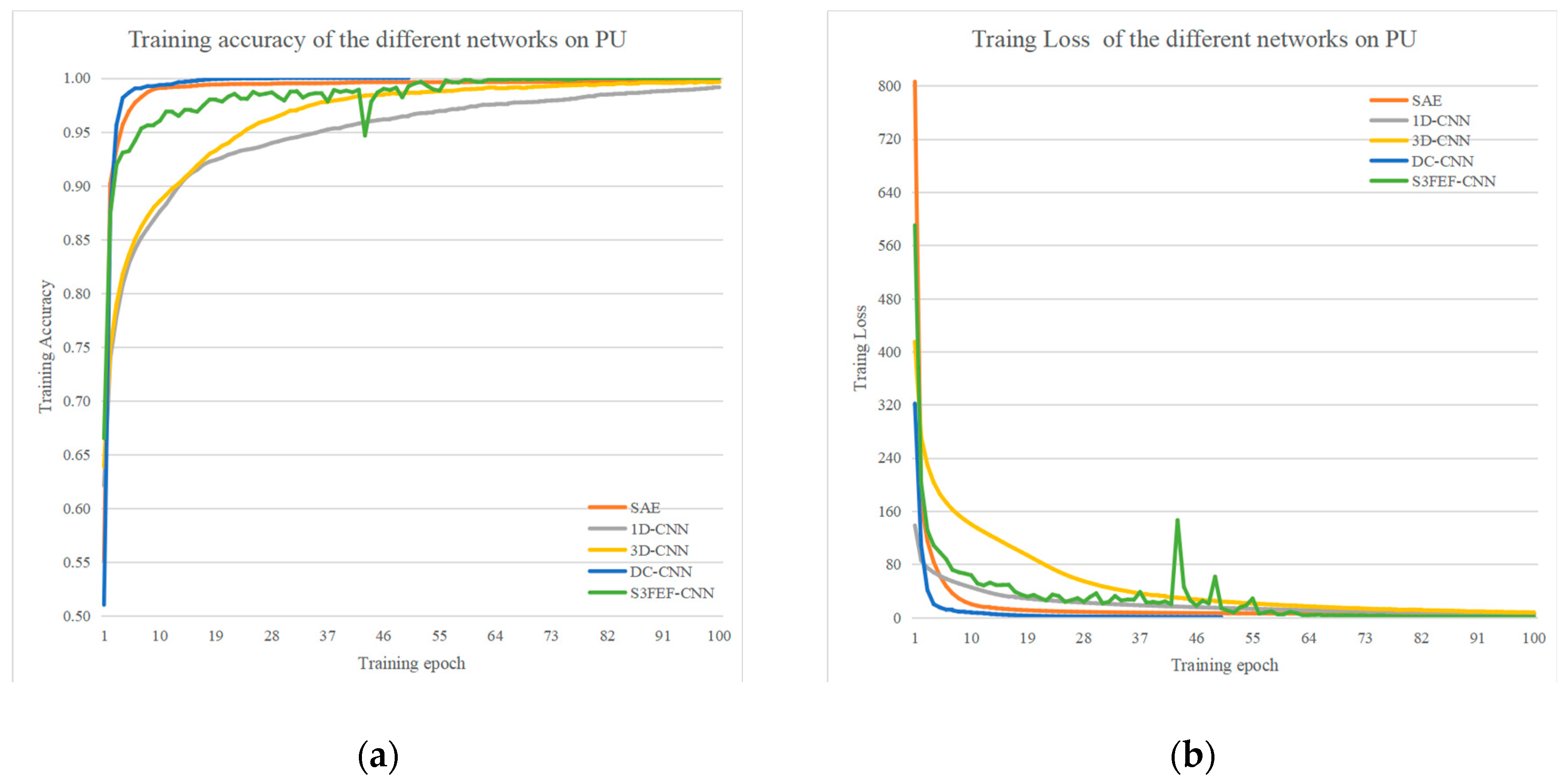
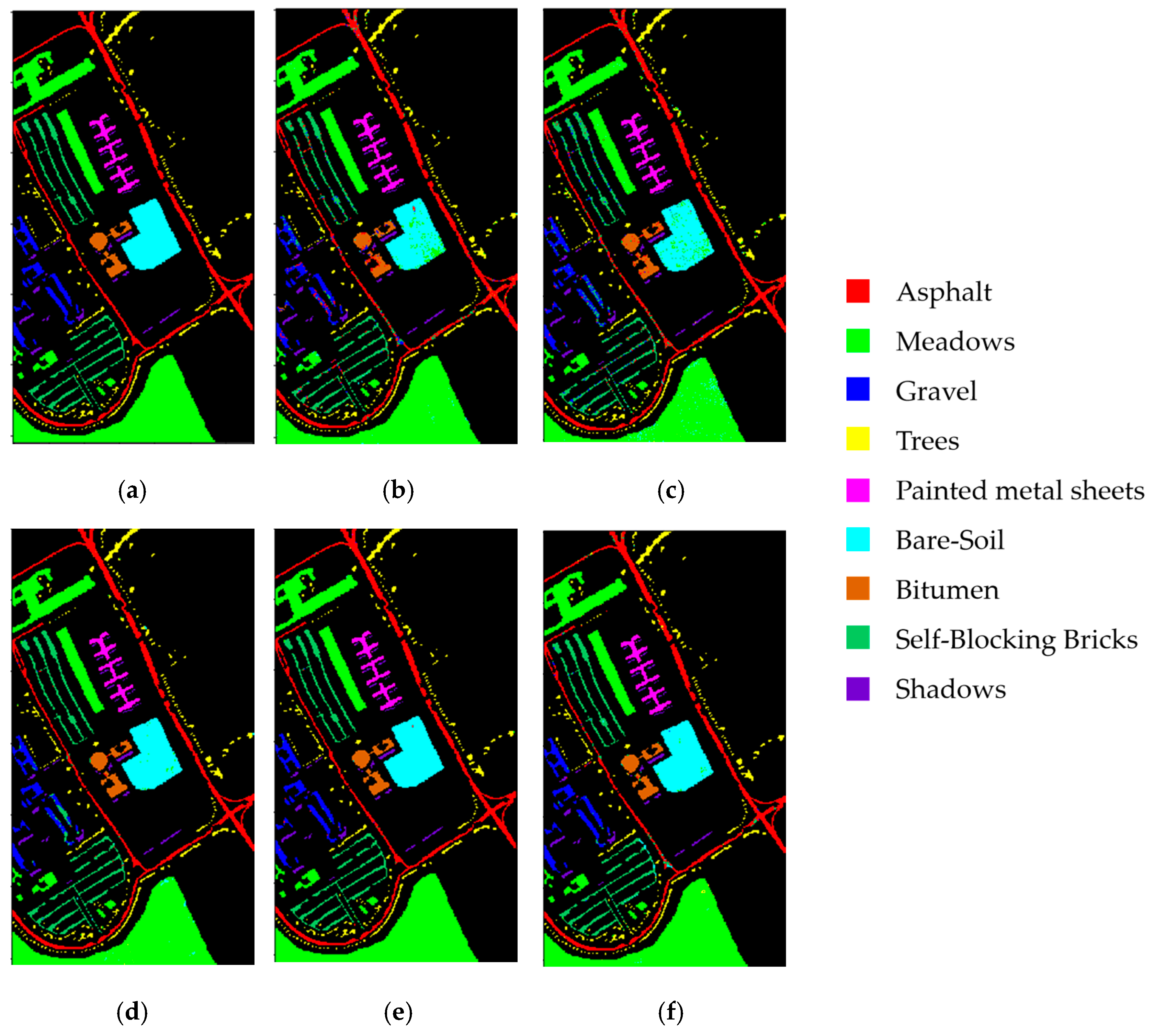
4.5. Results of the Pavia University Dataset
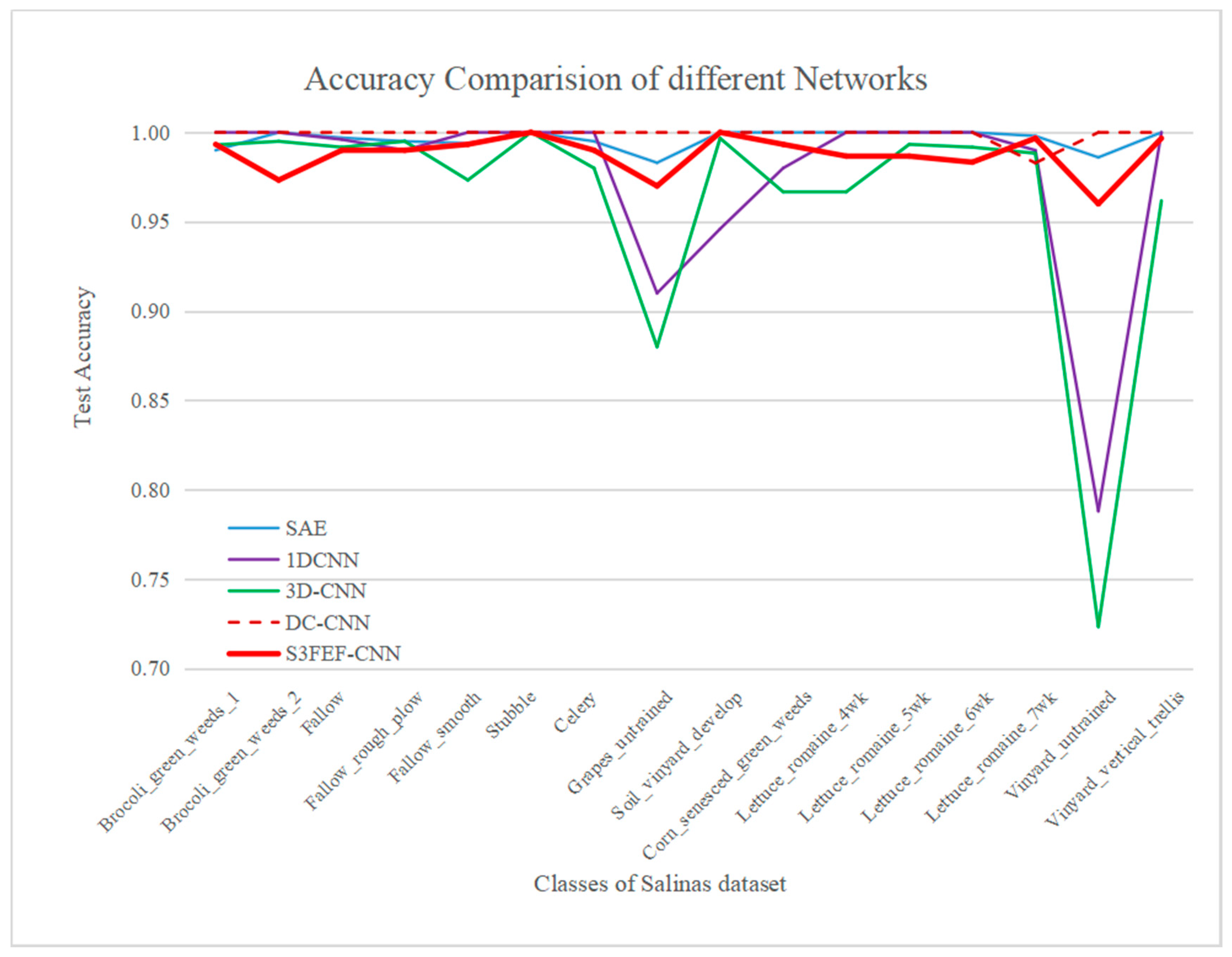
4.6. Results of the Salinas Dataset
4.7. Parameter Influence
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Liang, L.; Di, L.; Zhang, L.; Deng, M.; Qin, Z.; Zhao, S.; Lin, H. Estimation of crop LAI using hyperspectral vegetation indices and a hybrid inversion method. Remote Sens. Environ. 2015, 165, 123–134. [Google Scholar] [CrossRef]
- Tidke, S.; Kumar, A. New HyperSpectral Image Segmentation based on the Concept of Binary Partition Tree. Int. J. Adv. Technol. Eng. Explor. 2015, 2, 140–146. [Google Scholar]
- Lu, X.; Li, X.; Mou, L. Semi-supervised multitask learning for scene recognition. IEEE Trans. Cybern. 2015, 45, 1967–1976. [Google Scholar] [PubMed]
- Valero, S.; Salembier, P.; Chanussot, J. Object recognition in hyperspectral images using Binary Partition Tree representation. Pattern Recognit. Lett. 2015, 56, 4098–4101. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Song, W.; Fang, L.; Chen, Y.; Ghamisi, P.; Benediktsson, J. Deep learning for hyperspectral image classification: An overview. arXiv 2019, arXiv:1910.12861. [Google Scholar] [CrossRef] [Green Version]
- Hecker, C.; Meijde, M.; Werff, H.; Meer, F. Assessing the influence of reference spectra on synthetic SAM classification results. IEEE Trans. Geosci. Remote Sens. 2008, 46, 4162–4172. [Google Scholar] [CrossRef]
- Wang, K.; Gu, X.; Yu, T.; Meng, Q.; Zhao, L.; Feng, L. Classification of hyperspetral remote sensing images using frequency spectrum similarity. Sci. China Tech. Sci. 2013, 56, 980–988. [Google Scholar] [CrossRef]
- Demir, B.; Erturk, S. Hyperspectral image classification using relevance vector machines. IEEE Geosci. Remote Sens. Lett. 2007, 4, 586–590. [Google Scholar] [CrossRef]
- Camps-Valls, G.; Gomez-Chova, L.; Muñoz-Marí, J.; Vila-Francés, J.; Calpe-Maravilla, J. Composite kernels for hyper-spectral image classification. IEEE Geosci. Remote Sens. Lett. 2006, 3, 93–97. [Google Scholar] [CrossRef]
- Gόmez-Chova, L.; Camps-Valls, G.; Muoz-Mari, J.; Calpe, J. Semi-supervised image classification with Laplacian support vector machines. IEEE Geosci. Remote Sens. Lett. 2008, 5, 336–340. [Google Scholar] [CrossRef]
- Licciardi, G.; Marpu, P.; Chanussot, J.; Benediktsson, J. Linear versus nonlinear PCA for the classification of hyperspectral data based on the extended morphological profiles. IEEE Geosci. Remote Sens. Lett. 2012, 9, 447–451. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Chen, C.; Su, H.; Du, Q. Local binary patterns and extreme learning machine for hyperspectral imagery classification. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3681–3693. [Google Scholar] [CrossRef]
- Cao, X.; Xu, L.; Meng, D.; Zhao, Q.; Xu, Z. Integration of 3-dimensional discrete wavelet transform and markov random field for hyperspectral image classification. Neurocomputing 2017, 226, 90–100. [Google Scholar] [CrossRef]
- Li, W.; Wu, G.; Zhang, F.; Du, Q. Hyperspectral image classification using deep pixel-pair features. IEEE Trans. Geosci. Remote Sens. 2017, 55, 844–853. [Google Scholar] [CrossRef]
- Chen, Y.; Jiang, H.; Li, C.; Jia, X.; Ghamisi, P. Deep feature extraction and classification of hyperspectral images based on convolutional neural networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef] [Green Version]
- Liang, J.; Zhou, J.; Qian, Y.; Wen, L.; Bai, X.; Gao, Y. On the sampling strategy for valuation of spectral-spatial methods in hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 862–879. [Google Scholar] [CrossRef] [Green Version]
- Cheng, G.; Li, Z.; Han, J.; Yao, X.; Guo, L. Exploring hierarchical convolutional features for hyperspectral image classifification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6712–6722. [Google Scholar] [CrossRef]
- Kang, X.; Li, C.; Li, S.; Lin, H. Classification of hyperspectral images by gabor filtering based deep network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1166–1178. [Google Scholar] [CrossRef]
- Leng, J.; Li, T.; Bai, G.; Dong, Q.; Dong, H. Cube-CNN-SVM: A novel hyperspectral image classification method. In Proceedings of the IEEE 28th International Conference on Tools with Artificial Intelligence (ICTAI), San Jose, CA, USA, 6–8 November 2016; pp. 1027–1034. [Google Scholar]
- Yu, D.; Deng, L.; Wang, S. Learning in the deep-structured conditional random fields. In Proceedings of the Conference and Workshop on Neural Information Processing Systems (NIPS), Vancouver, BC, Canada, 7–10 December 2009; pp. 1848–1852. [Google Scholar]
- Mohamed, A.; Sainath, T.; Dahl, G.; Ramabhadran, B.; Hinton, G.E.; Picheny, M. Deep belief networks using discriminative features for phone recognition. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Prague, Czech, 22–27 May 2011; pp. 5060–5063. [Google Scholar]
- Dieleman, S.; Schrauwen, B. End-to-end learning for music audio. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Florence, Italy, 4–9 May 2014; pp. 6964–6968. [Google Scholar]
- Wang, T.; Wu, D.; Coates, A.; Ng, A. End-to-end text recognition with convolutional neural networks. In Proceedings of the 21st International Conference on Pattern Recognition (ICPR), Tsukuba, Japan, 11–15 November 2012; pp. 3304–3308. [Google Scholar]
- Hu, W.; Huang, Y.; Li, W.; Zhang, F.; Li, H. Deep convolutional neural networks for hyperspectral image classification. J. Sens. 2015, 2015, 258619. [Google Scholar] [CrossRef] [Green Version]
- Yue, J.; Zhao, W.; Mao, S.; Liu, H. Spectral-spatial classification of hyperspectral images using deep convolutional neural networks. IEEE Geosci. Remote Sens. Lett. 2015, 6, 468–477. [Google Scholar] [CrossRef]
- Mei, S.; Ji, J.; Bi, Q.; Hou, J.; Du, Q.; Li, W. Integrating spectral and spatial information into deep convolutional neural networks for hyperspectral classification. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 5067–5070. [Google Scholar]
- Haut, J.; Paoletti, M.; Plaza, J.; Li, J.; Plaza, A. Active learning with convolutional neural networks for hyperspectral image classification using a new bayesian approach. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6440–6461. [Google Scholar] [CrossRef]
- Liang, H.; Li, Q. Hyperspectral imagery classification using sparse representations of convolutional neural network features. Remote Sens. 2016, 8, 99. [Google Scholar] [CrossRef] [Green Version]
- Makantasis, K.; Protopapadakis, E.; Doulamis, A.; Doulamis, N.; Loupos, C. Deep convolutional neural networks for efficient vision based tunnel inspection. In Proceedings of the IEEE International Conference on Intelligent Computer Communication and Processing (ICCP), Cluj-Napoca, Romania, 3–5 September 2015; pp. 335–342. [Google Scholar]
- Li, Y.; Zhang, H.; Shen, Q. Spectral-spatial classification of hyperspectral imagery with 3d convolutional neural network. Remote Sens. 2017, 9, 67. [Google Scholar] [CrossRef] [Green Version]
- Zhong, Z.; Li, J.; Luo, Z.; Chapman, M. Spectral-spatial residual network for hyperspectral image classification: A 3-D deep learning framework. IEEE Trans. Geosci. Remote Sens. 2018, 56, 847–858. [Google Scholar] [CrossRef]
- Chen, C.; Zhang, J.; Zheng, C.; Yan, Q.; Xun, L. Classification of hyperspectral data using a multi-channel convolutional neural network. In Proceedings of the 14th International Conference on Intelligent Computing (ICIC), Wuhan, China, 15–18 August 2018; pp. 81–92. [Google Scholar]
- Paoletti, M.; Haut, J.; Plaza, J.; Plaza, A. A new deep convolutional neural network for fast hyperspectral image classification. ISPRS J. Photogramm. Remote Sens. 2018, 145, 120–147. [Google Scholar] [CrossRef]
- He, M.; Li, B.; Chen, H. Multi-scale 3d Deep Convolutional Neural Network for Hyperspectral image classification. In Proceedings of the IEEE International Conference on Image Processing (ICIP), Beijing, China, 17–20 September 2017; pp. 3904–3908. [Google Scholar]
- Yang, J.; Zhao, Y.; Chan, J. Learning and transferring deep joint spectral-spatial features for hyperspectral classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4729–4742. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Y.; Zhang, Y.; Shen, Q. Spectral-spatial classification of hyperspectral imagery using a dual-channel convolutional neural network. IEEE Geosci. Remote Sens. Lett. 2017, 8, 438–447. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Zhao, Y.; Chan, J.; Yi, C. Hyperspectral image classification using two-channel deep convolutional neural network. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 5079–5082. [Google Scholar]
- Roy, S.; Krishna, G.; Dubey, S.; Chaudhuri, B. HybridSN: Exploring 3D-2D CNN feature hierarchy for hyperspectral image classification. arXiv 2019, arXiv:1902.06701v2. [Google Scholar]
- Chen, Y.; Lin, Z.; Zhao, X.; Wang, G.; Gu, Y. Deep learning-based classification of hyperspectral data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2094–2107. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, X.; Jia, X. Spectral-spatial classification of hyperspectral data based on deep belief network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2381–2392. [Google Scholar] [CrossRef]
- Wu, Q.; Diao, W.; Dou, F.; Sun, X.; Zheng, X.; Fu, K.; Zhao, F. Shape-based object extraction in high-resolution remote-sensing images using deep Boltzmann machine. Int. J. Remote Sens. 2016, 37, 6012–6022. [Google Scholar] [CrossRef]
- Deng, F.; Pu, S.; Chen, X.; Shi, Y.; Yuan, T.; Pu, S. Hyperspectral image classification with capsule network using limited training samples. Sensors 2018, 18, 3153. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kang, X.; Zhuo, B.; Duan, P. Dual-path network-based hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2019, 16, 447–451. [Google Scholar] [CrossRef]
- Hamida, A.; Benoit, A.; Lambert, P.; Amar, C. 3-D deep learning approach for remote sensing image classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4420–4434. [Google Scholar] [CrossRef] [Green Version]
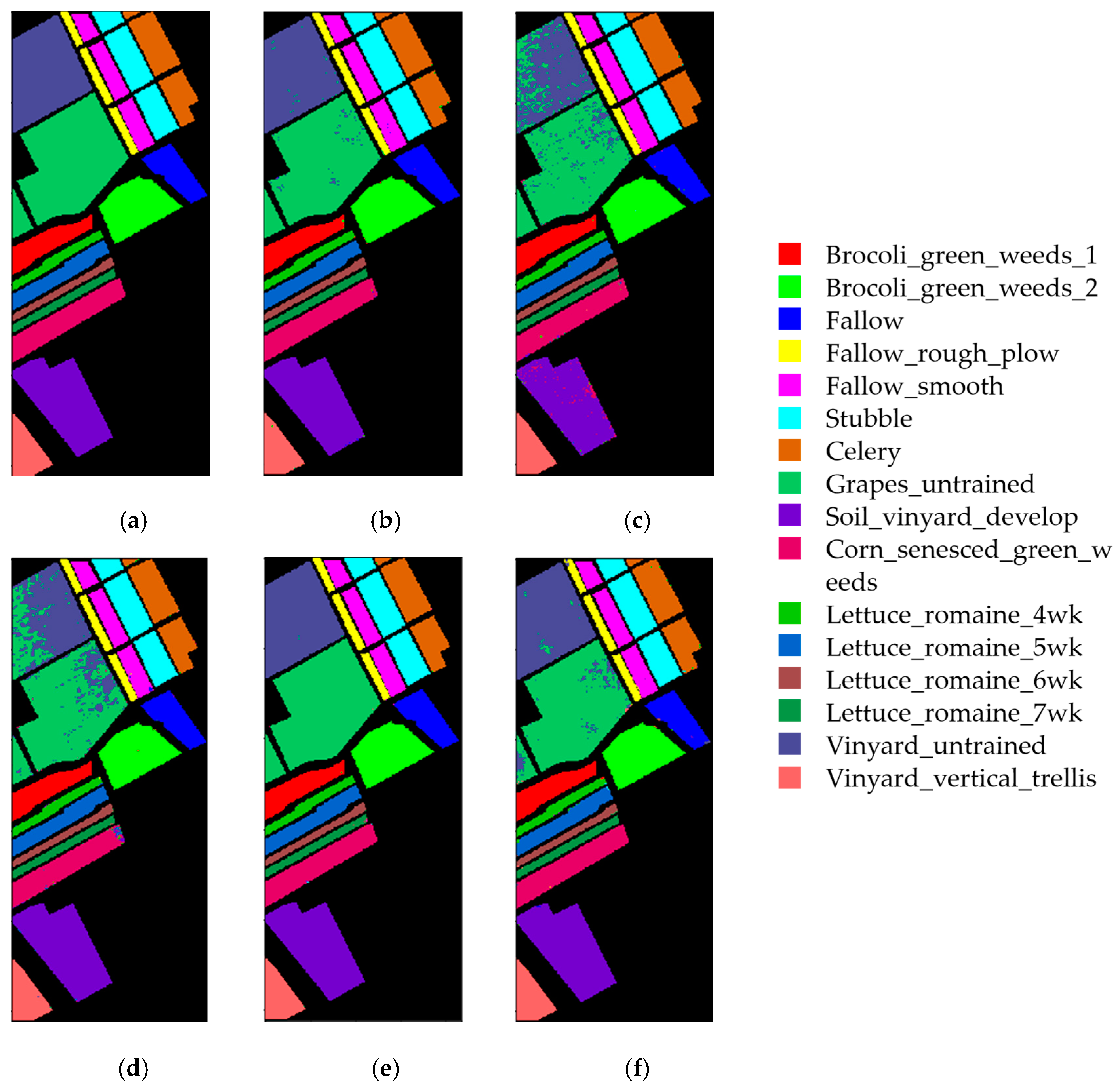
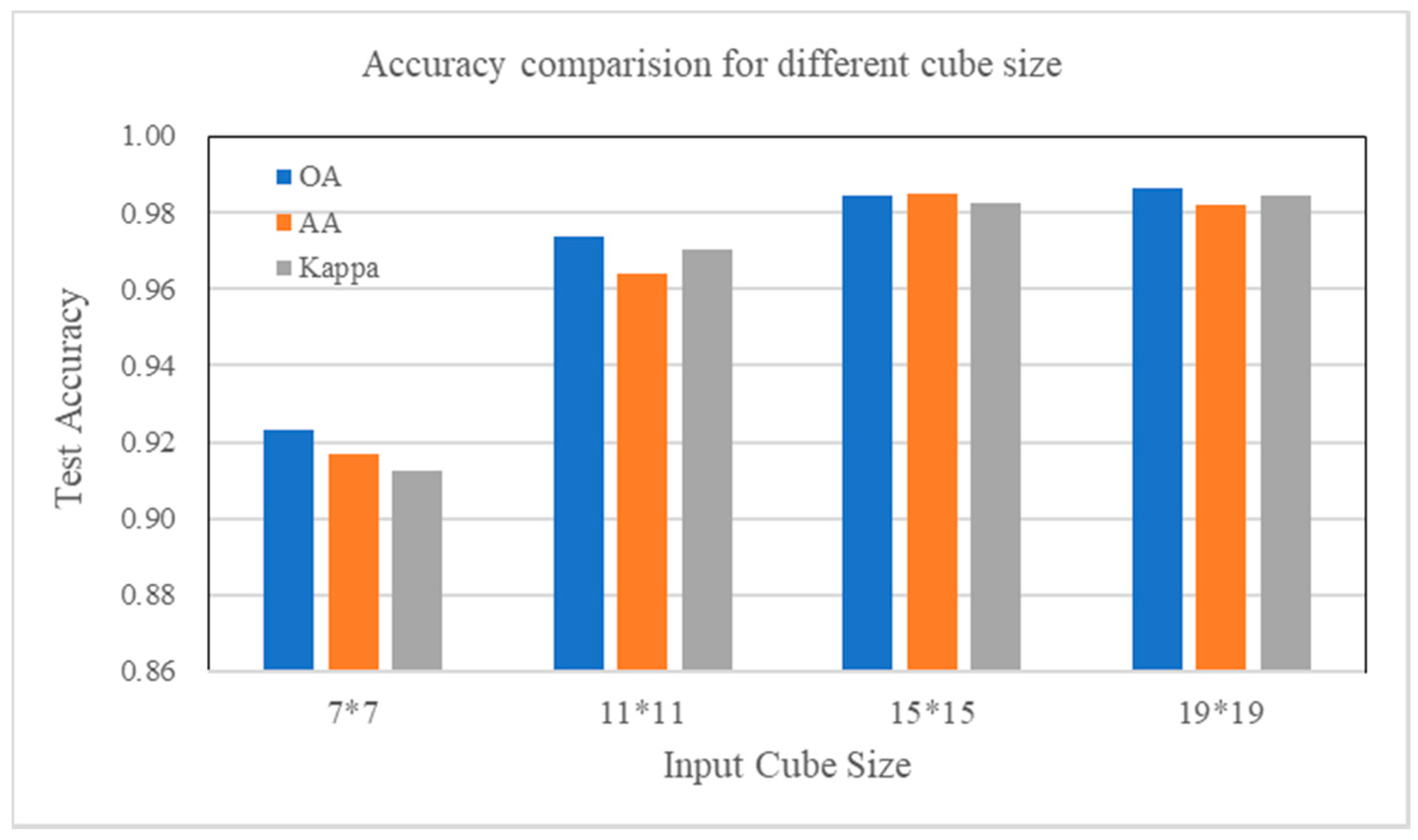
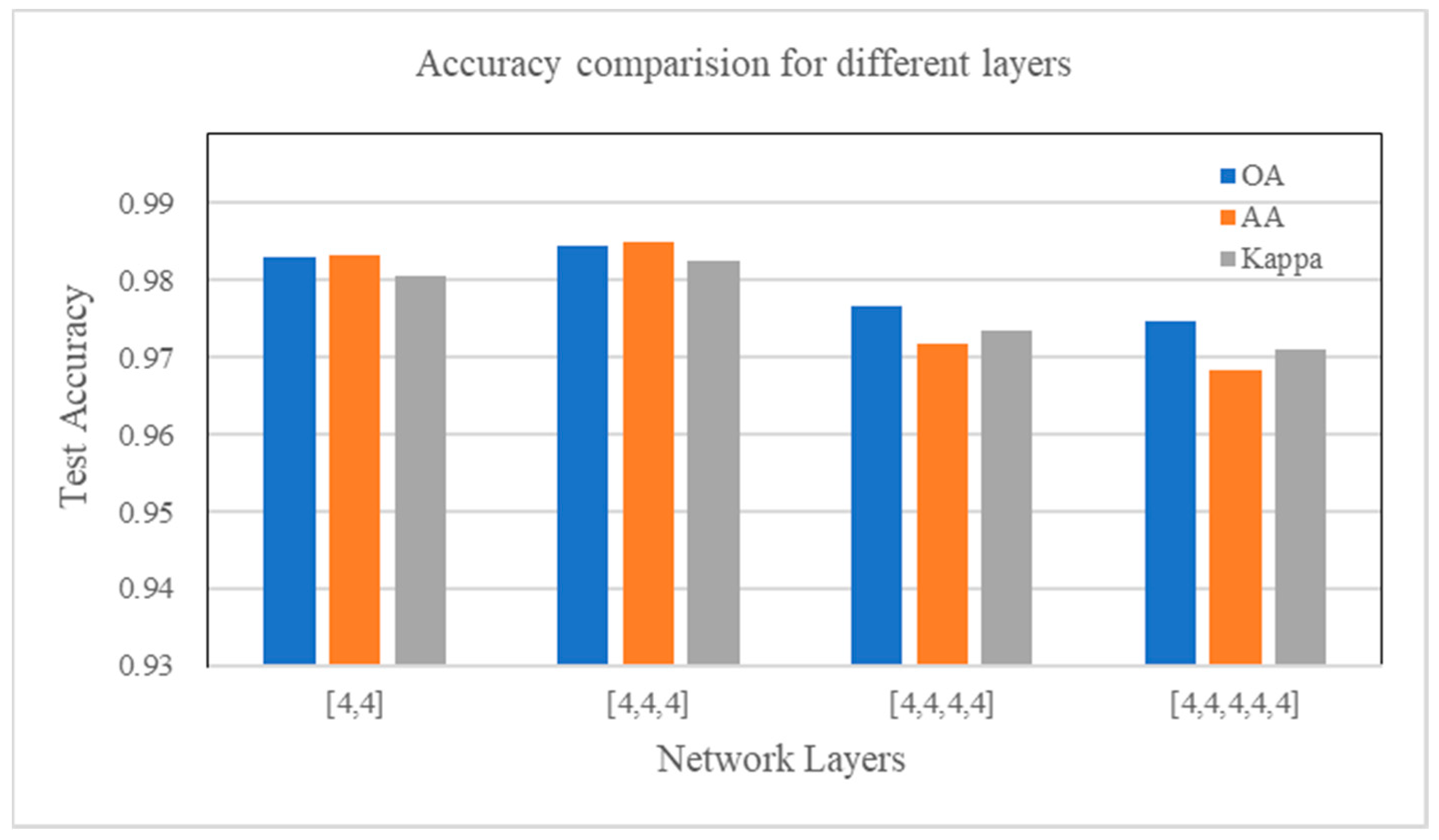
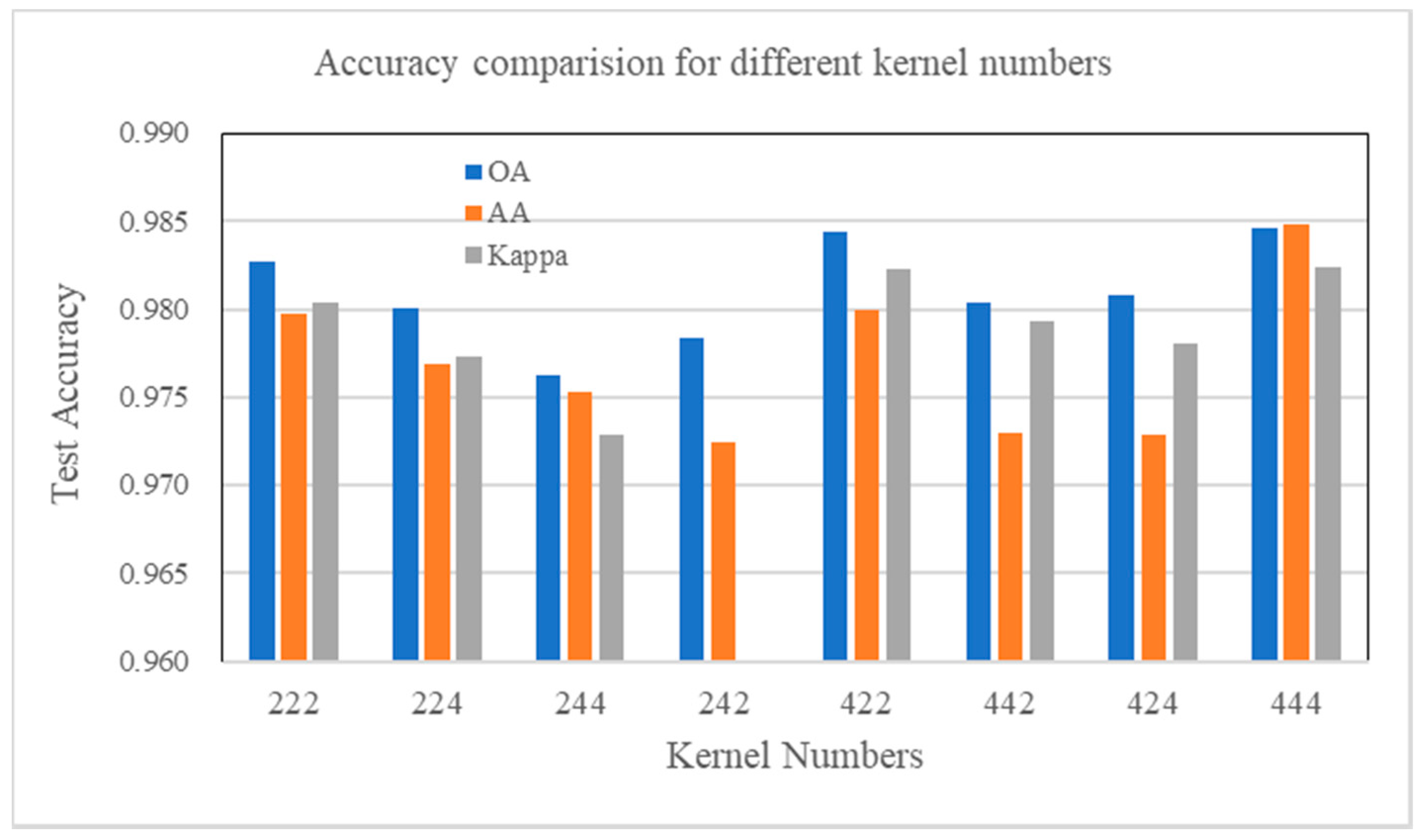
| Layer/Operation | Input | Kernel Size | Kernel Number | Output | Parameters |
|---|---|---|---|---|---|
| Spectral channel | 15 × 15 × N × 1 | 1 × 3 | 4 | 15 × 15 × N × 4 | 16 |
| Spatial channel | 15 × 15 × N × 1 | 3 × 3 | 4 | 15 × 15 × N × 4 | 40 |
| EWM | 15 × 15 × N × 4 | - | - | 15 × 15 × N × 4 | 0 |
| Batch normalization | 15 × 15 × N × 4 | - | - | 15 × 15 × N × 4 | 8 |
| Relu | 15 × 15 × N × 4 | 15 × 15 × N × 1 | 0 | ||
| Total | 64 |
| Layer/Operation | Indian Pines | Salinas | Pavia University |
|---|---|---|---|
| S2FEF Block1 | 64 | 64 | 64 |
| S2FEF Block2 | 64 | 64 | 64 |
| S2FEF Block3 | 64 | 64 | 64 |
| Max Pooling layers | 0 | 0 | 0 |
| Softmax layer | 5776 | 5792 | 1629 |
| Total | 5968 | 5984 | 1821 |
| Dataset | SAE | 1D-CNN | 3D-CNN | DC-CNN | S2FEF-CNN |
|---|---|---|---|---|---|
| IP | 129,856 | 81,408 | 199,040 | 278,552 | 5968 |
| PU | 129,856 | 61,249 | 111,129 | 153,117 | 1821 |
| SA | 123,609 | 82,216 | 199,040 | 278,552 | 5984 |
| Dataset | S2FEF-CNN/SAE | S2FEF-CNN/1D-CNN | S2FEF-CNN/3D-CNN | S2FEF-CNN/DC-CNN |
|---|---|---|---|---|
| IP | 4.60% | 7.33% | 3.00% | 2.14% |
| PU | 1.40% | 2.97% | 1.64% | 1.19% |
| SA | 4.84% | 7.27% | 3.01% | 2.14% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, L.; Wei, Z.; Xu, Y. A Lightweight Spectral–Spatial Feature Extraction and Fusion Network for Hyperspectral Image Classification. Remote Sens. 2020, 12, 1395. https://doi.org/10.3390/rs12091395
Chen L, Wei Z, Xu Y. A Lightweight Spectral–Spatial Feature Extraction and Fusion Network for Hyperspectral Image Classification. Remote Sensing. 2020; 12(9):1395. https://doi.org/10.3390/rs12091395
Chicago/Turabian StyleChen, Linlin, Zhihui Wei, and Yang Xu. 2020. "A Lightweight Spectral–Spatial Feature Extraction and Fusion Network for Hyperspectral Image Classification" Remote Sensing 12, no. 9: 1395. https://doi.org/10.3390/rs12091395
APA StyleChen, L., Wei, Z., & Xu, Y. (2020). A Lightweight Spectral–Spatial Feature Extraction and Fusion Network for Hyperspectral Image Classification. Remote Sensing, 12(9), 1395. https://doi.org/10.3390/rs12091395