Automated Filtering of Multibeam Water-Column Data to Detect Relative Abundance of Giant Kelp (Macrocystis pyrifera)
Abstract
1. Introduction
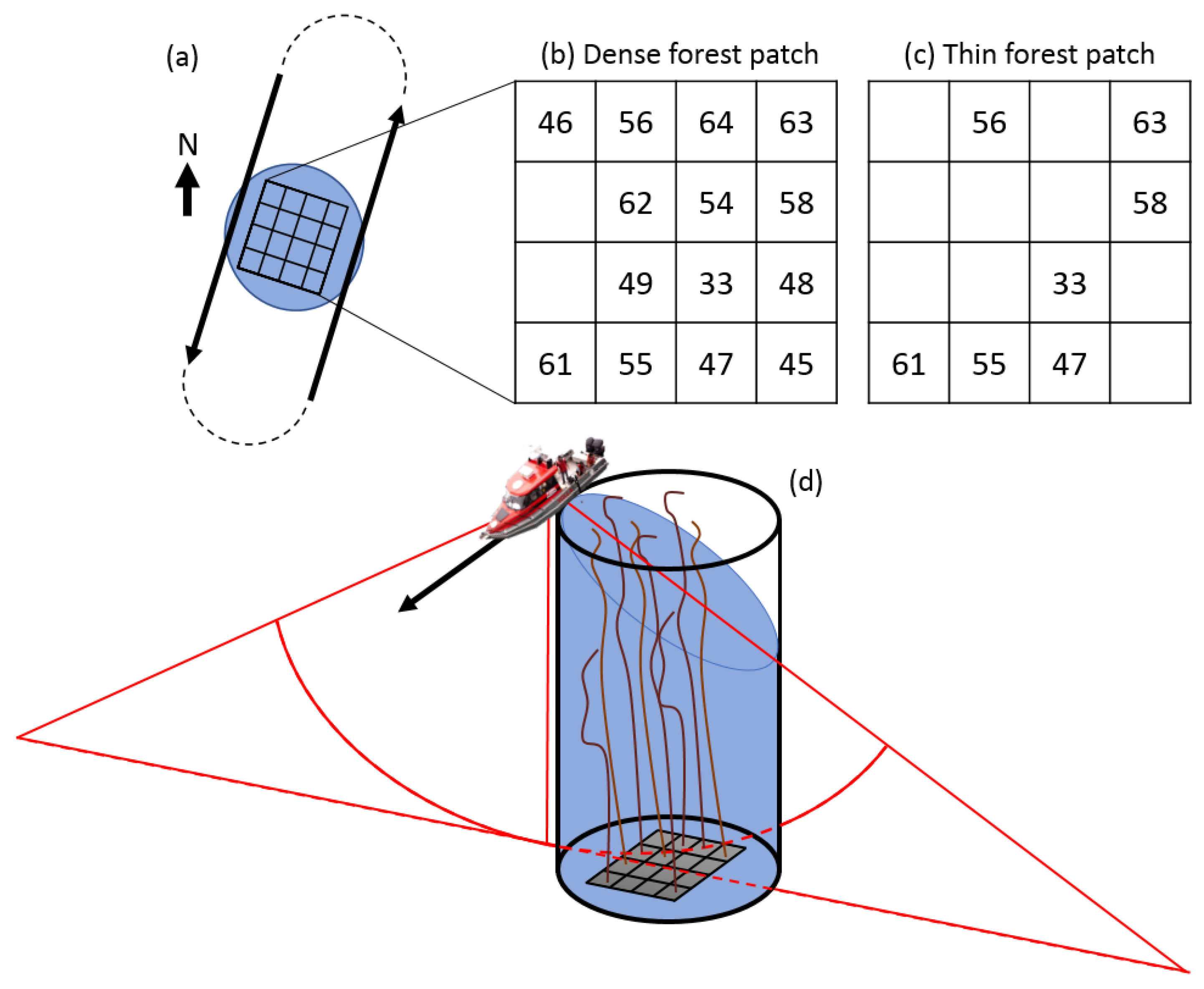
2. Materials and Methods
3. Results
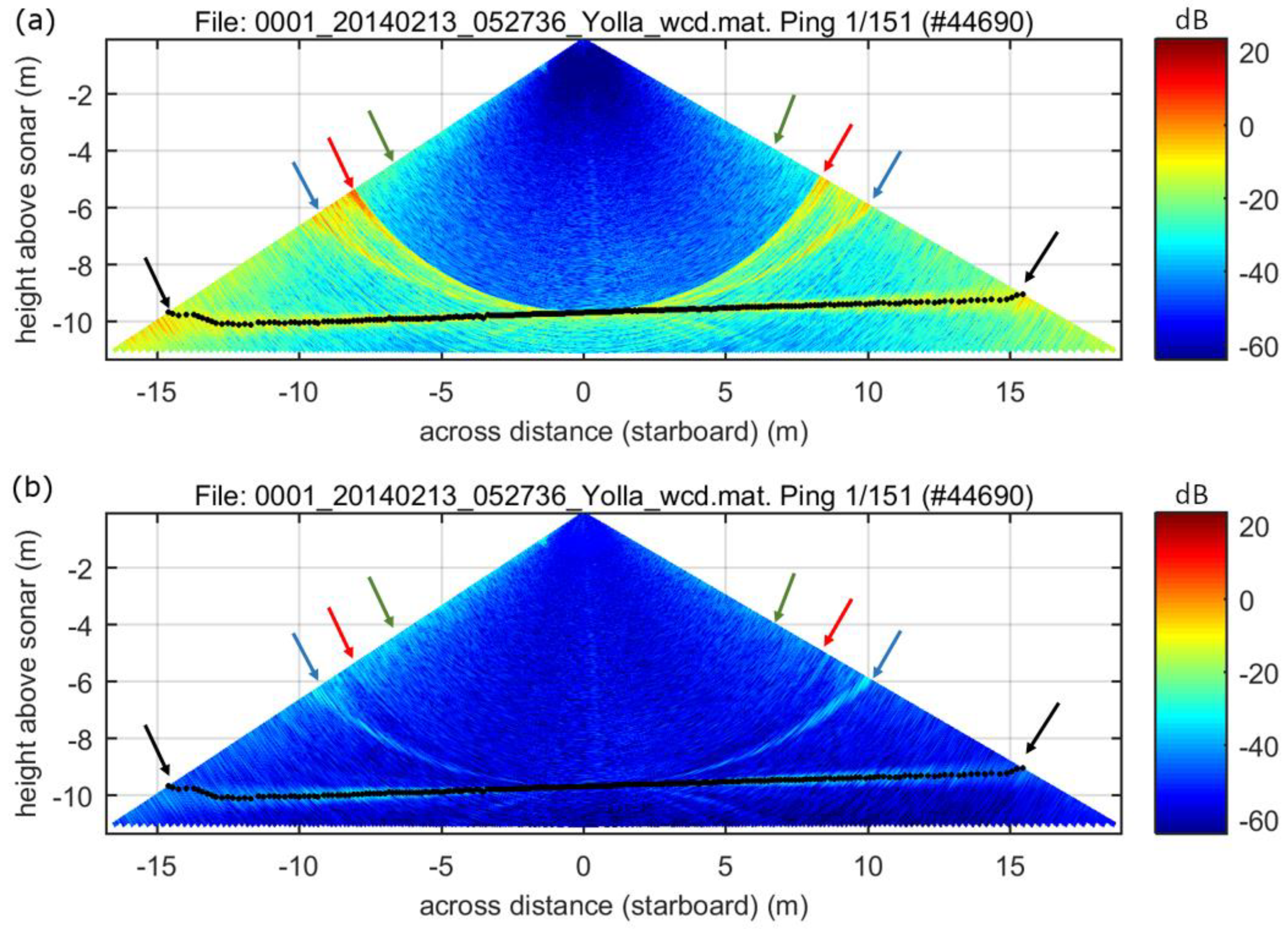
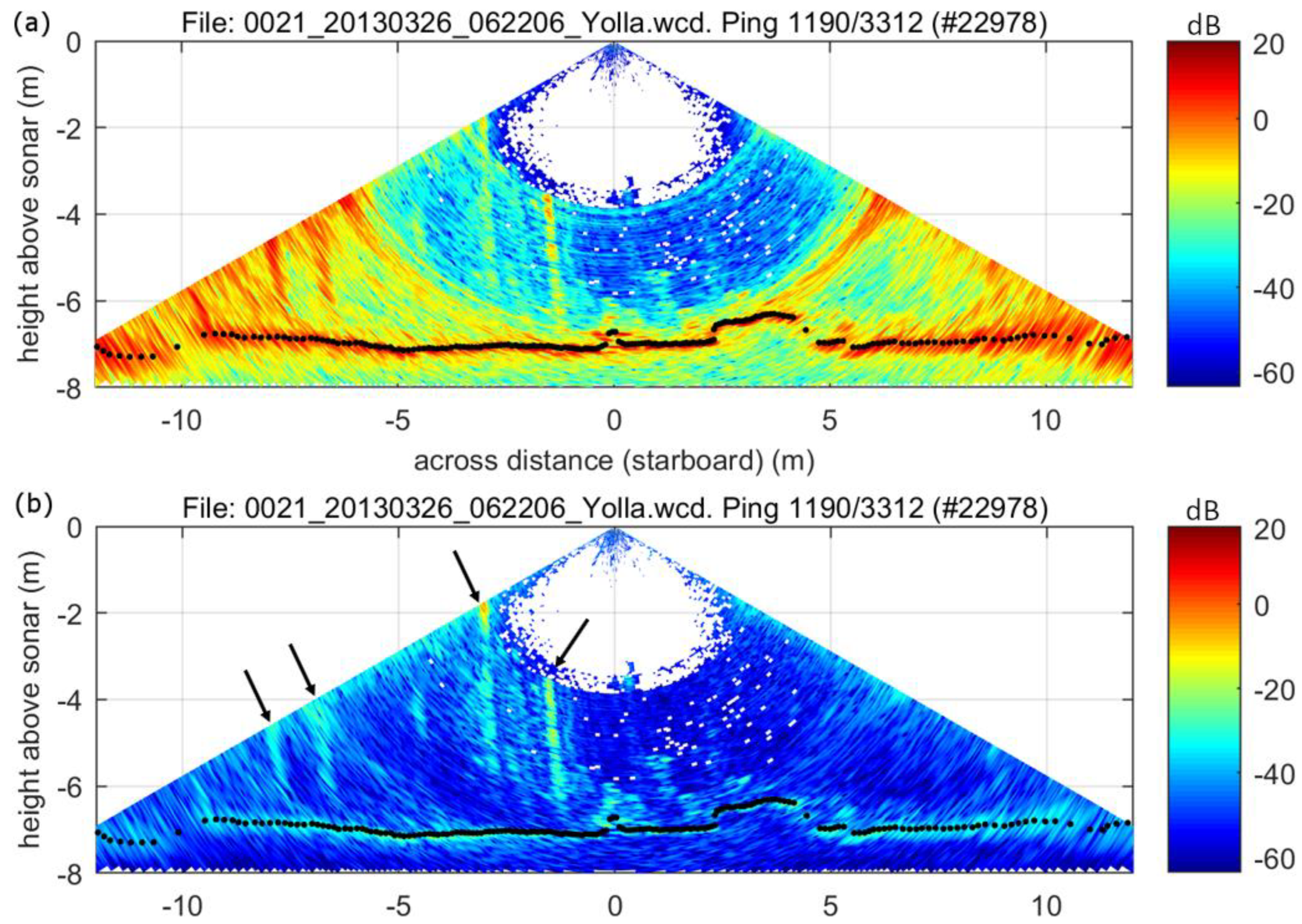
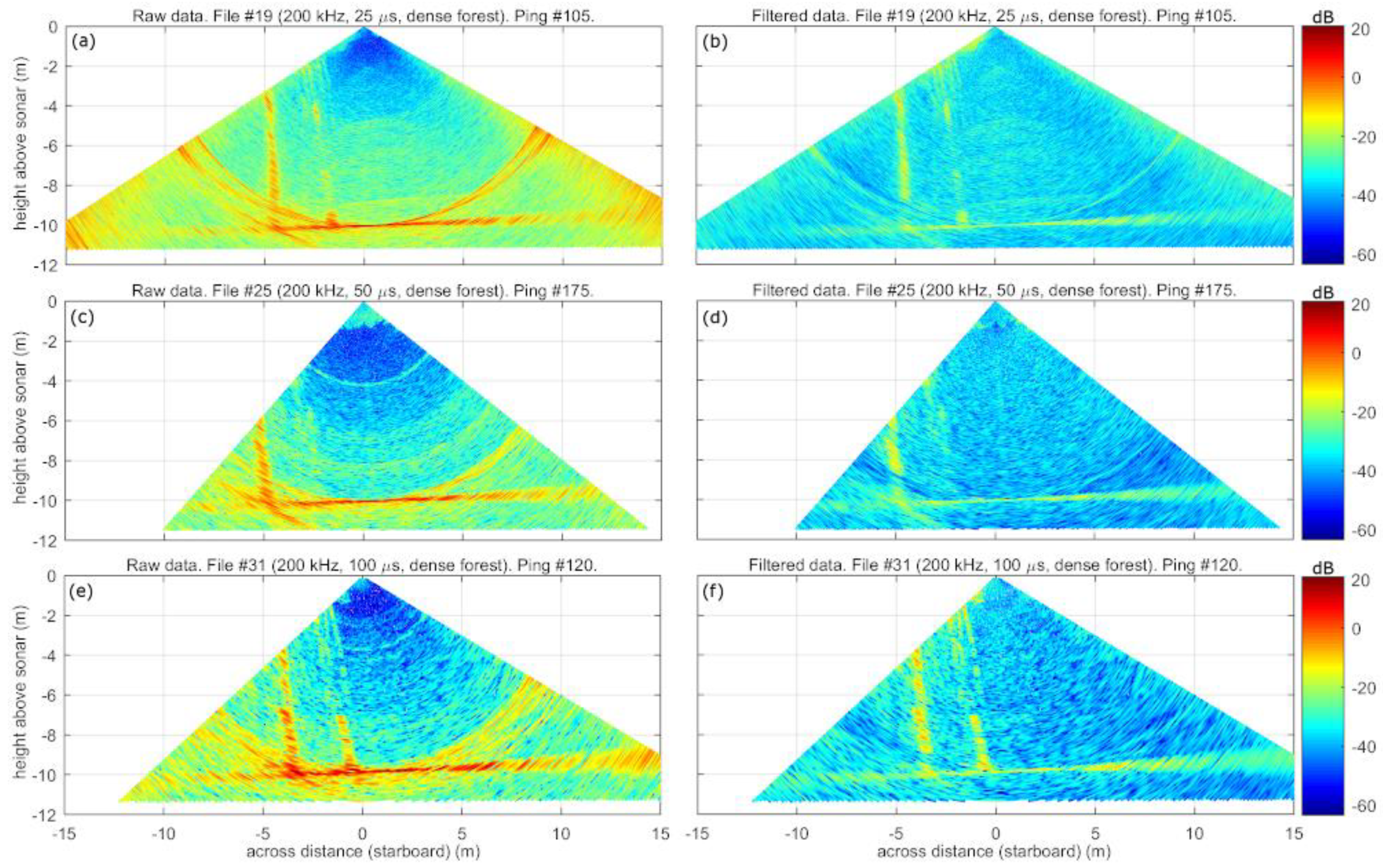
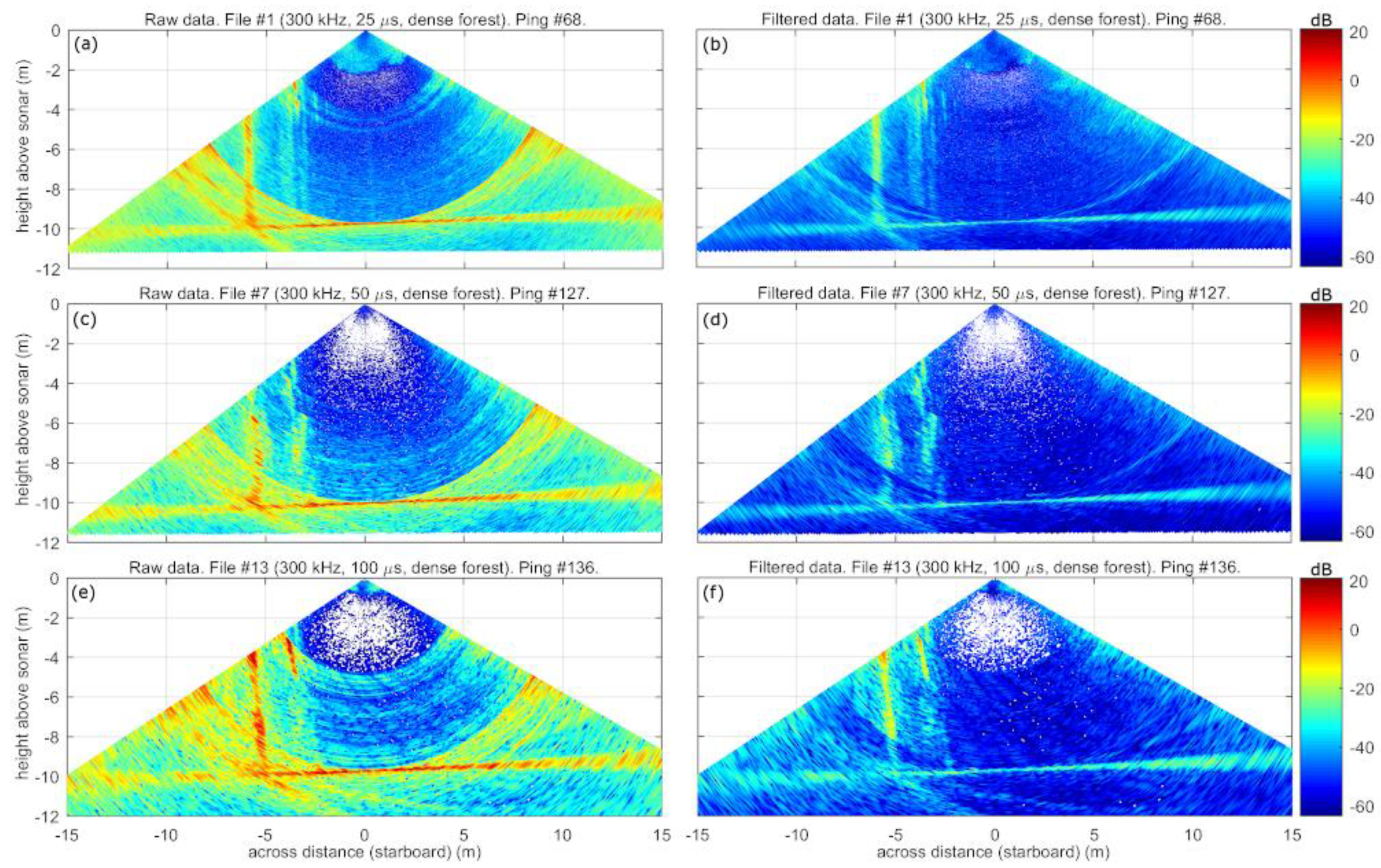
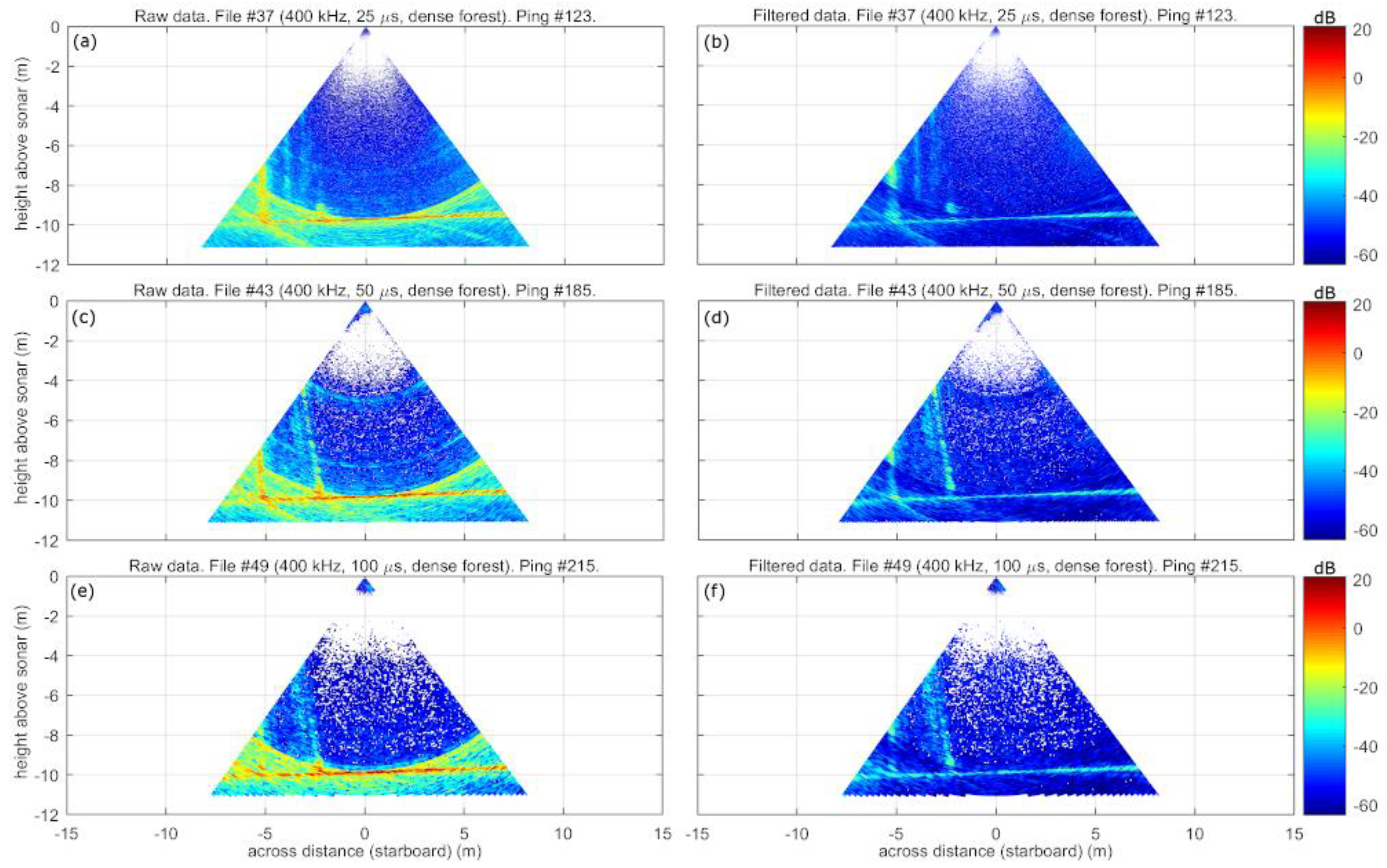
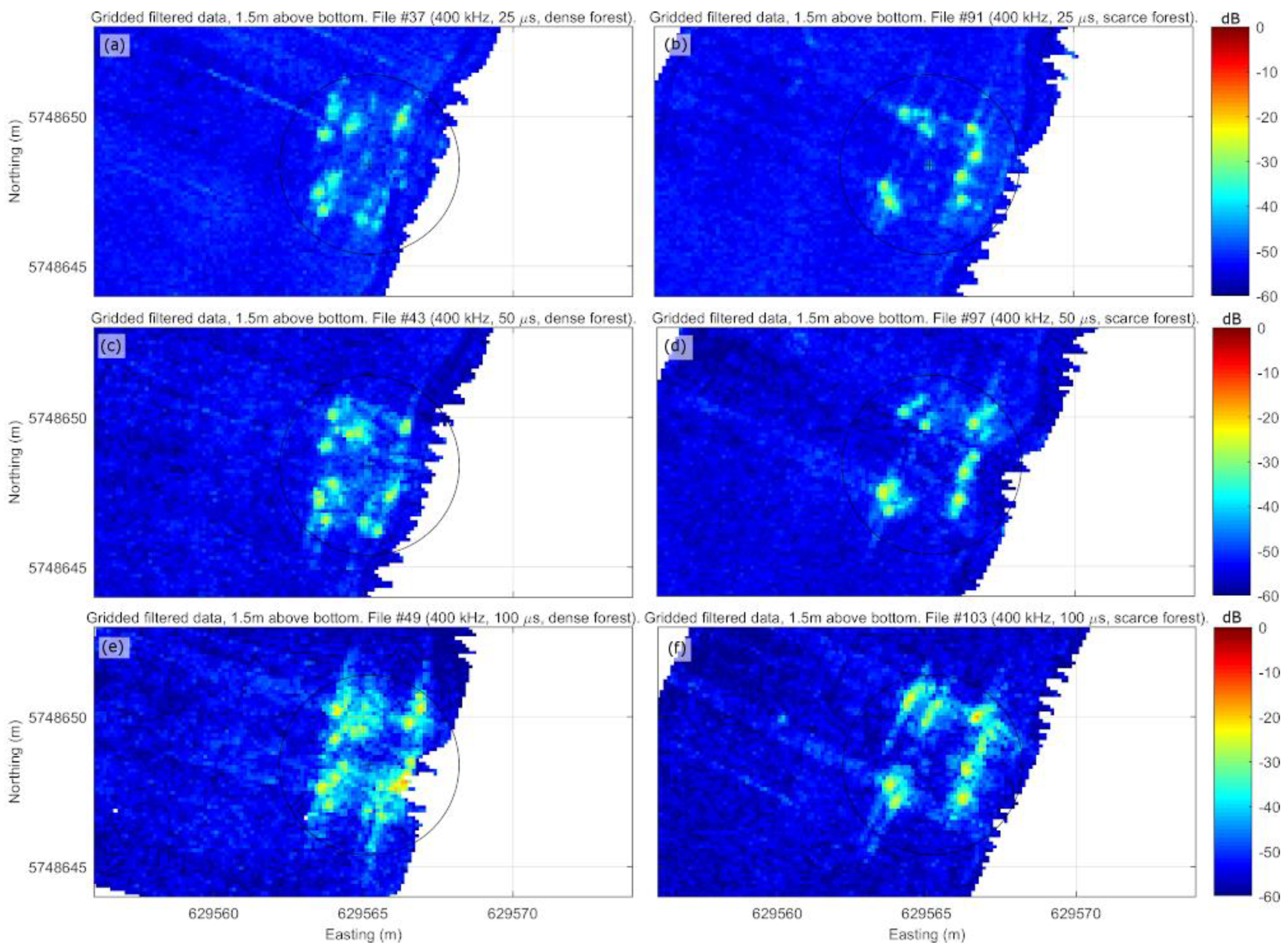
3.1. Water-column Data Examples and Effects of the SRSN Filter
3.2. Comparing Dense Against Thin Patch Results in Horizontal Slice View
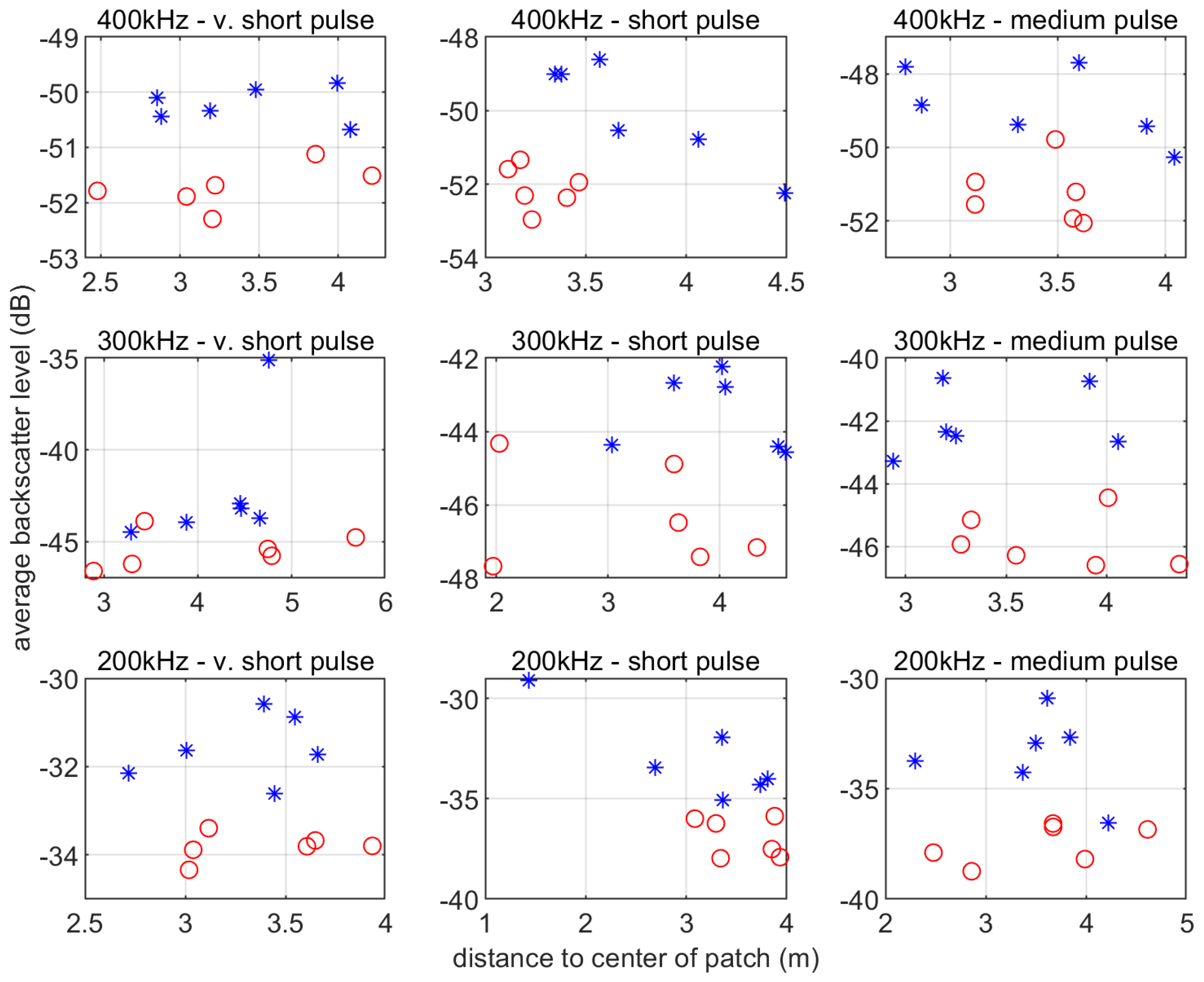
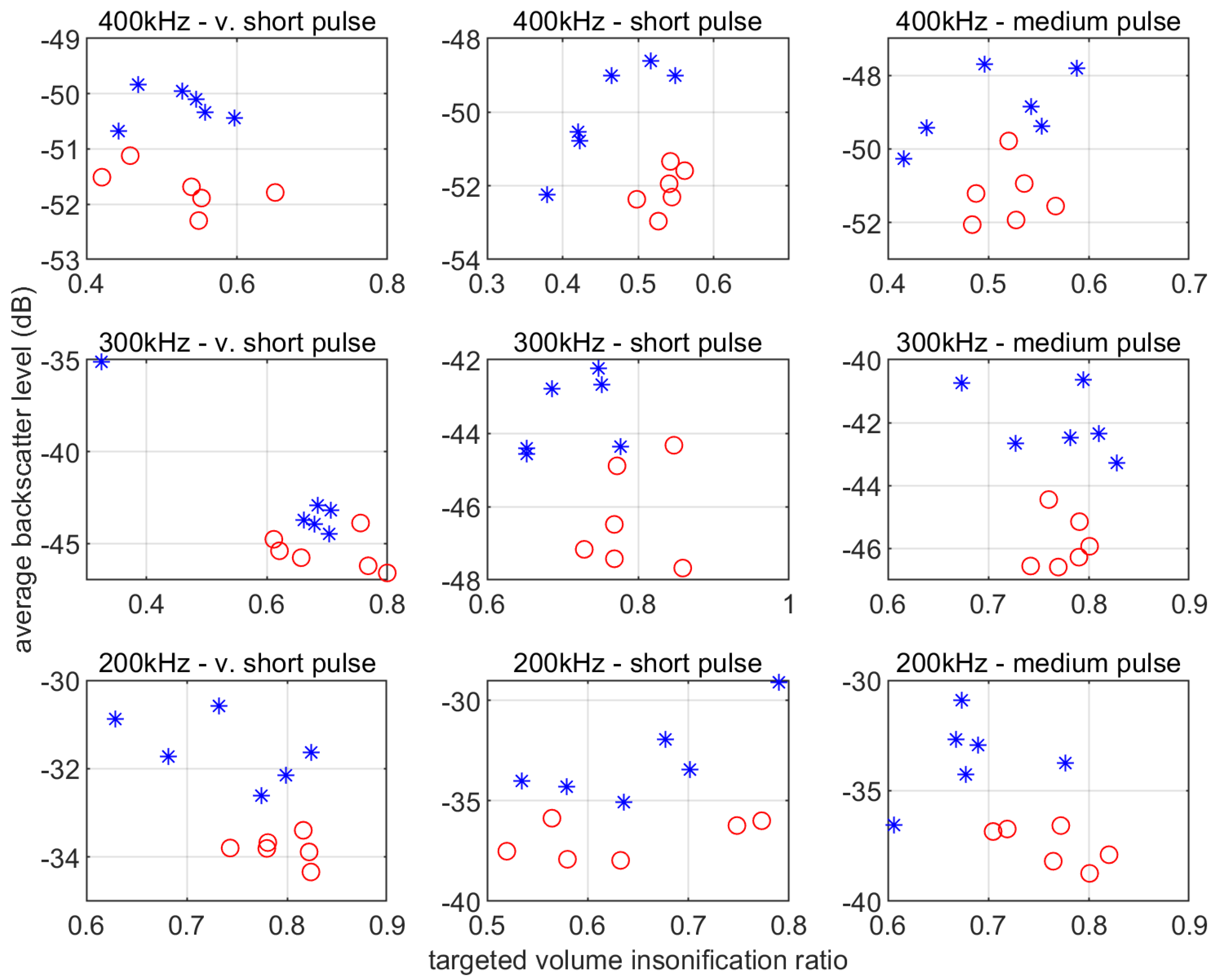
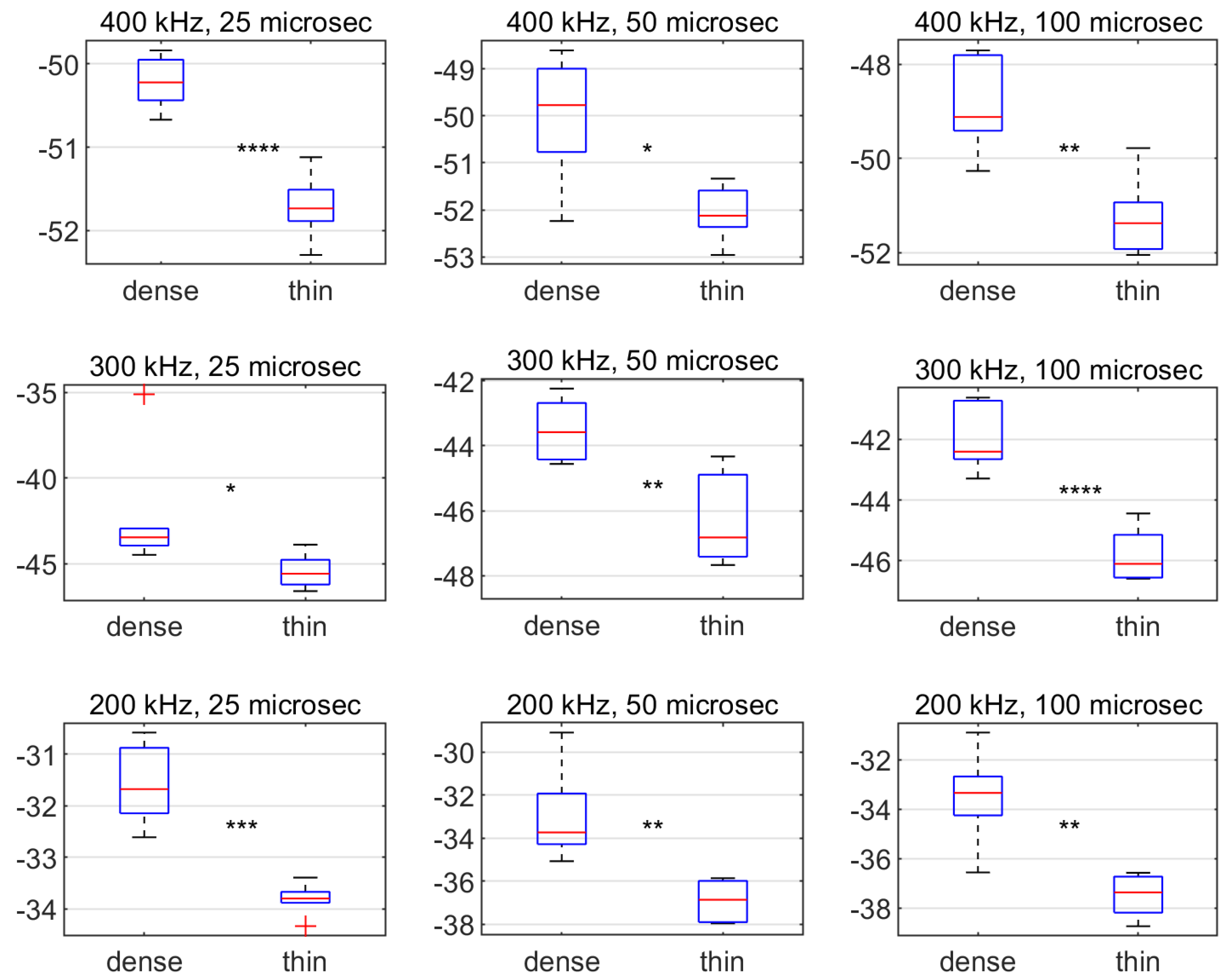
3.3. Average Backscatter Level in Target Volume
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mayer, L.A. Frontiers in Seafloor Mapping and Visualization. Mar. Geophys. Res. 2006, 27, 7–17. [Google Scholar] [CrossRef]
- Lurton, X.; Lamarche, G. Backscatter Measurements by Seafloor-Mapping Sonars; Guidelines and Recommendations. Technical Report. 2015. Available online: https://niwa.co.nz/static/BWSG_REPORT_MAY2015_web.pdf (accessed on 24 February 2020).
- Colbo, K.; Ross, T.; Brown, C.J.; Weber, T. A review of oceanographic applications of water column data from multibeam echosounders. Estuar. Coast. Shelf Sci. 2014, 145, 41–56. [Google Scholar] [CrossRef]
- Dayton, P.K. Ecology of Kelp Communities. Ann. Rev. Ecol. Syst. 1985, 16, 215–245. [Google Scholar] [CrossRef]
- Steneck, R.S.; Graham, M.H.; Bourque, B.J.; Corbett, D.; Erlandson, J.M.; Estes, J.A.; Tegner, M.J. Kelp forest ecosystems: Biodiversity, stability, resilience and future. Environ. Conserv. 2002, 29, 436–459. [Google Scholar] [CrossRef]
- Young, M.; Ierodiaconou, D.; Womersley, T. Forests of the sea: Predictive habitat modelling to assess the abundance of canopy forming kelp forests on temperate reefs. Remote Sens. Environ. 2015, 170, 178–187. [Google Scholar] [CrossRef]
- Wernberg, T.; Bennett, S.; Babcock, R.C.; de Bettignies, T.; Cure, K.; Depczynski, M.; Dufois, F.; Fromont, J.; Fulton, C.J.; Hovey, R.K.; et al. Climate-driven regime shift of a temperate marine ecosystem. Science 2016, 353, 169–172. [Google Scholar] [CrossRef]
- Cavanaugh, K.C.; Siegel, D.A.; Reed, D.C.; Dennison, P.E. Environmental controls of giant-kelp biomass in the Santa Barbara Channel, California. Mar. Ecol. Prog. Ser. 2011, 429, 1–17. [Google Scholar] [CrossRef]
- Edwards, M.S. Estimating scale-dependency in disturbance impacts: El Niños and giant kelp forests in the northeast Pacific. Oecologia 2004, 138, 436–447. [Google Scholar] [CrossRef]
- Edyvane, K. Conservation, Monitoring & Recovery of Threatened Giant Kelp (Macrocystis pyrifera) Beds in Tasmania—Final Report; Department of Primary Industries, Water and Environment: Tasmania, Australia, 2003. [Google Scholar]
- Deysher, L.E. Evaluation of remote sensing techniques for monitoring giant kelp populations. Hydrobiologia 1993, 260, 307–312. [Google Scholar] [CrossRef]
- Nijland, W.; Reshitnyk, L.; Rubidge, E. Satellite remote sensing of canopy-forming kelp on a complex coastline: A novel procedure using the Landsat image archive. Remote Sens. Environ. 2019, 220, 41–50. [Google Scholar] [CrossRef]
- Schroeder, S.B.; Boyer, L.; Juanes, F.; Costa, M. Spatial and temporal persistence of nearshore kelp beds on the west coast of British Columbia, Canada using satellite remote sensing. Remote Sens. Ecol. Conserv. 2019. [Google Scholar] [CrossRef]
- Bell, T.W.; Allen, J.G.; Cavanaugh, K.C.; Siegel, D.A. Three decades of variability in California’s giant kelp forests from the Landsat satellites. Remote Sens. Environ. 2020, 238, 110811. [Google Scholar] [CrossRef]
- Stekoll, M.S.; Deysher, L.E.; Hess, M. A remote sensing approach to estimating harvestable kelp biomass. J. Appl. Phycol. 2006, 18, 323–334. [Google Scholar] [CrossRef]
- Tait, L.; Bind, J.; Charan-Dixon, H.; Hawes, I.; Pirker, J.; Schiel, D. Unmanned Aerial Vehicles (UAVs) for Monitoring Macroalgal Biodiversity: Comparison of RGB and Multispectral Imaging Sensors for Biodiversity Assessments. Remote Sens. 2019, 11, 2332. [Google Scholar] [CrossRef]
- Bicknell, A.W.J.; Godley, B.J.; Sheehan, E.V.; Votier, S.C.; Witt, M.J. Camera technology for monitoring marine biodiversity and human impact. Front. Ecol. Environ. 2016, 14, 424–432. [Google Scholar] [CrossRef]
- Bennion, M.; Fisher, J.; Yesson, C.; Brodie, J. Remote Sensing of Kelp (Laminariales, Ochrophyta): Monitoring Tools and Implications for Wild Harvesting. Rev. Fish. Sci. Aquac. 2019, 27, 127–141. [Google Scholar] [CrossRef]
- Méléder, V.; Populus, J.; Guillaumont, B.; Perrot, T.; Mouquet, P. Predictive modelling of seabed habitats: Case study of subtidal kelp forests on the coast of Brittany, France. Mar. Biol. 2010, 157, 1525–1541. [Google Scholar] [CrossRef]
- Minami, K.; Yasuma, H.; Tojo, N.; Fukui, S.-I.; Ito, Y.; Nobetsu, T.; Miyashita, K. Estimation of kelp forest, Laminaria spp., distributions in coastal waters of the Shiretoko Peninsula, Hokkaido, Japan, using echosounder and geostatistical analysis. Fish. Sci. 2010, 76, 729–736. [Google Scholar] [CrossRef]
- Riegl, B.M.; Moyer, R.P.; Morris, L.J.; Virnstein, R.W.; Purkis, S.J. Distribution and seasonal biomass of drift macroalgae in the Indian River Lagoon (Florida, USA) estimated with acoustic seafloor classification (QTCView, Echoplus). J. Exp. Mar. Biol. Ecol. 2005, 326, 89–104. [Google Scholar] [CrossRef]
- Mielck, F.; Bartsch, I.; Hass, H.C.; Wölfl, A.-C.; Bürk, D.; Betzler, C. Predicting spatial kelp abundance in shallow coastal waters using the acoustic ground discrimination system RoxAnn. Estuar. Coast. Shelf Sci. 2014, 143, 1–11. [Google Scholar] [CrossRef]
- Parnell, P.E. The effects of seascape pattern on algal patch structure, sea urchin barrens, and ecological processes. J. Exp. Mar. Biol. Ecol. 2015, 465, 64–76. [Google Scholar] [CrossRef]
- Shao, H.; Minami, K.; Shirakawa, H.; Maeda, T.; Ohmura, T.; Fujikawa, Y.; Yotsukura, N.; Nakaoka, M.; Miyashita, K. Verification of echosounder measurements of thickness and spatial distribution of kelp forests. J. Mar. Sci. Technol. 2017, 25, 343–351. [Google Scholar] [CrossRef]
- Demer, D.A.; Berger, L.; Bernasconi, M.; Bethke, E.; Boswell, K.; Chu, D.; Domokos, R.; Dunford, A.; Fassler, S.; Gauthier, S.; et al. Calibration of Acoustic Instruments; ICES Cooperative Research Report No. 326; International Council for the Exploration of the Sea (ICES): Copenhagen, Denmark, 2015; 133p. [Google Scholar] [CrossRef]
- Simmonds, J.; MacLennan, D. Fisheries Acoustics Theory and Practice, 2nd ed.; Pitcher, T.J., Ed.; Blackwell Publishing: Oxford, UK, 2005; ISBN 9780632059942. [Google Scholar]
- Wilson, C.J.; Wilson, P.S.; Dunton, K.H. Assessing the low frequency acoustic characteristics of Macrocystis pyrifera, Egregia menziessi, and Laminaria solidungula. J. Acoust. Soc. Am. 2013, 133, 3819–3826. [Google Scholar] [CrossRef] [PubMed]
- Randall, J.; Hermand, J.-P.; Ernould, M.-E.; Ross, J.; Johnson, C. Measurement of acoustic material properties of macroalgae (Ecklonia radiata). J. Exp. Mar. Biol. Ecol. 2014, 461, 430–440. [Google Scholar] [CrossRef]
- Hermand, J.-P.; Randall, J. A Monte Carlo experiment for measuring acoustic properties of macroalgae living tissue. J. Acoust. Soc. Am. 2015, 137, EL314–EL319. [Google Scholar] [CrossRef] [PubMed]
- Shao, H.; Minami, K.; Shirakawa, H.; Kawauchi, Y.; Matsukura, R.; Tomiyasu, M.; Miyashita, K. Target strength of a common kelp species, Saccharina japonica, measured using a quantitative echosounder in an indoor seawater tank. Fish. Res. 2019, 214, 110–116. [Google Scholar] [CrossRef]
- Komatsu, T.; Igarashi, C.; Tatsukawa, K.; Sultana, S.; Matsuoka, Y.; Harada, S. Use of multi-beam sonar to map seagrass beds in Otsuchi Bay on the Sanriku Coast of Japan. Aquat. Liv. Resour. 2003, 16, 223–230. [Google Scholar] [CrossRef]
- Di Maida, G.; Tomasello, A.; Luzzu, F.; Scannavino, A.; Pirrotta, M.; Orestano, C.; Calvo, S. Discriminating between Posidonia oceanica meadows and sand substratum using multibeam sonar. ICES J. Mar. Sci. 2011, 68, 12–19. [Google Scholar] [CrossRef]
- McGonigle, C.; Grabowski, J.H.; Brown, C.J.; Weber, T.C.; Quinn, R. Detection of deep water benthic macroalgae using image-based classification techniques on multibeam backscatter at Cashes Ledge, Gulf of Maine, USA. Estuar. Coast. Shelf Sci. 2011, 91, 87–101. [Google Scholar] [CrossRef]
- Brown, C.J.; Smith, S.J.; Lawton, P.; Anderson, J.T. Benthic habitat mapping: A review of progress towards improved understanding of the spatial ecology of the seafloor using acoustic techniques. Estuar. Coast. Shelf Sci. 2011, 92, 502–520. [Google Scholar] [CrossRef]
- Che Hasan, R.; Ierodiaconou, D.; Laurenson, L.; Schimel, A. Integrating Multibeam Backscatter Angular Response, Mosaic and Bathymetry Data for Benthic Habitat Mapping. PLoS ONE 2014, 9, e97339. [Google Scholar] [CrossRef] [PubMed]
- Diesing, M.; Stephens, D. A multi-model ensemble approach to seabed mapping. J. Sea Res. 2015, 100, 62–69. [Google Scholar] [CrossRef]
- Ierodiaconou, D.; Schimel, A.C.G.; Kennedy, D.; Monk, J.; Gaylard, G.; Young, M.; Diesing, M.; Rattray, A. Combining pixel and object based image analysis of ultra-high resolution multibeam bathymetry and backscatter for habitat mapping in shallow marine waters. Mar. Geophys. Res. 2018, 39, 271–288. [Google Scholar] [CrossRef]
- Clarke, J.H. Applications of multibeam water column imaging for hydrographic survey. Hydrogr. J. 2006, 120, 3. [Google Scholar]
- Lurton, X. An Introduction to Underwater Acoustics: Principles and Applications; Springer: London, UK, 2002. [Google Scholar]
- Kruss, A.; Blondel, P.; Tegowski, J.; Wiktor, J.; Tatarek, A. Estimation of macrophytes using single-beam and multibeam echosounding for environmental monitoring of arctic fjords (Kongsfjord, West Svalbard Island). In Proceedings of the 9th European Conference on Underwater Acoustics, ECUA 2008, Paris, France, 29 June–4 July 2008. [Google Scholar]
- Kruss, A.; Blondel, P.; Tegowski, J. Acoustic properties of macrophytes: Comparison of single-beam and multibeam imaging with modeling results. In Proceedings of the 11th European Conference on Underwater Acoustics, ECUA 2012, Edinburgh, UK, 1–6 July 2012; Institute of Acoustics: St. Albans, UK, 2012; pp. 168–175. [Google Scholar]
- Kruss, A.; Tegowski, J.; Tatarek, A.; Wiktor, J.; Blondel, P. Spatial distribution of macroalgae along the shores of Kongsfjorden (West Spitsbergen) using acoustic imaging. Pol. Polar Res. 2017, 38, 205–229. [Google Scholar] [CrossRef][Green Version]
- Kennedy, D.M.; Ierodiaconou, D.; Schimel, A.C.G. Granitic coastal geomorphology: Applying integrated terrestrial and bathymetric LiDAR with multibeam sonar to examine coastal landscape evolution. Earth Surf. Process. Landf. 2014, 39, 1663–1674. [Google Scholar] [CrossRef]
- Schimel, A.C.G.; Ierodiaconou, D.; Hulands, L.; Kennedy, D.M. Accounting for uncertainty in volumes of seabed change measured with repeat multibeam sonar surveys. Cont. Shelf Res. 2015, 111, 52–68. [Google Scholar] [CrossRef]
- Schimel, A.C.G.; Healy, T.R.; McComb, P.; Immenga, D. Comparison of a Self-Processed EM3000 Multibeam Echosounder Dataset with a QTC View Habitat Mapping and a Sidescan Sonar Imagery, Tamaki Strait, New Zealand. J. Coast. Res. 2010, 26, 714–725. [Google Scholar] [CrossRef]
- CoFFee—An Open-Source Matlab Toolbox for Multibeam Sonar Data Processing. Available online: https://github.com/alexschimel/CoFFee (accessed on 24 February 2020).
- Kongsberg. EM Series. Multibeam Echo Sounders. Datagram Formats; 850-160692/W; Kongsberg: Kongsberg, Norway, 2018; 183p. [Google Scholar]
- Nau, A.W.; Lucieer, V.; Schimel, A.C.G. Modeling the along-track sidelobe interference artifact in multibeam sonar water-column data. In Proceedings of the OCEANS 2018 Charleston, Charleston, SC, USA, 22–25 October 2018. [Google Scholar] [CrossRef]
- Kongsberg. EM 2040C Multibeam Echo Sounder; 369468/G; Kongsberg: Kongsberg, Norway, 2017. [Google Scholar]
- Schimel, A.C.G.; Beaudoin, J.; Parnum, I.M.; Le Bas, T.; Schmidt, V.; Keith, G.; Ierodiaconou, D. Multibeam sonar backscatter data processing. Mar. Geophys. Res. 2018, 39, 121–137. [Google Scholar] [CrossRef]
- Rattray, A.; Ierodiaconou, D.; Monk, J.; Laurenson, L.; Kennedy, P. Quantification of Spatial and Thematic Uncertainty in the Application of Underwater Video for Benthic Habitat Mapping. Mar. Geod. 2014, 37, 315–336. [Google Scholar] [CrossRef]
- Urban, P.; Köser, K.; Greinert, J. Processing of multibeam water column image data for automated bubble/seep detection and repeated mapping. Limnol. Oceanogr. Methods 2017, 15, 1–21. [Google Scholar] [CrossRef]
- de Moustier, C. OS-CFAR detection of targets in the water column and on the seafloor with a multibeam echosounder. In Proceedings of the OCEANS 13 MTS, San Diego, CA, USA, 23–26 September 2013. [Google Scholar] [CrossRef]
- Multibeam Background Removal. Echoview Help File 10.0.38 for Echoview 10.0.257. 2019. Available online: https://support.echoview.com/WebHelp/Windows_and_Dialog_Boxes/Dialog_Boxes/Variable_properties_dialog_box/Operator_pages/Multibeam_Background_Removal.htm (accessed on 24 February 2020).
- Parsons, M.J.G.; Parnum, I.M.; McCauley, R.D. Visualizing Samsonfish (Seriola hippos) with a Reson 7125 Seabat multibeam sonar. ICES J. Mar. Sci. 2013, 70, 665–674. [Google Scholar] [CrossRef]
- Dunlop, K.M.; Jarvis, T.; Benoit-Bird, K.J.; Waluk, C.M.; Caress, D.W.; Thomas, H.; Smith, K.L., Jr. Detection and characterisation of deep-sea benthopelagic animals from an autonomous underwater vehicle with a multibeam echosounder: A proof of concept and description of data-processing methods. Deep Sea Res. Part I Oceanogr. Res. Pap. 2018, 134, 64–79. [Google Scholar] [CrossRef]

| Tag Number | Length (m) | Weight (kg) | Dense Forest exp. | Thin Forest exp. |
|---|---|---|---|---|
| 33 | 9.8 | 21.6 | X | X |
| 45 | 7.6 | 20.9 | X | |
| 46 | 9.6 | 17.1 | X | |
| 47 | 11 | 22.6 | X | X |
| 48 | 8.2 | 10.4 | X | |
| 49 | 11.3 | 13.8 | X | |
| 54 | 9.4 | 17.7 | X | |
| 55 | 10.4 | 9.2 | X | X |
| 56 | 9.4 | 14.5 | X | X |
| 58 | 7.55 | 10 | X | X |
| 61 | 10.4 | 19 | X | X |
| 62 | 9.1 | 11.3 | X | |
| 63 | 10.9 | 8.9 | X | X |
| 64 | 9.6 | 12.3 | X |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schimel, A.C.G.; Brown, C.J.; Ierodiaconou, D. Automated Filtering of Multibeam Water-Column Data to Detect Relative Abundance of Giant Kelp (Macrocystis pyrifera). Remote Sens. 2020, 12, 1371. https://doi.org/10.3390/rs12091371
Schimel ACG, Brown CJ, Ierodiaconou D. Automated Filtering of Multibeam Water-Column Data to Detect Relative Abundance of Giant Kelp (Macrocystis pyrifera). Remote Sensing. 2020; 12(9):1371. https://doi.org/10.3390/rs12091371
Chicago/Turabian StyleSchimel, Alexandre C. G., Craig J. Brown, and Daniel Ierodiaconou. 2020. "Automated Filtering of Multibeam Water-Column Data to Detect Relative Abundance of Giant Kelp (Macrocystis pyrifera)" Remote Sensing 12, no. 9: 1371. https://doi.org/10.3390/rs12091371
APA StyleSchimel, A. C. G., Brown, C. J., & Ierodiaconou, D. (2020). Automated Filtering of Multibeam Water-Column Data to Detect Relative Abundance of Giant Kelp (Macrocystis pyrifera). Remote Sensing, 12(9), 1371. https://doi.org/10.3390/rs12091371







