Abstract
The morphometric characteristics of the Kalvārī basin were analyzed to prioritize sub-basins based on their susceptibility to erosion by water using a remote sensing-based data and a GIS. The morphometric parameters (MPs)—linear, relief, and shape—of the drainage network were calculated using data from the Advanced Land-observing Satellite (ALOS) phased-array L-type synthetic-aperture radar (PALSAR) digital elevation model (DEM) with a spatial resolution of 12.5 m. Interferometric synthetic aperture radar (InSAR) was used to generate the DEM. These parameters revealed the network’s texture, morpho-tectonics, geometry, and relief characteristics. A complex proportional assessment of alternatives (COPRAS)-analytical hierarchy process (AHP) novel-ensemble multiple-criteria decision-making (MCDM) model was used to rank sub-basins and to identify the major MPs that significantly influence erosion landforms of the Kalvārī drainage basin. The results show that in evolutionary terms this is a youthful landscape. Rejuvenation has influenced the erosional development of the basin, but lithology and relief, structure, and tectonics have determined the drainage patterns of the catchment. Results of the AHP model indicate that slope and drainage density influence erosion in the study area. The COPRAS-AHP ensemble model results reveal that sub-basin 1 is the most susceptible to soil erosion (SE) and that sub-basin 5 is least susceptible. The ensemble model was compared to the two individual models using the Spearman correlation coefficient test (SCCT) and the Kendall Tau correlation coefficient test (KTCCT). To evaluate the prediction accuracy of the ensemble model, its results were compared to results generated by the modified Pacific Southwest Inter-Agency Committee (MPSIAC) model in each sub-basin. Based on SCCT and KTCCT, the ensemble model was better at ranking sub-basins than the MPSIAC model, which indicated that sub-basins 1 and 4, with mean sediment yields of 943.7 and 456.3 , respectively, have the highest and lowest SE susceptibility in the study area. The sensitivity analysis revealed that the most sensitive parameters of the MPSIAC model are slope (R2 = 0.96), followed by runoff (R2 = 0.95). The MPSIAC shows that the ensemble model has a high prediction accuracy. The method tested here has been shown to be an effective tool to improve sustainable soil management.
1. Introduction
Soil erosion (SE) threatens sustainable development [1]. More than three hundred years is needed to form a centimeter of soil [2], therefore the prevention of SE is vital to protect valuable resources [3]. In arid and semiarid regions, SE destroys soil fertility and threatens agriculture [4]. Defoliation, flooding, reduced effectiveness of dams, increasing economic losses, desertification, and land use changes are major consequences of SE [5]. The global rate of annual SE is approximated to be 75 billion tons [6]. Iran loses more than two billion tons every year, approximately three times the rates of other Asian countries. Approximately 125 million of the 165 million ha of the country experiences erosion [7]. This is roughly 75% of the entire country and 60% of Iran’s agricultural land. Iran’s average erosion is 30–32 ton/ha/year, which is 4.3 times the global average [7]. Economic losses caused by SE in Iran have been estimated to be 10 trillion rial [8]. Therefore, SE management and protection in Iran is urgently needed, in line with the United Nations Sustainable Development Goals [9]. This study prepared a SE risk map using effective factors to predict locations that are more likely to be SE “hot spots.”
A basin is the developmental unit used to effectively manage resources sustainably [10]. It is a natural hydrological feature within which runoff is directed into collecting channels, streams, or rivers [11]. The characteristics and conditions of a basin or drainage basin determine the development of the landforms within it. Therefore, identification of the most important characteristics of a basin is integral to understanding its geomorphology [12]. Basin management planning can strive to control losses from SE in a basin [13]. Although there are several factors that influence SE, the major agent is water. SE is not a new problem, but it has become common and is worsening in Iran. It is particularly visible in the Kalvārī river basin.
Soil, geomorphology, hydrology, and landscapes are intimately linked. Measurement and analysis of Earth’s surface through geomorphometry is undertaken to understand the relationships between the sizes and shapes of a region’s features [10]. SE, runoff, the evolution of rivers, sedimentation, and drainage geometry are reflections of hydrological and geomorphic processes, and are ultimately assessable using morphometry [10]. Therefore, the morphometry of a basin can explain its hydrological behaviors. The basin is the unit of morphometric analysis, which is a technique introduced by Horton [14,15] and elaborated upon by Strahler [16,17,18], Miller [19], and Schumm [20]. Together, they provided the foundations for the field of quantitative fluvial geomorphology [21].
Because resource development planning is generally conducted at the watershed scale, it is critical to prioritize management of natural resources for sustainable development [11]. Prioritization for soil or water conservation can be improved by quantitative analyses of morphometric watershed parameters [10]. Morphometric analysis quantitatively describes drainage systems to understand landform- and soil-development processes as well as erosional characteristics [22]. Morphometry is the quantitative measurement of the shapes and dimensions of Earth’s landforms. Areas, volumes, elevations, slopes, profiles, and textures of the surface are the characteristics of utmost interest [22]. River basin morphometry reflects the hydrological and geomorphic responses of runoff, SE, flooding, drought, sedimentation, fluvial bifurcation, the flow characteristics and flow volumes of drainages and rivers, and the capacities and sustainability of reservoirs within a basin. Conventional studies have explored the relationships between the properties of drainage networks and other influences like climate, relief, lithology, structure, and tectonics to interpret morphometrics [23,24,25]. The tectonics of river basins have been examined for links to the geomorphological processes that shape drainages [26]. Recently, stream network morphometry has been used more often to assess water, soil, and hazards in developing countries [27,28,29,30].
Geospatial analytical techniques (geographic information systems (GIS) and remote sensing (RS)), and multi-criteria decision-making models (MCDM) have enhanced quantitative assessments of drainage networks, thematic mapping of morphometry, and applied morphometric analyses [31,32,33,34,35,36]. Furthermore, other software designed to quantify and calculate linear, areal, shape, and relief MPs have also advanced the sophistication of morphometrics [37,38]. Comparisons of conventionally and manually collected data to automated geospatial methods have demonstrated that modern technologies are powerful and cost-effective for better management and processing of data and for creating maps for a variety of applications [39,40].
Digital elevation models (DEMs) are a standard source of data that can be used to discern the mechanisms behind geomorphological processes. DEMs are developed using several data sources. Ground surveys, photogrammetry, optical RS, radar, and lidar are the principal data acquisition methods. Synthetic aperture radar (SAR) data are analyzed using interferometry and radargrammetry, which detect phase discrepancies in each pixel. Elevation change is determined stereoscopically [41]. Highly detailed models of elevations are developed by comparing precise measurements of phase-shifts of reflected wavelengths from Earth’s surface using interferometric synthetic aperture radar (InSAR) [42]. Numerous studies have examined the use of methods to analyze radar data to produce DEMs [41]. First-order streams (Horton’s “fingertip” streams) can be delineated precisely using DEMs. GIS and RS can be used to measure and calculate drainage-basin MPs economically and can enable efficient analysis of large amounts of spatial information [43,44,45].
Few studies have used morphometric analysis of SE to prioritize sub-watersheds. Altaf and Meraj [46] combined an Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) DEM with 14 MPs in a multi-criteria analysis (MCA) to assess the susceptibility of a watershed in the western Himalaya to SE. They found that three sub-watersheds could be regarded as very high priority (highly susceptible to SE) for management. Ahmad Rather et al. [47] coupled 13 morphometric, land use, and slope parameters and data from a Shuttle-Radar Topography Mission (SRTM) DEM in an MCA to estimate SE susceptibility in the Jhelum basin of Kashmir. Gajbhiye et al. [13] used an SRTM DEM and morphometric analysis on 14 sub-watersheds of the Manot River catchment (a tributary of the Narmada River) to discern SE susceptibility. One sub-watershed had the lowest compound parameter value and was therefore most likely to experience the greatest amount of SE. This study combines a novel MCDM-based approach (the complex proportional assessment of alternatives (COPRAS)-analytical hierarchy process (AHP)) with MPs to prioritize sub-basins by their susceptibility to SE. SE was mapped: (1) to model non-quantitative parameters; (2) to devise a method to compare different types of variables and to handle data at different scales; (3) to eliminate strict assumptions behind the study; (4) to fill a gap in the scholarship wherein only a few studies have employed MCDM models to assess SE susceptibility; and (5) to undertake a comprehensive study of the capabilities of COPRAS-AHP ensemble models for SE susceptibility analysis. The study area is the Kalvārī Basin in Iran, an area that experiences high rates of SE. The main objectives of this study were: (1) to analyze the MPs of the Kalvārī Basin using GIS, RS, and a Phased-Array type L-band Synthetic Aperture Radar (PALSAR) DEM (spatial resolution 12.5 m); (2) to prioritize sub-basins and to identify the major MPs that influence SE in the Kalvārī Basin using the COPRAS-AHP novel ensemble MCDM model; and (3) to identify the sub-basin landscape parameters that dictate the SE potential of fluvial forces and SE susceptibility throughout the region. The results will provide better SE management and will enhance other environmental activities like land use planning, hazard management, and water conservation. This approach to morphometric analysis could be transferred to other, similar highland basins in other arid regions.
2. Materials and Methods
2.1. Study Area
The Kalvārī Basin, with an area of 70.21 km2, is approximately 187 km southwest of Shahrekord in Chaharmahal va Bakhtiari Province, Iran. It is located between 31˚32′33” and 31˚37′31”N and 50˚29′23” and 50˚38′E (Figure 1). The highest elevation is found in the western part of the basin at 1999 m above sea level (asl) and the lowest is in the southwestern part of the basin at 1100 m asl. Mean annual precipitation and temperature in the study area are 295 mm and 20.6˚C respectively [48]. The geology of the study area varies from Paleocene limestone, shale, and marl to Quaternary deposits, including low-level piedmont fan and valley-terrace deposits [49]. The Asmari Calcareous Formation, the Bakhtiari Clastic Formation, Quaternary sediments, and the Gachsaran Evaporite Formation are the most important formations in the study area [49]. The area’s surface is covered with rock outcrops and inceptisols [50]. The watershed includes several macro-faults, formed mainly by shale and phylite contact with granite and re-crystallized limestone formations. The main soil texture is silt loam covering the hills. Runoff height in the Kalvārī Basin is 109.8 mm. The average slope of the basin is 22.4˚. Land use/land cover classes in the study area include orchard (0.07%), low forest (23.05%), agriculture-dry farming (0.58%), dry farming (31.06%), moderate rangeland (0.009%), moderate forest (10.94%), and poor rangeland (34.27%).
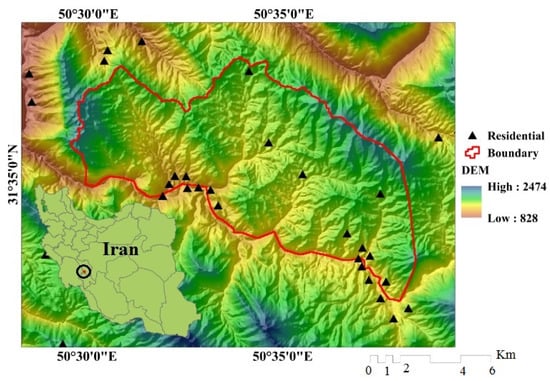
Figure 1.
Location of the study area in Iran.
2.2. Methodology
There are seven steps to this method (Figure 2), which are: (1) determine the boundaries of 11 sub-basins using topographic maps (1:50,000 scale and 20 m contours) and PALSAR DEM (12.5 m resolution); (2) extract basic MPs (basin area, basin length, numbers and lengths of streams of each order, basin perimeter, and bifurcation ratio) of the Kalvārī Basin from drainage networks, sub-basin polygons, and an elevation model generated from the PALSAR DEM; (3) extract linear, shape, and relief factors, including mean bifurcation ratio (Rbm), drainage density (Dd), stream frequency (Fu), texture ratio (T), length of overland flow (Lo), infiltration number (If), constant of channel maintenance (C), form factor (Rf), shape factor (Bs), elongation ratio (Re), compactness coefficient (Cc), circularity ratio (Rc), ruggedness number (Rn), basin relief (Bh), relief ratio (Rh), and slope (S) from the basic parameters and formula (Table 1); (4) apply the AHP model to determine the relative importance of the morphometric factors in SE; (5) calculate the relative weight of each alternative (for the sub-basins) and prioritize them using the COPRAS model; (6) prepare an SE susceptibility map using the AHP-COPRAS ensemble model; and (7) validate the results using the MPSIAC model and non-parametric correlation tests such as the Spearman correlation coefficient test (SCCT) and the Kendall Tau correlation coefficient test (KTCCT).
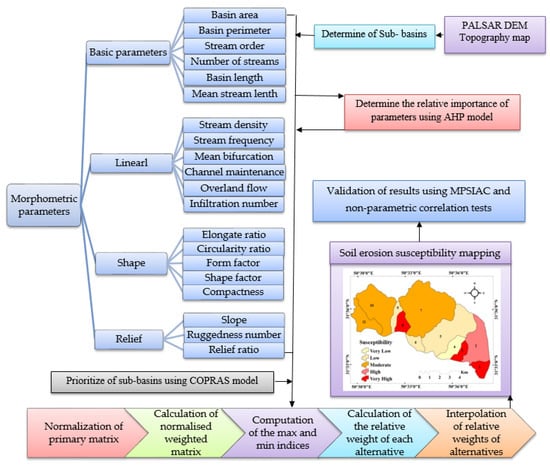
Figure 2.
Flowchart of research in the study area.

Table 1.
Computation of basic, linear, shape, and relief morphometric parameters.
Morphometric (elevation and slope) and hydrologic (drainage networks) parameters were estimated using an ALOS PALSAR DEM (12.5 m resolution). Detailed descriptions of the methodology used to produce the ALOS PALSAR DEM using InSAR are discussed in [51,52]. The key step in DEM generation is the transformation of phase-change measurements to elevations [53]. InSAR was developed by Graham [54]. In terms of economics, efficiency, and resolution, InSAR is the best DEM production technique [55]. InSAR calculates phase changes from two radar image pairs taken at different times and reveals changes in the surface quantitatively and qualitatively [56]. There are 6 steps in InSAR generation of DEMs from PALSAR data [52] (Figure 3), which are: (1) register radar images—in this study, two images (Slave (2008/07/11) and Master (2010/08/16)) were entered chronologically; (2) produce interferogram—the images iSRTMn SARScape4.8 are converted into single-look complex (SLC) format with the following settings, TB (745 days), SB (114.8 m), and critical baseline (2623.5 m); (3) remove flat effect—the DEM derived from the Shuttle Radar Topography Mission (SRTM) and its Doppler Orbitography and Radiopositioning Integrated by Satellite (DORIS) files are used to remove the topographic effect; (4) filter noise—adaptive filters are used to eliminate the effect of noise from the interferogram, as they may reduce its quality (this step will also produce a coherent image, coherence indicates interferogram quality and should be less than 0.5; the Goldstein filter was used in this study and the coherence value of the image was 0.20); (5) unwrap phase—region-growing and minimum cost-flow algorithms are the most common methods for phase correction, a region-growing algorithm was used in this study; and (6) convert phase to height—the ALOS PALSAR DEM is created by phase-to-height conversion, the PALSAR DEM of the study area was produced with the mosaicking tools in ENVI v4.8.
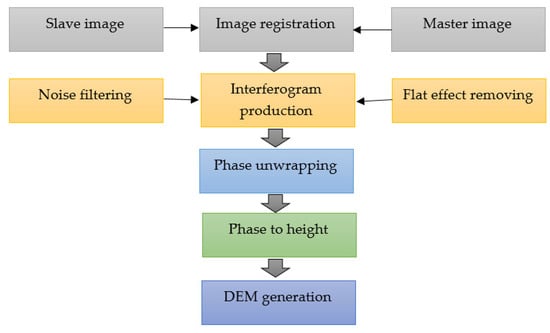
Figure 3.
Interferometric synthetic aperture radar (InSAR) data-processing procedure for digital elevation model (DEM) production.
An ALOS PALSAR DEM enhanced reproduction of the complex topography of the study area to improve approximations of morphometric and hydrological factors [57,58]. The vertical accuracy of the ALOS DEM was assessed by ground-truthing the model’s elevation values in ArcGIS 10.5 at selected 230 ground control points (GCPs) (Figure 4), following procedures used in [59]. The root mean square error (RMSE) of DEM generated based on comparisons with GCPs was 1.2 m.
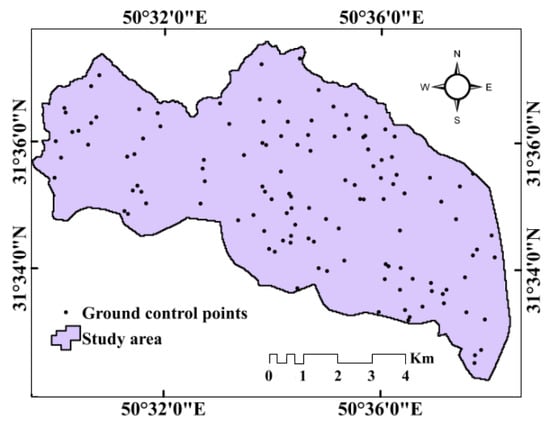
Figure 4.
Ground control points in the study area.
The boundaries of the sub-basins (Figure 5) were extracted by determining the pour point, the location where water drained from the basin flows into the main river. For drainage network extraction, the Arc Hydro package was used. Compared to the manual approach, this package provides a rational, effective, and consistent algorithm [46]. Generating the drainage network using Arc Hydro has been explained by Ahmad Rather et al. [47]. To do this, DEM sinks were specified and filled to designate the flow direction and locations of accumulation. Stream networks in the sub-basin were defined according to the cumulative number of upstream cells draining into each cell. A threshold of greater than 500 was used to extract the drainage; this critical threshold is the minimum upstream area necessary to produce a stream. The areas and perimeters of the sub-basins were extracted by computing the geometry of the sub-basin polygons. Strahler’s scheme was used for stream ordering [16].
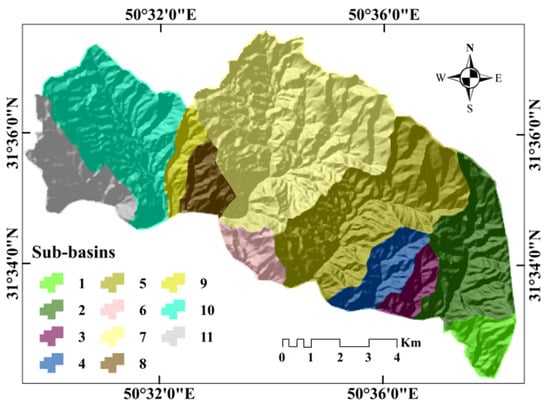
Figure 5.
Sub-basins of the Kalvārī basin.
2.3. Models
2.3.1. COPRAS
COPRAS is an MCDM method presented by Zavadskas and Kaklauskas in 1996 [60]. The COPRAS method assumes direct and commensurate affiliations of the levels of magnitude and usefulness of alternatives in the presence of conflicting criteria [61]. The COPRAS procedure consists of the following steps [62]:
Step 1: Prepare the primary matrix;
Step 2: Normalize the primary matrix using Equation (1):
where is the normalized quantity of the jth criterion, is the ith alternative performance of the jth criterion, and m denotes the alternative numbers;
Step 3: Determine the normalized weighted decision-making matrix (Equation (2)):
where is the efficiency of the ith alternative, and wj is the criterion weight;
Step 4: Compute the maximum and minimum indices for alternatives—in this step, alternatives are classified as maximising and minimising indices (Equations (3) and (4)):
where and are the weighted normalized qualities for advantageous and non-advantageous adjectives, respectively. In fact, the highest value of parameters that have a direct relationship with SE, such as slope, and the lowest value of parameters that have an inverse relationship with SE, such as shape factors, is and vice versa; and
Step 5: Calculate the relative weights of each alternative using (Equation (5)):
where is the minimum value of . and are maximum and minimum indices, respectively.
2.3.2. AHP
Several methods can characterize the weights of criteria, but in this study the AHP was used. Weights were calculated with a pair-wise variable comparison matrix developed from experts’ opinions. For this purpose, an AHP questionnaire was designed and was administered to 18 geomorphology and 15 hydrology experts. Initially, due to the incompatibility of some of the paired-comparison matrices from the experts’ votes, the questionnaire was redistributed to confirm the matrices’ compatibilities and the validity of the questionnaire. The expert judgments reflect a blend of rational thinking and experience [63]. Based on the AHP method, Saaty’s linguistic scales (Table 2) of pair-wise comparisons were converted to quantitative values [64]. Then, the weights of criteria were determined using Equations (6) and (7) [63]:
where is the weight of criteria by AHP, is normalized of pair-wise comparison matrix and is matrix element in row i and column j.

Table 2.
Saaty’s linguistic scales in the analytical hierarchy process (AHP) [64].
The consistency ratio (CR) is the mechanism by which the validity of the expert response is measured in the pair-wise comparison matrix [63]. A CR < 0.1 is acceptable. Equations (8) to (12) were used to calculate CR [4]:
where CR is consistency ratio, CI is consistency index, RI is a random index (extracted from Table 3), n is the number of criteria, is the largest special matrix value, is consistency vector, WSV is weighted sum vector, A is pair-wise comparison matrix, and W is weight of criteria vector.

Table 3.
Values of random index (RI).
2.4. Validation of Results
2.4.1. Non-Parametric Correlation Tests to Comparing Models Ranking
The non-parametric Spearman correlation coefficient test (SCCT) and Kendall Tau correlation coefficient test (KTCCT) were used to compare the ranks of the observed values of two independent variables within the models instead of comparing their values [65,66] to determine whether the variables are statistically dependent. A reciprocal comparison is made between each random pair of variables. The number of comparisons is equal to where n is the number of alternatives. KTCC (Equation (13)) is used to compare two variables with dissimilar ranks. When two variables have similar rankings of observed values, Equation (14) is used:
where C and D are the numbers of concordant pairs and the number of discordant pairs, respectively. T and U are the numbers of pairs having the same ranks within the two data sets.
The non-parametric SCCT test compares the ranked values of two variables. Equation (15) is used when the observations of two variables are never similarly ranked and Equation (16) is used when one set of observations for two variables have the same rank:
where di is the difference between the ranks of models for each alternative, and and are the mean of x and y model, respectively.
2.4.2. Validation of Results Using MPSIAC Model
To validate the model, the sediment-delivery ratio (SDR) was calculated for each sub-basin using the modified Pacific Southwest Inter-Agency Committee (MPSIAC) method. The PSIAC method was created in 1968 by the US Water Management Committee [67]. MPSIAC was used in Walnut Gulch basin in southeastern Arizona. In 1982, Johnson and Gembhart quantified the descriptive concepts of the first model and presented each of the factors mathematically. In this method, the effects of nine important effective parameters—surface geology (X1), soil (X2), climate (X3), runoff (X4), topography (X5), land cover (X6), land use (X7), upland SE (X8) and channel SE (X9)—are evaluated. Depending on the relative importance of each parameter, values are attributed and the sum of the values of each is used to estimate SE severity and sediment yield [68]. Details of the MPSIAC model have been reported elsewhere [69,70,71].
Estimation of Sediment Yield and Total Sediment Production
Each effective parameter is divided into classes. Based on the estimated impact of each class, augmentation values are assigned by consulting model tables. The SE severity and annual sediment yield are estimated by summation of the values. This is signified by R:
where R is ranking value () and Xi is each factor in the model.
To manage the accuracy of interpolations and extrapolations of the nine parameter values in the MPSIAC model, this equation was developed to estimate sediment yield [70]:
where Qs is rate of sediment yield () and R is ranking value ().
To calculate the total sediment production of a study area, the rate of sediment yield is multiplied by surface area:
where S is the total sediment production based on sediment yield (), Qs is the sediment rate (), and A is surface area.
3. Results
3.1. Analysis of MPs
The characteristics of physical processes in a basin drainage system significantly impact its infiltration capacity and runoff dimensions [14]. Basin morphometry describes the relationships between the geomorphic, hydrologic, and geologic surface processes and a landscape [16]. Quantitative analysis of the Kalvārī Basin and its 11 sub-basins was carried out to evaluate the basin’s morphometric characteristics and the characteristics of each sub-basin drainage network. This analysis enables prioritization of the variables in terms of conservation and management efforts. In this regard, 23 MPs that represent basic (Table 4), linear, shape, and relief characteristics of the basin were examined.

Table 4.
Basic morphometric parameters of Kalvārī basin.
3.2. Basic Parameters
The Kalvārī Basin is a 5th-order (Figure 6) basin with an area of 70.71 km2. The basin contains 2204 stream segments. The total length is 327.93 km. The number and length were determined by the drainage threshold defined during the extraction of the stream network from the DEM. These characteristics are indicative of Horton’s First Law [15], which states that the number of streams of different ranks in the basin tends to have an inverse geometric ratio. This inverse geometric relationship is shown in the form of straight lines when the logarithm of the number of streams is plotted on a regular graph (Figure 7a). Changes in stream rankings are strongly dependent on the morphological and structural features of the basin. The number and length of streams vary directly with the size of the sub-basins. The lengths of the stream (Lu) were calculated according to Horton’s law. The length indicates the temporal development of a stream interacting with tectonic disturbances. The higher the stream ranking, the greater the length of the stream. The characteristics of the basin length of the Kalvārī Basin conform to Horton’s Second Law [15], which states that the average flow length of each stream tends to have a straight geometric ratio relative to basin length. This linear geometrical relationship is shown when the logarithms of the basin length values are plotted on a regular graph (Figure 7b). The lengths of streams in the basin vary from 4.62 km (sub-basin 6) to a maximum of 91.62 km (sub-basin 7). Mean stream length ranges from 0.1216 (sub-basin 6) to 0.1877 (sub-basin 8). The minimum and maximum heights of the basin are 1100 m and 1999 m. A comparison of the areas and lengths of sub-basin waterways also reveals a direct relationship (Figure 7c).
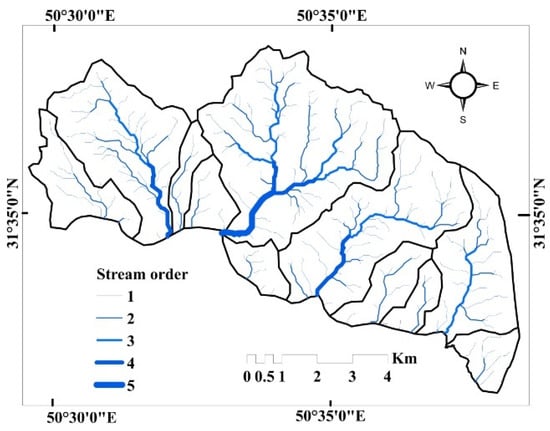
Figure 6.
Stream order in the Kalvārī basin.
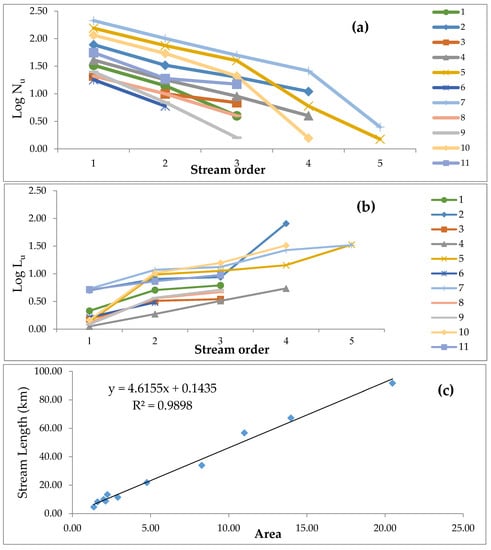
Figure 7.
(a) Correlation between stream orders and logarithm of the number of streams in sub-basins (Horton’s first law); (b) correlation between stream orders and logarithm of stream length in sub-basins (Horton’s second law); and (c) relationship between area and stream length in the Kalvārī Basin.
3.3. Linear Parameters
3.3.1. Stream Density (Dd)
Stream density reflects landscape dissection and a basin’s runoff potential. Slope angle and relative relief are the primary morphological factors that control drainage density. Strahler [16] concluded that Dd is low when basin relief is high. Lower Dd in a basin indicates highly permeable subsurface material, good vegetation, and low roughness, and the opposite conditions produce high Dd [72]. In the Kalvārī Basin, the lowest stream density was observed in sub-basin 4 (3.94 km). This sub-basin, therefore, has the highest infiltration among all sub-basins. If the condensation parameter alone is considered, it has the highest SE resistance and is the least susceptible to SE, and sub-basin 1 has the highest value. Sub-basins 10 (5.12), 3 (5.08), 9 (4.9), 5 (4.78), 11 (4.55), 7 (4.43), 8 (4.13), 2 (4.06), and 4 (3.94) are in the following categories of SE susceptibility (Table 5).

Table 5.
Shape, linear and relief geomorphometric parameters of the Kalvārī basin.
3.3.2. Stream Frequency (Fu)
Fu is the ratio of the number of streams in a basin to that basin’s area [15,73]. The Fu is inversely related to infiltration and is directly related to basin roughness [73]. High Fu indicates that the basin has a rocky surface and low permeability that contributes to further SE, and vice versa. Values of Fu in the study area vary from 22.15 streams/km2 for basin 8 to 41.06 for basin 3. Thus, sub-basin 3 has the lowest absorption capacity and is the most susceptible to SE, whereas basin 8 is least susceptible to SE. Sub-basins 9 (34), 1 (33.09), 5 (33.01), 7 (32.34), 10 (32.05), 2 (29.57), 6 (27.08) 11 (25.41) and 4 (24.4) rank second to tenth in susceptibility.
3.3.3. Mean Bifurcation Ratio (Rbm)
Rbm indicates that the infiltration of the basin are inversely correlated. A high Rbm value is the peak of the initial hydrograph when flooding results in high soil degradation. Rbm values are too high for all sub-basins in this study area, indicating that they are structurally complex and have low infiltration rates. Rbm values range from 3.66 for sub-basin 3 to 9.96 for sub-basin 5. Sub-basin 5 is the basin most susceptible to SE and sub-basins 6, 4, 7, 2, 1, 10, 8, 11 and 9 with values (8.96, 6.48, 6.01, 5.87, 5.81, 5.51, 4.56, 4.17, and 3.96) follow in rank.
3.3.4. Drainage Texture (T)
T depends on several physical factors—climate, rainfall, vegetation, rock, and soil type, infiltration capacity, and soil evolutionary stage. According to Smith [74], drainage texture is classified into four levels: rough (less than 4), moderate (4–10), soft (more than 10), and ultra-soft (or highland topography) (more than 15). According to this classification, the drainage texture of the basin is super soft (14/39). High drainage texture indicates soft rocks of low SE-resistance. The drainage texture values of this study area indicate the basin is highly sensitive to SE. The highest drainage texture is found in sub-basin 7 (31.33) and it, therefore is the sub-basin most sensitive to SE. Sub-basin 8 (7.55) is least sensitive to SE. Sub-basins 5 (22.32), 10 (22.03), 2 (16.74), 3 (11.23), 1 (11.09), 11 (10.95), 4 (8.6), 9 (8.3) and 6 (7.7) ranked second to tenth most sensitive to SE.
3.3.5. Constant of Channel Maintenance (C)
This indicator reflects infiltration and the control of flow to the basin outlet [19]. The relationship between this parameter and SE is analogous to the relationship of drainage density to stream frequency. The values of C range from a minimum (0.13) for sub-basin 1 to a maximum (0.26) for sub-basin 6. Sub-basin 6 is the most erodible sub-basins, and sub-basin 1 is not susceptible to SE. Sub-basins 4 (0.21), 2 (0.2), 8 (0.2), 7 (0.18), 11 (0.18), 5 (0.17), 9 (0.16), 3 (0.15), and 10 (0.15) are the next nine of the top ten.
3.3.6. Length of Overland Flow (Lo)
Lo affects the hydrological evalution of the basin [16]. This factor is lower for steeper slopes and higher for more mild slopes. Lo values for the basin range from 2.9 in sub-basin 1 to 1.65 in sub-basin 6. Higher values of Lo indicate greater susceptibility to SE. Sub-basins 10 (2.54), 3 (2.51), 9 (2.42), 5 (2.36), 11 (2.25), 7 (2.19), 8 (2.04), 2 (2.01), 4 (1.95), and 6 (1.65) are the next ten sub-basins ranked in terms of susceptibility to SE.
3.3.7. Infiltration Number (If)
Sub-basins with high infiltration values are less susceptible to SE. If values for the sub-basins range from the minimum (92.3) in sub-basin 8 to the maximum (240.16) in sub-basin 3. Sub-basin 8 is then most susceptible to SE. Sub-basins 6 (94.1), 4 (97.3), 11 (116.86), 2 (121.36), 7 (144.7), 5 (159), 10 (165.6), 9 (168), and 1 (197.66) are ranked next in terms of susceptibility to SE.
3.4. Shape Parameters
3.4.1. Elongation Ratio (Re)
The values of Re range from 0.6 to 1.0 based on climate and geological conditions [20]. Values of about 1 are typical of areas with very low roughness [15], mild topography, and little frictional resistance to flow, while values of 0.6 to 0.8 are associated with high roughness and steep terrain [75]. In the study area, sub-basin 9 is most the elongated sub-basin (0.78) and is therefore least susceptible to SE. Sub-basin 7 has the smallest elongation ratio (0.66) and is the most susceptible to SE. Sub-basins 5 (0.67), 10 (0.69), 2 (0.7), 11 (0.73), 4 (0.75), 1 (0.77), 8 (0.77), 6 (0.8) and 3 (0.79) fill out the top ten in terms of susceptibility.
3.4.2. Circularity Ratio (Rc)
Rc relates to several basin characteristics: stream length and frequency, geological structure, climate, roughness, and slope. High Rc indicates a circular basin with moderate to high roughness, high infiltration, less elongated, lower roughness, and low infiltration. Sub-basin 9, with the lowest Rc value (0.34), is least susceptible to SE due to high infiltration. Sub-basin 6, having the highest Rc value (0.67), is most susceptible to SE. In terms of Rc and susceptibility to SE, sub-basins 5 (0.37), 2 (0.45), 11 (0.45), 4 (0.5), 10(0.5), 7 (0.54), 3 (0.55), 1 (0.59), and 8 (0.65) were next in rank of the nine least susceptible to SE.
3.4.3. Form Factor (Rf)
The effect of the Rf parameter on SE is similar to the effect of the elongation factor: basins with the lowest Rf values are most susceptible to SE. The extracted Rf values are low in the study area and ranged from a minimum (0.34) in sub-basin 7, the most SE-susceptible sub-basin, to a maximum (0.5) in sub-basin 6. Sub-basins 5 (0.36), 10 (0.37), 2 (0.38), 11 (0.42), 4 (0.45), 1 (0.47), 8 (0.47), 9 (0.48), and 3 (0.49) ranked as the next most SE-susceptible.
3.4.4. Shape Factor (Bs)
The sediment- and runoff-production rates, drainage length, and roughness are influenced by Bs. Thus, in terms of SE response, Bs behaves like Rf. Among the sub-basins, the lowest Bs value (1.78) and therefore the highest erodibility is observed in sub-basin 6, while the highest (2.59) and least SE-susceptible is sub-basin 7. Sub-basins 3 (1.82), 9 (1.87), 8 (1.89), 1 (1.9), 4 (1.97), 11 (2.11), 2 (2.28), 10 (2.37), and 5 (2.45) complete the list of the ten most erodible.
3.4.5. Compactness Coefficient (Cc)
The Cc is directly linked to infiltration capacity. Therefore, the relationship between Cc and SE is the same as Rf and Bs. Sub-basin 6 has the lowest Cc value (1.14) and has surfaces with low permeability. Therefore sub-basin 6 is the most SE-susceptible basin. Sub-basin 9 has the highest Cc (1.58) and therefore is least SE-susceptible. Sub-basins 8 (1.15), 1 (1.21), 3 (1.25), 7 (1.27), 10 (1.31), 4 (1.31), 11 (1.37), 2 (1.38), and 5 (1.51) have the next lowest Cc values and are the next most susceptible to SE.
3.5. Relief Parameters
3.5.1. Basin Relief (Bh)
Bh indicates height difference [76]. This parameter has a significant role in hydrological characteristics [6]. The Bh indicates the overall slope of a basin and therefore the intensity of the SE forces operating on the slopes. The relationships of this parameter to SE is the same as Dd, and Fu. Sub-basin 4 has the lowest Bh (0.05) and sub-basin 1 has the highest Bh (0.40), thus sub-basin 1 is most susceptible and sub-basin 4 is least susceptible. Sub-basins 8 (0.32), 3 (0.24), 2 (0.15), 9 (0.13), 11 (0.1), 6 (0.08), 7 (0.05), and 5 (0.04) rank second to ninth in Bh values.
3.5.2. Slope (S)
In terms of SE response, slopes are drainage density and stream frequency factors. The steepest slope in the sub-basins is in sub-basin 1 (36.08°) which makes it the most susceptible to SE. The lowest slope is in sub-basin 4 (14.1°) which is least susceptible to SE. Sub-basins 5 (27.09°), 8 (26.17°), 3 (24.13°), 10 (24.09°), 6 (23.72°), 2 (23.61°), 11 (22.17°), 9 (21.3°), and 7 (19.1°), rank as the next nine SE-susceptible sub-basins.
3.5.3. Ruggedness Number (Rn)
Rn is used to calculate the flood potential of streams [16]. This parameter reflects the geometrical characteristics of the basin. The Rn is directly related to erodibility: increasing Rn increases erosivity. Rn ranged from a minimum of 0.079 for sub-basin 4 to a maximum of 5.41 for sub-basin 1. Sub-basin 1 is therefore most susceptible, followed by sub-basins 2, 10, 8, 7, 3, 11, 9, 4, and 6.
3.5.4. Relief Ratio (Rh)
Rh is directly related to slope. It affects hydrological processes and SE. Rh, like the other shape parameters, is direct related to a basin’s likelihood to be exposed to erosive fluvial forces. Sub-basin 1 has the highest value (13.72) and sub-basin 5 the lowest (2.28). Sub-basin 1 is most susceptible to SE and is followed by sub-basins 8 (11.86), 3 (8.1), 2 (5.61), 9 (4.08), 11 (4.15), 10 (3.89), 6 (3.72), 7 (3.08), and 4 (2.51).
3.6. Prioritization of Sub-Basins Using Novel AHP-COPRAS Ensemble Model
To determine the relative importance of the contribution that each MP makes to determining soil-SE potential, a set of academic experts were asked to express their informed opinions of expected importance of each variable. From their responses, a pairwise comparison matrix was created to determine the weight of each parameter using AHP (Table 6). The consistency ratio from this matrix was 0.05, indicating that the opinions were consistent. Based on the AHP results (Table 6 and Figure 8), Slope (0.122), Dd (0.120), and If (0.113) are the most important determinants of SE. By contrast, the parameters Re (0.022), Fu (0.029), and Rf (0.0316) were the least important influencers of sub-basin erosivity. This is consistent with the results of [23]. T (0.097), Lo (0.073), Bh (0.067), Rbm (0.063), Rh (0.056), Rn (0.045), C (0.042), Rc (0.04), Cc (0.037), and Bs (0.034) bridge the gap in these ranks. The scores obtained for all 11 sub-basins using the COPRAS model varied from the minimum (0.118) to the maximum (0.319) and were divided into 5 groups (Figure 8): very low (0.118–0.137), low (0.137–0.159), moderate (0.159–0.171), high (0.171–0.208) and very high (0.208–0.319) using the natural-break method (Figure 9). Accordingly, sub-basin 4 is in the very low-SE class. Sub-basins 5, 6, and 9 are in the low-SE group. Sub-basins 7, 10, and 11 have moderate SE potential. Sub-basin 2 is highly likely to be prone to SE, and sub-basins 1, 3, and 8 are very highly likely to experience SE.

Table 6.
Pair-wise comparison matrix.
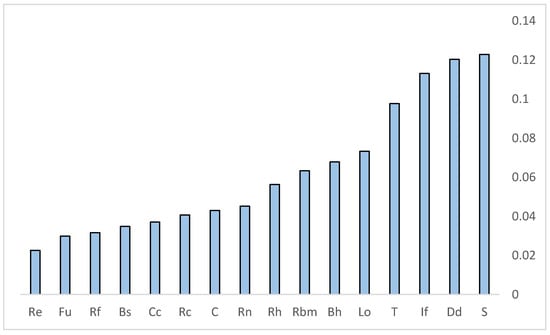
Figure 8.
Relative importance of geomorphometric parameters using AHP model.
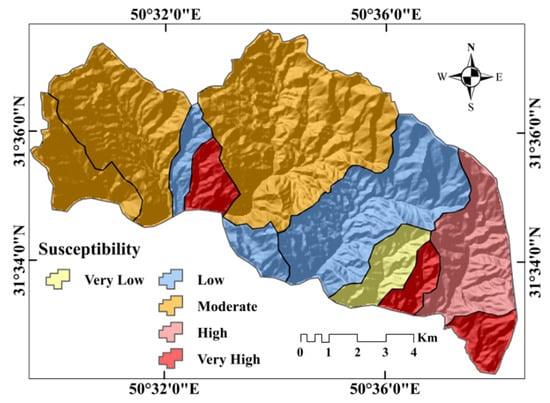
Figure 9.
Prioritization of sub-basins for conservation programs.
The COPRAS algorithm indicated (Table 7) that sub-basins 1 (0.319), 8 (0.257), and 3 (0.208) are the most susceptible to SE. Sub-basins 2, 10, 11, 7, and 9 rank next in terms of SE susceptibility. And sub-basins 4 (0.118), 6 (0.137), and 5 (0.147) are the least susceptible to SE.

Table 7.
Final weight of sub-basins using complex proportional assessment of alternatives (COPRAS) models.
3.7. Validation of Results
Results of mean sediment yield from the MPSIAC model (Table 8) show that sub-basins 1, 8, and 3, with mean sediment yields of 943.7, 845.2, and 715.8 , have the highest susceptibility to SE. By comparison, sub-basins of 4, 6, and 5, with mean sediment yields of 550.6, 511.4, and 456.3 , are the least susceptibility to SE. Sub-basins 2, 10, 11, 7, and 9, with mean sediment yields of 675.1, 645.2, 613.7, 601.8, and 581.3 , ranked fourth to eighth in terms of sensitivity to SE. The results of regressing the nine effective factors from the MPSIAC model against sediment yield at each sub-basin revealed high correlation coefficients with topography, runoff, upland SE, and channel SE (R2 = 0.92 − 0.96; Table 9). Comparing the results of sub-basin prioritization using the hybrid method and the MPSIAC method showed that the ensemble method prioritizes the sub-basins rather accurately (100%) (Figure 10). Non-parametric tests indicate that, compared to the AHP and COPRAS models, the AHP-COPRAS ensemble had the best correlation (Table 10).

Table 8.
Surface area, mean sediment yield, and sediment production at each sub-basin of the study area.

Table 9.
Correlation between sediment yield and modified Pacific Southwest Inter-Agency Committee (MPSIAC) factors in the study area.
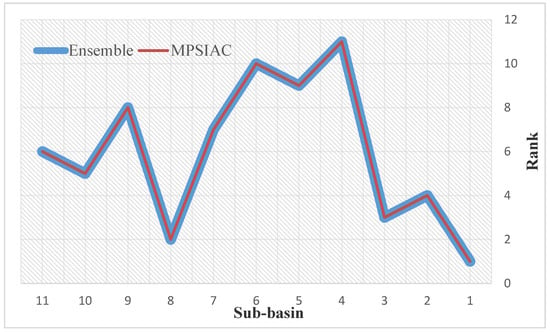
Figure 10.
Validation of ensemble model with MPSIAC model.

Table 10.
Comparison of models using non-parametric tests.
4. Discussion
The Kalvārī Basin was selected for study because of the extent to which it is impacted by SE. Erosion processes in the basin reflect its morphology—visible in its linear relief pattern, its shape, and its spatial extent. After determining its drainage network and MPs using RS, GIS, and a DEM, the AHP-COPRAS ensemble model was used to develop a map of SE susceptibility and to rank the sub-basins by the intensity of SE. The results of the map were compared to the results from two individual models.
Digitally estimating MPs provided an easier, more accurate, and more quantitative method to evaluate morphometric characteristics and to analyze the variations within the region. PALSAR DEM has been used previously for morphometric studies, especially in mountainous regions, as it provides more accurate elevation measurements and better morphometric and geomorphic details (compared to ASTER and SRTM DEMs) [77].
First-order streams comprise nearly 67% of the streams in the study area. That first-order streams are the most numerous of all orders indicates that there is a structural weakness in the basin in the form of lineaments [78]. Stream frequency in all sub-basins is moderate, which indicates that there is moderate run-off intensity and high drainage density. The terrain is highly dissected. Sub-basins are finely textured, indicating highly developed drainage and high rates of SE. Stream frequency, drainage density, and texture are very high in sub-basins 1 and 3, which indicates that these sub-basins experience intensive SE. The values of these three characteristics are lowest in sub-basin 4, a unit that is less prone to SE. Relief ratios generally depict a high-energy basin with substantial SE and high sediment loads. This parameter is very high in sub-basins 1 and 8, where SE rates are high, and slopes are moderate. By contrast, the relief ratios are very low in sub-basins 4 and 5, low-energy drainages as exhibited by their gentle topographies.
Despite the low mean slope for the region overall, both the maximum and minimum slope angles of the Kalvārī Basin are in sub-basin 4, where the gentle topography has attracted greater human activity. This has created a plateau-like terrain—a flat platform with steeply sloping edges on its perimeter. This unit is a low-energy landscape with less sediment in streams. Sub-basins 1, 11, and 8 have higher mean slopes, and provide favorable topography for higher SE potential. The ruggedness numbers of all the sub-basins reflect the mountainous nature of the region’s terrain, with significant amounts of SE and dissection. The lowest ruggedness value is found in sub-basin 4 and the highest is in sub-basin 8; these compliment the patterns of slope and relief ratios discussed above. Shape factors reflect the geomorphology of a landscape and provide evidence of run-off and infiltration processes [76]. Sub-basins 6, 3, 9, and 1 have the highest form factors of the sub-basins, reflecting their more ovate and less elongated shapes (these forms are consistent with the elongation measures and circulatory ratios for those units). The higher form-factor values of these sub-basins indicate more drainage development and more structural control.
Based on the results of the AHP model, we know that slope, drainage density, infiltration number, and texture ratio significantly impact SE in the study area, results which are consistent with others [12,79,80,81,82]. Arabameri et al. [82] used four MCDM-based models to rank the sub-basins’ SE susceptibilities by analyzing the MPs. The mean bifurcation ratio (Rbm), slope (S), and infiltration number (If) have key roles in SE rates. Slope is a morphometric factor associated with hydrology that indicates runoff volumes and runoff concentration time [76]. Soil infiltration-capacity and the initial resistance of a surface to SE depend on drainage density [73]. Infiltration number is very important for expressing a basin’s infiltration characteristics and depends directly on the basin’s runoff capacity [76]. Validation of the results by using non-parametric tests shows that the ensemble model performed better than the AHP and COPRAS individual models. This is consistent with the findings of Arabameri et al. [83] which indicated that ensemble MCDM-based models perform better than individual models.
Validation of the ensemble model with the MPSIAC model shows that the ensemble model very accurately prioritized sub-basins and could be used to prepare SE susceptibility maps. Sub-basins 1, 3, and 8 might be experiencing heavy SE and sedimentation due to either higher erodibility of hills in these areas, greater slopes, or land-cover changes (from compact to less compact pastures). The sub-basins with slight and moderate SE and sedimentation may be less affected because of ultrabasic and crystallized limestone formations, rock outcrops, or cultivated lands. The results provide ways to identify very erosive areas and open new horizons in watershed management and sediment control by providing greater evidence to support conservation-project prioritization.
Compared to other commonly used approaches to produce SE susceptibility maps, this ensemble approach can be achieved with much simpler input data, specifically morphometric data, that can be easily extracted from DEMs. Our approach does not need other SE parameters that might necessitate a soil-inventory map, a source that is very time-consuming and expensive create. One limitation of this method is that it ignores human activities that interfere with hydrologic processes (e.g., reducing a river’s flow capacity), actions that often amplify SE. Moreover, additional information derived from land use analyses that can be used to detail soil-erosion history would be beneficial, as they would clarify the connection between spatial patterns of activities and SE zones. But suitable results can be achieved without the best information.
5. Conclusions
The common approaches to assess the problem of SE, to develop management plans to address it, require quantitative SE rate data at regional and global scales. In this research, the morphometric characteristics of the Kalvārī Basin were determined for use in an MCDM-based ensemble model. A PALSAR DEM was input into a GIS, allowing for the development of quantitative and qualitative morphometric analyses and the extraction of the spatial patterns of MPs. An AHP model was used to evaluate the importance of each of the 16 parameters and revealed that slope, drainage density, and infiltration number were the most important predictors of SE potential. A COPRAS-AHP ensemble model indicated that sub-basins 1, 3, and 8 are highly susceptible to SE. Validation of the modeled results using MPSIAC and non-parametric tests show that the ensemble model and the ranking of MPs achieved strong prediction accuracy of SE susceptibility and this enables a faster and less expensive prioritization of sub-basins for management actions. The method presented here takes advantage of computer-assisted extraction and computation of morphometric characteristics to predict the spatial patterns of the intensity of SE potential. A significant advantage is that only high-quality empirical topographical data are employed. In this way, one can produce assessments for catchments that either lack stream gages and extensive, large-scale records of past SE patterns, or are remote and difficult to access. This, in fact, describes most of the watercourses in Iran. Given the predicted high SE-susceptibility of sub-basins 1, 3, and 8, it is recommended that protective measures be taken to arrest SE, reduce sedimentation in reservoirs, stabilize slopes against mass wasting, and reduce flood risk.
Author Contributions
Conceptualization, A.A.; Data curation, A.A.; Formal analysis, A.A.; Investigation, A.A.; and D.T.B.; Methodology, A.A.; Resources, A.A.; Software, A.A.; Supervision, A.A., B.P., and D.T.B.; Validation, A.A.; Writing—Original draft, A.A.; Writing—Review and editing, A.A., J.P.T., B.P., T.B., and D.T.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partly funded by the Austrian Science Fund (FWF) through the Doctoral College GIScience (DK W 1237-N23) at the University of Salzburg.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Masselink, R.; Temme, A.J.A.M.; Giménez, R.; Casalí, J.; Keesstra, S.D. Assessing hillslope-channel connectivity in an agricultural catchment using rare-earth oxide tracers and random forests models. Cuadernos de Investigación Geográfica 2017, 43, 19–39. [Google Scholar] [CrossRef]
- Tripathi, R.P. Soil Erosion and Conservation; New Age International Ltd.: New Dehli, India, 2001; p. 350. [Google Scholar]
- Morgan, R. Soil Erosion and Conservation; Longman Scientific and Technical: London, UK, 1986; p. 298. [Google Scholar]
- Novara, A.; Gristina, L.; Saladino, S.S.; Santoro, A.; Cerdà, A. Soil erosion assessment on tillage and alternative soil managements in a Sicilian vineyard. Soil Tillage Res. 2011, 117, 140–147. [Google Scholar] [CrossRef]
- Kuhn, N.J.; Armstrong, E.K.; Ling, A.C.; Connolly, K.L.; Heckrath, G. Interrill erosion of carbon and phosphorus from conventionally and organically farmed Devon silt soils. Catena 2012, 91, 94–103. [Google Scholar] [CrossRef]
- Pimentel, D.; Burgess, M. Soil Erosion Threatens Food Production. J. Agric. 2013, 3, 443–463. [Google Scholar] [CrossRef]
- FAO. Forest resources of the world. Unasylva 1984, 2, 161–182. [Google Scholar]
- National Geosciences Database. 2017. Available online: www.ngdir.ir (accessed on 12 February 2019).
- Keesstra, S.D.; Bouma, J.; Wallinga, J.; Tittonell, P.; Smith, P.; Cerdà, A.; Montanarella, L.; Quinton, J.N.; Pachepsky, Y.; Van Der Putten, W.H.; et al. The significance of soils and soil science towards realization of the United Nations Sustainable Development Goals. Soil 2016, 2, 111–128. [Google Scholar] [CrossRef]
- UNEP. World Atlas of Desertification, 2nd ed.; Arnold: London, UK, 1997; p. 77. [Google Scholar]
- Chopra, R.; Dhiman, R.D.; Sharma, P.K. Morphometric Analysis of Sub-Watersheds in Gurdaspur District, Punjab Using Remote Sensing and GIS Techniques. J. Indian Soc. Remote Sens. 2005, 33, 531–539. [Google Scholar] [CrossRef]
- Patel, D.; Dholakia, M.; Naresh, N.; Srivastava, P. Water Harvesting Structure Positioning by Using Geo- Visualization Concept and Prioritization of Mini-Watersheds through Morphometric Analysis in the Lower Tapi Basin. J. Indian Soc. Remote Sens. 2012, 40, 299–312. [Google Scholar] [CrossRef]
- Gajbhiye, S.; Mishra, S.K.; Pandey, A. Prioritizing erosion-prone area through morphometric analysis: An RS and GIS perspective. Appl. Water Sci. 2014, 4, 51–61. [Google Scholar] [CrossRef]
- Horton, R. Drainage Basin Characteristics. Trans. Am. Geophys. Union 1932, 13, 350–361. [Google Scholar] [CrossRef]
- Horton, R. Erosional Development of Streams and Their Drainage Basins; Hydrophysical Approach to Quantitative Morphology. Geol. Soc. Am. Bull. 1945, 56, 275–370. [Google Scholar] [CrossRef]
- Strahler, A. Dynamic Basis of Geomorphology. Geol. Soc. Am. Bull. 1952, 63, 923–938. [Google Scholar] [CrossRef]
- Strahler, A. Quantitative Analysis of Watershed Geomorphology. Trans. Am. Geophys. Union 1957, 38, 913–920. [Google Scholar] [CrossRef]
- Strahler, A. Quantitative Geomorphology of Drainage Basins and Channel Networks. In Handbook of Applied Hydrology; Chow, V., Ed.; McGraw Hill: New York, NY, USA, 1964; pp. 439–476. [Google Scholar]
- Miller, V. A Quantitative Geomorphic Study of Drainage Basin Characteristics in the Clinch Mountain Area, Virginia and Tennessee; Project NR 389–402, Technical Report 3; Columbia University, Department of Geology, ONR: New York, NY, USA, 1953. [Google Scholar]
- Schumm, S. Evolution of Drainage Systems and Slopes in Badlands at Perth Amboy, New Jersey. Geol. Soc. Am. Bull. 1956, 67, 597–646. [Google Scholar] [CrossRef]
- Kouli, M.; Vallianatos, F.; Soupios, P.; Alexakis, D. GIS-Based Morphometric Analysis of Two Major Watersheds, Western Crete, Greece. J. Environ. Hydrol. 2007, 15, 1–17. [Google Scholar]
- Clark, J. Morphometry from Maps. In Essays in Geomorphology; Heinemann: London, UK, 1966; pp. 235–274. [Google Scholar]
- Nageswara, R.; Swarna, L.; Arun, K.; Hari, K. Morphometric Analysis of Gostani River Basin in AndhraPradesh State, India Using Spatial Information Technology. Int. J. Geomat. Geosci. 2010, 1, 179–187. [Google Scholar]
- Ivanoua, E.; Nedkov, R.; Ivanova, I.; Radeva, K. Morpho-Hydrographic Analyze of Black Sea Catchment Area in Bulgaria. Procedia Environ. Sci. 2012, 14, 143–153. [Google Scholar] [CrossRef][Green Version]
- Thomas, J.; Joseph, S.; Thrivikramji, K.; Abe, G.; Kannan, N. Morphometrical Analysis of Two Tropical River Basins of Contrasting Environmental Settings, the Southern Western Ghats, India. Environ. Earth Sci. 2012, 66, 2353–2366. [Google Scholar] [CrossRef]
- Manu, M.; Anirudhan, S. Drainage Characteristics of Achankovil River Basin, Kerala. J. Geol. Soc. India 2008, 71, 841–850. [Google Scholar]
- Ozdemir, H.; Bird, D. Evaluation of Morphometric Parameters of Drainage Networks Derived from Topographic Maps and DEM in Point of Floods. Environ. Geol. 2009, 56, 1405–1415. [Google Scholar] [CrossRef]
- Arnous, M.; Aboulela, H.; Green, D. Geo-Enviornmental Hazards Assessment of the North Western Gulf of Suez, Egypt. J. Coast. Conserv. 2011, 15, 37–50. [Google Scholar] [CrossRef]
- Youssef, A.; Pradhan, B.; Hassan, A. Flash Flood Risk Estimation along the St. Katherine Road, Southern Sinai, Egypt Using GIS Based Morphometry and Satellite Imagery. Environ. Earth Sci. 2011, 62, 611–623. [Google Scholar] [CrossRef]
- Abdel-Lattif, A.; Sherief, Y. Morphometric Analysis and Flash Floods of Wadi Sudr and Wadi Wardan, Gulf of Suez, Egypt: Using Digital Elevation Model. Arab. J. Geosci. 2012, 5, 181–195. [Google Scholar] [CrossRef]
- Arabameri, A. Application of the Analytic Hierarchy Process (AHP) for locating fire stations: Case Study Maku City. Merit Res. J. Arts Soc. Sci. Humanit. 2014, 2, 1–10. [Google Scholar]
- Arabameri, A. Zoning Mashhad Watershed for Artificial Recharge of Underground Aquifers Using Topsis Model and GIS Technique. Glob. J. Hum. Soc. Sci. B Geogr. Geo Sci. Environ. Sci. Disaster Manag. 2014, 14, 45–53. [Google Scholar]
- Arabameri, A.; Pourghasemi, H.R.; Yamani, M. Applying different scenarios for landslide spatial modeling using computational intelligence methods. Environ. Earth Sci. 2017, 76, 832. [Google Scholar] [CrossRef]
- Arabameri, A.; Pradhan, B.; Pourghasemi, H.R.; Rezaei, K. Identification of erosion-prone areas using different multi-criteria decision-making techniques and GIS. Geomat. Nat. Hazards Risk 2018, 9, 1129–1155. [Google Scholar] [CrossRef]
- Arabameri, A.; Rezaei, K.; Cerda, A.; Conoscenti, C.; Kalantari, Z. A comparison of statistical methods and multi-criteria decision making to map flood hazard susceptibility in Northern Iran. Sci. Total Environ. 2019, 660, 443–458. [Google Scholar] [CrossRef]
- Arabameri, A.; Rezaei, K.; Cerda, A.; Lombardo, L.; Rodrigo-Comino, J. GIS-based groundwater potential mapping in Shahroud plain, Iran. A comparison among statistical (bivariate and multivariate), data mining and MCDM approaches. Sci. Total Environ. 2019, 658, 160–177. [Google Scholar] [CrossRef]
- Prasannakumar, V.; Vijith, H.; Geetha, N. Terrain Evaluation through the Assessment of Morphometric Parameters Using DEM and GIS: Case Study of Two Major Sub-Watersheds in Attapady, South India. Arab. J. Geosci. 2013, 6, 1141–1151. [Google Scholar] [CrossRef]
- Markose, V.; Dinesh, A.; Jayappa, K. Quantitative Analysis of Morphometric Parameters of Kali River Basin, Sothern India, Using Bearing Azimuth and Drainage (bAd) Calculator and GIS. Environ. Earth Sci. 2014, 72, 2887–2903. [Google Scholar] [CrossRef]
- Apaydin, H.; Ozturk, F.; Merdun, H.; Aziz, N. Determination of the Drainage Basin Characteristics Using Vector GIS. Nord. Hydrol. 2006, 37, 129–142. [Google Scholar] [CrossRef]
- Saeedrashed, Y.; Guven, A. Estimation of Geomorphological Parameters of Lower Zab Riverk-Basin by Using GIS Based Remotely Sensed Image. Water Resour. Manag. 2013, 27, 209–219. [Google Scholar] [CrossRef]
- Johansen, K.S.; Taihei, D.; Tindall, S.; Phinn, S. Object-based Monitoring of Gully Extent and Volume in North Austrailia using LIDAR Data. GEOBIA 2012, 1, 168–173. [Google Scholar]
- Chu, T.; Lindenschmidt, K.E. Comparison and Validation of Digital Elevation Models Derived from InSAR for a Flat Inland Delta in the High Latitudes of Northern Canada. Can. J. Remote Sens. 2017, 43, 109–123. [Google Scholar] [CrossRef]
- Franklin, S. Morphometric Processing of Digital Elevation Model. Comput. Geosci. 1987, 13, 603–609. [Google Scholar] [CrossRef]
- Kamp, U.; Bolch, T.; Olsenholler, J. Geomorphometry of Cerro Sillajhauy (Andes, Chile/Bolivia): Comparison of Digital Elevation Models (DEMs) from ASTER Remote Sensing Data and Contour Maps. Geocarto Int. 2005, 20, 23–33. [Google Scholar] [CrossRef]
- Singh, P.; Thakur, J.; Singh, U. Morphometric Analysis of Morar River Basin, Madhya Pradesh, India, Using Remote Sensing and GIS Techniques. Environ. Earth Sci. 2013, 68, 1967–1977. [Google Scholar] [CrossRef]
- Altaf, S.; Meraj, G.; Ahmad Romshoo, S. Morphometry and land cover based multicriteria analysis for assessing the soil erosion susceptibility of the western Himalayan watershed. Environ. Monit. Assess. 2014, 186, 8391–8412. [Google Scholar] [CrossRef]
- Ahmad Rather, M.; Satish Kumar, J.; Farooq, M.; Rashid, H. Assessing the influence of watershed characteristics on soil erosion susceptibility of Jhelum basin in Kashmir Himalayas. Arab. J. Geosci. 2017, 10, 59. [Google Scholar] [CrossRef]
- I.R. of Iran Meteorological Organization (IRIMO). 2012. Available online: http://www.mazandaranmet.ir (accessed on 15 July 2019).
- Geology Survey of Iran (GSI). 1997. Available online: http://www.gsi.ir/Main/Lang_en/index.html (accessed on 15 July 2019).
- Soil Survey Staff. Keys to Soil Taxonomy, 12th ed.; USDA-Natural Resources Conservation Service: Washington, DC, USA, 2014. [Google Scholar]
- Gesch, D.; Oimoen, M.; Zhang, Z.; Meyer, D.; Danielson, J. Validation of the ASTER global digital elevation model version 2 over the conterminous United States. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 4, 281–286. [Google Scholar] [CrossRef]
- Zhou, C.; Ge, L.E.D.; Chang, H.C. A case study of using external DEM in InSAR DEM generation. Geo Spat. Inf. Sci. 2005, 8, 14–18. [Google Scholar]
- Zhang, W.; Wang, W.; Chen, L. Constructing DEM based on InSAR and the relationship between InSAR DEM’s precision and terrain factors. Energy Procedia 2012, 16, 184–189. [Google Scholar] [CrossRef]
- Graham, L.C. Synthetic Interferometer Radar for Topographic Mapping. Proc. IEEE 1974, 62, 763. [Google Scholar] [CrossRef]
- Raucoules, D.; Colesanti, C.; Carnec, C. Use of SAR interferometry for detecting and assessing ground subsidence. Comptes Rendus Geosci. 2007, 339, 289–302. [Google Scholar] [CrossRef]
- Pacheco-Martínez, J.; Arzate-Flores, J.; Rojas, E.; Arroyo, M.; Yutsis, V.; Ochoa, G. Delimitation of Ground Failure Zones due to Land Subsidence Using Gravity Data and Finite Element Modeling in the Querétaro Valley, Mexico. Eng. Geol. 2006, 84, 143–160. [Google Scholar] [CrossRef]
- Arabameri, A.; Pradhan, B.; Rezaei, K. Spatial prediction of gully erosion using ALOS PALSAR data and ensemble bivariate and data mining models. Geosci. J. 2019, 23, 669–686. [Google Scholar] [CrossRef]
- Boreggio, M.; Bernard, M.; Gregoretti, C. Evaluating the influence of gridding techniques for Digital Elevation Models generation on the debris flow routing modeling: A case study from Rovina di Cancia basin (North-eastern Italian Alps). Front. Earth Sci. 2018, 6, 89. [Google Scholar] [CrossRef]
- Wu, C.Y.; Mossa, J.; Mao, L.; Almulla, M. Comparison of different spatial interpolation methods for historical hydrographic data of the lowermost Mississipi River. Ann. GIS 2019, 25, 133–151. [Google Scholar] [CrossRef]
- Podvezko, V. The comparative analysis of MCDA methods SAW and COPRAS. Inz. Ekon. Eng. Econ. 2011, 22, 134–146. [Google Scholar] [CrossRef]
- Chatterjee, P. Gear material selection using complex proportional assessment and additive ratio assessment-based approaches: A comparative study. Int. J. Mater. Sci. Eng. 2013, 1, 104–111. [Google Scholar] [CrossRef]
- Ress, E.Y. Performance Evaluation of Research Assistants by Copras Method. Eur. Sci. J. 2016, 4, 102–109. [Google Scholar]
- Arabameri, A.; Pradhan, B.; Rezaei, K.; Conoscenti, C. Gully erosion susceptibility mapping using GIS-based multi-criteria decision analysis techniques. Catena. 2019, 180, 282–297. [Google Scholar] [CrossRef]
- Saaty, T.L. The Analytic Hierarchy Process; McGraw-Hill: New York, NY, USA, 1980; pp. 20–25. [Google Scholar]
- Szmidt, E.; Kacprzyk, J. The Spearman and Kendall rank correlation coefficients between intuitionist fuzzy sets. In Aix-Les-Bains; Atlantis Press: Paris, France, 2011; pp. 521–528. [Google Scholar]
- Chitsaz, N.; Banihabib, M.E. Comparison of different multi criteria decision-making models in prioritizing flood management alternatives. Water Resour. Manag. 2015, 29, 2503–2525. [Google Scholar] [CrossRef]
- Pacific Southwest Inter-Agency Committee. Report on Factors Affecting Sediment Yield in the Pacific Southwest Area and Selection and Evaluation of Measures for the Reduction of Erosion and Sediment Yield; Water Management Subcommittee, Sedimentation Task Force, The Committee Publisher: Paris, France, 1968. [Google Scholar]
- PSIAC Report. Sediment Assessment and Evaluation Study for Lake Louise and Cottonwood Lake Hand, Hyde, Faulk, and Spink Counties South Dakota, United States Department of Agriculture Natural Recourses Conservation Service South Dakota in Cooperation with South Dakota; Department of Environment and Natural Resources and Hand County Conservation District: Miller, SD, USA, 2000. [Google Scholar]
- Daneshvar, M.R.M.; Bagherzadeh, A. Evaluation of sediment yield in PSIAC and MPSIAC models by using GIS at Toroq Watershed, Northeast of Iran. Front. Earth Sci. 2012, 6, 83–94. [Google Scholar] [CrossRef]
- Noori, H.; Karami, H.; Farzin, S.; Siadatmousavi, S.M.; Mojaradi, B.; Kisi, O. Investigation of RS and GIS techniques on MPSIAC model to estimate soil erosion. Nat. Hazards 2018, 91, 221–238. [Google Scholar] [CrossRef]
- Zarei, A.; Mokarram, M.; Shahabi, A. Evaluation of sediment yield (Qs) in Bishezard watershed located southwest of Iran, using PSIAC and MPSIAC models. Int. J. Glob. Environ. Issues 2019, 18, 1–23. [Google Scholar] [CrossRef]
- Prasad, R.K.; Mondal, N.C.; Banerjee, P.; Nandakumar, M.V.; Singh, V.S. Deciphering Potential Groundwater Zone in Hard Rock through the Application of GIS. Environ. Geol. 2008, 55, 467–475. [Google Scholar] [CrossRef]
- Magesh, N.S.; Chandrasekar, N.; Soundranayagam, J.P. Morphometric Evaluation of Papanasam and Manimuthar Watersheds, Part of Western Ghats, Tirunelueli Distric, Tamil Nadu, India: A GIS Approach. Environ. Earth Sci. 2011, 64, 373–381. [Google Scholar] [CrossRef]
- Smith, K. Standards for Grading Textures of Erosional Topography. Am. J. Sci. 1950, 248, 655–668. [Google Scholar] [CrossRef]
- Singh, S.; Singh, M.C. Morphometric Analysis of Kanhar River Basin. Natl. Geogr. J. India 1997, 43, 31–43. [Google Scholar]
- Mesa, L.M. Morphometric analysis of a subtropical Andean basin (Tucumam, Argentina). Environ. Geol. 2006, 50, 1235–1242. [Google Scholar] [CrossRef]
- Sharifikia, M.; Shayan, S.; Yamani, M.; Arabameri, A. Morphometric parameter extraction and analysis for watershed periodization over the Naka Roud Catchment. Iran. J. Ecohydrol. 2018, 5, 69–83. [Google Scholar]
- Patel, D.; Gajjar, C.; Srivastava, P. Prioritization of Malesari Mini-Watersheds through Morphometric Analysis: A Remote Sensing and GIS Perspective. Environ. Earth Sci. 2013, 69, 2643–2656. [Google Scholar] [CrossRef]
- Khare, D.; Mondal, A.; Kumar Mishra, P.; Kundu, S.; Kumar Meena, P. Morphometric Analysis for Prioritization using Remote Sensing and GIS Techniques in a Hilly Catchment in the State of Uttarakhand, India. Indian J. Sci. Technol. 2014, 7, 1650–1662. [Google Scholar]
- Abdul Rahaman, S.; Abdul Ajeez, S.; Aruchamy, S.; Jegankumar, R. Prioritization of sub-watersheds based on morphometric characteristics using fuzzy analytical hierarchy process and geographical information system—a study of Kallar Watershed. Tamil Nadu. Aquat. Procedia 2015, 4, 1322–1330. [Google Scholar] [CrossRef]
- Farhan, Y.; Anaba, O. A remote sensing and GIS approach for prioritization ofWadi Shueib Mini-Watersheds (Central Jordan) based on morphometric and Soil erosion susceptibility analysis. J. Geogr. Inf. Syst. 2016, 8, 1–19. [Google Scholar]
- Arabameri, A.; Pourghasemi, H.R.; Cerda, A. Erodibility prioritization of subwatersheds using morphometric parameters analysis and its mapping: A comparison among TOPSIS, VIKOR, SAW, and CF multi-criteria decision making models. Sci. Total Environ. 2017, 613–614, 1385–1400. [Google Scholar]
- Arabameri, A.; Cerda, A.; Rodrigo-Comino, J.; Pradhan, B.; Sohrabi, M.; Blaschke, T.; Tien Bui, D. Proposing a Novel Predictive Technique for Gully Erosion Susceptibility Mapping in Arid and Semi-arid Regions (Iran). Remote Sens. 2019, 11, 2577. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).