1. Introduction
Soil erosion (SE) threatens sustainable development [
1]. More than three hundred years is needed to form a centimeter of soil [
2], therefore the prevention of SE is vital to protect valuable resources [
3]. In arid and semiarid regions, SE destroys soil fertility and threatens agriculture [
4]. Defoliation, flooding, reduced effectiveness of dams, increasing economic losses, desertification, and land use changes are major consequences of SE [
5]. The global rate of annual SE is approximated to be 75 billion tons [
6]. Iran loses more than two billion tons every year, approximately three times the rates of other Asian countries. Approximately 125 million of the 165 million ha of the country experiences erosion [
7]. This is roughly 75% of the entire country and 60% of Iran’s agricultural land. Iran’s average erosion is 30–32 ton/ha/year, which is 4.3 times the global average [
7]. Economic losses caused by SE in Iran have been estimated to be 10 trillion rial [
8]. Therefore, SE management and protection in Iran is urgently needed, in line with the United Nations Sustainable Development Goals [
9]. This study prepared a SE risk map using effective factors to predict locations that are more likely to be SE “hot spots.”
A basin is the developmental unit used to effectively manage resources sustainably [
10]. It is a natural hydrological feature within which runoff is directed into collecting channels, streams, or rivers [
11]. The characteristics and conditions of a basin or drainage basin determine the development of the landforms within it. Therefore, identification of the most important characteristics of a basin is integral to understanding its geomorphology [
12]. Basin management planning can strive to control losses from SE in a basin [
13]. Although there are several factors that influence SE, the major agent is water. SE is not a new problem, but it has become common and is worsening in Iran. It is particularly visible in the Kalvārī river basin.
Soil, geomorphology, hydrology, and landscapes are intimately linked. Measurement and analysis of Earth’s surface through geomorphometry is undertaken to understand the relationships between the sizes and shapes of a region’s features [
10]. SE, runoff, the evolution of rivers, sedimentation, and drainage geometry are reflections of hydrological and geomorphic processes, and are ultimately assessable using morphometry [
10]. Therefore, the morphometry of a basin can explain its hydrological behaviors. The basin is the unit of morphometric analysis, which is a technique introduced by Horton [
14,
15] and elaborated upon by Strahler [
16,
17,
18], Miller [
19], and Schumm [
20]. Together, they provided the foundations for the field of quantitative fluvial geomorphology [
21].
Because resource development planning is generally conducted at the watershed scale, it is critical to prioritize management of natural resources for sustainable development [
11]. Prioritization for soil or water conservation can be improved by quantitative analyses of morphometric watershed parameters [
10]. Morphometric analysis quantitatively describes drainage systems to understand landform- and soil-development processes as well as erosional characteristics [
22]. Morphometry is the quantitative measurement of the shapes and dimensions of Earth’s landforms. Areas, volumes, elevations, slopes, profiles, and textures of the surface are the characteristics of utmost interest [
22]. River basin morphometry reflects the hydrological and geomorphic responses of runoff, SE, flooding, drought, sedimentation, fluvial bifurcation, the flow characteristics and flow volumes of drainages and rivers, and the capacities and sustainability of reservoirs within a basin. Conventional studies have explored the relationships between the properties of drainage networks and other influences like climate, relief, lithology, structure, and tectonics to interpret morphometrics [
23,
24,
25]. The tectonics of river basins have been examined for links to the geomorphological processes that shape drainages [
26]. Recently, stream network morphometry has been used more often to assess water, soil, and hazards in developing countries [
27,
28,
29,
30].
Geospatial analytical techniques (geographic information systems (GIS) and remote sensing (RS)), and multi-criteria decision-making models (MCDM) have enhanced quantitative assessments of drainage networks, thematic mapping of morphometry, and applied morphometric analyses [
31,
32,
33,
34,
35,
36]. Furthermore, other software designed to quantify and calculate linear, areal, shape, and relief MPs have also advanced the sophistication of morphometrics [
37,
38]. Comparisons of conventionally and manually collected data to automated geospatial methods have demonstrated that modern technologies are powerful and cost-effective for better management and processing of data and for creating maps for a variety of applications [
39,
40].
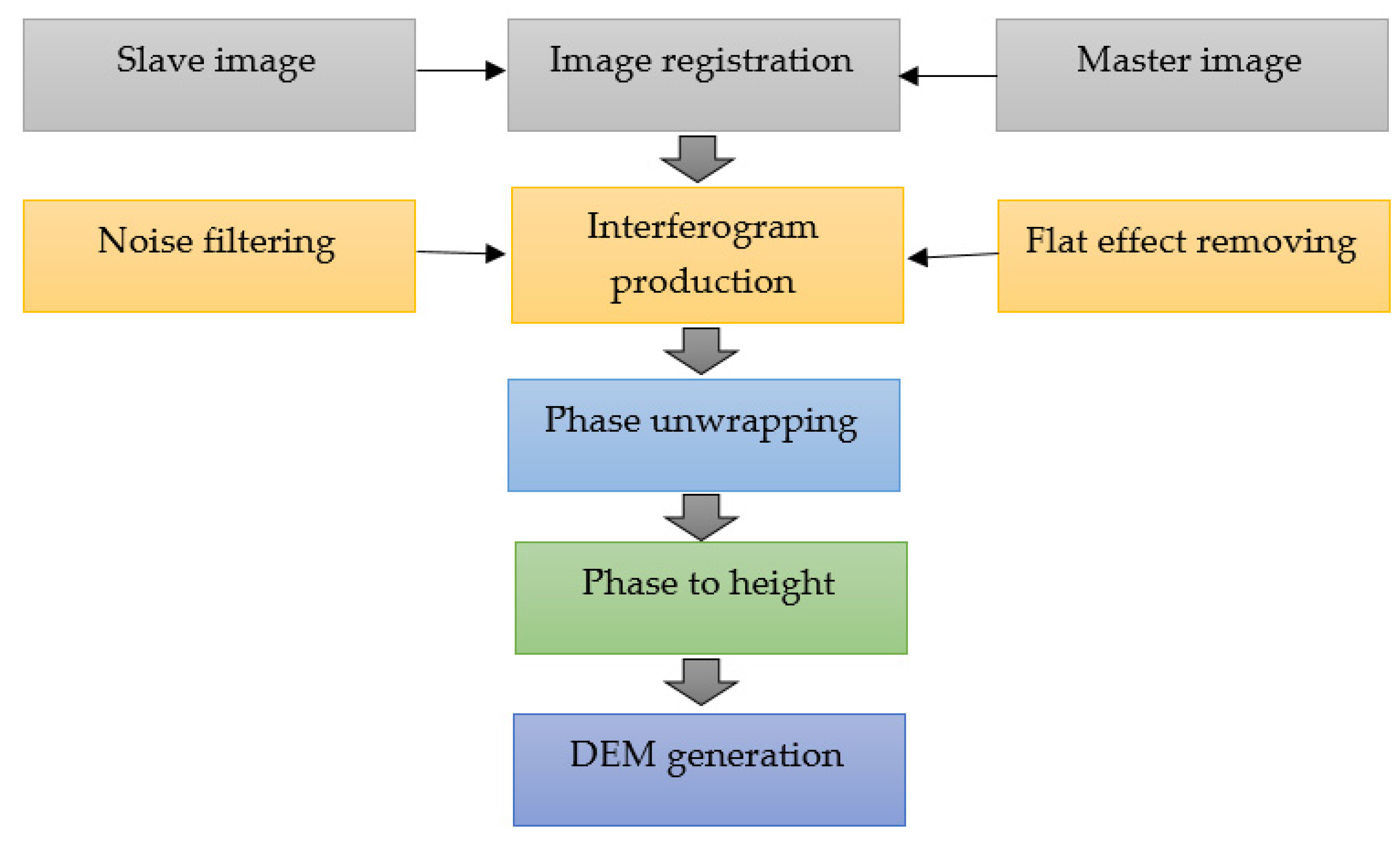
Digital elevation models (DEMs) are a standard source of data that can be used to discern the mechanisms behind geomorphological processes. DEMs are developed using several data sources. Ground surveys, photogrammetry, optical RS, radar, and lidar are the principal data acquisition methods. Synthetic aperture radar (SAR) data are analyzed using interferometry and radargrammetry, which detect phase discrepancies in each pixel. Elevation change is determined stereoscopically [
41]. Highly detailed models of elevations are developed by comparing precise measurements of phase-shifts of reflected wavelengths from Earth’s surface using interferometric synthetic aperture radar (InSAR) [
42]. Numerous studies have examined the use of methods to analyze radar data to produce DEMs [
41]. First-order streams (Horton’s “fingertip” streams) can be delineated precisely using DEMs. GIS and RS can be used to measure and calculate drainage-basin MPs economically and can enable efficient analysis of large amounts of spatial information [
43,
44,
45].
Few studies have used morphometric analysis of SE to prioritize sub-watersheds. Altaf and Meraj [
46] combined an Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) DEM with 14 MPs in a multi-criteria analysis (MCA) to assess the susceptibility of a watershed in the western Himalaya to SE. They found that three sub-watersheds could be regarded as very high priority (highly susceptible to SE) for management. Ahmad Rather et al. [
47] coupled 13 morphometric, land use, and slope parameters and data from a Shuttle-Radar Topography Mission (SRTM) DEM in an MCA to estimate SE susceptibility in the Jhelum basin of Kashmir. Gajbhiye et al. [
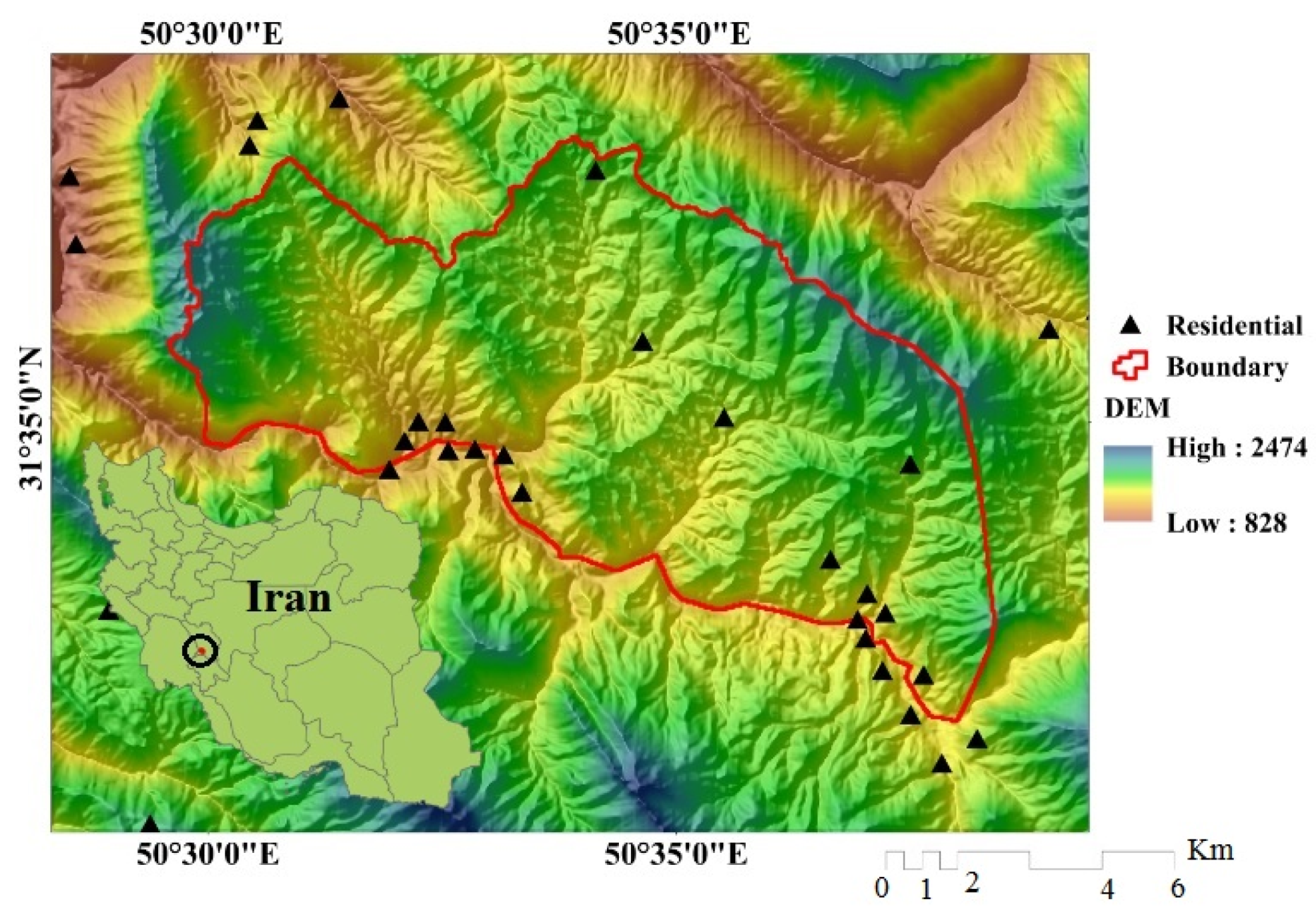
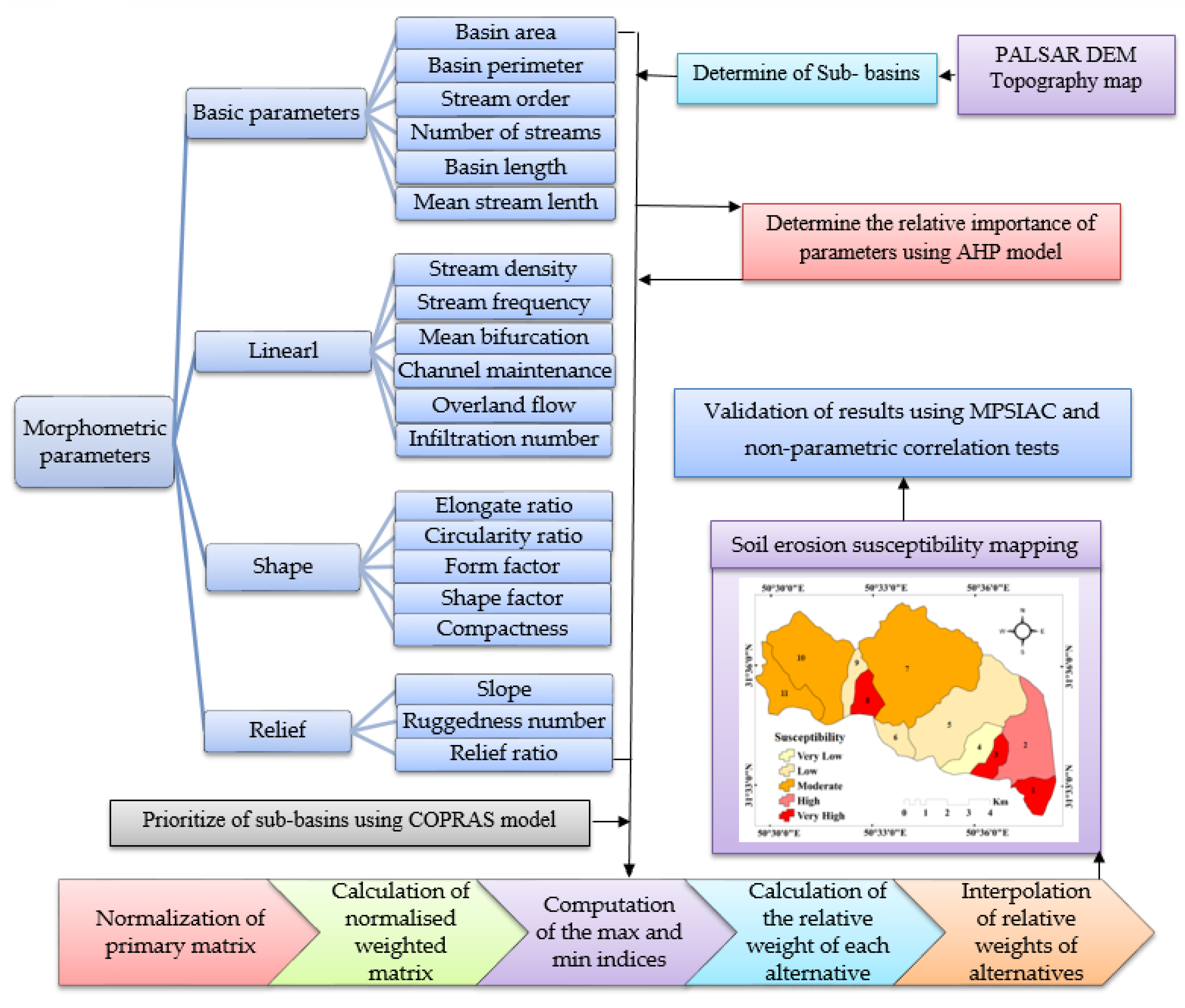
13] used an SRTM DEM and morphometric analysis on 14 sub-watersheds of the Manot River catchment (a tributary of the Narmada River) to discern SE susceptibility. One sub-watershed had the lowest compound parameter value and was therefore most likely to experience the greatest amount of SE. This study combines a novel MCDM-based approach (the complex proportional assessment of alternatives (COPRAS)-analytical hierarchy process (AHP)) with MPs to prioritize sub-basins by their susceptibility to SE. SE was mapped: (1) to model non-quantitative parameters; (2) to devise a method to compare different types of variables and to handle data at different scales; (3) to eliminate strict assumptions behind the study; (4) to fill a gap in the scholarship wherein only a few studies have employed MCDM models to assess SE susceptibility; and (5) to undertake a comprehensive study of the capabilities of COPRAS-AHP ensemble models for SE susceptibility analysis. The study area is the Kalvārī Basin in Iran, an area that experiences high rates of SE. The main objectives of this study were: (1) to analyze the MPs of the Kalvārī Basin using GIS, RS, and a Phased-Array type L-band Synthetic Aperture Radar (PALSAR) DEM (spatial resolution 12.5 m); (2) to prioritize sub-basins and to identify the major MPs that influence SE in the Kalvārī Basin using the COPRAS-AHP novel ensemble MCDM model; and (3) to identify the sub-basin landscape parameters that dictate the SE potential of fluvial forces and SE susceptibility throughout the region. The results will provide better SE management and will enhance other environmental activities like land use planning, hazard management, and water conservation. This approach to morphometric analysis could be transferred to other, similar highland basins in other arid regions.
4. Discussion
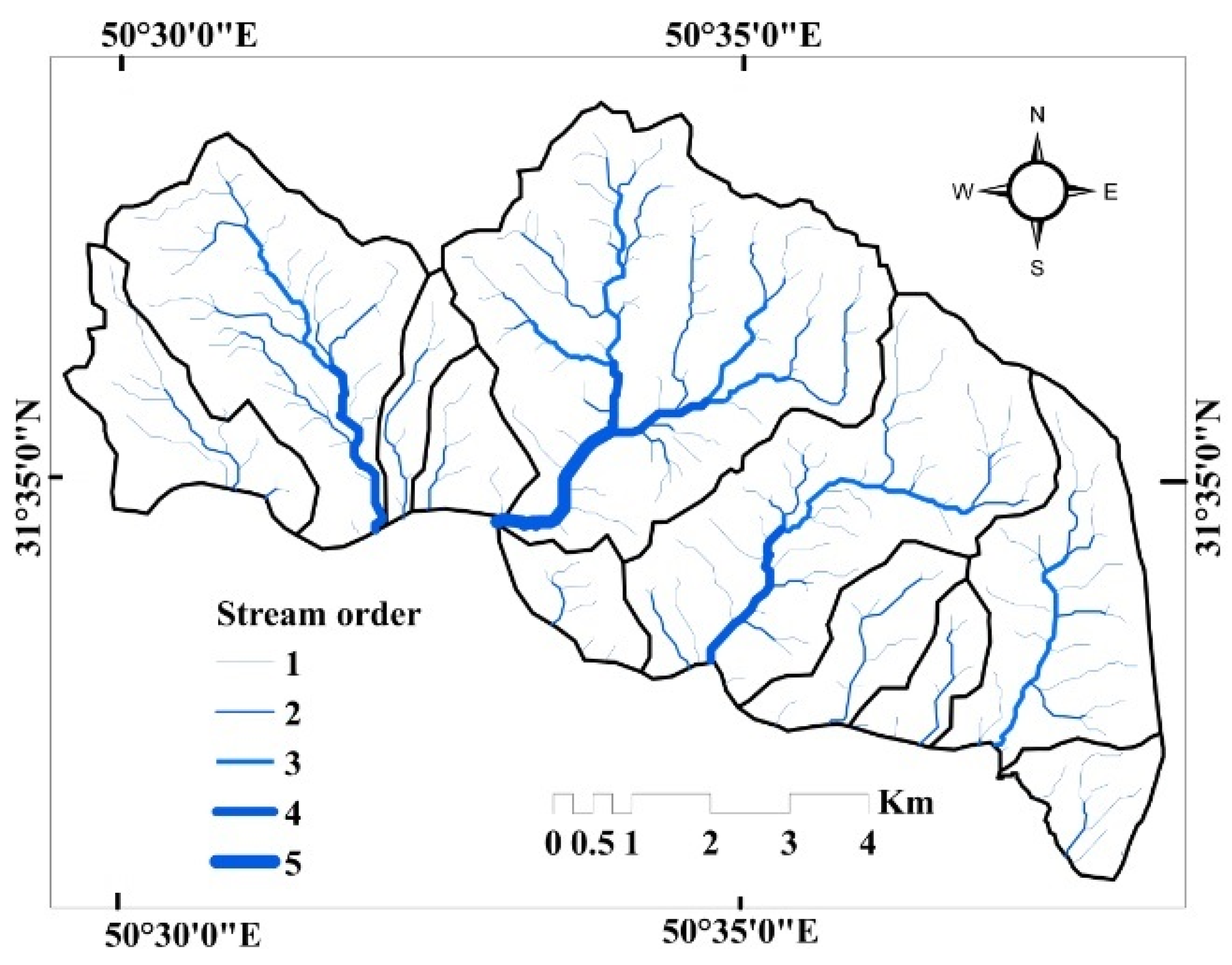
The Kalvārī Basin was selected for study because of the extent to which it is impacted by SE. Erosion processes in the basin reflect its morphology—visible in its linear relief pattern, its shape, and its spatial extent. After determining its drainage network and MPs using RS, GIS, and a DEM, the AHP-COPRAS ensemble model was used to develop a map of SE susceptibility and to rank the sub-basins by the intensity of SE. The results of the map were compared to the results from two individual models.
Digitally estimating MPs provided an easier, more accurate, and more quantitative method to evaluate morphometric characteristics and to analyze the variations within the region. PALSAR DEM has been used previously for morphometric studies, especially in mountainous regions, as it provides more accurate elevation measurements and better morphometric and geomorphic details (compared to ASTER and SRTM DEMs) [
77].
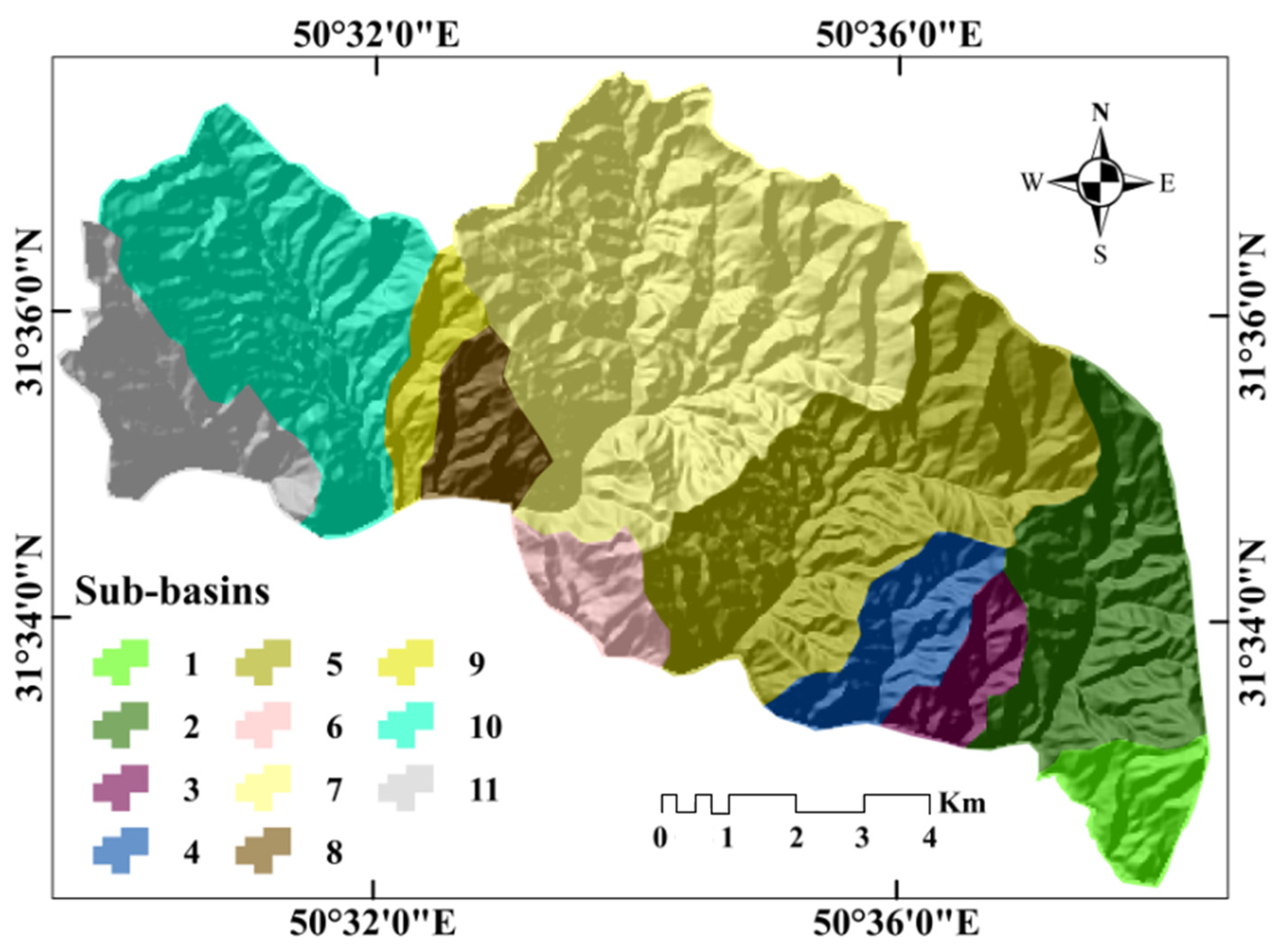
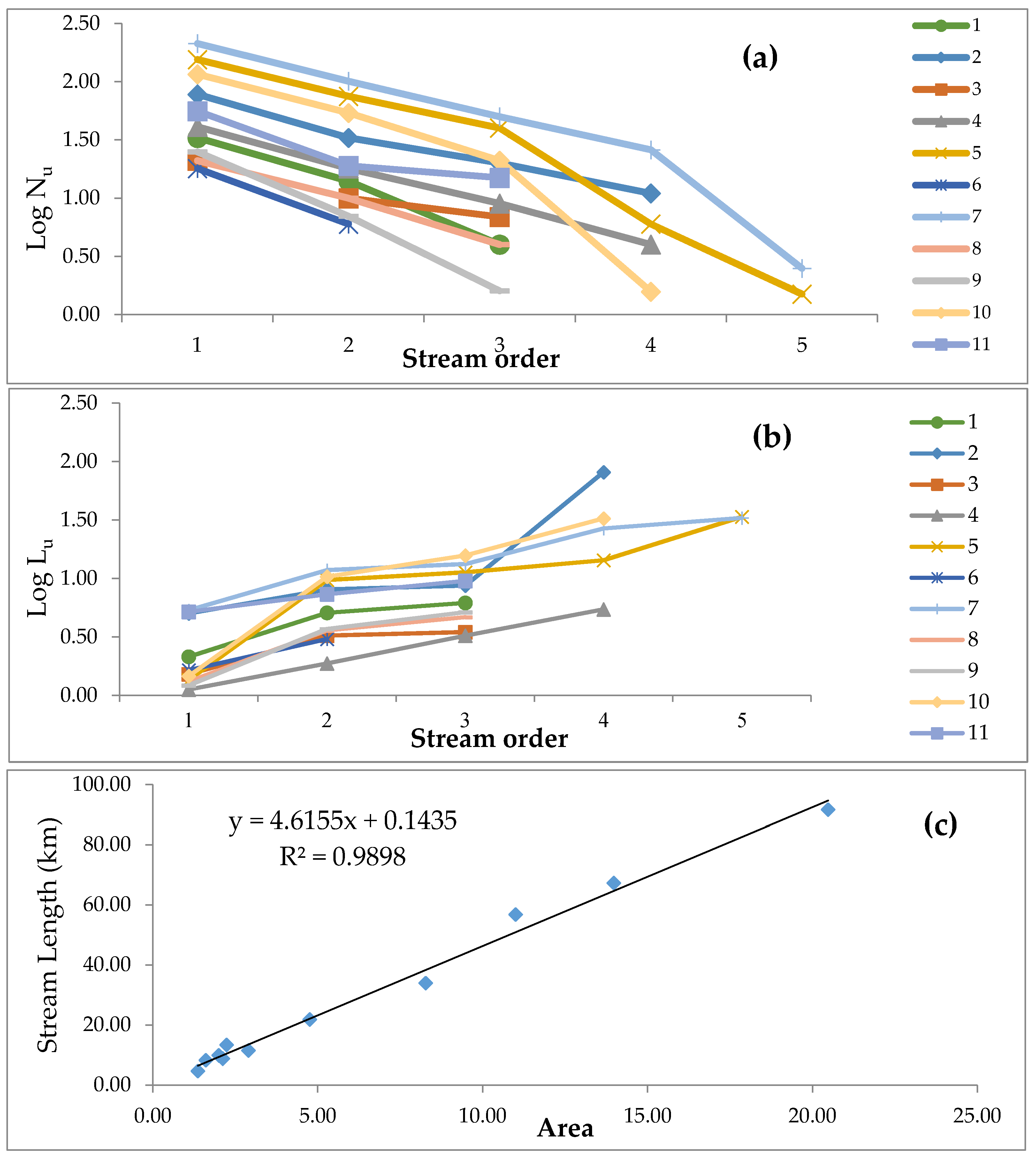
First-order streams comprise nearly 67% of the streams in the study area. That first-order streams are the most numerous of all orders indicates that there is a structural weakness in the basin in the form of lineaments [
78]. Stream frequency in all sub-basins is moderate, which indicates that there is moderate run-off intensity and high drainage density. The terrain is highly dissected. Sub-basins are finely textured, indicating highly developed drainage and high rates of SE. Stream frequency, drainage density, and texture are very high in sub-basins 1 and 3, which indicates that these sub-basins experience intensive SE. The values of these three characteristics are lowest in sub-basin 4, a unit that is less prone to SE. Relief ratios generally depict a high-energy basin with substantial SE and high sediment loads. This parameter is very high in sub-basins 1 and 8, where SE rates are high, and slopes are moderate. By contrast, the relief ratios are very low in sub-basins 4 and 5, low-energy drainages as exhibited by their gentle topographies.
Despite the low mean slope for the region overall, both the maximum and minimum slope angles of the Kalvārī Basin are in sub-basin 4, where the gentle topography has attracted greater human activity. This has created a plateau-like terrain—a flat platform with steeply sloping edges on its perimeter. This unit is a low-energy landscape with less sediment in streams. Sub-basins 1, 11, and 8 have higher mean slopes, and provide favorable topography for higher SE potential. The ruggedness numbers of all the sub-basins reflect the mountainous nature of the region’s terrain, with significant amounts of SE and dissection. The lowest ruggedness value is found in sub-basin 4 and the highest is in sub-basin 8; these compliment the patterns of slope and relief ratios discussed above. Shape factors reflect the geomorphology of a landscape and provide evidence of run-off and infiltration processes [
76]. Sub-basins 6, 3, 9, and 1 have the highest form factors of the sub-basins, reflecting their more ovate and less elongated shapes (these forms are consistent with the elongation measures and circulatory ratios for those units). The higher form-factor values of these sub-basins indicate more drainage development and more structural control.
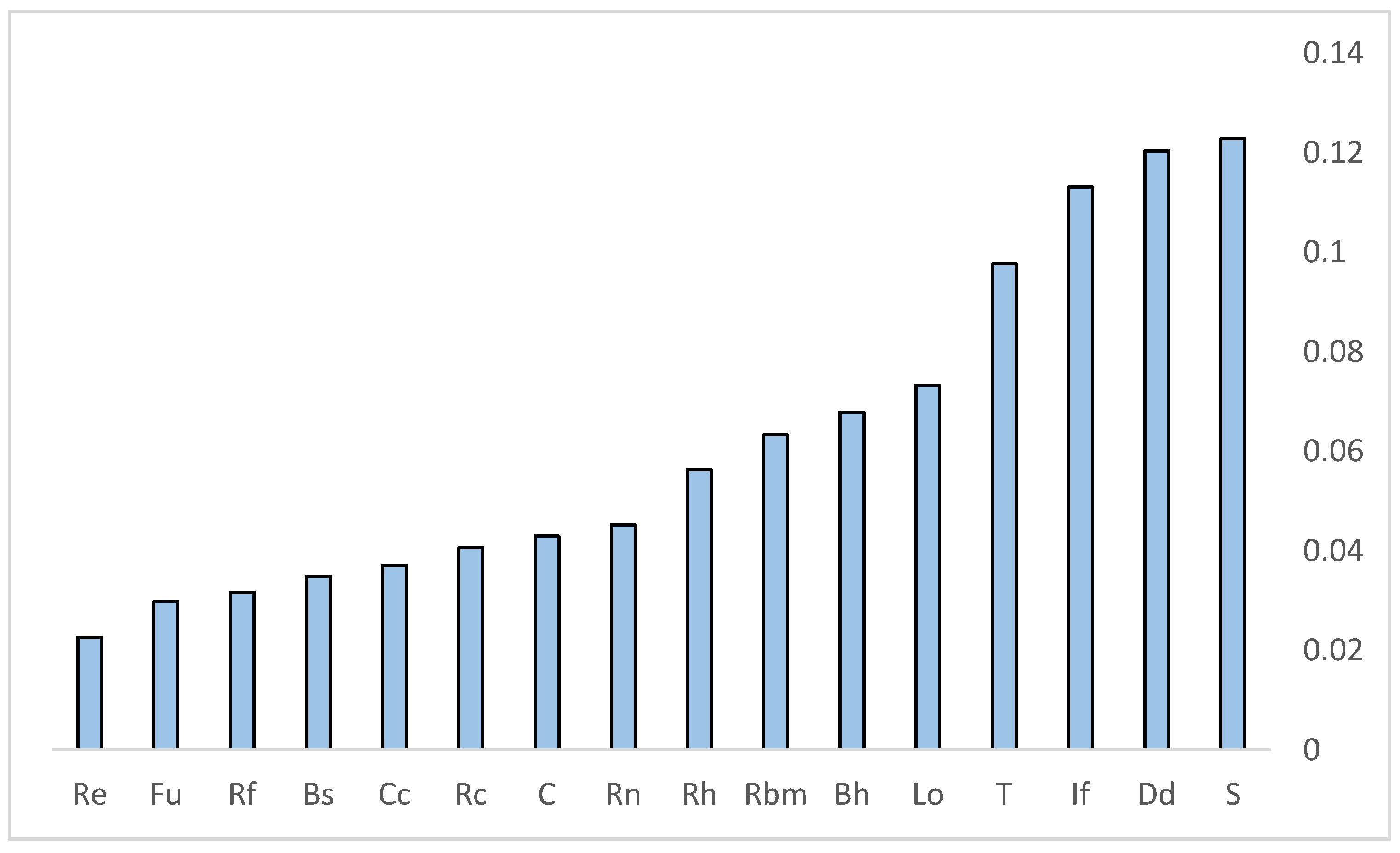
Based on the results of the AHP model, we know that slope, drainage density, infiltration number, and texture ratio significantly impact SE in the study area, results which are consistent with others [
12,
79,
80,
81,
82]. Arabameri et al. [
82] used four MCDM-based models to rank the sub-basins’ SE susceptibilities by analyzing the MPs. The mean bifurcation ratio (Rbm), slope (S), and infiltration number (If) have key roles in SE rates. Slope is a morphometric factor associated with hydrology that indicates runoff volumes and runoff concentration time [
76]. Soil infiltration-capacity and the initial resistance of a surface to SE depend on drainage density [
73]. Infiltration number is very important for expressing a basin’s infiltration characteristics and depends directly on the basin’s runoff capacity [
76]. Validation of the results by using non-parametric tests shows that the ensemble model performed better than the AHP and COPRAS individual models. This is consistent with the findings of Arabameri et al. [
83] which indicated that ensemble MCDM-based models perform better than individual models.
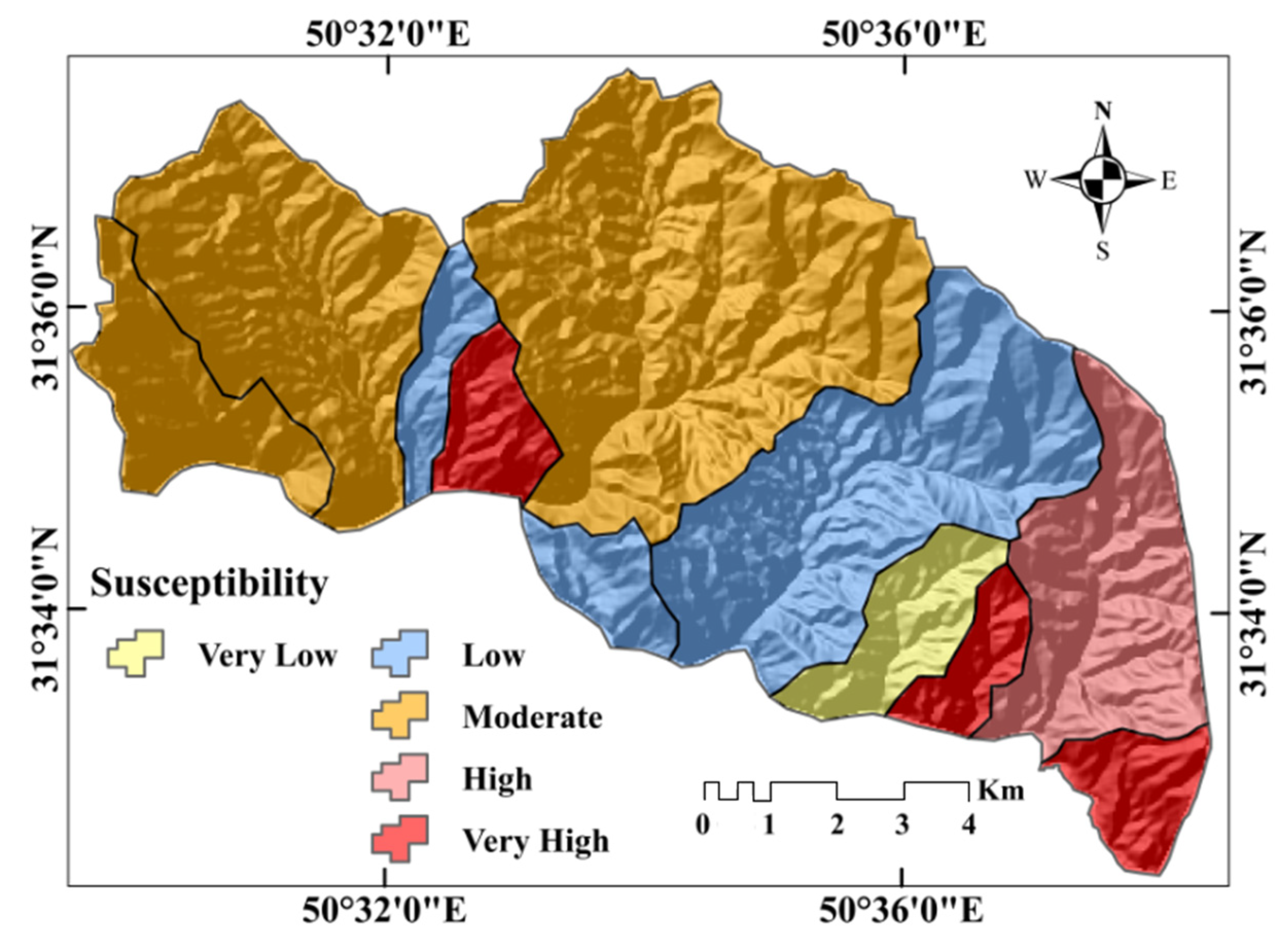
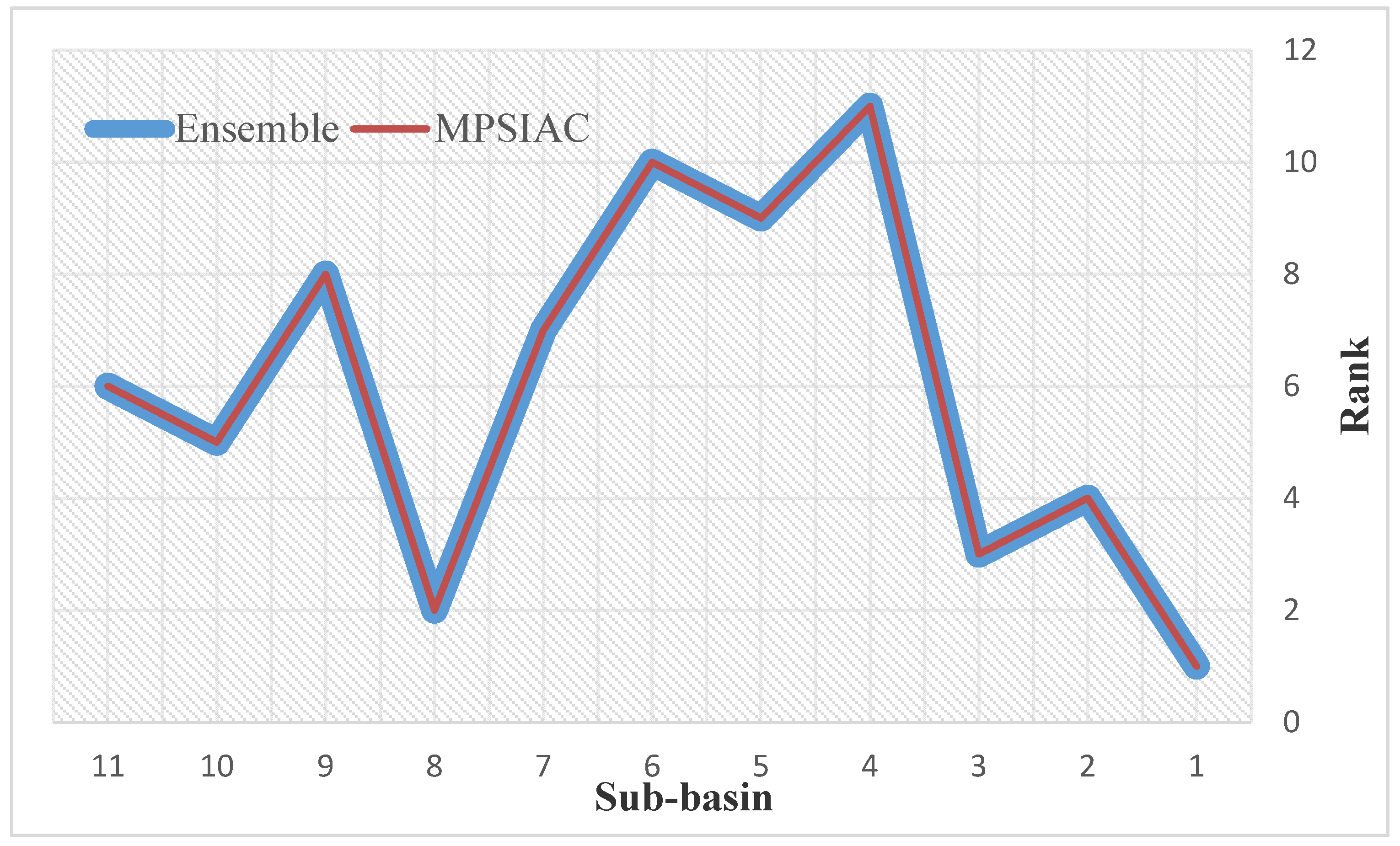
Validation of the ensemble model with the MPSIAC model shows that the ensemble model very accurately prioritized sub-basins and could be used to prepare SE susceptibility maps. Sub-basins 1, 3, and 8 might be experiencing heavy SE and sedimentation due to either higher erodibility of hills in these areas, greater slopes, or land-cover changes (from compact to less compact pastures). The sub-basins with slight and moderate SE and sedimentation may be less affected because of ultrabasic and crystallized limestone formations, rock outcrops, or cultivated lands. The results provide ways to identify very erosive areas and open new horizons in watershed management and sediment control by providing greater evidence to support conservation-project prioritization.
Compared to other commonly used approaches to produce SE susceptibility maps, this ensemble approach can be achieved with much simpler input data, specifically morphometric data, that can be easily extracted from DEMs. Our approach does not need other SE parameters that might necessitate a soil-inventory map, a source that is very time-consuming and expensive create. One limitation of this method is that it ignores human activities that interfere with hydrologic processes (e.g., reducing a river’s flow capacity), actions that often amplify SE. Moreover, additional information derived from land use analyses that can be used to detail soil-erosion history would be beneficial, as they would clarify the connection between spatial patterns of activities and SE zones. But suitable results can be achieved without the best information.
5. Conclusions
The common approaches to assess the problem of SE, to develop management plans to address it, require quantitative SE rate data at regional and global scales. In this research, the morphometric characteristics of the Kalvārī Basin were determined for use in an MCDM-based ensemble model. A PALSAR DEM was input into a GIS, allowing for the development of quantitative and qualitative morphometric analyses and the extraction of the spatial patterns of MPs. An AHP model was used to evaluate the importance of each of the 16 parameters and revealed that slope, drainage density, and infiltration number were the most important predictors of SE potential. A COPRAS-AHP ensemble model indicated that sub-basins 1, 3, and 8 are highly susceptible to SE. Validation of the modeled results using MPSIAC and non-parametric tests show that the ensemble model and the ranking of MPs achieved strong prediction accuracy of SE susceptibility and this enables a faster and less expensive prioritization of sub-basins for management actions. The method presented here takes advantage of computer-assisted extraction and computation of morphometric characteristics to predict the spatial patterns of the intensity of SE potential. A significant advantage is that only high-quality empirical topographical data are employed. In this way, one can produce assessments for catchments that either lack stream gages and extensive, large-scale records of past SE patterns, or are remote and difficult to access. This, in fact, describes most of the watercourses in Iran. Given the predicted high SE-susceptibility of sub-basins 1, 3, and 8, it is recommended that protective measures be taken to arrest SE, reduce sedimentation in reservoirs, stabilize slopes against mass wasting, and reduce flood risk.