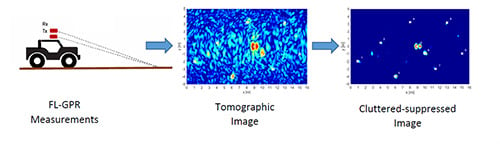
Coherence-Factor-Based Rough Surface Clutter Suppression for Forward-Looking GPR Imaging
Abstract
1. Introduction
2. Methods
2.1. Matched-Filtering-Based Near-Field Tomographic Imaging
2.2. Back-Projection Algorithm
2.3. Coherence-Factor-Based Image Enhancement
3. Results
3.1. Radar Configuration
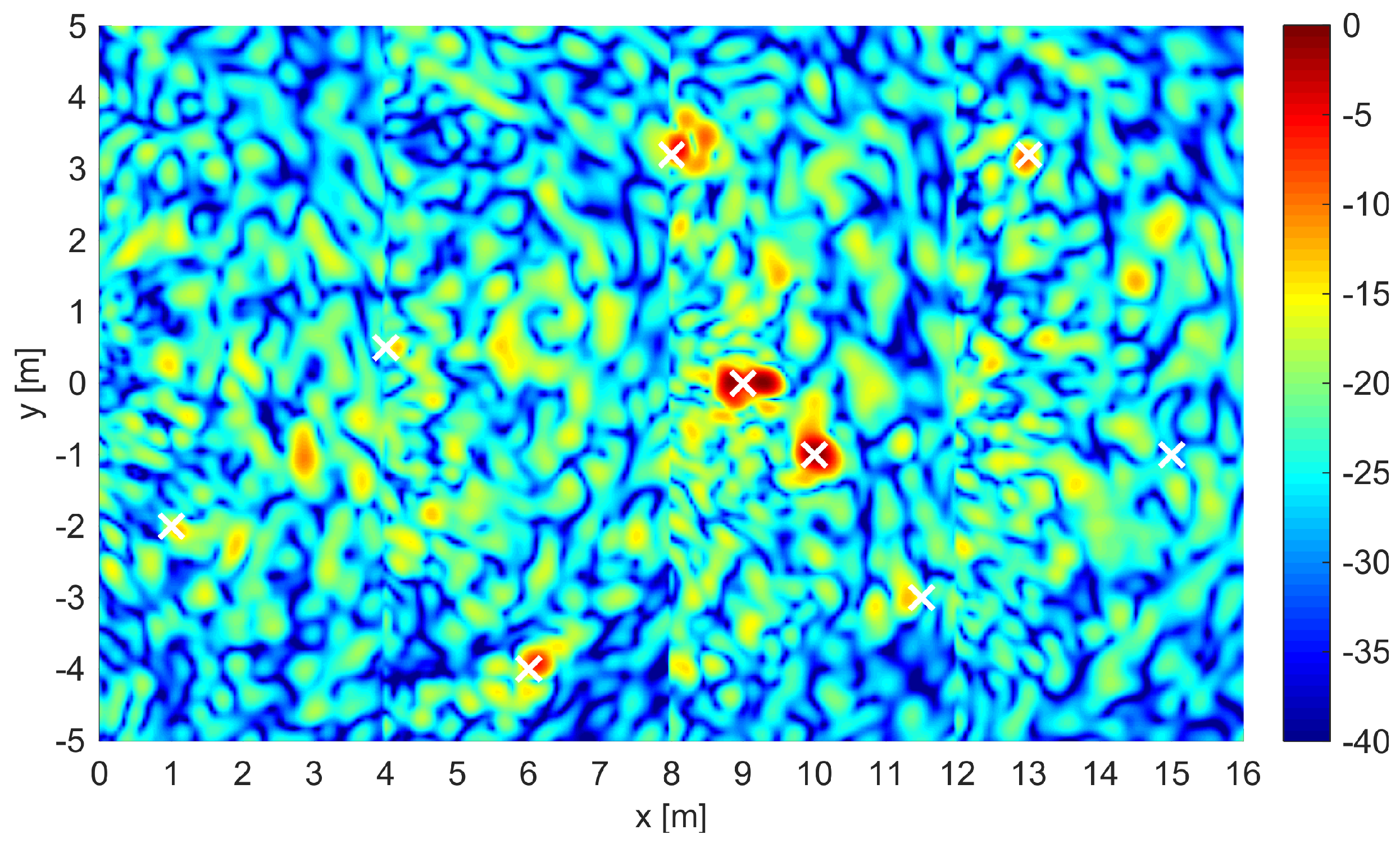
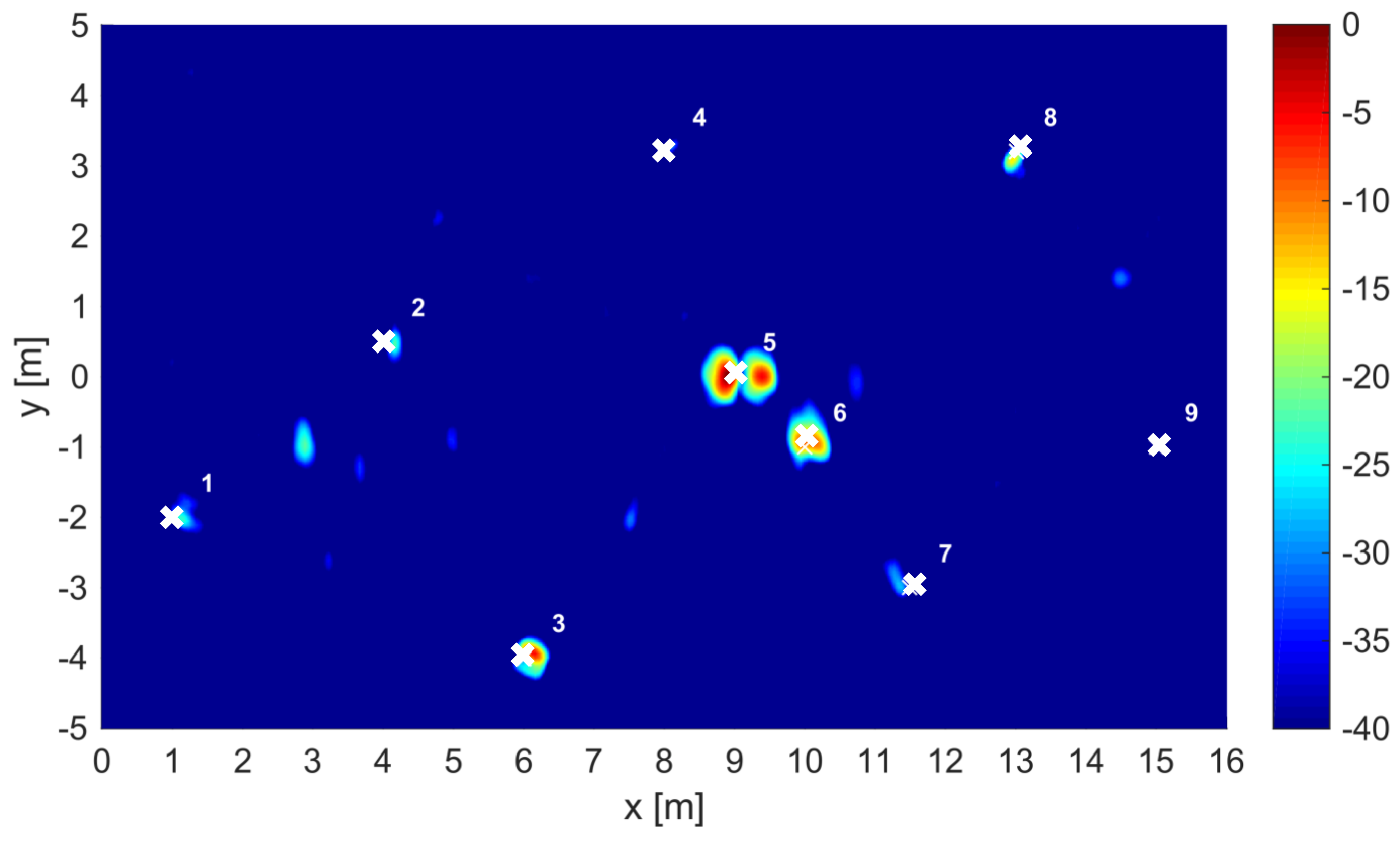
3.2. Image Formation Results
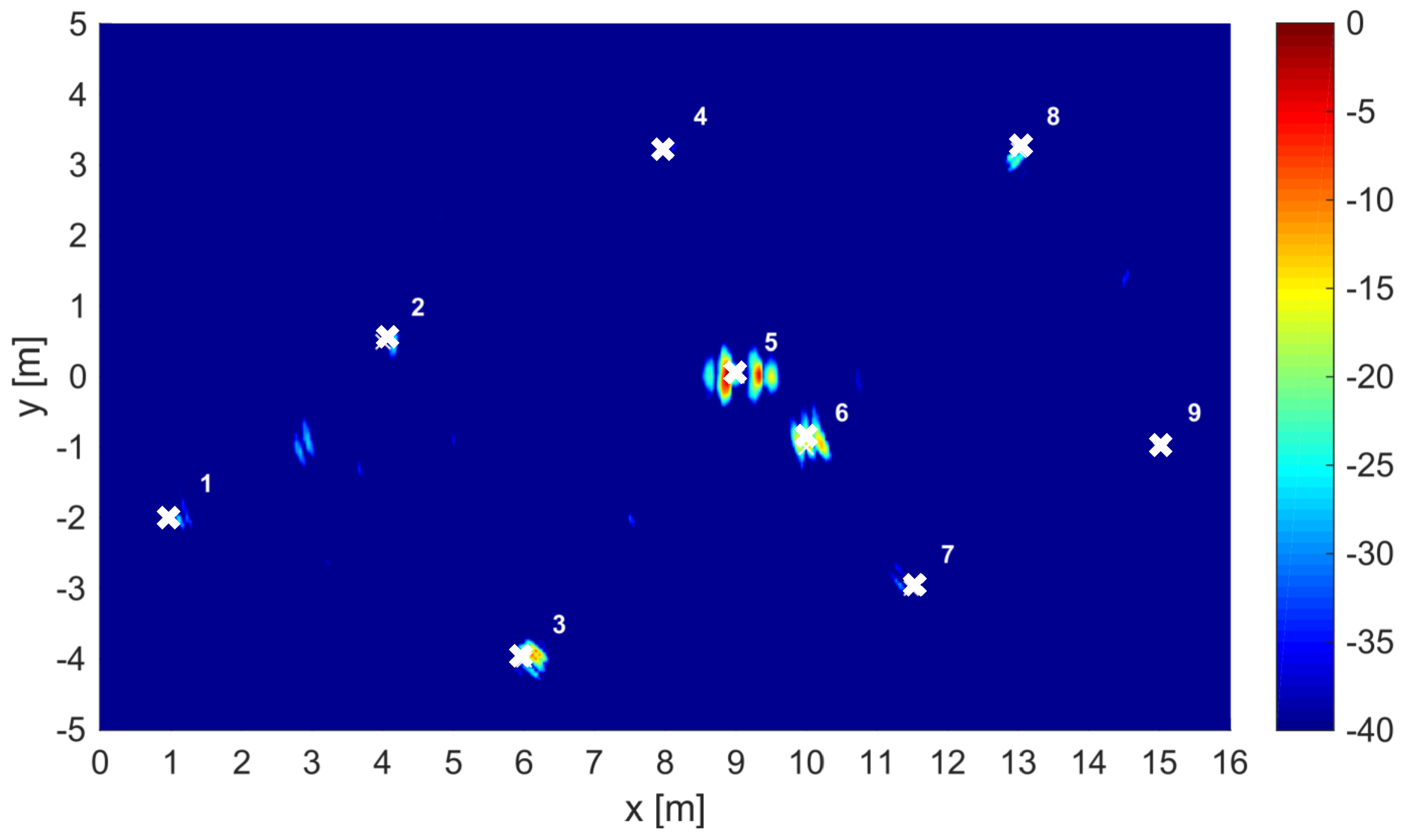
3.3. CF Enhanced Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Pastorino, M. Microwave Imaging; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2010. [Google Scholar]
- Jin, S.; Haghighipour, N.; Ip, W.-H. (Eds.) Planetary Exploration and Science: Recent Results and Advances; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Amin, M.G. Through-the-Wall Radar Imaging; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Solimene, R.; Catapano, I.; Gennarelli, G.; Cuccaro, A.; Dell Aversano, A.; Soldovieri, F. SAR imaging algorithms and some unconventional applications. IEEE Signal Process. Mag. 2014, 31, 90–98. [Google Scholar] [CrossRef]
- Persico, R. Introduction to Ground Penetrating Radar: Inverse Scattering and Data Processing; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2014. [Google Scholar]
- Lo Monte, L.; Erricolo, D.; Soldovieri, F.; Wicks, M.C. Radio frequency tomography for tunnel detection. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1128–1137. [Google Scholar] [CrossRef]
- Garcia-Fernandez, M.; Morgenthaler, A.; Alvarez-Lopez, Y.; Las Heras, F.; Rappaport, C. Bistatic landmine and IED detection combining vehicle and drone mounted GPR sensors. Remote Sens. 2019, 11, 2299. [Google Scholar] [CrossRef]
- Kositsky, J.; Cosgrove, R.; Amazeen, C.; Milanfar, P. Results from a forward-looking GPR mine detection system. Proc. SPIE 2002, 4742, 206–217. [Google Scholar]
- Kositsky, E.M.; Rotondo, F.S.; Elizabeth, A. Testing and evaluation of forward-looking GPR countermine systems. Proc. SPIE 2005, 5794, 901–911. [Google Scholar]
- Wang, Y.; Sun, Y.; Li, J.; Stoica, P. Adaptive imaging for forward-looking ground penetrating radar. IEEE Trans. Aerosp. Electron. Syst. 2005, 41, 922–936. [Google Scholar] [CrossRef]
- Wang, T.; Keller, J.M.; Gader, P.D.; Sjahputera, O. Frequency sub-band processing and feature analysis of forward-looking ground penetrating radar signals for land-mine detection. IEEE Trans. Geosci. Remote Sens. 2007, 45, 718–729. [Google Scholar] [CrossRef]
- Soldovieri, F.; Gennarelli, G.; Catapano, I.; Liao, D.; Dogaru, T. Forward-looking radar imaging: A comparison of two data processing strategies. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 562–571. [Google Scholar] [CrossRef]
- Ogworonjo, H.C.; Anderson, J.M.M.; Nguyen, L.H. An iterative parameter-free MAP algorithm with an application to forward looking GPR imaging. IEEE Trans. Geosci. Remote Sens. 2017, 55, 1573–1586. [Google Scholar] [CrossRef]
- Comite, D.; Ahmad, F.; Liao, D.; Dogaru, T.; Amin, M.G. Multiview imaging for low-signature target detection in rough-surface clutter environment. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5220–5229. [Google Scholar] [CrossRef]
- Catapano, I.; Affinito, A.; Del Moro, A.; Alli, G.; Soldovieri, F. Forward-looking ground-penetrating radar via a linear inverse scattering approach. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5624–5633. [Google Scholar] [CrossRef]
- Sun, Y.; Li, J. Time-frequency analysis for plastic landmine detection via forward-looking ground penetrating radar. Proc. Inst. Elect. Eng. Radar Sonar Navig. 2003, 150, 253–261. [Google Scholar] [CrossRef]
- Nguyen, L. SAR imaging technique for reduction of sidelobes and noise. Proc. SPIE 2009, 7308, 73080U. [Google Scholar]
- Liao, D.; Dogaru, T.; Sullivan, A. Large-scale, full-wave-based emulation of step-frequency forward-looking radar imaging in rough terrain environments. Sens. Imag. 2014, 15, 88. [Google Scholar] [CrossRef]
- Ton, T.; Wong, D.; Soumekh, M. ALARIC forward-looking ground penetrating radar system with standoff capability. In Proceedings of the 2010 IEEE International Conference on Wireless Information Technology and Systems, Honolulu, HI, USA, 8 August–3 September 2010. [Google Scholar]
- Yang, J.; Jin, T.; Huang, X.; Thompson, J.; Zhou, Z. Sparse MIMO array forward-looking GPR imaging based on compressed sensing in clutter environment. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4480–4494. [Google Scholar] [CrossRef]
- Tajdini, M.M.; Gonzalez-Valdes, B.; Martinez-Lorenzo, J.A.; Morgenthaler, A.W.; Rappaport, C.M. Real-time modeling of forward-looking synthetic aperture ground penetrating radar scattering from rough terrain. IEEE Trans. Geosci. Remote Sens. 2019, 57, 2754–2765. [Google Scholar] [CrossRef]
- Comite, D.; Ahmad, F.; Dogaru, T.; Amin, M.G. Adaptive detection of low-signature targets in forward-looking GPR imagery. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1520–1524. [Google Scholar] [CrossRef]
- Pambudi, A.D.; Fauss, M.; Ahmad, F.; Zoubir, A.M. Robust detection for forward-looking GPR in rough-surface clutter environments. In Proceedings of the 52nd Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 28–31 October 2018; pp. 2077–2080. [Google Scholar]
- Keller, S.K.; Ho, K.C.; Busch, M.; Gader, P.D. On the registration of FLGPR and IR data for a forward-looking landmine detection system and its use in eliminating FLGPR false alarms. Proc. SPIE 2008, 6953, 695314. [Google Scholar]
- Li, L.; Zhang, W.; Li, F. Derivation and discussion of the SAR migration algorithm within inverse scattering problem: Theoretical analysis. IEEE Trans. Geosci. Remote Sens. 2010, 48, 415–422. [Google Scholar]
- Gilmore, C.; Jeffrey, I.; Lo Vetri, J. Derivation and comparison of SAR and frequency-wavenumber migration within a common inverse scalar wave problem formulation. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1454–1461. [Google Scholar] [CrossRef]
- Leuschen, C.J.; Plumb, R.G. A matched-filter-based reverse-time migration algorithm for ground-penetrating radar data. IEEE Trans. Geosci. Remote Sens. 2001, 39, 929–936. [Google Scholar] [CrossRef]
- Hollman, K.W.; Rigby, K.W.; O Donnell, M. Coherence factor of speckle from a multi-row probe. In Proceedings of the 1999 IEEE Ultrasonics Symposium, Caesars Tahoe, NV, USA, 17–20 October 1999; pp. 1257–1260. [Google Scholar]
- Klemm, M.; Leendertz, J.A.; Gibbins, D.; Craddock, I.J.; Preece, A.; Benjamin, R. Microwave radar-based breast cancer detection: Imaging in inhomogeneous breast phantoms. IEEE Antennas Wireless. Prop. Lett. 2009, 8, 1949–1952. [Google Scholar] [CrossRef]
- Burkholder, R.J.; Browne, K.E. Coherence factor enhancement of through-wall radar images. IEEE Antennas Wirel. Prop. Lett. 2010, 9, 842–845. [Google Scholar] [CrossRef]
- Liao, D.; Dogaru, T. Full-wave characterization of rough terrain surface scattering for forward-looking radar applications. IEEE Trans. Antennas Propag. 2012, 60, 3853–3866. [Google Scholar] [CrossRef]
- Comite, D.; Ahmad, F.; Dogaru, T.; Amin, M.G. Coherence factor for rough surface clutter mitigation in forward-looking GPR. In Proceedings of the 2017 IEEE Radar Conference (RadarConf), Seattle, WA, USA, 8–12 May 2017; pp. 1803–1806. [Google Scholar]
- Li, S.; Amin, M.; An, Q.; Zhao, G.; Sun, H. 2-D coherence factor for sidelobe and ghost suppressions in radar imaging. IEEE Trans. Antennas Propag. 2019, 68, 1204–1209. [Google Scholar] [CrossRef]
- Chew, W.C. Waves and Fields in Inhomogeneous Media; Wiley-IEEE Press: Hoboken, NJ, USA, 1995. [Google Scholar]
- Lu, B.Y.; Sun, X.; Zhao, Y.; Zhou, Z.M. Phase coherence factor for mitigation of sidelobe artifacts in through-the-wall radar imaging. J. Electromagn. Waves Appl. 2013, 27, 716–725. [Google Scholar] [CrossRef]
- Camacho, J.; Parrilla, M.; Fritsch, C. Phase coherence imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2009, 56, 958–974. [Google Scholar] [CrossRef]
- Liu, J.; Jia, Y.; Kong, L.; Yang, X.; Liu, Q.H. Sign-coherence-factor-based suppression for grating lobes in through-wall radar imaging. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1681–1685. [Google Scholar] [CrossRef]
- Yoon, Y.S.; Amin, M.G. Spatial filtering for wall-clutter mitigation in through-the-wall radar imaging. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3192–3208. [Google Scholar] [CrossRef]
- Adams, R.; Bischof, L. Seeded region growing. IEEE Trans. Pattern Anal. Mach. Intell. 1994, 16, 64–647. [Google Scholar] [CrossRef]
- Chan, C.H.; Tsang, L. Monte Carlo simulations of large-scale one-dimensional random rough-surface scattering at near-grazing incidence: Penetrable case. IEEE Trans. Antennas Propag. 1998, 46, 142–149. [Google Scholar] [CrossRef]
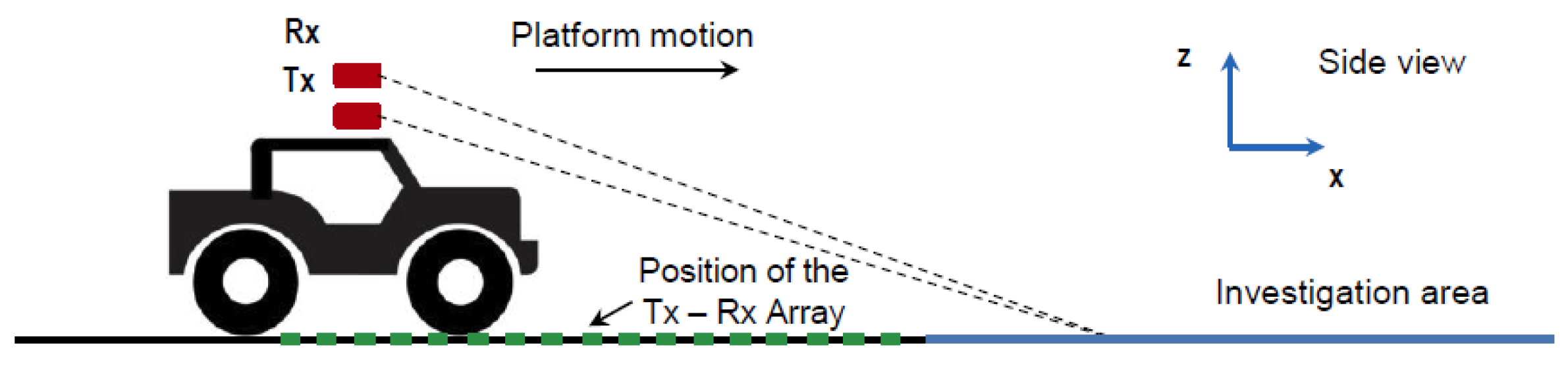

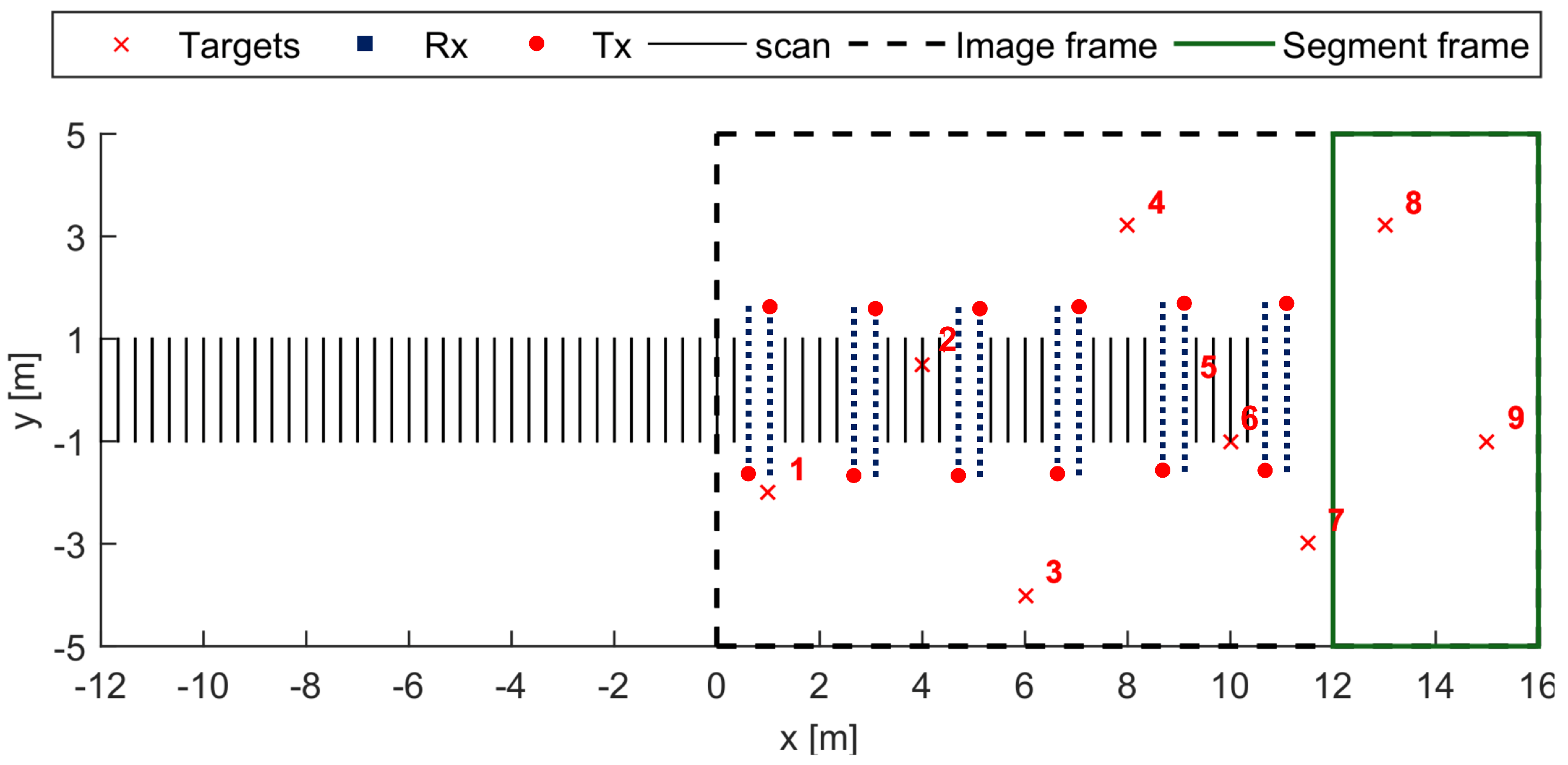

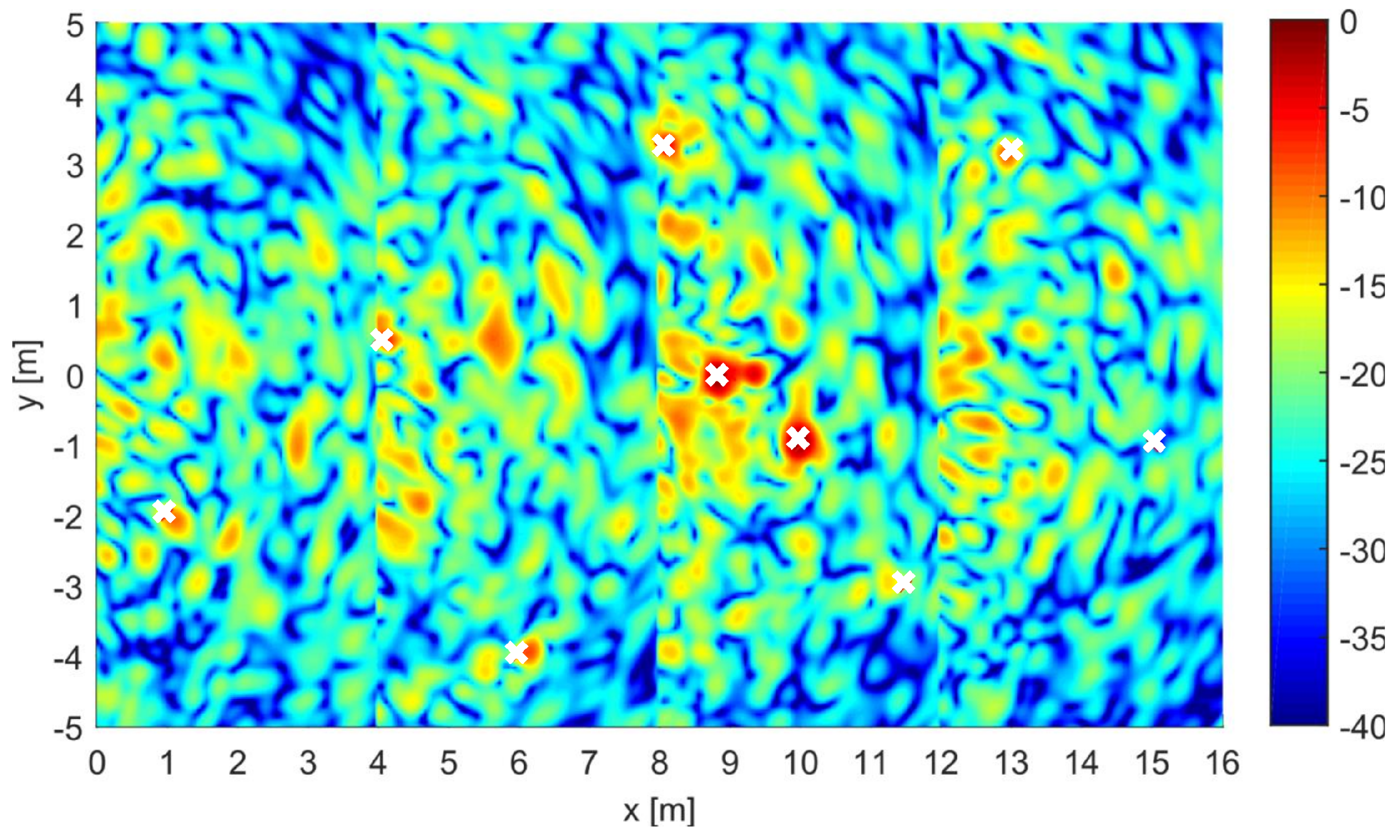
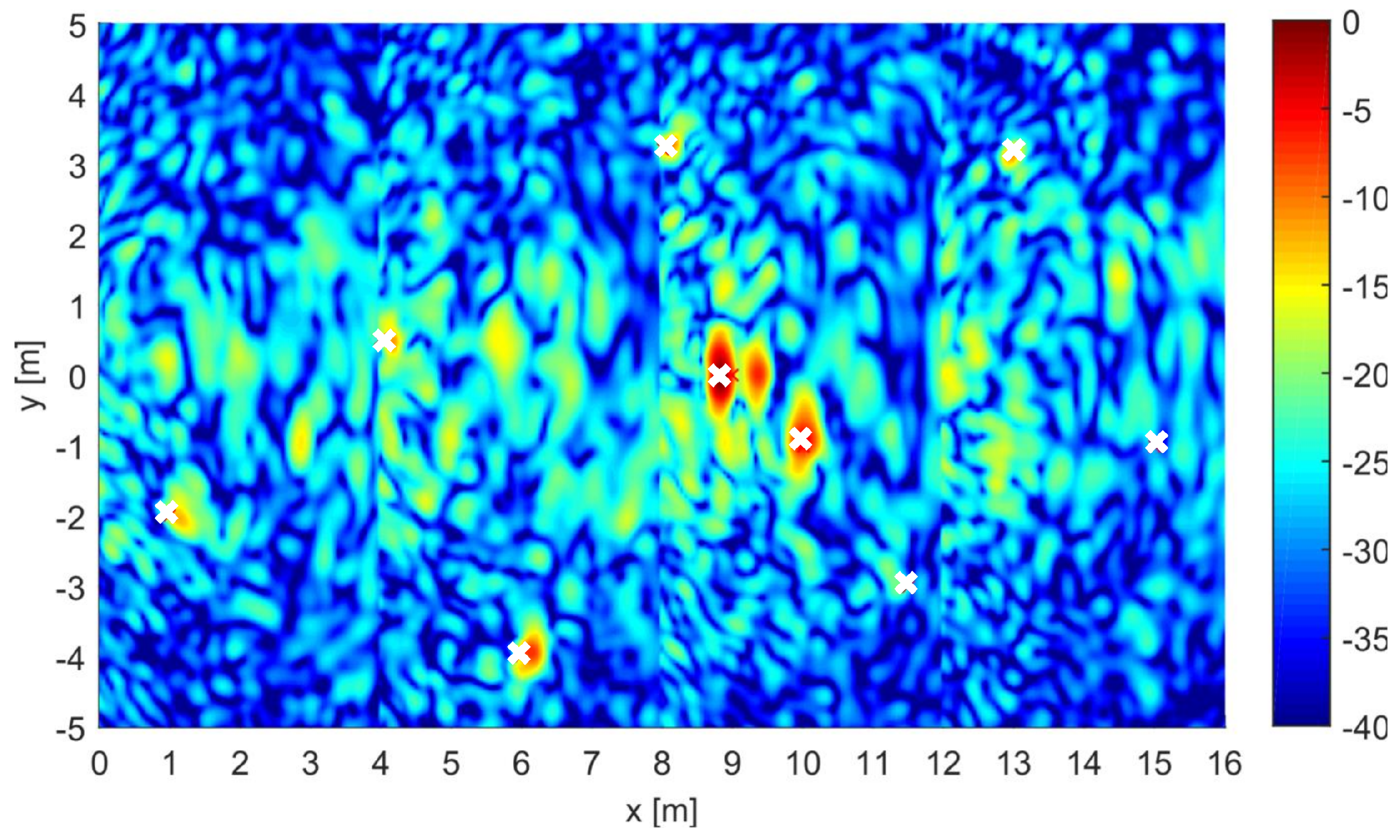

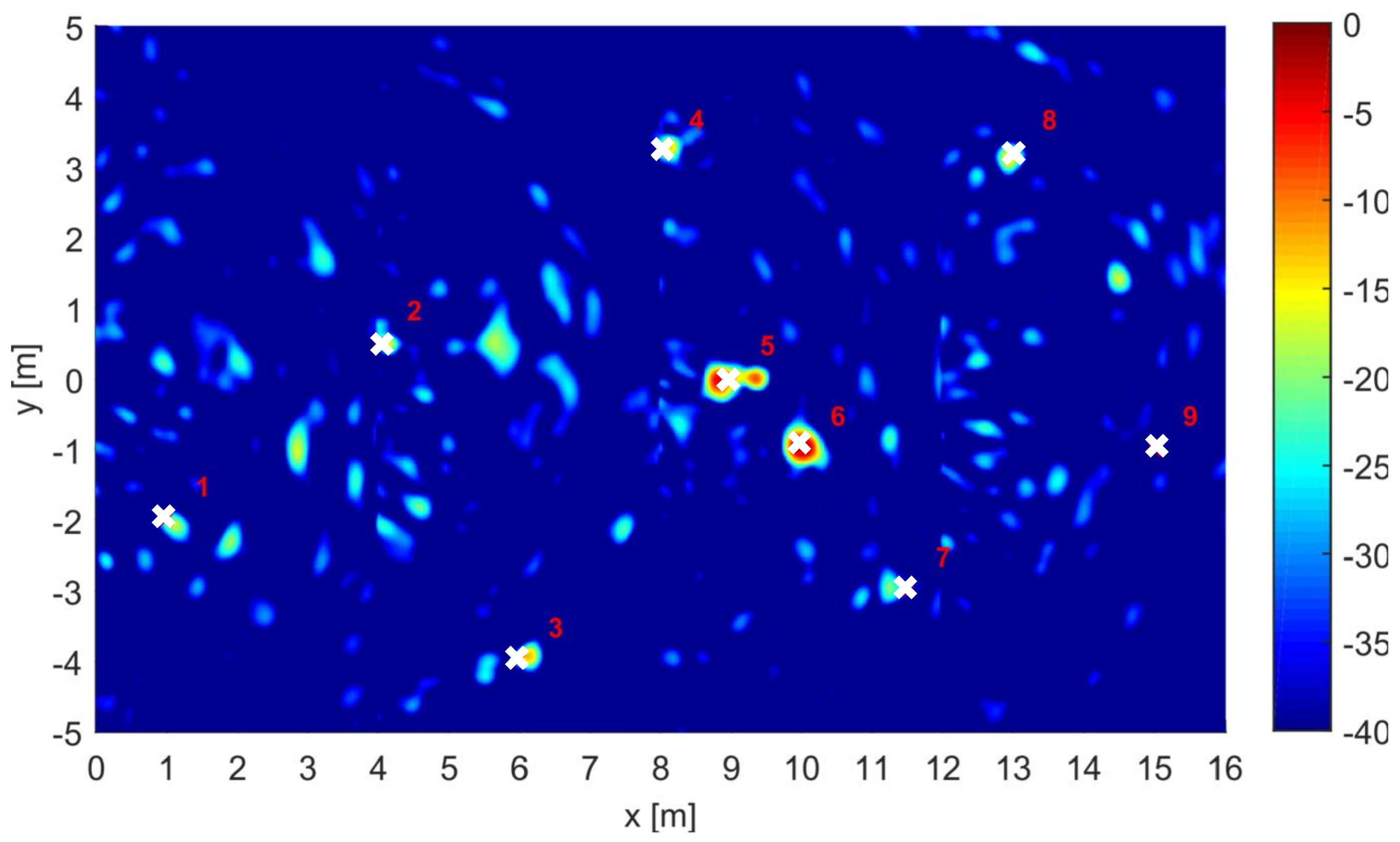

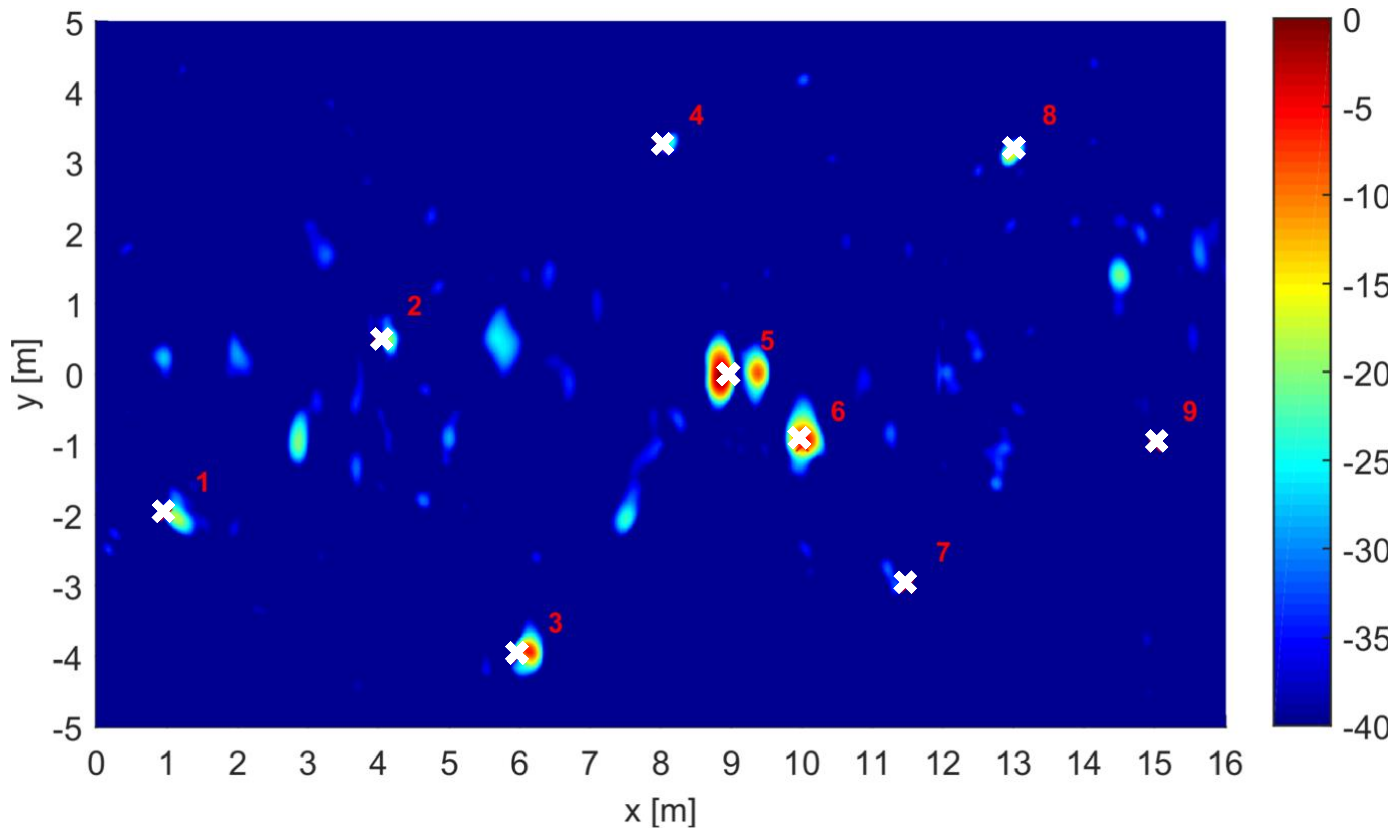
| Investigation area | Size: m | 1.8 cm, cm | |
| Antenna height | Tx antennas: 1.9 m | Rx antennas: 2 m | |
| Linear antenna array | Aperture extent: 2 m | Rx antennas: 16 | Tx antennas: 2 |
| System parameters | Frequency: 0.3–1.5 GHz | Coverage angle: 5–20 |
| Target No. | Type | State | Size |
|---|---|---|---|
| 1 | Metallic anti-personnel landmine | Buried | Diameter: 100 mm; Height: 55 mm |
| 2 | Plastic anti-personnel landmine | On surface | Diameter: 100 mm; Height: 55 mm |
| 3 | Metallic artillery shell | Buried | Diameter: 155 mm; Length: 585 mm |
| 4 | Metallic anti-tank landmine | Buried | Diameter: 300 mm; Height: 125 mm |
| 5 | Metallic anti-tank landmine | On surface | Diameter: 300 mm; Height: 125 mm |
| 6 | Metallic artillery shell | Buried | Diameter: 155 mm; Length: 585 mm |
| 7 | Metallic artillery shell | Buried | Diameter: 155 mm; Length: 585 mm |
| 8 | Plastic anti-personnel landmine | On surface | Diameter: 100 mm; Height: 55 mm |
| 9 | Plastic anti-tank landmine | Buried | Diameter: 300 mm; Height: 125 mm |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Comite, D.; Ahmad, F.; Dogaru, T.; Amin, M. Coherence-Factor-Based Rough Surface Clutter Suppression for Forward-Looking GPR Imaging. Remote Sens. 2020, 12, 857. https://doi.org/10.3390/rs12050857
Comite D, Ahmad F, Dogaru T, Amin M. Coherence-Factor-Based Rough Surface Clutter Suppression for Forward-Looking GPR Imaging. Remote Sensing. 2020; 12(5):857. https://doi.org/10.3390/rs12050857
Chicago/Turabian StyleComite, Davide, Fauzia Ahmad, Traian Dogaru, and Moeness Amin. 2020. "Coherence-Factor-Based Rough Surface Clutter Suppression for Forward-Looking GPR Imaging" Remote Sensing 12, no. 5: 857. https://doi.org/10.3390/rs12050857
APA StyleComite, D., Ahmad, F., Dogaru, T., & Amin, M. (2020). Coherence-Factor-Based Rough Surface Clutter Suppression for Forward-Looking GPR Imaging. Remote Sensing, 12(5), 857. https://doi.org/10.3390/rs12050857