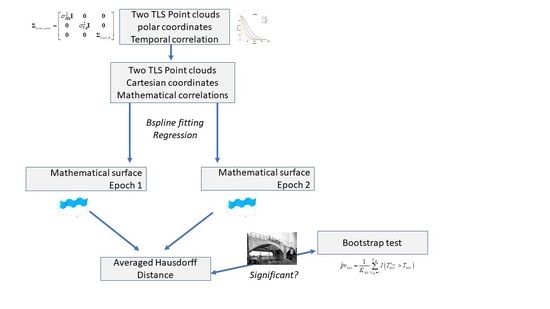
Deformation Analysis Using B-Spline Surface with Correlated Terrestrial Laser Scanner Observations—A Bridge Under Load
Abstract
1. Introduction
- choice of the mathematical approximation of the PC. In the field of geodesy, the regression B-spline approximation, as introduced by Reference [20], allows great flexibility to model raw TLS observations: no predetermined geometric primitives, such as circles, planes or cylinders, restrict the fitting [21]. Other strategies exist, such as penalized splines [22] or patches splines [23]. They seem less suitable for applications with noisy and scattered observations from TLS PC: please refer to Reference [24] for a short review of the different methods);
- choice of the distance [25]. The distance chosen has to fulfil certain conditions, such as being robust against noise and outliers to ensure its trustworthiness, particularly when the objects are close to each other [26]. Furthermore, it should correspond to the problem under consideration, that is, shape recognition or image comparisons may require another definition than object matching applications [27]. When a complex object is modelled, maps that allow for a visualization of pointwise deformation magnitudes to detect changes are more relevant than a global measure of distance [28]. Distances based on the maximum norm of parametric representations may not estimate the real distance correctly [29] and cannot be applied to piecewise algebraic spline curves [30]. An alternative is the widely used Hausdorff distance (HD) to estimate either the distance between two raw PC or their B-spline approximations [31]. Unfortunately, the traditional HD only provides a global measure of the distance and is known to be sensitive to outliers. Alternatives were proposed, including the Hausdorff quantile [32], for close objects [26], for the specific case of B-spline curves [33], spatially coherent matching [34] or the averaged Hausdorff distance (AHD; [27]).
- (1)
- Is a mathematical approximation of the noisy TLS PC beneficial for a trustworthy distance computation?
- (2)
- How does correlated noise affect the distance between mathematical surfaces? Which metric is better suited in the case of correlated observations?
- (3)
- Which specific statistical test has to be applied when testing for deformation based on a distance between mathematical approximations of TLS PC?
2. Mathematical Background
2.1. Approximation of Observations with B-Splines Basis Functions
2.1.1. B-Spline Curves
2.1.2. Approximation of Scattered Points with B-Spline Curves
The Least-Square Problem
The Parametrization of the Point Cloud
The Number of CP
2.2. B-Spline Surfaces
2.3. Deformation Analysis
2.3.1. Suboptimal Intuitive Approaches
- The first one makes use a gridded PC and is defined as the difference between the co-ordinates of and , , where is the Euclidian norm. and are the values of and at grid points and , respectively. We note that and may have been computed with different optimal numbers of CP, i.e., we may have . Due to the gridding, should only be used when the deformation can be assumed to be unidirectional (i.e., in the z-direction).
- A second idea is to define the distance at the parameter level between the estimated vectors of CP and for and , respectively, as . Clearly, is meaningless when , since the size of the two control polygons differs.
2.3.2. The Hausdorff Distance
2.3.3. The Averaged Hausdorff Distance
Note
3. Simulations
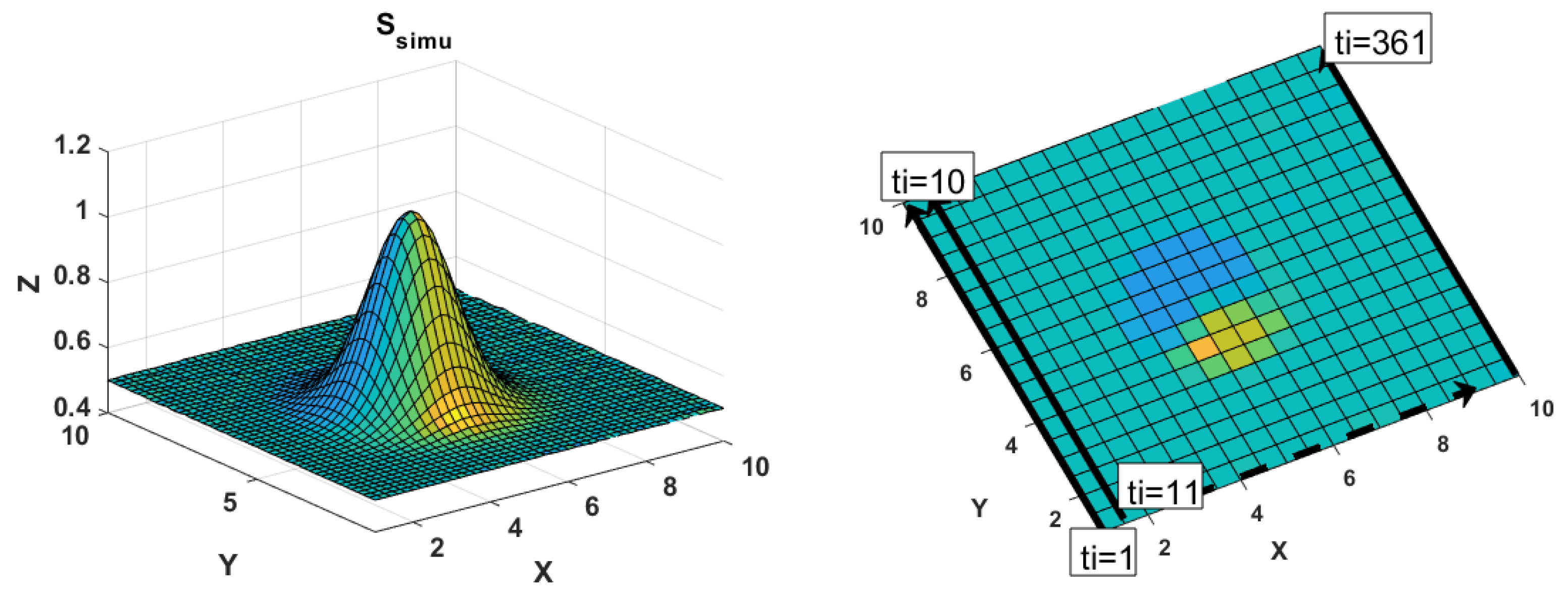
3.1. Generating Noisy Surfaces

3.2. Generating the Reference Noise VCM Σnoise
- (i)
- Simple VCM: . The Identity matrix is scaled by a factor defined in the next section.
- (ii)
- Complex VCM degree 1:, assuming heteroscedasticity of the raw polar observations and mathematical correlations (MAC) due to the transformation to Cartesian coordinates in the B-spline approximation.
- (iii)
- Complex VCM degree 2:, assuming, in addition to (ii), also temporally correlated polar observations.
3.2.1. Case (ii)
3.2.2. Case (iii)
Our Assumptions
- We model the correlation of the range as being temporal, that is, time-dependent. Range measurements are a measure of time [49]: any spatial effects stemming from the reflected surface can be included in the variance factor. This latter could exemplarily follow the physically plausible intensity model, as proposed in Reference [12].
- The covariance function proposed is said to be separable, that is, it separates the temporal from the spatial effects [50]. We will here assume a temporal spacing of 1 s between the simulated observations.
Building the VCM
3.3. Approximated VCM in the LS Adjustment
3.4. Determining the Optimal Number of CP Using Information Criteria
3.5. Results
3.5.1. Impact of the Simplified Stochastic Model on HD and AHD: Mathematical Approximations
Use of a Correct VCM
Use of An Approximated VCM
- under correlated noise, the approximated VCM used in the LS computation affects the determination of both the HD and the AHD strongly: the difference ratio reaches for the case iii) more than 75% for the HD and 200% for the AHD. This result was found to hold true for all cases under consideration, that is, independently of the correlation structure and the variance factor. Thus, a correct stochastic model is unavoidable for a trustworthy distance. Exemplarily for case (iii) with and m, the ratio of the difference between the approximated and the reference distance to the reference for or reaches 200% for the AHD (Table 3). Decreasing the correlation length decreases the ratio: for case iii) and , this latter is found only 7% smaller than the reference value when the VCM is mis-specified ( or ). This result is found to be independent of the chosen. For m, the same ratio is 10% smaller: a small range variance impacts the distance computed with a mis-specified VCM less strongly.
- When the observations are only MC, simplifying the stochastic model by neglecting the mathematical correlations, that is, taking , did not affect the HD or the AHD significantly for m. By increasing the range STD to m, the ratio for the AHD was increased by 15%. This result highlights the importance of accounting for mathematical correlations under unfavorable scanning conditions, that is, high range variance.
3.5.2. Impact of the Simplified Stochastic Model on the HD and AHD: PC
3.5.3. Statistical Testing for Deformation
3.6. Conclusions of the Simulations
- How does correlated noise affect the distance? Which distance is better suited in the case of noisy observations?
- Why should we use a mathematical approximation of the noisy PC?
4. Case Study
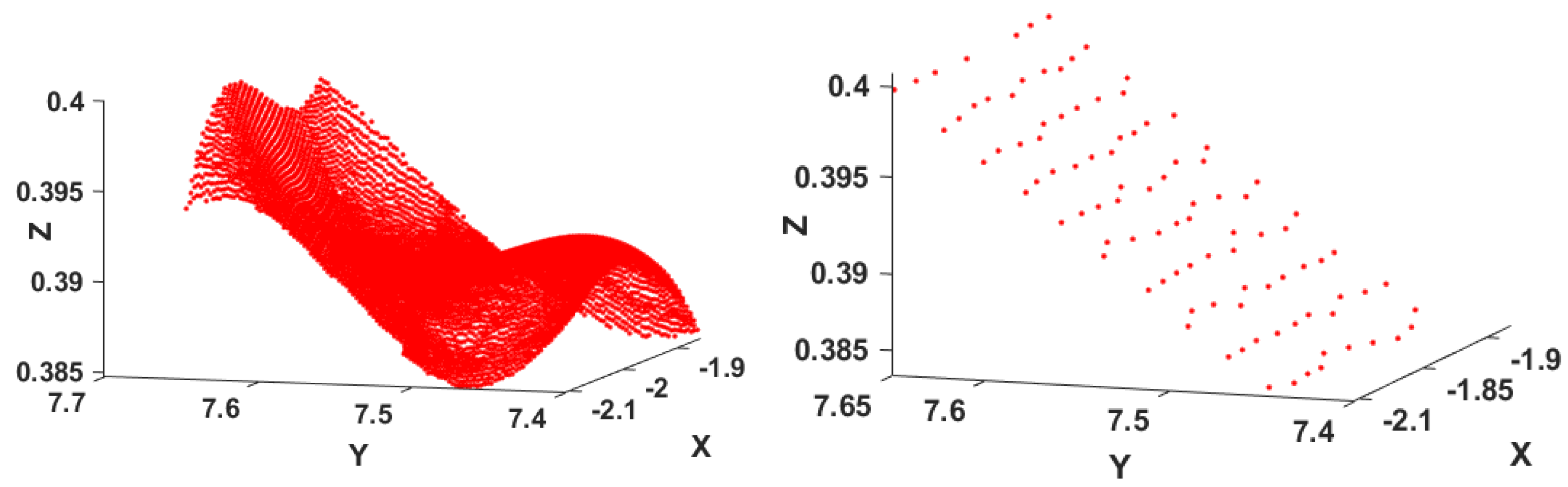
4.1. A Bridge Under Load
- their comparable and small deformation magnitudes of approximately 4 mm between step E00 and 55 around the reference LT point and
- the two different scanning geometries.
4.2. Mathematical Modelling
- In a pre-processing step, the extracted PC were gridded, that is, the X- and Y-axis were each divided into ten steps. For each of the 100 cells, the means of the X, Y, Z values were computed to reduce the number of observations. The value of 10 was chosen as the highest one leading to the occurrence of at least one point in each cell.
- The PC extracted were gridded similarly to (i) but the X- and Y-axis were divided into 5, which corresponds to 25 cells.
- The whole PC were used without gridding, that is, no reduction of the PC point density was performed.
Note on the Stochastic Model:
4.3. Computation of the HD and AHD
Gridded Observations: Case (i) and (ii)
No Gridding, Case (iii)
4.4. Testing for Deformation
4.5. Discussion
- an optimal grid setting for a good correspondence between the deformation magnitudes computed from two different sensors exists: a higher point density may lead to different point correspondences in the two epochs, particularly in the case of a small deformation. The optimal size of the cell depends on the point density inside one cell and could be assigned by means of calibration based on sensors comparison (LT and TLS).
- We further pointed out that the AHD is less influenced by a suboptimal fitting, that is, inappropriate parametrization, knot vector or number of CP and is more trustworthy for local deformation analysis than the HD. This finding confirms the results from the previous simulations: the AHD is more appropriate than a maximum value (the HD) for the sake of comparison with LT values. This is due to the averaging of the AHD when a local deformation analysis is performed. A statistical test of significance of deformation should be based on this distance.
5. Conclusions
- A mathematical approximation of the noisy TLS PC is beneficial for a trustworthy distance computation: B-spline surface approximation from scattered PC acts as filtering the correlated and heteroscedastic noise from TLS observations. The AHD computed was closer to the reference one for both simulated and real data analysis when a B-spline surface fitting was performed. Additionally, a pre-gridding of the raw PC for a real scenario affected the distance computation positively by further reducing the observations available.
- Rigorous statistical test for deformation can only be performed based on parametric surfaces. That is one of the most significant advantages of mathematical approximation. Because the distribution of the test statistics for deformation based on the AHD is not tractable: we proposed and validated a novel bootstrap approach for the test decision.
- Correlated noise affects the distance computation between PC for both raw and approximated observations. In the case of an approximation of the PC with regression B-spline surfaces, an optimal stochastic model in the LS adjustment is mandatory to reach the optimal value of the distance: both mathematical and temporal correlations should be accounted for.
Author Contributions
Funding
Conflicts of Interest
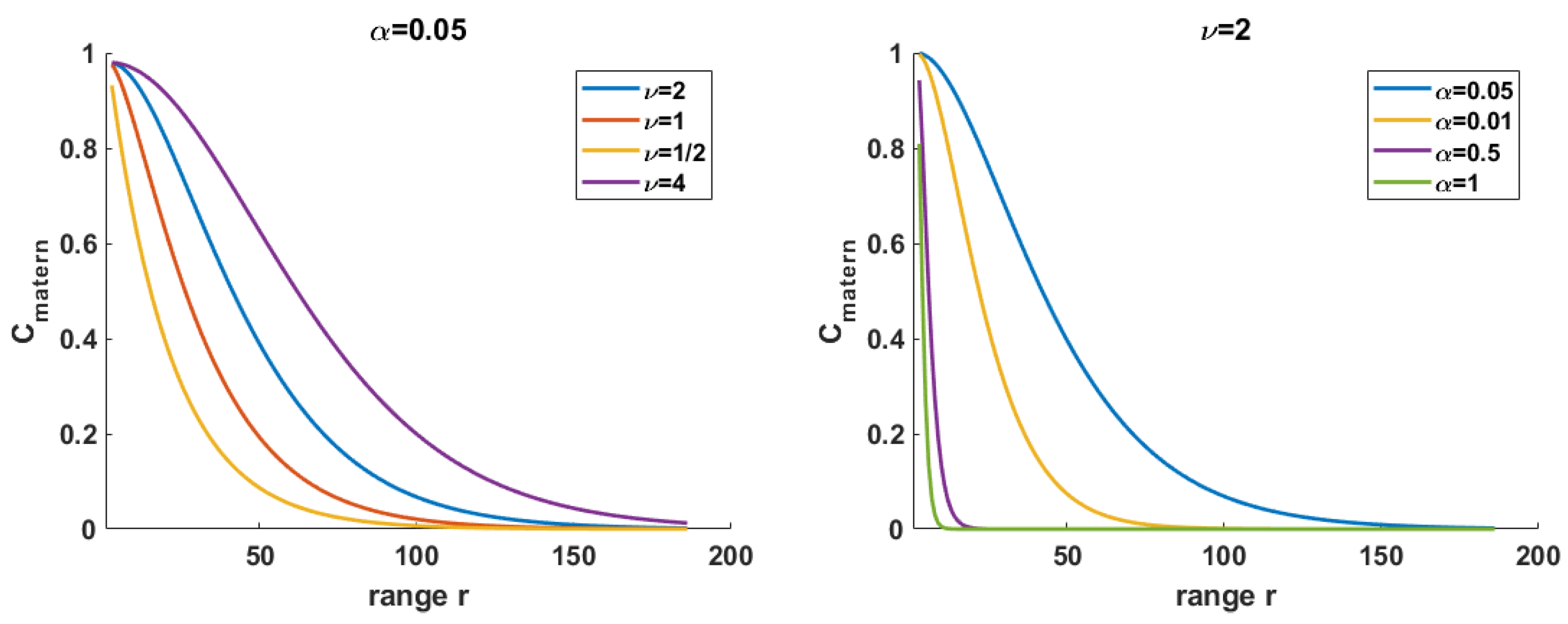
Appendix A. The Matérn Model
- corresponds to the exponential covariance function, that is, a strong decay at the origin
- to the Markov process of first order
- is the squared exponential covariance function, which corresponds to a physically less plausible infinitely differentiable random field at the origin. The case of Figure A1 left highlights the meaning of this assumption, that is, a low decaying at the origin, leading potentially to some numerical problems when corresponding VCM have to be inverted.
Appendix B. Bootstrap Statistical Test for Deformation
Appendix B.1. Test Statistics and the Null Hypothesis
Appendix B.2. Bootstrap Approach
- Testing step: the bootstrapping approach starts by computing and or their a posteriori counterparts for the two estimated surfaces. Because these quantities are to be compared to a critical value that is not available, a large number of observation vectors are generated under . A so-called bootstrap sample is defined, which is here taken as the mean of the surface differences, that is, . We consider, therefore, that the mean surface as not being deformed, that is, generated under .
- Generating step: the generating step begins with the computation of and following the methodology of Section 3.1. Added to , we generate, thus, two noised surfaces, which we approximate with regression B-splines surfaces. Finally, the HD and AHD between the two approximations are computed. For one iteration , we call the corresponding test statistics and . Please note that we make use of a parametric approach, that is, the random numbers are generated independently, so that no replacement is made by using the residuals of the LS approximation.
- Evaluation steps: iterations are carried out. Following [57], the loss of power of the test is proportional to the inverse of . We fixed to keep the computation manageable. The p-value is estimated by , according to Reference [56], to determine how extreme the test values and are in comparison to the of and generated under . is an indicator function, which takes the value 1 when and 0, vice versa.
- Decision test: A large indicates a large support of by the observations. is rejected if , where is the specified significance level, usually taken as 0.05.

References
- Hu, S.; Wallner, J. A second order algorithm for orthogonal projection onto curves and surfaces. Comput. Aided Geom. Des. 2005, 22, 251–260. [Google Scholar] [CrossRef]
- Guthe, M.; Borodin, P.; Klein, R. Fast and accurate Hausdorff distance calculation between meshes. J. WSCG 2005, 13, 41–48. [Google Scholar]
- Alt, H.; Scharf, L. Computing the Hausdorff distance between sets of curves. In Proceedings of the 20th European Workshop on Computational Geometry (EWCG), Seville, Spain, 24–25 March 2004; pp. 233–236. [Google Scholar]
- Pelzer, H. Zur Analyze Geodatischer Deformations-messungen; Verlag der Bayer. Akad. D. Wiss: München, Germany, 1971; p. 86. [Google Scholar]
- Paffenholz, J.A.; Huge, J.; Stenz, U. Integration von Lasertracking und Laserscanning zur optimalen Bestimmung von lastinduzierten Gewölbeverformungen. AVN Allg. Vermess.-Nachr. 2018, 125, 75–89. [Google Scholar]
- Alba, M.; Fregonese, L.; Prandi, F.; Scaioni, M.; Valgoi, P. Structural monitoring of a large dam by terrestrial laser scanning. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2006, 36, 1–6. [Google Scholar]
- Caballero, D.; Esteban, J.; Izquierdo, B. ORCHESTRA: A unified and open architecture for risk management applications. Geophys. Res. Abstr. 2007, 9, 08557. [Google Scholar]
- Besl, P.J.; McKay, N.D. A method for registration of 3D shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 239–256. [Google Scholar] [CrossRef]
- Holst, C.; Kuhlmann, H. Challenges and present fields of action at laser scanner based deformation analysis. J. Appl. Geod. 2016, 10, 17–25. [Google Scholar]
- Lague, D.; Brodu, N.; Leroux, J. Accurate 3D comparison of complex topography with terrestrial laser scanner. Application to the Rangitikei canyon (N-Z). ISPRS J. Photogramm. Remote Sens. 2013, 82, 10–26. [Google Scholar] [CrossRef]
- Soudarissanane, S.; Lindenbergh, R.; Menenti, M.; Teunissen, P. Scanning geometry: Influencing factor on the quality of terrestrial laser scanning points. ISPRS J. Photogramm. Remote Sens. 2011, 66, 389–399. [Google Scholar] [CrossRef]
- Wujanz, D.; Burger, M.; Mettenleiter, M.; Neitzel, F. An intensity-based stochastic model for terrestrial laser scanners. ISPRS J. Photogramm. Remote Sens. 2017, 125, 146–155. [Google Scholar] [CrossRef]
- Wujanz, D.; Burger, M.; Tschirschwitz, F.; Nietzschmann, T.; Neitzel, F.; Kersten, T.P. Determination of intensity-based stochastic models for terrestrial laser scanners utilizing 3D-point clouds. Sensors 2018, 18, 2187. [Google Scholar] [CrossRef] [PubMed]
- Holst, C.; Artz, T.; Kuhlmann, H. Biased and unbiased estimates based on laser scans of surfaces with unknown deformations. J. Appl. Geod. 2014, 8, 169–183. [Google Scholar] [CrossRef]
- Jurek, T.; Kuhlmann, H.; Host, C. Impact of spatial correlations on the surface estimation based on terrestrial laser scanning. J. Appl. Geod. 2017, 11, 143–155. [Google Scholar] [CrossRef]
- Kermarrec, G.; Schön, S. On the Matérn covariance family: A proposal for modelling temporal correlations based on turbulence theory. J. Geod. 2014, 88, 1061–1079. [Google Scholar] [CrossRef]
- Kermarrec, G.; Neumann, I.; Alkhatib, H.; Schön, S. The stochastic model for Global Navigation Satellite Systems and terrestrial laser scanning observations: A proposal to account for correlations in least squares adjustment. J. Appl. Geod. 2018, 13, 93–104. [Google Scholar] [CrossRef]
- Mémoli, F.; Sapiro, G. Comparing point clouds. In The 2004 Eurographics/ACM SIGGRAPH Symposium; Boissonnat, J.-D., Alliez, P., Eds.; ACM: New York, NY, USA, 2004; p. 32. [Google Scholar]
- Monserrat, O.; Crosetto, M. Deformation measurement using terrestrial laser scanning data and least squares 3D surface matching. ISPRS J. Photogramm. 2008, 63, 142–154. [Google Scholar] [CrossRef]
- Koch, K.R. Fitting free-form surfaces to laserscan data by NURBS. AVN Allg. Vermess.-Nachr. 2009, 116, 134–140. [Google Scholar]
- Lindenbergh, R.; Pietrzyk, P. Change detection and deformation analysis using static and mobile laser scanning. Appl. Geomat. 2015, 7, 65–74. [Google Scholar] [CrossRef]
- Eilers, P.H.C.; Marx, B.D. Flexible smoothing with B-splines and penalties. Stat. Sci. 1996, 11, 89–121. [Google Scholar] [CrossRef]
- Engleitner, N.; Jüttler, B. Patchwork B-spline refinement. Comput. Aided Des. 2017, 90, 168–179. [Google Scholar] [CrossRef]
- Aguilera, A.M.; Aguilera-Morillo, M.C. Comparative study of different B-spline approaches for functional data. Math. Comput. Model. 2013, 58, 1568–1579. [Google Scholar] [CrossRef]
- Bogacki, P.; Weinstein, S.E. Generalized Fréchet distance between curves. In Mathematical Methods for Curves and Surfaces II; Daehlen, M., Lyche, T., Schumaker, L.L., Eds.; Vanderbilt University Press: Nashville, Tennessee, 1998; pp. 25–32. [Google Scholar]
- Kim, Y.-J.; Oh, Y.-T.; Yoon, S.-H.; Kim, M.-S.; Elber, G. Efficient Hausdorff distance computation for freeform geometric models in close proximity. Comput. Aided Des. 2013, 45, 270–276. [Google Scholar] [CrossRef]
- Dubuisson, M.P.; Jain, A.K. A modified Hausdorff distance for object matching. In Proceedings of the 12th IAPR International Conference on Pattern Recognition, Jerusalem, Israel, 9–13 October 1994; Volume 1, pp. 566–568. [Google Scholar]
- Scaioni, M.; Roncella, R.; Alba, M.I. Change detection and deformation analysis in point clouds: Application to rock face monitoring. Photogramm. Eng. Remote Sens. 2013, 79, 441–455. [Google Scholar] [CrossRef]
- Jüttler, B. Bounding the Hausdorff distance of implicitly defined and/or parametric curves. In Mathematical Methods in CAGD; Lyche, T., Schumaker, L.L., Eds.; Academic Press: Oslo, Norway, 2000; pp. 1–10. [Google Scholar]
- Elber, G.; Grandine, T. Hausdorff and minimal distances between parametric free forms in R2 and R3. In Advances in Geometric Modeling and Processing, Proceedings of the 5th International Conference, GMP 2008, Hangzhou, China, 23–25 April 2008; Chen, F., Juettler, B., Eds.; Lecture Notes in Computer Science 4975; Springer: Berlin, Germany, 2008; pp. 191–204. [Google Scholar]
- Shapiro, M.D.; Blaschko, M.B. On Hausdorff Distance Measures; Technical Report, UM-CS-2004-071; Department of Computer Science, University of Massachusetts Amherst: Amherst, MA, USA, 2004. [Google Scholar]
- Huttenlocher, D.P.; Klanderman, G.A.; Rucklidge, W.J. Comparing images using the Hausdorff distance. IEEE TPAMI 1993, 15, 850–862. [Google Scholar] [CrossRef]
- Chen, X.D.; Ma, W.; Xu, G.; Paul, J.C. Computing the Hausdorff distance between two B-spline curves. Comput. Aided Des. 2010, 42, 1197–1206. [Google Scholar] [CrossRef]
- Boykov, Y.; Huttenlocher, D. A new Bayesian framework for object recognition. IEEE CVPR 1999, 2, 517–523. [Google Scholar]
- Boehler, W.; Marbs, A.A. 3D Scanning instruments. In Proceedings of the CIPA WG6 International Workshop on Scanning for Cultural Heritage Recording, Corfu, Greece, 1–2 September 2002. [Google Scholar]
- Kauker, S.; Schwieger, V. A synthetic covariance matrix for monitoring by terrestrial laser scanning. J. Appl. Geod. 2017, 11, 77–87. [Google Scholar] [CrossRef]
- Kermarrec, G.; Alkhatib, H.; Neumann, I. On the sensitivity of the parameters of the intensity-based stochastic model for terrestrial laser scanner. Case study: B-spline approximation. Sensors 2018, 18, 2964. [Google Scholar] [CrossRef]
- Stein, M.L. Interpolation of Spatial Data: Some Theory for Kriging; Springer: New York, NY, USA, 1999. [Google Scholar]
- De Boor, C. On calculating with B-splines. J. Approx. Theory 1972, 6, 50–62. [Google Scholar] [CrossRef]
- Piegl, L.; Tiller, W. The NURBS Book; Springer Science & Business Media: Berlin, Germany, 1997. [Google Scholar]
- Harmening, C.; Neuner, H. Choosing the optimal number of B-spline control points (Part 1 Methodology and approximation of curves). J. Appl. Geod. 2016, 10, 139–157. [Google Scholar] [CrossRef]
- Alkhatib, H.; Kargoll, B.; Bureick, J.; Paffenholz, J.A. Statistical evaluation of the B-Splines approximation of 3D point clouds. In Proceedings of the 2018 FIG-Congress, Istanbul, Turkey, 6–11 May 2018. [Google Scholar]
- Burnham, K.P.; Anderson, D.R. Model Selection and Multimodel Inference; Springer: New York, NY, USA, 2002. [Google Scholar]
- Aspert, N.; Santa-Cruz, D.; Ebrahimi, T. Measuring errors between surfaces using the Hausdorff distance. In Proceedings of the IEEE International Conference on Multimedia and Expo, Lausanne, Switzerland, 26–29 August 2002; Volume 1, pp. 705–708. [Google Scholar]
- Kermarrec, G.; Alkhatib, H.; Paffenholz, J.-A. Original 3D-Punktwolken oder Approximation mit B-Splines: Verformungsanalyse mit CloudCompare. In Tagungsband GeoMonitoring 2019, Proceedings of the GeoMonitoring, Hannover, Germany, 14–15 March 2019; Alkhatib, H., Paffenholz, J.A., Eds.; Leibniz Universität Hannover: Hanover, Germany, 2019; pp. 165–176. [Google Scholar]
- Zhao, X.; Kermarrec, G.; Kargoll, B.; Alkhatib, H.; Neumann, I. Statistical evaluation of the influence of stochastic model on geometry based deformation analysis. J. Appl. Geod. 2017, 11, 4. [Google Scholar]
- Gentle, J.E. Random Number Generation and Monte Carlo Methods; Springer: Berlin, Germany, 1998. [Google Scholar]
- Matérn, B. Spatial variation – stochastic models and their applications to some problems in forest survey sampling investigations. Rep. For. Res. Inst. Swede 1960, 49, 1–144. [Google Scholar]
- Rueger, J.M. Electronic Distance Measurement; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Gelfand, A.E.; Diggle, P.J.; Fuentes, M.; Guttorp, P. Handbook of Spatial Statistics; Chapman & Hall/CRC Handbooks of Modern Statistical Methods: London, UK, 2010. [Google Scholar]
- Kermarrec, G.; Paffenholz, J.-A.; Alkhatib, H. How significant are differences obtained by neglecting correlations when testing for deformation: A real case study using bootstrapping with terrestrial laser scanner observations approximated by B-spline surfaces. Sensors 2019, 19, 3640. [Google Scholar] [CrossRef] [PubMed]
- Schacht, G.; Piehler, J.; Müller, J.Z.A.; Marx, S. Belastungsversuche an einer historischen Eisenbahn-Gewölbebrücke. Bautechnik 2017, 94, 125–130. [Google Scholar] [CrossRef]
- Lenzmann, L.; Lenzmann, E. Strenge Auswertung des nichtlinearen GaußHelmert-Modells. AVN Allg. Vermess.-Nachr. 2004, 111, 68–73. [Google Scholar]
- Kaufman, C.G.; Shaby, B.A. The role of the range parameter for estimation and prediction in geostatistics. Biometrika 2012, 100, 473–484. [Google Scholar] [CrossRef]
- Efron, B. Bootstrap methods: Another look at the jackknife. Ann. Stat. 1979, 7, 1–26. [Google Scholar] [CrossRef]
- McKinnon, J. Bootstrap Hypothesis Testing; Queen’s Economics Department Working Paper, No. 1127; Queen’s University: Kingston, ON, Canada, 2007. [Google Scholar]
- Davidson, R.; MacKinnon, J.G. Bootstrap tests: How many bootstraps? Econom. Rev. 2000, 19, 55–68. [Google Scholar] [CrossRef]

| Case (i) | Case (ii) | Case (iii) |
|---|---|---|
| True VCM | Simplification 1 | Simplification 1 |
| True VCM | Simplification 2 | |
| True VCM |
| Case (i) | Case (ii) | |
| BIC (n/m) | 9/10 | 11/10 |
| Case (iii) | (Case iii) | |
| BIC (n/m) | 11/10 | 11/10 |
| HD (%)/STD | AHD (%)/STD | |
|---|---|---|
| reference VCM | 0.0084 3.6 × 103 | 0.0029 1.3 × 103 |
| only MAC | 0.0175 (107%) 6.2 × 103 | 0.0090 (207%) 4.8 × 103 |
| no correlation | 0.0148 (76%) 6.1 × 103 | 0.0090 (207%) 4.9 × 103 |
| PC no approximation | 0.0153 (82%) 5.7 × 103 | 0.0092 (135%) 4.8 × 103 |
| L13mm | AHD [mm] | HD [mm] | LT [mm] | M3C2 [mm] |
| Gridded observations | ||||
| B-Splines (i): 74 points/cell B-Splines (ii): 300 points/cell | 4.90 4.80 | 5.62 5.53 | ||
| No gridding | ||||
| B-splines (iii) no gridding PC or raw obs. | 5.21 5.58 | 6.70 7.24 | Ref: 4.96 | 4.70 |
| L8mm | AHD [mm] | HD [mm] | LT [mm] | M3C2 [mm] |
| Gridded observations | ||||
| B-Splines (i): 16 points/cell B-Splines (ii): 66 points/cell | 4.29 4.06 | 9.71 5.39 | ||
| No gridding | ||||
| B-splines (iii) no gridding PC or raw obs. | 4.51 5.09 | 11.00 9.82 | Ref: 4.07 | 3.20 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kermarrec, G.; Kargoll, B.; Alkhatib, H. Deformation Analysis Using B-Spline Surface with Correlated Terrestrial Laser Scanner Observations—A Bridge Under Load. Remote Sens. 2020, 12, 829. https://doi.org/10.3390/rs12050829
Kermarrec G, Kargoll B, Alkhatib H. Deformation Analysis Using B-Spline Surface with Correlated Terrestrial Laser Scanner Observations—A Bridge Under Load. Remote Sensing. 2020; 12(5):829. https://doi.org/10.3390/rs12050829
Chicago/Turabian StyleKermarrec, Gaël, Boris Kargoll, and Hamza Alkhatib. 2020. "Deformation Analysis Using B-Spline Surface with Correlated Terrestrial Laser Scanner Observations—A Bridge Under Load" Remote Sensing 12, no. 5: 829. https://doi.org/10.3390/rs12050829
APA StyleKermarrec, G., Kargoll, B., & Alkhatib, H. (2020). Deformation Analysis Using B-Spline Surface with Correlated Terrestrial Laser Scanner Observations—A Bridge Under Load. Remote Sensing, 12(5), 829. https://doi.org/10.3390/rs12050829