Parallel Regional Segmentation Method of High-Resolution Remote Sensing Image Based on Minimum Spanning Tree
Abstract
1. Introduction
2. Methods
2.1. Parallel MHR Method
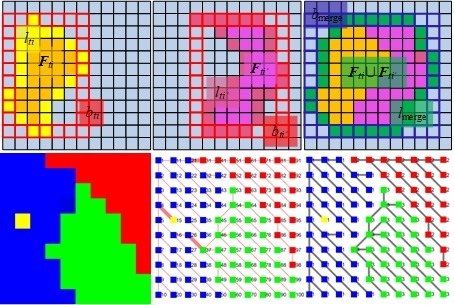
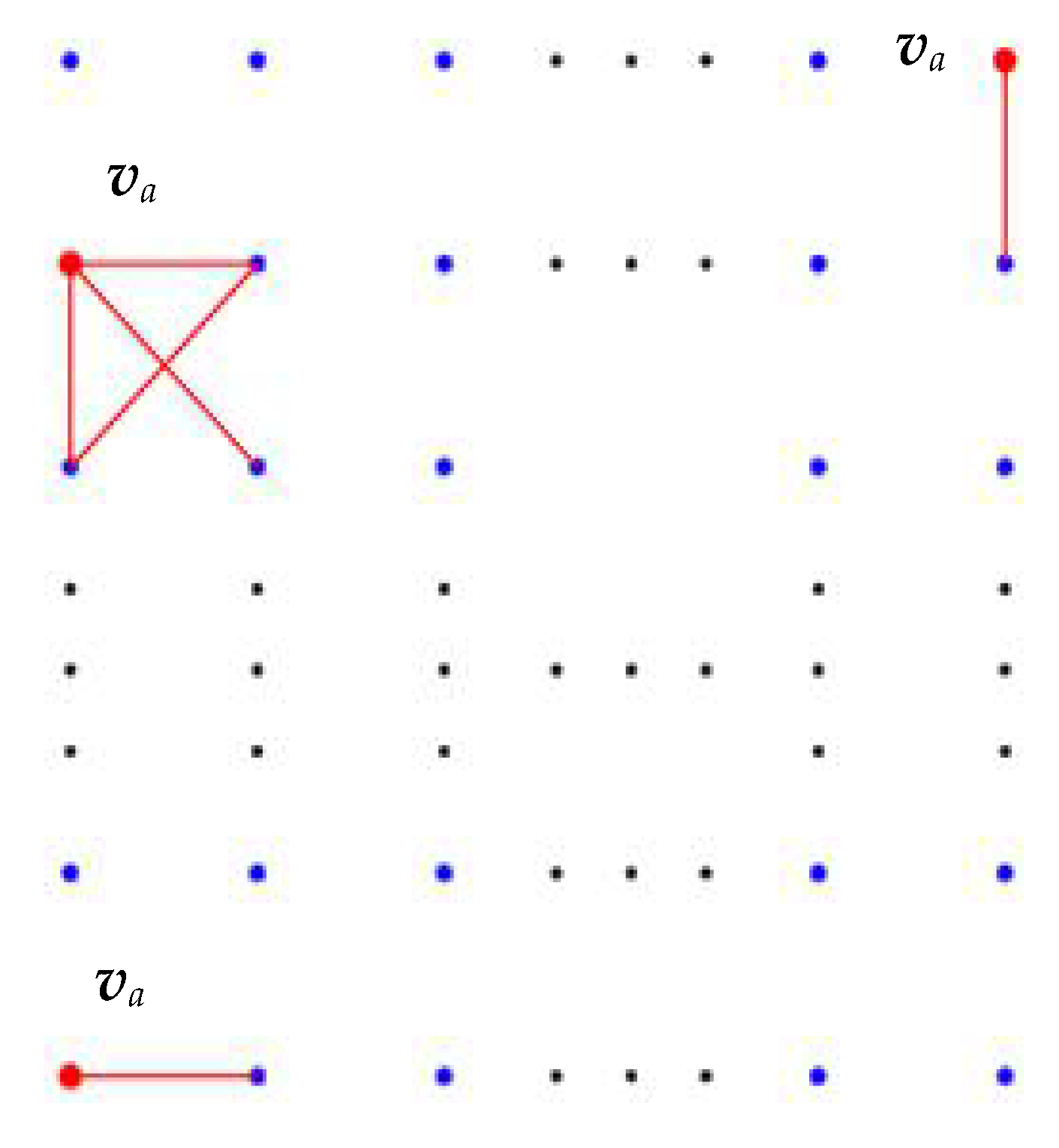
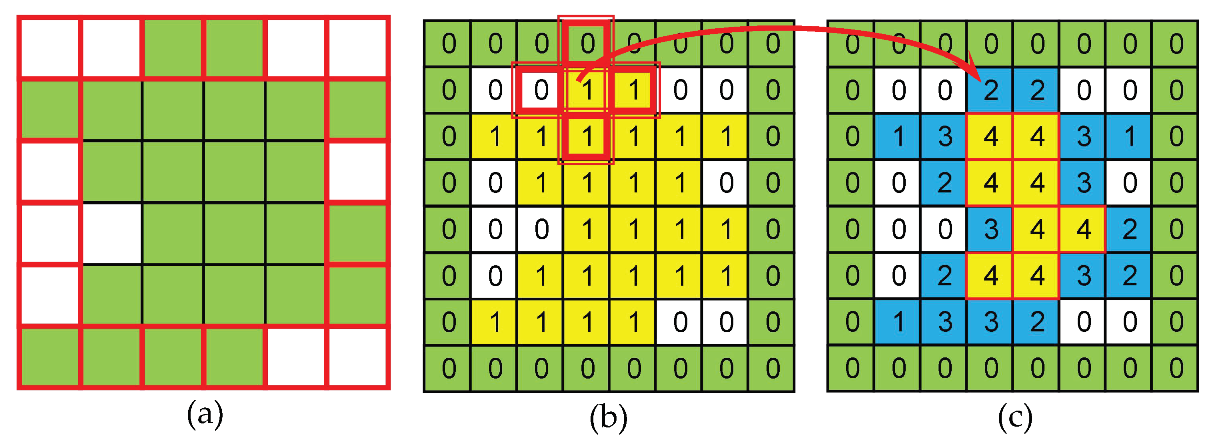
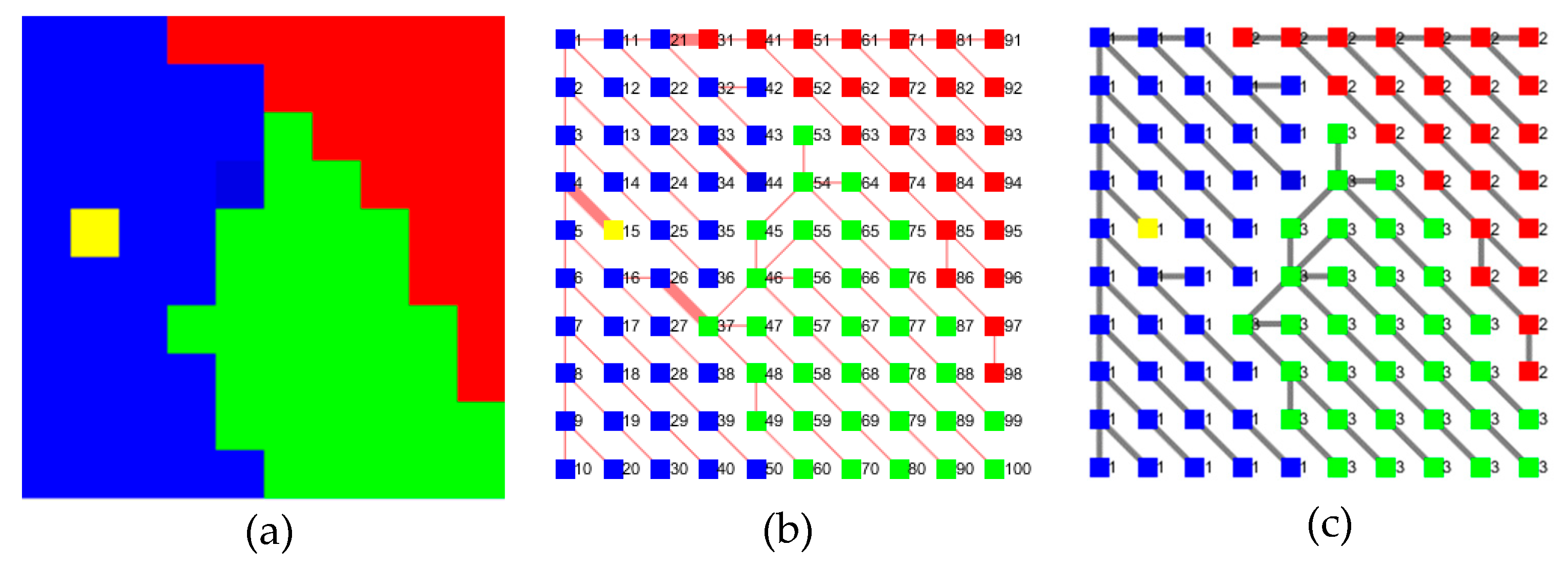
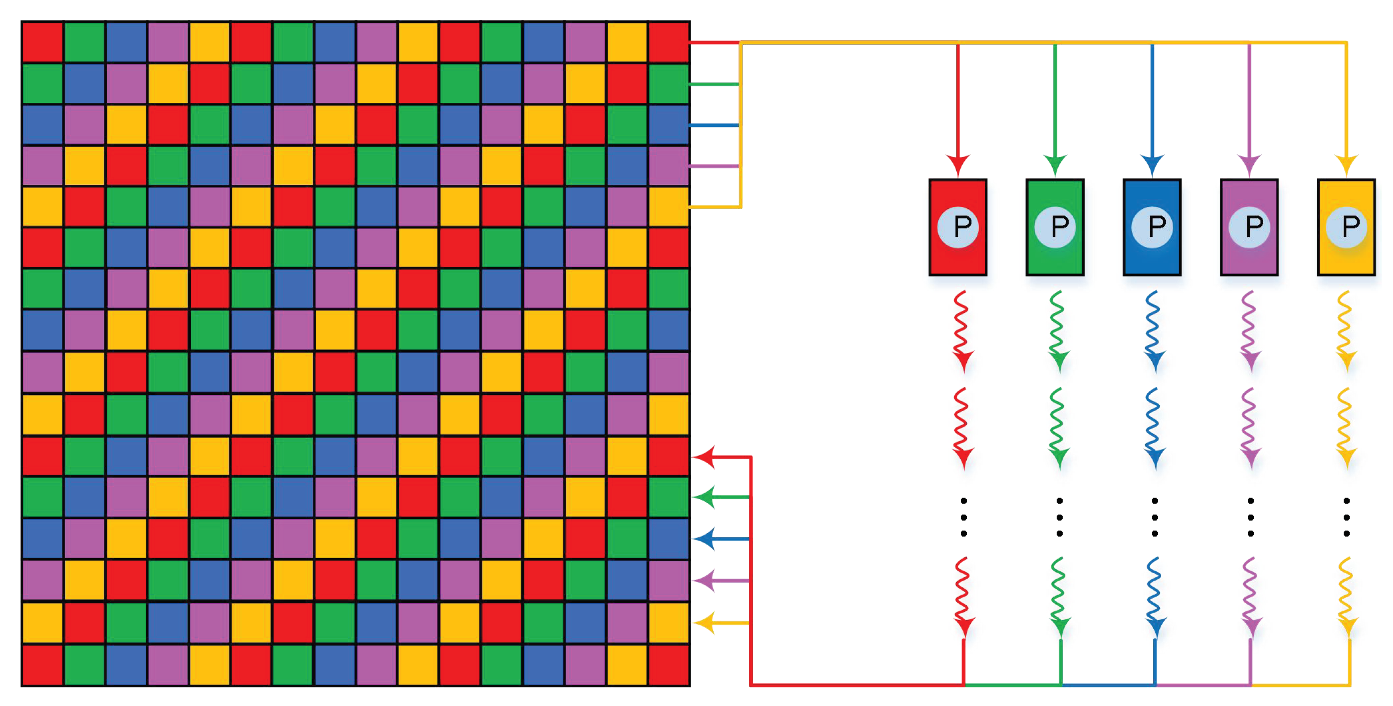
2.1.1. Block Partitioning
- (1).
- The operation time complexity based on Tt is O(|Vt¯|), which has linear complexity.
- (2).
- Every edge of Et¯ is a cut edge, such that deleting or restoring an edge will increase or decrease a region, which greatly simplifies the complexity of the partition operation, and each region corresponds to a tree.
- (3).
- The boundary of the target on Tt is generated along the edge, which is helpful to express the complex and irregular boundary of the target.
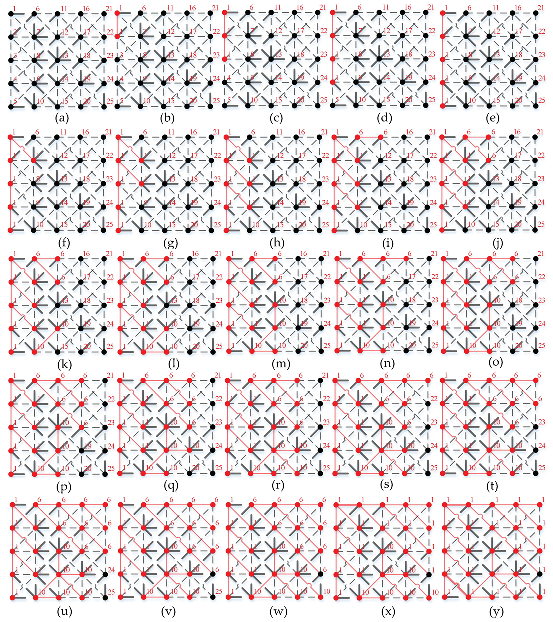
| Algorithm 1. Proposed image MST generation method based on Kruskal algorithm |
| Input: graph Ɠt = (Vt, Et, Ψt) |
| Output: MST Tt = (Vt¯, Et¯, Ψt¯) |
| Initialization: Vt¯ = ∅, Et¯ = ∅, Ψt¯= ∅, t = {1, 2, …, |Vt¯|} |
| 1. do Et = sortrows(Et, Ψt, “ascending”) |
| 2. for each ec = (vc1, vc2) ∈ Et |
| 3. do if t(vc1) ≠ t(vc2) |
| 4. do Et¯ =Et¯ ∪ {ec}, Ψt¯ = Ψt¯ ∪ {φc}, Vt¯ = Vt¯∪ {vc1, vc2}, Vt¯ = unique(Vt¯) |
| 5. do t(t = t(vc2)) = t(vc1)// all markers of the vertices t(vc2) are changed to t(vc1) |
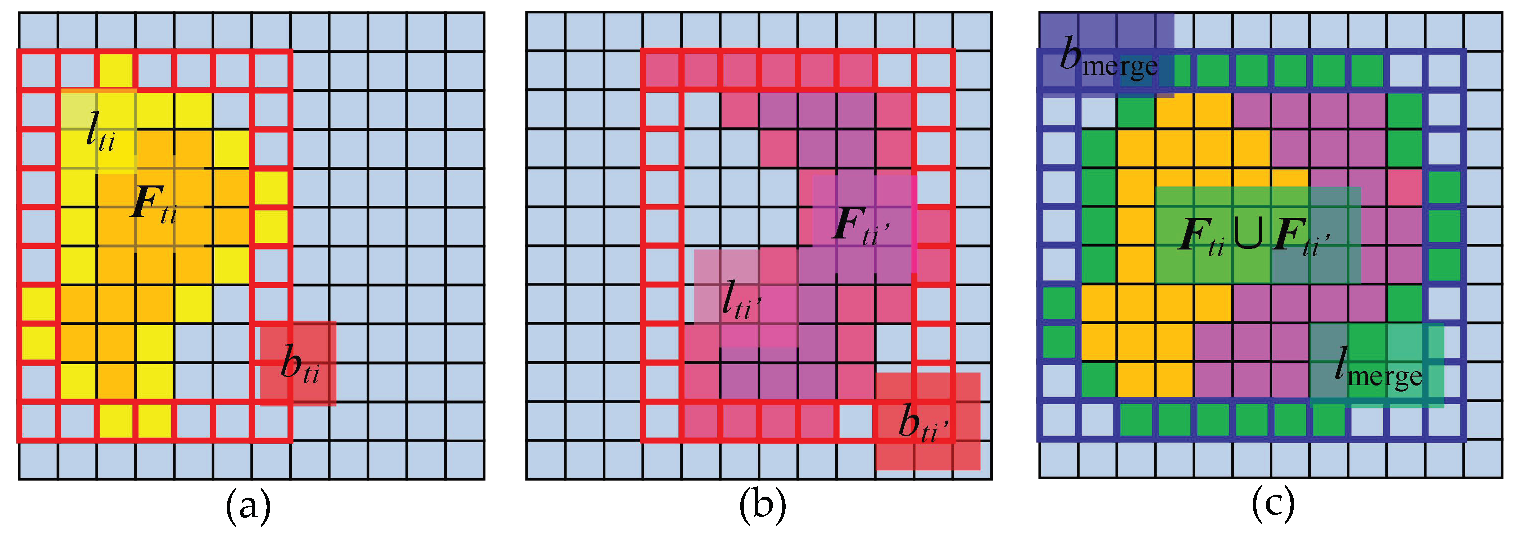
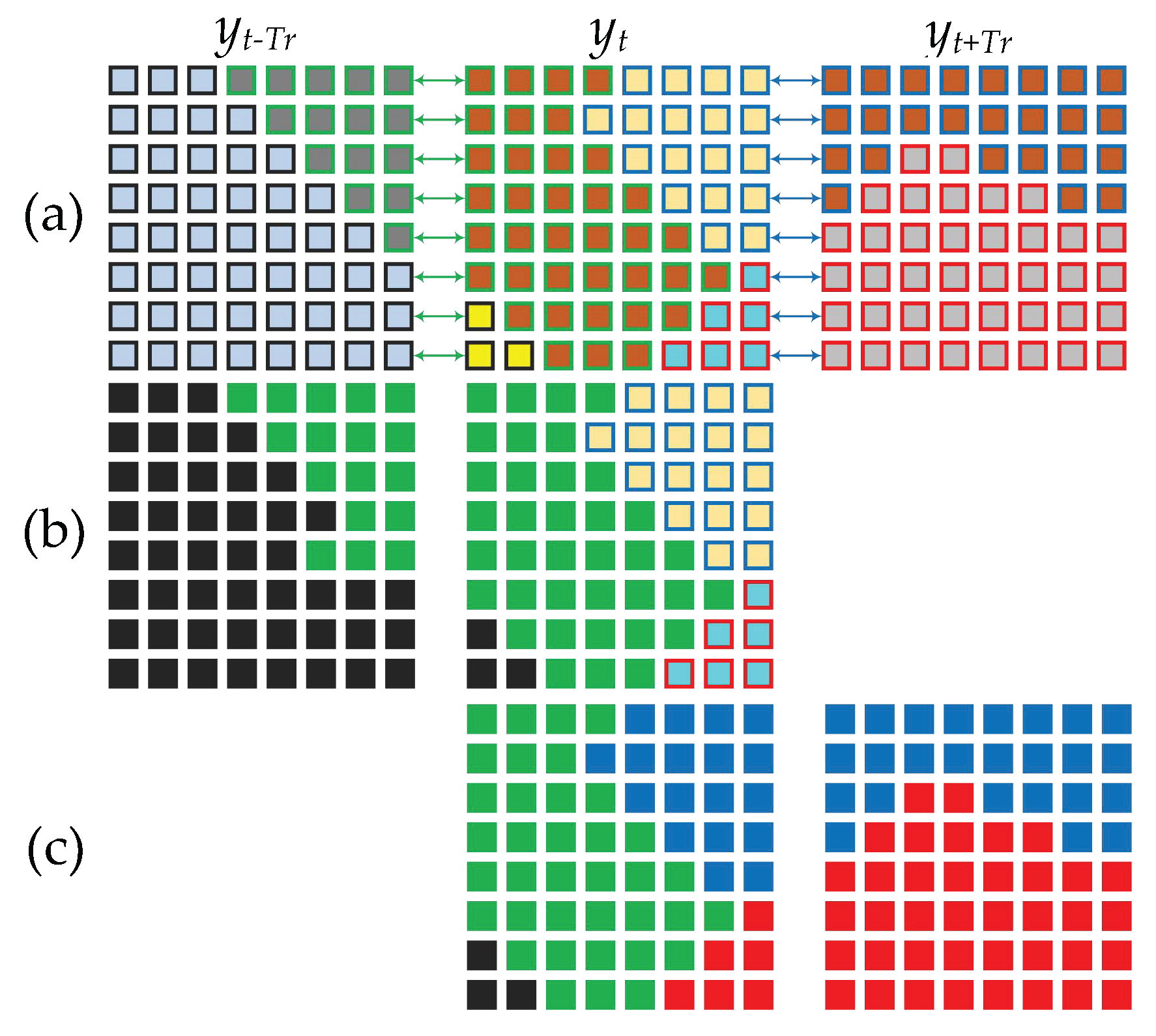
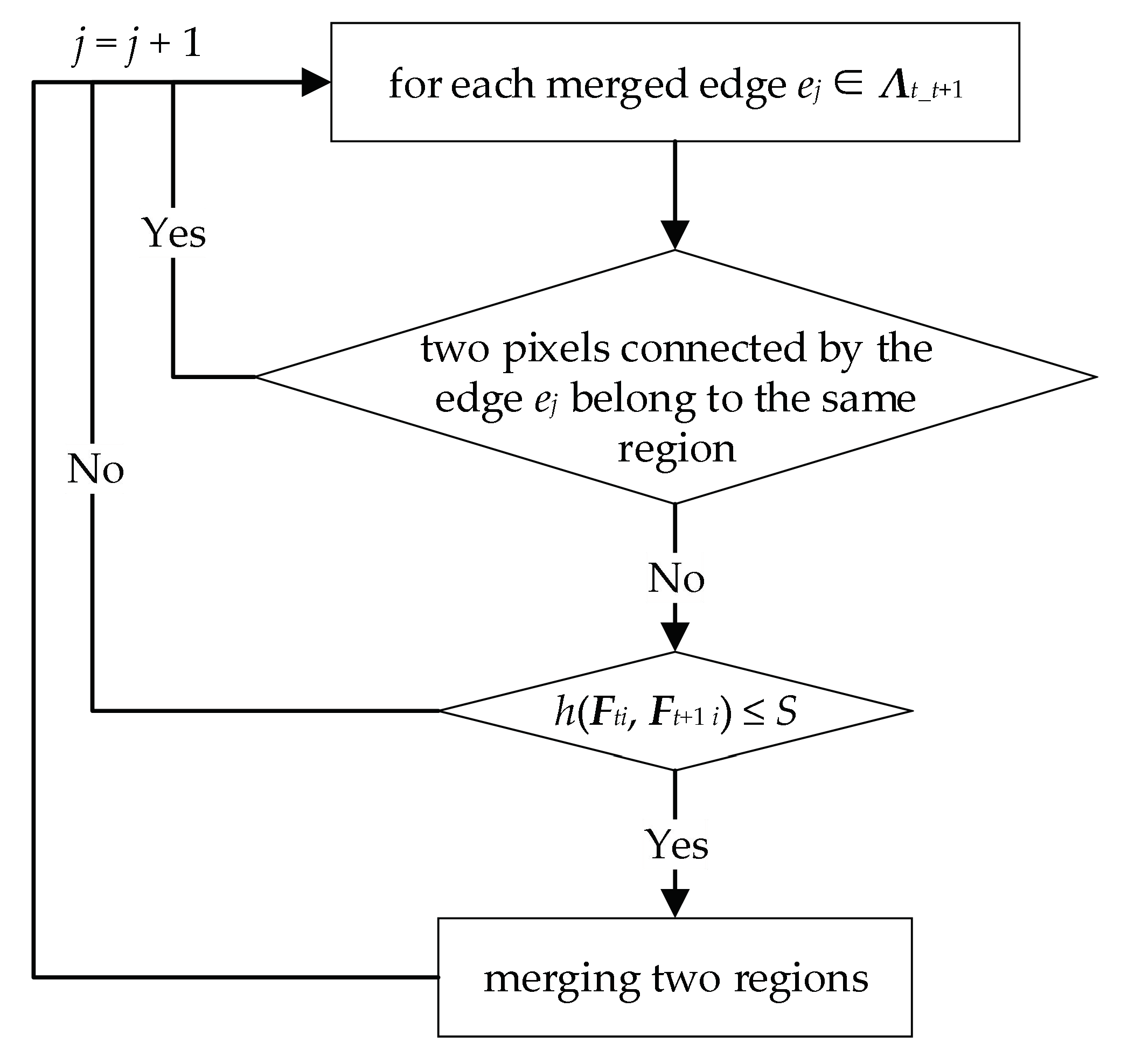
2.1.2. Block Merging
2.2. Regional Hidden Markov Random Field–Fuzzy C-Means (RHMRF-FCM) Segmentation
2.2.1. RHMRF-FCM Segmentation
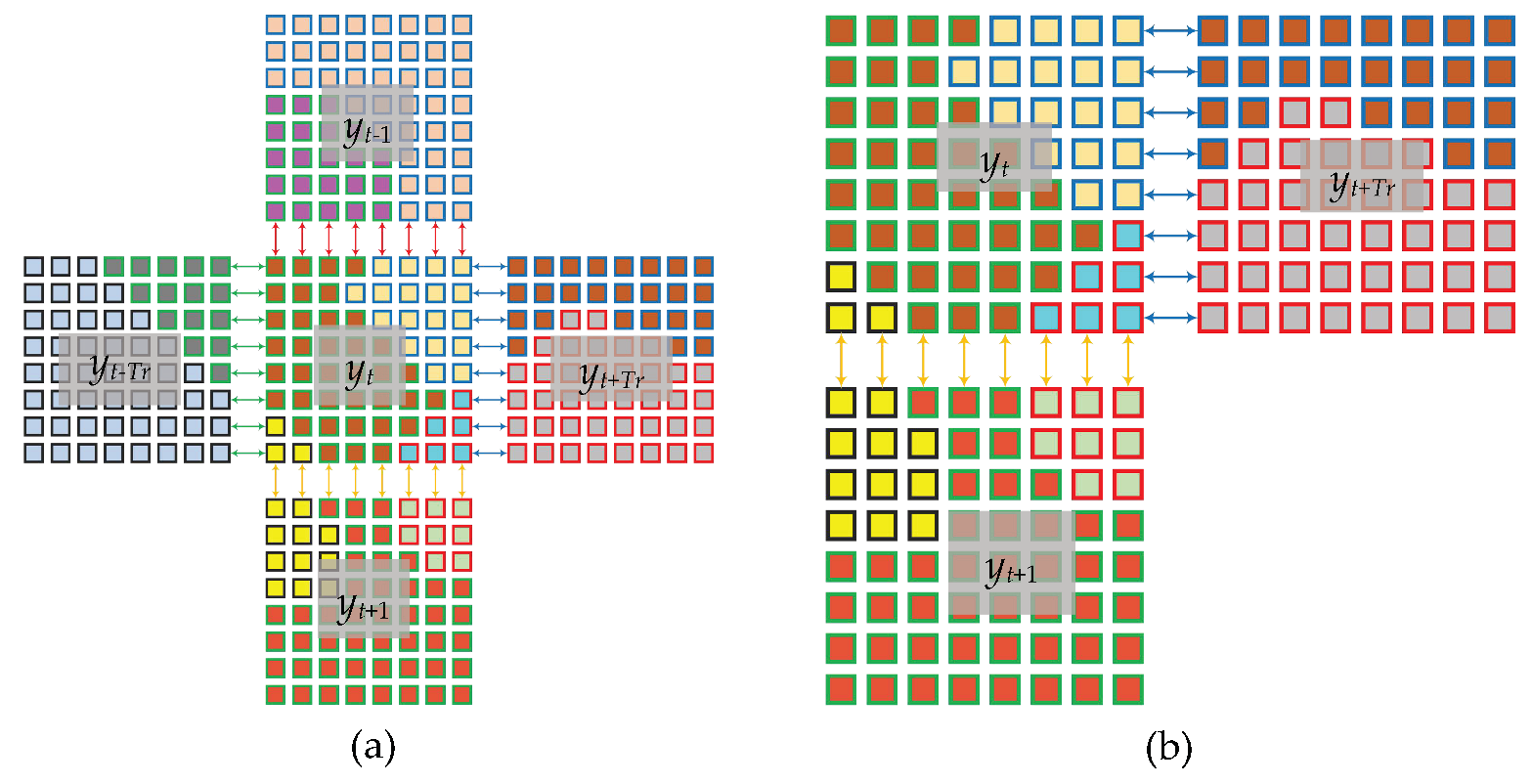
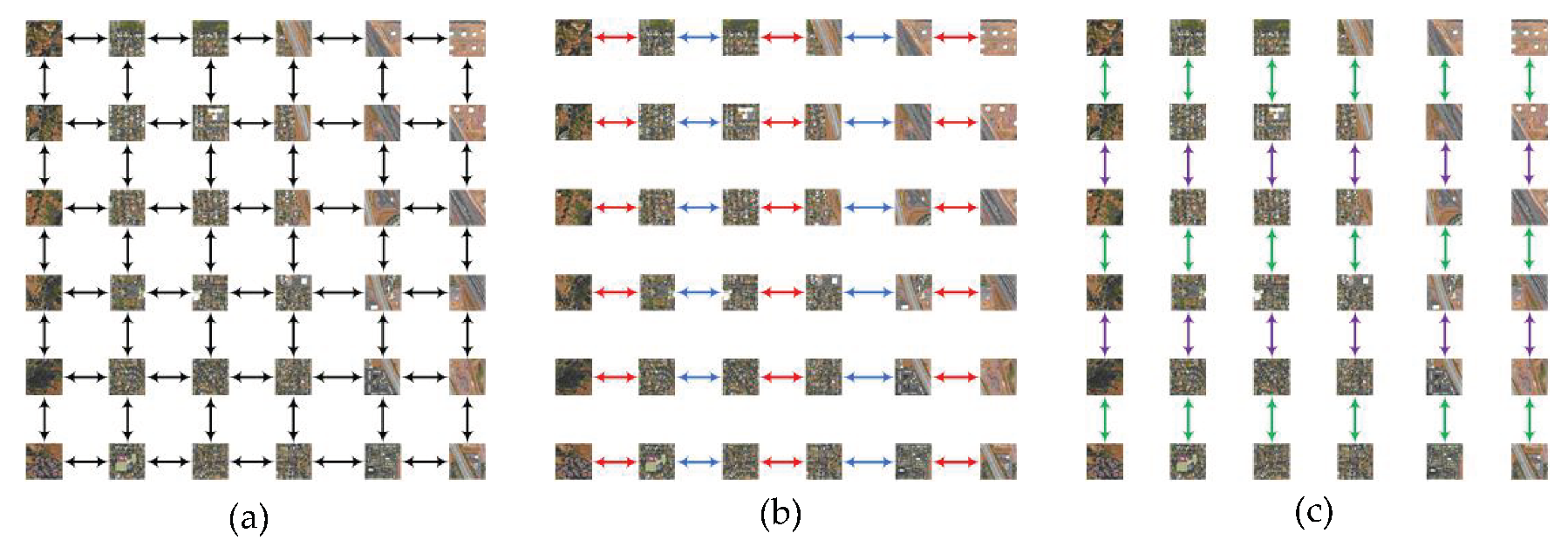
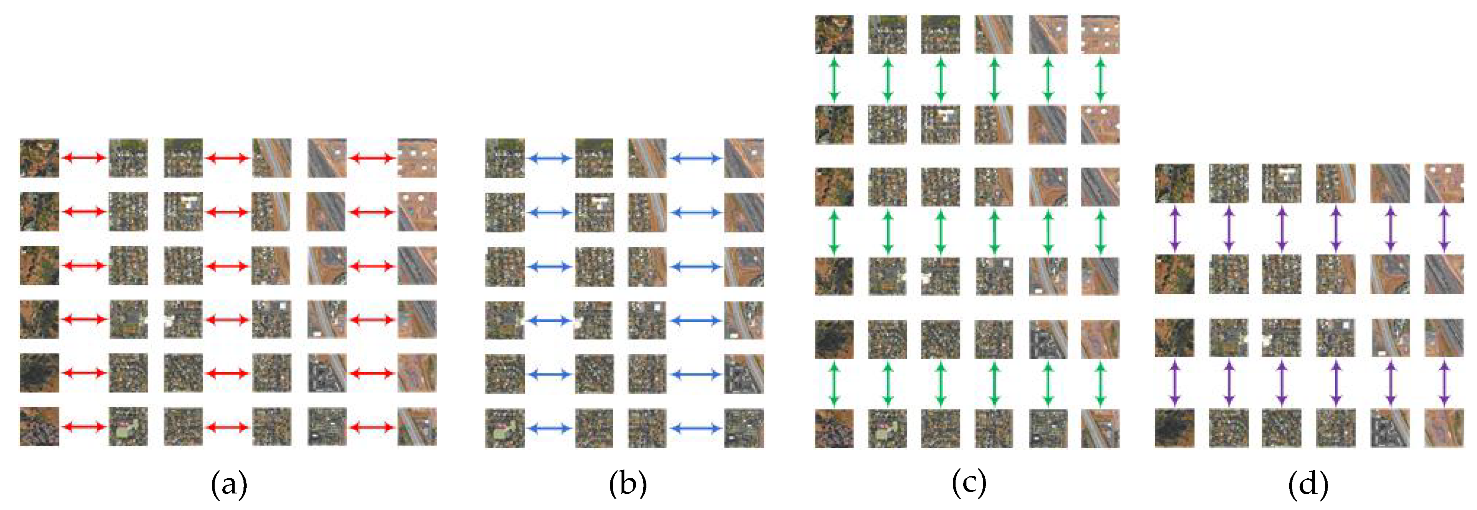
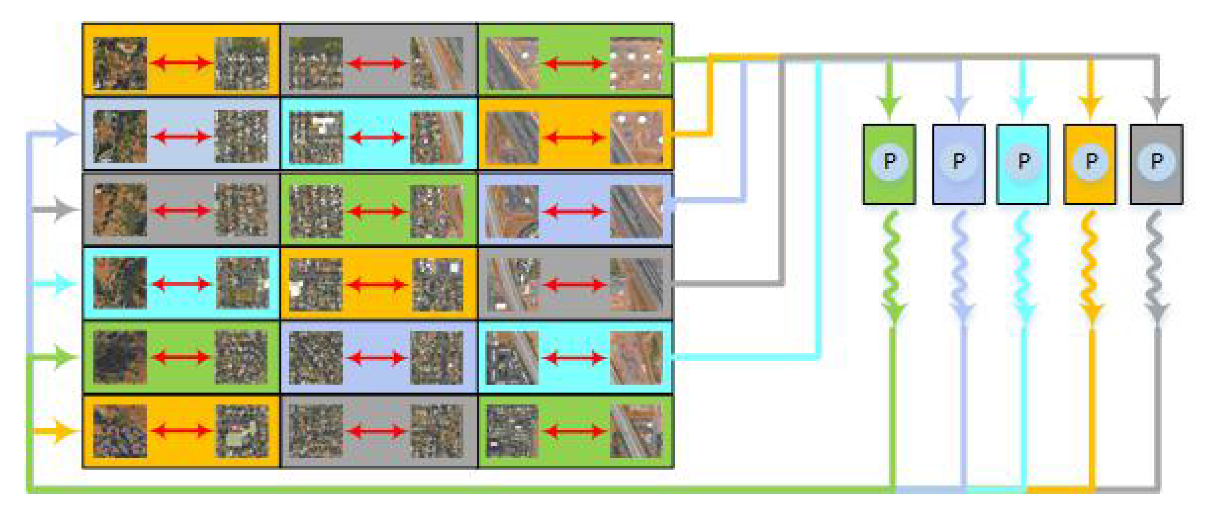
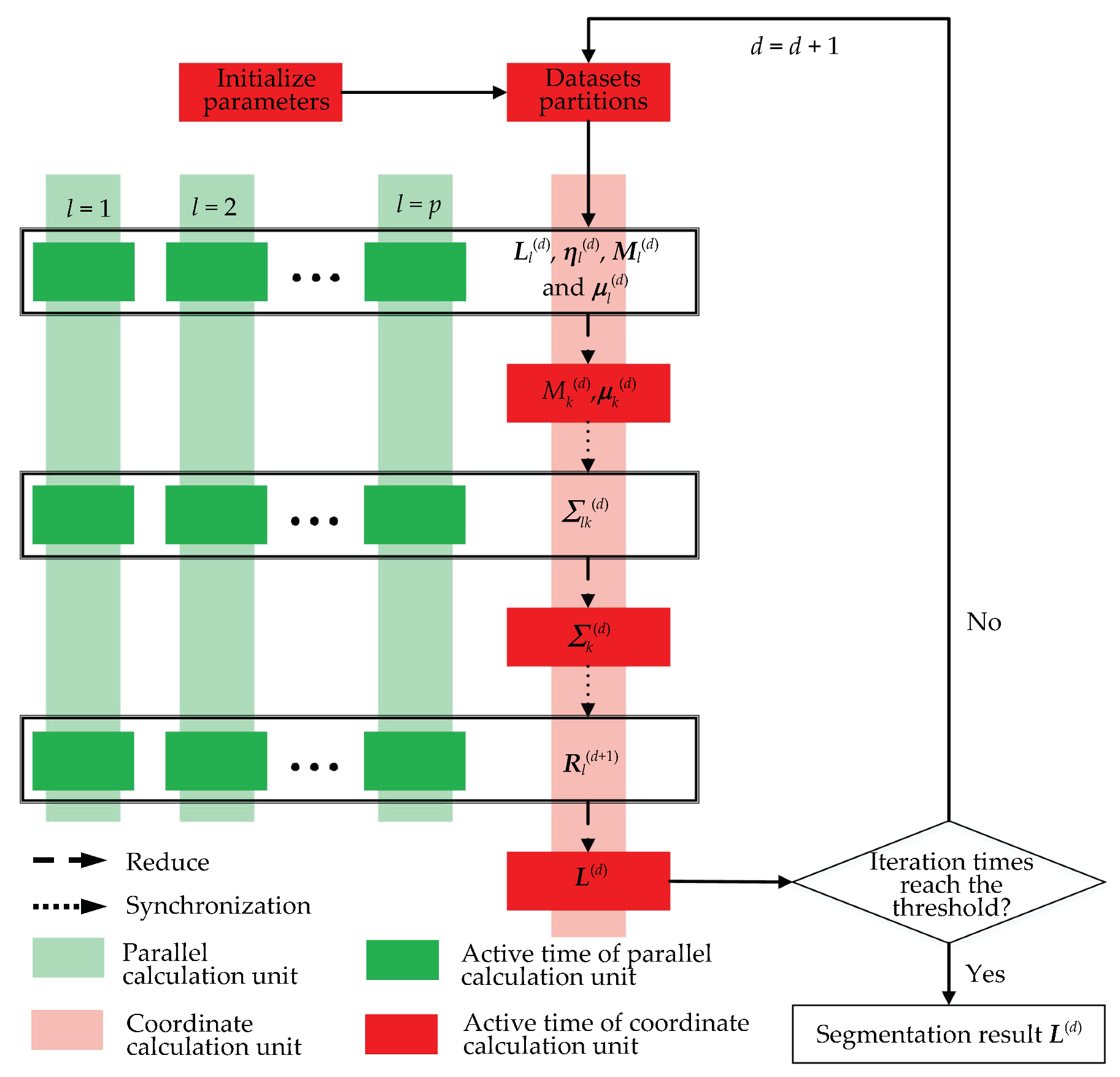
2.2.2. Parallel RHMRF-FCM Segmentation
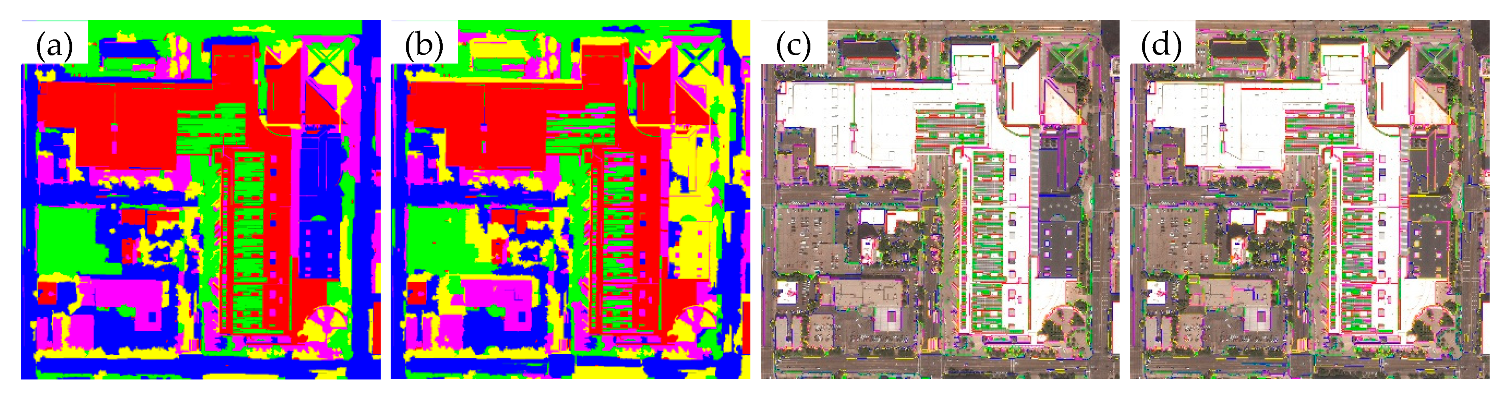
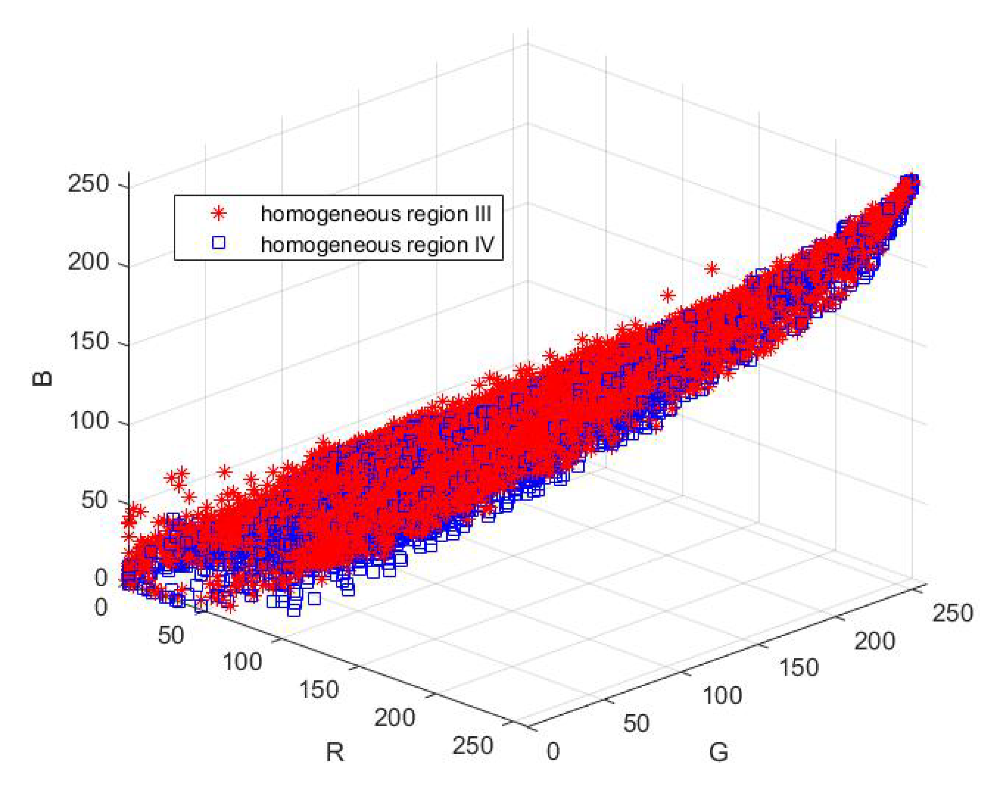
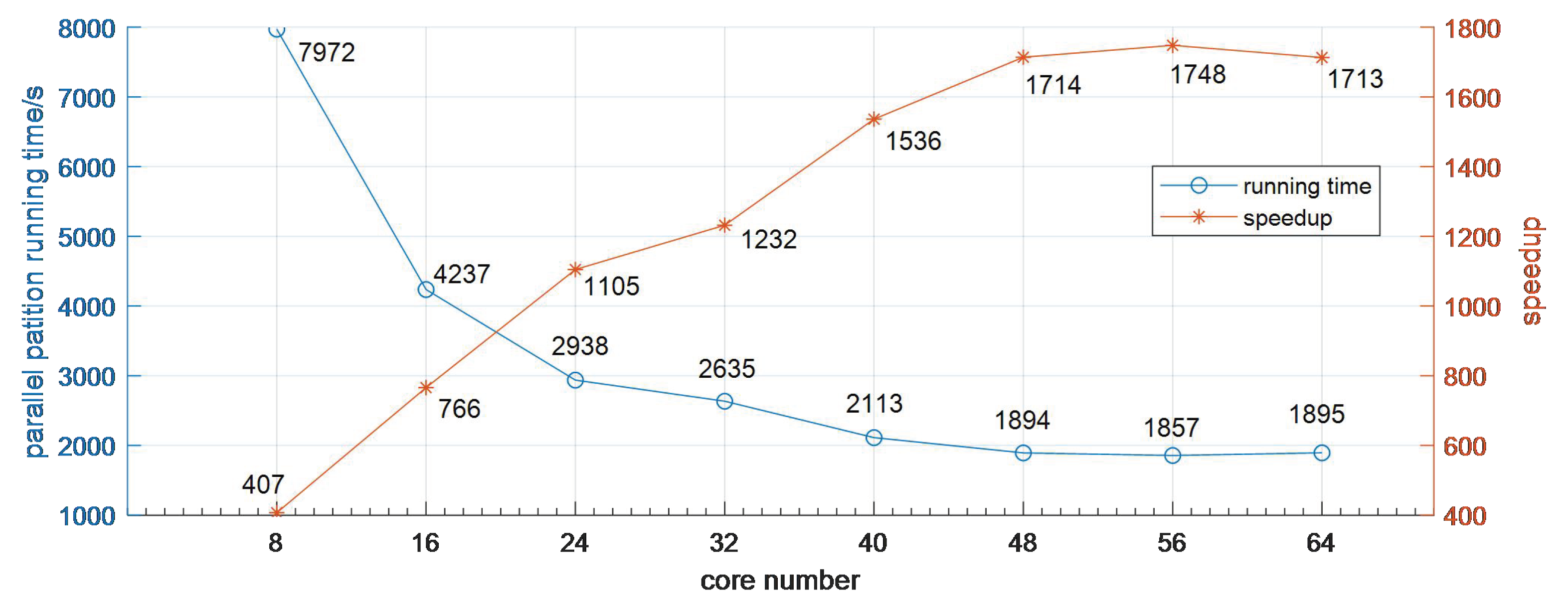
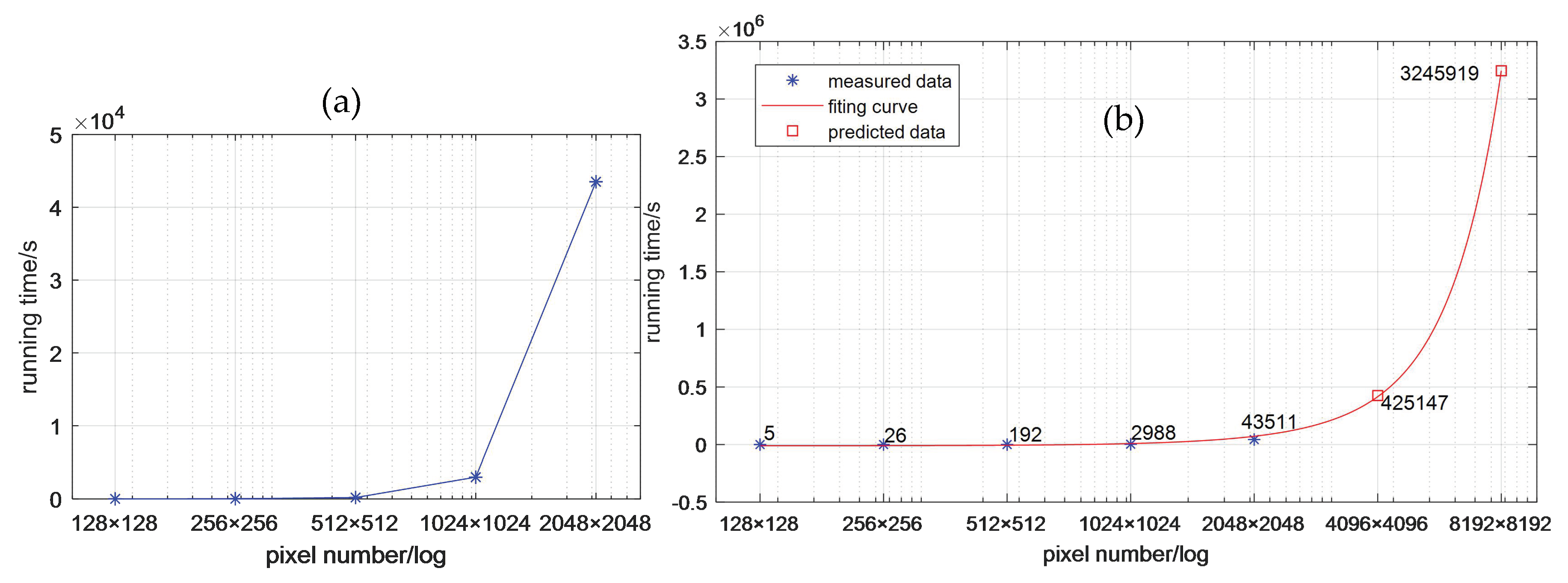
3. Results and Discussion
3.1. Cost Analysis
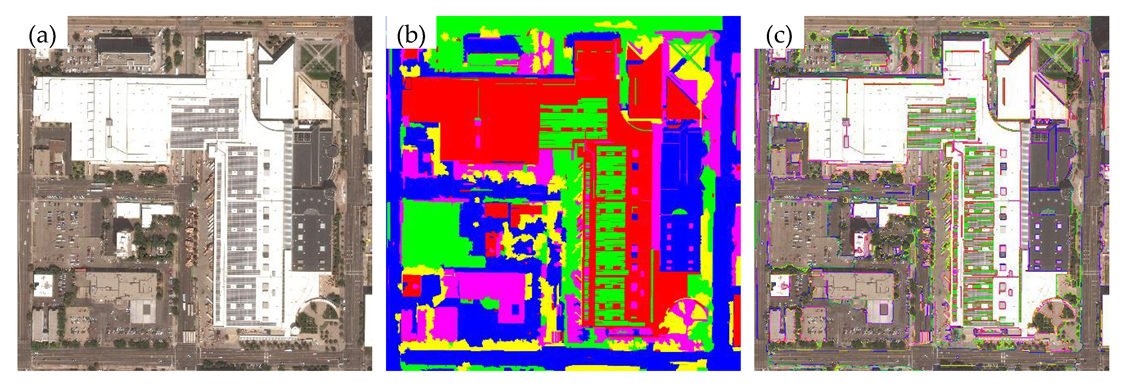
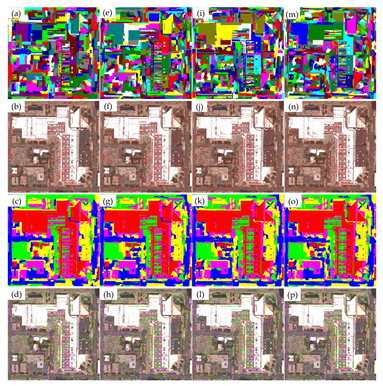
3.2. Performance Analysis
3.3. Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jensen, J. Introductory Digital Image Processing: A Remote Sensing Perspective, 3rd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2005. [Google Scholar]
- Zhao, X.; Li, Y.; Zhao, Q. Mahalanobis distance based on fuzzy clustering algorithm for image segmentation. Digit. Signal Process. 2015, 43, 8–16. [Google Scholar] [CrossRef]
- Li, Y. Remotely Sensed Data Segmentation under a Spatial Statistics Framework. Ph.D. Thesis, University of Waterloo, Waterloo, Ontario, 2009. [Google Scholar]
- Curran, P. Remote sensing: Using the spatial domain. Environ. Ecol. Stat. 2001, 8, 331–344. [Google Scholar] [CrossRef]
- Wang, C.; Xu, A.; Li, X. Supervised classification high-resolution remote-sensing image based on interval type-2 fuzzy membership function. Remote Sens. 2018, 10, 710. [Google Scholar] [CrossRef]
- Li, D.; Tong, Q.; Li, R.; Gong, J.Y.; Zhnag, L. Current issues in high-resolution earth observation technology. Sci. China Earth Sci. 2012, 55, 1043–1051. (In Chinese) [Google Scholar] [CrossRef]
- Benediktsson, J.; Chanussot, J.; Moon, W. Very high-resolution remote sensing: Challenges and opportunities. Proc. IEEE 2012, 100, 1907–1910. [Google Scholar] [CrossRef]
- Ma, Y.; Wu, H.; Wang, L.; Huang, B.; Rangjan, R.; Zomaya, A.; Jie, W. Remote sensing big data computing: Challenges and opportunities. Future Gener. Comput. Syst. 2015, 51, 47–60. [Google Scholar] [CrossRef]
- Rathore, M.; Paul, A.; Ahmad, A.; Chen, B.W.; Huang, B.; Ji, W. Real-time big data analytical architecture for remote sensing application. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 4610–4621. [Google Scholar] [CrossRef]
- Lin, W.; Li, Y.; Zhao, Q. High-resolution remote sensing image segmentation using minimum spanning tree tessellation and RHMRF-FCM algorithm. Acta Geod. Cartogr. Sin. 2019, 48, 64–74. (In Chinese) [Google Scholar]
- Dearo, G.; Coelho, N. Multiple parallel mapreduce k-means clustering with validation and selection. In Proceedings of the 2014 Brazilian Conference on Intelligent Systems, IEEE Computer Society, Sao Paulo, Brazil, 18–22 October 2014; pp. 432–437. [Google Scholar]
- Gu, H.; Han, Y.; Yang, Y.; Li, H.; Liu, Z.; Soergel, U.; Blaschke, T.; Cui, S. An efficient parallel multi-scale segmentation method for remote sensing imagery. Remote Sens. 2018, 10, 590. [Google Scholar] [CrossRef]
- Du, Z.; Gu, Y.; Zhang, C.; Zhang, F.; Liu, R.; Sequeira, J.; Li, W. ParSymG: A parallel clustering approach for unsupervised classification of remotely sensed imagery. Int. J. Digit. Earth 2016, 1–19. [Google Scholar] [CrossRef]
- Guan, Q.; Clarke, K. A general-purpose parallel raster processing programming library test application using a geographic cellular automata model. Int. J. Geogr. Inf. Sci. 2010, 24, 695–722. [Google Scholar] [CrossRef]
- Xing, J.; Sieber, R.; Kalacska, M. The challenges of image segmentation in big remotely sensed imagery data. Ann. GIS 2014, 20, 233–244. [Google Scholar] [CrossRef]
- Peng, B.; Zhang, L.; Zhang, D. A survey of graph theoretical approaches to image segmentation. Pattern Recognit. 2013, 46, 1020–1038. [Google Scholar] [CrossRef]
- Geetha, M.; Rakendu, R. An improved method for segmentation of point cloud using minimum spanning tree. In Proceedings of the 2014 International Conference on Communications & Signal Processing, Melmaruvathur, India, 3–5 April 2014; pp. 833–837. [Google Scholar]
- Sharifi, M.; Kiani, K.; Kheirkhahan, M. A Graph-Based Image Segmentation Approach for Image Classification and Its Application on SAR Images. Prz. Elektrotech. 2013, 89, 202–205. [Google Scholar]
- Wu, Z.; Leahy, R. An optimal graph theoretic approach to data clustering: Theory and its application to image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 1993, 15, 1101–1113. [Google Scholar] [CrossRef]
- Banerjee, B.; Varma, S.; Buddhiraju, K.; Eeti, L.N. Unsupervised multi-spectral satellite image segmentation combining modified mean-shift and a new minimum spanning tree based clustering technique. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 888–894. [Google Scholar] [CrossRef]
- Cui, W.; Zhang, Y. An effective graph-based hierarchy image segmentation. Intell. Autom. Soft Comput. 2011, 17, 969–981. [Google Scholar] [CrossRef]
- Baatz, M.; Schäpe, A. Multiresolution segmentaion: An optimization approach for high quality multi-scale image segmentation. In Angewandte Geographische Informationsverarbeitung XII; Strobl, J., Blaschke, T., Griesebner, G., Eds.; Wichmann: Heidelberg, Germany, 2000; pp. 12–23. [Google Scholar]
- Judah, A.; Hu, B.X.; Wang, J.G. An Algorithm for Boundary Adjustment toward Multi-Scale AdaptiveSegmentation of Remotely Sensed Imagery. Remote Sens. 2014, 6, 3583–3610. [Google Scholar] [CrossRef]
- Wang, P.; Wei, Z.; Cui, W.; Lin, Z. A image segmentation method based on statistics learning theory and minimum spanning tree. Geomat. Inf. Sci. Wuhan Univ. 2017, 42, 877–883. (In Chinese) [Google Scholar]
- Zhao, Q.; Li, X.; Zhao, X.; Li, Y. Fuzzy ISODATA Image Segmentation Intergrating Voronoi Tessellation HMRF Model. J. Signal Process. 2016, 32, 1233–1243. [Google Scholar]
- Zhao, Q.; Li, X.; Zhao, X.; Li, Y. Remote Sensing Image Segmentation Algorithm with Regional Fuzzy Cluster and Mahalanobis Distance. J. China Univ. Min. Technol. 2017, 46, 222–228. [Google Scholar]
- Lucarini, V. Symmetry-Break in Voronoi Tessellations. Symmetry 2009, 1, 21–54. [Google Scholar] [CrossRef]
- Schneider, R. Weighted faces of Poisson Hyperplane Tessellations. Adv. Appl. Probab. 2009, 41, 682–694. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Y.; Zhao, Q. SAR Image Segmentation Combined Regular Tessellation and M-H Algorithm. Geomat. Inf. Sci. Wuhan Univ. 2016, 41, 1491–1497. [Google Scholar]
- Achanta, R.; Shaji, A.; Smith, K. SLIC Superpixels Compared to State-of-the-Art Superpixel Methods. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 2274–2282. [Google Scholar] [CrossRef] [PubMed]
- Baatz, M.; Schäpe, A. An optimization approach for high quality multi-scale image segmentation. In Beiträge Zum AGIT-Symposium; Herber Wichmann-Verlag: Berlin, Germany, 2000; pp. 12–23. [Google Scholar]
- Li, H.; Tang, Y.; Liu, Q.; Ding, H.; Jing, L. An improved algorithm based on minimum spanning tree for multi-scale segmentation of remote sensing imagery. Acta Geod. Cartogr. Sin. 2015, 44, 791–796. (In Chinese) [Google Scholar]
- Zhao, Q.; Li, X.; Li, Y.; Zhao, X. A fuzzy clustering image segmentation algorithm based on Hidden Markov Random Field models and Voronoi Tessellation. Pattern Recognit. Lett. 2017, 85, 49–55. [Google Scholar] [CrossRef]
- Cannon, R.L.; Dave, J.V.; Bezdek, J.C.; Trivedi, M.M. Segmentation of a thematic mapper image using the fuzzy c-means clustering algorithm. IEEE Trans. Geosci. Remote Sens. 1986, 24, 400–408. [Google Scholar] [CrossRef]
- Miyamoto, S.; Ichihashi, H.; Honda, K. Algorithms for Fuzzy Clustering; Springer: Heidelberg, Germany, 2008. [Google Scholar]
- Prim, R. Shortest connection networks and some generalizations. Bell Syst. Tech. J. 1957, 36, 1389–1401. [Google Scholar] [CrossRef]
- Kruskal, J. On the shortest spanning subtree of a graph and the traveling salesman problem. Proc. Am. Math. Soc. 1956, 7, 48–50. [Google Scholar] [CrossRef]
- Kruskal’s Minimum Spanning Tree Algorithm|Greedy Algo-2. Available online: https://www.geeksforgeeks.org/kruskals-minimum-spanning-tree-algorithm-greedy-algo-2/ (accessed on 20 January 2020).
- Thomas, H.; Charles, E.; Ronald, L.; Clifford, S. Introduction to Algorithms, 3rd ed.; The MIT Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Chatzis, S.; Varvarigou, T. A fuzzy clustering approach toward hidden Markov random field models for enhanced spatially constrained image segmentation. IEEE Trans. Fuzzy Syst. 2008, 16, 1351–1361. [Google Scholar] [CrossRef]
- Rosu, R.-G.; Giovannelli, J.-F.; Giremus, A.; Vacar, A. Potts model parameter estimation in Bayesian segmentation of piecewise constant images. In Proceedings of the 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), IEEE, Brisbane, Australia, 19–24 April 2015; pp. 4080–4084. [Google Scholar]
- Chen, W.; Ostrouchov, G.; Pugmire, D.; Prabhat, M.; Wehner, M.F. A parallel EM algorithm for model-based clustering applied to the exploration of large spatio-temporal data. Technometrics 2013, 55, 513–523. [Google Scholar] [CrossRef]
- Trobec, R.; Slivnik, B.; Bulić, P.; Robic, B. Introduction to Parallel Computing: From Algorithms to Programming on State-of-the-Art Platforms; Springer: Beilin, Germany, 2018. [Google Scholar]
- Congalton, R.; Green, K. Assessing the Accuracy of Remotely Sensed Data: Principles and Practices; Lewis Publishers: Boca Raton, FL, USA, 1999. [Google Scholar]


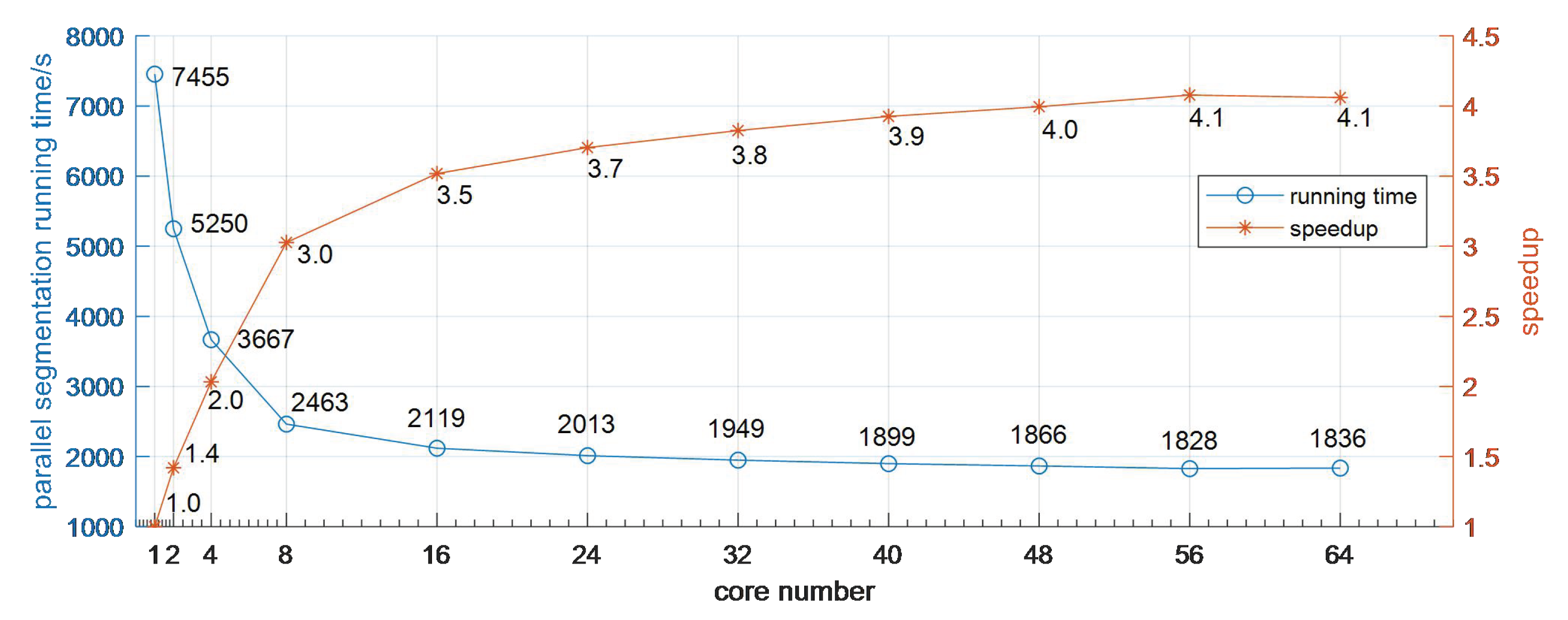
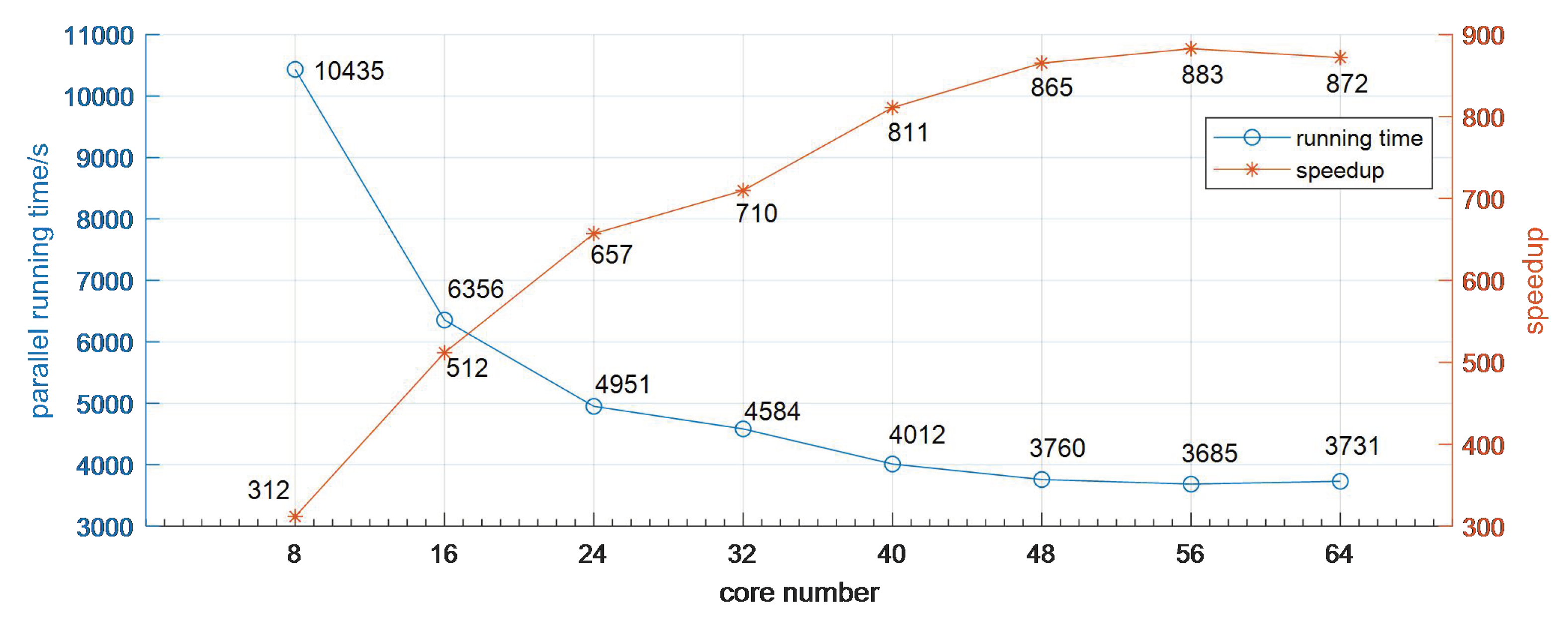
| Block Size | Accuracy | Homogeneous Region | ||||
|---|---|---|---|---|---|---|
| I | II | III | IV | V | ||
| 128 × 128 | User’s | 0.98 | 0.69 | 0.86 | 0.39 | 0.86 |
| Producer’s | 0.98 | 0.81 | 0.57 | 0.80 | 0.76 | |
| Overall | 0.76 | |||||
| Kappa | 0.72 | |||||
| 256 × 256 | User’s | 0.99 | 0.78 | 0.89 | 0.44 | 0.94 |
| Producer’s | 0.99 | 0.88 | 0.64 | 0.83 | 0.82 | |
| Overall | 0.82 | |||||
| Kappa | 0.78 | |||||
| 512 × 512 | User’s | 0.99 | 0.80 | 0.93 | 0.46 | 0.96 |
| Producer’s | 0.99 | 0.89 | 0.65 | 0.90 | 0.84 | |
| Overall | 0.83 | |||||
| Kappa | 0.80 | |||||
| 1024 × 1024 | User’s | 0.99 | 0.83 | 0.94 | 0.48 | 0.96 |
| Producer’s | 0.99 | 0.89 | 0.67 | 0.92 | 0.86 | |
| Overall | 0.85 | |||||
| Kappa | 0.82 | |||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, W.; Li, Y. Parallel Regional Segmentation Method of High-Resolution Remote Sensing Image Based on Minimum Spanning Tree. Remote Sens. 2020, 12, 783. https://doi.org/10.3390/rs12050783
Lin W, Li Y. Parallel Regional Segmentation Method of High-Resolution Remote Sensing Image Based on Minimum Spanning Tree. Remote Sensing. 2020; 12(5):783. https://doi.org/10.3390/rs12050783
Chicago/Turabian StyleLin, Wenjie, and Yu Li. 2020. "Parallel Regional Segmentation Method of High-Resolution Remote Sensing Image Based on Minimum Spanning Tree" Remote Sensing 12, no. 5: 783. https://doi.org/10.3390/rs12050783
APA StyleLin, W., & Li, Y. (2020). Parallel Regional Segmentation Method of High-Resolution Remote Sensing Image Based on Minimum Spanning Tree. Remote Sensing, 12(5), 783. https://doi.org/10.3390/rs12050783