Building Extraction from High Spatial Resolution Remote Sensing Images via Multiscale-Aware and Segmentation-Prior Conditional Random Fields

Abstract

Building extraction is a binary classification task that separates the building area from the background in remote sensing images. The conditional random field (CRF) is directly modelled by the maximum posterior probability, which can make full use of the spatial neighbourhood information of both labelled and observed images. CRF is widely used in building footprint extraction. However, edge oversmoothing still exists when CRF is directly used to extract buildings from high spatial resolution (HSR) remote sensing images. Based on a computer vision multi-scale semantic segmentation network (D-LinkNet), a novel building extraction framework is proposed, named multiscale-aware and segmentation-prior conditional random fields (MSCRF). To solve the problem of losing building details in the downsampling process, D-LinkNet connecting the encoder and decoder is correspondingly used to generate the unary potential. By integrating multi-scale building features in the central module, D-LinkNet can integrate multiscale contextual information without loss of resolution. For the pairwise potential, the segmentation prior is fused to alleviate the influence of spectral diversity between the building and the background area. Moreover, the local class label cost term is introduced. The clear boundaries of the buildings are obtained by using the larger-scale context information. The experimental results demonstrate that the proposed MSCRF framework is superior to the state-of-the-art methods and performs well for building extraction of complex scenes.

1. Introduction

With the rapid development of city construction, buildings have become one of the most changeable artificial target types in basic geographical data [1]. In recent years, many series of high-resolution satellites have been launched worldwide. The availability and accessibility of HSR images have been significantly improved [2]. The timely and accurate extraction of buildings from HSR is of great significance for urban planning, disaster management, digital city and geographic database updates [3,4].

In the 1980s, researchers began to study the basic theory of building extraction using remote sensing images. In recent decades, many scholars worldwide have proposed a variety of accurate and rapid building extraction methods. During this period, information was applied to building extraction such as edge extraction, image segmentation, digital surface model (DSM) data, light detection and ranging (LiDAR) point clouds, and the spatial information and features of HSR images [5]. In addition, building extraction methods that use spatial information and features such as the geometry and texture of HSR images were gradually developed. An a priori shape model of typical buildings with respect to their geometric attributes was introduced by Karantzalos and Paragios [6]. This model, which combines level set segmentation, can achieve better extraction results, but its application in urban areas with dense buildings is limited. Akçay et al. [7] combined probabilistic latent semantic analysis (PLSA) and morphological analysis to identify features of HSR images, which can simultaneously extract urban buildings, roads and vegetation areas, avoiding the difficulty of establishing regular geometric shapes. However, the extracted building outline is irregular. A conditional random field (CRF) was applied to building extraction in 2015. Li et al. combined pixel-level information and segmentation level to identify roofs, which can improve the performance of roof extraction and can also effectively handle complex-shaped buildings [8,9]. A CRF was developed on the basis of a Markov random field, which eliminates the strict independence assumption of the Markov random field. Its good overall nature can link local features well and realize the organic integration of bottom-up and top-down target semantics. However, due to the lack of large-scale spatial interactive information modelling capabilities of CRF, it easily produces different degrees of smoothing problems [10].

With the increasing maturity of deep learning technology, it is possible to learn representative high-level features in images by training a large number of samples, and deep learning has also been introduced into building extraction research. Vakalopoulou et al. [11] implemented remote sensing image building target detection based on a convolutional neural network in 2015. Aiming at the regular shape, diverse appearance and complex distribution of buildings, Chen et al. [12] designed a 27-layer-deep convolutional neural network with convolution and deconvolution to achieve pixel-level extraction of buildings on high-resolution images. Deep learning networks have powerful feature extraction capabilities. Complex neural networks have high extraction accuracy, but often require considerable computing time, and the existing deep learning methods are not ideal for extracting building boundaries with regular geometric structures.

The ability to use contextual information from CRF can compensate for the shortcomings of deep learning in extracting buildings. Shrestha S et al. improved the full convolutional network by introducing an exponential linear unit (ELU) to improve the performance of the fully convolutional networks (FCNs). This is combined with CRF to make full use of context information and enhance building boundaries [13,14]. Sun et al. [15] designed a multitask network to enable FCN to generate mask and edge information simultaneously. It used a CRF to refine the results of the FCN. Then, a new time-efficient end-to-end model was obtained. Li et al. [16] proposed a feature pair conditional random field (FPCRF) framework, which uses convolutional neural networks (CNNs) as a feature extractor to achieve fine-grained building segmentation. These methods generally use traditional neural networks combined with traditional CRF. However, existing deep learning models of building extraction easily lose detailed information in the process of downsampling, which is difficult to recover during upsampling. In addition, the pixel-based processing of CRF may cause discontinuities inside the building and lead to the loss of detailed information.

In this paper, a multiscale-aware and segmentation-prior conditional random field (MSCRF) framework is proposed. For buildings of different scales, it is difficult to extract sufficient features from a single receptive field. This framework introduces D-LinkNet (LinkNet with a pretrained encoder and dilated convolution) [17] to model the relationship between the observed image data and the label for the first time. The pairwise potential models the linear combination of the spatial smoothing term and the local class label cost term. Moreover, this paper fuses segmentation prior to extracting buildings using larger-scale context information. Finally, the $\alpha -\mathrm{expansion}$ algorithm based on graph cuts is introduced for model inference.

The major contributions of this paper are as follows:

(1)

The MSCRF framework is proposed to obtain buildings with clear boundaries and maintain the continuity inside the buildings. In MSCRF, D-LinkNet is used to model the correspondence between the image and its label. Using D-LinkNet to extract buildings still has problems, such as discontinuities inside the buildings. The CRF compensates for the shortcomings of D-LinkNet. The segmentation prior and the local class label cost are merged into the pairwise potential of the traditional CRF in the MSCRF.

(2)

Multiscale building features are integrated by D-LinkNet based on multiple parallel dilated convolution modules in the MSCRF framework. D-LinkNet can avoid losing many details in the subsampling process, and solve the problem of boundary blur. This is beneficial for extracting small-scale dense buildings. To obtain a stronger feature expression of the building areas, the feature map of D-LinkNet is used to replace the unary potential of the traditional CRF in MSCRF.

(3)

The local class label cost term is introduced. The pairwise potential reflect the linear combination of the spatial relationship of adjacent pixels and the local class label cost term. It can effectively maintain the detailed information inside the buildings. Moreover, to solve the problem of the spectral similarity between buildings and noise, the segmentation prior is fused to extract buildings by using larger-scale context information.

The rest of this paper is organized as follows. In Section 2, building extraction methods are described in detail. Section 3 describes the proposed MSCRF framework for HSR imagery building extraction. A description of the datasets and a discussion of the experimental results are presented in Section 4. Section 5 presents the discussion. Finally, conclusions are drawn in Section 6.

2. Related Works

High-resolution remote sensing images contain much detailed information, but there are also certain noise problems. Therefore, originally, object-oriented methods were widely used in the field of building extraction. Then, the building extraction mode based on segmentation gradually developed. Qiao et al. [18] adopted an object-oriented strategy and proposed a multiscale segmentation methodology based on IKONOS images. Wegne et al. [19] proposed a combination of region segmentation and the Markov random field algorithm for image scene modelling and building extraction.

To further improve the accuracy of building extraction, auxiliary information was introduced into the extraction methods. Data collection using LiDAR while concurrently capturing very high-resolution optical images is one of the options. Mohamad et al. [20] fused high-resolution optical images with LiDAR data. An innovative technique for improving the fusion process, which relies on wavelet transform techniques, was proposed. In 2018, a deep learning (DL)-based building detection method was proposed that used the fusion of LiDAR data and orthophotos [21]. This improved the accuracy of building recognition in the fused LiDAR–orthophoto data by using an automatic encoder. In addition, Maruyama et al. [22] extracted earthquake-damaged buildings based on DSM data. Li et al. [23] used public geographic information system (GIS) map datasets to improve building extraction results. Several strategies have been designed and combined with the U-Net semantic segmentation model, including data augmentation and postprocessing. Gao et al. proposed a method that could automatically extract building samples using building shadows and accurately verified buildings. This method has high accuracy, especially for suburban areas. In recent years, building extraction has become an important part of the LiDAR point cloud processing field. LiDAR point clouds combined with texture features, Markov random fields, etc., can effectively extract building information in a variety of complex environments [24,25].

The development of deep learning has greatly promoted the progress of building extraction. Xu et al. [26] proposed a new neural network framework called Res-U-Net. This framework is an alternative technology of urban area object labelling combined with deep learning and guided filtering. It can extract buildings in urban areas with very high-resolution (VHR) remote sensing images. Huang et al. [27] proposed an end-to-end trainable gated residual refinement network (GRRNet). This network is based on the excellent feature learning and end-to-end pixel-level labelling capabilities of FCN, and combines high-resolution aerial images and LiDAR point clouds for building extraction. Combined with edge detection technology, convolutional neural networks can effectively deal with the recognition and segmentation of complex buildings [28].

3. MSCRF Framework for HSR Imagery Building Extraction

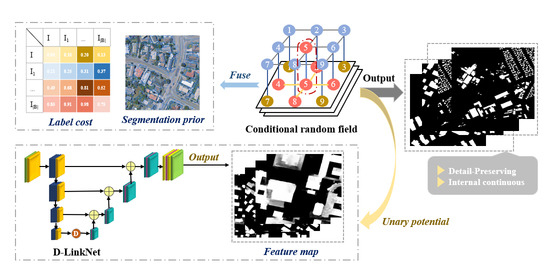
This paper proposes a multiscale-aware and segmentation-prior conditional random field, which is used to extract buildings from high-resolution remote sensing images. As shown in Figure 1, the building extraction process can be divided into three steps. (1) We train the D-LinkNet network and build the unary potential of the CRF based on D-LinkNet. (2) The segmentation prior is obtained based on the feature map using the connected region labelling algorithm. While using image spatial context information, the label cost is introduced. Then, when the uncertainty of the image label is strong, the category label is obtained by referring to the image neighbourhood label information. (3) The $\alpha -\mathrm{expansion}$ algorithm based on graph cuts is used for model inference to obtain the final labelling result.

3.1. Unary Potential Based on D-LinkNet

Let $x$ be the labels of the whole image and $y$ be the observed data from the input image. When the observation field $y$ is given and the random variable $x_i$ obeys the definition of a Markov random field, the model constitutes a CRF. CRF is a probabilistic discriminative framework that directly models the posterior probability of the labels. Given the observed image data $y$, the Gibbs distribution of $x$ can be expressed as the following form:

$$p\left(x|y\right)=\frac{1}{Z\left(y\right)}\exp \left\{-{\displaystyle \sum _{c\in C}{\psi }_c\left(X_c,y\right)}\right\}$$

(1)

where the partition function is defined as $Z\left(y\right)={\displaystyle {\sum }_x\exp }\left\{-{\displaystyle {\sum }_{c\in C}{\psi }_c\left(x_c,y\right)}\right\}$, which can adjust the calculation result of the posterior probability to between 0 and 1. ${\psi }_c\left(x_c,y\right)$ is the potential function.

The unary potential models the relationship between the label sequence and the observation sequence. It calculates the probability that the pixel obtains a building label or a nonbuilding label based on the feature of the pixel. The commonly used unary potential can be defined as:

$${\psi }_i\left(x_i,y\right)=-\ln \left(P\left(x_i=b_k|f_i\left(y\right)\right)\right)$$

(2)

where $x_i$ is the label at pixel $i$, $i\in V=\left\{1,2,\cdots ,N\right\}$, and the parameter $N$ is the number of pixels in the image. The set of labels is $B=\left\{\left(k=0,1\right)|b_k\right\}$, and the value of $k$ is 0 or 1, which indicates that the pixel category is building or nonbuilding, respectively. The function $f$ is the feature mapping function, which corresponds to the image block to the feature vector. Finally, $f_i\left(y\right)$ represents the feature at pixel $i$.

The early method of segmentation using CRF was to directly process each pixel as a unit [29]. In a typical CRF-based segmentation method [30], first, select and extract appropriate features from the input image. Then use a structured support vector machine (SSVM) [29] or other classifiers to learn the coefficients of CRF for segmentation [31,32]. These methods do not need to extract features, but the number of calculations is large. In addition, the existing potential functions cannot fully consider the characteristics of high-resolution images and lack large-scale spatial interactive information modelling capabilities. D-LinkNet not only has fewer parameters and is computationally efficient, but it can also use the multiscale spatial building features of the image. Therefore, this paper uses D-LinkNet to learn image features and calculate the probability $P\left(x_i=b_k|f_i\left(y\right)\right)$ of obtaining the marker $b_k$ at pixel $x_i$ based on its feature vector.

3.1.1. Encoder and Decoder

Zhou et al. (2018) proposed a new network D-LinkNet based on the LinkNet (exploiting encoder representations for efficient semantic segmentation) network [28,33]. D-LinkNet obtains efficient calculation and storage capabilities by building a dilated convolutional layer in the central module. Moreover, it integrates multiscale contextual information of buildings without reducing the resolution of the feature map. D-LinkNet is divided into three parts, A, B, and C, which are named the encoder, the centre module, and the decoder, respectively, as shown in Figure 2.

The encoder of D-LinkNet is ResNet34 (residual neural network) [34], which is pretrained on the ImageNet [35] dataset. First, start with an initial block. This block uses a convolution kernel with a kernel size of 7 × 7 and a step size of 2 to convolve the input image. Then it uses a convolution kernel with a kernel size of 3 × 3 and a step size of 2 for space maximum pooling. The latter part of the D-LinkNet encoder is composed of ResNet34 residual blocks, and the hierarchical structure is shown in Figure 3.

The decoder of D-LinkNet is consistent with LinkNet [33], and the hierarchical structure is shown in Figure 4. The decoder uses a full convolution structure, and each operation in the decoder module has at least three parameters.

After performing multiple subsampled operations in the encoder, some spatial information will be lost. It is difficult to recover the lost information using only the upsampling output of the decoder. Therefore, in D-LinkNet, each encoder is connected to the decoder so that each layer of the decoder can obtain the learning results of the encoder, thereby preserving the detailed features of the building. The probability of calculating the label $b_k$ based on its feature vector at pixel $x_i$ can be expressed as $P\left(x_i=b_k|f_i\left(y\right)\right)$. After the calculation of the entire image is completed, the decoder outputs a feature map. The eigenvalues of the feature map are further processed into probability values. Finally, the probability map is used as the input of the unary potential of the CRF.

3.1.2. Multiparallel Dilated Convolution Module

Building detail information is easily lost in the process of subsampling. In addition, there are differences in different building scales, which makes it difficult to extract sufficient features from a single receptive field. To solve this problem, a multiparallel dilated convolution module is used. This module supports the exponential growth of the receptive field and can capture building features from multiple scales.

As shown in Figure 5, if the dilation rates of the stacked dilated convolution layers are 1, 2, 4, and 8, then the receptive field of each layer will be 3, 7, 15, and 31, respectively. The central dilation convolution module of D-LinkNet includes dilation convolution in the cascade mode and parallel mode. It uses different dilation rates in each branch to extract building features in parallel and finally obtains the final feature extraction by fusing all branch results. Since the acceptance domain of each path is different, the network can integrate building features of different scales. The loss of details due to subsampling is alleviated.

3.2. Detail-Preserving Pairwise Potential

The introduction of pairwise potential ${\psi }_i\left(x_i,y_i,y\right)$ makes it possible to consider the spatial interaction of local pixels in the building extraction process. The pairwise potential constructs the relationship between the current node and its neighbouring nodes. However, due to the influence of spectral variability and noise, the spectral values of adjacent pixels in the homogeneous image area are not completely equal. Based on the spatial correlation of features, adjacent pixels always tend to be of the same feature category. Pairwise potential models this kind of spatial neighbourhood relationship, and it considers the constraints of pixel category labels and the scale of image segmentation. Therefore, pairwise potential can make full use of the large-scale spatial context information of the observed image data.

3.2.1. The Local Class Label Cost Term

In this paper, the local class label cost term is introduced into the pairwise potential. The label of each pixel can be fully considered in the classification iteration process to maintain detailed information. It is defined as follows:

$${\psi }_i\left(x_i,y_i,y\right)=\{\begin{array}{cc}0& x_i=x_j\\ g_{ij}\left(y\right)+\theta \times {\mathrm{\Theta }}_B\left(x_i,y_i|y\right)& \mathrm{otherwise}\end{array}$$

(3)

where $g_{ij}\left(y\right)$ represents the spatial smoothing term of modelling adjacent pixels. ${\mathrm{\Theta }}_B\left(x_i,x_j|y\right)$ is the label cost term of size $\left|B\right|\times \left|B\right|$, which represents the cost between the corresponding labels of adjacent pixels $x_i$ and $x_j$. $\theta$ is a parameter that controls the degree of the category labelling cost in the pairwise potential.

The function $g_{ij}\left(y\right)$ models the spatial interaction between neighbouring pixels $i$ and $j$, which can be expressed as [36]:

$$g_{ij}\left(y\right)=dist{\left(i,j\right)}^{-1}\exp \left(-\beta {\Vert y_i-y_j\Vert }^2\right)$$

(4)

where $\left(i,j\right)$ represents the coordinate pair of the neighbouring pixels, and the function $dist\left(i,j\right)$ is its corresponding Euclidean distance. $y_i$ and $y_j$ represent the spectral vectors at positions $i$ and $j$. The parameter $\beta$ is set to the mean square difference between the spectral vectors of all the adjacent pixels in the image.

The local class label cost term uses observation image data to model the spatial relationship of each neighbourhood category label $x_i$ and $x_j$, defined as follows:

$${\mathrm{\Theta }}_L\left(x_i,x_j|y\right)=\frac{\min \left\{P\left(x_i|f_i\left(y\right)\right),P\left(x_j|f_j\left(y\right)\right)\right\}}{\max \left\{P\left(x_i|f_i\left(y\right)\right),P\left(x_j|f_j\left(y\right)\right)\right\}}$$

(5)

Similar to the unary potential, the category probability $P\left(x_i|f_i\left(y\right)\right)$ is obtained by D-LinkNet. Therefore, the local class label cost term is the interactive influence of the current label between the adjacent nodes $i$ and $j$ using the observation image data $y$. The label of each pixel can be fully considered and the detailed information in the classification iteration process can be kept.

3.2.2. Segmentation Prior

When the precision and richness of the sample are limited, the pairwise potential of the traditional CRF has difficulty accurately distinguishing the details of the ground from the image noise. The object-oriented methods can use a larger-scale spatial information, which can effectively alleviate the influence of the spectral difference between buildings and background areas [18].

The segmentation prior is based on the feature map and is obtained by using the connected-component labelling algorithm. The algorithm uses the connected regions with the same value in the feature map as the segmentation region, thereby avoiding the selection of the segmentation scale. This paper uses the classical connected-component algorithm with an 8-neighbourhood to obtain the segmentation object [37]. Then, based on the original building extraction map, the label of each segmented object can be obtained through the maximum voting strategy. The segmentation prior can be defined as:

$$P\left(x_i=b_{seg}\right)=\max \left\{P\left(x_i=b_k\right)\right\},k\in \left|B\right|$$

(6)

where $b_{seg}$ represents the object label category of the segmented area where the pixel is located.

The segmentation prior requires that the objects in each area are marked as the maximum value of all the pixel category labels in the area. It has a similar strategy for processing category probabilities as object-oriented probabilities.

3.3. The Inference of MSCRF

In the MSCRF, the potential functions are constructed for building extraction according to the characteristics of high-resolution images. After parameter estimation, model inference needs to be used to predict the optimal building extraction effect of the test image. That is, the pixel obtains the optimal label $x$, which is defined relative to finding the minimum value of the energy function [38]. To obtain the optimal label, researchers have proposed many reasoning methods, such as iterative conditional modes (ICMs) and graph cuts. However, the ICM is more sensitive to the selection of the initial value and easily falls into a local minimum. Therefore, we use the $\alpha -\mathrm{expansion}$ algorithm based on graph cuts [39] for inference.

Define $G=\langle V,E\rangle$ as a weighted graph with two distinguished vertices called terminals. The cut $E_0\subset E$ is a set of edges in which the terminals are separated in the induced graph $G=\langle V,E-E_0\rangle$. For energy functions with metric attributes, the $\alpha -\mathrm{expansion}$ algorithm based on graph cuts sets up a local search strategy. The strategy can solve the problem that the algorithm tends to fall into a local minimum solution when the moving space is small. The $\alpha -\mathrm{expansion}$ algorithm continuously iterates through the graph cuts algorithm in the loop according to the local search strategy. At each iteration, the global minimum of the binary labelling problem is calculated, as shown in Algorithm 1.

Algorithm 1 The $\alpha -\mathrm{expansion}$ algorithm based on graph cuts
1:	Input $x^i$ := arbitrary labelling
2:	set mark := 0
3:	for$\alpha \in B=\left\{1,\dots ,K\right\}$
4:	$x^j$:=$\arg \min E\left(x^i\right)$
5:	if $E\left(x^j\right)<E\left(x^i\right)$, set $x^i$:= $x^j$and mark := 1
6:	if mark = 1 goto 2
7:	return  $x^i$

First, initialize the current label. In the $\alpha -\mathrm{expansion}$ algorithm, there are two strategies for each pixel: keeping the current label and changing the label to a specific value $\alpha \in B=\left\{1,\dots ,K\right\}$. By using the graph-cut algorithm to optimize the energy function $E\left(x^i\right)$, the optimal solution of the binary labelling problem is obtained. Since all pixels are processed simultaneously, there are an exponential number of possible moves with respect to any particular label (building or non-building). Therefore, the strong local minimum property of the algorithm is effectively guaranteed. The problem of the ICM algorithm easily falling into the local minimum can be solved.

4. Experiments and Analysis

4.1. Dataset Description

This paper uses the WHU building dataset and the Massachusetts building dataset for experimental analysis [40,41]. The WHU building dataset was taken in New Zealand and covers an area of approximately 450 square kilometres. The ground resolution is downsampled to 0.3 m and contains more than 187,000 well-marked buildings. The images in the area are cropped into 8189 images of 512 × 512 pixels. Following Ji et al. [40], the samples are divided into 4736 images for training, 1036 images for validation and 2416 images for testing, respectively.

The Massachusetts building dataset consists of 151 aerial images and corresponding single-channel labelled images, including 137 training images, 10 test images, and 4 validation images. The size of all images in the dataset is 1500 × 1500 pixels, and the resolution of images is 1 m. The entire dataset covers an area of approximately 340 km², and each image covers 2.25 km².

4.2. Experimental Design

D-LinkNet [28], convolution conditional random field (ConvCRF) [42], detail-preserving smoothing classifier based on conditional random fields (DPSCRF) [18] and fully connected conditional random field (FullCRF) [43] were selected for the comparative experiment of MSCRF. Of these, DPSCRF uses a support vector machine (SVM) to construct unary potential. Although SVM is simple to operate, its pixel-based classification has problems such as salt-and-pepper noise. The pairwise potential of DPSCRF models the linear combination of the spatial smoothing term and the local class label cost term. In addition, DPSCRF adopts object-oriented thinking to integrate the segmentation prior. FullCRF constructs a fully connected CRF model of the complete image pixel set. On the basis of FullCRF, ConvCRF uses ResNet to construct unary potential. Moreover, ConvCRF adds conditional independence assumptions to CRF reasoning, which can formalize most of the inferencing into convolutions. D-LinkNet uses pretrained ResNet34 as its encoder, and its decoder remains the same as LinkNet. All methods take the RGB images as input in this paper.

A total of 4736 images in the training set of the WHU building dataset were used to train the network, including the unary of MSCRF and D-LinkNet. In the experiment, ENVI was used directly to obtain the SVM classification result. First, the region of interest was selected, and the SVM classifier was used to classify the image based on the colour characteristics of images. Then, the classification map was used to construct the unary potential of DPSCRF. The unary potential of ConvCRF was constructed using ResNet, and the pretrained network model was used in the experiment. Finally, the filter size k was set to 3 in the inference part of ConvCRF.

In the experiments using the Massachusetts building dataset, except for DPSCRF and MSCRF, all other methods directly used the images of 1500 × 1500 pixels for training or testing. DPSCRF used images cropped to 750 × 750 pixels for testing and calculating accuracy. MSCRF used 137 images with a size of 1500 × 1500 pixels for training the unary. The images in the training set were cropped to 750 × 750 pixels for iterative inferencing of the MSCRF.

In the experiment, three kinds of accuracy evaluation indicators were selected as the evaluation criteria for building extraction. The three evaluation indicators were precision (the ratio of the correct prediction within the category), IoU (the ratio of the intersection and union of a category prediction result and the true value), and recall (a measure of coverage, which measures the number of positive samples classified as positive samples).

4.3. Experiment 1: WHU Building Dataset

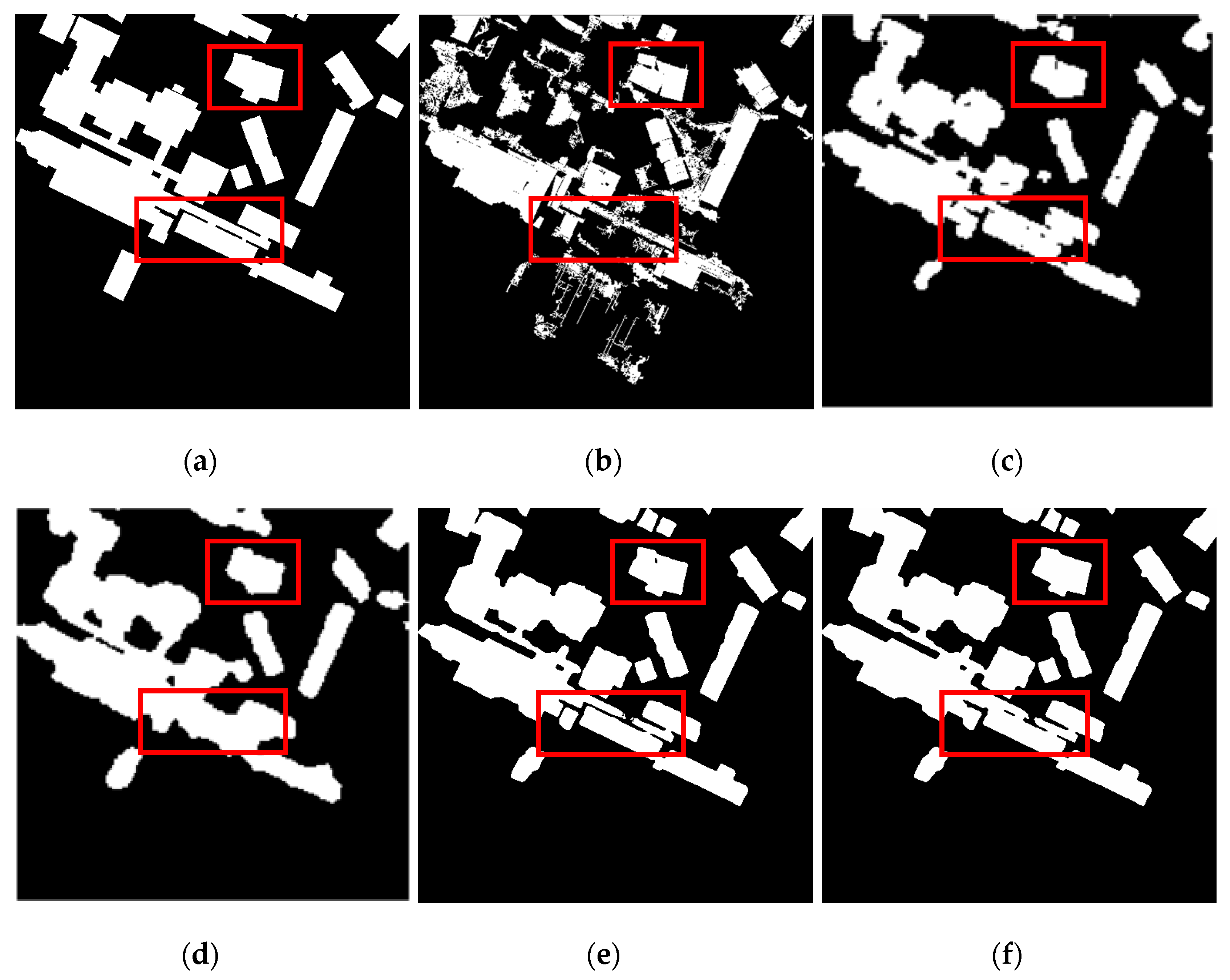
This article only shows the building extraction results of two groups of images. The original image is shown in Figure 6a, and the corresponding manually labelled building area is shown in Figure 6b. Figure 7 and Figure 8 show the results of building extraction on two sets of images using different models.

It can be seen in the figure that the extraction performance of DPSCRF is somewhat poor: there are more discrete pixels, and the boundaries are relatively rough. The effect of FullCRF is average. Although there is no obvious salt-and-pepper noise, there are also blurred boundaries. The building extraction performance of the ConvCRF algorithm is better. There is basically no noise, and the boundary blur problem is greatly improved. However, for a few small buildings, the extracted boundary is relatively rough. In contrast, D-LinkNet and MSCRF can extract clearer building boundaries without noise. In addition, MSCRF removes the small buildings that D-LinkNet misextracts and can effectively maintain detailed information.

In this paper, the recall, precision and IoU of the methods are calculated to quantitatively evaluate the performance of the building extracted from the model, as shown in

Table 1. Quantitative evaluation of building extraction from the WHU dataset.

Method	Recall (%)	Precision (%)	IoU (%)
DPSCRF [18]	76.33	80.00	67.74
FullCRF [43]	\	81.04	80.01
ConvCRF [42]	89.21	94.98	87.31
SRI-Net [44]	\	95.21	89.09
DE-Net [45]	\	95.00	90.12
EU-Net [46]	\	94.98	90.56
D-LinkNet [28]	96.30	93.72	90.58
MSCRF	96.47	95.07	91.99

.

It can be seen in the table that the performance of DPSCRF is slightly worse, the IoU of ConvCRF reaches 87.31%, and other indicators are relatively high. The recall and IoU of D-LinkNet are both higher than those of ConvCRF, but the precision is slightly lower than that of ConvCRF. The accuracy evaluation results of both are significantly higher than DPSCRF and FullCRF, indicating that they can be well applied to the field of building extraction. For our MSCRF, it can be seen that the recall, precision, and IoU are all higher than those of the other seven models, which are also significantly improved compared to D-LinkNet. In addition, it can be seen that MSCRF performs better than the current state-of-the-art methods, i.e., SRI-Net (spatial residual inception convolutional neural network) [44], DE-Net (deep encoding network) [45] and EU-Net (efficient fully convolutional network) [46].

4.4. Experiment 2: Massachusetts Building Dataset

The scene of the Massachusetts building dataset is more complex, with many small-scale dense buildings, as shown in Figure 9. Figure 10 shows the visual performance of different models for extracting buildings. It can be seen in the figure that the buildings extracted by each model are incomplete, especially in the cases of FullCRF and ConvCRF, both of which have a weak ability to extract small-scale buildings. The buildings extracted by DPSCRF not only have serious boundary blur problems but also contain more noise. In contrast, the D-LinkNet and MSCRF methods give more complete and accurate building extraction results. D-LinkNet has a better extraction performance for small and dense building areas, while MSCRF can more accurately extract large-scale buildings and effectively improve the problem of blurry building boundaries.

The quantitative evaluation of building extraction performance is shown in

Table 2. Quantitative evaluation of buildings extracted from the Massachusetts dataset.

Method	Recall (%)	Precision (%)	IoU (%)
DPSCRF [18]	49.70	49.07	34.85
Pruned FCN-2s [47]	61.00	78.00	52.00
FullCRF [43]	\	55.86	54.02
ConvCRF [42]	78.63	65.89	56.64
D-LinkNet [28]	85.88	73.36	65.54
GMEDN [48]	\	\	70.39
MSCRF	89.93	80.14	71.19

. In addition, to further verify the effectiveness of the model, some state-of-the-art methods in the field of building extraction were compared, including pruned FCN-2s [47] and GMEDN(global and multiscale encoder-decoder network) [48]. It can be clearly seen that the performance of the MSCRF proposed in this article is better than other comparison methods, such as DPSCRF, FullCRF, and ConvCRF. Although the IoU of pruned FCN-2s is significantly lower than that of GMEDN and other methods, its precision is higher. Compared with D-LinkNet, our model improves IoU by nearly 6%, and there are also significant improvements in other evaluation indicators.

The scene of the Massachusetts building dataset is more complex, including large, medium, and small building areas. The shadow projection of high-rise buildings also creates great difficulties in extraction. Additionally, compared with the WHU building dataset, the label accuracy and image resolution of this dataset are lower. Therefore, the quantitative evaluation results of all methods in the Massachusetts building dataset are much lower.

5. Discussion

5.1. Detailed Comparative Analysis of Building Extraction Results

As shown in Figure 11, the building boundaries extracted by D-LinkNet are relatively complete. D-LinkNet uses multiparallel dilated convolution modules to integrate multiscale building features, which is conducive to extracting small-scale dense building targets. However, only using D-LinkNet for building extraction still has the problem of discontinuity inside the building, and the extraction results often show small fragments. The framework proposed in this paper combines D-LinkNet with CRF. The ability to use CRF spatial context information can effectively smooth the boundaries of buildings and remove small fragments. In addition, this paper introduces the local class label cost term in the CRF. The term is able to fully consider the label of each pixel and maintain the detailed information of the building. Moreover, the fusion of segmentation priors is beneficial to obtain continuous building interior labels. As seen in Figure 11, compared with D-LinkNet, the boundaries of the building extracted by MSCRF are smoother, and the fine parts near the building are effectively removed.

5.2. Analysis of Building Extraction Results with Different Sample Sizes

The WHU building dataset is divided into three parts: a training set (4736 tiles with 130,500 buildings), a validation set (1036 tiles with 14,500 buildings) and a test set (2416 tiles with 42,000 buildings) [40]. Sample data is shown in Figure 12. In general, the more training samples there are, the higher the testing accuracy of the deep learning network. However, with the gradual increase in training samples, the model may overfit. The MSCRF framework combines deep learning networks with traditional methods. Considering whether the performance of the framework is affected by the laws of deep learning networks, this paper discusses the following experiments.

As shown in Figure 13, when the training sample size is 58% of the total number of images, the performance of MSCRF is excellent. When the proportion of training samples increases to 68%, not only the performance of MSCRF is not significantly improved, but the time cost becomes much higher; that is, the current sample division method is most suitable for our method. Moreover, the changing trend of MSCRF is consistent with the deep learning network D-LinkNet. Regardless of how the sample size is divided, the performance of MSCRF is always better than that of D-LinkNet, which fully reflects the superiority of our method.

6. Conclusions

This paper proposes a high-resolution remote sensing image-based multiscale-aware and segmentation-prior conditional random field framework. The framework introduces D-LinkNet into the field of building extraction, and uses D-LinkNet to model the unary potential of the CRF to make full use of the multiscale building features. In the construction of pairwise potential, segmentation prior is added to effectively deal with the problems of noise and spectral difference of the images. Moreover, the local class label cost term is introduced to extract detailed building information. Finally, after parameter estimation and model inference based on the $\alpha -\mathrm{expansion}$ algorithm, the final building extraction result is obtained. For testing, this paper used the WHU building dataset and the Massachusetts building dataset. The results show that MSCRF has excellent extraction performance. The detailed information of the building can be effectively preserved during the extraction, and the problem of blurry building boundaries also effectively improves. In the future, we will use larger-scale datasets, such as the Inria aerial image dataset [49], to test model performance. In addition, it is also a good idea to fuse the additional satellite imagery information and geographic information system map data to extract clearer building boundaries.