QCam: sUAS-Based Doppler Radar for Measuring River Discharge
Abstract
1. Introduction
2. Materials and Methods
2.1. QCam Specifications
2.2. QCam Integration
2.3. QCam Flight Envelope
2.4. Science Flights at Collocated USGS Streamgages
2.5. Field and Computational Methods
2.5.1. Conventional Streamgaging
2.5.2. QCam Deployment
2.5.3. Velocity and Discharge Algorithms
3. Results
3.1. QCam Integration
3.2. QCam Flight Envelope
3.3. Science Flights
3.3.1. Probability Concept Parameters
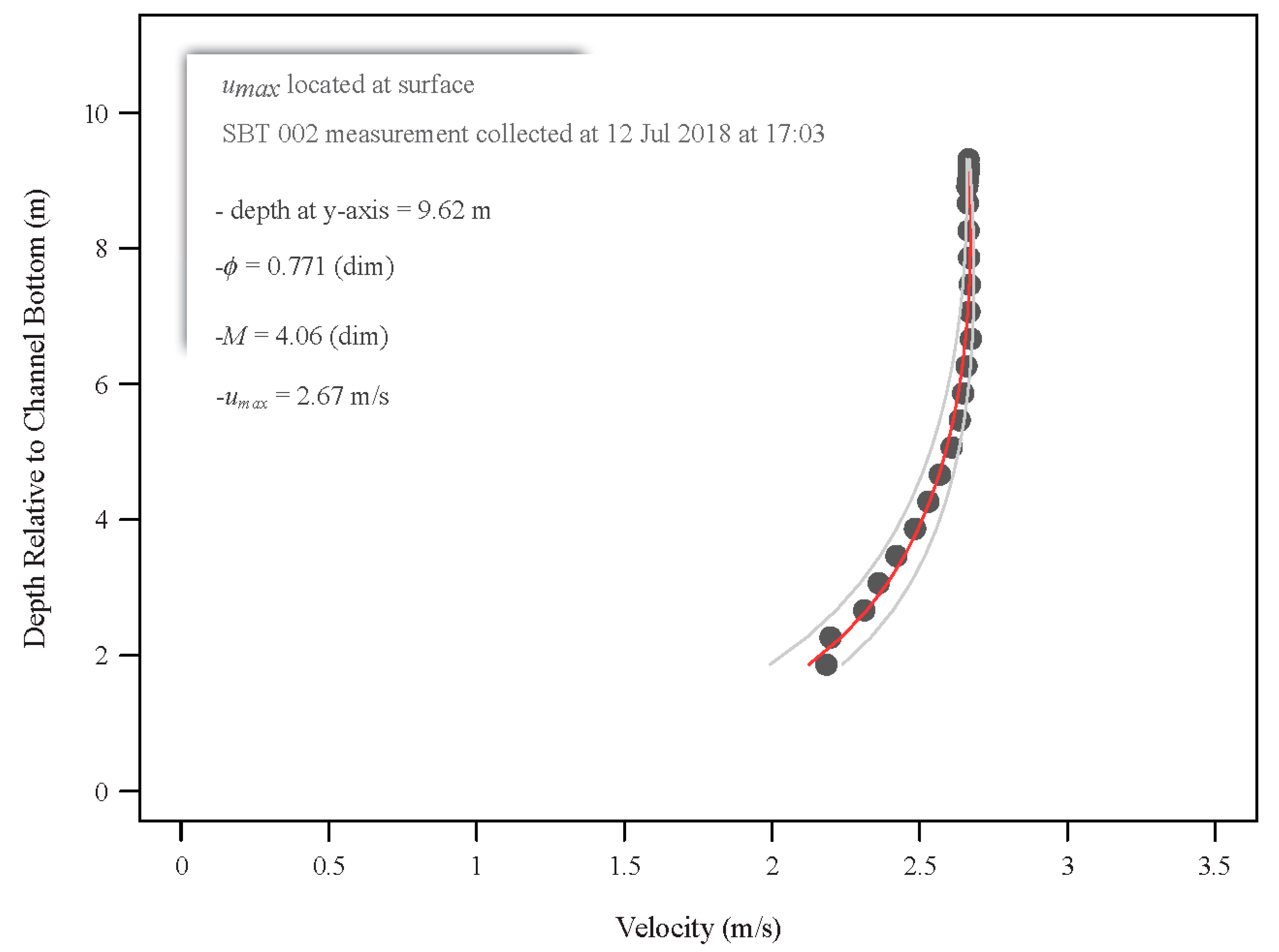
3.3.2. Velocity, Cross-sectional Area, and River Discharge
3.3.3. sUAS Measurements
4. Discussion
4.1. Velocity and River Discharge
4.2. Uncertainty
4.2.1. Surface-Scatterer Quality
4.2.2. Flight Altitude and Propwash
4.2.3. Wind Drift
4.2.4. Sample Duration
4.3. QCam Applications and Evolution
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Durand, M.; Gleason, C.J.; Garambois, P.A.; Bjerklie, D.M.; Smith, L.C.; Roux, H.; Rodriguez, E.; Bates, P.D.; Pavelsky, T.M.; Monnier, J.; et al. An intercomparison of remote sensing river discharge estimation algorithms from measurements of river height, width, and slope. Water Resour. Res. 2016, 52, 4527–4549. [Google Scholar] [CrossRef]
- Frazier, A.H.; Heckler, W.E. New Mexico, Birthplace of Systematic Stream Gaging; Geological Survey Professional Paper 778; GPO: Washington, DC, USA, 1972; p. 23. [Google Scholar] [CrossRef]
- Eberts, S.; Woodside, M.; Landers, M.; Wagner, C. Monitoring the Pulse of Our Nation’s Rivers and Streams—The U.S. Geological Survey Streamgaging Network; US Geological Survey Fact Sheet 2018-3021; USGS: Reston, VA, USA, 2018. [Google Scholar] [CrossRef]
- Buchanan, T.J.; Somers, W.P. Discharge Measurements at Gaging Stations; U.S. Geological Survey Techniques of Water-Resources Investigations, Book 3, Chapter A8; GPO: Washington, DC, USA, 1969. Available online: http://pubs.usgs.gov/twri/twri3a8/ (accessed on 30 December 2019).
- Rantz, S. Measurement and Computation of Streamflow: Volume 1. Measurement of Stage and Discharge; US. Geological Survey Water Supply Paper 2175; Department of the Interior: Washington, DC, USA, 1982; p. 284. [Google Scholar]
- Turnipseed, D.P.; Sauer, V.B. Discharge Measurements at Gaging Stations; US Geological Survey Techniques and Methods Book 3, Chapter A8; USGS: Reston, VA, USA, 2010; Volume 87. Available online: http://pubs.usgs.gov/tm/tm3-a8/ (accessed on 30 December 2019).
- Christensen, J.L.; Herrick, L.E. Mississippi River Test: Volume 1; Final Report DCP4400/300 Prepared for the US Geological Survey; AMETEK/Straza Division: El Cajon, CA, USA, 1982. [Google Scholar]
- Simpson, M.R. Evaluation of a vessel-mounted acoustic Doppler current profiler for use in rivers and estuaries. In Proceedings of the 3rd Working Conference on Current Measurement, Washington, DC, USA, 22–24 January 1986; pp. 106–121. [Google Scholar]
- Gordon, R.L. Acoustic measurement of river discharge. J. Hydraul. Eng. 1989, 115, 925–936. [Google Scholar] [CrossRef]
- Simpson, M.R.; Oltmann, R.N. Discharge-Measurement System Using an Acoustic Doppler Current Profiler with Applications to Large Rivers and Estuaries; US Geological Survey Water Supply Paper 2395; USGS: Reston, VA, USA, 1993; p. 32. [Google Scholar]
- Oberg, K.A.; Morlock, S.E.; Caldwell, W.S. Quality Assurance Plan for Discharge Measurements Using Acoustic Doppler Current Profilers; US Geological Survey Scientific Investigations Report 5135; USGS: Reston, VA, USA, 2005; p. 35. [Google Scholar]
- Mueller, D.S. QRev—Software for Computation and Quality Assurance of Acoustic Doppler Current Profiler Moving-Boat Streamflow Measurements—User’s Manual for Version 2.8; US Geological Survey Open-File Report 2016–1052; USGS: Reston, VA, USA, 2016; p. 50. [Google Scholar] [CrossRef]
- Mueller, D.S. Extrap: Software to assist the selection of extrapolation methods for moving-boat ADCP streamflow measurements. Comput. Geosci. 2013, 54, 211–218. [Google Scholar] [CrossRef]
- Mueller, D.S.; Wagner, C.R.; Rehmel, M.S.; Oberg, K.A.; Rainville, F. Measuring Discharge with Acoustic Doppler Current Profilers from a Moving Boat (Version 2.0, December 2013); U.S. Geological Survey Techniques and Methods, Book 3, Chap. A22; USGS: Reston, VA, USA, 2013; p. 95. [Google Scholar] [CrossRef]
- Smith, L.C.; Isacks, B.L.; Bloom, A.L.; Murray, A.B. Estimation of discharge from three braided rivers using synthetic aperture radar satellite imagery. Water Resour. Res. 1996, 32, 2021–2034. [Google Scholar] [CrossRef]
- Leon, J.G.; Calmant, S.; Seyler, F.; Bonnet, M.P.; Cauhope, M.; Frappart, F. Rating curves and estimation of average water depth at the upper Negro River based on satellite altimeter data and modeled discharges. J. Hydrol. 2006, 328, 481–496. [Google Scholar] [CrossRef]
- Getirana, A.C.V.; Bonnet, M.P.; Calmant, S.; Roux, H.; Filho, O.C.R.; Mansur, W.J. Hydrological monitoring of poorly gauged basins based on rainfall–runoff modeling and spatial altimetry. J. Hydrol. 2009, 379, 205–219. [Google Scholar] [CrossRef]
- Birkinshaw, S.J.; O’Donnell, G.M.; Moore, P.; Kilsby, C.G.; Fowler, H.J.; Berry, P.A.M. Using satellite altimetry data to augment flow estimation techniques on the Mekong River. Hydrol. Process. 2010, 24, 3811–3825. [Google Scholar] [CrossRef]
- Getirana, A.C.V.; Peters-Lidard, C. Estimating water discharge from large radar altimetry datasets. Hydrol. Earth Syst. Sci. 2013, 17, 923–933. [Google Scholar] [CrossRef]
- Paiva, R.C.D.; Buarque, D.C.; Colischonn, W.; Bonnet, M.-P.; Frappart, F.; Calmant, S.; Mendes, C.A.B. Large-scale hydrological and hydrodynamics modelling of the Amazon River basin. Water Resour. Res. 2013, 49, 1226–1243. [Google Scholar] [CrossRef]
- Tarpanelli, A.; Barbetta, S.; Brocca, L.; Moramarco, T. River discharge estimation by using altimetry data and simplified flood routing modeling. Remote Sens. 2013, 5, 4145–4162. [Google Scholar] [CrossRef]
- Birkinshaw, S.J.; Moore, P.; Kilsby, C.G.; O’Donnell, G.M.; Hardy, A.J.; Berry, P.A.M. Daily discharge estimation at ungauged river sites using remote sensing. Hydrol. Process. 2014, 28, 1043–1054. [Google Scholar] [CrossRef]
- Pavelsky, T.M. Using width-based rating curves from spatially discontinuous satellite imagery to monitor river discharge. Hydrol. Process. 2014, 28, 3035–3040. [Google Scholar] [CrossRef]
- Paris, A.; Dias de Paiva, R.; Santos da Silva, J.; Medeiros Moreira, D.; Calmant, S.; Garambois, P.-A.; Collischonn, W.; Bonnet, M.-P.; Seyler, F. Stage-discharge rating curves based on satellite altimetry and modeled discharge in the Amazon basin. Water Resour. Res. 2016, 52, 3787–3814. [Google Scholar] [CrossRef]
- Bjerklie, D.M.; Birkett, C.M.; Jones, J.W.; Carabajal, C.; Rover, J.A.; Fulton, J.W.; Garambois, P.-A. Satellite remote sensing estimation of river discharge: Application to the Yukon River Alaska. J. Hydrol. 2018, 561, 1000–1018. [Google Scholar] [CrossRef]
- Bogning, S.; Frappart, F.; Blarel, F.; Niño, F.; Mahé, G.; Bricquet, J.-P.; Seyler, F.; Onguéné, R.; Etamé, J.; Paiz, M.-C.; et al. Monitoring water levels and discharges using radar altimetry in an ungauged river basin: The case of the Ogooué. Remote Sens. 2018, 10, 350. [Google Scholar] [CrossRef]
- Moramarco, T.; Barbetta, S.; Bjerklie, D.M.; Fulton, J.W.; Tarpanelli, A. River bathymetry estimate and discharge assessment from remote sensing. Water Resour. Res. 2019, 55, 6692–6711. [Google Scholar] [CrossRef]
- Birkett, C.M. Contribution of the TOPEX NASA radar altimeter to the global monitoring of large rivers and wetlands. Water Resour. Res. 1998, 34, 1223–1239. [Google Scholar] [CrossRef]
- Birkett, C.M.; Mertes, L.A.K.; Dunne, T.; Costa, M.H.; Jasinski, M.J. Surface water dynamics in the Amazon Basin: Application of satellite radar altimetry. J. Geophys. Res. 2002, 107, 8059. [Google Scholar] [CrossRef]
- Kouraev, A.V.; Zakharova, E.A.; Samain, O.; Mognard, N.M.; Cazenave, A. Ob’ river discharge from TOPEX/Poseidon satellite altimetry (1992–2002). Remote Sens. Environ. 2004, 93, 238–245. [Google Scholar] [CrossRef]
- Papa, F.; Bala, S.K.; Kumar Pandey, R.; Durand, F.; Rahman, A.; Rossow, W.B. Ganga-Brahmaputra river discharge from Jason-2 radar altimetry: An update to the long-term satellite-derived estimates of continental freshwater forcing flux into the Bay of Bengal. Geophys. Res. 2012, 117. [Google Scholar] [CrossRef]
- Tulbure, M.G.; Broich, M. Spatiotemporal dynamic of surface water bodies using Landsat time-series data from 1999 to 2011. ISPRS J. Photogramm. Remote Sens. 2013, 79, 44–52. [Google Scholar] [CrossRef]
- Gleason, C.J.; Smith, L.C. Toward global mapping of river discharge using satellite images and at-many-stations hydraulic geometry. Proc. Natl. Acad. Sci. USA 2014, 111, 4788–4791. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.-W.; Lu, Z.; Jones, J.W.; Shum, C.K.; Lee, H.; Jia, Y. Monitoring Everglades freshwater marsh water level using L-band synthetic aperture radar backscatter. Remote Sens. Environ. 2014, 150, 66–81. [Google Scholar] [CrossRef]
- Jones, J.W. Efficient wetland surface water detection and monitoring via Landsat: Comparison with in situ data from the Everglades Depth Estimation Network. Remote Sens. 2015, 7, 12503–12538. [Google Scholar] [CrossRef]
- Carroll, M.; Wooten, M.; DiMiceli, C.; Sohlberg, R.; Kelly, M. Quantifying surface water dynamics at 30 meter spatial resolution in the North American high northern latitudes 1991–2011. Remote Sens. 2016, 8, 622. [Google Scholar] [CrossRef]
- Brakenridge, G.R.; Nghiem, S.V.; Anderson, E.; Mic, R. Orbital microwave measurement of river discharge and ice status. Water Resour. Res. 2007, 43, W04405. [Google Scholar] [CrossRef]
- Durand, M.; Neal, J.; Rodríguez, E.; Andreadis, K.M.; Smith, L.C.; Yoon, Y. Estimating reach-averaged discharge for the River Severn from measurements of river water surface elevation and slope. J. Hydrol. 2014, 511, 92–104. [Google Scholar] [CrossRef]
- Biancamaria, S.; Lettenmaier, D.P.; Pavelsky, T. The SWOT Mission and its capabilities for land hydrology. Surv. Geophys. 2015, 37, 307–337. [Google Scholar] [CrossRef]
- Garambois, P.-A.; Monnier, J. Inference of effective river properties from remotely sensed observations of water surface. Adv. Water Resour. 2015, 79, 103–120. [Google Scholar] [CrossRef]
- Bonnema, M.G.; Sikder, S.; Hossain, F.; Durand, M.; Gleason, C.J.; Bjerklie, D.M. Benchmarking wide swath altimetry-based river discharge estimation algorithms for the Ganges river system. Water Resour. Res. 2016, 52, 2439–2461. [Google Scholar] [CrossRef]
- National Aeronautics and Space Administration (NASA). Surface Water and Ocean Topography. 2018. Available online: https://swot.jpl.nasa.gov/home.htm (accessed on 17 July 2018).
- Spicer, K.R.; Costa, J.E.; Placzek, G. Measuring flood discharge in unstable channels using ground-penetrating radar. Geology 1997, 25, 423–426. [Google Scholar] [CrossRef]
- Costa, J.E.; Spicer, K.R.; Cheng, R.T.; Haeni, F.P.; Melcher, N.B.; Thurman, E.M.; Plant, W.J.; Keller, W.C. Measuring stream discharge by non-contact methods: A Proof-of-Concept Experiment. Geophys. Res. Lett. 2000, 27, 553–556. [Google Scholar] [CrossRef]
- Haeni, F.; Buursink, M.L.; Costa, J.E.; Melcher, N.B.; Cheng, R.T.; Plant, W.J. Ground-Penetrating Radar Methods Used in Surface-Water Discharge Measurements. In Proceedings of the 8th International Conference on Ground Penetrating Radar, Gold Coast, Australia, 23–26 May 2000; pp. 494–500. [Google Scholar]
- Melcher, N.B.; Costa, J.; Haeni, F.; Cheng, R.; Thurman, E.; Buursink, M.; Spicer, K.; Hayes, E.; Plant, W.; Keller, W.; et al. River discharge measurements by using helicopter mounted radar. Geophys. Res. Lett. 2002, 29, 41–44. [Google Scholar] [CrossRef]
- Plant, W.J.; Keller, W.C.; Hayes, K. Measurement of river surface currents with coherent microwave systems. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1242–1257. [Google Scholar] [CrossRef]
- Costa, J.E.; Cheng, R.T.; Haeni, F.P.; Melcher, N.; Spicer, K.R.; Hayes, E.; Plant, W.; Hayes, K.; Teague, C.; Barrick, D. Use of radars to monitor stream discharge by noncontact methods. Water Resour. Res. 2006, 42, 14. [Google Scholar] [CrossRef]
- Fujita, I.; Komura, S. Application of video image analysis for measurements of river-surface flows. Proc. Hydraul. Eng. JSCE 1994, 38, 733–738. [Google Scholar] [CrossRef]
- Hauet, A.; Morlot, T.; Daubagnan, L. Velocity Profile and Depth-Averaged to Surface Velocity in Natural Streams: A Review Over a Large Sample of Rivers; E3S Web of Conferences 40 06015 River Flow; EDP Sciences: Paris, France, 2018. [Google Scholar] [CrossRef]
- Engel, F.L. Guidelines for the collection of video for Large Scale Particle Velocimetry (LSPIV). 2018. Available online: https://my.usgs.gov/confluence/pages/viewpage.action?pageId=546865360 (accessed on 30 December 2019).
- Lin, D.; Grundmann, J.; Eltner, A. Evaluating image tracking approaches for surface velocimetry with thermal tracers. Water Resour. Res. 2019, 55, 3122–3136. [Google Scholar] [CrossRef]
- Dugan, J.P.; Anderson, S.P.; Piotrowski, C.C.; Zuckerman, S.B. Airborne infrared remote sensing of riverine currents. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3895–3907. [Google Scholar] [CrossRef]
- Tauro, F.; Pagano, C.; Phamduy, P.; Grimaldi, S.; Porfiri, M. Large-scale particle image velocimetry from an unmanned aerial vehicle. IEEE/Asme Trans. Mechatron. 2015, 20, 3269–3275. [Google Scholar] [CrossRef]
- Tauro, F.; Porfiri, M.; Grimaldi, S. Surface flow measurements from drones. J. Hydrol. 2016, 540, 240–245. [Google Scholar] [CrossRef]
- Kinzel, P.J.; Legleiter, C.J. sUAS-based remote sensing of river discharge using thermal particle image velocimetry and bathymetric lidar. Remote Sens. 2019, 11, 2317. [Google Scholar] [CrossRef]
- Fulton, J.W.; Ostrowski, J. Measuring real-time streamflow using emerging technologies: Radar, hydroacoustics, and the probability concept. J. Hydrol. 2008, 357, 1–10. [Google Scholar] [CrossRef]
- Moramarco, T.; Barbetta, S.; Tarpanelli, A. From surface flow velocity measurements to discharge assessment by the entropy theory. Water 2017, 9, 120. [Google Scholar] [CrossRef]
- Welber, M.; Le Coz, J.; Laronne, J.B.; Zolezzi, G.; Zamler, D.; Dramais, G.; Hauet, A.; Salvaro, M. Field assessment of noncontact stream gauging using portable surface velocity radars (SVR). Water Resour. Res. 2016, 2, 1108–1126. [Google Scholar] [CrossRef]
- Fulton, J.W.; Mason, C.A.; Eggleston, J.R.; Nicotra, M.J.; Chiu, C.-L.; Henneberg, M.F.; Best, H.R.; Cederberg, J.R.; Holnbeck, S.R.; Lotspeich, R.R.; et al. Near-Field Remote Sensing of Surface Velocity and River Discharge Using Radars and the Probability Concept at 10 U.S. Geological Survey Streamgages. Remote Sens. 2020, 12, 1296. [Google Scholar] [CrossRef]
- Lane, J.W.; Dawson, C.B.; White, E.A.; Fulton, J.W. Non-contact measurement of river bathymetry using sUAS Radar: Recent developments and examples from the Northeastern United States. In Proceedings of the Fifth International Conference on Engineering Geophysics (ICEG), Al Ain, UAE, 21–24 October 2019; pp. 119–122. [Google Scholar]
- Federal Institute of Metrology METAS. Certificate of Calibration. Certificate numbers 136-32600–136-32603 and 136-32676–136-32677. 3 November 2015; unpublished. [Google Scholar]
- McDermott, W.R.; Fulton, J.W. Drone- and Ground-Based Measurements of Velocity, Depth, and Discharge Collected during 2017-18 at the Arkansas and South Platte Rivers in Colorado and the Salcha and Tanana Rivers in Alaska, USA, U.S. Geological Survey Data Release. 2020. [Google Scholar] [CrossRef]
- U.S. Geological Survey. USGS Water Data for the Nation; U.S. Geological Survey National Water Information System Database; USGS: Reston, VA, USA, 2013. [CrossRef]
- Chiu, C.-L.; Chiou, J.-D. Structure of 3--D Flow in rectangular open channels. J. Hydraul. Eng. 1986, 112, 1050–1068. [Google Scholar] [CrossRef]
- Chiu, C.-L. Entropy and probability concepts in hydraulics. J. Hydraul. Eng. 1987, 113, 583–600. [Google Scholar] [CrossRef]
- Chiu, C.-L. Velocity distribution in open channel flow. J. Hydraul. Eng. 1989, 115, 576–594. [Google Scholar] [CrossRef]
- Chiu, C.-L. Probability and Entropy Concepts in Fluid Flow Modeling and Measurement; ROC: Taipei, Taiwan, 1995. [Google Scholar]
- Chiu, C.-L.; Tung, N.C.; Hsu, S.M.; Fulton, J.W. Comparison and Assessment of Methods of Measuring Discharge in Rivers and Streams; Research Report No CEEWR-4; Dept. of Civil & Environmental Engineering, University of Pittsburgh: Pittsburgh, PA, USA, 2001. [Google Scholar]
- Chiu, C.-L.; Tung, N.C. Velocity and regularities in open-channel flow. J. Hydraul. Eng. 2002, 128, 390–398. [Google Scholar] [CrossRef]
- Moramarco, T.; Saltalippi, C.; Singh, V.P. Estimation of mean velocity in natural channel based on Chiu’s velocity distribution equation. J. Hydrol. Eng. 2004, 9, 42–50. [Google Scholar] [CrossRef]
- Chiu, C.-L.; Hsu, S.M.; Tung, N.C. Efficient methods of discharge measurements in rivers and streams based on the probability concept. Hydrol. Process. Wiley Intersci. 2005, 19, 3935–3946. [Google Scholar] [CrossRef]
- Chiu, C.-L.; Hsu, S.-M. Probabilistic approach to modeling of velocity distributions in fluid flows. J. Hydrol. 2006, 316, 28–42. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 623–656. [Google Scholar] [CrossRef]
- Moramarco, T.; Dingman, S.L. On the theoretical velocity distribution and flow resistance in natural channels. J. Hydrol. 2017, 555, 777–785. [Google Scholar] [CrossRef]
- Fulton, J.W. Comparison of Conventional and Probability-Based Modeling of Open-Channel Flow in the Allegheny River, Pennsylvania, USA. Unpublished Thesis, University of Pittsburgh, Pittsburgh, PA, USA, April 1999. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019; Available online: https://www.R-project.org/ (accessed on 9 February 2020).
- Fulton, J.W.; Henneberg, M.F.; Mills, T.J.; Kohn, M.S.; Epstein, B.; Hittle, E.A.; Damschen, W.C.; Laveau, C.D.; Lambrecht, J.M.; Farmer, W.H. Computing under-ice discharge: A proof-of-concept using hydroacoustics and the Probability Concept. J. Hydrol. 2018, 562, 733–748. [Google Scholar] [CrossRef]
- Blodgett, J.C. Rock Riprap Design for Protection of Stream Channels Near Highway Structures, Volume 1: Hydraulic Characteristics of Open Channels; US Geological Survey Water-Resources Investigations Report 86-4127; USGS: Reston, VA, USA, 1986; p. 60. [Google Scholar]
- SommerMESSTECHNIK. RQ-30, RQ-30A Discharge Measurement System: User Manual. 2014. Available online: https://www.sommer.at/en/products/water/rq-30-rq-30a (accessed on 25 August 2020).
- González, J.A.; Melching, C.S.; Oberg, K.A. Analysis of open-channel velocity measurements collected with an acoustic Doppler current profiler; Reprint from RIVERTECH 96. In Proceedings of the 1st International Conference on New/Emerging Concepts for Rivers Organized by the International Water Resources Association, Chicago, IL, USA, 22–26 September 1996. [Google Scholar]
- Guo, J.; Julien, P.Y. Application of the modified log-wake law in open-channels. J. Appl. Fluid Mech. 2008, 1, 17–23. [Google Scholar]
- Jarrett, R.D. Wading measurements of vertical velocity profiles. Geomorphology 1991, 4, 243–247. [Google Scholar] [CrossRef]
- Murphy, E.C. Accuracy of Stream Measurements; Water Supply Irrigation Paper No. 95 Series M, General Hydrographic Investigations, 10; USGS: Reston, VA, USA, 1904; Volume 58, pp. 58–163. [Google Scholar]
- Plant, W.J.; Wright, J.W. Phase speeds of upwind and downwind traveling short gravity waves. J. Geophys. Res. 1980, 85, 3304–3310. [Google Scholar] [CrossRef]
- Canova, M.G.; Fulton, J.W.; Bjerklie, D.M. USGS HYDRoacoustic Dataset in Support of the Surface Water Oceanographic Topography Satellite Mission (HYDRoSWOT); US Geological Survey Data Release; USGS: Reston, VA, USA, 2016. [CrossRef]
- Bjerklie, D.M.; Fulton, J.W.; Dingman, S.L.; Canova, M.G.; Minear, J.T.; Moramarco, T. Fundamental hydraulics of cross sections in natural rivers: Preliminary analysis of a large data set of acoustic Doppler measurements. Water Resour. Res. 2020, 56. [Google Scholar] [CrossRef]


| Velocity Measurement | Comment |
| Detectable measurement range | 0.10 to 15 m/s |
| Accuracy | ±0.01 m/s; ±1% |
| Resolution | 1 mm/s |
| Direction recognition | +/– |
| Measurement duration | 5 to 240 s |
| Measurement frequency | 24 GHz (K-Band) |
| Radar opening angle | 12° |
| Distance to water surface | minimum 0.50 m |
| Necessary minimum ripple height | 3 mm |
| Vertical inclination | measured internally |
| Automatic Vertical Angle Compensation | Comment |
| Accuracy | ± 1° |
| Resolution | ± 0.1° |
| 3DR© Solo | Comment |
| Solo 3DR™ with battery | 957.84 gm |
| Battery | 495 gm |
| Center of lift imaginary weight | 1 gm |
| Leg extensions, propellers, and vibrational dampeners | 30 gm |
| QCam and 3D mount | 545.12 gm |
| Total | 2028.96 gm |
| USGS Streamgage Identification Number | Date Collected | USGS Streamgage | Latitude | Longitude | Drainage Area (km2) |
|---|---|---|---|---|---|
| 07094500 | 20 March 2018 | Arkansas River at Parkdale, Colorado | 38.4872265 | −105.3736086 | 6369 |
| 07094500 | 28 June 2018 | Arkansas River at Parkdale, Colorado | 38.4872265 | −105.3736086 | 6369 |
| 15484000 | 10 July 2018 | Salcha River near Salchaket, Alaska | 64.471528 | −146.928056 | 5698 |
| 06701900 | 24 October 2017 | South Platte River below Brush Creek near Trumbull, Colorado | 39.2599913 | −105.2219365 | 5252 |
| 15515500 | 12 July 2018 | Tanana River near Nenana, Alaska | 64.5649444 | −149.0940000 | 66,200 |
| Parameter | Arkansas River at Parkdale, Colorado Mar 2018 | Arkansas River at Parkdale, Colorado Jun 2018 | Salcha River near Salchaket, Alaska | South Platte River below Brush Creek near Trumbull, Colorado | Tanana River at Nenana, Alaska |
|---|---|---|---|---|---|
| M(dim) | 2.59 | 2.59 | 3.00 | 1.12 | 4.06 |
| ϕ(dim) | 0.695 | 0.695 | 0.719 | 0.591 | 0.771 |
| Parameter | Source of Data | Arkansas River at Parkdale, Colorado 20 March 2018, 1126 MST | Arkansas River at Parkdale, Colorado 28 June 2018, 0922 MDT | Salcha River near Salchaket, Alaska 10 July 2018, 1518 AKDT | South Platte River below Brush Creek near Trumbull, Colorado 24 October 2017, 1058 MDT | Tanana River at Nenana, Alaska 12 July 2018, 1700 AKDT |
|---|---|---|---|---|---|---|
| uD (m/s) | QCam | 1.02 [−1.0%] | 1.43 | 1.58 | 0.90 [1.1%] | 2.17 |
| uD (m/s) | Hydroacoustics | 1.03 | -- | -- | 0.89 | -- |
| umax (m/s) | QCam | 1.02 | 1.43 | 1.58 | 0.90 | 2.17 |
| umax (m/s) | Computed | 1.03 | -- | 1.78 | 0.82 | 2.69 |
| umean (m/s) | QCam | 0.709 [0.3%] | 0.99 [2.5%] | 1.14 [−10.4%] | 0.53 [7.3%] | 1.67 [−18.8%] |
| umean (m/s) | Computed | 0.718 [1.6%] | -- | 1.28 [0.8%] | 0.48 [−2.5%] | 2.07 [0.5%] |
| umean (m/s) | Hydroacoustics | 0.707 | 0.97 A | 1.27 | 0.50 | 2.06 |
| Gage height (m) | -- | -- | 0.96 | -- | -- | -- |
| Area (m2) | -- | 13.4 | 20.4 A | 54.7 | 6.42 | 944 |
| Q (m3/s) | QCam | 9.48 [0.3%] | 20.3 [2.5%] | 62.1 [−10.4%] | 3.42 [7.3%] | 1579 [−18.8%] |
| Q (m3/s) | Computed | 9.61 [1.6%] | -- | 69.9 [0.8%] | 3.10 [−2.5%] | 1954 [0.5%] |
| Q (m3/s) | Hydroacoustics | 9.45 | 19.8 A | 69.3 | 3.18 | 1944 |
| Surface Velocity | |||||
|---|---|---|---|---|---|
| Time (MDT) | Station (m) | FT2 Near-Surface Velocity (m/s) | SVR Surface Velocity (m/s) | QCam Surface Velocity (m/s) | Measurement Location |
| 10:15 a.m. | 14 | 0.86 | 0.88 | 0.90 | Total depth of the vertical that contains the maximum velocity = 0.5 m; all instream point velocity measurements were obtained from this station; all station distances are relative to a permanent post located approximately 9 m from the REW; flights conducted at approximately 5 m above the water surface and correlate with the software (RPCommander) used to parameterize and process QCam radar spectra 1–4; propwash was not observed; s.d. = 0.01 m/s. |
| 11:02 a.m. | 14 | 0.83 | 0.85 | 0.80 | Flights conducted at approximately 8 m above the water surface and correlate with RPCommander radar spectra 6–10; propwash was not observed; radar footprint encountered low velocity regions and vegetation near the REW; s.d. = 0.02 m/s. |
| 11:43 a.m. | 22 | 0.59 | -- | 0.60 | Measurements collected near the LEW, which is characterized by shallow depths and low velocities and correlate with RPCommander radar spectra 11–15; flights conducted at approximately 5 m above the water surface; propwash was observed; total depth of the vertical at station = 0.23 m. |
| 12:27 p.m. | 22 | -- | -- | 0.66 | Flights conducted at approximately 8 m above the water surface and correlate with RPCommander radar spectra 16–21; radar footprint encountered high velocity regions away from the LEW; propwash was not observed. |
| USGS Streamgage | |||||
|---|---|---|---|---|---|
| Spectrum Information | Arkansas River at Parkdale, Colorado March 2018 | Arkansas River at Parkdale, Colorado June 2018 | Salcha River near Salchaket, Alaska | South Platte River below Brush Creek near Trumbull, Colorado | Tanana River at Nenana, Alaska |
| Approach | |||||
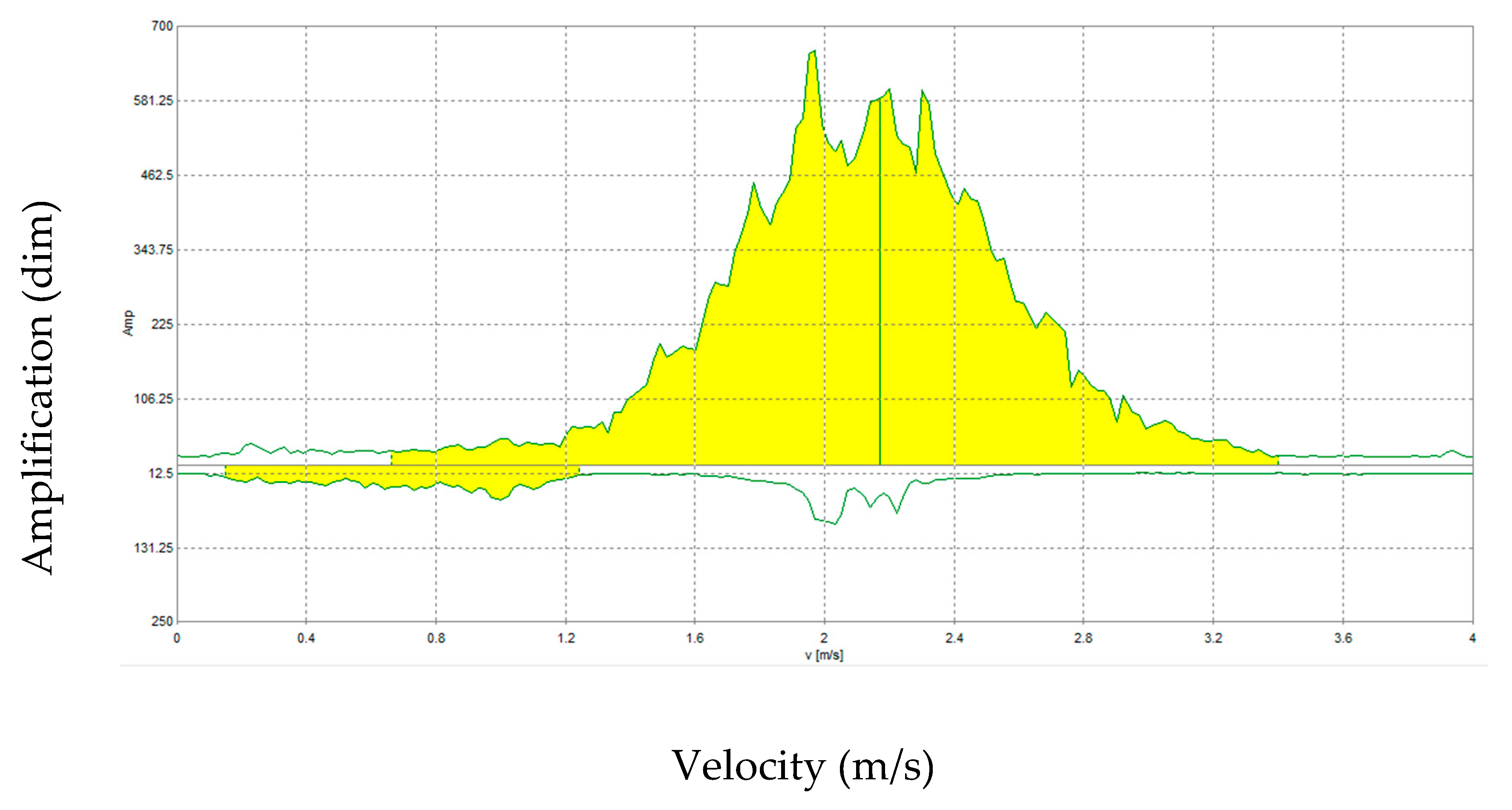
| Spectrum no. (dim) | 1 | 5 | 1 | 1 | 3 |
| Surface velocity (m/s) | 1.02 | 1.43 | 1.58 | 0.900 | 2.17 |
| Min velocity (m/s) | 0.190 | 0.160 | 0.430 | 0.170 | 0.660 |
| Mean velocity (umean) (m/s) | 1.03 | 1.44 | 1.59 | 0.90 | 2.17 |
| Max velocity (umax) (m/s) | 1.91 | 3.26 | 2.72 | 1.70 | 3.40 |
| Signal-to-noise ratio (dB) | 52.0 | 71.0 | 64.0 | 60.0 | 68.0 |
| Delta (δ) (m/s) | 1.72 | 3.10 | 2.29 | 1.53 | 2.74 |
| Departing | |||||
| Spectrum no. (dim) | 1 | 5 | 1 | 1 | 3 |
| Surface velocity (m/s) | -- | -- | -- | -- | -- |
| Min velocity (m/s) | 0.430 | 0.350 | 0.140 | 0.500 | 0.150 |
| Mean velocity (umean) (m/s) | 2.21 | 1.35 | 1.96 | 2.58 | 0.00 |
| Max velocity (umax) (m/s) | 2.86 | 2.26 | 2.42 | 3.33 | 1.24 |
| Signal-to-noise ratio (dB) | 41.0 | 60.0 | 45.0 | 40.0 | 52.0 |
| Delta (δ) (m/s) | 2.43 | 1.98 | 2.28 | 2.83 | 1.09 |
This work was authored as part of the Contributor’s official duties as an Employee of the United States Government and is therefore a work of the United States Government. In accordance with 17 U.S.C. 105, no copyright protection is available for such works under U.S. Law. This is an Open Access article that has been identified as being free of known restrictions under copyright law, including all related and neighboring rights (https://creativecommons.org/publicdomain/mark/1.0/). You can copy, modify, distribute and perform the work, even for commercial purposes, all without asking permission.
Share and Cite
Fulton, J.W.; Anderson, I.E.; Chiu, C.-L.; Sommer, W.; Adams, J.D.; Moramarco, T.; Bjerklie, D.M.; Fulford, J.M.; Sloan, J.L.; Best, H.R.; et al. QCam: sUAS-Based Doppler Radar for Measuring River Discharge. Remote Sens. 2020, 12, 3317. https://doi.org/10.3390/rs12203317
Fulton JW, Anderson IE, Chiu C-L, Sommer W, Adams JD, Moramarco T, Bjerklie DM, Fulford JM, Sloan JL, Best HR, et al. QCam: sUAS-Based Doppler Radar for Measuring River Discharge. Remote Sensing. 2020; 12(20):3317. https://doi.org/10.3390/rs12203317
Chicago/Turabian StyleFulton, John W., Isaac E. Anderson, C.-L. Chiu, Wolfram Sommer, Josip D. Adams, Tommaso Moramarco, David M. Bjerklie, Janice M. Fulford, Jeff L. Sloan, Heather R. Best, and et al. 2020. "QCam: sUAS-Based Doppler Radar for Measuring River Discharge" Remote Sensing 12, no. 20: 3317. https://doi.org/10.3390/rs12203317
APA StyleFulton, J. W., Anderson, I. E., Chiu, C.-L., Sommer, W., Adams, J. D., Moramarco, T., Bjerklie, D. M., Fulford, J. M., Sloan, J. L., Best, H. R., Conaway, J. S., Kang, M. J., Kohn, M. S., Nicotra, M. J., & Pulli, J. J. (2020). QCam: sUAS-Based Doppler Radar for Measuring River Discharge. Remote Sensing, 12(20), 3317. https://doi.org/10.3390/rs12203317






