A Dual-Wavelength Ocean Lidar for Vertical Profiling of Oceanic Backscatter and Attenuation
Abstract
1. Introduction
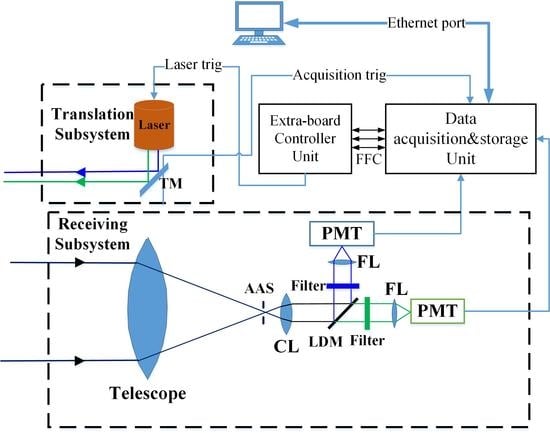
2. Instrument Configuration
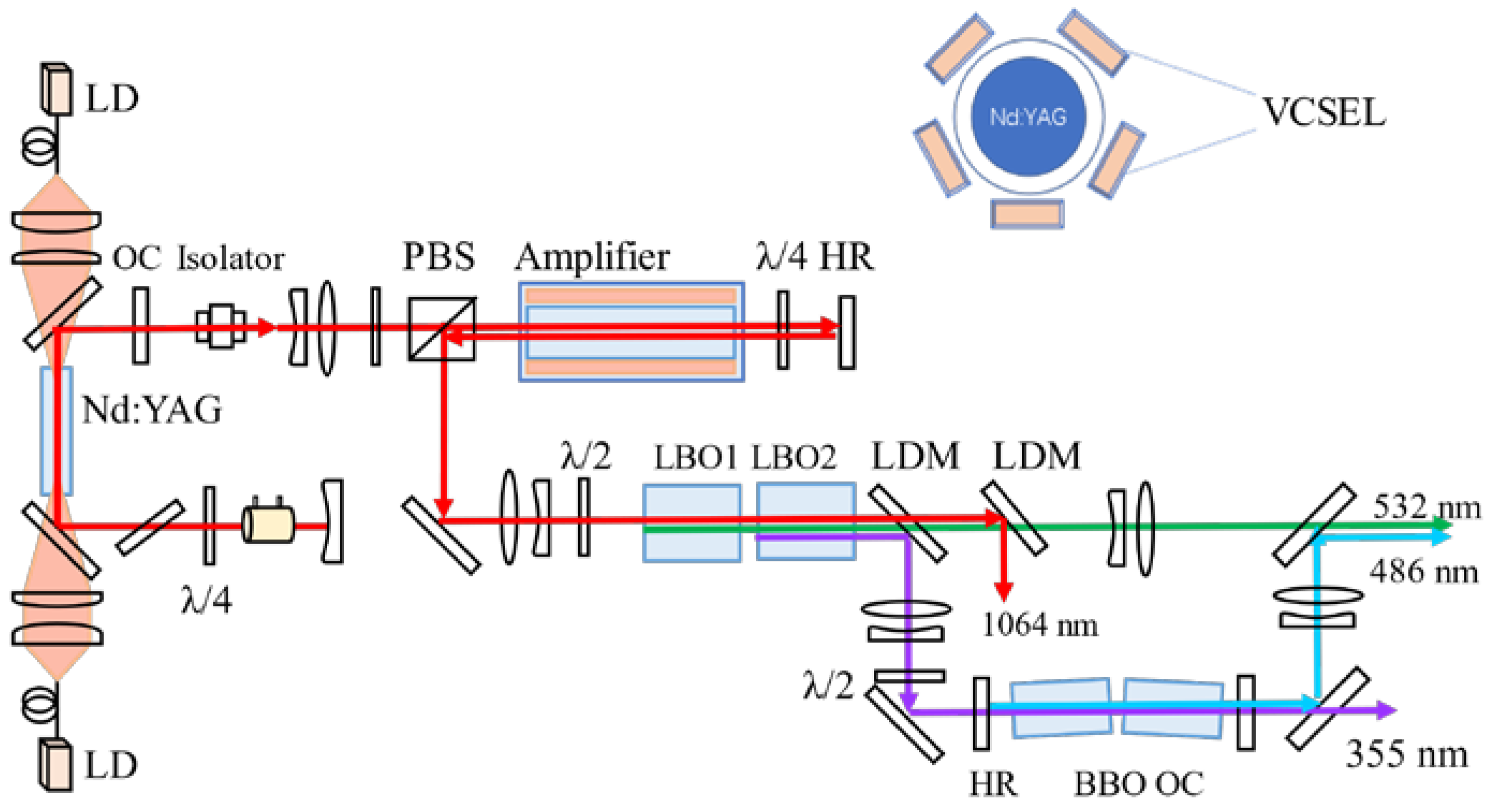
2.1. Transmitter Subsystem
2.2. Receiver Subsystem
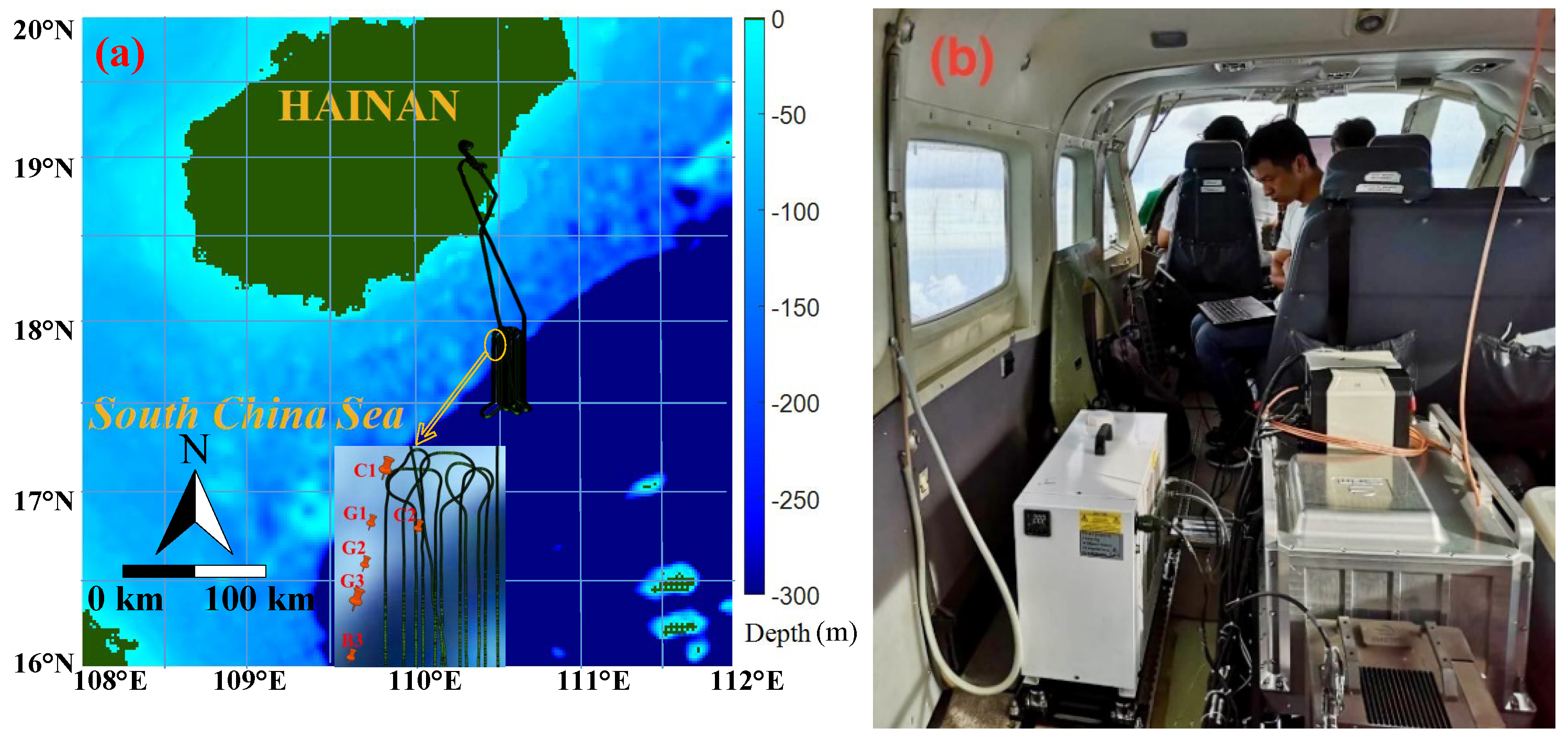
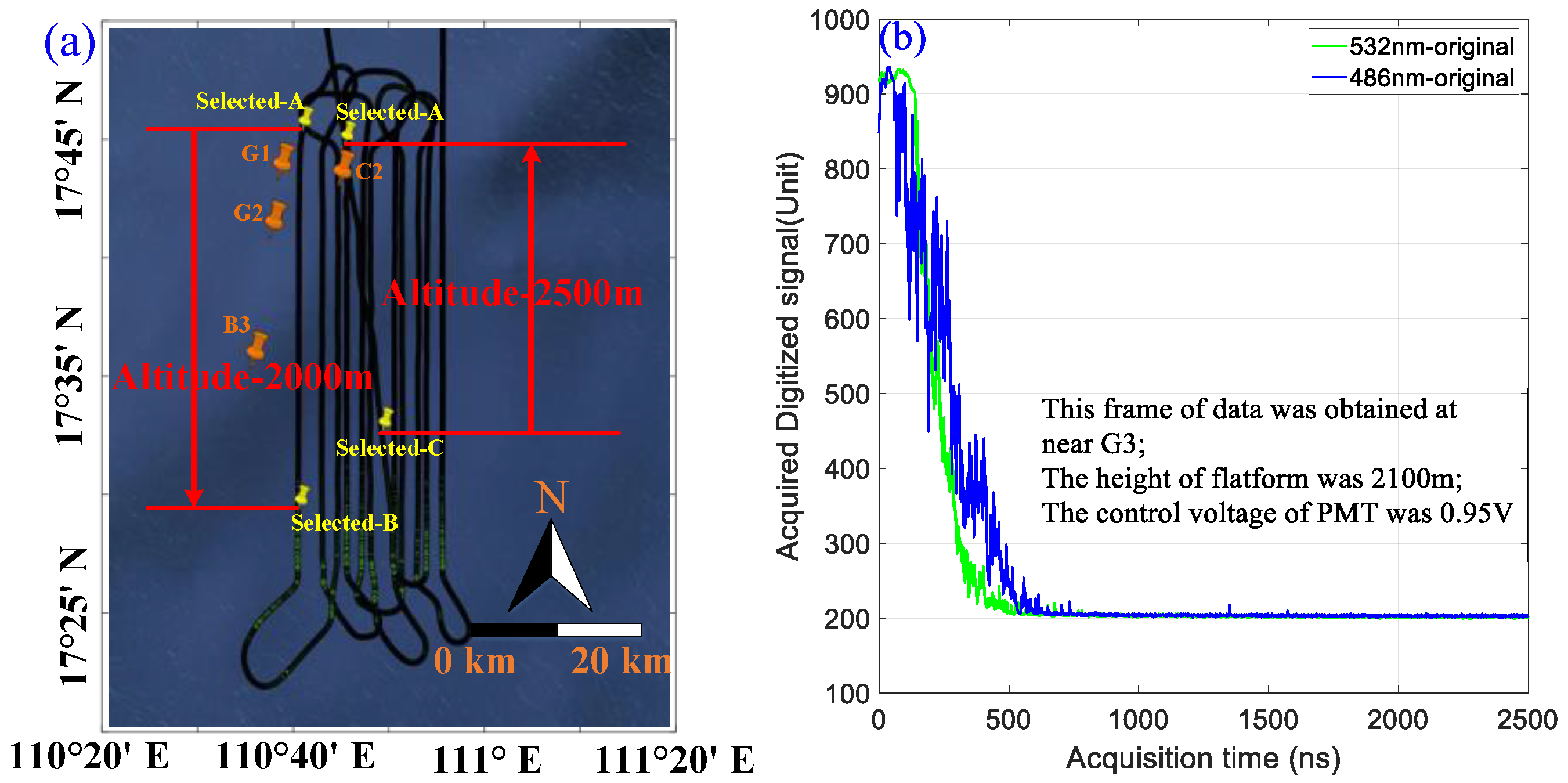
3. Experiment Validation
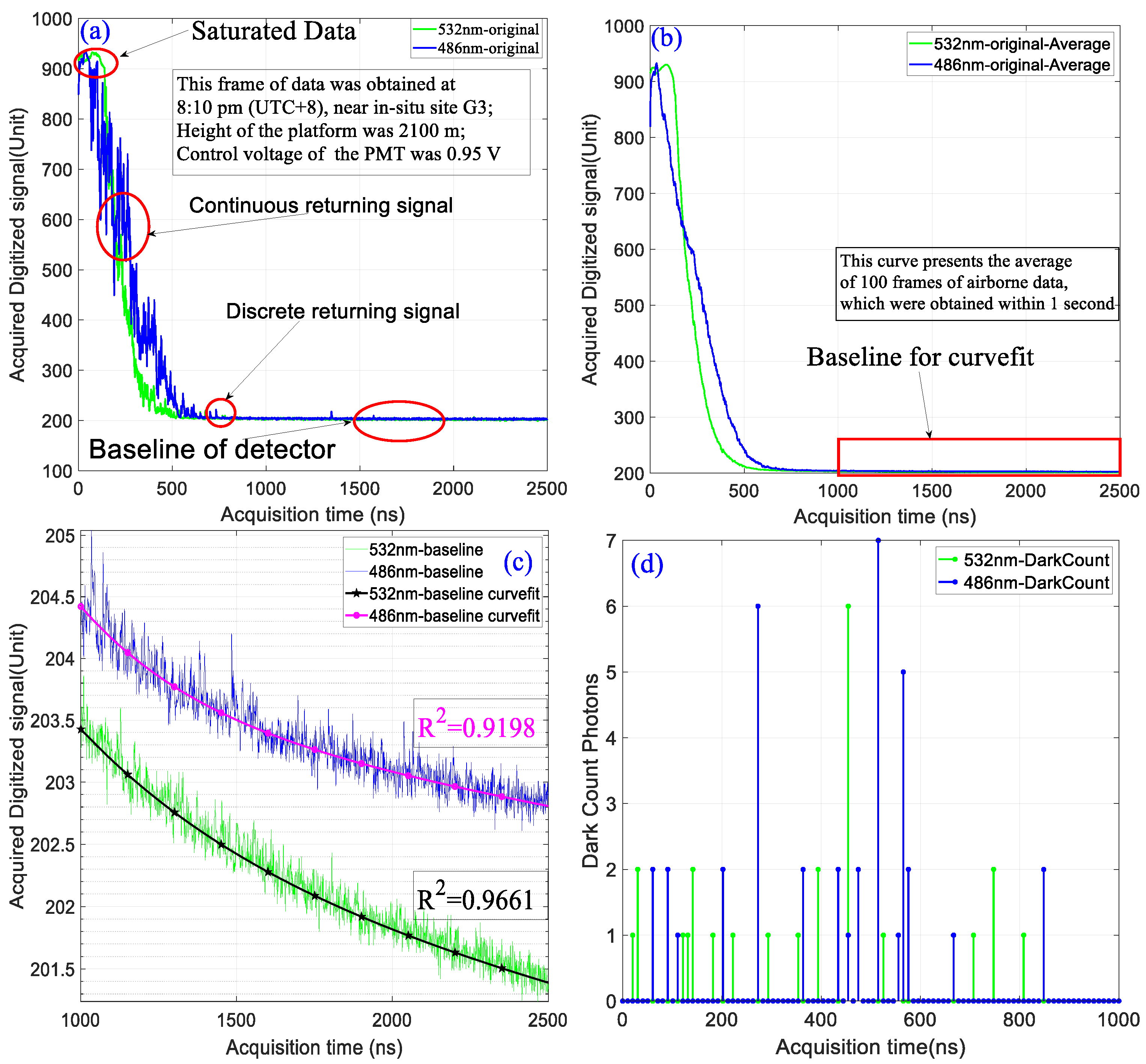
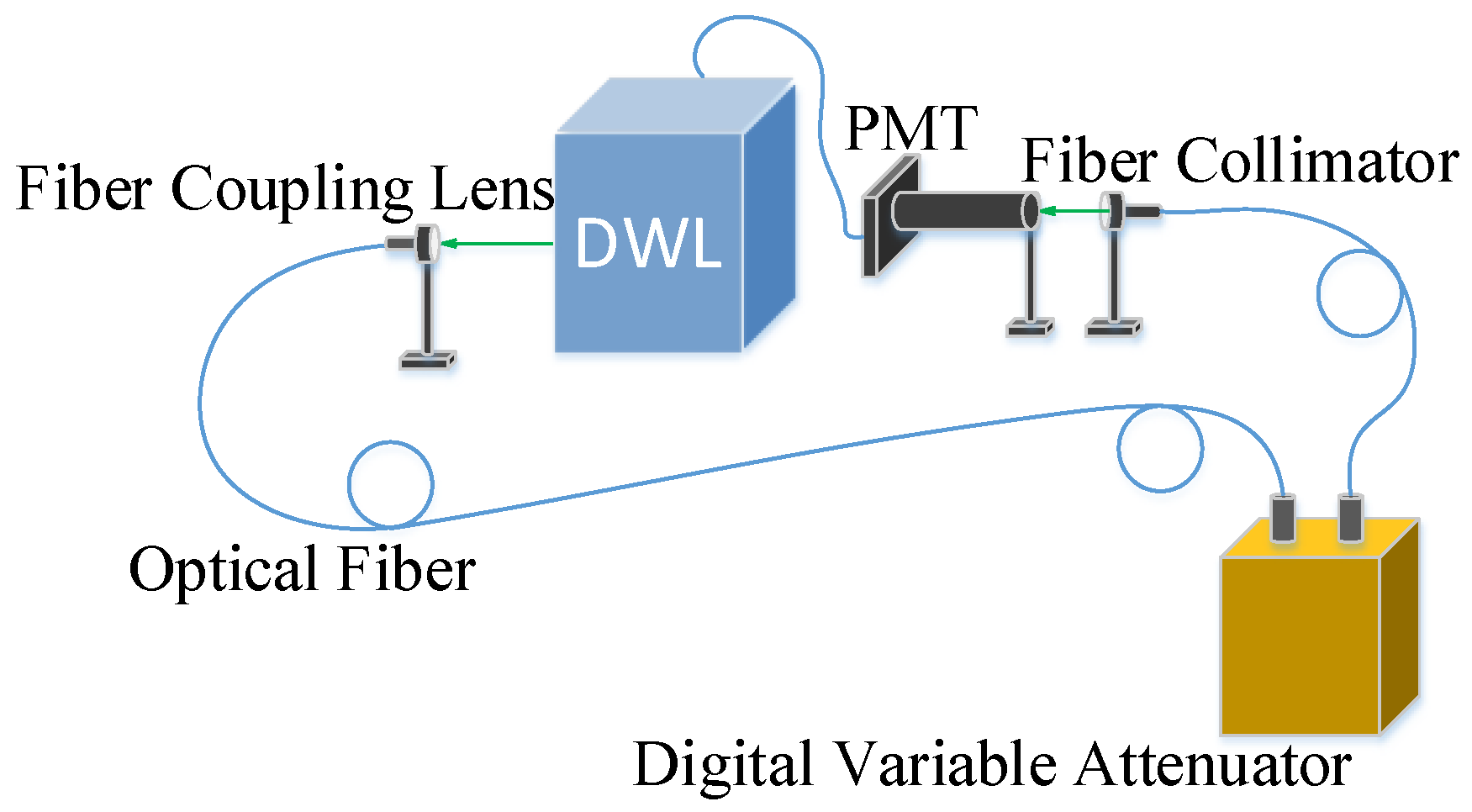
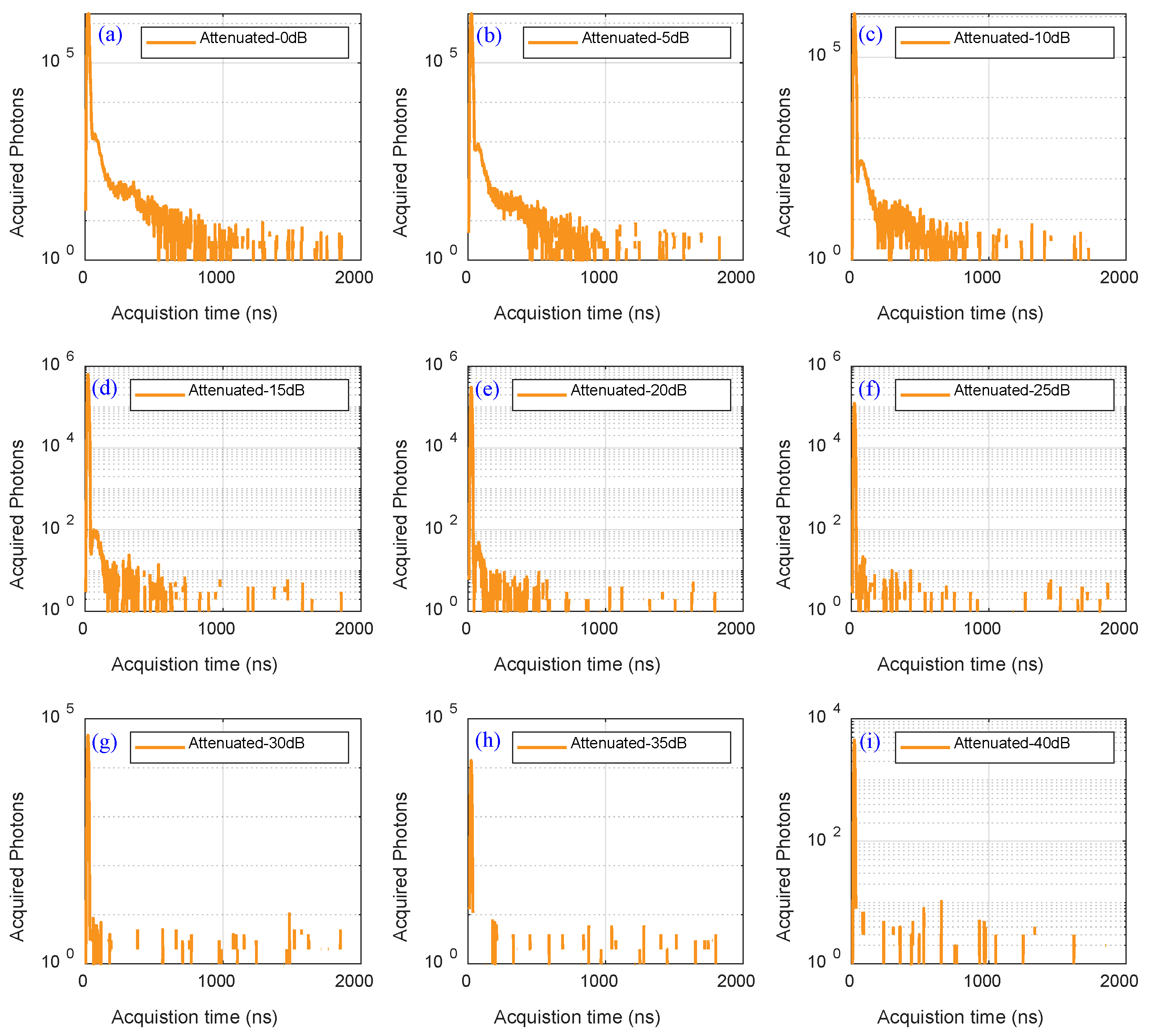
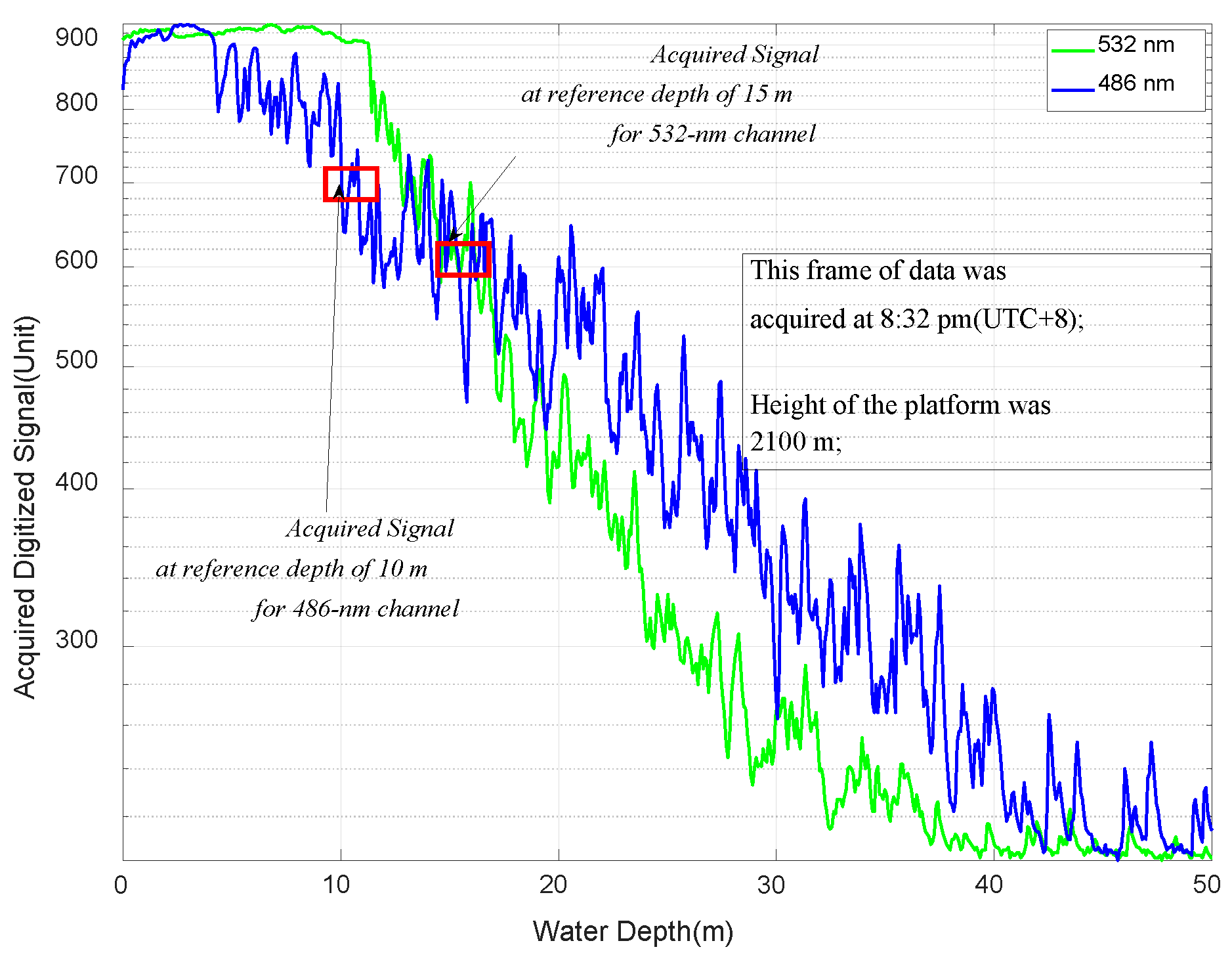
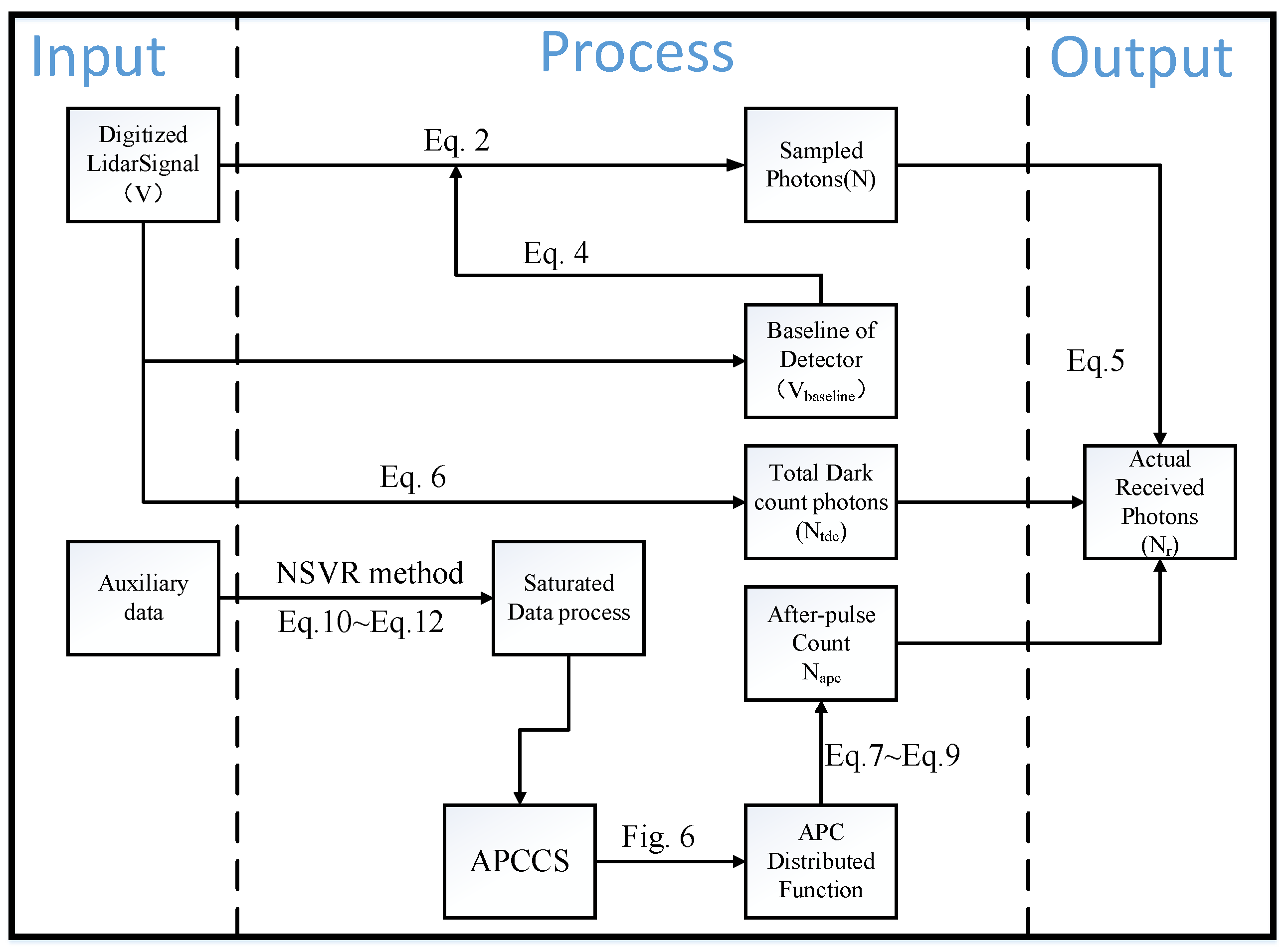
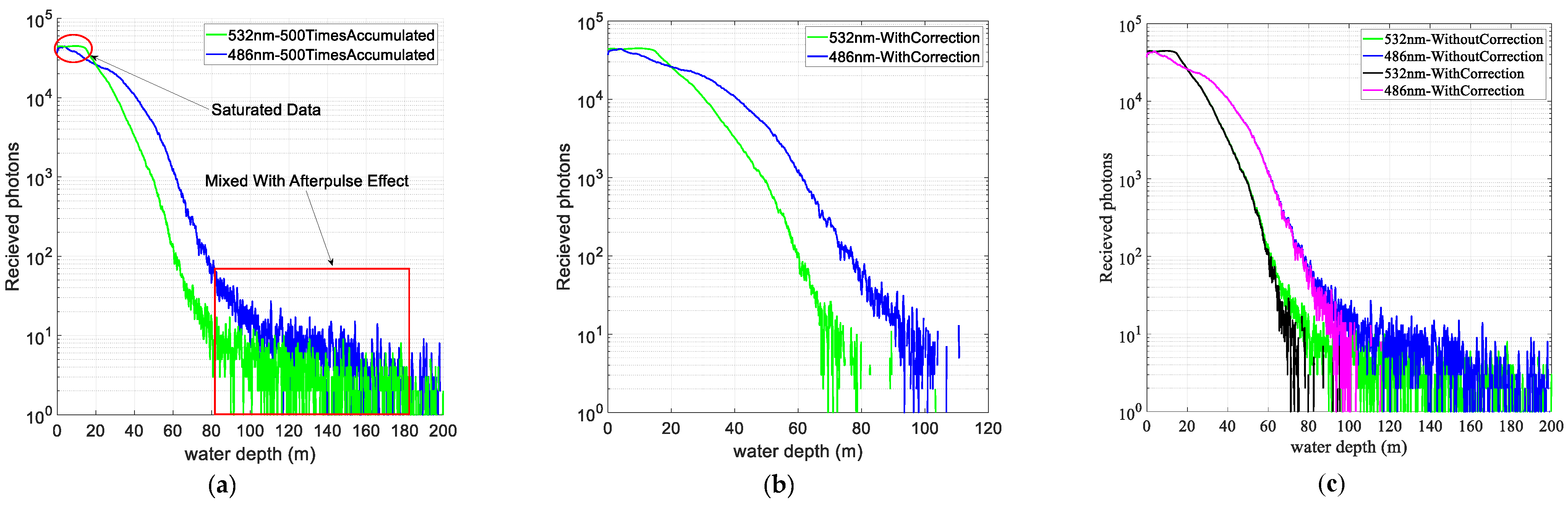
3.1. Conversion from the Sampled Digitized Voltage Values to the Corresponding Photon Number
3.2. APC Correction
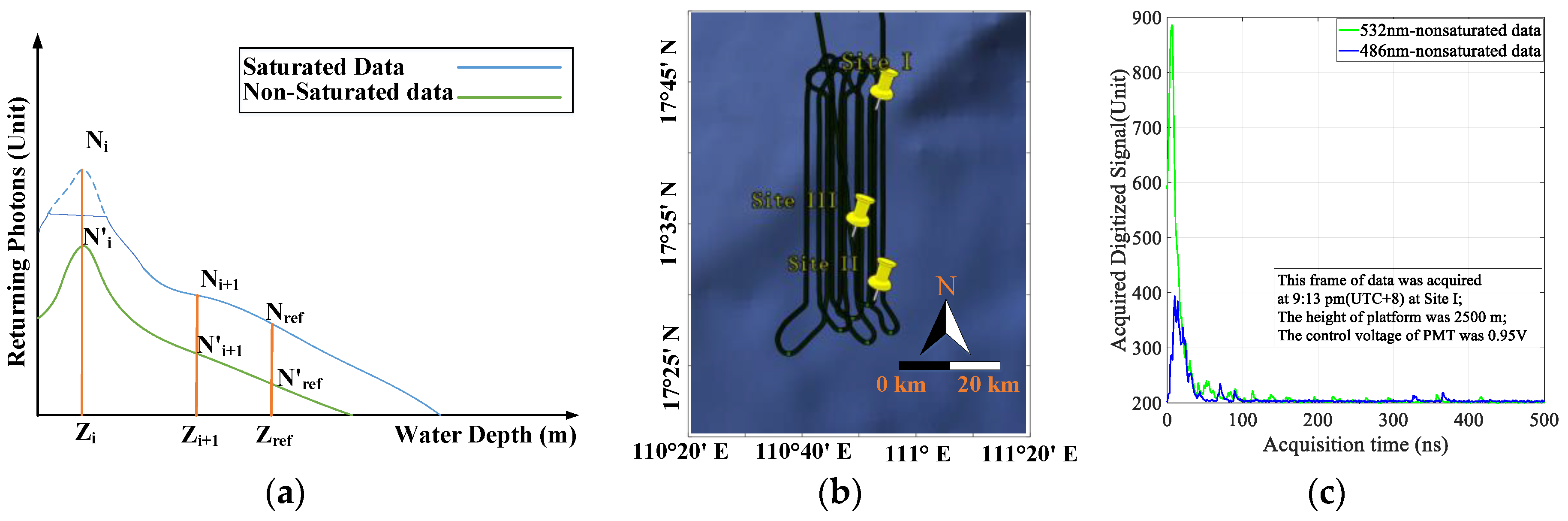
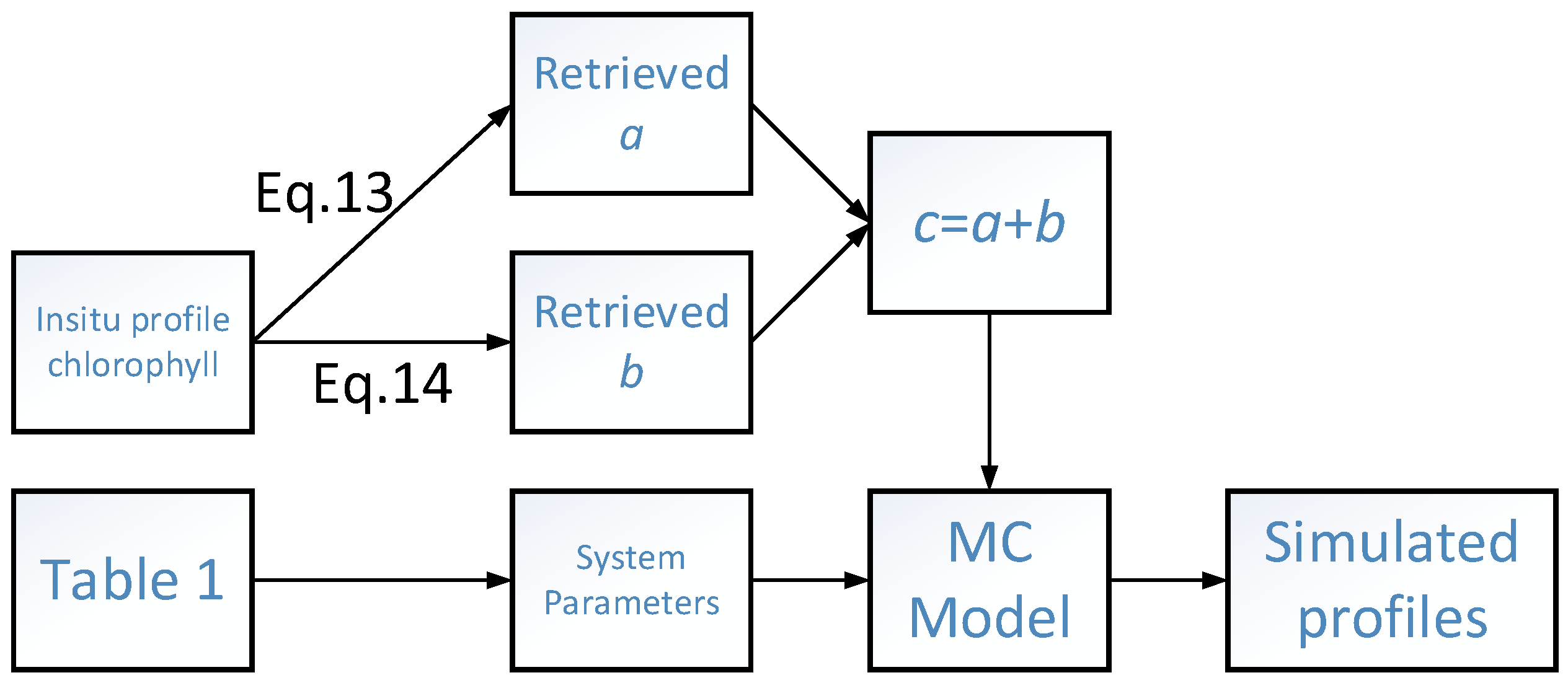
3.3. Monte Carlo Model Based on In Situ Shipborne Data
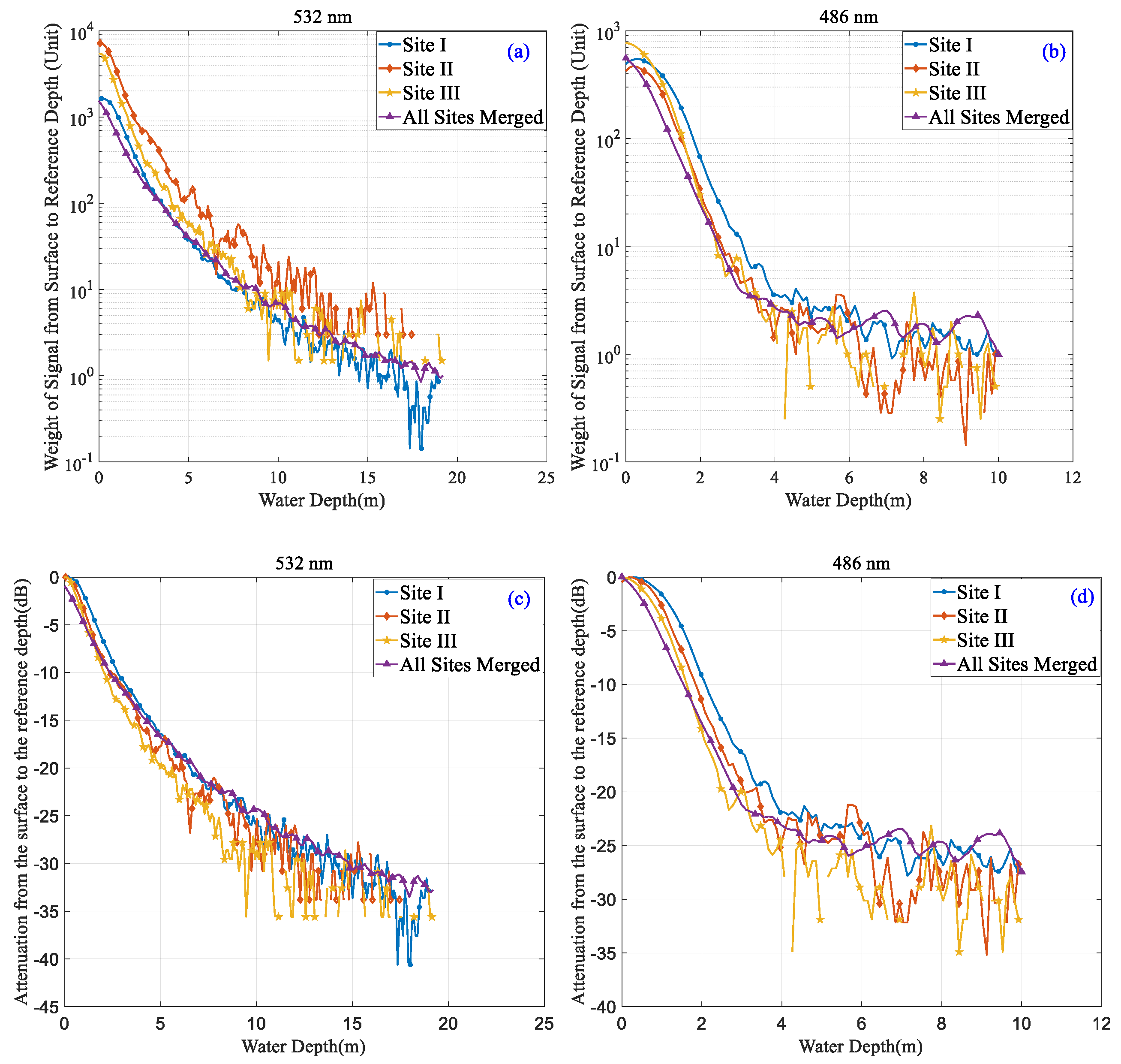
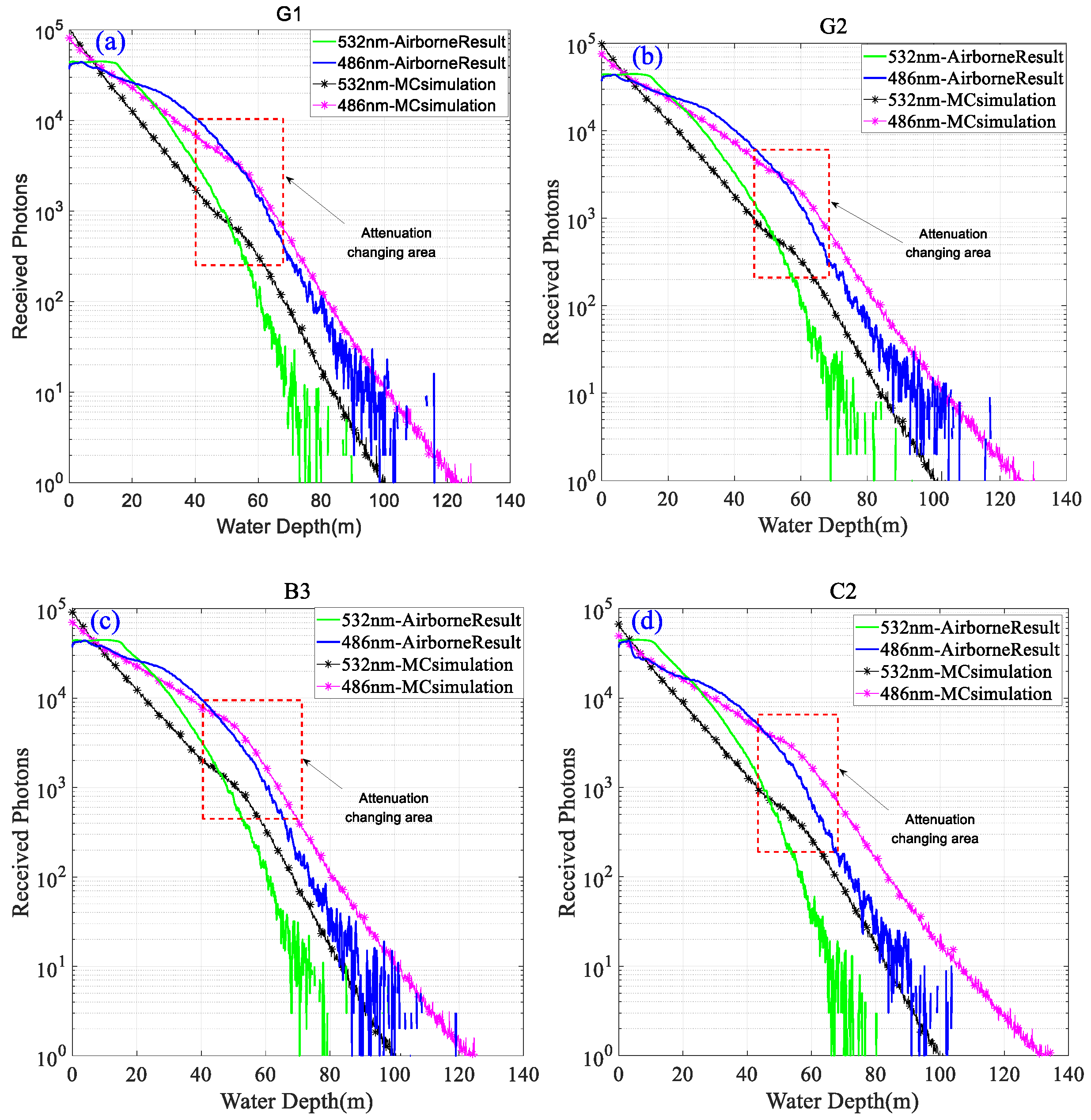
3.4. Airborne Experiment Results and Comparison with MC Simulation Results
4. Discussion
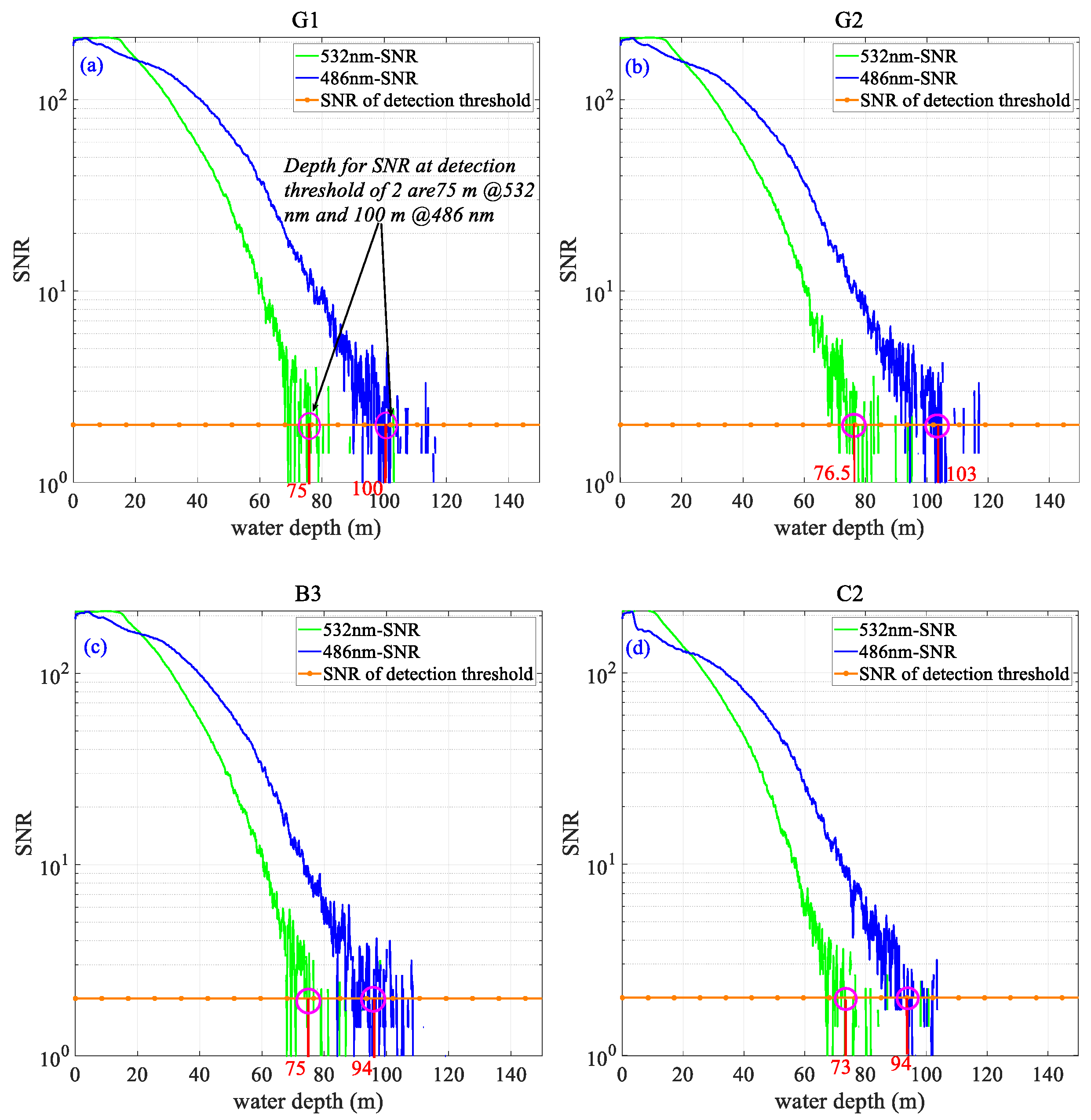
4.1. Signal-to-Noise Ratio
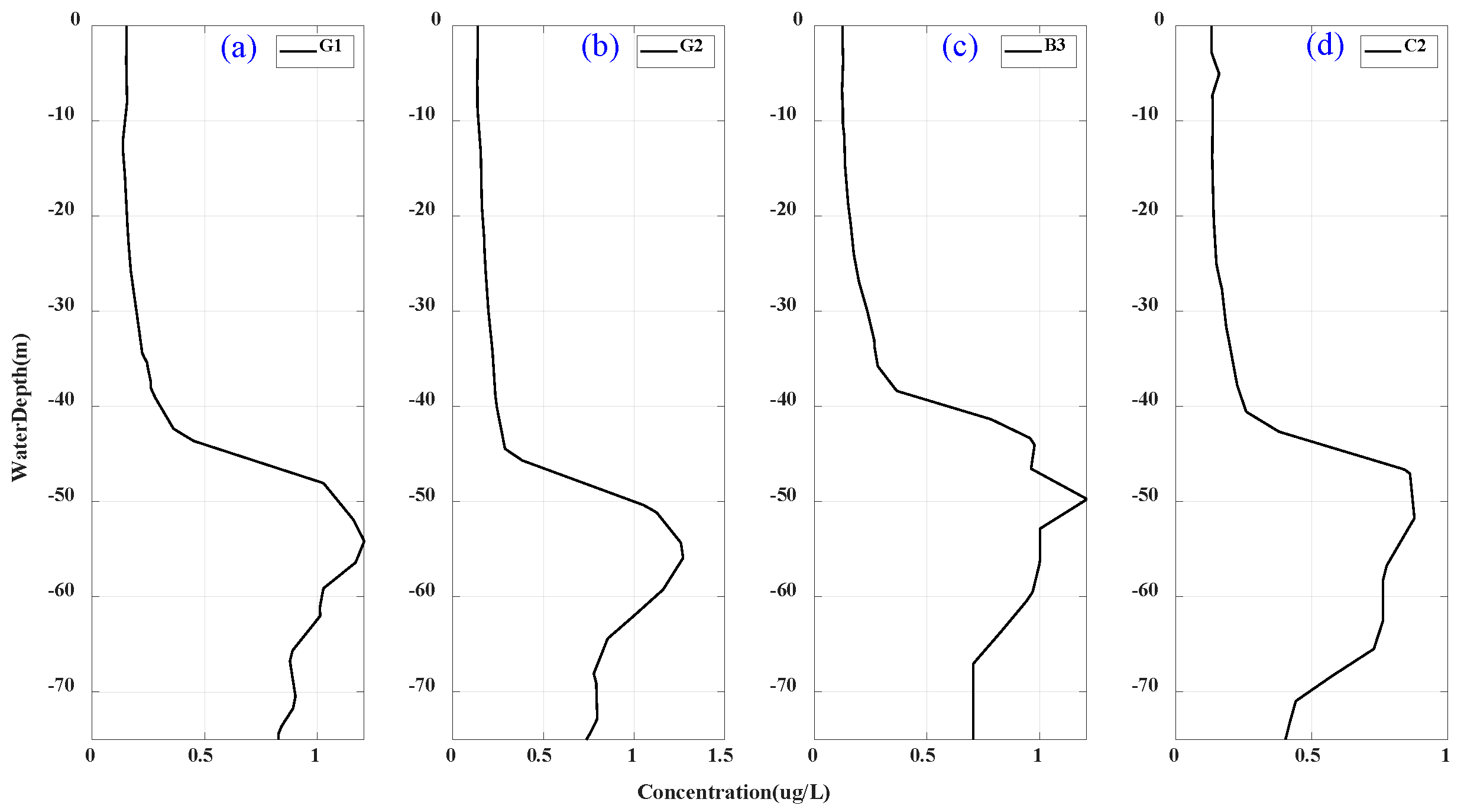
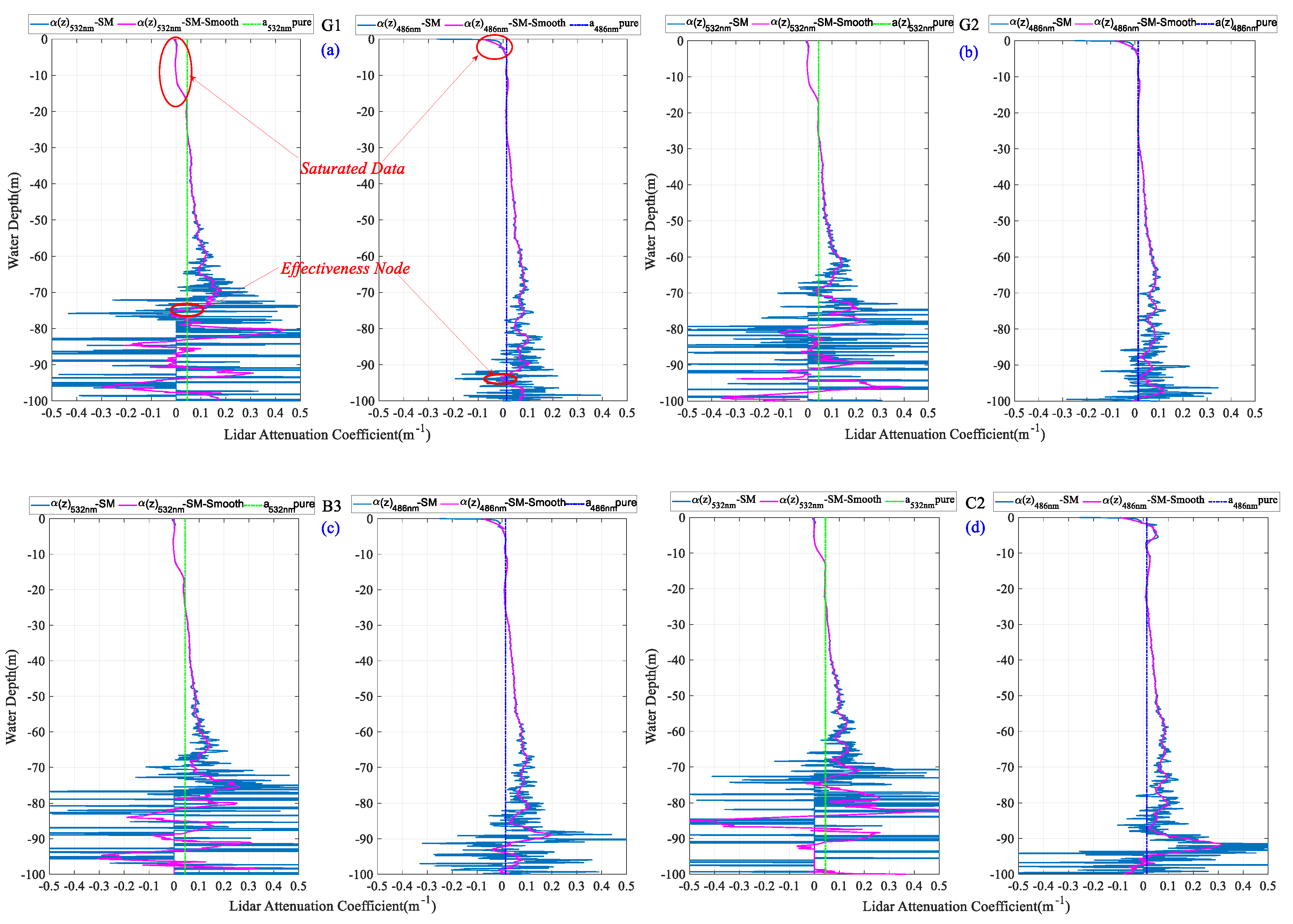
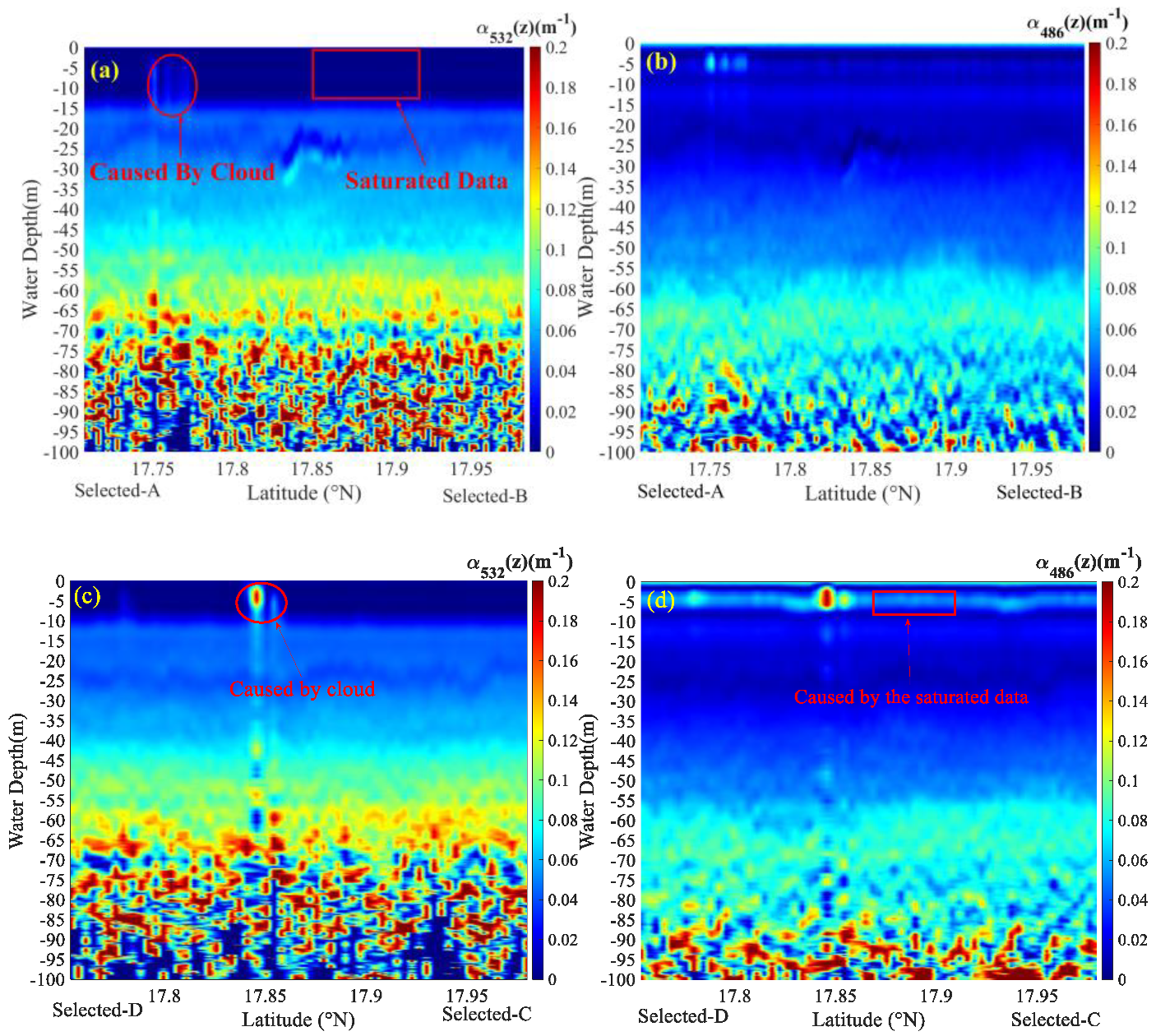
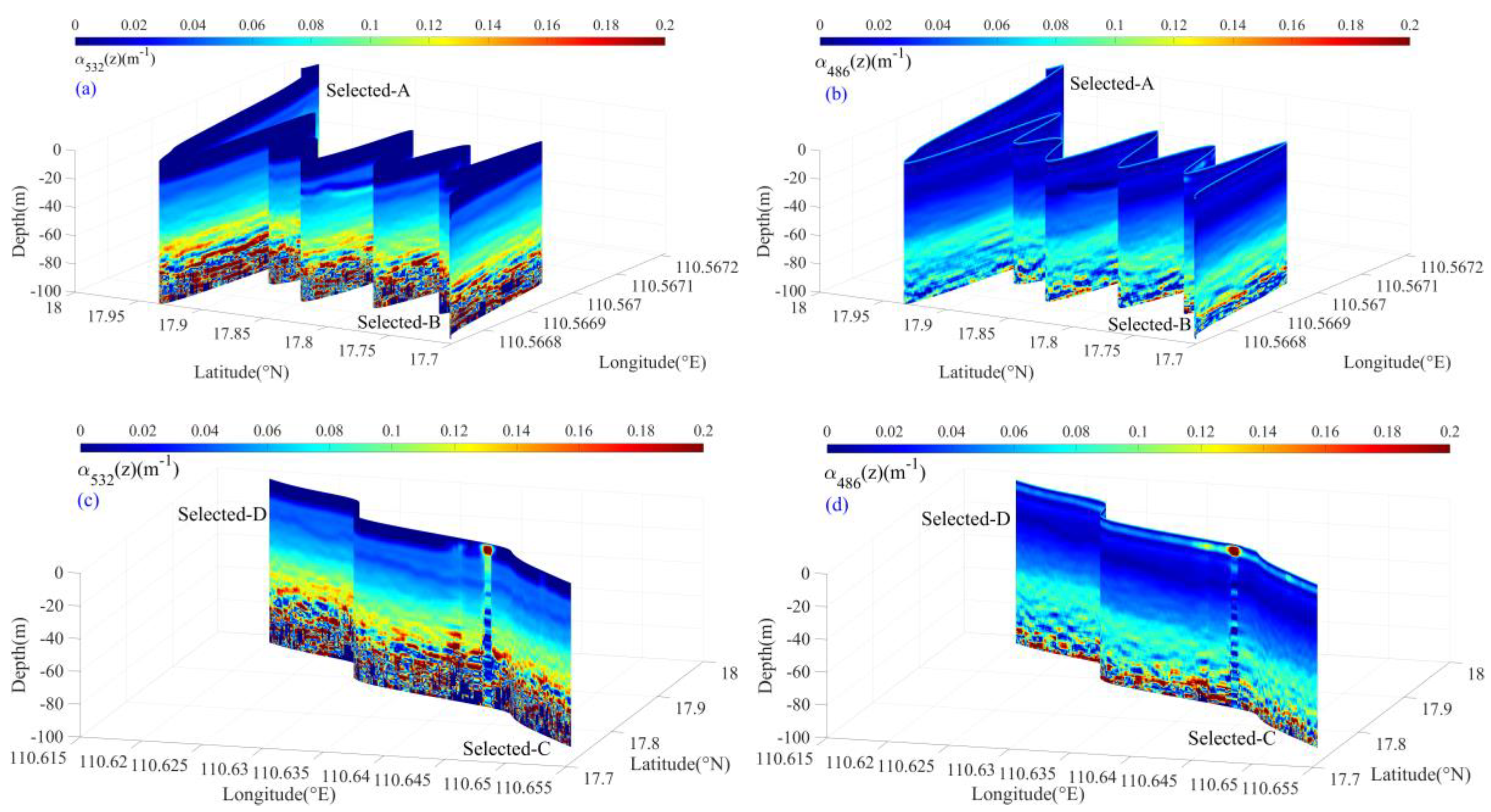
4.2. Inversion and Analysis of Water Column Parameters
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- McClain, C.R. A decade of satellite ocean color observations. Annu. Rev. Mar. Sci. 2009, 1, 19–42. [Google Scholar] [CrossRef] [PubMed]
- Siegel, D.A.; Behrenfeld, M.J.; Maritorena, S.; McClain, C.R.; Antoine, D.; Bailey, S.W.; Bontempi, P.S.; Boss, E.S.; Dierssen, H.M.; Doney, S.C. Regional to global assessments of phytoplankton dynamics from the SeaWiFS mission. Remote Sens. Environ. 2013, 135, 77–91. [Google Scholar] [CrossRef]
- De Boyer Montégut, C.; Madec, G.; Fischer, A.S.; Lazar, A.; Iudicone, D. Mixed layer depth over the global ocean: An examination of profile data and a profile-based climatology. J. Geophys. Res. Oceans 2004, 109. [Google Scholar] [CrossRef]
- Brainerd, K.E.; Gregg, M.C. Surface mixed and mixing layer depths. Deep Sea Res. Part I Oceanogr. Res. Pap. 1995, 42, 1521–1544. [Google Scholar] [CrossRef]
- Morel, A.; Berthon, J.F. Surface pigments, algal biomass profiles, and potential production of the euphotic layer: Relationships reinvestigated in view of remote-sensing applications. Limnol. Oceanogr. 1989, 34, 1545–1562. [Google Scholar] [CrossRef]
- Winker, D.M.; Vaughan, M.A.; Omar, A.; Hu, Y.; Powell, K.A.; Liu, Z.; Hunt, W.H.; Young, S.A. Overview of the CALIPSO mission and CALIOP data processing algorithms. J. Atmos. Ocean. Technol. 2009, 26, 2310–2323. [Google Scholar] [CrossRef]
- Hu, Y. Ocean, Land and Meteorology Studies Using Space-Based Lidar Measurements; NASA Langley Research Center: Hampton, VA, USA, 2009.
- Morel, A. Light and marine photosynthesis: A spectral model with geochemical and climatological implications. Prog. Oceanogr. 1991, 26, 263–306. [Google Scholar] [CrossRef]
- Roesler, C.S.; Perry, M.J.; Carder, K.L. Modeling in situ phytoplankton absorption from total absorption spectra in productive inland marine waters. Limnol. Oceanogr. 1989, 34, 1510–1523. [Google Scholar] [CrossRef]
- Bricaud, A.; Morel, A.; Prieur, L. Absorption by dissolved organic matter of the sea (yellow substance) in the UV and visible domains 1. Limnol. Oceanogr. 1981, 26, 43–53. [Google Scholar] [CrossRef]
- Chen, S.; Xue, C.; Zhang, T.; Hu, L.; Chen, G.; Tang, J. Analysis of the Optimal Wavelength for Oceanographic Lidar at the Global Scale Based on the Inherent Optical Properties of Water. Remote Sens. 2019, 11, 2705. [Google Scholar] [CrossRef]
- Wu, S.; Song, X.; Liu, B. Fraunhofer lidar prototype in the green spectral region for atmospheric boundary layer observations. Remote Sens. 2013, 5, 6079–6095. [Google Scholar] [CrossRef]
- Kattawar, G.W.; Xu, X. Filling in of Fraunhofer lines in the ocean by Raman scattering. Appl. Opt. 1992, 31, 6491–6500. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Fan, R.; Ye, G.; Luo, T.; Guan, J.; Zhou, Z.; Chen, D. Depth resolution improvement of streak tube imaging lidar system using three laser beams. Chin. Opt. Lett. 2018, 16, 041101. [Google Scholar] [CrossRef]
- Gray, D.J.; Anderson, J.; Nelson, J.; Edwards, J. Using a multiwavelength LiDAR for improved remote sensing of natural waters. Appl. Opt. 2015, 54, F232–F242. [Google Scholar] [CrossRef]
- Burton, S.; Ferrare, R.; Hostetler, C.; Hair, J.; Rogers, R.; Obland, M.; Butler, C.; Cook, A.; Harper, D.; Froyd, K. Aerosol classification using airborne High Spectral Resolution Lidar measurements-methodology and examples. Atmos. Meas. Tech. 2012, 5, 73. [Google Scholar] [CrossRef]
- Sasano, Y.; Browell, E.V. Light scattering characteristics of various aerosol types derived from multiple wavelength lidar observations. Appl. Opt. 1989, 28, 1670–1679. [Google Scholar] [CrossRef]
- Acharya, Y.; Sharma, S.; Chandra, H. Signal induced noise in PMT detection of lidar signals. Measurement 2004, 35, 269–276. [Google Scholar] [CrossRef]
- Zhao, Y. Signal-induced fluorescence in photomultipliers in differential absorption lidar systems. Appl. Opt. 1999, 38, 4639–4648. [Google Scholar] [CrossRef]
- Concannon, B.M.; Contarino, V.M.; Allocca, D.M.; Mullen, L.J. Characterization of signal-induced artifacts in photomultiplier tubes for underwater lidar applications. In Proceedings of Airborne and In-Water Underwater Imaging; SPIE: Denver, CO, USA, 1999; pp. 167–173. [Google Scholar]
- Donovan, D.; Whiteway, J.; Carswell, A.I. Correction for nonlinear photon-counting effects in lidar systems. Appl. Opt. 1993, 32, 6742–6753. [Google Scholar] [CrossRef]
- Lu, X.; Hu, Y.; Yang, Y.; Bontempi, P.; Omar, A.; Baize, R. Antarctic spring ice-edge blooms observed from space by ICESat-2. Remote Sens. Environ. 2020, 245, 111827. [Google Scholar] [CrossRef]
- Yu, C.; Shangguan, M.; Xia, H.; Zhang, J.; Dou, X.; Pan, J.-W. Fully integrated free-running InGaAs/InP single-photon detector for accurate lidar applications. Opt. Express 2017, 25, 14611–14620. [Google Scholar] [CrossRef] [PubMed]
- Lu, X.; Hu, Y.; Pelon, J.; Trepte, C.; Liu, K.; Rodier, S.; Zeng, S.; Lucker, P.; Verhappen, R.; Wilson, J. Retrieval of ocean subsurface particulate backscattering coefficient from space-borne CALIOP lidar measurements. Opt. Express 2016, 24, 29001–29008. [Google Scholar] [CrossRef] [PubMed]
- Churnside, J.H.; McCarty, B.J.; Lu, X. Subsurface ocean signals from an orbiting polarization lidar. Remote Sens. 2013, 5, 3457–3475. [Google Scholar] [CrossRef]
- Schutz, B.E.; Zwally, H.J.; Shuman, C.A.; Hancock, D.; DiMarzio, J.P. Overview of the ICESat mission. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Chen, G.; Tang, J.; Zhao, C.; Wu, S.; Yu, F.; Ma, C.; Xu, Y.; Chen, W.; Zhang, Y.; Liu, J. Concept Design of the “Guanlan” Science Mission: China’s Novel Contribution to Space Oceanography. Front. Mar. Sci. 2019, 6, 194. [Google Scholar] [CrossRef]
- Ma, J.; Lu, T.; He, Y.; Jiang, Z.; Hou, C.; Li, K.; Liu, F.; Zhu, X.; Chen, W. Compact dual-wavelength blue-green laser for airborne ocean detection lidar. Appl. Opt. 2020, 59, C87–C91. [Google Scholar] [CrossRef]
- Amante, C.; Eakins, B.W. ETOPO1 Arc-Minute Global Relief Model: Procedures, Data Sources and Analysis; 2009. Available online: http://www.ngdc.noaa.gov/mgg/global/global.html (accessed on 1 September 2020).
- Wang, L.; Jacques, S.L.; Zheng, L. MCML—Monte Carlo modeling of light transport in multi-layered tissues. Comput. Methods Programs Biomed. 1995, 47, 131–146. [Google Scholar] [CrossRef]
- Lee, Z.; Carder, K.L.; Mobley, C.D.; Steward, R.G.; Patch, J.S. Hyperspectral remote sensing for shallow waters. I. A semianalytical model. Appl. Opt. 1998, 37, 6329–6338. [Google Scholar] [CrossRef]
- Morel, A. Optical modeling of the upper ocean in relation to its biogenous matter content (case I waters). J. Geophys. Res. Ocean 1988, 93, 10749–10768. [Google Scholar] [CrossRef]
- Pope, R.M.; Fry, E.S. Absorption spectrum (380–700 nm) of pure water. II. Integrating cavity measurements. Appl. Opt. 1997, 36, 8710–8723. [Google Scholar] [CrossRef]
- Morel, A. Optical properties of pure water and pure sea water. Opt. Asp. Oceanogr. 1974, 1, 1–24. [Google Scholar]
- Churnside, J.H. Review of profiling oceanographic lidar. Opt. Eng. 2013, 53. [Google Scholar] [CrossRef]
- SAVITZKY, A. Smoothing and Differentiation of Data by Simplified Least Squares Procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
| Transmitter | |
| Wavelength | 532 nm and 486 nm |
| Pulse energy | 5.4 mJ (532 nm) and 2.7 mJ (486 nm) |
| Laser repetition rate | 100 Hz |
| Pulse width | 4 ns (532 nm) and 8.7 ns (486 nm) |
| Beam divergence | 2.4 mRad (532 nm) and 4.7 mRad (486 nm) |
| Receiver | |
| Telescope diameter | 200 mm |
| Maximal field of view | 25 mRad |
| Diameter of FOV spot size at the water surface | 50–75 m |
| Optical efficiency | 0.6 |
| Detector | PMT |
| Detector efficiency | 0.10 |
| Sampling time resolution | 1 ns |
| Plane height | 2000–3000 m |
| Plane speed | 200 km/h |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, K.; He, Y.; Ma, J.; Jiang, Z.; Hou, C.; Chen, W.; Zhu, X.; Chen, P.; Tang, J.; Wu, S.; et al. A Dual-Wavelength Ocean Lidar for Vertical Profiling of Oceanic Backscatter and Attenuation. Remote Sens. 2020, 12, 2844. https://doi.org/10.3390/rs12172844
Li K, He Y, Ma J, Jiang Z, Hou C, Chen W, Zhu X, Chen P, Tang J, Wu S, et al. A Dual-Wavelength Ocean Lidar for Vertical Profiling of Oceanic Backscatter and Attenuation. Remote Sensing. 2020; 12(17):2844. https://doi.org/10.3390/rs12172844
Chicago/Turabian StyleLi, Kaipeng, Yan He, Jian Ma, Zhengyang Jiang, Chunhe Hou, Weibiao Chen, Xiaolei Zhu, Peng Chen, Junwu Tang, Songhua Wu, and et al. 2020. "A Dual-Wavelength Ocean Lidar for Vertical Profiling of Oceanic Backscatter and Attenuation" Remote Sensing 12, no. 17: 2844. https://doi.org/10.3390/rs12172844
APA StyleLi, K., He, Y., Ma, J., Jiang, Z., Hou, C., Chen, W., Zhu, X., Chen, P., Tang, J., Wu, S., Liu, F., Luo, Y., Zhang, Y., & Chen, Y. (2020). A Dual-Wavelength Ocean Lidar for Vertical Profiling of Oceanic Backscatter and Attenuation. Remote Sensing, 12(17), 2844. https://doi.org/10.3390/rs12172844