Sensitivity of Altimeter Wave Height Assessment to Data Selection
Abstract
1. Introduction
2. Datasets
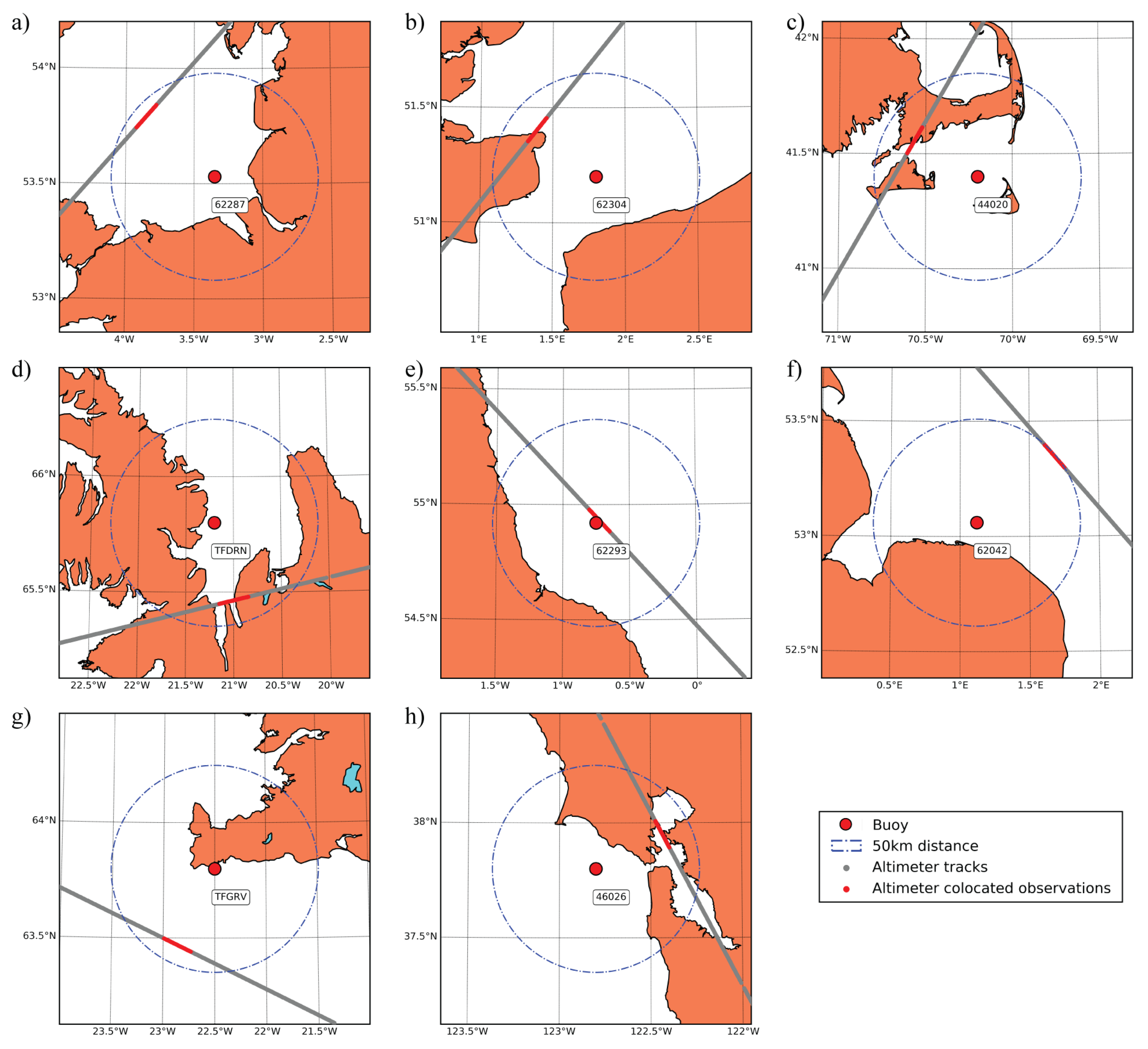
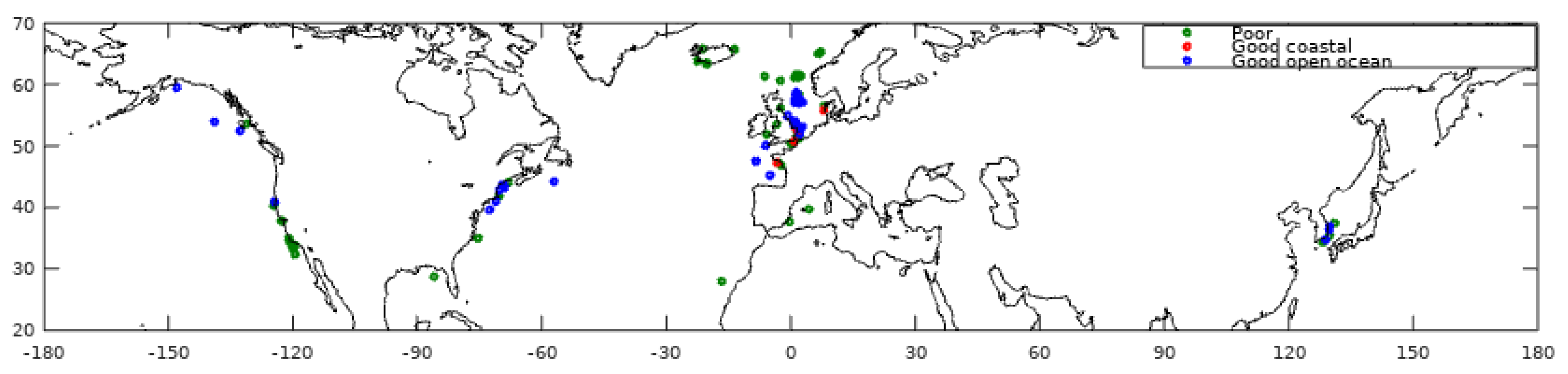
2.1. Buoy Data
2.2. Altimeter Data
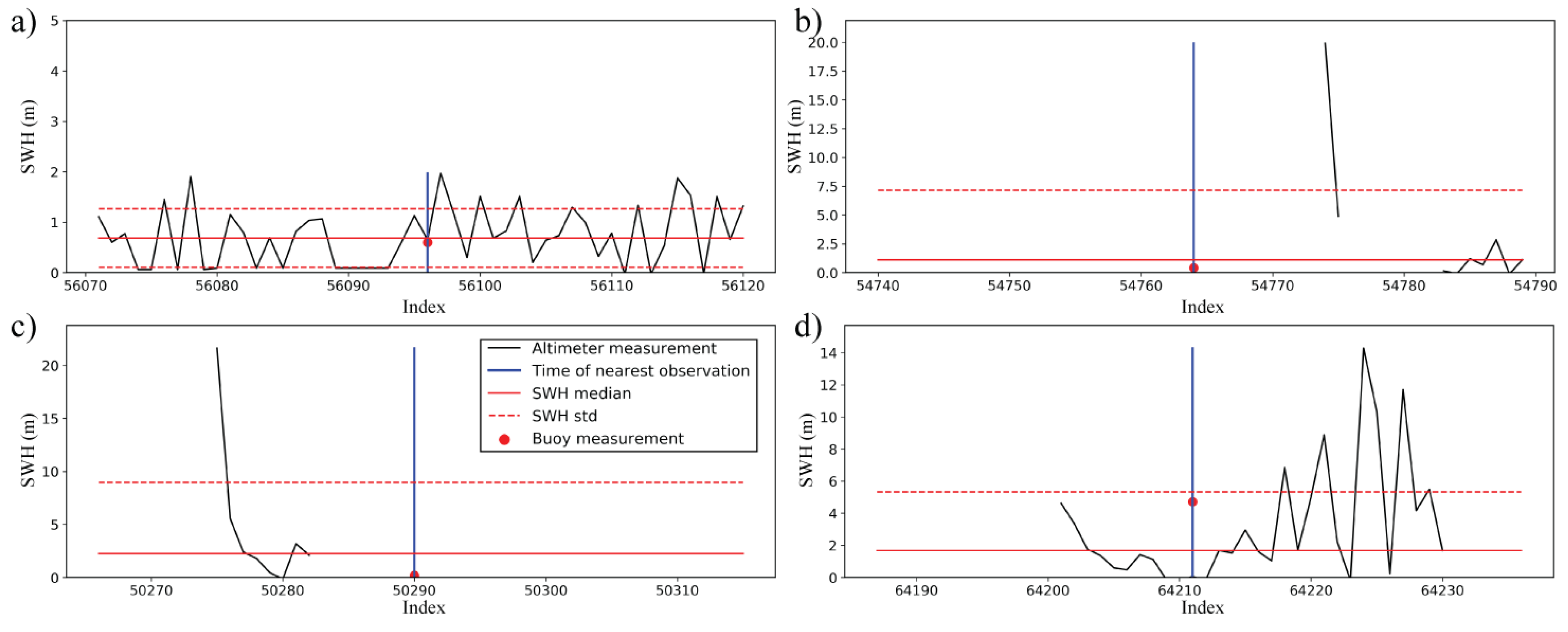
2.3. Data Match-Up
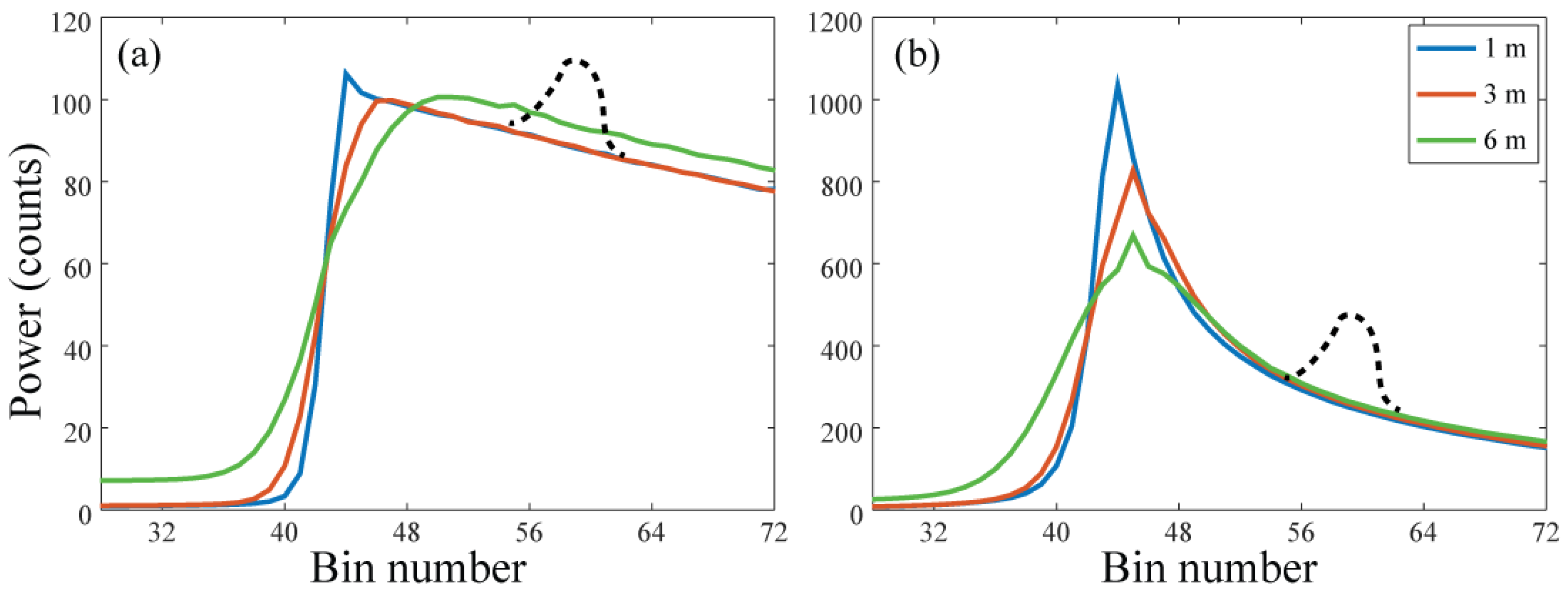
3. Factors Affecting Comparisons
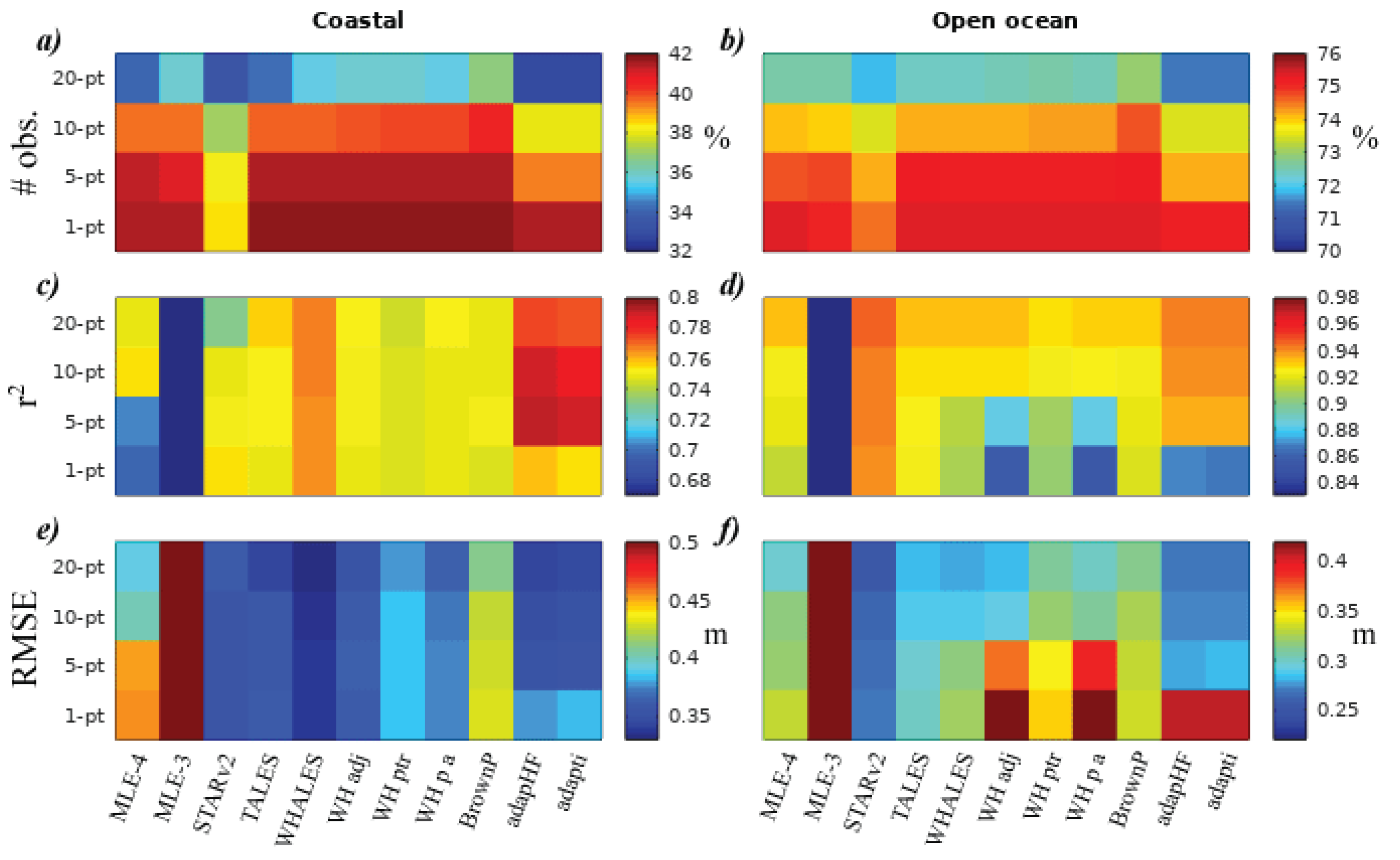
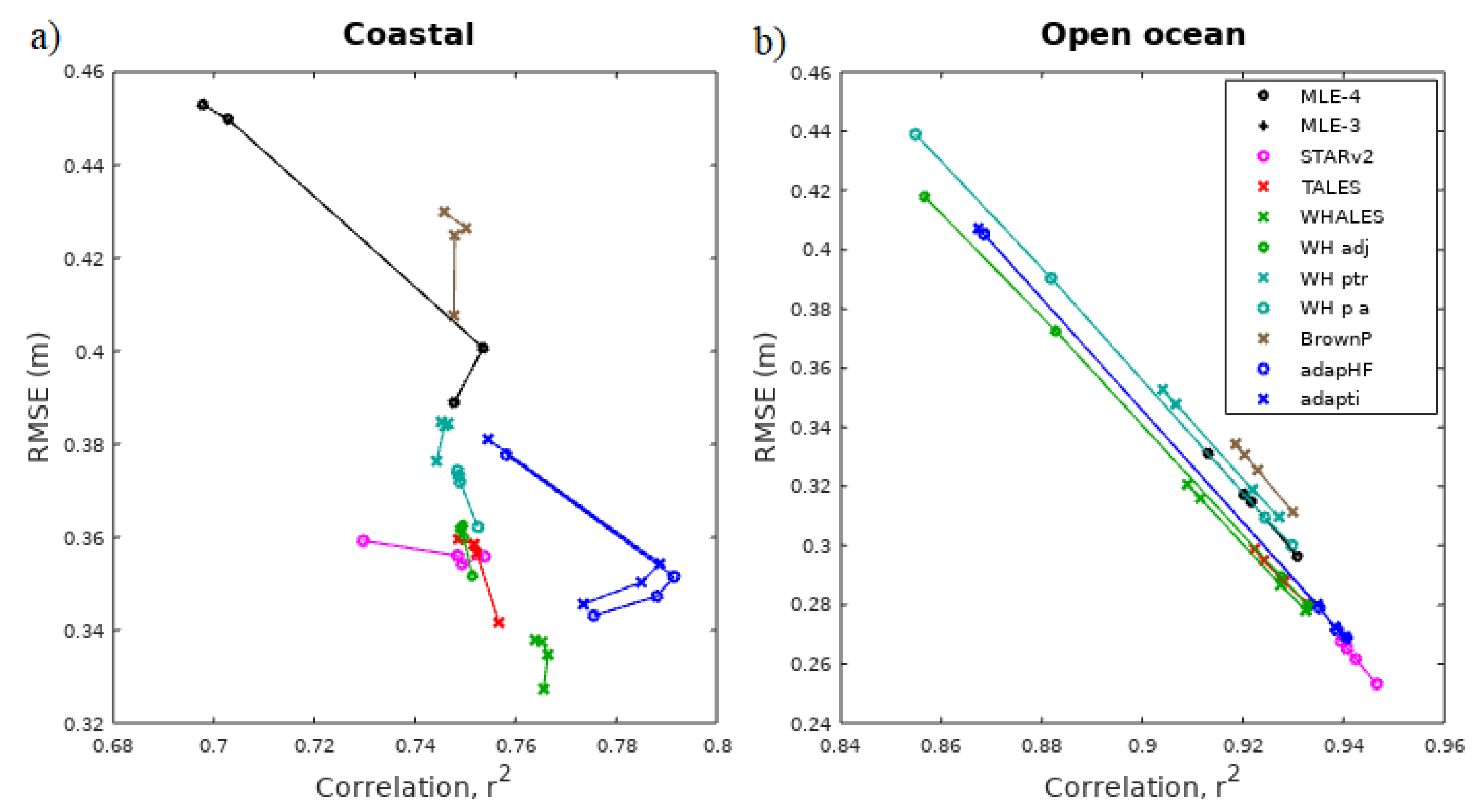
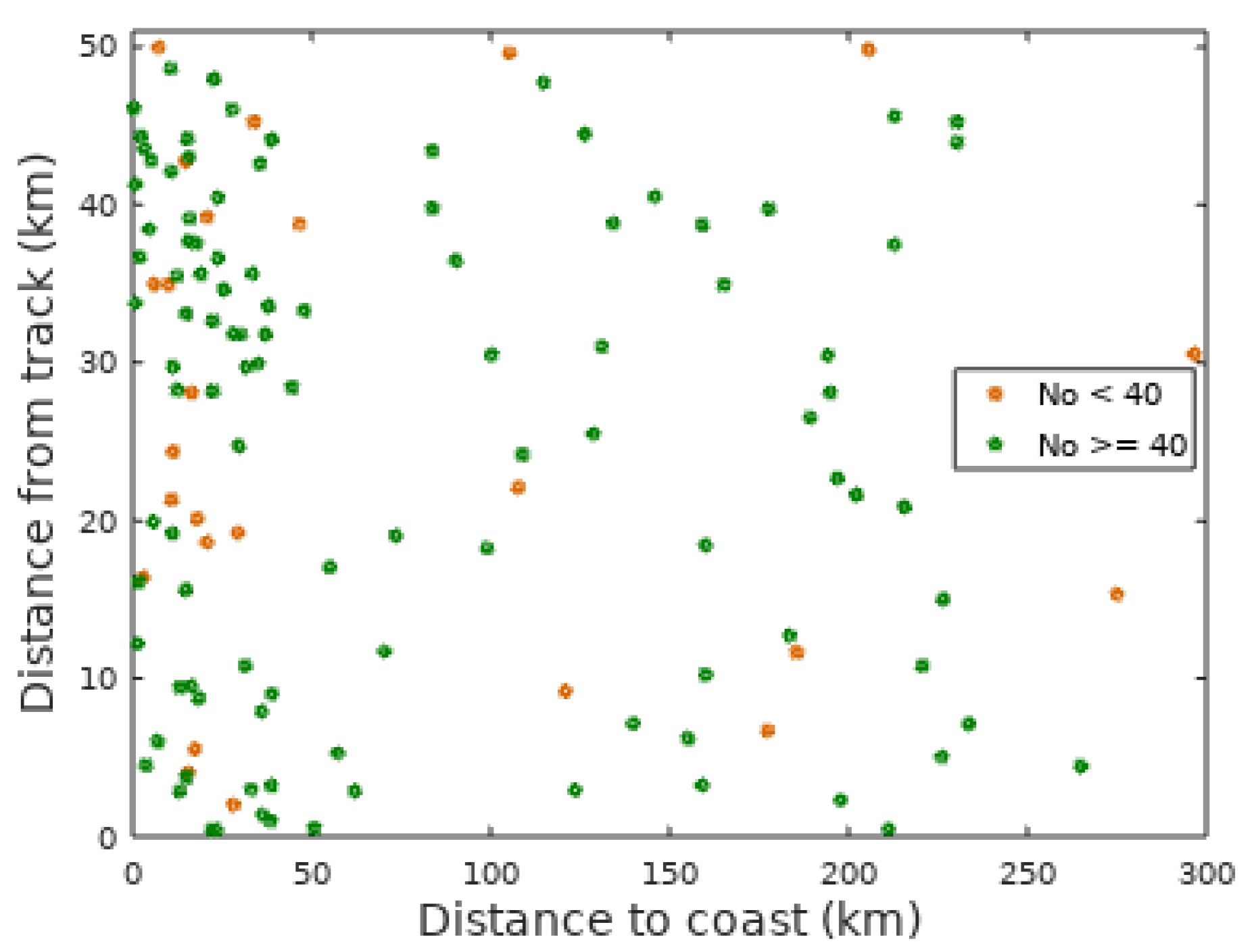
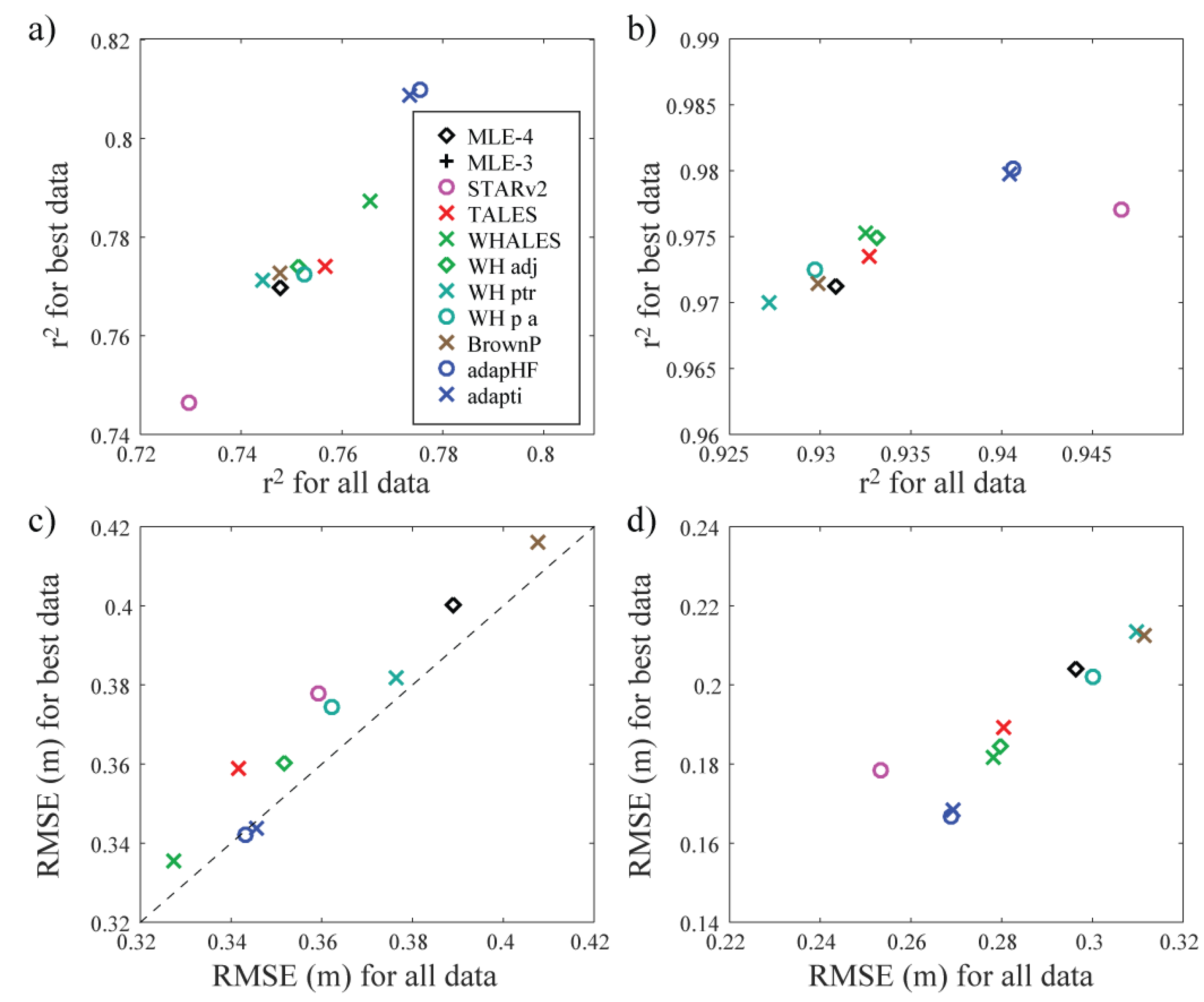
3.1. Effect of Changing Minimum No. of Match Ups
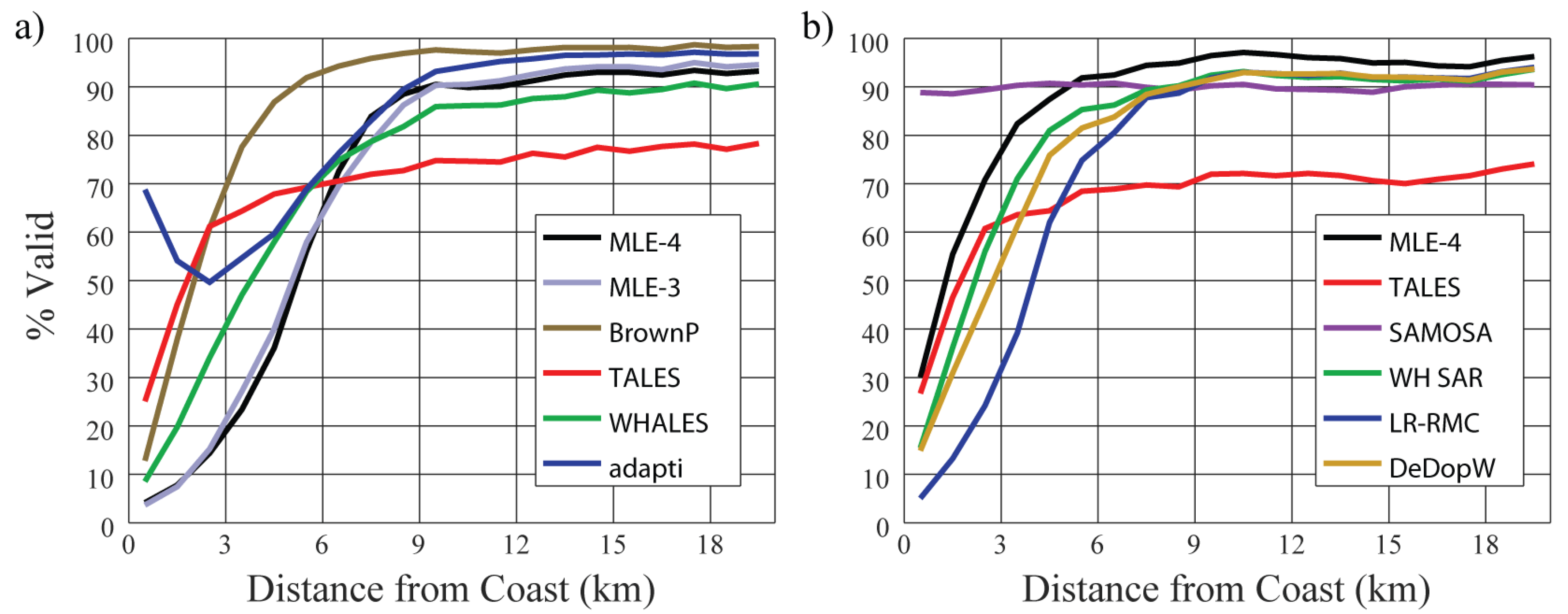
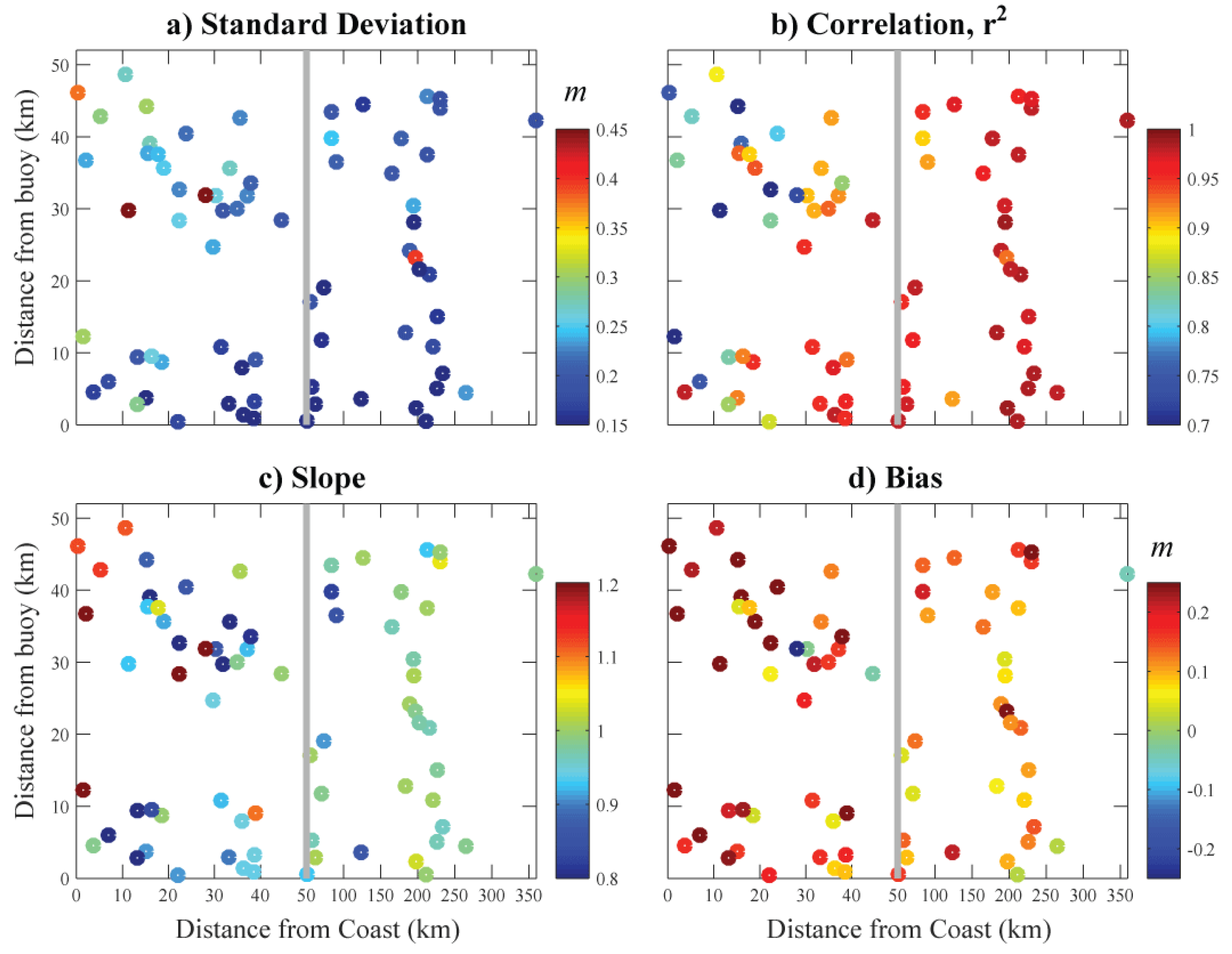
3.2. Automatic Selection of Best Buoys
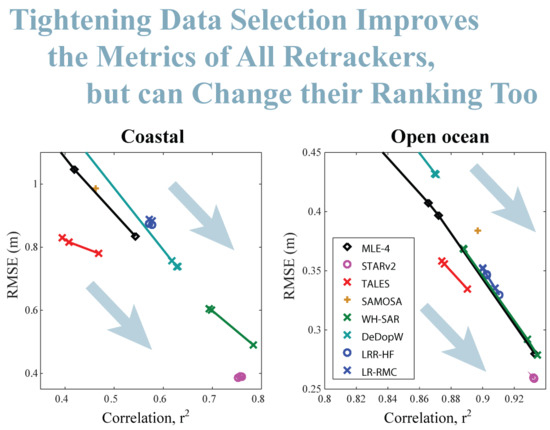
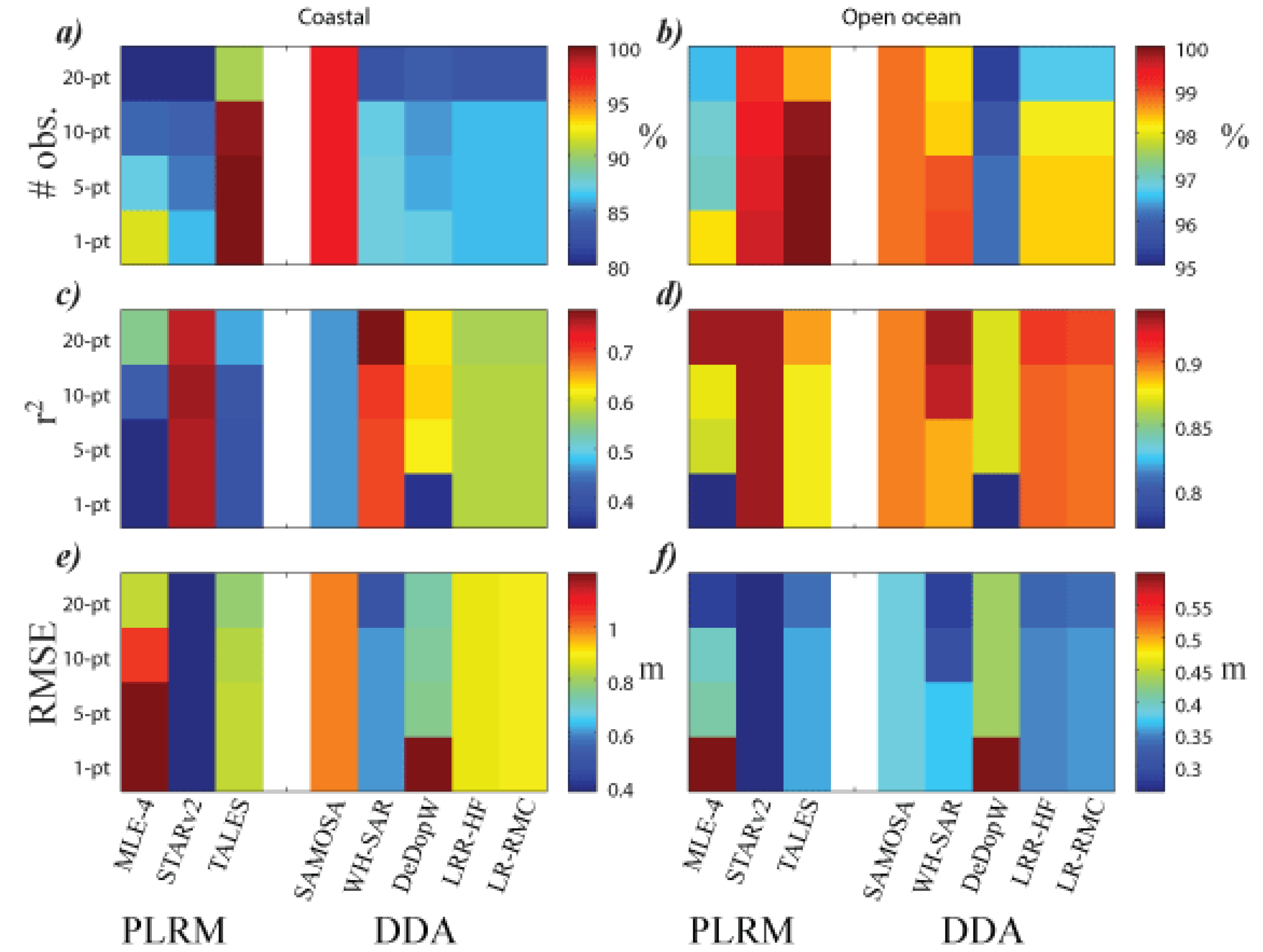
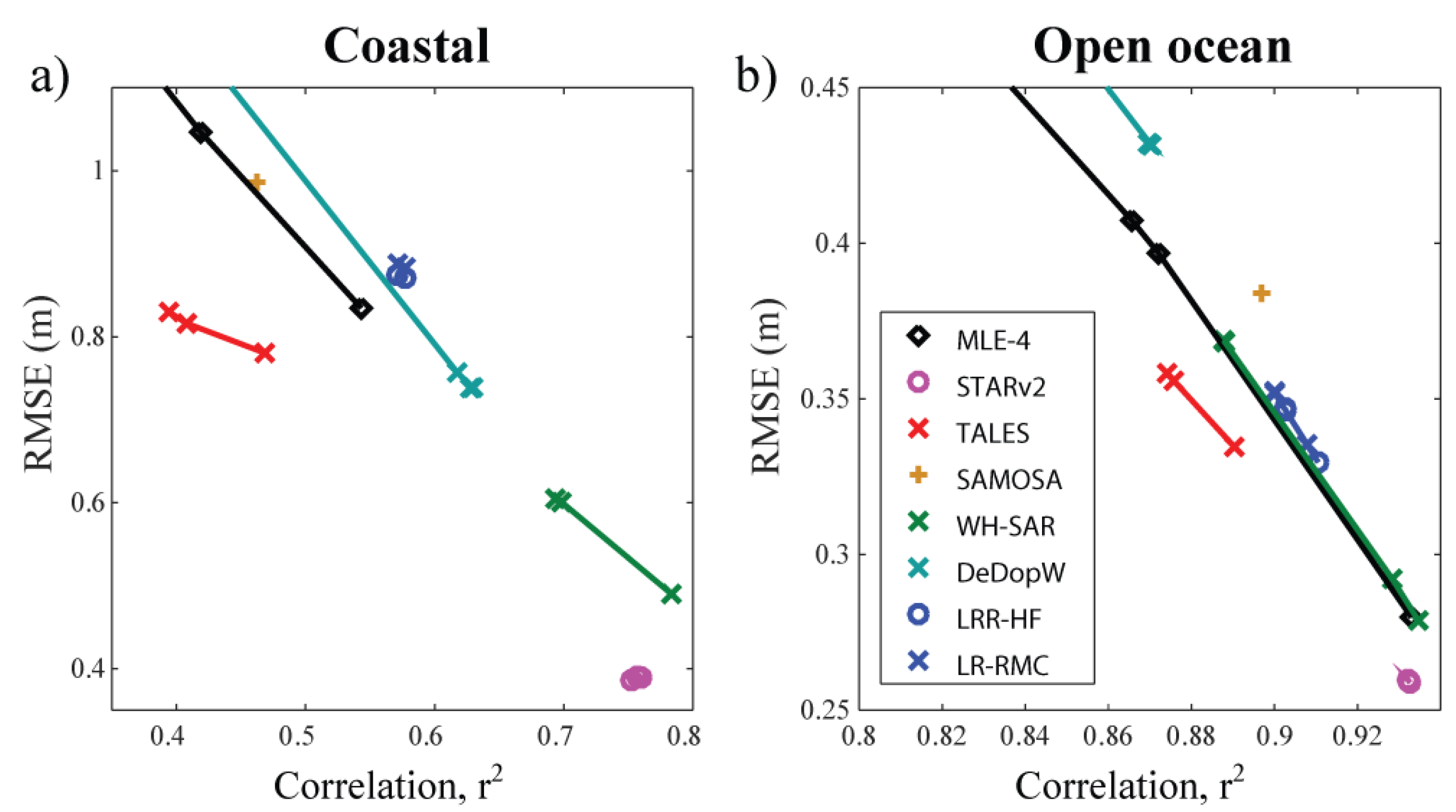
3.3. Effect on Assessment of Retrackers
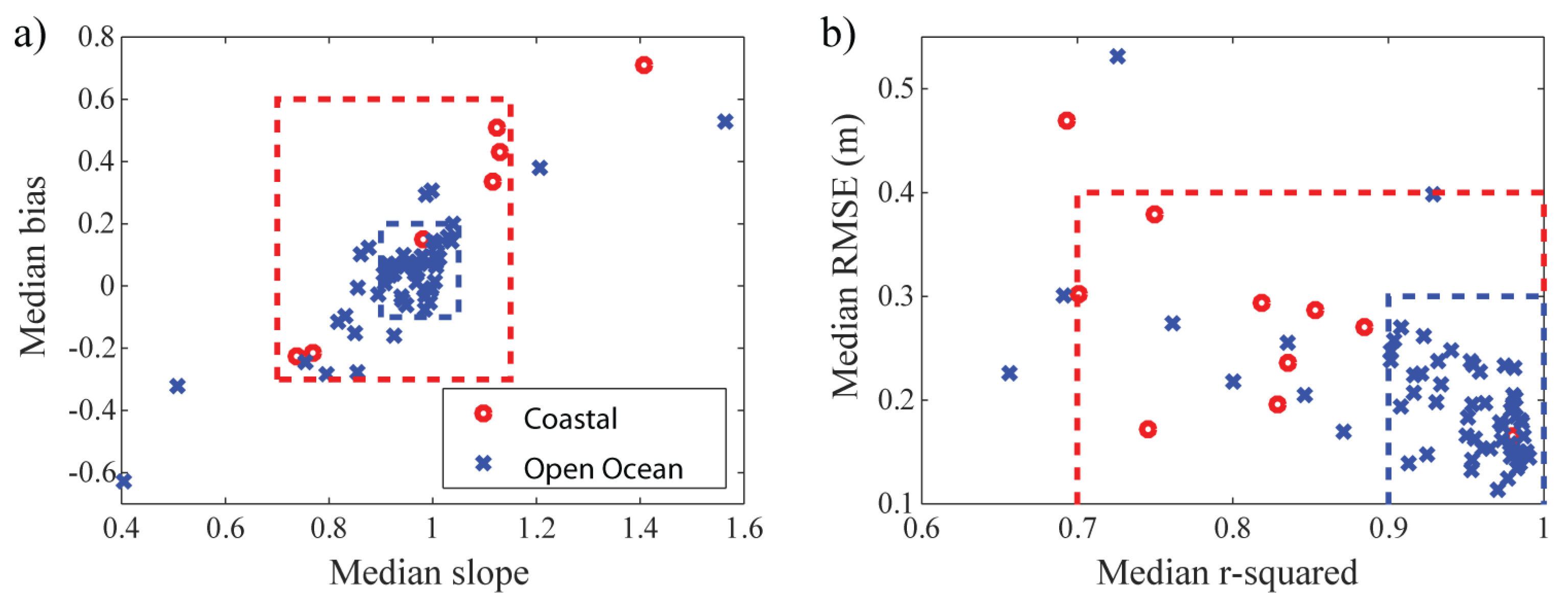
4. Summary and Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ALES | Adaptive Leading-Edge Subwaveform |
| CCI | Climate Change Initiative |
| DDA | Delay-Doppler Altimetry |
| ESA | European Space Agency |
| J3 | Jason-3 |
| LR-RMC | Low-Resolution with Range Migration Correction |
| LRM | Low Resolution Mode |
| MLE | Maximum Likelihood Estimator |
| PLRM | Pseudo Low Resolution Mode |
| RMSE | Root mean square error |
| S3A | Sentinel-3A |
| SAR | Synthetic Aperture Radar |
| S.D. | Standard Deviation |
| STAR | Spatio-Temporal Altimetry Retracking |
| SWH | Significant Wave Height |
References
- Global Climate Observing System. Systematic Observation Requirements for Satellite-Based Data Products for Climate (2011 Update). Available online: https://library.wmo.int/doc_num.php?explnum_id=3710 (accessed on 1 May 2020).
- Ardhuin, F.; Stopa, J.E.; Chapron, B.; Collard, F.; Husson, R.; Jensen, R.E.; Johannessen, J.; Mouche, A.; Passaro, M.; Quartly, G.D.; et al. Observing sea states. Front. Mar. Sci. 2019, 6, 124. [Google Scholar] [CrossRef]
- Young, I.R.; Ribal, A. Multiplatform evaluation of global trends in wind speed and wave height. Science 2019, 364, 548–552. [Google Scholar] [CrossRef] [PubMed]
- Dodet, G.; Piolle, J.F.; Quilfen, Y.; Abdalla, S.; Accensi, M.; Ardhuin, F.; Ash, E.; Bidlot, J.R.; Gommenginger, C.; Marechal, G.; et al. The Sea State CCI dataset v1: Towards a sea state climate data record based on satellite observations. Earth Syst. Sci. Data Discuss. 2020, 2020, 1–28. [Google Scholar] [CrossRef]
- Schlembach, F.; Passaro, M.; Quartly, G.D.; Kurekin, A.; Nencioli, F.; Dodet, G.; Piollé, J.F.; Ardhuin, F.; Bidlot, J.; Schwatke, C.; et al. Round robin assessment of radar altimeter Low Resolution Mode and delay-Doppler retracking algorithms for significant wave height. Remote Sens. 2020, 12, 1254. [Google Scholar] [CrossRef]
- Durrant, T.H.; Greenslade, D.J.M.; Simmonds, I. Validation of Jason-1 and Envisat remotely sensed wave heights. J. Atmos. Ocean. Technol. 2009, 26, 123–134. [Google Scholar] [CrossRef]
- Zieger, S.; Vinoth, J.; Young, I.R. Joint calibration of multiplatform altimeter measurements of wind speed and wave height over the past 20 years. J. Atmos. Ocean. Technol. 2009, 26, 2549–2564. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, J. Validation of Sentinel-3A/3B satellite altimetry wave heights with buoy and Jason-3 data. Sensors 2019, 19, 2914. [Google Scholar] [CrossRef]
- Gomez-Enri, J.; Vignudelli, S.; Quartly, G.D.; Gommenginger, C.P.; Cipollini, P.; Challenor, P.G.; Benveniste, J. Modeling Envisat RA-2 waveforms in the coastal zone: Case study of calm water contamination. IEEE Geosci. Remote Sens. Lett. 2010, 7, 474–478. [Google Scholar] [CrossRef]
- Wang, X.; Ichikawa, K. Coastal waveform retracking for Jason-2 altimeter data based on along-track echograms around the Tsushima Islands in Japan. Remote Sens. 2017, 9, 762. [Google Scholar] [CrossRef]
- ESA. Round Robin: Final Selection and Ranking of Algorithms. Available online: http://cci.esa.int/sites/default/files/Sea_State_cci_RR_Final_Selection_v1.1-signed.pdf (accessed on 3 July 2020).
- Queffeulou, P. Long-term validation of wave height measurements from altimeters. Mar. Geod. 2004, 27, 495–510. [Google Scholar] [CrossRef]
- Challenor, P.G.; Cotton, P.D. The Joint Calibration of Altimeter and In Situ Wave Heights. Advances in the Application of Marine Climatology. Available online: https://www.wmo.int/pages/prog/amp/mmop/documents/JCOMM-TR/J-TR-10-CLIMAR-99/Presentations/session_03/03.2_Challenor.pdf (accessed on 13 July 2020).
- Raney, R.K. The delay/Doppler radar altimeter. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1578–1588. [Google Scholar] [CrossRef]
- Quartly, G.D.; Nencioli, F.; Raynal, M.; Bonnefond, P.; Nilo Garcia, P.; Garcia-Mondéjar, A.; Flores de la Cruz, A.; Crétaux, J.F.; Taburet, N.; Frery, M.L.; et al. The roles of the S3MPC: Monitoring, validation and evolution of Sentinel-3 altimetry observations. Remote Sens. 2020, 12, 1763. [Google Scholar] [CrossRef]
- Amarouche, L.; Thibaut, P.; Zanife, O.Z.; Dumont, J.P.; Vincent, P.; Steunou, N. Improving the Jason-1 ground retracking to better account for attitude effects. Mar. Geod. 2004, 27, 171–197. [Google Scholar] [CrossRef]
- Passaro, M.; Cipollini, P.; Vignudelli, S.; Quartly, G.D.; Snaith, H.M. ALES: A multi-mission adaptive subwaveform retracker for coastal and open ocean altimetry. Remote Sens. Environ. 2014, 145, 173–189. [Google Scholar] [CrossRef]
- ESA. Algorithm Theoretical Basis Document. Available online: http://cci.esa.int/sites/default/files/Sea_State_cci_ATBD_v1.1-signed_0.pdf (accessed on 28 June 2020).
- Dinardo, S.; Fenoglio-Marc, L.; Buchhaupt, C.; Becker, M.; Scharroo, R.; Fernandes, M.J.; Benveniste, J. Coastal SAR and PLRM altimetry in German Bight and West Baltic Sea. Adv. Space Res. 2018, 62, 1371–1404. [Google Scholar] [CrossRef]
- Peng, F.; Deng, X. A new retracking technique for Brown Peaky altimetric waveforms. Mar. Geod. 2018, 41, 99–125. [Google Scholar] [CrossRef]
- Peng, F.; Deng, X. Validation of improved significant wave heights from the Brown-Peaky (BP) retracker along the east coast of Australia. Remote Sens. 2018, 10, 1072. [Google Scholar] [CrossRef]
- Poisson, J.; Quartly, G.D.; Kurekin, A.A.; Thibaut, P.; Hoang, D.; Nencioli, F. Development of an ENVISAT altimetry processor providing sea level continuity between open ocean and Arctic leads. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5299–5319. [Google Scholar] [CrossRef]
- Sandwell, D.T.; Smith, W.H.F. Retracking ERS-1 altimeter waveforms for optimal gravity field recovery. Geophys. J. Int. 2005, 163, 79–89. [Google Scholar] [CrossRef]
- Quartly, G.D. Removal of covariant errors from altimetric wave height data. Remote Sens. 2019, 11, 2319. [Google Scholar] [CrossRef]
- Roscher, R.; Uebbing, B.; Kusche, J. STAR: Spatio-temporal altimeter waveform retracking using sparse representation and conditional random fields. Remote Sens. Environ. 2017, 201, 148–164. [Google Scholar] [CrossRef]
- Ray, C.; Martin-Puig, C.; Clarizia, M.P.; Ruffini, G.; Dinardo, S.; Gommenginger, C.; Benveniste, J. SAR altimeter backscattered waveform model. IEEE Trans. Geosci. Remote Sens. 2015, 53, 911–919. [Google Scholar] [CrossRef]
- Moreau, T.; Tran, N.; Aublanc, J.; Tison, C.; Le Gac, S.; Boy, F. Impact of long ocean waves on wave height retrieval from SAR altimetry data. Adv. Space Res. 2018, 62, 1434–1444. [Google Scholar] [CrossRef]
- Makhoul, E.; Roca, M.; Ray, C.; Escolà, R.; Garcia-Mondéjar, A. Evaluation of the precision of different delay-Doppler processor (DDP) algorithms using CryoSat-2 data over open ocean. Adv. Space Res. 2018, 62, 1464–1478. [Google Scholar] [CrossRef]
- Monaldo, F. Expected differences between buoy and radar altimeter estimates of wind speed and significant wave height and their implications on buoy-altimeter comparisons. J. Geophys. Res. Ocean. 1988, 93, 2285–2302. [Google Scholar] [CrossRef]
- Nencioli, F.; Quartly, G.D. Evaluation of Sentinel-3A wave height observations near the coast of southwest England. Remote Sens. 2019, 11, 2998. [Google Scholar] [CrossRef]
- Passaro, M.; Fenoglio-Marc, L.; Cipollini, P. Validation of significant wave height from improved satellite altimetry in the German Bight. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2146–2156. [Google Scholar] [CrossRef]
- Guymer, T.H.; Quartly, G.D.; Srokosz, M.A. The effects of rain on ERS-1 radar altimeter data. J. Atmos. Ocean. Technol. 1995, 12, 1229–1247. [Google Scholar] [CrossRef]
- Janssen, P.A.E.; Abdalla, S.; Hersbach, H.; Bidlot, J.-R. Error estimation of buoy, satellite, and model wave height data. J. Atmos. Ocean. Technol. 2007, 24, 1665–1677. [Google Scholar] [CrossRef]
| Short Name | Waveform | Data | Brief Description | |
|---|---|---|---|---|
| Type | Source | |||
| 1 | MLE-4 | LRM | J3, S3A | Maximum Likelihood Estimator for 4 unknowns |
| 2 | MLE-3 | LRM | J3 | Maximum Likelihood Estimator for 3 unknowns |
| 3 | STARv2 | LRM | J3, S3A | Finds best route through a cloud of subwaveform solutions |
| 4 | TALES | LRM | J3, S3A | TU-Darmstadt version of ALES retracker |
| 5 | WHALES | LRM | J3 | Wave Height optimised version of ALES retracker |
| 6 | WH adj | LRM | J3 | WHALES output adjusted for variations in estimated range |
| 7 | WH ptr | LRM | J3 | WHALES output corrected for real PTR |
| 8 | WH p aj | LRM | J3 | WHALES output corrected for real PTR and variations in estimated range |
| 9 | BrownP | LRM | J3 | Brown-Peaky: discards data around spurious peaks and fits Brown model |
| 10 | adapti | LRM | J3 | Adaptive waveform fitting, using numerical description of real PTR |
| 11 | adapHF | LRM | J3 | adapti adjusted for variations in estimated range |
| 12 | SAMOSA | SAR | S3A | Default algorithm for S3A DDA waveforms |
| 13 | WH-SAR | SAR | S3A | Adaption of WHALES approach for SAR waveforms |
| 14 | DWaver | SAR | S3A | Implementation of Level 1B processing using DeDop toolbox |
| 15 | LR-RMC | SAR | S3A | Range Migration Correction and Compression + numerical retracking |
| 16 | LR-RHF | SAR | S3A | LR-RMC output adjusted for variations in estimated range |
| Retracker | All Coastal | Best Coastal | All Open Ocean | Best Open Ocean |
|---|---|---|---|---|
| MLE-4 | 0.748 | 0.770 | 0.931 | 0.971 |
| MLE-3 | 0.547 | 0.583 | 0.790 | 0.859 |
| STARv2 | 0.730 | 0.746 | 0.947 | 0.977 |
| TALES | 0.757 | 0.774 | 0.933 | 0.974 |
| WHALES | 0.766 | 0.787 | 0.933 | 0.975 |
| WH adj | 0.751 | 0.774 | 0.933 | 0.975 |
| WH ptr | 0.744 | 0.771 | 0.927 | 0.970 |
| WH p a | 0.753 | 0.772 | 0.930 | 0.972 |
| BrownP | 0.748 | 0.773 | 0.930 | 0.971 |
| adapHF | 0.775 | 0.810 | 0.941 | 0.980 |
| adapti | 0.773 | 0.809 | 0.940 | 0.980 |
| RMSE (m) | ||||
| Retracker | All Coastal | Best Coastal | All Open Ocean | Best Open Ocean |
| MLE-4 | 0.389 | 0.400 | 0.296 | 0.204 |
| MLE-3 | 0.564 | 0.567 | 0.547 | 0.471 |
| STARv2 | 0.359 | 0.378 | 0.253 | 0.178 |
| TALES | 0.342 | 0.359 | 0.280 | 0.189 |
| WHALES | 0.327 | 0.336 | 0.278 | 0.182 |
| WH adj | 0.352 | 0.360 | 0.280 | 0.185 |
| WH ptr | 0.376 | 0.382 | 0.310 | 0.213 |
| WH p a | 0.362 | 0.374 | 0.300 | 0.202 |
| BrownP | 0.408 | 0.416 | 0.311 | 0.213 |
| adapHF | 0.343 | 0.342 | 0.269 | 0.167 |
| adapti | 0.346 | 0.344 | 0.269 | 0.168 |
| Retracker | All Coastal | Best Coastal | All Open Ocean | Best Open Ocean |
|---|---|---|---|---|
| MLE-4 | 0.612 | 0.902 | 0.934 | 0.961 |
| STARv2 | 0.752 | 0.896 | 0.932 | 0.957 |
| TALES | 0.468 | 0.904 | 0.890 | 0.962 |
| WH-SAR | 0.783 | 0.915 | 0.935 | 0.966 |
| DeDopW | 0.627 | 0.901 | 0.870 | 0.963 |
| LR-HF | 0.571 | 0.925 | 0.911 | 0.953 |
| LR-RMC | 0.571 | 0.923 | 0.908 | 0.951 |
| RMSE (m) | ||||
| Retracker | All Coastal | Best Coastal | All Open Ocean | Best Open Ocean |
| MLE-4 | 0.768 | 0.274 | 0.276 | 0.215 |
| STARv2 | 0.386 | 0.232 | 0.259 | 0.210 |
| TALES | 0.780 | 0.241 | 0.335 | 0.198 |
| WH-SAR | 0.490 | 0.239 | 0.279 | 0.203 |
| DeDopW | 0.738 | 0.276 | 0.432 | 0.231 |
| LR-HF | 0.875 | 0.238 | 0.330 | 0.241 |
| LR-RMC | 0.888 | 0.243 | 0.335 | 0.249 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quartly, G.D.; Kurekin, A.A. Sensitivity of Altimeter Wave Height Assessment to Data Selection. Remote Sens. 2020, 12, 2608. https://doi.org/10.3390/rs12162608
Quartly GD, Kurekin AA. Sensitivity of Altimeter Wave Height Assessment to Data Selection. Remote Sensing. 2020; 12(16):2608. https://doi.org/10.3390/rs12162608
Chicago/Turabian StyleQuartly, Graham D., and Andrey A. Kurekin. 2020. "Sensitivity of Altimeter Wave Height Assessment to Data Selection" Remote Sensing 12, no. 16: 2608. https://doi.org/10.3390/rs12162608
APA StyleQuartly, G. D., & Kurekin, A. A. (2020). Sensitivity of Altimeter Wave Height Assessment to Data Selection. Remote Sensing, 12(16), 2608. https://doi.org/10.3390/rs12162608