Modeling and Analysis of an Echo Laser Pulse Waveform for the Orientation Determination of Space Debris
Abstract
1. Introduction
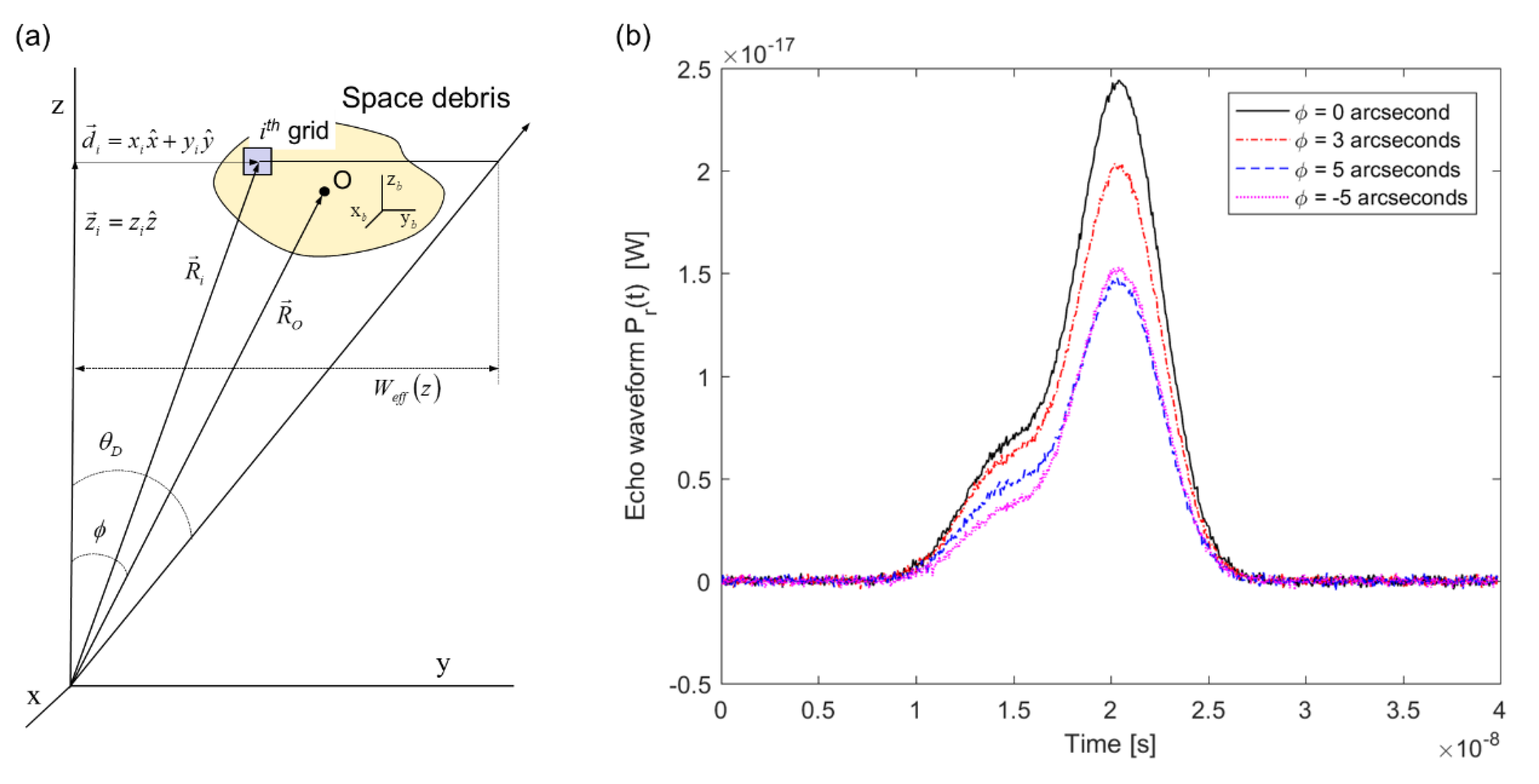
2. Mathematical Model
2.1. Echo Laser Pulse Waveform
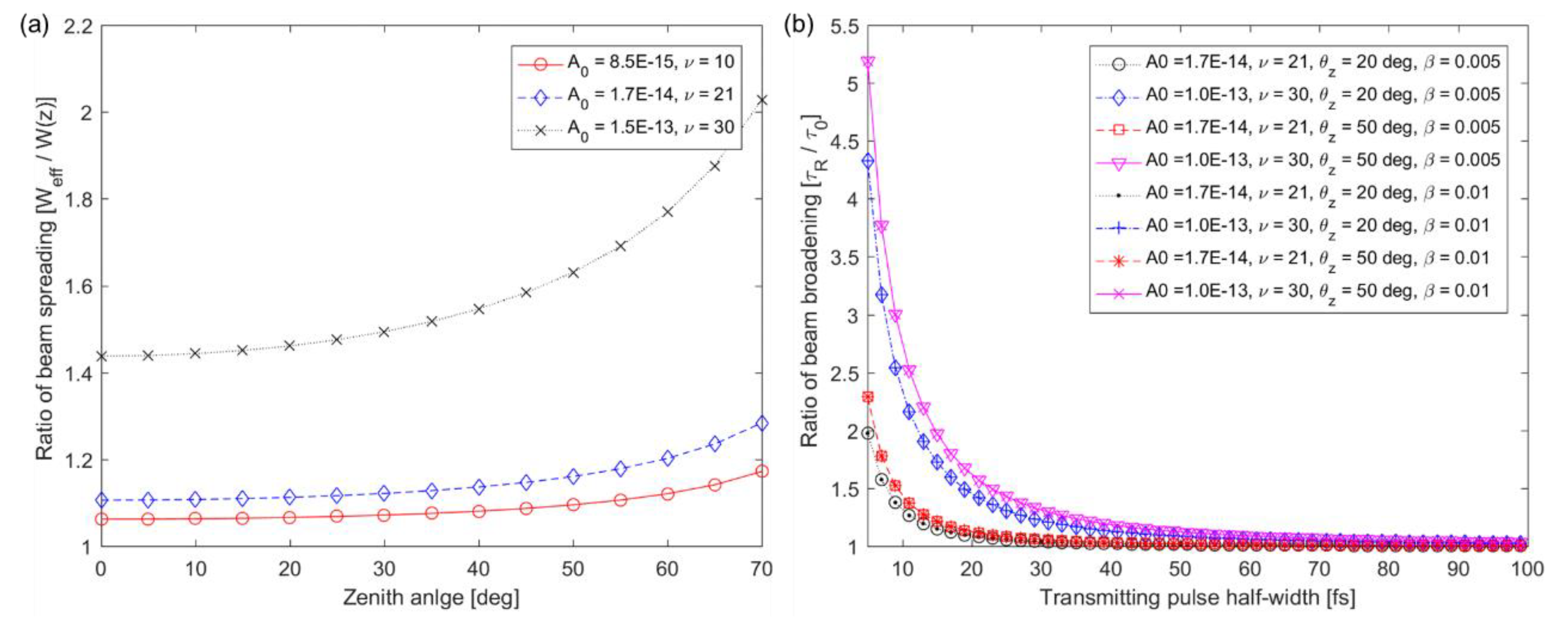
2.2. Laser Beam Spreading and Broadening
2.3. Noise Equivalent Power
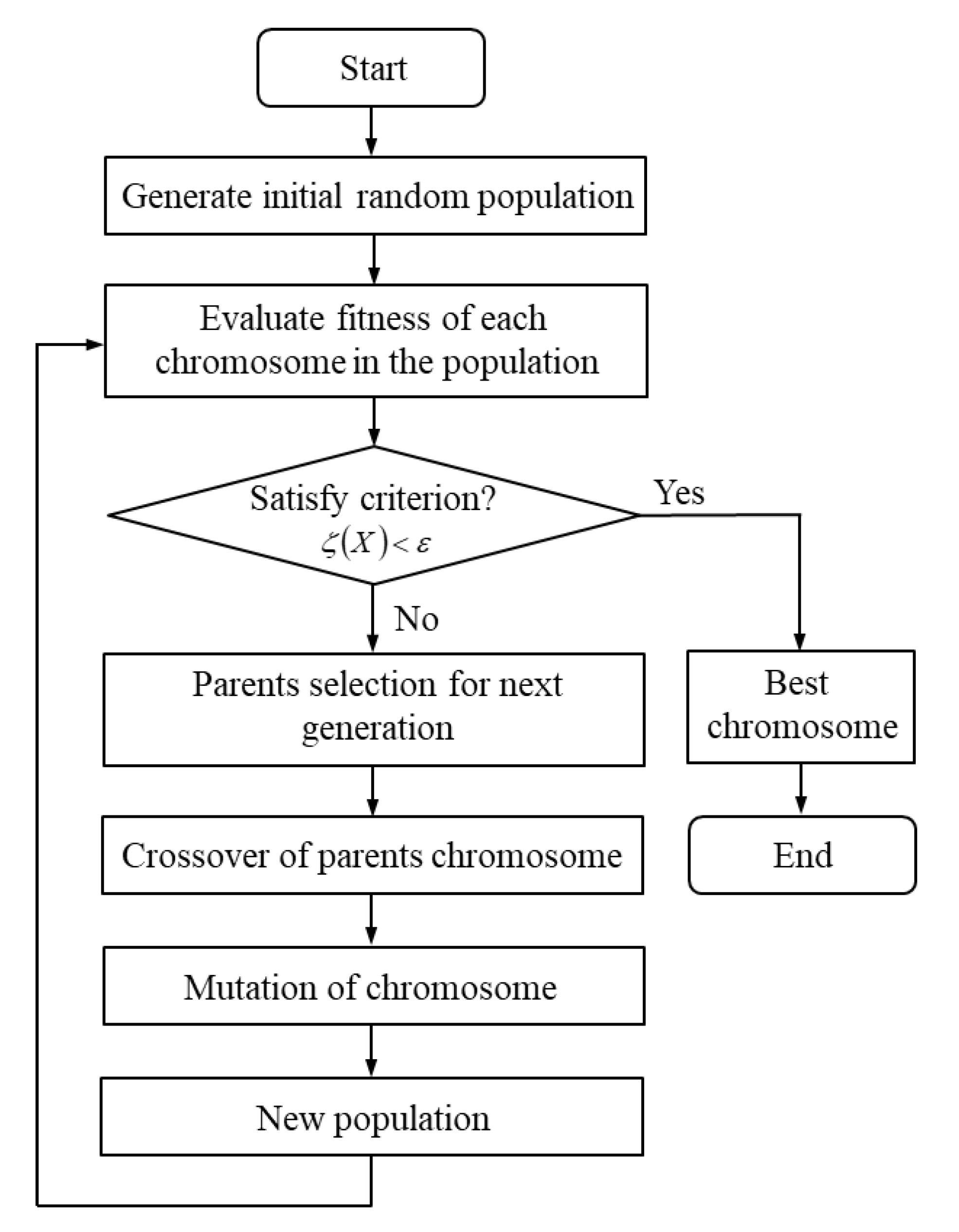
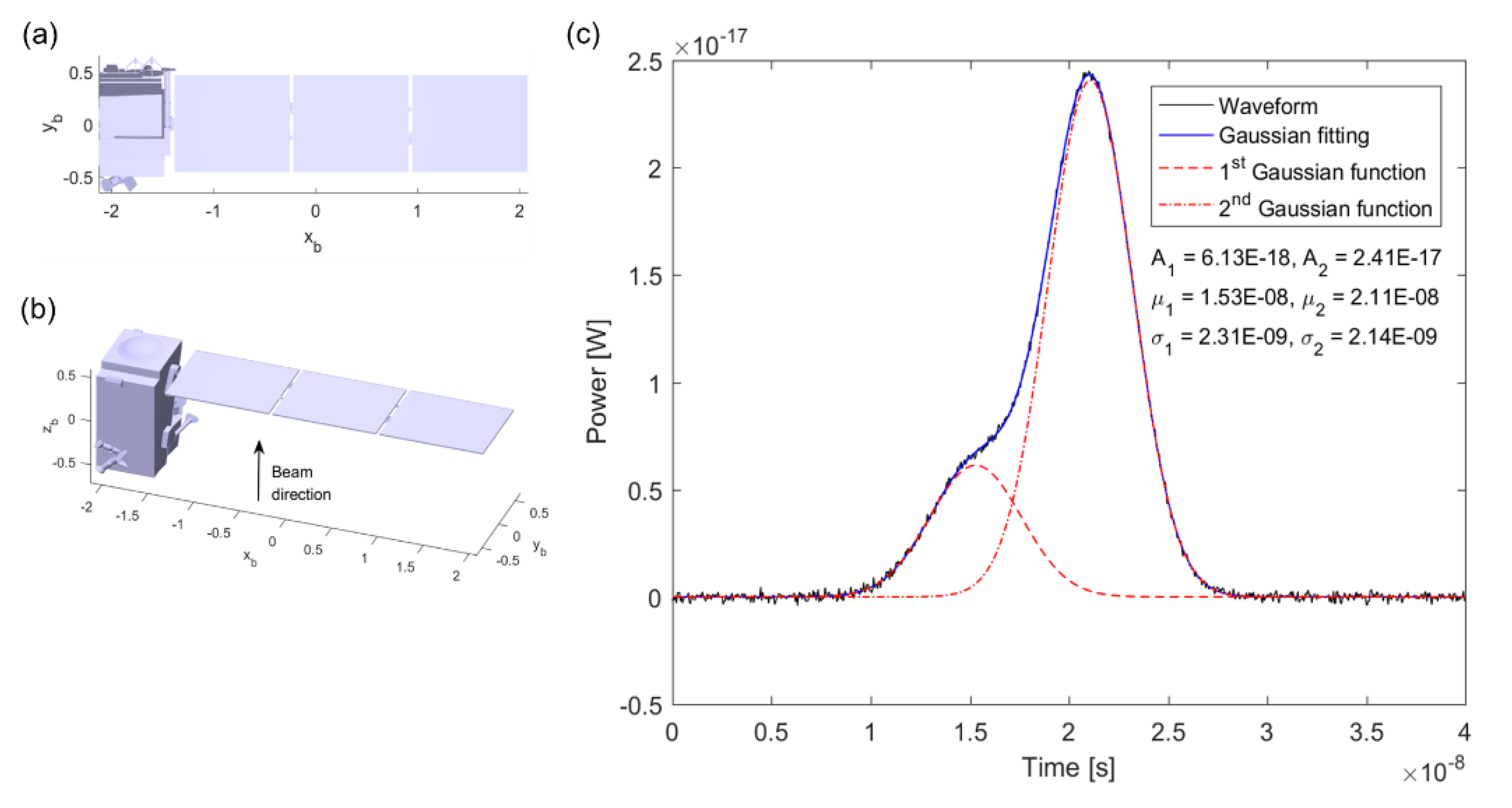
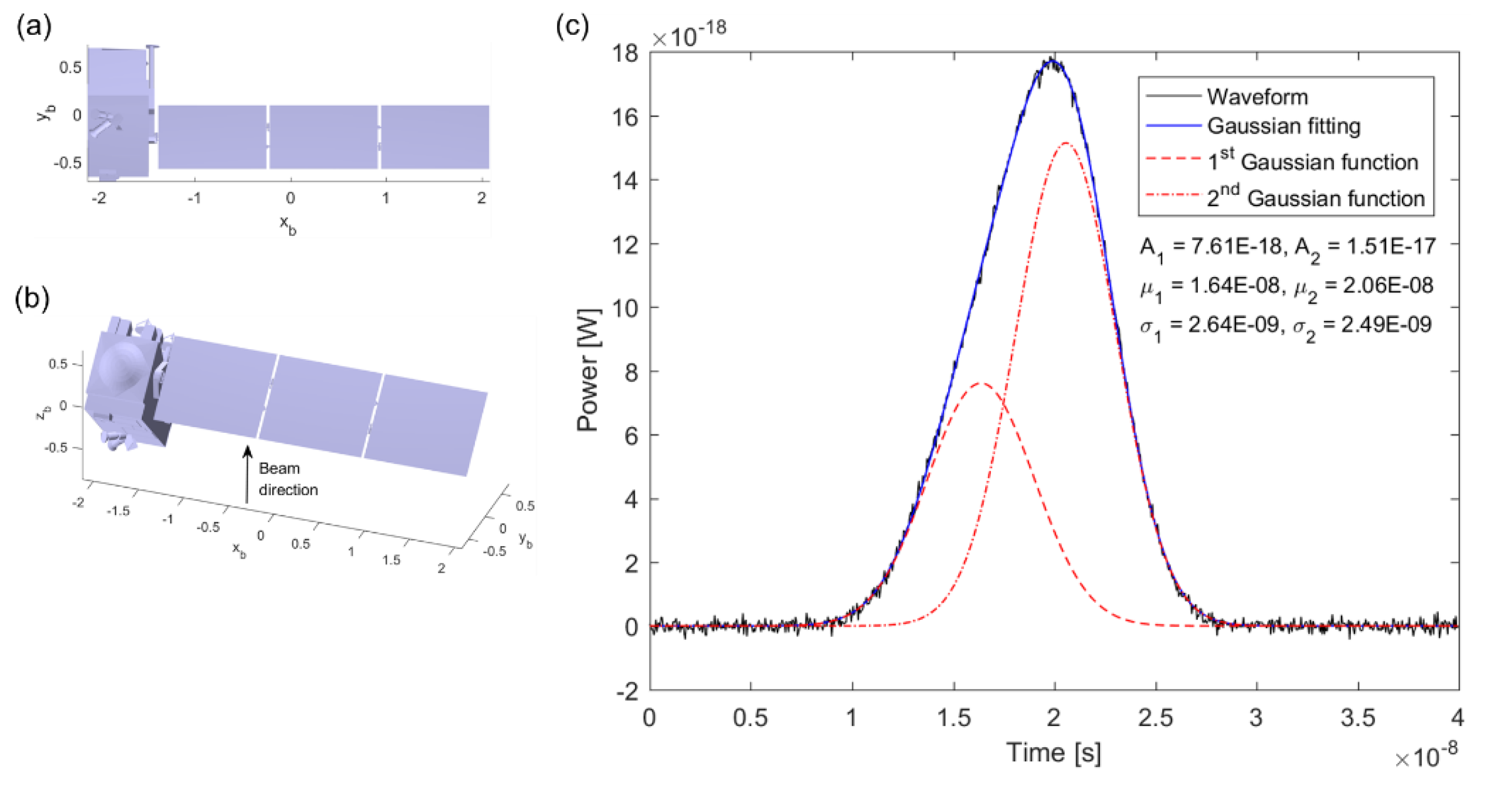
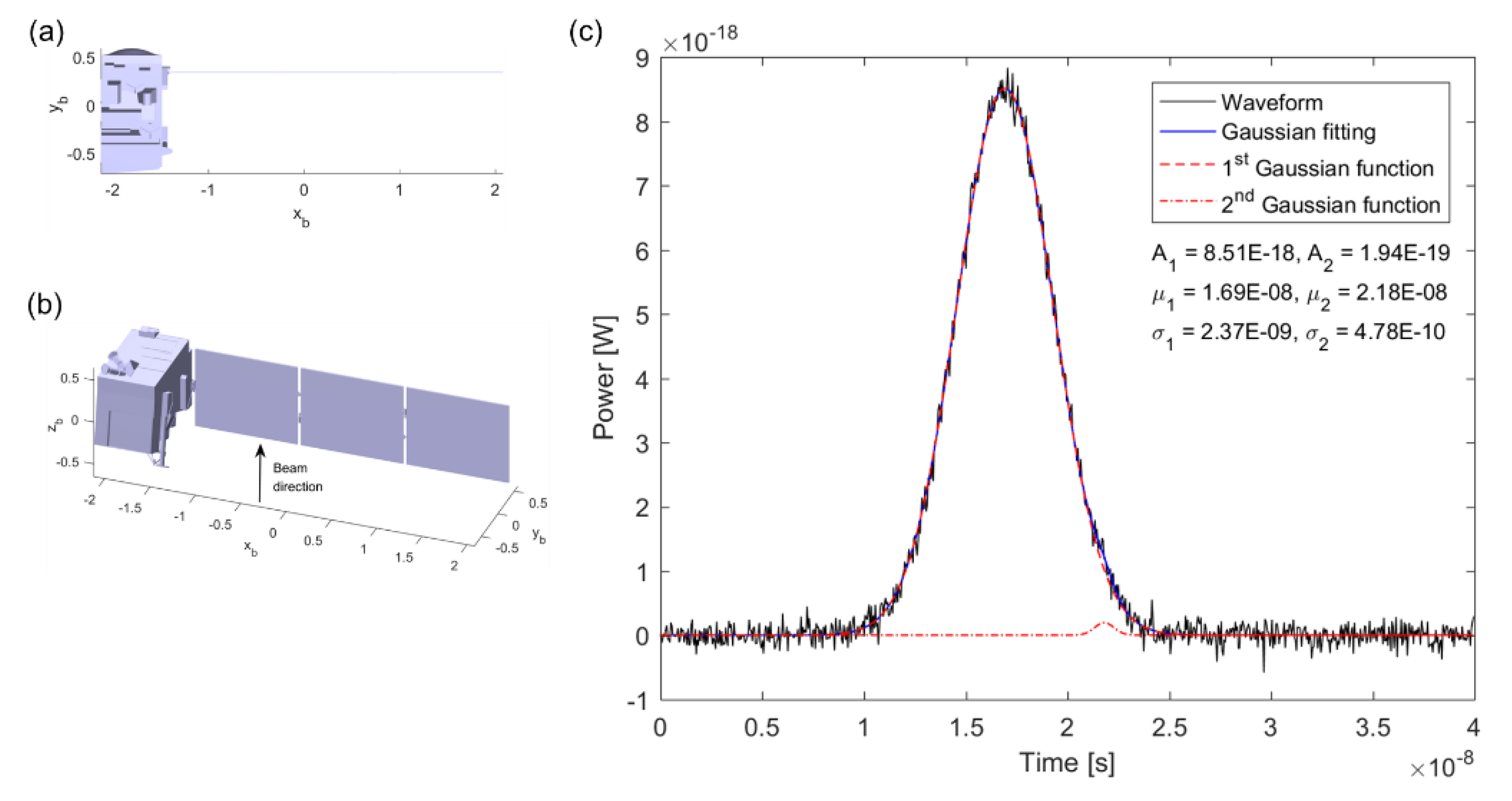
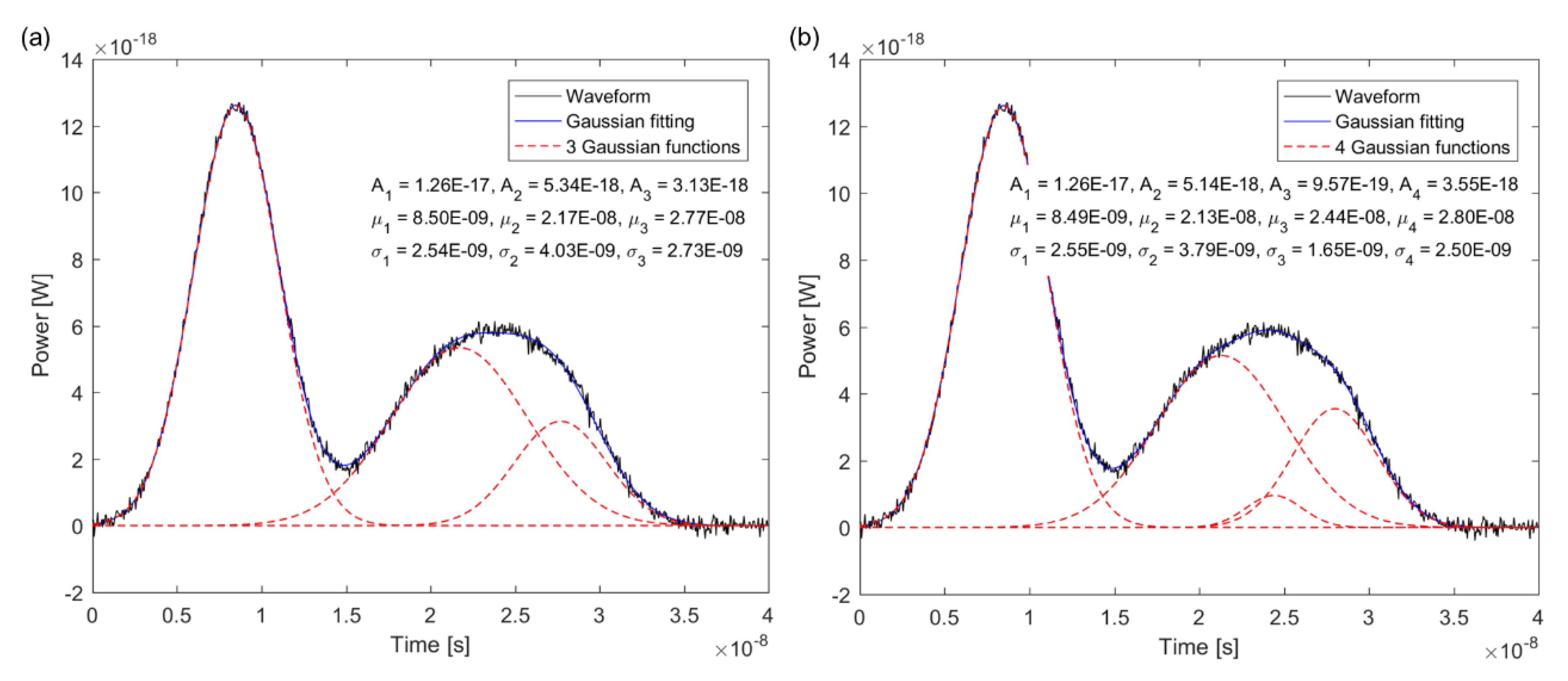
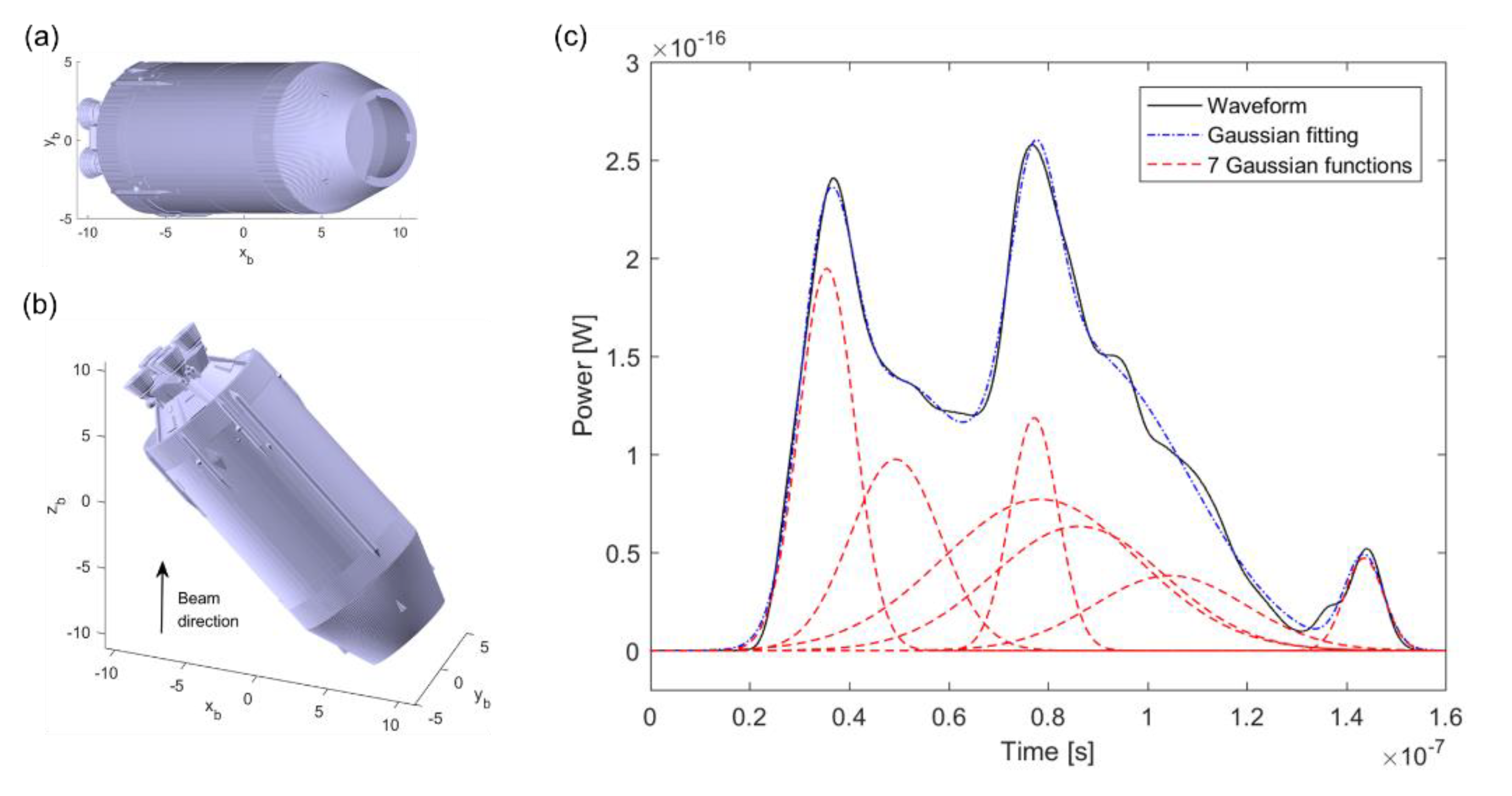
3. Genetic Algorithm for Gaussian Decomposition
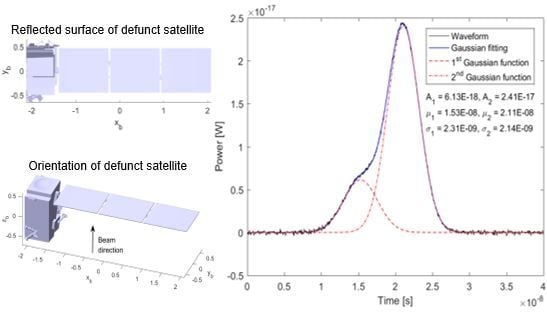
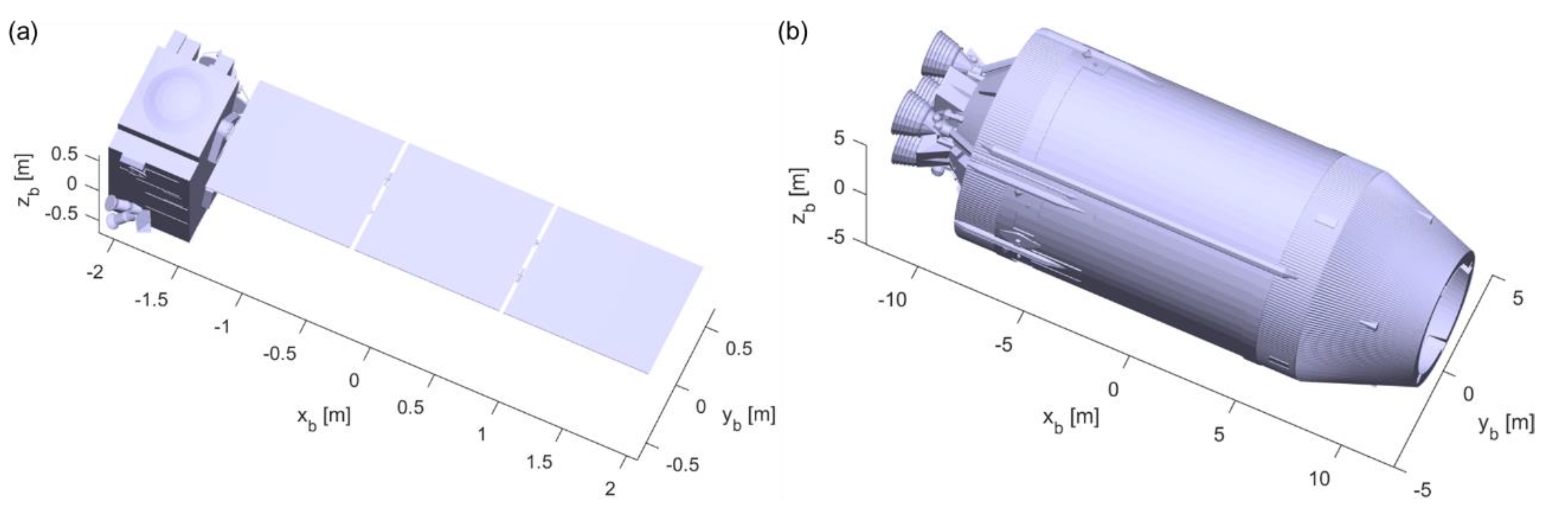
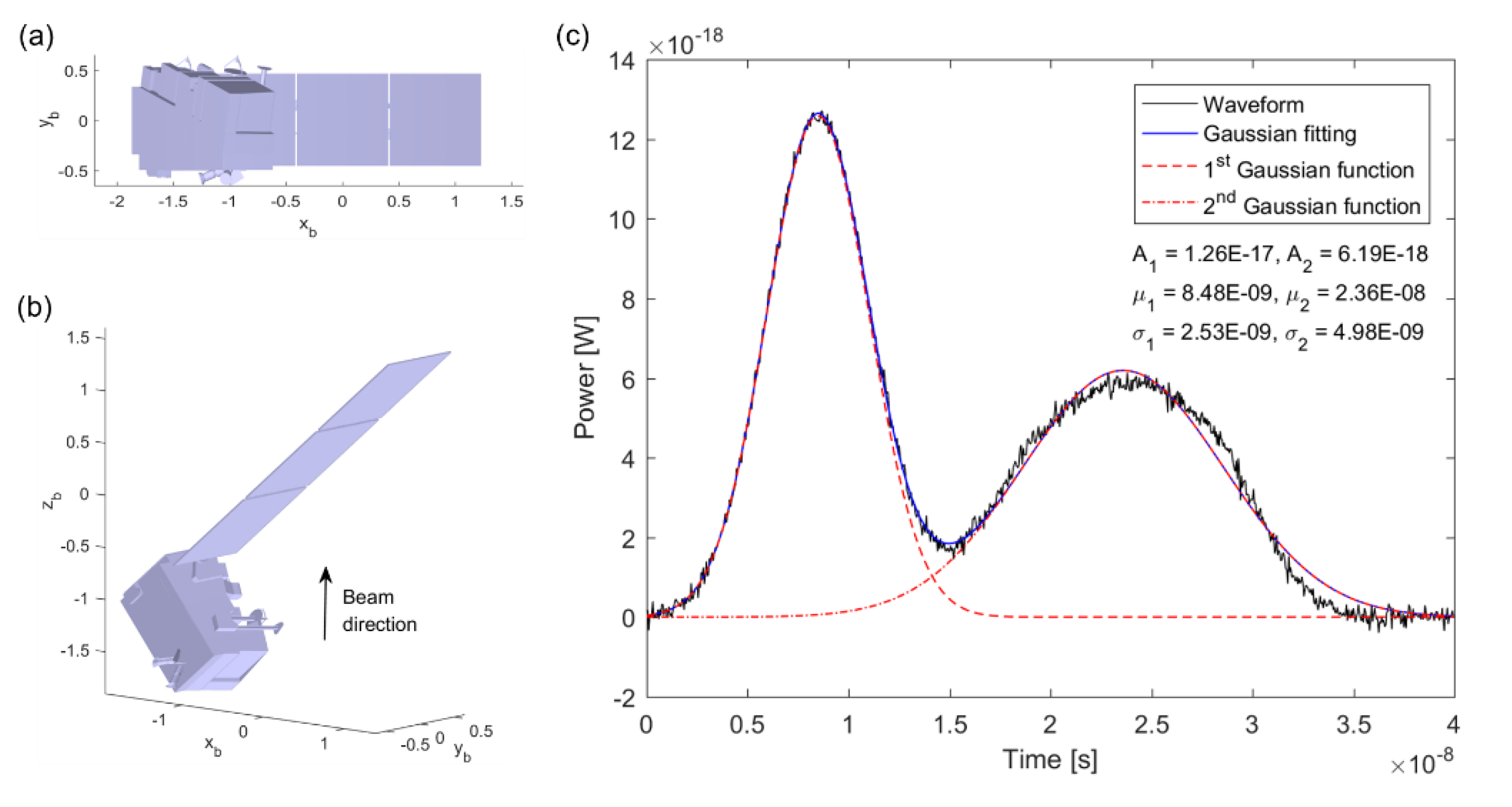
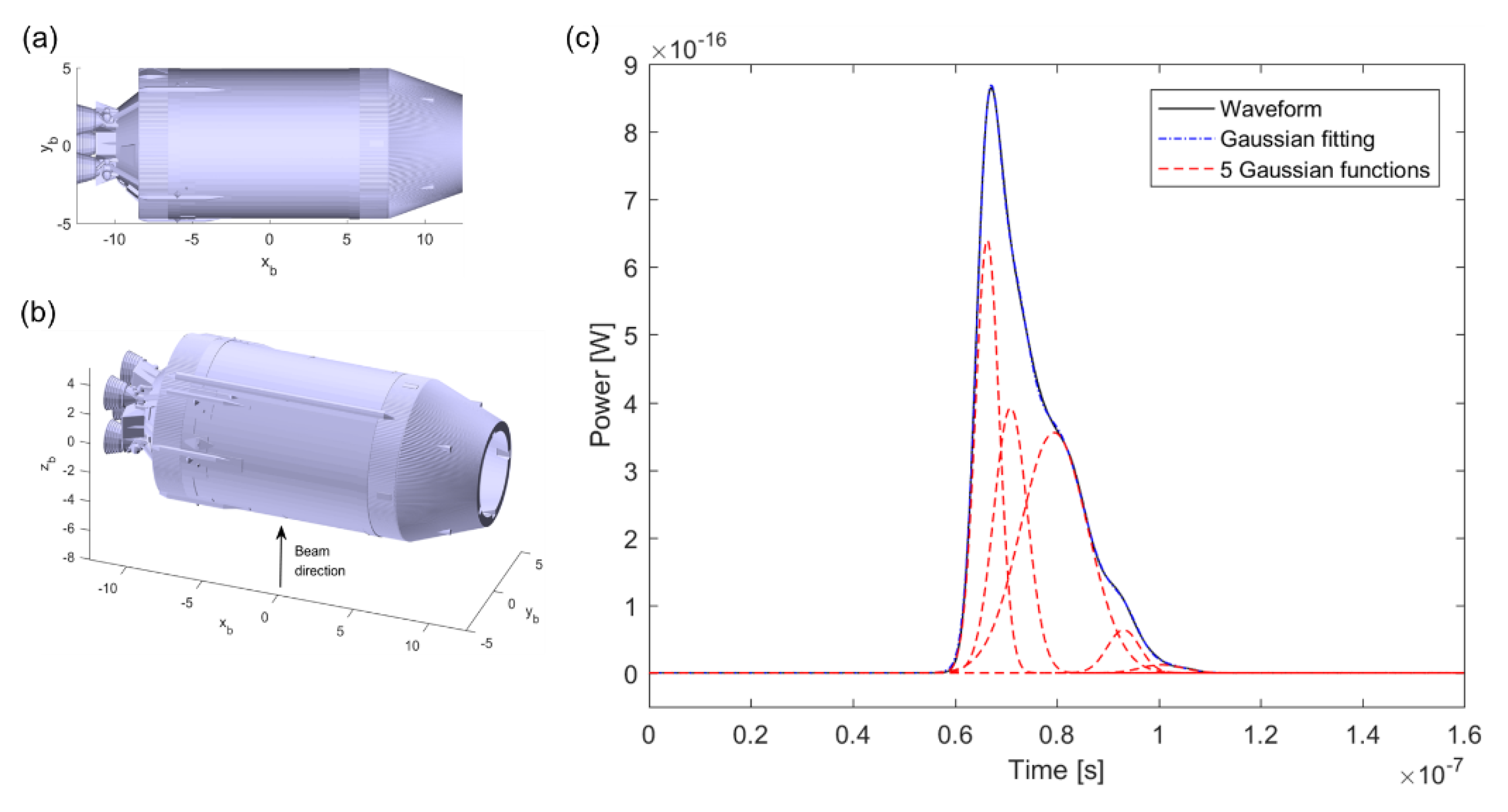
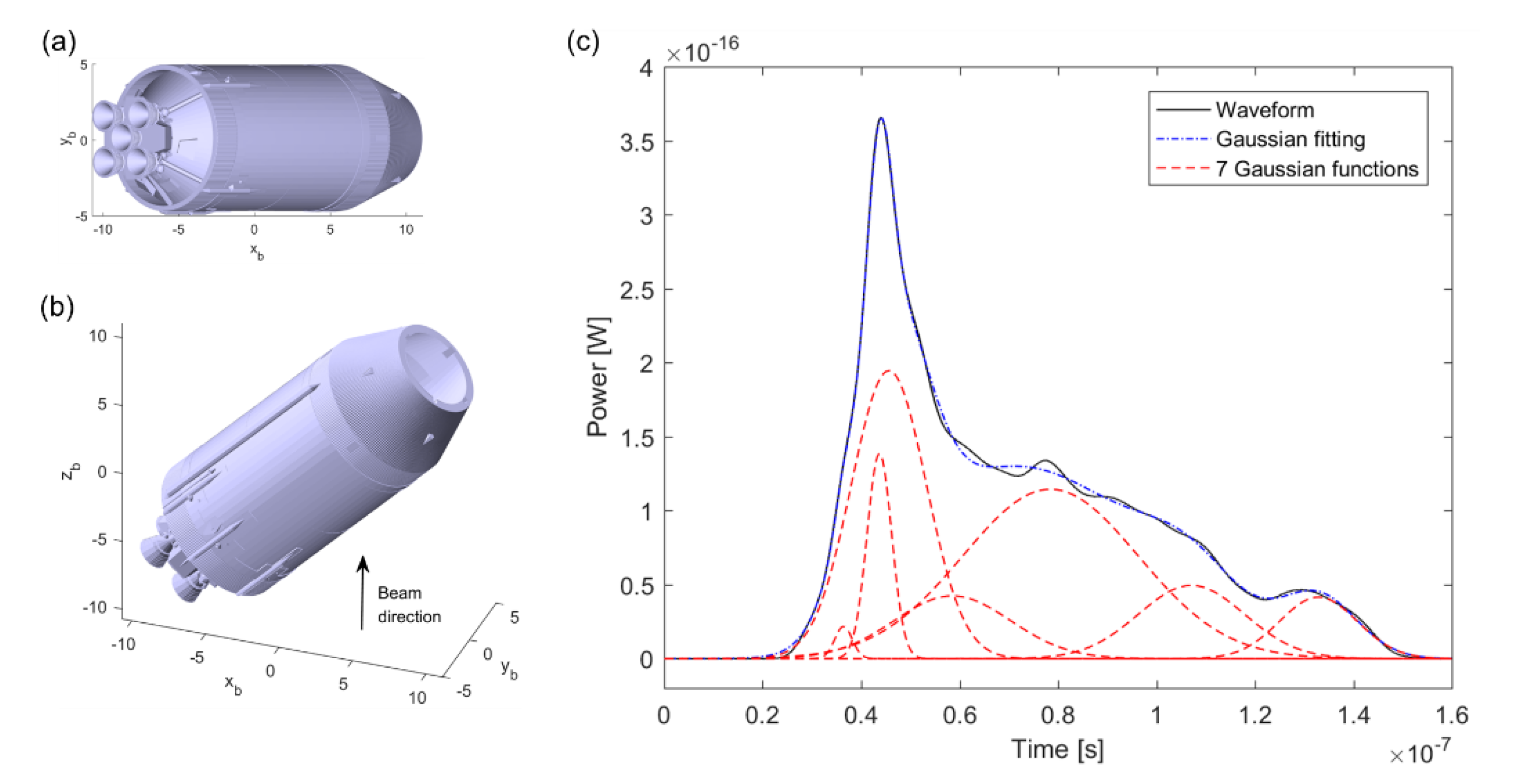
4. Simulation and Analysis of Laser Pulse Waveform
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Vallado, D.A.; Finkleman, D. A critical assessment of satellite drag and atmospheric density modeling. Acta Astronautica 2014, 95, 141–165. [Google Scholar] [CrossRef]
- Yanagisawa, T.; Kurosaki, H. Shape and motion estimate of LEO debris using light curves. Adv. Space Res. 2012, 50, 136–145. [Google Scholar] [CrossRef]
- Santoni, F.; Cordelli, E.; Piergentili, F. Determination of disposed upper-stage attitude motion by ground-based optical observations. J. Spacecraft Rock. 2013, 50, 701–708. [Google Scholar] [CrossRef]
- Kanzler, R.; Silha, J.; Schildknecht, T.; Fritsche, B.; Lips, T.; Krag, H. Space debris attitude simulation-iOTA (In-Orbit Tumbling Analysis). In Proceedings of the 15th Advanced Maui Optical and Space Surveillance Technologies (AMOS) Conference, Maui, HI, USA, 15–18 September 2015. [Google Scholar]
- Koshkin, N.; Korobeynikova, E.; Shakun, L.; Strakhova, S.; Tang, Z.H. Remote sensing of the EnviSat and Cbers-2B satellites rotation around the centre of mass by photometry. Adv. Space Res. 2016, 58, 358–371. [Google Scholar] [CrossRef]
- Koshkin, N.; Shakun, L.; Burlak, N. Ajisai spin-axis precession and rotation-period variations from photometric observations. Adv. Space Res. 2017, 60, 1389–1399. [Google Scholar] [CrossRef]
- Silha, J.; Pittet, J.-N.; Hamara, M.; Schildknecht, T. Apparent rotation properties of space debris extracted from photometric measurements. Adv. Space Res. 2018, 61, 844–861. [Google Scholar] [CrossRef]
- Bennet, F.; D’Orgeville, C.; Price, I.; Rigaut, F.; Ritchie, I.; Smith, C. Adaptive optics for satellite imaging and space debris ranging. In Proceedings of the 15th Annual Advanced Maui Optical and Space Surveillance Technologies (AMOS) Conference, Maui, HI, USA, 15–18 September 2015. [Google Scholar]
- Copeland, M.; Bennet, F.; Zovaro, A.; Riguat, F.; Piatrou, P.; Korkiakoski, V.; Smith, C. Adaptive Optics for Satellite and Debris Imaging in LEO and GEO. In Proceedings of the 17th Annual Advanced Maui Optical and Space Surveillance Technologies (AMOS), Maui, HI, USA, 19–22 September 2017. [Google Scholar]
- Copeland, M.; Bennet, F.; Rigaut, F.; Korkiakoski, V.; d’Orgeville, C.; Smith, C. Adaptive optics corrected imaging for satellite and debris characterization. In Proceedings of the SPIE 10703, Adaptive Optics Systems VI, Austin, TX, USA, 11 July 2018; p. 1070333. [Google Scholar]
- Kucharski, D.; Otsubo, T.; Kirchner, G.; Koidl, F. Spin axis orientation of Ajisai determined from Graz 2 kHz SLR data. Adv. Space Res. 2010, 46, 251–256. [Google Scholar] [CrossRef]
- Kucharski, D.; Kirchner, G.; Koidl, F. Spin parameters of nanosatellite BLITS determined from Graz 2 kHz SLR data. Adv. Space Res. 2011, 48, 343–348. [Google Scholar] [CrossRef]
- Kucharski, D.; Otsubo, T.; Kirchner, G.; Bianco, G. Spin rate and spin axis orientation of LARES spectrally determined from satellite laser ranging data. Adv. Space Res. 2012, 50, 1473–1477. [Google Scholar] [CrossRef]
- Kucharski, D.; Lim, H.-C.; Kirchner, G.; Hwang, J.-Y. Spin parameters of LAGEOS-1 and LAGEOS-2 spectrally determined from Satellite Laser Ranging data. Adv. Space Res. 2013, 52, 1332–1338. [Google Scholar] [CrossRef]
- Kucharski, D.; Kirchner, G.; Koidl, F.; Fan, C.; Carman, R.; Moore, C.; Dmytrotsa, A.; Ploner, M.; Bianco, G.; Medvedskij, M. Attitude and spin period of space debris envisat measured by satellite laser ranging. IEEE Trans. Geosci. Rem. Sens. 2014, 52, 7651–7657. [Google Scholar] [CrossRef]
- Kirchner, G.; Steindorfer, M.; Wang, P.; Koidl, F.; Kucharski, D.; Silha, J.; Schildknecht, T.; Krag, H.; Flohrer, T. Determination of attitude and attitude motion of space debris, using laser ranging and single-photon light curve data. In Proceedings of the 7th European Conference on Space Debris, Darmstadt, Germany, 18–21 April 2017. [Google Scholar]
- Kucharski, D.; Kirchner, G.; Bennett, J.; Lachut, M.; Sos’nica, K.; Koshkin, N.; Shakun, L.; Koidl, F.; Steindorfer, M.; Wang, P. Photon pressure force on space debris TOPEX/Poseidon measured by Satellite Laser Ranging. Earth Space Sci. 2017, 4, 661–668. [Google Scholar] [CrossRef]
- Schildknecht, T.; Linder, E.; Silha, J.; Hager, M.; Koshkin, N.; Korobeinikova, E.; Melikiants, S.; Shakun, L.; Strakhov, S. Photometric monitoring of non-resolved space debris and databases of optical light curves. In Proceedings of the 15th Advanced Maui Optical and Space Surveillance Technologies (AMOS) Conference, Maui, HI, USA, 15–18 September 2015. [Google Scholar]
- Schildknecht, T.; Silha, J.; Pittet, J.-N.; Rachman, A. Attitude states of space debris determined from optical light curve observations. In Proceedings of the 1st IAA Conference on Space Situational Awareness (ICSSA), Orlando, FL, USA, 13–15 November 2017. [Google Scholar]
- Zhao, S.; Steindorfer, M.; Kirchner, G.; Zheng, Y.; Koidl, F.; Wang, P.; Shang, W.; Zhang, Z.; Li, T. Attitude analysis of space debris using SLR and light curve data measured with single-photon detector. Adv. Space Res. 2020, 65, 1518–1527. [Google Scholar] [CrossRef]
- Zhang, Z.-P.; Yang, F.-M.; Zhang, H.-F.; Wu, Z.-B.; Chen, J.-P.; Li, P.; Meng, W.-D. The use of laser range to measure space debris. Res. Astron. Astrophys. 2012, 12, 212–218. [Google Scholar] [CrossRef]
- Sang., J.; Smith, C. Performance Assessment of the EOS Space Debris Tracking System. In Proceedings of the AIAA 2012-5018, AIAA/AAS Astrodynamics Specialist Conference, Minneapolis, MN, USA, 3–16 August 2012. [Google Scholar]
- Kirchner, G.; Koidl, F.; Friederich, F.; Buske, I.; Volker, U.; Riede, W. Laser measurements to space debris from Graz SLR station. Adv. Space Res. 2013, 51, 21–24. [Google Scholar] [CrossRef]
- Lim, H.-C.; Park, J.-U.; Kim, D.-J.; Seong, K.; Ka, N.-H. Laser Tracking Analysis of Space Debris using SOLT System at Mt. Gamak. J. Korean Soc. Aeronaut. Space Sci. 2015, 43, 830–837. [Google Scholar]
- Li, Y.; Wu, Z. Targets recognition using subnanosecond pulse laser range profiles. Opt. Express 2010, 18, 16788–16796. [Google Scholar] [CrossRef]
- Johnson, S.E. Effect of target surface orientation on the range precision of laser detection and ranging systems. J. Appl. Remote Sens. 2009, 3, 033564. [Google Scholar] [CrossRef]
- Richmond, R.D.; Cain, S.C. Direct-Detection LADAR Systems; SPIE: Washington, DC, USA, 2010. [Google Scholar]
- Abshire, J.B.; Sun, X.; Afzal, R.S. Mars orbiter laser altimeter: Receiver model and performance analysis. Appl. Opt. 2000, 39, 2449–2460. [Google Scholar] [CrossRef]
- Wagner, W.; Ullrich, A.; Ducic, V.; Melzer, T.; Studnicka, N. Gaussian decomposition and calibration of a novel small-footprint full-waveform digitizing airborne laser scanner. ISPRS J. Photogramm. Remote Sens. 2006, 60, 100–112. [Google Scholar] [CrossRef]
- Hao, Q.; Cheng, Y.; Cao, J.; Zhang, F.; Zhang, X.; Yu, H. Analytical and numerical approaches to study echo laser pulse profile affected by target and atmospheric turbulence. Opt. Express 2016, 24, 25026–25042. [Google Scholar] [CrossRef] [PubMed]
- Degnan, J.J. Milimeter Accuracy Satellite Laser Ranging: A Review. Geodyn. Ser. 1993, 25, 133–162. [Google Scholar]
- Gao, M.; Li, Y.; Gong, L.; Lv, H. Pulse broadening and beam spread of polarized laser pulse beam on slant path in turbulence atmospheric. Optik 2015, 126, 4651–4657. [Google Scholar] [CrossRef]
- Andrews, L.C.; Phillips, R.L. Laser Beam Propagation through Random Media; SPIE Optical Engineering Press: Bellingham, WA, USA, 1998. [Google Scholar]
- Kaushal, H.; Kaddoum, G. Optical Communication in Space: Challenges and Mitigation Techniques. IEEE Commun. Surv. Tutor. 2016, 19, 57–96. [Google Scholar] [CrossRef]
- Young, C.Y.; Andrews, L.C.; Ishimaru, A. Time-of-arrival fluctuations of a space-time Gaussian pulse in weak optical turbulence: An analytic solution. Appl. Opt. 1998, 37, 7655–7660. [Google Scholar] [CrossRef]
- Der, S.; Redman, B.; Chellappa, R. Simulation of error in optical radar range measurements. Appl. Opt. 1997, 36, 6869–6874. [Google Scholar] [CrossRef] [PubMed]
- Hemmati, H. Deep Space Optical Communications; Jet Propulsion Laboratory, California Institute of Technology: Pasadena, CA, USA, 2006.
- Mallet, C.; Bretar, F. Full-waveform topographic LiDAR: State-of-the-art. ISPRS J. Photogramm. Remote Sens. 2009, 64, 1–16. [Google Scholar] [CrossRef]
- Zhou, T.; Popescu, S. waveformlidar: An R Package for Waveform LiDAR Processing and Analysis. Remote Sens. 2019, 11, 2552. [Google Scholar] [CrossRef]
- Davies, L. Handbook of Genetic Algorithms; Van Nostrand Reinhold: New York, NY, USA, 1991. [Google Scholar]
- Man, K.F.; Tang, K.S.; Kwong, S. Genetic algorithms: Concepts and applications. IEEE Trans. Ind. Electron. 1996, 43, 519–534. [Google Scholar] [CrossRef]
- Houck, C.; Joines, J.; Kay, M. A Genetic Algorithm for Function Optimization: A Matlab Implementation, NCSU-IE Technical Report 95-09; North Carolina State University: Raleigh, NC, USA, 1996. [Google Scholar]
- Gori, F. Flattened gaussian beam. Opt. Commun. 1994, 107, 335–341. [Google Scholar] [CrossRef]
- Gardner, C.S. Ranging performance of satellite laser altimeters. IEEE Trans. Geosci. Remote Sens. 1992, 30, 1061–1072. [Google Scholar] [CrossRef]

| Parameter Description | Symbol | Value |
|---|---|---|
| Laser wavelength | 1064 nm | |
| Transmitted power | 60 W | |
| Pulse energy (repetition rate) | - | 60 J (1 Hz) |
| Full width at half maximum | FWHM | 5 ns |
| Transmitting optical efficiency | 0.8 | |
| Divergence half angle | 10 arcsec | |
| Telescope area | 0.25π m2 | |
| Receiving optical efficiency | 0.7 | |
| Optical filter transmittance | 0.5 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lim, H.-C.; Zhang, Z.-P.; Sung, K.-P.; Park, J.U.; Kim, S.; Choi, C.-S.; Choi, M. Modeling and Analysis of an Echo Laser Pulse Waveform for the Orientation Determination of Space Debris. Remote Sens. 2020, 12, 1659. https://doi.org/10.3390/rs12101659
Lim H-C, Zhang Z-P, Sung K-P, Park JU, Kim S, Choi C-S, Choi M. Modeling and Analysis of an Echo Laser Pulse Waveform for the Orientation Determination of Space Debris. Remote Sensing. 2020; 12(10):1659. https://doi.org/10.3390/rs12101659
Chicago/Turabian StyleLim, Hyung-Chul, Zhong-Ping Zhang, Ki-Pyoung Sung, Jong Uk Park, Simon Kim, Chul-Sung Choi, and Mansoo Choi. 2020. "Modeling and Analysis of an Echo Laser Pulse Waveform for the Orientation Determination of Space Debris" Remote Sensing 12, no. 10: 1659. https://doi.org/10.3390/rs12101659
APA StyleLim, H.-C., Zhang, Z.-P., Sung, K.-P., Park, J. U., Kim, S., Choi, C.-S., & Choi, M. (2020). Modeling and Analysis of an Echo Laser Pulse Waveform for the Orientation Determination of Space Debris. Remote Sensing, 12(10), 1659. https://doi.org/10.3390/rs12101659