Bayesian Harmonic Modelling of Sparse and Irregular Satellite Remote Sensing Time Series of Vegetation Indexes: A Story of Clouds and Fires
Abstract
1. Introduction
2. Materials
2.1. Study Areas
2.2. Satellites Time Series
3. Methods
3.1. Harmonic Models
Summary Descriptors of the Seasonal Dynamics
3.2. Models Fitting
| Algorithm 1: Pseudocode of fitting strategy for the Bayesian model. YSM and YAM are the harmonic model defined in the text, while TM is a simple trend model. When the model is fit with no explicit prior definition a flat prior was used. |
 |
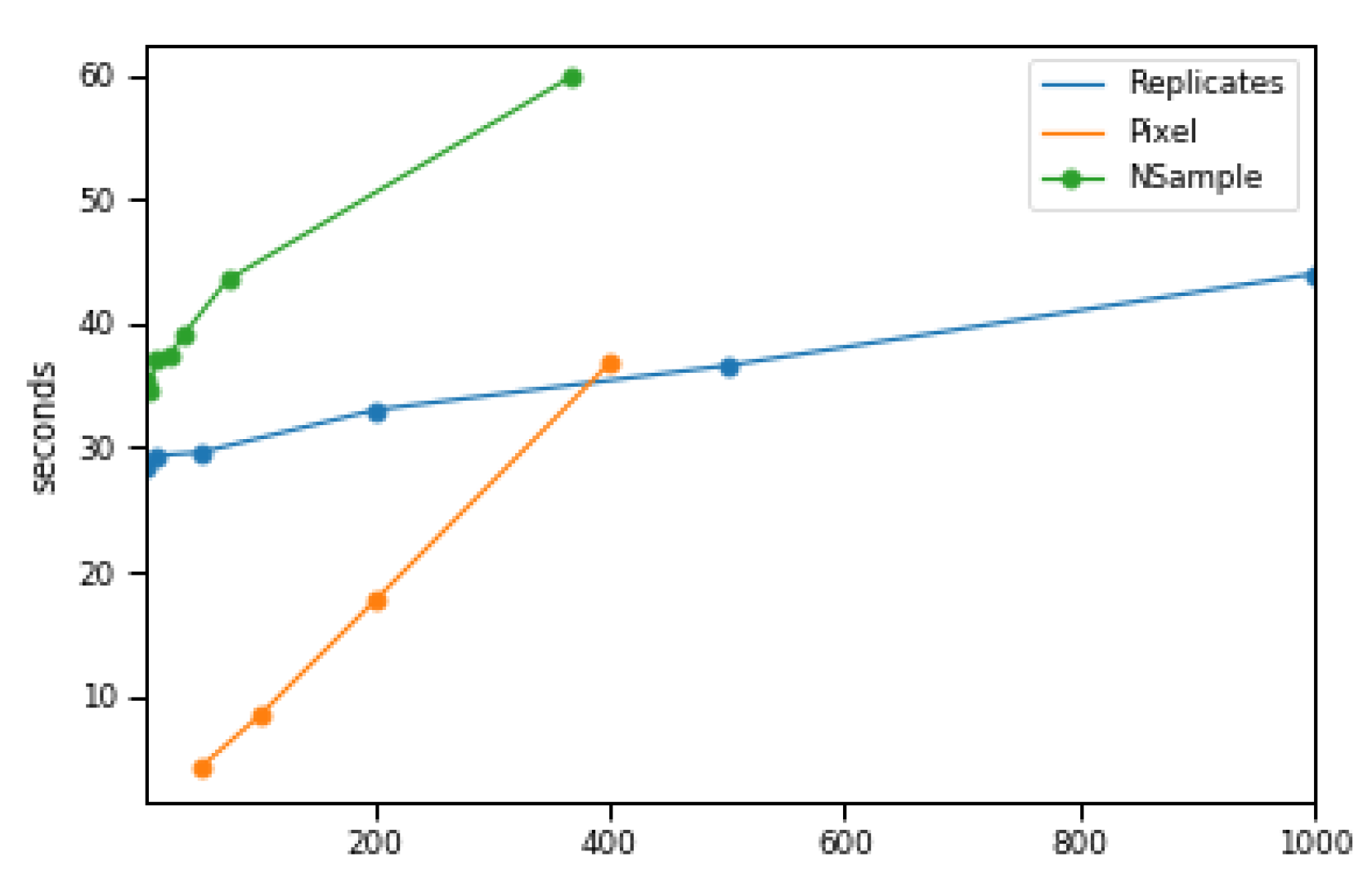
3.3. Cost of Model Fitting
4. Results and Discussion
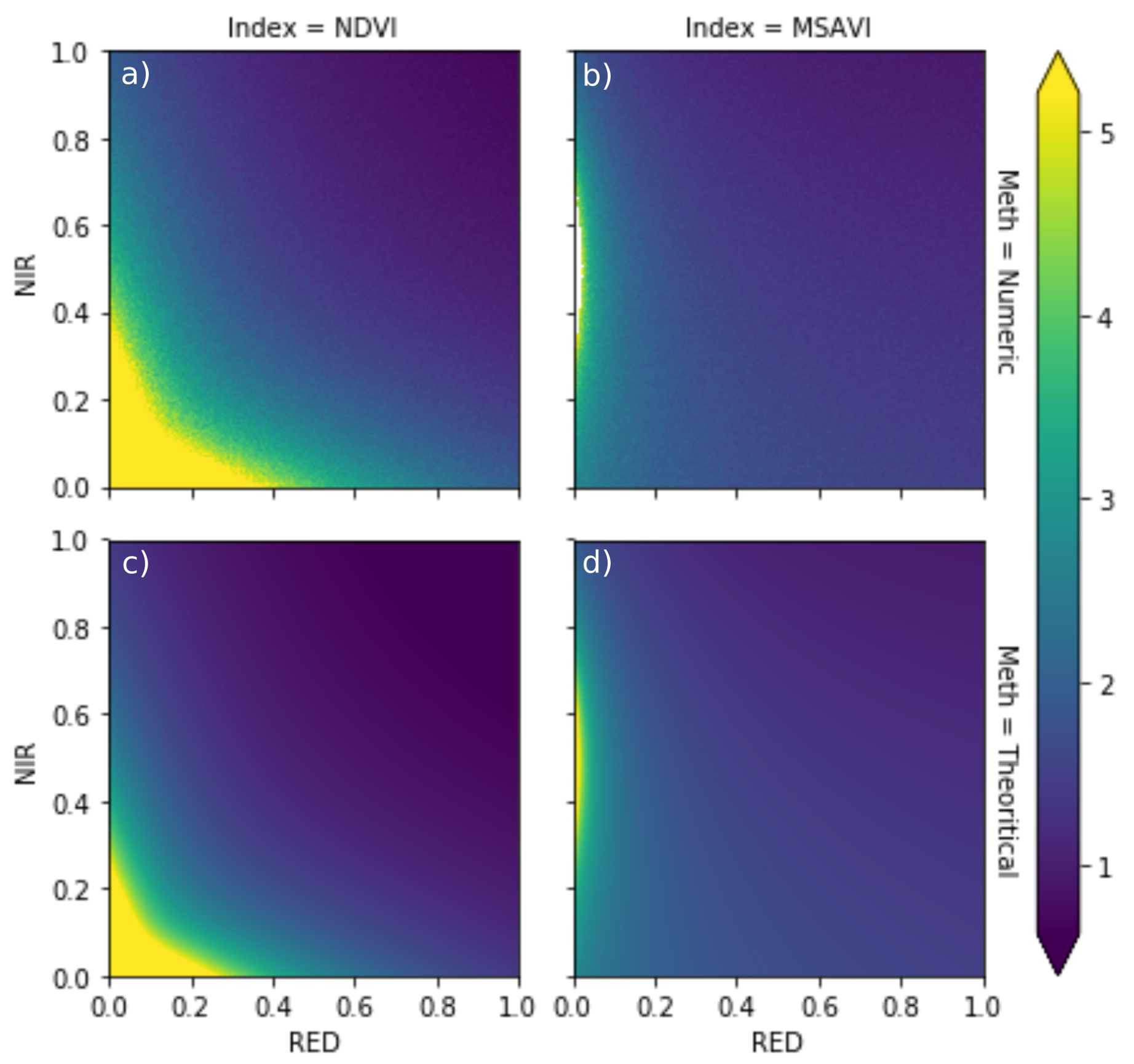
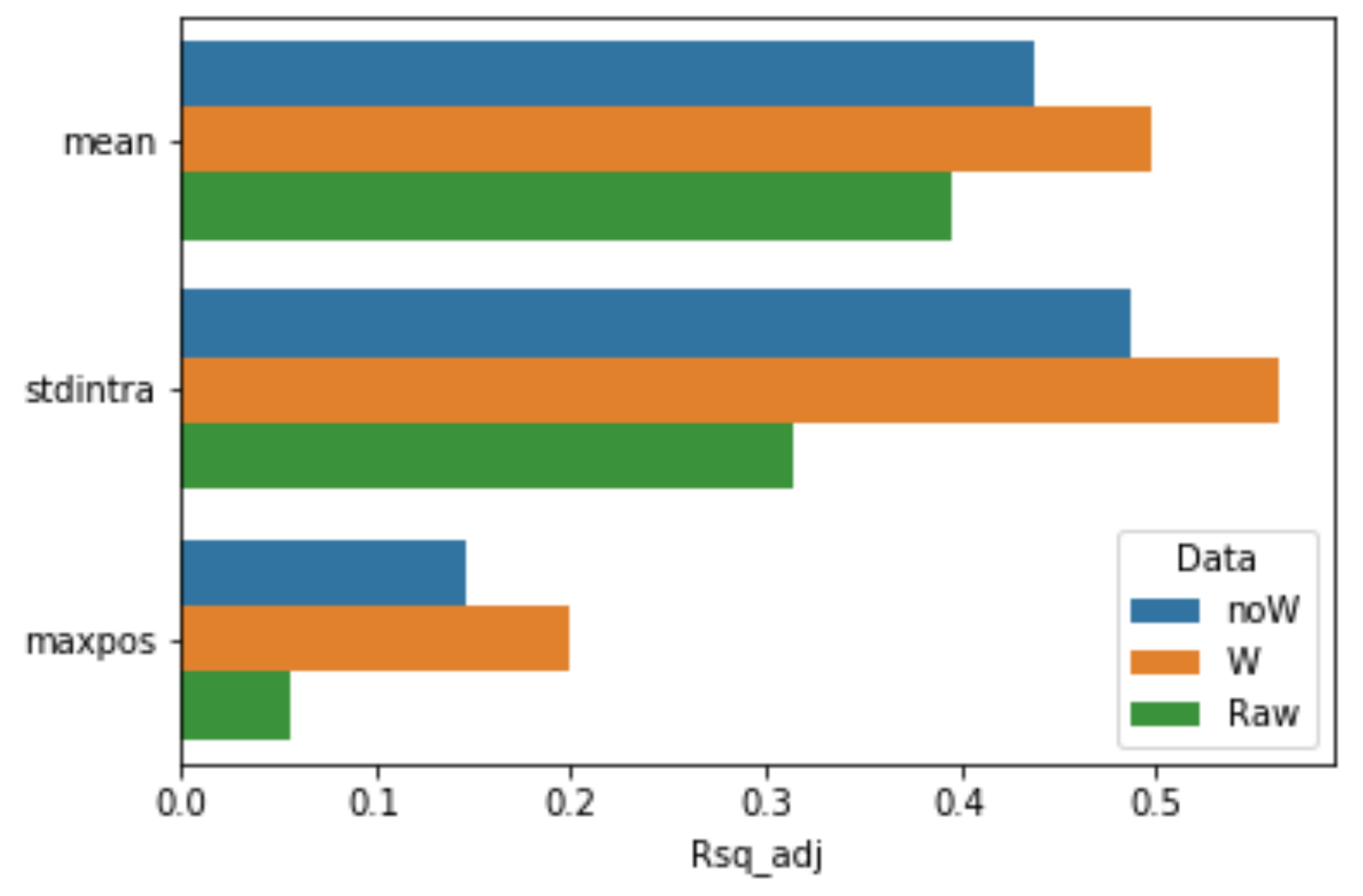
4.1. Selection of Vegetation Index
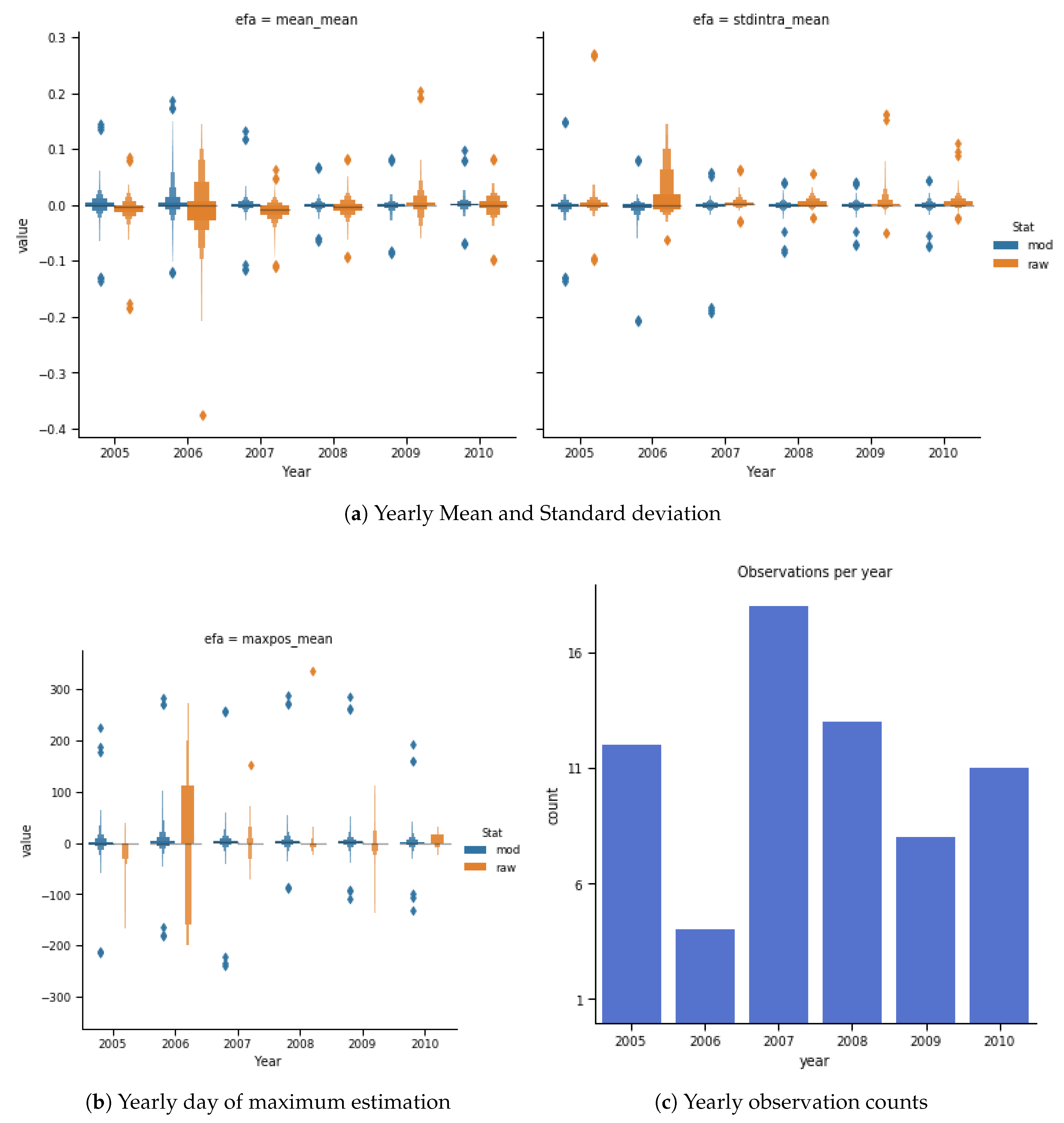
4.2. Simulation of Cloud Cover Experiment
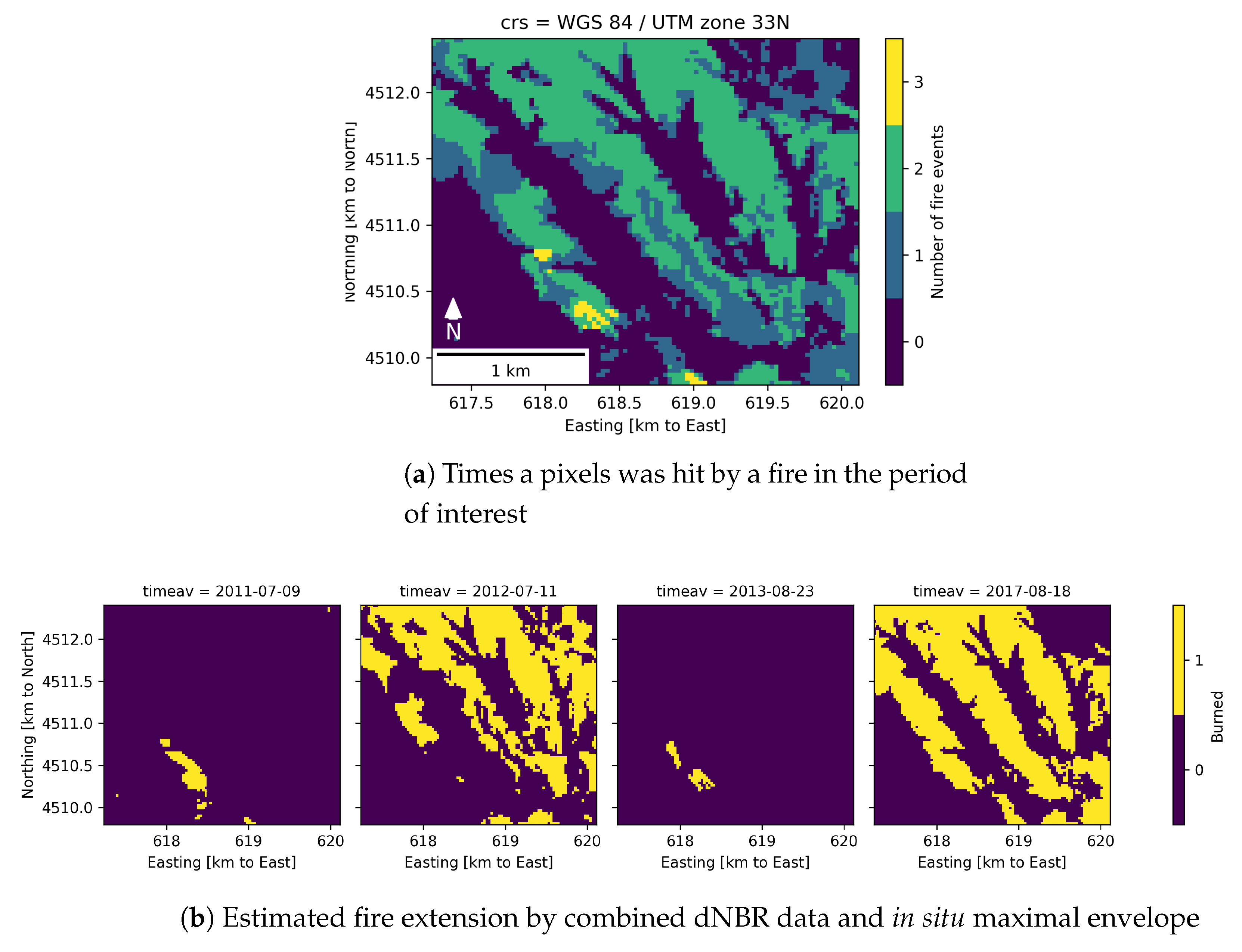
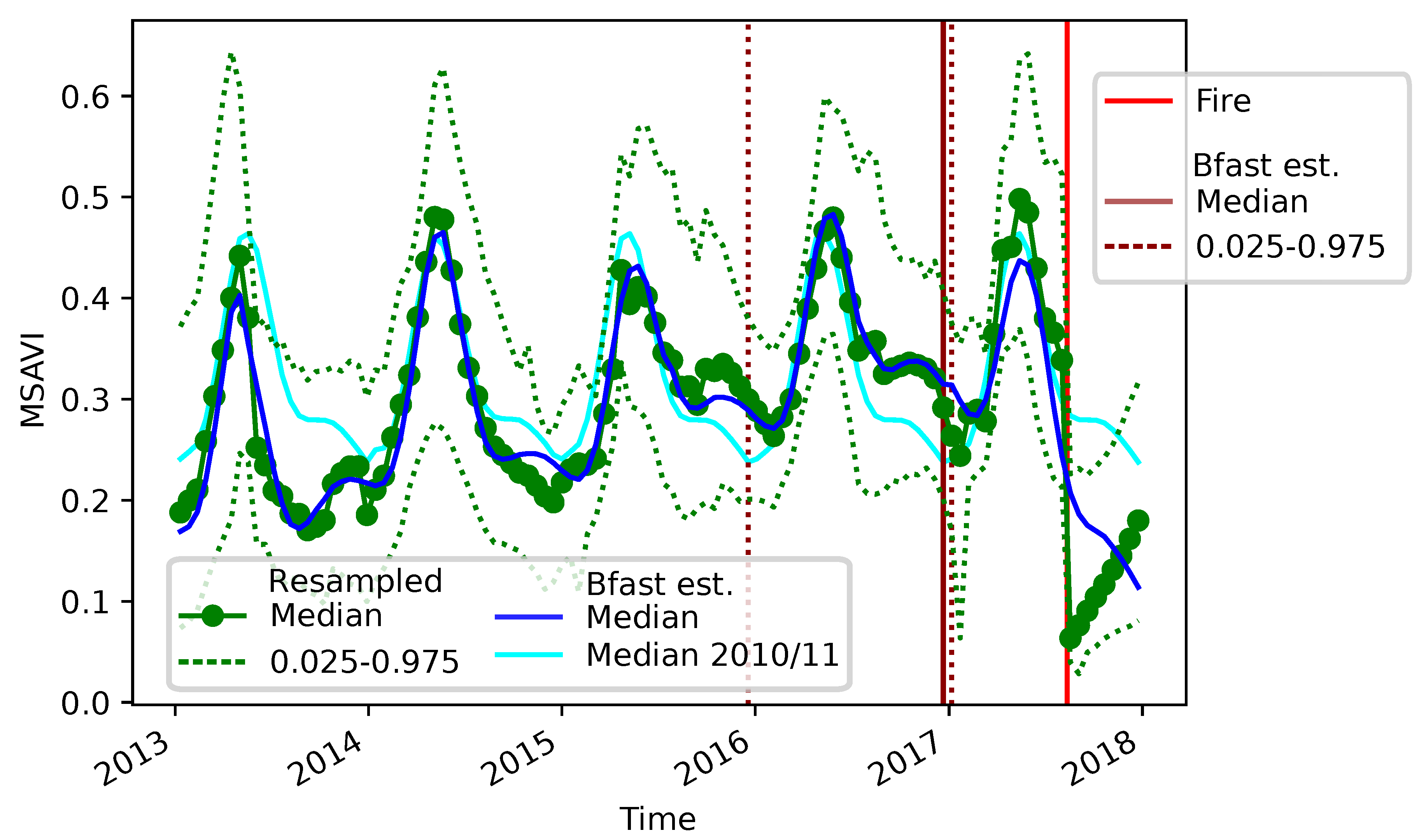
4.3. Testing over Forest Fires
4.4. Effect of Land Cover on Vegetation Phenology
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
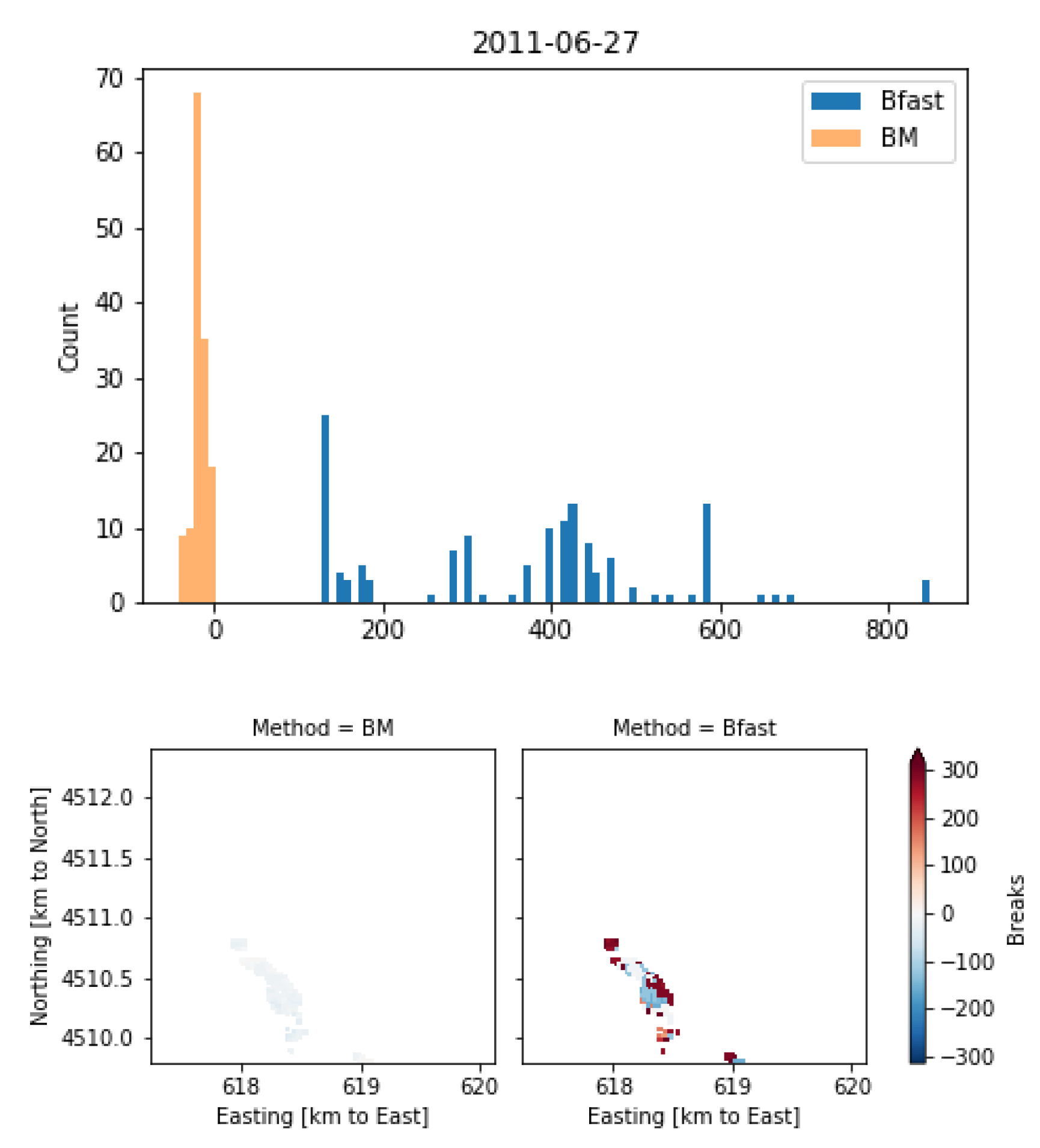
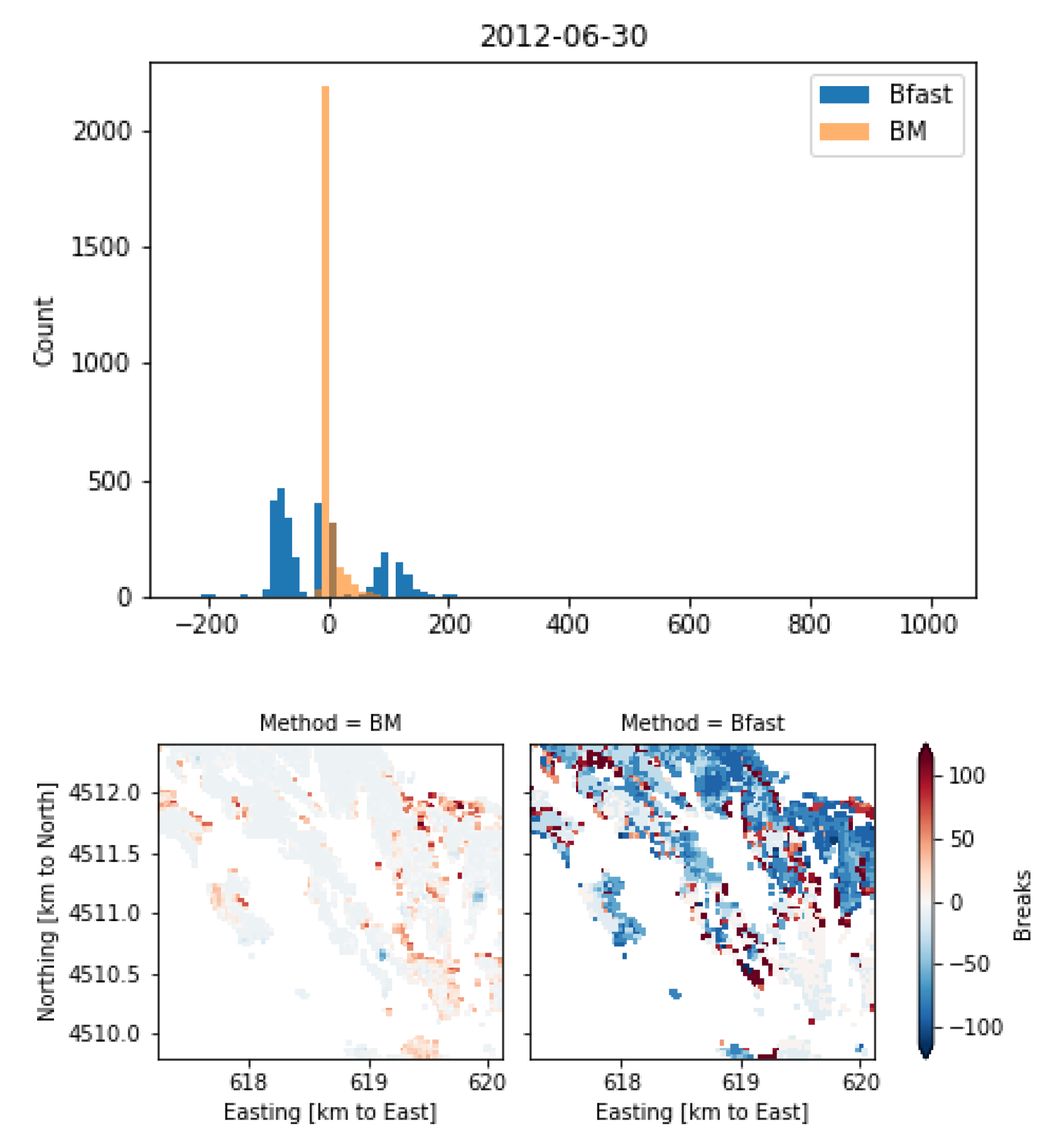
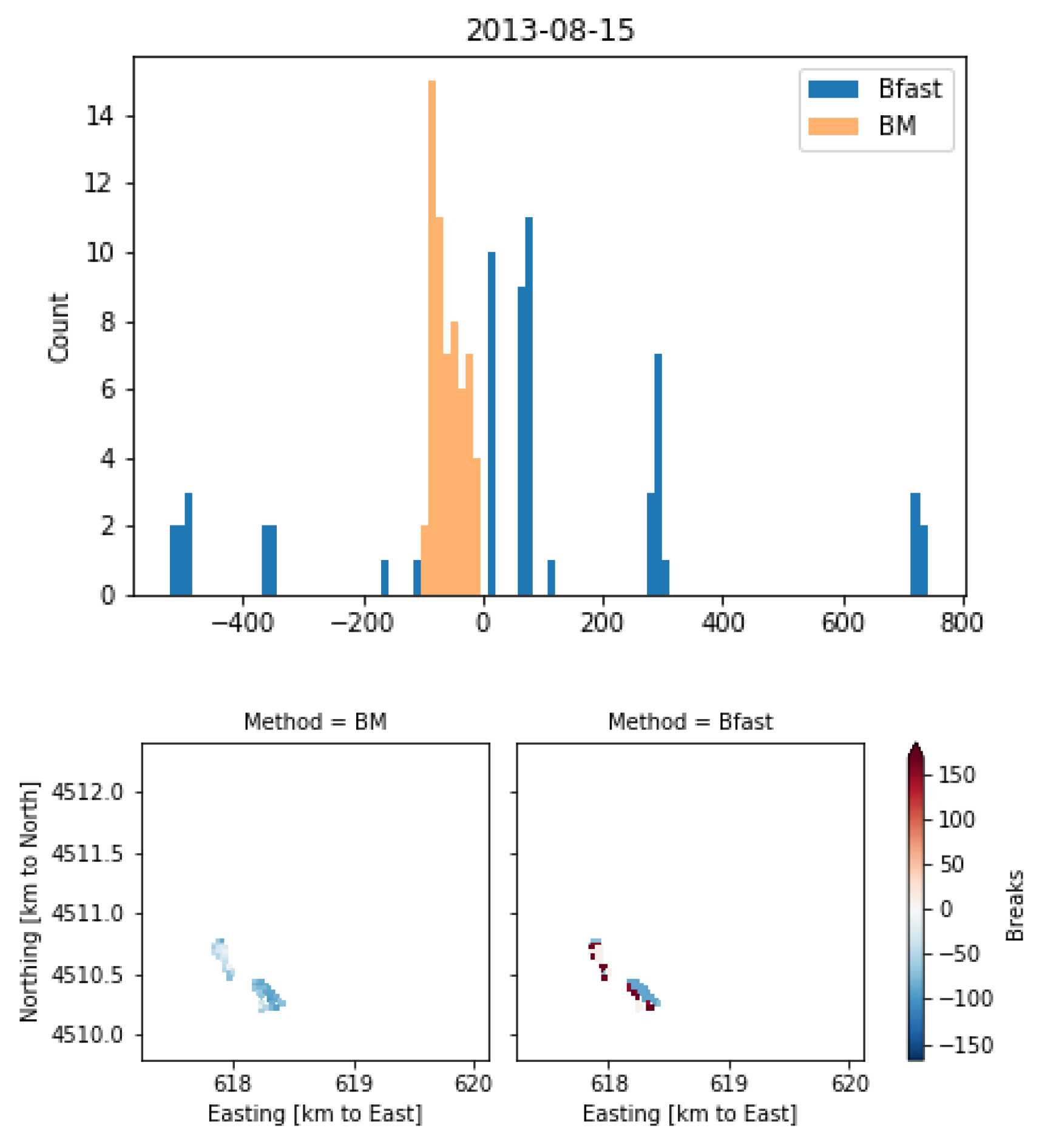
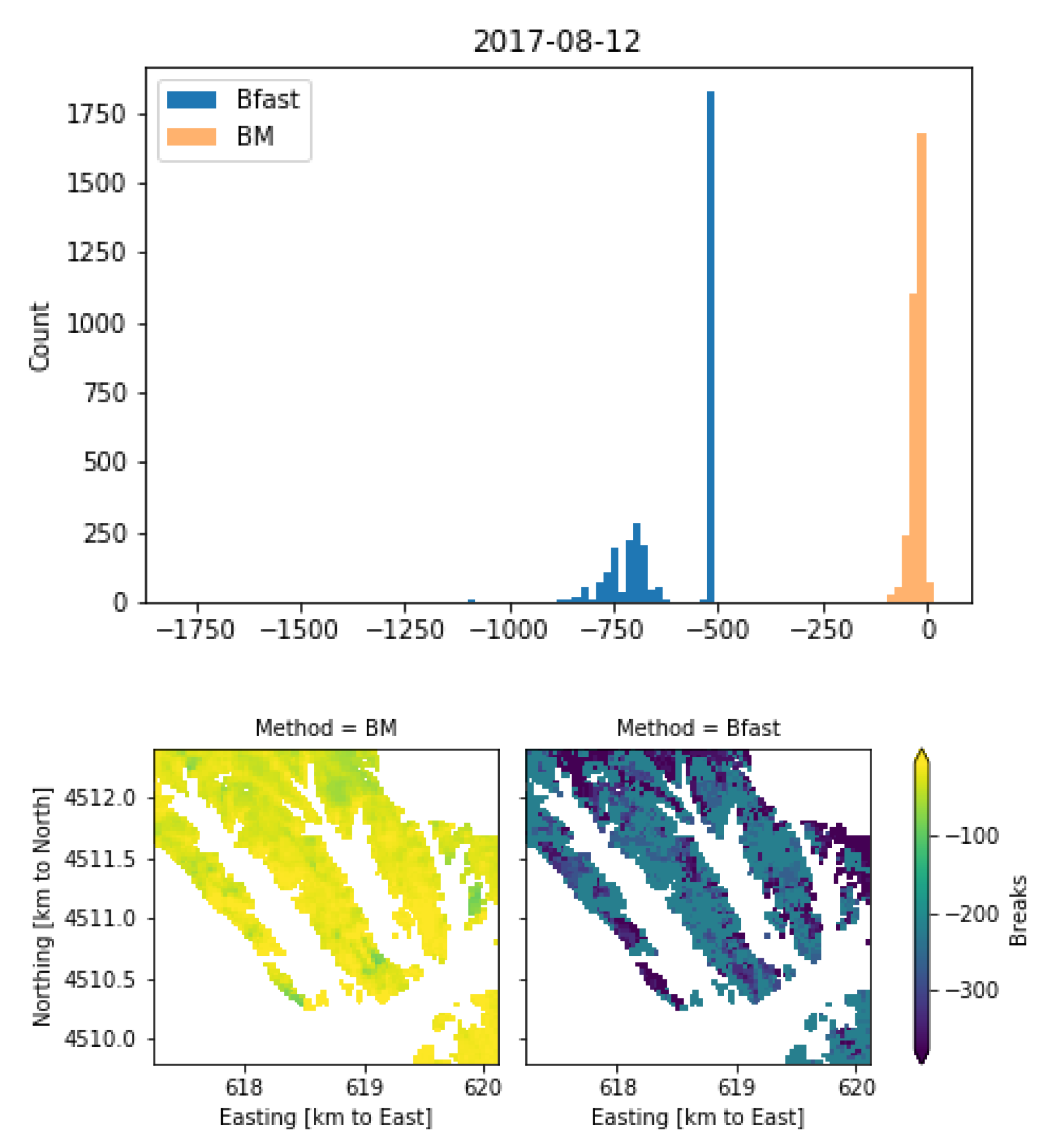
Appendix A. Detailed Comparison of Fire Breaks
References
- Ju, J.; Roy, D.P.; Vermote, E.; Masek, J.; Kovalskyy, V. Continental-scale validation of MODIS-based and LEDAPS Landsat ETM+ atmospheric correction methods. Remote Sens. Environ. 2012, 122, 175–184. [Google Scholar] [CrossRef]
- Forkel, M.; Carvalhais, N.; Verbesselt, J.; Mahecha, M.D.; Neigh, C.S.; Reichstein, M. Trend Change detection in NDVI time series: Effects of interannual variability and methodology. Remote Sens. 2013, 5, 2113–2144. [Google Scholar] [CrossRef]
- De Keersmaecker, W.; Lhermitte, S.; Honnay, O.; Farifteh, J.; Somers, B.; Coppin, P. How to measure ecosystem stability? An evaluation of the reliability of stability metrics based on remote sensing time series across the major global ecosystems. Glob. Chang. Biol. 2014, 20, 2149–2161. [Google Scholar] [CrossRef] [PubMed]
- Jianwen, L.; Yuke, Z. Comparison and application of NDVI time-series reconstruction methods at site scale on the Tibetan Plateau. Prog. Geogr. 2018, 37, 427–437. [Google Scholar] [CrossRef]
- Zhou, J.; Jia, L.; Menenti, M. Reconstruction of global MODIS NDVI time series: Performance of Harmonic ANalysis of Time Series (HANTS). Remote Sens. Environ. 2015, 163, 217–228. [Google Scholar] [CrossRef]
- Menenti, M.; Azzali, S.; Verhoef, W.; van Swol, R. Mapping agroecological zones and time lag in vegetation growth by means of fourier analysis of time series of NDVI images. Adv. Space Res. 1993, 13, 233–237. [Google Scholar] [CrossRef]
- Verbesselt, J.; Hyndman, R.; Zeileis, A.; Culvenor, D. Phenological change detection while accounting for abrupt and gradual trends in satellite image time series. Remote Sens. Environ. 2010, 114, 2970–2980. [Google Scholar] [CrossRef]
- Jönsson, P.; Eklundh, L. TIMESAT—A program for analyzing time-series of satellite sensor data. Comput. Geosci. 2004, 30, 833–845. [Google Scholar] [CrossRef]
- Nemani, R.R.; Keeling, C.D.; Hashimoto, H.; Jolly, W.M.; Piper, S.C.; Tucker, C.J.; Myneni, R.B.; Running, S.W. Climate-driven increases in global terrestrial net primary production from 1982 to 1999. Science 2003, 300, 1560–1563. [Google Scholar] [CrossRef] [PubMed]
- Alcaraz, D.; Paruelo, J.; Cabello, J. Identification of current ecosystem functional types in the Iberian Peninsula. Glob. Ecol. Biogeogr. 2006, 15, 200–212. [Google Scholar] [CrossRef]
- Regos, A.; Gagne, L.; Alcaraz-Segura, D.; Honrado, J.P.; Domínguez, J. Effects of species traits and environmental predictors on performance and transferability of ecological niche models. Sci. Rep. 2019, 9, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Alcaraz-Segura, D.; Lomba, A.; Sousa-Silva, R.; Nieto-Lugilde, D.; Alves, P.; Georges, D.; Vicente, J.R.; Honrado, J.P. Potential of satellite-derived ecosystem functional attributes to anticipate species range shifts. Int. J. Appl. Earth Obs. Geoinf. 2017, 57, 86–92. [Google Scholar] [CrossRef]
- Arenas-Castro, S.; Regos, A.; Gonçalves, J.F.; Alcaraz-Segura, D.; Honrado, J. Remotely Sensed Variables of Ecosystem Functioning Support Robust Predictions of Abundance Patterns for Rare Species. Remote Sens. 2019, 11, 2086. [Google Scholar] [CrossRef]
- Walter, G.; Augustin, T. Bayesian linear regression—Different conjugate models and their (In)sensitivity to prior-data conflict. In Statistical Modelling and Regression Structures: Festschrift in Honour of Ludwig Fahrmeir; Physica-Verlag HD: Heidelberg, Germany, 2010; pp. 59–78. [Google Scholar] [CrossRef]
- Asher Bender. Bayesian Linear Model. Available online: https://github.com/asherbender/bayesian-linear-model (accessed on 6 November 2019).
- Borgogno-Mondino, E.; Lessio, A.; Gomarasca, M.A. A fast operative method for NDVI uncertainty estimation and its role in vegetation analysis. Eur.J. Remote Sens. 2016, 49, 137–156. [Google Scholar] [CrossRef]
- Wolfram. Wolframalpha. Available online: https://www.wolframalpha.com (accessed on 6 November 2019).
- Qi, J.; Chehbouni, A.; Huete, A.; Kerr, Y.; Sorooshian, S. A modified soil adjusted vegetation index. Remote Sens. Environ. 1994, 48, 119–126. [Google Scholar] [CrossRef]
- Catasto Incendi. Available online: http://www.simontagna.it/portalesim/catastoincendi.jsp (accessed on 6 November 2019).
- Keeley, J.E. Fire intensity, fire severity and burn severity: A brief review and suggested usage. Int. J. Wildland Fire 2009, 18, 116–126. [Google Scholar] [CrossRef]
- Heisig, J. Step by Step: Burn Severity mapping in Google Earth Engine. Available online: http://www.un-spider.org/advisory-support/recommended-practices/recommended-practice-burn-severity/burn-severity-earth-engine (accessed on 6 November 2019).
- Adamo, M.; Tarantino, C.; Lucas, R.M.; Tomaselli, V.; Sigismondi, A.; Mairota, P.; Blonda, P. Combined use of expert knowledge and earth observation data for the land cover mapping of an Italian grassland area: An EODHaM system application. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 16–31 July 2015; IEEE: Piscataway, NJ, USA; pp. 3065–3068. [Google Scholar] [CrossRef]
- Jönsson, P.; Cai, Z.; Melaas, E.; Friedl, M.A.; Eklundh, L. A method for robust estimation of vegetation seasonality from Landsat and Sentinel-2 time series data. Remote Sens. 2018, 10, 635. [Google Scholar] [CrossRef]
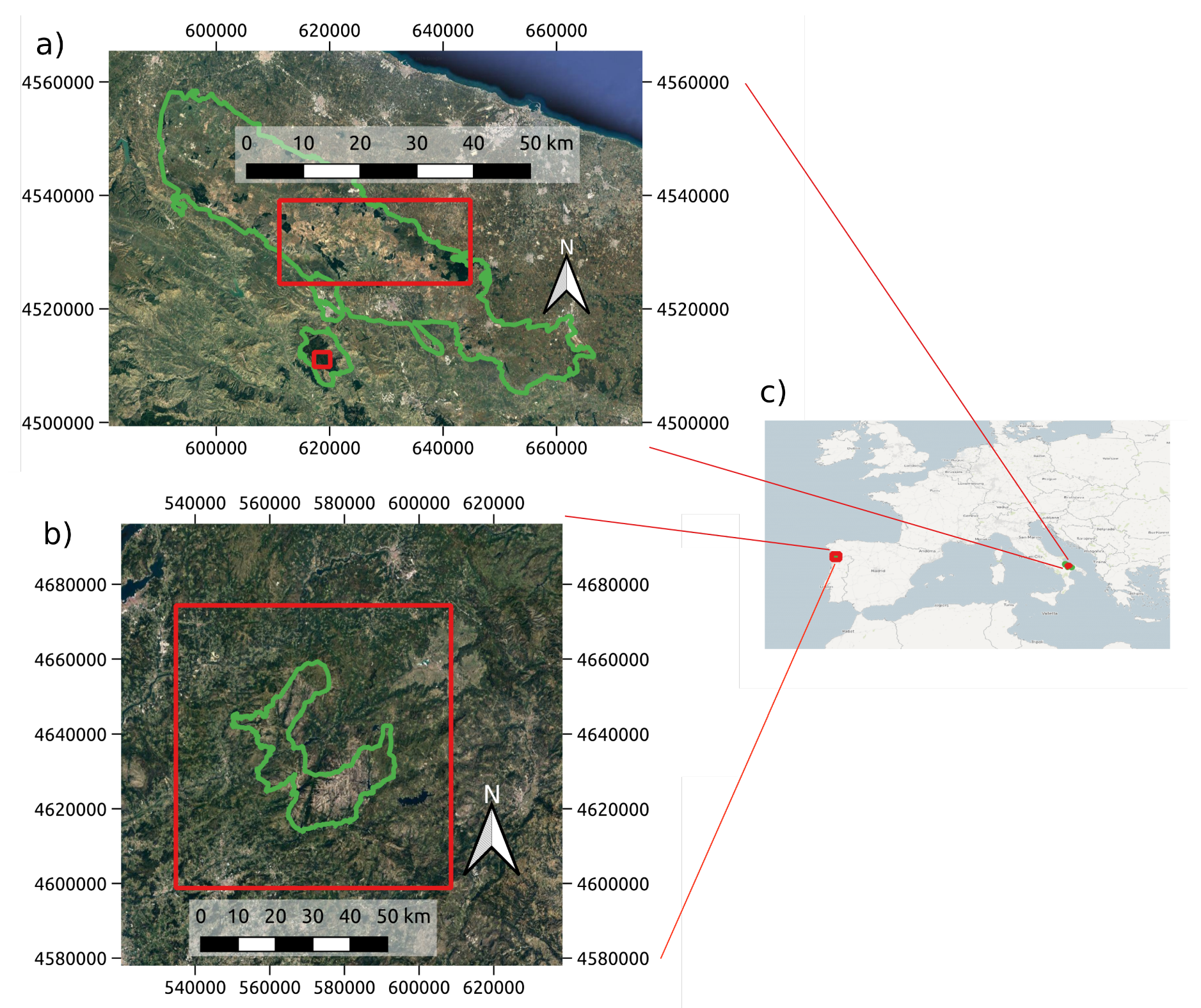
| Name Locality | Scenes | X Cells | Y Cells | Years Span |
|---|---|---|---|---|
| Peneda Gerês | 66 | 2521 | 2458 | 2005–2010 |
| Murgia Alta | 538 | 1122 | 488 | 2000–2018 |
| Bosco Difesa Grande | 192 | 87 | 96 | 2010–2017 |
| Bias | Std | |||
|---|---|---|---|---|
| Method Fire Event | BM | BFAST | BM | BFAST |
| 27 June 2011 | 33.3 | 118.2 | 51.2 | 196.1 |
| 30 June 2012 | 21.4 | −29.9 | 47.6 | 110.6 |
| 15 August 2013 | −17.7 | 15.7 | 62.5 | 245.6 |
| 12 August 2017 | −3.1 | −422.1 | 51.4 | 271.1 |
| mean_mean | stdintra_mean | maxpos_mean | ||||
|---|---|---|---|---|---|---|
| BM | BFAST | BM | BFAST | BM | BFAST | |
| Intercept (2011:nofire) | 0.330 | 0.322 | 0.090 | 0.080 | 144.206 | 145.140 |
| 2012:nofire | −0.038 | −0.053 | −0.007 | −0.006 | −4.431 | −13.457 |
| 2013:nofire | −0.053 | −0.041 | −0.005 | 0.004 | −8.722 | 3.898 |
| 2017:nofire | −0.011 | 0.006 | 0.006 | 0.007 | 5.722 | −8.013 |
| fire | −0.076 | −0.069 | −0.003 | −0.000 | −26.258 | −29.640 |
| 2012:fire | 0.023 | 0.029 | 0.004 | 0.011 | 13.924 | 34.929 |
| 2013:fire | 0.071 | 0.077 | 0.012 | −0.008 | 4.703 | 35.068 |
| 2017:fire | 0.027 | 0.013 | 0.018 | −0.006 | 19.348 | 26.071 |
| Rsq_adj | 0.162 | 0.182 | 0.048 | 0.013 | 0.065 | 0.041 |
| Space | Time | ||||
|---|---|---|---|---|---|
| BFAST | BM | BFAST | BM | ||
| maxpos | kernSD | 18.289 | 5.945 | 1.247 | 4.490 |
| TotSD | 27.787 | 28.748 | 6.819 | 6.986 | |
| Rate | 0.658 | 0.207 | 0.183 | 0.643 | |
| mean | kernSD | 0.021 | 0.021 | 0.027 | 0.022 |
| TotSD | 0.067 | 0.066 | 0.036 | 0.029 | |
| Rate | 0.319 | 0.321 | 0.747 | 0.766 | |
| std intra | kernSD | 0.014 | 0.014 | 0.007 | 0.007 |
| TotSD | 0.036 | 0.038 | 0.009 | 0.013 | |
| Rate | 0.386 | 0.378 | 0.708 | 0.560 | |
| std inter | kernSD | 0.006 | 0.006 | - | - |
| TotSD | 0.036 | 0.038 | - | - | |
| Rate | 0.153 | 0.146 | - | - | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vicario, S.; Adamo, M.; Alcaraz-Segura, D.; Tarantino, C. Bayesian Harmonic Modelling of Sparse and Irregular Satellite Remote Sensing Time Series of Vegetation Indexes: A Story of Clouds and Fires. Remote Sens. 2020, 12, 83. https://doi.org/10.3390/rs12010083
Vicario S, Adamo M, Alcaraz-Segura D, Tarantino C. Bayesian Harmonic Modelling of Sparse and Irregular Satellite Remote Sensing Time Series of Vegetation Indexes: A Story of Clouds and Fires. Remote Sensing. 2020; 12(1):83. https://doi.org/10.3390/rs12010083
Chicago/Turabian StyleVicario, Saverio, Maria Adamo, Domingo Alcaraz-Segura, and Cristina Tarantino. 2020. "Bayesian Harmonic Modelling of Sparse and Irregular Satellite Remote Sensing Time Series of Vegetation Indexes: A Story of Clouds and Fires" Remote Sensing 12, no. 1: 83. https://doi.org/10.3390/rs12010083
APA StyleVicario, S., Adamo, M., Alcaraz-Segura, D., & Tarantino, C. (2020). Bayesian Harmonic Modelling of Sparse and Irregular Satellite Remote Sensing Time Series of Vegetation Indexes: A Story of Clouds and Fires. Remote Sensing, 12(1), 83. https://doi.org/10.3390/rs12010083






