Designing and Evaluating a User-Oriented Calibration Field for the Target-Based Self-Calibration of Panoramic Terrestrial Laser Scanners
Abstract
1. Introduction
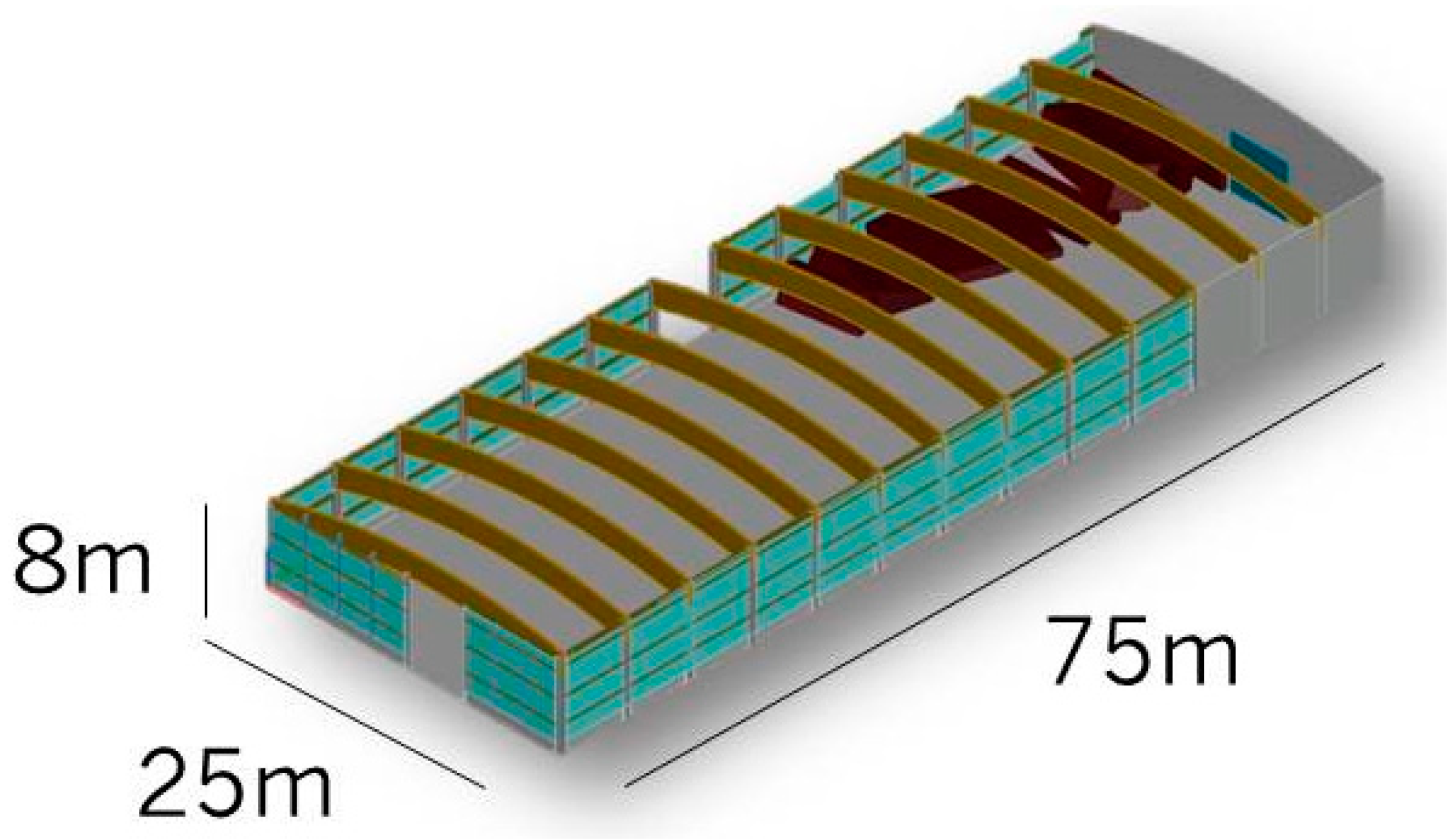
- To design a user-oriented calibration field (in sense of cost-efficiency) that fulfills certain design criteria;
- To evaluate this calibration field based on several calibration attempts using a wide range of TLSs with a special focus on high-end instruments;
- To demonstrate the usability of the calibration parameters in situ and a posteriori.
2. Materials and Methods
2.1. Basics of TLS Calibration
2.1.1. Calibration Parameters (CPs)
2.1.2. Functional Model
2.1.3. Stochastic Model
2.2. TLS Calibration in the Context of Geodetic Networks
2.2.1. Optimization of Geodetic Networks
2.2.2. Design Criteria
Efficiency
Precision of CPs
Correlations
Reliability
3. Results and Discussion
3.1. Simulation Experiments—Designing the Calibration Field
3.1.1. Simulated Design for High-End TLS
3.1.2. Comparison to Previous Calibration Fields
3.1.3. Simulation Results for Non-High-End TLS
3.2. Empirical Experiments—Evaluating the Calibration Field
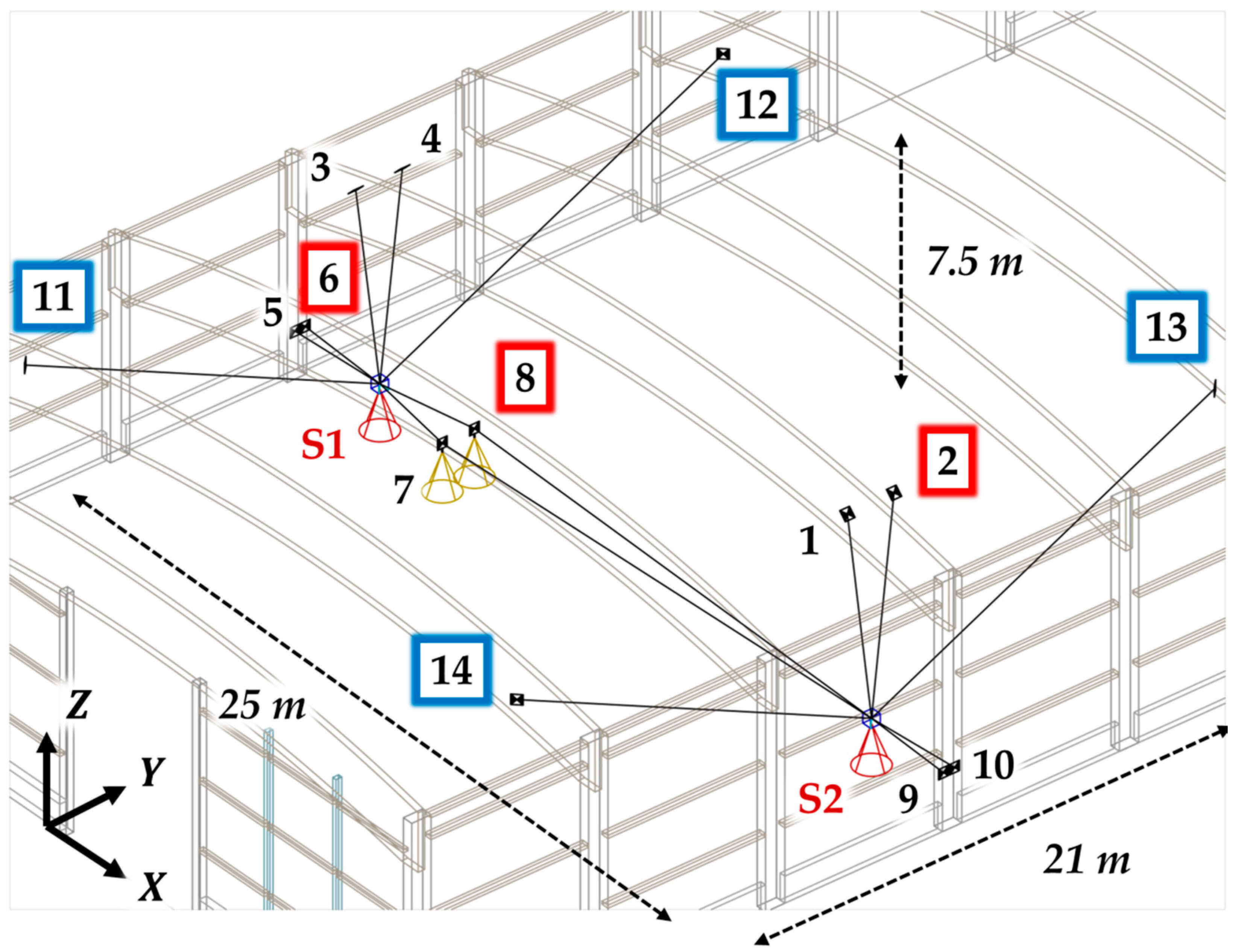
3.2.1. Experiment setup
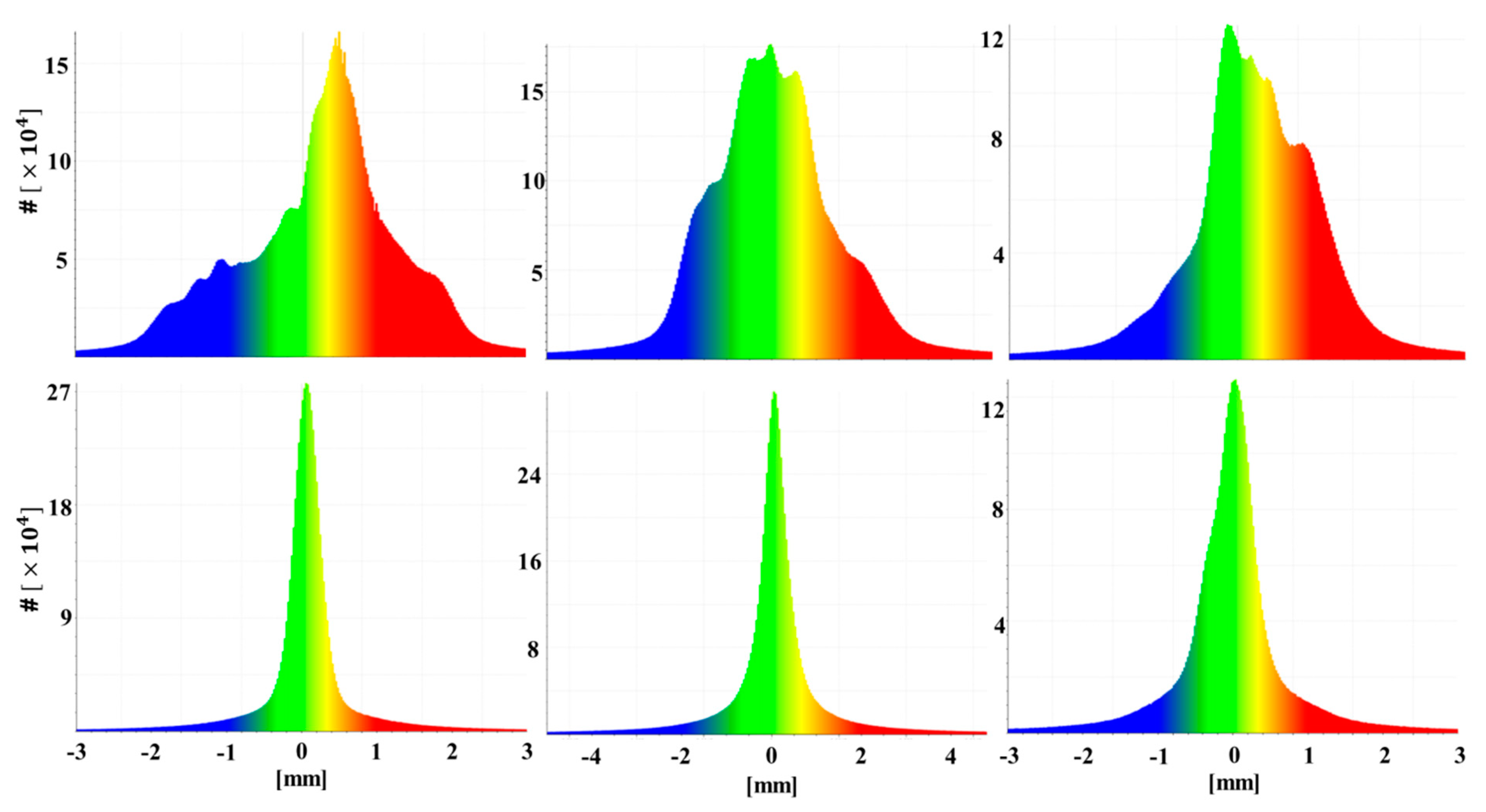
3.2.2. Experiment Results for All TLSs
3.2.3. Reproducibility of Results for the Leica ScanStation P50
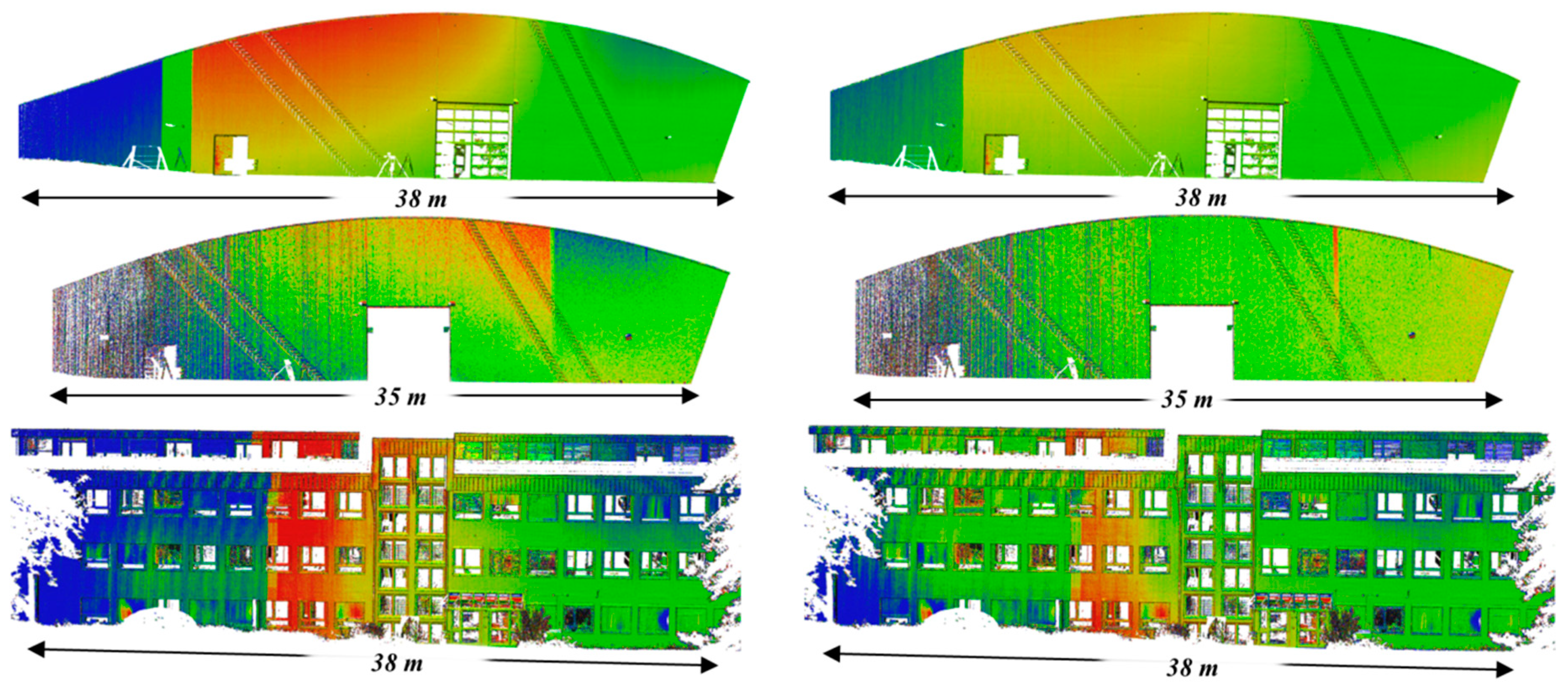
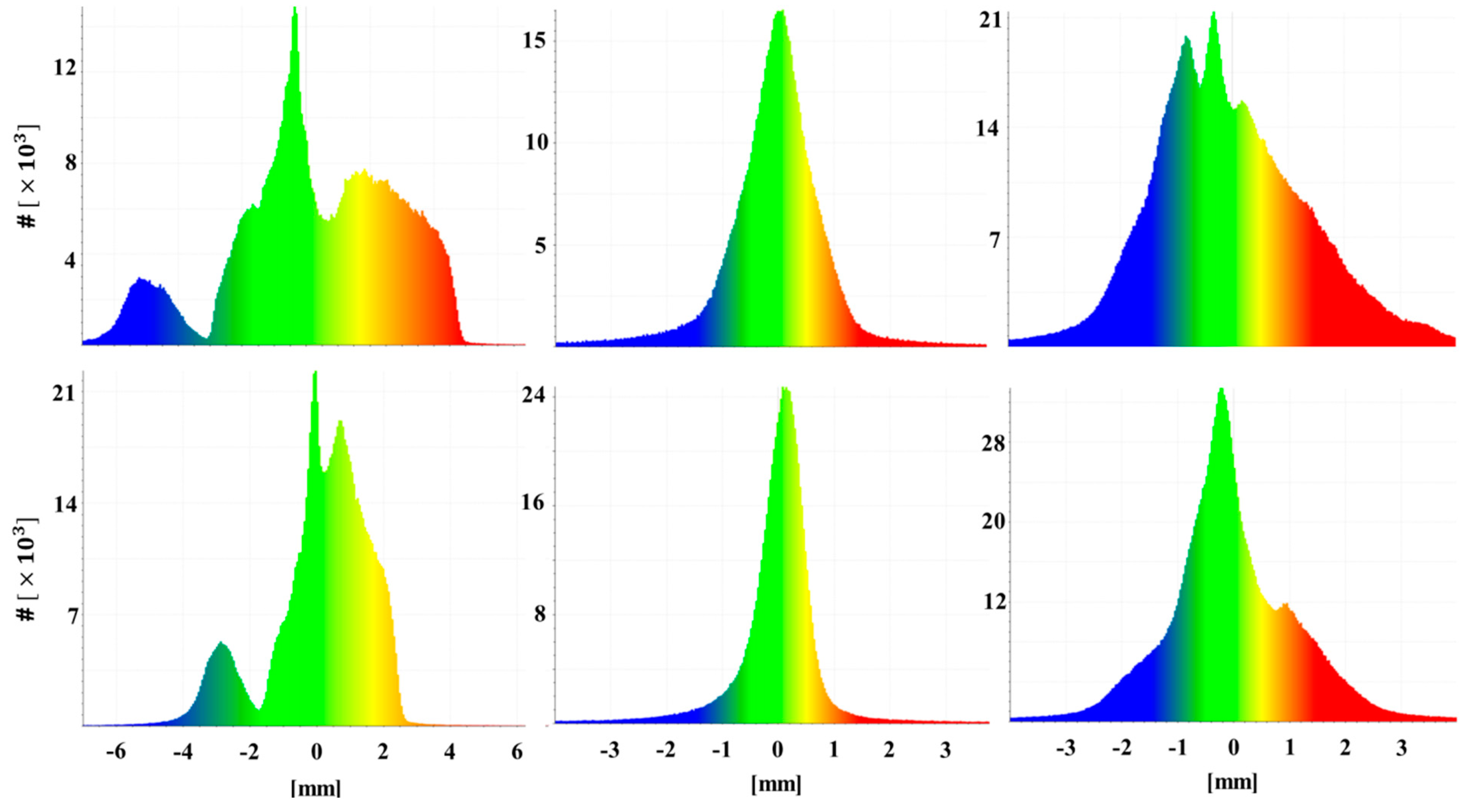
3.2.4. Point Cloud Quality Improvement
3.2.5. A Posteriori Use of Calibration Parameters
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Target # | X [m] | Y [m] | Z [m] | Target # | X [m] | Y [m] | Z [m] |
|---|---|---|---|---|---|---|---|
| 1 | 22.05 | 16.25 | 7.61 | 10 | 25.03 | 17.05 | 1.41 |
| 2 | 22.02 | 17.69 | 7.62 | 11 | 3.34 | 27.60 | 7.43 |
| 3 | 3.31 | 16.19 | 7.32 | 12 | 3.32 | 6.39 | 7.46 |
| 4 | 3.32 | 17.63 | 7.31 | 13 | 22.04 | 27.61 | 7.48 |
| 5 | 0.34 | 16.74 | 1.40 | 14 | 22.02 | 6.39 | 7.44 |
| 6 | 0.33 | 17.05 | 1.41 | Station | X [m] | Y [m] | Z [m] |
| 7 | 6.32 | 16.44 | 1.43 | S1 | 22.04 | 16.97 | 1.40 |
| 8 | 6.31 | 17.43 | 1.39 | S2 | 3.31 | 16.93 | 1.41 |
| 9 | 25.04 | 16.76 | 1.43 |
References
- Mukupa, W.; Roberts, G.W.; Hancock, C.M.; Al-Manasir, K. A review of the use of terrestrial laser scanning application for change detection and deformation monitoring of structures. Surv. Rev. 2017, 49, 99–116. [Google Scholar] [CrossRef]
- Bianculli, D.; Humphries, D.; Berkeley, L. Application of terrestrial laser scanner in particle accelerator and reverse engineering solutions. In Proceedings of the 14th International Workshop Accelerator Alignment, Grenoble, France, 3–7 October 2016. [Google Scholar]
- Chow, J.C.K.; Lichti, D.D.; Glennie, C.; Hartzell, P. Improvements to and comparison of static terrestrial LiDAR self-calibration methods. Sensors 2013, 13, 7224–7249. [Google Scholar] [CrossRef]
- Gielsdorf, F.; Rietdorf, A.; Gruendig, L. A Concept for the Calibration of Terrestrial Laser Scanners. In Proceedings of the FIG Working Week, Athens, Greece, 22–27 May 2004; pp. 1–10. [Google Scholar]
- Bae, K.; Lichti, D.D. On-site self-calibration using planar features for terrestrial laser scanners. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci 2007, 36, 14–19. [Google Scholar]
- Chan, T.O.; Lichti, D.D. Cylinder-Based Self-Calibration of a Panoramic Terrestrial Laser Scanner. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, XXXIX, 169–174. [Google Scholar] [CrossRef]
- Holst, C.; Medić, T.; Kuhlmann, H. Dealing with systematic laser scanner errors due to misalignment at area-based deformation analyses. J. Appl. Geod. 2018, 12, 169–185. [Google Scholar] [CrossRef]
- Lichti, D.D. Error modelling, calibration and analysis of an AM-CW terrestrial laser scanner system. ISPRS J. Photogramm. Remote Sens. 2007, 61, 307–324. [Google Scholar] [CrossRef]
- Reshetyuk, Y. Self-Calibration and Direct Georeferencing in Terrestrial Laser Scanning; KTH Stockholm: Stockholm, Sweden, 2009. [Google Scholar]
- Abbas, M.A.; Lichti, D.D.; Chong, A.K.; Setan, H.; Majid, Z. An on-site approach for the self-calibration of terrestrial laser scanner. Measurement 2014, 52, 111–123. [Google Scholar] [CrossRef]
- Lerma, J.L.; García-San-Miguel, D. Self-calibration of terrestrial laser scanners: Selection of the best geometric additional parameters. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, II-5, 219–226. [Google Scholar] [CrossRef]
- Neitzel, F. Investigation of Axes Errors of Terrestrial Laser Scanners. In Proceedings of the 5th International Symposium Turkish-German Joint Geodetic Days, Berlin, Germany, 28–31 March 2006. [Google Scholar]
- Wang, L.; Muralikrishnan, B.; Rachakonda, P.; Sawyer, D. Determining geometric error model parameters of a terrestrial laser scanner through two-face, length-consistency, and network methods. Meas. Sci. Technol. 2017, 28, 065016. [Google Scholar] [CrossRef]
- Muralikrishnan, B.; Wang, L.; Rachakonda, P.; Sawyer, D. Terrestrial laser scanner geometric error model parameter correlations in the Two-face, Length-consistency, and Network methods of self-calibration. Precis. Eng. 2018, 52, 15–29. [Google Scholar] [CrossRef]
- Medić, T.; Kuhlmann, H.; Holst, C. Automatic in-situ self-calibration of a panoramic TLS from a single station using 2D keypoints. In ISPRS Annals of the Photogrammetry, Remote Sensing and Spatial Information Sciences; ISPRS: Enschede, The Netherlands, 2019. [Google Scholar]
- Li, X.; Li, Y.; Xie, X.; Xu, L. Terrestrial Laser Scanner Autonomous Self-Calibration with No Prior Knowledge of Point-Clouds. IEEE Sens. J. 2018, 18, 9277–9285. [Google Scholar] [CrossRef]
- Garcia-San-Miguel, D.; Lerma, J.L. Geometric calibration of a terrestrial laser scanner with local additional parameters: An automatic strategy. ISPRS J. Photogramm. Remote Sens. 2013, 79, 122–136. [Google Scholar] [CrossRef]
- Lichti, D.D. Terrestrial laser scanner self-calibration: Correlation sources and their mitigation. ISPRS J. Photogramm. Remote Sens. 2010, 65, 93–102. [Google Scholar] [CrossRef]
- Lichti, D.D.; Chow, J.; Lahamy, H. Parameter de-correlation and model-identification in hybrid-style terrestrial laser scanner self-calibration. ISPRS J. Photogramm. Remote Sens. 2011, 66, 317–326. [Google Scholar] [CrossRef]
- Medić, T.; Kuhlmann, H.; Holst, C. Sensitivity Analysis and Minimal Measurement Geometry for the Target-Based Calibration of High-End Panoramic Terrestrial Laser Scanners. Remote Sens. 2019, 11, 1519. [Google Scholar] [CrossRef]
- Muralikrishnan, B.; Ferrucci, M.; Sawyer, D.; Gerner, G.; Lee, V.; Blackburn, C.; Phillips, S.; Petrov, P.; Yakovlev, Y.; Astrelin, A.; et al. Volumetric performance evaluation of a laser scanner based on geometric error model. Precis. Eng. 2015, 40, 139–150. [Google Scholar] [CrossRef]
- Chan, T.O.; Lichti, D.D.; Belton, D. A rigorous cylinder-based self-calibration approach for terrestrial laser scanners. ISPRS J. Photogramm. Remote Sens. 2015, 99, 84–99. [Google Scholar] [CrossRef]
- Chow, J.C.K.; Teskey, W.F.; Lovse, J.W. In-situ Self-calibration of Terrestrial Laser Scanners and Deformation Analysis Using Both Signalized Targets and Intersection of Planes for Indoor Applications. In Proceedings of the 14th FIG Symposium on Deformation Measurements and Analysis, Hong Kong, China, 2–4 November 2011. [Google Scholar]
- Chow, J.C.K.; Lichti, D.D.; Glennie, C. Point-based versus plane-based self-calibration of static terrestrial laser scanners. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2011, 38, 121–126. [Google Scholar] [CrossRef]
- Abbas, M.A.; Lichti, D.D.; Chong, A.K.; Setan, H.; Majid, Z.; Lau, C.L.; Idris, K.M.; Ariff, M.F.M. Improvements to the accuracy of prototype ship models measurement method using terrestrial laser scanner. Meas. J. Int. Meas. Confed. 2017, 100, 301–310. [Google Scholar] [CrossRef]
- Lichti, D.D.; Chow, J.C.K. Inner Constraints for Planar Features. Photogramm. Rec. 2013, 28, 74–85. [Google Scholar] [CrossRef]
- Ge, X. Terrestrial Laser Scanning Technology from Calibration to Registration with Respect to Deformation Monitoring; Technical University of Munich: Munich, Germany, 2016. [Google Scholar]
- Medić, T.; Holst, C.; Kuhlmann, H. Towards System Calibration of Panoramic Laser Scanners from a Single Station. Sensors 2017, 17, 1145. [Google Scholar] [CrossRef]
- Lichti, D.D. The impact of angle parameterisation on terrestrial laser scanner self-calibration. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci 2009, 38, 171–176. [Google Scholar]
- Medić, T.; Holst, C.; Kuhlmann, H. Improving the results of terrestrial laser scanner calibration by an optimized calibration process. In Photogrammetrie Laserscanning Optische 3DMesstechnik—Beiträge der Oldenburger 3D-Tage; Wichmann Verlag: Oldenburg/Berlin, Germany, 2019; pp. 36–50. [Google Scholar]
- Parian, J.A. Sensor Modeling, Calibration and Point Positioning with Terrestrial Panoramic Cameras; Inst. für Geodäsie und Photogrammetrie: Zürich, Switzerland, 2007; p. 121. [Google Scholar]
- Holst, C.; Kuhlmann, H. Aiming at self-calibration of terrestrial laser scanners using only one single object and one single scan. J. Appl. Geod. 2014, 8, 295–310. [Google Scholar] [CrossRef]
- Muralikrishnan, B.; Rachakonda, P.; Shilling, M.; Lee, V.; Blackburn, C.; Sawyer, D.; Cheok, G.; Cournoyer, L. Report on the May 2016 ASTM E57.02 Instrument Runoff at NIST, Part 1—Background Information and Key Findings; US Department of Commerce, National Institute of Standards and Technology: Washington, DC, USA, 2016. [Google Scholar] [CrossRef]
- Walsh, G. Leica ScanStation P-Series—Details that matter. Leica ScanStation—White Paper. Available online: http://blog.hexagongeosystems.com/wp-content/uploads/2015/12/Leica_ScanStation_P-Series_details_that_matter_white_paper_en-4.pdf (accessed on 21 May 2019).
- Schofield, W.; Breach, M. Engineering Surveying, 6th ed.; Elsevier: Oxford, UK, 2007; ISBN 9780750669498. [Google Scholar]
- Förstner, W.; Wrobel, B.P. Photogrammetric Computer Vision; Springer International Publishing: Cham, Switzerland, 2016; ISBN 9783319115498. [Google Scholar]
- Medić, T.; Holst, C.; Janßen, J.; Kuhlmann, H. Empirical stochastic model of detected target centroids: Influence on registration and calibration of terrestrial laser scanners. J. Appl. Geod. 2019. [Google Scholar] [CrossRef]
- Kuang, S. Geodetic Network Analysis and Optimal Design: Concepts and Applications; Ann Arbor Press: Chelsea, UK, 1996. [Google Scholar]
- Grafarend, E.W.; Sanso, F. Optimization and Design of Geodetic Networks, 1st ed.; Springer: Berlin/Heidelberg, Germany, 1985; ISBN 9783642706615. [Google Scholar]
- Saleh, H.A.; Chelouah, R. The design of the global navigation satellite system surveying networks using genetic algorithms. Eng. Appl. Artif. Intell. 2004, 17, 111–122. [Google Scholar] [CrossRef]
- Baselga, S. Second order design of geodetic networks by the simulated annealing method. J. Surv. Eng. 2011, 137, 167–173. [Google Scholar] [CrossRef]
- Niemeier, W. Ausgleichungsrechnung: Statistische Auswertemethoden; Walter de Gruyter: Berlin, Germany, 2008; ISBN 3110206781. [Google Scholar]
- Abbas, M.A.; Setan, H.; Majid, Z.; Idris, K.M.; Chong, A.K.; Lichti, D.D. The Effect of Datum Constraints for Terrestrial Laser Scanner Self-Calibration The Effect of Datum Constraints for Terrestrial Laser Scanners Self-Calibration. In Proceedings of the FIG Congress 2014, Kuala Lumpur, Malaysia, 16–21 June 2014. [Google Scholar]
- Abbas, M.A.; Setan, H.; Majid, Z.; Chong, A.K.; Lichti, D.D. Improvement in measurement accuracy for hybrid scanner. IOP Conf. Ser. Earth Environ. Sci. 2014, 18, 012066. [Google Scholar] [CrossRef]
- Jia, F.; Lichti, D.D. An Efficient, Hierarchical Viewpoint Planning Strategy for Terrestrial Laser Scanner Networks. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, 4. [Google Scholar] [CrossRef]
- Soudarissanane, S.; Lindenbergh, R. Optimizing Terrestrial Laser Scanning Measurement Set-Up. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, XXXVIII-5, 127–132. [Google Scholar] [CrossRef]
- Díaz-Vilariño, L.; Frías, E.; Balado, J.; González-Jorge, H. SCAN Planning and Route Optimization for Control of Execution of As-Designed Bim. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, XLII-4, 143–148. [Google Scholar]
- Jia, F.; Lichti, D. A comparison of simulated annealing, genetic algorithm and particle swarm optimization in optimal first-order design of indoor TLS networks. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 4, 75–82. [Google Scholar] [CrossRef]
- Amiri-Simkooei, A.R.; Asgari, J.; Zangeneh-Nejad, F.; Zaminpardaz, S. Basic Concepts of Optimization and Design of Geodetic Networks. J. Surv. Eng. 2012, 138, 172–183. [Google Scholar] [CrossRef]
- González-Aguilera, D.; Rodríguez-Gonzálvez, P.; Armesto, J.; Arias, P. Trimble GX200 and Riegl LMS-Z390i sensor self-calibration. Opt. Express 2011, 19, 2676–2693. [Google Scholar] [CrossRef]
- Baarda, W. A Testing Procedure for Use in Geodetic Networks. Netherlands Geod. Comm. 1968, 2, 64–71. [Google Scholar]
- Baarda, W. Statistical Concepts in Geodesy’, Netherlands Geod; Commission New Series; Publications on Geodesy: Waltman, The Netherlands, 1967; Volume 2. [Google Scholar]
- Heinz, E.; Eling, C.; Wieland, M.; Klingbeil, L.; Kuhlmann, H. Analysis of different reference plane setups for the calibration of a mobile laser scanning system. In Proceedings of the Internationalen Ingenieurvermessungskurs, Graz, Austria, 17–20 April 2017; pp. 25–29. [Google Scholar]
- Langley, R.B. Dilution of precision. GPS World 1999, 10, 52–59. [Google Scholar]
- Janßen, J.; Medić, T.; Kuhlmann, H.; Holst, C. Decreasing the uncertainty of the target centre estimation at terrestrial laser scanning by choosing the best algorithm and by improving the target design. Remote Sens. 2019, 11, 845. [Google Scholar] [CrossRef]
- Schwintzer, P. Zur Bestimmung der Signifikanten Parameter in Approximationsfunktionen. Inst. für Geodäsie der UniBW München München, Ger. 1984, 10, 71–91. [Google Scholar]
- Chow, J.C.K.; Lichti, D.D.; Teskey, W.F.; Key, C. Accuracy assessment of the FARO Focus 3D and Leica HDS6100 panoramic-type terrestrial laser scanners through point-based and plane-based user self-calibration. In Proceedings of the FIG Working Week: Knowing to Manage the Territory, Protect the Environment, Evaluate the Cultural Heritage, Rome, Italy, 6–10 May 2012. [Google Scholar]
- Lague, D.; Brodu, N.; Leroux, J. Accurate 3D comparison of complex topography with terrestrial laser scanner: Application to the Rangitikei canyon (NZ). ISPRS J. Photogramm. Remote Sens. 2013, 82, 10–26. [Google Scholar] [CrossRef]
- Mikhail, E.W. Observations and Least Squares; IEP Don-Donnelley: New York, NY, USA, 1976. [Google Scholar]
- Nocerino, E.; Menna, F.; Remondino, F.; Toschi, I.; Rodríguez-Gonzálvez, P. Investigation of indoor and outdoor performance of two portable mobile mapping systems. In Videometrics, Range Imaging, and Applications XIV; SPIE: Munich, Germany, 2017; Volume 10332, p. 103320I. [Google Scholar]
- Toschi, I.; Rodríguez-Gonzálvez, P.; Remondino, F.; Minto, S.; Orlandini, S.; Fuller, A. Accuracy evaluation of a mobile mapping system with advanced statistical methods. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, 40, 245. [Google Scholar] [CrossRef]
| CP | Description |
|---|---|
| x1n | Horizontal beam offset ** |
| x1z | Vertical beam offset ** |
| x2 | Horizontal axis offset |
| x3 | Mirror offset |
| x4 | Vertical index offset |
| x5n | Horizontal beam tilt |
| x5z | Vertical beam tilt ** |
| x6 | Mirror tilt |
| x7 | Horizontal axis error (tilt) |
| x10 | Rangefinder offset * |
| CP | with | |||||
|---|---|---|---|---|---|---|
| [mm] | –2.00 | –1.99 | 0.02 | 0.39 | 0.02 | |
| [mm] | –0.20 | –0.21 | 0.01 | –0.49 | 0.01 | |
| [mm] | –0.20 | –0.20 | 0.00 | –0.67 | 0.01 | |
| [ “ ] | –8.00 | –7.99 | 0.05 | 0.72 | 0.06 | |
| [mm] | –0.20 | –0.20 | 0.01 | 0.72 | 0.02 | |
| [ “ ] | 8.00 | 7.36 | 0.47 | 0.75 | 0.46 | |
| [ “ ] | –8.00 | –8.58 | 0.39 | 0.75 | 0.46 | |
| [mm] | –0.20 | –0.20 | 0.01 | –0.50 | 0.01 | |
| [ “ ] | –8.00 | –7.39 | 0.29 | –0.68 | 0.35 | |
| [ “ ] | –8.00 | –8.06 | 0.07 | –0.68 | 0.10 |
| CP | with | |||||
|---|---|---|---|---|---|---|
| [mm] | –2.00 | –2.02 | 0.01 | 0.05 | 0.00 | |
| [mm] | –0.20 | –0.20 | 0.00 | –0.28 | 0.00 | |
| [mm] | –0.20 | –0.20 | 0.00 | –0.70 | 0.00 | |
| [ “ ] | –8.00 | –7.97 | 0.03 | –0.70 | 0.03 | |
| [mm] | –0.20 | –0.20 | 0.00 | 0.53 | 0.01 | |
| [ “ ] | 8.00 | 8.07 | 0.46 | 0.72 | 0.29 | |
| [ “ ] | –8.00 | –8.02 | 0.35 | 0.72 | 0.09 | |
| [mm] | –0.20 | –0.20 | 0.00 | –0.62 | 0.00 | |
| [ “ ] | –8.00 | –8.13 | 0.29 | –0.62 | 0.27 | |
| [ “ ] | –8.00 | –7.92 | 0.06 | –0.06 | 0.08 |
| CP | with | |||||
|---|---|---|---|---|---|---|
| [mm] | –2.00 | –1.96 | 0.06 | 0.41 | 0.06 | |
| [mm] | –0.20 | –0.22 | 0.03 | –0.45 | 0.02 | |
| [mm] | –0.20 | –0.17 | 0.02 | –0.61 | 0.04 | |
| [ “ ] | –8.00 | –8.25 | 0.19 | 0.71 | 0.31 | |
| [mm] | –0.20 | –0.19 | 0.03 | 0.71 | 0.10 | |
| [ “ ] | 8.00 | 6.39 | 1.96 | 0.78 | 2.03 | |
| [ “ ] | –8.00 | –10.70 | 1.69 | 0.78 | 1.77 | |
| [mm] | –0.20 | –0.16 | 0.03 | –0.48 | 0.03 | |
| [ “ ] | –8.00 | –9.04 | 1.18 | –0.51 | 1.06 | |
| [ “ ] | –8.00 | –7.41 | 0.33 | –0.51 | 0.64 |
| Instrument | P50 | P20 | Imager 5016 | HDS6100 | Focus3D | BLK360 |
|---|---|---|---|---|---|---|
| Date | 16 April 2019 | 8 August 2018 | 27 May 2019 | 7 August 2018 | 7 August 2018 | 7 August 2018 |
| Duration | 1 h | 1 h | 1 h | 2 h | 2 h | 40 min |
| Scans # | 4 | 4 | 4 | 4** | 8 | 8 |
| Observations # | 168 | 168 | 168 | 168 | 336 | 336 |
| Two-face m. | yes | yes | yes | yes | no | no |
| Compensator | yes | yes | yes | no | no | no |
| Resolution [mm @ 10 m] | 1.6 | 1.6 | 1.6 | 1.6 | 1.6 | 5.0 |
| [mm] | 1.2 | 1.0 | 1.0 | 2.0 | 2.0 | 4.0 |
| [ ″ ] | 8.0 | 8.0 | 14.4 | 26.0 | 19.0 | 41.0 |
| [ ″ ] | 1.5 | 1.5 | 14.4 | - | - | - |
| Temperature* | 17.9 | 28.0 | 16.8 | 31.2 | 33.1 | 33.1 |
| Pressure* | 996.2 | 991.5 | 990.1 | 989.0 | 988.3 | 988.3 |
| Humidity* | 42.5 | 54.0 | 75.0 | 31.5 | 27.5 | 27.5 |
| CP | P50 | P20 | Imager | HDS6100 | Focus3D | BLK360 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| sgf. | sgf. | sgf. | sgf. | sgf. | sgf. | |||||||
| [mm] | –0.03 | N | 0.58 | Y | 0.37 | Y | 0.11 | N | 0.23 | Y | 4.29 | Y |
| [mm] | –0.14 | Y | –0.09 | N | 0.03 | N | 0.03 | N | 0.05 | N | 0.04 | N |
| [mm] | 0.14 | N | –0.23 | Y | 0.59 | Y | –0.01 | N | 0.87 | N | 1.37 | Y |
| [mm] | –0.03 | N | 0.16 | Y | –0.15 | N | –0.64 | N | –0.28 | N | –0.41 | N |
| [ “ ] | –33.50 | Y | 3.78 | N | 26.49 | Y | –85.77 | Y | 122.14 | Y | –16.97 | N |
| [ “ ] | 3.41 | Y | 0.55 | N | 0.40 | N | 8.00 | Y | 10.28 | Y | –19.98 | Y |
| [mm] | 0.01 | N | 0.08 | N | –0.45 | Y | –0.54 | N | –0.17 | N | 0.05 | N |
| [ “ ] | 4.51 | Y | –6.70 | Y | –6.44 | Y | –8.13 | Y | –57.31 | Y | 52.03 | Y |
| [ “ ] | 5.38 | Y | –18.05 | Y | 12.74 | N | 57.07 | Y | –2.51 | N | –20.72 | Y |
| [ “ ] | –16.78 | Y | –2.53 | N | 2.66 | N | –64.81 | Y | 36.08 | Y | –3.49 | N |
| P50 | P20 | Imager 5016 | |||||||
| [ ″ ] | [ ″ ] | [ ″ ] | [ ″ ] | [ ″ ] | [ ″ ] | ||||
| no CPs | 0.15 | 93.73 | 18.36 | 0.28 | 26.14 | 8.79 | 0.12 | 32.07 | 4.82 |
| CPs | 0.06 | 24.72 | 1.86 | 0.25 | 13.39 | 4.47 | 0.06 | 17.73 | 3.40 |
| % | 56.76 | 73.62 | 89.87 | 10.87 | 48.79 | 49.22 | 48.98 | 44.70 | 29.50 |
| HDS6100 | FOCUS 3D | BLK360 | |||||||
| [mm] | [ ″ ] | [ ″ ] | [mm] | [ ″ ] | [ ″ ] | [mm] | [ ″ ] | [ ″ ] | |
| no CPs | 0.27 | 84.02 | 17.23 | 0.11 | 218.02 | 21.50 | 2.16 | 58.05 | 25.40 |
| CPs | 0.20 | 26.31 | 8.88 | 0.10 | 70.60 | 11.26 | 1.72 | 24.07 | 16.08 |
| % | 24.24 | 68.69 | 48.45 | 5.87 | 67.62 | 47.60 | 20.34 | 58.53 | 36.68 |
| CP | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| [mm] | –0.16 | 0.03 | 0.01 | –0.03 | –0.04 | 0.09 | 0.06 | 0.37 | 0.10 |
| [mm] | –0.12 | –0.11 | –0.12 | –0.14 | –0.12 | 0.01 | 0.02 | –0.23 | 0.02 |
| [mm] | 0.08 | 0.31 | 0.21 | 0.14 | 0.19 | 0.10 | 0.07 | 0.64 | 0.10 |
| [mm] | –0.02 | 0 | –0.06 | –0.03 | –0.03 | 0.03 | 0.05 | –0.77 | 0.08 |
| [ “ ] | –22.35 | –25.38 | –26.31 | –33.5 | –26.89 | 4.72 | 2.02 | 0.61 | 2.66 |
| [ “ ] | 4.19 | 3.59 | 4.11 | 3.41 | 3.83 | 0.38 | 0.31 | –0.77 | 0.46 |
| [mm] | 0.07 | 0.08 | 0.05 | 0.01 | 0.05 | 0.03 | 0.05 | –0.64 | 0.07 |
| [ “ ] | 4.2 | 5.1 | 5.17 | 4.51 | 4.75 | 0.47 | 0.32 | –0.70 | 0.64 |
| [ “ ] | 4.5 | 4.67 | 5.62 | 5.38 | 5.04 | 0.54 | 1.48 | –0.70 | 1.29 |
| [ “ ] | –12 | –14.71 | –14.33 | –16.78 | –14.46 | 1.96 | 1.07 | 0.18 | 0.86 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Medić, T.; Kuhlmann, H.; Holst, C. Designing and Evaluating a User-Oriented Calibration Field for the Target-Based Self-Calibration of Panoramic Terrestrial Laser Scanners. Remote Sens. 2020, 12, 15. https://doi.org/10.3390/rs12010015
Medić T, Kuhlmann H, Holst C. Designing and Evaluating a User-Oriented Calibration Field for the Target-Based Self-Calibration of Panoramic Terrestrial Laser Scanners. Remote Sensing. 2020; 12(1):15. https://doi.org/10.3390/rs12010015
Chicago/Turabian StyleMedić, Tomislav, Heiner Kuhlmann, and Christoph Holst. 2020. "Designing and Evaluating a User-Oriented Calibration Field for the Target-Based Self-Calibration of Panoramic Terrestrial Laser Scanners" Remote Sensing 12, no. 1: 15. https://doi.org/10.3390/rs12010015
APA StyleMedić, T., Kuhlmann, H., & Holst, C. (2020). Designing and Evaluating a User-Oriented Calibration Field for the Target-Based Self-Calibration of Panoramic Terrestrial Laser Scanners. Remote Sensing, 12(1), 15. https://doi.org/10.3390/rs12010015







