Spatiotemporal Modeling of Urban Growth Using Machine Learning
Abstract
1. Introduction
2. Materials and Methods
2.1. Input Variables
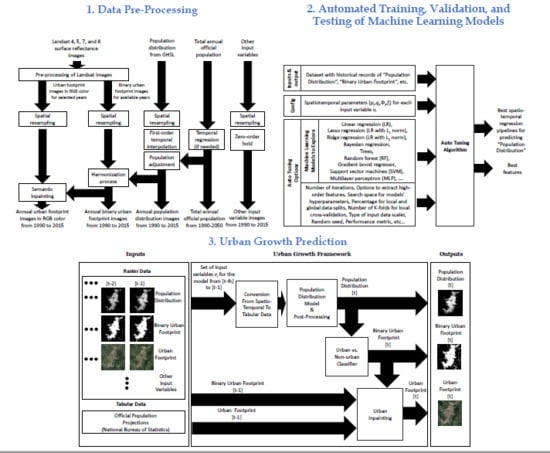
2.2. Data Pre-Processing
- Using images from Landsat missions to obtain a set of initial estimates of the urban footprint in RGB color and the binary urban footprint. This is covered in Section 2.2.1.
- Performing a content-aware spatial resampling of all input variables for getting digital images with a common coordinate reference system, geographic extent, and spatial resolution. This is explained in Section 2.2.2.
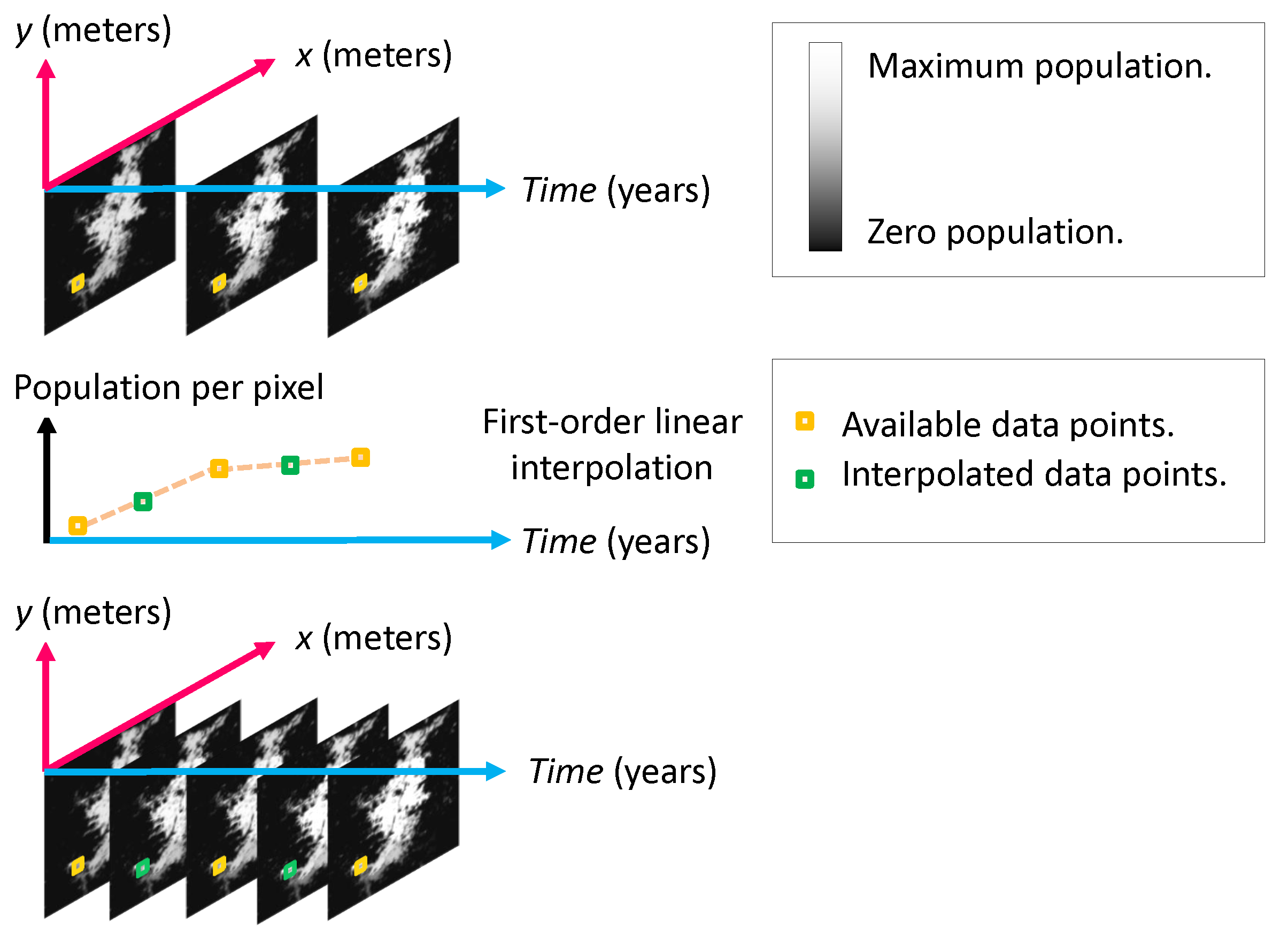
- Applying a first-order temporal interpolation to the population distribution for getting annual estimates, and optionally if available, applying an adjustment of the annual population distribution estimates to match the total population defined by the corresponding National Bureau of Statistics (see Section 2.2.3). Notice that, if the official population values are only available for a subset of the years of interest, then a temporal regression is applied to estimate the values in missing years.
- Estimating the binary urban footprint for missing years by harmonizing it with the historical population distribution. This process is detailed in Section 2.2.4;
- Using a semantic-inpainting algorithm for estimating the urban footprint in RGB color for missing years. The block in this pre-processing stage is the same to the one explained in Section 2.6.
- Applying a zero-order hold to get annual estimates of the other input variables in missing years.
2.2.1. Pre-Processing of Landsat Images
2.2.2. Content-Aware Spatial Resampling of Images
2.2.3. Temporal Interpolation of the Population Distribution and Official Adjustment
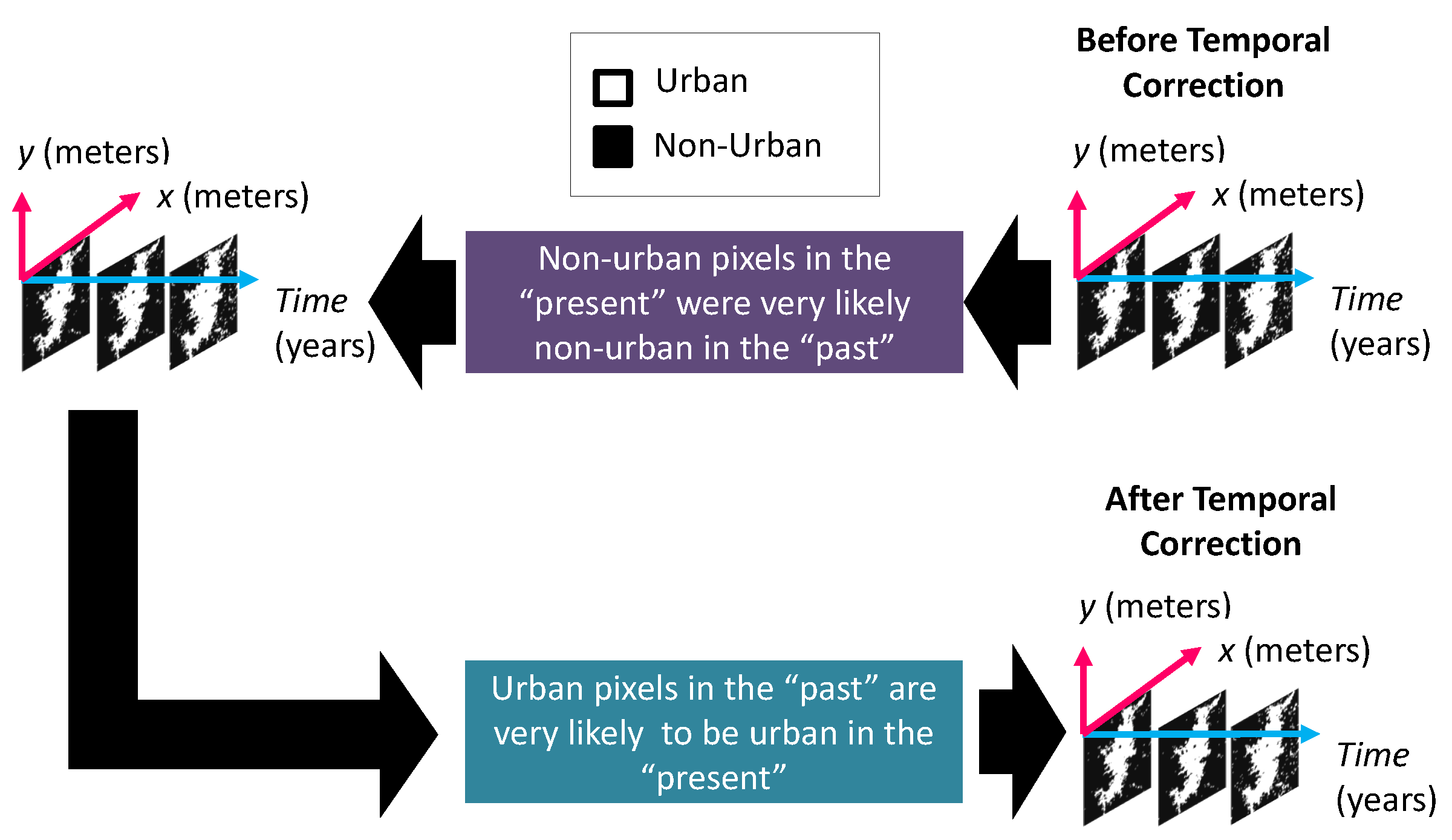
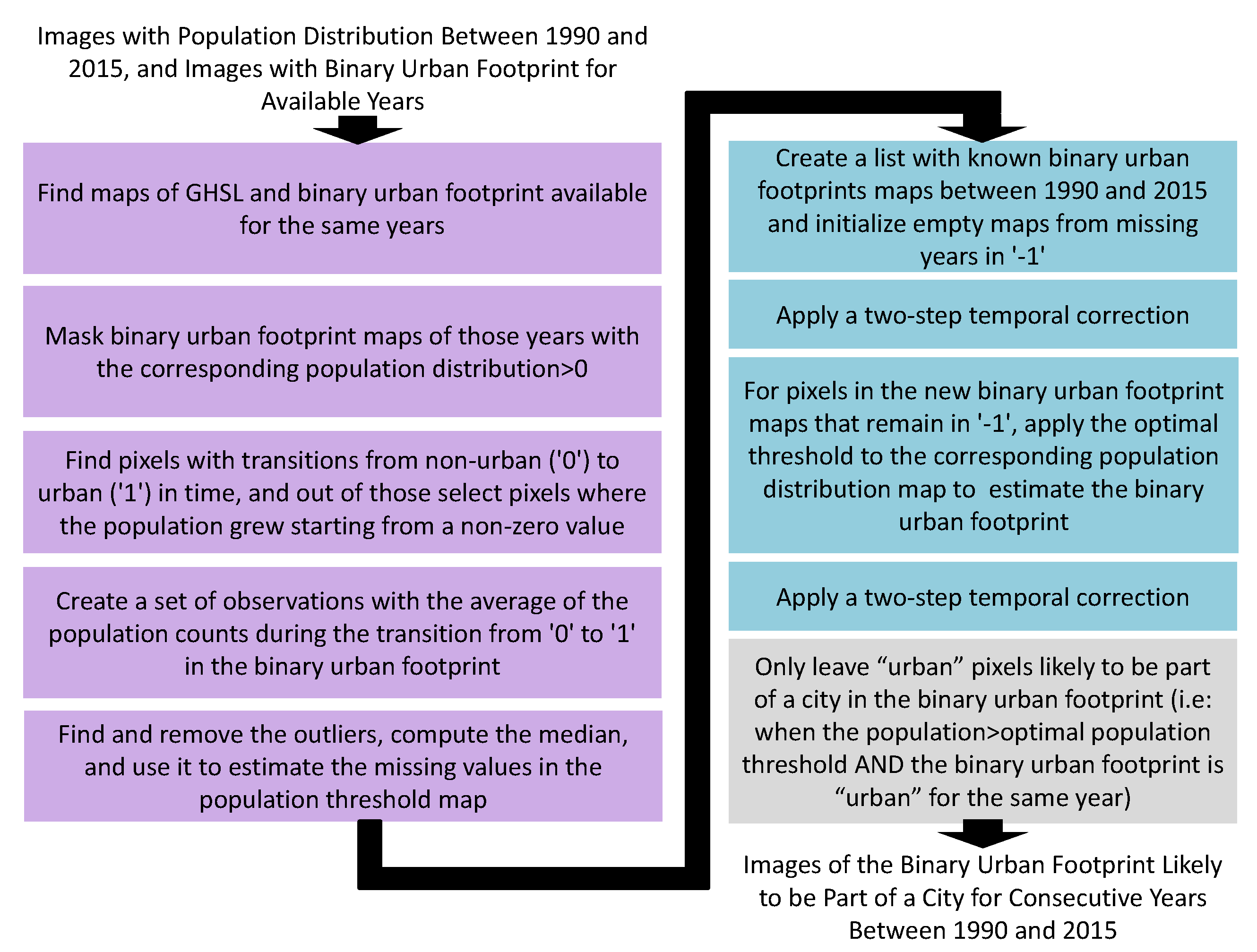
2.2.4. Harmonization Between the Binary Urban Footprint and the Population Distribution
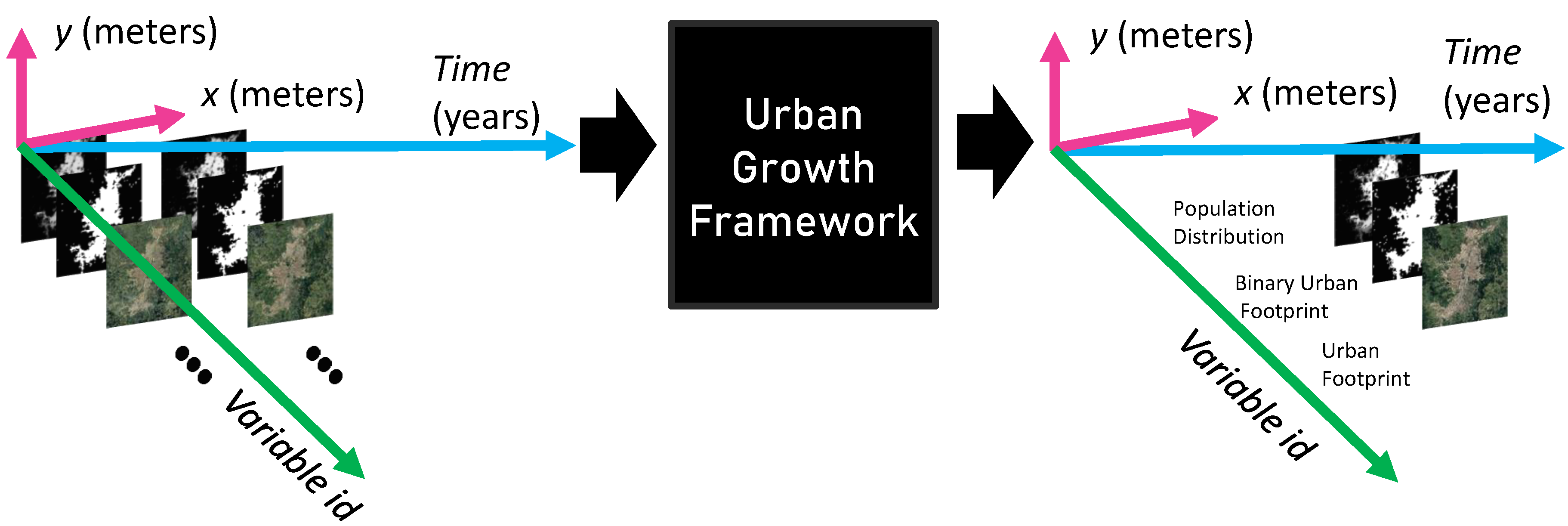
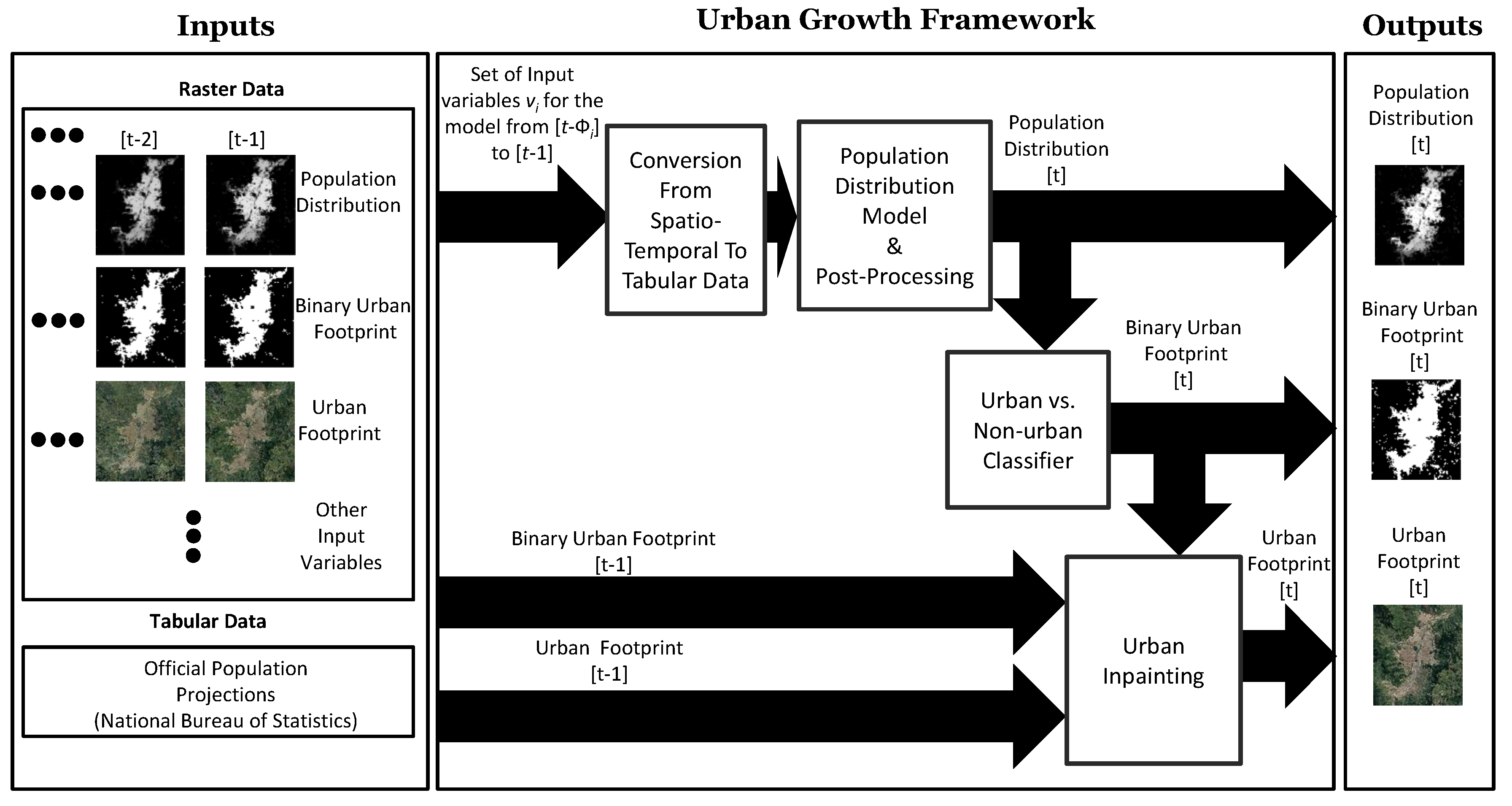
2.3. Urban Growth Model
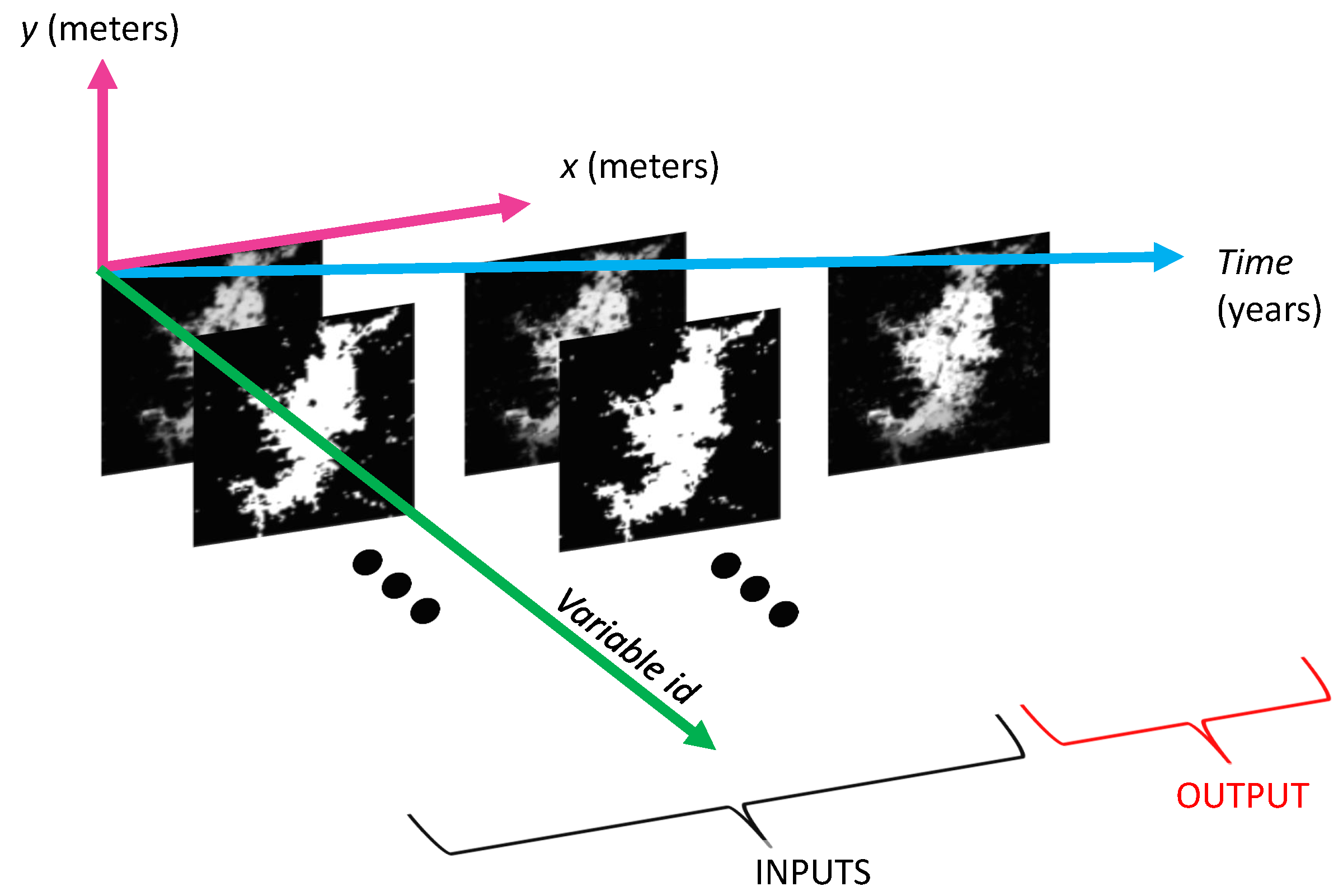
2.4. Spatiotemporal Regression Model for the Population Distribution
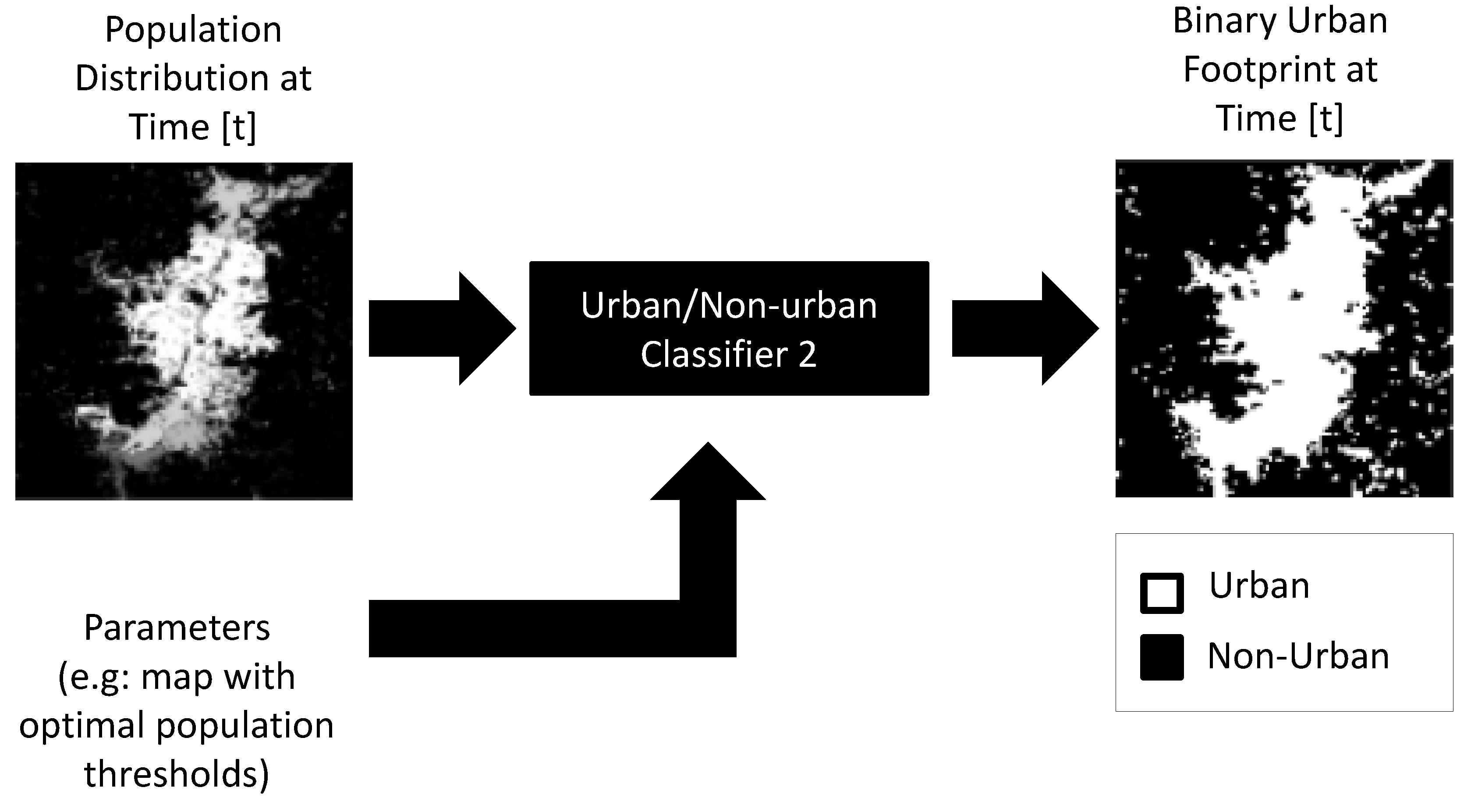
2.5. Binary Urban Footprint Estimation
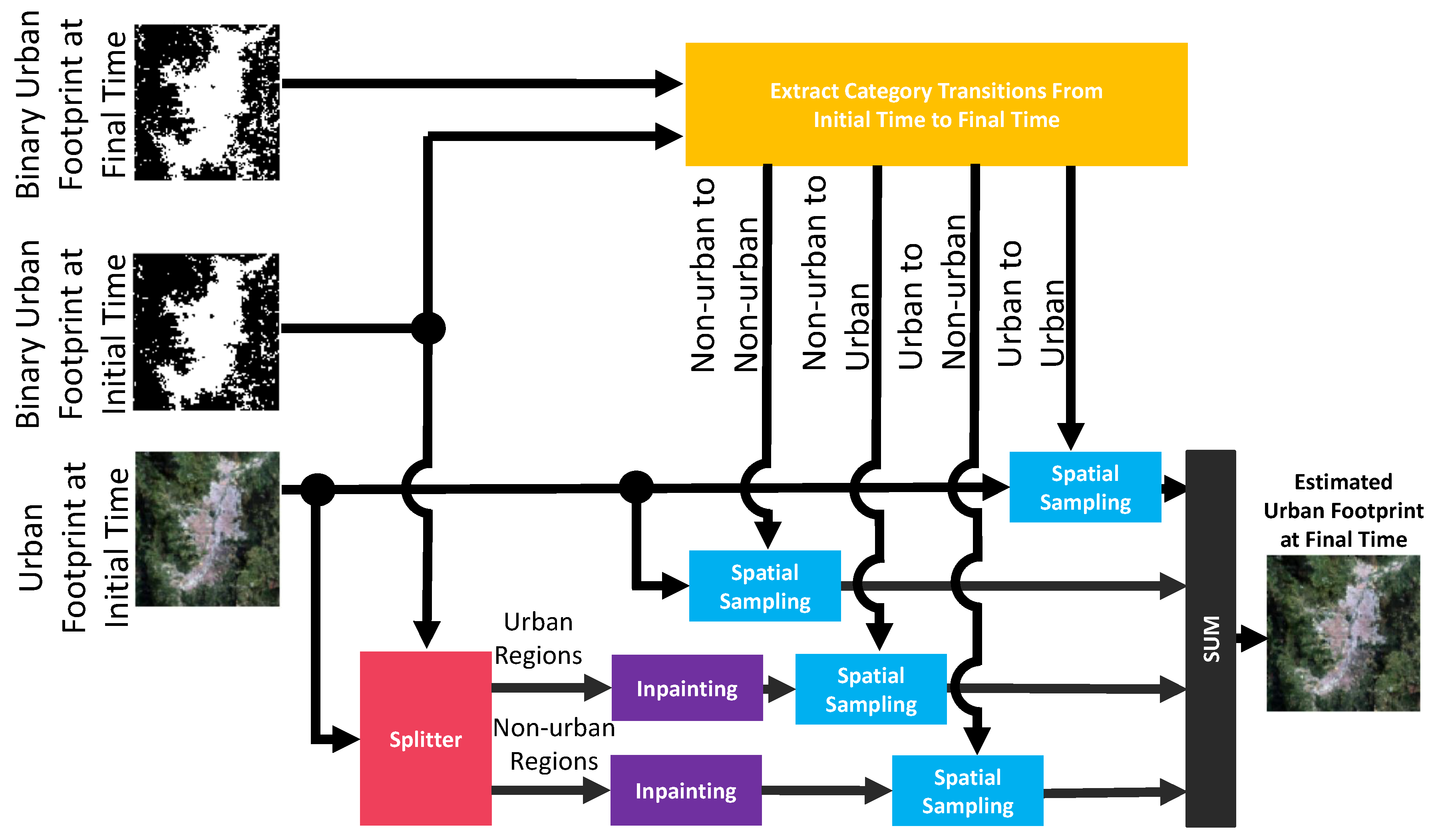
2.6. Urban Footprint Estimation
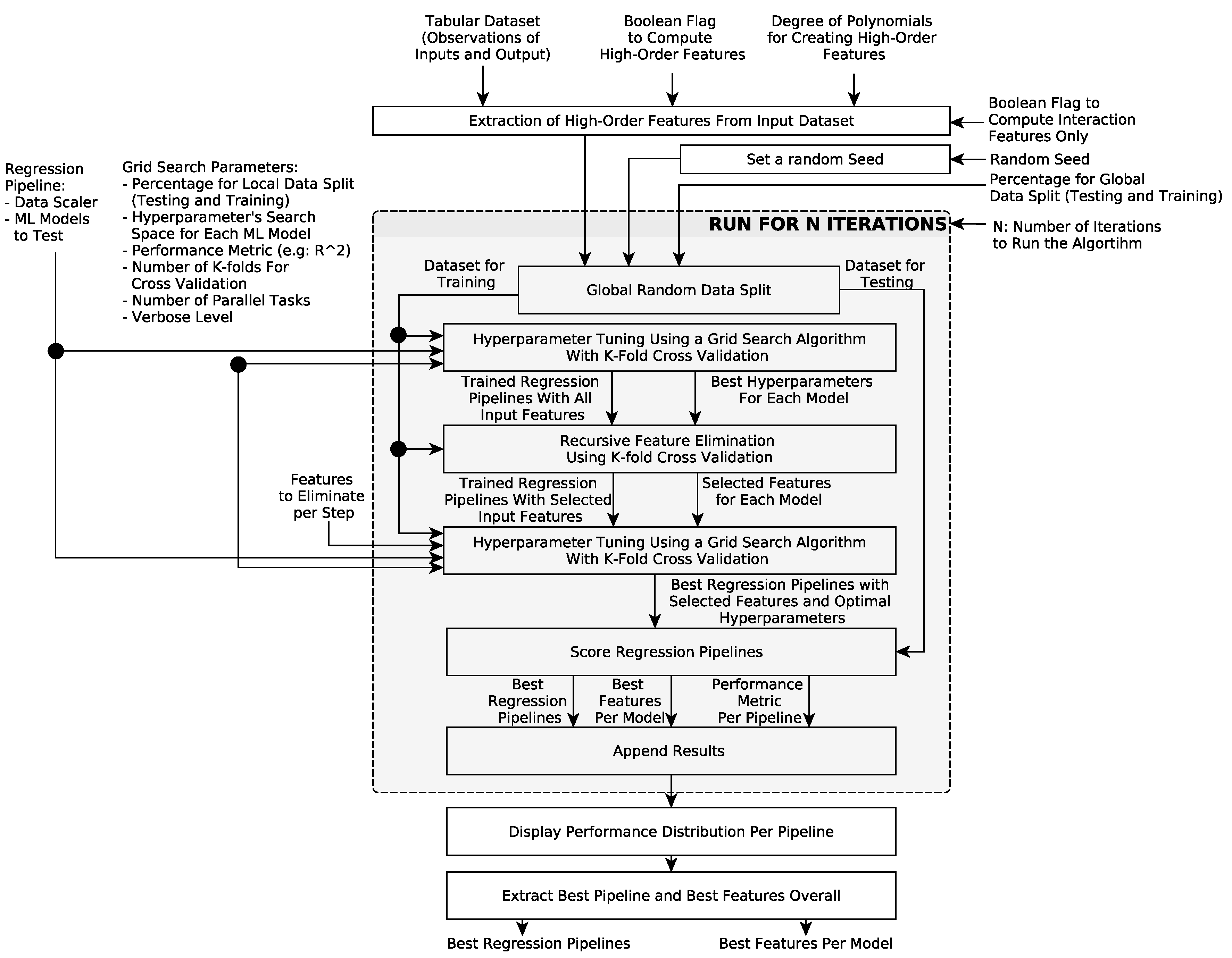
2.7. Training, Model Selection, and Testing Strategies
2.8. Implementation Details
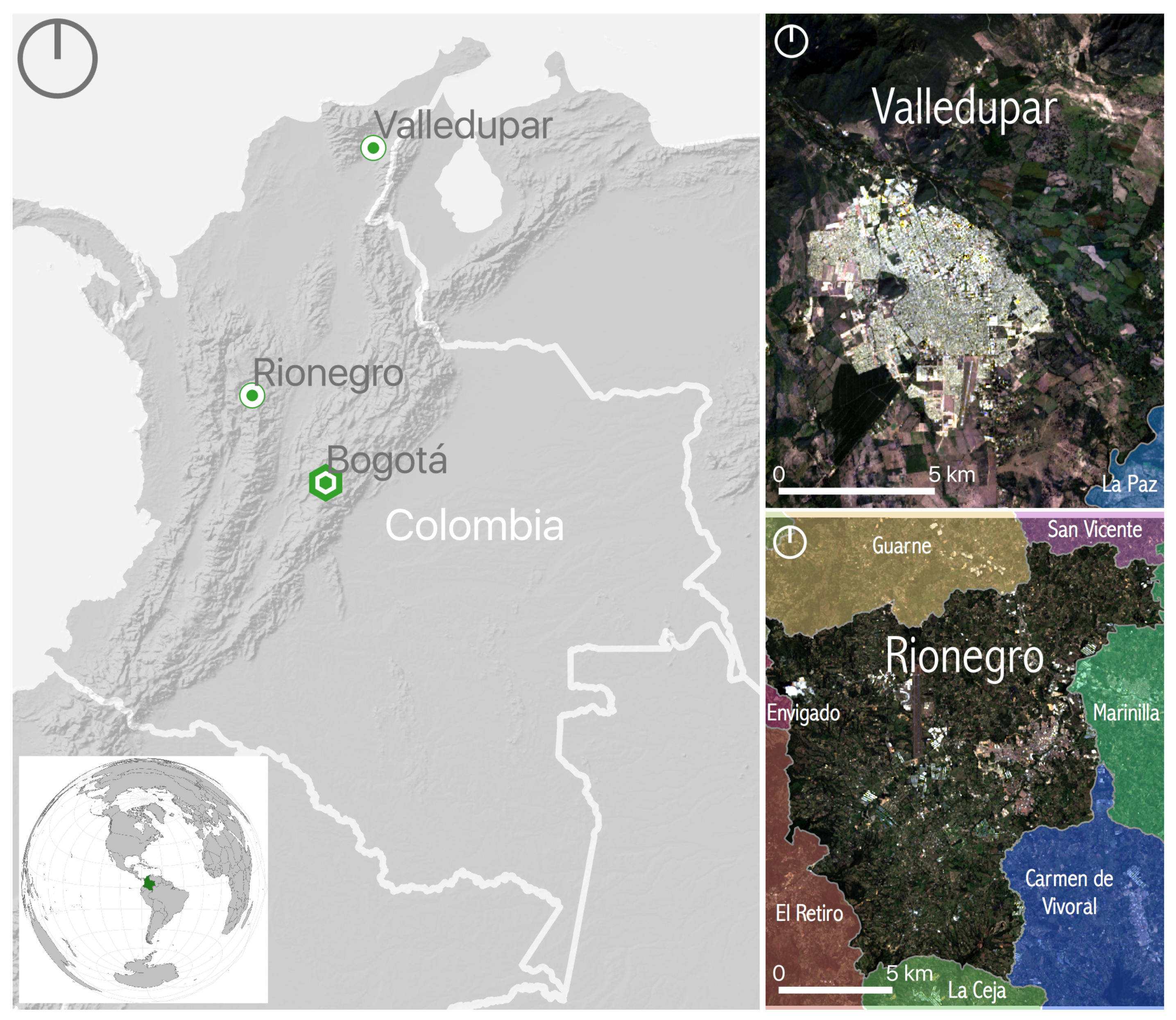
2.9. Case Studies
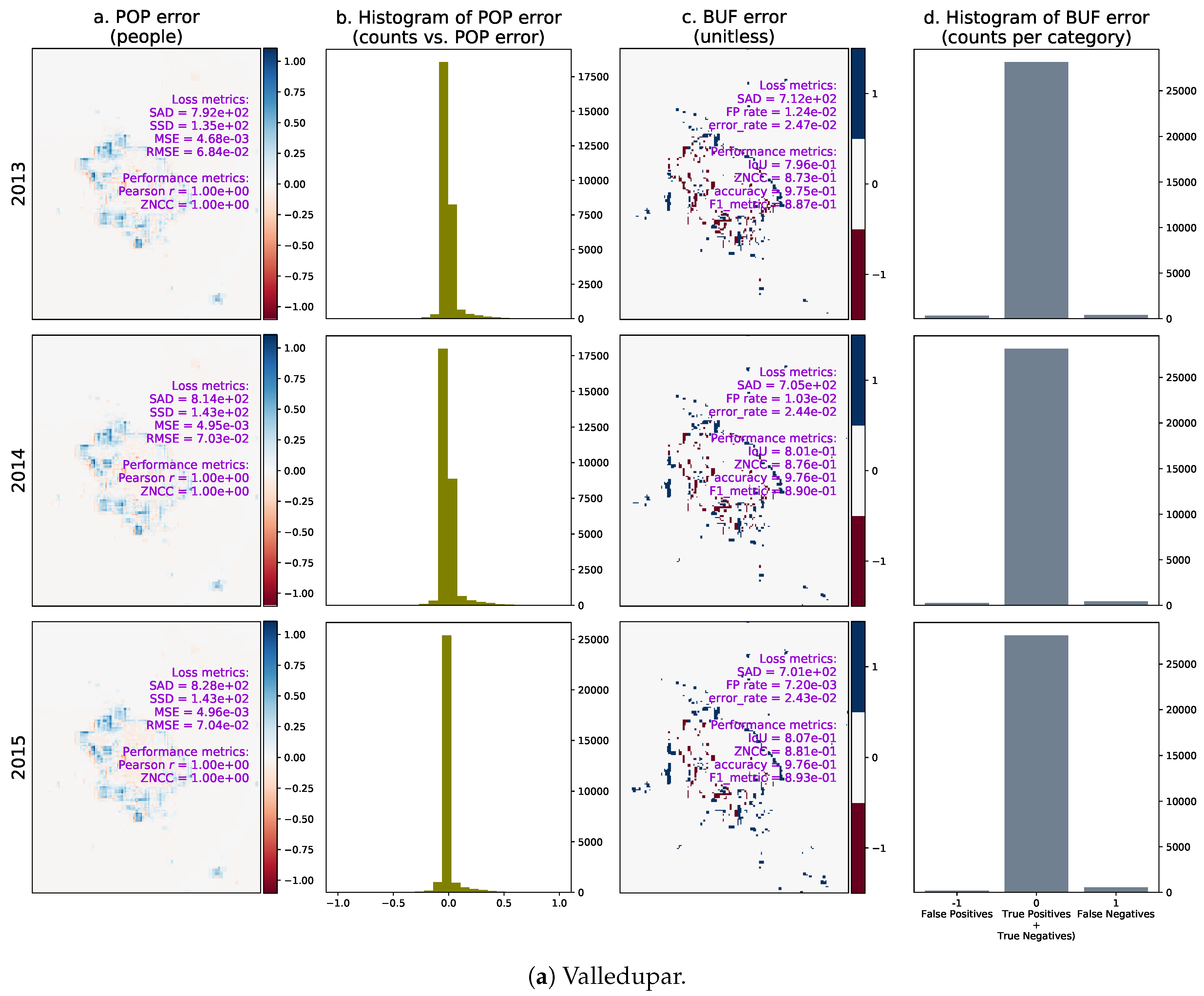
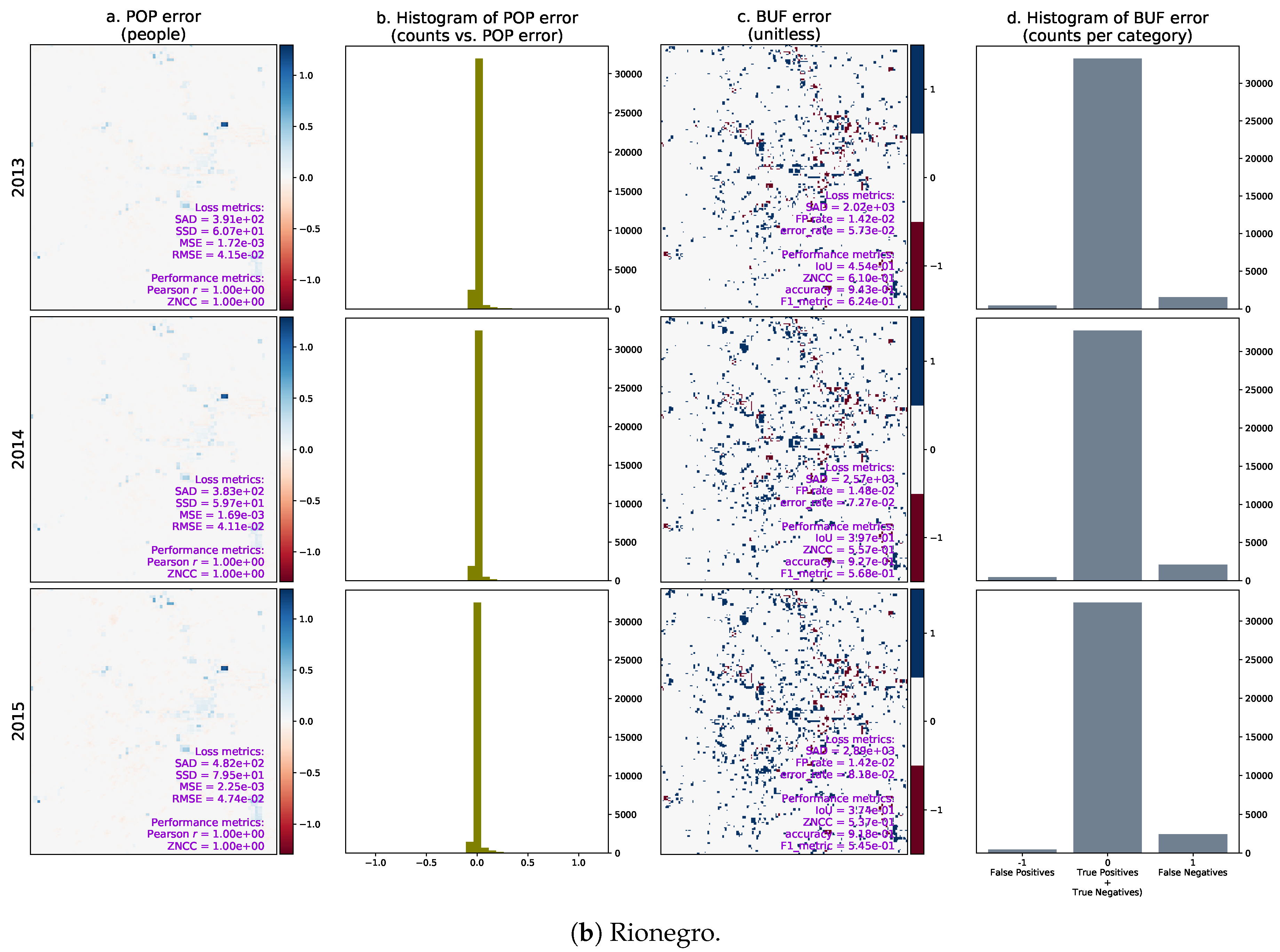
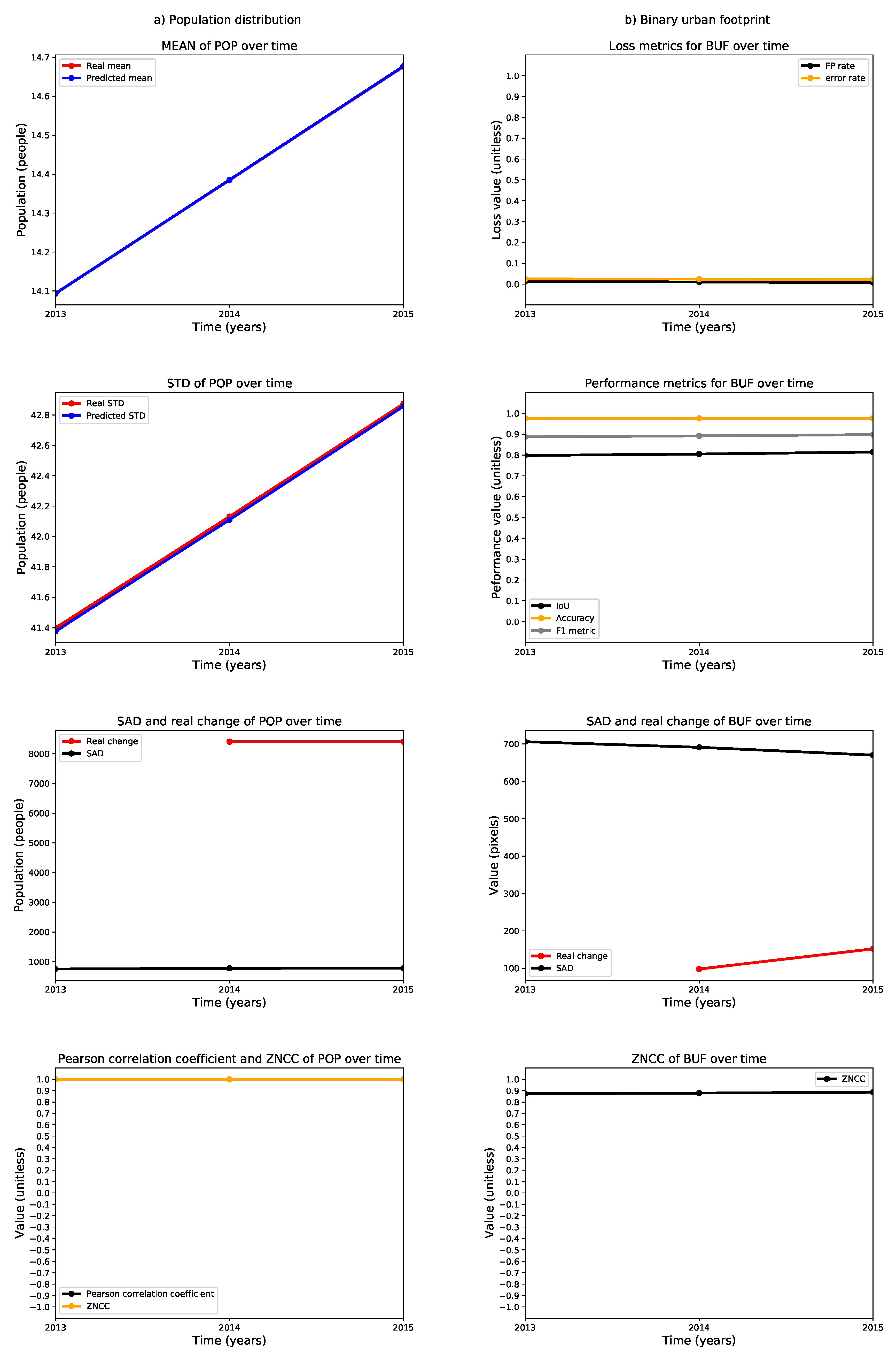
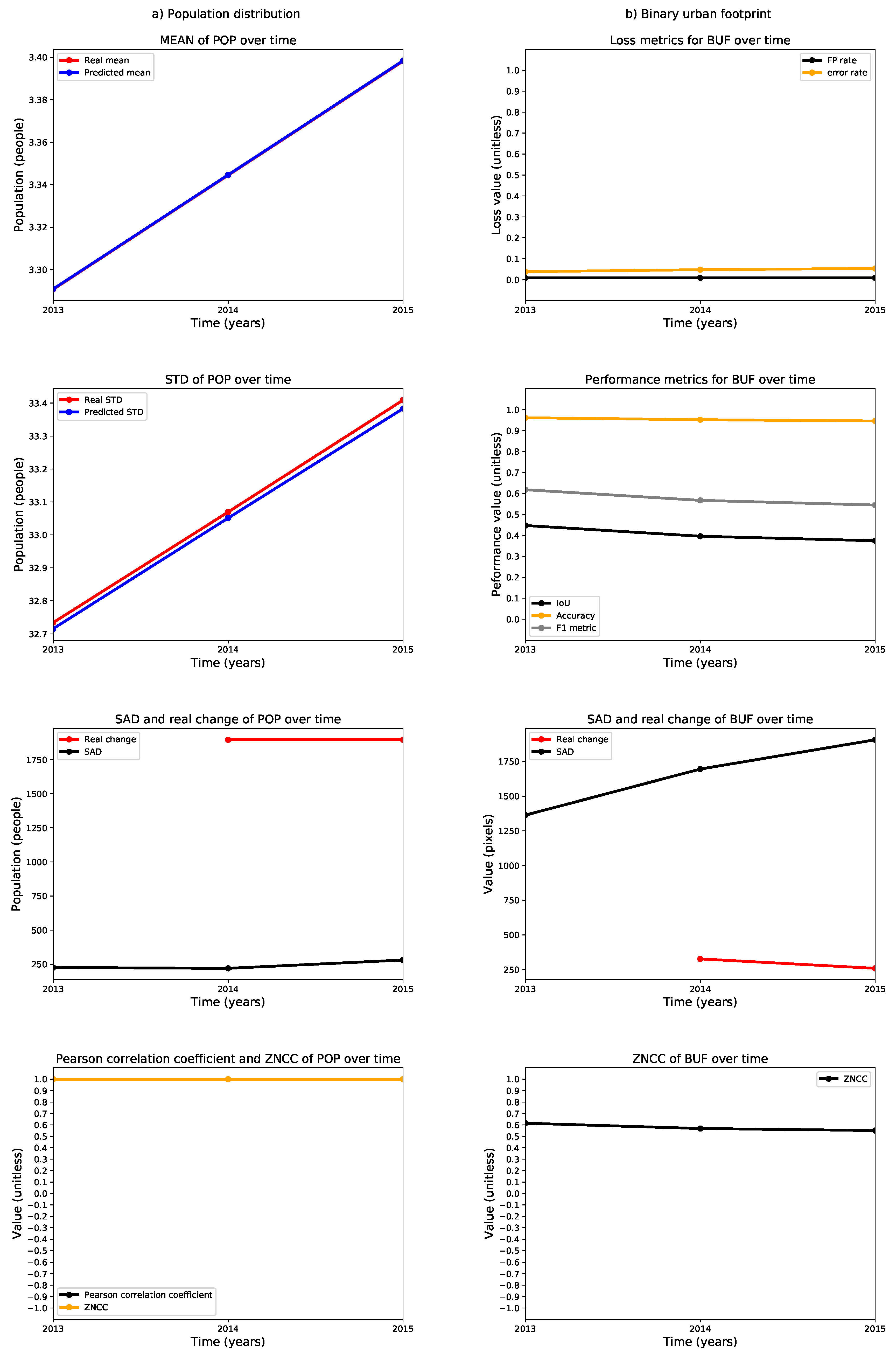
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| GHSL | Global human settlement layer |
| BUF | Binary urban footprint |
| POP | Population distribution |
| SAD | Sum of absolute differences |
| SSD | Sum of square differences |
| FP | False positive |
| ZNCC | Zero-mean normalized cross correlation |
| IoU | Intersection over Union |
| KDE | Kernel density estimation |
| Probability density function | |
| LAC | Latin American cities |
| ML | Machine learning |
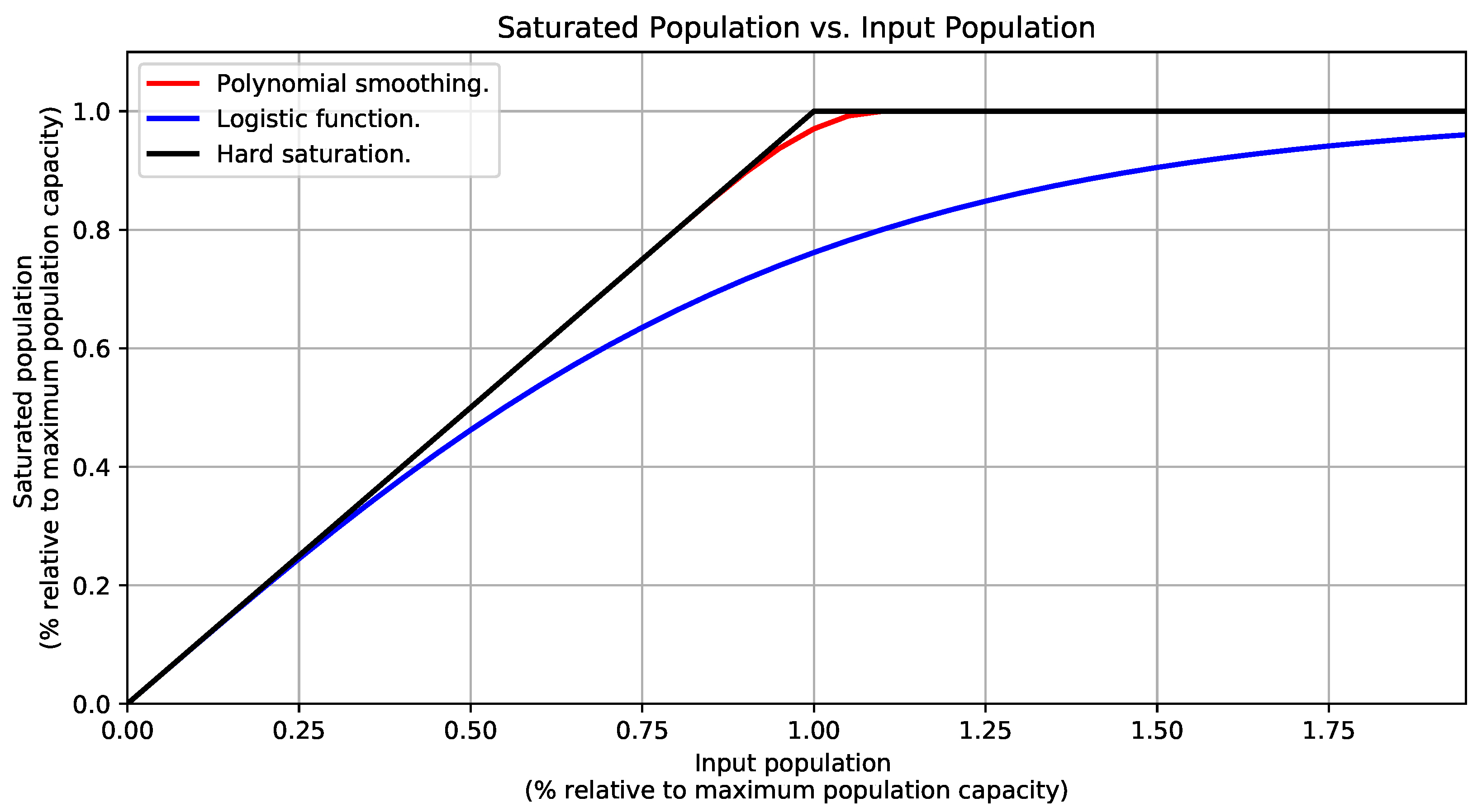
Appendix A. Saturation Functions for the Population Distribution
References
- United Nations. World Population Prospects 2019: Data Booket. ST/ESA/SER.A/424; Technical Report; United Nations, Department of Economic and Social Affairs, Population Division: New York, NY, USA, 2019. Available online: https://population.un.org/wpp/Publications/Files/WPP2019_DataBooklet.pdf (accessed on 30 November 2019).
- United Nations. Population Facts; Technical Report 4; United Nations, Department of Economic and Social Affairs: New York, NY, USA, 2019. Available online: https://www.un.org/en/development/desa/population/migration/publications/populationfacts/docs/MigrationStock2019_PopFacts_2019-04.pdf (accessed on 30 November 2019).
- United Nations. International Migration Report 2017: Highlights (ST/ESA/SER.A/404); Technical Report; United Nations, Department of Economic and Social Affairs: New York, NY, USA, 2017. Available online: https://www.un.org/en/development/desa/population/migration/publications/migrationreport/docs/MigrationReport2017_Highlights.pdf (accessed on 30 November 2019).
- Grant, U. Spatial Inequality and Urban Poverty Traps; Technical Report; Overseas Development Institute: London, UK, 2010; Available online: https://www.odi.org/publications/4526-spatial-inequality-and-urban-poverty-traps (accessed on 30 November 2019).
- Moore, M.; Gould, P.; Keary, B.S. Global urbanization and impact on health. Int. J. Hygiene Environ. Health 2003, 206, 269–278. [Google Scholar] [CrossRef] [PubMed]
- Huang, W.; Huang, Y.; Lin, S.; Chen, Z.; Gao, B.; Cui, S. Changing urban cement metabolism under rapid urbanization—A flow and stock perspective. J. Clean. Prod. 2018, 173, 197–206. [Google Scholar] [CrossRef]
- Flörke, M.; Schneider, C.; McDonald, R.I. Water competition between cities and agriculture driven by climate change and urban growth. Nat. Sustain. 2018, 1, 51. [Google Scholar] [CrossRef]
- DeFries, R.S.; Rudel, T.; Uriarte, M.; Hansen, M. Deforestation driven by urban population growth and agricultural trade in the twenty-first century. Nat. Geosci. 2010, 3, 178. [Google Scholar] [CrossRef]
- Panagopoulos, T.; González Duque, J.A.; Bostenaru Dan, M. Urban planning with respect to environmental quality and human well-being. Environ. Pollut. 2016, 208, 137–144. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Chen, B.; Fath, B.D. Urban ecosystem modeling and global change: Potential for rational urban management and emissions mitigation. Environ. Pollut. 2014, 190, 139–149. [Google Scholar] [CrossRef]
- Fang, C.; Wang, S.; Li, G. Changing urban forms and carbon dioxide emissions in China: A case study of 30 provincial capital cities. Appl. Energy 2015, 158, 519–531. [Google Scholar] [CrossRef]
- Seto, K.C.; Pandey, B. Urban Land Use: Central to Building a Sustainable Future. ONE Earth 2019, 1, 168–170. [Google Scholar] [CrossRef]
- Ahrend, R.; Farchy, E.; Kaplanis, I.; Lembcke, A.C. What Makes Cities More Productive? Evidence on the Role of Urban Governance from Five OECD Countries. OECD Reg. Dev. Work. Papers 2014, 5, 1–33. [Google Scholar] [CrossRef]
- Potere, D. Mapping the World’s cities: An Examination of Global Urban Maps And Their Implications for Conservation Planning. Ph.D. Thesis, Princeton University, Princeton, NJ, USA, 2009. [Google Scholar]
- Glaeser, E.L. Are Cities Dying? J. Econ. Perspect. 1998, 12, 139–160. [Google Scholar] [CrossRef]
- Jaffe, A.B.; Trajtenberg, M.; Henderson, R. Geographic Localization of Knowledge Spillovers as Evidenced by Patent Citations. Q. J. Econ. 1993, 108, 577–598. Available online: http://oup.prod.sis.lan/qje/article-pdf/108/3/577/5318741/108-3-577.pdf (accessed on 30 November 2019). [CrossRef]
- Lynch, K. A Theory of Good City Form; MIT Press: Cambridge, MA, USA; London, UK, 1981. [Google Scholar]
- Colsaet, A.; Laurans, Y.; Levrel, H. What drives land take and urban land expansion? A systematic review. Land Use Policy 2018, 79, 339–349. [Google Scholar] [CrossRef]
- He, Q.; He, W.; Song, Y.; Wu, J.; Yin, C.; Mou, Y. The impact of urban growth patterns on urban vitality in newly built-up areas based on an association rules analysis using geographical ‘big data’. Land Use Policy 2018, 78, 726–738. [Google Scholar] [CrossRef]
- Khanal, N.; Uddin, K.; Matin, M.; Tenneson, K. Automatic Detection of Spatiotemporal Urban Expansion Patterns by Fusing OSM and Landsat Data in Kathmandu. Remote Sens. 2019, 11, 2296. [Google Scholar] [CrossRef]
- Goldstein, N.C.; Candau, J.; Clarke, K. Approaches to simulating the “March of Bricks and Mortar”. Comput. Environ. Urban Syst. 2004, 28, 125–147. [Google Scholar] [CrossRef]
- Barredo, J.I.; Demicheli, L. Urban sustainability in developing countries’ megacities: Modelling and predicting future urban growth in Lagos. Cities 2003, 20, 297–310. [Google Scholar] [CrossRef]
- Duwal, S.; Amer, S.; Kuffer, M. Modelling urban growth in the Kathmandu Valley, Nepal. In Gis in Sustainable Urban Planning and Management: A Golbal Perspective, 1st ed.; van Maarseveen, M., Martinez, J., Flacke, J., Eds.; CRC Press: Boca Raton, MA, USA, 2018; Chapter 12; pp. 205–223. [Google Scholar] [CrossRef]
- Weng, Q. Remote sensing of impervious surfaces in the urban areas: Requirements, methods, and trends. Remote Sens. Environ. 2012, 117, 34–49. [Google Scholar] [CrossRef]
- Al-Darwish, Y.; Ayad, H.; Taha, D.; Saadallah, D. Predicting the future urban growth and it’s impacts on the surrounding environment using urban simulation models: Case study of Ibb city—Yemen. Alexandria Eng. J. 2018, 57. [Google Scholar] [CrossRef]
- Pérez-Molina, E.; Sliuzas, R.; Flacke, J.; Jetten, V. Developing a cellular automata model of urban growth to inform spatial policy for flood mitigation: A case study in Kampala, Uganda. Comput. Environ. Urban Syst. 2017, 65, 53–65. [Google Scholar] [CrossRef]
- Xia, C.; Zhang, A.; Wang, H.; Liu, J. Land Use Policy Delineating early warning zones in rapidly growing metropolitan areas by integrating a multiscale urban growth model with biogeography-based optimization. Land Use Policy 2019, 90, 104332. [Google Scholar] [CrossRef]
- Cosentino, C.; Amato, F.; Murgante, B. Population-based simulation of urban growth: The Italian case study. Sustainability 2018, 10, 4838. [Google Scholar] [CrossRef]
- Gounaridis, D.; Chorianopoulos, I.; Koukoulas, S. Exploring prospective urban growth trends under different economic outlooks and land-use planning scenarios: The case of Athens. Appl. Geogr. 2018, 90, 134–144. [Google Scholar] [CrossRef]
- Zhang, C.; Miao, C.; Zhang, W.; Chen, X. Spatiotemporal patterns of urban sprawl and its relationship with economic development in China during 1990–2010. Habit. Int. 2018, 79, 51–60. [Google Scholar] [CrossRef]
- Aghion, P.; Durlauf, S. Handbook of Economic Growth, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2005; Volume 2. [Google Scholar]
- Lung, T.; Lübker, T.; Ngochoch, J.K.; Schaab, G. Human population distribution modelling at regional level using very high resolution satellite imagery. Appl. Geogr. 2013, 41, 36–45. [Google Scholar] [CrossRef]
- Bhowmick, A.R.; Sardar, T.; Bhattacharya, S. Estimation of growth regulation in natural populations by extended family of growth curve models with fractional order derivative: Case studies from the global population dynamics database. Ecol. Inform. 2019, 53, 100980. [Google Scholar] [CrossRef]
- Wu, J.; Li, R.; Ding, R.; Li, T.; Sun, H. City expansion model based on population diffusion and road growth. Appl. Math. Model. 2017, 43, 1–14. [Google Scholar] [CrossRef]
- Tobler, W.R. A computer movie simulating urban growth in the Detroit region. Economic Geography 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Nduwayezu, G.; Sliuzas, R.; Kuffer, M. Modeling urban growth in Kigali city Rwanda. Rwanda J. 2017, 1. [Google Scholar] [CrossRef]
- Herold, M.; Goldstein, N.C.; Clarke, K.C. The spatiotemporal form of urban growth: Measurement, analysis and modeling. Remote Sens. Environ. 2003, 86, 286–302. [Google Scholar] [CrossRef]
- Ayazli, I.E.; Kilic, F.; Lauf, S.; Demir, H.; Kleinschmit, B. Simulating urban growth driven by transportation networks: A case study of the Istanbul third bridge. Land Use Policy 2015, 49, 332–340. [Google Scholar] [CrossRef]
- Thapa, R.B.; Murayama, Y. Scenario based urban growth allocation in Kathmandu Valley, Nepal. Landscape Urban Plan. 2012, 105, 140–148. [Google Scholar] [CrossRef]
- Makse, H.A.; Havlin, S.; Stanley, H.E. Modelling urban growth patterns. Nature 1995, 377, 608. [Google Scholar] [CrossRef]
- Tobler, W.R. Geographical filters and their inverses. Geogr. Anal. 1969, 1, 234–253. [Google Scholar] [CrossRef]
- Hu, Z.; Lo, C. Modeling urban growth in Atlanta using logistic regression. Comput. Environ. Urban Syst. 2007, 31, 667–688. [Google Scholar] [CrossRef]
- Clarke, K.C.; Hoppen, S.; Gaydos, L. A self-modifying cellular automaton model of historical urbanization in the San Francisco Bay area. Environ. Plan. B Plan. Des. 1997, 24, 247–261. [Google Scholar] [CrossRef]
- Clarke, K.C.; Gaydos, L.J. Loose-coupling a cellular automaton model and GIS: Long-term urban growth prediction for San Francisco and Washington/Baltimore. Int. J. Geogr. Inform. Sci. 1998, 12, 699–714. [Google Scholar] [CrossRef]
- Schiavina, M.; Freire, S.; MacManus, K. GHS Population Grid Multitemporal (1975, 1990, 2000, 2015) R2019A; Technical Report; European Commission, Joint Research Centre (JRC): Brussels, Belgium, 2019; Available online: http://data.europa.eu/89h/0c6b9751-a71f-4062-830b-43c9f432370f (accessed on 30 November 2019).
- Florczyk, A.J.; Melchiorri, M.; Corbane, C.; Schiavina, M.; Maffenini, M.; Pesaresi, M.; Politis, P.; Sabo, S.; Freire, S.; Ehrlich, D.; et al. Description of the GHS Urban Centre Database 2015, Public Release 2019, Version 1.0; Technical Report; Publications Office of the European Union: Luxembourg, 2019. [Google Scholar] [CrossRef]
- NASA; U.S. Geological Survey. Landsat Missions; Technical Report; NASA; U.S. Geological Survey: Reston, VA, USA, 2019. Available online: https://www.usgs.gov/land-resources/nli/landsat (accessed on 30 November 2019).
- DANE. Estimation and Projection of the Total National, Departmental, and Municipal Population by Area 1985–2020; Technical Report; National Administrative Department of Statistics (DANE): Bogotá, Colombia, 2019. Available online: https://www.dane.gov.co/index.php/estadisticas-por-tema/demografia-y-poblacion/proyecciones-de-poblacion (accessed on 30 November 2019).
- Rionegro Town Hall. Master Plan of Rionegro; Technical Report; Rionegro Town Hall: Rionegro, Colombia, 2018. Available online: https://www.rionegro.gov.co/Paginas/plan-de-ordenamiento-territorial.aspx (accessed on 30 November 2019).
- Valledupar Town Hall. Master Plan of Valledupar; Technical Report; Valledupar Town Hall: Valledupar, Colombia, 2013. Available online: https://sites.google.com/a/valledupar-cesar.gov.co/pot_valledupar/batx-2-1 (accessed on 30 November 2019).
- Corbane, C.; Florczyk, A.; Pesaresi, M.; Politis, P.; Syrris, V. GHS Built-Up Grid, Derived from Landsat, Multitemporal (1975-1990-2000-2014), R2018A; Technical Report; European Commission, Joint Research Centre (JRC): Brussels, Belgium, 2018; Available online: http://data.europa.eu/89h/jrc-ghsl-10007 (accessed on 30 November 2019). [CrossRef]
- Jarvis, A.; Reuter, H.I.; Nelson, A.; Guevara, E. Hole-Filled SRTM for the Globe Version 4; Technical Report; International Centre for Tropical Agriculture (CIAT): Palmira, Colombia, 2008; Available online: http://srtm.csi.cgiar.org (accessed on 30 November 2019).
- OpenStreetMap Contributors. 2017. Planet OSM. Available online: https://planet.osm.org (accessed on 30 November 2019).
- IGAC. Open Data Cartography and Geography; Technical Report; Agustín Codazzi Geographic Institute: Bogotá, Colombia, 2019. Available online: https://geoportal.igac.gov.co/contenido/datos-abiertos-cartografia-y-geografia (accessed on 30 November 2019).
- UNEP-WCMC; IUCN. Protected Planet: The World Database on Protected Areas (WDPA); Technical Report; UNEP-WCMC; IUCN: Cambridge, UK, 2019; Available online: www.protectedplanet.net (accessed on 30 November 2019).
- Young, N.E.; Anderson, R.S.; Chignell, S.M.; Vorster, A.G.; Lawrence, R.; Evangelista, P.H. A survival guide to Landsat preprocessing. Ecology 2017, 98, 920–932. [Google Scholar] [CrossRef]
- Goslee, S.C. Analyzing remote sensing data in R: The landsat package. J. Stat. Softw. 2011, 43, 1–25. [Google Scholar] [CrossRef]
- Cao, Z.; Wu, Z.; Kuang, Y.; Huang, N.; Wang, M. Coupling an intercalibration of radiance-calibrated nighttime light images and land use/cover data for modeling and analyzing the distribution of GDP in Guangdong, China. Sustainability 2016, 8, 108. [Google Scholar] [CrossRef]
- Liu, F.T.; Ting, K.M.; Zhou, Z.H. Isolation-Based Anomaly Detection. ACM Trans. Knowl. Discov. Data 2012, 6, 3:1–3:39. [Google Scholar] [CrossRef]
- Breunig, M.; Kriegel, H.P.; Ng, R.; Sander, J. LOF: Identifying Density-Based Local Outliers. ACM Sigmod Record 2000, 29, 93–104. [Google Scholar] [CrossRef]
- Bak, P.; Tang, C.; Wiesenfeld, K. Self-organized criticality. Phys. Rev. A 1988, 38, 364–374. Available online: https://link.aps.org/doi/10.1103/PhysRevA.38.364 (accessed on 30 November 2019). [CrossRef] [PubMed]
- Telea, A. An image inpainting technique based on the fast marching method. J. Graph. Tools 2004, 9, 23–34. [Google Scholar] [CrossRef]
- Bertalmio, M.; Bertozzi, A.L.; Sapiro, G. Navier-stokes, fluid dynamics, and image and video inpainting. In Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, CVPR 2001, Kauai, HI, USA, 8–14 December 2001; Volume 1. [Google Scholar]
- Damelin, S.B.; Hoang, N.S. On Surface Completion and Image Inpainting by Biharmonic Functions: Numerical Aspects. Int. J. Math. Math. Sci. 2018, 2018, 3950312. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: New York, NY, USA, 2009. [Google Scholar]
- Nakhmani, A.; Tannenbaum, A. A new distance measure based on generalized image normalized cross-correlation for robust video tracking and image recognition. Pattern Recognit. Lett. 2013, 34, 315–321. [Google Scholar] [CrossRef]
- Di Stefano, L.; Mattoccia, S.; Tombari, F. ZNCC-based template matching using bounded partial correlation. Pattern Recognit. Lett. 2005, 26, 2129–2134. [Google Scholar] [CrossRef]
- DANE. Results From National Population and Housing Census 2018 for Valledupar, Cesar; Techreport; National Administrative Department of Statistics (DANE): Bogotá, Colombia, 2019. Available online: https://www.dane.gov.co/files/censo2018/informacion-tecnica/presentaciones-territorio/050919-CNPV-presentacion-Cesar.pdf (accessed on 30 November 2019).
- Angel, S.; Arango Franco, S.; Liu, Y.; Blei, A.M. The shape compactness of urban footprints. Progress Plan. 2018, in press. [Google Scholar] [CrossRef]
- DANE. Results From National Population and Housing Census 2018 For Antioquia; Techreport; National Administrative Department of Statistics (DANE): Bogotá, Colombia, 2019. Available online: https://www.dane.gov.co/files/censo2018/informacion-tecnica/presentaciones-territorio/190719-CNPV-presentacion-Antioquia-2.pdf (accessed on 30 November 2019).
- Duque, J.C.; Lozano-Gracia, N.; Patino, J.E.; Restrepo, P.; Velasquez, W.A. Spatiotemporal Dynamics of Urban Growth in Latin American Cities: An Analysis Using Nighttime Lights Imagery. Landsc. Urban Plan. 2019, 191, 103640. [Google Scholar] [CrossRef]
- Inostroza, L.; Baur, R.; Csaplovics, E. Urban sprawl and fragmentation in Latin America: A dynamic quantification and characterization of spatial patterns. J. Environ. Manag. 2013, 115, 87–97. [Google Scholar] [CrossRef]
- Berrigan, D.; Tatalovich, Z.; Pickle, L.W.; Ewing, R.; Ballard-Barbash, R. Urban sprawl, obesity, and cancer mortality in the United States: Cross-sectional analysis and methodological challenges. Int. J. Health Geogr. 2014, 13, 1–14. [Google Scholar] [CrossRef]
- Ewing, R.; Hamidi, S.; Grace, J.B.; Wei, Y.D. Does urban sprawl hold down upward mobility? Landsc. Urban Plan. 2016, 148, 80–88. [Google Scholar] [CrossRef]
- Fallah, B.N.; Partridge, M.D.; Olfert, M.R. Urban sprawl and productivity: Evidence from US metropolitan areas. Papers Reg. Sci. 2011, 90, 451–472. [Google Scholar] [CrossRef]
- Marconcini, M.; Metz-Marconcini, A.; Üreyen, S.; Palacios-Lopez, D.; Hanke, W.; Bachofer, F.; Zeidler, J.; Esch, T.; Gorelick, N.; Kakarla, A.; et al. Outlining where humans live—The World Settlement Footprint 2015. arXiv 2019, arXiv:1910.12707. [Google Scholar]
- Liu, G.; Reda, F.A.; Shih, K.J.; Wang, T.C.; Tao, A.; Catanzaro, B. Image Inpainting for Irregular Holes Using Partial Convolutions. arXiv 2018, arXiv:cs.CV/1804.07723. [Google Scholar]



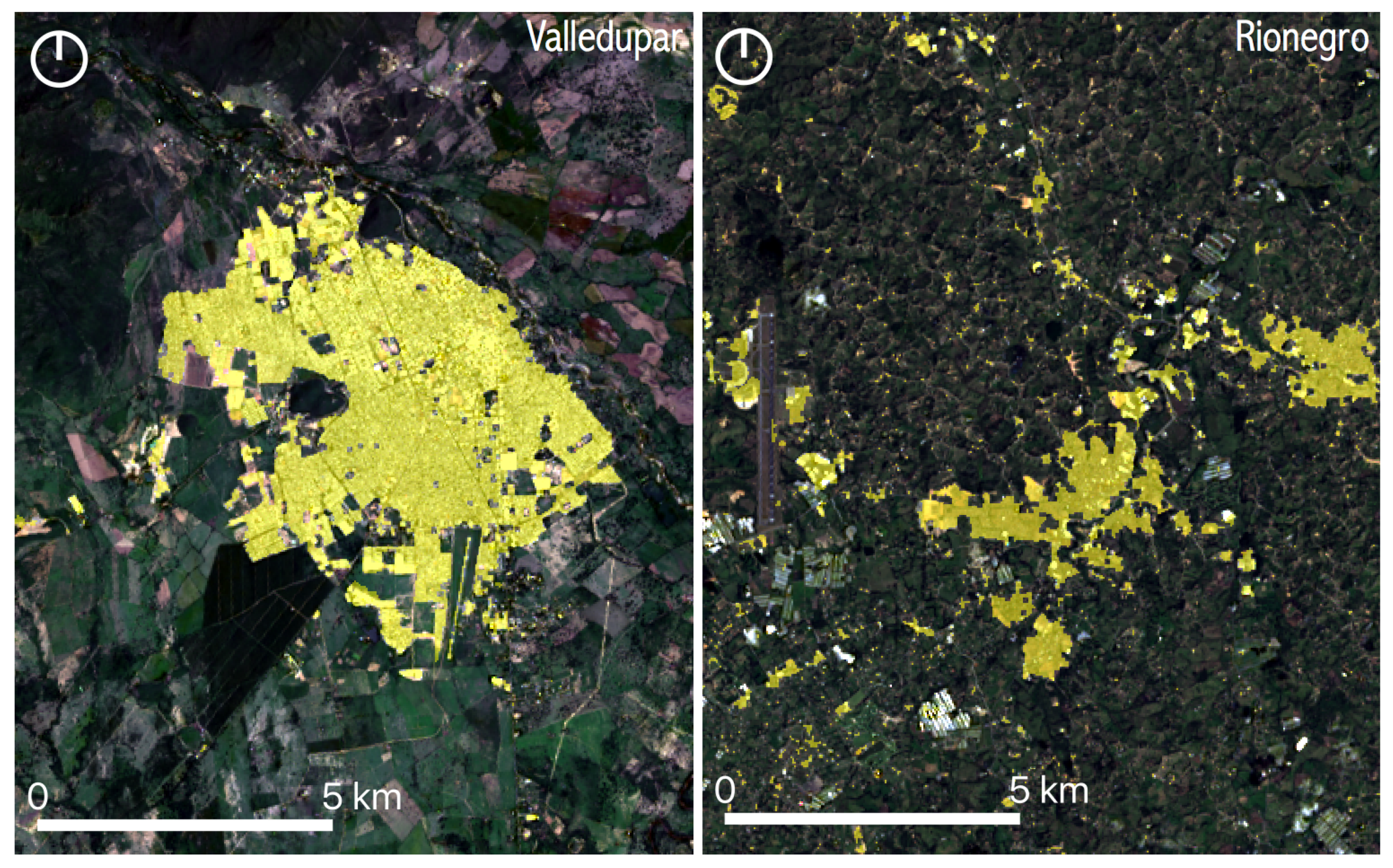
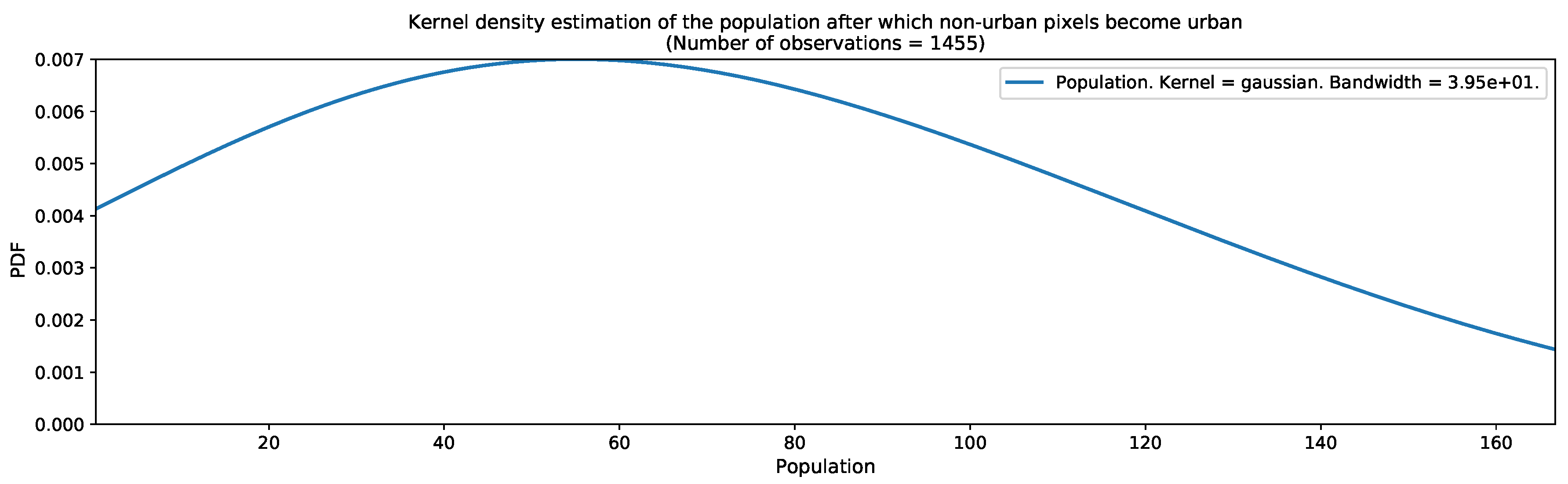
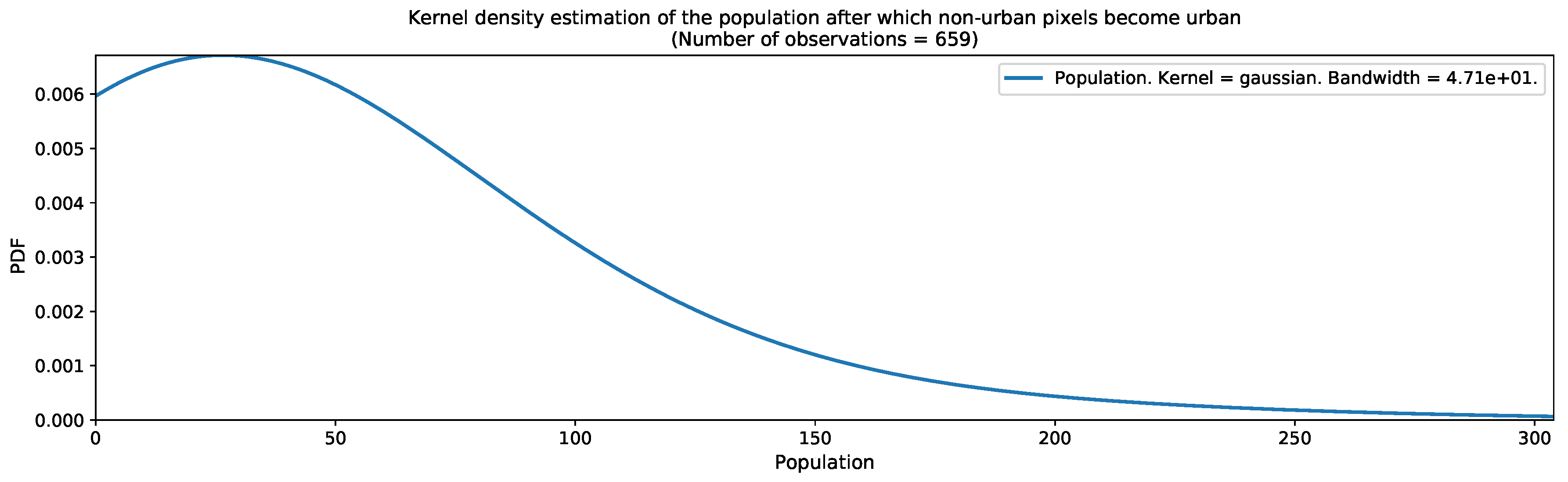
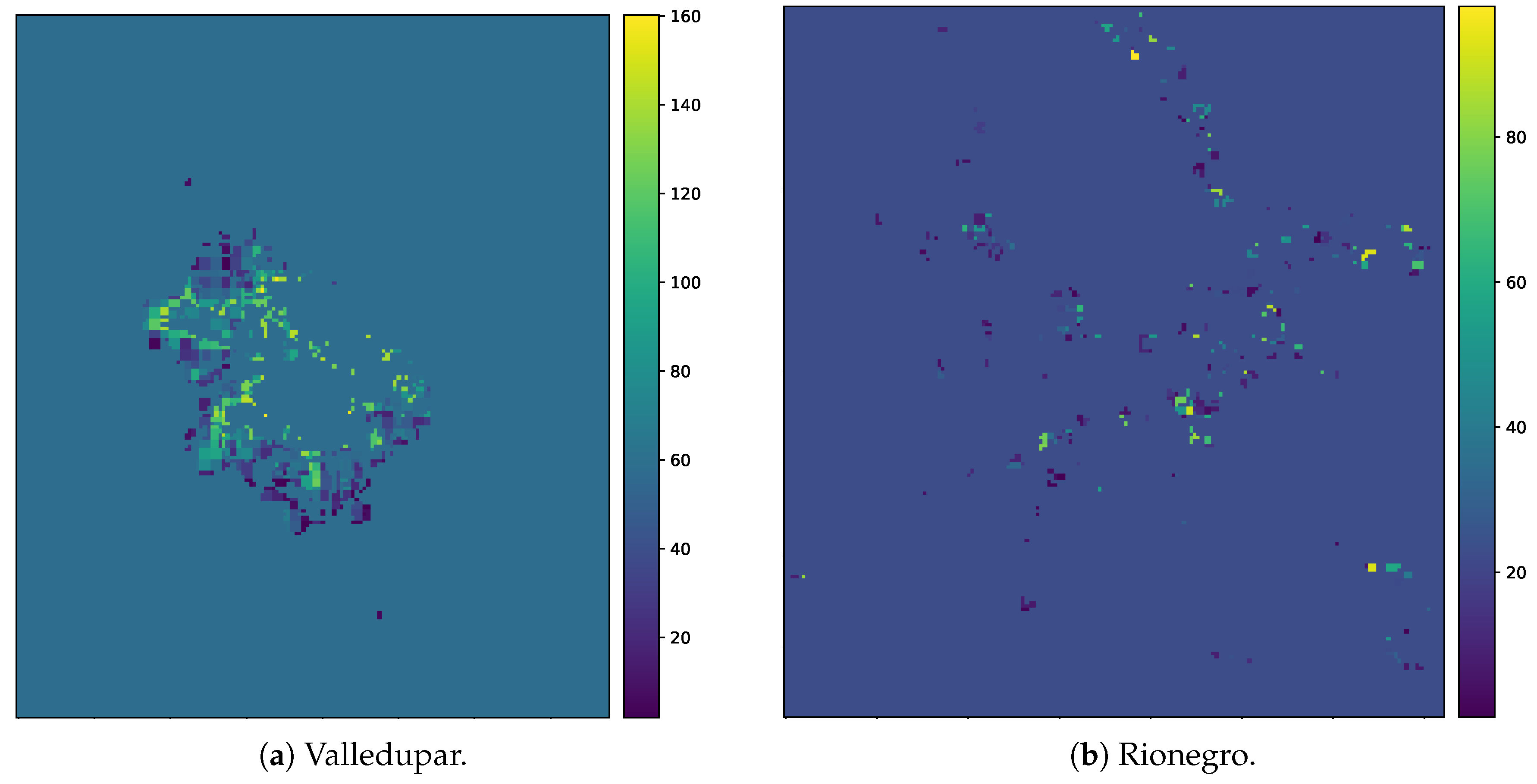
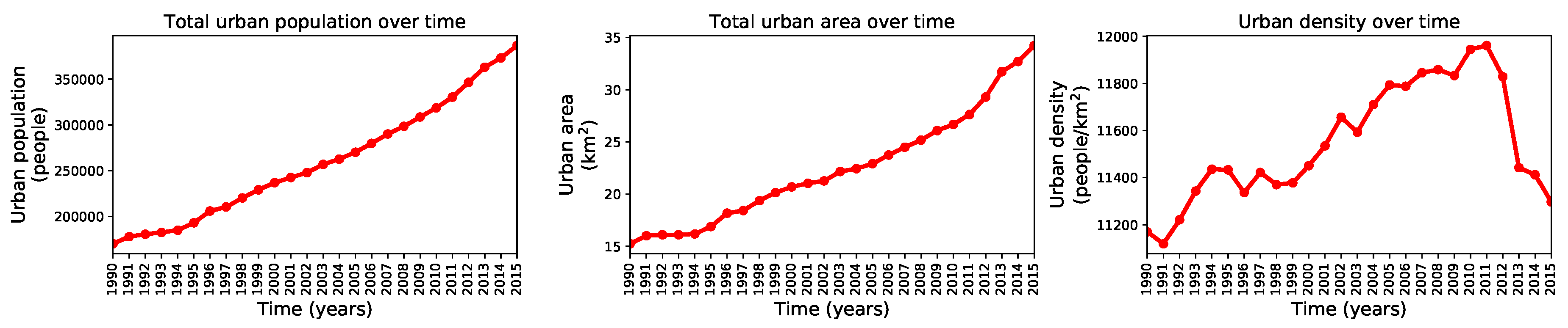
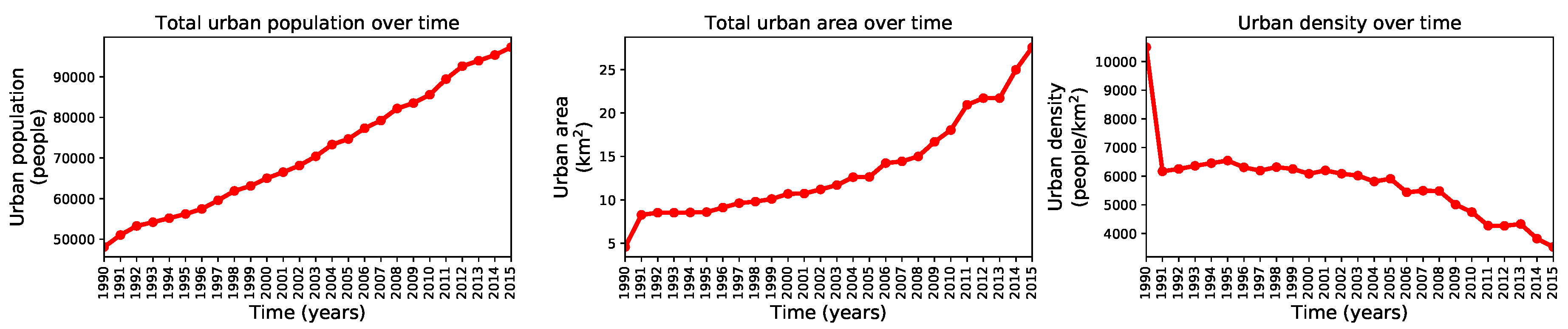
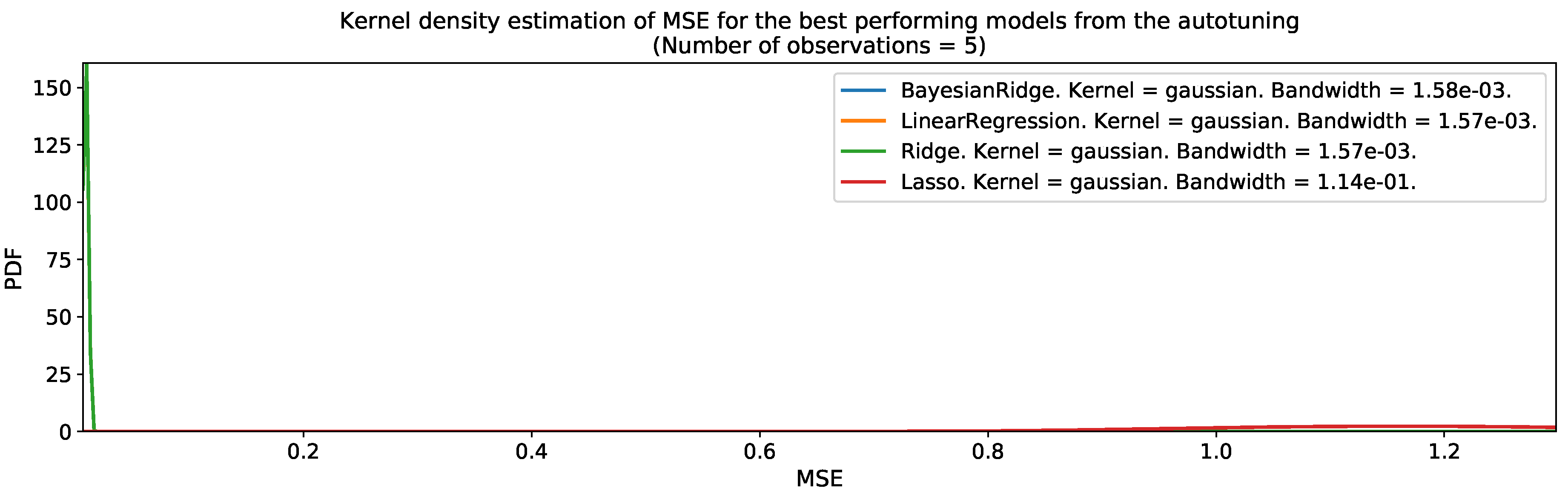
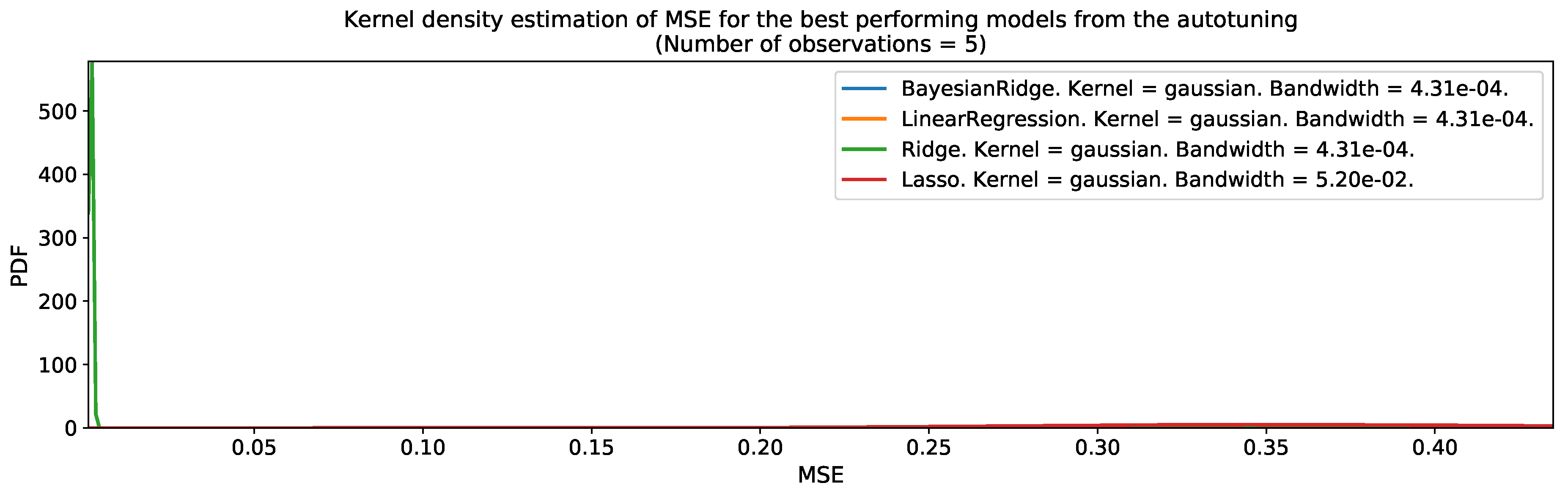


| Variable Name | Data Source | Digital Format | Resolution | Availability | Importance |
|---|---|---|---|---|---|
| Population distribution. | GHSL pop [45]. | Raster. | 250 m × 250 m. | Global. | Essential. |
| Urban footprint. | Landsat [47]. | Raster. | 30 m × 30 m. | Global. | Essential. |
| Binary urban footprint. | Derived from the urban footprint through a binary classifier. | Raster. | 30 m × 30 m. | Global. | Essential. |
| Official population projections. | National Bureau of Statistics [48]. | Tabular. | Administrative units. | National. | Optional. |
| Maximum population capacity. | Master plan [49,50]. | Vector. | - | Local. | Optional. |
| Land use (residential, industrial, commercial, official, and special). | Master plan [49,50]. | Vector. | - | Local. | Optional. |
| Built-up urban ratio. | GHSL built-up [51]. | Raster. | 250 m × 250 m. | Global. | Optional. |
| Terrain slope. | SRTM [52]. | Raster. | 90 m × 90 m. | Global. | Optional. |
| Distances to nearest populated towns. | Derived from binary urban footprint. | Raster. | 30 m × 30 m. | Global. | Optional. |
| Roads. | OSM [53], IGAC [54]. | Vector. | - | Global, National. | Optional. |
| Natural hazard (flooding, landslide, fire, volcanic eruption, earthquake.). | Master plan [49,50]. | Vector. | - | Local. | Optional. |
| Water bodies. | Master plan [49,50], IGAC [54]. | Vector. | - | Local. | Optional. |
| Protected areas. | Master plan [49,50], WDPA [55]. | Vector. | - | Global, Local. | Optional. |
| Urban development projects. | Master plan [49,50], others. | Vector. | - | Local. | Optional. |
| Variables | Description |
|---|---|
| t | Time in years. |
| r | Number of consecutive years of historical data records available for training. |
| Spatial coordinates along the East and North directions, respectively. | |
| Width and height of the spatial extent under study in meters. | |
| Spatial sampling period in meters along the x and y directions, respectively. | |
| Number of rows and columns of each digital image. | |
| Auxiliary variables. | |
| Population distribution. | |
| Binary urban footprint (black and white). | |
| Urban footprint (color). | |
| i-th input variable. | |
| Number of rows and columns of the spatial window for . | |
| Number of consecutive temporal lags in years for . | |
| Mathematical function applied to each possible spatial window of pixels in . In the naïve feature sampling, it corresponds to a reshape operation to convert the data dimensions from to . In other scenarios it can be a spatial-filtering function that processes and reduces the number of features (e.g., an element-wise multiplication of the spatial window by a fixed spatial kernel of the same dimensions followed by a sum of its elements). | |
| Number of temporal windows that can be extracted from the historical data records for all variables given the maximum consecutive temporal lag in the regression model. | |
| Number of rows (i.e., observations) and columns (i.e., input features) of the resulting tabular dataset for training the population distribution growth model based on machine learning. | |
| Population threshold after which a region can be considered as urbanized. |
| Predicted Class | |||||
|---|---|---|---|---|---|
| built-up | bare soil | vegetation | water | ||
| True class | built-up | 2094 | 45 | 3 | 0 |
| bare soil | 28 | 9339 | 7 | 0 | |
| vegetation | 0 | 24 | 17,504 | 6 | |
| water | 0 | 6 | 43 | 89 | |
| Predicted Class | |||||
| urban | non-urban | ||||
| True class | urban | 2094 | 48 | ||
| non-urban | 28 | 27,018 | |||
| Predicted Class | |||||
|---|---|---|---|---|---|
| built-up | bare soil | vegetation | water | ||
| True class | built-up | 1355 | 29 | 11 | 1 |
| bare soil | 61 | 535 | 15 | 1 | |
| vegetation | 0 | 10 | 5557 | 0 | |
| water | 1 | 7 | 3 | 73 | |
| Predicted Class | |||||
| urban | non-urban | ||||
| True class | urban | 1355 | 41 | ||
| non-urban | 62 | 6201 | |||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gómez, J.A.; Patiño, J.E.; Duque, J.C.; Passos, S. Spatiotemporal Modeling of Urban Growth Using Machine Learning. Remote Sens. 2020, 12, 109. https://doi.org/10.3390/rs12010109
Gómez JA, Patiño JE, Duque JC, Passos S. Spatiotemporal Modeling of Urban Growth Using Machine Learning. Remote Sensing. 2020; 12(1):109. https://doi.org/10.3390/rs12010109
Chicago/Turabian StyleGómez, Jairo A., Jorge E. Patiño, Juan C. Duque, and Santiago Passos. 2020. "Spatiotemporal Modeling of Urban Growth Using Machine Learning" Remote Sensing 12, no. 1: 109. https://doi.org/10.3390/rs12010109
APA StyleGómez, J. A., Patiño, J. E., Duque, J. C., & Passos, S. (2020). Spatiotemporal Modeling of Urban Growth Using Machine Learning. Remote Sensing, 12(1), 109. https://doi.org/10.3390/rs12010109