DisCountNet: Discriminating and Counting Network for Real-Time Counting and Localization of Sparse Objects in High-Resolution UAV Imagery
Abstract
:1. Introduction
- We developed a novel end-to-end architecture for counting and localizing small and sparse objects in high-resolution aerial images. This architecture can allow for a real-time implementation on board the UAV, while maintaining comparable accuracy to state-of-the-art techniques.
- Our DisCount network discards a large amount of background information, limiting expensive calculations to important foreground areas.
- The hard example training part of our algorithm addresses the issues of shadow and occluded animals.
- We collected a novel UAV dataset, prepared the ground truth for it, and conducted a comprehensive evaluation.
2. Related Work
2.1. Counting Methods
2.1.1. Counting Via Detection
2.1.2. Counting Via Density Map
2.1.3. Counting on Image Level
2.2. Counting Applications
2.3. Unmanned Aerial Systems
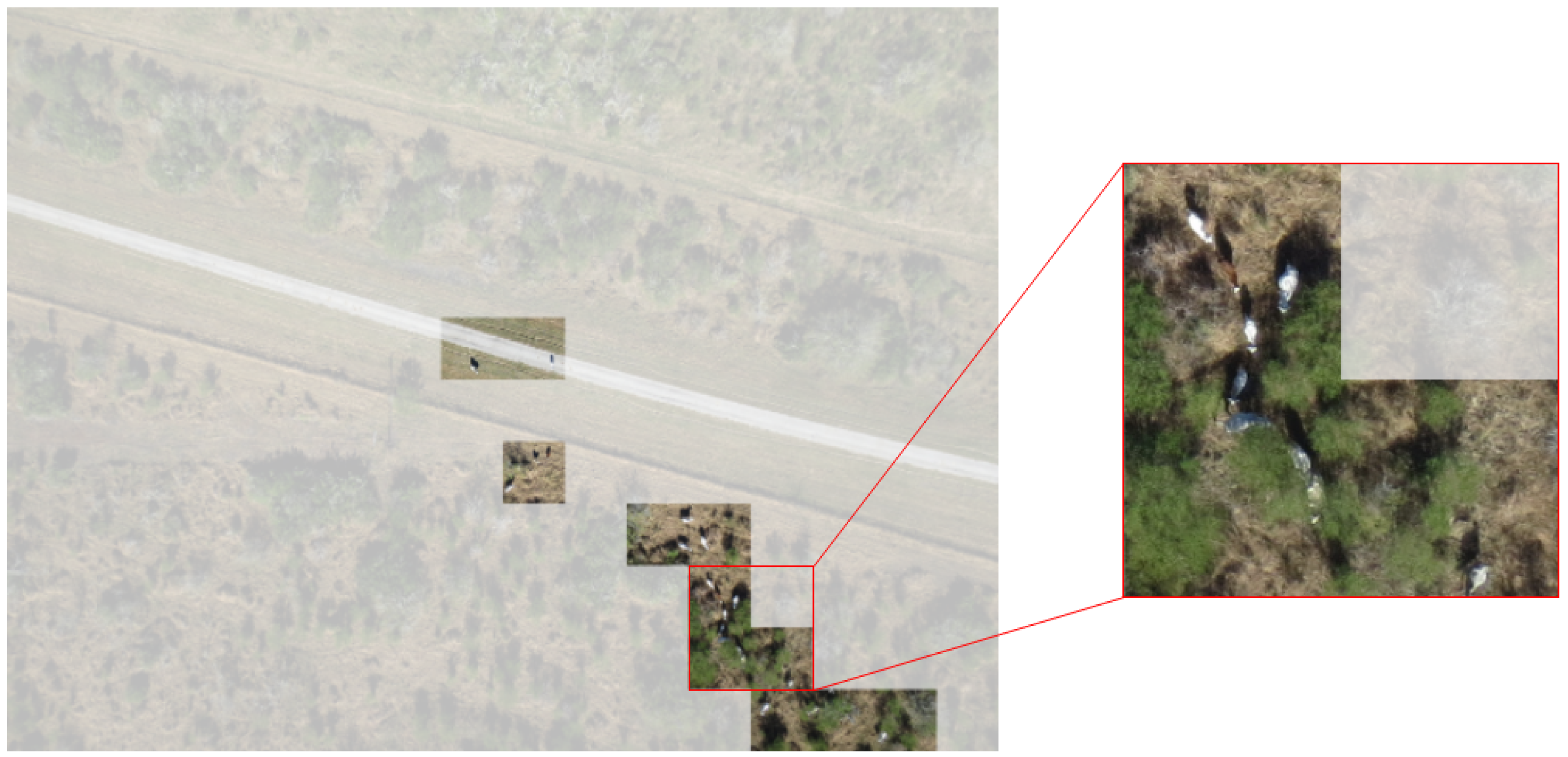
3. Data Set
3.1. Data Collection
3.2. Dataset Feature Description
3.3. Dataset Preparation
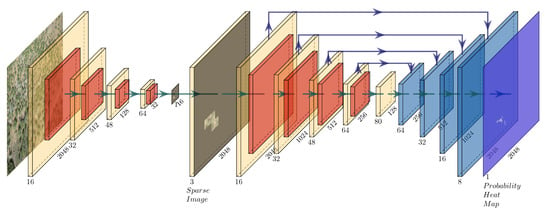
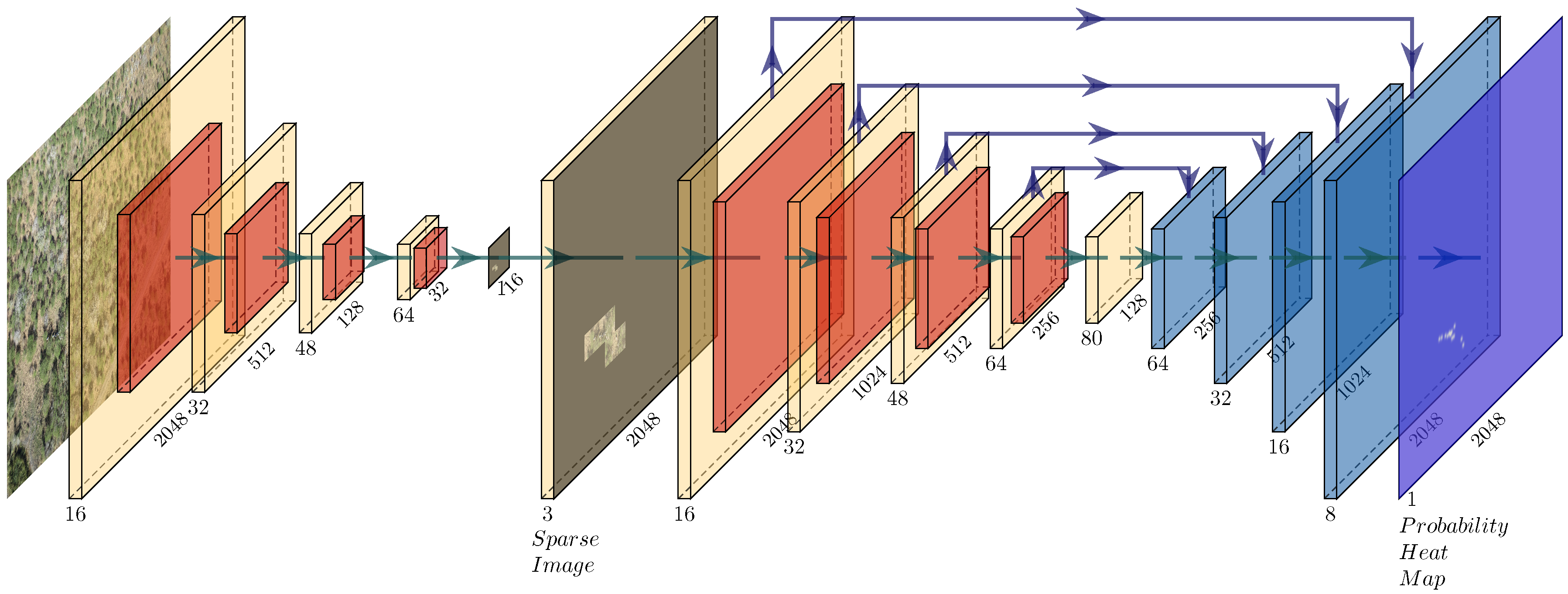
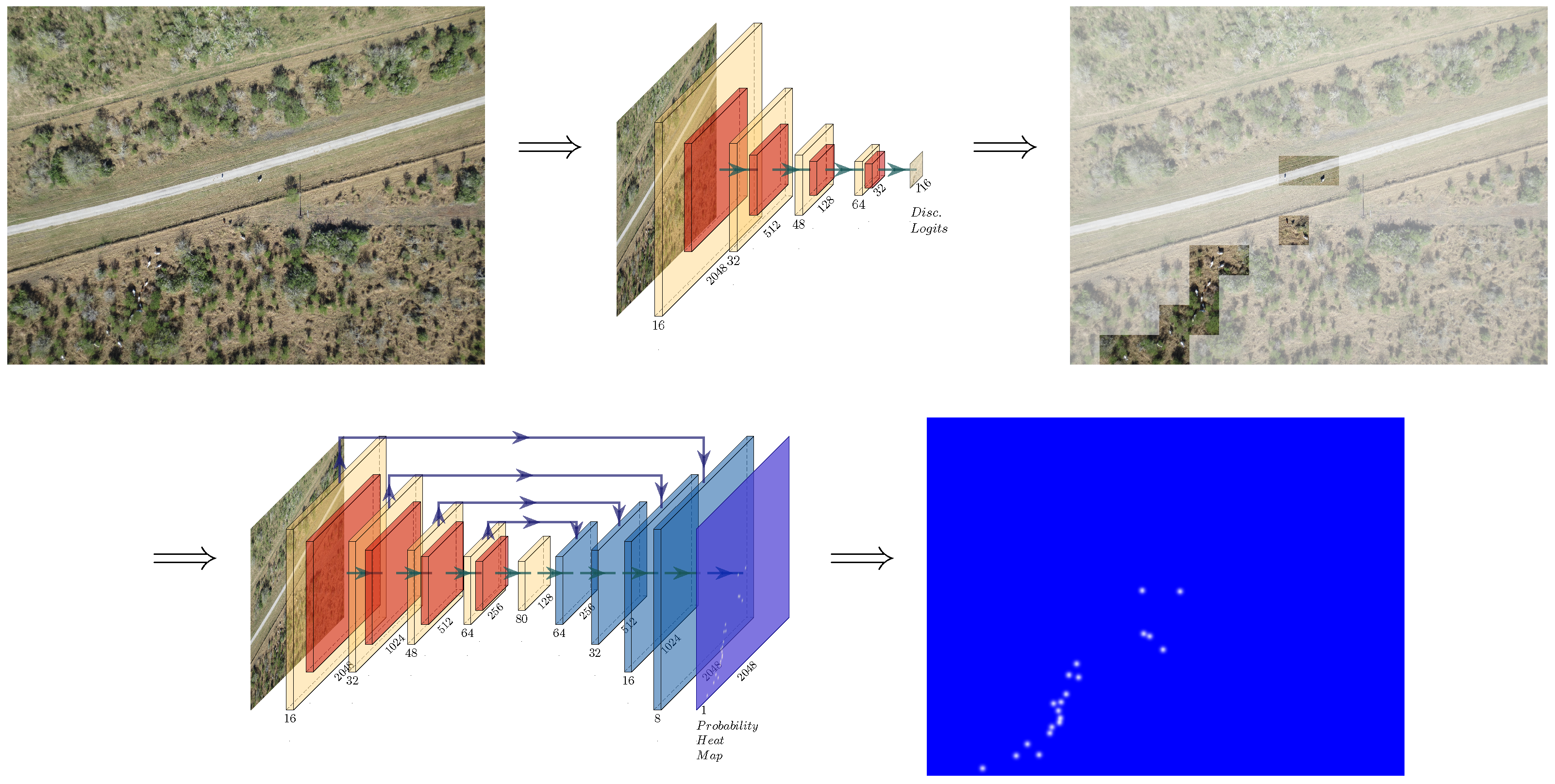
4. Our Approach
- The data can be accurately described as a set of two distributions.
- The majority of our data can be classified as background information.
- Background information can be safely discarded without losing contextual details.
- Foreground information can be densely packed.
4.1. Implementation and Training
| Algorithm 1: DisCount training algorithm is illustrated here. |
 |
4.2. Hard Example Training
5. Evaluation Metrics
5.1. Image Level Label Metrics
5.2. Image Region Level Metric
5.3. Density Map Quality Comparison
6. Results
6.1. Experimental Setup
6.2. Qualitative and Quantitative Results
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chan, A.B.; Liang, Z.S.J.; Vasconcelos, N. Privacy preserving crowd monitoring: Counting people without people models or tracking. In Proceedings of the 2008 IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008; pp. 1–7. [Google Scholar]
- Idrees, H.; Saleemi, I.; Seibert, C.; Shah, M. Multi-source multi-scale counting in extremely dense crowd images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 2547–2554. [Google Scholar]
- Shen, Z.; Xu, Y.; Ni, B.; Wang, M.; Hu, J.; Yang, X. Crowd counting via adversarial cross-scale consistency pursuit. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 5245–5254. [Google Scholar]
- Boominathan, L.; Kruthiventi, S.S.; Babu, R.V. Crowdnet: A deep convolutional network for dense crowd counting. In Proceedings of the 24th ACM international conference on Multimedia, Amsterdam, The Netherlands, 15–19 October 2016; pp. 640–644. [Google Scholar]
- Liu, J.; Gao, C.; Meng, D.; Hauptmann, A.G. Decidenet: Counting varying density crowds through attention guided detection and density estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 5197–5206. [Google Scholar]
- Guerrero-Gómez-Olmedo, R.; Torre-Jiménez, B.; López-Sastre, R.; Maldonado-Bascón, S.; Onoro-Rubio, D. Extremely overlapping vehicle counting. In Pattern Recognition and Image Analysis; Springer: Cham, Switzerland, 2015; pp. 423–431. [Google Scholar]
- Xie, W.; Noble, J.A.; Zisserman, A. Microscopy cell counting and detection with fully convolutional regression networks. Comput. Methods Biomech. Biomed. Eng. Imaging Vis. 2018, 6, 283–292. [Google Scholar] [CrossRef]
- Rahnemoonfar, M.; Sheppard, C. Deep count: Fruit counting based on deep simulated learning. Sensors 2017, 17, 905. [Google Scholar] [CrossRef] [PubMed]
- Rahnemoonfar, M.; Sheppard, C. Real-time yield estimation based on deep learning. Proc. SPIE 2017, 10218. [Google Scholar] [CrossRef]
- Huang, L.C.; Kulkarni, K.; Jha, A.; Lohit, S.; Jayasuriya, S.; Turaga, P. CS-VQA: Visual Question Answering with Compressively Sensed Images. In Proceedings of the 2018 25th IEEE International Conference on Image Processing (ICIP), Athens, Greece, 7–10 October 2018; pp. 1283–1287. [Google Scholar]
- Fukui, A.; Park, D.H.; Yang, D.; Rohrbach, A.; Darrell, T.; Rohrbach, M. Multimodal compact bilinear pooling for visual question answering and visual grounding. arXiv 2016, arXiv:1606.01847. [Google Scholar]
- Sheppard, C.; Rahnemoonfar, M. Real-time scene understanding for UAV imagery based on deep convolutional neural networks. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 2243–2246. [Google Scholar]
- Redmon, J.; Farhadi, A. YOLO9000: Better, faster, stronger. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 7263–7271. [Google Scholar]
- Lin, T.Y.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal loss for dense object detection. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2980–2988. [Google Scholar]
- Kamangir, H.; Rahnemoonfar, M.; Dobbs, D.; Paden, J.; Fox, G.C. Detecting ice layers in Radar images with deep hybrid networks. In Proceedings of the IEEE Conference on Geoscience and Remote Sensing (IGARSS), Valencia, Spain, 22–27 July 2018. [Google Scholar]
- Rahnemoonfar, M.; Robin, M.; Miguel, M.V.; Dobbs, D.; Adams, A. Flooded area detection from UAV images based on densely connected recurrent neural networks. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 3743–3746. [Google Scholar]
- Chattopadhyay, P.; Vedantam, R.; Selvaraju, R.R.; Batra, D.; Parikh, D. Counting everyday objects in everyday scenes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1135–1144. [Google Scholar]
- Zhang, C.; Li, H.; Wang, X.; Yang, X. Cross-scene crowd counting via deep convolutional neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 833–841. [Google Scholar]
- Hu, P.; Ramanan, D. Finding tiny faces. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 951–959. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. In Advances in Neural Information Processing Systems 28; Cortes, C., Lawrence, N.D., Lee, D.D., Sugiyama, M., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2015; pp. 91–99. [Google Scholar]
- Zhang, Y.; Zhou, D.; Chen, S.; Gao, S.; Ma, Y. Single-image crowd counting via multi-column convolutional neural network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 589–597. [Google Scholar]
- Fiaschi, L.; Köthe, U.; Nair, R.; Hamprecht, F.A. Learning to count with regression forest and structured labels. In Proceedings of the 21st International Conference on Pattern Recognition (ICPR2012), Tsukuba, Japan, 11–15 November 2012; pp. 2685–2688. [Google Scholar]
- Sam, D.B.; Surya, S.; Babu, R.V. Switching convolutional neural network for crowd counting. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 4031–4039. [Google Scholar]
- Idrees, H.; Tayyab, M.; Athrey, K.; Zhang, D.; Al-Maadeed, S.; Rajpoot, N.; Shah, M. Composition loss for counting, density map estimation and localization in dense crowds. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 532–546. [Google Scholar]
- Walach, E.; Wolf, L. Learning to count with cnn boosting. In Computer Vision—ECCV 2016; Springer: Cham, Switzerland, 2016; pp. 660–676. [Google Scholar]
- Deb, D.; Ventura, J. An aggregated multicolumn dilated convolution network for perspective-free counting. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 18–22 June 2018; pp. 195–204. [Google Scholar]
- Wawerla, J.; Marshall, S.; Mori, G.; Rothley, K.; Sabzmeydani, P. Bearcam: Automated wildlife monitoring at the arctic circle. Mach. Vis. Appl. 2009, 20, 303–317. [Google Scholar] [CrossRef]
- Shang, C.; Ai, H.; Bai, B. End-to-end crowd counting via joint learning local and global count. In Proceedings of the 2016 IEEE International Conference on Image Processing (ICIP), Phoenix, AZ, USA, 25–28 September 2016; pp. 1215–1219. [Google Scholar]
- Liu, X.; van de Weijer, J.; Bagdanov, A.D. Leveraging unlabeled data for crowd counting by learning to rank. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 7661–7669. [Google Scholar]
- Babu Sam, D.; Sajjan, N.N.; Venkatesh Babu, R.; Srinivasan, M. Divide and grow: Capturing huge diversity in crowd images with incrementally growing CNN. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 3618–3626. [Google Scholar]
- Shi, Z.; Zhang, L.; Liu, Y.; Cao, X.; Ye, Y.; Cheng, M.M.; Zheng, G. Crowd counting with deep negative correlation learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 5382–5390. [Google Scholar]
- Tayara, H.; Soo, K.G.; Chong, K.T. Vehicle detection and counting in high-resolution aerial images using convolutional regression neural network. IEEE Access 2018, 6, 2220–2230. [Google Scholar] [CrossRef]
- Chen, S.W.; Shivakumar, S.S.; Dcunha, S.; Das, J.; Okon, E.; Qu, C.; Taylor, C.J.; Kumar, V. Counting apples and oranges with deep learning: A data-driven approach. IEEE Robot. Autom. Lett. 2017, 2, 781–788. [Google Scholar] [CrossRef]
- Lu, H.; Cao, Z.; Xiao, Y.; Zhuang, B.; Shen, C. TasselNet: Counting maize tassels in the wild via local counts regression network. Plant Methods 2017, 13, 79. [Google Scholar] [CrossRef] [PubMed]
- Chamoso, P.; Raveane, W.; Parra, V.; González, A. UAVs applied to the counting and monitoring of animals. In Ambient Intelligence-Software and Applications; Springer: Cham, Switzerland, 2014; pp. 71–80. [Google Scholar]
- Rivas, A.; Chamoso, P.; González-Briones, A.; Corchado, J. Detection of Cattle Using Drones and Convolutional Neural Networks. Sensors 2018, 18, 2048. [Google Scholar] [CrossRef] [PubMed]
- Longmore, S.; Collins, R.; Pfeifer, S.; Fox, S.; Mulero-Pázmány, M.; Bezombes, F.; Goodwin, A.; De Juan Ovelar, M.; Knapen, J.; Wich, S. Adapting astronomical source detection software to help detect animals in thermal images obtained by unmanned aerial systems. Int. J. Remote Sens. 2017, 38, 2623–2638. [Google Scholar] [CrossRef]
- Koskowich, B.J.; Rahnemoonfar, M.; Starek, M. Virtualot—A Framework Enabling Real-Time Coordinate Transformation & Occlusion Sensitive Tracking Using UAS Products, Deep Learning Object Detection & Traditional Object Tracking Techniques. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium(IGARSS), Valencia, Spain, 22–27 July 2018; pp. 6416–6419. [Google Scholar]
- Wallace, L.; Lucieer, A.; Watson, C.; Turner, D. Development of a UAV-LiDAR system with application to forest inventory. Remote Sens. 2012, 4, 1519–1543. [Google Scholar] [CrossRef]
- D’Oleire Oltmanns, S.; Marzolff, I.; Peter, K.; Ries, J. Unmanned aerial vehicle (UAV) for monitoring soil erosion in Morocco. Remote Sens. 2012, 4, 3390–3416. [Google Scholar] [CrossRef]
- Chabot, D.; Bird, D.M. Wildlife research and management methods in the 21st century: Where do unmanned aircraft fit in? J. Unmanned Veh. Syst. 2015, 3, 137–155. [Google Scholar] [CrossRef]
- Barbedo, J.G.A.; Koenigkan, L.V. Perspectives on the use of unmanned aerial systems to monitor cattle. Outlook Agric. 2018, 47, 214–222. [Google Scholar] [CrossRef]
- Jin, X.; Davis, C.H. Vehicle detection from high-resolution satellite imagery using morphological shared-weight neural networks. Image Vis. Comput. 2007, 25, 1422–1431. [Google Scholar] [CrossRef]
- Jiang, Q.; Cao, L.; Cheng, M.; Wang, C.; Li, J. Deep neural networks-based vehicle detection in satellite images. In Proceedings of the 2015 International Symposium on Bioelectronics and Bioinformatics (ISBB), Beijing, China, 14–17 October 2015; pp. 184–187. [Google Scholar]
- Miyamoto, H.; Uehara, K.; Murakawa, M.; Sakanashi, H.; Nasato, H.; Kouyama, T.; Nakamura, R. Object Detection in Satellite Imagery Using 2-Step Convolutional Neural Networks. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium(IGARSS), Valencia, Spain, 22–27 July 2018; pp. 1268–1271. [Google Scholar]
- Starek, M.J.; Davis, T.; Prouty, D.; Berryhill, J. Small-scale UAS for geoinformatics applications on an island campus. In Proceedings of the 2014 Ubiquitous Positioning Indoor Navigation and Location Based Service (UPINLBS), Corpus Christi, TX, USA, 20–21 November 2014; pp. 120–127. [Google Scholar]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- United States Department of Agriculture. Balancing Animals with Your Forage; United States Department of Agriculture: Washington, DC, USA, 2009.
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015; Springer: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
- Li, Y.; Zhang, X.; Chen, D. Csrnet: Dilated convolutional neural networks for understanding the highly congested scenes. In Proceedings of the IEEE conference on computer vision and pattern recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 1091–1100. [Google Scholar]
- Wang, Z.; Simoncelli, E.P.; Bovik, A.C. Multiscale structural similarity for image quality assessment. In Proceedings of the Thrity-Seventh Asilomar Conference on Signals, Systems & Computers, Pacific Grove, CA, USA, 9–12 November 2003; Volume 2, pp. 1398–1402. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]






| Network | mAE | mSE | Parameters |
|---|---|---|---|
| CSRNet [50] | 1.58 | 4.49 | 16.7M |
| RetinaNet [14] | 1.24 | 3.54 | 36.4M |
| DisCountNet | 1.65 | 4.98 | 206k |
| Network | GAME1 | GAME2 | GAME3 | GAME4 |
|---|---|---|---|---|
| CSRNet [50] | 1.520 | 0.3800 | 0.0950 | 0.0237 |
| DisCountNet | 1.359 | 0.3396 | 0.0849 | 0.0212 |
| Network | SSIM | PSNR |
|---|---|---|
| CSRNet [50] | 0.9991 | 41.33 |
| DisCountNet | 0.9999 | 41.14 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rahnemoonfar, M.; Dobbs, D.; Yari, M.; Starek, M.J. DisCountNet: Discriminating and Counting Network for Real-Time Counting and Localization of Sparse Objects in High-Resolution UAV Imagery. Remote Sens. 2019, 11, 1128. https://doi.org/10.3390/rs11091128
Rahnemoonfar M, Dobbs D, Yari M, Starek MJ. DisCountNet: Discriminating and Counting Network for Real-Time Counting and Localization of Sparse Objects in High-Resolution UAV Imagery. Remote Sensing. 2019; 11(9):1128. https://doi.org/10.3390/rs11091128
Chicago/Turabian StyleRahnemoonfar, Maryam, Dugan Dobbs, Masoud Yari, and Michael J. Starek. 2019. "DisCountNet: Discriminating and Counting Network for Real-Time Counting and Localization of Sparse Objects in High-Resolution UAV Imagery" Remote Sensing 11, no. 9: 1128. https://doi.org/10.3390/rs11091128
APA StyleRahnemoonfar, M., Dobbs, D., Yari, M., & Starek, M. J. (2019). DisCountNet: Discriminating and Counting Network for Real-Time Counting and Localization of Sparse Objects in High-Resolution UAV Imagery. Remote Sensing, 11(9), 1128. https://doi.org/10.3390/rs11091128