Evaluation of the Performance of SM2RAIN-Derived Rainfall Products over Brazil
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Rainfall Datasets
2.2.1. Ground Observation Dataset
2.2.2. SM2RAIN-CCI Rainfall Product
2.2.3. SM2RAIN-ASCAT Rainfall Product
2.2.4. TRMM TMPA Rainfall Product
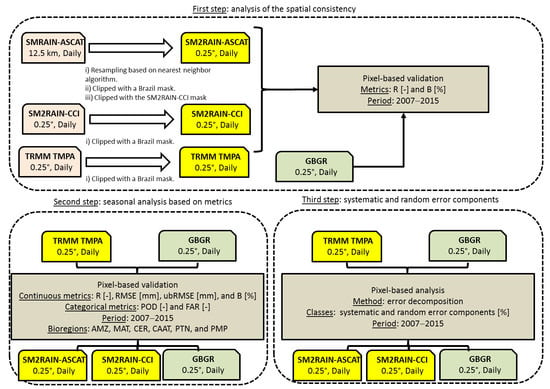
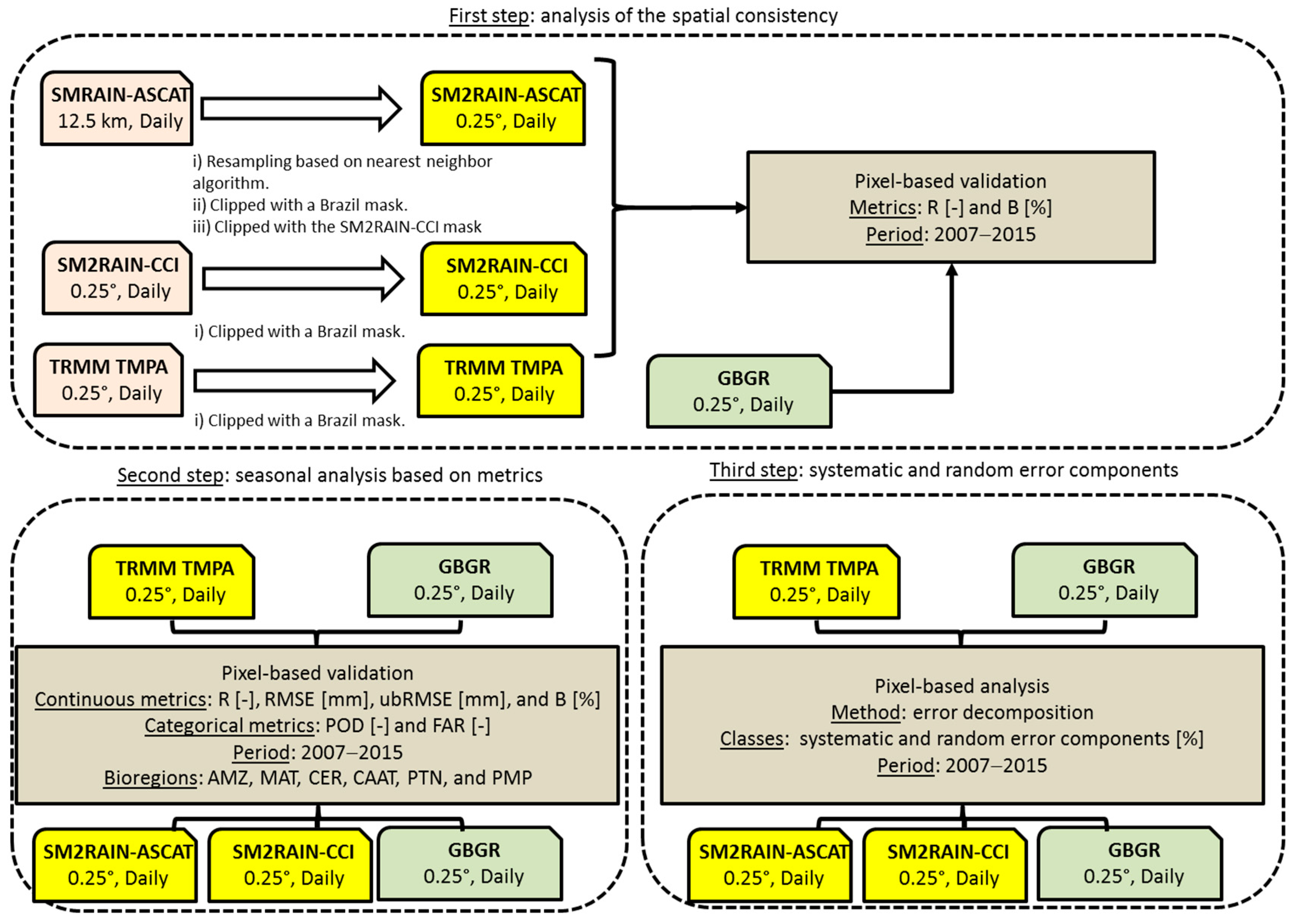
2.3. Dataset Pre-Processing
2.4. Performance Evaluation Methods
3. Results
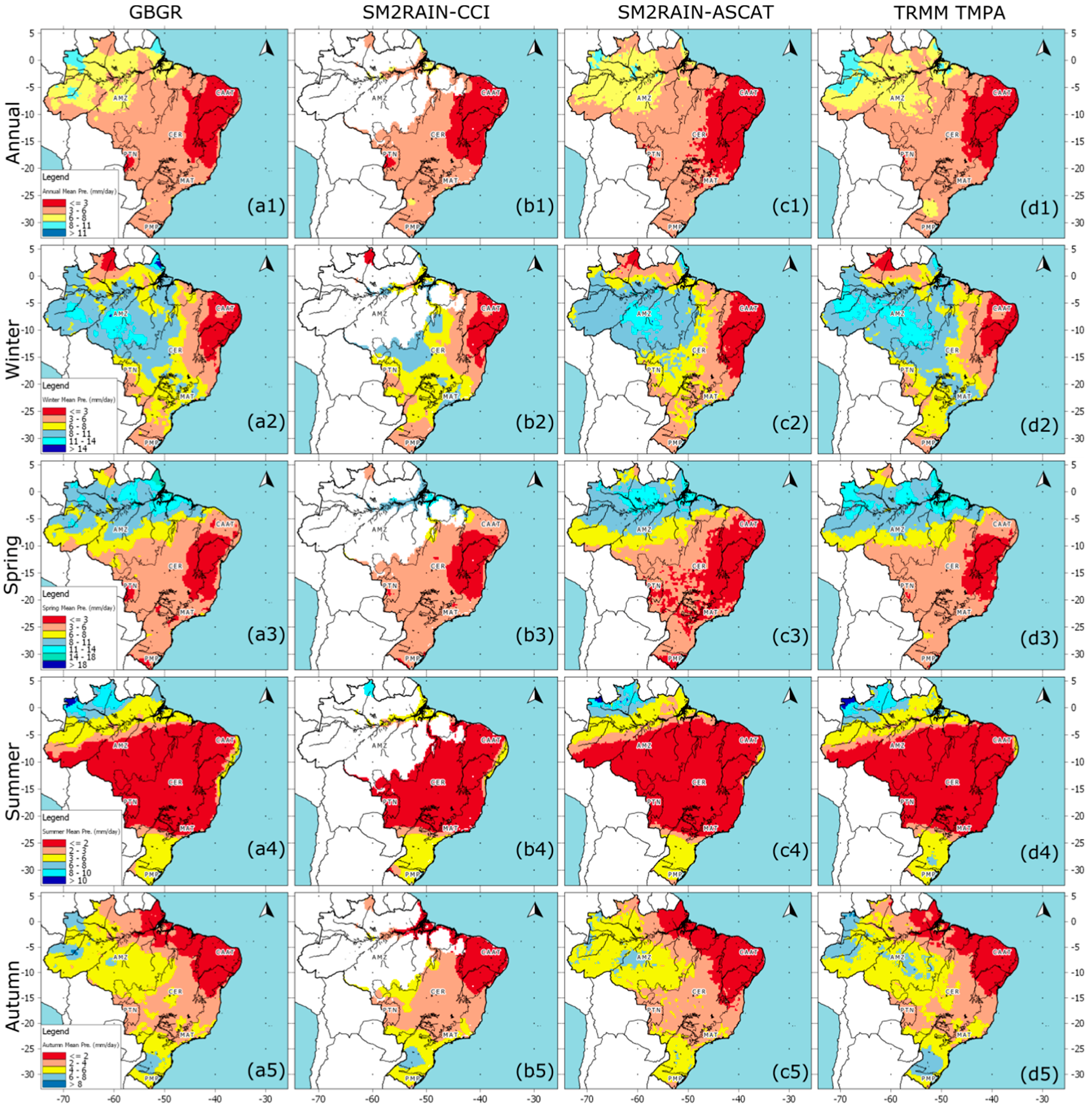
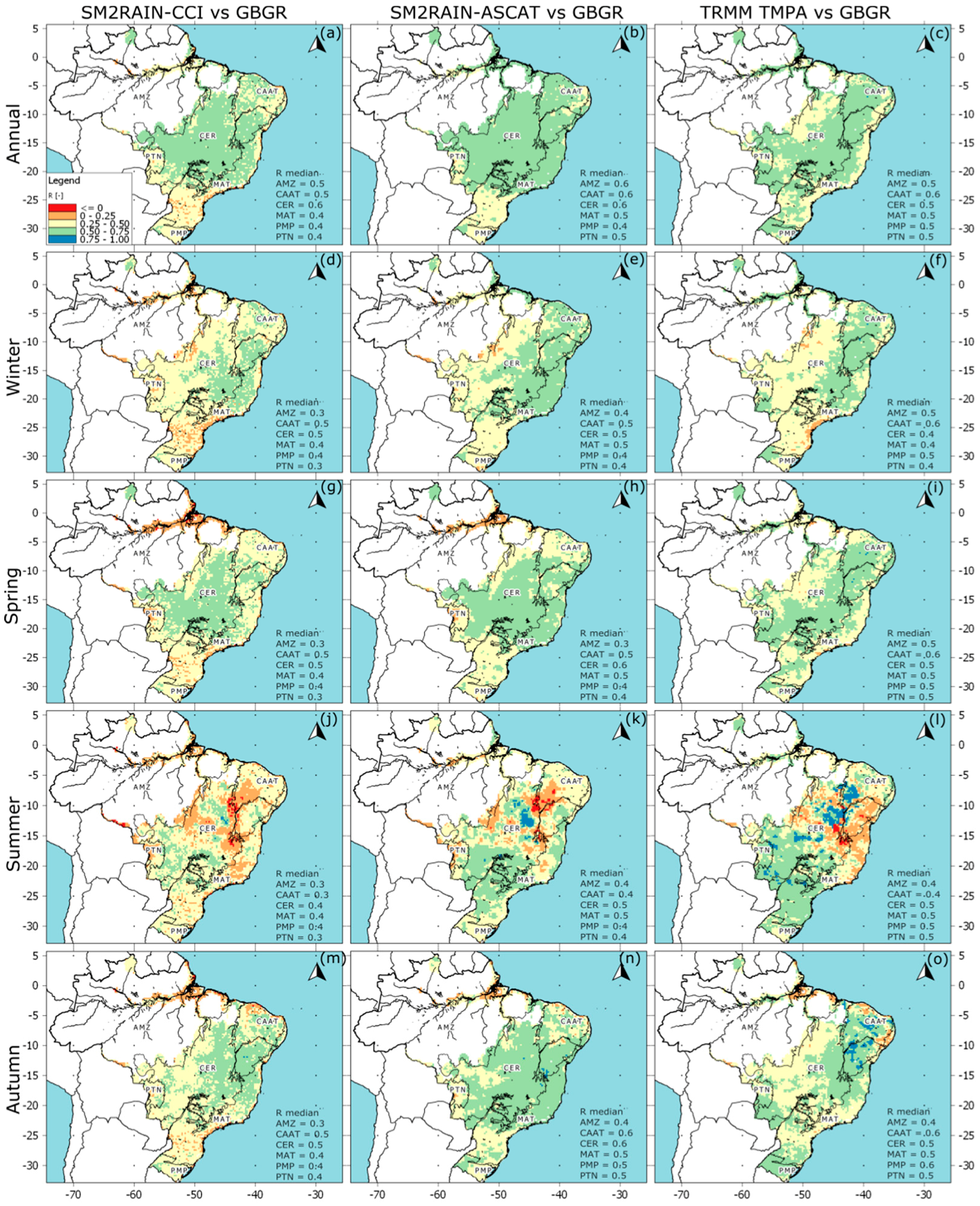
3.1. Annual and Seasonal Mean Precipitation
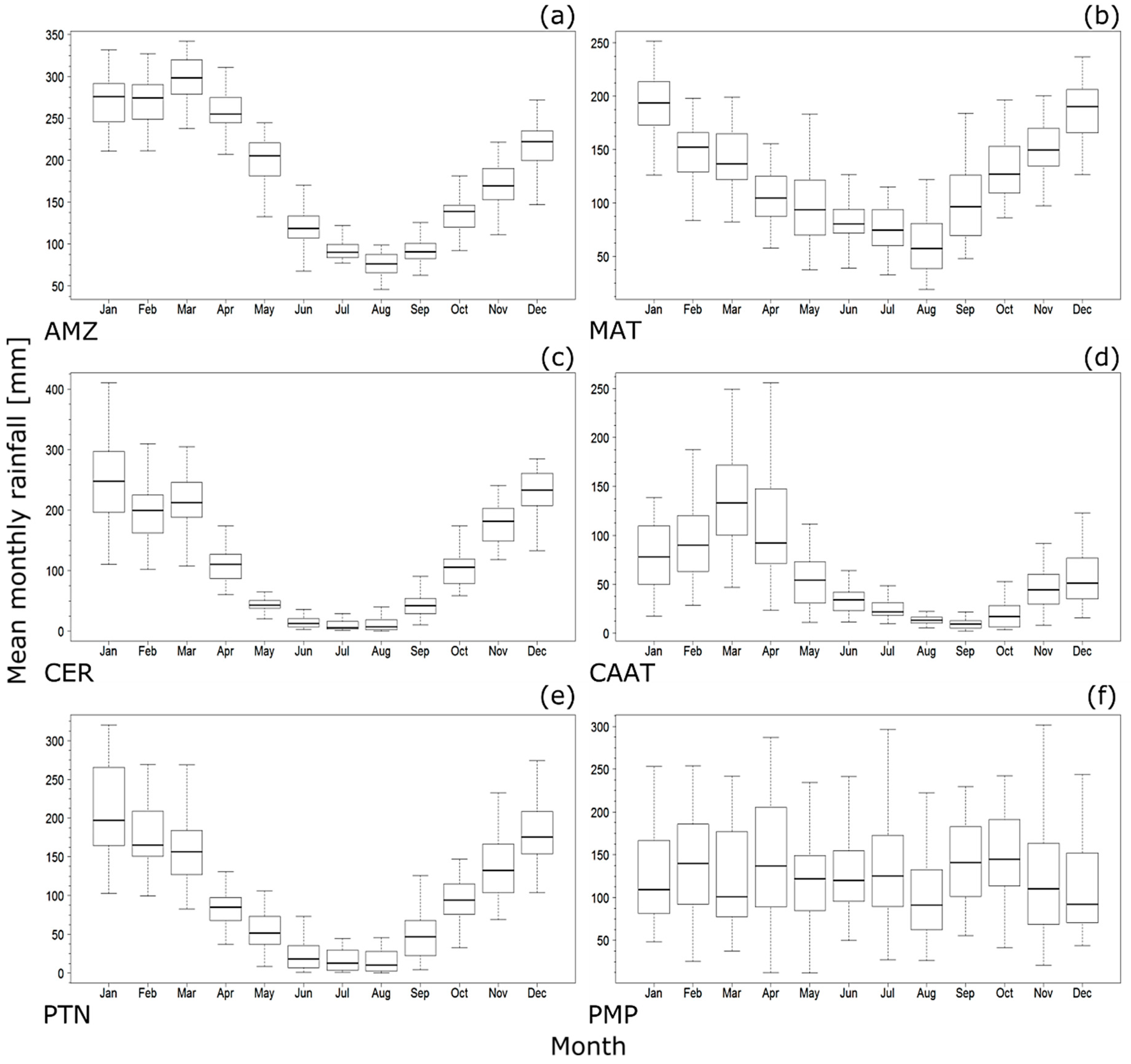
3.2. Monthly Mean Precipitation
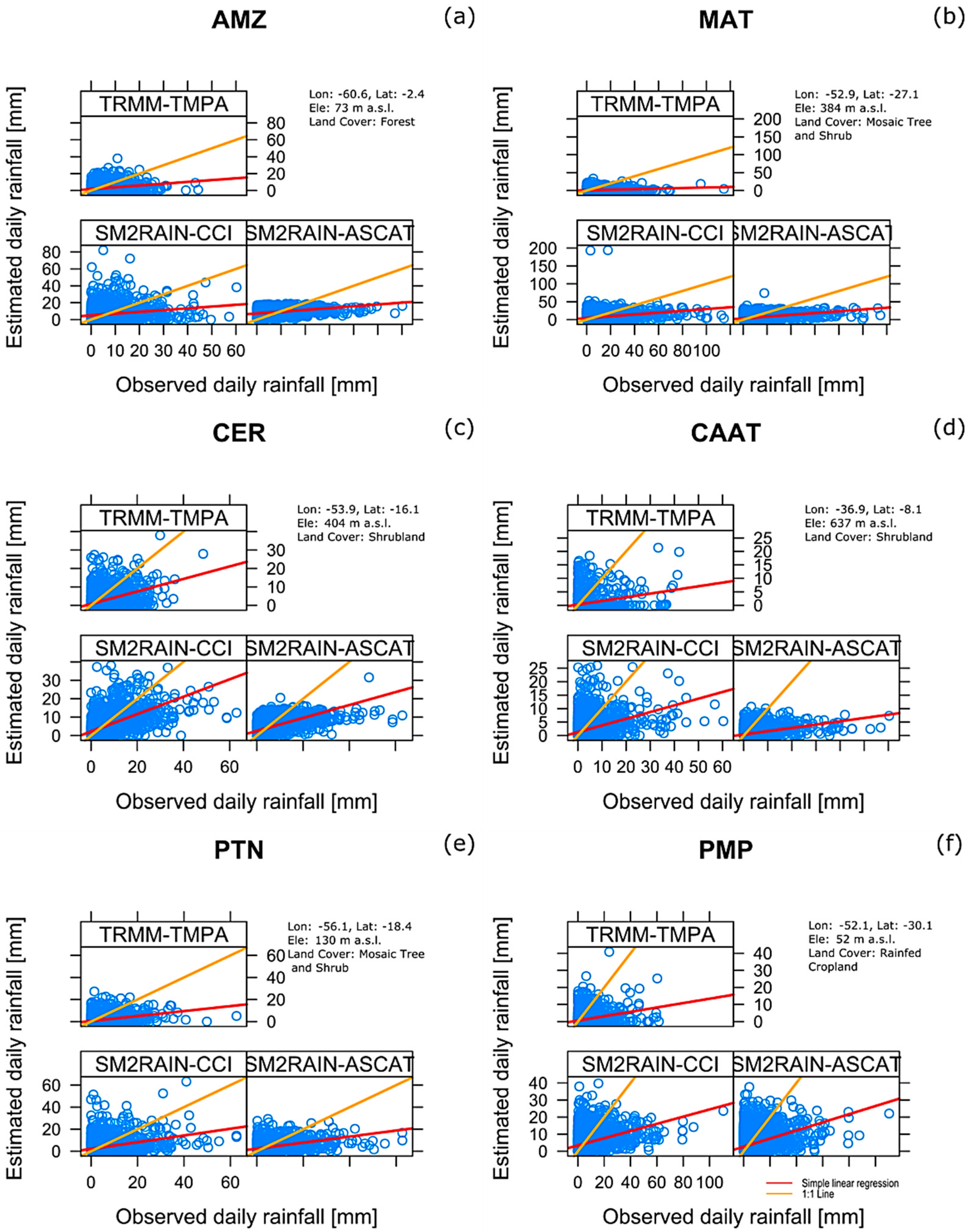
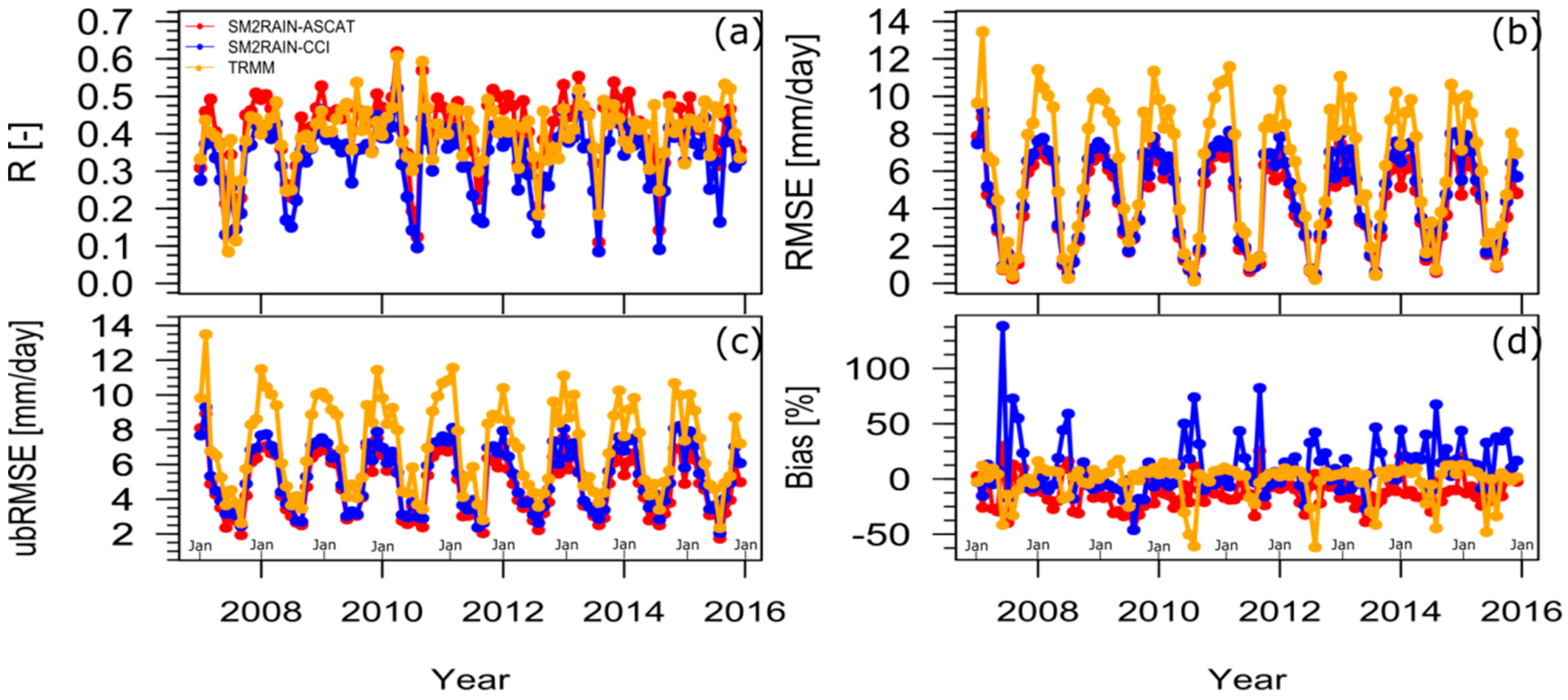
3.3. Error Characteristics of Daily Precipitation
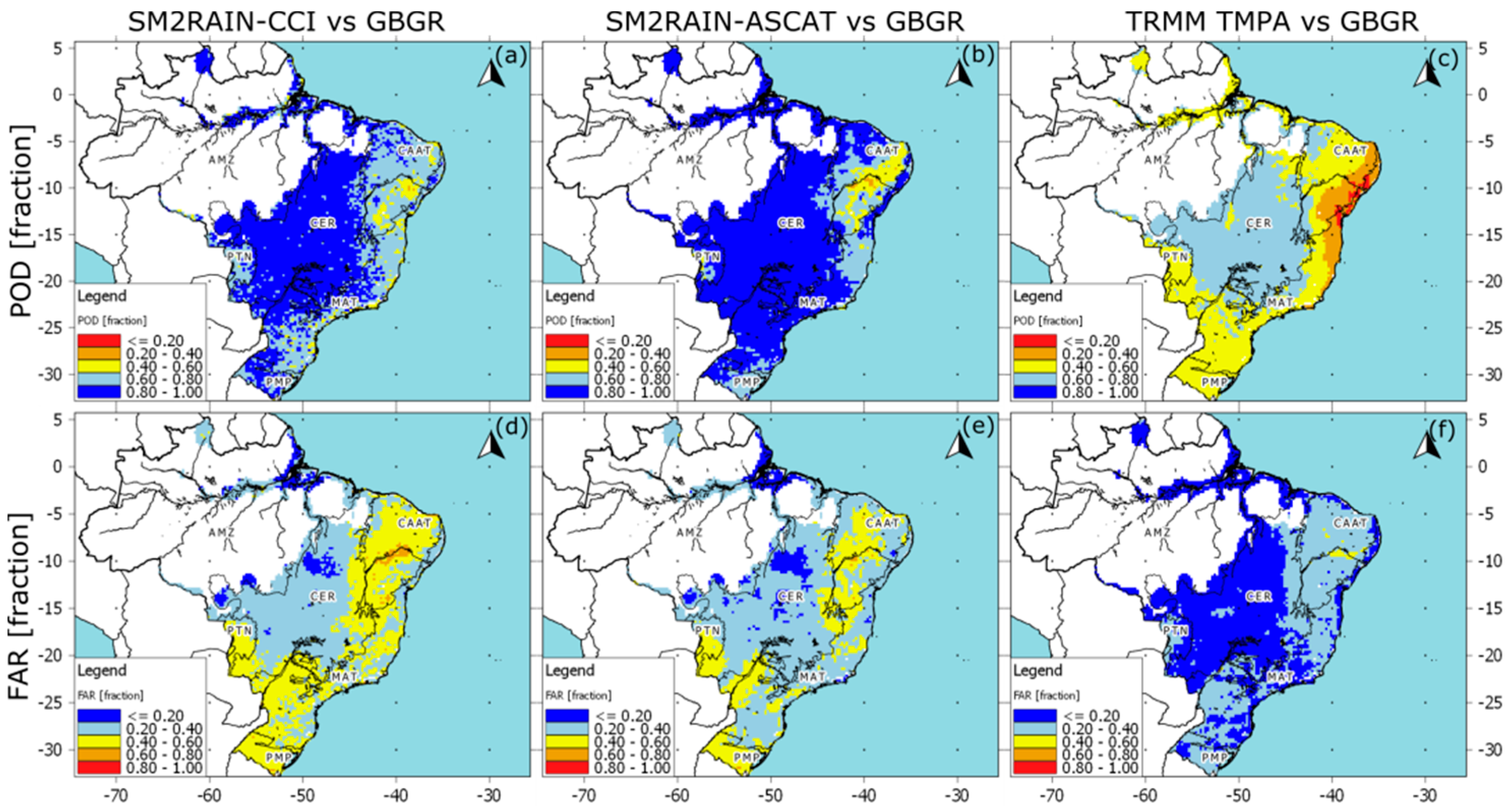
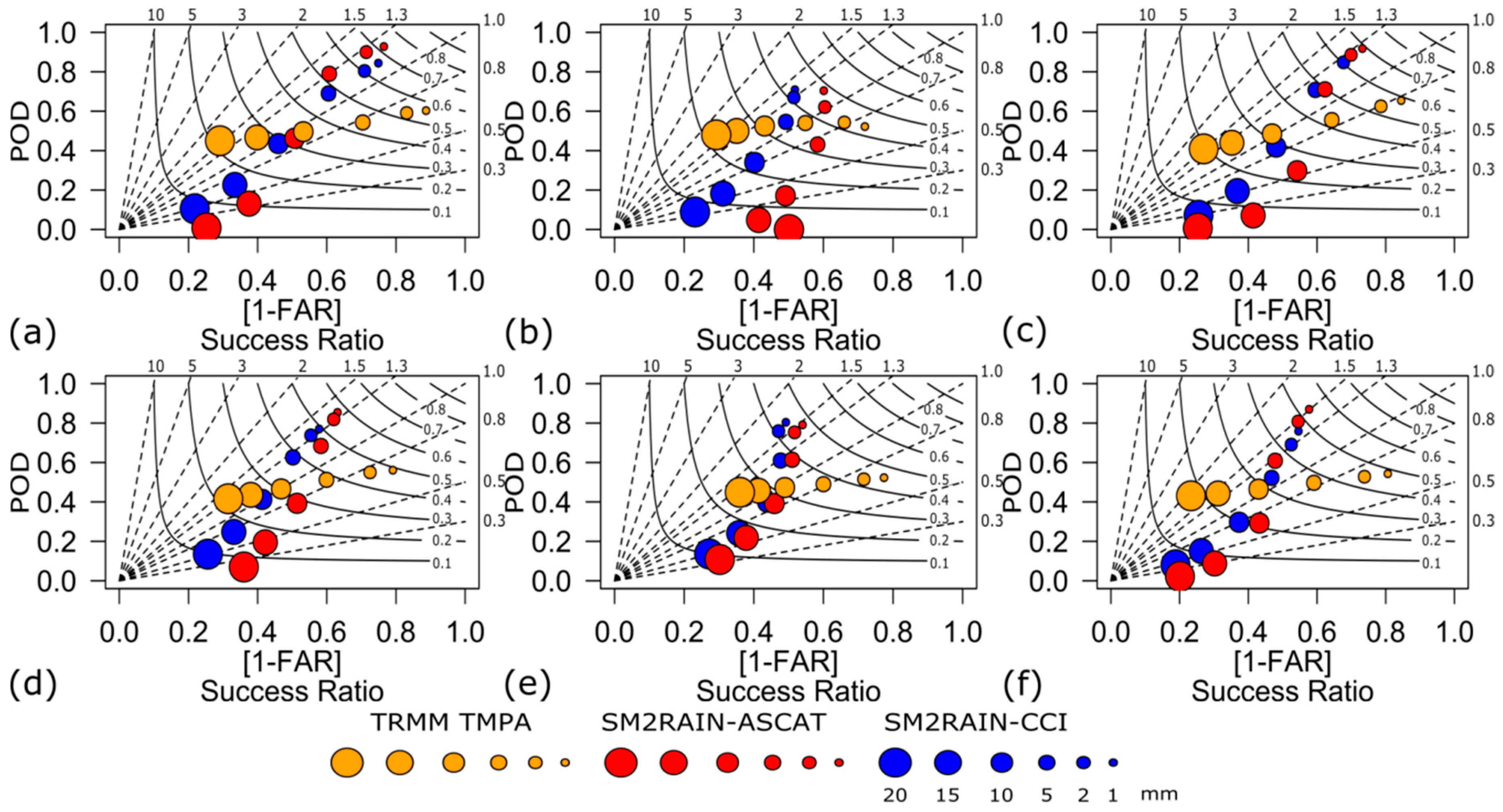
3.4. Performance of Precipitation Product in Detecting the Rainy Events
4. Discussion
5. Conclusions
- (1).
- (2).
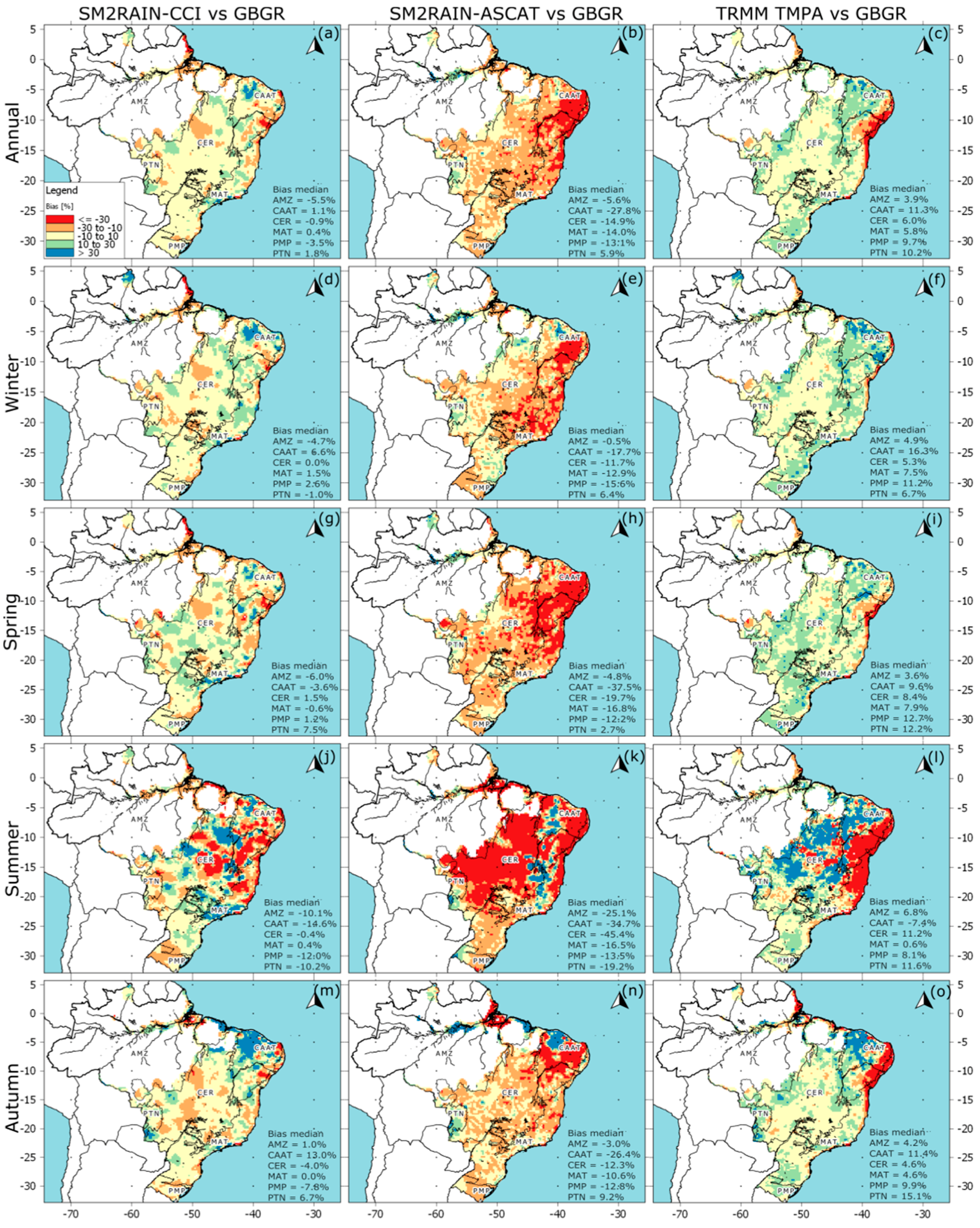
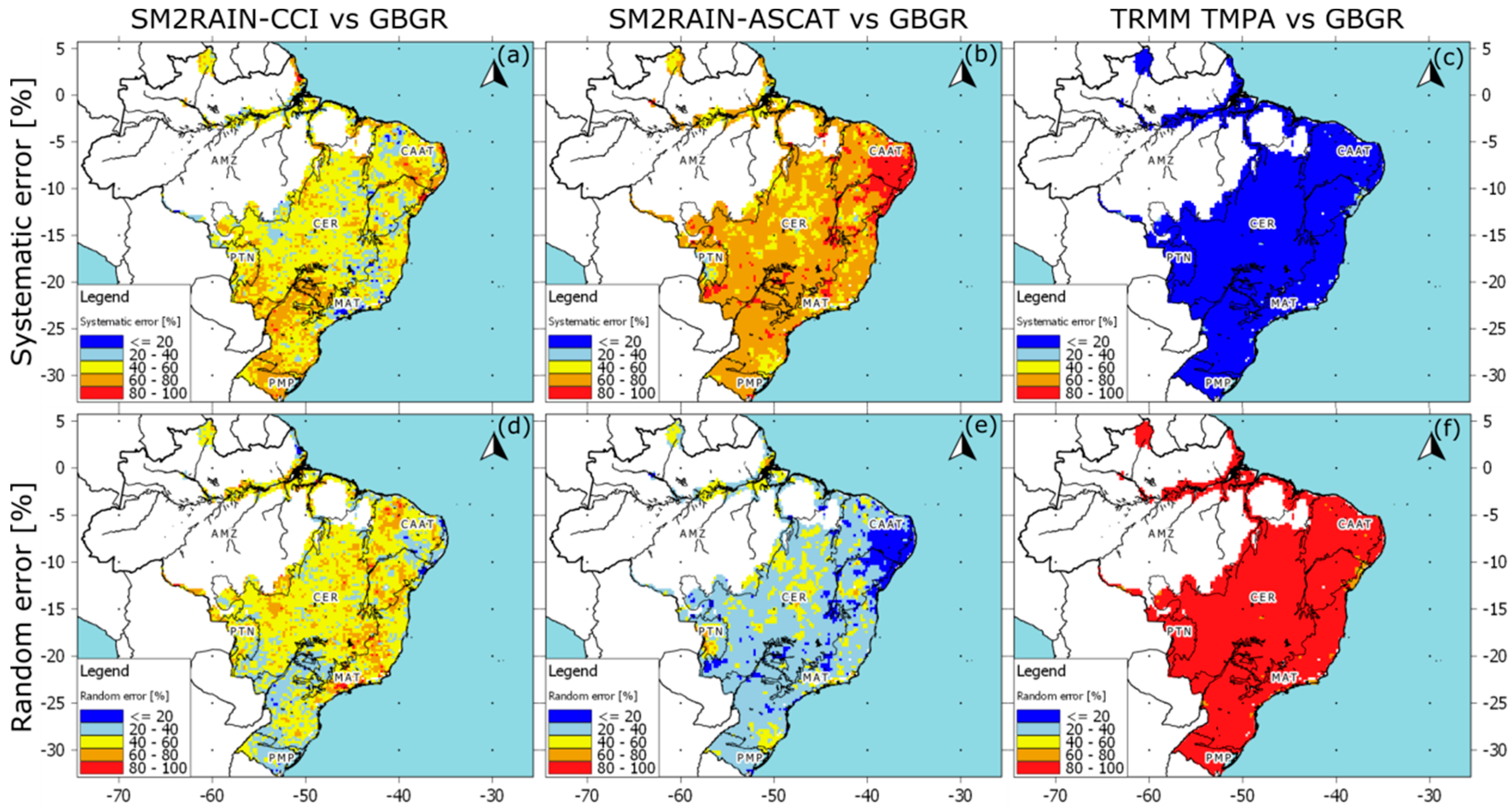
- The reliability of rainfall products was partially dependent on the topography and types of land use/land cover (biomes); for instance, they tended to fail to estimate the amount of rainfall in those regions dominated by a semiarid climate at the CAAT and CER biomes (see Figure 1c and Figure 6, and Table 5).
- (3).
- These products showed the highest (lowest) values of error in terms of RMSE and ubRMSE in winter and autumn (summer and spring), as expected because these scores are strongly dependent on the rainfall magnitude (see Figure 8).
- (4).
- SM2RAIN-CCI tended to show higher overestimation during the transition from summer to autumn, while a general underestimation characterized SM2RAIN-ASCAT throughout the year, and was significantly noticeable in spring (see Figure 8). TRMM TMPA tended to overestimate the seasonal daily mean rainfall in all biomes, excepting the CAAT biome in summer, where a moderate underestimation of the rainfall amount was observed (see Figure 5 and Figure 6).
- (5).
- The systematic error component in SM2RAIN-CCI and SM2RAIN-ASCAT was dominant to the random error component in all-Brazil (see Figure 9), suggesting the need for bias correction to these rainfall products before integrating them in any operational application. By contrast, TRMM TMPA showed a larger contribution of random error components than systematic error components.
- (6).
- In terms of POD, the results of the two SM2RAIN-based rainfall products were quite similar (excepting the CAAT biome) when a rainfall threshold of 1 mm/day was used (see Figure 10). Interestingly, the SM2RAIN-based and TRMM TMPA products tended to show decreased POD with the rainfall threshold increased (i.e., from 1–20 mm/day) over all biomes of Brazil. Thus, indicating that the performance of each product in detecting the rain occurrence declined with the rainfall threshold increased (see Figure 11). In terms of the detection of rainfall events, the two SM2RAIN-based SPPs performed better than TRMM TMPA (see Figure 10).
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Skofronick-Jackson, G.; Petersen, W.A.; Berg, W.; Kidd, C.; Stocker, E.F.; Kirschbaum, D.B.; Kakar, R.; Braun, S.A.; Huffman, G.J.; Iguchi, T.; et al. The global precipitation measurement (GPM) mission for science and society. Bull. Am. Meteorol. Soc. 2017, 98, 1679–1695. [Google Scholar] [CrossRef]
- Zhao, X.; Jing, W.; Zhang, P. Mapping Fine Spatial Resolution Precipitation from TRMM Precipitation Datasets Using an Ensemble Learning Method and MODIS Optical Products in China. Sustainability 2017, 9, 1912. [Google Scholar] [CrossRef]
- Prakash, S. Performance assessment of CHIRPS, MSWEP, SM2RAIN-CCI, and TMPA precipitation products across India. J. Hydrol. 2019, 571, 50–59. [Google Scholar] [CrossRef]
- Beck, H.E.; Vergopolan, N.; Pan, M.; Levizzani, V.; Van Dijk, A.I.J.M.; Weedon, G.P.; Brocca, L.; Pappenberger, F.; Huffman, G.J.; Wood, E.F. Global-scale evaluation of 22 precipitation datasets using gauge observations and hydrological modeling. Hydrol. Earth Syst. Sci. 2017, 21, 6201–6217. [Google Scholar] [CrossRef]
- Zambrano, F.; Wardlow, B.; Tadesse, T.; Lillo-Saavedra, M.; Lagos, O. Evaluating satellite-derived long-term historical precipitation datasets for drought monitoring in Chile. Atmos. Res. 2017, 186, 26–42. [Google Scholar] [CrossRef]
- Funk, C.; Verdin, A.; Michaelsen, J.; Peterson, P.; Pedreros, D.; Husak, G. A global satellite assisted precipitation climatology. Earth Syst. Sci. Data Discuss. 2015, 8, 401–425. [Google Scholar] [CrossRef]
- Villarini, G.; Mandapaka, P.V.; Krajewski, W.F.; Moore, R.J. Rainfall and sampling uncertainties: A rain gauge perspective. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef]
- Maggioni, V.; Sapiano, M.R.P.; Adler, R.F.; Tian, Y.; Huffman, G.J. An Error Model for Uncertainty Quantification in High-Time-Resolution Precipitation Products. J. Hydrometeorol. 2014, 15, 1274–1292. [Google Scholar] [CrossRef]
- Ciabatta, L.; Brocca, L.; Massari, C.; Moramarco, T.; Gabellani, S.; Puca, S.; Wagner, W. Rainfall-runoff modelling by using SM2RAIN-derived and state-of-the-art satellite rainfall products over Italy. Int. J. Appl. Earth Obs. Geoinf. 2016, 48, 163–173. [Google Scholar] [CrossRef]
- Munzimi, Y.A.; Hansen, M.C.; Adusei, B.; Senay, G.B. Characterizing Congo basin rainfall and climate using Tropical Rainfall Measuring Mission (TRMM) satellite data and limited rain gauge ground observations. J. Appl. Meteorol. Climatol. 2015, 54, 541–555. [Google Scholar] [CrossRef]
- Kidd, C.; Becker, A.; Huffman, G.J.; Muller, C.L.; Joe, P.; Skofronick-Jackson, G.; Kirschbaum, D.B. So, how much of the Earth’s surface is covered by rain gauges? Bull. Am. Meteorol. Soc. 2017, 98, 69–78. [Google Scholar] [CrossRef] [PubMed]
- Maggioni, V.; Meyers, P.C.; Robinson, M.D. A Review of Merged High-Resolution Satellite Precipitation Product Accuracy during the Tropical Rainfall Measuring Mission (TRMM) Era. J. Hydrometeorol. 2016, 17, 1101–1117. [Google Scholar] [CrossRef]
- Ciabatta, L.; Marra, A.C.; Panegrossi, G.; Casella, D.; Sanò, P.; Dietrich, S.; Massari, C.; Brocca, L. Daily precipitation estimation through different microwave sensors: Verification study over Italy. J. Hydrol. 2017, 545, 436–450. [Google Scholar] [CrossRef]
- Ciabatta, L.; Brocca, L.; Massari, C.; Moramarco, T.; Puca, S.; Rinollo, A.; Gabellani, S.; Wagner, W. Integration of Satellite Soil Moisture and Rainfall Observations over the Italian Territory. J. Hydrometeorol. 2015, 16, 1341–1355. [Google Scholar] [CrossRef]
- Paredes, F.; Barbosa, H.A.; Lakshmi-Kumar, T. Validating CHIRPS-based satellite precipitation estimates in Northeast Brazil. J. Arid Environ. 2016, 139, 26–40. [Google Scholar] [CrossRef]
- Sahoo, A.K.; Sheffield, J.; Pan, M.; Wood, E.F. Evaluation of the Tropical Rainfall Measuring Mission Multi-Satellite Precipitation Analysis (TMPA) for assessment of large-scale meteorological drought. Remote Sens. Environ. 2015, 159, 181–193. [Google Scholar] [CrossRef]
- Liu, X.; Chang, P.; Kurian, J.; Saravanan, R.; Lin, X. Satellite-observed precipitation response to ocean mesoscale eddies. J. Clim. 2018, 31, 6879–6895. [Google Scholar] [CrossRef]
- Zambrano-Bigiarini, M.; Nauditt, A.; Birkel, C.; Verbist, K.; Ribbe, L. Temporal and spatial evaluation of satellite-based rainfall estimates across the complex topographical and climatic gradients of Chile. Hydrol. Earth Syst. Sci. 2017, 21, 1295–1320. [Google Scholar] [CrossRef]
- Maggioni, V.; Sapiano, M.R.P.; Adler, R.F. Estimating Uncertainties in High-Resolution Satellite Precipitation Products: Systematic or Random Error? J. Hydrometeorol. 2016, 17, 1119–1129. [Google Scholar] [CrossRef]
- Abera, W.; Brocca, L.; Rigon, R. Comparative evaluation of different satellite rainfall estimation products and bias correction in the Upper Blue Nile (UBN) basin. Atmos. Res. 2016, 178–179, 471–483. [Google Scholar] [CrossRef]
- Kimani, M.W.; Hoedjes, J.C.B.; Su, Z. An assessment of satellite-derived rainfall products relative to ground observations over East Africa. Remote Sens. 2017, 9, 430. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-Global, Multiyear, Combined-Sensor Precipitation Estimates at Fine Scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Hsu, K.; Gao, X.; Sorooshian, S.; Gupta, H.V. Precipitation estimation from remotely sensed information using artificial neural networks. J. Appl. Meteorol. 1997, 36, 1176–1190. [Google Scholar] [CrossRef]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A Method that Produces Global Precipitation Estimates from Passive Microwave and Infrared Data at High Spatial and Temporal Resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef] [PubMed]
- Beck, H.E.; Van Dijk, A.I.J.M.; Levizzani, V.; Schellekens, J.; Miralles, D.G.; Martens, B.; De Roo, A. MSWEP: 3-hourly 0.25° global gridded precipitation (1979–2015) by merging gauge, satellite, and reanalysis data. Hydrol. Earth Syst. Sci. 2017, 21, 589–615. [Google Scholar] [CrossRef]
- Brocca, L.; Ciabatta, L.; Massari, C.; Dorigo, W.; Hahn, S. Soil as a natural raingauge: Estimating rainfall from global satellite soil moisture data. J. Geophys. Res. Atmos. 2014, 119, 5128–5141. [Google Scholar] [CrossRef]
- Brocca, L.; Moramarco, T.; Melone, F.; Wagner, W. A new method for rainfall estimation through soil moisture observations. Geophys. Res. Lett. 2013, 40, 853–858. [Google Scholar] [CrossRef]
- Brocca, L.; Massari, C.; Ciabatta, L.; Moramarco, T.; Penna, D.; Zuecco, G.; Pianezzola, L.; Borga, M.; Matgen, P.; Martínez-Fernández, J. Rainfall estimation from in situ soil moisture observations at several sites in Europe: An evaluation of the SM2RAIN algorithm. J. Hydrol. Hydromech. 2015, 63, 201–209. [Google Scholar] [CrossRef]
- Paredes-Trejo, F.; Barbosa, H.; Rossato, L. Assessment of SM2RAIN-Derived and State-of-the-Art Satellite Rainfall Products over Northeastern Brazil. Remote Sens. 2018, 10, 1093. [Google Scholar] [CrossRef]
- Koster, R.D.; Brocca, L.; Crow, W.T.; Burgin, M.S.; De Lannoy, G.J.M. Precipitation estimation using L-band and C-band soil moisture retrievals. Water Resour. Res. 2016, 52, 7213–7225. [Google Scholar] [CrossRef] [PubMed]
- Ciabatta, L.; Massari, C.; Brocca, L.; Gruber, A.; Reimer, C.; Hahn, S.; Paulik, C.; Dorigo, W.; Kidd, R.; Wagner, W. SM2RAIN-CCI: A new global long-term rainfall dataset derived from ESA CCI soil moisture. Earth Syst. Sci. Data 2018, 10, 267–280. [Google Scholar] [CrossRef]
- Brocca, L.; Pellarin, T.; Crow, W.T.; Ciabatta, L.; Massari, C.; Ryu, D.; Su, C.-H.; Rüdiger, C.; Kerr, Y. Rainfall estimation by inverting SMOS soil moisture estimates: A comparison of different methods over Australia. J. Geophys. Res. Atmos. 2016, 121, 12–62. [Google Scholar] [CrossRef]
- Brocca, L.; Ciabatta, L.; Massari, C.; Camici, S.; Tarpanelli, A. Soil moisture for hydrological applications: Open questions and new opportunities. Water 2017, 9, 140. [Google Scholar] [CrossRef]
- Brocca, L.; National, I.; Ciabatta, L.; National, I.; Massari, C.; National, I.; Italian, M.; View, D.W.; Brocca, L. Integration of H05 and H16 Products through SM2RAIN Algorithm for Improving Rainfall Estimate; European Organisation for the Exploitation of Meteorological Satellites: Darmstadt, Germany, 2016. [Google Scholar]
- Liu, Y.Y.; Parinussa, R.M.; Dorigo, W.A.; De Jeu, R.A.M.; Wagner, W.; Van Dijk, A.I.J.M.; McCabe, M.F.; Evans, J.P. Developing an improved soil moisture dataset by blending passive and active microwave satellite-based retrievals. Hydrol. Earth Syst. Sci. 2011, 15, 425–436. [Google Scholar] [CrossRef]
- Dorigo, W.A.; Gruber, A.; De Jeu, R.A.M.; Wagner, W.; Stacke, T.; Loew, A.; Albergel, C.; Brocca, L.; Chung, D.; Parinussa, R.M.; et al. Evaluation of the ESA CCI soil moisture product using ground-based observations. Remote Sens. Environ. 2015, 162, 380–395. [Google Scholar] [CrossRef]
- Wagner, W.; Hahn, S.; Kidd, R.; Melzer, T.; Bartalis, Z.; Hasenauer, S.; Figa-Saldaña, J.; de Rosnay, P.; Jann, A.; Schneider, S.; et al. The ASCAT soil moisture product: A review of its specifications, validation results, and emerging applications. Meteorol. Z. 2013, 22, 5–33. [Google Scholar] [CrossRef]
- Melo, D.d.C.D.; Xavier, A.C.; Bianchi, T.; Oliveira, P.T.S.; Scanlon, B.R.; Lucas, M.C.; Wendland, E. Performance evaluation of rainfall estimates by TRMM multi-satellite precipitation analysis 3B42V6 and V7 over Brazil. J. Geophys. Res. 2015, 120, 9426–9436. [Google Scholar] [CrossRef]
- Ayehu, G.T.; Tadesse, T.; Gessesse, B.; Dinku, T. Validation of new satellite rainfall products over the Upper Blue Nile Basin, Ethiopia. Atmos. Meas. Tech. Discuss. 2017, 11, 1–24. [Google Scholar] [CrossRef]
- Nogueira, S.M.C.; Moreira, M.A.; Volpato, M.M.L. Evaluating precipitation estimates from Eta, TRMM and CHRIPS data in the south-southeast region of Minas Gerais state-Brazil. Remote Sens. 2018, 10, 313. [Google Scholar] [CrossRef]
- Souto, J.; Beltrão, N.; Teodoro, A.; Souto, J.; Beltrão, N.; Teodoro, A. Performance of Remotely Sensed Soil Moisture for Temporal and Spatial Analysis of Rainfall over São Francisco River Basin, Brazil. Geosciences 2019, 9, 144. [Google Scholar] [CrossRef]
- Ciabatta, L.; Massari, C.; Brocca, L.; Gruber, A.; Reimer, C.; Hahn, S.; Paulik, C.; Dorigo, W.; Kidd, R.; Wagner, W. SM2RAIN-CCI (1 Jan 1998–31 December 2015) global daily rainfall dataset 2018. Available online: https://zenodo.org/record/846260#.XNOpPZoRWUk (accessed on 8 May 2019).
- Brocca, L.; Filippucci, P.; Hahn, S.; Ciabatta, L.; Massari, C.; Camici, S.; Schüller, L.; Bojkov, B.; Wagner, W. Wolfgang SM2RAIN-ASCAT (2007–2018): Global daily satellite rainfall from ASCAT soil moisture. Earth Syst. Sci. Data 2019. in review. [Google Scholar] [CrossRef]
- Instituto Brasileiro de Geografia e Estatística 2010 Census (Censo 2010). Available online: https://ww2.ibge.gov.br/home/estatistica/populacao/censo2010/default.shtm (accessed on 7 March 2019).
- Salazar, L.; Nobre, C.; Oyama, M. Climate change consequences on the biome distribution in tropical South America. Geophys. Res. Lett. 2007, 34, 1–6. [Google Scholar] [CrossRef]
- Oliveira-Filho, A.T.; Ratter, J.A. Vegetation Physiognomies and Woody Flora of the Cerrado Biome. Cerrados Brazil Ecol. Nat. Hist. a Neotrop. Savanna 2002, 42, 91–120. [Google Scholar]
- Scarano, F.R.; Ceotto, P. Brazilian Atlantic forest: Impact, vulnerability, and adaptation to climate change. Biodivers. Conserv. 2015, 24, 2319–2331. [Google Scholar] [CrossRef]
- Barbosa, H.A.; Huete, A.R.; Baethgen, W.E. A 20-year study of NDVI variability over the Northeast Region of Brazil. J. Arid Environ. 2006, 67, 288–307. [Google Scholar] [CrossRef]
- Mariano, D.A.; dos Santos, C.A.C.; Wardlow, B.D.; Anderson, M.C.; Schiltmeyer, A.V.; Tadesse, T.; Svoboda, M.D. Use of remote sensing indicators to assess effects of drought and human-induced land degradation on ecosystem health in Northeastern Brazil. Remote Sens. Environ. 2018, 213, 129–143. [Google Scholar] [CrossRef]
- Souza, R.; Feng, X.; Antonino, A.; Montenegro, S.; Souza, E.; Porporato, A. Vegetation response to rainfall seasonality and interannual variability in tropical dry forests. Hydrol. Process. 2016, 30, 3583–3595. [Google Scholar] [CrossRef]
- Alho, C.J.R. Biodiversity of the Pantanal: Response to seasonal flooding regime and to environmental degradation. Braz. J. Biol. 2008, 68, 957–966. [Google Scholar] [CrossRef]
- Cruz, J.C.; Valente, M.L.; Baggiotto, C.; Baumhardt, E. Qualitative characteristics of water resulting from the introduction of Eucalyptus silviculture in Pampa biome, RS. RBRH 2016, 21, 636–645. [Google Scholar] [CrossRef]
- Barbosa, H.A.; Lakshmi Kumar, T.V.; Silva, L.R.M. Recent trends in vegetation dynamics in the South America and their relationship to rainfall. Nat. Hazards 2015, 77, 883–899. [Google Scholar] [CrossRef]
- Barbosa, H.A.; Lakshmi Kumar, T.V. Influence of rainfall variability on the vegetation dynamics over Northeastern Brazil. J. Arid Environ. 2016, 124, 377–387. [Google Scholar] [CrossRef]
- Barbosa, H.A.; Lakshmi Kumar, T.; Paredes, F.; Elliott, S.; Ayuga, J.G. Assessment of Caatinga response to drought using Meteosat-SEVIRI Normalized Difference Vegetation Index (2008–2016). ISPRS J. Photogramm. Remote Sens. 2019, 148, 235–252. [Google Scholar] [CrossRef]
- Houghton, R.A.; Bontemps, S.; Peng, S.; Lamarche, C.; Li, W.; MacBean, N.; Defourny, P.; Ciais, P. Gross and net land cover changes based on plant functional types derived from the annual ESA CCI land cover maps. Earth Syst. Sci. Data Discuss. 2017, 10, 1–23. [Google Scholar]
- Berry, P.A.M.; Garlick, J.D.; Smith, R.G. Near-global validation of the SRTM DEM using satellite radar altimetry. Remote Sens. Environ. 2007, 106, 17–27. [Google Scholar] [CrossRef]
- Xavier, A.C.; King, C.W.; Scanlon, B.R. Daily gridded meteorological variables in Brazil (1980–2013). Int. J. Climatol. 2016, 36, 2644–2659. [Google Scholar] [CrossRef]
- Marengo, J.A. Interannual variability of surface climate in the Amazon basin. Int. J. Climatol. 1992, 12, 853–863. [Google Scholar] [CrossRef]
- Tomaziello, A.C.N.; Carvalho, L.M.V.; Gandu, A.W. Intraseasonal variability of the Atlantic Intertropical Convergence Zone during austral summer and winter. Clim. Dyn. 2016, 47, 1717–1733. [Google Scholar] [CrossRef]
- Ledru, M.-P.; Montade, V.; Blanchard, G.; Hély, C. Long-term spatial changes in the distribution of the Brazilian Atlantic Forest. Biotropica 2016, 48, 159–169. [Google Scholar] [CrossRef]
- Kousky, V.E. Frontal Influences on Northeast Brazil. Mon. Weather Rev. 1979, 107, 1140–1153. [Google Scholar] [CrossRef]
- Carvalho, L.M.V.; Jones, C.; Liebmann, B. The South Atlantic convergence zone: Intensity, form, persistence, and relationships with intraseasonal to interannual activity and extreme rainfall. J. Clim. 2004, 17, 88–108. [Google Scholar] [CrossRef]
- Rao, V.B.; Franchito, S.H.; Santo, C.M.E.; Gan, M.A. An update on the rainfall characteristics of Brazil: Seasonal variations and trends in 1979–2011. Int. J. Climatol. 2016, 36, 291–302. [Google Scholar] [CrossRef]
- Uvo, C.B.; Repelli, C.A.; Zebiak, S.E.; Kushnir, Y. The relationships between tropical Pacific and Atlantic SST and northeast Brazil monthly precipitation. J. Clim. 1998, 11, 551–562. [Google Scholar] [CrossRef]
- Xavier, A.C.; King, C.W.; Scanlon, B.R. Brazil Gridded Meteorological Data from 1980–2013, 2016. Available online: https://pdfs.semanticscholar.org/9e4c/b88ee4d2c6d574c9eb1ccd7d4f81d1aa1029.pdf (accessed on 8 May 2019).
- Hofstra, N.; New, M. Spatial variability in correlation decay distance and influence on angular-distance weighting interpolation of daily precipitation over Europe. Int. J. Climatol. 2009, 29, 1872–1880. [Google Scholar] [CrossRef]
- Xavier, A.C. An update of Xavier, King and Scanlon (2016) daily precipitation gridded dataset for the Brazil. In Proceedings of the 18th Brazilian Symposium on Remote Sensing, Santos, São Paulo, Brazil, 28–31 May 2017. [Google Scholar]
- Loew, A.; Bell, W.; Brocca, L.; Bulgin, C.E.; Burdanowitz, J.; Calbet, X.; Donner, R.V.; Ghent, D.; Gruber, A.; Kaminski, T.; et al. Validation practices for satellite-based Earth observation data across communities. Rev. Geophys. 2017, 55, 779–817. [Google Scholar] [CrossRef]
- Brocca, L.; Crow, W.T.; Ciabatta, L.; Massari, C.; De Rosnay, P.; Enenkel, M.; Hahn, S.; Amarnath, G.; Camici, S.; Tarpanelli, A.; et al. A review of the applications of ASCAT soil moisture products. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2285–2306. [Google Scholar] [CrossRef]
- Massari, C.; Camici, S.; Ciabatta, L.; Brocca, L. Exploiting satellite-based surface soil moisture for flood forecasting in the Mediterranean area: State update versus rainfall correction. Remote Sens. 2018, 10, 292. [Google Scholar] [CrossRef]
- GES DISC. Mirador—Goddard Earth Sciences (GES) Data and Information Center (DISC). Available online: https://mirador.gsfc.nasa.gov/ (accessed on 8 May 2019).
- Rozante, J.; Vila, D.; Barboza Chiquetto, J.; Fernandes, A.; Souza Alvim, D. Evaluation of TRMM/GPM blended daily products over Brazil. Remote Sens. 2018, 10, 882. [Google Scholar] [CrossRef]
- AghaKouchak, A.; Mehran, A.; Norouzi, H.; Behrangi, A. Systematic and random error components in satellite precipitation datasets. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Huang, A.; Zhao, Y.; Zhou, Y.; Yang, B.; Zhang, L.; Dong, X.; Fang, D.; Wu, Y. Evaluation of multisatellite precipitation products by use of ground-based data over China. J. Geophys. Res. Atmos. 2016, 121, 10–654. [Google Scholar] [CrossRef]
- Toté, C.; Patricio, D.; Boogaard, H.; van der Wijngaart, R.; Tarnavsky, E.; Funk, C. Evaluation of satellite rainfall estimates for drought and flood monitoring in Mozambique. Remote Sens. 2015, 7, 1758–1776. [Google Scholar] [CrossRef]
- Roebber, P.J. Visualizing multiple measures of forecast quality. Weather Forecast. 2009, 24, 601–608. [Google Scholar] [CrossRef]
- Rodriguez-Fernández, N.J.; Kerr, Y.H.; van der Schalie, R.; Al-Yaari, A.; Wigneron, J.-P.; de Jeu, R.; Richaume, P.; Dutra, E.; Mialon, A.; Drusch, M.; et al. Long Term Global Surface Soil Moisture Fields Using an SMOS-Trained Neural Network Applied to AMSR-E Data. Remote Sens. 2016, 8, 959. [Google Scholar] [CrossRef]
- Chen, M.; Shi, W.; Xie, P.; Silva, V.B.S.; Kousky, V.E.; Wayne Higgins, R.; Janowiak, J.E. Assessing objective techniques for gauge-based analyses of global daily precipitation. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef]
- Zeng, Q.; Wang, Y.; Chen, L.; Wang, Z.; Zhu, H.; Li, B. Inter-comparison and evaluation of remote sensing precipitation products over China from 2005 to 2013. Remote Sens. 2018, 10, 168. [Google Scholar] [CrossRef]
- Schneider, U.; Becker, A.; Finger, P.; Meyer-Christoffer, A.; Ziese, M.; Rudolf, B. GPCC’s new land surface precipitation climatology based on quality controlled in situ data and its role in quantifying the global water cycle. Theor. Appl. Climatol. 2014, 115, 15–40. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Bolvin, D.T.; Nelkin, E.J. The TRMM multi-satellite precipitation analysis (TMPA). In Satellite Rainfall Applications for Surface Hydrology; Springer: Dordrecht, The Netherlands, 2010; pp. 3–22. [Google Scholar]
- Vittucci, C.; Ferrazzoli, P.; Kerr, Y.; Richaume, P.; Guerriero, L.; Rahmoune, R.; Laurin, G.V. SMOS retrieval over forests: Exploitation of optical depth and tests of soil moisture estimates. Remote Sens. Environ. 2016, 180, 115–127. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Waldteufel, P.; Wigneron, J.-P.; Martinuzzi, J.; Font, J.; Berger, M. Soil moisture retrieval from space: The Soil Moisture and Ocean Salinity (SMOS) mission. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1729–1735. [Google Scholar] [CrossRef]
- Rodríguez-Fernández, N.; Muñoz Sabater, J.; Richaume, P.; de Rosnay, P.; Kerr, Y.; Albergel, C.; Drusch, M.; Mecklenburg, S. SMOS near real time soil moisture product: Processor overview and first validation results. Hydrol. Earth Syst. Sci. Discuss. 2017, 21, 1–23. [Google Scholar] [CrossRef]
- Obregon, G.O.; Nobre, C.A. Rainfall trends in Brazil. Bull. Am. Meteorol. Soc. 2003, 84, 1008. [Google Scholar]
- Bhatti, H.; Rientjes, T.; Haile, A.; Habib, E.; Verhoef, W. Evaluation of bias correction method for satellite-based rainfall data. Sensors 2016, 16, 884. [Google Scholar] [CrossRef] [PubMed]
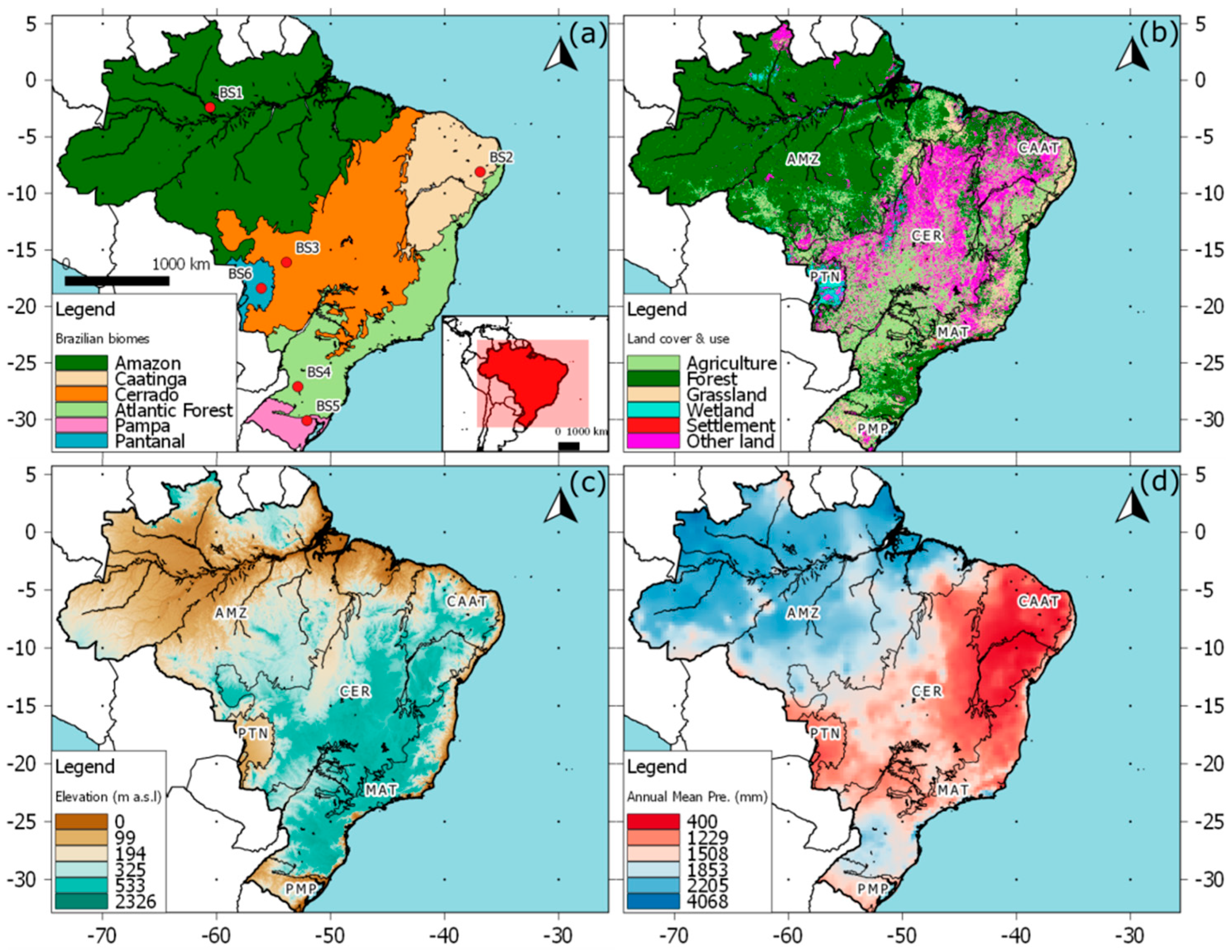
| Biome | Area (km2/1000) * | Median Elevation (m a.s.l.) ** | Dominant Land Cover/Use 1 (Name/%) | MAR 2 (mm) | Wettest Trimester 3 |
|---|---|---|---|---|---|
| AMZ | 4094 | 176 | Forest/82% | 2215 | JFM |
| CER | 2089 | 504 | Agriculture/43% | 1400 | DJF |
| MAT | 1166 | 550 | Agriculture/40% | 1457 | DJF |
| CAAT | 825 | 418 | Agriculture/36% | 639 | FMA |
| PTN | 156 | 127 | Forest/25% | 1145 | DJF |
| PMP | 186 | 152 | Agriculture/41% | 1433 | SON |
| Name | Formula | Perfect Score |
|---|---|---|
| Pearson correlation coefficient | 1 | |
| Root mean square error | 0 | |
| Unbiased root mean square error | 0 | |
| Bias | 0 |
| Gauge ≥ Threshold | Gauge < Threshold | |
|---|---|---|
| Satellite ≥ Threshold | A | B |
| Satellite < Threshold | C | D |
| Name | Formula | Perfect Score |
|---|---|---|
| Probability of Detection | 1 | |
| False Alarm Ratio | 0 | |
| Critical Success Index | 1 | |
| Bias Score | 1 |
| R | BIAS | ||||||
|---|---|---|---|---|---|---|---|
| Elevation Range 1 | Land Cover/Use 2 | CCI | ASCAT | TMRR | CCI | ASCAT | TMRR |
| Very Low (≤141 m a.s.l.)* | Bare Area | 0.33 | 0.50 | 0.52 | 24.60 | −19.05 | −5.80 |
| Forest | 0.44 | 0.54 | 0.50 | −5.60 | −8.00 | 5.90 | |
| Grassland | 0.46 | 0.54 | 0.50 | −5.85 | −18.50 | 2.70 | |
| Mosaic Cropland | 0.47 | 0.54 | 0.52 | −3.70 | −14.40 | 5.30 | |
| Mosaic Natural Vegetation | 0.46 | 0.52 | 0.52 | −4.20 | −14.30 | 5.30 | |
| Mosaic Tree and Shrub | 0.46 | 0.54 | 0.53 | −4.50 | −10.70 | 3.80 | |
| Rainfed Cropland | 0.50 | 0.55 | 0.51 | −1.20 | −11.80 | 6.60 | |
| Settlement | 0.47 | 0.58 | 0.48 | −6.15 | −21.50 | 1.85 | |
| Shrubland | 0.52 | 0.55 | 0.50 | 0.40 | −11.20 | 8.10 | |
| Sparse Vegetation | 0.38 | 0.51 | 0.55 | 7.30 | −18.60 | −0.50 | |
| Tree Cover Flooded | 0.34 | 0.54 | 0.43 | −11.70 | −17.30 | 6.00 | |
| Tree Cover Flooded Saline | 0.34 | 0.60 | 0.60 | −16.80 | −9.80 | 3.35 | |
| Water | 0.40 | 0.49 | 0.53 | −1.05 | −5.55 | 3.75 | |
| Wetland | 0.42 | 0.49 | 0.50 | 0.20 | 0.65 | 6.45 | |
| Low (142–438 m a.s.l.) | Bare Area | 0.49 | 0.55 | 0.61 | 18.60 | −25.50 | 16.60 |
| Forest | 0.52 | 0.57 | 0.54 | 2.55 | −14.00 | 10.55 | |
| Grassland | 0.51 | 0.57 | 0.52 | 1.80 | −19.05 | 5.05 | |
| Mosaic Cropland | 0.53 | 0.57 | 0.54 | −0.30 | −18.90 | 5.30 | |
| Mosaic Natural Vegetation | 0.50 | 0.55 | 0.56 | −0.15 | −20.95 | 7.10 | |
| Mosaic Tree and Shrub | 0.52 | 0.58 | 0.52 | 1.50 | −14.90 | 7.70 | |
| Rainfed Cropland | 0.53 | 0.58 | 0.53 | −0.80 | −13.75 | 6.60 | |
| Settlement | 0.51 | 0.58 | 0.51 | −5.80 | −8.50 | 3.60 | |
| Shrubland | 0.55 | 0.59 | 0.53 | 1.50 | −17.30 | 9.10 | |
| Sparse Vegetation | 0.54 | 0.56 | 0.60 | 1.40 | −48.60 | −4.00 | |
| Tree Cover Flooded | 0.49 | 0.53 | 0.55 | 41.30 | 7.60 | 22.90 | |
| Water | 0.52 | 0.56 | 0.54 | −1.95 | −20.25 | 0.50 | |
| Wetland | 0.33 | 0.50 | 0.50 | 1.70 | −12.50 | 5.40 | |
| Medium (439–740 m a.s.l.) | Forest | 0.49 | 0.57 | 0.52 | 1.60 | −14.60 | 8.15 |
| Grassland | 0.48 | 0.61 | 0.52 | 1.70 | −16.80 | 6.00 | |
| Mosaic Cropland | 0.55 | 0.62 | 0.54 | −2.00 | −16.90 | 7.40 | |
| Mosaic Natural Vegetation | 0.57 | 0.62 | 0.56 | 0.25 | −19.00 | 6.05 | |
| Mosaic Tree and Shrub | 0.50 | 0.58 | 0.52 | 3.40 | −14.50 | 9.10 | |
| Rainfed Cropland | 0.57 | 0.62 | 0.55 | −0.10 | −16.65 | 6.60 | |
| Settlement | 0.38 | 0.53 | 0.49 | 2.40 | −18.10 | 5.00 | |
| Shrubland | 0.60 | 0.64 | 0.57 | 0.00 | −18.40 | 5.50 | |
| Water | 0.60 | 0.63 | 0.56 | −0.30 | −28.35 | 1.90 | |
| Wetland | 0.63 | 0.63 | 0.61 | −1.10 | −9.30 | 2.80 | |
| High (741–994 m a.s.l.) | Forest | 0.36 | 0.48 | 0.51 | 2.05 | −10.30 | 9.65 |
| Grassland | 0.51 | 0.58 | 0.54 | −0.30 | −17.70 | 6.30 | |
| Mosaic Cropland | 0.56 | 0.61 | 0.54 | −0.85 | −14.40 | 4.65 | |
| Mosaic Natural Vegetation | 0.54 | 0.66 | 0.55 | 2.35 | −15.85 | 4.25 | |
| Mosaic Tree and Shrub | 0.53 | 0.63 | 0.52 | 0.05 | −13.05 | 5.25 | |
| Rainfed Cropland | 0.58 | 0.64 | 0.55 | −0.30 | −13.20 | 4.25 | |
| Settlement | 0.53 | 0.65 | 0.58 | 8.80 | −18.50 | 10.90 | |
| Shrubland | 0.58 | 0.65 | 0.56 | −1.40 | −20.35 | 4.40 | |
| Very High (≥995 m a.s.l.) | Forest | 0.41 | 0.59 | 0.48 | -0.70 | −5.45 | 6.85 |
| Grassland | 0.46 | 0.56 | 0.53 | -3.65 | −0.15 | 6.15 | |
| Mosaic Cropland | 0.39 | 0.57 | 0.40 | 2.55 | 2.70 | 9.70 | |
| Mosaic Natural Vegetation | 0.48 | 0.62 | 0.45 | 3.40 | −15.50 | 4.20 | |
| Mosaic Tree and Shrub | 0.35 | 0.48 | 0.53 | 1.60 | −5.70 | 13.20 | |
| Rainfed Cropland | 0.62 | 0.65 | 0.55 | -0.50 | −10.40 | −0.50 | |
| Shrubland | 0.56 | 0.65 | 0.55 | 1.05 | −17.35 | 0.60 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paredes-Trejo, F.; Barbosa, H.; dos Santos, C.A.C. Evaluation of the Performance of SM2RAIN-Derived Rainfall Products over Brazil. Remote Sens. 2019, 11, 1113. https://doi.org/10.3390/rs11091113
Paredes-Trejo F, Barbosa H, dos Santos CAC. Evaluation of the Performance of SM2RAIN-Derived Rainfall Products over Brazil. Remote Sensing. 2019; 11(9):1113. https://doi.org/10.3390/rs11091113
Chicago/Turabian StyleParedes-Trejo, Franklin, Humberto Barbosa, and Carlos A. C. dos Santos. 2019. "Evaluation of the Performance of SM2RAIN-Derived Rainfall Products over Brazil" Remote Sensing 11, no. 9: 1113. https://doi.org/10.3390/rs11091113
APA StyleParedes-Trejo, F., Barbosa, H., & dos Santos, C. A. C. (2019). Evaluation of the Performance of SM2RAIN-Derived Rainfall Products over Brazil. Remote Sensing, 11(9), 1113. https://doi.org/10.3390/rs11091113