Scene Classification from Synthetic Aperture Radar Images Using Generalized Compact Channel-Boosted High-Order Orderless Pooling Network
Abstract
1. Introduction
- We present a generalized compact channel-boosted high-order orderless pooling network (GCCH) which learns the high-order vector of parameterized locally constrain affine subspace coding by a kernelled outer product. It enables low-dimensional but highly discriminative feature descriptors, and the dimension of the final feature descriptors can be set by us.
- We employ the squeeze and excitation block to learn the channel information of the parameterized LASC statistic representation by explicitly modelling the interdependencies between channels; the block obtains the importance of each feature channel by the adaptive learning network.
- All of the layers can be trained by back-propagation, and some important parameters on the proposed network are made to obtain better experimental parameter settings, and research on the SAR image scene classification dataset demonstrates the competitive performance.
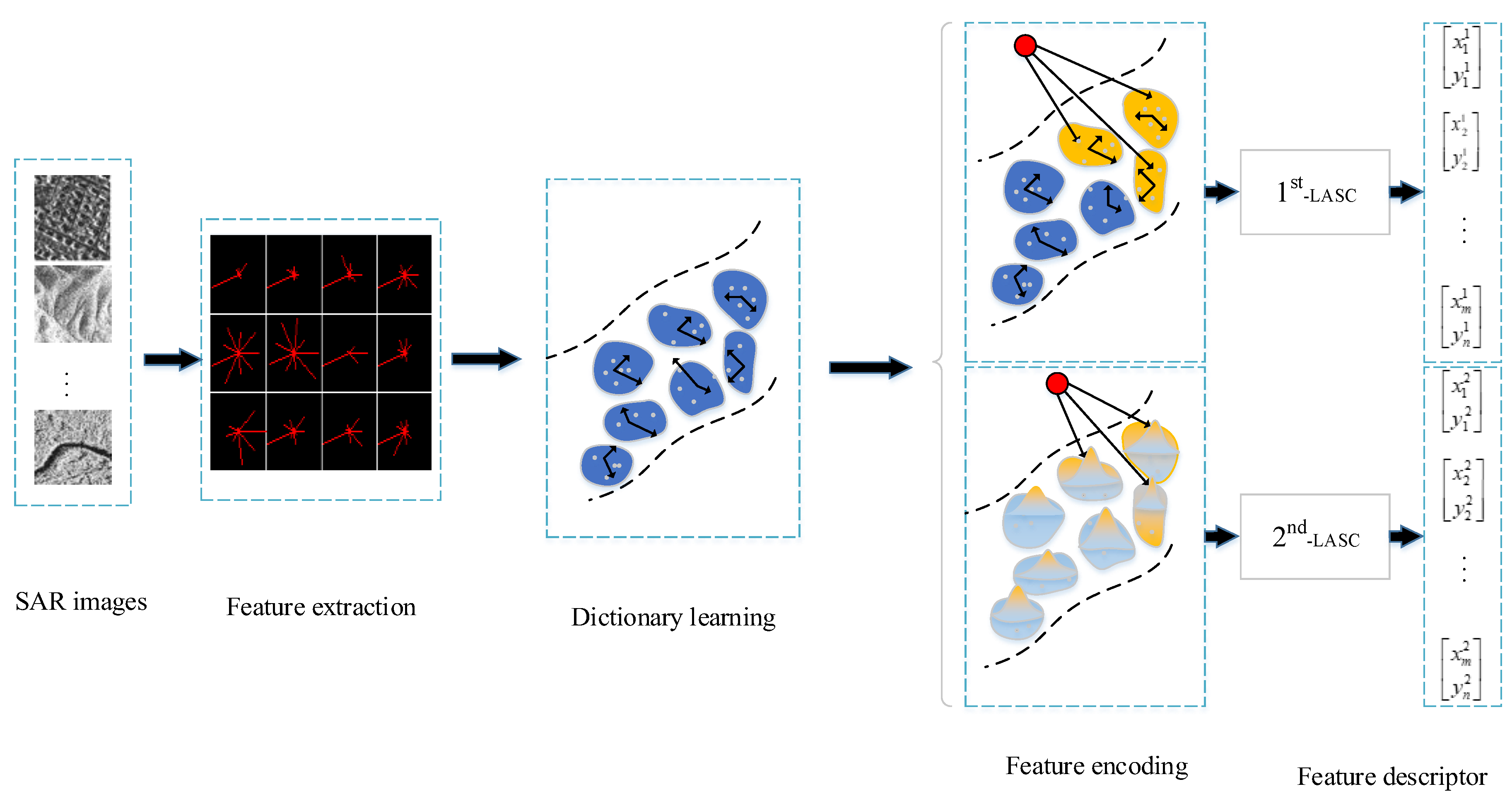
2. Traditional LASC Method
3. Generalized Compact Channel-Boosted High-Order Orderless Pooling Network
3.1. The Second-Order Generalized Layer (Parameterized Lasc Layer)
- Step1.
- Normalize by the -norm layer.
- Step2.
- The first-order LASC static information is obtained by rescaling the output of the soft assignment layer with the affine subspace layer.
- Step3.
- The second-order LASC static information is obtained by rescaling the output of the soft assignment layer with the affine subspace layer and activation layer.
- Step4.
- Cascading both and .
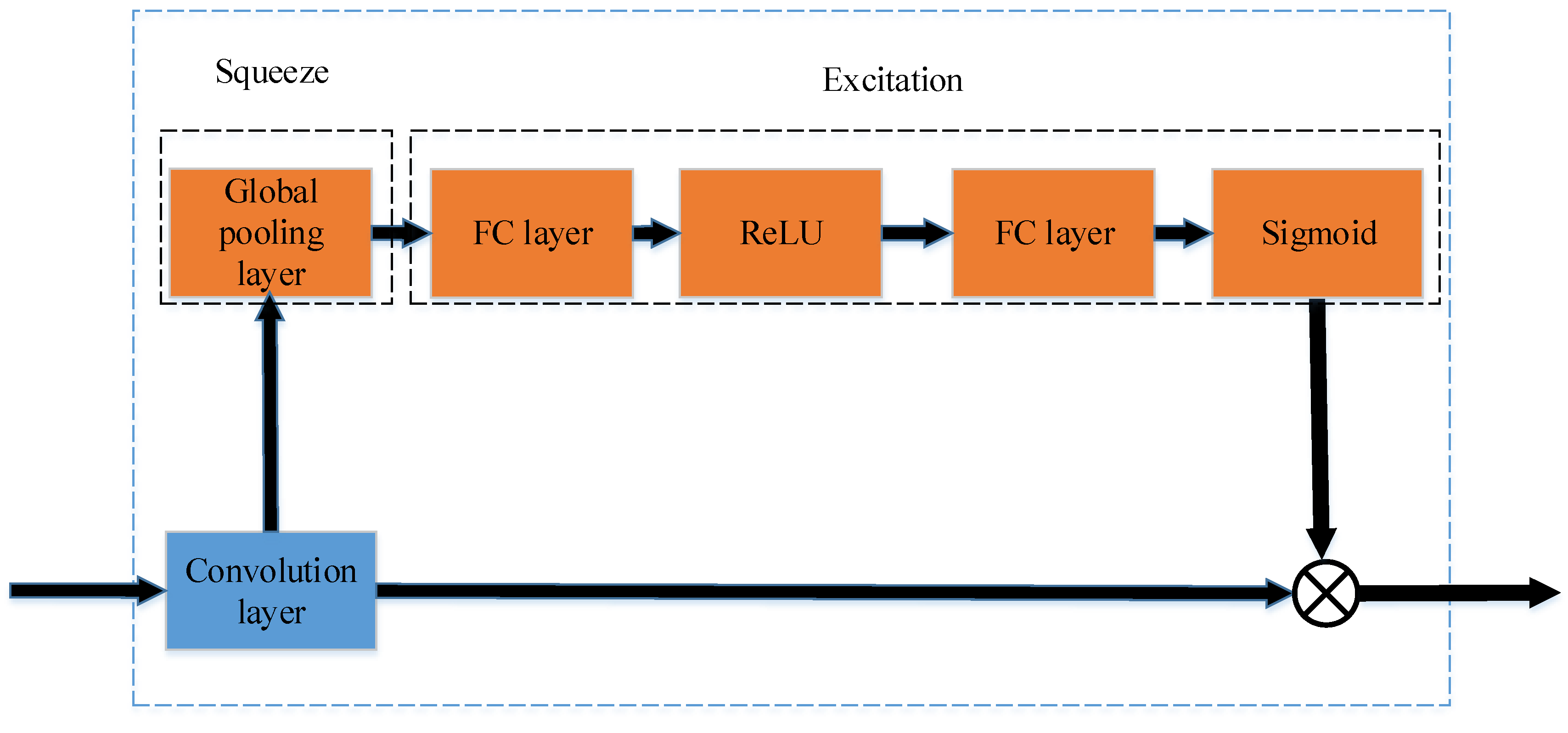
3.2. Squeeze and Excitation Block
- Step1.
- The squeeze operation is calculated by Equation (15).
- Step2.
- The excitation operation is obtained by Equation (16).
- Step3.
- Then, the output () is obtained by rescaling the convolution output with .
3.3. Compact High-Order Generalized Orderless Pooling Layer
- Step1.
- Generate random (the parameters needed to be learned), and make each entry be either or with equal probability.
- Step2.
- Let , and denotes element-wise multiplication.
4. Experimental Results and Discussion
4.1. Date Set
4.2. Experimental Setup
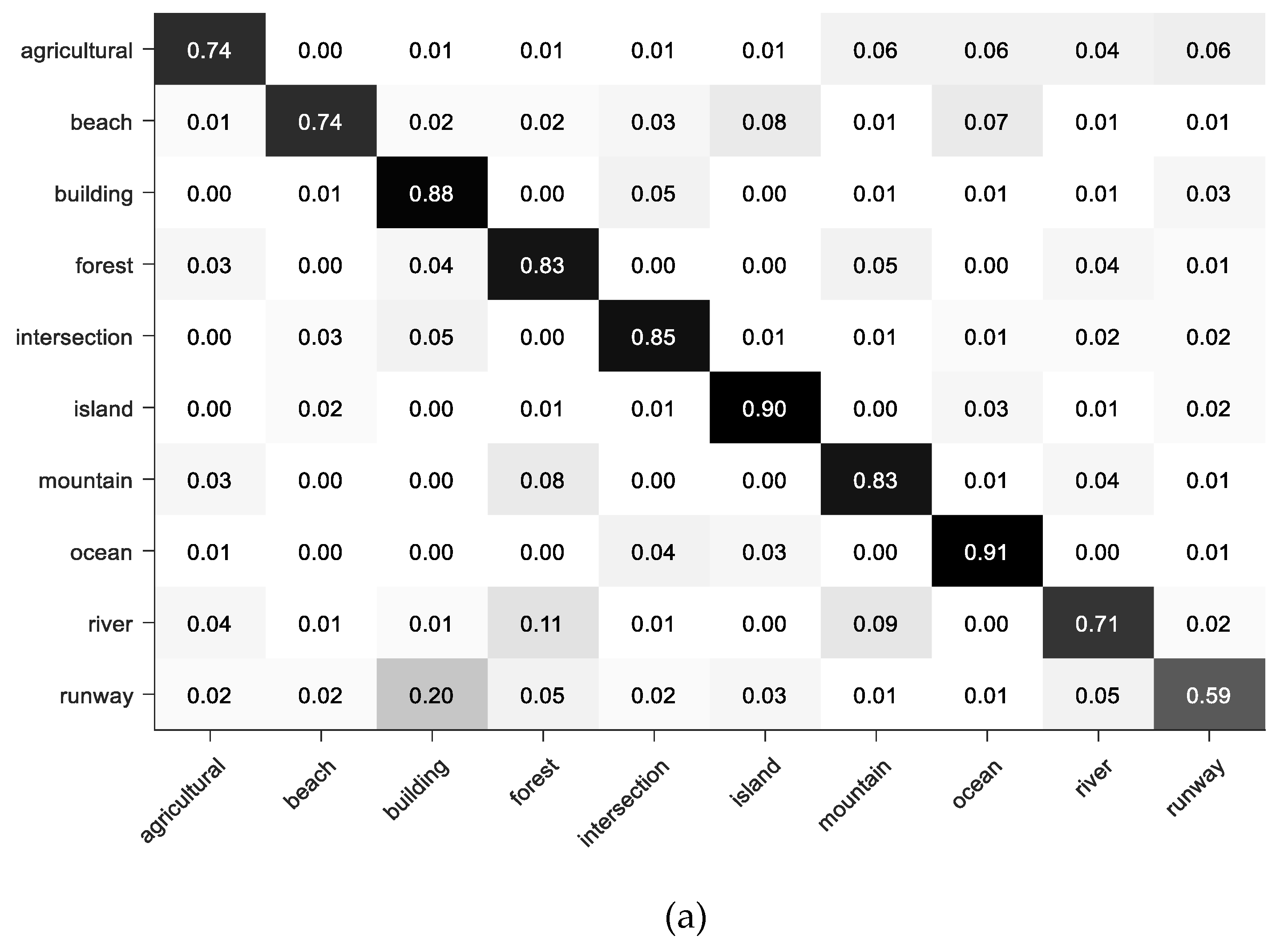
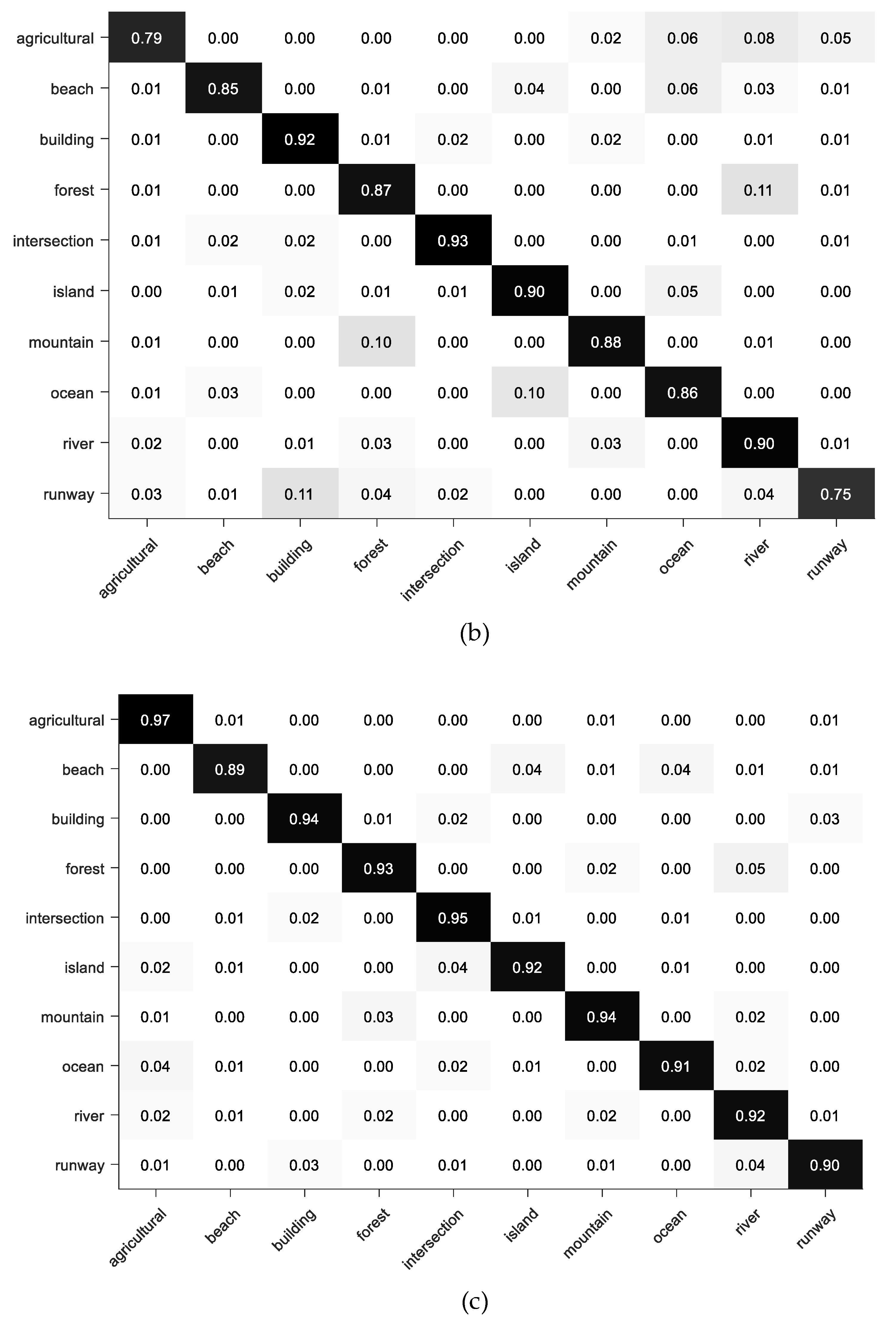
4.3. Experimental Results and Discussion
4.3.1. Evaluation of Projected Dimensions
4.3.2. Evaluation of the Ratio of Reduction
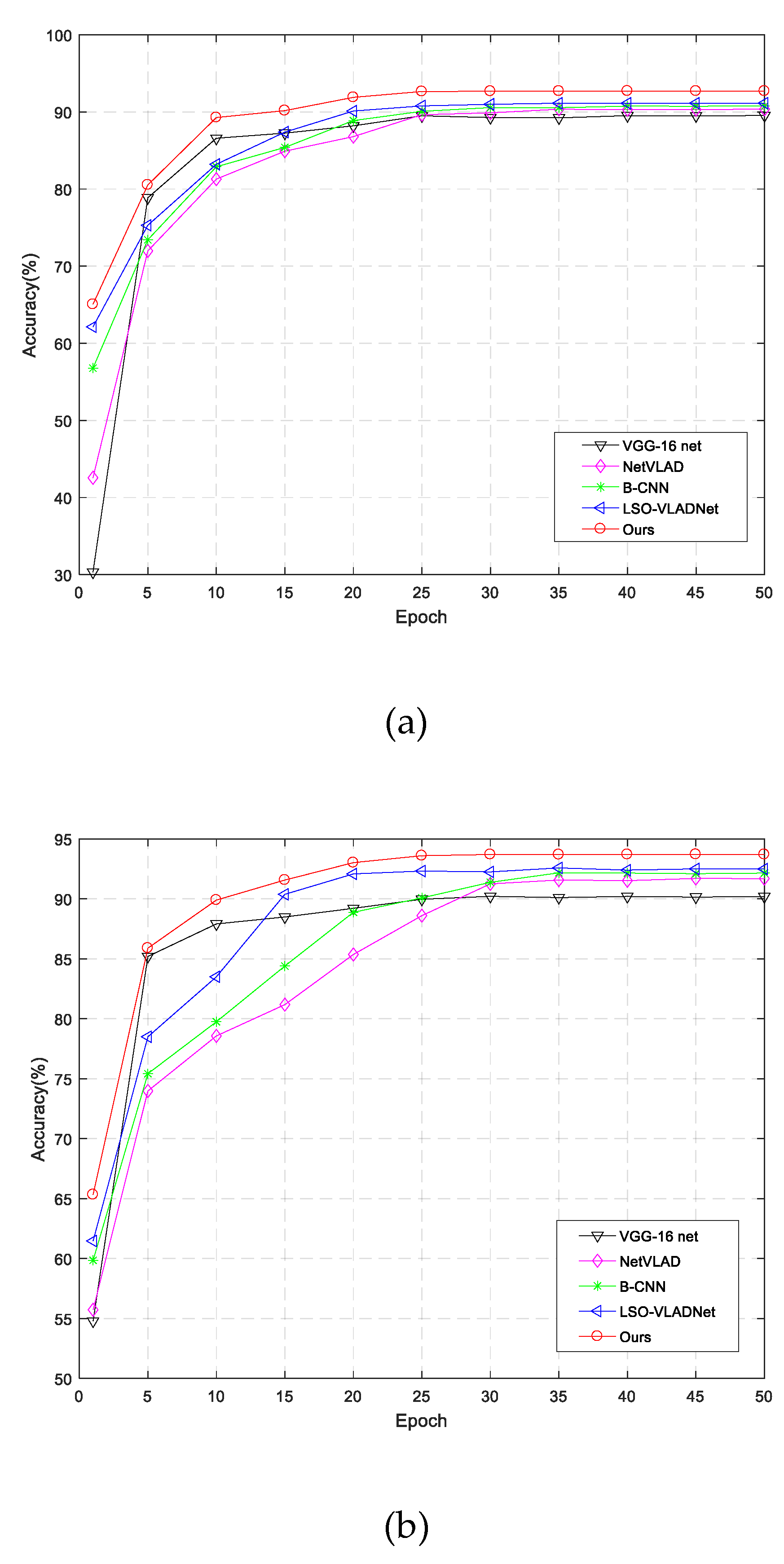
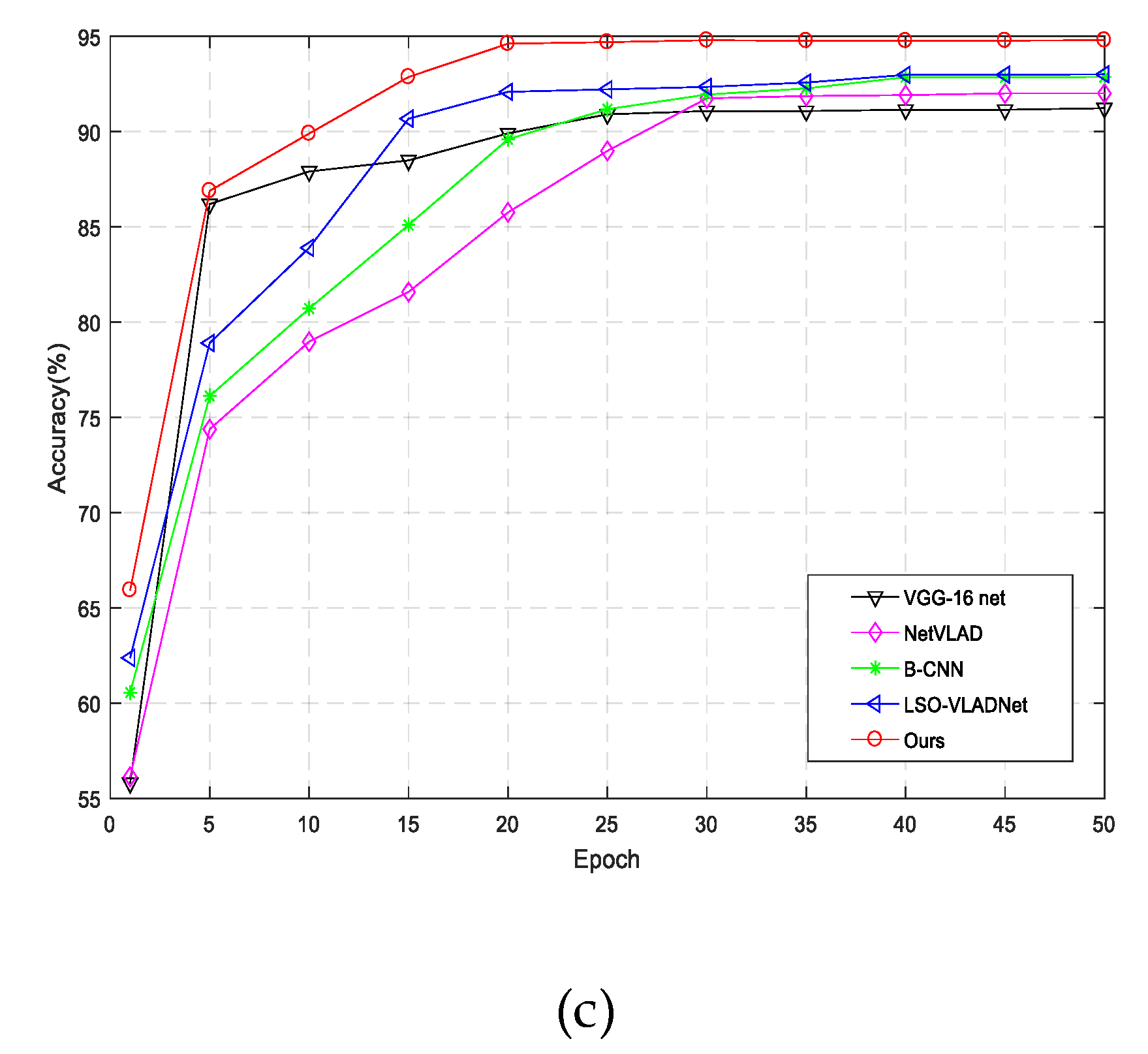
4.3.3. Comparison with Other State-of-the Art Methods
4.3.4. Comparison with Other Mid-Level Feature Representation Methods
4.3.5. The Ablation and Combined Experiments
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ren, Z.L.; Hou, B.; Wen, Z.D.; Jiao, L.C. Patch-sorted deep feature learning for high resolution SAR image classification. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2018, 11, 3113–3126. [Google Scholar] [CrossRef]
- Esch, T.; Schenk, A.; Ullmann, T.; Thiel, M.; Roth, A.; Dech, S. Characterization of land cover types in terrasar-x images by combined analysis of speckle statistics and intensity information. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1911–1925. [Google Scholar] [CrossRef]
- Kwon, T.J.; Li, J.; Wong, A. Etvos: An enhanced total variation optimization segmentation approach for SAR sea-ice image segmentation. IEEE Trans. Geosci. Remote Sens. 2013, 51, 925–934. [Google Scholar] [CrossRef]
- Yang, X.; Clausi, D. Evaluating SAR sea ice image segmentation using edge-preserving region-based MRFs. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2012, 5, 1383–1393. [Google Scholar] [CrossRef]
- Knuth, R.; Thiel, C.; Thiel, C.; Eckardt, R.; Richter, N.; Schmullius, C. Multisensor SAR analysis for forest monitoring in boreal and tropical forest environments. In Proceedings of the IEEE International Geoscience & Remote Sensing Symposium, Cape Town, South Africa, 12–17 July 2009. [Google Scholar]
- Yang, S.; Wang, M.; Feng, Z.; Liu, Z.; Li, R. Deep sparse tensor filtering network for synthetic aperture radar images classification. IEEE T Neural Netw. Learn. Syst. 2018, 29, 3919–3924. [Google Scholar] [CrossRef]
- Yang, S.; Wang, M.; Long, H.; Liu, Z. Sparse robust filters for scene classification of synthetic aperture radar (SAR) images. Neurocomputing 2006, 184, 91–98. [Google Scholar] [CrossRef]
- Geng, J.; Wang, H.; Fan, J.; Ma, X. SAR image classification via deep recurrent encoding neural networks. IEEE Trans. Geosci. Remote Sens. 2017, 56, 2255–2269. [Google Scholar] [CrossRef]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef] [PubMed]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 25, 1097–1105. [Google Scholar] [CrossRef]
- Li, E.Z.; Xia, J.S.; Du, P.J.; Lin, C.; Samat, A. Integrating multilayer features of convolutional neural networks for remote sensing scene classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5653–5665. [Google Scholar] [CrossRef]
- He, N.J.; Fang, L.Y.; Li, S.T.; Plaza, A.; Plaza, J. Remote sensing scene classification using multilayer stacked covariance pooling. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6899–6910. [Google Scholar] [CrossRef]
- Matthew, D.Z.; Rob, F. Visualizing and understanding convolutional networks. In European Conference on Computer Vision; Springer: Berlin, Germany, 2014; pp. 818–833. [Google Scholar]
- Gong, Y.C.; Wang, L.W.; Guo, R.Q.; Lazebnik, S. Multi-scale orderless pooling of deep convolutional activation features. In European Conference on Computer Vision; Springer: Berlin, Germany, 2014; pp. 392–407. [Google Scholar]
- Silva, F.B.; Werneck, R.D.O.; Goldenstein, S.; Tabbone, S.A. Graph-based bag-of-words for classification. Pattern Recogn. 2017, 74, 266–285. [Google Scholar] [CrossRef]
- Xie, X.M.; Zhang, Y.Z.; Wu, J.J.; Shi, G.M.; Dong, W.S. Bag-of-words feature representation for blind image quality assessment with local quantized pattern. Neurocomputing 2017, 266, 176–187. [Google Scholar] [CrossRef]
- Sun, H.; Sun, X.; Wang, H.; Li, Y.; Li, X. Automatic target detection in high-resolution remote sensing images using spatial sparse coding bag-of-words model. IEEE Geosci. Remote Sens. Lett. 2012, 9, 109–113. [Google Scholar] [CrossRef]
- Li, Y.; Liu, L.Q.; Shen, C.H.; Hengel, A.V.D. Mining mid-level visual patterns with deep CNN activations. Int. J. Comput. Vis. 2015, 121, 971–980. [Google Scholar] [CrossRef]
- Sivic, J. A text retrieval approach to object matching in videos. In Proceedings of the Ninth IEEE International Conference on Computer Vision, Nice, France, 13–16 October 2003. [Google Scholar]
- Lazebnik, S. Beyond bags of features: Spatial pyramid matching for recognizing natural scene categories. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, New York, NY, USA, 17–22 June 2006. [Google Scholar]
- Sheng, G.F.; Yang, W.; Xu, T.; Sun, H. High-resolution satellite scene classification using a sparse coding based multiple feature combination. Int. J. Remote Sens. 2012, 33, 2395–2412. [Google Scholar] [CrossRef]
- Wang, J.; Yang, J.; Kai, Y.; Lv, F.; Huang, T.; Gong, Y. Locality-constrained Linear Coding for image classification. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010. [Google Scholar]
- Zhou, X.; Yu, K.; Zhang, T.; Huang, T.S. Image classification using super-vector coding of local image descriptors. In European Conference on Computer Vision; Springer: Berlin, Germany, 2010; Volume 6315, pp. 141–154. [Google Scholar]
- Sánchez, J.; Perronnin, F.; Mensink, T.; Verbeek, J. Image classification with the fisher vector: Theory and practice. Int. J. Comput. Vis. 2013, 105, 222–245. [Google Scholar] [CrossRef]
- Li, P.; Lu, X.; Wang, Q. From dictionary of visual words to subspaces: Locality-constrained affine subspace coding. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015. [Google Scholar]
- Zhu, Q.; Zhong, Y.; Zhao, B.; Xia, G.S.; Zhang, L. Bag-of-visual-words scene classifier with local and global features for high spatial resolution remote sensing imagery. IEEE Geosci. Remote Sens. Lett. 2016, 13, 747–751. [Google Scholar] [CrossRef]
- Hu, F.; Xia, G.S.; Hu, J.W.; Zhang, L.P. Transferring deep Convolutional Neural Networks for the scene classification of high-resolution remote sensing imagery. Remote Sens. 2015, 7, 14680–14707. [Google Scholar] [CrossRef]
- Qi, K.; Wu, H.; Shen, C.; Gong, J. Land-use scene classification in high-resolution remote sensing images using improved correlatons. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2403–2407. [Google Scholar]
- Bian, X.; Chen, C.; Tian, L.; Du, Q. Fusing local and global features for high-resolution scene classification. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2017, 10, 2889–2901. [Google Scholar] [CrossRef]
- Mekhalfi, M.L.; Melgani, F.; Bazi, Y.; Alajian, N. Land-use classification with compressive sensing multifeature fusion. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2155–2159. [Google Scholar] [CrossRef]
- Cheng, G.; Li, Z.; Yao, X.; Guo, L.; Wei, Z. Remote sensing image scene classification using bag of convolutional features. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1735–1739. [Google Scholar] [CrossRef]
- Yuan, B.; Li, S.; Li, N. Multiscale deep features learning for land-use scene recognition. J. Appl. Remote Sens. 2018, 12, 015010. [Google Scholar] [CrossRef]
- Banerjee, B.; Chaudhuri, S. Scene recognition from optical remote sensing images using mid-level deep feature mining. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1080–1084. [Google Scholar] [CrossRef]
- Yang, Y.; Newsam, S. Bag-of-visual-words and spatial extensions for land-use classification. In Proceedings of the 18th Sigspatial International Conference on Advances in Geographic Information Systems, New York, NY, USA, 2–5 November 2010. [Google Scholar]
- Fan, J.; Chen, T.; Lu, S. Unsupervised feature learning for land-use scene recognition. IEEE Trans. Geosci. Remote Sens. 2017, 50, 2250–2261. [Google Scholar] [CrossRef]
- Dalal, N.; Triggs, B. Histograms of oriented gradients for human detection. In Proceedings of the Computer Society Conference on Computer Vision and Pattern Recognition, San Diego, CA, USA, 20–25 June 2005. [Google Scholar]
- Arandjelovic, R.; Gronat, P.; Torii, A.; Pajdla, T.; Sivic, J. Netvlad: CNN architecture for weakly supervised place recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 1437–1451. [Google Scholar] [CrossRef]
- Jegou, H.; Douze, M.; Schmid, C.; Perez, P. Aggregating local descriptors into a compact image representation. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010. [Google Scholar]
- Chen, B.; Li, J.; Wei, G.; Ma, B. A novel localized and second order feature coding network for image recognition. Pattern Recogn. 2018, 76, 339–348. [Google Scholar] [CrossRef]
- Ni, K.; Wang, P.; Wu, Y.Q. High-order generalized orderless pooling networks for synthetic-aperture radar scene classification. Available online: http://openaccess.thecvf.com/content_cvpr_2018/html/Hu_Squeeze-and-Excitation_Networks_CVPR_2018_paper.html (accessed on 23 April 2019).
- Hu, J.; Shen, L.; Albanie, S.; Sun, G.; Wu, E. Squeeze-and-excitation networks. Available online: https://ieeexplore.ieee.org/abstract/document/8695749 (accessed on 29 April 2019).
- Nogueira, K.; Penatti, O.A.B.; Santos, J.A.D. Towards better exploiting Convolutional Neural Networks for remote sensing scene classification. Pattern Recogn. 2017, 61, 539–556. [Google Scholar] [CrossRef]
- Lin, R.; Xiao, J.; Fan, J. Nextvlad: An efficient neural network to aggregate frame-level features for large-scale video classification. In Proceedings of the Workshop on Statistical Learning in Computer Vision ECCV, Munuch, Germany, 8–14 September 2018. pp. 206–218.
- Lin, T.Y.; Roychowdhury, A.; Maji, S. Bilinear cnn models for fine-grained visual recognition. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015. pp. 1449–1457.
- Kong, S.; Fowlkes, C. Low-rank bilinear pooling for fine-grained classification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Gao, Y.; Beijbom, O.; Zhang, N.; Darrell, T. Compact bilinear pooling. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las, Vegas, NV, USA, 27–30 June 2016. pp. 317–326.
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las, Vegas, NV, USA, 27–30 June 2016. pp. 770–778.
- Zegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015. pp. 1–9.
- Sun, Y.; Liu, Z.P.; Todorovic, S.; Li, J. Adaptive boosting for SAR automatic target recognition. IEEE T Aero Elec Sys. 2005, 43, 112–125. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]





| Method | Include Layers | Channel Learning | High-Order Feature | Parameters Learning | Feature | End to end Training |
|---|---|---|---|---|---|---|
| Traditional LASC [25] | \ | \ | No | No | hand crafted | No |
| BoCF [31] | \ | \ | No | No | deep feature | No |
| NetVLAD [37] | VLAD [38] (first-order) | No | No | Yes | deep feature | Yes |
| GCCH (Ours) | LASC (second-order) | Yes | Yes | Yes | deep feature | Yes |
| TerraSAR-X Dataset | |||
|---|---|---|---|
| 10% Training Ratio | 20% Training Ratio | Parameters | |
| 2 | 92.73% | 93.75% | 395K |
| 4 | 92.71% | 93.73% | 198K |
| 8 | 92.70% | 93.70% | 100K |
| 16 | 92.31% | 92.89% | 50K |
| Method | TerraSAR-X Dataset | ||
|---|---|---|---|
| 10% | 20% | 30% | |
| ResNet-50(fine-tuning) [47] | 90.10 | 91.28 | 92.23 |
| GoogleNet(fine-tuning) [48] | 89.71 | 90.40 | 91.74 |
| VGG-16net(fine-tuning) [10] | 89.53 | 90.21 | 91.23 |
| NetVLAD [37] | 90.36 | 91.75 | 92.01 |
| B-CNN [44] | 90.76 | 92.35 | 92.87 |
| LSO-VLADNet [39] | 91.14 | 92.58 | 92.91 |
| Ours | 92.70 | 93.70 | 94.80 |
| Method | TerraSAR-X Dataset | ||
|---|---|---|---|
| 10% | 20% | 30% | |
| Bow [49]+SIFT [50] | 80.39 ± 1.03 | 83.22 ± 0.53 | 85.06 ± 0.23 |
| SC [21]+SIFT [50] | 81.09 ± 0.89 | 83.50 ± 0.27 | 86.21 ± 0.31 |
| LLC [22]+SIFT [50] | 75.51 ± 0.64 | 78.33 ± 0.21 | 79.88 ± 0.38 |
| VLAD [38]+SIFT [50] | 84.90 ± 0.82 | 88.87 ± 0.84 | 91.25 ± 0.67 |
| FV [24]+SIFT [50] | 86.65 ± 0.81 | 91.13 ± 0.60 | 92.48 ± 0.42 |
| GCCH(Ours) | 92.70 | 93.70 | 94.80 |
| Method | Time (Second) | TerraSAR-X Dataset | ||
|---|---|---|---|---|
| 10% | 20% | 30% | ||
| vgg-16(finetuning) | 4.92 | 89.53 | 90.21 | 91.23 |
| vgg-16+PLASC | 1.77 | 91.14 | 92.58 | 92.91 |
| vgg-16+CHG | 1.53 | 90.51 | 92.12 | 92.38 |
| vgg-16+PLASC+SE | 3.58 | 91.42 | 92.60 | 93.12 |
| vgg-16+PLASC+CHG | 2.98 | 91.55 | 92.65 | 93.38 |
| GCCH(Ours) | 4.14 | 92.70 | 93.70 | 94.80 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ni, K.; Wu, Y.; Wang, P. Scene Classification from Synthetic Aperture Radar Images Using Generalized Compact Channel-Boosted High-Order Orderless Pooling Network. Remote Sens. 2019, 11, 1079. https://doi.org/10.3390/rs11091079
Ni K, Wu Y, Wang P. Scene Classification from Synthetic Aperture Radar Images Using Generalized Compact Channel-Boosted High-Order Orderless Pooling Network. Remote Sensing. 2019; 11(9):1079. https://doi.org/10.3390/rs11091079
Chicago/Turabian StyleNi, Kang, Yiquan Wu, and Peng Wang. 2019. "Scene Classification from Synthetic Aperture Radar Images Using Generalized Compact Channel-Boosted High-Order Orderless Pooling Network" Remote Sensing 11, no. 9: 1079. https://doi.org/10.3390/rs11091079
APA StyleNi, K., Wu, Y., & Wang, P. (2019). Scene Classification from Synthetic Aperture Radar Images Using Generalized Compact Channel-Boosted High-Order Orderless Pooling Network. Remote Sensing, 11(9), 1079. https://doi.org/10.3390/rs11091079






