Figure 1.
Reference undistorted multi-spectral images scenes used for the subjective study obtained from [
42].
Figure 1.
Reference undistorted multi-spectral images scenes used for the subjective study obtained from [
42].
Figure 2.
Example of distortion levels. Three different levels of distortion for (a–c) blur.
Figure 2.
Example of distortion levels. Three different levels of distortion for (a–c) blur.
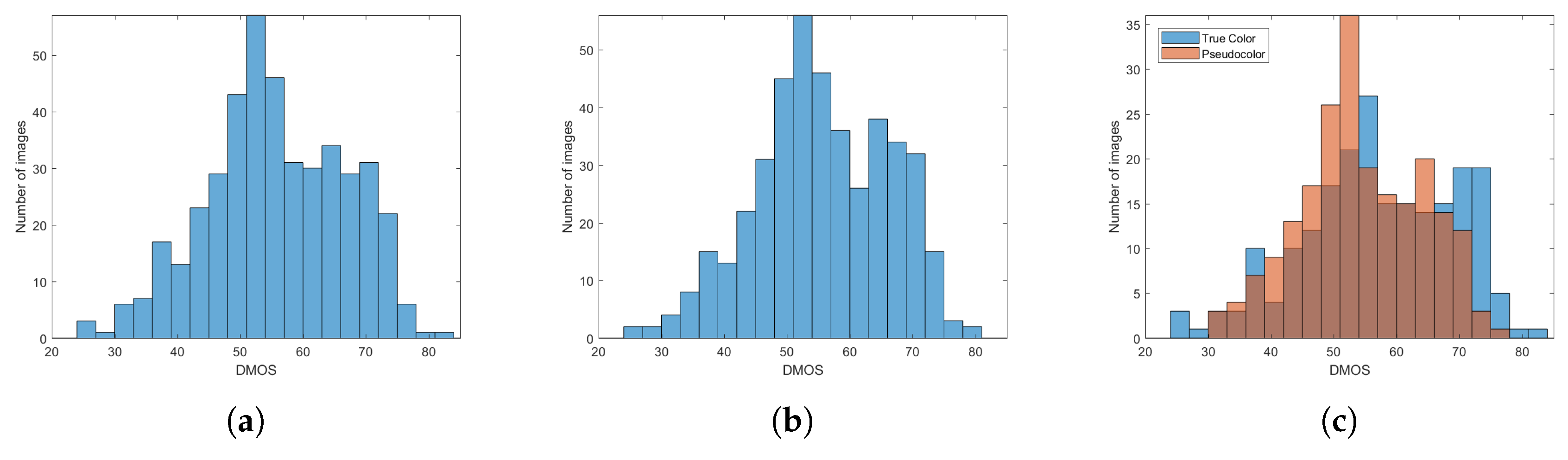
Figure 3.
Histograms of the differential mean opinion scores (DMOS) in 33 equally-spaced bins for (a) scores obtained for all images before subject rejection, (b) scores obtained for all images after subject rejection, and (c) scores after subject rejection for true color and pseudo-color image representation in the subjective study.
Figure 3.
Histograms of the differential mean opinion scores (DMOS) in 33 equally-spaced bins for (a) scores obtained for all images before subject rejection, (b) scores obtained for all images after subject rejection, and (c) scores after subject rejection for true color and pseudo-color image representation in the subjective study.
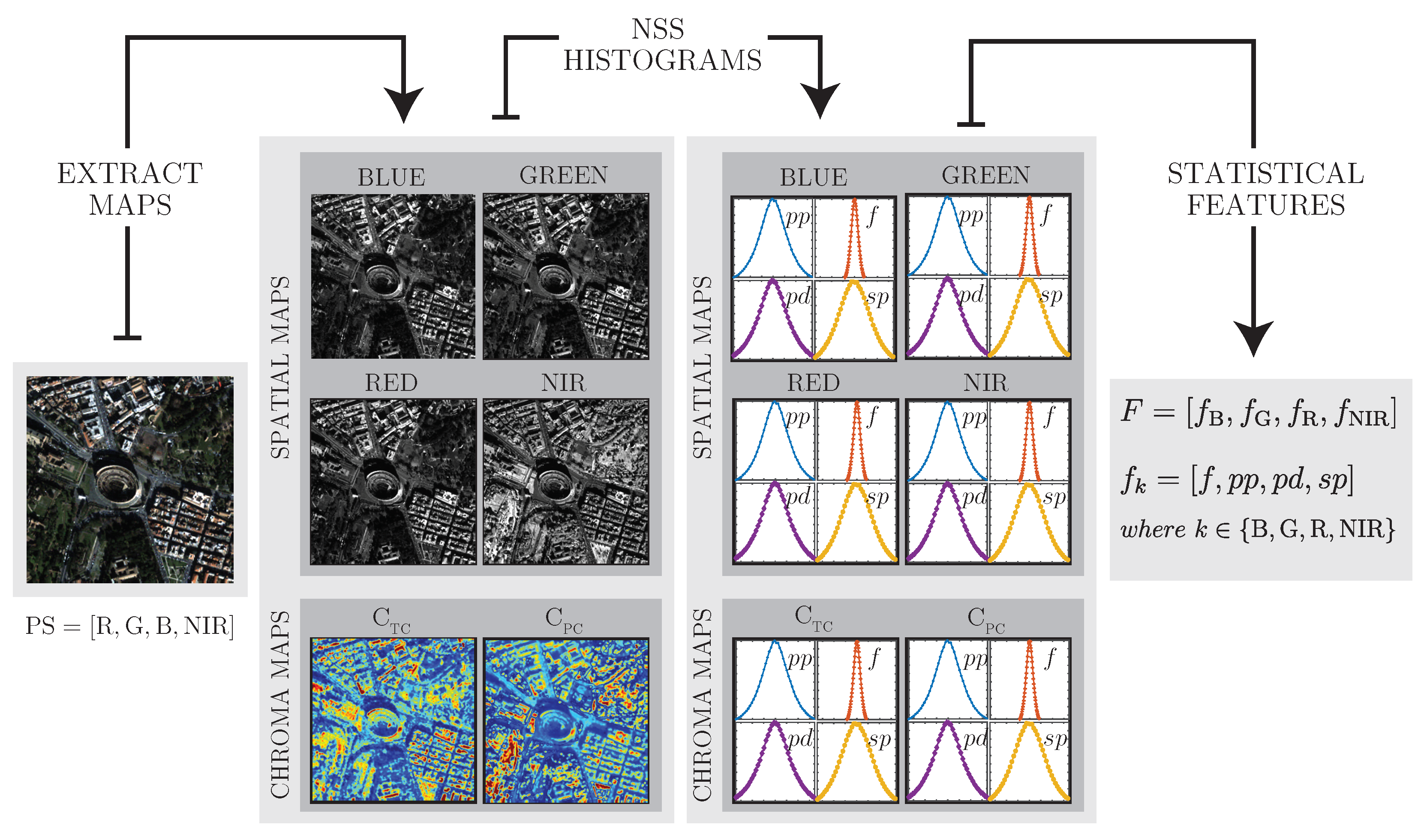
Figure 4.
The perceptual feature space obtains empirical histograms from space maps (B, G, R, NIR) and chroma true color () and chroma pseudo-color () maps. Chroma maps result from the chrominance components of the TC and PC representations, respectively. Then, the processing models extract statistical features in the vector F. NSS, natural scene statistics.
Figure 4.
The perceptual feature space obtains empirical histograms from space maps (B, G, R, NIR) and chroma true color () and chroma pseudo-color () maps. Chroma maps result from the chrominance components of the TC and PC representations, respectively. Then, the processing models extract statistical features in the vector F. NSS, natural scene statistics.
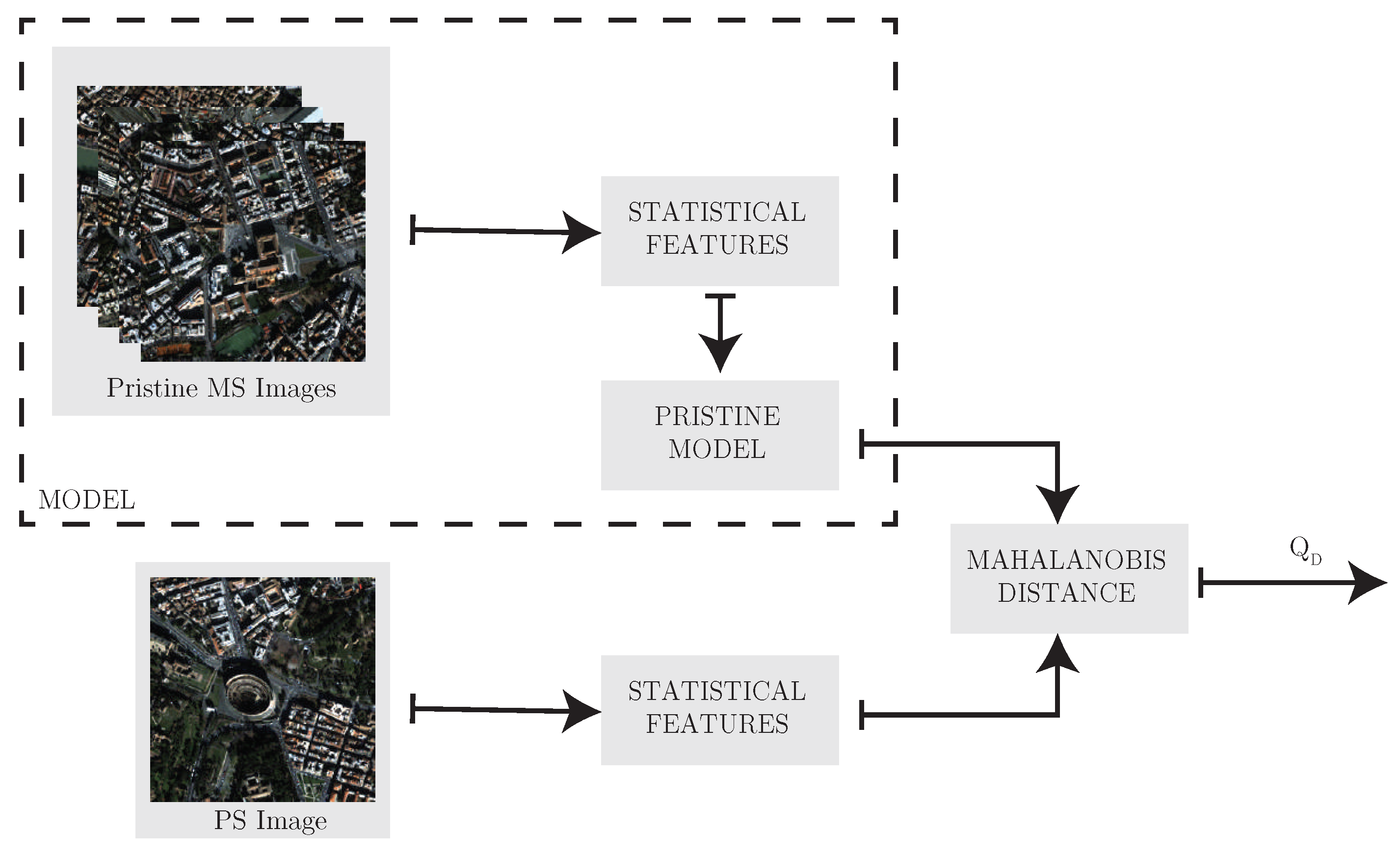
Figure 5.
Flowchart of the opinion- and distortion-unaware quality analyzer.
Figure 5.
Flowchart of the opinion- and distortion-unaware quality analyzer.
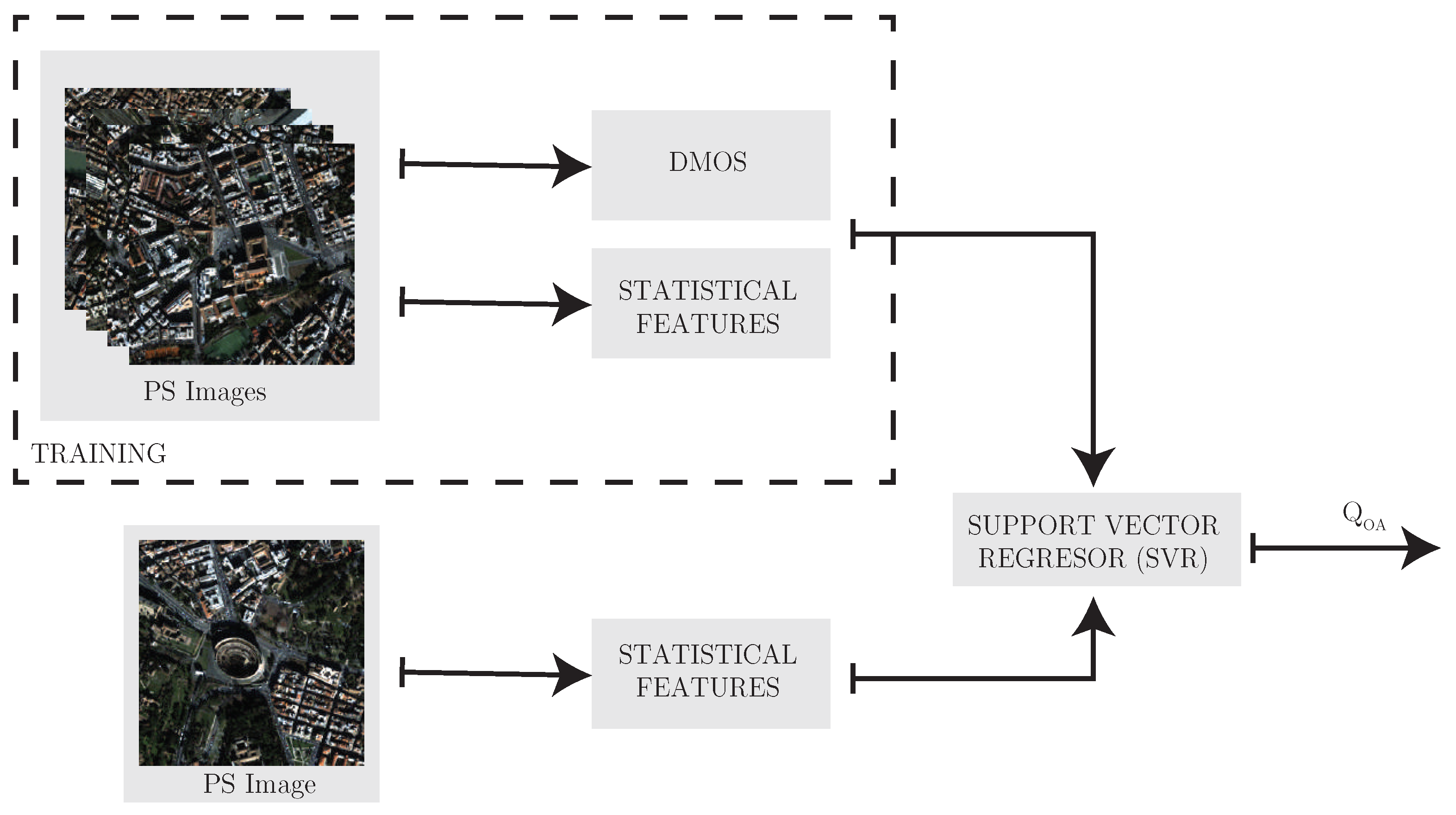
Figure 6.
Flow chart of the ODAquality analyzer.
Figure 6.
Flow chart of the ODAquality analyzer.
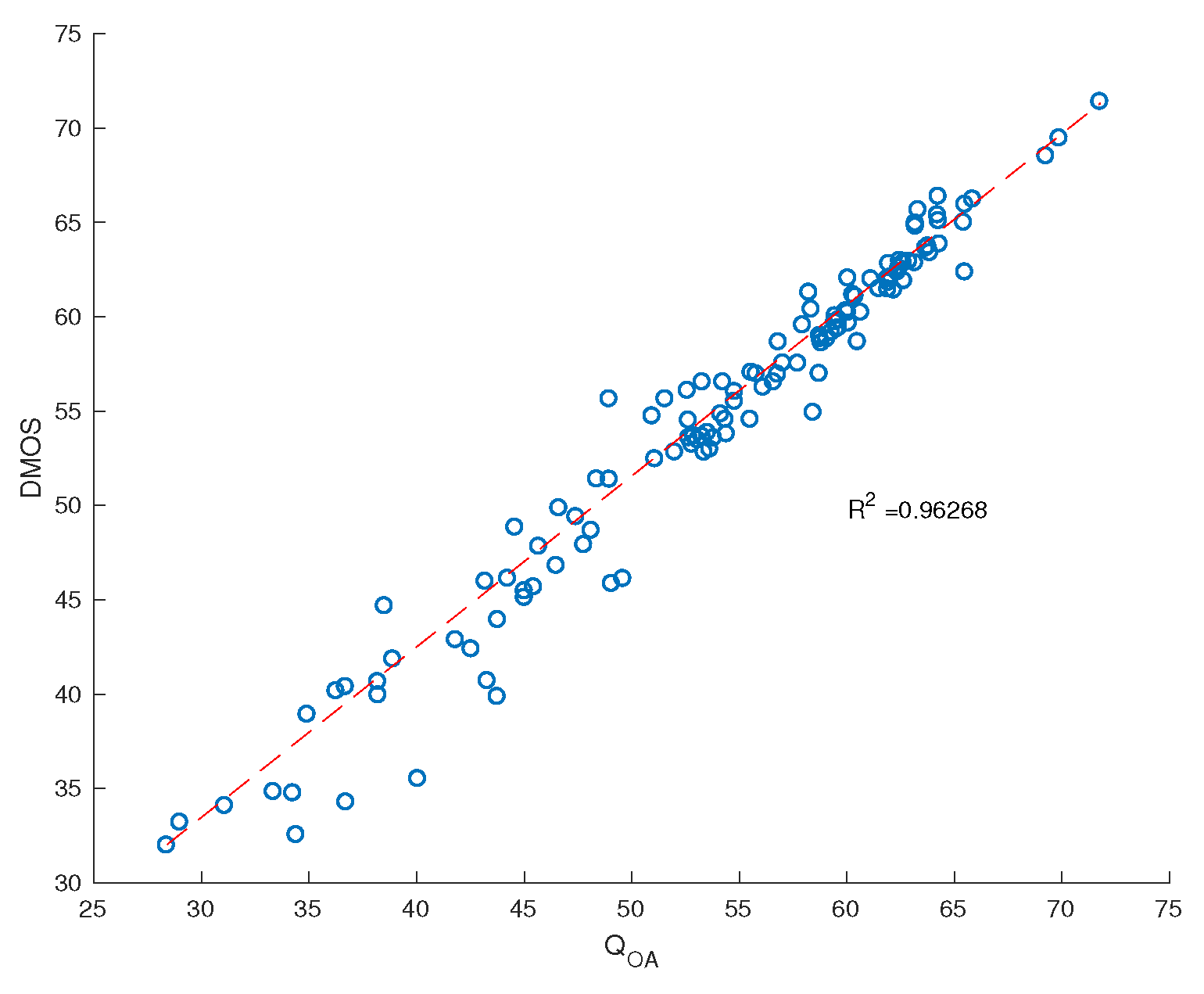
Figure 7.
Scatter plot of prediction scores versus the DMOS for all images assessed in the subjective human study and the best fitting logistic function. Notice the linear relationship with .
Figure 7.
Scatter plot of prediction scores versus the DMOS for all images assessed in the subjective human study and the best fitting logistic function. Notice the linear relationship with .
Table 1.
Description of images employed in the subjective study. TC, true color; PC, pseudo-color; MS, multi-spectral; PS, pan-sharpening.
Table 1.
Description of images employed in the subjective study. TC, true color; PC, pseudo-color; MS, multi-spectral; PS, pan-sharpening.
| | TC | PC |
|---|
| EXP | 5 | 5 |
| Undistorted MS | 5 | 5 |
| PS images | 125 | 125 |
| Total | 135 | 135 |
Table 2.
Means and standard deviations of quality scores from 11 reduced resolution and full-resolution quality metrics. In this case, each algorithm analyzed 125 PS images affected by three different levels of blur distortion.
Table 2.
Means and standard deviations of quality scores from 11 reduced resolution and full-resolution quality metrics. In this case, each algorithm analyzed 125 PS images affected by three different levels of blur distortion.
| | | |
|---|
| 0.75 | 0.10 |
| 9.25 | 1.91 |
| 0.80 | 0.11 |
| 0.50 | 0.26 |
| 0.11 | 0.08 |
| 0.84 | 0.07 |
| 722.66 | 351.80 |
| 457.36 | 126.26 |
| 1508.58 | 443.02 |
| 5.38 | 1.40 |
| 54.95 | 8.83 |
Table 3.
Means and standard deviations of quality scores from 11 reduced resolution and full-resolution quality metrics. In this case, each algorithm analyzed 35 PS undistorted images (6 PS algorithms + EXP) in five different scenarios.
Table 3.
Means and standard deviations of quality scores from 11 reduced resolution and full-resolution quality metrics. In this case, each algorithm analyzed 35 PS undistorted images (6 PS algorithms + EXP) in five different scenarios.
| | | |
|---|
| 0.79 | 0.13 |
| 8.38 | 2.42 |
| 0.85 | 0.15 |
| 0.54 | 0.25 |
| 0.14 | 0.08 |
| 0.81 | 0.09 |
| 479.95 | 259.90 |
| 418.99 | 126.44 |
| 1182.35 | 379.18 |
| 4.38 | 1.22 |
| 47.54 | 11.36 |
Table 4.
IKONOS Roma Villa scene, reduced resolution metrics quantitative results. IHS, intensity-hue-saturation; BDSD, band-dependent spatial detail; ATWT-M2, a trous wavelet transform using Model 2; HPF, high-pass filtering; MTF-GLP-CBD, modulation transfer function Laplacian pyramid with context-based decision. The bold number indicates the best performing PS method according to each quality metric.
Table 4.
IKONOS Roma Villa scene, reduced resolution metrics quantitative results. IHS, intensity-hue-saturation; BDSD, band-dependent spatial detail; ATWT-M2, a trous wavelet transform using Model 2; HPF, high-pass filtering; MTF-GLP-CBD, modulation transfer function Laplacian pyramid with context-based decision. The bold number indicates the best performing PS method according to each quality metric.
| | | | | |
|---|
| EXP | 0.51 | 13.45 | 0.51 | 0.88 |
| 0.73 | 10.16 | 0.93 | 0.88 |
| IHS | 0.73 | 10.32 | 0.91 | 0.88 |
| BDSD | 0.93 | 5.61 | 0.95 | 0.87 |
| ATWT-M2 | 0.63 | 11.72 | 0.86 | 0.88 |
| HPF | 0.81 | 8.94 | 0.91 | 0.88 |
| MTF-GLP-CBD | 0.93 | 5.83 | 0.94 | 0.93 |
Table 5.
IKONOS Roma Urban scene, reduced resolution metrics quantitative results. The bold number indicates the best performing PS method according to each quality metric.
Table 5.
IKONOS Roma Urban scene, reduced resolution metrics quantitative results. The bold number indicates the best performing PS method according to each quality metric.
| | | | | |
|---|
| EXP | 0.60 | 11.89 | 0.50 | 0.48 |
| 0.80 | 8.63 | 0.93 | 0.49 |
| IHS | 0.80 | 8.58 | 0.93 | 0.49 |
| BDSD | 0.94 | 5.31 | 0.94 | 0.70 |
| ATWT-M2 | 0.70 | 10.27 | 0.86 | 0.48 |
| HPF | 0.86 | 7.58 | 0.91 | 0.51 |
| MTF-GLP-CBD | 0.94 | 5.39 | 0.94 | 0.71 |
Table 6.
IKONOS Roma Road scene, reduced resolution quantitative results. The bold number indicates the best performing PS method according to each quality metric.
Table 6.
IKONOS Roma Road scene, reduced resolution quantitative results. The bold number indicates the best performing PS method according to each quality metric.
| | | | | |
|---|
| EXP | 0.58 | 11.63 | 0.52 | 0.59 |
| 0.82 | 8.30 | 0.93 | 0.60 |
| IHS | 0.83 | 8.16 | 0.94 | 0.60 |
| BDSD | 0.94 | 5.18 | 0.95 | 0.70 |
| ATWT-M2 | 0.68 | 10.10 | 0.85 | 0.59 |
| HPF | 0.86 | 7.15 | 0.92 | 0.62 |
| MTF-GLP-CBD | 0.94 | 5.24 | 0.94 | 0.73 |
Table 7.
IKONOS Roma River scene, reduced resolution quantitative results. The bold number indicates the best performing PS method according to each quality metric.
Table 7.
IKONOS Roma River scene, reduced resolution quantitative results. The bold number indicates the best performing PS method according to each quality metric.
| | | | | |
|---|
| EXP | 0.58 | 10.43 | 0.51 | 0.09 |
| 0.81 | 7.42 | 0.93 | 0.08 |
| IHS | 0.81 | 7.51 | 0.93 | 0.07 |
| BDSD | 0.95 | 4.45 | 0.95 | 0.61 |
| ATWT-M2 | 0.68 | 9.07 | 0.84 | 0.08 |
| HPF | 0.86 | 6.58 | 0.91 | 0.21 |
| MTF-GLP-CBD | 0.94 | 4.54 | 0.94 | 0.55 |
Table 8.
IKONOS Roma Coliseum scene, reduced resolution quantitative results. The bold number indicates the best performing PS method according to each quality metric.
Table 8.
IKONOS Roma Coliseum scene, reduced resolution quantitative results. The bold number indicates the best performing PS method according to each quality metric.
| | | | | |
|---|
| EXP | 0.58 | 12.12 | 0.51 | 0.30 |
| 0.73 | 10.34 | 0.87 | 0.31 |
| IHS | 0.77 | 9.58 | 0.90 | 0.30 |
| BDSD | 0.88 | 6.51 | 0.92 | 0.57 |
| ATWT-M2 | 0.68 | 10.74 | 0.83 | 0.30 |
| HPF | 0.83 | 7.98 | 0.89 | 0.35 |
| MTF-GLP-CBD | 0.88 | 6.61 | 0.91 | 0.51 |
Table 9.
IKONOS Roma Villa scene, full-resolution, image quality assessment metrics, and quantitative results. The bold number indicates the best performing PS method according to each quality metric.
Table 9.
IKONOS Roma Villa scene, full-resolution, image quality assessment metrics, and quantitative results. The bold number indicates the best performing PS method according to each quality metric.
| | | | | | | | | DMOS-GM |
|---|
| EXP | 0.40 | 0.59 | 1055.62 | 524.89 | 2266.59 | 5.79 | 69.75 | 69.44 |
| 0.13 | 0.84 | 531.40 | 385.05 | 988.53 | 4.85 | 42.96 | 42.86 |
| IHS | 0.13 | 0.84 | 604.92 | 377.77 | 1208.89 | 4.78 | 51.27 | 46.10 |
| BDSD | 0.05 | 0.88 | 447.97 | 312.53 | 908.14 | 5.77 | 43.88 | 43.92 |
| ATWT-M2 | 0.26 | 0.71 | 1001.56 | 486.65 | 1625.02 | 7.53 | 59.24 | 58.81 |
| HPF | 0.10 | 0.85 | 488.97 | 290.10 | 865.49 | 4.53 | 53.77 | 53.44 |
| MTF-GLP-CBD | 0.06 | 0.85 | 481.73 | 445.63 | 1120.57 | 5.58 | 45.33 | 45.10 |
Table 10.
IKONOS Roma Urban scene, full-resolution, image quality assessment metrics, and quantitative results. The bold number indicates the best performing PS method according to each quality metric.
Table 10.
IKONOS Roma Urban scene, full-resolution, image quality assessment metrics, and quantitative results. The bold number indicates the best performing PS method according to each quality metric.
| | | | | | | | | DMOS-GM |
|---|
| EXP | 0.26 | 0.74 | 993.92 | 400.93 | 1841.59 | 6.17 | 71.32 | 71.38 |
| 0.07 | 0.90 | 273.39 | 255.64 | 801.77 | 3.56 | 39.31 | 38.90 |
| IHS | 0.06 | 0.91 | 261.11 | 305.48 | 965.23 | 3.47 | 46.61 | 40.69 |
| BDSD | 0.07 | 0.88 | 265.99 | 311.59 | 843.91 | 4.42 | 42.20 | 39.93 |
| ATWT-M2 | 0.10 | 0.88 | 486.16 | 369.68 | 1148.38 | 6.46 | 61.52 | 60.21 |
| HPF | 0.05 | 0.89 | 271.42 | 203.53 | 828.77 | 3.80 | 50.14 | 49.84 |
| MTF-GLP-CBD | 0.09 | 0.82 | 251.77 | 362.45 | 911.05 | 4.23 | 47.19 | 39.84 |
Table 11.
IKONOS Roma Road scene, full-resolution, image quality assessment metrics, and quantitative results. The bold number indicates the best performing PS method according to each quality metric.
Table 11.
IKONOS Roma Road scene, full-resolution, image quality assessment metrics, and quantitative results. The bold number indicates the best performing PS method according to each quality metric.
| | | | | | | | | DMOS-GM |
|---|
| EXP | 0.26 | 0.73 | 975.01 | 568.75 | 2023.48 | 5.31 | 65.33 | 64.98 |
| 0.09 | 0.86 | 297.67 | 345.64 | 913.40 | 2.71 | 32.04 | 33.19 |
| IHS | 0.08 | 0.87 | 272.50 | 444.76 | 1094.48 | 2.62 | 32.11 | 31.97 |
| BDSD | 0.07 | 0.86 | 293.88 | 344.67 | 855.00 | 4.05 | 36.30 | 32.53 |
| ATWT-M2 | 0.11 | 0.87 | 381.90 | 364.40 | 1127.49 | 4.35 | 54.08 | 53.83 |
| HPF | 0.06 | 0.88 | 335.78 | 312.76 | 861.62 | 2.61 | 44.79 | 42.37 |
| MTF-GLP-CBD | 0.09 | 0.83 | 279.91 | 371.91 | 925.52 | 3.70 | 41.69 | 35.50 |
Table 12.
IKONOS Roma River scene, full-resolution, image quality assessment metrics, and quantitative results. The bold number indicates the best performing PS method according to each quality metric.
Table 12.
IKONOS Roma River scene, full-resolution, image quality assessment metrics, and quantitative results. The bold number indicates the best performing PS method according to each quality metric.
| | | | | | | | | DMOS-GM |
|---|
| EXP | 0.07 | 0.92 | 998.36 | 556.13 | 1872.33 | 4.96 | 68.88 | 68.50 |
| 0.20 | 0.79 | 301.85 | 468.15 | 947.26 | 2.50 | 39.39 | 40.14 |
| IHS | 0.20 | 0.78 | 307.58 | 579.74 | 1252.39 | 2.49 | 40.98 | 40.63 |
| BDSD | 0.07 | 0.88 | 298.84 | 499.56 | 954.65 | 3.61 | 39.36 | 40.37 |
| ATWT-M2 | 0.08 | 0.91 | 461.56 | 765.40 | 1438.87 | 3.71 | 59.04 | 56.96 |
| HPF | 0.14 | 0.81 | 312.69 | 521.22 | 978.25 | 2.59 | 47.73 | 48.82 |
| MTF-GLP-CBD | 0.11 | 0.81 | 276.91 | 497.61 | 930.82 | 3.42 | 41.15 | 41.83 |
Table 13.
IKONOS Roma Coliseum scene, full-resolution, image quality assessment metrics, and quantitative results. The bold number indicates the best performing PS method according to each quality metric.
Table 13.
IKONOS Roma Coliseum scene, full-resolution, image quality assessment metrics, and quantitative results. The bold number indicates the best performing PS method according to each quality metric.
| | | | | | | | | DMOS-GM |
|---|
| EXP | 0.10 | 0.86 | 978.35 | 641.87 | 1787.43 | 5.20 | 63.04 | 62.91 |
| 0.27 | 0.63 | 616.29 | 210.12 | 1244.64 | 4.75 | 35.28 | 34.26 |
| IHS | 0.26 | 0.65 | 396.08 | 621.18 | 1396.54 | 4.08 | 35.22 | 34.74 |
| BDSD | 0.16 | 0.73 | 291.14 | 346.07 | 874.35 | 4.94 | 33.39 | 34.07 |
| ATWT-M2 | 0.09 | 0.84 | 451.73 | 458.47 | 1313.14 | 4.95 | 54.03 | 53.64 |
| HPF | 0.20 | 0.69 | 464.43 | 316.12 | 1143.46 | 4.44 | 40.65 | 44.65 |
| MTF-GLP-CBD | 0.20 | 0.66 | 389.77 | 398.16 | 1123.17 | 5.46 | 34.91 | 34.81 |
Table 14.
Clustering of pan-sharpening algorithms applied to IKONOS Roma Villa, Urban, Road, River, and Coliseum scenes’ data into high, medium, and low performance. Input data for clustering are the reduced resolution scores indexes
,
,
, and
in
Table 4,
Table 5,
Table 6,
Table 7 and
Table 8.
Table 14.
Clustering of pan-sharpening algorithms applied to IKONOS Roma Villa, Urban, Road, River, and Coliseum scenes’ data into high, medium, and low performance. Input data for clustering are the reduced resolution scores indexes
,
,
, and
in
Table 4,
Table 5,
Table 6,
Table 7 and
Table 8.
| | High | Medium | Low |
|---|
| Villa | MTF-GLP-CBD | BDSD | HPF |
| Urban | BDSD | MTF-GLP-CBD | HPF |
| Road | BDSD | MTF-GLP-CBD | HPF |
| River | BDSD | MTF-GLP-CBD | HPF |
| Coliseum | BDSD | MTF-GLP-CBD | HPF |
Table 15.
Clustering of pan-sharpening algorithms applied to IKONOS Roma Villa, Urban, Road, River, and Coliseum scenes’ data into high, medium, and low performance. Input data for clustering are the full-resolution index
in
Table 9,
Table 10,
Table 11,
Table 12 and
Table 13.
Table 15.
Clustering of pan-sharpening algorithms applied to IKONOS Roma Villa, Urban, Road, River, and Coliseum scenes’ data into high, medium, and low performance. Input data for clustering are the full-resolution index
in
Table 9,
Table 10,
Table 11,
Table 12 and
Table 13.
| | High | Medium | Low |
|---|
| Villa | BDSD | MTF-GLP-CBD | HPF |
| Urban | IHS | PCA | HPF |
| Road | HPF | IHS | ATWT-M2 |
| River | ATWT-M2 | BDSD | MTF-GLP-CBD |
| Coliseum | ATWT-M2 | BDSD | HPF |
Table 16.
Clustering of pan-sharpening algorithms applied to IKONOS Roma Villa, Urban, Road, River, and Coliseum scenes’ data into high, medium, and low performance. Input data for clustering are the full-resolution image quality assessment (IQA)-based indexes
,
,
, and
,
in
Table 9,
Table 10,
Table 11,
Table 12 and
Table 13.
Table 16.
Clustering of pan-sharpening algorithms applied to IKONOS Roma Villa, Urban, Road, River, and Coliseum scenes’ data into high, medium, and low performance. Input data for clustering are the full-resolution image quality assessment (IQA)-based indexes
,
,
, and
,
in
Table 9,
Table 10,
Table 11,
Table 12 and
Table 13.
| | High | Medium | Low |
|---|
| Villa | BDSD | HPF | PCA |
| Urban | PCA | IHS | BDSD |
| Road | PCA | BDSD | IHS |
| River | PCA | BDSD | MTF-GLP-CBD |
| Coliseum | BDSD | IHS | HPF |
Table 17.
Clustering of pan-sharpening algorithms applied to IKONOS Roma Villa, Urban, Road, River, and Coliseum scenes’ data into high, medium, and low performance. Input data for clustering are the
IQA-based indexes
,
,
,
, and
in
Table 9,
Table 10,
Table 11,
Table 12 and
Table 13.
Table 17.
Clustering of pan-sharpening algorithms applied to IKONOS Roma Villa, Urban, Road, River, and Coliseum scenes’ data into high, medium, and low performance. Input data for clustering are the
IQA-based indexes
,
,
,
, and
in
Table 9,
Table 10,
Table 11,
Table 12 and
Table 13.
| | High | Medium | Low |
|---|
| Villa | PCA | BDSD | MTF-GLP-CBD |
| Urban | PCA | BDSD | MTF-GLP-CBD |
| Road | PCA | IHS | BDSD |
| River | PCA | IHS | BDSD |
| Coliseum | PCA | IHS | BDSD |
Table 18.
Means () and standard deviations () of for each PS technique extracted from 30 PS undistorted images (6 PS algorithms) in five different scenarios). The PS techniques are organized from high to low performance.
Table 18.
Means () and standard deviations () of for each PS technique extracted from 30 PS undistorted images (6 PS algorithms) in five different scenarios). The PS techniques are organized from high to low performance.
| | | |
|---|
| BDSD | 37.87 | 4.07 |
| PCA | 38.16 | 4.74 |
| IHS | 38.82 | 5.55 |
| MTF-GLP-CBD | 39.41 | 4.33 |
| ATWT-M2 | 47.82 | 4.37 |
| HPF | 56.69 | 2.93 |
Table 19.
Median and standard deviation of the Spearman rank correlation coefficient (SRCC) and the linear correlation coefficient (LCC) between DMOS and spatial quality indices measured over 1000 iterations.
Table 19.
Median and standard deviation of the Spearman rank correlation coefficient (SRCC) and the linear correlation coefficient (LCC) between DMOS and spatial quality indices measured over 1000 iterations.
| | | | | | | |
|---|
| 0.6692 | 0.1040 | 0.6739 | 0.1029 | 7.1022 | 1.1542 |
| 0.6146 | 0.1171 | 0.6352 | 0.1191 | 7.4441 | 1.2732 |
| 0.8408 | 0.0633 | 0.8668 | 0.0487 | 4.7596 | 0.8503 |
| 0.1502 | 0.1126 | 0.1249 | 0.1034 | 9.3622 | 1.1801 |
| 0.1482 | 0.1201 | 0.1379 | 0.1145 | 9.2684 | 1.3716 |
| 0.1564 | 0.1281 | 0.1515 | 0.1214 | 9.1547 | 1.3583 |
| 0.8096 | 0.0753 | 0.8229 | 0.0810 | 5.6903 | 1.3099 |
| 0.2153 | 0.1446 | 0.2264 | 0.1428 | 9.0588 | 1.2170 |
| 0.7762 | 0.0727 | 0.7671 | 0.0931 | 6.3339 | 1.2881 |
| 0.5496 | 0.1350 | 0.5931 | 0.1257 | 7.6390 | 1.1749 |
| 0.9262 | 0.0416 | 0.9374 | 0.0289 | 4.8784 | 1.0508 |
Table 20.
Statistical significance matrix of SRCC between DMOS and quality indices.
Table 20.
Statistical significance matrix of SRCC between DMOS and quality indices.
| | | | | | | | | | | | |
|---|
| - | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 |
| 0 | - | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 |
| 1 | 1 | - | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| 0 | 0 | 0 | - | - | - | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | - | - | - | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | - | - | - | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 | 1 | - | 1 | 1 | 1 | 0 |
| 0 | 0 | 0 | 1 | 1 | 1 | 0 | - | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | - | 1 | 0 |
| 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | - | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | - |