Monitoring Spatial and Temporal Variabilities of Gross Primary Production Using MAIAC MODIS Data
Abstract
1. Introduction
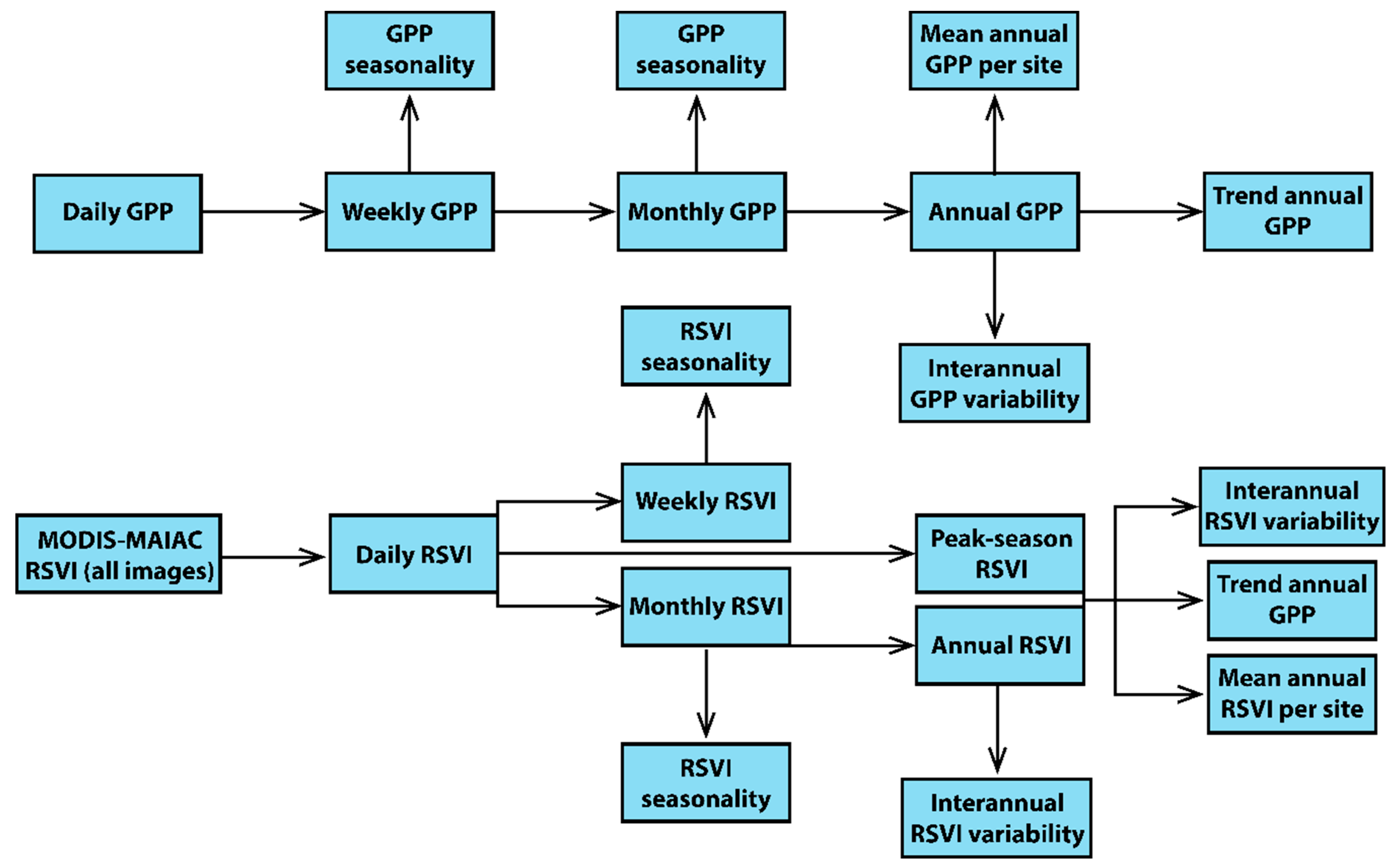
2. Materials and Methods
2.1. Carbon Flux, Weather, and Remotely Sensed Data
2.2. Statistical Analysis
3. Results
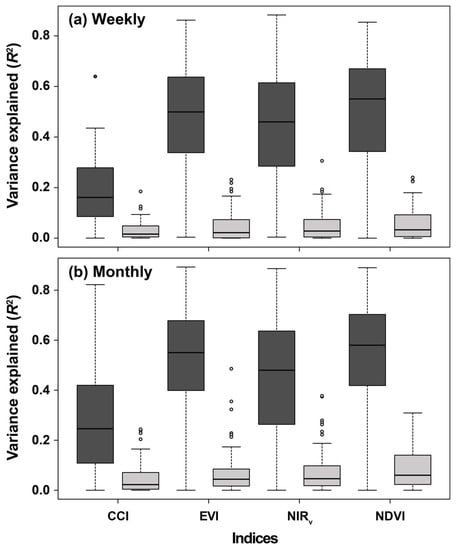
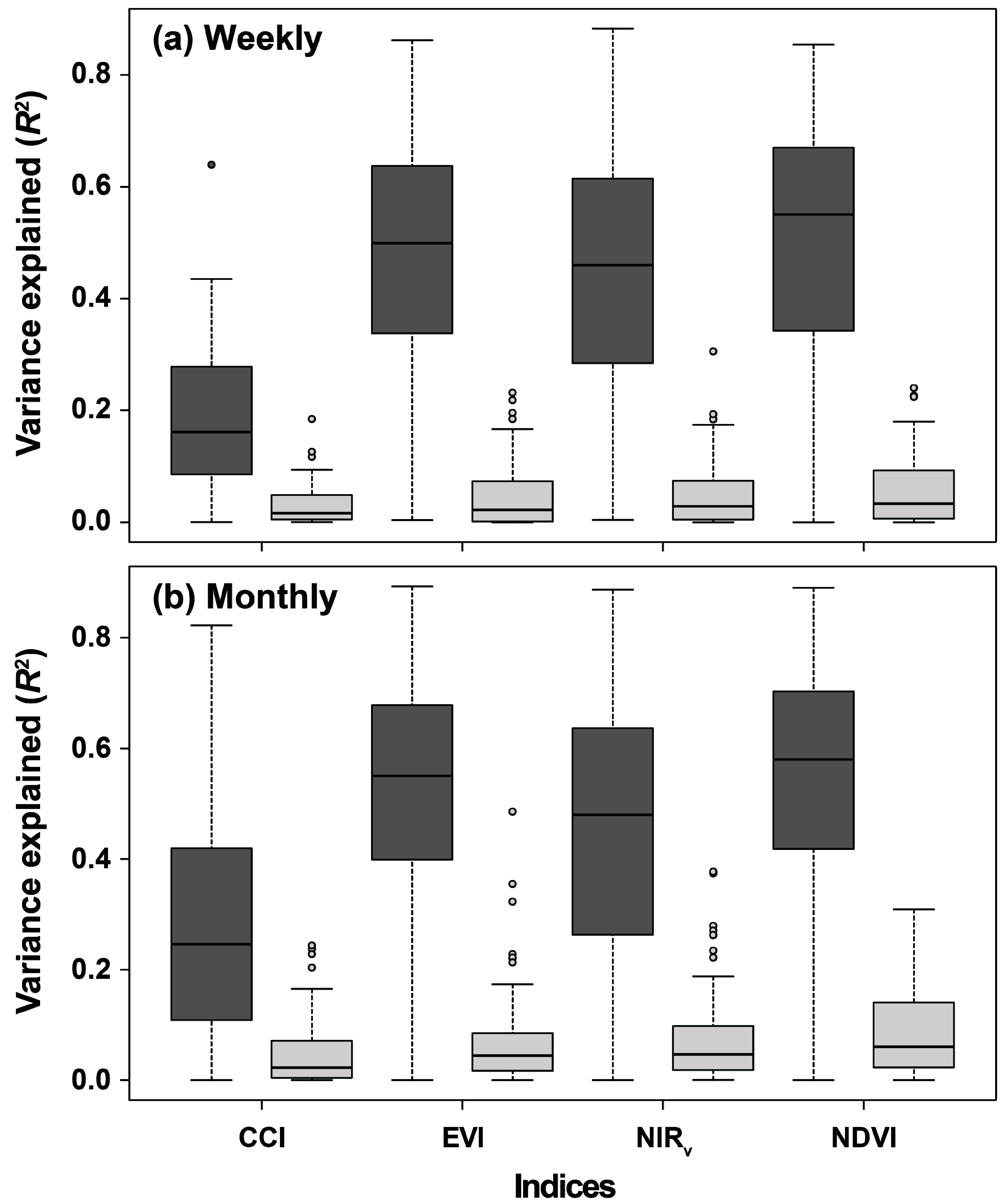
3.1. Monitoring Weekly and Monthly Temporal Variability of GPP Using the RSVIs
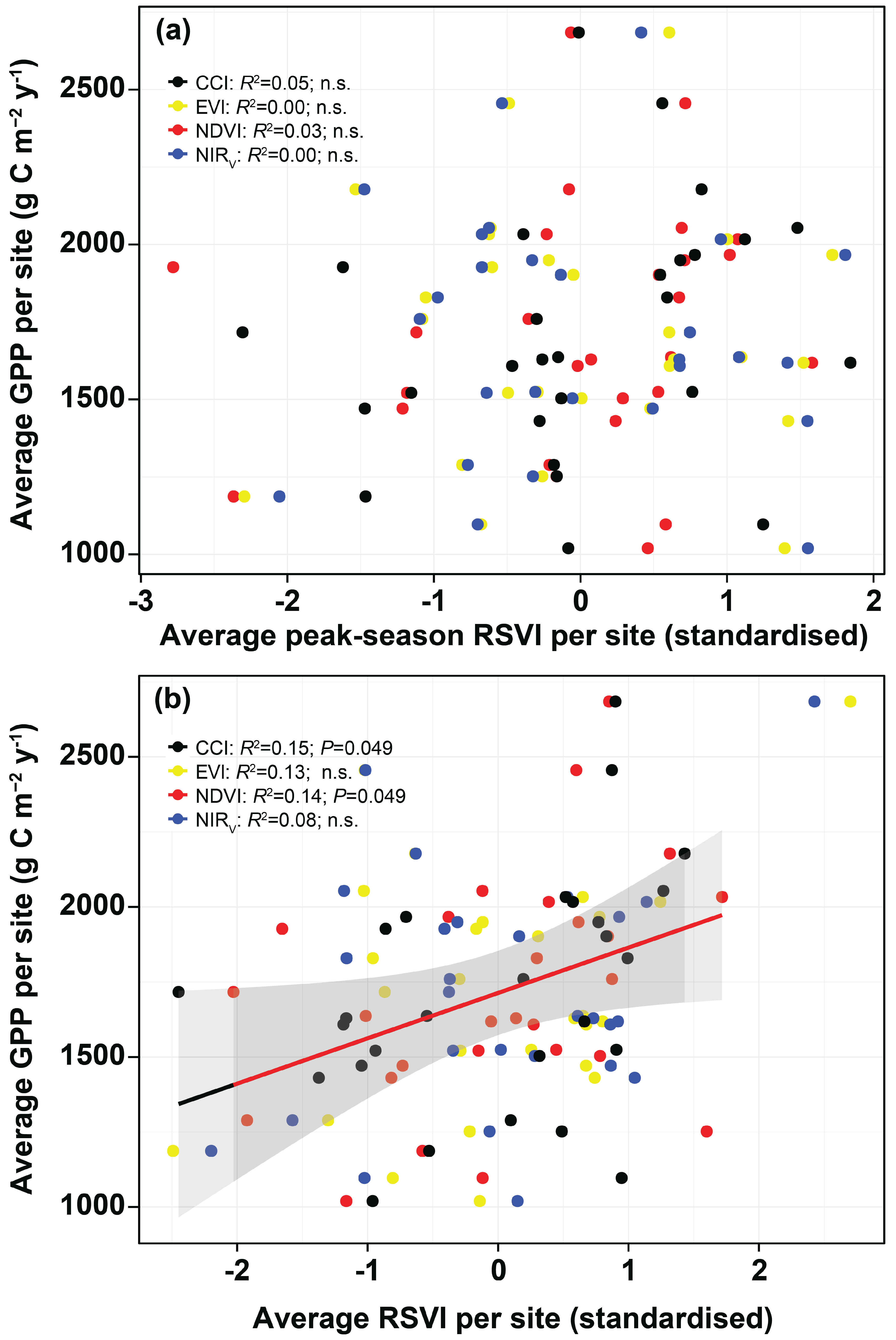
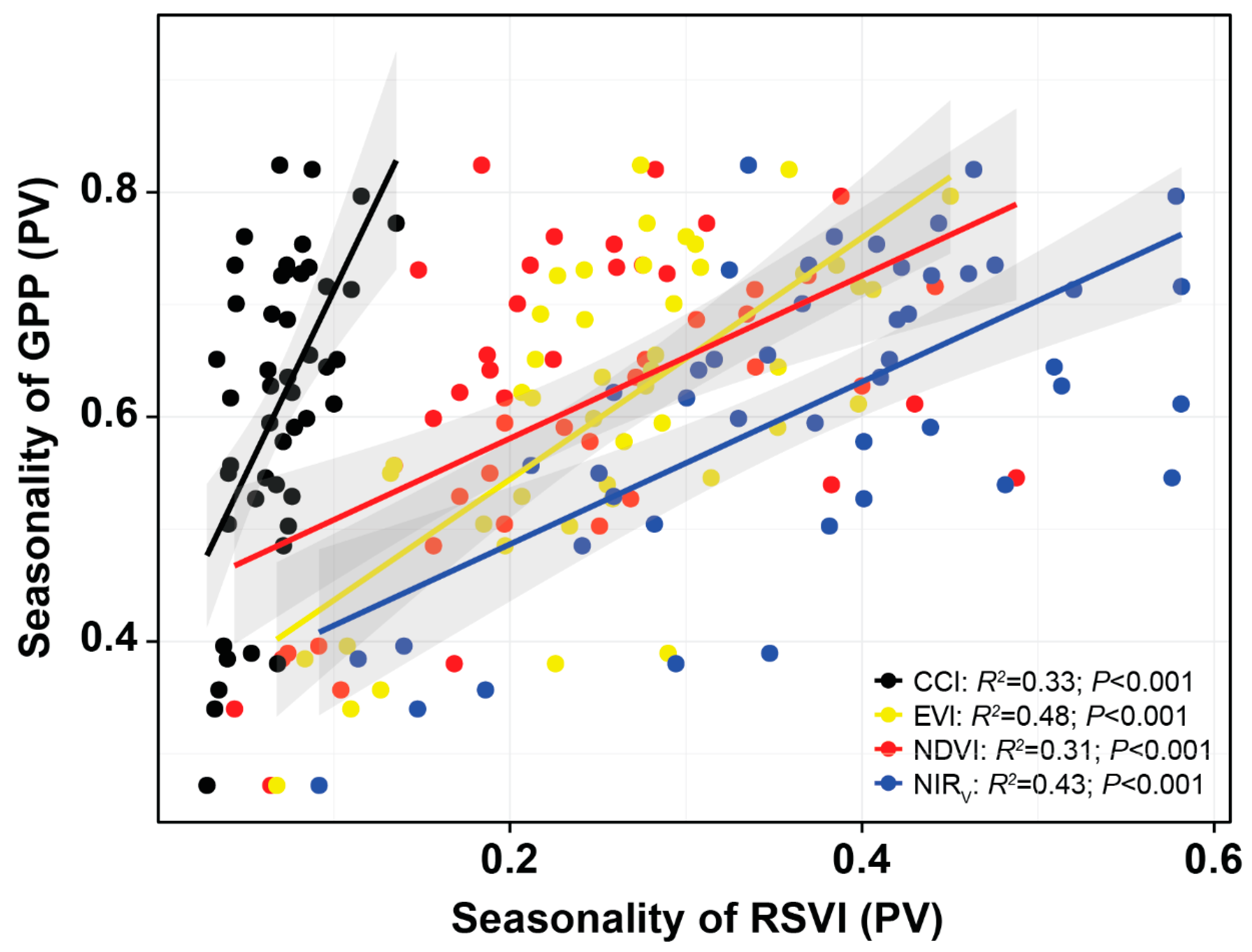
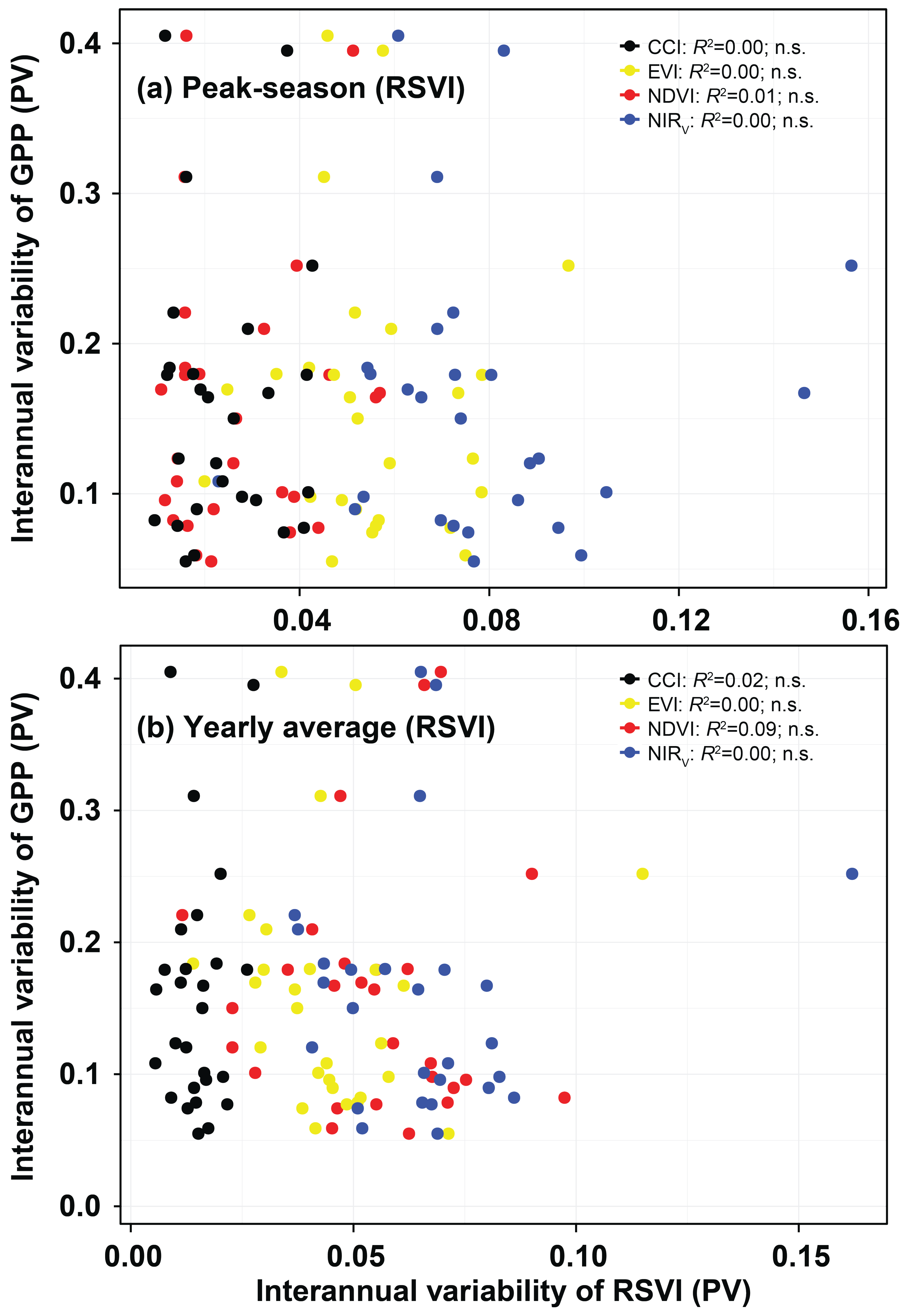
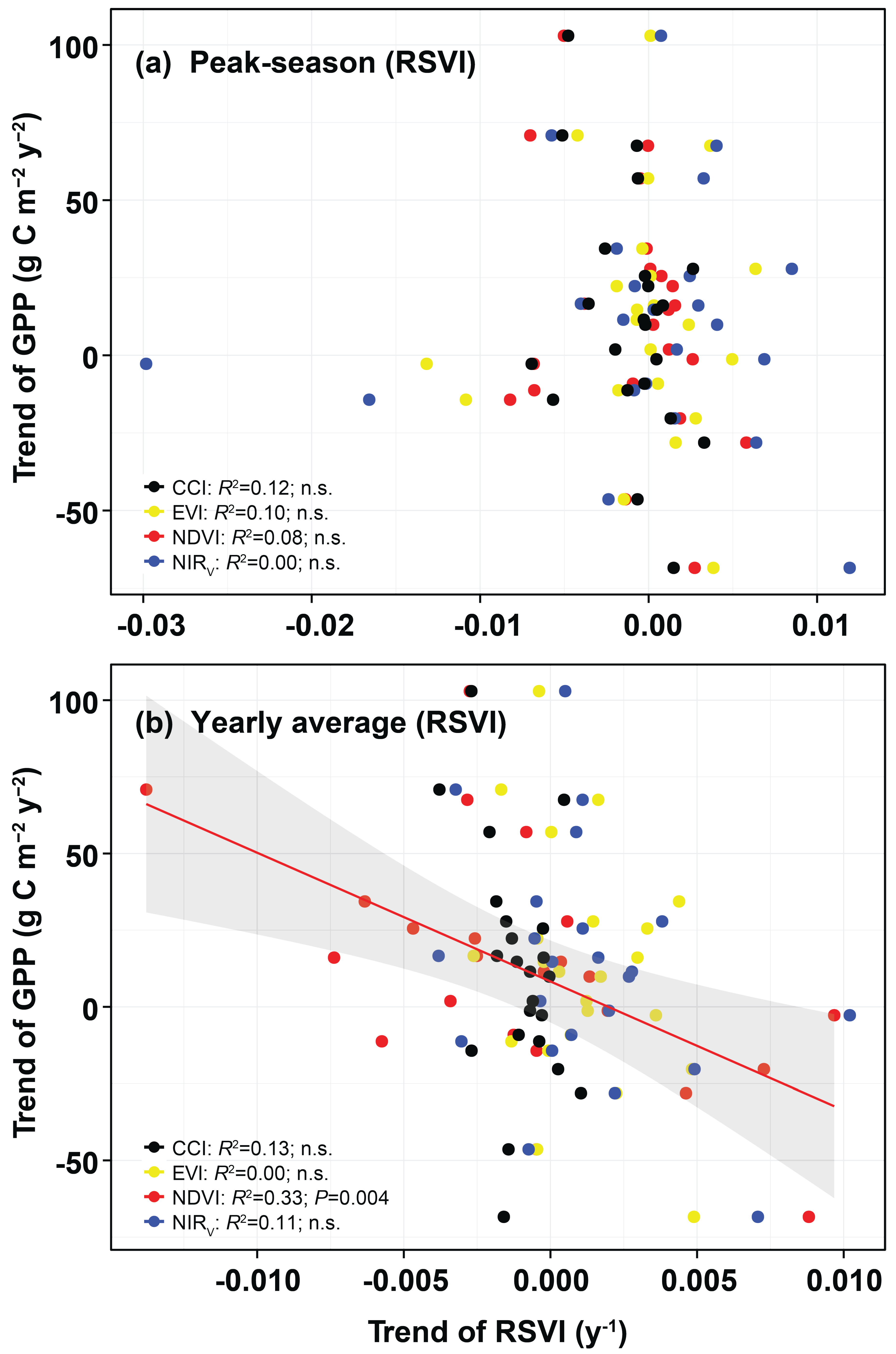
3.2. Monitoring Spatial Variability, Seasonality, Interannual Variability, and Trends
4. Discussion
4.1. Seasonality Induces Temporal Correlations between GPP and the RSVIs
4.2. Performance of the RSVIs in Explaining the Spatial Variabilities of Seasonality, Interannual Variability, and Trends of GPP
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhu, Z.; Piao, S.; Myneni, R.B.; Huang, M.; Zeng, Z.; Canadell, J.G.; Ciais, P.; Sitch, S.; Friedlingstein, P.; Arneth, A.; et al. Greening of the Earth and its drivers. Nat. Clim. Chang. 2016, 6, 791–795. [Google Scholar] [CrossRef]
- Fernández-Martínez, M.; Garbulsky, M.; Peñuelas, J.; Peguero, G.; Espelta, J.M. Temporal trends in the enhanced vegetation index and spring weather predict seed production in Mediterranean oaks. Plant Ecol. 2015, 216, 1061–1072. [Google Scholar] [CrossRef]
- Martínez-Jauregui, M.; San Miguel-Ayanz, A.; Mysterud, A.; Rodríguez-Vigal, C.; Clutton-Brock, T.; Langvatn, R.; Coulson, T. Are local weather, NDVI and NAO consistent determinants of red deer weight across three contrasting European countries? Glob. Chang. Biol. 2009, 15, 1727–1738. [Google Scholar] [CrossRef]
- Wiegand, T.; Naves, J.; Garbulsky, M.; Fernández, N. Animal habitat quality and ecosystem functioning: Exploring seasonal patterns using NDVI. Ecol. Monogr. 2008, 78, 87–103. [Google Scholar] [CrossRef]
- Garbulsky, M.F.; Peñuelas, J.; Gamon, J.; Inoue, Y.; Filella, I. The photochemical reflectance index (PRI) and the remote sensing of leaf, canopy and ecosystem radiation use efficiencies A review and meta-analysis. Remote Sens. Environ. 2011, 115, 281–297. [Google Scholar] [CrossRef]
- Balzarolo, M.; Vicca, S.; Nguy-Robertson, A.L.; Bonal, D.; Elbers, J.A.; Fu, Y.H.; Grünwald, T.; Horemans, J.A.; Papale, D.; Peñuelas, J.; et al. Matching the phenology of Net Ecosystem Exchange and vegetation indices estimated with MODIS and FLUXNET in-situ observations. Remote Sens. Environ. 2016, 174, 290–300. [Google Scholar] [CrossRef]
- Balzarolo, M.; Anderson, K.; Nichol, C.; Rossini, M.; Vescovo, L.; Arriga, N.; Wohlfahrt, G.; Calvet, J.C.; Carrara, A.; Cerasoli, S.; et al. Ground-based optical measurements at European flux sites: A review of methods, instruments and current controversies. Sensors 2011, 11, 7954–7981. [Google Scholar] [CrossRef]
- Peñuelas, J.; Filella, I. Visible and near-infrared reflectance techniques for diagnosing plant physiological status. Trends Plant Sci. 1998, 3, 151–156. [Google Scholar] [CrossRef]
- Gamon, J.A.; Huemmrich, K.F.; Wong, C.Y.S.; Ensminger, I.; Garrity, S.; Hollinger, D.Y.; Noormets, A.; Peñuelas, J. A remotely sensed pigment index reveals photosynthetic phenology in evergreen conifers. Proc. Natl. Acad. Sci. USA 2016, 113, 13087–13092. [Google Scholar] [CrossRef]
- Wehlage, D.C.; Gamon, J.A.; Thayer, D.; Hildebrand, D.V. Interannual variability in dry mixed-grass prairie yield: A comparison of MODIS, SPOT, and field measurements. Remote Sens. 2016, 8, 872. [Google Scholar] [CrossRef]
- Filella, I.; Zhang, C.; Seco, R.; Karl, T.; Guenther, A.; Potosnak, M.; Pallardy, S.; Gu, L.; Kim, S.; Balzarolo, M.; et al. Photochemical reflectance index (PRI) as an estimator of isoprenoid emissions in a temperate deciduous forest. Remote Sens. 2018, 10, 557. [Google Scholar] [CrossRef]
- Garbulsky, M.F.; Peñuelas, J.; Ogaya, R.; Filella, I. Leaf and stand-level carbon uptake of a Mediterranean forest estimated using the satellite-derived reflectance indices EVI and PRI. Int. J. Remote Sens. 2013, 34, 1282–1296. [Google Scholar] [CrossRef]
- Myneni, R.B.; Keeling, C.D.; Tucker, C.J.; Asrar, G.; Nemani, R.R. Increased plant growth inthe northern high latitudes from 1981 to 1991. Nature 1997, 386, 698–702. [Google Scholar] [CrossRef]
- Nemani, R.R.; Keeling, C.D.; Hashimoto, H.; Jolly, W.M.; Piper, S.C.; Tucker, C.J.; Myneni, R.B.; Running, S.W. Climate-driven increases in global terrestrial net primary production from 1982 to 1999. Science 2003, 300, 1560–1563. [Google Scholar] [CrossRef]
- Zhao, M.; Running, S.W. Drought-induced reduction in global terrestrial net primary production from 2000 through 2009. Science 2010, 329, 940–943. [Google Scholar] [CrossRef] [PubMed]
- Myneni, R.B.; Dong, J.; Tucker, C.J.; Kaufmann, R.K.; Kauppi, P.E.; Liski, J.; Zhou, L.; Alexeyev, V.; Hughes, M.K. A large carbon sink in the woody biomass of Northern forests. Proc. Natl. Acad. Sci. USA 2001, 98, 14784–14789. [Google Scholar] [CrossRef] [PubMed]
- Viana, H.; Aranha, J.; Lopes, D.; Cohen, W.B. Estimation of crown biomass of Pinus pinaster stands and shrubland above-ground biomass using forest inventory data, remotely sensed imagery and spatial prediction models. Ecol. Model. 2012, 226, 22–35. [Google Scholar] [CrossRef]
- Jin, Y.; Yang, X.; Qiu, J.; Li, J.; Gao, T.; Wu, Q.; Zhao, F.; Ma, H.; Yu, H.; Xu, B. Remote sensing-based biomass estimation and its spatio-temporal variations in temperate Grassland, Northern China. Remote Sens. 2014, 6, 1496–1513. [Google Scholar] [CrossRef]
- Paruelo, J.M.; Epstein, H.E.; Lauenroth, W.K.; Burke, I.C. ANPP estimates from NDVI for the central grassland region of the United States. Ecology 1997, 78, 953–958. [Google Scholar] [CrossRef]
- Meng, J.; Du, X.; Wu, B. Generation of high spatial and temporal resolution NDVI and its application in crop biomass estimation. Int. J. Digit. Earth 2013, 6, 203–218. [Google Scholar] [CrossRef]
- White, M.; Nemani, R. Canopy duration has little influence on annual carbon storage in the deciduous broad leaf forest. Glob. Chang. Biol. 2003, 9, 967–972. [Google Scholar] [CrossRef]
- Gamon, J.A.; Field, C.B.; Goulden, M.L.; Griffin, K.L. Relationships Between NDVI, Canopy Structure, and Photosynthesis in Three Californian Vegetation Types. Ecol. Appl. 1995, 5, 28–41. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.; Gao, X.; Ferreira, L. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Badgley, G.; Field, C.B.; Berry, J.A. Canopy near-infrared reflectance and terrestrial photosynthesis. Sci. Adv. 2017, 3, e1602244. [Google Scholar] [CrossRef]
- Lyapustin, A.I.; Martonchik, J.; Wang, Y.; Laszlo, I.; Korkin, S. Multiangle implementation of atmospheric correction (MAIAC): 1. Radiative transfer basis and look-up tables. J. Geophys. Res. 2011, 116, D03210. [Google Scholar] [CrossRef]
- Lyapustin, A.I.; Wang, Y.; Laszlo, I.; Kahn, R.; Korkin, S.; Remer, L.; Levy, R.; Reid, J.S. Multiangle implementation of atmospheric correction (MAIAC): 2. Aerosol algorithm. J. Geophys. Res. Atmos. 2011, 116, 1–15. [Google Scholar] [CrossRef]
- Lyapustin, A.I.; Wang, Y.; Laszlo, I.; Hilker, T.; Hall, F.G.; Sellers, P.J.; Tucker, C.J.; Korkin, S.V. Multi-angle implementation of atmospheric correction for MODIS (MAIAC): 3. Atmospheric correction. Remote Sens. Environ. 2012, 127, 385–393. [Google Scholar] [CrossRef]
- Soegaard, H.; Otto, N.; Boegh, E.; Bay, C.; Schelde, K.; Thomsen, A. Carbon dioxide exchange over agricultural landscape using eddy correlation and footprint modelling. Agric. For. Meteorol. 2003, 114, 153–173. [Google Scholar] [CrossRef]
- Joiner, J.; Yoshida, Y.; Zhang, Y.; Duveiller, G.; Jung, M.; Lyapustin, A.; Wang, Y.; Tucker, C.; Joiner, J.; Yoshida, Y.; et al. Estimation of Terrestrial Global Gross Primary Production (GPP) with Satellite Data-Driven Models and Eddy Covariance Flux Data. Remote Sens. 2018, 10, 1346. [Google Scholar] [CrossRef]
- Heath, J.P. Quantifying temporal variability in population abundances. Oikos 2006, 115, 573–581. [Google Scholar] [CrossRef]
- Fernández-Martínez, M.; Vicca, S.; Janssens, I.A.; Martín-Vide, J.; Peñuelas, J. The consecutive disparity index, D, as measure of temporal variability in ecological studies. Ecosphere 2018, 9, e02527. [Google Scholar] [CrossRef]
- Keenan, T.F.; Hollinger, D.Y.; Bohrer, G.; Dragoni, D.; Munger, J.W.; Schmid, H.P.; Richardson, A.D. Increase in forest water-use efficiency as atmospheric carbon dioxide concentrations rise. Nature 2013, 499, 324–327. [Google Scholar] [CrossRef]
- Ohlson, J.A.; Kim, S. Linear valuation without OLS: The Theil-Sen estimation approach. Rev. Account. Stud. 2015, 20, 395–435. [Google Scholar] [CrossRef]
- R Core Team. R: A Lenguage and Environment for Stasitical Computing; R Core Team: St. Louis, MO, USA, 2018. [Google Scholar]
- Grömping, U. Estimators of Relative Importance in Linear Regression Based on Variance Decomposition. Am. Stat. 2007, 61, 139–147. [Google Scholar] [CrossRef]
- Grömping, U. Relative importance for linear regression in R: The package relaimpo. J. Stat. Softw. 2006, 17, 1–27. [Google Scholar] [CrossRef]
- Luyssaert, S.; Inglima, I.; Jung, M.; Richardson, D.; Reichstein, M.; Papale, D.; Piao, S.L.; Schulze, E.-D.; Wingate, L.; Matteucci, G.; et al. CO2 balance of boreal, temperate, and tropical forests derived from a global database. Glob. Chang. Biol. 2007, 13, 2509–2537. [Google Scholar] [CrossRef]
- Reverter, B.R.; Sánchez-Cañete, E.P.; Resco, V.; Serrano-Ortiz, P.; Oyonarte, C.; Kowalski, A.S. Analyzing the major drivers of NEE in a Mediterranean alpine shrubland. Biogeosciences 2010, 7, 2601–2611. [Google Scholar] [CrossRef]
- Momeni, M.; Saradjian, M.R. Evaluating NDVI-based emissivities of MODIS bands 31 and 32 using emissivities derived by Day/Night LST algorithm. Remote Sens. Environ. 2007, 106, 190–198. [Google Scholar] [CrossRef]
- Goerner, A.; Reichstein, M.; Tomelleri, E.; Hanan, N.; Rambal, S.; Papale, D.; Dragoni, D.; Schmullius, C. Remote sensing of ecosystem light use efficiency with MODIS-based PRI. Biogeosciences 2011, 8, 189–202. [Google Scholar] [CrossRef]
- Garbulsky, M.F.; Peñuelas, J.; Papale, D.; Filella, I. Remote estimation of carbon dioxide uptake by a Mediterranean forest. Glob. Chang. Biol. 2008, 14, 2860–2867. [Google Scholar] [CrossRef]
- Kross, A.; Fernandes, R.; Seaquist, J.; Beaubien, E. The effect of the temporal resolution of NDVI data on season onset dates and trends across Canadian broadleaf forests. Remote Sens. Environ. 2011, 115, 1564–1575. [Google Scholar] [CrossRef]
- Zhang, Y.; Song, C.; Band, L.E.; Sun, G.; Li, J. Reanalysis of global terrestrial vegetation trends from MODIS products: Browning or greening? Remote Sens. Environ. 2017, 191, 145–155. [Google Scholar] [CrossRef]
- Ulsig, L.; Nichol, C.J.; Huemmrich, K.F.; Landis, D.R.; Middleton, E.M.; Lyapustin, A.I.; Mammarella, I.; Levula, J.; Porcar-Castell, A. Detecting inter-annual variations in the phenology of evergreen conifers using long-term MODIS vegetation index time series. Remote Sens. 2017, 9, 49. [Google Scholar] [CrossRef]

| Ecosystem | NDVI | EVI | NIRv | CCI | N |
|---|---|---|---|---|---|
| Weekly | |||||
| ENF | 0.42 ± 0.07 | 0.43 ± 0.05 | 0.46 ± 0.06 | 0.13 ± 0.03 | 16 |
| EBF | 0.19 ± 0.07 | 0.20 ± 0.08 | 0.19 ± 0.08 | 0.11 ± 0.02 | 3 |
| DBF | 0.42 ± 0.09 | 0.53 ± 0.10 | 0.54 ± 0.10 | 0.24 ± 0.07 | 10 |
| MF | 0.48 ± 0.01 | 0.68 ± 0.01 | 0.66 ± 0.01 | 0.30 ± 0.07 | 3 |
| OSH | 0.51 ± NA | 0.47 ± NA | 0.50 ± NA | 0.00 ± NA | 2 |
| GRA | 0.62 ± 0.05 | 0.56 ± 0.05 | 0.55 ± 0.05 | 0.25 ± 0.04 | 9 |
| CRO | 0.35 ± 0.06 | 0.39 ± 0.05 | 0.40 ± 0.06 | 0.14 ± 0.03 | 10 |
| WET | 0.48 ± 0.07 | 0.55 ± 0.07 | 0.56 ± 0.08 | 0.25 ± 0.05 | 5 |
| Mean | 0.43 ± 0.03 | 0.48 ± 0.03 | 0.49 ± 0.03 | 0.19 ± 0.02 | 58 |
| Weekly anomalies | |||||
| ENF | 0.03 ± 0.01 | 0.02 ± 0.01 | 0.03 ± 0.01 | 0.01 ± 0.00 | 16 |
| EBF | 0.02 ± 0.01 | 0.01 ± 0.01 | 0.01 ± 0.01 | 0.06 ± 0.03 | 3 |
| DBF | 0.07 ± 0.02 | 0.07 ± 0.02 | 0.07 ± 0.02 | 0.07 ± 0.01 | 10 |
| MF | 0.02 ± 0.01 | 0.01 ± 0.01 | 0.02 ± 0.02 | 0.01 ± 0.00 | 3 |
| OSH | 0.05 ± NA | 0.05 ± NA | 0.03 ± NA | 0.00 ± NA | 2 |
| GRA | 0.10 ± 0.03 | 0.08 ± 0.02 | 0.09 ± 0.03 | 0.02 ± 0.01 | 9 |
| CRO | 0.08 ± 0.02 | 0.11 ± 0.03 | 0.10 ± 0.03 | 0.06 ± 0.02 | 10 |
| WET | 0.00 ± 0.00 | 0.00 ± 0.00 | 0.01 ± 0.00 | 0.02 ± 0.01 | 5 |
| Mean | 0.05 ± 0.00 | 0.05 ± 0.01 | 0.06 ± 0.01 | 0.03 ± 0.01 | 58 |
| Monthly | |||||
| ENF | 0.43 ± 0.06 | 0.49 ± 0.06 | 0.50 ± 0.06 | 0.20 ± 0.04 | 16 |
| EBF | 0.16 ± 0.07 | 0.23 ± 0.12 | 0.23 ± 0.12 | 0.10 ± 0.04 | 3 |
| DBF | 0.43 ± 0.09 | 0.55 ± 0.11 | 0.56 ± 0.11 | 0.35 ± 0.10 | 10 |
| MF | 0.45 ± 0.03 | 0.77 ± 0.02 | 0.74 ± 0.02 | 0.48 ± 0.06 | 3 |
| OSH | 0.32 ± NA | 0.27 ± NA | 0.35 ± NA | 0.21 ± NA | 2 |
| GRA | 0.61 ± 0.06 | 0.65 ± 0.04 | 0.65 ± 0.04 | 0.42 ± 0.07 | 9 |
| CRO | 0.41 ± 0.07 | 0.38 ± 0.06 | 0.43 ± 0.06 | 0.21 ± 0.03 | 10 |
| WET | 0.53 ± 0.05 | 0.57 ± 0.05 | 0.60 ± 0.07 | 0.35 ± 0.08 | 5 |
| Mean | 0.44 ± 0.03 | 0.51 ± 0.03 | 0.52 ± 0.03 | 0.28 ± 0.03 | 58 |
| Monthly anomalies | |||||
| ENF | 0.06 ± 0.02 | 0.05 ± 0.03 | 0.07 ± 0.02 | 0.02 ± 0.01 | 16 |
| EBF | 0.03 ± 0.02 | 0.04 ± 0.03 | 0.04 ± 0.02 | 0.07 ± 0.03 | 3 |
| DBF | 0.11 ± 0.04 | 0.10 ± 0.03 | 0.10 ± 0.03 | 0.08 ± 0.02 | 10 |
| MF | 0.04 ± 0.03 | 0.02 ± 0.01 | 0.06 ± 0.03 | 0.01 ± 0.01 | 3 |
| OSH | 0.02 ± NA | 0.08 ± NA | 0.15 ± NA | 0.02 ± NA | 2 |
| GRA | 0.12 ± 0.05 | 0.10 ± 0.04 | 0.12 ± 0.04 | 0.10 ± 0.01 | 9 |
| CRO | 0.10 ± 0.02 | 0.13 ± 0.02 | 0.15 ± 0.03 | 0.05 ± 0.03 | 10 |
| WET | 0.06 ± 0.02 | 0.03 ± 0.01 | 0.03 ± 0.01 | 0.05 ± 0.03 | 5 |
| Mean | 0.08 ± 0.01 | 0.08 ± 0.01 | 0.09 ± 0.01 | 0.05 ± 0.01 | 58 |
| MAT | VPD | IGBP | GPP | GPP PV | RSVI PV | GPP PV% | RSVI PV% | GPP IPV | RSVI IPV | R2 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Weekly | |||||||||||
| NDVI | GRA | 0.49 ± 0.12 | 0.45 ± 0.11 | 0.24 ± 0.08 | 0.81 | ||||||
| EVI | 0.63 ± 0.08 | 0.51 ± 0.07 | 0.26 ± 0.08 | 0.76 | |||||||
| NIRv | 0.60 ± 0.09 | 0.47 ± 0.09 | 0.25 ± 0.09 | 0.72 | |||||||
| CCI | 0.36 ± 0.12 | 0.44 ± 0.12 | 0.47 ± 0.10 | 0.48 | |||||||
| Weekly anomalies | |||||||||||
| NDVI | 0.00 | ||||||||||
| EVI | 0.24 ± 0.12 | 0.27 ± 0.12 | 0.43 ± 0.13 | 0.33 | |||||||
| NIRv | 0.41 ± 0.12 | 0.17 | |||||||||
| CCI | 0.50 ± 0.12 | 0.25 ± 0.12 | 0.29 | ||||||||
| Monthly | |||||||||||
| NDVI | 0.95 ± 0.09 | 0.56 ± 0.09 | 0.68 | ||||||||
| EVI | 0.63 ± 0.09 | 0.52 ± 0.09 | 0.19 ± 0.09 | 0.65 | |||||||
| NIRv | 0.67 ± 0.12 | 0.31 ± 0.10 | 0.30 ± 0.11 | 0.59 | |||||||
| CCI | 0.38 ± 0.13 | 0.47 ± 0.12 | 0.50 ± 0.10 | 0.36 ± 0.15 | 0.48 | ||||||
| Monthly anomalies | |||||||||||
| NDVI | 0.00 | ||||||||||
| EVI | 0.34 ± 0.15 | 0.43 ± 0.15 | 0.31 ± 0.15 | 0.21 | |||||||
| NIRv | 0.30 ± 0.13 | 0.09 | |||||||||
| CCI | 0.33 ± 0.14 | −0.51 ± 0.14 | 0.20 | ||||||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fernández-Martínez, M.; Yu, R.; Gamon, J.; Hmimina, G.; Filella, I.; Balzarolo, M.; Stocker, B.; Peñuelas, J. Monitoring Spatial and Temporal Variabilities of Gross Primary Production Using MAIAC MODIS Data. Remote Sens. 2019, 11, 874. https://doi.org/10.3390/rs11070874
Fernández-Martínez M, Yu R, Gamon J, Hmimina G, Filella I, Balzarolo M, Stocker B, Peñuelas J. Monitoring Spatial and Temporal Variabilities of Gross Primary Production Using MAIAC MODIS Data. Remote Sensing. 2019; 11(7):874. https://doi.org/10.3390/rs11070874
Chicago/Turabian StyleFernández-Martínez, Marcos, Rong Yu, John Gamon, Gabriel Hmimina, Iolanda Filella, Manuela Balzarolo, Benjamin Stocker, and Josep Peñuelas. 2019. "Monitoring Spatial and Temporal Variabilities of Gross Primary Production Using MAIAC MODIS Data" Remote Sensing 11, no. 7: 874. https://doi.org/10.3390/rs11070874
APA StyleFernández-Martínez, M., Yu, R., Gamon, J., Hmimina, G., Filella, I., Balzarolo, M., Stocker, B., & Peñuelas, J. (2019). Monitoring Spatial and Temporal Variabilities of Gross Primary Production Using MAIAC MODIS Data. Remote Sensing, 11(7), 874. https://doi.org/10.3390/rs11070874