Long-Term Variations in the Pixel-to-Pixel Variability of NOAA AVHRR SST Fields from 1982 to 2015
Abstract
1. Introduction
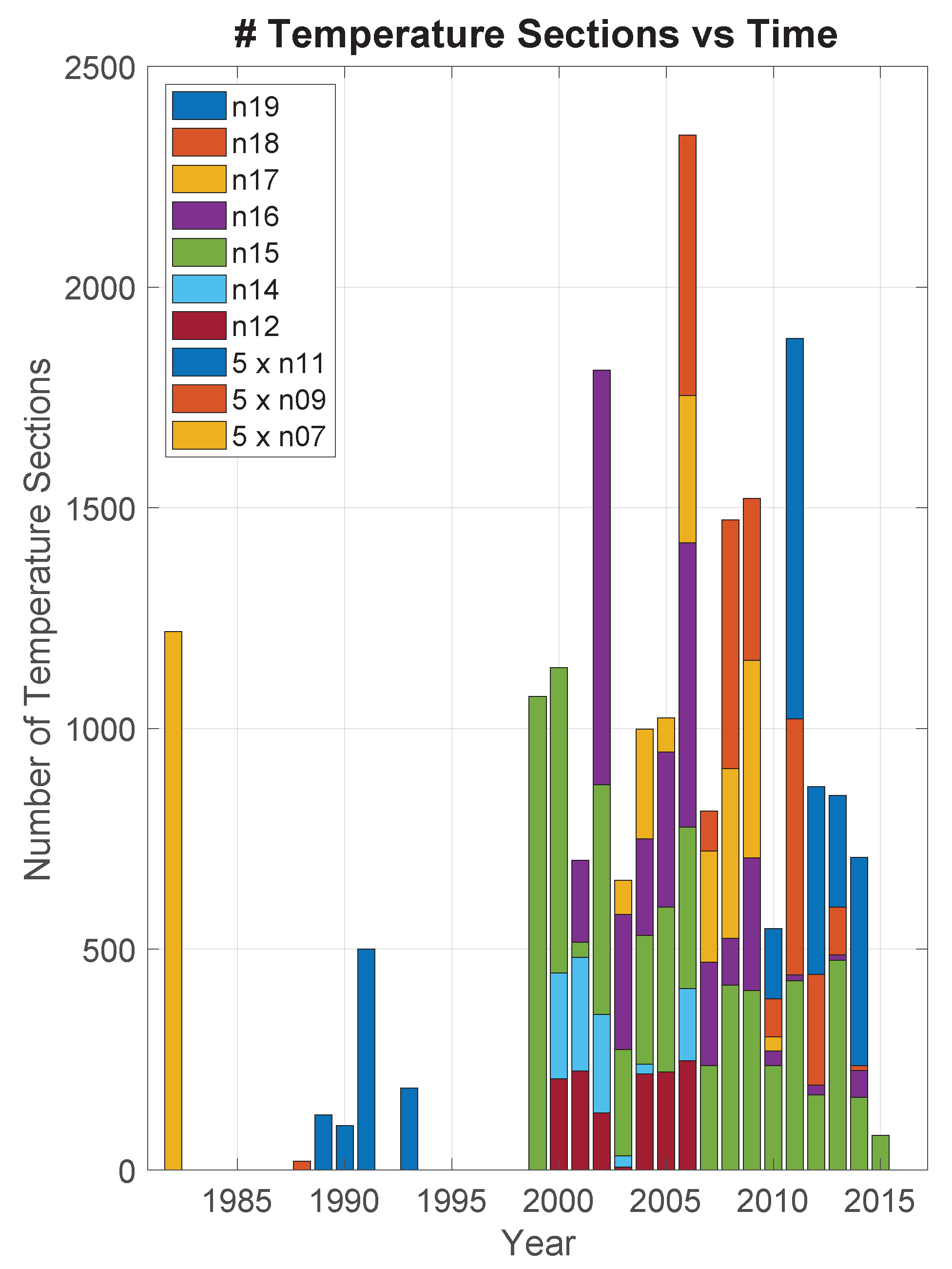
2. Data
3. Processing
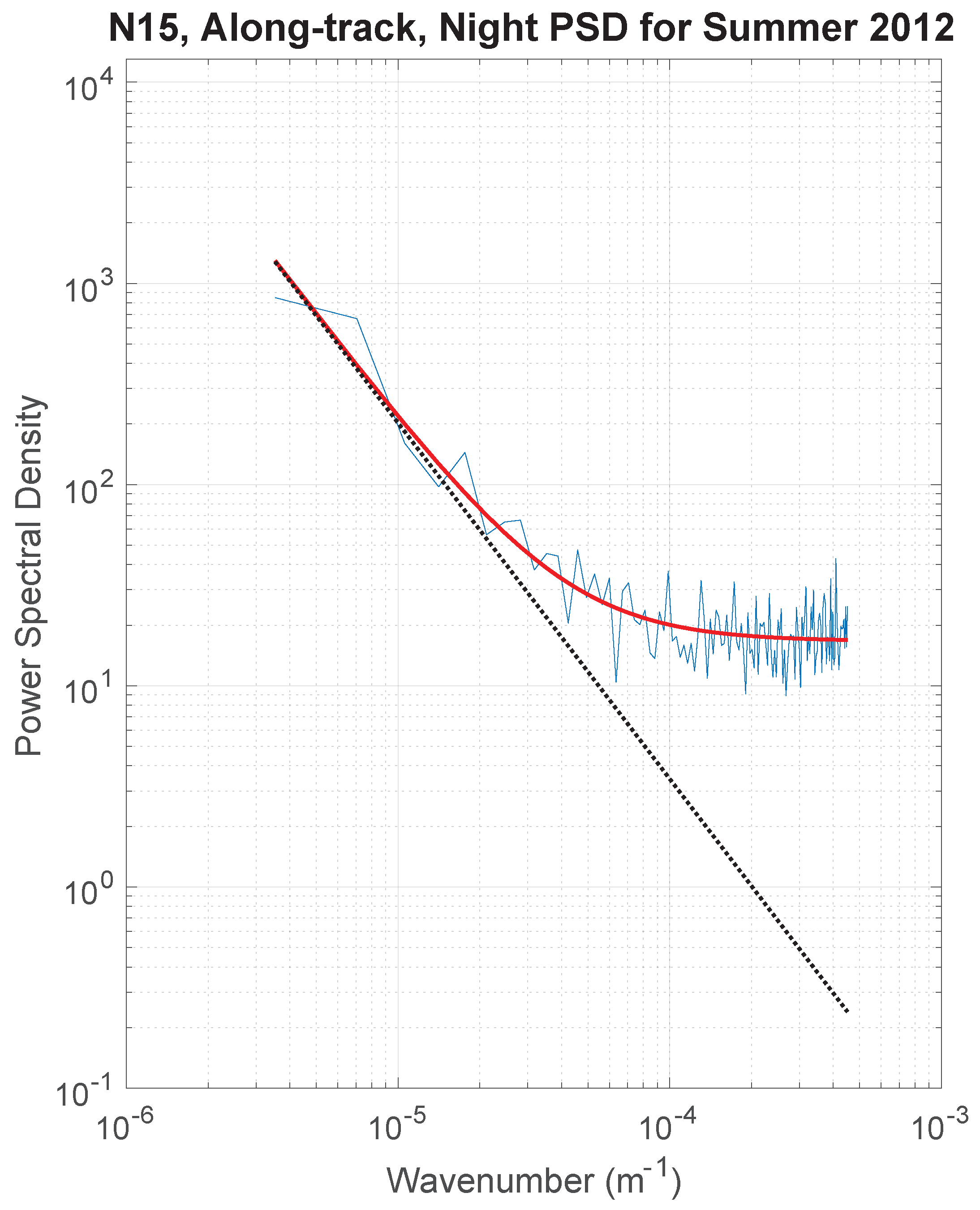
4. Results
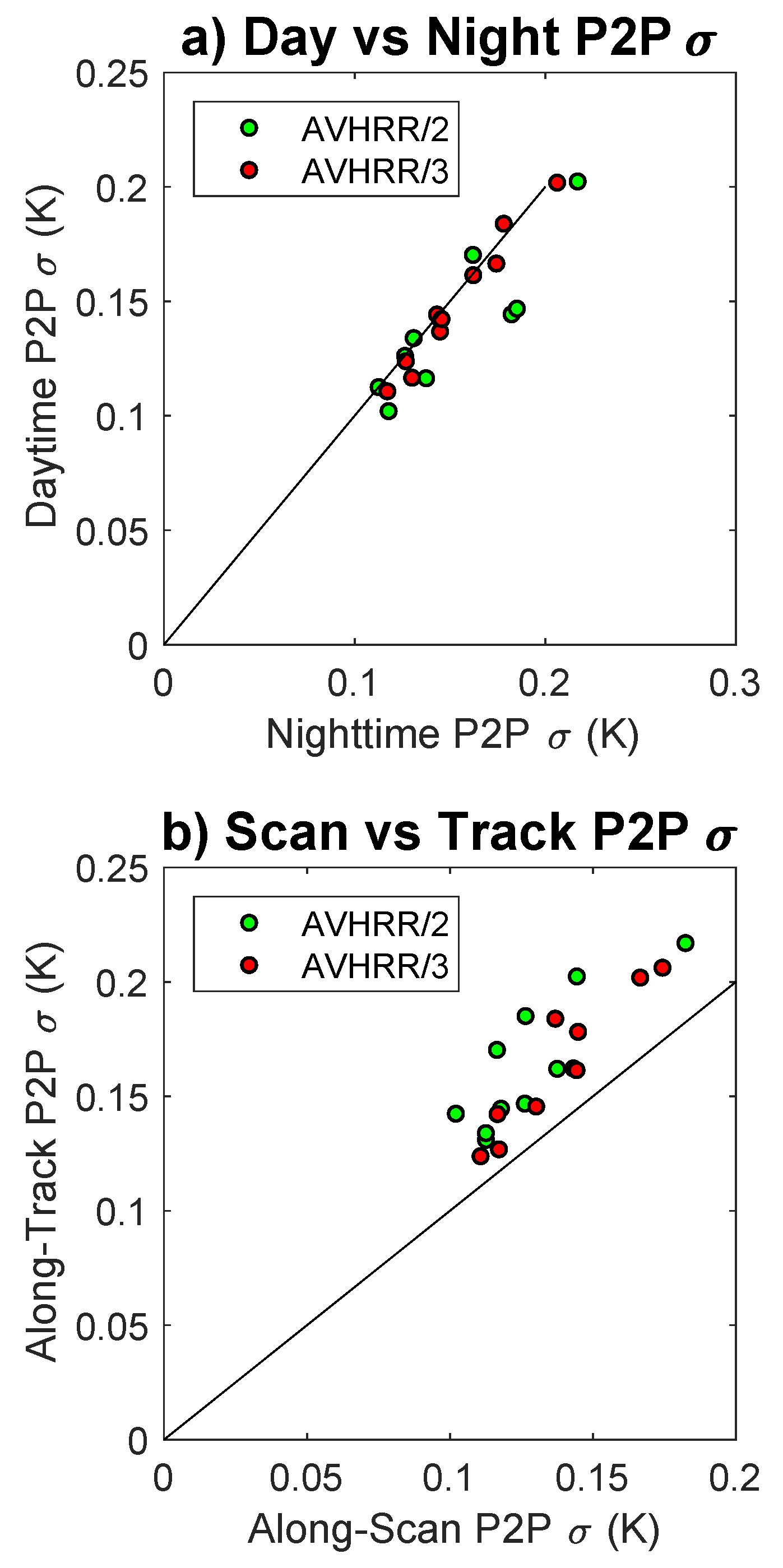
4.1. P2P by Satellite
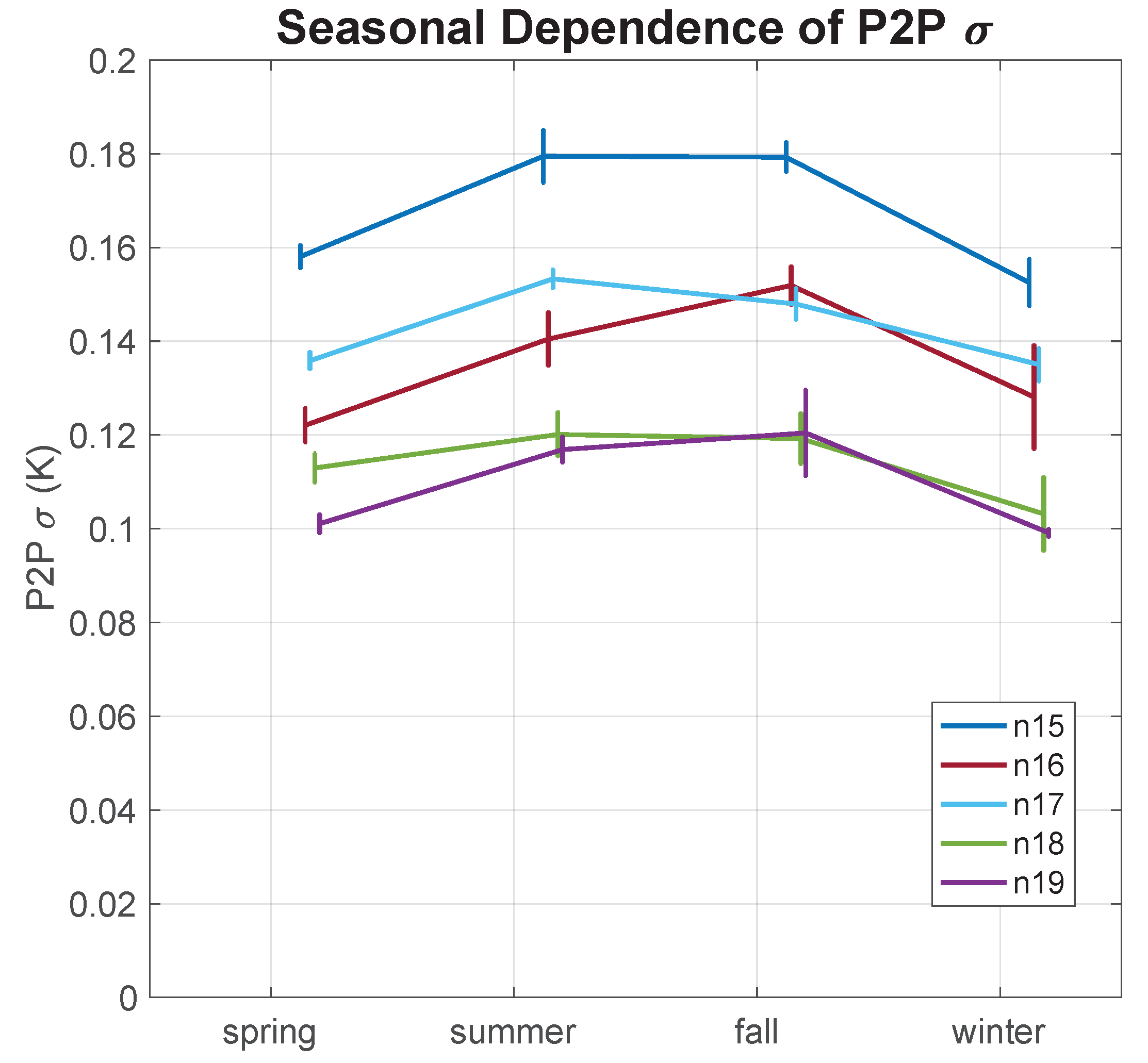
4.2. Seasonal Dependence of P2P by Satellite
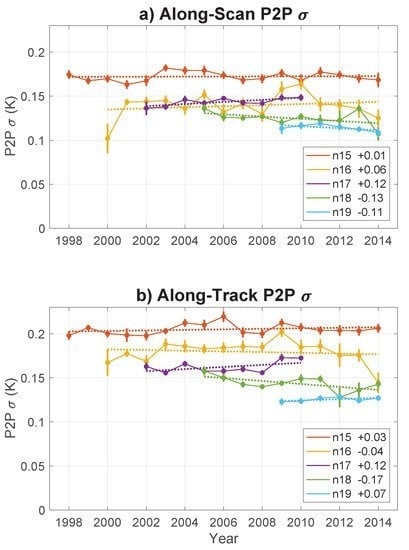
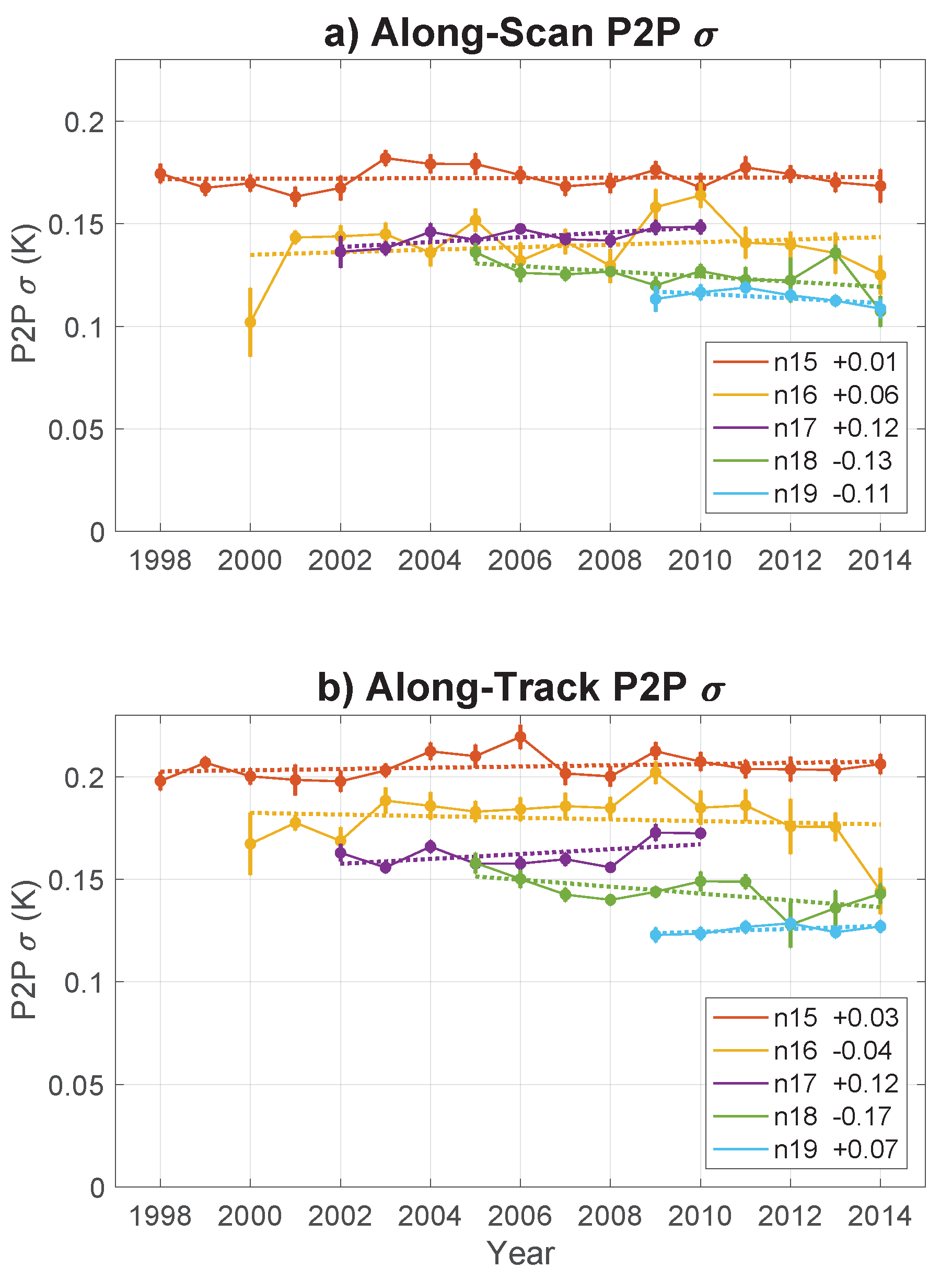
4.3. Temporal Trend in P2P by Satellite
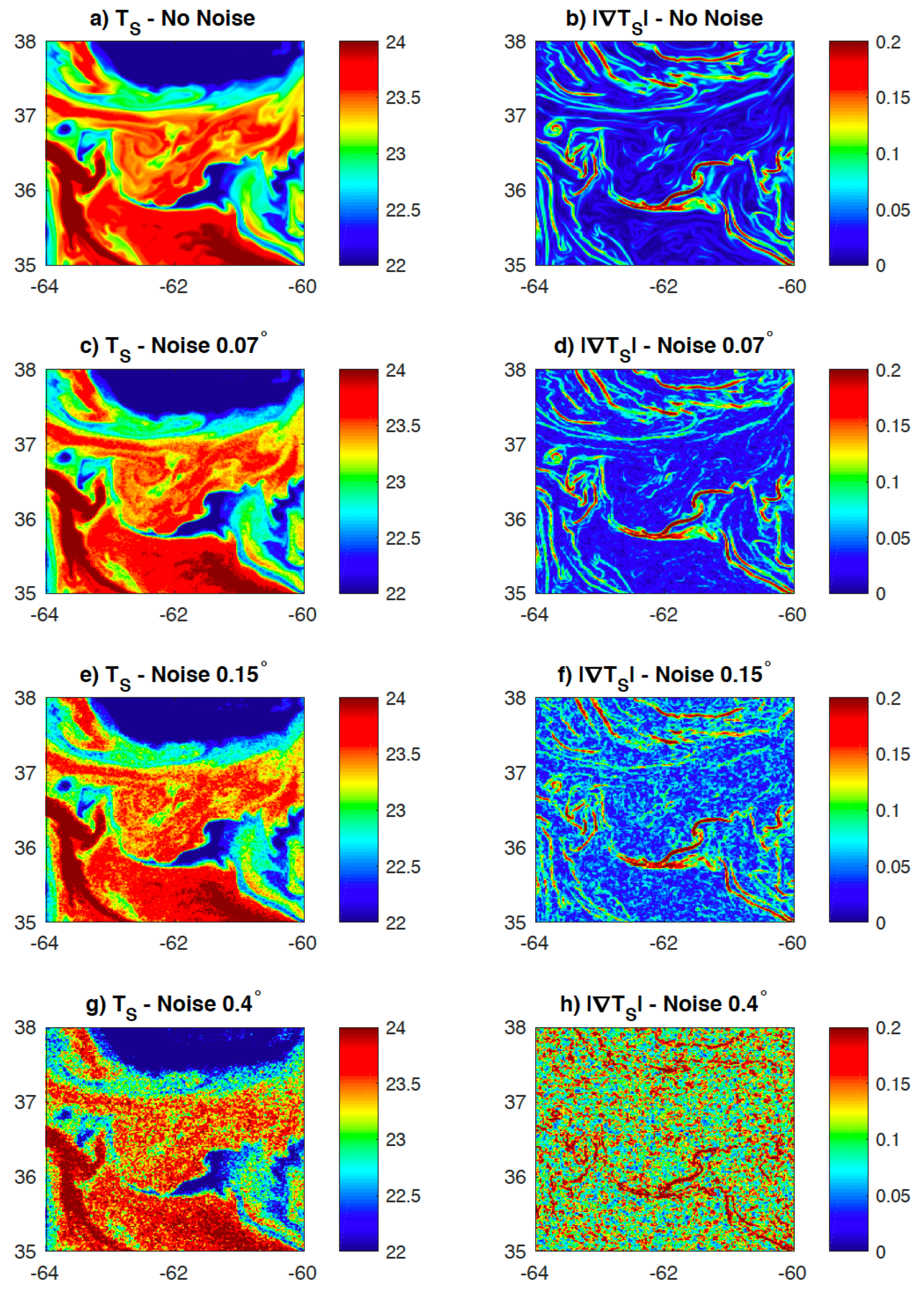
5. Discussion
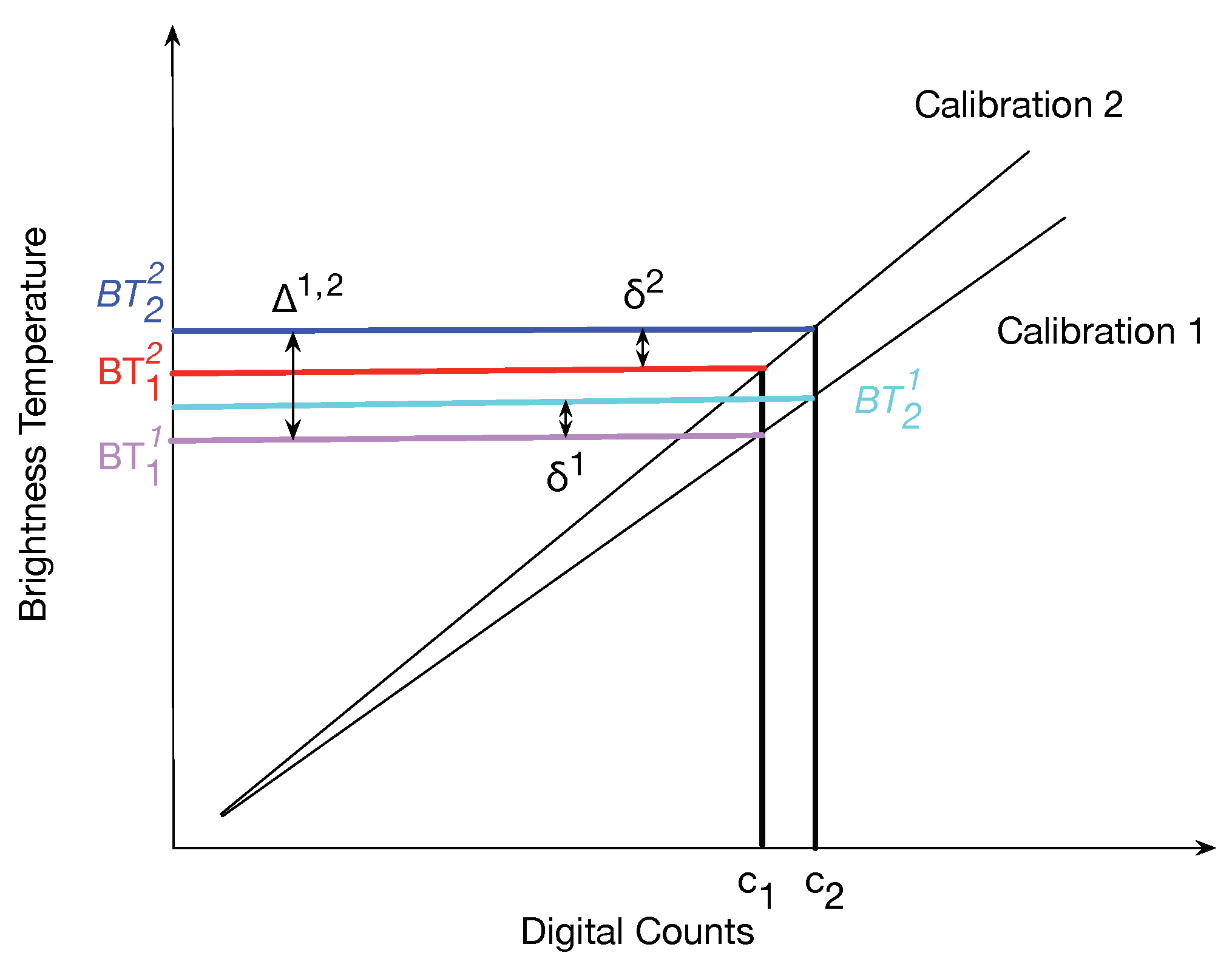
5.1. Pathfinder Retrieval Algorithm
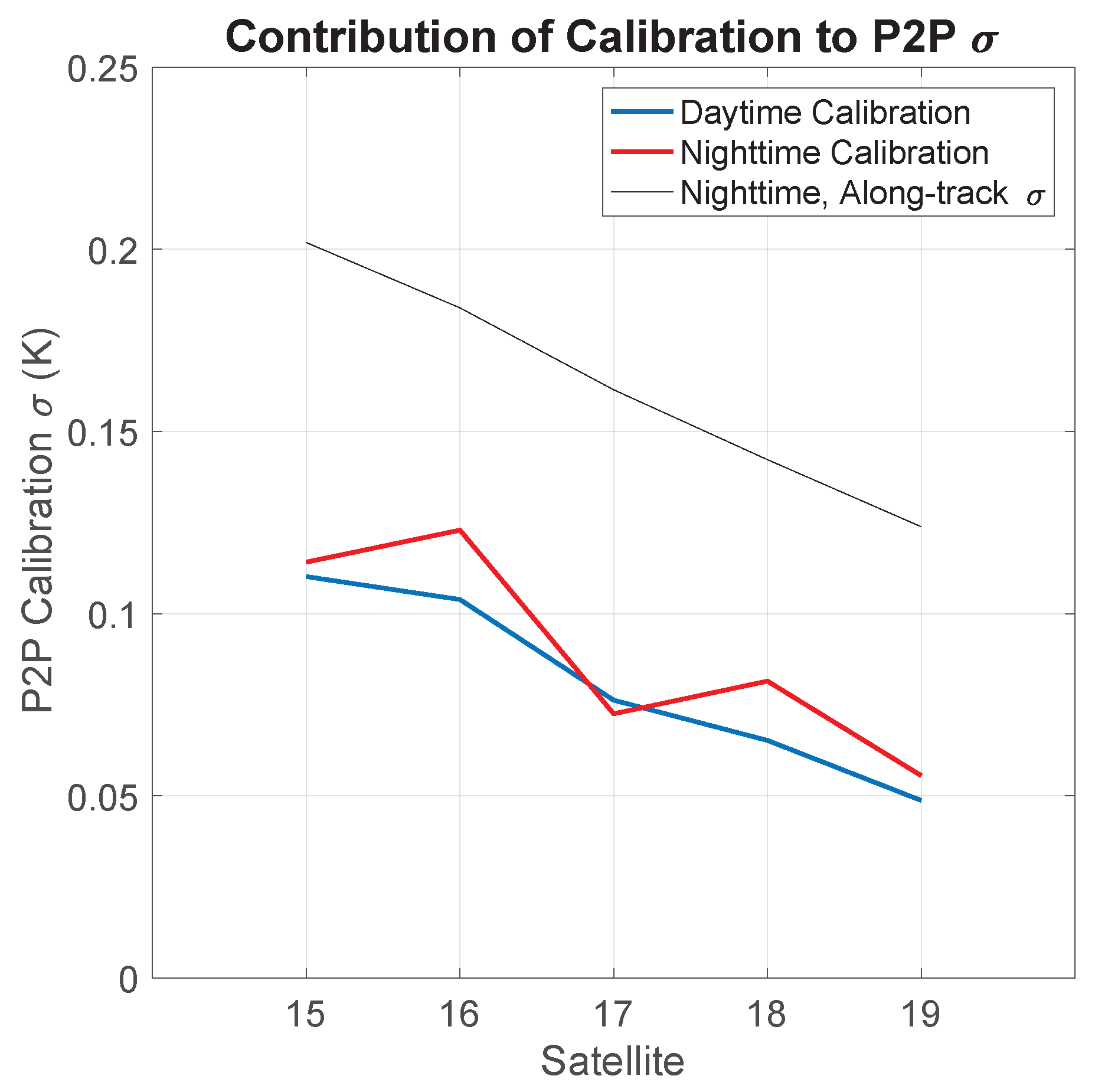
5.2. Uncertainties in Brightness Temperature (BT)
5.3. Putting It All Together
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AVHRR | Advanced Very High Resolution Radiometer |
| BT | Brightness Temperature |
| CLASS | Comprehensive Large Array-data Stewardship System |
| CMS | Centre de Météorologie Spatiale |
| FFT | Fast Fourier Transform |
| GHRSST | Group for High Resolution Sea Surface Temperature |
| HRPT | High Resolution Picture Transmission |
| ICT | Internal Calibration Target |
| LLC | Latitude/Longitude/polar-Cap |
| LLC-4320 | Latitude/Longitude/polar-Cap (LLC)-4320 |
| NASA | National Aeronautics and Space Administration |
| NEΔT | Noise Equivalent Temperature |
| NOAA | National Oceanic and Atmospheric Administration |
| NPP | National Polar-orbiting Partnership |
| p2p | pixel-to-pixel |
| PRT | Platinum Resistance Thermistor |
| PSD | power spectral density |
| SEVIRI | Spinning Enhanced Visible and Infra-Red Imager |
| 3S | Sensor Stability for SST |
| SST | sea surface temperature |
| URI | University of Rhode Island |
| VIIRS | Visible-Infrared Imager-Radiometer Suite |
| WOA05 | World Ocean Atlas 2005 |
References and Notes
- Wu, F.; Cornillon, P.C.; Boussidi, B.; Guan, L. Determining the Pixel-to-Pixel Uncertainty in Satellite-Derived SST Fields. Remote Sens. 2017, 9, 877. [Google Scholar] [CrossRef]
- ‘Level-2’ refers to the processing level of the data, a nomenclature used extensively for satellite-derived datasets, although the precise meaning of the level of processing varies by organization. The definition used here, http://science.nasa.gov/earth-science/earth-science-data/data-processing-levels-for-eosdis-data-products/, is that promulgated by the GHRSST.
- Cornillon, P.; Castro, S.; Gentemann, C.; Jessup, A.; Kaplan, A.; Lindstrom, E.; Maturi, E. SST Error Budget—White Paper; Technical Report; University of Rhode Island: Kingston, RI, USA, 2010; Available online: https://works.bepress.com/peter-cornillon/1/ (accessed on 24 February 2019).
- Obenour, K.M. Temporal Trends in Global Sea Surface Temperature Trends. Master’s Thesis, University of Rhode Island, Kingston, RI, USA, 2013. [Google Scholar]
- Kahru, M.; Di Lorenzo, E. Spatial and temporal statistics of sea surface temperature and chlorophyll fronts in the California Current. J. Plankton Res. 2012, 34, 749–760. [Google Scholar] [CrossRef]
- Rocha, C.B.; Chereskin, T.K.; Gille, S.T.; Menemenlis, D. Mesoscale to Submesoscale Wavenumber Spectra in Drake Passage. J. Phys. Oceanogr. 2016, 46, 601–620. [Google Scholar] [CrossRef]
- Vazquez-Cuervo, J.; Torres, H.S.; Menemenlis, D.; Chin, T.M.; Armstrong, E.M. Relationship between SST Gradients and Upwelling off Peru and Chile: Model/Satellite Data Analysis. Int. J. Remote Sens. 2017, 38, 6599–6622. [Google Scholar] [CrossRef]
- Kilpatrick, K.A.; Podestá, G.P.; Evans, R. Overview of the NOAA/NASA advanced very high resolution radiometer Pathfinder algorithm for sea surface temperature and associated matchup database. J. Geophys. Res. 2001, 106, 9179–9198. [Google Scholar] [CrossRef]
- Reynolds, R.W.; Smith, T.M.; Liu, C.; Chelton, D.B.; Casey, K.S.; Schlax, M.G. Daily High-Resolution-Blended Analyses for Sea Surface Temperature. J. Clim. 2007, 20, 5473–5496. [Google Scholar] [CrossRef]
- The noise in channels 4 and 5 may be correlated. Furthermore, there are a number of other characteristics affecting the calibration, which are not included in the brief overview of calibration presented in Section 5.2. Jonathan Mittaz, personal communication, 24 January 2019.
- Issues related to in-flight calibration are more complicated than suggested here. Jonathan Mittaz, personal communication, 24 January 2019. However, with the exception of the possible correlation between channels and of the non-Gaussian nature of the noise, the extra complexity does not play a significant role in the analysis presented here.
- Rama Varma Raja, M.K.; Battles, D.; Wu, X.; Bauch, H.; Yu, F.; Lambeck, R.W.; Sun, N.; Perez Albinana, A.; Montagner, F. In-Orbit Health and Performance of Operational AVHRR Instruments; SPIE Optical Engineering + Applications, Strojnik, M., Paez, G., Eds.; SPIE: Bellingham, WA, USA, 2010; p. 780814. [Google Scholar]
- He, K.; Ignatov, A.; Kihai, Y.; Cao, C.; Stroup, J. Sensor Stability for SST (3S): Toward Improved Long-Term Characterization of AVHRR Thermal Bands. Remote Sens. 2016, 8, 346. [Google Scholar] [CrossRef]
- Brown, O.B.; Brown, J.W.; Evans, R.H. Calibration of advanced very high resolution radiometer infrared observations. J. Geophys. Res. Oceans 1985, 90, 11667–11677. [Google Scholar] [CrossRef]
- Steyn-Ross, D.A.; Steyn-Ross, M.L.; Clift, S. Radiance calibrations for advanced very high resolution radiometer infrared channels. J. Geophys. Res. 1992, 97, 5551–5568. [Google Scholar] [CrossRef]
- Brown, J.W.; Brown, O.B.; Evans, R.H. Calibration of advanced very high resolution radiometer infrared channels: A new approach to nonlinear correction. J. Geophys. Res. Oceans 1993, 98, 18157–18269. [Google Scholar] [CrossRef]
- Trishchenko, A.P.; Fedosejevs, G.; Li, Z.; Cihlar, J. Trends and uncertainties in thermal calibration of AVHRR radiometers onboard NOAA-9 to NOAA-16. J. Geophys. Res. 2002, 107, 4778. [Google Scholar] [CrossRef]
- Mittaz, J.P.D.; Harris, A.R.; Sullivan, J.T. A Physical Method for the Calibration of the AVHRR/3 Thermal IR Channels 1: The Prelaunch Calibration Data. J. Atmospheric Ocean. Technol. 2009, 26, 996–1019. [Google Scholar] [CrossRef]
- Minnett, P.J.; Smith, D.L. Chapter 2.4—Postlaunch Calibration and Stability: Thermal Infrared Satellite Radiometers; Elsevier: Amsterdam, The Netherlands, 2014; Volume 47. [Google Scholar]
- Trishchenko, A.P.; Li, Z. A method for the correction of AVHRR onboard IR calibration in the event of short-term radiative contamination. Int. J. Remote Sens. 2001, 22, 3619–3624. [Google Scholar] [CrossRef]
- Mittaz, J.; Harris, A. A Physical Method for the Calibration of the AVHRR/3 Thermal IR Channels. Part II: An In-Orbit Comparison of the AVHRR Longwave Thermal IR Channels on board MetOp-Awith IASI. J. Atmos. Ocean. Technol. 2011, 28, 1072–1087. [Google Scholar] [CrossRef]
- Chang, T.; Wu, X.; Weng, F. Modeling thermal emissive bands radiometric calibration impact with application to AVHRR. J. Geophys. Res. Atmos. 2017, 122, 2831–2843. [Google Scholar] [CrossRef]
- Lauritson, L.; Nelson, G.J.; Porto, F.W. Data Extraction and Calibration of TIROS-N/NOAA Radiometers; Technical Report NESS 107; National Oceanographic and Atmospheric Administration: Silver Spring, ML, USA, 1979; Rev. 1 (1988) by W.G. Planet. [Google Scholar]
- PRT values are provided on a five scan cycle, with PRT1 on scan 1, PRT2 on scan 2, PRT3 on scan 3, PRT4 on scan 4 and no PRT value on scan 5. The sequence then repeats.
- The T4 − T5 ≥ 0.7 °C regime is more representative of the water vapor environment in the study area than the T4 − T5 < 0.7 °C regime hence its use. c tends to be larger for the T4 − T5 < 0.7 °C leading to slightly larger estimates of the p2p σ uncertainties, but the general trends are similar.
- Barton, I.J. Digitization effects in AVHRR and MCSST data. Remote Sens. Environ. 1988, 29, 87–89. [Google Scholar] [CrossRef]
- Miller, P.I.; Groom, S.; Mcmanus, A.; Selley, J.; Mironnet, N. Panorama: A Semi-Automated Avhrr and Czcs System for Observation of Coastal and Ocean Processes. In Proceedings of the Remote Sensing Society, San Diego, CA, USA, 30 July–1 August 1997; pp. 539–544. [Google Scholar]
- Detailed in an internal CMS report “Radiometric noise and atmospheric correction smoothing in the case of Meteosat08/SEVIRI”. Pierre Le Borgne, personal communication, 3 February 2019.
- T4 and T5 refer to the brightness temperatures of spectral channels 4 and 5 on AVHRRs. The corresponding channels on SEVIRI are labeled differently but, for consistency, we continue to refer to this as the T4 − T5 term.
- SEVIRI is an infrared radiometer in a geosynchronous orbit with similar spectral channels to the AVHRR. The basic form of the SEVIRI retrieval algorithm is similar to that of the Pathfinder retrieval algorithm.
- Saux Picart, S. Algorithm Theoretical Basis Document for MSG/SEVIRI Sea Surface Temperature Data Record; Technical Report OSI-250; EUMETSAT: Darmstadt, Germany, 2018. [Google Scholar]
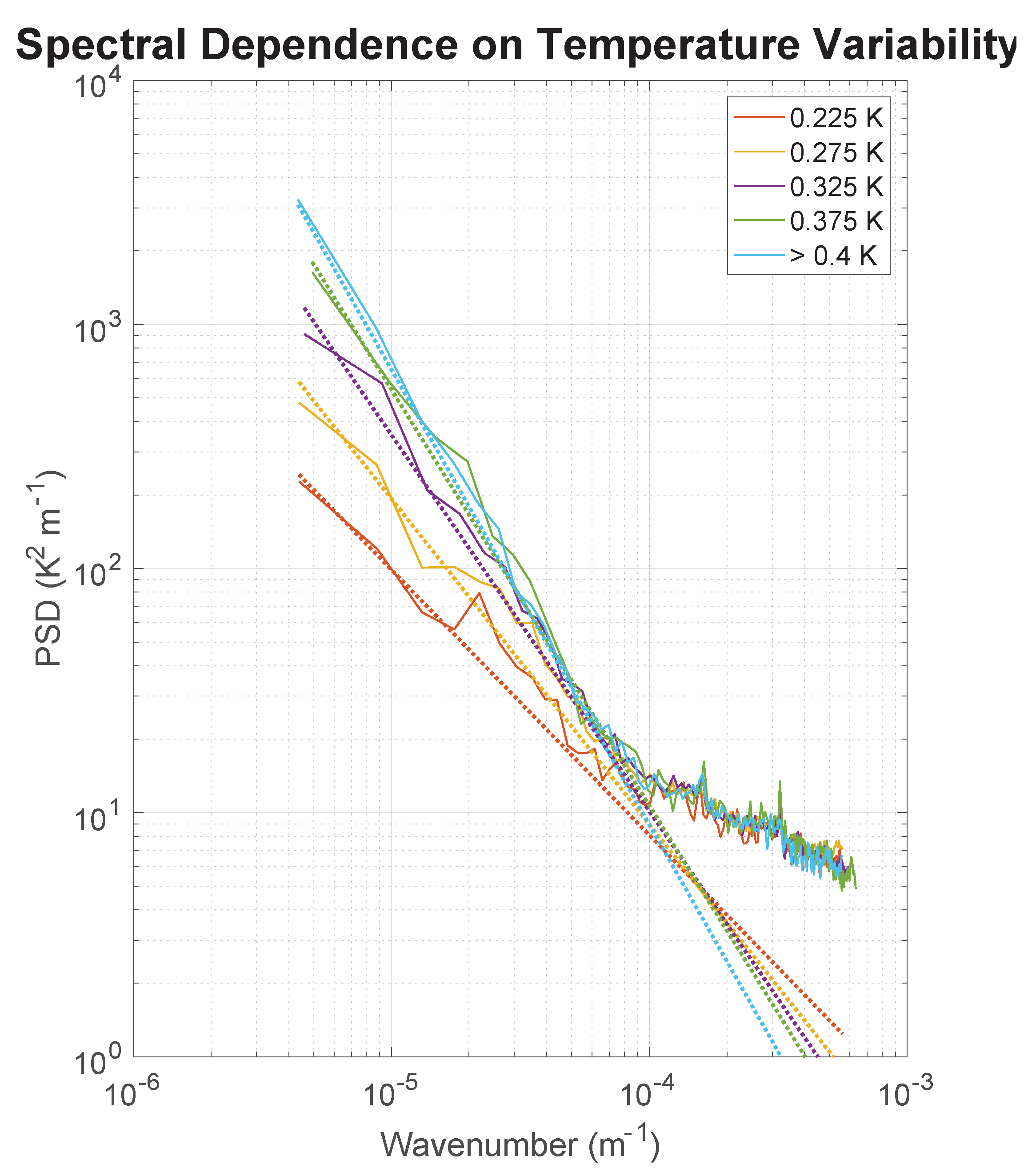
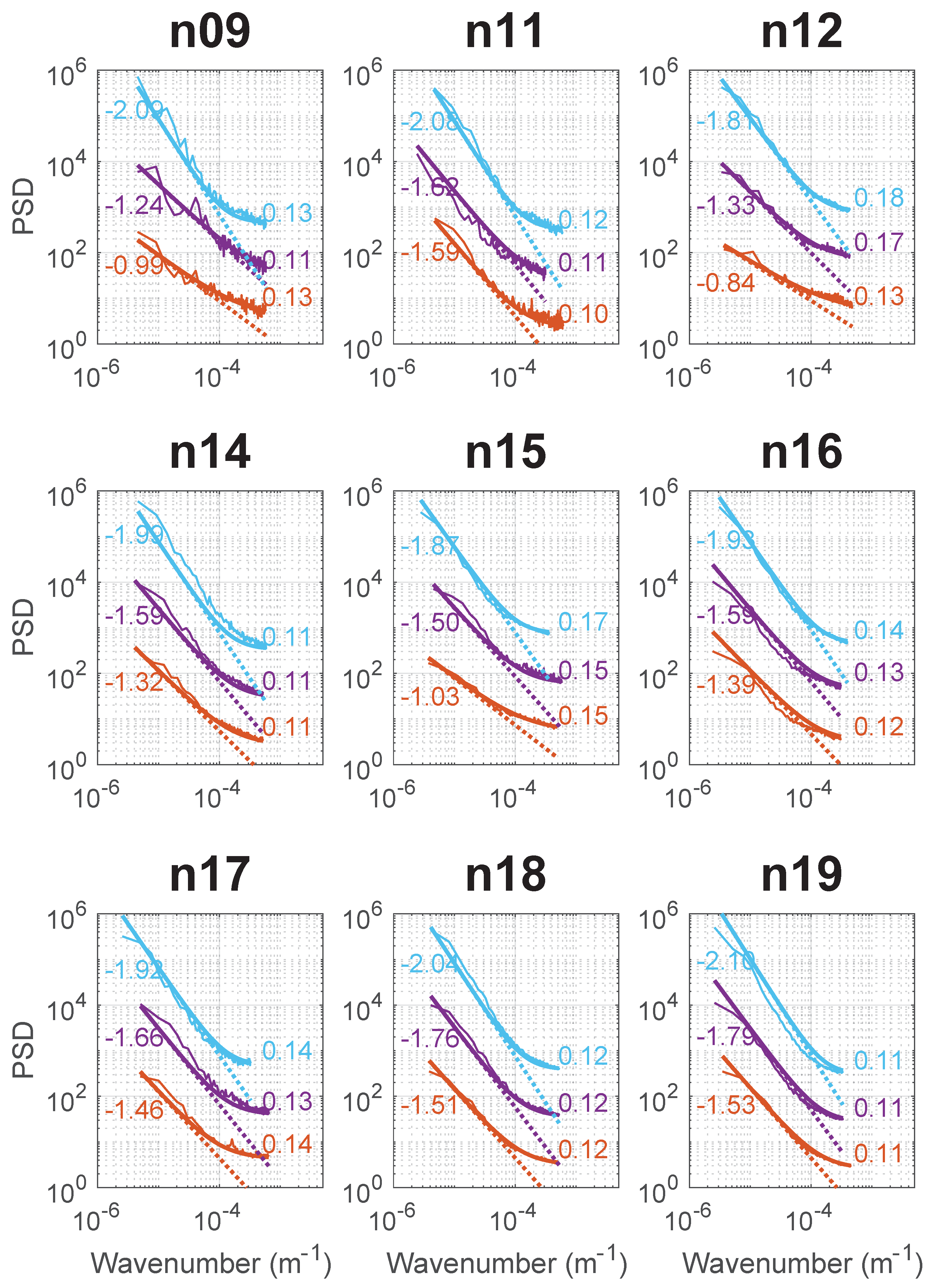
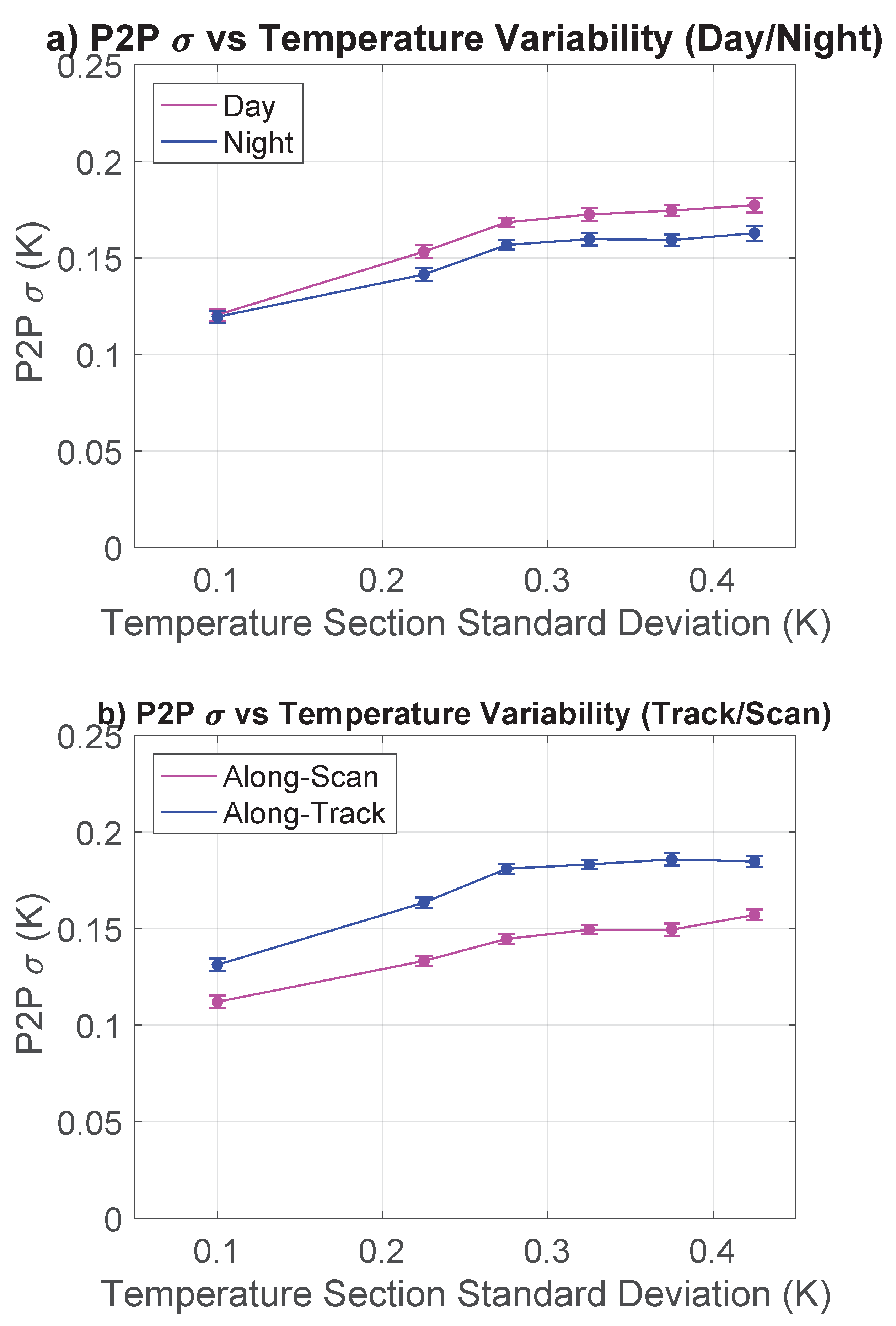
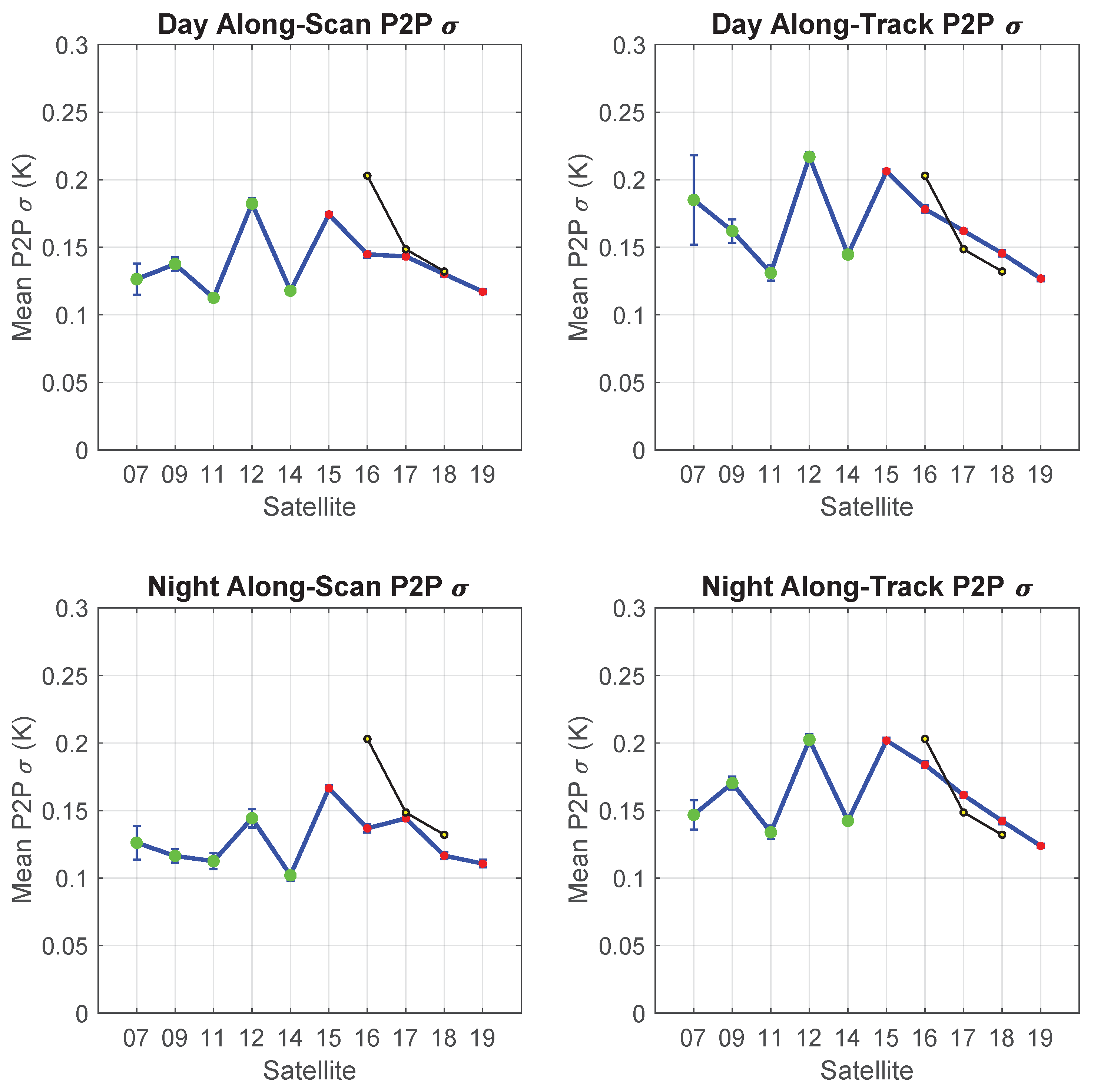
| Satellite | Period Covered | Number of Sections | ||||
|---|---|---|---|---|---|---|
| Start | End | Day | Night | |||
| Along-Scan | Along-Track | Along-Scan | Along-Track | |||
| NOAA-07 | 01/04/82 | 07/09/82 | 233 | 89 | 25 | 68 |
| NOAA-09 | 05/20/85 | 10/25/88 | 716 | 280 | 273 | 741 |
| NOAA-11 | 02/22/89 | 08/14/94 | 1085 | 704 | 136 | 229 |
| NOAA-12 | 01/02/00 | 10/09/06 | 7370 | 8079 | 682 | 2600 |
| NOAA-14 | 07/28/95 | 09/28/06 | 6378 | 7495 | 1405 | 1786 |
| NOAA-15 | 11/10/98 | 05/10/15 | 30,337 | 33,307 | 7873 | 11,370 |
| NOAA-16 | 01/09/01 | 05/10/14 | 19,666 | 20,192 | 5682 | 10,881 |
| NOAA-17 | 07/17/02 | 09/25/10 | 7267 | 16,618 | 17,604 | 14,551 |
| NOAA-18 | 06/09/05 | 10/04/14 | 19,002 | 14,804 | 4556 | 9198 |
| NOAA-19 | 04/04/09 | 09/19/14 | 13,891 | 11,306 | 2371 | 6204 |
| Satellite | Day, Along-Scan | Day, Along-Track | Night, Along-Scan | Night, Along-Track | ||||
|---|---|---|---|---|---|---|---|---|
| Mean | Sigma | Mean | Sigma | Mean | Sigma | Mean | Sigma | |
| NOAA-07 | 0.126 | 0.012 | 0.185 | 0.033 | 0.126 | 0.013 | 0.147 | 0.011 |
| NOAA-09 | 0.137 | 0.005 | 0.162 | 0.009 | 0.116 | 0.005 | 0.170 | 0.005 |
| NOAA-11 | 0.113 | 0.003 | 0.131 | 0.006 | 0.113 | 0.006 | 0.134 | 0.005 |
| NOAA-12 | 0.182 | 0.004 | 0.217 | 0.004 | 0.144 | 0.007 | 0.202 | 0.004 |
| NOAA-14 | 0.118 | 0.002 | 0.145 | 0.002 | 0.102 | 0.004 | 0.142 | 0.003 |
| NOAA-15 | 0.174 | 0.002 | 0.206 | 0.002 | 0.167 | 0.002 | 0.202 | 0.002 |
| NOAA-16 | 0.145 | 0.002 | 0.178 | 0.003 | 0.137 | 0.003 | 0.184 | 0.002 |
| NOAA-17 | 0.143 | 0.002 | 0.162 | 0.001 | 0.144 | 0.002 | 0.161 | 0.002 |
| NOAA-18 | 0.130 | 0.002 | 0.146 | 0.002 | 0.117 | 0.003 | 0.142 | 0.002 |
| NOAA-19 | 0.117 | 0.002 | 0.127 | 0.002 | 0.111 | 0.003 | 0.124 | 0.002 |
| All | 0.139 | 0.004 | 0.166 | 0.006 | 0.128 | 0.005 | 0.161 | 0.004 |
| AVHRR/2 | 0.135 | 0.005 | 0.168 | 0.011 | 0.120 | 0.007 | 0.159 | 0.005 |
| AVHRR/3 | 0.142 | 0.002 | 0.164 | 0.002 | 0.135 | 0.002 | 0.163 | 0.002 |
| Satellite | NOAA-16 | NOAA-17 | NOAA-18 | |
|---|---|---|---|---|
| (K) | Range | 0.063–0.071 | 0.048–0.055 | 0.034–0.055 |
| Mean | 0.067 | 0.053 | 0.052 | |
| (K) | Range | 0.085–0.091 | 0.056–0.061 | 0.054–0.059 |
| Mean | 0.088 | 0.057 | 0.057 | |
| 1.89 | 1.71 | 1.44 | ||
| p2p (K) | 0.22 | 0.14 | 0.12 | |
| Seasonal Ratio: Spectral | 0.16 | 0.11 | 0.10 | |
| Seasonal Ratio: Equation (3) | 0.21 | 0.19 | 0.19 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, F.; Cornillon, P.; Guan, L.; Kilpatrick, K. Long-Term Variations in the Pixel-to-Pixel Variability of NOAA AVHRR SST Fields from 1982 to 2015. Remote Sens. 2019, 11, 844. https://doi.org/10.3390/rs11070844
Wu F, Cornillon P, Guan L, Kilpatrick K. Long-Term Variations in the Pixel-to-Pixel Variability of NOAA AVHRR SST Fields from 1982 to 2015. Remote Sensing. 2019; 11(7):844. https://doi.org/10.3390/rs11070844
Chicago/Turabian StyleWu, Fan, Peter Cornillon, Lei Guan, and Katherine Kilpatrick. 2019. "Long-Term Variations in the Pixel-to-Pixel Variability of NOAA AVHRR SST Fields from 1982 to 2015" Remote Sensing 11, no. 7: 844. https://doi.org/10.3390/rs11070844
APA StyleWu, F., Cornillon, P., Guan, L., & Kilpatrick, K. (2019). Long-Term Variations in the Pixel-to-Pixel Variability of NOAA AVHRR SST Fields from 1982 to 2015. Remote Sensing, 11(7), 844. https://doi.org/10.3390/rs11070844