Towards a Long-Term Reanalysis of Land Surface Variables over Western Africa: LDAS-Monde Applied over Burkina Faso from 2001 to 2018
Abstract
1. Introduction
2. Materials and Methods
2.1. LDAS-Monde
2.1.1. ISBA Land Surface Model
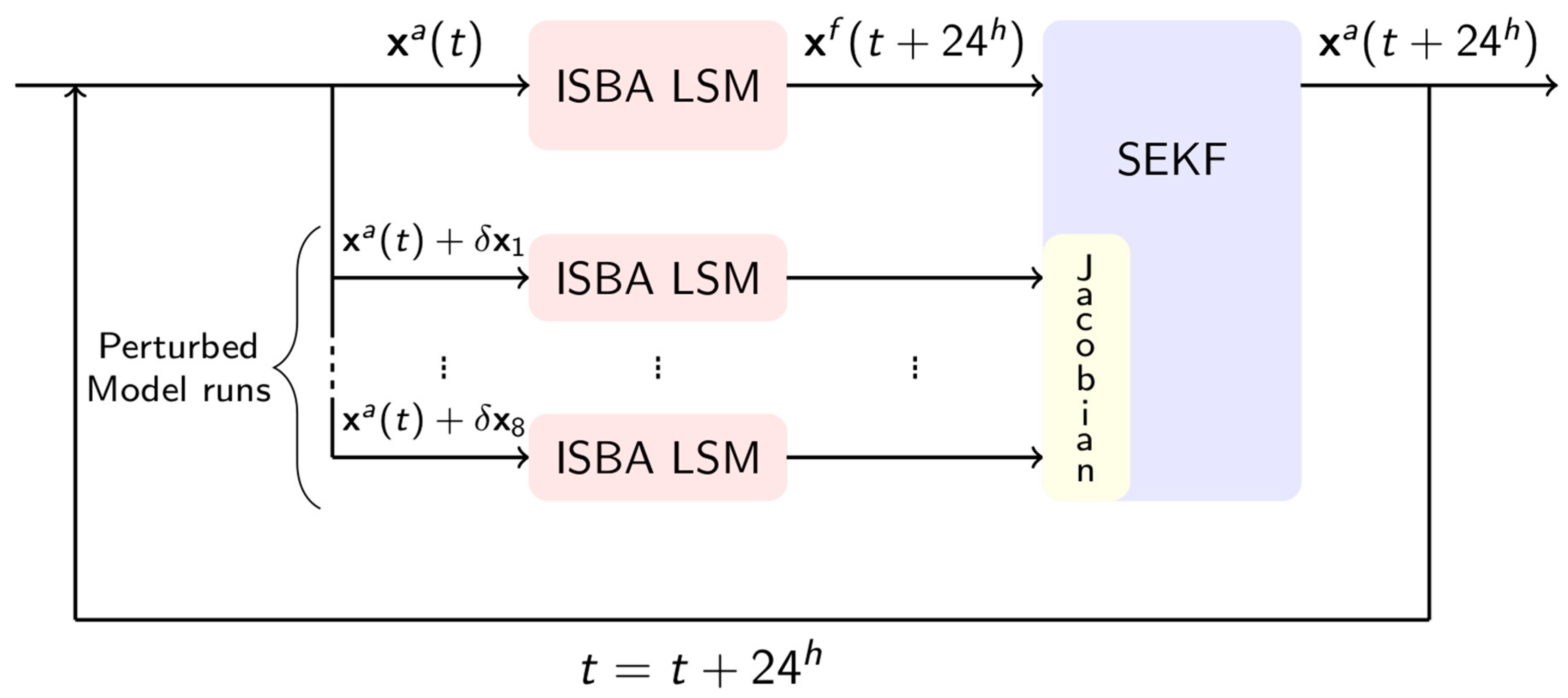
2.1.2. Data Assimilation
2.2. Datasets and Data Processing
2.2.1. In Situ Measurements
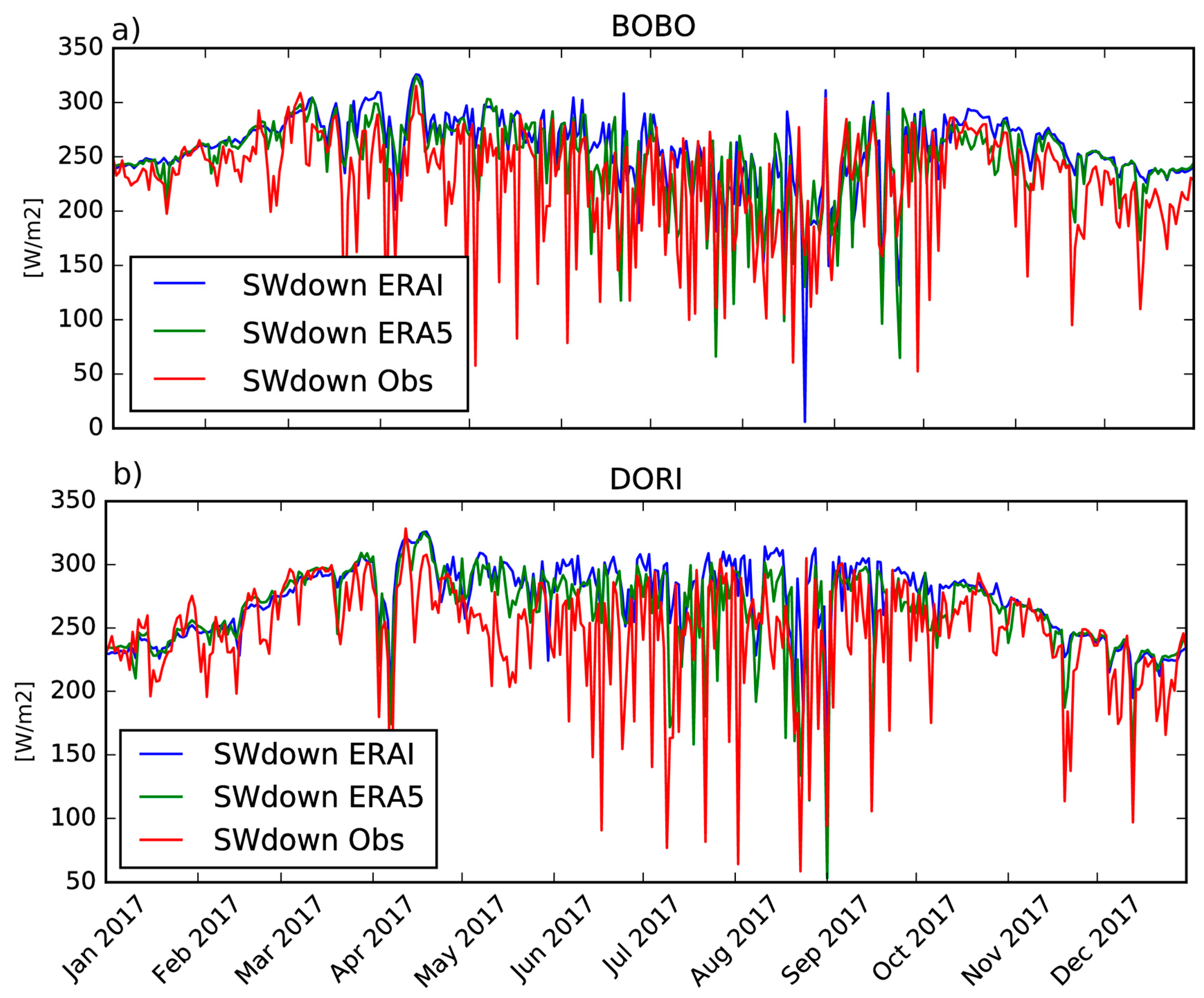
2.2.2. ERA-Interim and ERA5 Atmospheric Reanalyses
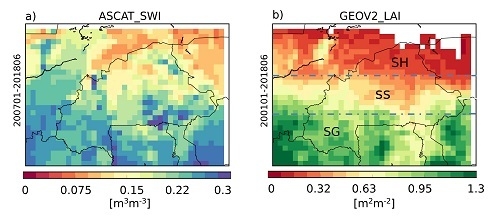
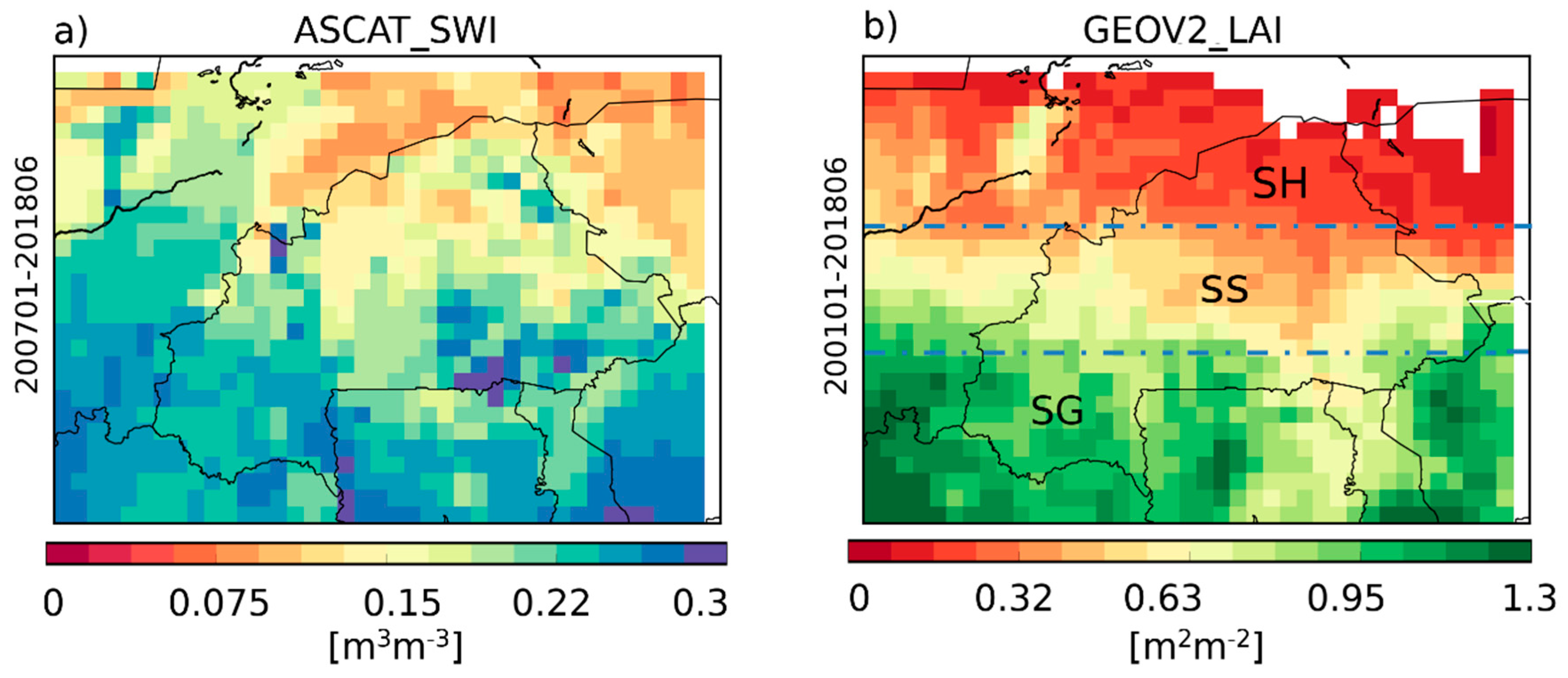
2.2.3. ASCAT Soil Water Index and GEOV2 Leaf Area Index
2.2.4. Evapotranspiration, Gross Primary Production, and Sun-Induced Fluorescence
2.3. Experimental Setup and Evaluation Strategies
3. Results
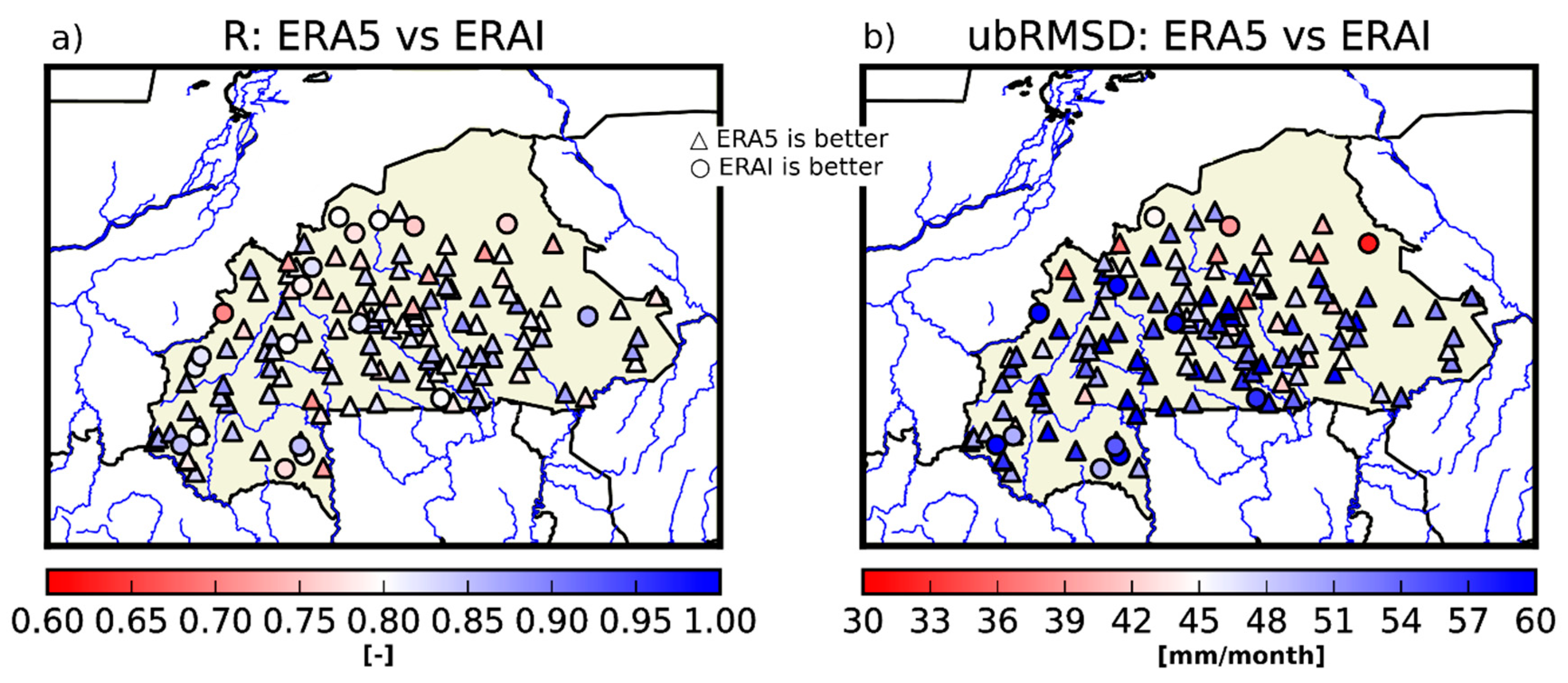
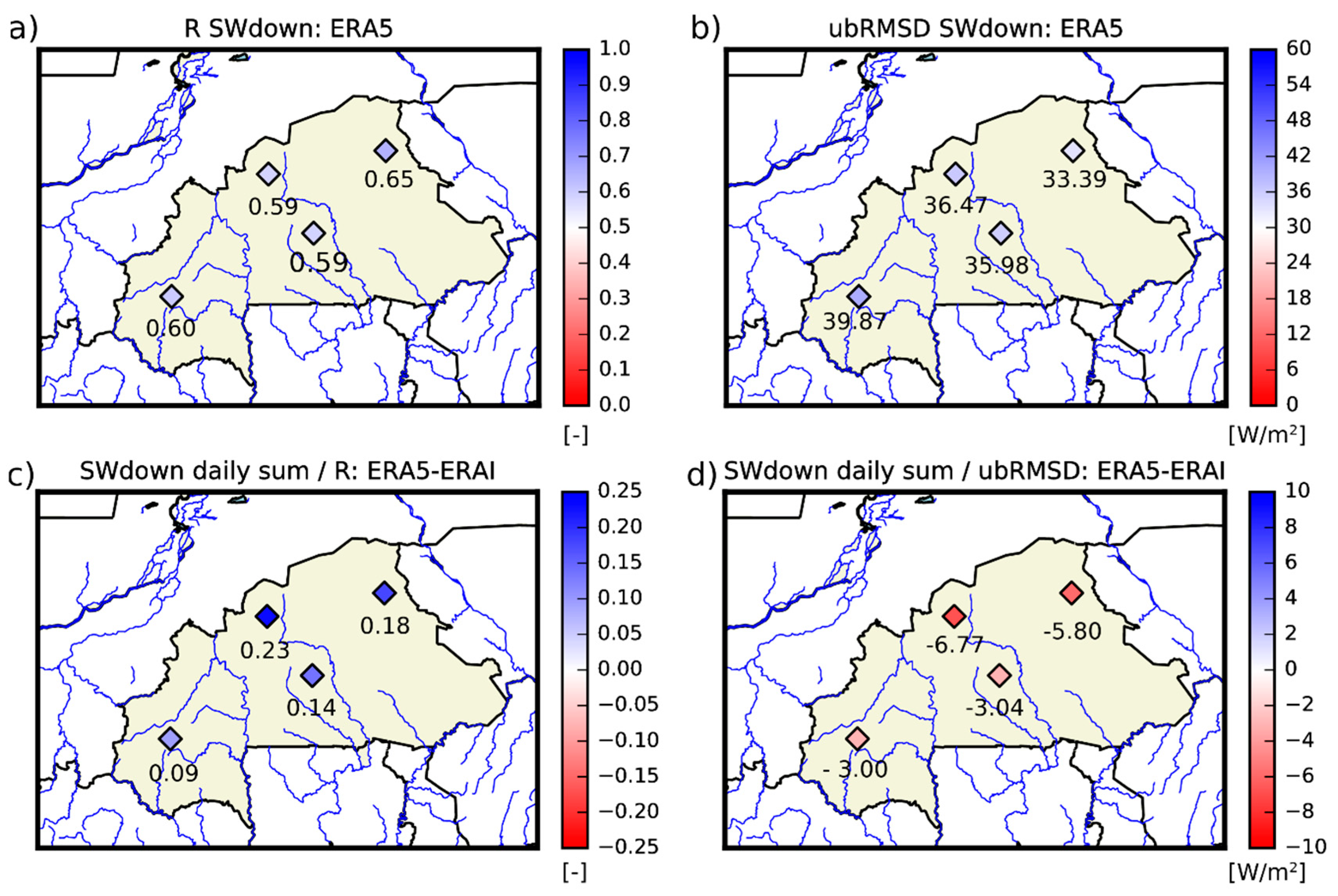
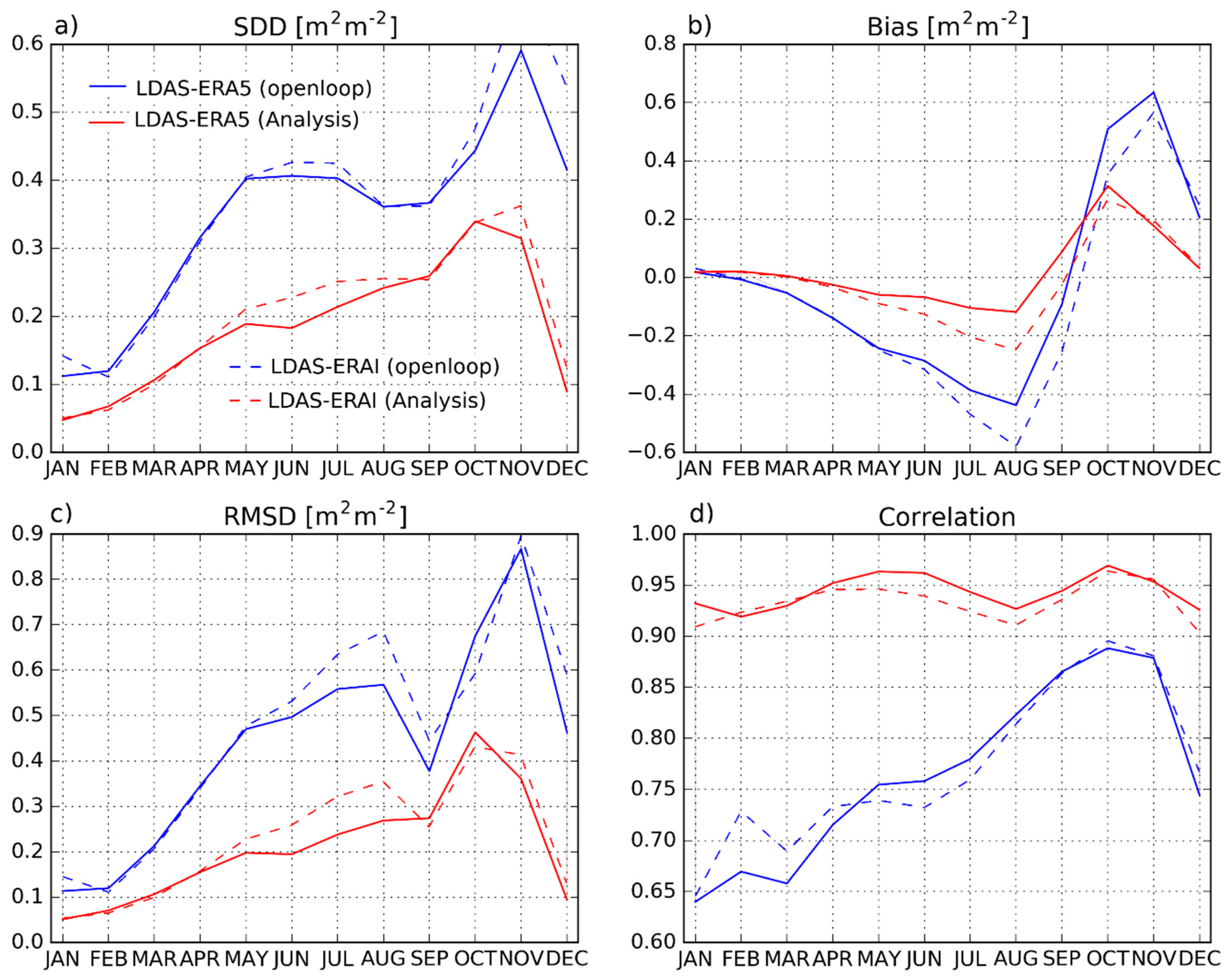
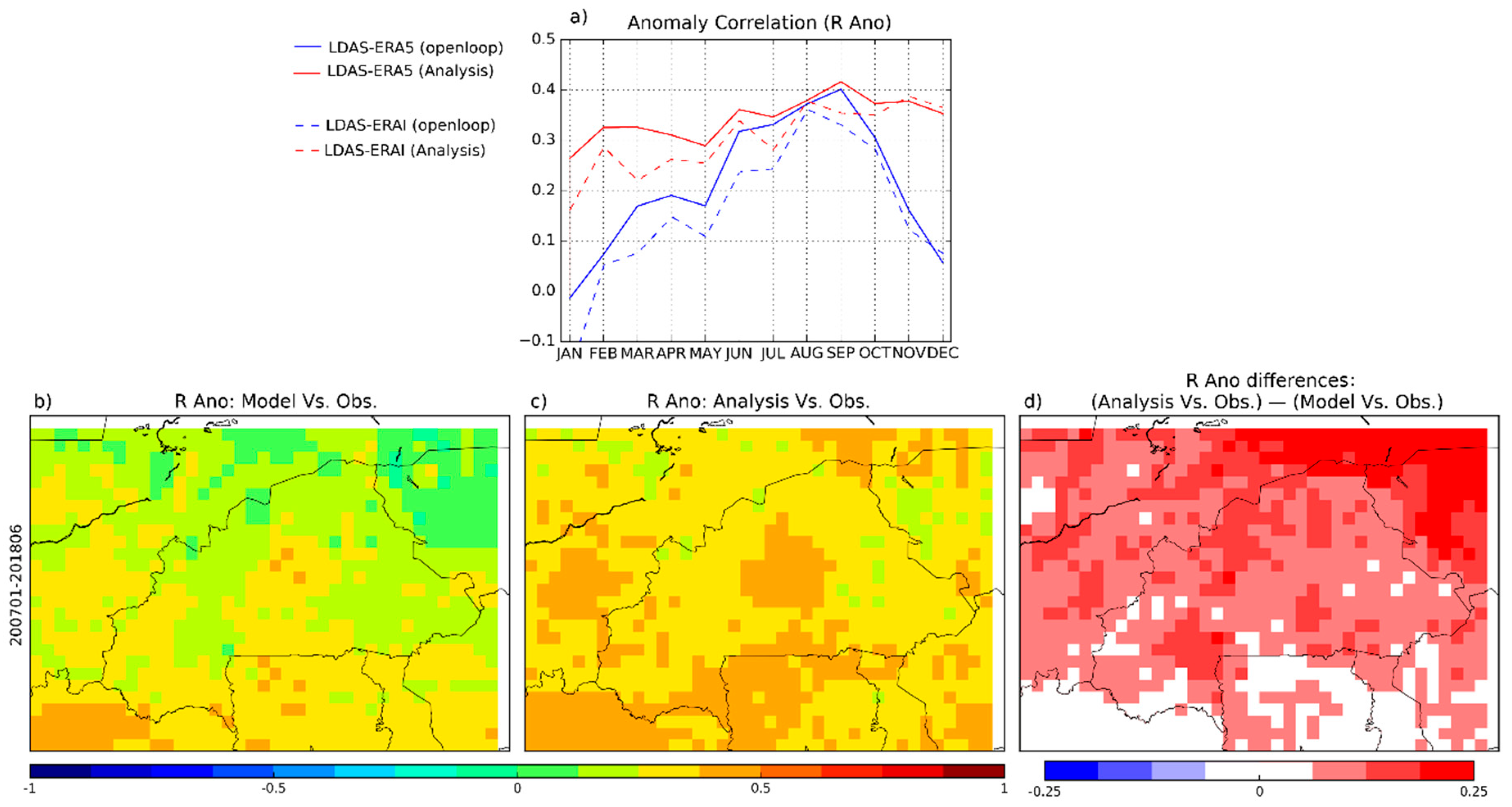
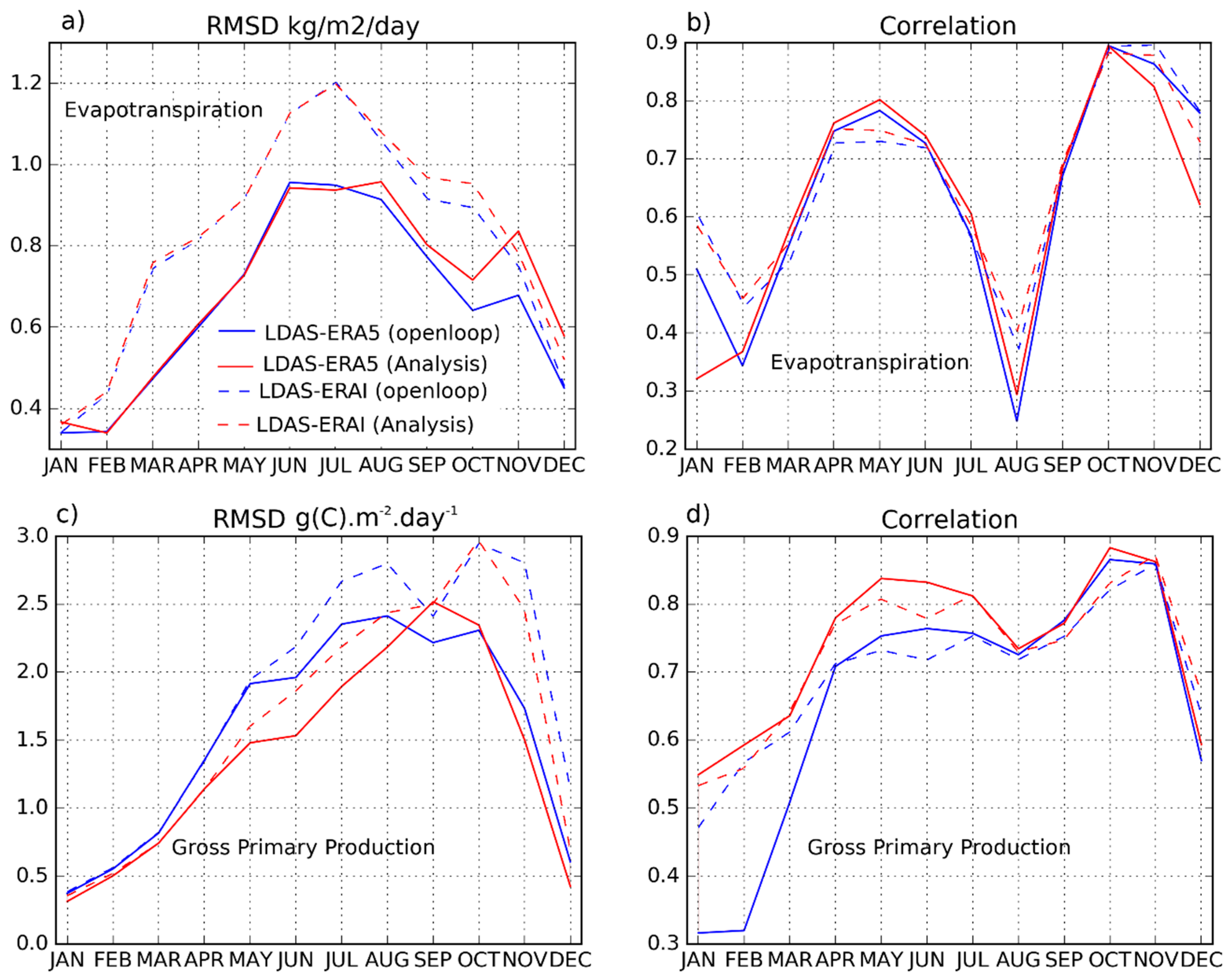
3.1. Evaluation of ERA5 and ERA-Interim Reanalyses
3.2. LDAS-Monde Impact
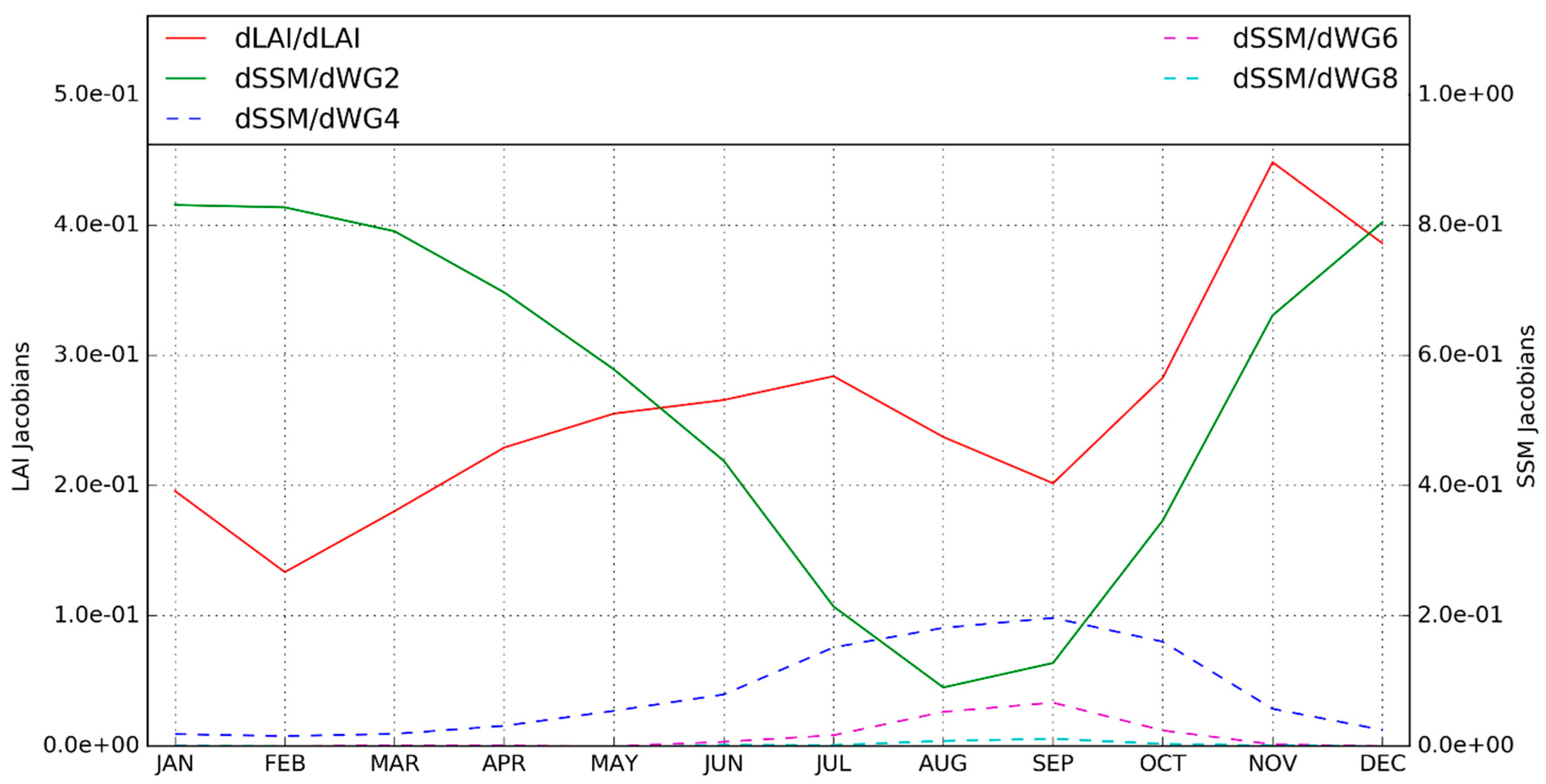
3.2.1. Model Sensitivity to the Observations
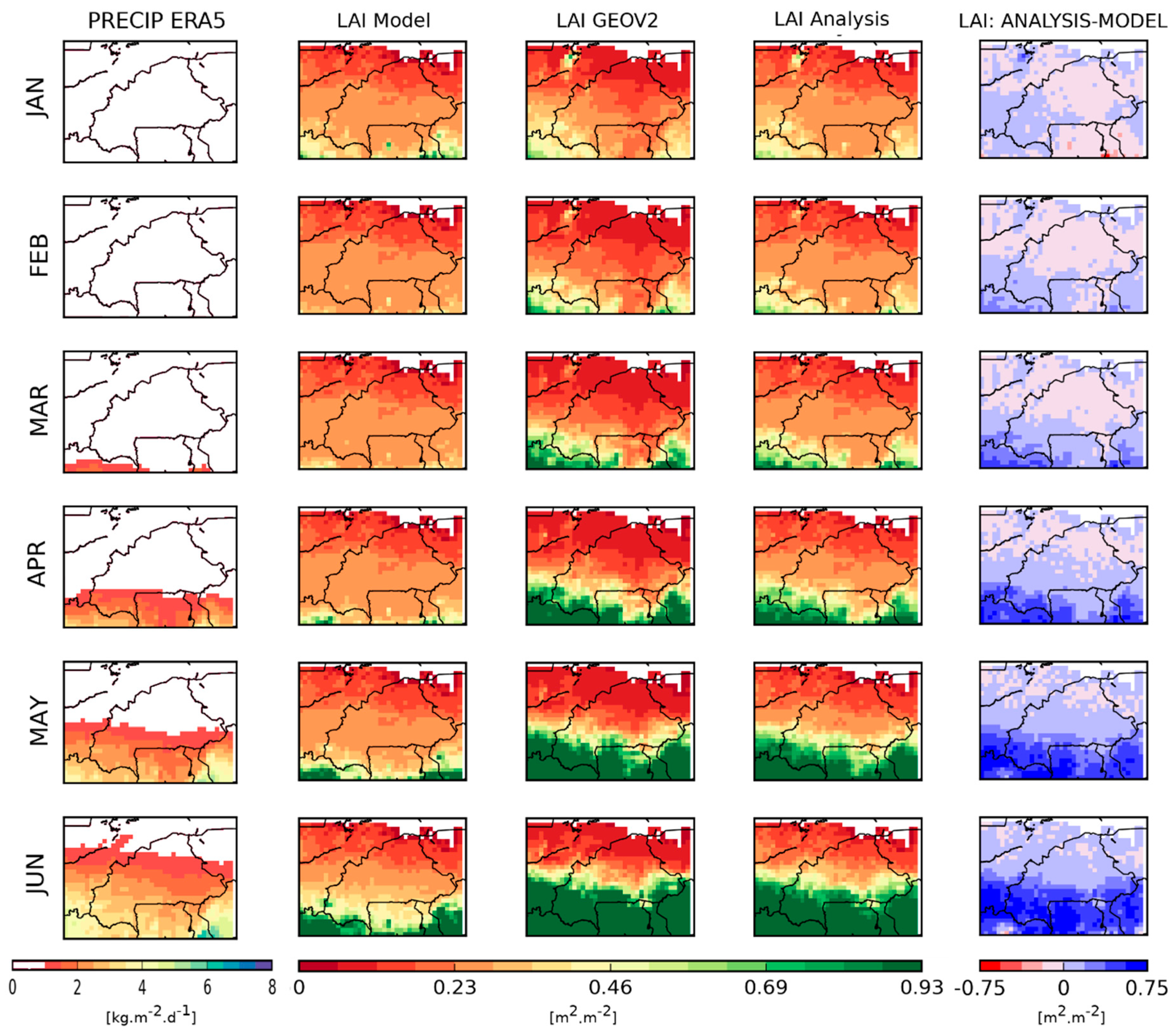
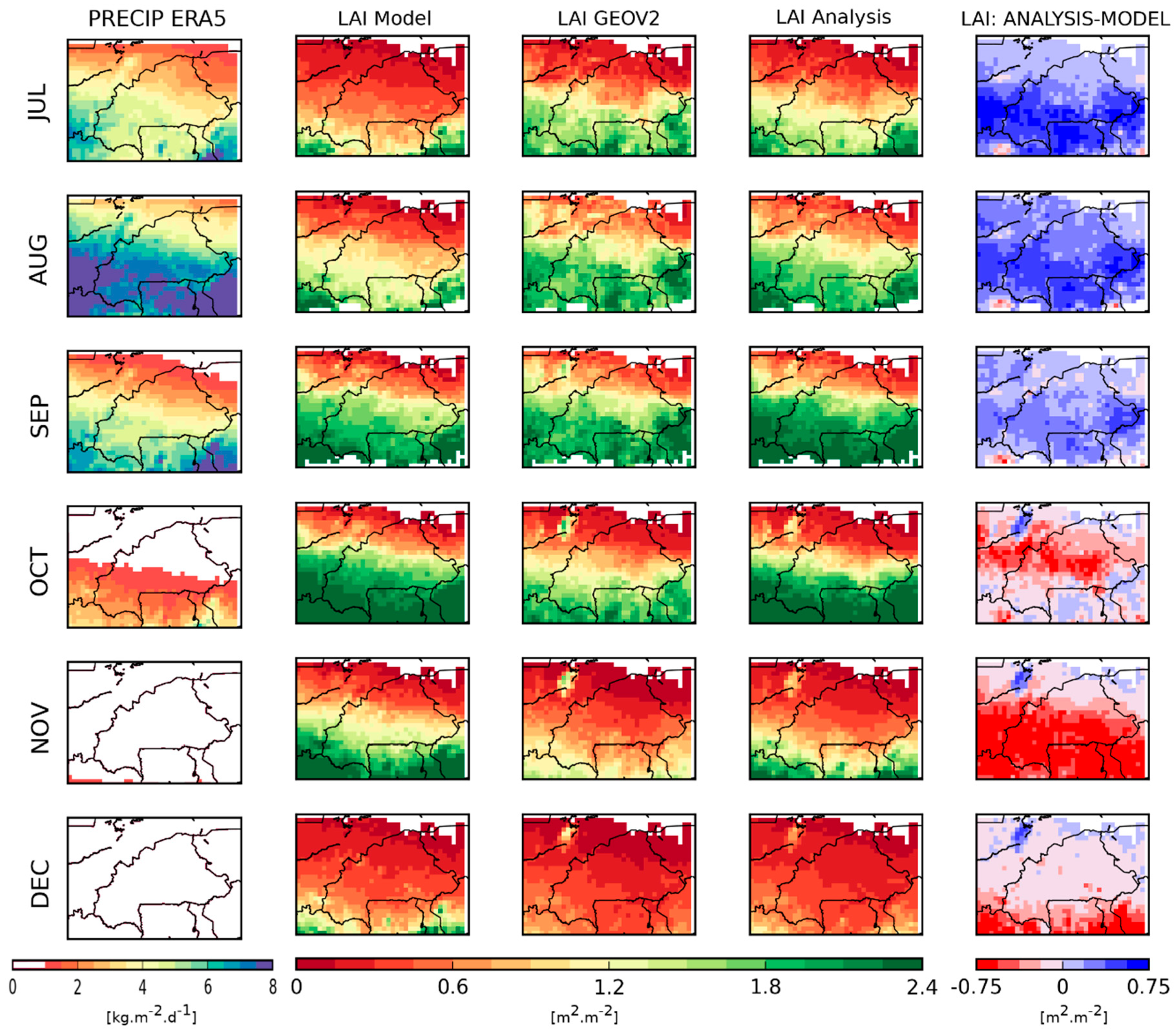
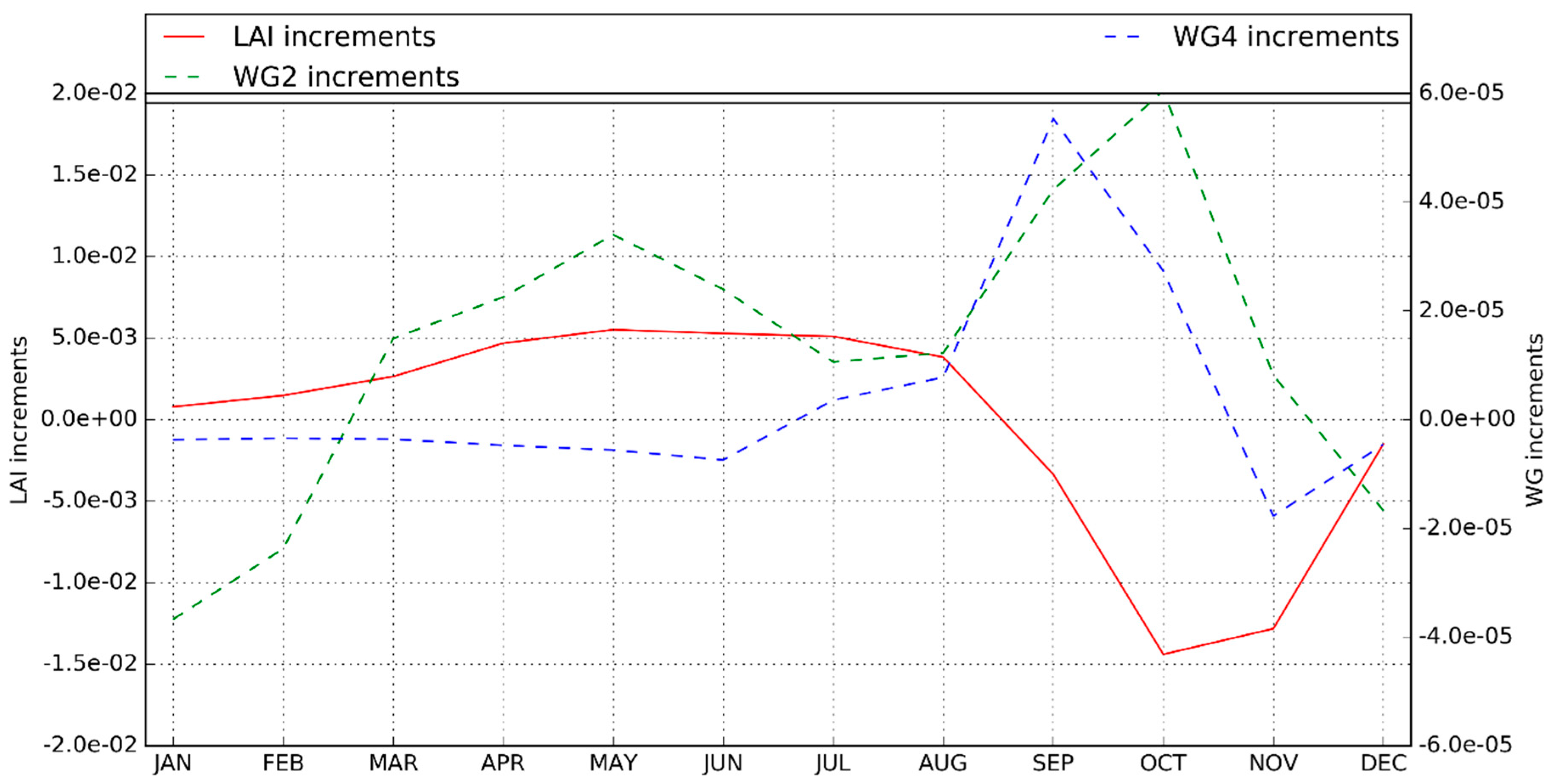
3.2.2. Assimilation Impact on LAI and Soil Moisture
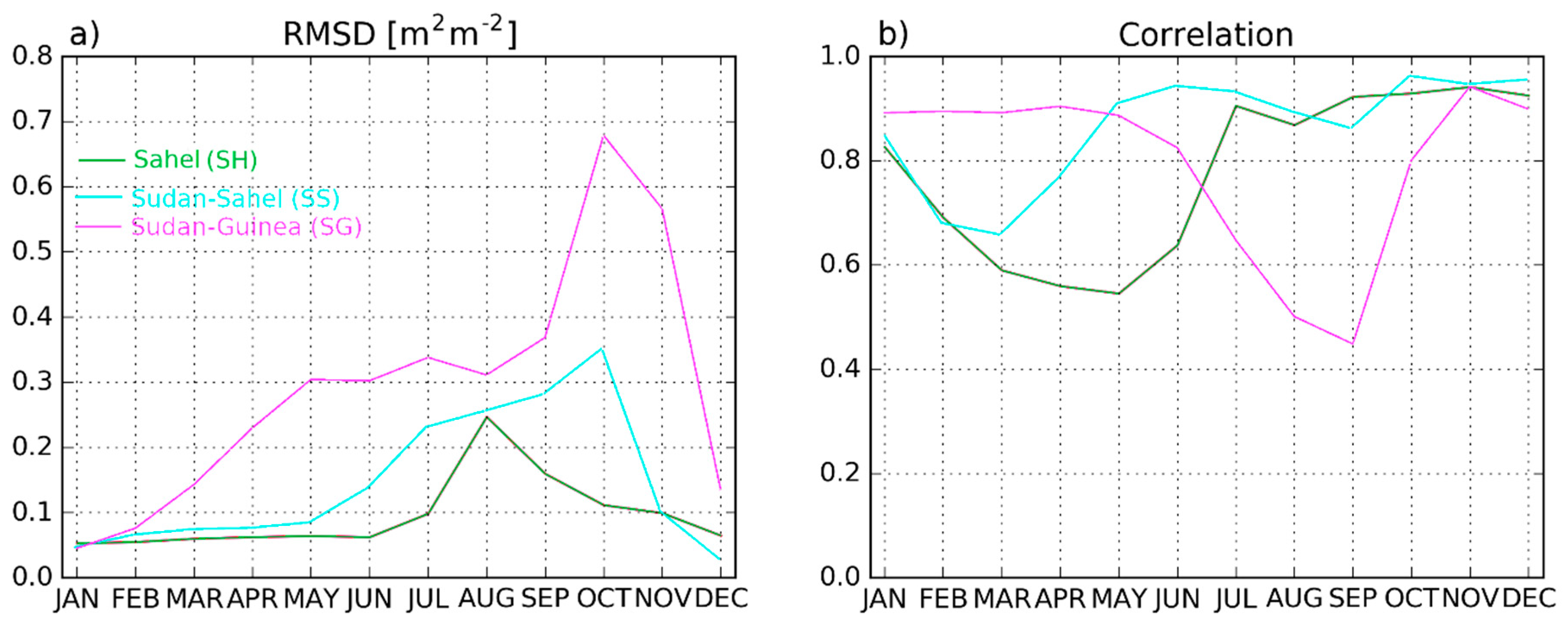
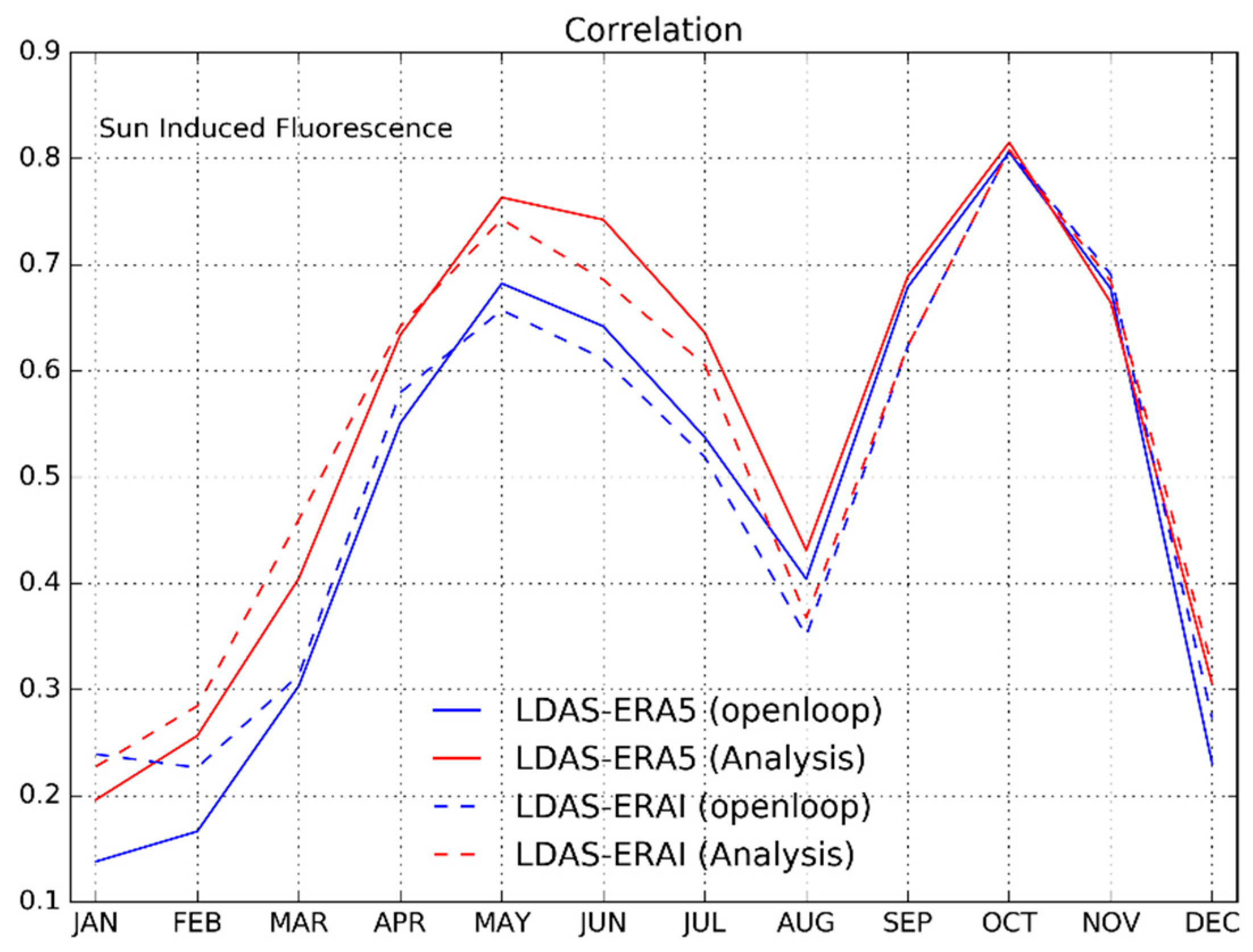
3.2.3. Evaluation Using Independent Datasets
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Rodell, M.; Houser, P.R.; Jambor, U.E.A.; Gottschalck, J.; Mitchell, K.; Meng, C.-J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M. The global land data assimilation system. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef]
- Schellekens, J.; Dutra, E.; Martínez-de la Torre, A.; Balsamo, G.; van Dijk, A.; Weiland, F.S.; Minvielle, M.; Calvet, J.-C.; Decharme, B.; Eisner, S. A global water resources ensemble of hydrological models: The eartH2Observe Tier-1 dataset. Earth Syst. Sci. Data 2017, 9, 389–413. [Google Scholar] [CrossRef]
- Dirmeyer, P.A.; Gao, X.; Zhao, M.; Guo, Z.; Oki, T.; Hanasaki, N. GSWP-2: Multimodel analysis and implications for our perception of the land surface. Bull. Am. Meteorol. Soc. 2006, 87, 1381–1398. [Google Scholar] [CrossRef]
- Albergel, C.; Dutra, E.; Munier, S.; Calvet, J.-C.; Munoz-Sabater, J.; de Rosnay, P.; Balsamo, G. ERA-5 and ERA-Interim driven ISBA land surface model simulations: Which one performs better? Hydrol. Earth Syst. Sci. 2018, 22, 3515–3532. [Google Scholar] [CrossRef]
- Boone, A.; De Rosnay, P.; Balsamo, G.; Beljaars, A.; Chopin, F.; Decharme, B.; Delire, C.; Ducharne, A.; Gascoin, S.; Grippa, M. The AMMA land surface model intercomparison project (ALMIP). Bull. Am. Meteorol. Soc. 2009, 90, 1865–1880. [Google Scholar] [CrossRef]
- Boone, A.; Getirana, A.C.; Demarty, J.; Cappelaere, B.; Galle, S.; Grippa, M.; Lebel, T.; Mougin, E.; Peugeot, C.; Vischel, T. The african monsoon multidisciplinary analyses (AMMA) land surface model intercomparison project phase 2 (ALMIP2). GEWEX News 2009, 19, 9–10. [Google Scholar]
- Koster, R.D.; Guo, Z.; Yang, R.; Dirmeyer, P.A.; Mitchell, K.; Puma, M.J. On the nature of soil moisture in land surface models. J. Clim. 2009, 22, 4322–4335. [Google Scholar] [CrossRef]
- Koster, R.D.; Mahanama, S.P.P.; Yamada, T.J.; Balsamo, G.; Berg, A.A.; Boisserie, M.; Dirmeyer, P.A.; Doblas-Reyes, F.J.; Drewitt, G.; Gordon, C.T. The second phase of the global land–atmosphere coupling experiment: Soil moisture contributions to subseasonal forecast skill. J. Hydrometeorol. 2011, 12, 805–822. [Google Scholar] [CrossRef]
- Diallo, F.B.; Hourdin, F.; Rio, C.; Traore, A.-K.; Mellul, L.; Guichard, F.; Kergoat, L. The surface energy budget computed at the grid-scale of a climate model challenged by station data in West Africa. J. Adv. Model. Earth Syst. 2017, 9, 2710–2738. [Google Scholar] [CrossRef]
- Charney, J.G. Dynamics of deserts and drought in the Sahel. Q. J. R. Meteorol. Soc. 1975, 101, 193–202. [Google Scholar] [CrossRef]
- Taylor, C.M.; Gounou, A.; Guichard, F.; Harris, P.P.; Ellis, R.J.; Couvreux, F.; De Kauwe, M. Frequency of Sahelian storm initiation enhanced over mesoscale soil-moisture patterns. Nat. Geosci. 2011, 4, 430–433. [Google Scholar] [CrossRef]
- Reichle, R.H.; Koster, R.D.; Liu, P.; Mahanama, S.P.; Njoku, E.G.; Owe, M. Comparison and assimilation of global soil moisture retrievals from the advanced microwave scanning radiometer for the Earth observing system (AMSR-E) and the scanning multichannel microwave radiometer (SMMR). J. Geophys. Res. Atmos. 2007, 112. [Google Scholar] [CrossRef]
- Lahoz, W.A.; De Lannoy, G.J. Closing the gaps in our knowledge of the hydrological cycle over land: Conceptual problems. Surv. Geophys 2014, 35, 623–660. [Google Scholar] [CrossRef]
- Kaminski, T.; Knorr, W.; Rayner, P.J.; Heimann, M. Assimilating atmospheric data into a terrestrial biosphere model: A case study of the seasonal cycle. Glob. Biogeochem. Cycles 2002, 16, 14-1–14-16. [Google Scholar] [CrossRef]
- Sawada, Y.; Koike, T. Simultaneous estimation of both hydrological and ecological parameters in an ecohydrological model by assimilating microwave signal. J. Geophys. Res. Atmos. 2014, 119, 8839–8857. [Google Scholar] [CrossRef]
- Sawada, Y.; Koike, T.; Walker, J.P. A land data assimilation system for simultaneous simulation of soil moisture and vegetation dynamics. J. Geophys. Res. Atmos. 2015, 120, 5910–5930. [Google Scholar] [CrossRef]
- Sawada, Y. Quantifying drought propagation from soil moisture to vegetation dynamics using a newly developed ecohydrological land reanalysis. Remote Sens. 2018, 10, 1197. [Google Scholar] [CrossRef]
- Kumar, S.V.; Jasinski, M.; Mocko, D.; Rodell, M.; Borak, J.; LI, B.; Kato Beaudoing, H.; Peters-Lidard, C.D. NCA-LDAS land analysis: Development and performance of a multisensor, multivariate land data assimilation system for the National Climate Assessment. J. Hydrometeorol. 2018. [Google Scholar] [CrossRef]
- Albergel, C.; Munier, S.; Leroux, D.J.; Dewaele, H.; Fairbairn, D.; Barbu, A.L.; Gelati, E.; Dorigo, W.; Faroux, S.; Meurey, C. Sequential assimilation of satellite-derived vegetation and soil moisture products using SURFEX_v8. 0: LDAS-Monde assessment over the Euro-Mediterranean area. Geosci. Model Dev. 2017, 10, 3889–3912. [Google Scholar] [CrossRef]
- Yin, J.; Zhan, X.; Liu, J.; Schull, M. An Inter-comparison of Noah model skills with benefits of assimilating SMOPS blended and individual soil moisture retrievals. Water Resour. Res. 2019. [Google Scholar] [CrossRef]
- Pinnington, E.; Quaife, T.; Black, E. Impact of remotely sensed soil moisture and precipitation on soil moisture prediction in a data assimilation system with the JULES land surface model. Hydrol. Earth Syst. Sci. 2018, 22, 2575–2588. [Google Scholar] [CrossRef]
- Waongo, M.; Laux, P.; Traoré, S.B.; Sanon, M.; Kunstmann, H. A crop model and fuzzy rule based approach for optimizing maize planting dates in Burkina Faso, West Africa. J. Appl. Meteorol. Climatol. 2014, 53, 598–613. [Google Scholar] [CrossRef]
- Sivakumar, M.V.; Gnoumou, F. Agroclimatology of West Africa: Burkina Faso; International Crops Research Institute for the Semi-Arid Tropics: Hyderabad, India, 1987; ISBN 92-9066-122-4. [Google Scholar]
- Noilhan, J.; Mahfouf, J.-F. The ISBA land surface parameterisation scheme. Glob. Planet. Chang. 1996, 13, 145–159. [Google Scholar] [CrossRef]
- Calvet, J.-C.; Noilhan, J.; Roujean, J.-L.; Bessemoulin, P.; Cabelguenne, M.; Olioso, A.; Wigneron, J.-P. An interactive vegetation SVAT model tested against data from six contrasting sites. Agric. For. Meteorol. 1998, 92, 73–95. [Google Scholar] [CrossRef]
- Calvet, J.-C.; Rivalland, V.; Picon-Cochard, C.; Guehl, J.-M. Modelling forest transpiration and CO2 fluxes—Response to soil moisture stress. Agric. For. Meteorol. 2004, 124, 143–156. [Google Scholar] [CrossRef]
- Gibelin, A.-L.; Calvet, J.-C.; Roujean, J.-L.; Jarlan, L.; Los, S.O. Ability of the land surface model ISBA-A-gs to simulate leaf area index at the global scale: Comparison with satellites products. J. Geophys. Res. Atmos. 2006, 111. [Google Scholar] [CrossRef]
- Masson, V.; Le Moigne, P.; Martin, E.; Faroux, S.; Alias, A.; Alkama, R.; Belamari, S.; Barbu, A.; Boone, A.; Bouyssel, F. The SURFEXv7. 2 land and ocean surface platform for coupled or offline simulation of earth surface variables and fluxes. Geosci. Model Dev. 2013, 6, 929–960. [Google Scholar] [CrossRef]
- Wagner, W.; Hahn, S.; Kidd, R.; Melzer, T.; Bartalis, Z.; Hasenauer, S.; Figa-Saldaña, J.; de Rosnay, P.; Jann, A.; Schneider, S. The ASCAT soil moisture product: A review of its specifications, validation results, and emerging applications. Meteorol. Z. 2013, 22, 5–33. [Google Scholar] [CrossRef]
- Balsamo, G.; Albergel, C.; Beljaars, A.; Boussetta, S.; Brun, E.; Cloke, H.; Dee, D.; Dutra, E.; Muñoz-Sabater, J.; Pappenberger, F. ERA-Interim/Land: A global land surface reanalysis data set. Hydrol. Earth Syst. Sci. 2015, 19, 389–407. [Google Scholar] [CrossRef]
- Balsamo, G.; Agusti-Panareda, A.; Albergel, C.; Arduini, G.; Beljaars, A.; Bidlot, J.; Bousserez, N.; Boussetta, S.; Brown, A.; Buizza, R. Satellite and in situ observations for advancing global Earth surface modelling: A Review. Remote Sens. 2018, 10, 2038. [Google Scholar] [CrossRef]
- Rienecker, M.M.; Suarez, M.J.; Gelaro, R.; Todling, R.; Bacmeister, J.; Liu, E.; Bosilovich, M.G.; Schubert, S.D.; Takacs, L.; Kim, G.-K. MERRA: NASA’s modern-era retrospective analysis for research and applications. J. Clim. 2011, 24, 3624–3648. [Google Scholar] [CrossRef]
- Gelaro, R.; McCarty, W.; Suárez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.A.; Darmenov, A.; Bosilovich, M.G.; Reichle, R. The modern-era retrospective analysis for research and applications, version 2 (MERRA-2). J. Clim. 2017, 30, 5419–5454. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, D.P. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Beck, H.E.; Pan, M.; Roy, T.; Weedon, G.P.; Pappenberger, F.; van Dijk, A.; Huffman, G.J.; Adler, R.F.; Wood, E.F. Daily evaluation of 26 precipitation datasets using Stage-IV gauge-radar data for the CONUS. Hydrol. Earth Syst. Sci. Discuss 2019, 23, 207–214. [Google Scholar] [CrossRef]
- Urraca, R.; Huld, T.; Gracia-Amillo, A.; Martinez-de-Pison, F.J.; Kaspar, F.; Sanz-Garcia, A. Evaluation of global horizontal irradiance estimates from ERA5 and COSMO-REA6 reanalyses using ground and satellite-based data. Sol. Energy 2018, 164, 339–354. [Google Scholar] [CrossRef]
- Barbu, A.L.; Calvet, J.-C.; Mahfouf, J.-F.; Lafont, S. Integrating ASCAT surface soil moisture and GEOV1 leaf area index into the SURFEX modelling platform: A land data assimilation application over France. Hydrol. Earth Syst. Sci. 2014, 18, 173–192. [Google Scholar] [CrossRef]
- Mahfouf, J.-F.; Bergaoui, K.; Draper, C.; Bouyssel, F.; Taillefer, F.; Taseva, L. A comparison of two off-line soil analysis schemes for assimilation of screen level observations. J. Geophys. Res. Atmos. 2009, 114. [Google Scholar] [CrossRef]
- Albergel, C.; Calvet, J.-C.; De Rosnay, P.; Balsamo, G.; Wagner, W.; Hasenauer, S.; Naeimi, V.; Martin, E.; Bazile, E.; Bouyssel, F. Cross-evaluation of modelled and remotely sensed surface soil moisture with in situ data in southwestern France. Hydrol. Earth Syst. Sci. 2010, 14, 2177–2191. [Google Scholar] [CrossRef]
- Barbu, A.L.; Calvet, J.-C.; Mahfouf, J.-F.; Albergel, C.; Lafont, S. Assimilation of soil wetness index and leaf area index into the ISBA-A-gs land surface model: Grassland case study. Biogeosciences 2011, 8, 1971–1986. [Google Scholar] [CrossRef]
- Fairbairn, D.; Barbu, A.L.; Napoly, A.; Albergel, C.; Mahfouf, J.-F.; Calvet, J.-C. The effect of satellite-derived surface soil moisture and leaf area index land data assimilation on streamflow simulations over France. Hydrol. Earth Syst. Sci. 2017, 21, 2015–2033. [Google Scholar] [CrossRef]
- Albergel, C.; Munier, S.; Bocher, A.; Bonan, B.; Zheng, Y.; Draper, C.; Leroux, D.; Calvet, J.-C. LDAS-Monde sequential assimilation of satellite derived observations applied to the contiguous US: An ERA-5 driven reanalysis of the land surface variables. Remote Sens. 2018, 10, 1627. [Google Scholar] [CrossRef]
- Leroux, D.; Calvet, J.-C.; Munier, S.; Albergel, C. Using satellite-derived vegetation products to evaluate LDAS-monde over the Euro-Mediterranean area. Remote Sens. 2018, 10, 1199. [Google Scholar] [CrossRef]
- Boone, A.; Masson, V.; Meyers, T.; Noilhan, J. The influence of the inclusion of soil freezing on simulations by a soil-vegetation-atmosphere transfer scheme. J. Appl. Meteorol. 2000, 39, 1544–1569. [Google Scholar] [CrossRef]
- Decharme, B.; Martin, E.; Faroux, S. Reconciling soil thermal and hydrological lower boundary conditions in land surface models. J. Geophys. Res. Atmos. 2013, 118, 7819–7834. [Google Scholar] [CrossRef]
- Faroux, S.; Kaptué Tchuenté, A.T.; Roujean, J.-L.; Masson, V.; Martin, E.; Moigne, P.L. ECOCLIMAP-II/Europe: A twofold database of ecosystems and surface parameters at 1 km resolution based on satellite information for use in land surface, meteorological and climate models. Geosci. Model Dev. 2013, 6, 563–582. [Google Scholar] [CrossRef]
- Draper, C.; Mahfouf, J.-F.; Calvet, J.-C.; Martin, E.; Wagner, W. Assimilation of ASCAT near-surface soil moisture into the SIM hydrological model over France. Hydrol. Earth Syst. Sci. 2011, 15, 3829–3841. [Google Scholar] [CrossRef]
- De Jeu, R.A.; Wagner, W.; Holmes, T.R.H.; Dolman, A.J.; Van De Giesen, N.C.; Friesen, J. Global soil moisture patterns observed by space borne microwave radiometers and scatterometers. Surv. Geophys. 2008, 29, 399–420. [Google Scholar] [CrossRef]
- Gruber, A.; Su, C.-H.; Zwieback, S.; Crow, W.; Dorigo, W.; Wagner, W. Recent advances in (soil moisture) triple collocation analysis. Int. J. Appl. Earth Obs. Geoinf. 2016, 45, 200–211. [Google Scholar] [CrossRef]
- Berrisford, P.; Dee, D.; Fielding, K.; Fuentes, M.; Kallberg, P.; Kobayashi, S.; Uppala, S. The ERA-interim archive; ERA Report Series; ERA: Shinfield Park, UK, 2009; pp. 1–16. [Google Scholar]
- Hersbach, H.; Dee, D. ERA5 reanalysis is in production. ECMWF Newsletters. April 2016. Number 147. Available online: https://www.ecmwf.int/en/newsletter/147/news/era5-reanalysis-production (accessed on 26 March 2019).
- Albergel, C.; Rüdiger, C.; Pellarin, T.; Calvet, J.-C.; Fritz, N.; Froissard, F.; Suquia, D.; Petitpa, A.; Piguet, B.; Martin, E. From near-surface to root-zone soil moisture using an exponential filter: An assessment of the method based on in-situ observations and model simulations. Hydrol. Earth Syst. Sci. 2008, 12, 1323–1337. [Google Scholar] [CrossRef]
- Bartalis, Z.; Wagner, W.; Naeimi, V.; Hasenauer, S.; Scipal, K.; Bonekamp, H.; Figa, J.; Anderson, C. Initial soil moisture retrievals from the METOP-A advanced scatterometer (ASCAT). Geophys. Res. Lett. 2007, 34, L20401. [Google Scholar] [CrossRef]
- Reichle, R.H.; Koster, R.D. Bias reduction in short records of satellite soil moisture. Geophys. Res. Lett. 2004, 31, L19501. [Google Scholar] [CrossRef]
- Owe, M.; de Jeu, R.; Holmes, T. Multisensor historical climatology of satellite-derived global land surface moisture. J. Geophys. Res. Earth Surf. 2008, 113, F01002. [Google Scholar] [CrossRef]
- Haas, E.M.; Bartholomé, E.; Combal, B. Time series analysis of optical remote sensing data for the mapping of temporary surface water bodies in Sub-Saharan Western Africa. J. Hydrol. 2009, 370, 52–63. [Google Scholar] [CrossRef]
- Tappan, G.G.; Cushing, W.M.; Cotillon, S.E.; Mathis, M.L.; Hutchinson, J.A.; Dalsted, K.J. West Africa Land Use Land Cover Time Series; U.S. Geological Survey: Reston, VA, USA, 2016.
- Drusch, M.; Wood, E.F.; Gao, H. Observation operators for the direct assimilation of TRMM microwave imager retrieved soil moisture. Geophys. Res. Lett. 2005, 32, L15403. [Google Scholar] [CrossRef]
- Scipal, K.; Drusch, M.; Wagner, W. Assimilation of a ERS scatterometer derived soil moisture index in the ECMWF numerical weather prediction system. Adv. Water Resour. 2008, 31, 1101–1112. [Google Scholar] [CrossRef]
- Verger, A.; Baret, F.; Weiss, M. Near real-time vegetation monitoring at global scale. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 3473–3481. [Google Scholar] [CrossRef]
- Martens, B.; Gonzalez Miralles, D.; Lievens, H.; Van Der Schalie, R.; De Jeu, R.A.; Fernández-Prieto, D.; Beck, H.E.; Dorigo, W.; Verhoest, N. GLEAM v3: Satellite-based land evaporation and root-zone soil moisture. Geosci. Model Dev. 2017, 10, 1903–1925. [Google Scholar] [CrossRef]
- Greve, P.; Orlowsky, B.; Mueller, B.; Sheffield, J.; Reichstein, M.; Seneviratne, S.I. Global assessment of trends in wetting and drying over land. Nat. Geosci. 2014, 7, 716–721. [Google Scholar] [CrossRef]
- Miralles, D.G.; Teuling, A.J.; Van Heerwaarden, C.C.; de Arellano, J.V.-G. Mega-heatwave temperatures due to combined soil desiccation and atmospheric heat accumulation. Nat. Geosci. 2014, 7, 345–349. [Google Scholar] [CrossRef]
- Zhang, Y.; Peña-Arancibia, J.L.; McVicar, T.R.; Chiew, F.H.; Vaze, J.; Liu, C.; Lu, X.; Zheng, H.; Wang, Y.; Liu, Y.Y. Multi-decadal trends in global terrestrial evapotranspiration and its components. Sci. Rep. 2016, 6, 19124. [Google Scholar] [CrossRef] [PubMed]
- Miralles, D.G.; Van Den Berg, M.J.; Gash, J.H.; Parinussa, R.M.; De Jeu, R.A.; Beck, H.E.; Holmes, T.R.; Jiménez, C.; Verhoest, N.E.; Dorigo, W.A. El Niño-La Niña cycle and recent trends in continental evaporation. Nat. Clim. Chang. 2014, 4, 122–126. [Google Scholar] [CrossRef]
- Guillod, B.P.; Orlowsky, B.; Miralles, D.G.; Teuling, A.J.; Seneviratne, S.I. Reconciling spatial and temporal soil moisture effects on afternoon rainfall. Nat. Commun. 2015, 6, 6443. [Google Scholar] [CrossRef] [PubMed]
- Jung, M.; Reichstein, M.; Schwalm, C.R.; Huntingford, C.; Sitch, S.; Ahlström, A.; Arneth, A.; Camps-Valls, G.; Ciais, P.; Friedlingstein, P. Compensatory water effects link yearly global land CO2 sink changes to temperature. Nature 2017, 541, 516–520. [Google Scholar] [CrossRef] [PubMed]
- Munro, R.; Eisinger, M.; Anderson, C.; Callies, J.; Corpaccioli, E.; Lang, R.; Lefebvre, A.; Livschitz, Y.; Perez Albinana, A. GOME-2 on MetOp: From In-Orbit Verification to Routine Operations. In Proceedings of the EUMETSAT Meteorological Satellite Conference, Helsinki, Finland, 12–16 June 2006. [Google Scholar]
- Joiner, J.; Yoshida, Y.; Guanter, L.; Middleton, E.M. New methods for the retrieval of chlorophyll red fluorescence from hyperspectral satellite instruments: Simulations and application to GOME-2 and SCIAMACHY. Atmos. Meas. Tech. 2016, 9, 3939–3967. [Google Scholar] [CrossRef]
- Bechtold, P. Convection in Global Numerical Weather Prediction. In Parameterization of Atmospheric Convection: Volume 2: Current Issues and New Theories; World Scientific: Singapore, 2016; pp. 5–45. [Google Scholar]
- Guichard, F.; Kergoat, L.; Mougin, E.; Timouk, F.; Baup, F.; Hiernaux, P.; Lavenu, F. Surface thermodynamics and radiative budget in the Sahelian Gourma: Seasonal and diurnal cycles. J. Hydrol. 2009, 375, 161–177. [Google Scholar] [CrossRef]
- Slingo, A.; White, H.E.; Bharmal, N.A.; Robinson, G.J. Overview of observations from the RADAGAST experiment in Niamey, Niger: 2. Radiative fluxes and divergences. J. Geophys. Res. Atmos. 2009, 114. [Google Scholar] [CrossRef]
- Agustí-Panareda, A.; Beljaars, A.; Ahlgrimm, M.; Balsamo, G.; Bock, O.; Forbes, R.; Ghelli, A.; Guichard, F.; Köhler, M.; Meynadier, R. The ECMWF re-analysis for the AMMA observational campaign. Q. J. R. Meteorol. Soc. 2010, 136, 1457–1472. [Google Scholar] [CrossRef]
- Hogan, R.J.; Bozzo, A. A flexible and efficient radiation scheme for the ECMWF model. J. Adv. Model. Earth Syst. 2018, 10, 1990–2008. [Google Scholar] [CrossRef]
- Rüdiger, C.; Albergel, C.; Mahfouf, J.-F.; Calvet, J.-C.; Walker, J.P. Evaluation of Jacobians for leaf area index data assimilation with an extended Kalman filter. J. Geophys. Res. 2010. [Google Scholar] [CrossRef]
- Shackleton, C.M. Rainfall and topo-edaphic influences on woody community phenology in South African savannas. Glob. Ecol. Biogeogr. 1999, 8, 125–136. [Google Scholar] [CrossRef]
- Seghieri, J.; Vescovo, A.; Padel, K.; Soubie, R.; Arjounin, M.; Boulain, N.; De Rosnay, P.; Galle, S.; Gosset, M.; Mouctar, A.H. Relationships between climate, soil moisture and phenology of the woody cover in two sites located along the West African latitudinal gradient. J. Hydrol. 2009, 375, 78–89. [Google Scholar] [CrossRef]
- Awessou, B.K.; Peugeot, C.; Agbossou, E.K.; Seghieri, J. Consommation en eau d’une Espèce Agroforestière en Zone Soudanienne; Agropolis: Montpellier, France, 2017. [Google Scholar]
- Peugeot, C. (HSM, IRD, Univ. Montpellier, CNRS, 34000 Montpellier, France). Personal communication, 2018.
- Pierre, C.; Grippa, M.; Mougin, E.; Guichard, F.; Kergoat, L. Changes in Sahelian annual vegetation growth and phenology since 1960: A modeling approach. Glob. Planet. Chang. 2016, 143, 162–174. [Google Scholar] [CrossRef]
- Kergoat, L.; Guichard, F.; Pierre, C.; Vassal, C. Influence of dry-season vegetation variability on Sahelian dust during 2002–2015. Geophys. Res. Lett. 2017, 44, 5231–5239. [Google Scholar] [CrossRef]
- Pagán, B.R.; Maes, W.H.; Gentine, P.; Martens, B.; Miralles, D.G. Exploring the potential of satellite solar-induced fluorescence to constrain global transpiration estimates. Remote Sens. 2019, 11, 413. [Google Scholar] [CrossRef]
- Munier, S.; Carrer, D.; Planque, C.; Camacho, F.; Albergel, C.; Calvet, J.-C. Satellite leaf area index: Global scale analysis of the tendencies per vegetation type over the last 17 years. Remote Sens. 2018, 10, 424. [Google Scholar] [CrossRef]
- Lievens, H.; De Lannoy, G.J.M.; Al Bitar, A.; Drusch, M.; Dumedah, G.; Franssen, H.-J.H.; Kerr, Y.H.; Tomer, S.K.; Martens, B.; Merlin, O. Assimilation of SMOS soil moisture and brightness temperature products into a land surface model. Remote Sens. Environ. 2016, 180, 292–304. [Google Scholar] [CrossRef]
- Albergel, C.; Dutra, E.; Bonan, B.; Zheng, Y.; Munier, S.; Balsamo, G.; de Rosnay, P.; Muñoz-Sabater, J.; Calvet, J.-C. Monitoring and Forecasting the Impact of the 2018 Summer Heatwave on Vegetation. Remote Sens. 2019, 11, 520. [Google Scholar] [CrossRef]


| 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SWI | 36,154 | 39,624 | 38,761 | 41,687 | 41,699 | 41,652 | 41,086 | 41,129 | 173,818 | 319,565 | 319,097 | 157,476 |
| LAI | 37,107 | 37,500 | 37,342 | 37,425 | 37,269 | 36,706 | 37,024 | 38,778 | 38,839 | 38,757 | 38,243 | 19,908 |
| Median R 1, 95% Confidence Interval 2 (% of Stations for Which This Configuration Is the Best) | Median ubRMSD 1 on Precipitation Time Series (in mm/month) and Incoming Solar Radiation (in w·m−2), 95% Confidence Interval 2 (% of Stations for Which This Configuration is the Best) | Median Bias 1 on Precipitation Time Series (in mm/month) and Incoming Solar Radiation (in w·m−2), 95% Confidence Interval 2 (% of Stations for Which This Configuration is Better) | Median RMSD 1 on Precipitation Time Series (in mm/month) and Incoming Solar Radiation (in w·m−2), 95% Confidence Interval 2 (% of Stations for Which This Configuration is Better) | |
|---|---|---|---|---|
| ERA5 (precipitation) | 0.82 ± 0.009 (84%) | 52.02 ± 1.39 (89%) | −15.00 ± 3.27 (83%) | 56.15 ± 3.60 (86%) |
| ERA-Interim (precipitation) | 0.77 ± 0.010 (16%) | 58.44 ± 1.42 (11%) | −19.85 ± 3.77 (17%) | 63.89 ± 3.25 (14%) |
| ERA5 (incoming solar radiation) | 0.59 ± 0.07 (100%) | 36.23 ± 6.48 (100%) | 19.40 ± 32.43 (100%) | 42.24 ± 21.76 (100%) |
| ERAI (incoming solar radiation) | 0.46 ± 0.15 (0%) | 41.03 ± 4.22 (0%) | 28.12 ± 29.80 (0%) | 50.72 ± 18.63 (0%) |
| January 2001 to June 2018 | 1–4 cm | 4–10 cm | 10–20 cm | 20–40 cm | 40–60 cm | 60–80 cm | 80–100 cm | |
| Mean | –0.0006 | 0.5372 | 0.2033 | 0.0818 | 0.0441 | 0.0142 | 0.0049 | 0.0020 |
1–4 cm | 4–10 cm | 10–20 cm | 20–40 cm | 40–60 cm | 60–80 cm | 80–100 cm | ||
| Mean | 0.2578 | 0.0134 | 0.0223 | 0.0432 | 0.0911 | 0.0522 | 0.0318 | 0.0188 |
| Jan. | Feb. | Mar. | Apr. | May | Jun. | Jul. | Aug. | Sep. | Oct. | Nov. | Dec. | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| BF | 59,724 | 59,723 | 59,724 | 59,715 | 58,914 | 53,840 | 48,140 | 48,006 | 46,022 | 54,265 | 56,406 | 56,406 |
| SH | 18,684 | 18,683 | 18,684 | 18,679 | 18,674 | 18,678 | 17,638 | 17,644 | 17,646 | 17,646 | 17,646 | 17,646 |
| SS | 19,440 | 19,440 | 19,440 | 19,440 | 19,440 | 19,440 | 18,334 | 18,357 | 18,319 | 18,360 | 18,360 | 18,360 |
| SD | 21,600 | 21,600 | 21,600 | 21,596 | 20,800 | 15,722 | 12,168 | 12,005 | 10,057 | 18,259 | 20,400 | 20,400 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tall, M.; Albergel, C.; Bonan, B.; Zheng, Y.; Guichard, F.; Dramé, M.S.; Gaye, A.T.; Sintondji, L.O.; Hountondji, F.C.C.; Nikiema, P.M.; et al. Towards a Long-Term Reanalysis of Land Surface Variables over Western Africa: LDAS-Monde Applied over Burkina Faso from 2001 to 2018. Remote Sens. 2019, 11, 735. https://doi.org/10.3390/rs11060735
Tall M, Albergel C, Bonan B, Zheng Y, Guichard F, Dramé MS, Gaye AT, Sintondji LO, Hountondji FCC, Nikiema PM, et al. Towards a Long-Term Reanalysis of Land Surface Variables over Western Africa: LDAS-Monde Applied over Burkina Faso from 2001 to 2018. Remote Sensing. 2019; 11(6):735. https://doi.org/10.3390/rs11060735
Chicago/Turabian StyleTall, Moustapha, Clément Albergel, Bertrand Bonan, Yongjun Zheng, Françoise Guichard, Mamadou Simina Dramé, Amadou Thierno Gaye, Luc Olivier Sintondji, Fabien C. C. Hountondji, Pinghouinde Michel Nikiema, and et al. 2019. "Towards a Long-Term Reanalysis of Land Surface Variables over Western Africa: LDAS-Monde Applied over Burkina Faso from 2001 to 2018" Remote Sensing 11, no. 6: 735. https://doi.org/10.3390/rs11060735
APA StyleTall, M., Albergel, C., Bonan, B., Zheng, Y., Guichard, F., Dramé, M. S., Gaye, A. T., Sintondji, L. O., Hountondji, F. C. C., Nikiema, P. M., & Calvet, J.-C. (2019). Towards a Long-Term Reanalysis of Land Surface Variables over Western Africa: LDAS-Monde Applied over Burkina Faso from 2001 to 2018. Remote Sensing, 11(6), 735. https://doi.org/10.3390/rs11060735