Estimation of Carbon Fluxes from Eddy Covariance Data and Satellite-Derived Vegetation Indices in a Karst Grassland (Podgorski Kras, Slovenia)
Abstract
1. Introduction
- (i)
- Evaluate the ability of different VIs retrieved from remote sensing platforms to represent GPP and NEE trends in a karst grassland;
- (ii)
- Compare the performance of different models, integrating VIs in the estimation of GPP and NEE;
- (iii)
- Apply obtained results to map NEE and GPP for the grassland area in the Podgorski Kras Plateau comparing the suitability of different remote platforms.
2. Materials and Methods
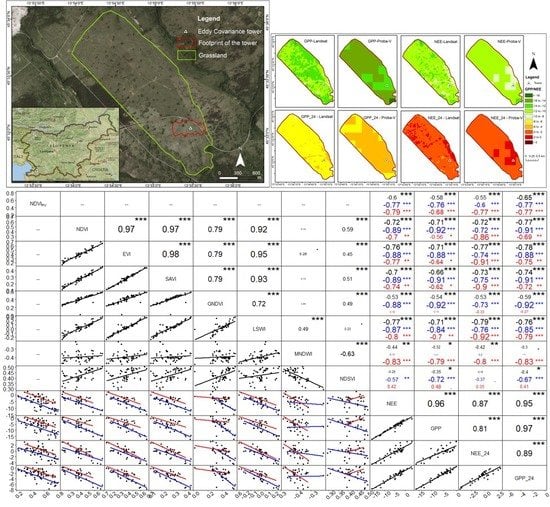
2.1. Study Area
2.2. Data Acquisition
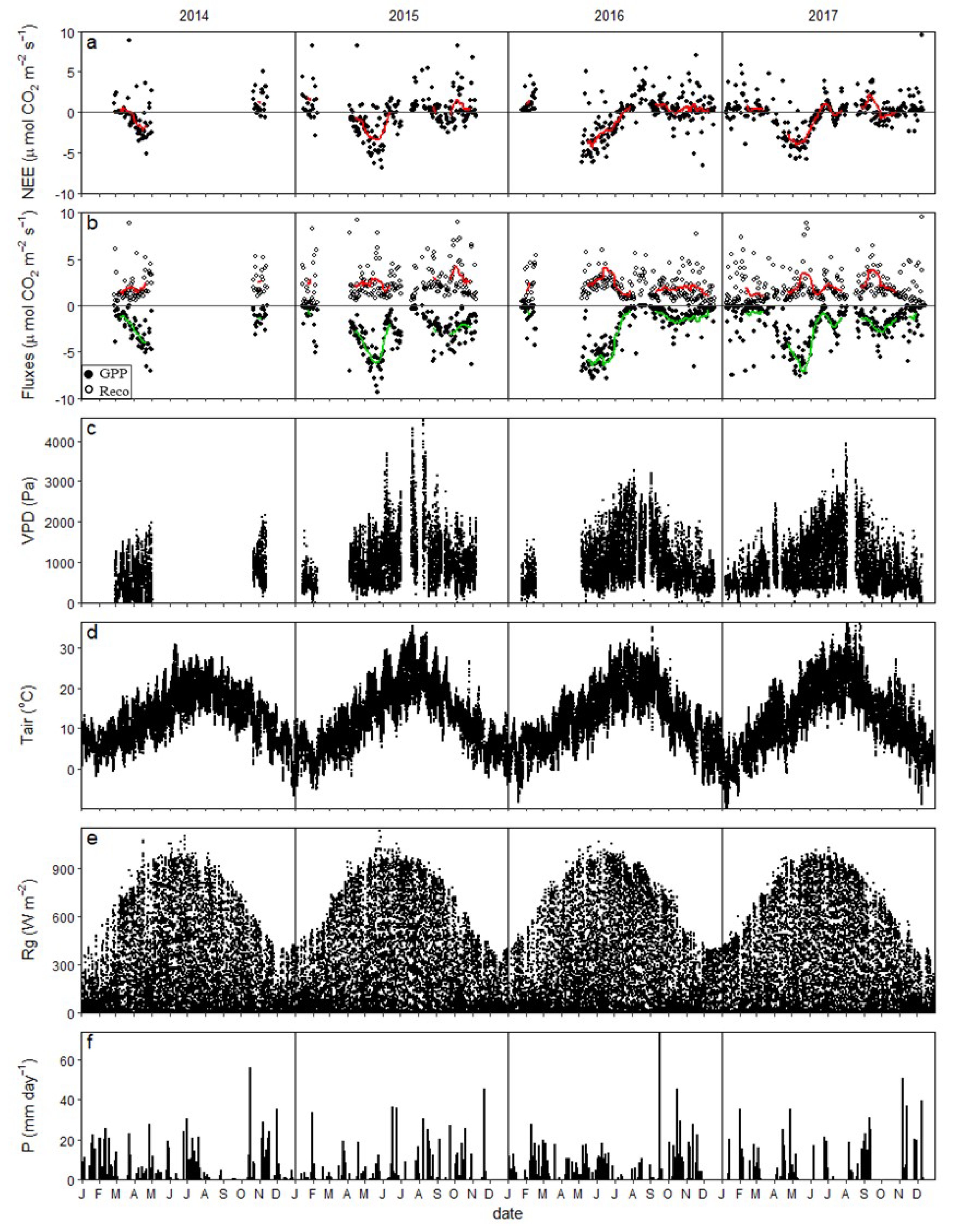
2.2.1. Eddy Covariance and Meteorological Data
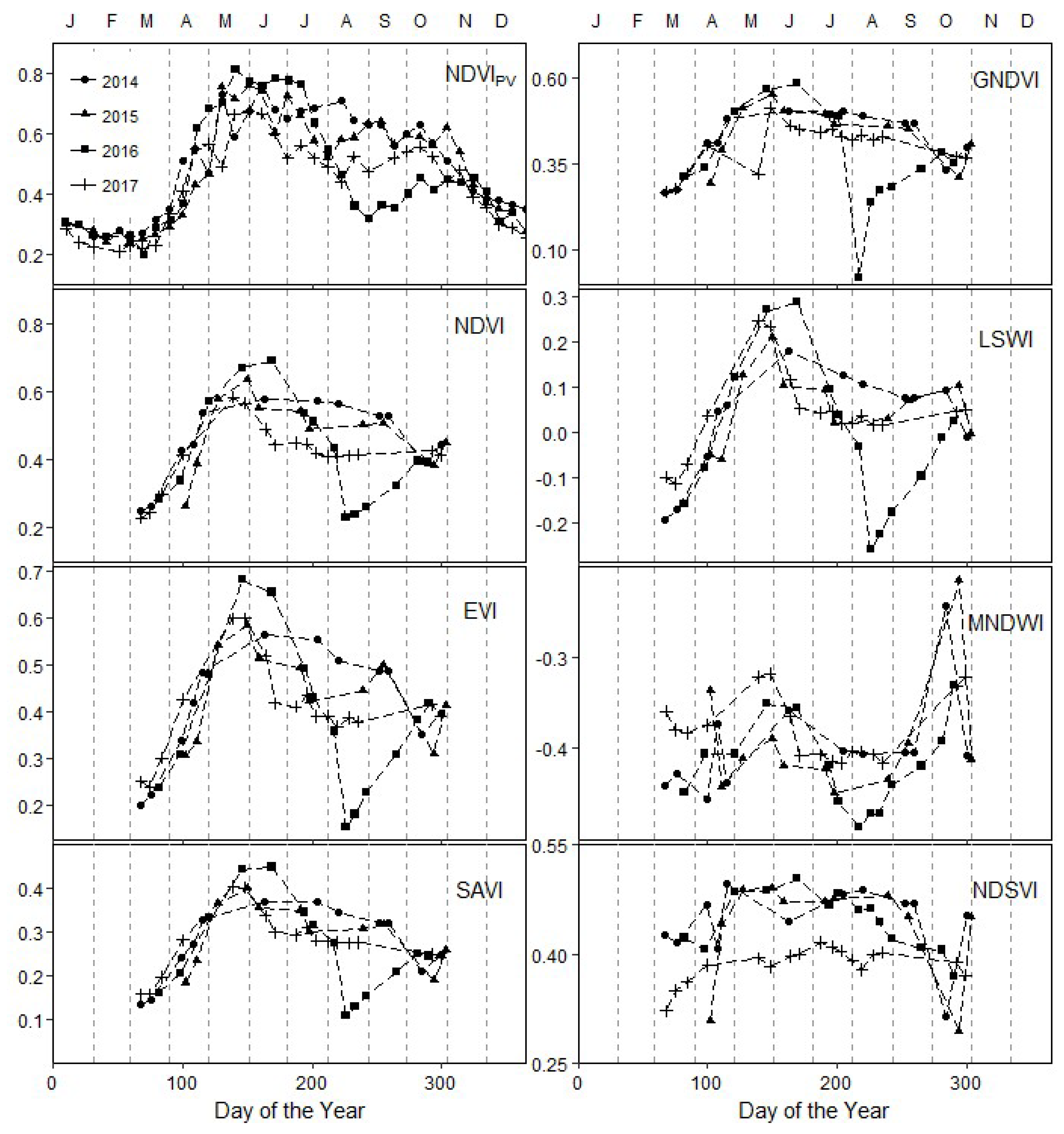
2.2.2. Spectral Vegetation Indices
2.3. Data Analysis and Modelling
- (i) Model 1 assuming a direct linear relationship between GPP or NEE and a vegetation indexwhere NEE is the net ecosystem exchange, GPP is the gross primary production, VI is a vegetation index, a and b are regression constants.NEE or GPP = a*VI + b,
- (ii) Model 2 assuming a direct linear relationship between GPP and the product of a VI and incoming PAR or Rg in this studywhere GPP is the gross primary production, VI is a vegetation index, Rg is the short-wave radiation, a and b are regression constants.GPP = a*(VI*Rg) + b,
- (iii) Model 3, a simplified LUE model, in which the LUE term is considered a constant (integrated in the model) and APAR is obtained by multiplying the fraction of absorbed photosynthetically active radiation (fAPAR), estimated as a linear function of a VI, by PAR (replaced by Rg in this study). By this approach, LUE and fAPAR estimates are conceptually independent.where GPP is the gross primary production, LUE is the light use efficiency, VI is a vegetation index, Rg is the short-wave radiation, a and b are regression constants.GPP = LUE* (a*VI + b)*Rg,
2.4. Mapping of Carbon Fluxes
3. Results
3.1. Carbon Fluxes and Environmental Variables Measured by the EC Tower
3.2. Vegetation Indices
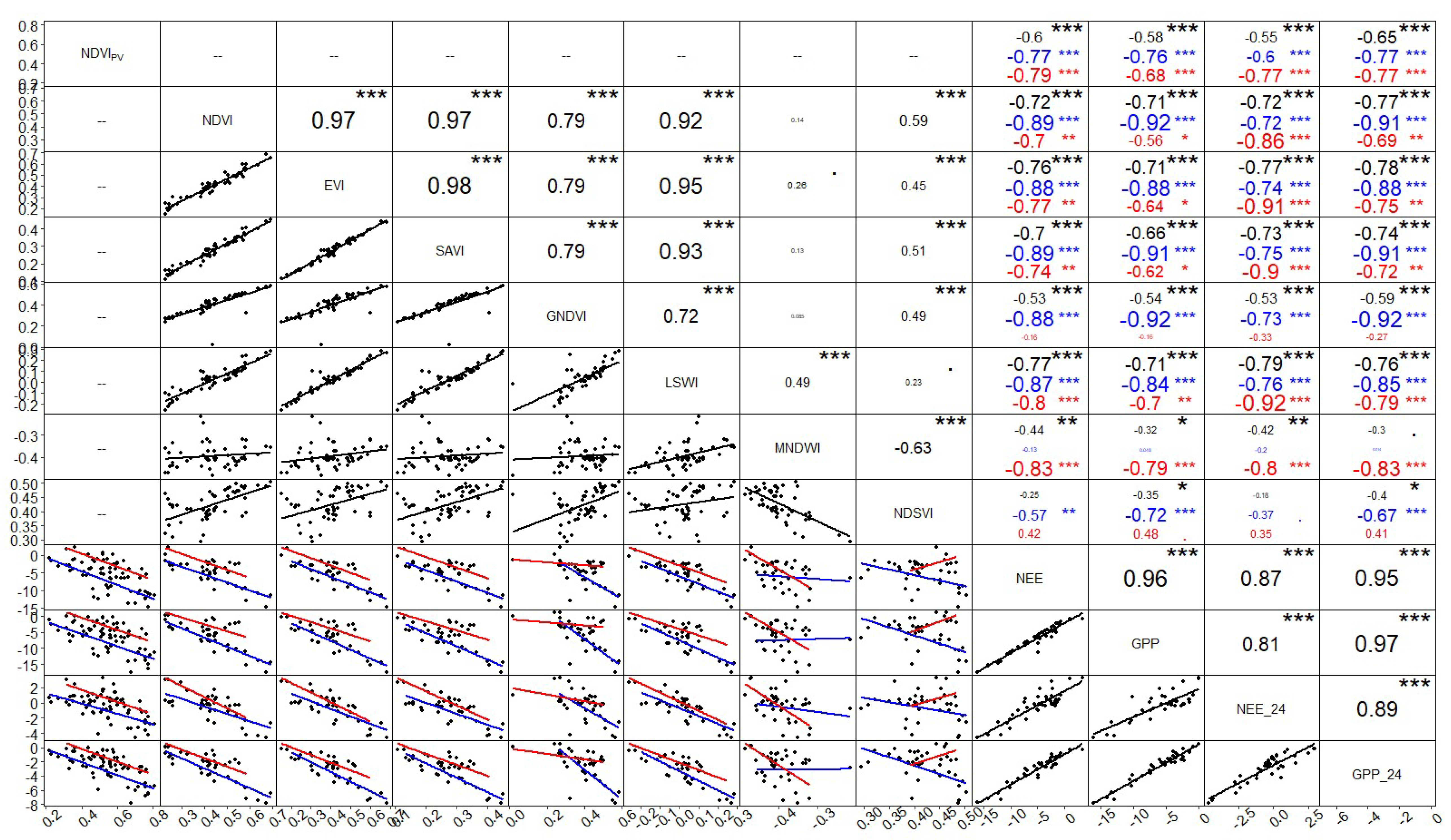
3.3. Correlation Charts of Fluxes and Vegetation Indices
3.4. Comparison of the Different Models
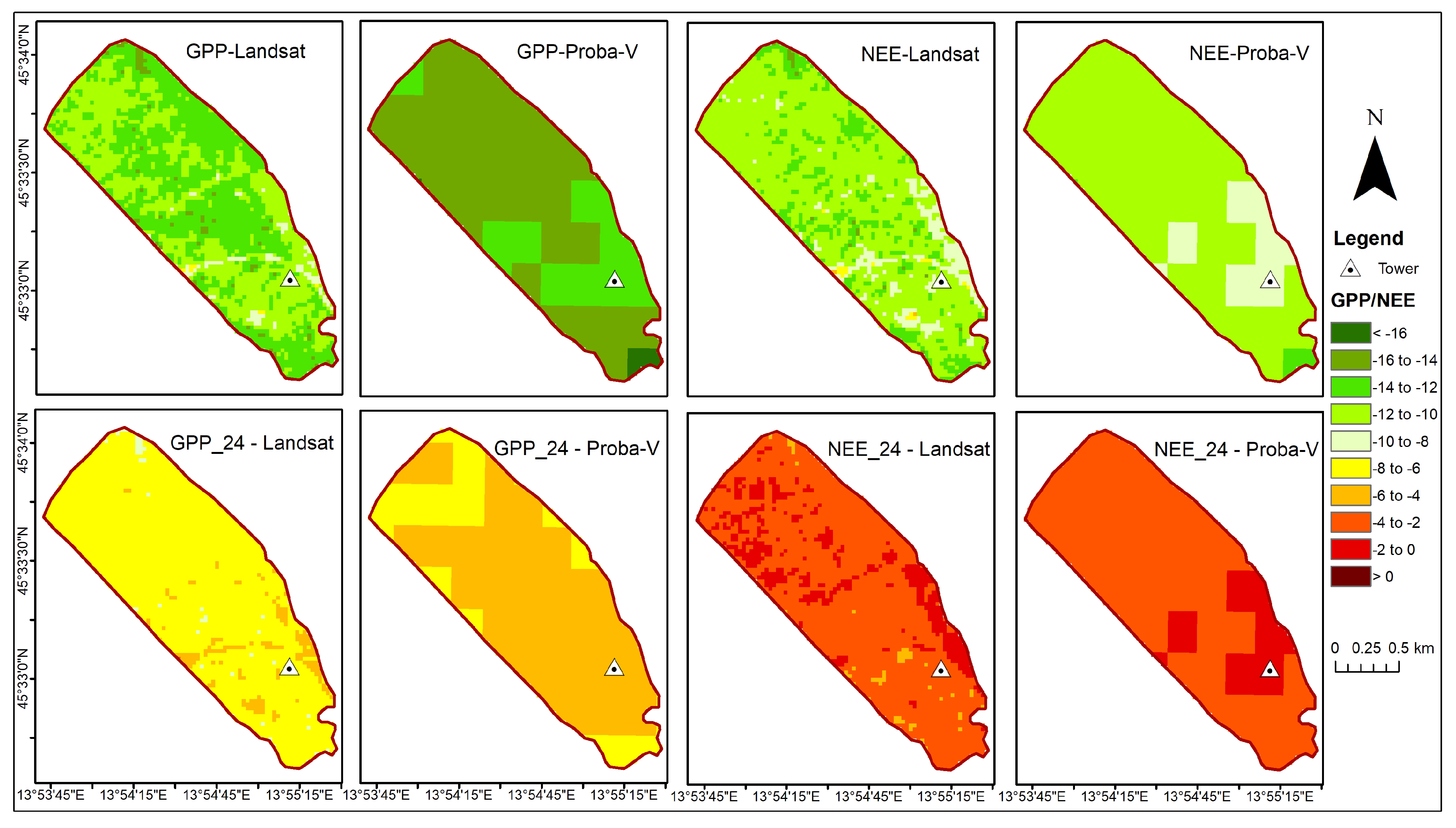
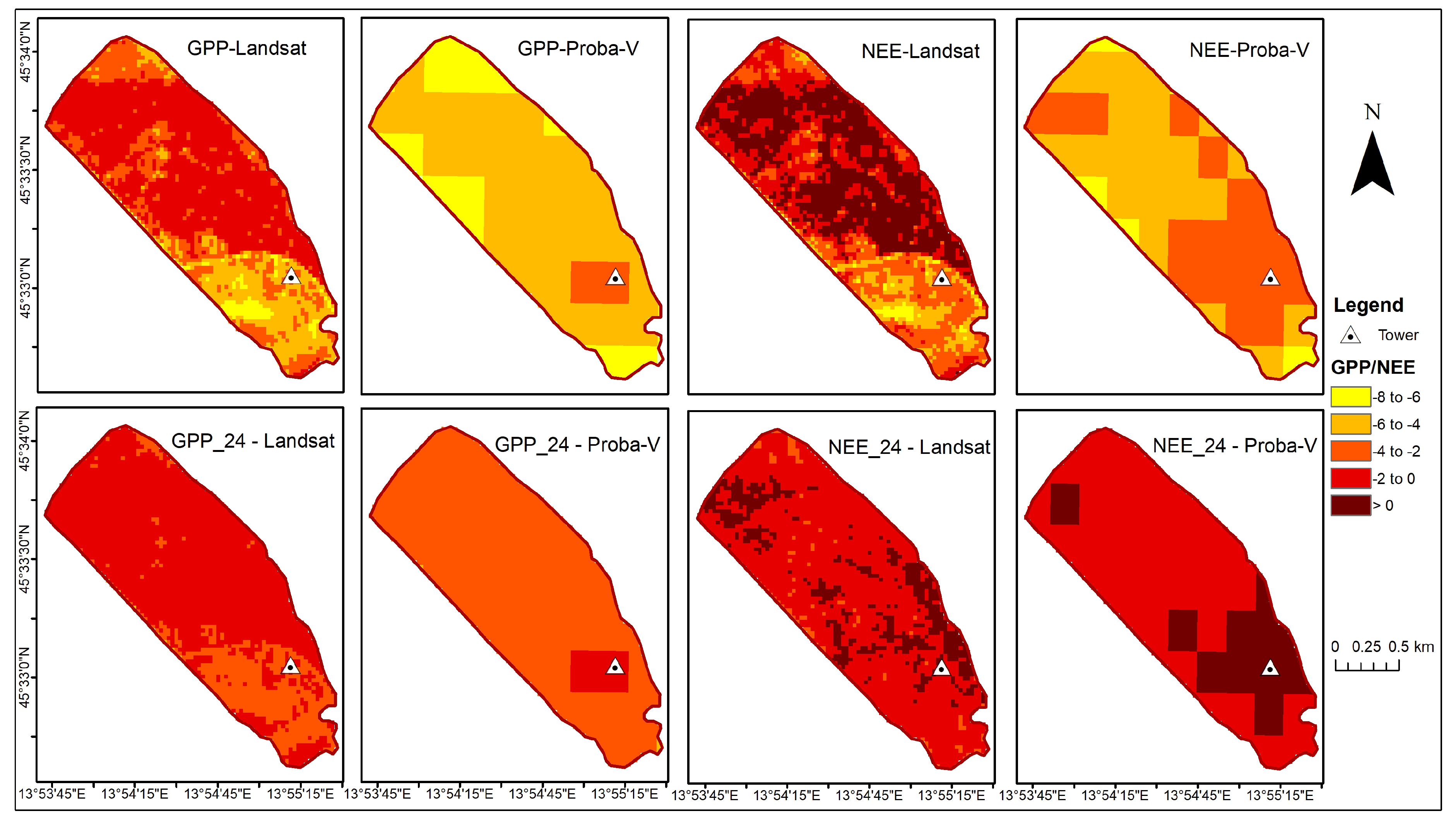
3.5. Flux Maps Using the Best Models
4. Discussion
4.1. Performance of the Different Vegetation Indices
4.2. Performance of the Different Models
4.3. GPP and NEE Maps
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mason, J.A.; Zanner, C.W. Grassland soils. In Encyclopedia of Soils in the Environment; Elsevier: Amsterdam, The Netherlands, 2005; pp. 138–145. ISBN 9780123485304. [Google Scholar]
- Scurlock, J.M.O.; Hall, D.O. The global carbon sink: A grassland perspective. Glob. Chang. Biol. 1998, 4, 229–233. [Google Scholar] [CrossRef]
- Buringh, P. Organic Carbon in Soils of the World. In The role of Terrestrial Vegetation in the Global Carbon Cycle: Measurement by Remote Sensing; Woodwell, G.M., Ed.; SCOPE 23; Wiley: Chichester, UK, 1984; pp. 41–109. [Google Scholar]
- Papale, D.; Reichstein, M.; Aubinet, M.; Canfora, E.; Bernhofer, C.; Kutsch, W.; Longdoz, B.; Rambal, S.; Valentini, R.; Vesala, T.; et al. Towards a standardized processing of Net Ecosystem Exchange measured with eddy covariance technique: Algorithms and uncertainty estimation. Biogeosciences 2006, 3, 571–583. [Google Scholar] [CrossRef]
- Burba, G.; Anderson, D. A Brief Practical Guide to Eddy Covariance Flux Measurements: Principles and Workflow Examples for Scientific and Industrial Applications; LI-COR Biosciences: Lincoln, NB, USA, 2010. [Google Scholar]
- Kirschbaum, M.U.F.; Eamus, D.; Gifford, R.M.; Roxburgh, S.H.; Sands, P.J. Definitions of Some Ecological Terms Commonly Used in Carbon Accounting. In Proceedings of the Net Ecosystem Exchange, Canberra, Australia, 18–20 April 2001; pp. 1–144. [Google Scholar]
- Aubinet, M.; Vesala, T.; Papale, D. Eddy Covariance A Practical Guide to Measurement and Data Analysis; Springer: New York, NY, USA, 2012; ISBN 9789400723504. [Google Scholar]
- Myneni, R.B.; Williams, D.L. On the relationship between FAPAR and NDVI. Remote Sens. Environ. 1994, 49, 200–211. [Google Scholar] [CrossRef]
- Nestola, E.; Calfapietra, C.; Emmerton, C.A.; Wong, C.Y.S.; Thayer, D.R.; Gamon, J.A. Monitoring grassland seasonal carbon dynamics, by integrating MODIS NDVI, proximal optical sampling, and eddy covariance measurements. Remote Sens. 2016, 8, 25. [Google Scholar] [CrossRef]
- Running, S.W.; Nemani, R.R.; Heinsch, F.A.; Zhao, M.; Reeves, M.; Hashimoto, H. A Continuous Satellite-Derived Measure of Global Terrestrial Primary Production. Bioscience 2004, 54, 547. [Google Scholar] [CrossRef]
- Yuan, W.; Cai, W.; Xia, J.; Chen, J.; Liu, S.; Dong, W.; Merbold, L.; Law, B.; Arain, A.; Beringer, J.; et al. Global comparison of light use efficiency models for simulating terrestrial vegetation gross primary production based on the LaThuile database. Agric. For. Meteorol. 2014, 192–193, 108–120. [Google Scholar] [CrossRef]
- Zhou, X.; Zhu, Q.; Tang, S.; Chen, X.; Wu, M. Interception of PAR and relationship between FPAR and LAI in summer maize canopy. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Toronto, ON, Canada, 24–28 June 2002; Volume 6, pp. 3252–3254. [Google Scholar]
- Yan, W.; Hu, Z.; Zhao, Y.; Zhang, X.; Fan, Y.; Shi, P. Modeling Net Ecosystem Carbon Exchange of Alpine Grasslands with a Satellite-Driven Model. PLoS ONE 2015, 10, e0122486. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Zhang, L.; Xiao, J.; Chen, S.; Kato, T.; Zhou, G. A comparison of satellite-derived vegetation indices for approximating gross primary productivity of grasslands. Rangel. Ecol. Manag. 2014, 67, 9–18. [Google Scholar] [CrossRef]
- Rocha, A.V.; Shaver, G.R. Advantages of a two band EVI calculated from solar and photosynthetically active radiation fluxes. Agric. For. Meteorol. 2009, 149, 1560–1563. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Kaufman, Y.J.; Merzlyak, M.N. Use of a green channel in remote sensing of global vegetation from EOS-MODIS. Remote Sens. Environ. 1996, 58, 289–298. [Google Scholar] [CrossRef]
- Cerasoli, S.; Campagnolo, M.; Faria, J.; Nogueira, C.; Caldeira, M.D.C. On estimating the gross primary productivity of Mediterranean grasslands under different fertilization regimes using vegetation indices and hyperspectral reflectance. Biogeosciences 2018, 15, 5455–5471. [Google Scholar] [CrossRef]
- Jovanović, D.; Govedarica, M.; Sabo, F.; Važić, R.; Popović, D. Impact analysis of pansharpening Landsat ETM+, Landsat OLI, WorldView-2, and Ikonos images on vegetation indices. In Proceedings of the Fourth International Conference on Remote Sensing and Geoinformation of the Environment (RSCy2016), Paphos, Cyprus, 4–6 April 2016; Themistocleous, K., Hadjimitsis, D.G., Michaelides, S., Papadavid, G., Eds.; 2016; Volume 9688, p. 10. [Google Scholar]
- Rossini, M.; Cogliati, S.; Meroni, M.; Migliavacca, M.; Galvagno, M.; Busetto, L.; Cremonese, E.; Julitta, T.; Siniscalco, C.; Morra, U.; et al. Remote sensing-based estimation of gross primary production in a subalpine grassland. Biogeosciences 2012, 9, 2565–2584. [Google Scholar] [CrossRef]
- Sakowska, K.; Vescovo, L.; Marcolla, B.; Juszczak, R.; Olejnik, J.; Gianelle, D. Monitoring of carbon dioxide fluxes in a subalpine grassland ecosystem of the Italian Alps using a multispectral sensor. Biogeosciences 2014, 11, 4695–4712. [Google Scholar] [CrossRef]
- John, R.; Chen, J.; Lu, N.; Guo, K.; Liang, C.; Wei, Y.; Noormets, A.; Ma, K.; Han, X. Predicting plant diversity based on remote sensing products in the semi-arid region of Inner Mongolia. Remote Sens. Environ. 2008, 112, 2018–2032. [Google Scholar] [CrossRef]
- Hill, M.J. Vegetation index suites as indicators of vegetation state in grassland and savanna: An analysis with simulated SENTINEL 2 data for a North American transect. Remote Sens. Environ. 2013, 137, 94–111. [Google Scholar] [CrossRef]
- Bajgain, R.; Xiao, X.; Wagle, P.; Basara, J.; Zhou, Y. Sensitivity analysis of vegetation indices to drought over two tallgrass prairie sites. ISPRS J. Photogramm. Remote Sens. 2015, 108, 151–160. [Google Scholar] [CrossRef]
- Wagle, P.; Zhang, Y.; Jin, C.; Xiao, X. Comparison of solar-induced chlorophyll fluorescence, light-use efficiency, and process-based GPP models in maize. Ecol. Appl. 2016, 26, 1211–1222. [Google Scholar] [CrossRef]
- Sims, D.A.; Rahman, A.F.; Cordova, V.D.; El-Masri, B.Z.; Baldocchi, D.D.; Bolstad, P.V.; Flanagan, L.B.; Goldstein, A.H.; Hollinger, D.Y.; Misson, L.; et al. A new model of gross primary productivity for North American ecosystems based solely on the enhanced vegetation index and land surface temperature from MODIS. Remote Sens. Environ. 2008, 112, 1633–1646. [Google Scholar] [CrossRef]
- Goerner, A.; Reichstein, M.; Tomelleri, E.; Hanan, N.; Rambal, S.; Papale, D.; Dragoni, D.; Schmullius, C. Remote sensing of ecosystem light use efficiency with MODIS-based PRI. Biogeosciences 2011, 8, 189–202. [Google Scholar] [CrossRef]
- Li, Z.; Yu, G.; Xiao, X.; Li, Y.; Zhao, X.; Ren, C.; Zhang, L.; Fu, Y. Modeling gross primary production of alpine ecosystems in the Tibetan Plateau using MODIS images and climate data. Remote Sens. Environ. 2007, 107, 510–519. [Google Scholar] [CrossRef]
- Gilmanov, T.; Tieszen, L.L.; Wylie, B.K.; Flanagan, L.B.; Frank, A.B.; Haferkamp, M.R.; Meyers, T.P.; Morgan, J.A. Integration of CO2 flux and remotely-sensed data for primary production and ecosystem respiration analyses in the Northern Great Plains: Potential for quantitative spatial extrapolation. Glob. Ecol. Biogeogr. 2005, 14, 271–292. [Google Scholar] [CrossRef]
- Baldocchi, D.D. “Breathing” of the terrestrial biosphere: Lessons learned from a global network of carbon dioxide flux measurement systems. Aust. J. Bot. 2008, 56, 1. [Google Scholar] [CrossRef]
- Baldocchi, D.D.; Sturtevant, C. Fluxnet contributors Does day and night sampling reduce spurious correlation between canopy photosynthesis and ecosystem respiration? Agric. For. Meteorol. 2015, 207, 117–126. [Google Scholar] [CrossRef]
- Ma, S.; Baldocchi, D.D.; Wolf, S.; Verfaillie, J. Slow ecosystem responses conditionally regulate annual carbon balance over 15 years in Californian oak-grass savanna. Agric. For. Meteorol. 2016, 228–229, 252–264. [Google Scholar] [CrossRef]
- Gabrovšek, K. People with Nature, Nature for People—Biodiversity is Our Life; Institute of the Republic of Slovenia for Nature Conservation: Ljubljana, Slovenia, 2010. [Google Scholar]
- Ferlan, M. The Use of Micro-Meteorological Methods for the Monitoring of the Carbon Fluxes in Karst Ecosystems. Ph.D. Thesis, University of Ljubljana, Ljubljana, Slovenia, 2013. [Google Scholar]
- Knez, M.; Petrič, M.; Slabe, T.; Šebela, S. The Beka-Ocizla Cave System: Karstological Railway Planning in Slovenia; Springer: New York, NY, USA, 2015; ISBN 9783319044552. [Google Scholar]
- EARS Environmental Agency of the Republic of Slovenia. Available online: http://meteo.arso.gov.si (accessed on 1 March 2019).
- Ferlan, M.; Alberti, G.; Eler, K.; Batič, F.; Miglietta, F.; Zaldei, A.; Simončič, P. Comparing carbon fluxes between different stages of secondary succession of a karst grassland. Agric. Ecosyst. Environ. 2011, 140, 199–207. [Google Scholar] [CrossRef]
- Schuepp, P.H.; Leclerc, M.Y.; MacPherson, J.I.; Desjardins, R.L. Footprint prediction of scalar fluxes from analytical solutions of the diffusion equation. Boundary-Layer Meteorol. 1990, 50, 355–373. [Google Scholar] [CrossRef]
- Aubinet, M.; Grelle, A.; Ibrom, A.; Rannik, Ü.; Moncrieff, J.; Foken, T.; Kowalski, A.S.; Martin, P.H.; Berbigier, P.; Bernhofer, C.; et al. Estimates of the Annual Net Carbon and Water Exchange of Forests: The EUROFLUX Methodology. Adv. Ecol. Res. 1999, 30, 113–175. [Google Scholar]
- Webb, E.K.; Pearman, G.I.; Leuning, R. Correction of flux measurements for density effects due to heat and water vapour transfer. Q. J. R. Meteorol. Soc. 1980, 106, 85–100. [Google Scholar] [CrossRef]
- Burba, G.; Mcdermitt, D.K.; Grelle, A.; Anderson, D.J.; Xu, L. Addressing the influence of instrument surface heat exchange on the measurements of CO2 flux from open-path gas analyzers. Glob. Chang. Biol. 2008, 14, 1854–1876. [Google Scholar] [CrossRef]
- University of Edinburgh EdiRe Software for Micrometeorological Applications(App. Note Code: 3C-R); Campbell Scientific: Logan, UT, USA, 1999.
- Foken, T.; Wichura, B. Tools for quality assessment of surface-based flux measurements. Agric. For. Meteorol. 1996, 78, 83–105. [Google Scholar] [CrossRef]
- Meek, D.W.; Hatfield, J.L.; Howell, T.A.; Idso, S.B.; Reginato, R.J. A Generalized Relationship between Photosynthetically Active Radiation and Solar Radiation1. Agron. J. 1984, 76, 939–945. [Google Scholar] [CrossRef]
- Lasslop, G.; Reichstein, M.; Papale, D.; Richardson, A.D.; Arneth, A.; Barr, A.; Stoy, P.; Wohlfahrt, G. Separation of net ecosystem exchange into assimilation and respiration using a light response curve approach: Critical issues and global evaluation. Glob. Chang. Biol. 2010, 16, 187–208. [Google Scholar] [CrossRef]
- CGLSP Copernicus Global Land Service Portal. Available online: http://land.copernicus.vgt.vito.be/PDF/portal/Application.html#Browse;Root=513186;Collection=1000063;Time=NORMAL,NORMAL,-1,,,-1,, (accessed on 20 December 2017).
- USGS United States Geological Survey. Available online: https://glovis.usgs.gov/ (accessed on 5 January 2018).
- Saranya, M. Cloud Removal from Satellite Images Using Information Cloning. Int. J. Comput. Sci. Mob. Comput. 2014, 32, 681–688. [Google Scholar]
- Sun, L.; Mi, X.; Wei, J.; Wang, J.; Tian, X.; Yu, H.; Gan, P. A cloud detection algorithm-generating method for remote sensing data at visible to short-wave infrared wavelengths. ISPRS J. Photogramm. Remote Sens. 2017, 124, 70–88. [Google Scholar] [CrossRef]
- USGS United States Geological Survey. Available online: https://earthexplorer.usgs.gov/ (accessed on 1 March 2019).
- Chavez, P.S.J. Image-based atmospheric corrections—Revisited and improved. Photogramm. Eng. Remote Sens. 1996, 62, 1025–1036. [Google Scholar]
- R Core Team R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing. Available online: http://www.r-project.org/ (accessed on 1 March 2019).
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring vegetation systems in the Great Plains with ERTS. In Proceedings of the 3rd Earth Resources Satellite-1 Symposium (NASA SP-351), Washington, DC, USA, 10–14 December 1973. [Google Scholar]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Xiao, X.; Boles, S.; Liu, J.; Zhuang, D.; Frolking, S.; Li, C.; Salas, W.; Moore, B. Mapping paddy rice agriculture in southern China using multi-temporal MODIS images. Remote Sens. Environ. 2005, 95, 480–492. [Google Scholar] [CrossRef]
- Xu, H. Modification of normalised difference water index (NDWI) to enhance open water features in remotely sensed imagery. Int. J. Remote Sens. 2006, 27, 3025–3033. [Google Scholar] [CrossRef]
- Sulman, B.N.; Roman, D.T.; Yi, K.; Wang, L.; Phillips, R.P.; Novick, K.A. High atmospheric demand for water can limit forest carbon uptake and transpiration as severely as dry soil. Geophys. Res. Lett. 2016, 43, 9686–9695. [Google Scholar] [CrossRef]
- Will, R.E.; Wilson, S.M.; Zou, C.B.; Hennessey, T.C. Increased vapor pressure deficit due to higher temperature leads to greater transpiration and faster mortality during drought for tree seedlings common to the forest-grassland ecotone. New Phytol. 2013, 200, 366–374. [Google Scholar] [CrossRef] [PubMed]
- Maherali, H.; Maherali, H.; Johnson, H.B.; Jackson, R.B. Stomatal sensitivity to vapour pressure difference over a subambient to elevated CO2 gradient in a C3/C4 grassland. Plant Cell Environ. 2003, 26, 1297–1306. [Google Scholar] [CrossRef]
- Anderson, L.J.; Maherali, H.; Johnson, H.B.; Polley, H.W.; Jackson, R.B. Gas exchange and photosynthetic acclimation over subambient to elevated CO2 in a C3-C4 grassland. Glob. Chang. Biol. 2001, 7, 693–707. [Google Scholar] [CrossRef]
- Richter, K.; Atzberger, C.; Hank, T.B.; Mauser, W. Derivation of biophysical variables from Earth observation data: Validation and statistical measures. J. Appl. Remote Sens. 2012, 6, 063557. [Google Scholar] [CrossRef]
- Tagesson, T.; Ardö, J.; Cappelaere, B.; Kergoat, L.; Abdi, A.; Horion, S.; Fensholt, R. Modelling spatial and temporal dynamics of gross primary production in the Sahel from earth-observation-based photosynthetic capacity and quantum efficiency. Biogeosciences 2017, 14, 1333–1348. [Google Scholar] [CrossRef]
- Bagaram, M.; Giuliarelli, D.; Chirici, G.; Giannetti, F.; Barbati, A. UAV Remote Sensing for Biodiversity Monitoring: Are Forest Canopy Gaps Good Covariates? Remote Sens. 2018, 10, 1397. [Google Scholar]
- Gamon, J.A.; Field, C.B.; Goulden, M.L.; Griffin, K.L.; Hartley, A.E.; Joel, G.; Penuelas, J.; Valentini, R. Relationships Between NDVI, Canopy Structure, and Photosynthesis in Three Californian Vegetation Types. Ecol. Appl. 1995, 5, 28–41. [Google Scholar] [CrossRef]
- Myneni, R.B.; Hall, F.G.; Sellers, P.J.; Marshak, A.L. The interpretation of spectral vegetation indexes. IEEE Trans. Geosci. Remote Sens. 1995, 33, 481–486. [Google Scholar] [CrossRef]
- Gianelle, D.; Vescovo, L.; Marcolla, B.; Manca, G.; Cescatti, A. Ecosystem carbon fluxes and canopy spectral reflectance of a mountain meadow. Int. J. Remote Sens. 2009, 30, 435–449. [Google Scholar] [CrossRef]
- Vescovo, L.; Wohlfahrt, G.; Balzarolo, M.; Pilloni, S.; Sottocornola, M.; Rodeghiero, M.; Gianelle, D. New spectral vegetation indices based on the near-infrared shoulder wavelengths for remote detection of grassland phytomass. Int. J. Remote Sens. 2011, 33, 2178–2195. [Google Scholar] [CrossRef] [PubMed]
- Sonmez, N.K.; Slater, B. European Journal of Remote Sensing Measuring Intensity of Tillage and Plant Residue Cover Using Remote Sensing. Eur. J. Remote Sens. 2016, 49, 121–135. [Google Scholar] [CrossRef]
- Li, Z.; Guo, X. Non-photosynthetic vegetation biomass estimation in semiarid Canadian mixed grasslands using ground hyperspectral data, Landsat 8 OLI, and Sentinel-2 images. Int. J. Remote Sens. 2018, 39, 6893–6913. [Google Scholar] [CrossRef]
- Keeley, J.E.; Keeley, S.C. Postfire Recovery of California Coastal Sage Scrub. Source Am. Midl. Nat. 1984, 111, 105–117. [Google Scholar] [CrossRef]
- Xu, L.; Baldocchi, D.D. Seasonal variation in carbon dioxide exchange over a Mediterranean annual grassland in California. Agric. For. Meteorol. 2004, 123, 79–96. [Google Scholar] [CrossRef]
- Lei, T.; Pang, Z.; Wang, X.; Li, L.; Fu, J.; Kan, G.; Zhang, X.; Ding, L.; Li, J.; Huang, S.; et al. Drought and Carbon Cycling of Grassland Ecosystems under Global Change: A Review. Water 2016, 8, 460. [Google Scholar] [CrossRef]
| Name | Landsat Range (µm) | Proba-V Range (µm) |
|---|---|---|
| Ultra Blue (coastal/aerosol) | Band 1 (0.435–0.451) | – |
| Blue | Band 2 (0.452–0.512) | Band 1 (0.438–0.486) |
| Green | Band 3 (0.533–0.590) | – |
| Red | Band 4 (0.636–0.673) | Band 2 (0.615–0.696) |
| Near Infrared (NIR) | Band 5 (0.851–0.879) | Band 3 (0.772–0.914) |
| Shortwave Infrared (SWIR) 1 | Band 6 (1.566–1.651) | Band 4 (1.564–1.634) |
| Shortwave Infrared (SWIR) 2 | Band 7 (2.107–2.294) | – |
| Panchromatic | Band 8 (0.503–0.676) | – |
| Cirrus | Band 9 (1.363–1.384) | – |
| Thermal Infrared (TIRS) 1 | Band 10 (10.60–11.19 | – |
| Thermal Infrared (TIRS) 2 | Band 11 (11.50–12.51) | – |
| Satellite | Index | Formula | Reference |
|---|---|---|---|
| Proba-V | NDVIPV | NDVIPV = (b3 − b2)/(b2 + b3) | [52] |
| Landsat 8 | NDVI | NDVI = (b5 − b4)/(b5 + b4) | [52] |
| Landsat 8 | GNDVI | GNDVI = (b5 − b3)/(b5 + b3) | [16] |
| Landsat 8 | EVI | EVI = (2.5*(b5 − b4))/(b5 + 6*b4 − 7.5*b2 + 1) | [53] |
| Landsat 8 | NDSVI | NDSVI = (b6 − b4)/(b6 + b4) | [21] |
| Landsat 8 | SAVI | SAVI = ((1 + L)(b5 − b4))/(b5 + b4 + L) | [54] |
| Landsat 8 | LSWI | LSWI = (b5 − b6)/(b5 + b6) | [55] |
| Landsat 8 | MNDWI | MNDWI = (b3 − b6)/(b3 + b6) | [56] |
| R2 | R2boot | RMSE | AIC | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Model | Flux | VIs | Single | Wet | Dry | Single | Wet | Dry | Single | Wet | Dry | Single | Wet | Dry |
| 1 | NEE | NDVIPV | 0.36 | 0.59 | 0.62 | 0.36 ± 0.00 | 0.6 ± 0.01 | 0.63 ± 0.01 | 3.34 | 2.51 | 1.72 | 172.83 | 81.40 | 34.40 |
| Flux = a*VI + b | NDVI | 0.52 | 0.80 | 0.49 | 0.51 ± 0.01 | 0.79 ± 0.00 | 0.53 ± 0.01 | 2.87 | 1.68 | 2.67 | 88.46 | 30.96 | 31.54 | |
| EVI | 0.58 | 0.78 | 0.59 | 0.55 ± 0.01 | 0.77 ± 0.01 | 0.64 ± 0.01 | 2.70 | 1.75 | 2.40 | 83.60 | 33.05 | 28.50 | ||
| SAVI | 0.48 | 0.79 | 0.55 | 0.46 ± 0.01 | 0.78 ± 0.01 | 0.61 ± 0.01 | 2.99 | 1.73 | 2.51 | 91.71 | 32.52 | 29.76 | ||
| GNDVI | 0.29 | 0.78 | 0.03 | 0.28 ± 0.01 | 0.77 ± 0.01 | 0.17 ± 0.01 | 3.52 | 1.76 | 3.68 | 104.77 | 33.32 | 40.49 | ||
| LSWI | 0.59 | 0.75 | 0.64 | 0.56 ± 0.01 | 0.74 ± 0.01 | 0.69 ± 0.01 | 2.68 | 1.88 | 2.23 | 82.96 | 36.73 | 26.52 | ||
| MNDWI | 0.19 | 0.02 | 0.69 | 0.19 ± 0.01 | 0.03 ± 0.00 | 0.66 ± 0.01 | 3.74 | 3.72 | 2.09 | 109.60 | 72.31 | 24.68 | ||
| NDSVI | 0.06 | 0.33 | 0.18 | 0.1 ± 0.01 | 0.4 ± 0.01 | 0.2 ± 0.01 | 4.04 | 3.07 | 3.38 | 115.73 | 62.35 | 38.14 | ||
| GPP | NDVIPV | 0.33 | 0.58 | 0.46 | 0.34 ± 0.00 | 0.58 ± 0.01 | 0.48 ± 0.01 | 3.53 | 2.53 | 2.47 | 180.56 | 82.10 | 54.57 | |
| NDVI | 0.50 | 0.85 | 0.32 | 0.5 ± 0.01 | 0.85 ± 0.00 | 0.34 ± 0.01 | 2.81 | 1.42 | 2.83 | 84.48 | 21.65 | 33.17 | ||
| EVI | 0.51 | 0.77 | 0.41 | 0.5 ± 0.01 | 0.77 ± 0.01 | 0.42 ± 0.01 | 2.78 | 1.74 | 2.64 | 83.62 | 31.83 | 31.18 | ||
| SAVI | 0.44 | 0.82 | 0.38 | 0.44 ± 0.01 | 0.82 ± 0.00 | 0.4 ± 0.01 | 2.97 | 1.54 | 2.71 | 88.81 | 25.64 | 31.88 | ||
| GNDVI | 0.30 | 0.85 | 0.02 | 0.31 ± 0.01 | 0.85 ± 0.00 | 0.15 ± 0.01 | 3.32 | 1.43 | 3.39 | 97.69 | 22.04 | 38.19 | ||
| LSWI | 0.50 | 0.71 | 0.48 | 0.49 ± 0.01 | 0.7 ± 0.01 | 0.49 ± 0.01 | 2.80 | 1.99 | 2.47 | 84.29 | 38.33 | 29.29 | ||
| MNDWI | 0.10 | 0.00 | 0.63 | 0.12 ± 0.01 | 0.03 ± 0.00 | 0.59 ± 0.01 | 3.76 | 3.67 | 2.10 | 107.24 | 68.96 | 24.77 | ||
| NDSVI | 0.12 | 0.52 | 0.23 | 0.15 ± 0.01 | 0.54 ± 0.01 | 0.27 ± 0.01 | 3.71 | 2.54 | 3.01 | 106.23 | 50.53 | 34.81 | ||
| 2 | GPP | NDVIPV | 0.10 | 0.73 | 0.37 | 0.11 ± 0.00 | 0.73 ± 0.01 | 0.38 ± 0.01 | 4.10 | 2.03 | 2.67 | 201.57 | 63.61 | 58.99 |
| GPP = a*(VI*Rg) + b | NDVI | 0.19 | 0.81 | 0.19 | 0.2 ± 0.01 | 0.8 ± 0.00 | 0.22 ± 0.01 | 3.56 | 1.61 | 3.10 | 103.07 | 27.92 | 35.66 | |
| EVI | 0.22 | 0.75 | 0.26 | 0.23 ± 0.01 | 0.74 ± 0.01 | 0.28 ± 0.01 | 3.50 | 1.82 | 2.95 | 101.64 | 33.96 | 34.32 | ||
| SAVI | 0.18 | 0.77 | 0.24 | 0.19 ± 0.01 | 0.76 ± 0.01 | 0.27 ± 0.01 | 3.60 | 1.76 | 2.99 | 103.83 | 32.30 | 34.67 | ||
| GNDVI | 0.10 | 0.73 | 0.01 | 0.12 ± 0.01 | 0.72 ± 0.01 | 0.12 ± 0.01 | 3.75 | 1.92 | 3.41 | 107.11 | 36.55 | 38.39 | ||
| LSWI | 0.48 | 0.74 | 0.47 | 0.47 ± 0.01 | 0.72 ± 0.01 | 0.47 ± 0.01 | 2.85 | 1.89 | 2.51 | 85.64 | 35.71 | 29.76 | ||
| MNDWI | 0.03 | 0.22 | 0.61 | 0.05 ± 0.00 | 0.23 ± 0.01 | 0.56 ± 0.01 | 3.90 | 3.25 | 2.13 | 110.15 | 62.90 | 25.21 | ||
| NDSVI | 0.01 | 0.55 | 0.13 | 0.03 ± 0.00 | 0.56 ± 0.01 | 0.17 ± 0.01 | 3.94 | 2.45 | 3.20 | 110.92 | 48.83 | 36.53 | ||
| 3 | GPP | NDVIPV | 0.11 | 0.73 | 0.45 | 0.13 ± 0.01 | 0.72 ± 0.01 | 0.46 ± 0.01 | 4.45 | 2.07 | 2.49 | 212.88 | 64.97 | 55.10 |
| GPP=LUE*(a*VI+b)*Rg | NDVI | 0.26 | 0.84 | 0.25 | 0.27 ± 0.01 | 0.84 ± 0.00 | 0.28 ± 0.01 | 3.75 | 1.67 | 2.98 | 107.03 | 29.72 | 34.58 | |
| EVI | 0.26 | 0.76 | 0.33 | 0.28 ± 0.01 | 0.76 ± 0.01 | 0.34 ± 0.01 | 3.72 | 1.92 | 2.84 | 106.41 | 36.71 | 33.24 | ||
| SAVI | 0.18 | 0.77 | 0.31 | 0.2 ± 0.01 | 0.77 ± 0.01 | 0.33 ± 0.01 | 3.92 | 1.90 | 2.87 | 110.48 | 36.03 | 33.52 | ||
| GNDVI | 0.11 | 0.80 | 0.01 | 0.14 ± 0.01 | 0.8 ± 0.01 | 0.12 ± 0.01 | 4.10 | 1.81 | 3.46 | 114.01 | 33.80 | 38.73 | ||
| LSWI | 0.27 | 0.74 | 0.40 | 0.28 ± 0.01 | 0.73 ± 0.01 | 0.41 ± 0.01 | 3.68 | 1.99 | 2.67 | 105.69 | 38.32 | 31.45 | ||
| MNDWI | 0.08 | 0.26 | 0.53 | 0.12 ± 0.01 | 0.3 ± 0.01 | 0.49 ± 0.01 | 3.90 | 3.15 | 2.38 | 110.08 | 61.45 | 28.26 | ||
| NDSVI | 0.03 | 0.67 | 0.18 | 0.07 ± 0.00 | 0.68 ± 0.01 | 0.22 ± 0.01 | 4.24 | 2.13 | 3.13 | 116.69 | 41.80 | 35.92 | ||
| R2 | R2boot | RMSE | AIC | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Model | Flux | VIs | Single | Wet | Dry | Single | Wet | Dry | Single | Wet | Dry | Single | Wet | Dry |
| 1 | NEE | NDVIPV | 0.30 | 0.36 | 0.59 | 0.3 ± 0.00 | 0.37 ± 0.01 | 0.59 ± 0.01 | 1.45 | 1.42 | 0.80 | 55.86 | 33.36 | −8.48 |
| Flux = a*VI + b | NDVI | 0.52 | 0.52 | 0.74 | 0.5 ± 0.01 | 0.5 ± 0.01 | 0.74 ± 0.01 | 1.23 | 1.21 | 0.85 | 20.70 | 13.92 | −0.61 | |
| EVI | 0.59 | 0.55 | 0.82 | 0.56 ± 0.01 | 0.51 ± 0.01 | 0.82 ± 0.01 | 1.13 | 1.17 | 0.71 | 13.80 | 12.31 | −5.69 | ||
| SAVI | 0.54 | 0.57 | 0.81 | 0.52 ± 0.01 | 0.53 ± 0.01 | 0.82 ± 0.01 | 1.20 | 1.15 | 0.74 | 18.98 | 11.19 | −4.61 | ||
| GNDVI | 0.28 | 0.53 | 0.11 | 0.3 ± 0.01 | 0.5 ± 0.01 | 0.26 ± 0.02 | 1.49 | 1.20 | 1.58 | 36.85 | 13.46 | 16.79 | ||
| LSWI | 0.62 | 0.58 | 0.86 | 0.61 ± 0.01 | 0.55 ± 0.01 | 0.85 ± 0.01 | 1.08 | 1.13 | 0.63 | 10.52 | 10.19 | −8.72 | ||
| MNDWI | 0.18 | 0.04 | 0.64 | 0.17 ± 0.01 | 0.03 ± 0.00 | 0.6 ± 0.01 | 1.60 | 1.71 | 1.00 | 42.41 | 31.89 | 4.02 | ||
| NDSVI | 0.03 | 0.14 | 0.13 | 0.06 ± 0.00 | 0.2 ± 0.01 | 0.16 ± 0.01 | 1.73 | 1.62 | 1.56 | 49.18 | 29.07 | 16.48 | ||
| GPP | NDVIPV | 0.43 | 0.60 | 0.59 | 0.43 ± 0.00 | 0.59 ± 0.01 | 0.6 ± 0.01 | 1.41 | 1.18 | 0.90 | 51.77 | 17.58 | −1.92 | |
| NDVI | 0.59 | 0.82 | 0.47 | 0.61 ± 0.01 | 0.82 ± 0.00 | 0.5 ± 0.01 | 1.09 | 0.71 | 1.07 | 11.18 | −12.88 | 5.79 | ||
| EVI | 0.62 | 0.78 | 0.57 | 0.62 ± 0.01 | 0.77 ± 0.00 | 0.59 ± 0.01 | 1.06 | 0.80 | 0.96 | 9.02 | −7.37 | 2.98 | ||
| SAVI | 0.54 | 0.83 | 0.52 | 0.56 ± 0.01 | 0.82 ± 0.00 | 0.56 ± 0.01 | 1.16 | 0.71 | 1.01 | 15.93 | −13.46 | 4.33 | ||
| GNDVI | 0.35 | 0.84 | 0.07 | 0.4 ± 0.01 | 0.84 ± 0.00 | 0.25 ± 0.02 | 1.39 | 0.68 | 1.41 | 30.31 | −15.27 | 13.69 | ||
| LSWI | 0.58 | 0.73 | 0.62 | 0.61 ± 0.01 | 0.72 ± 0.01 | 0.65 ± 0.01 | 1.11 | 0.88 | 0.90 | 12.36 | −2.34 | 1.08 | ||
| MNDWI | 0.09 | 0.00 | 0.69 | 0.11 ± 0.01 | 0.02 ± 0.00 | 0.65 ± 0.01 | 1.64 | 1.70 | 0.82 | 43.39 | 30.47 | −1.55 | ||
| NDSVI | 0.16 | 0.46 | 0.17 | 0.16 ± 0.01 | 0.46 ± 0.01 | 0.2 ± 0.01 | 1.57 | 1.25 | 1.34 | 40.27 | 15.28 | 12.15 | ||
| 2 | GPP | NDVIPV | 0.19 | 0.78 | 0.52 | 0.2 ± 0.00 | 0.78 ± 0.01 | 0.52 ± 0.01 | 1.67 | 0.87 | 0.98 | 75.59 | −7.60 | 2.61 |
| GPP=a*(VI*Rg)+b | NDVI | 0.30 | 0.85 | 0.32 | 0.33 ± 0.01 | 0.84 ± 0.00 | 0.35 ± 0.01 | 1.43 | 0.66 | 1.21 | 32.78 | −16.99 | 9.37 | |
| EVI | 0.34 | 0.81 | 0.40 | 0.37 ± 0.01 | 0.8 ± 0.01 | 0.43 ± 0.01 | 1.39 | 0.74 | 1.13 | 30.53 | −10.95 | 7.52 | ||
| SAVI | 0.28 | 0.82 | 0.37 | 0.32 ± 0.01 | 0.81 ± 0.01 | 0.41 ± 0.01 | 1.46 | 0.71 | 1.16 | 34.06 | −12.92 | 8.14 | ||
| GNDVI | 0.17 | 0.78 | 0.05 | 0.22 ± 0.01 | 0.78 ± 0.01 | 0.2 ± 0.01 | 1.56 | 0.79 | 1.43 | 39.57 | −7.94 | 14.00 | ||
| LSWI | 0.57 | 0.76 | 0.61 | 0.59 ± 0.01 | 0.74 ± 0.01 | 0.63 ± 0.01 | 1.13 | 0.83 | 0.92 | 13.47 | −5.47 | 1.53 | ||
| MNDWI | 0.01 | 0.25 | 0.55 | 0.02 ± 0.00 | 0.27 ± 0.01 | 0.51 ± 0.01 | 1.71 | 1.47 | 0.98 | 47.02 | 23.16 | 3.42 | ||
| NDSVI | 0.05 | 0.59 | 0.06 | 0.08 ± 0.00 | 0.59 ± 0.01 | 0.09 ± 0.00 | 1.67 | 1.08 | 1.42 | 45.02 | 7.98 | 13.89 | ||
| 3 | GPP | NDVIPV | 0.17 | 0.80 | 0.60 | 0.19 ± 0.01 | 0.8 ±0.01 | 0.6 ± 0.01 | 1.74 | 0.83 | 0.89 | 81.90 | −11.55 | −2.36 |
| GPP = LUE*(a*VI+b)*Rg | NDVI | 0.36 | 0.91 | 0.42 | 0.35 ± 0.01 | 0.9 ± 0.00 | 0.45 ± 0.01 | 1.52 | 0.57 | 1.12 | 37.41 | −24.15 | 7.28 | |
| EVI | 0.38 | 0.86 | 0.49 | 0.37 ± 0.01 | 0.85 ± 0.00 | 0.52 ± 0.01 | 1.50 | 0.67 | 1.06 | 36.36 | −15.84 | 5.52 | ||
| SAVI | 0.28 | 0.87 | 0.47 | 0.27 ± 0.01 | 0.86 ± 0.00 | 0.51 ± 0.01 | 1.61 | 0.66 | 1.08 | 41.89 | −17.14 | 6.05 | ||
| GNDVI | 0.18 | 0.89 | 0.06 | 0.19 ± 0.01 | 0.88 ± 0.00 | 0.26 ± 0.01 | 1.71 | 0.61 | 1.42 | 46.84 | −20.45 | 13.87 | ||
| LSWI | 0.36 | 0.86 | 0.55 | 0.35 ± 0.01 | 0.84 ± 0.00 | 0.58 ± 0.01 | 1.51 | 0.68 | 0.98 | 36.94 | −15.28 | 3.52 | ||
| MNDWI | 0.17 | 0.50 | 0.60 | 0.19 ± 0.01 | 0.51 ± 0.01 | 0.57 ± 0.01 | 1.59 | 1.24 | 0.93 | 41.14 | 14.66 | 2.09 | ||
| NDSVI | 0.09 | 0.77 | 0.16 | 0.12 ± 0.01 | 0.76 ± 0.01 | 0.21 ± 0.01 | 1.74 | 0.82 | 1.35 | 48.11 | −5.65 | 12.36 | ||
| Aggregate | VI Source | Flux | Wet Phase | Dry Phase |
|---|---|---|---|---|
| Midday | Landsat | GPP | −26.34*NDVI + 4.17, R2 = 0.85 | −64.9*MNDWI − 30.7, R2 = 0.63 |
| Proba-V | −0.03*(NDVIPV*Rg) − 0.71, R2 = 0.73 | −19.17*NDVIPV + 7.17, R2 = 0.46 | ||
| Landsat | NEE | −26.03*NDVI + 4.76, R2 = 0.80 | −73.81*MNDWI − 33.52, R2 = 0.69 | |
| Proba-V | −19.35*NDVIPV + 3.13, R2 = 0.59 | −18.49*NDVIPV + 7.75, R2 = 0.62 | ||
| Daily | Landsat | GPP | (−0.044*NDVI + 0.004)*Rg, R2 = 0.91 | −29.05*MNDWI − 13.93, R2 = 0.69 |
| Proba-V | (−0.033*NDVIPV)*Rg, R2 = 0.80 | (−0.028*NDVIPV + 0.01)*Rg, R2 = 0.60 | ||
| Landsat | NEE | −10.72*LSWI − 0.57, R2 = 0.58 | −12.34*LSWI + 0.3, R2 = 0.86 | |
| Proba-V | −6.81*NDVIPV + 2.61, R2 = 0.36 | −7.97*NDVIPV + 4.88, R2 = 0.59 |
| Flux Estimates (g C m−2 Growing Season−1) | ||||
|---|---|---|---|---|
| Year | GPP | GPP_24 | NEE | NEE_24 |
| 2014 | −394.13 | −709.63 | −351.76 | −259.57 |
| 2015 | −391.71 | −727.15 | −331.97 | −212.51 |
| 2016 | −368.15 | −702.08 | −312.16 | −161.44 |
| 2017 | −379.05 | −703.35 | −309.71 | −161.99 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Noumonvi, K.D.; Ferlan, M.; Eler, K.; Alberti, G.; Peressotti, A.; Cerasoli, S. Estimation of Carbon Fluxes from Eddy Covariance Data and Satellite-Derived Vegetation Indices in a Karst Grassland (Podgorski Kras, Slovenia). Remote Sens. 2019, 11, 649. https://doi.org/10.3390/rs11060649
Noumonvi KD, Ferlan M, Eler K, Alberti G, Peressotti A, Cerasoli S. Estimation of Carbon Fluxes from Eddy Covariance Data and Satellite-Derived Vegetation Indices in a Karst Grassland (Podgorski Kras, Slovenia). Remote Sensing. 2019; 11(6):649. https://doi.org/10.3390/rs11060649
Chicago/Turabian StyleNoumonvi, Koffi Dodji, Mitja Ferlan, Klemen Eler, Giorgio Alberti, Alessandro Peressotti, and Sofia Cerasoli. 2019. "Estimation of Carbon Fluxes from Eddy Covariance Data and Satellite-Derived Vegetation Indices in a Karst Grassland (Podgorski Kras, Slovenia)" Remote Sensing 11, no. 6: 649. https://doi.org/10.3390/rs11060649
APA StyleNoumonvi, K. D., Ferlan, M., Eler, K., Alberti, G., Peressotti, A., & Cerasoli, S. (2019). Estimation of Carbon Fluxes from Eddy Covariance Data and Satellite-Derived Vegetation Indices in a Karst Grassland (Podgorski Kras, Slovenia). Remote Sensing, 11(6), 649. https://doi.org/10.3390/rs11060649