Decision Fusion Framework for Hyperspectral Image Classification Based on Markov and Conditional Random Fields
Abstract
1. Introduction
2. Methodology
2.1. Preliminaries
2.1.1. MRF Regularization
2.1.2. CRF Regularization
2.2. The Decision Sources
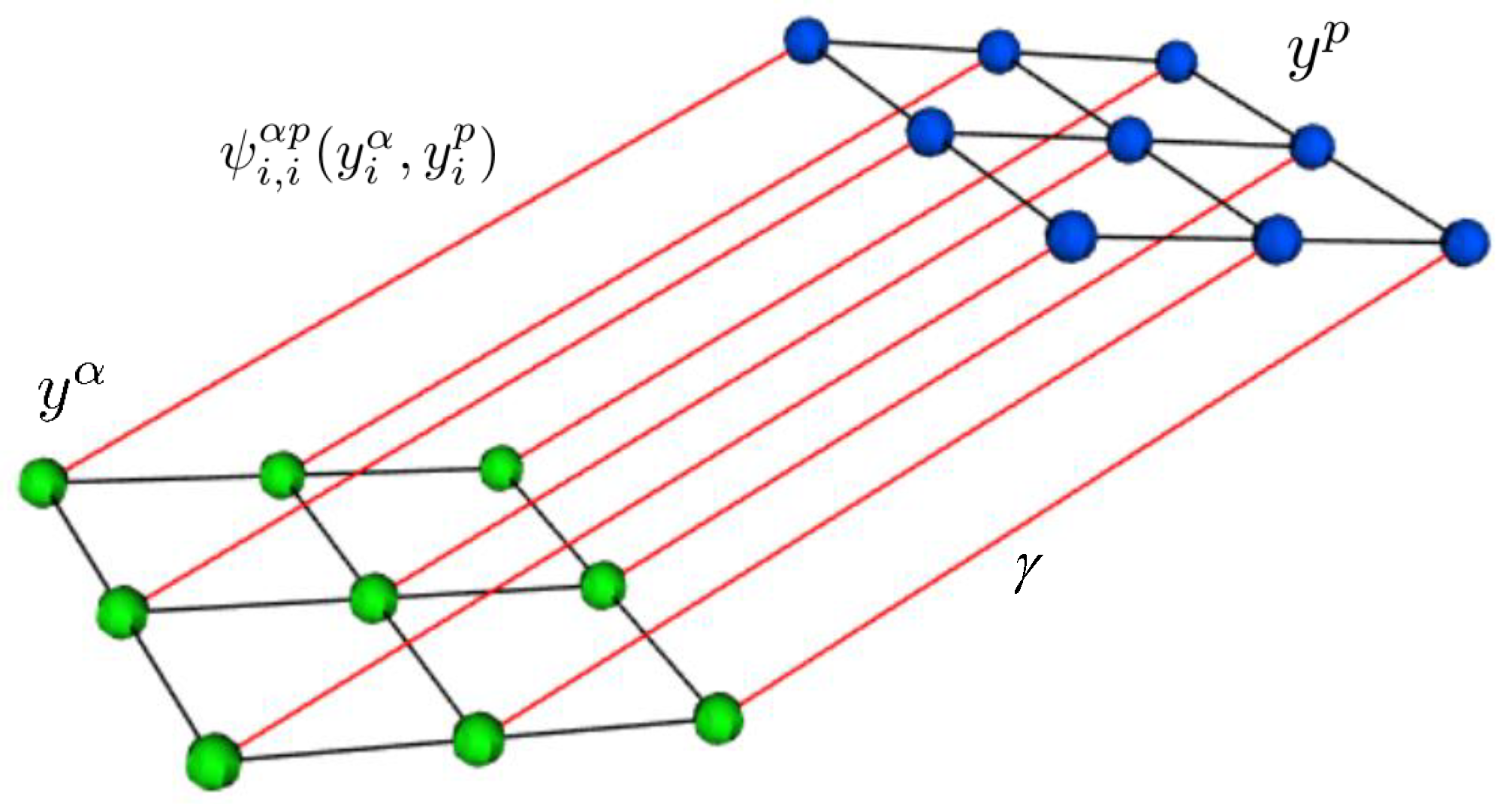
2.3. MRF with Cross Links for Fusion (MRFL)
2.4. CRF with Cross Links for Fusion (CRFL)
3. Experimental Results and Discussion
3.1. Hyperspectral Data Sets
3.1.1. University of Pavia
3.1.2. Indian Pines
3.2. Parameter Settings
- the performance of the sparse representation obtained by the pixels fractional abundances from SunSAL as decisions, when combined with classification probabilities in a decision fusion scheme;
- the comparison of the performances of MRFL and CRFL as decision fusion methods;
- the flexibility of the proposed fusion methods, by including additional decision sets;
- the performance of the method in the case of small training sample sizes.
- The OA initially improves with increasing and , proving the effectiveness of incorporating the spatial neighborhood and the consistency terms in our proposed methods, to correct for the wrongly initially assigned labels from the individual sources.
- In general, the OA is more sensitive to changes of , and remains relatively stable for a large range of values of .
- A significant accuracy drop can be observed for higher values of and in the MRFL method, whereas the CRFL method produces more stable results for different combinations of and . This allows for applying the CRFL method to other images without having to perform extensive and exhaustive parameter grid searches.
- The optimal values of and are substantially higher for CRFL than for MRFL. This is because the CRFL method inherently uses observed data in the pairwise potentials, and thus heavily penalizes small differences between decisions that correspond to different class labels.
- For the Indian Pines image, is much higher than in the case of CRFL. This can be attributed to the presence of large homogeneous regions that imply a low influence of the spatial neighborhood compared to the consistency terms. In contrast, the University of Pavia image contains less large homogeneous regions, leading to an increase of the influence of the spatial neighborhood, with larger values of in the case of CRFL.
3.3. Experiments
3.3.1. Experiment 1: Complementarity of the Abundances
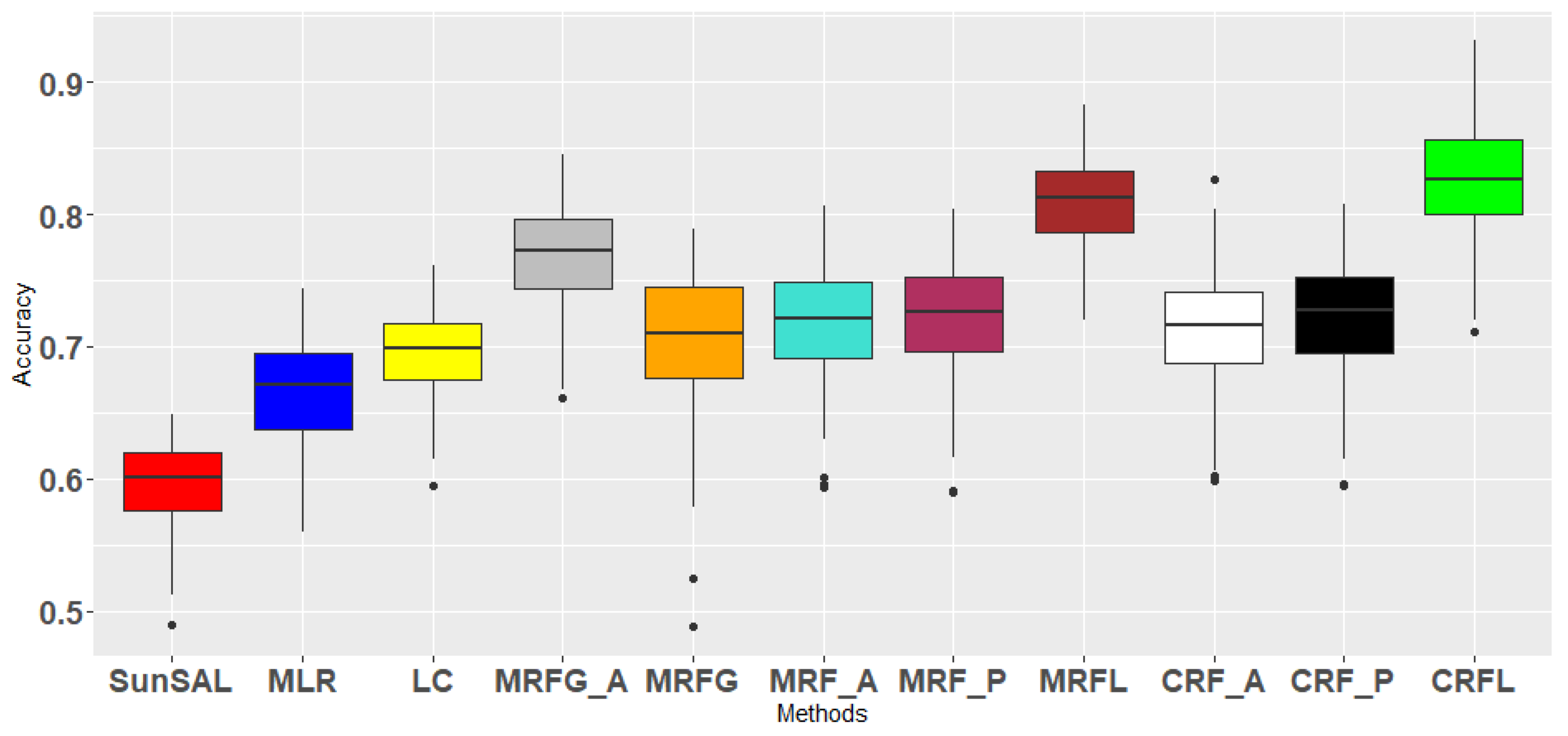
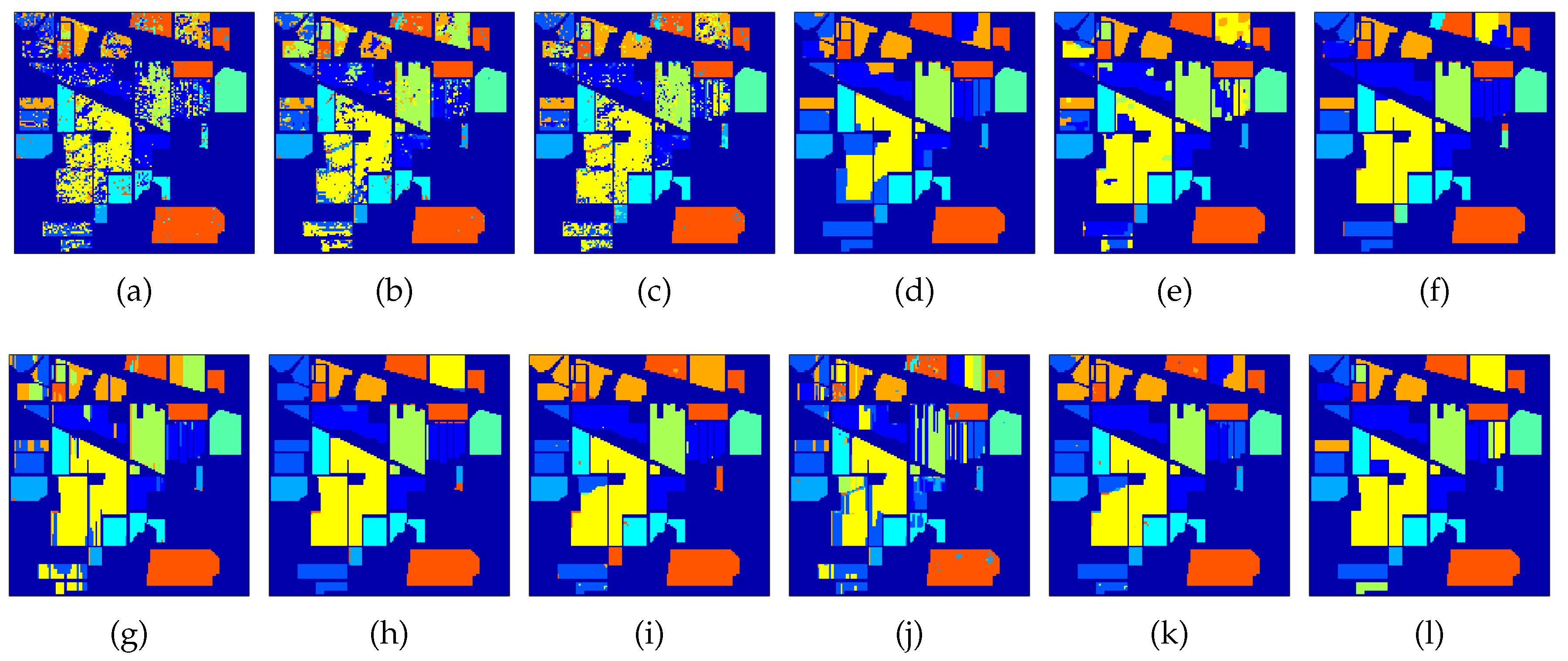
3.3.2. Experiment 2: Validation of the Decision Fusion Framework
- SunSAL [29]—sparse spectral unmixing is applied to each test pixel, obtaining the abundance vector . From this vector, the pixel is labeled as the class corresponding to the largest abundance value: . This is a single source, spectral only method.
- MLR—Multinomial Logistic Regression classifier [36] generating the class probabilities . From this vector, the pixel is labeled as the class corresponding to the largest probability . This is also a single source, spectral only method.
- LC—linear combination, a simple decision fusion approach, using a linear combination of the obtained abundances and class probabilities by applying the linear opinion pool rule from: [15]. This is a spectral only fusion method. This method was applied in [30] on the same sources as initialisation for a semi-supervised approach.
- MRFG_a [23]—a decision fusion framework from the recent literature. The principle of this method is to linearly combine different decision sources, weighted by the accuracies of each of the sources. The obtained single source is then regularized by a MRF, as in Equation (1). In [23], three different sources were applied. For a fair comparison, we apply their fusion method with the abundances and class probabilities from our method as decision sources.
- MRFG—the same decision fusion method as MRFG_a, but this time, the posterior classification probabilities from the abundances as obtained in [23] are employed. In that work, the abundances were obtained with a matched filtering technique. To produce the posterior classification probabilities, the MLR classifier was used.
- MRF_a—this method applies a MRF regularization on the output of SunSAL as a single source. This is a spatial-spectral single source method.
- MRF_p—a spatial-spectral single source method, applying MRF as a regularizer on the output of the MLR classifier.
- CRF_a—a spatial-spectral single source method, applying CRF as a regularizer on the output of SunSAL.
- CRF_p—a spatial-spectral single source method, applying CRF as a regularizer on the output of the MLR classifier.
(a) University of Pavia dataset
(b) Indian Pines dataset
3.3.3. Experiment 3: Comparison of Different Decision Sources
- Pair 1: probabilities based on the spectra and probabilities based on the fractional abundances.The first source is the same as in the previous experiments and the fractional abundances were obtained using SunSAL. Subsequently, the abundances were used as input to an MLR classifier, to produce posterior classification probabilities for this set. Ultimately, these two sources of information were fused with the proposed MRFL and CRFL fusion schemes. Therefore, the only difference with the previous experiment is that, instead of the abundances, classification probabilities from the abundances are used.
- Pair 2: probabilities based on morphological profiles and probabilities based on the fractional abundances. Initially, (partial) morphological profiles were extracted as in [6] and used as input to an MLR classifier, to produce posterior classification probabilities. These were fused with the probabilities from the abundances using the proposed MRFL and CRFL fusion schemes. The difference with before is that the morphological profiles contain spatial-spectral information.
- Pair 3: probabilities based on morphological profiles and probabilities based on the spectra.
- Pair 4: For the CRFL pairwise fusion, we conducted one additional pairwise fusion, between the the pure fractional abundances and the probabilities based on the morphological profiles.
- In general, accuracies go down when the abundances are not directly used, but, instead, class probabilities are calculated from them (Pair 1).
- For the University of Pavia image, accuracies slightly improve when the spectral features are replaced by contextual features, but part of the effect disappears again because of the above-mentioned effect (Pair 2 and Pair 3). The best result is obtained with a direct use of abundances along with contextual features (CRF_Pair4).
- For the Indian Pines image, no improvement is observed when including contextual features.
3.3.4. Experiment 4: Additional Sources in the Fusion Framework
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hughes, G. On the Mean Accuracy of Statistical Pattern Recognizers. IEEE Trans. Inf. Theor. 2006, 14, 55–63. [Google Scholar] [CrossRef]
- Plaza, A.; Martinez, P.; Plaza, J.; Perez, R. Dimensionality reduction and classification of hyperspectral image data using sequences of extended morphological transformations. IEEE Trans. Geosci. Remote Sens. 2005, 43, 466–479. [Google Scholar] [CrossRef]
- Dalla Mura, M.; Benediktsson, J.A.; Waske, B.; Bruzzone, L. Extended profiles with morphological attribute filters for the analysis of hyperspectral data. Int. J. Remote Sens. 2010, 31, 5975–5991. [Google Scholar] [CrossRef]
- Liao, W.; Bellens, R.; Pizurica, A.; Philips, W.; Pi, Y. Classification of Hyperspectral Data Over Urban Areas Using Directional Morphological Profiles and Semi-Supervised Feature Extraction. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 1177–1190. [Google Scholar] [CrossRef]
- Benediktsson, J.A.; Palmason, J.A.; Sveinsson, J.R. Classification of hyperspectral data from urban areas based on extended morphological profiles. IEEE Trans. Geosci. Remote Sens. 2005, 43, 480–491. [Google Scholar] [CrossRef]
- Liao, W.; Chanussot, J.; Dalla Mura, M.; Huang, X.; Bellens, R.; Gautama, S.; Philips, W. Taking optimal advantage of fine spatial information: promoting partial image reconstruction for the morphological analysis of very-high-resolution images. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–28. [Google Scholar] [CrossRef]
- Licciardi, G.; Marpu, P.R.; Chanussot, J.; Benediktsson, J.A. Linear versus nonlinear PCA for the classification of hyperspectral data based on the extended morphological profiles. IEEE Geosci. Remote Sens. Lett. 2012, 9, 447–451. [Google Scholar] [CrossRef]
- Song, B.; Li, J.; Dalla Mura, M.; Li, P.; Plaza, A.; Bioucas-Dias, J.M.; Benediktsson, J.A.; Chanussot, J. Remotely sensed image classification using sparse representations of morphological attribute profiles. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5122–5136. [Google Scholar] [CrossRef]
- Fauvel, M.; Benediktsson, J.; Chanussot, J.; Sveinsson, J. Spectral and spatial classification of hyperspectral data using SVMs and morphological profiles. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3804–3814. [Google Scholar] [CrossRef]
- Tuia, D.; Matasci, G.; Camps-Valls, G.; Kanevski, M. Learning the relevant image features with multiple kernels. In Proceedings of the 2009 IEEE International Geoscience and Remote Sensing Symposium, Cape Town, South Africa, 12–17 July 2009; Volume 2, pp. II-65–II-68. [Google Scholar]
- Li, J.; Huang, X.; Gamba, P.; Bioucas-Dias, J.M.; Zhang, L.; Benediktsson, J.A.; Plaza, A.J. Multiple feature learning for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1592–1606. [Google Scholar] [CrossRef]
- Licciardi, G.; Pacifici, F.; Tuia, D.; Prasad, S.; West, T.; Giacco, F.; Thiel, C.; Inglada, J.; Christophe, E.; Chanussot, J.; et al. Decision fusion for the classification of hyperspectral data: outcome of the 2008 GRSS data fusion contest. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3857–3865. [Google Scholar] [CrossRef]
- Song, B.; Li, J.; Li, P.; Plaza, A. Decision fusion based on extended multi-attribute profiles for hyperspectral image classification. In Proceedings of the 5th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Gainesville, FL, USA, 26–28 June 2013. [Google Scholar]
- Li, W.; Prasad, S.; Tramel, E.W.; Fowler, J.E.; Du, Q. Decision fusion for hyperspectral image classification based on minimum-distance classifiers in the wavelet domain. In Proceedings of the 2014 IEEE China Summit & International Conference on Signal and Information Processing (ChinaSIP), Xi’an, China, 9–13 July 2014; pp. 162–165. [Google Scholar]
- Benediktsson, J.A.; Kanellopoulos, I. Classification of multisource and hyperspectral data based on decision fusion. IEEE Trans. Geosci. Remote Sens. 1999, 37, 1367–1377. [Google Scholar] [CrossRef]
- Kalluri, H.R.; Prasad, S.; Bruce, L.M. Decision-level fusion of spectral reflectance and derivative information for robust hyperspectral land cover classification. IEEE Trans. Geosci. Remote Sens. 2010, 48, 4047–4058. [Google Scholar] [CrossRef]
- Yang, H.; Du, Q.; Ma, B. Decision fusion on supervised and unsupervised classifiers for hyperspectral imagery. IEEE Geosci. Remote Sens. Lett. 2010, 7, 875–879. [Google Scholar] [CrossRef]
- Li, S.; Lu, T.; Fang, L.; Jia, X.; Benediktsson, J.A. Probabilistic fusion of pixel-level and superpixel-level hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2016, 54, 7416–7430. [Google Scholar] [CrossRef]
- Khodadadzadeh, M.; Li, J.; Ghassemian, H.; Bioucas-Dias, J.; Li, X. Spectral-spatial classification of hyperspectral data using local and global probabilities for mixed pixel characterization. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6298–6314. [Google Scholar] [CrossRef]
- Khodadadzadeh, M.; Li, J.; Plaza, A.; Ghassemian, H.; Bioucas-Dias, J.M. Spectral-spatial classification for hyperspectral data using SVM and subspace MLR. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium—IGARSS, Melbourne, Australia, 21–26 July 2013; pp. 2180–2183. [Google Scholar]
- Xia, J.; Chanussot, J.; Du, P.; He, X. Spectral–spatial classification for hyperspectral data using rotation forests with local feature extraction and markov random fields. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2532–2546. [Google Scholar] [CrossRef]
- Lu, Q.; Huang, X.; Li, J.; Zhang, L. A novel MRF-based multifeature fusion for classification of remote sensing images. IEEE Geosci. Remote Sens. Lett. 2016, 13, 515–519. [Google Scholar] [CrossRef]
- Lu, T.; Li, S.; Fang, L.; Jia, X.; Benediktsson, J.A. From subpixel to superpixel: a novel fusion framework for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4398–4411. [Google Scholar] [CrossRef]
- Gómez-Chova, L.; Tuia, D.; Moser, G.; Camps-Valls, G. Multimodal classification of remote sensing images: a review and future directions. Proc. IEEE 2015, 103, 1560–1584. [Google Scholar] [CrossRef]
- Solberg, A.H.S.; Taxt, T.; Jain, A.K. A markov random field model for classification of multisource satellite imagery. IEEE Trans. Geosci. Remote Sens. 1996, 34, 100–113. [Google Scholar] [CrossRef]
- Wegner, J.D.; Hansch, R.; Thiele, A.; Soergel, U. Building detection from one orthophoto and high-resolution InSAR data using conditional random fields. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2011, 4, 83–91. [Google Scholar] [CrossRef]
- Albert, L.; Rottensteiner, F.; Heipke, C. A higher order conditional random field model for simultaneous classification of land cover and land use. Int. J. Photogramm. Remote Sens. 2017, 130, 63–80. [Google Scholar] [CrossRef]
- Tuia, D.; Volpi, M.; Moser, G. Decision fusion with multiple spatial supports by conditional random fields. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3277–3289. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.; Figueiredo, M. Alternating direction algorithms for constrained sparse regression: Application to hyperspectral unmixing. In Proceedings of the 2nd Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Reykjavik, Iceland, 14–16 June 2010. [Google Scholar]
- Dopido, I.; Li, J.; Gamba, P.; Plaza, A. A new hybrid strategy combining semisupervised classification and unmixing of hyperspectral data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 3619–3629. [Google Scholar] [CrossRef]
- Chen, Y.; Nasrabadi, N.M.; Tran, T.D. Hyperspectral image classification using dictionary-based sparse representation. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3973–3985. [Google Scholar] [CrossRef]
- Li, W.; Du, Q. Joint within-class collaborative representation for hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2200–2208. [Google Scholar] [CrossRef]
- Sun, X.; Qu, Q.; Nasrabadi, N.M.; Tran, T.D. Structured priors for sparse-representation-based hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1235–1239. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Scheunders, P.; Tuia, D.; Moser, G. Contributions of machine learning to remote sensing data analysis. In Comprehensive Remote Sensing; Liang, S., Ed.; Elsevier: Amsterdam, The Netherlands, 2017; Volume 2, Chapter 10. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning; Springer: New York, NY, USA, 2009. [Google Scholar]
- Namin, S.T.; Najafi, M.; Salzmann, M.; Petersson, L. A multi-modal graphical model for scene analysis. In Proceedings of the 2015 IEEE Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 5–9 January 2015; pp. 1006–1013. [Google Scholar] [CrossRef]
- Boykov, Y.; Kolmogorov, V. An experimental comparison of min-cut/max-flow algorithms for energy minimization in vision. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 1124–1137. [Google Scholar] [CrossRef]
- Boykov, Y.; Veksler, O.; Zabih, R. Fast approximation energy minimization via graph cuts. IEEE Trans. Pattern Anal. Mach. Intell. 2001, 23, 1222–1239. [Google Scholar] [CrossRef]
- Kohli, P.; Ladicky, L.; Torr, P. Robust higher order potentials for enforcing label consistency. Int. J. Comp. Vis. 2009, 82, 302–324. [Google Scholar] [CrossRef]
- Kohli, P.; Ladicky, L.; Torr, P. Graph Cuts for Minimizing Robust Higher Order Potentials; Technical Report; Oxford Brookes University: Oxford, UK, 2008. [Google Scholar]
- Boykov, Y.; Jolly, M.P. Interactive graph cuts for optimal boundary and region segmentation of objects in n-D images. In Proceedings of the Eighth IEEE International Conference on Computer Vision, Vancouver, BC, Canada, 7–14 July 2001. [Google Scholar]
- Weinmann, M.; Schmidt, A.; Mallet, C.; Hinz, S.; Rottensteiner, F.; Jutzi, B. Contextual classification of point cloud data by exploiting individual 3D neighborhoods. ISPRS Ann. Photogramm. Remote Sensi. Spat. Inf. Sci. 2015, II-3/W4, 271–278. [Google Scholar] [CrossRef]
- Iordache, M.D.; Bioucas-Dias, J.; Plaza, A. Collaborative sparse regression for hyperspectral unmixing. IEEE Trans. Geosci. Remote Sens. 2013, 52, 341–354. [Google Scholar] [CrossRef]
- Iordache, M.D.; Bioucas-Dias, J.; Plaza, A. Total variation spatial regularization for sparse hyperspectral unmixing. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4484–4502. [Google Scholar] [CrossRef]






| Image | |||||
|---|---|---|---|---|---|
| University of Pavia | 1.0 | 1.0 | 25 | 25 | |
| Indian Pines | 1.0 | 0.8 | 5 | 25 |
| Class | Train | Test | SunSAL | MLR | LC | MRFG_a | MRFG | MRF_a | MRF_p | MRFL | CRF_a | CRF_p | CRFL |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Asphalt | 10 | 6621 | 33.04 | 50.72 | 50.42 | 66.60 | 58.05 | 52.26 | 58.80 | 77.56 | 50.40 | 59.28 | 77.86 |
| Meadows | 10 | 18,639 | 68.95 | 67.16 | 73.46 | 78.08 | 71.18 | 80.97 | 71.80 | 82.13 | 81.66 | 72.70 | 88.74 |
| Gravel | 10 | 2089 | 60.59 | 70.93 | 77.01 | 87.85 | 71.18 | 88.30 | 78.82 | 90.90 | 86.49 | 76.86 | 92.71 |
| Trees | 10 | 3054 | 84.61 | 88.95 | 91.49 | 91.79 | 91.72 | 91.56 | 88.92 | 91.95 | 90.80 | 88.76 | 89.51 |
| Metal Sheet | 10 | 1335 | 95.43 | 97.81 | 98.71 | 98.96 | 98.85 | 99.30 | 98.11 | 99.46 | 98.59 | 97.88 | 99.28 |
| Bare Soil | 10 | 5019 | 46.80 | 55.85 | 56.10 | 59.9 | 59.90 | 53.44 | 59.18 | 61.29 | 52.20 | 59.04 | 63.07 |
| Bitumen | 10 | 1320 | 48.80 | 80.75 | 83.24 | 95.43 | 87.82 | 91.07 | 90.98 | 97.14 | 90.15 | 89.87 | 96.55 |
| Bricks | 10 | 3672 | 36.74 | 61.60 | 55.99 | 71.85 | 63.11 | 34.75 | 72.33 | 72.64 | 34.72 | 72.64 | 58.25 |
| Shadows | 10 | 937 | 98.61 | 95.52 | 99.31 | 99.83 | 99.66 | 99.96 | 96.88 | 99.88 | 99.92 | 96.74 | 99.97 |
| OA (OA-SD) | - | - | 59.56 | 66.53 | 69.45 | 76.74 | 70.59 | 71.71 | 71.88 | 80.67 | 71.39 | 72.19 | 82.47 |
| AA (AA-SD) | - | - | 63.73 | 74.37 | 76.19 | 83.37 | 81.35 | 76.84 | 79.55 | 85.88 | 76.11 | 79.31 | 85.10 |
| (-SD) | - | - | 0.48 | 0.57 | 0.61 | 0.70 | 0.70 | 0.63 | 0.64 | 0.74 | 0.63 | 0.64 | 0.77 |
| Class | Train | Test | SunSAL | MLR | LC | MRFG_a | MRFG | MRF_a | MRF_p | MRFL | CRF_a | CRF_p | CRFL |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Corn-notill | 10 | 1418 | 53.97 | 55.83 | 64.71 | 61.85 | 58.39 | 70.13 | 60.96 | 75.12 | 73.01 | 63.27 | 74.50 |
| Corn-mintill | 10 | 820 | 43.20 | 59.15 | 59.57 | 68.86 | 63.91 | 58.74 | 66.48 | 69.46 | 60.00 | 65.64 | 69.53 |
| Grass pasture | 10 | 473 | 81.02 | 82.41 | 84.83 | 89.50 | 89.27 | 80.52 | 84.23 | 82.38 | 78.97 | 83.49 | 81.60 |
| Grass trees | 10 | 720 | 88.24 | 91.75 | 96.12 | 97.31 | 96.47 | 98.45 | 95.66 | 99.52 | 99.15 | 94.94 | 98.94 |
| Hey Windrowed | 10 | 468 | 99.62 | 99.82 | 100 | 100 | 100 | 100 | 99.98 | 100 | 100 | 99.9 | 100 |
| Soybean-notill | 10 | 962 | 49.08 | 58.56 | 64.28 | 68.50 | 65.87 | 71.24 | 64.85 | 75.23 | 75.81 | 68.74 | 76.47 |
| Soybean-mintill | 10 | 2445 | 47.98 | 48.15 | 55.24 | 55.83 | 53.76 | 62.88 | 51.54 | 65.73 | 66.07 | 53.47 | 67.80 |
| Soybean-clean | 10 | 583 | 64.55 | 62.75 | 79.55 | 77.18 | 72.54 | 81.72 | 69.10 | 89.05 | 86.19 | 71.23 | 88.20 |
| Woods | 10 | 1255 | 78.41 | 84.04 | 88.39 | 89.85 | 89.00 | 91.99 | 87.04 | 92.38 | 92.34 | 86.32 | 92.42 |
| Buildings | 10 | 376 | 56.36 | 59.92 | 63.48 | 71.54 | 69.24 | 70.86 | 69.30 | 80.12 | 70.38 | 64.15 | 70.00 |
| OA (OA-SD) | - | - | 61.11 | 64.86 | 71.06 | 72.45 | 70.16 | 75.11 | 69.31 | 78.95 | 77.22 | 70.22 | 79.00 |
| AA (AA-SD) | - | - | 66.21 | 70.23 | 75.62 | 78.04 | 75.85 | 78.65 | 74.90 | 82.90 | 80.20 | 75.12 | 81.95 |
| (-SD) | - | - | 0.55 | 0.59 | 0.66 | 0.68 | 0.65 | 0.71 | 0.65 | 0.75 | 0.73 | 0.66 | 0.75 |
| MRF_Pair1 | MRF_Pair2 | MRF_Pair3 | CRF_Pair1 | CRF_Pair2 | CRF_Pair3 | CRF_Pair4 | |
|---|---|---|---|---|---|---|---|
| University of Pavia | 74.70 | 80.59 | 80.69 | 76.73 | 78.50 | 79.07 | 83.22 |
| Indian Pines | 76.51 | 77.70 | 77.26 | 73.70 | 73.25 | 74.70 | 77.03 |
| MRFL_3 | CRFL_3 | |
|---|---|---|
| University of Pavia | 83.52 | 88.51 |
| Indian Pines | 82.85 | 82.16 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andrejchenko, V.; Liao, W.; Philips, W.; Scheunders, P. Decision Fusion Framework for Hyperspectral Image Classification Based on Markov and Conditional Random Fields. Remote Sens. 2019, 11, 624. https://doi.org/10.3390/rs11060624
Andrejchenko V, Liao W, Philips W, Scheunders P. Decision Fusion Framework for Hyperspectral Image Classification Based on Markov and Conditional Random Fields. Remote Sensing. 2019; 11(6):624. https://doi.org/10.3390/rs11060624
Chicago/Turabian StyleAndrejchenko, Vera, Wenzhi Liao, Wilfried Philips, and Paul Scheunders. 2019. "Decision Fusion Framework for Hyperspectral Image Classification Based on Markov and Conditional Random Fields" Remote Sensing 11, no. 6: 624. https://doi.org/10.3390/rs11060624
APA StyleAndrejchenko, V., Liao, W., Philips, W., & Scheunders, P. (2019). Decision Fusion Framework for Hyperspectral Image Classification Based on Markov and Conditional Random Fields. Remote Sensing, 11(6), 624. https://doi.org/10.3390/rs11060624






