A Hierarchical Convolution Neural Network (CNN)-Based Ship Target Detection Method in Spaceborne SAR Imagery
Abstract
:1. Introduction
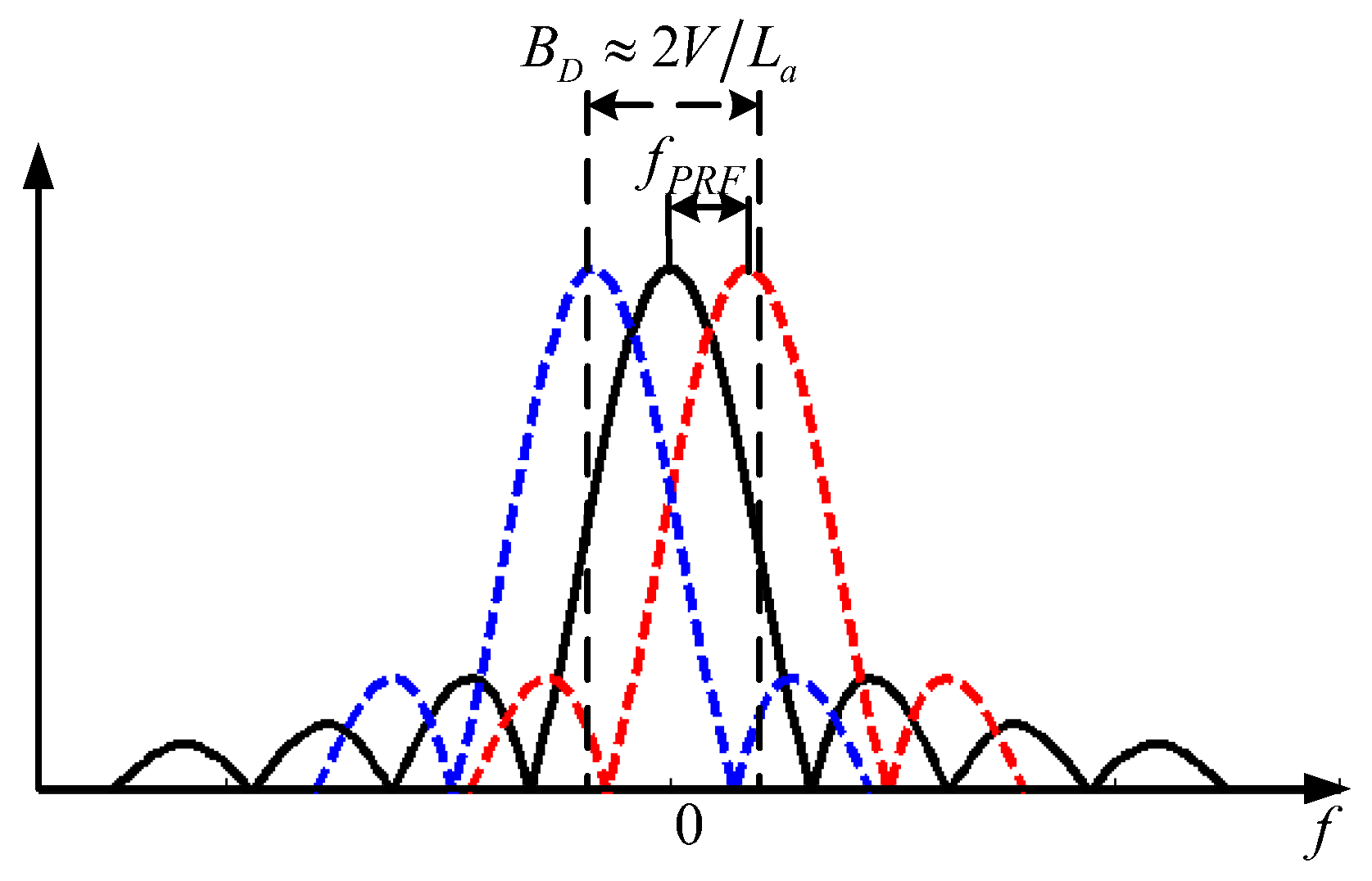
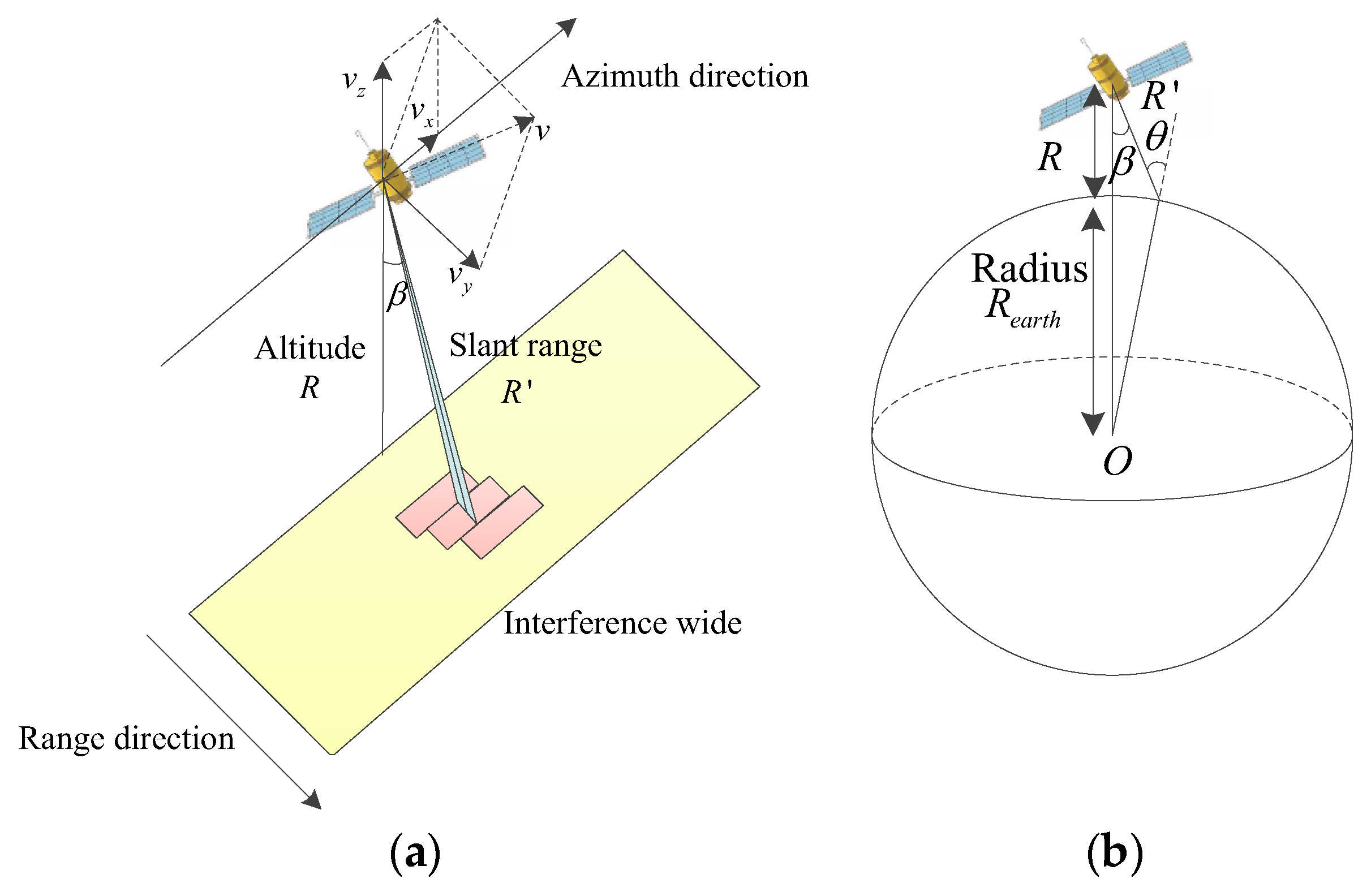
2. Ghost Phenomenon in Spaceborne SAR
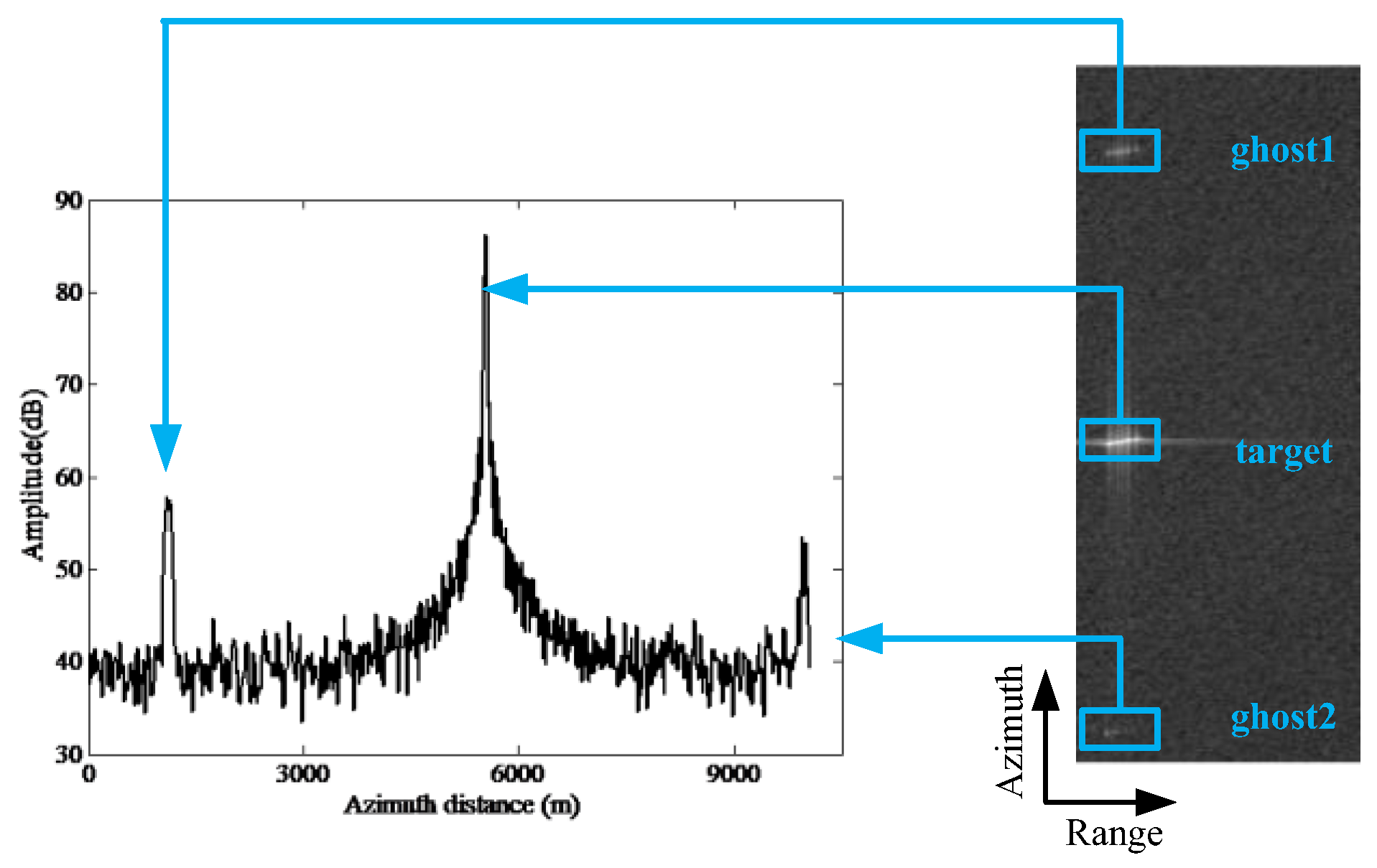
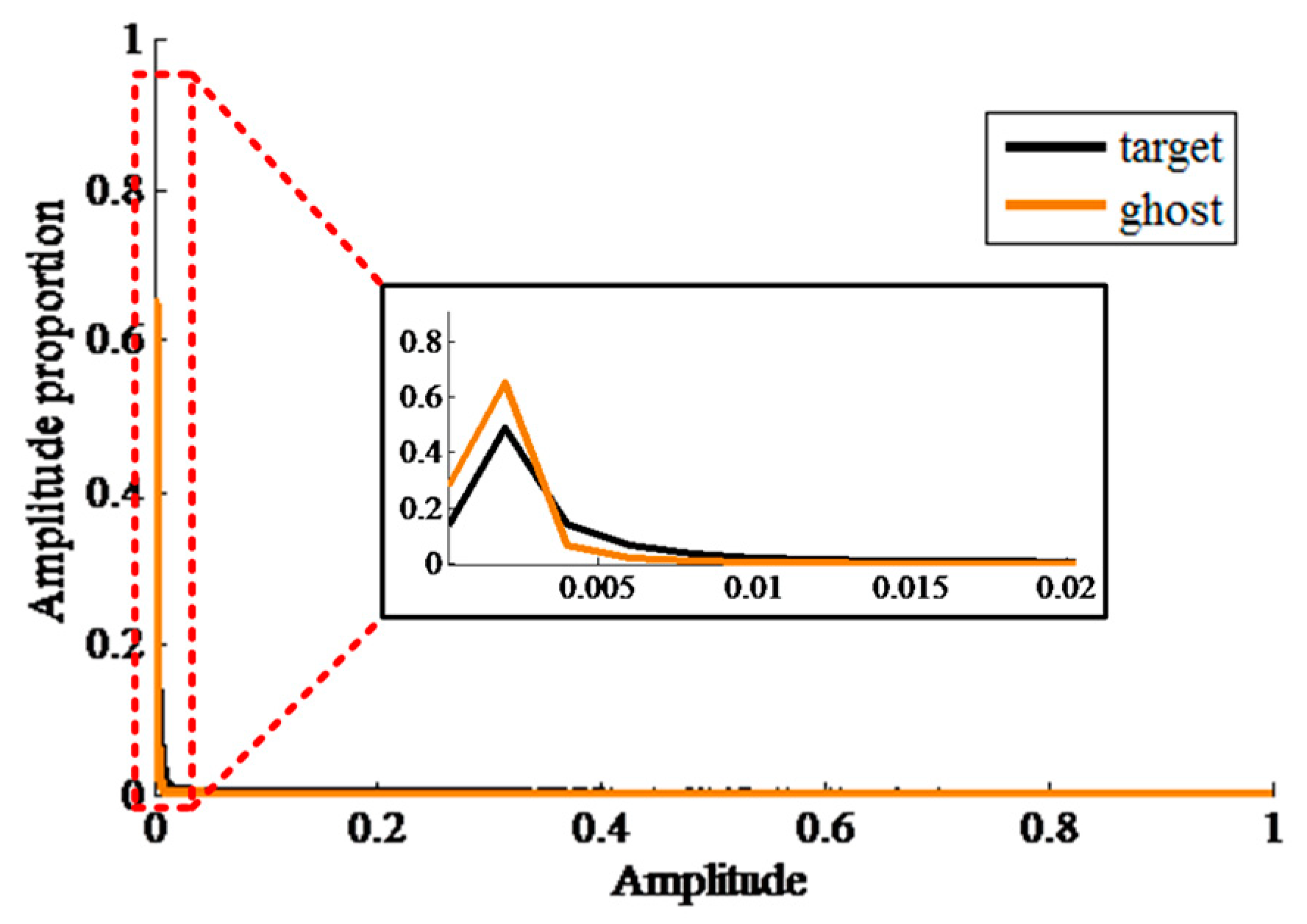
3. Property Analyses of Ship Target and Ghost Replica
4. Architecture of the H-CNN Model
5. Experiments and Results
5.1. Dataset
5.2. Discussion of Parameter Configuration of H-CNN
5.3. Analyses of Feature Extraction by H-CNN
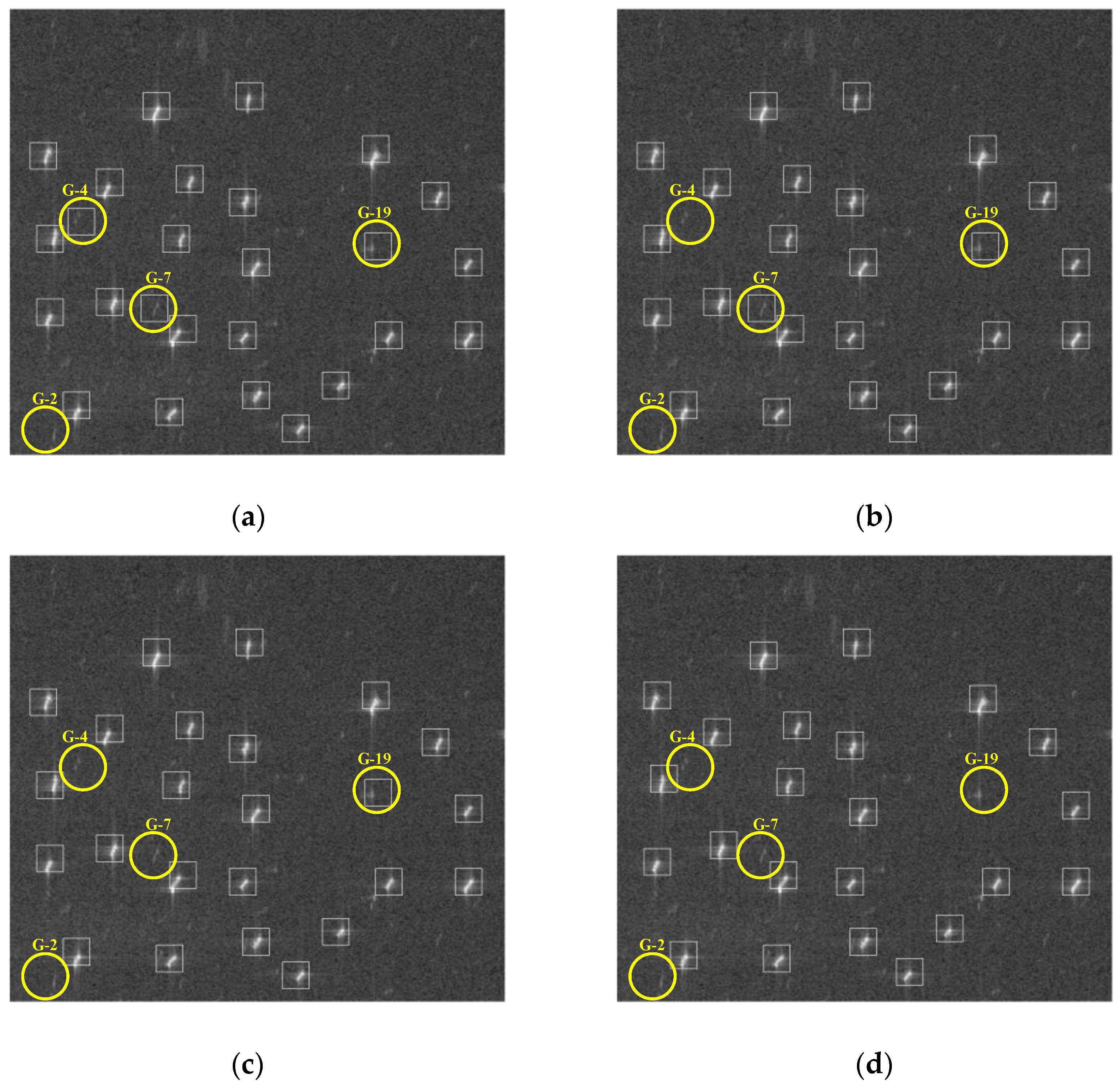
5.4. Detection Result Comparison
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Schwartz, G.; Alvarez, M.; Varfis, A.; Kourti, N. Elimination of false positives in vessels detection and identification by remote sensing. In Proceedings of the 2002 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Toronto, ON, Canada, 24–28 June 2002; pp. 116–118. [Google Scholar]
- Tu, S.; Su, Y.; Wang, W.; Xiong, B.; Li, Y. Automatic target recognition scheme for a high-resolution and large-scale synthetic aperture radar image. J. Appl. Remote Sens. 2015, 9, 096039. [Google Scholar] [CrossRef]
- Dale, A.A. Digital vs. optical techniques in synthetic aperture radar data processing. J. Appl. Remote Sens. 1977, 19, 238–257. [Google Scholar]
- El-Darymli, K.; McGuire, P.; Power, D.; Moloney, C.R. Target detection in synthetic aperture radar imagery: A state-of-the-art survey. J. Appl. Remote Sens. 2016, 7, 071598. [Google Scholar] [CrossRef]
- Wu, L.; Wang, L.; Min, L.; Hou, W.; Guo, Z.; Zhao, J.; Li, N. Discrimination of Algal-bloom using spaceborne SAR observations of Great Lakes in China. Remote Sens. 2018, 10, 767. [Google Scholar] [CrossRef]
- Santoro, M.; Cartus, O. Research pathways of forest above-ground biomass estimation based on SAR backscatter and interferometric SAR observations. Remote Sens. 2018, 10, 608. [Google Scholar] [CrossRef]
- Jin, T.T.; Qiu, X.L.; Hu, D.H.; Ding, C.B. An ML-based radial velocity estimation algorithm for moving targets in spaceborne high-resolution and wide-swath SAR systems. Remote Sens. 2017, 9, 404. [Google Scholar] [CrossRef]
- Zhao, R.; Zhang, G.; Deng, M.; Yang, F.; Chen, Z.; Zheng, Y. Multimode hybrid geometric calibration of spaceborne SAR considering atmospheric propagation delay. Remote Sens. 2017, 9, 464. [Google Scholar] [CrossRef]
- Xu, Y.; Hou, C.; Yan, S.; Li, J.; Hao, C. Fuzzy statistical normalization CFAR detector for non-Rayleigh data. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 383–396. [Google Scholar] [CrossRef]
- Hu, C.; Ferro-Famil, L.; Kuang, G. Ship discrimination using polarimetric SAR data and coherent time-frequency analysis. Remote Sens. 2013, 5, 6899–6920. [Google Scholar] [CrossRef]
- Yuan, X.; Tang, T.; Xiang, D.; Li, Y.; Su, Y. Target recognition in SAR imagery based on local gradient ratio pattern. J. Appl. Remote Sens. 2014, 35, 857–870. [Google Scholar] [CrossRef]
- Wang, C.; Jiang, S.; Zhang, H.; Wu, F.; Zhang, B. Ship detection for high-resolution SAR images based on feature analysis. IEEE Geosci. Remote Sens. Lett. 2014, 11, 119–123. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Hwang, J.-I.; Jung, H.-S. Automatic ship detection using the artificial neural network and support vector machine from X-band SAR satellite images. Remote Sens. 2018, 10, 1799. [Google Scholar] [CrossRef]
- LeCun, Y.; Boser, J.; Denker, J.S.; Henderson, D.; Howard, R.E.; Hubbard, W.; Jackel, L.D. Backpropagation applied to handwritter zip code recognition. Neural Comput. 1989, 1, 541–551. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, M.-H.; Xu, P.; Guo, Z.-W. SAR ship detection using sea-land segmentation-based convolutional neural network. In Proceedings of the 2017 International Workshop on Remote Sensing with Intelligent Processing (RSIP 2017), Shanghai, China, 18–21 May 2017; pp. 1–4. [Google Scholar]
- Zhao, B.; Li, Z.; Zhao, B.; Feng, F.; Deng, C. Spaceborne SAR ship detection based on low complexity convolution neural network. J. Beijing Jiaotong Univ. 2017, 41, 1–7. [Google Scholar]
- Li, W.; Qu, C.; Shao, J. Ship detection in SAR images based on an improved faster R-CNN. In Proceedings of the 2017 SAR in Big Data Era: Models, Methods & Applications (BIGSARDATA 2017), Beijing, China, 13–14 November 2017; pp. 1–6. [Google Scholar]
- Jiao, J.; Zhang, Y.; Sun, H.; Yang, X.; Gao, X.; Hong, W.; Fu, K.; Sun, X. A densely connected end-to-end neural network for multiscale and multiscene SAR ship detection. IEEE Access 2018, 6, 20881–20892. [Google Scholar] [CrossRef]
- Cui, Z.; Dang, S.; Cao, Z.; Wang, S.; Liu, N. SAR target recognition in large scene images via region-based convolutional neural networks. Remote Sens. 2018, 10, 776. [Google Scholar] [CrossRef]
- Hamza, M.K.; Cai, Y.Z. Ship detection in SAR image using YOLOv2. In Proceedings of the 37th Chinese Control Conference (CCC 2018), Wuhan, China, 25–27 July 2018; pp. 9495–9499. [Google Scholar]
- Zénere, M.P. SAR Image Quality Assessment; Universidad Nacional de Córdoba: Córdoba, Argentina, 2012. [Google Scholar]
- Freeman, A. On Ambiguities in SAR Design. In Proceedings of the 6th European Conference on Synthetic Aperture Radar (EUSAR 2006), Dresden, Germany, 16–18 May 2006; pp. 1–4. [Google Scholar]
- Franceschetti, G.; Lanari, R.; Pascazio, V. Wide angle SAR processors and their quality assessment. In Proceedings of the 1991 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Espoo, Finland, 3–6 June 1991; pp. 287–290. [Google Scholar]
- Guarnieri, A.M. Adaptive removal of azimuth ambiguities in SAR images. IEEE Trans. Geosci. Electron. 2005, 43, 625–633. [Google Scholar] [CrossRef]
- Franceschetti, G.; Lanari, R. Synthetic Aperture Radar Processing, 2nd ed.; CRC Press, Inc.: Boca Raton, FL, USA, 2016. [Google Scholar]
- Copernicus Open Access Hub. Available online: https://scihub.copernicus.eu/ (accessed on 24 December 2018).
- Elachi, C.; Bicknell, T.; Jordan, R.L.; Wu, C. Spaceborne synthetic aperture imaging radars: Applications, techniques, and technology. Proc. IEEE 1982, 70, 1174–1209. [Google Scholar] [CrossRef]
- Yu, Z.; Wang, S.; Li, Z. An imaging compensation algorithm for spaceborne high-resolution SAR based on a continuous tangent motion model. Remote Sens. 2016, 8, 223. [Google Scholar] [CrossRef]
- Vespe, M.; Greidanus, H. SAR image quality assessment and indicators for vessel and oil spill detection. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4726–4734. [Google Scholar] [CrossRef]
- Stastny, J.; Hughes, M.; Garcia, D.; Bagnall, B.; Pifko, K.; Buck, H.; Sharghi, E. A novel adaptive synthetic aperture radar ship detection system. In Proceedings of the OCEANS, Waikoloa, HI, USA, 19–22 September 2011; pp. 1–7. [Google Scholar]
- Liu, C.; Gierull, C.H. A new application for PolSAR imagery in the field of moving target indication/ship detection. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3426–3436. [Google Scholar] [CrossRef]
- Bamler, R.; Runge, H. PRF-ambiguity resolving by wavelength diversity. IEEE Trans. Geosci. Remote Sens. 1991, 29, 997–1003. [Google Scholar] [CrossRef]
- Moreira, A. Suppressing the azimuth ambiguities in synthetic aperture radar images. IEEE Trans. Geosci. Remote Sens. 1993, 31, 885–895. [Google Scholar] [CrossRef]
- Avolio, C.; Constantini, M.; Martino, G.D.; Iodice, A.; Macina, F.; Ruello, G.; Riccio, D.; Zavagli, M. A method for the reduction of ship-detection false alarms due to SAR azimuth ambiguity. In Proceedings of the 2014 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Quebec City, QC, Canada, 13–18 July 2014; pp. 3694–3697. [Google Scholar]
- Chen, J.; Wang, K.; Yang, W.; Liu, W. Accurate reconstruction and suppression for azimuth ambiguities in spaceborne stripmap SAR images. IEEE Geosci. Remote Sens. Lett. 2017, 14, 102–106. [Google Scholar] [CrossRef]
- Hu, C.; Xiong, B.; Lu, J.; Li, Z.; Zhao, L.; Kuang, G. SAR azimuth ambiguities removal for ship detection using time-frequency techniques. In Proceedings of the 2014 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Quebec City, QC, Canada, 13–18 July 2014; pp. 982–985. [Google Scholar]
- Nair, V.; Hinton, G.E. Rectified linear units improve restricted Boltzmann machines. In Proceedings of the International Conference on International Conference on Machine Learning, Haifa, Israel, 21–24 June 2010; pp. 807–814. [Google Scholar]
- Xue, Z.; Du, P.; Su, H.; Zhou, S. Discriminative sparse representation for hyperspectral image classification: A semi-supervised perspective. Remote Sens. 2017, 9, 386. [Google Scholar] [CrossRef]
- Hollstein, A.; Segl, K.; Guanter, L.; Brell, M.; Enesco, M. Ready-to-use methods for the detection of clouds, cirrus, snow, shadow, water and clear sky pixels in Sentinel-2 MSI images. Remote Sens. 2016, 8, 666. [Google Scholar] [CrossRef]
- Neubeck, A.; Gool, L.J.V. Efficient non-maximum suppression. In Proceedings of the 18th International Conference on Pattern Recognition (ICPR 2006), Hong Kong, China, 20–24 August 2006. [Google Scholar]
- Australian Government. AMSA Online Service. Available online: http://www.operations.amsa.gov.au/ (accessed on 19 November 2018).
- Wang, Z.; Zhang, H.; Wang, C.; Wu, F. Ship surveillance with Radarsat-2 ScanSAR. In Proceedings of the SAR Image Analysis, Modeling & Techniques XIV., International Society for Optics and Photonics, Amsterdam, The Netherlands, 22–25 September 2014; pp. 41–45. [Google Scholar]
- Fukunaga, K. Introduction to Statistical Pattern Recognition, 2nd ed.; Academic Press: New York, NY, USA, 1990. [Google Scholar]
- Xing, X.; Ji, K.; Zou, H.; Sun, J. A fast ship detection algorithm in SAR imagery for wide area ocean surveillance. In Proceedings of the 2012 IEEE Radar Conference, Atlanta, GA, USA, 7–11 May 2012; pp. 570–574. [Google Scholar]
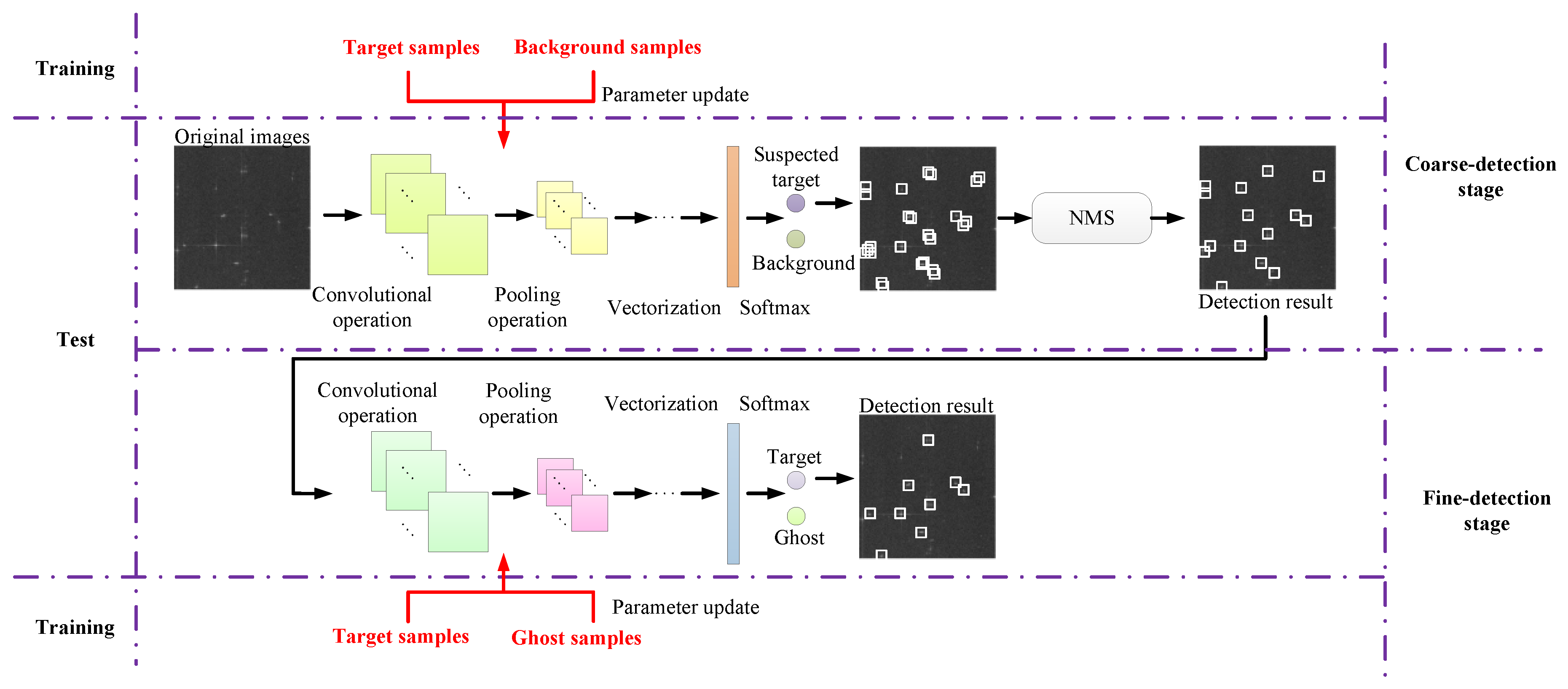
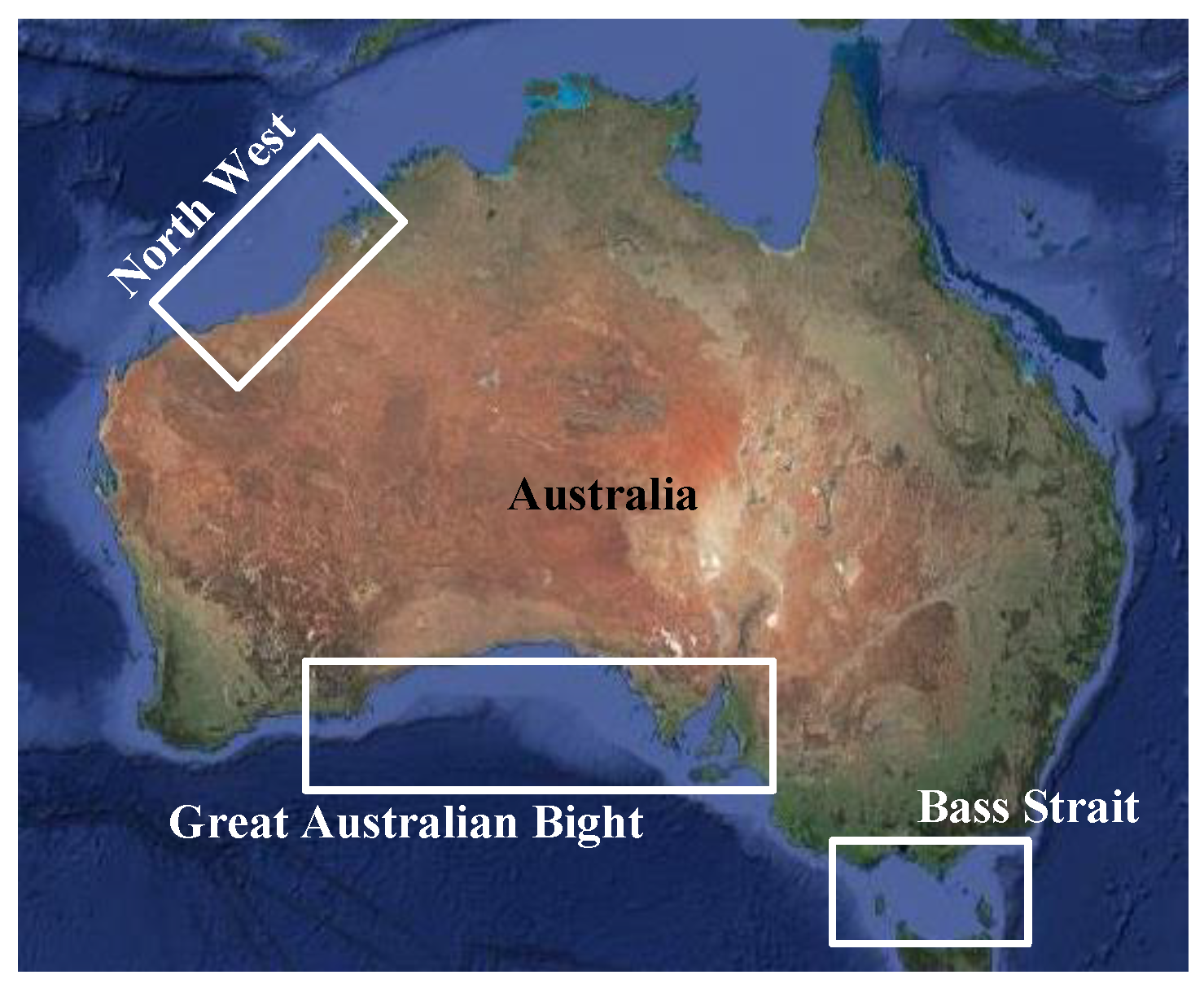


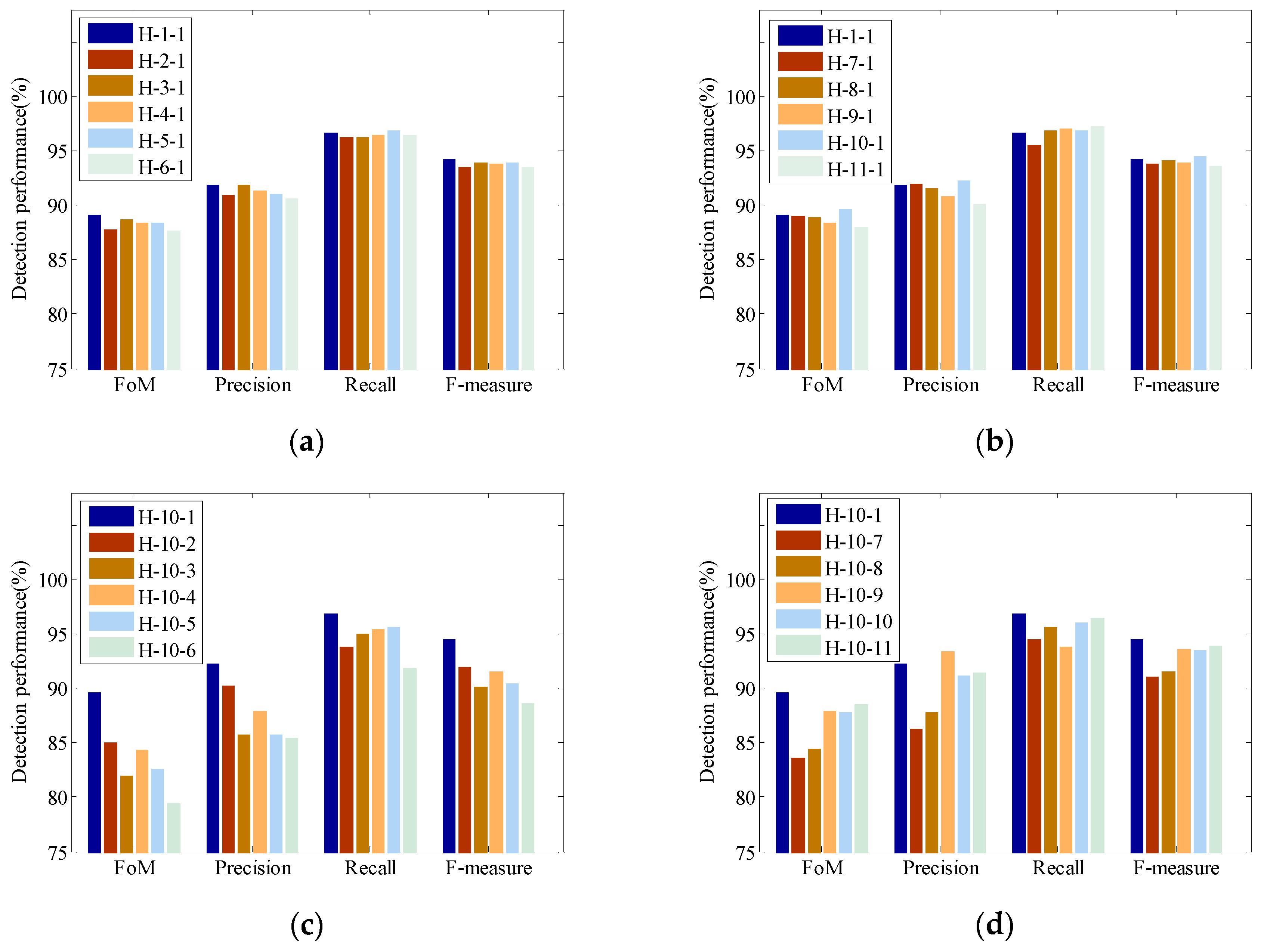

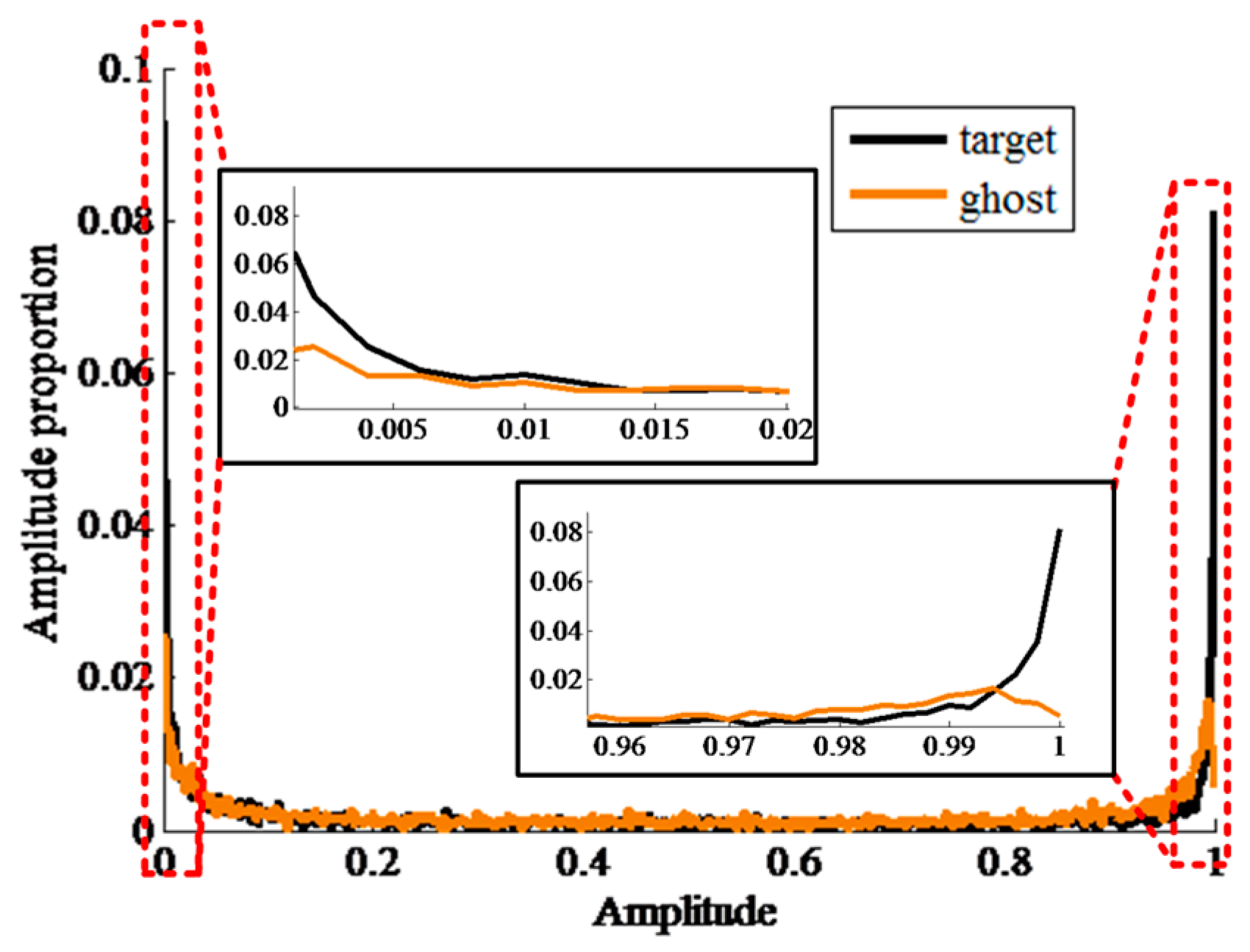
| (a) | |||||
| Parameters | Symbols | Values | Parameters | Symbols | Values |
| Altitude of satellite | R | 693 km | Radius of curvature | Rearth | 6371 km |
| Velocity in x direction | vx | 2.3455 103 m/s | Radar wavelength | λ | 5.55 10−2 m |
| Velocity in y direction | vy | −1.5613 103 m/s | PRF | fPRF1 | 1.717 kHz |
| Velocity in z direction | vz | 7.0588 103 m/s | fPRF2 | 1.452 kHz | |
| Elevation angle | β | 27.4967° | fPRF3 | 1.686 kHz | |
| Incidence angle | θ | 30.8312° | |||
| (b) | |||||
| Velocity of the ship | 17.2 nk | Type | Cargo ship | ||
| Latitude | −38.3061° | Time | 18/12/2016: 00:34:59 | ||
| Longitude | 144.8005° | ||||
| (a) | ||||||||
| Case | H-1-1 | H-2-1 | H-3-1 | H-4-1 | H-5-1 | H-6-1 | ||
| Input | 40 × 40 | |||||||
| Coarse-detection stage | L1 | Conv. | 3@9 × 9 | 4@9 × 9 | 6@9 × 9 | 8@9 × 9 | 9@9 × 9 | 12@9 × 9 |
| Maxpool | 2 × 2 | |||||||
| L2 | Conv. | 3@9 × 9 | 4@9 × 9 | 6@9 × 9 | 8@9 × 9 | 9@9 × 9 | 12@9 × 9 | |
| Maxpool | 2 × 2 | |||||||
| L3 | Fully connection | |||||||
| Fine-detection stage | L1 | Conv. | 3@7 × 7 | |||||
| Maxpool | 2 × 2 | |||||||
| L2 | Conv. | 3@8 × 8 | ||||||
| Maxpool | 2 × 2 | |||||||
| L3 | Fully connection | |||||||
| Output | 2 × 1 | |||||||
| (b) | ||||||||
| Case | H-1-1 | H-7-1 | H-8-1 | H-9-1 | H-10-1 | H-11-1 | ||
| Input | 40 × 40 | |||||||
| Coarse-detection stage | L1 | Conv. | 3@9 × 9 | 3@3 × 3 | 3@5 × 5 | 3@7 × 7 | 3@11 × 11 | 3@13 × 13 |
| Maxpool | 2 × 2 | |||||||
| L2 | Conv. | 3@9 × 9 | 3@4 × 4 | 3@7 × 7 | 3@8 × 8 | 3@8 × 8 | 3@7 × 7 | |
| Maxpool | 2 × 2 | |||||||
| L3 | Fully connection | |||||||
| Fine-detection stage | L1 | Conv. | 3@7 × 7 | |||||
| Maxpool | 2 × 2 | |||||||
| L2 | Conv. | 3@8 × 8 | ||||||
| Maxpool | 2 × 2 | |||||||
| L3 | Fully connection | |||||||
| Output | 2 × 1 | |||||||
| (c) | ||||||||
| Case | H-10-1 | H-10-2 | H-10-3 | H-10-4 | H-10-5 | H-10-6 | ||
| Input | 40 × 40 | |||||||
| Coarse-detection stage | L1 | Conv. | 3@11 × 11 | |||||
| Maxpool | 2 × 2 | |||||||
| L2 | Conv. | 3@8 × 8 | ||||||
| Maxpool | 2 × 2 | |||||||
| L3 | Fully connection | |||||||
| Fine-detection stage | L1 | Conv. | 3@7 × 7 | 4@7 × 7 | 6@7 × 7 | 8@7 × 7 | 9@7 × 7 | 12@7 × 7 |
| Maxpool | 2 × 2 | |||||||
| L2 | Conv. | 3@8 × 8 | 4@8 × 8 | 6@8 × 8 | 8@8 × 8 | 9@8 × 8 | 12@8 × 8 | |
| Maxpool | 2 × 2 | |||||||
| L3 | Fully connection | |||||||
| Output | 2 × 1 | |||||||
| (d) | ||||||||
| Case | H-10-1 | H-10-7 | H-10-8 | H-10-9 | H-10-10 | H-10-11 | ||
| Input | 40 × 40 | |||||||
| Coarse-detection stage | L1 | Conv. | 3@11 × 11 | |||||
| Maxpool | 2 × 2 | |||||||
| L2 | Conv. | 3@8 × 8 | ||||||
| Maxpool | 2 × 2 | |||||||
| L3 | Fully connection | |||||||
| Fine-detection stage | L1 | Conv. | 3@7 × 7 | 3@3 × 3 | 3@5 × 5 | 3@9 × 9 | 3@11 × 11 | 3@13 × 13 |
| Maxpool | 2 × 2 | |||||||
| L2 | Conv. | 3@8 × 8 | 3@4 × 4 | 3@7 × 7 | 3@9 × 9 | 3@8 × 8 | 3@7 × 7 | |
| Maxpool | 2 × 2 | |||||||
| L3 | Fully connection | |||||||
| Output | 2 × 1 | |||||||
| Layer | L1 | L2 |
|---|---|---|
| 0.1915 | 1.0728 | |
| 0.0306 | 0.0486 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Zheng, T.; Lei, P.; Bai, X. A Hierarchical Convolution Neural Network (CNN)-Based Ship Target Detection Method in Spaceborne SAR Imagery. Remote Sens. 2019, 11, 620. https://doi.org/10.3390/rs11060620
Wang J, Zheng T, Lei P, Bai X. A Hierarchical Convolution Neural Network (CNN)-Based Ship Target Detection Method in Spaceborne SAR Imagery. Remote Sensing. 2019; 11(6):620. https://doi.org/10.3390/rs11060620
Chicago/Turabian StyleWang, Jun, Tong Zheng, Peng Lei, and Xiao Bai. 2019. "A Hierarchical Convolution Neural Network (CNN)-Based Ship Target Detection Method in Spaceborne SAR Imagery" Remote Sensing 11, no. 6: 620. https://doi.org/10.3390/rs11060620
APA StyleWang, J., Zheng, T., Lei, P., & Bai, X. (2019). A Hierarchical Convolution Neural Network (CNN)-Based Ship Target Detection Method in Spaceborne SAR Imagery. Remote Sensing, 11(6), 620. https://doi.org/10.3390/rs11060620





