Abstract
Rangelands cover ~23 million hectares and support a $3.4 billion annual cattle industry in California. Large variations in forage production from year to year and across the landscape make grazing management difficult. We here developed optimized methods to map high-resolution forage production using multispectral remote sensing imagery. We conducted monthly flights using a Small Unmanned Aerial System (sUAS) in 2017 and 2018 over a 10-ha deferred grazing rangeland. Daily maps of NDVI at 30-cm resolution were first derived by fusing monthly 30-cm sUAS imagery and more frequent 3-m PlanetScope satellite observations. We estimated aboveground net primary production as a product of absorbed photosynthetically active radiation (APAR) derived from NDVI and light use efficiency (LUE), optimized as a function of topography and climate stressors. The estimated forage production agreed well with field measurements having a R2 of 0.80 and RMSE of 542 kg/ha. Cumulative NDVI and APAR were less correlated with measured biomass ( = 0.68). Daily forage production maps captured similar seasonal and spatial patterns compared to field-based biomass measurements. Our study demonstrated the utility of aerial and satellite remote sensing technology in supporting adaptive rangeland management, especially during an era of climatic extremes, by providing spatially explicit and near-real-time forage production estimates.
1. Introduction
Rangelands are a key global resource, both in terms of extent and ecological and economic impact. In California, over 60% of the land area is rangeland, which provides a wide range of ecological services, including forage production for livestock and wildlife, water quality protection, biodiversity, recreation, and wildlife habitat [1]. More than half of California rangelands are grazed [2], supporting a $3.4-billion per year livestock industry [3]. Rangeland forage production is characteristically variable and depends on a multitude of drivers—most notably climate, soils and topography, which together regulate plant-available water [4]. Most California rangelands are rain fed, and thus highly vulnerable to irregular precipitation patterns [5]. For example, large year-to-year variations in forage production (from 33 to 11503 kg/ha) were observed in a 14-year record from the California Central Coast region [6]. Warming, drought, and increasing climate variability [7,8] are predicted to become more prevalent in the future, and therefore, raise the critical need for cost-effective; timely; and robust tools for monitoring, predicting and optimizing use of forage while maintaining proper stewardship of the land.
Several studies have examined factors controlling forage production of California’s annual grass-dominated rangelands. Temperature was found to be an important regulator for timing of four distinct forage growth stages: germination season, winter growth, rapid spring growth, and peak forage production [4]. Amount and timing of precipitation are closely related to forage production with highest yields occurring when sufficient precipitation is received in April (to support rapid spring growth) [9]. Sensitivity of forage production to weather also varies spatially with soil characteristics and topography. In Mediterranean climates, such as California, annual systems are highly dependent on moisture stored in the upper 25~30 cm of soil [10]. Medium texture soils (e.g., loams, clay loams, and silt loams) have higher plant-available water-holding capacity, which can provide a buffer for plants when precipitation is sparsely spaced [11]. Topography affects forage production through two pathways: influencing soil properties such as soil depth, fertility and temperature, and controlling photosynthetically active radiation (PAR) [12]. Thus, spatial and temporal heterogeneity of forage production can only be fully explained by coupling these key drivers: temperature, amount and timing of precipitation, soil characteristics and topography.
Traditional methods for measuring forage biomass rely on time-consuming hand clipping and drying of quadrats randomly selected across the landscape. Advancements in technology could facilitate modeling as an alternative for forage production monitoring and prediction. Empirical statistical models relating observed production with key environmental determinants have been developed from large datasets of field measurements [9,13,14,15]. Growing degree days (GDD) and precipitation were used as inputs to predict California’s rangeland production dating back to the 1970s [9,14]. These empirical models usually do not consider landscape characteristics, and thus, performance is limited when extrapolating to larger areas with heterogeneity in climate, soils and topography.
Mechanistic models have also been developed to simulate complex biophysical processes in rangelands [16]. For example, the Simulation of Production and Utilization of Rangelands model [17] is able to predict forage production in different regions reasonably well (R2 = 0.3~0.9, depending on the species and location) [18,19,20]. However, the model accuracy is often limited by the assumptions made to simplify the processes and the uncertainties in the model parameters tuned with field measurements. They also require a large number of site-specific environmental variables, e.g., climate, and soil hydrological properties as inputs. Therefore, it is logistically challenging for land managers to implement simulation models because spatially-explicit data are difficult to obtain for large heterogeneous areas.
On the other hand, simplified eco-physiological models provide a robust approach over different regions and time, by converting photosynthetically active radiative (PAR) energy into biomass based on light use efficiency (LUE). Forage production is estimated as a product of absorbed PAR (APAR) and LUE [21]. APAR can be easily estimated from remote sensing data [22,23,24,25,26] and the LUE calibrated to field measurements; therefore it serves as a good candidate for mapping forage production [22,23,26,27,28,29,30,31,32]. The main challenge is parameterizing LUE as a function of environmental variables, since the proportion of APAR converted to biomass is down-regulated under various environmental stressors, such as soil moisture deficits and extreme temperatures. For example, LUE is derived as a function of potential LUE and the combined effects of low air temperature, high water vapor deficits, and soil moisture in the Global Production Efficiency Model (GLO-PEM) [32]. In the MODIS Gross Primary Production algorithm, LUE is calculated as the product of biome-specific maximum LUE and several down-regulators controlled by air temperature and vapor deficit [26]. In two Mediterranean grassland sites, Eddy Covariance data were used to calibrate the dominant LUE stress terms from air temperature and soil moisture, where soil moisture was identified as the dominant factor controlling LUE [31]. While different studies apply different forms of LUE calculation, this critical metric needs to be calibrated rigorously in different ecosystems and with different input datasets, because of its high model sensitivity.
Remotely sensed imagery from satellites provides a relatively reliable source for obtaining spatiotemporal inputs for LUE-based models. Landsat remote sensing data, with a 30-m resolution and a 16-day revisiting frequency, have been widely used for many vegetation monitoring studies worldwide [23,33,34,35,36]. However, coincidence of rainfall and growing season in California’s Mediterranean climate greatly limits the availability of cloud-free Landsat images during critical plant growth stages from November to April. Moreover, the spatial resolution of traditional satellite remote sensing generally ranges from a kilometer to 10s of meters, whereas most field biomass measurements are at a scale of 10s of centimeters. This scale mismatch poses challenges for developing and validating the LUE optimization.
Recent advances in small unmanned aerial system (sUAS) technology and image processing make it possible to overcome many challenges involved in quantifying forage production across the landscape. Compared to satellites, sUAS can be deployed quickly, repeatedly, and flexibly. A 20-minute flight is sufficient to map a 10-ha area, and with advanced software, data processing can be completed in a few hours. Cameras designed for sUAS vegetation monitoring capture spectral information in visible and near infrared (NIR) bands, from which critical information on plant vigor and growth can be extracted. Users can easily customize the spatiotemporal resolution by adjusting the flight height and frequency. High-resolution digital surface models (DSMs) generated from sUAS data allow accounting for topo-edaphic conditions in forage production modeling and related analysis. A few pilot studies have explored the applications of sUAS technology in monitoring agricultural production for soybean [37], rice and wheat [38,39], barley [40,41], and mango [42]. However, there is currently limited research concerning the efficacy of sUASs for rangeland forage production quantification and modeling.
The primary aim of this paper was to develop LUE-based models to map forage production at very high spatial (30 cm) and temporal (daily) resolutions using multispectral data collected from sUAS, augmented with more frequent satellite data from PlanetScope satellites at 3-m resolution [43]. Specifically, our objectives included (1) imaging a Mediterranean-type semi-arid annual rangeland using sUAS and fusing the sUAS data with PlanetScope data to obtain daily sUAS resolution images; (2) investigating the connection between ground-based plant biophysical measurements and remote sensing vegetation indices, (3) building and evaluating forage production models to map daily rangeland production at 30-cm resolution, and (4) analyzing the predicted spatial and temporal patterns of estimated forage production to explore the relationship between forage production and its environmental and climatic drivers.
2. Materials and Methods
2.1. Study Site
Our study focused on a privately-owned, annual grassland (no trees or shrubs), located 56 km east of the coast in San Luis Obispo County, California (35.5N, 120.3W) (Figure 1), which has been grazed by beef cattle for more than 15 years. A 10-ha parcel was fenced in November 2016 to exclude grazing during the growing season. Following peak forage biomass growth, 50 cow-calf pairs grazed the fenced area for 30 days in the summer of 2017 to prepare the site for a repeated study during the 2018 growing season.
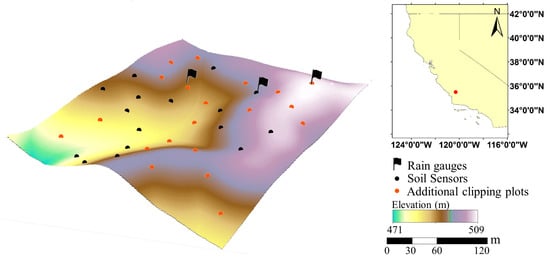
Figure 1.
Topography of the study area (35.5N, 120.3W) on Central Coast, California, from sUAS-derived digital surface model. The study area features large topographic variation including a valley, a hilltop, and many concave and convex slopes. The soil sensors (in black) and additional 20 biomass clipping plots (in red) were distributed in multiple topographic positions.
Soils were dominated by the loamy Balcom-Nacimiento complex [6]. The climate is Mediterranean with hot, dry summers and mild, moderately wet winters. Mean annual rainfall during 2001–2018 was 213 mm, mostly occurring from December through March. Annual rainfall at the site was 176, 139, 57, and 130 mm during the 2012–2016 drought years, respectively, and 287 and 123 mm during the study years of 2017 and 2018, respectively. Annual grasses and forbs at the site typically germinate in late fall with the onset of the rainy season (~November) and grow rapidly (March–April) to reach peak biomass in late spring (April-May), depending on the timing and length of the rainy season. Historical forage production for the site shows a large fluctuation, varying from 132 to 4204 kg/ha (mean = 1866 kg/ha) during 2001–2014 [6]. The study site was selected to include complex topography, including valley, hilltop and concave/convex hillslopes with slopes ranging from 10 to 20 degrees (Figure 1). Overall, 45% of the total area was south facing, 29% west facing, 24% north facing, and 2% east facing.
2.2. Field Measurements
In November 2016, 16 pairs of ECH2O 5TM sensors were installed to measure soil moisture and temperature across the study area (Figure 1). Locations were selected based on a digital elevation model to capture the spatial variation of topography and soil conditions. At each location, duplicate sensors were deployed in the shallow rooting zone at a 7-cm depth (most roots occurred in the upper 15 cm soil layer). Data-loggers recorded sensor readings every 15 minutes. Three tipping bucket rain gauges recorded rainfall, and three time-lapse cameras followed forage germination and growth at the hilltop, south-facing slope, and north-facing slope positions (Figure 1).
We measured forage production immediately after each of the 10 sUAS flight missions (except for 11/11/2016). Two replicate 30 cm × 30 cm quadrats at opposite cardinal angles were selected at a 1.5-m radius of the 16 soil sensors, resulting in two sample points per plot [44]. All aboveground plant biomass was harvested and dried at 60 ˚C for 48 hours before weighing to record dry biomass values. To further capture the spatial variation in topography and forage production, we classified the site into five categories based on clustering of topographical features including aspect, slope, flow accumulation, and elevation, using Iterative Self-Organizing Data Analysis Technique classification [45]. We selected an additional 20 plots for biomass clipping to ensure that each topographical cluster had at least eight plots. We collected 32~52 biomass clip-plot samples on each sUAS observation date and retained a total of 330 (200 and 130 in 2017 and 2018 growing seasons) biomass measurements after removing outliers (e.g., samples affected by strong rodent activity). For the cumulative NDVI & APAR and biomass analysis and LUE modeling, we further averaged the plots that had two samples near soil sensors, resulting 220 data points to work with.
2.3. sUAS Flights and Image Preprocessing
We integrated a MicaSense RedEdge camera with a 3DR Solo quadcopter for monthly aerial flights over the study area during the 2017 and 2018 growing seasons (November–April). MicaSense RedEdge is a multispectral camera with five spectral bands including blue, green, red, red-edge, and NIR. A sun irradiance sensor was included to measure band-specific incoming solar irradiance for radiometric correction. Flights were scheduled with the closest overpass dates of PlanetScope satellites when weather permitted it. A total of 10 missions were performed: six from 11 November 2016 to 30 April 2017, and four from 18 January 2018 to 14 April 2018.
We followed the same flight plan with a side- and front-overlap of 85% for all missions. Each mission was flown at 91-m (350-ft) above ground level (from the launching point) to acquire imagery at a 7.5 ~ 7.9 cm resolution and cover the whole study area in less than 30 minutes due to the payload constraint. Flying speed was set at 7 m/s along a fixed direction parallel to the east/west site boundary (Figure S1). Flights were conducted around solar noon to minimize the impacts of sun-angle variation throughout the season. Images of a calibrated white reflectance panel were recorded before and after each flight to calibrate raw pixel values to absolute reflectance values. To ensure the accuracy of the sUAS image geo-registration, we established eight permanent landmarks as ground control points (GCPs) evenly distributed at the corners (and center) of the study area. Coordinates of GCPs, forage clip-plot samples and soil sensors were recorded using a Trimble Geo 7x Series Handheld Data Collector.
Raw sUAS images were stitched and processed in Pix4dMapper Pro to generate orthomosaic maps of surface reflectance and DSM. The software converts the raw data in digital number (DN) to surface reflectance using images of the calibration panel, incoming sunlight irradiance, and camera parameters (e.g., ISO, aperture, shutter speed, and vignetting) recorded in the EXIF metadata [46]. DSMs were based on a dense point cloud generated from tie points that were automatically identified by the software. Mean average error (MAE) between GPS measurements and derived elevation was 3.5 cm across the study area.
A two-step geo-registration was performed on the time series of sUAS images to ensure spatial alignment of all aerial images. Images were first geo-registered in Pix4dMapper Pro using the eight GCPs to minimize the spatial mismatch when relating images to ground measurements. A mean Root Mean Square error (RMSE) of less than 3 cm was achieved. Reliability of this GCP-based geo-registration is highly dependent on the accuracy of the GPS. Since we did not upgrade our GPS to centimeter accuracy until the summer of 2017, we then used the Image to Image Registration function in ENVI 5.3 (using the 4/6/2017 image as the base image and second-order cubic) to align the images acquired in the 2017 growing season on different dates. In the Image to Images registration, we selected GCPs visually for each pair of images. The resulting RMSE was maintained at ~3 cm, less than 0.3 pixels at the original 8-cm resolution for all pairs of images. The geo-registered 8-cm resolution surface reflectance maps were then aggregated to 30-cm resolution to match the plant biomass field measurement plots and used for further analysis, which resulted in a <10% geolocation displacement in the final 30-cm maps.
Standard reflectance calibration assumes similar incoming solar radiation for all pixels. However, the complex topography of the study site led to significant variation in illumination conditions among pixels at different topographic positions. We applied the C model [47] to correct pixel reflectance based on its illumination condition (IC) for each spectral band (supplemental online material, SOM). The C model has been applied for correcting Landsat satellite data [47,48,49,50], but its feasibility and accuracy in correcting sUAS has not been fully evaluated. We used our 30-cm resolution DSM derived from the sUAS data to perform the illumination correction. The illumination-corrected red and NIR reflectance values were then used to calculate sUAS NDVI.
2.4. High Resolution Satellite Imagery and Data Fusion
Relatively high temporal frequency of remote sensing imagery is needed to capture the rapid growth cycle of annual plants. We downloaded a total of 174 cloud-free PlanetScope (PS) orthorectified scenes (level 3A) from Planet at 3.125-m spatial resolution for the 2017 and 2018 growing seasons. With a constellation of around 120 CubeSats, PS aims to provide daily images of three visible bands and one NIR band for any place on Earth. We converted the DN to the Top of Atmosphere (TOA) reflectance, using the TOA reflectance coefficients embedded in the metadata XML for each individual scene. The NDVI was then calculated with red and NIR reflectance.
To compensate for the limited temporal acquisition of sUAS data, we combined PS satellite data with monthly sUAS data to obtain a complete time series of daily NDVI at the 30-cm sUAS resolution. Our goal was to predict a sUAS-resolution NDVI map U(x,y,tp), for any particular date (tp), using (1) two pairs of coincident sUAS and PS images during the nearest two sUAS flight dates on tb1 and tb2 and (2) a PS-based image on the prediction date tp. We followed the basic concept of the Spatial and Temporal Adaptive Reflectance Fusion Model (STARFM) [51] to take advantage of the complementary spatial and temporal information from PS and sUAS. We first took advantage of the PS’s high temporal frequency and linearly interpolated temporally the available cloud-free PS NDVI images to obtain a continuous daily time series. To facilitate the pixel-based process, daily PS data were reprojected and bi-linearly resampled, denoted as P(x,y,t) to match the resolution, projection, and extent of the sUAS data. Since the study area has a relatively homogeneous landcover, we assumed that the temporal change from the daily PS NDVI images was similar at the 30-cm resolution:
The sUAS-resolution NDVI for a given location (x,y) and day (tp) was then estimated as a weighted sum of the two closest pairs of sUAS base NDVI images at 30-cm resolution (Figure 2), each adjusted for temporal change derived from the PS NDVI time series:
where tb1 and tb2 are the dates for the base image pair, and w1 and w2 are the temporal weights representing the contribution of each base image pair to the estimated NDVI, based on a linear function of the correlations between the base PS NDVI images on tb1 and tb2 and the PS NDVI image on tp (SOM).
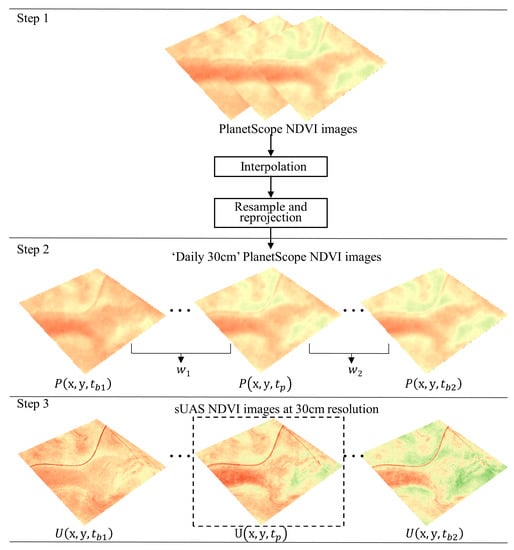
Figure 2.
Flowchart for the data fusion method to combine the monthly sUAS imagery and more frequent PlanetScope imagery. (Step 1) PS imageries are first interpolated daily and preprocessed to the same projection and resolution as the sUAS imageries. (Step 2) The preprocessed daily PS imageries are used to calculated weights based on correlations between base imageries (on tb1 and tb2) and the imagery on tp. (Step 3). Finally, the predicted NDVI values are computed from the weighted NDVI values from both PS and sUAS (Equation (1)).
We tested the performance of our data fusion method using a leave-one-out method. Within each iteration, we left out one sUAS NDVI image and predicted that image using the nearest neighboring image pairs and the PS NDVI image taken on the same day. The accuracy of the method was evaluated by comparing the predicted sUAS NDVI image to the observed sUAS NDVI image.
2.5. Forage Production Estimation Methods and Assessment
2.5.1. Empirical Statistical Analysis
We first examined the relationship between the measured biomass and two types of remote sensing metrics derived from the fused data, namely NDVI and APAR. NDVI was used as a proxy for net primary production and biomass [52,53,54,55]. Specifically, we used univariate linear regression (in R) to quantify the spatial variance in biomass across various plots explained by the corresponding coincident NDVI and the spatial and temporal variance explained when pooling data from all sites and dates together. When analyzing the coincident NDVI–biomass relationship, we did not average the paired samples taken close to the soil sensors, considering the limited number of samples on a single observation day. We investigated the relationship between biomass and cumulative NDVI integrated from the beginning of the growing season to the date of observation. Critical phenological days, such as the beginning (germination date) and end of the growing season were identified by fitting a logistic function (SOM) to the fused NDVI time series [56]. A similar statistical analysis was performed for cumulative APAR derived from the fused daily data and the California Irrigation Management Information System (CIMIS) spatial solar radiation.
2.5.2. Light Use Efficiency (LUE) Models
We estimated forage production based on LUE theory, as the cumulative product of APAR and LUE [22]:
where, tp is the date of prediction, and t0 is the corresponding germination date.
APAR was estimated as the product of fPAR and PAR. We calculated fPAR as a function of NDVI [57]:
where fPARmax = 0.95, fPARmin = 0.001, and NDVImax and NDVImin are the NDVI values corresponding to the upper and lower 2% of the NDVI histogram. NDVImin and NDVImax were set to 0.23 and 0.8, respectively, based on the NDVI distribution of sUAS data.
PAR was calculated as 50% of the daily shortwave incoming solar radiation, available from the CIMIS Spatial dataset at a 2-km resolution [58], assuming a constant ratio of 0.5 for PAR over incoming solar radiation [59,60,61,62,63,64]. The CIMIS Spatial incoming solar radiation showed an R2 of 0.99 when validated with CIMIS measured incoming solar radiation. The 2-km PAR was further sharpened to 30-cm resolution using the sUAS DSM to account for topography-induced illumination, and thus, PAR variations. We first generated daily solar radiation maps of the study area using the Area Solar Radiation function in the Arcpy package in Python, based on the sUAS-derived 30-cm DSM, latitude, and day of year [65]. Similar maps were derived for a simulated flat surface assuming DSM at the average elevation of the study area (491 m). For each 30-cm pixel and each day, the ratio of the daily 30-cm solar radiation from the actual DSM over the simulated flat DSM was used to multiply the corresponding CIMIS spatial solar radiation to derive solar radiation and PAR at 30-cm resolution.
We developed two semi-empirical statistical models to estimate LUE, depending on availability of the input data. All parameters in LUE models were optimized with field measurements. We first parameterized LUE as a function of topographic variables (Equation (4), Model I), which were derived from the DSM generated from sUAS data:
LUE0 is the LUE at the optimal topographic position. LUE0 is estimated by scaling f(Topo,x,y) from 0 to 1. We used topographic variables to drive an empirical scalar because we did not have the spatial soil moisture and air temperature data that are traditionally used for LUE down-regulators. We explored a suite of topographic features including cosine aspect, slope, flow accumulation, IC, and elevation, and enumerated the possible combinations of these variables in the equation.
We further added time-varying controls of soil moisture (W) and air temperature (T) on LUE, in addition to significant topographic features (Equation (5), Model II), as shown below:
where , , and range from 0 to 1. Forms of the W and T scalar functions were set to the same as those in Reference [22] but coefficients were optimized using field-measured biomass. The temperature (T) stress scalar was based on deviation from optimal air temperature (Topt):
where a is the coefficient to be calibrated, Ta is the air temperature (˚C), and (x, y, ) denotes the location and time. Topt is here defined as the average temperature during the month with the highest NDVI. We used daily mean air temperature from the 2-km CIMIS spatial dataset. The T scalar decreases from 1 to 0 as temperature deviates from Topt, with the rate of decrease represented by a.
The water stress (W) scalar represents the down regulation of light use efficiency under drought conditions, and was parameterized as a function of soil moisture (M) (Equation (7)):
where b is the coefficient to be calibrated; M is the derived soil moisture, represented by volumetric water content (VWC); and WP is the wilting point. W ranges from 0.5 to 1 as soil moisture varies from the wilting point to field capacity. The wilting point was set to a water content of 0.14 cm3 cm−3 determined by averaging soil moisture content in June during the dry season when grass and forbs had desiccated and soil moisture was at its water-year minimum [66]. For operational mapping purposes, we required soil moisture for every pixel. We estimated the daily soil moisture using a simple bucket model (SOM) following Reference [22], based primarily on precipitation data from PRISM [67] and potential evapotranspiration from CIMIS Spatial [58]. The topographic control term is a linear function of elevation and IC for Model II. Elevation and IC were selected because they had the highest statistical significance for minimizing differences between measured and predicted biomass among topographic variables.
As a comparison to Model II, we also built a Model III by replacing the air temperature and derived soil moisture with measured soil temperature and soil moisture in the LUE parameterization. As for the topographic variable, we selected elevation because it had the highest statistical significance on minimizing model error.
We optimized the model coefficients using the Stochastic Gradient Descent (SGD) method [68,69]. We used 70% of the data for training and the remaining 30% for validation of the SGD LUE optimization. Model performance was evaluated by comparing model estimates with measured biomass values in the validation dataset. We used R-squared (R2) and RMSE to quantify the uncertainty of models for estimating forage production. The LUE scalars and their corresponding coefficients may be site-specific as they were specifically optimized for our study area.
2.6. Forage Production Mapping and Patterns
We implemented Model II to generate daily forage production maps for the study area. The maps were compared against the concurrent RGB images from sUAS to determine if prediction captured a similar spatial pattern. To further study the interaction between topography (aspect and slope) and forage production, we calculated the predicted biomass for topographic zones divided by aspect (north and south) and slope (flat, moderate, and steep) and performed zonal statistical analysis.
3. Results
3.1. Terrain Correction
The wavelength-specific C model significantly removed the topographic varying illumination effect present in the original sUAS images (Figure 3). For example, pixels on the north-facing slopes, when displayed in true color composite, appeared very dark due to terrain shadows, especially for early season images when the sun angle was relatively low, e.g., 16 January 2017. This shadowing effect was minimized after applying the correction. Raw reflectance was significantly correlated with IC (p < 0.01 in most cases), but the correlation was minimized and not significant after correction (Figure 4). For example, R2 was reduced from 0.33 (p < 0.01) to 0.12 (p = 0.02) in the red and from 0.80 (p < 0.01) to 0.01 (p = 0.5) in the NIR for January 2017 imagery (Figure 4). The topographic illumination effects were found to be more pronounced in the NIR band and early in the growing season.
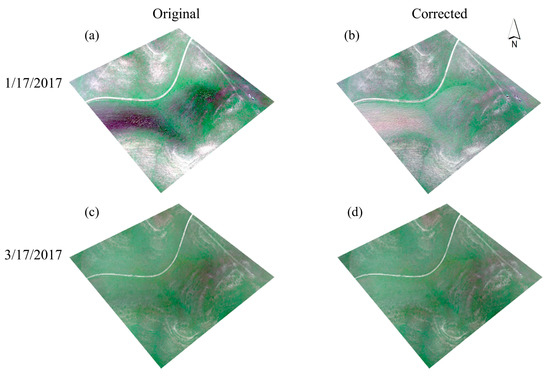
Figure 3.
Original (a,c) and terrain corrected (b,d) example images, in true color composite, acquired from the sUAS on (a,b) 17 January 2017 and (c,d) 17 March 2017. The C model removed most of the topographic illumination effect (b,d) as presented in the original images (a,c). The shadow (pixels in very dark color) on the north-facing slopes is removed in the corrected images.
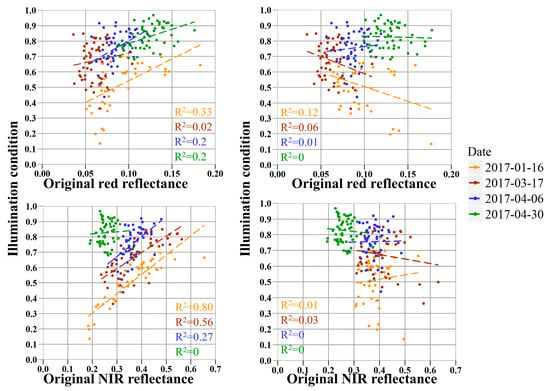
Figure 4.
Scatterplots of red (top panels) and NIR reflectance (bottom panels) vs. the illumination condition (IC) for 200 pixels with biomass clipping as shown in Figure 1. Raw reflectances are shown in left column (a,c), and corrected reflectances in right column (b,d).
3.2. sUAS and PlanetScope Data Fusion
We combined all available 30-cm sUAS NDVI images and satellite NDVI images from the two growing seasons to generate daily 30-cm NDVI time series from 11 November 2016 to 30 April 2017 and from 1 January to 14 April 2018. The fused daily NDVI curve had a similar magnitude to those from sUAS imagery, and a quantitative comparison showed that the predicted 30-cm NDVI agreed well with the original sUAS NDVI images (R2 = 0.87 and RMSE = 0.06) (SOM, Section 2). The fused time series followed similar temporal patterns with those from PS data. For a selected plant pixel within a relatively homogeneous patch, Figure 5 shows three sets of NDVI values from PS and sUAS sensors at 30-cm resolution and data fusion. The sUAS NDVI values were typically higher than those from the concurrent PS imagery, e.g., 0.65 vs. 0.46 on 6 April 2017. This difference was most likely due to lower atmospheric effects on surface reflectance from the low-altitude sUAS flights. The fused time series was able to conserve the sUAS NDVI values, e.g., 0.65 on the same day. Due to its higher temporal frequency, the PS NDVI time series captured more detailed temporal dynamics of plant growth than the less frequent sUAS snapshots. Both fused and original PS NDVI time series in 2018 showed a unique bimodal shape, with peaks on January 25th and March 19th. This variation was consistent with a gap in precipitation that greatly reduced plant growth in February, but growth resumed following late March rainfall. The smoothed and fused NDVI time series successfully captured the rapid changes in phenology, while preserving the magnitude of NDVI values with minimal atmospheric contamination (Figure 5).
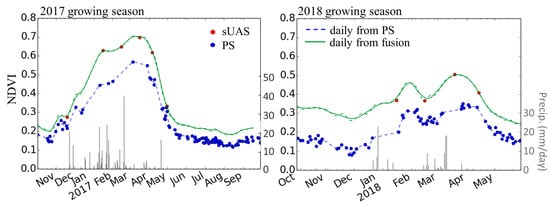
Figure 5.
NDVI time series of a randomly selected grass pixel over a relatively homogeneous area, from 10 sUAS missions (6 and 4 in the 2017 and 2018 growing season respectively), PlanetScope (PS), and data fusion. Also shown is daily precipitation (grey bar) from the on-site rain gauge measurement.
NDVI maps derived from sUAS imagery showed similar spatiotemporal patterns to those from the PS satellite, as shown by the coincident images acquired by both sensors on 19 November 2016, and 16 January 2017 (Figure 6). However, the sUAS NDVI map revealed greater spatial details. The sUAS-resolution NDVI map on 15 December 2016 (Figure 6e), predicted by the simplified STARFM, demonstrated that the prediction retained sUAS spatial resolution, as the road boundary and patterns of NDVI heterogeneity were preserved, and at the same time, captured phenological changes shown in the PS time series.
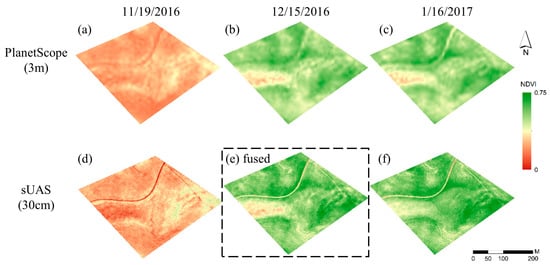
Figure 6.
NDVI maps at PlanetScope resolution (upper panels) and sUAS resolution (bottom panels). Concurrent images were available on 19 November 2016 (a,d) and 16 January 2017 (c,f), while only a PlanetScope image was available on 15 December 2016 (b). The predicted NDVI image from data fusion at 30-cm resolution on 15 December 2016 is shown in (e).
3.3. Relationships Between Remote Sensing Metrics and Biomass Measurements
Daily fused NDVI was positively related (with varying significance) to biomass measurements (mean = 1122 kg/ha; range = 17 - 4483 kg/ha) taken on the same day over all the clipping sites, with R2 ranging from 0.01 to 0.33 on various sUAS image acquisition dates (Figure S4). The highest R2, 0.33 (p < 0.05, N = 21), was found for February 2018. The varying R2 among different dates suggests limited performance for using instantaneous NDVI to predict biomass over the growing season. NDVI values were typically lower in 2018 than those in 2017 for the same month, consistent with differences in corresponding biomass measurements.
When integrated from the germination date to the date of observation (using the fused time series), the cumulative NDVI explained 68% of the variance in measured biomass among all field sampling plots during the two growing seasons (Figure 7a), and the cumulative APAR explained 69% of spatial and temporal variance (Figure 7b) (N = 220). The linear regression model, based on 70% of the randomly selected data points, showed that cumulative APAR predicted biomass with an R2 of 0.67 ± 0.06 and a RMSE of 631 ± 82 kg/ha, when compared with the remaining 30% of the data (N = 66). Similarly, predictions from cumulative NDVI showed an R2 of 0.67 ± 0.05 and an RMSE of 627 ± 73 kg/ha. However, the empirical NDVI-only and APAR-only methods may have large uncertainties when extrapolated to other areas or time periods.
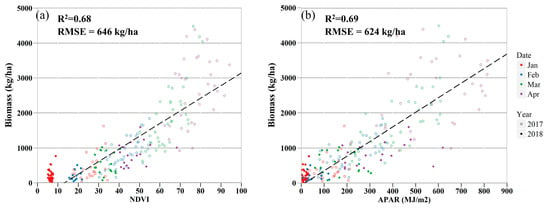
Figure 7.
Scatterplots of measured biomass versus the cumulated NDVI (a) and cumulated APAR (b) over 220 clip-plot samples in 2017 and 2018.
3.4. Forage Production Models
Optimization of the topography-based LUE model (Model I) with 70% of randomly selected data resulted in the following forage production model:
LUE decreased with both elevation and IC. When compared with the remaining 30% of the data (N = 66), predicted biomass showed an R2 of 0.70 and an RMSE of 567 kg/ha (Figure 8a), suggesting a better performance (a decrease of 56 kg/ha in RMSE) than the linear model driven only by APAR (Figure 7b).
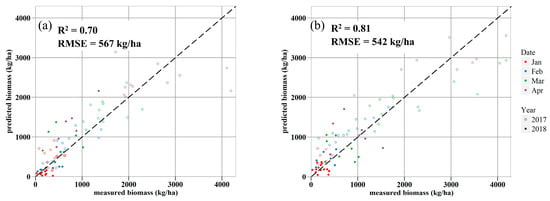
Figure 8.
Biomass predicted by models with LUE optimized as functions of (a) elevation and IC (Model I); and (b) elevation, IC, and air temperature and soil moisture stress terms (Model II). Each point represents a pair of the predicted and observed biomass from the validation dataset.
The final optimized LUE Model II was generated as a function of soil moisture (SM), air temperature (Ta), elevation and IC:
The soil moisture scalar showed that decreasing moisture down-regulated LUE. The W scalar increases logistically from 0.5 to 1 as soil moisture changes from wilting point (θv = 0.14 cm3 cm−3) to field capacity (θv = 0.29 cm3 cm−3). The T scalar dropped to 0.5 when air temperature was 1˚C below or above the optimal temperature of 10.33 ˚C. This full model resulted in improved accuracy for predicting biomass with greater explanation of variance (81%) and lower RMSE (542 kg/ha) compared with the topography-based LUE model (Figure 8b). This suggests that time-varying controllers of soil moisture and air temperature captured environmental stress impacts on forage production.
When using field-measured soil moisture and soil temperature, Model III:
predicted biomass with an RMSE of 472 kg/ha and R2 of 0.77 (Figure S5).
3.5. Forage Production Mapping and Patterns
We summarized forage production across the study area based on daily biomass maps generated from Model II. Forage production increased gradually during the growing season, but followed an unstable trajectory with bursts and plateaus (Figure 9). Most rapid growth was from 20 March to 2 April 2017 (averaging 107 kg/ha/d) and from 10 March to 19 March 2018 (averaging 15 kg/ha/d). The 2017 growing season had higher overall growth rates than 2018, which resulted in a mean peak standing biomass of 3216 (±678SD) kg/ha versus 1054 (±374SD) kg/ha, respectively. This large difference in peak standing biomass was linked to higher precipitation in 2017 (287 mm) compared to 2018 (123 mm). The standard deviation of biomass for the sUAS flight dates (Figure 9) showed increasing spatial variability in biomass as the growing season progressed.
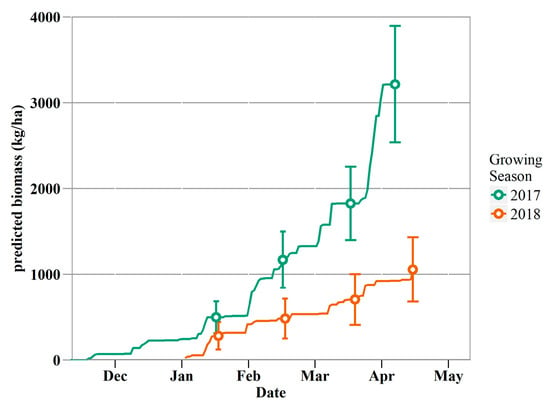
Figure 9.
Daily time series of the estimated biomass averaged across the study area in 2017 and 2018 growing seasons. Error bars, denoting the standard deviation, were added to the eight sUAS flight dates, indicating the increase of spatial variability in biomass as plants grow.
Predicted biomass maps at 30-cm resolution provided a visual representation of spatial variation across the landscape (Figure 10). At peak biomass in 2017 (Figure 10d), high biomass production was predicted at low elevation (Figure 10i) and high IC (Figure 10j) regions, whereas in 2018, high biomass production was predicted in low elevation and low IC regions. Lower elevation regions often have higher soil moisture because lower slope positions receive runoff and throughflow from upper hillslope positions. IC values are positively related to PAR with higher PAR leading to higher biomass when plants are not water stressed. However, when water is limited, high PAR could contribute to lower biomass production (i.e., greater plant water stress). The maps also captured human disturbance on biomass production, such as the road having very low biomass compared to the surrounding area.
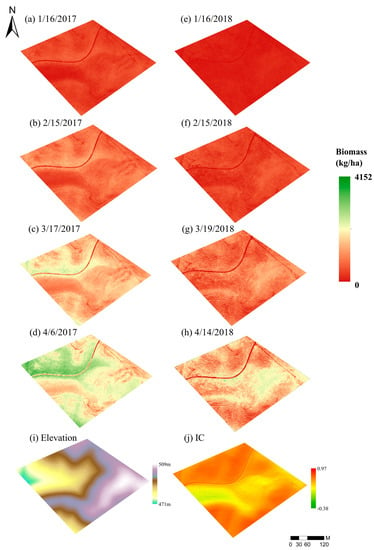
Figure 10.
Spatial distribution of the estimated biomass on days with sUAS flights during 2017 and 2018 growing seasons (a–h). Also shown are elevation (i) and illumination condition (IC) maps (j).
A zonal statistical analysis was performed on Biomass-Slope and Biomass-Aspect to examine interactions between topography and biomass. The model predicted higher biomass in flatter areas (Figure 11a) while the steeper group had lower biomass than the other two groups in both years. However, the model predicted similar biomass values for the flat and moderate groups in 2017 (wetter year). The model predicted lower biomass on north-facing slopes than south-facing slopes in 2017; however, an opposite effect was observed in 2018 (Figure 11b).
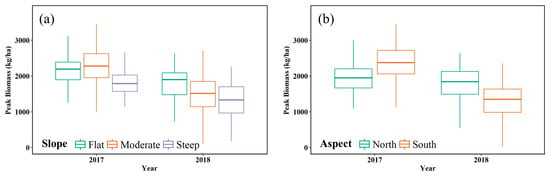
Figure 11.
Variation of the predicted peak biomass by (a) slope and (b) aspect. The area was divided into three categories of slopes: flat terrain (0~5°), moderate (5~15°), and steep (>15°).
4. Discussion
In this pioneering study, we developed two remote sensing data-driven LUE models that accurately predicted daily forage production at centimeter-scale resolution. We also streamlined preprocessing and fusing approaches for raw sUAS data with high-resolution satellite remote sensing data to obtain high-spatiotemporal data. We successfully implemented preprocessing and fusing methods and frameworks (e.g., the C model for illumination correction and the simplified STARFM) that were developed for satellite remote sensing data on the sUAS data. From the model predicted forage production maps, we observed unique patterns in productivity related to different environmental and climatic drivers. The following discussion section expands on additional findings in sUAS data preprocessing (Section 4.1) and fusing with PlanetScope data (Section 4.2), and the response of forage plants to precipitation (Section 4.3) and soil moisture and temperature (Section 4.4).
4.1. Variations in the Illumination Effect
This study demonstrated a successful application of the C model for correcting sUAS data for illumination effects. Reflectance in visible bands was generally less affected by terrain than NIR and red-edge bands. The same phenomenon was found for topographic illumination effects on Landsat images [50]. The authors concluded that the lower correlation for visible bands was caused by their lower reflectance rate and a more significant atmospheric scattering effect on visible bands than longer-wavelength bands. From the temporal analysis, the topographic illumination effect intensity was not consistent over the entire growing season for a given band, but rather diminished as the growing season progressed. In addition to changes in vegetation density, the diminishing trend is probably related to changes in sun angle. Since the study site is at 35.5N, the solar-noon sun elevation angle increases from 31˚ in December to >80° in June. Therefore, the theoretical intensity of illumination effects should decrease as the growing season progresses.
Notably, the R2 between red band surface reflectance and IC was very low (0.02) for the March flight, and the corresponding corrected R2 (0.06) was higher than the original R2. Although both R2 values were small, this raises caution that applying the C model may lead to overcorrection when the illumination effect is weak. Therefore, a test of the illumination effect intensity, for example, a correlation analysis on the surface reflectance and IC, is recommended before applying illumination correction to models. In this study, since the corrected red band surface reflectance-IC R2 value was very low, we used the corrected red band reflectance to maintain temporal consistency among data.
4.2. Fusing Satellite and sUAS Data
We found that the PS NDVI values were generally lower than those from sUAS, especially when NDVI was higher than 0.5. This results from PS NDVI being calculated from the Top of Atmosphere (TOA) reflectance while the sUAS NDVI is determined from the surface reflectance. Several studies document a lower TOA NDVI compared to NDVI at the surface [70,71] due to the atmospheric scattering effect. In the simplified STARFM, we used the temporal change of PS TOA NDVI, which reduced the noise from TOA reflectance, while the absolute value relies heavily on the sUAS. Smaller differences between December and February sUAS instantaneous NDVI and PS NDVI datasets may result from the use of a sun light irradiance (SLR) sensor on sUAS flights after March 2017. We initially relied on a white calibration panel for radiometric and atmospheric correction when preprocessing data from the first two flights before installation of the SLR sensor.
Data fusion of sUAS and high spatial-resolution images has great potential to lower the cost of operating frequent sUAS flights, especially given increasing availability of high-spatial resolution data (e.g., RapidEye data and PS data by Planet and WorldView data by DigitalGlobe). However, much of the high-spatial resolution satellite (including PS) data is only available in DN or TOA due to the lack of shortwave NIR bands for atmospheric correction. Therefore, it is important to develop robust data fusion methods that work on multi-source data with systematic differences. Future release of atmospherically-corrected PS surface reflectance products, i.e., using the concurrent MODIS data, will further reduce uncertainties in sUAS-satellite data fusion methods. Moreover, a more sophisticated fusion method is needed to take into account the spatial details embedded in sUAS data for the temporal interpolation of PS data.
4.3. LUE Parameterization
We observed improvements in model accuracy when including additional model terms. RMSEs of forage production estimates from APAR-only, Model I, Model II, and Model III were 624 kg/ha, 567 kg/ha, 542 kg/ha, and 472 kg/ha, respectively. We selected Model II to map forage production because it had the highest accuracy and does not require ground measured soil moisture and temperature. Model III, which uses locally measured soil moisture and soil temperature, achieved a higher accuracy than Model II, which uses estimated soil moisture and coarse-resolution air temperature. We believe that the main source of error in Model II is from the use of a simple bucket model for estimating soil moisture and/or the coarse resolution of air temperature.
Comparing the stressing scalars in Model II and III, the W scalar functions have very similar controls on LUE; however, the T scalar behaves quite differently. In Model II, the T scalar is driven by air temperature and is more sensitive to deviations from optimal air temperature. The estimated LUE0 across the three models showed large discrepancies, ranging from 0.32 to 1.8 g/MJ APAR with Model I having the highest LUE0 and Model II the lowest. Over the years, maximal LUE has been estimated using different methods for different biomes [72]. However, maximal LUE used in existing LUE models varies a lot [31] because researchers used different methods to estimate this metric [72]. In addition, maximal LUE also varies across scales. Currently, the number of LUE studies at the watershed scale is very limited. We expect to see increasingly more relevant studies on LUE modeling with advances in sUAS technology.
Using measured soil temperature and moisture in Model III achieved the highest accuracy among the three models, but this model cannot be applied to directly generate biomass maps because it requires point measurement data to parameterize input variables. As of now, daily soil moisture maps at high spatial resolution are not available, but with the continuous expanding constellations of satellites, new remote sensing products are being produced that could provide daily spatial patterns for soil moisture. For example, a past study demonstrated the potential for retrieving soil moisture from C-band synthetic aperture radar (SAR) data [73]. Additional studies have developed algorithms for mapping high-resolution (<1 km) soil moisture locally using the sentinel-1 C-band SAR data at a 10-m resolution [74,75]. Therefore, inclusion of near real-time soil moisture estimates may be forthcoming as new remote sensing technologies emerge.
4.4. Response of Forage Production and Plant Phenology to Moisture
Moisture is the primary controlling factor of forage production in Mediterranean annual range systems [6,31,76]. The different precipitation regimes in the 2017 and 2018 growing seasons triggered very different biomass-aspect relationships. South-facing slopes were expected to have a lower peak biomass than north-facing slopes because of increased temperatures leading to higher ET and lower soil moisture on south-facing slopes. However, we observed a higher peak biomass on south-facing slopes in the 2017 growing season (Figure 10b). This resulted from the high precipitation (287 mm) that was well distributed throughout the 2017 growing season. With sufficient precipitation to maintain soil moisture content (Figure S6), plants experienced little water deficit. With sufficient water supply, PAR became the primary limiting factor. Therefore, south-facing slopes, where more solar radiation is received, were able to produce higher peak biomass than north-facing slopes. In contrast, the 2018 growing season received only 108 mm of precipitation with large gaps between rainfall events. The majority of the precipitation was received in January, March and early April resulting in an extremely dry February (Figures S5 and S6). This precipitation distribution hindered plant growth on the radiation-rich south-facing slopes by intensifying the soil moisture deficit. Therefore, a lower peak biomass was observed on south-facing slopes in the 2018 growing season.
Time series biomass maps provided insights on plant phenology changes in response to different precipitation regimes during the 2017 and 2018 growing seasons. Germination and growth can be very different interannually in annual range systems. Peak growth is highly dependent on the amount and timing of precipitation. The November 2017 rainfall resulted in germination (11/11/2016) of the plants about 2 months earlier than the 2018 growing season (1/1/2018) (Figure 5 and Figure 12). The predicted germination dates are close to actual gemination dates (11/6/2016 and 1/13/2018) captured by the time lapse camera. Although the two growing seasons had a 1.5-month difference in their germination date, they both had peak growth in April. We predicted 4/6/2017 and 4/14/2018 as the peak growth dates for the 2017 and 2018 growing season, which were close to the camera observed peak growth dates (4/12/2017 and 4/25/2018). In addition to having a longer growing season, plants also accumulated biomass faster in 2017 than in 2018 (Figure 9). This higher biomass accumulation rate is largely due to the higher and more evenly distributed precipitation pattern during 2017. Plant growth on south-facing slopes was very sensitive to soil moisture availability. During the 2017 growing season and in January 2018, when moisture was sufficient, plants on south-facing slopes accumulated biomass faster than those on north-facing slopes. However, when soil moisture became limiting, for example, starting in February 2018, biomass accumulation on south-facing slopes was distinctly lower than north-facing slopes.
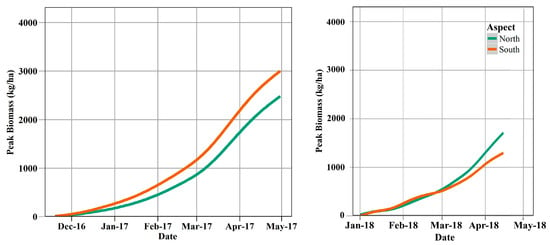
Figure 12.
Daily average biomass time series of biomass averaged over 500 randomly selected pure forage pixels (at 30cm resolution) in the study area during 2017-2018 growing season. The time series shows a different phenology for plants growing on south- and north-facing slopes.
5. Conclusions
This pilot study demonstrates the synergistic use of complementary sUAS and satellite remote sensing technology to map daily forage production at 30-cm resolution on a delayed grazing rangeland. Remote sensing-based APAR estimates were the primary driver for both LUE-based models developed here. LUE was optimized as a function of elevation and illumination conditions in Model I, achieving an R2 of 0.70 and an RMSE of 567 kg/ha when comparing predicted forage production with measured forage biomass. By further incorporating moisture and temperature stress terms to the LUE parameterization (Model II), Model II predicted forage production with higher accuracy (R2 = 0.81) and lower RMSE (542 kg/ha). Both LUE approaches showed improved prediction accuracy compared to the univariate linear regression with cumulative APAR. Finally, the inclusion of measured soil moisture and soil temperature into the LUE model (Model III) achieved the lowest RMSE (472 kg/ha) with a similar R2 of 0.77.
The fusion of high spatial resolution sUAS data and high temporal PlanetScope satellite imagery enabled us to generate daily forage production maps at a 30-cm resolution. The maps allowed the analysis of landscape-derived zonal statistics to assess (a) interactions between topography and biomass and (b) the response of forage production and plant phenology to changing precipitation regimes. Our analysis showed higher forage production and biomass accumulation rates in landscape positions experiencing less environmental stress (e.g., soil water deficit), with several differences occurring between wet and dry years. The forage production maps can be implemented in decision support tools to help ranchers better anticipate weather-driven changes in forage production and optimize their decisions on proactive practices, such as stocking conservatively, resting pasture, and incorporating yearling cattle. This study provides basic tools that can be further developed and scaled to statewide regions to provide near real time forage availability delivered to users via internet apps.
Supplementary Materials
The following are available online at https://www.mdpi.com/2072-4292/11/5/595/s1, Figure S1: sUAS flight plan; Figure S2: (a) Observed and (b) predicted NDVI image on 4/6/2017, and the (c) corresponding difference image; Figure S3: Scatter plot (N = 10000) of (a) observed and predicted NDVI on 4/6/2017 and scatter plot of (b) observed NDVI on 4/6/2017 and 4/30/2017; Figure S4: Scatterplots of instantaneous sUAS NDVI and measured biomass on the eight flight days. Each data point represents a single ground sampling point on a specific day; Figure S5: Scatterplot of the Model III predicted biomass versus measured biomass; Figure S6: Calibrated soil moisture time series for the 2017 and 2018 growing seasons.
Author Contributions
H.L., Y.J., and R.A.D. conceived and designed the research. H.L., S.M.D., R.E.L., R.A.D., S.C., and A.J.Y.W. carried out the field measurement. H.L. and A.J.Y.W. conducted the sUAS flights. H.L. processed the data and developed the LUE models. H.L. and Y.J. analyzed the results and drafted the manuscript. H.L., R.A.D., R.E.L., S.M.D., L.M.R., A.T.G., A.J.Y.W., S.C. and Y.J. provided critical feedback and helped edited the manuscript.
Funding
This study was supported by the University of California—Davis Russell L. Rustici Rangeland and Cattle Research Endowment.
Acknowledgments
We thank the Morrison Family for permitting access to Camatta Ranch for data collection and their cooperation throughout this study period. We also thank Mui Lay and Karl Linsteadt for their help with field measurements.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Roche, L.M.; Schohr, T.K.; Derner, J.D.; Lubell, M.N.; Cutts, B.B.; Kachergis, E.; Eviner, V.T.; Tate, K.W. Sustaining Working Rangelands: Insights from Rancher Decision Making. Rangel. Ecol. Manag. 2015, 68, 383–389. [Google Scholar] [CrossRef]
- Schwarzenegger, A.; Snow, L.; Walters, D. California’s Forests and Rangelands: 2010 Assessment. Available online: http://frap.fire.ca.gov/data/assessment2010/pdfs/california_forest_assessment_nov22.pdf (accessed on 17 April 2017).
- California Department of Food & Agriculture. 2015 Crop Year Report; California Department of Food & Agriculture: Sacramento, CA, USA, 2015.
- Becchetti, T.; George, M.; McDougald, N.; Dudley, D.M.; Connor, M.; Flavell, D.K.; Vaughn, C.E.; Forero, L.C.; Frost, B.; Oneto, S.R.; et al. Annual Range Forage Production. Univ. Calif. Agric. Nat. Resour. Publ. 2016, 8018, 1–12. [Google Scholar]
- Sloat, L.L.; Gerber, J.S.; Samberg, L.H.; Smith, W.K.; Herrero, M.; Ferreira, L.G.; Godde, C.M.; West, P.C. Increasing Importance of Precipitation Variability on Global Livestock Grazing Lands. Nat. Clim. Chang. 2018, 8, 214–218. [Google Scholar] [CrossRef]
- Larsen, R.; Striby, K.; Horney, M. Fourteen Years of Frage Monitoring on the California Central Coast Shows Tremendous Variation; General Technical Reports PSW-GTR-251; US Department of Agriculture, Forest Service, Pacific Southwest Research Station: Berkeley, CA, USA, 2014; pp. 273–281.
- Intergovernmental Panel on Climate Change [IPCC]. Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T., Qin, D., Plattner, G., Tignor, M., Allen, S., Bosching, J., Nauels, A., Xia, Y., Bex, V., Midgley, P., Eds.; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Coppock, D.L.; Fernández-Giménez, M.; Hiernaux, P.; Huber-Sannwald, E.; Schloeder, C.; Valdivia, C.; Arredondo, J.T.; Jacobs, M.; Turin, C.; Turner, M. Rangeland Systems in Developing Nations: Conceptual Advances and Societal Implications. In Rangeland Systems; Briske, D.D., Ed.; Springer: Cham, Switzerland, 2017; pp. 569–641. ISBN 978-3-319-46707-8. [Google Scholar]
- George, M.R.; Williams, W.A.; McDougald, N.K.; Clawson, W.J.; Murphy, A.H. Predicting Peak Standing Crop on Annual Range Using Weather Variables. J. Range Manag. 1989, 42, 508–512. [Google Scholar] [CrossRef]
- Liacos, L.G. Soil Moisture Depletion in the Annual Grass Type. J. Range Manag. 1962, 15, 67–72. [Google Scholar] [CrossRef]
- O’ Geen, A.T. Soil Water Dynamics. Nat. Educ. Knowl. 2012, 3, 12. [Google Scholar]
- Beaudette, D.E.; O’Geen, A.T. Quantifying the Aspect Effect: An Application of Solar Radiation Modeling for Soil Survey. Soil Sci. Soc. Am. J. 2009, 73, 1755. [Google Scholar] [CrossRef]
- Wang, J.Y. A Critique of the Heat Unit Approach to Plant Response Studies. Ecology 1960, 41, 785–790. [Google Scholar] [CrossRef]
- George, M.R.; Raguse, C.A.; Clawson, W.J.; Wilson, C.B.; Willoughby, R.L.; McDougald, N.K.; Duncan, D.A.; Murphy, A.H. Correlation of Degree-Days with Annual Herbage Yields and Livestock Gains. J. Range Manag. 1988, 41. [Google Scholar] [CrossRef]
- Murphy, A.H. Predicted Forage Yield Based on Fall Precipitation in California Annual Grasslands. J. Range Manag. 1970, 23, 363–365. [Google Scholar] [CrossRef]
- Woodmansee, R.G. Critique and Analyses of the Grassland Ecosystem Model ELM. In Grassland Simulation Model; Innis, G.S., Ed.; Springer: New York, NY, USA, 1978; pp. 257–281. ISBN 978-1-4612-9929-5. [Google Scholar]
- Wright, J.; Skiles, J. SPUR Simulation of Production and Utilization of Rangelands: Documentation and User Guide; USDA-Agricultural Research Service: Washington, DC, USA, 1987.
- Pierson, F.B.; Carlson, D.H.; Spaeth, K.E. A Process-based Hydrology Submodel Dynamically Linked to the Plant Component of the Simulation of Production and Utilization on Rangelands SPUR Model. Ecol. Model. 2001, 141, 241–260. [Google Scholar] [CrossRef]
- Stout, W.L.; Vona, L.C.; Skiles, J.W.; Shaffer, J.A.; Jung, G.A.; Reid, R.L. Evaluating SPUR Model for Predicting Animal Gains and Biomass on Eastern Hill Land Pastures. Agric. Syst. 1990, 34, 169–178. [Google Scholar] [CrossRef]
- Corson, M.S.; Skinner, R.H.; Rotz, C.A. Modification of the SPUR Rangeland Model to Simulate Species Composition and Pasture Productivity in Humid Temperate Regions. Agric. Syst. 2006, 87, 169–191. [Google Scholar] [CrossRef]
- Monteith, J.L. Solar Radiation and Productivity in Tropical Ecosystems. J. Appl. Ecol. 1972, 9, 747. [Google Scholar] [CrossRef]
- Potter, C.S.; Randerson, J.T.; Field, C.B.; Matson, P.A.; Vitousek, P.M.; Mooney, H.A.; Klooster, S.A. Terresrial Ecosystem Production: A Process Model Based on Global Satellite and Surface Data. Glob. Biogeochem. Cycles 1993, 7, 811–841. [Google Scholar] [CrossRef]
- Li, S. Monitoring of Net Primary Production in California Rangelands Using Landsat and MODIS Satellite Remote Sensing. Nat. Resour. 2012, 3, 56–65. [Google Scholar] [CrossRef]
- Goetz, S.J.; Prince, D.; Goward, N.; Thawley, M.M.; Small, J.; Johnston, A. Mapping Net Primary Production and Related Biophysical Variables with Remote Sensing: Application to the BOREAS region. J. Geophys. Res. 1999, 104, 27719–27734. [Google Scholar] [CrossRef]
- Grigera, G.; Oesterheld, M.; Pacín, F. Monitoring Forage Production for Farmers’ Decision Making. Agric. Syst. 2007, 94, 637–648. [Google Scholar] [CrossRef]
- Running, S.W.; Thornton, P.E.; Nemani, R.; Glassy, J.M. Global Terrestrial Gross and Net Primary Productivity from the Earth Observing System. In Methods in Ecosystem Science; Springer: New York, NY, USA, 2000; pp. 44–57. [Google Scholar]
- Turner, D.; Gower, S.; Cohen, W.; Gregory, M.; Maiersperger, T. Effects of Spatial Variability in Light Use Efficiency on Satellite-based NPP Monitoring. Remote Sens. Environ. 2002, 80, 397–405. [Google Scholar] [CrossRef]
- Lobell, D.B.; Hicke, J.A.; Asner, G.P.; Field, C.B.; Tucker, C.J.; Los, S.O. Satellite Estimates of Productivity and Light Use Efficiency in United States Agriculture, 1982-98. Glob. Chang. Biol. 2002, 8, 722–735. [Google Scholar] [CrossRef]
- Nestola, E.; Calfapietra, C.; Emmerton, C.A.; Wong, C.Y.S.; Thayer, D.R.; Gamon, J.A. Monitoring Grassland Seasonal Carbon Dynamics, by Integrating MODIS NDVI, Proximal Optical Sampling, and Eddy Covariance Measurements. Remote Sens. 2016, 8, 260. [Google Scholar] [CrossRef]
- Hilker, T.; Coops, N.C.; Wulder, M.A.; Black, T.A.; Guy, R.D. The Use of Remote Sensing in Light Use Efficiency Based Models of Gross Primary Production: A Review of Current Status and Future Requirements. Sci. Total Environ. 2008, 404, 411–423. [Google Scholar] [CrossRef]
- Yuan, W.; Liu, S.; Zhou, G.G.; Zhou, G.G.; Tieszen, L.L.; Baldocchi, D.; Bernhofer, C.; Gholz, H.; Goldstein, A.H.; Goulden, M.L.; et al. Deriving a Light Use Efficiency Model from Eddy Covariance Flux Data for Predicting Daily Gross Primary Production Across Biomes. Agric. For. Meteorol. 2007, 143, 189–207. [Google Scholar] [CrossRef]
- Prince, S.D.; Goward, S.N. Global Primary Production: A Remote Sensing Approach. Source J. Biogeogr. 1995, 22, 815–835. [Google Scholar] [CrossRef]
- Fisher, J.I.; Mustard, J.F.; Vadeboncoeur, M.A. Green Leaf Phenology at Landsat Resolution: Scaling from the Field to the Satellite. Remote Sens. Environ. 2006, 100, 265–279. [Google Scholar] [CrossRef]
- Gärtner, P.; Förster, M.; Kleinschmit, B. The Benefit of Synthetically Generated RapidEye and Landsat 8 data Fusion Time Series for Riparian Forest Disturbance Monitoring. Remote Sens. Environ. 2016, 177, 237–247. [Google Scholar] [CrossRef]
- Hunt, E.R.; Everitt, J.H.; Ritchie, J.C.; Moran, M.S.; Booth, D.T.; Anderson, G.L.; Clark, P.E.; Seyfried, M.S. Applications and Research Using Remote Sensing for Rangeland Management. Photogramm. Eng. Remote Sens. 2003, 69, 675–693. [Google Scholar] [CrossRef]
- Walker, J.J.; De Beurs, K.M.; Wynne, R.H. Dryland Vegetation Phenology across An Elevation Gradient in Arizona, USA, Investigated with Fused MODIS and Landsat Data. Remote Sens. Environ. 2014, 144, 85–97. [Google Scholar] [CrossRef]
- Yu, N.; Li, L.; Schmitz, N.; Tian, L.F.; Greenberg, J.A.; Diers, B.W. Development of methods to improve soybean yield estimation and predict plant maturity with an unmanned aerial vehicle based platform. Remote Sens. Environ. 2016, 187, 91–101. [Google Scholar] [CrossRef]
- Guan, S.; Fukami, K.; Matsunaka, H.; Okami, M.; Tanaka, R.; Nakano, H.; Sakai, T.; Nakano, K.; Ohdan, H.; Takahashi, K.; et al. Assessing Correlation of High-Resolution NDVI with Fertilizer Application Level and Yield of Rice and Wheat Crops using Small UAVs. Remote Sens. 2019, 11, 112. [Google Scholar] [CrossRef]
- Yue, J.; Yang, G.; Li, C.; Li, Z.; Wang, Y.; Feng, H.; Xu, B.; Yue, J.; Yang, G.; Li, C.; et al. Estimation of Winter Wheat Above-Ground Biomass Using Unmanned Aerial Vehicle-Based Snapshot Hyperspectral Sensor and Crop Height Improved Models. Remote Sens. 2017, 9, 708. [Google Scholar] [CrossRef]
- Näsi, R.; Viljanen, N.; Kaivosoja, J.; Alhonoja, K.; Hakala, T.; Markelin, L.; Honkavaara, E.; Näsi, R.; Viljanen, N.; Kaivosoja, J.; et al. Estimating Biomass and Nitrogen Amount of Barley and Grass Using UAV and Aircraft Based Spectral and Photogrammetric 3D Features. Remote Sens. 2018, 10, 1082. [Google Scholar] [CrossRef]
- Brocks, S.; Bareth, G.; Brocks, S.; Bareth, G. Estimating Barley Biomass with Crop Surface Models from Oblique RGB Imagery. Remote Sens. 2018, 10, 268. [Google Scholar] [CrossRef]
- Sarron, J.; Malézieux, É.; Sané, C.; Faye, É.; Sarron, J.; Malézieux, É.; Sané, C.A.B.; Faye, É. Mango Yield Mapping at the Orchard Scale Based on Tree Structure and Land Cover Assessed by UAV. Remote Sens. 2018, 10, 1900. [Google Scholar] [CrossRef]
- Planet. Planet Imagery Product Specification: PlanetScope and RapidEye; Planet Labs Inc.: San Francisco, CA, USA, 2018. [Google Scholar]
- Bartolome, J.; Frost, W.; Mcdougald, N. Guidelines for Residual Dry Matter on Coastal and Foothill Rangelands in California. Agric. Nat. Resour. Publ. 2002, 8092, 1–7. [Google Scholar]
- Ball, G.H.; Hall, D.J. ISODATA, A Novel Method of Data Analysis and Pattern Classification; Stanford Research Institute: Menlo Park, CA, USA, 1965. [Google Scholar]
- Pix4D Support Radiometric Corrections. Available online: https://support.pix4d.com/hc/en-us/articles/202559509-Radiometric-corrections#%23label2 (accessed on 26 September 2018).
- Teillet, P.M.; Guindon, B.; Goodenough, D.G. On the Slope-Aspect Correction of Multispectral Scanner Data. Can. J. Remote Sens. 1982, 8, 84–106. [Google Scholar] [CrossRef]
- Meyer, P.; Itten, K.I.; Kellenberger, T.; Sandmeier, S.; Sandmeier, R. Radiometric Corrections of Topographically Induced Effects on Landsat TM Data in an Alpine Environment. ISPRS J. Photogramm. Remote Sens. 1993, 48, 17–28. [Google Scholar] [CrossRef]
- Soenen, S.A.; Peddle, D.R.; Coburn, C.A. SCS+C: A Modified Sun-canopy-sensor Topographic Correction in Forested Terrain. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2148–2159. [Google Scholar] [CrossRef]
- Tan, B.; Masek, J.G.; Wolfe, R.; Gao, F.; Huang, C.; Vermote, E.F.; Sexton, J.O.; Ederer, G. Improved Forest Change Detection with Terrain Illumination Corrected Landsat Images. Remote Sens. Environ. 2013, 136, 469–483. [Google Scholar] [CrossRef]
- Gao, F.; Masek, J.; Schwaller, M.; Hall, F. On the Blending of The landsat and MODIS Surface Reflectance: Predicting Daily Landsat Surface Reflectance. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2207–2218. [Google Scholar] [CrossRef]
- Paruelo, J.M.; Epstein, H.E.; Lauenroth, W.K.; Burke, I.C. ANPP Estimates from NDVI for the Central Grassland Region of the United States ANPP. Ecology 1997, 78, 953–958. [Google Scholar] [CrossRef]
- Anderson, G.; Hanson, J.; Haas, R. Evaluating Landsat Thematic Mapper Derived Vegetation Indices for Estimating Above-Ground Biomass on Semiarid Rangelands. Remote Sens. Environ. 1993, 45, 165–175. [Google Scholar] [CrossRef]
- Moulin, S.; Kergoat, L.; Viovy, N.; Dedieu, G. Global-scale Assessment of Vegetation Phenology using NOAA/AVHRR Satellite Measurements. J. Clim. 1997, 10, 1154–1170. [Google Scholar] [CrossRef]
- Tucker, C.J.; Sellers, P.J. Satellite Remote Sensing of Primary Production. Int. J. Remote Sens. 1986, 7, 1395–1416. [Google Scholar] [CrossRef]
- Zhang, X.; Friedl, M.A.; Schaaf, C.B.; Strahler, A.H.; Hodges, J.C.F.; Gao, F.; Reed, B.C.; Huete, A. Monitoring Vegetation Phenology using MODIS. Remote Sens. Environ. 2003, 84, 471–475. [Google Scholar] [CrossRef]
- Sellers, P.J.; Los, S.O.; Tucker, C.J.; Justice, C.O.; Dazlich, D.A.; Collatz, G.J.; Randall, D.A. A Revised Land Surface Parameterization (SiB2) Ffor Atmospheric GCMs. Part II: The Generation of Global Fields of Terrestrial Biophysical Parameters from Datellite Data. J. Clim. 1996, 9, 706–737. [Google Scholar] [CrossRef]
- Hart, Q.J.; Brugnach, M.; Temesgen, B.; Rueda, C.; Ustin, S.L.; Frame, K. Daily Reference Evapotranspiration for California using Satellite Imagery and Weather Station Measurement Interpolation. Civ. Eng. Environ. Syst. 2009, 26, 19–33. [Google Scholar] [CrossRef]
- Akitsu, T.; Kume, A.; Hirose, Y.; Ijima, O.; Nasahara, K.N. On the Stability of Radiometric Ratios of Photosynthetically Active Radiation to Global Solar Radiation in Tsukuba, Japan. Agric. For. Meteorol. 2015, 209, 59–68. [Google Scholar] [CrossRef]
- Blackburn, W.J.; Proctor, J.T.A. Estimating Photosynthetically Active Radiation from Measured Solar Irradlance. Sol. Energy 1983, 3183, 233–234. [Google Scholar] [CrossRef]
- Li, R.; Zhao, L.; Ding, Y.; Wang, S.; Ji, G.; Xiao, Y.; Liu, G.; Sun, L. Monthly Ratios of PAR to Global Solar Radiation Measured at Northern Tibetan Plateau, China. Sol. Energy 2010, 84, 964–973. [Google Scholar] [CrossRef]
- Papaioannou, G.; Papanikolaou, N.; Retalis, D. Relationships of Photosynthetically Active Radiation and Shortwave Irradiance. Theor. Appl. Climatol. 1993, 48, 23–27. [Google Scholar] [CrossRef]
- Tsubo, M.; Walker, S. Relationships between Photosynthetically Active Radiation and Clearness Index at Bloemfontein, South Africa. Theor. Appl. Climatol. 2005, 80, 17–25. [Google Scholar] [CrossRef]
- Frouin, R.; Pinker, R.T. Estimating Photosynthetically Active Radiation (PAR) at the Earth’s Surface from Satellite Observations. Remote Sens. Environ. 1995, 51, 98–107. [Google Scholar] [CrossRef]
- ArcGIS for Desktop Area Solar Radiation. Available online: http://desktop.arcgis.com/en/arcmap/10.3/tools/spatial-analyst-toolbox/area-solar-radiation.htm (accessed on 11 March 2019).
- Klute, A.; Cassel, D.K.; Nielsen, D.R. Field Capacity and Available Water Capacity. In Methods of Soil Analysis: Part 1—Physical and Mineralogical Methods; Soil Science Society of America, American Society of Agronomy: Madison, WI, USA, 1986; pp. 901–926. [Google Scholar]
- Gibson, W.; Daly, C.; Kittel, T.; Nychka, D.; Johns, C.; Rosenbloom, N.; McNab, A.; Taylor, G. Development of A 103-year high-resolution Climate Data Set for the Conterminous United States. In AMS Conference on Applied Climatology; American Meteorological Society: Portland, OR, USA, 2002; pp. 181–183. [Google Scholar]
- Robbins, H.; Monro, S. A Stochastic Approximation Method. Annu. Math. Stat. 1951, 22, 400–407. [Google Scholar] [CrossRef]
- Bottou, L. Stochastic gradient descent tricks. In Neural Networks: Tricks of the Trade; Springer: Berlin/Heidelberg, Germany, 2012; pp. 421–436. ISBN 9783642352881. [Google Scholar]
- Trishchenko, A.P.; Cihlar, J.; Li, Z. Effects of Spectral Response Function on Surface Reflectance and NDVI Measured with Moderate Resolution Satellite Sensors. Remote Sens. Environ. 2002, 81, 1–18. [Google Scholar] [CrossRef]
- Roy, D.P.; Kovalskyy, V.; Zhang, H.K.; Vermote, E.F.; Yan, L.; Kumar, S.S.; Egorov, A. Characterization of Landsat-7 to Landsat-8 Reflective Wavelength and Normalized Difference Vegetation Index Continuity. Remote Sens. Environ. 2016, 185, 57–70. [Google Scholar] [CrossRef]
- Li, A.; Bian, J.; Lei, G.; Huang, C. Estimating the Maximal Light Use Efficiency for Different Vegetation Through the CASA Model Combined with Time-series Remote Sensing Data and Ground Measurements. Remote Sens. 2012, 4, 3857–3876. [Google Scholar] [CrossRef]
- Paloscia, S.; Pettinato, S.; Santi, E.; Notarnicola, C.; Pasolli, L.; Reppucci, A. Soil Moisture Mapping using Sentinel-1 Images: Algorithm and Rreliminary Validation. Remote Sens. Environ. 2013, 134, 234–248. [Google Scholar] [CrossRef]
- Wagner, W.; Sabel, D.; Doubkova, M.; Bartsch, A.; Pathe, C. The Potential of Sentinel-1 for Monitoring Soil Moisture With a High Spatial Resolution At Global Scale. Earth Obs. Water Cycle Sci. 2009, 2009, 18–20. [Google Scholar]
- Balenzano, A.; Mattia, F.; Satalino, G.; Pauwels, V.; Snoeij, P. SMOSAR Algorithm for Soil Moisture Retrival using Sentinel-1 Data. In Proceedings of the2012 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Munich, Germany, 22–27 July 2012; pp. 1200–1203. [Google Scholar]
- Chaplin-Kramer, R.; George, M.R. Effects of Climate Change on Range Forage Production in the San Francisco Bay Area. PLoS ONE 2013, 8, 1–11. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).