A Comparison of Three Sediment Acoustic Models Using Bayesian Inversion and Model Selection Techniques
Abstract
1. Introduction
2. Geoacoustic Models and Acoustic Scattering Models
2.1. Fluid Model
2.1.1. EDFM
2.1.2. Fluid Interface Roughness Scattering Model
2.1.3. Fluid Volume Scattering Model
2.2. Grain-Shearing Elastic Model
2.2.1. VGS(λ)
2.2.2. Elastic Scattering Model
2.3. Poroelastic Model
2.3.1. CREB
2.3.2. Poroelastic Scattering Model
2.4. Sensitivity Analysis
3. Bayesian Inference
3.1. Parameter Inversion
3.2. Convergence Criterion
3.3. Model Selection
4. Experimental Measurements, Results, and Discussion
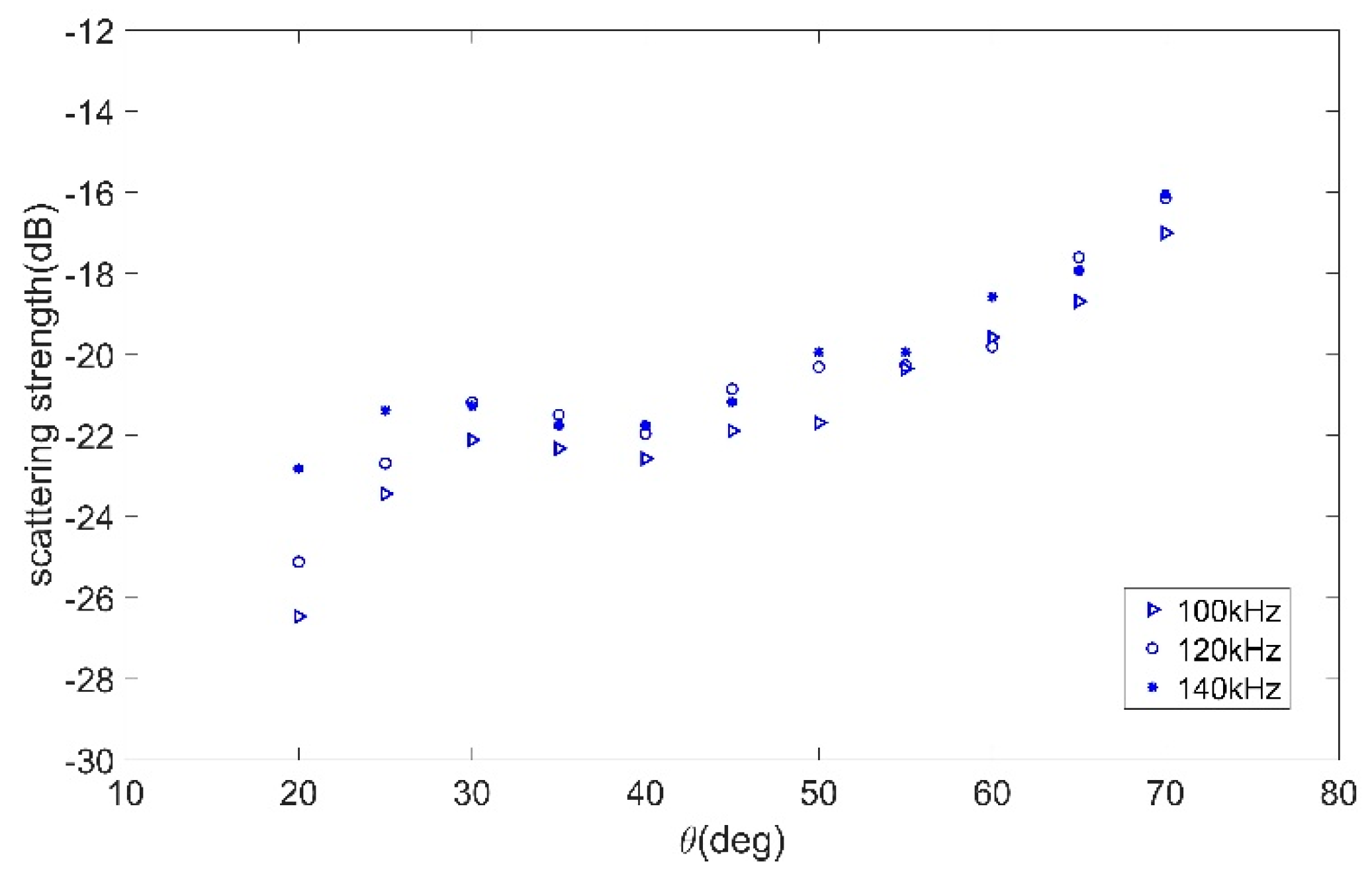
4.1. Experiment Description
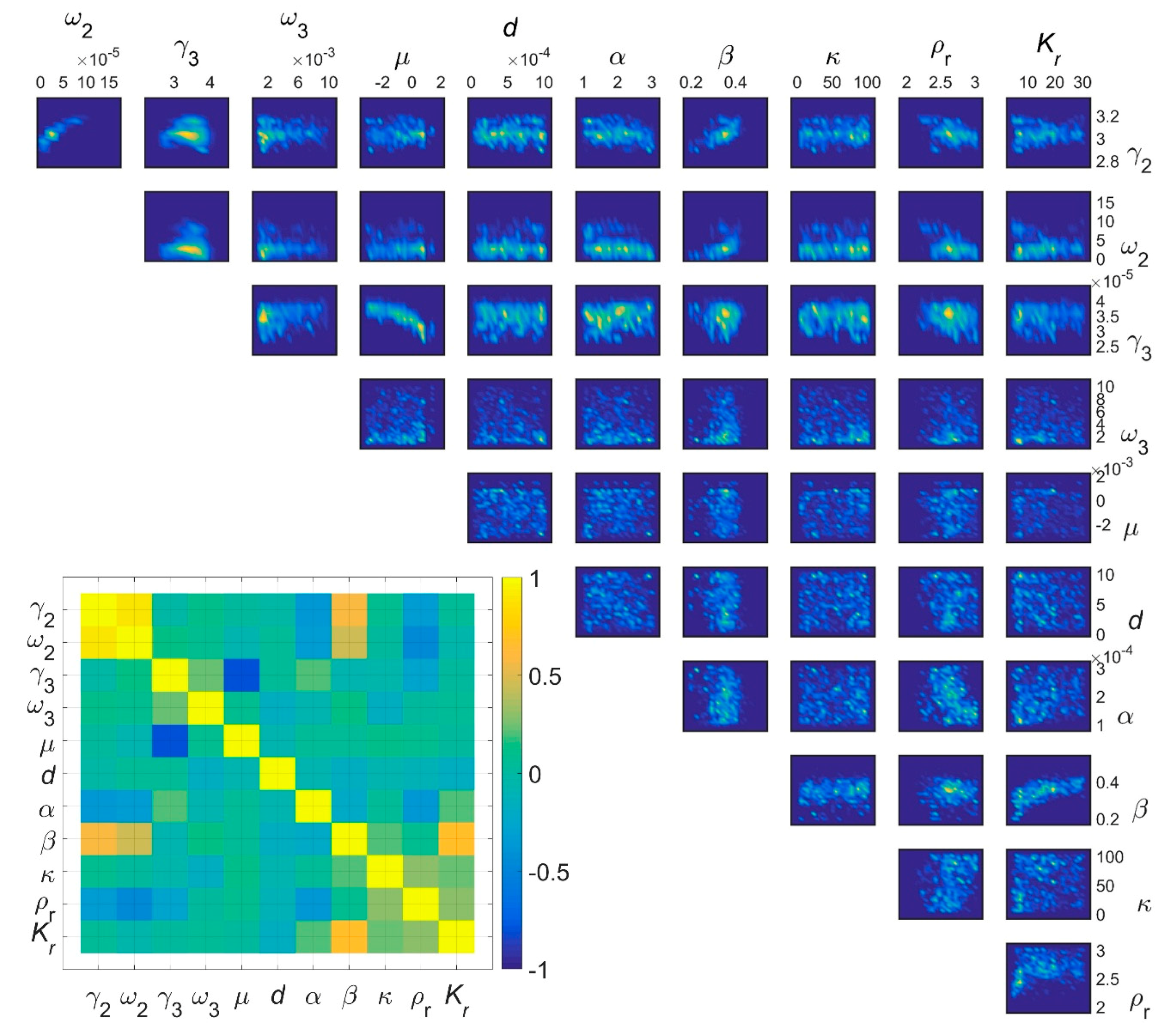
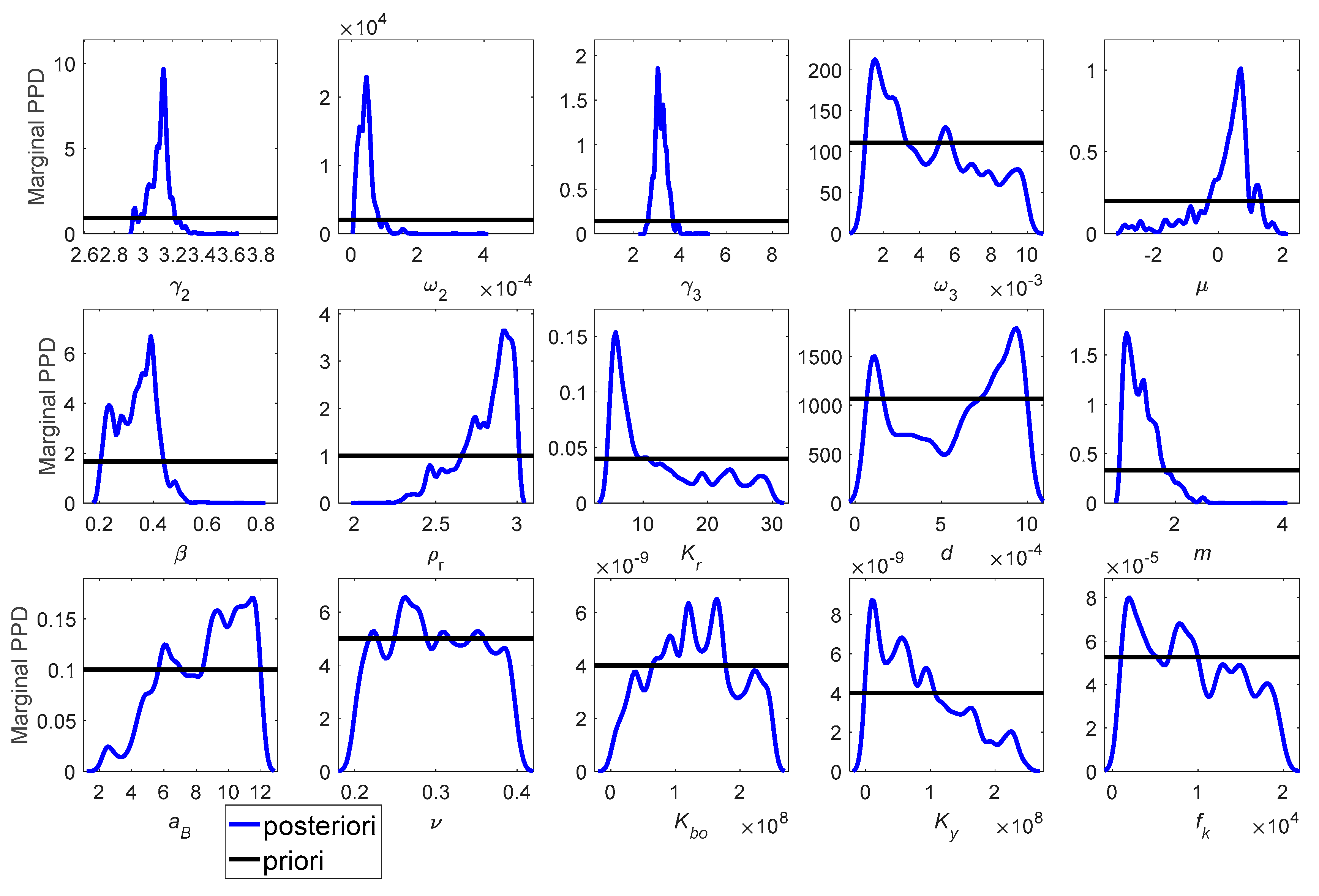
4.2. Parameter Inversion
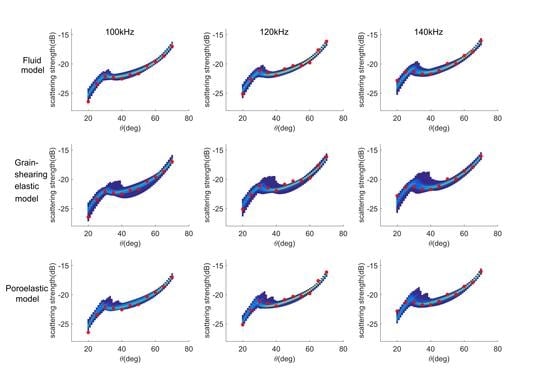
4.2.1. Fluid Model
4.2.2. Grain-Shearing Elastic Model
4.2.3. Poroelastic Model
4.3. Model Comparison and Selection
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A

Appendix B
References
- Anderson, J.T.; Van Holliday, D.; Kloser, R.; Reid, D.G.; Simard, Y. Acoustic seabed classification: Current practice and future directions. ICES J. Mar. Sci. 2008, 65, 1004–1011. [Google Scholar] [CrossRef]
- Siemes, K.; Hermand, J.P.; Snellen, M.; Simons, D.G. Toward an Efficient and Comprehensive Assessment of Marine Sediments through Combining Hydrographic Surveying and Geoacoustic Inversion. IEEE J. Ocean. Eng. 2016, 41, 190–203. [Google Scholar]
- Jackson, D.R.; Richardson, M.D. High-Frequency Seafloor Acoustics; Springer: New York, NY, USA, 2007. [Google Scholar]
- Chotiros, N.P.; Isakson, M.J. A broadband model of sandy ocean sediments: Biot–Stoll with contact squirt flow and shear drag. J. Acoust. Soc. Am. 2004, 116, 2011–2022. [Google Scholar] [CrossRef]
- Buckingham, M.J. Compressional and shear wave properties of marine sediments: Comparisons between theory and data. J. Acoust. Soc. Am. 2005, 117, 137–152. [Google Scholar] [CrossRef] [PubMed]
- Buckingham, M.J. On pore-fluid viscosity and the wave properties of saturated granular materials including marine sediments. J. Acoust. Soc. Am. 2007, 122, 1486. [Google Scholar] [CrossRef] [PubMed]
- Williams, K.L. Adding thermal and granularity effects to the effective density fluid model. J. Acoust. Soc. Am. 2013, 133, EL431–EL437. [Google Scholar] [CrossRef] [PubMed]
- Buckingham, M.J. Analysis of shear-wave attenuation in unconsolidated sands and glass beads. J. Acoust. Soc. Am. 2014, 136, 2478–2488. [Google Scholar] [CrossRef] [PubMed]
- Chotiros, N.P.; Isakson, M.J. Shear wave attenuation and micro-fluidics in water-saturated sand and glass beads. J. Acoust. Soc. Am. 2014, 135, 3264–3279. [Google Scholar] [CrossRef] [PubMed]
- Williams, K.L.; Jackson, D.R.; Thorsos, E.I.; Tang, D.J.; Briggs, K.B. Acoustic backscattering experiments in a well characterized sand sediment: Data/model comparisons using sediment fluid and Biot models. IEEE J. Ocean. Eng. 2002, 27, 376–387. [Google Scholar] [CrossRef]
- Ohkawa, K.; Yamaoka, H.; Yamamoto, T. Acoustic backscattering from a sandy seabed. IEEE J. Ocean. Eng. 2005, 30, 700–708. [Google Scholar] [CrossRef]
- Williams, K.L.; Jackson, D.R.; Dajun, T.; Briggs, K.B.; Thorsos, E.I. Acoustic Backscattering From a Sand and a Sand/Mud Environment: Experiments and Data/Model Comparisons. IEEE J. Ocean. Eng. 2009, 34, 388–398. [Google Scholar] [CrossRef]
- Williams, K.L.; Thorsos, E.I.; Jackson, D.R.; Hefner, B.T. Thirty years of sand acoustics: A perspective on experiments, models and data/model comparisons. AIP Conf. Proc. 2012, 1495, 166–192. [Google Scholar]
- Biot, M. Theory of Propagation of Elastic Waves in a Fluid-Saturated Porous Solid. I. Low-Frequency Range. J. Acoust. Soc. Am. 1956, 28, 168–178. [Google Scholar] [CrossRef]
- Biot, M. Theory of Propagation of Elastic Waves in a Fluid-Saturated Porous Solid. II. Higher Frequency Range. Acoust. Soc. Am. J. 1956, 28, 179–191. [Google Scholar] [CrossRef]
- Stoll, R.D. Sediment Acoustics. Lecture Notes in Earth Sciences; Springer: Berlin, Germany, 1989; pp. 1–101. [Google Scholar]
- Chotiros, N.P. Acoustics of the Seabed as a Poroelastic Medium; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Bonomo, A.L.; Isakson, M.J. A comparison of three geoacoustic models using Bayesian inversion and selection techniques applied to wave speed and attenuation measurements. J. Acoust. Soc. Am. 2018, 143, 2501. [Google Scholar] [CrossRef] [PubMed]
- Williams, K.L. An effective density fluid model for acoustic propagation in sediments derived from Biot theory. J. Acoust. Soc. Am. 2001, 110, 2276–2281. [Google Scholar] [CrossRef] [PubMed]
- Williams, K.L.; Jackson, D.R.; Thorsos, E.I.; Dajun, T.; Schock, S.G. Comparison of sound speed and attenuation measured in a sandy sediment to predictions based on the Biot theory of porous media. IEEE J. Ocean. Eng. 2002, 27, 413–428. [Google Scholar] [CrossRef]
- Bonomo, A.L.; Chotiros, N.P.; Isakson, M.J. On the validity of the effective density fluid model as an approximation of a poroelastic sediment layer. J. Acoust. Soc. Am. 2015, 138, 748–757. [Google Scholar] [CrossRef] [PubMed]
- Buckingham, M.J. Wave propagation, stress relaxation, and grain-to-grain shearing in saturated, unconsolidated marine sediments. J. Acoust. Soc. Am. 2000, 108, 2796–2815. [Google Scholar] [CrossRef]
- Buckingham, M.J. Response to “Comments on ‘Pore fluid viscosity and the wave properties of saturated granular materials including marine sediments [J. Acoust. Soc. Am. 127, 2095–2098 (2010)]’”. J. Acoust. Soc. Am. 2010, 127, 2099. [Google Scholar] [CrossRef]
- Dettmer, J.; Dosso, S.E.; Holland, C.W. Model selection and Bayesian inference for high-resolution seabed reflection inversion. J. Acoust. Soc. Am. 2009, 125, 706–716. [Google Scholar] [CrossRef]
- Dosso, S.E.; Nielsen, P.L.; Harrison, C.H. Bayesian inversion of reverberation and propagation data for geoacoustic and scattering parameters. J. Acoust. Soc. Am. 2009, 125, 2867–2880. [Google Scholar] [CrossRef] [PubMed]
- Dosso, S.E.; Dettmer, J.; Steininger, G.; Holland, C.W. Efficient trans-dimensional Bayesian inversion for geoacoustic profile estimation. Inverse Probl. 2014, 30, 114018. [Google Scholar] [CrossRef]
- Simons, D.G.; Snellen, M. A Bayesian approach to seafloor classification using multi-beam echo-sounder backscatter data. Appl. Acoust. 2009, 70, 1258–1268. [Google Scholar] [CrossRef]
- Landmark, K.; Solberg, A.H.S.; Austeng, A.; Hansen, R.E. Bayesian Seabed Classification Using Angle-Dependent Backscatter Data From Multibeam Echo Sounders. IEEE J. Ocean. Eng. 2014, 39, 724–739. [Google Scholar] [CrossRef]
- Bourbie, T.; Coussy, O.; Zinszner, B. Acoustics of Porous Media; Editions Technip: Paris, France, 1987. [Google Scholar]
- Stoll, R.D. Acoustic Waves in Saturated Sediments; Springer: Boston, MA, USA, 1974. [Google Scholar]
- Zou, D.P.; Williams, K.L.; Thorsos, E.I. Influence of Temperature on Acoustic Sound Speed and Attenuation of Seafloor Sand Sediment. IEEE J. Ocean. Eng. 2015, 40, 969–980. [Google Scholar]
- Thorsos, E.I.; Jackson, D.R. The validity of the perturbation approximation for rough surface scattering using a Gaussian roughness spectrum. J. Acoust. Soc. Am. 1989, 86, 261–277. [Google Scholar] [CrossRef]
- Thorsos, E.I. The Validity of the Kirchoff Approximation for Rough Surface Scattering Using a Gaussian Roughness Spectrum. J. Acoust. Soc. Am. 1998, 86 (Suppl. 1), 20. [Google Scholar]
- Voronovich, A. Small-slope approximation in wave scattering by rough surfaces. Sov. Phys. JETP 1985, 62, 65–70. [Google Scholar]
- Williams, K.L.; Jackson, D.R. Bistatic bottom scattering: Model, experiments, and model/data comparison. J. Acoust. Soc. Am. 1998, 103, 169–181. [Google Scholar] [CrossRef]
- Pouliquen, E.; Lyons, A.P.; Pace, N.G. Penetration of acoustic waves into rippled sandy seafloors. J. Acoust. Soc. Am. 2000, 1 Pt 1, 2071–2081. [Google Scholar] [CrossRef]
- Hamilton, E.L. Elastic properties of marine sediments. J. Geophys. Res. 1971, 76, 579–604. [Google Scholar] [CrossRef]
- Hamilton, E.L.; Bachman, R.T. Sound velocity and related properties of marine sediments. J. Acoust. Soc. Am. 1982, 72, 1891–1904. [Google Scholar] [CrossRef]
- Williams, K.L.; Grochocinski, J.M.; Jackson, D.R. Interface scattering by poroelastic seafloors: First-order theory. J. Acoust. Soc. Am. 2001, 110, 2956–2963. [Google Scholar] [CrossRef]
- Borgonovo, E. A new uncertainty importance measure. Reliab. Eng. Syst. Saf. 2007, 92, 771–784. [Google Scholar] [CrossRef]
- Sobol, I.M. Theorems and examples on high dimensional model representation. Reliab. Eng. Syst. Saf. 2003, 79, 187–193. [Google Scholar] [CrossRef]
- Sobol, I.M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates. Math. Comput. Simul. 2001, 55, 271–280. [Google Scholar] [CrossRef]
- Saltelli, A.; Tarantola, S.; Campolongo, F. Sensitivity anaysis as an ingredient of modeling. Stat. Sci. 2000, 15, 377–395. [Google Scholar]
- Rabitz, H.; Aliş, Ö.F. General foundations of high-dimensional model representations. J. Math. Chem. 1999, 25, 197–233. [Google Scholar] [CrossRef]
- Hefner, B.T.; Williams, K.L. Sound speed and attenuation measurements in unconsolidated glass-bead sediments saturated with viscous pore fluids. J. Acoust. Soc. Am. 2006, 120, 2538–2549. [Google Scholar] [CrossRef]
- Helton, J.C.; Davis, F.J. Latin hypercube sampling and the propagation of uncertainty in analyses of complex systems. Reliab. Eng. Syst. Saf. 2003, 81, 23–69. [Google Scholar] [CrossRef]
- Dosso, S.E. Quantifying uncertainty in geoacoustic inversion. I. A fast Gibbs sampler approach. J. Acoust. Soc. Am. 2002, 111, 129–142. [Google Scholar] [CrossRef] [PubMed]
- Dosso, S.E.; Dettmer, J. Bayesian matched-field geoacoustic inversion. Inverse Probl. 2011, 27, 055009. [Google Scholar] [CrossRef]
- Yang, K.D.; Xiao, P.; Duan, R.; Ma, Y.L. Bayesian Inversion for Geoacoustic Parameters from Ocean Bottom Reflection Loss. J. Comput. Acoust. 2017, 25. [Google Scholar] [CrossRef]
- Hastings, W.K. Monte Carlo Sampling Methods Using Markov Chains and Their Applications. Biometrika 1970, 57, 97. [Google Scholar] [CrossRef]
- Haario, H.; Saksman, E.; Tamminen, J. Adaptive proposal distribution for random walk Metropolis algorithm. Comput. Stat. 1999, 14, 375–395. [Google Scholar] [CrossRef]
- Haario, H.; Saksman, E.; Tamminen, J. An adaptive Metropolis algorithm. Bernoulli 2001, 7, 223–242. [Google Scholar] [CrossRef]
- Haario, H.; Laine, M.; Mira, A.; Saksman, E. DRAM: Efficient adaptive MCMC. Stat. Comput. 2006, 16, 339–354. [Google Scholar] [CrossRef]
- Braak, C.J.F.T. A Markov Chain Monte Carlo version of the genetic algorithm Differential Evolution: Easy Bayesian computing for real parameter spaces. Stat. Comput. 2006, 16, 239–249. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Braak, C.J.F.T.; Diks, C.G.H.; Robinson, B.A.; Hyman, J.M.; Higdon, D. Accelerating Markov Chain Monte Carlo Simulation by Differential Evolution with Self-Adaptive Randomized Subspace Sampling. Int. J. Nonlinear Sci. Numer. Simul. 2009, 10, 273–290. [Google Scholar] [CrossRef]
- Dosso, S.E.; Nielsen, P.L. Quantifying uncertainty in geoacoustic inversion. II. Application to broadband, shallow-water data. J. Acoust. Soc. Am. 2002, 111, 143–159. [Google Scholar] [CrossRef] [PubMed]
- Vrugt, J.A. Markov chain Monte Carlo simulation using the DREAM software package: Theory, concepts, and MATLAB implementation. Environ. Model. Softw. 2016, 75, 273–316. [Google Scholar] [CrossRef]
- Gelman, A.; Rubin, D.B. Inference from Iterative Simulation Using Multiple Sequences. Stat. Sci. 1992, 7, 457–472. [Google Scholar] [CrossRef]
- Brooks, S.P.; Gelman, A. General methods for monitoring convergence of iterative simulations. J. Comput. Graph. Stat. 1998, 7, 434–455. [Google Scholar]
- Kass, R.E.; Raftery, A.E. Bayes Factors. J. Am. Stat. Assoc. 1995, 90, 773–795. [Google Scholar] [CrossRef]
- Brunetti, C.; Linde, N.; Vrugt, J.A. Bayesian model selection in hydrogeophysics: Application to conceptual subsurface models of the South Oyster Bacterial Transport Site, Virginia, USA. Adv. Water Resour. 2017, 102, 127–141. [Google Scholar] [CrossRef]
- Jackson, D.R.; Baird, A.M.; Crisp, J.J.; Thomson, P.A.G. High-frequency bottom backscatter measurements in shallow water. J. Acoust. Soc. Am. 1986, 80, 1188–1199. [Google Scholar] [CrossRef]
- Zou, B.; Zhai, J.; Xu, J.; Li, Z.; Gao, S. A Method for Estimating Dominant Acoustic Backscatter Mechanism of Water-Seabed Interface via Relative Entropy Estimation. Math. Probl. Eng. 2018, 2018, 10. [Google Scholar] [CrossRef]







| Parameter | Symbol | Lower Bound | Upper Bound | Unit | |
|---|---|---|---|---|---|
| Common parameters | Roughness spectral exponent | 2 | 4 | dimensionless | |
| Roughness spectral strength | 0.00001 | 0.0005 | |||
| Density fluctuation spectral exponent | 1 | 8 | dimensionless | ||
| Density fluctuation spectral strength | 0.001 | 0.01 | |||
| Ratio of compressibility to density fluctuation | −3 | 2 | dimensionless | ||
| Porosity | 0.2 | 0.8 | dimensionless | ||
| Ratio of mass density of grains to water | 2 | 3 | dimensionless | ||
| Ratio of bulk modulus of grains to water | 5 | 30 | dimensionless | ||
| Fluid model parameters | Mean grain diameter | m | |||
| Tortuosity | 1 | 3 | dimensionless | ||
| Permeability | |||||
| Grain-shearing elastic model parameters | Material exponent | 0.02 | 0.2 | dimensionless | |
| Compressional rigidity coefficient | Pa | ||||
| Shear rigidity coefficient | Pa | ||||
| Compressional viscoelastic relaxation time | s | ||||
| Poroelastic model parameters | Mean grain diameter | m | |||
| Cementation exponent | 1 | 4 | dimensionless | ||
| Pore shape factor | 2 | 12 | dimensionless | ||
| Poisson’s ratio of grains | 0.2 | 0.4 | dimensionless | ||
| Low-frequency asymptotic frame bulk modulus | 0 | Pa | |||
| High-frequency asymptotic increase | 0 | Pa | |||
| Bulk relaxation frequency | Hz |
| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Mass density | 1000 | ||
| Bulk modulus | |||
| Dynamic viscosity | 0.001 | ||
| Compressional wave speed | 1493 |
| Evidence in favor of | |
|---|---|
| <0 | is favored |
| 0 to 0.5 | Not worth more than a bare mention |
| 0.5 to 1 | Substantial |
| 1 to 2 | Strong |
| >2 | Decisive |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, B.; Zhai, J.; Qi, Z.; Li, Z. A Comparison of Three Sediment Acoustic Models Using Bayesian Inversion and Model Selection Techniques. Remote Sens. 2019, 11, 562. https://doi.org/10.3390/rs11050562
Zou B, Zhai J, Qi Z, Li Z. A Comparison of Three Sediment Acoustic Models Using Bayesian Inversion and Model Selection Techniques. Remote Sensing. 2019; 11(5):562. https://doi.org/10.3390/rs11050562
Chicago/Turabian StyleZou, Bo, Jingsheng Zhai, Zhanfeng Qi, and Zhaoxing Li. 2019. "A Comparison of Three Sediment Acoustic Models Using Bayesian Inversion and Model Selection Techniques" Remote Sensing 11, no. 5: 562. https://doi.org/10.3390/rs11050562
APA StyleZou, B., Zhai, J., Qi, Z., & Li, Z. (2019). A Comparison of Three Sediment Acoustic Models Using Bayesian Inversion and Model Selection Techniques. Remote Sensing, 11(5), 562. https://doi.org/10.3390/rs11050562