Study of the Seasonal Effect of Building Shadows on Urban Land Surface Temperatures Based on Remote Sensing Data
Abstract
1. Introduction
2. Materials and Methods
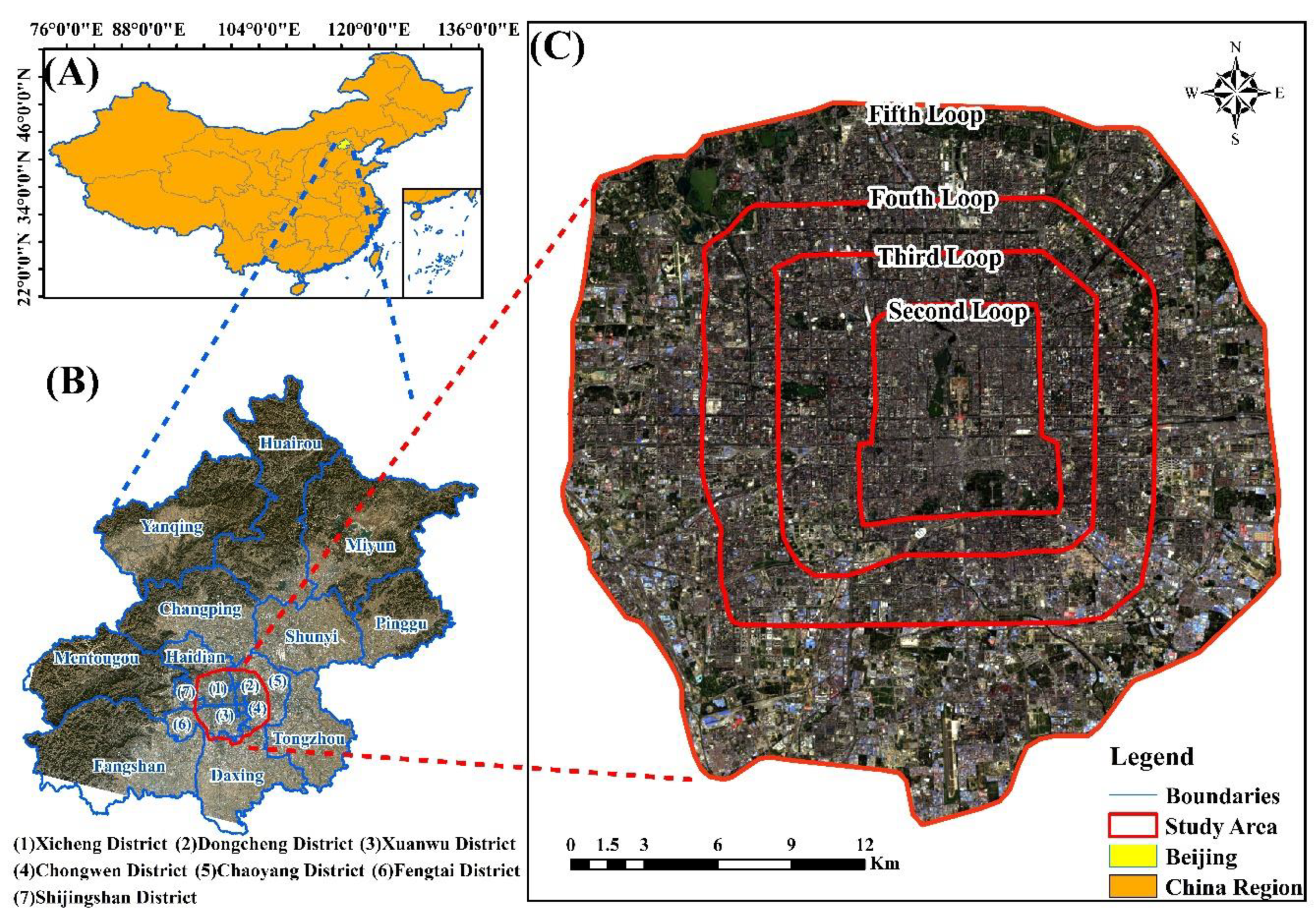
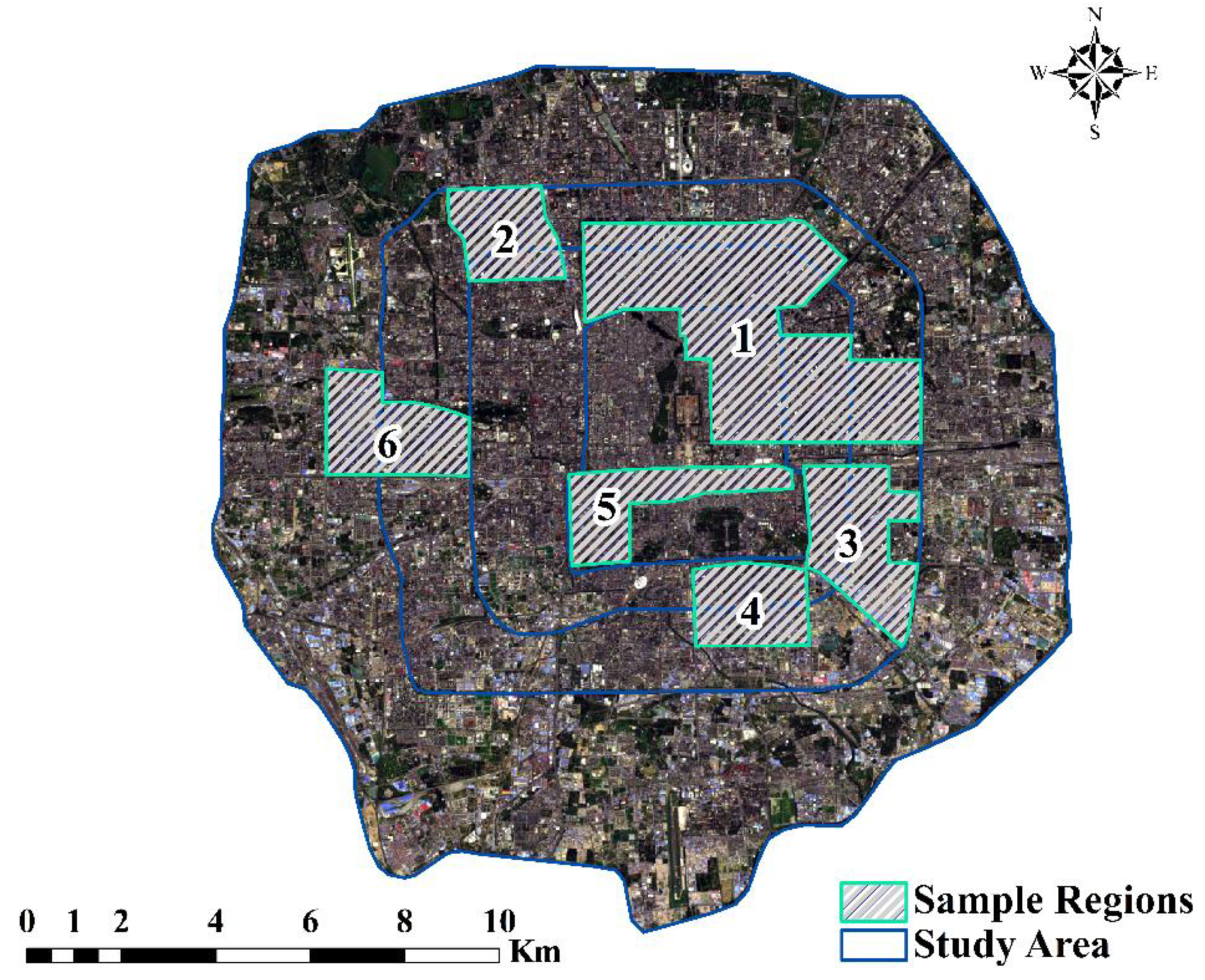
2.1. Study Area
2.2. Data
2.2.1. DSM Data
2.2.2. Landsat-8 Thermal Infrared Sensor Data
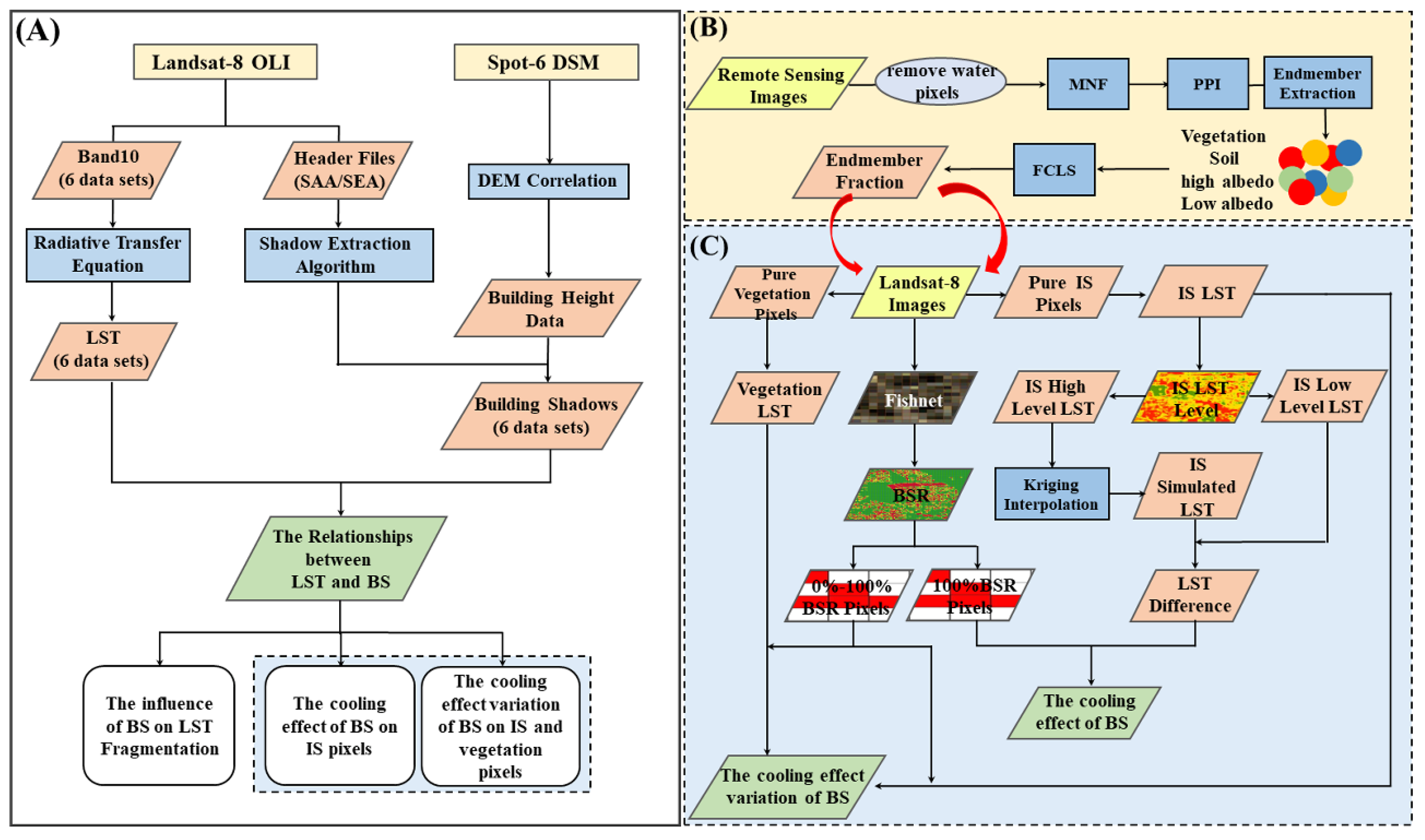
2.3. Methods
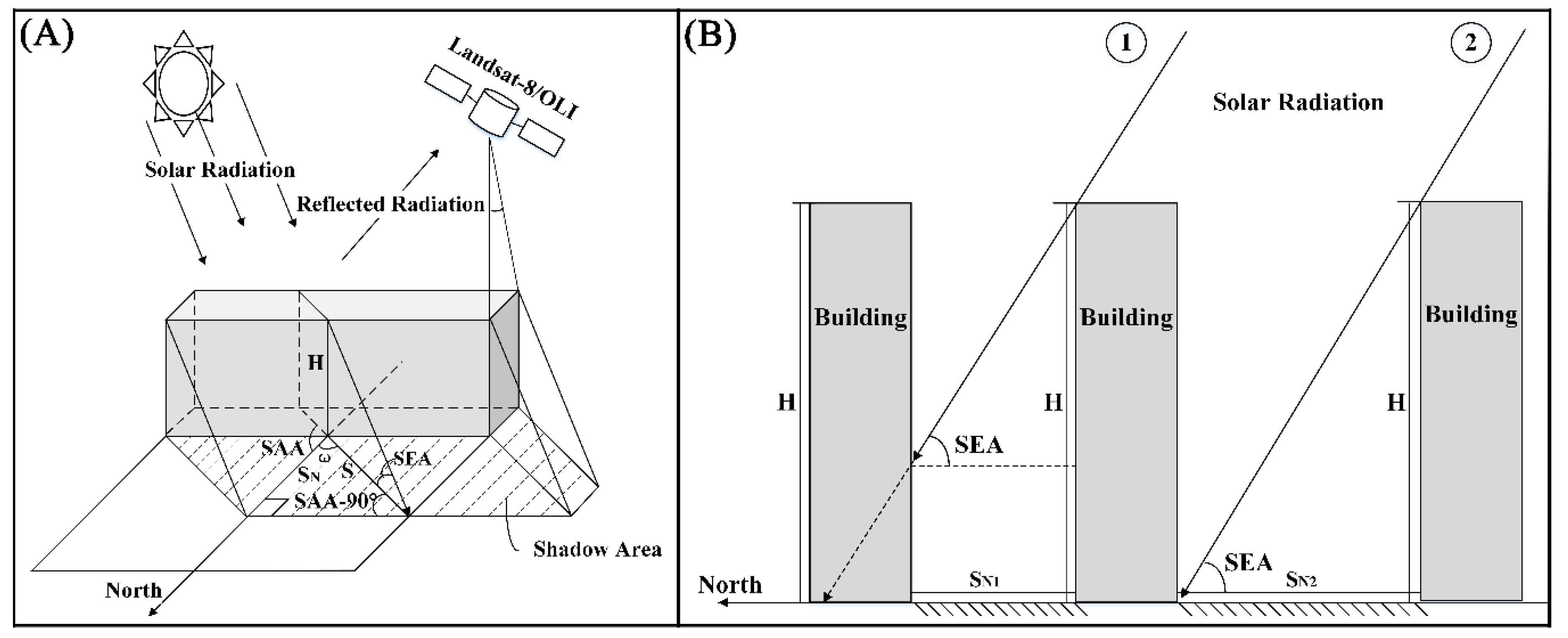
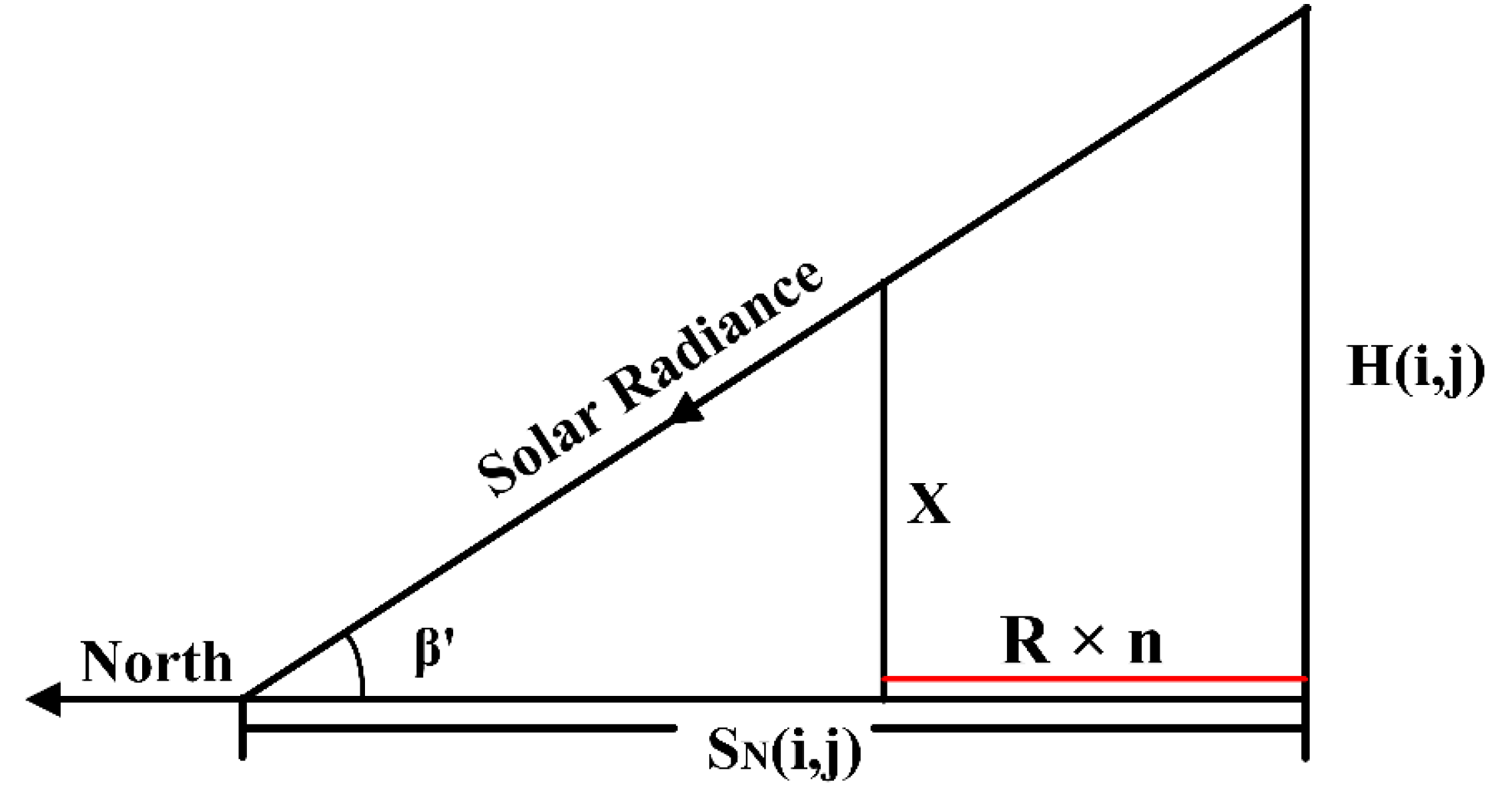
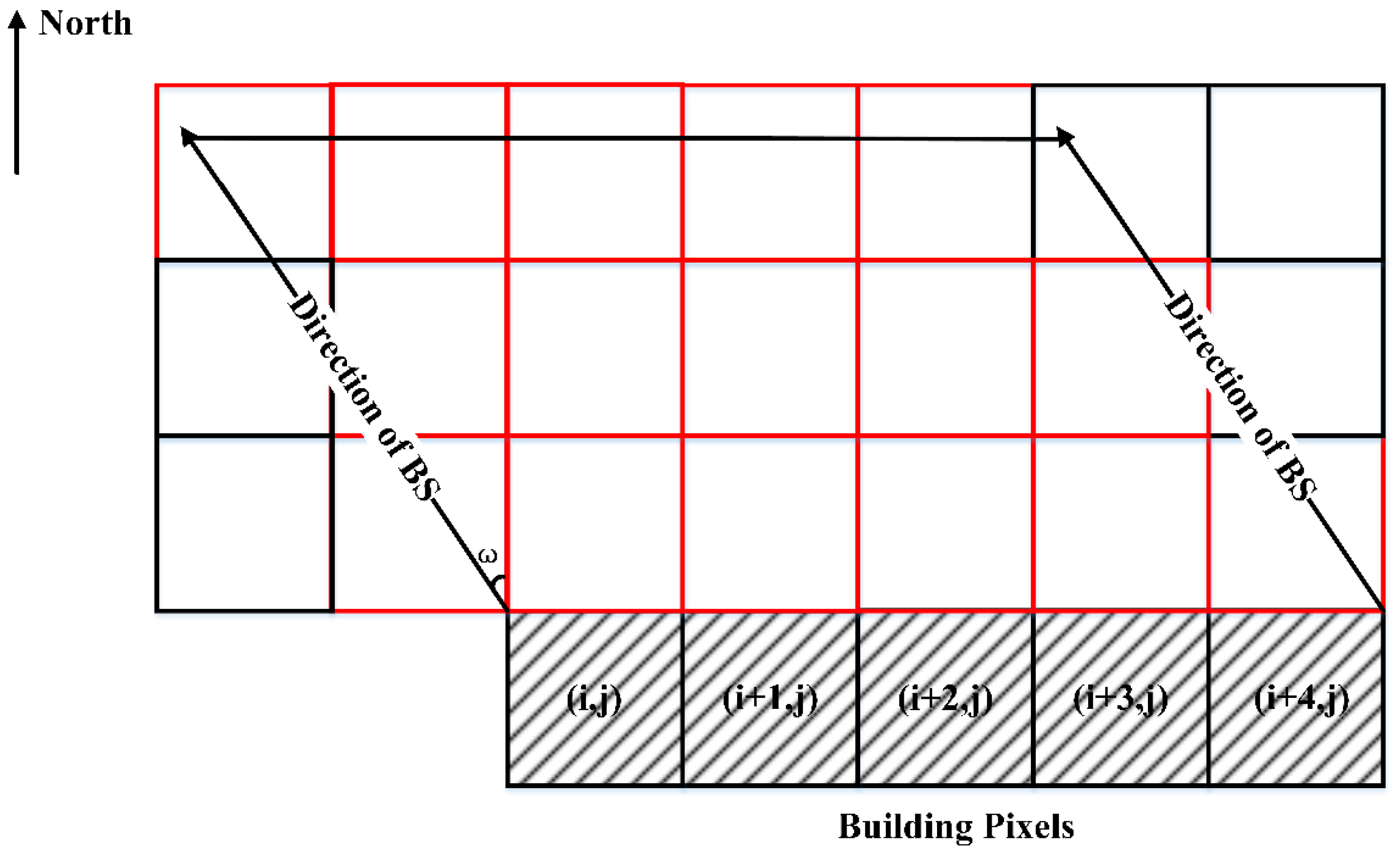
2.3.1. Extraction of Building Shadows
2.3.2. LST Retrieval from Landsat-8 Thermal Infrared Sensor Data
2.3.3. Definition of Thermal Landscape Fragmentation
2.3.4. Extraction of Pure Is and Vegetation Pixels
2.3.5. Quantification of the Cooling Effect of BSs from LST Data
3. Results
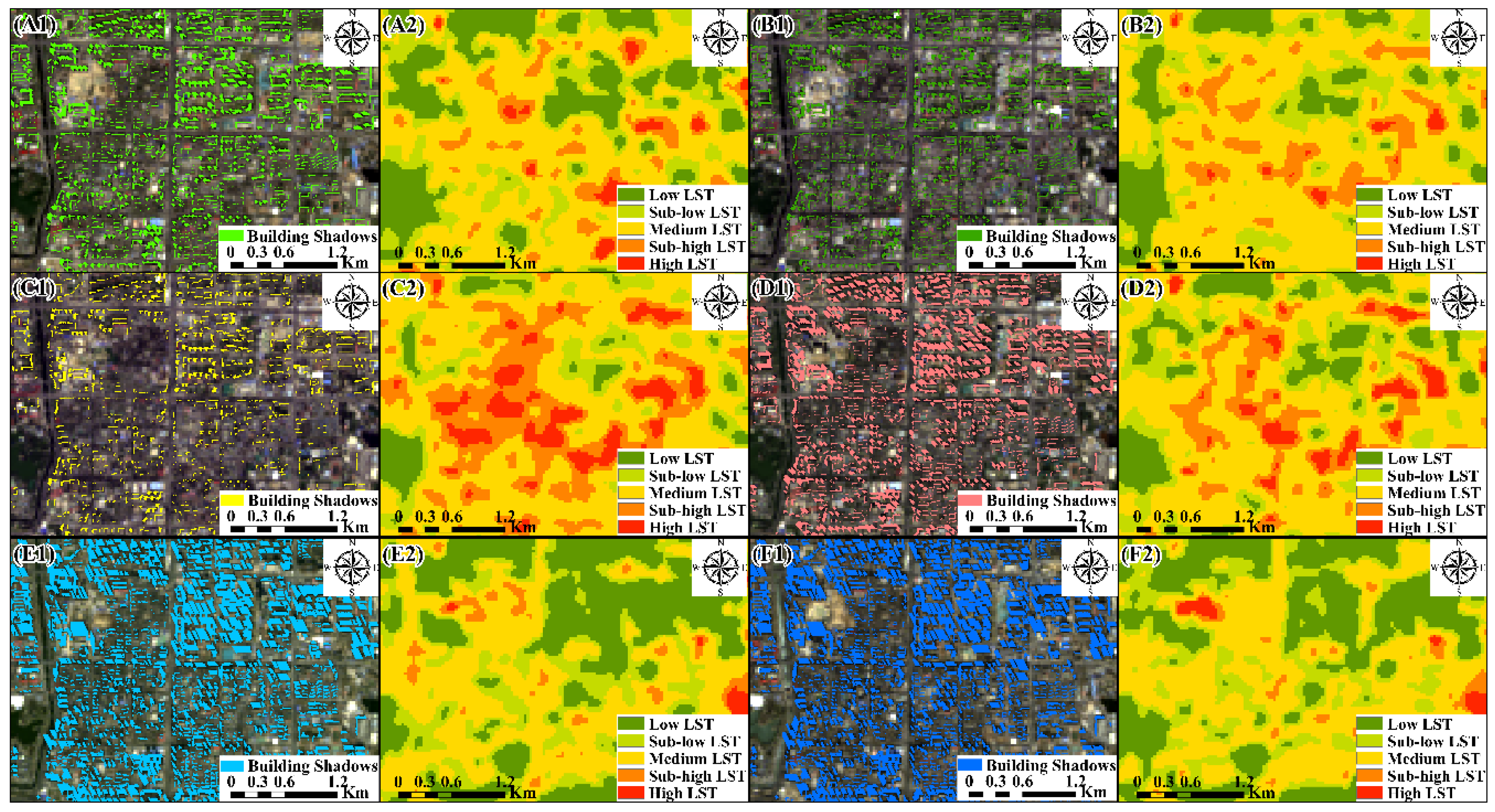
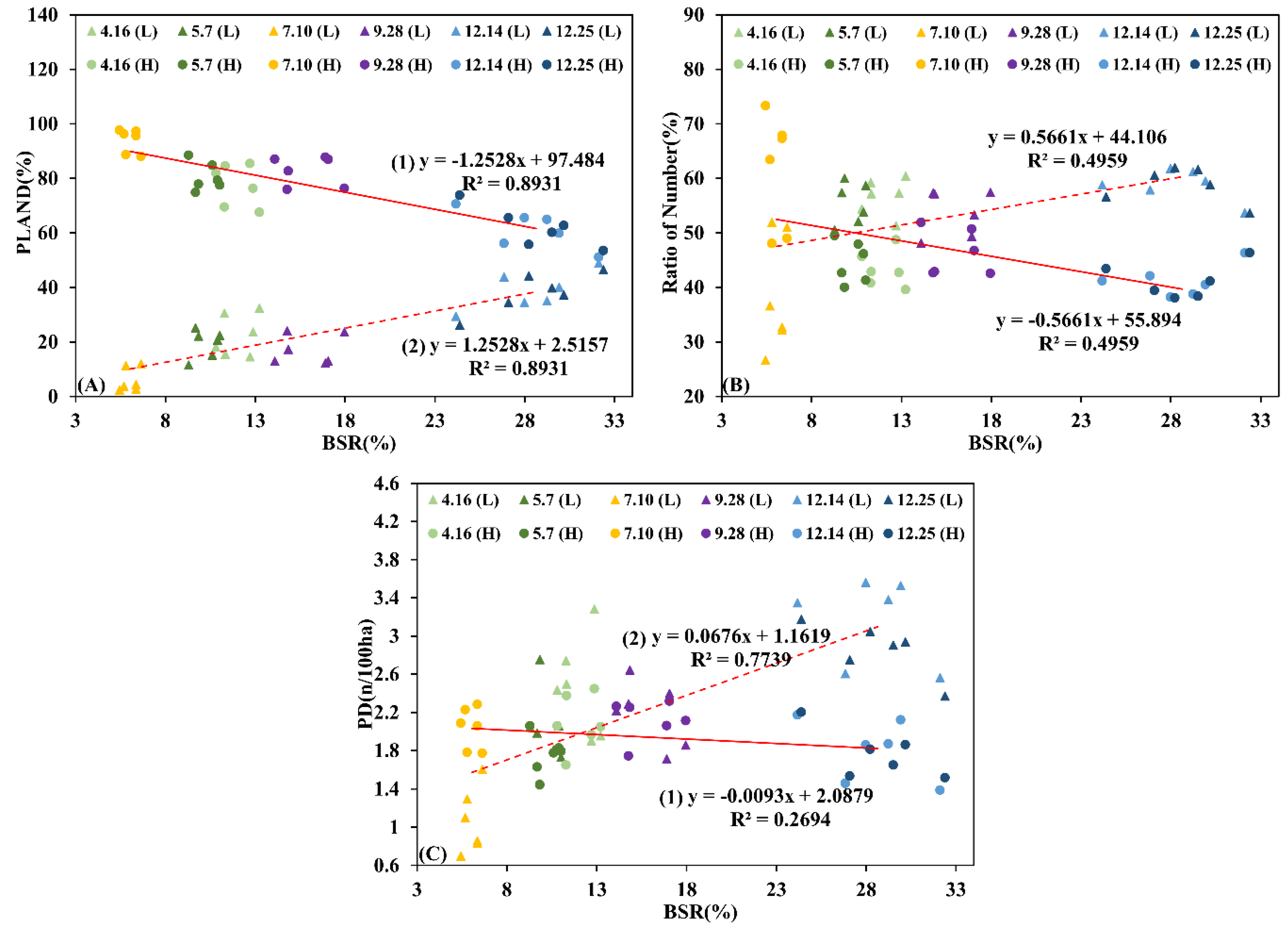
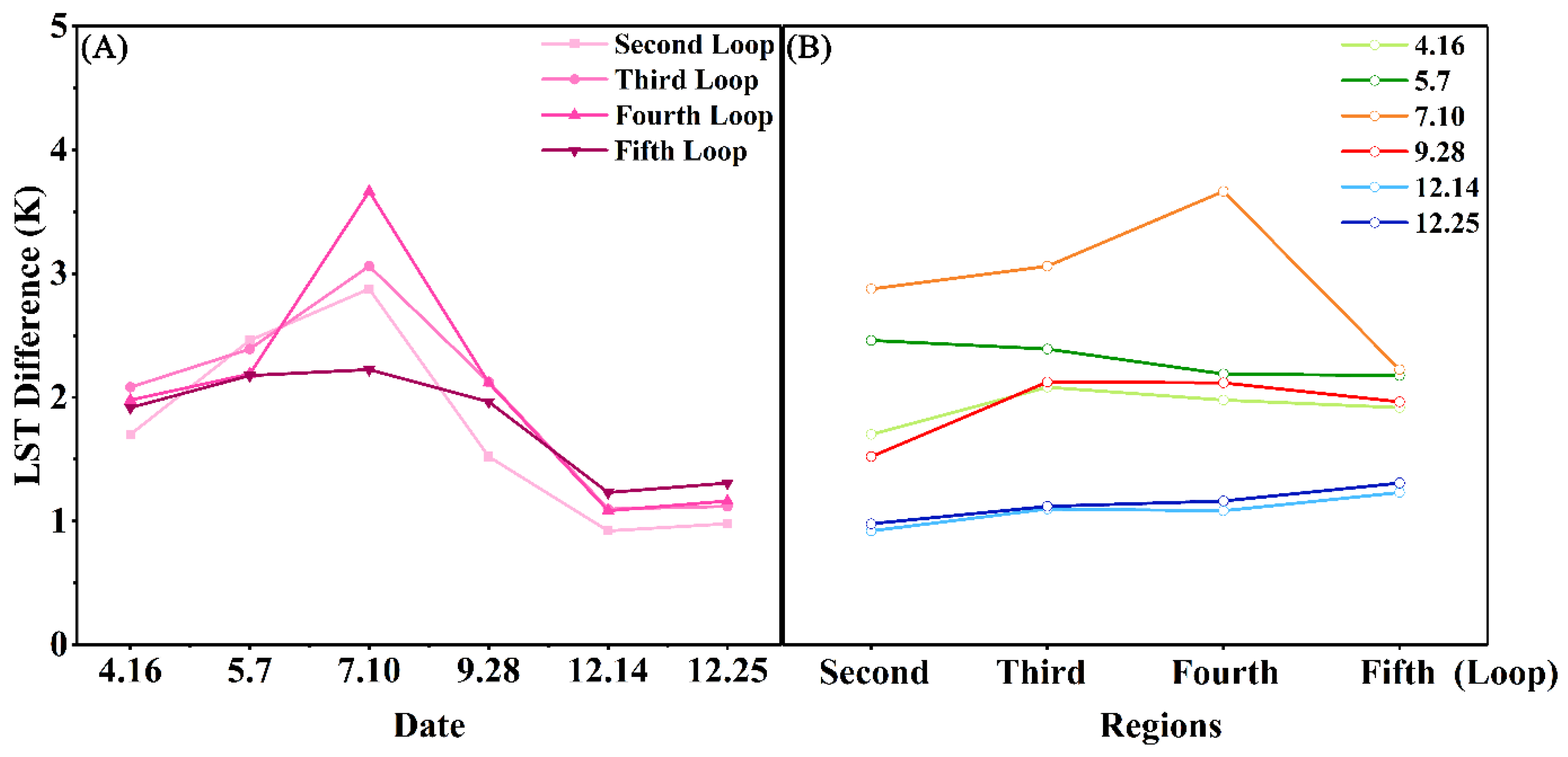
3.1. Seasonal Characteristics of BSs Areas and LST
3.2. Seasonal Influence of BSs on Thermal Landscape Fragmentation
3.3. Seasonal Influence of BSs on Mitigating LST
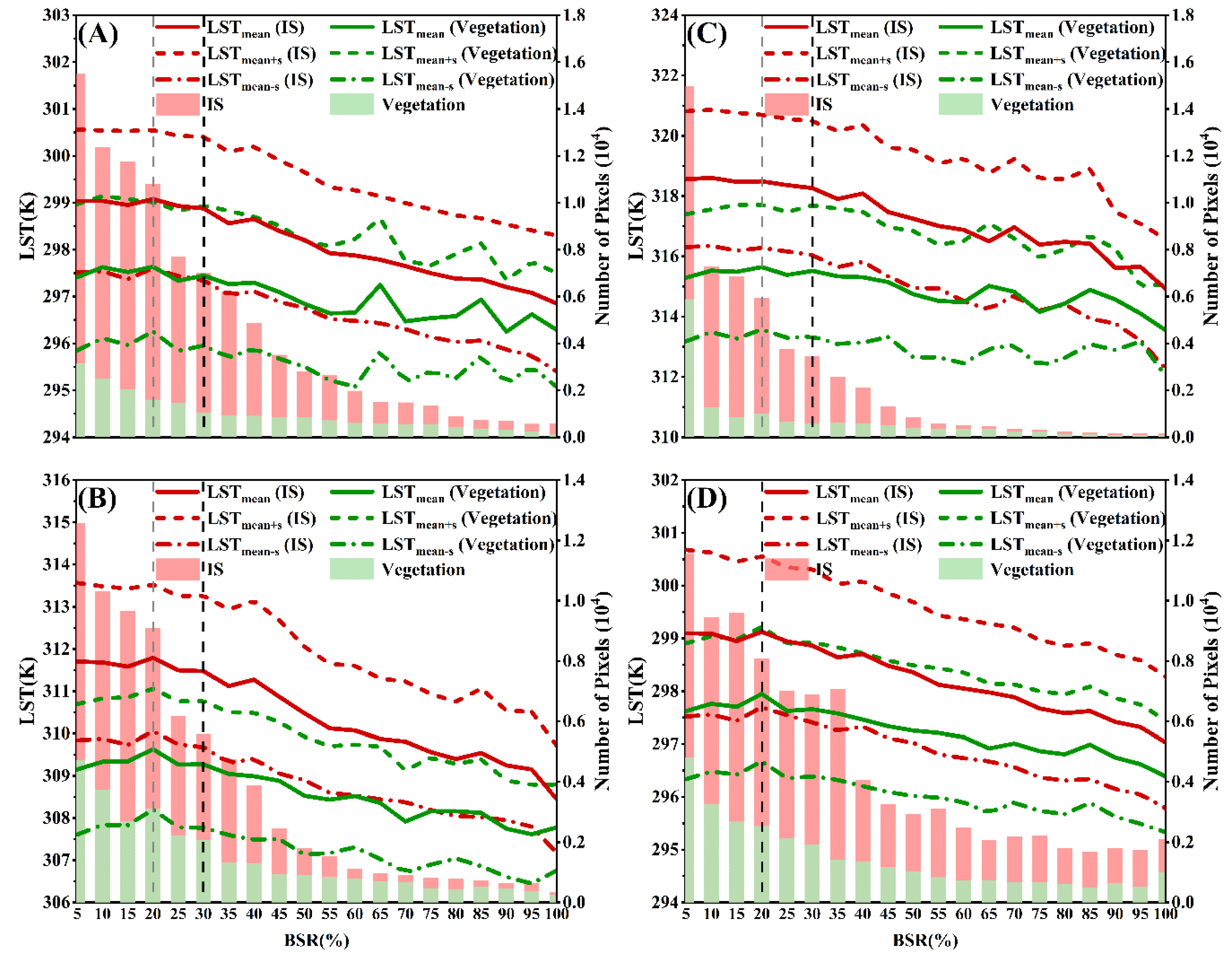
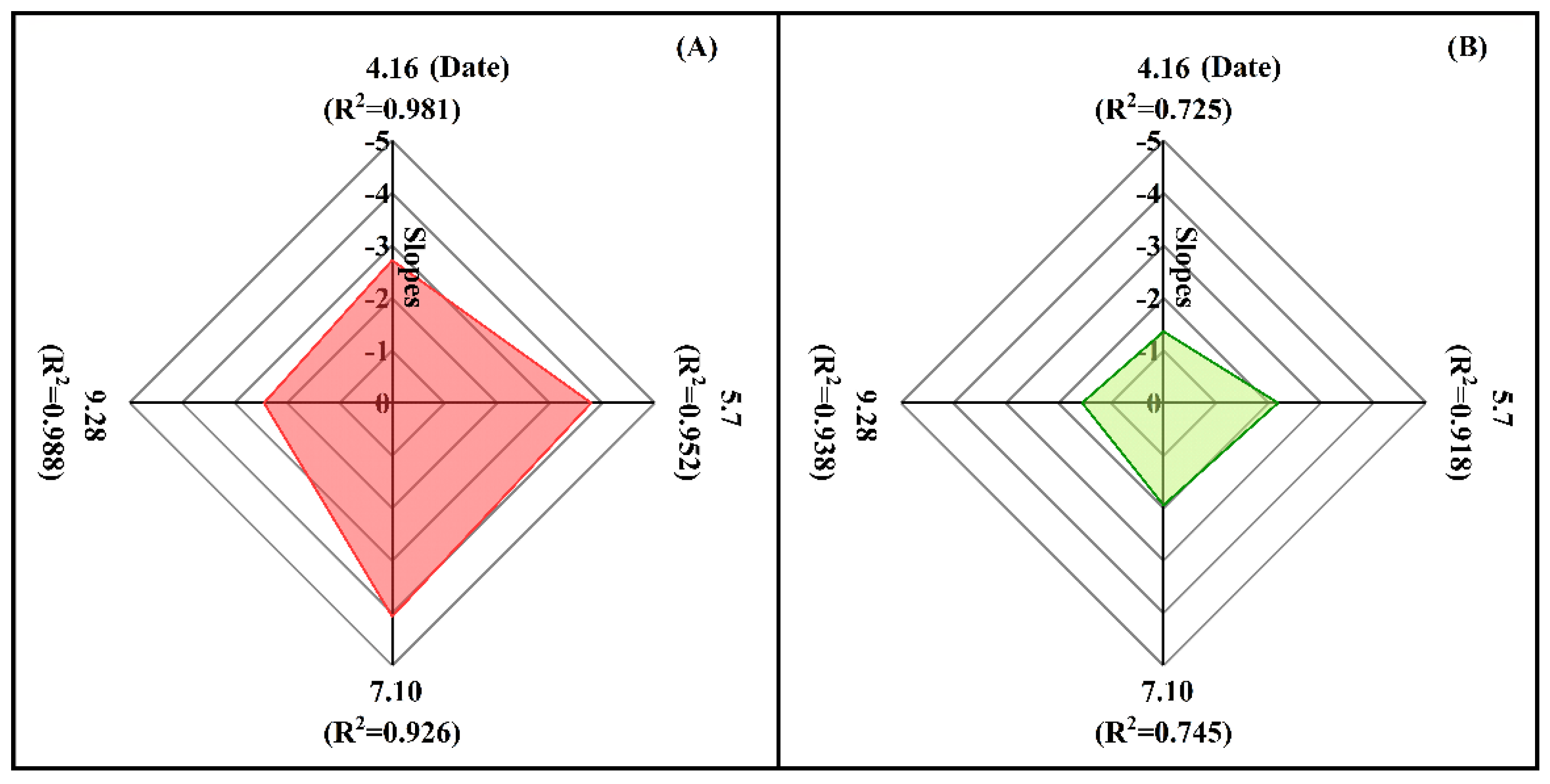
3.3.1. LST Mitigation of IS Pixels Totally Covered by BS
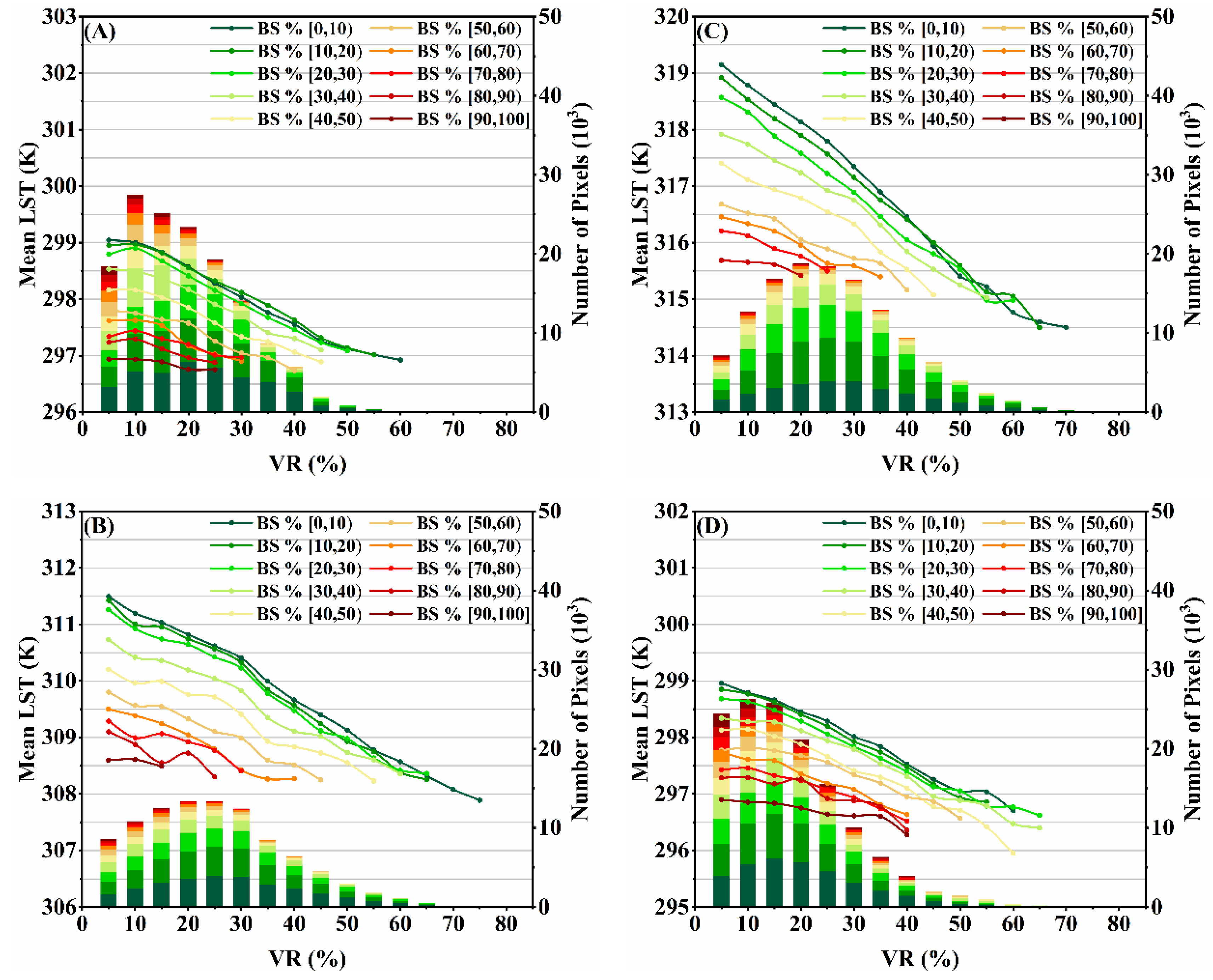
3.3.2. Cooling Variation of BSs with Changed BSR in Pure IS and Vegetation Pixels
3.3.3. Sensitivity Analysis of BSs on LST of IS and Vegetation Pixels
4. Discussion
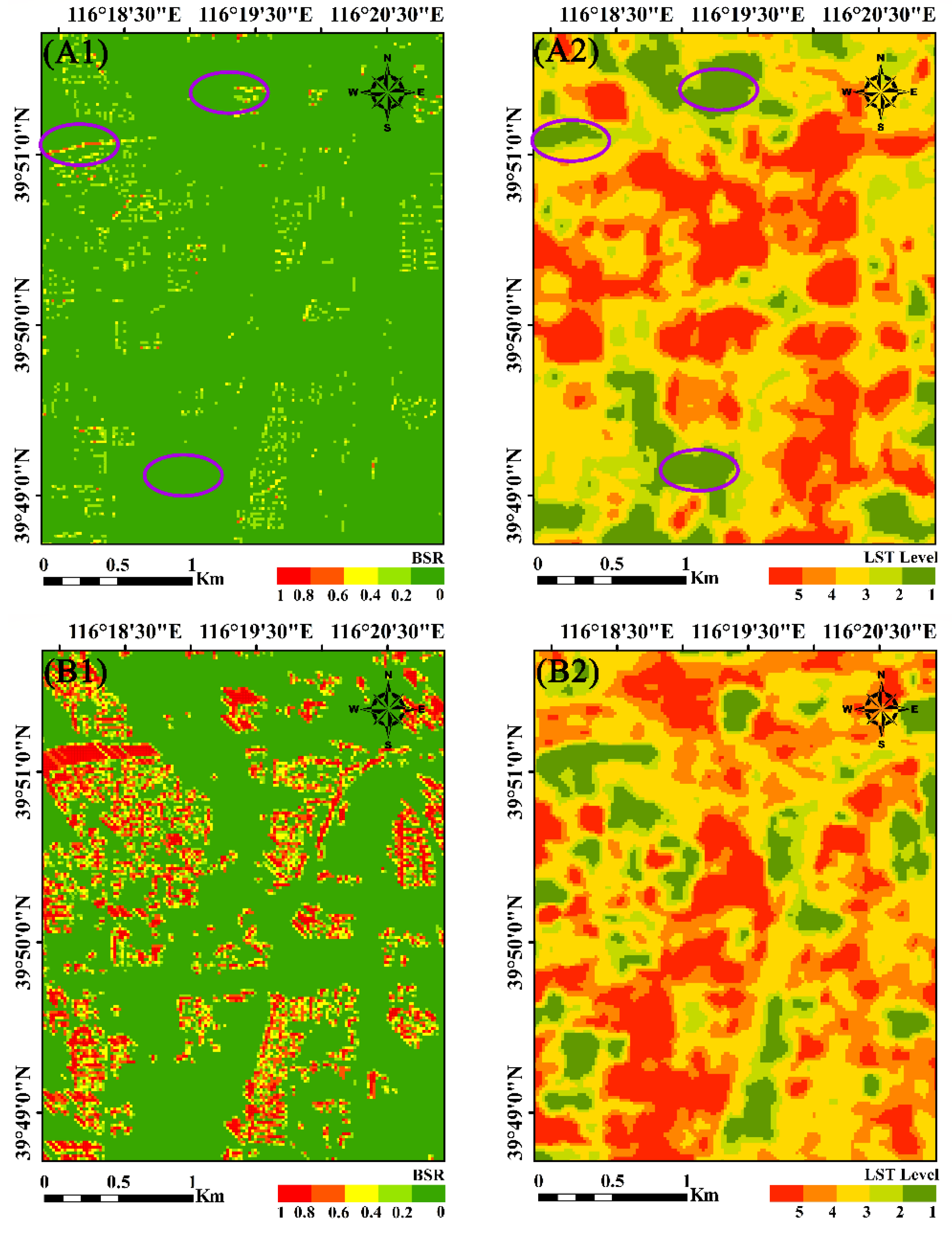
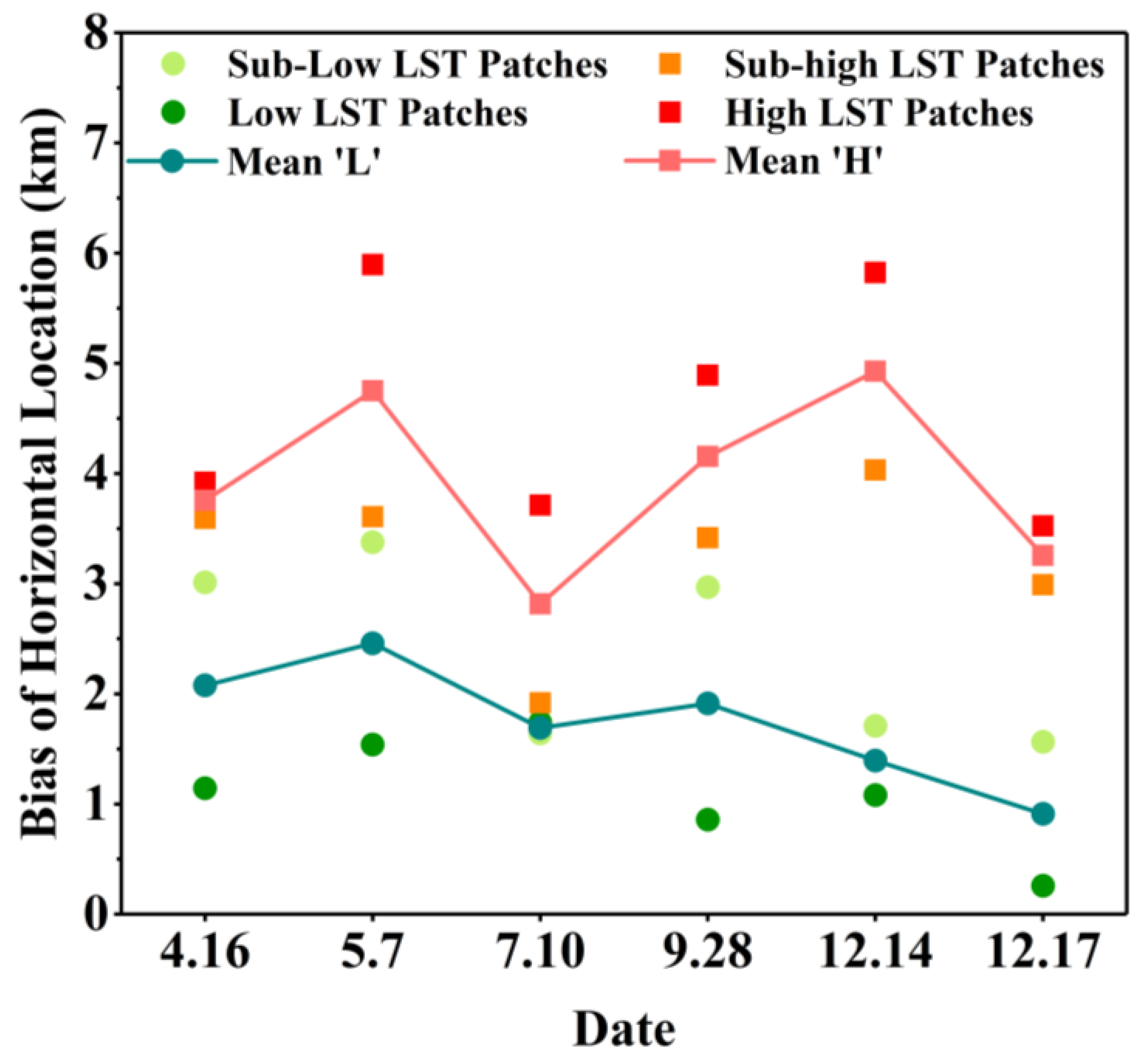
4.1. Relationship Between the Thermal Patch Centroid and BS
4.2. Effect of Adjacent Land Cover Types on BS Cooling at the Pixel Scale
4.3. Influence of BSs on the Cooling Effect of Vegetation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Santamouris, M. Analyzing the heat island magnitude and characteristics in one hundred Asian and Australian cities and regions. Sci. Total Environ. 2015, 512, 582–598. [Google Scholar] [CrossRef] [PubMed]
- Voogt, J.A.; Oke, T.R. Thermal remote sensing of urban climates. Remote Sens. Environ. 2003, 86, 370–384. [Google Scholar] [CrossRef]
- Bowler, D.E.; Buyung-Ali, L.; Knight, T.M.; Pullin, A.S. Urban greening to cool towns and cities: A systematic review of the empirical evidence. Landscape Urban Plan. 2010, 97, 147–155. [Google Scholar] [CrossRef]
- Cai, Z.; Han, G.F.; Chen, M.C. Do water bodies play an important role in the relationship between urban form and land surface temperature? Sustain. Cities Soc. 2018, 39, 487–498. [Google Scholar] [CrossRef]
- Peng, J.; Jia, J.L.; Liu, Y.X.; Li, H.L.; Wu, J.S. Seasonal contrast of the dominant factors for spatial distribution of land surface temperature in urban areas. Remote Sens. Environ. 2018, 215, 255–267. [Google Scholar] [CrossRef]
- Hsieh, C.M.; Li, J.J.; Zhang, L.; Schwegler, B. Effects of tree shading and transpiration on building cooling energy use. Energy Build. 2018, 159, 382–397. [Google Scholar] [CrossRef]
- Zhou, W.; Wang, J.; Cadenasso, M.L. Effects of the spatial configuration of trees on urban heat mitigation: A comparative study. Remote Sens. Environ. 2017, 195, 1–12. [Google Scholar] [CrossRef]
- Bonafoni, S.; Keeratikasikorn, C. Land Surface Temperature and Urban Density: Multiyear Modeling and Relationship Analysis Using MODIS and Landsat Data. Remote Sens. 2018, 10, 1471. [Google Scholar] [CrossRef]
- Alobaydi, D.; Bakarman, M.A.; Obeidat, B. The Impact of Urban Form Configuration on the Urban Heat Island: The Case Study of Baghdad, Iraq. Procedia Eng. 2016, 145, 820–827. [Google Scholar] [CrossRef]
- Hendel, M.; Parison, S.; Grados, A.; Royon, L. Which pavement structures are best suited to limiting the UHI effect? A laboratory-scale study of Parisian pavement structures. Build. Environ. 2018, 144, 216–229. [Google Scholar] [CrossRef]
- Sun, Y.W.; Gao, C.; Li, J.L.; Li, W.F.; Ma, R.F. Examining urban thermal environment dynamics and relations to biophysical composition and configuration and socio-economic factors: A case study of the Shanghai metropolitan region. Sustain. Cities Soc. 2018, 40, 284–295. [Google Scholar] [CrossRef]
- Zhou, D.C.; Xiao, J.F.; Bonafoni, S.; Berger, C.; Deilami, K.; Zhou, Y.Y.; Frolking, S.; Yao, R.; Qiao, Z.; Sobrino, J.A. Satellite Remote Sensing of Surface Urban Heat Islands: Profress, Challenges, and Perspectives. Remote Sens. 2019, 11, 48. [Google Scholar] [CrossRef]
- Yin, C.H.; Yuan, M.; Lu, Y.P.; Huang, Y.P.; Liu, Y.F. Effects of urban form on the urban heat island effect based on spatial regression model. Sci. Total Environ. 2018, 634, 696–704. [Google Scholar] [CrossRef] [PubMed]
- Taleghani, M.; Kleerekoper, L.; Tenpierik, M.; Dobbelsteen, A.V.D. Outdoor thermal comfort within five different urban forms in The Netherlands. Build. Environ. 2015, 83, 65–78. [Google Scholar] [CrossRef]
- Lin, T.P.; Matzarakis, A.; Hwang, R.L. Shading effect on long-term outdoor thermal comfort. Build. Environ. 2010, 45, 213–221. [Google Scholar] [CrossRef]
- Ichinose, T.; Lei, L.; Lin, Y. Impacts of shading effect from nearby buildings on heating and cooling energy consumption in hot summer and cold winter zone of China. Energy Build. 2017, 136, 199–210. [Google Scholar] [CrossRef]
- Martinelli, L.; Lin, T.P.; Matzarakis, A. Assessment of the influence of daily shadings pattern on human thermal comfort and attendance in Rome during summer period. Build. Environ. 2015, 92, 30–38. [Google Scholar] [CrossRef]
- Villadiego, K.; Velay-Dabat, M.A. Outdoor thermal comfort in a hot and humid climate of Colombia: A field study in Barranquilla. Build. Environ. 2014, 75, 142–152. [Google Scholar] [CrossRef]
- Chun, B.; Guldmann, J.M. Impact of greening on the urban heat island: Seasonal variations and mitigation strategies. Comput. Environ. Urban 2018, 84, 1199–1209. [Google Scholar] [CrossRef]
- Akbari, H.; Kolokotsa, D. Three decades of urban heat islands and mitigation technologies research. Energy Build. 2016, 133, 834–842. [Google Scholar] [CrossRef]
- Li, D.H.W.; Wong, S.L. Daylighting and energy implications due to shading effects from nearby buildings. Appl. Energy 2007, 136, 199–210. [Google Scholar] [CrossRef]
- Shahidan, M.F.; Jones, P.J.; Gwilliam, J.; Salleh, E. An evaluation of outdoor and building environment cooling achieved through combination modification of trees with ground materials. Build. Environ. 2012, 58, 245–257. [Google Scholar] [CrossRef]
- Watanabe, S.; Nagano, K.; Ishii, J.; Horikoshi, T. Evaluation of outdoor thermal comfort in sunlight, building shade, and pergola shade during summer in a humid subtropical region. Build. Environ. 2014, 82, 556–565. [Google Scholar] [CrossRef]
- Hwang, R.L.; Lin, T.P.; Matzarakis, A. Seasonal effects of urban street shading on long-term outdoor thermal comfort. Build. Environ. 2011, 46, 863–870. [Google Scholar] [CrossRef]
- Johansson, E. Influence of urban geometry on outdoor thermal comfort in a hot dry climate: A studyin Fez, Morocco. Build. Environ. 2006, 41, 1326–1338. [Google Scholar] [CrossRef]
- Ali-Toudert, F.; Mayer, H. Numerical Study on the effects of aspect ratio and orientation on an urban street canyon on outdoor thermal comfort in hot and dry climate. Build. Environ. 2006, 41, 94–108. [Google Scholar] [CrossRef]
- Ali-Toudert, F.; Mayer, H. Thermal comfort in an east–west oriented street canyon in Freiburg (Germany) under hot summer conditions. Theor. Appl. Climatol. 2007, 87, 223–237. [Google Scholar] [CrossRef]
- Hamdi, R.; Schayes, G. Sensitivity study of the urban heat island intensity to urban characteristics. Int. J. Climatol. 2008, 28, 973–982. [Google Scholar] [CrossRef]
- Appelbaum, J.; Bany, J. Shadow effect of adjacent solar collectors in large scale systems. Sol. Energy 1979, 23, 497–507. [Google Scholar] [CrossRef]
- Ok, V. A procedure for calculating cooling load due to solar radiation: The shading effects from adjacent or nearby buildings. Energy Build. 1992, 19, 11–20. [Google Scholar] [CrossRef]
- Chan, A.L.S. Effect of adjacent shading on the thermal performance of residential buildings in a subtropical region. Appl. Energy 2012, 92, 516–522. [Google Scholar] [CrossRef]
- Lam, J.C. Shading effects due to nearby buildings and energy implications. Energy Convers. Manag. 2000, 41, 647–659. [Google Scholar] [CrossRef]
- Cao, X.; Onishi, A.; Chen, J.; Imura, H. Quantifying the cool island intensity of urban parks using ASTER and IKONOS data. Landsc. Urban Plan. 2010, 96, 224–231. [Google Scholar] [CrossRef]
- Dare, P.M. Shadow Analysis in High-Resolution Satellite Imagery of Urban Areas. Photogramm. Eng. Remote Sens. 2005, 71, 169–177. [Google Scholar] [CrossRef]
- Li, Y.Z.; Gong, X.Q.; Guo, Z.; Xu, K.P.; Hu, D.; Zhou, X.H. An index and approach for water extraction using Landsat–OLI data. Int. J. Remote Sens. 2016, 37, 3611–3635. [Google Scholar] [CrossRef]
- Chung, K.L.; Lin, Y.R.; Huang, Y.H.; Wang, L.J.; He, X.H. Efficient shadow detection of color aerial images based on successive thresholding scheme. IEEE Trans. Geosci. Remote Sens. 2009, 47, 671–682. [Google Scholar] [CrossRef]
- Liasis, G.; Stavrou, S. Satellite images analysis for shadow detection and building height estimation. ISPRS J. Photogramm. Remote Sens. 2016, 119, 437–450. [Google Scholar] [CrossRef]
- Hu, Y.F.; Zhang, Q.L. The Extraction of Building Shadow and the Estimation of Building Heights Based on Morphology and Spectral Characteristic Parameters. Bull. Surv. Mapp. 2018, 6, 22–26. [Google Scholar] [CrossRef]
- Hu, L.Q.; Monaghan, A.; Voogt, J.A.; Barlage, M. A first satellite-based observational assessment of urban thermal anisotropy. Remote Sens. Environ. 2016, 181, 111–121. [Google Scholar] [CrossRef]
- Lagouarde, J.P.; Hénon, A.; Irvine, M.; Voogt, J.; Pigeon, G.; Moreau, P.; Masson, V.; Mestayer, P. Experimental characterization and modelling of the nighttime directional anisotropy of thermal infrared measurements over an urban area: Case study of Toulouse (France). Remote Sens. Environ. 2012, 117, 19–33. [Google Scholar] [CrossRef]
- Degerickx, J.; Roberts, D.A.; Somers, B. Enhancing the performance of Multiple Endmember Spectral Mixture Analysis (MESMA) for urban land cover mapping using airborne lidar data and band selection. Remote Sens. Environ. 2019, 221, 260–273. [Google Scholar] [CrossRef]
- Fernández-Manso, A.; Quintano, C.; Roberts, D. Evaluation of potential of multiple endmember spectral mixture analysis (MESMA) for surface coal mining affected area mapping in different world forest ecosystems. Remote Sens. Environ. 2012, 127, 181–193. [Google Scholar] [CrossRef]
- Quintano, C.; Fernandez-Manso, A.; Roberts, D.A. Burn severity mapping from Landsat MESMA fraction images and Land Surface Temperature. Remote Sens. Environ. 2017, 190, 83–95. [Google Scholar] [CrossRef]
- Xiao, R.B.; Weng, Q.H.; Ouyang, Z.Y.; Li, W.F.; Schienke, E.W.; Zhang, Z.M. Land Surface Temperature Variation and Major Factors in Beijing, China. Photogramm. Eng. Remote Sens. 2008, 74, 451–461. [Google Scholar] [CrossRef]
- Du, H.Y.; Song, X.J.; Jiang, H.; Kan, Z.H.; Wang, Z.B.; Cai, Y.L. Research on the cooling island effects of water body: A case study of Shanghai, China. Ecol. Indic. 2016, 67, 31–38. [Google Scholar] [CrossRef]
- Yu, X.L.; Guo, X.L.; Wu, Z.C. Land Surface Temperature Retrieval from Landsat 8 TIRS—Comparison between Radiative Transfer Equation-Based Method, Split Window Algorithm and Single Channel Method. Remote Sens. 2014, 6, 9829–9852. [Google Scholar] [CrossRef]
- García-Santos, V.; Cuxart, J.; Martínez-Villagrasa, D.; Antònia Jiménez, M.; Simó, G. Comparison of Three Methods for Estimating Land Surface Temperature from Landsat 8-TIRS Sensor Data. Remote Sens. 2018, 10, 1450. [Google Scholar] [CrossRef]
- Chander, G.; Markham, B. Revised landsat-5 tm radiometric calibration procedures and postcalibration dynamic ranges. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2674–2677. [Google Scholar] [CrossRef]
- Jaeger, J.A.G. Landscape division, splitting index, and effective mesh size: New measures of landscape fragmentation. Landsc. Ecol. 2000, 15, 115–130. [Google Scholar] [CrossRef]
- Han, B.L.; Liu, H.X.; Wang, R.S. Urban ecological security assessment for cities in the Beijing–Tianjin–Hebei metropolitan region based on fuzzy and entropy methods. Ecol. Model. 2015, 318, 217–225. [Google Scholar] [CrossRef]
- Peng, J.; Xie, P.; Liu, Y.X.; Ma, J. Urban thermal environment dynamics and associated landscape pattern factors: A case study in the Beijing metropolitan region. Remote Sens. Environ. 2016, 173, 145–155. [Google Scholar] [CrossRef]
- Quan, J.L.; Chen, Y.H.; Zhan, W.F.; Wang, J.F.; Voogt, J.; Wang, M.J. Multi-temporal trajectory of the urban heat island centroid in Beijing, China based on a Gaussian volume model. Remote Sens. Environ. 2014, 149, 33–46. [Google Scholar] [CrossRef]
- Raines, G.L. Description and comparison of geologic maps with FRAGSTATS-a spatial statistics program. Comput. Geosci. 2002, 28, 169–177. [Google Scholar] [CrossRef]
- Macdonald, D.W.; Bothwell, H.M.; Hearn, A.J.; Cheyne, S.M.; Haidir, I.; Hunter, L.T.B.; Kaszta, Z.; Linkie, M.; Macdonald, E.A.; Ross, J.; et al. Multi-scale habitat selection modeling identifies threats and conservation opportunities for the Sunda clouded leopard (Neofelisdiardi). Biol. Conserv. 2018, 227, 92–103. [Google Scholar] [CrossRef]
- Chen, X.; Wang, D.W.; Chen, J.; Wang, C.; Shen, M.G. The mixed pixel effect in land surface phenology: A simulation study. Remote Sens. Environ. 2018, 211, 338–344. [Google Scholar] [CrossRef]
- Li, X.M.; Chen, L.; Yang, M. A priori fully constrained least squares spectral unmixing based on sparsity. In Proceedings of the IEEE International Conference on Computer & Communications, Chengdu, China, 14–17 October 2016; IEEE Computer Society: Washington, DC, USA, 2016. [Google Scholar] [CrossRef]
- Xie, H.; Luo, X.; Xu, X.; Pan, H.Y.; Tong, X.H. Automated Subpixel Surface Water Mapping from Heterogeneous Urban Environments Using Landsat 8 OLI Imagery. Remote Sens. 2016, 8, 584. [Google Scholar] [CrossRef]
- Liu, W.Y.; Gong, A.D.; Zhou, J.; Zhan, W.F. Investigation on Relationships between Urban Building Materials and Land Surface Temperature through a Multi-resource Remote Sensing Approach. Remote Sens. Inf. 2011, 31, 46–53. [Google Scholar] [CrossRef]
- Wu, C.S.; Murray, A.T. Estimating impervious surface distribution by spectral mixture analysis. Remote Sens. Environ. 2003, 84, 493–505. [Google Scholar] [CrossRef]
- Chen, F.; Jiang, H.J.; Voorde, T.V.D. Land cover mapping in urban environments using hyperspectralAPEX data: A study case in Baden, Switzerland. Int. J. Appl. Earth Obs. 2018, 71, 70–82. [Google Scholar] [CrossRef]
- Graceline, J.S.; Pattabiraman, V. Improved pure pixel identification algorithms to determine the endmembers in hyperspectral images. Comput. Electr. Eng. 2018, 71, 515–532. [Google Scholar] [CrossRef]
- Svensson, M.K. Sky view factor analysis—Implications for urban air temperature differences. Meteorol. Appl. 2010, 11, 201–211. [Google Scholar] [CrossRef]
- Wetherley, E.B.; McFadden, J.P.; Roberts, D.A. Megacity-scale analysis of urban vegetation temperatures. Remote Sens. Environ. 2018, 213, 18–33. [Google Scholar] [CrossRef]
- Voogt, J.A. Assessment of an Urban Sensor View Model for thermal anisotropy. Remote Sen. Environ. 2008, 112, 482–495. [Google Scholar] [CrossRef]
- Vera, S.; Pinto, C.; Tabares-Velasco, P.C.; Bustamante, W.; Victorero, F.; Gironas, J.; Bonilla, C.A. Influence of Vegetation, Substrate, and Thermal Insulation of an Extensive Vegetated Roof on the Thermal Performance of Retail Stores in Semiarid and Marine Climates. Energy Build. 2017, 146, 312–321. [Google Scholar] [CrossRef]
- Catoni, R.; Gratani, L. Variations in leaf respiration and photosynthesis ratio in response to air temperature and water availability among Mediterranean evergreen species. J. Arid Environ. 2014, 102, 82–88. [Google Scholar] [CrossRef]
- Simó, G.; García-Santos, V.; Jiménez, M.A.; Martínez-Villagrasa, D.; Picos, R.; Caselles, V.; Cuxart, J. Landsat and Local Land Surface Temperature in a Heterogeneous Terrain Compared to MODIS Value. Remote Sens. 2016, 8, 849. [Google Scholar] [CrossRef]
- García-Santos, V.; Joan, C.; Jiménez, M.A.; Martínez-Villagrasa, D.; Simó, G.; Picos, R.; Caselles, V. Study of Temperature Heterogeneities at Sub-Kilometric Scales and Influence on Surface-Atmosphere Energy Interactions. IEEE Trans. Geosci. Remote 2018, 57, 640–654. [Google Scholar] [CrossRef]
- Niethammer, U.; James, M.R.; Rothmund, S.; Travelletti, J.; Joswig, M. UAV-based remote sensing of the Super-Sauze landslide: Evaluation and results. Eng. Geol. 2012, 128, 2–11. [Google Scholar] [CrossRef]
| Sensor | Date | Time (CST) | Spatial Resolution (M) | Solar Azimuth Angle (°) | Solar Elevation Angle (°) |
|---|---|---|---|---|---|
| Landsat-8 | 25 December 2014 | 10:53 | 100 | 160.11 | 23.64 |
| Landsat-8 | 16 April 2015 | 10:52 | 100 | 143.05 | 54.80 |
| Landsat-8 | 14 December 2016 | 10:53 | 100 | 161.35 | 24.14 |
| Landsat-8 | 7 May 2017 | 10:52 | 100 | 138.19 | 61.23 |
| Landsat-8 | 10 July 2017 | 10:53 | 100 | 128.81 | 64.47 |
| Landsat-8 | 28 September 2017 | 10:53 | 100 | 154.95 | 44.68 |
| Class of LST | Division Interval of LST |
|---|---|
| High LST | T > M + S |
| Sub-high LST | M + 0.5 × S < T <= M + S |
| Medium LST | M − 0.5 × S < T <= M + 0.5 × S |
| Sub-low LST | M − S < T <= M − 0.5 × S |
| Low LST | T < M − S |
| Metric | Formula |
|---|---|
| PLAND | PLAND = A is the total area of landscape, Ai is the total area of landscape i (same as below); and M is the total number of landscape classes. |
| PDi | PDi is the patch density of landscape i; and Ni is the number of landscape i. |
| Date | Pure Pixels | |
|---|---|---|
| Vegetation | IS | |
| 16 April 2015 | 37,887 | 166,620 |
| 7 May 2017 | 83,635 | 120,863 |
| 10 July 2017 | 124,952 | 100,513 |
| 28 September 2017 | 105,556 | 138,958 |
| Statistics | Mean (K) | Std Dev 1 (K) | |
|---|---|---|---|
| Date | |||
| 16 April 2015 | 310.383 | 1.608 | |
| 7 May 2017 | 312.301 | 2.327 | |
| 10 July 2017 | 318.797 | 2.607 | |
| 28 September 2017 | 299.429 | 1.782 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, K.; Chen, Y.; Wang, D.; Chen, Z.; Gong, A.; Li, J. Study of the Seasonal Effect of Building Shadows on Urban Land Surface Temperatures Based on Remote Sensing Data. Remote Sens. 2019, 11, 497. https://doi.org/10.3390/rs11050497
Yu K, Chen Y, Wang D, Chen Z, Gong A, Li J. Study of the Seasonal Effect of Building Shadows on Urban Land Surface Temperatures Based on Remote Sensing Data. Remote Sensing. 2019; 11(5):497. https://doi.org/10.3390/rs11050497
Chicago/Turabian StyleYu, Ke, Yunhao Chen, Dandan Wang, Zixuan Chen, Adu Gong, and Jing Li. 2019. "Study of the Seasonal Effect of Building Shadows on Urban Land Surface Temperatures Based on Remote Sensing Data" Remote Sensing 11, no. 5: 497. https://doi.org/10.3390/rs11050497
APA StyleYu, K., Chen, Y., Wang, D., Chen, Z., Gong, A., & Li, J. (2019). Study of the Seasonal Effect of Building Shadows on Urban Land Surface Temperatures Based on Remote Sensing Data. Remote Sensing, 11(5), 497. https://doi.org/10.3390/rs11050497






