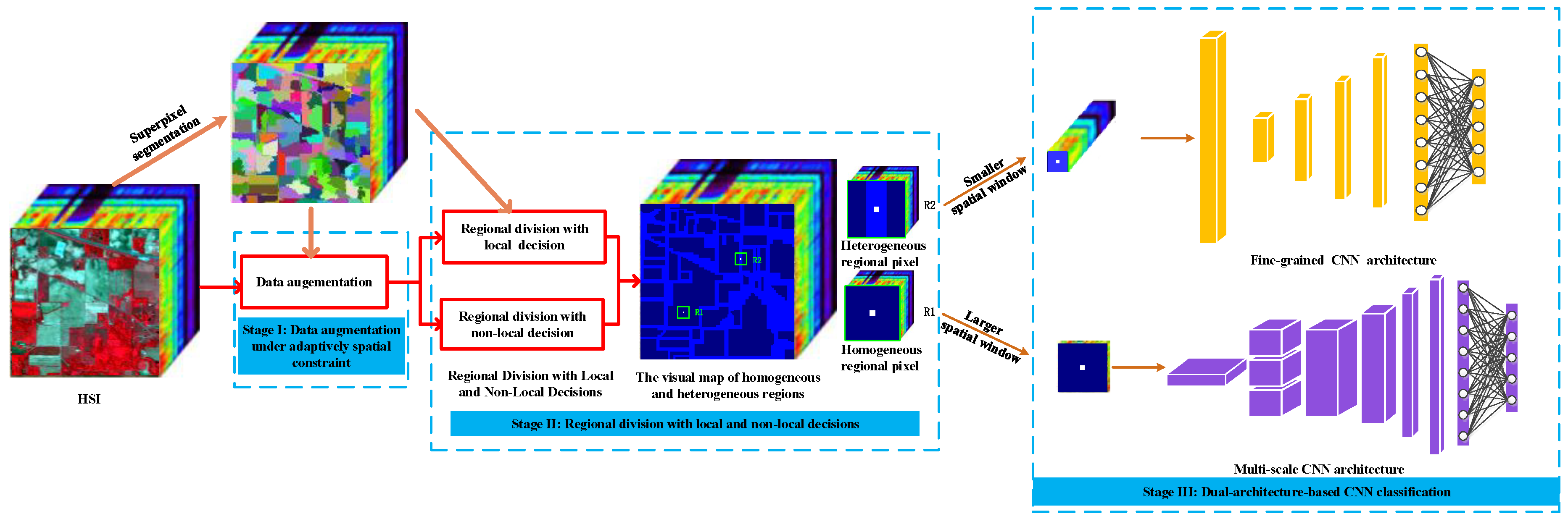
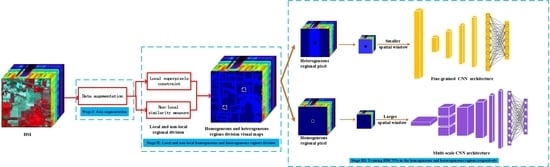
Figure 1.
The flowchart of proposed divide-and-conquer dual-architecture convolutional neural network (DDCNN).
Figure 1.
The flowchart of proposed divide-and-conquer dual-architecture convolutional neural network (DDCNN).
Figure 2.
Procedure of the superpixel segmentation.
Figure 2.
Procedure of the superpixel segmentation.
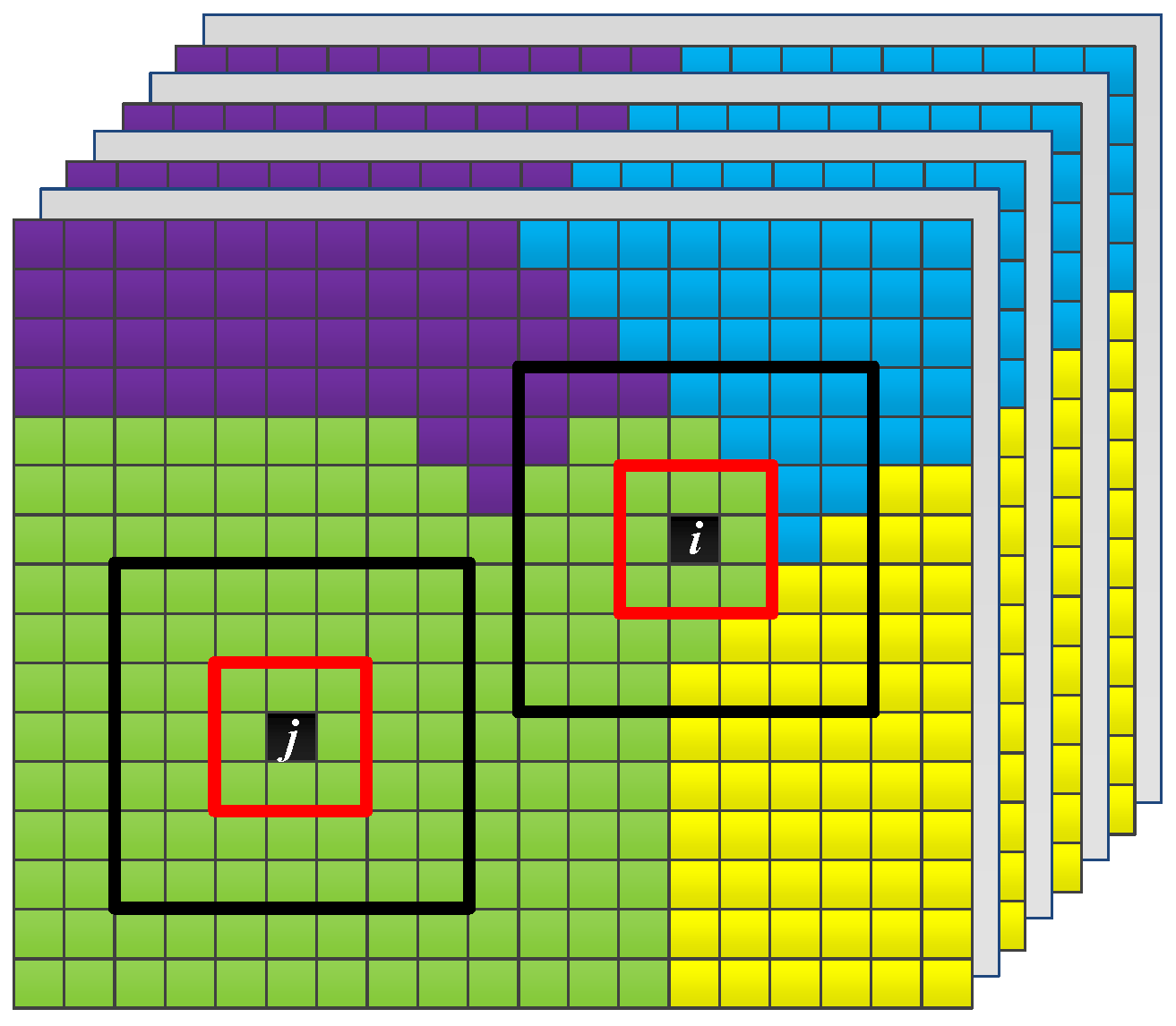
Figure 3.
Illustration of samples in the homogeneous and heterogeneous regions.
Figure 3.
Illustration of samples in the homogeneous and heterogeneous regions.
Figure 4.
Illustration of local regional division based on superpixel segmentation: (a) ground truth; (b) superpixel segmentation map; (c) the filter of samples in the homogeneous region; (d) the filter of samples in the heterogeneous region; (e) the filter of samples in the “false boundary”.
Figure 4.
Illustration of local regional division based on superpixel segmentation: (a) ground truth; (b) superpixel segmentation map; (c) the filter of samples in the homogeneous region; (d) the filter of samples in the heterogeneous region; (e) the filter of samples in the “false boundary”.
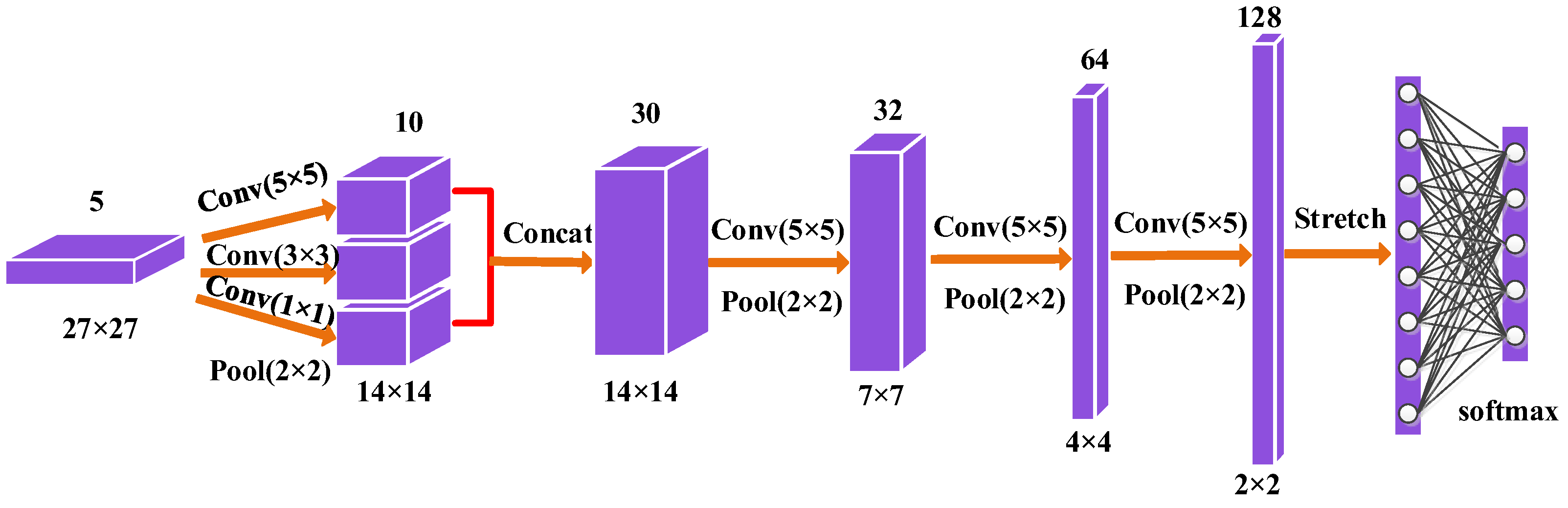
Figure 5.
The construction of multi-scale convolutional neural network (CNN).
Figure 5.
The construction of multi-scale convolutional neural network (CNN).
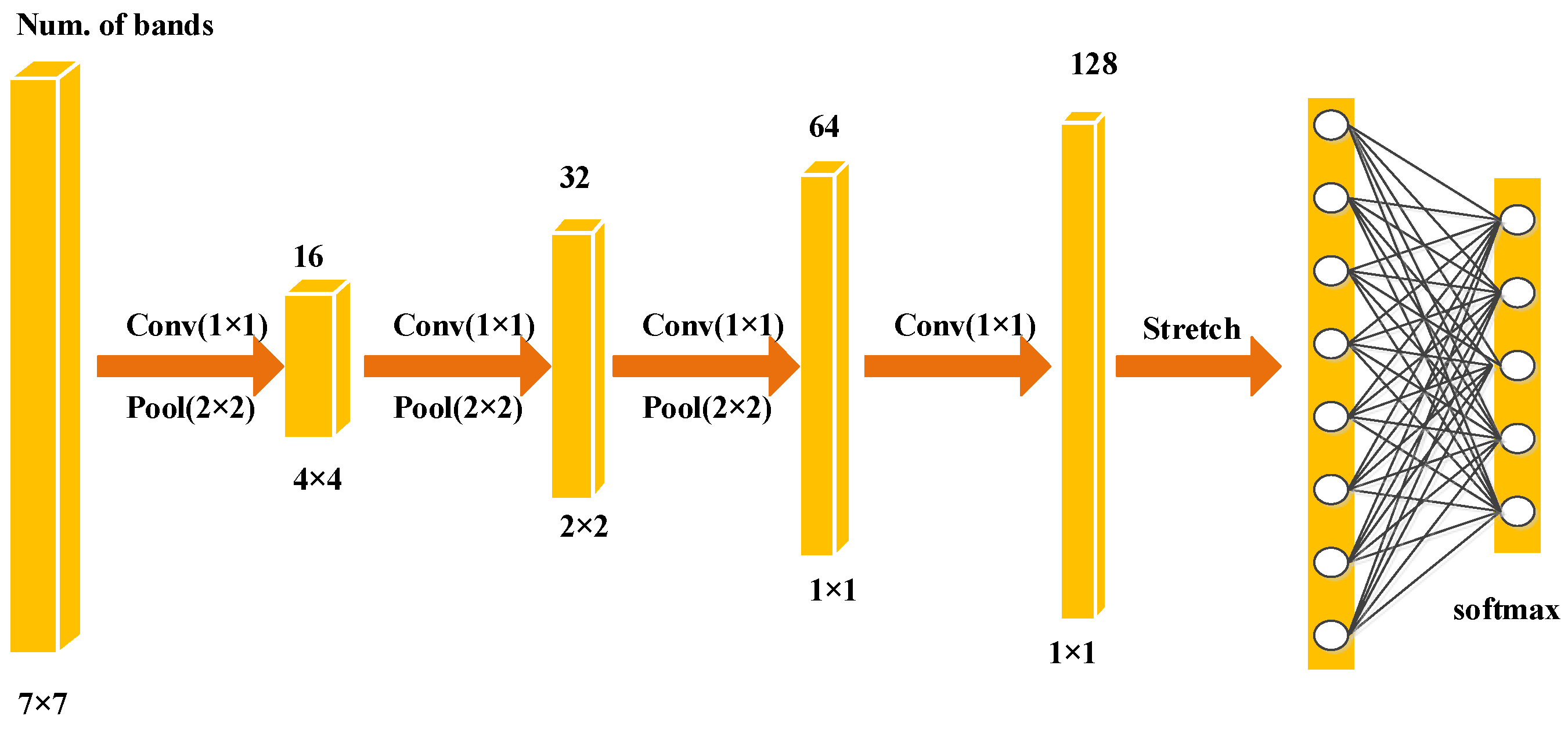
Figure 6.
The construction of fine-grained CNN.
Figure 6.
The construction of fine-grained CNN.
Figure 7.
The false-color composite images of (a) the Indian Pines; (b) the Pavia University; (c) the Salinas valley.
Figure 7.
The false-color composite images of (a) the Indian Pines; (b) the Pavia University; (c) the Salinas valley.
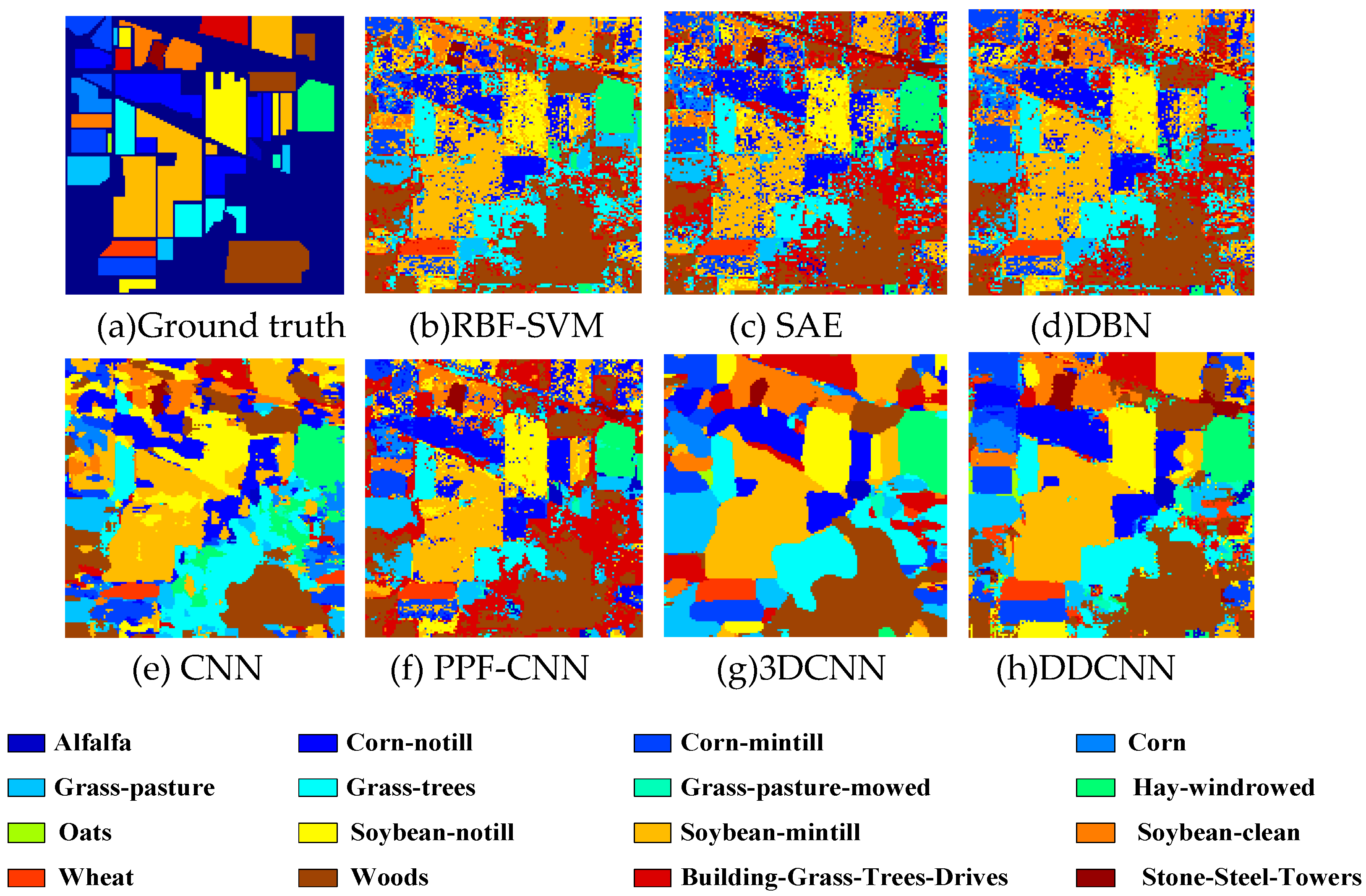
Figure 8.
(a) Ground truth and (b–h) classification visual maps of the Indian Pines dataset by RBF-SVM, SAE, DBN, PPF-CNN, CNN, 3DCNN, and DDCNN, respectively.
Figure 8.
(a) Ground truth and (b–h) classification visual maps of the Indian Pines dataset by RBF-SVM, SAE, DBN, PPF-CNN, CNN, 3DCNN, and DDCNN, respectively.
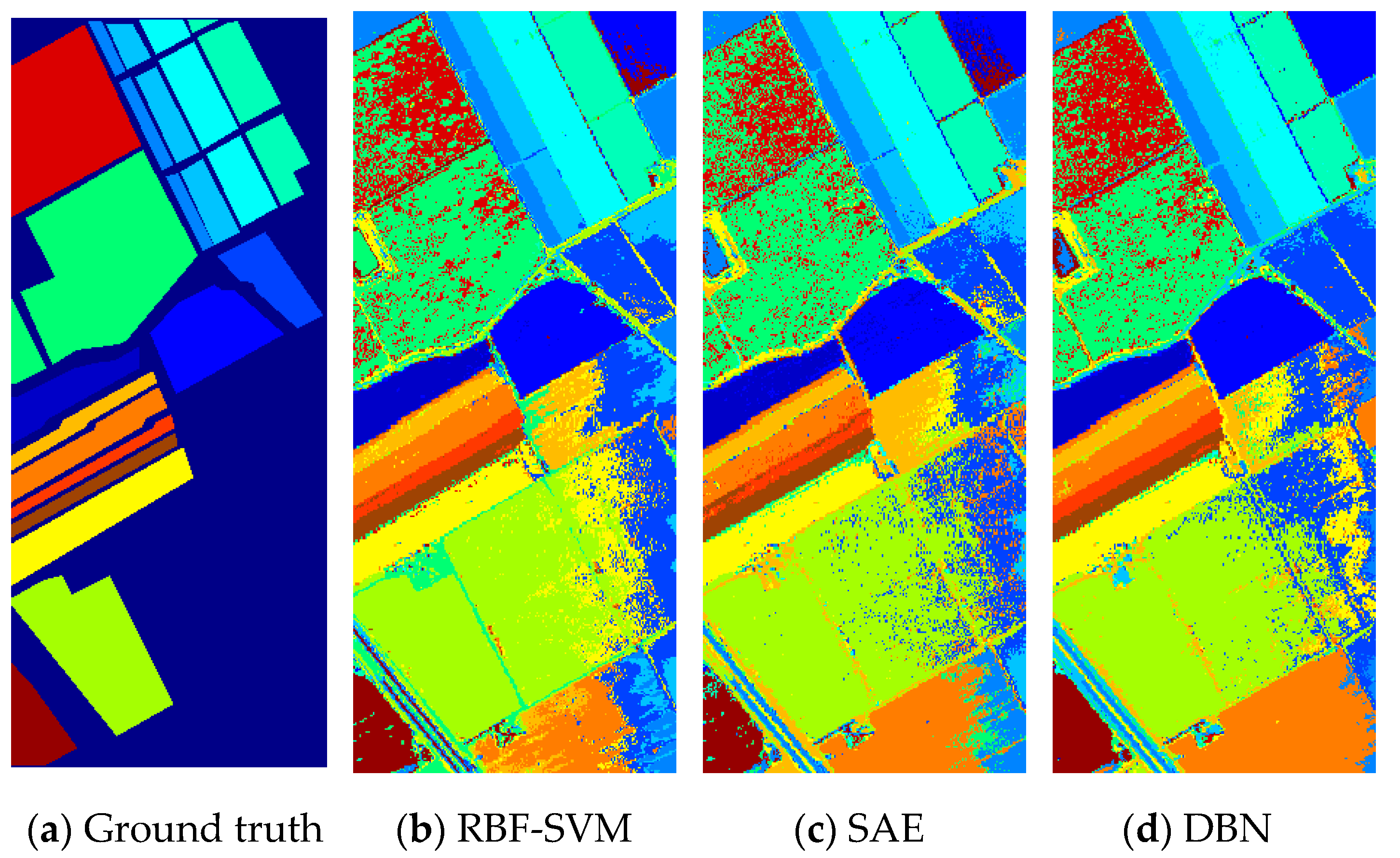
Figure 9.
(a) Ground truth and (b–h) classification visual maps of the Pavia University dataset by RBF-SVM, SAE, DBN, CNN, PPF-CNN, 3DCNN, and DDCNN, respectively.
Figure 9.
(a) Ground truth and (b–h) classification visual maps of the Pavia University dataset by RBF-SVM, SAE, DBN, CNN, PPF-CNN, 3DCNN, and DDCNN, respectively.
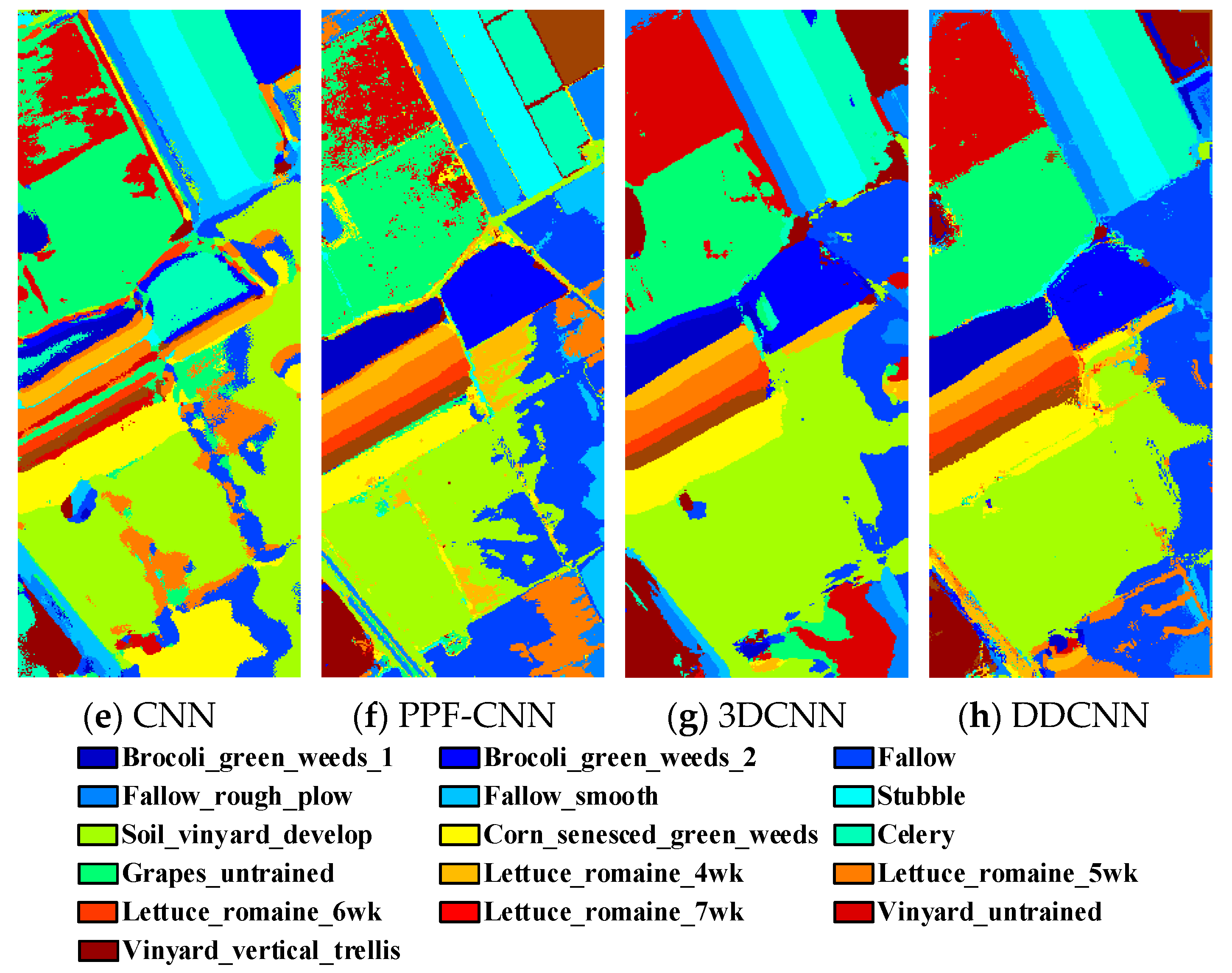
Figure 10.
(a) Ground truth and (b–h classification visual maps of the Salinas dataset by RBF-SVM, SAE, DBN, CNN, PPF-CNN, 3DCNN, and DDCNN, respectively.
Figure 10.
(a) Ground truth and (b–h classification visual maps of the Salinas dataset by RBF-SVM, SAE, DBN, CNN, PPF-CNN, 3DCNN, and DDCNN, respectively.
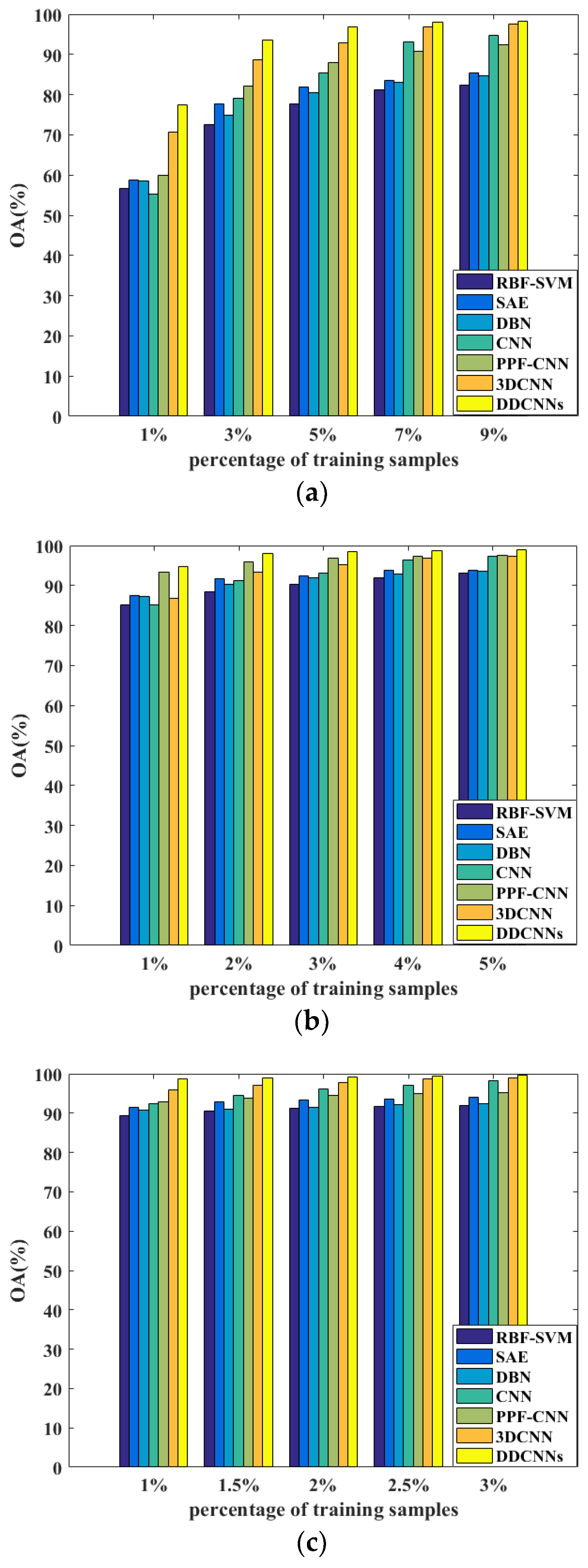
Figure 11.
The OA results of RBF-SVM, SAE, DBN, CNN, PPF-CNN, 3DCNN, and DDCNN with different ratios of training samples on the (a) Indian Pines, (b) Pavia University, and (c) Salinas datasets.
Figure 11.
The OA results of RBF-SVM, SAE, DBN, CNN, PPF-CNN, 3DCNN, and DDCNN with different ratios of training samples on the (a) Indian Pines, (b) Pavia University, and (c) Salinas datasets.
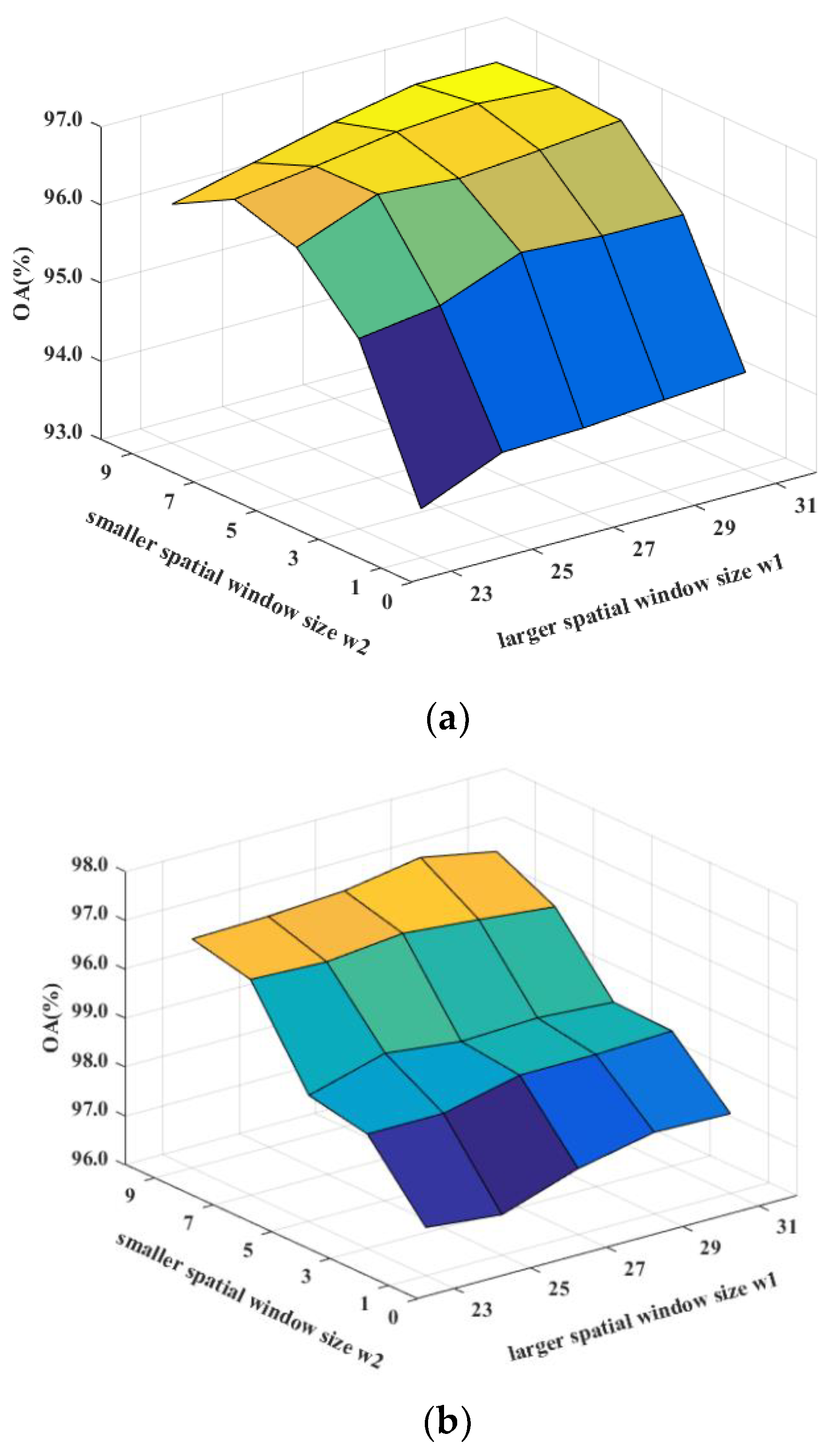
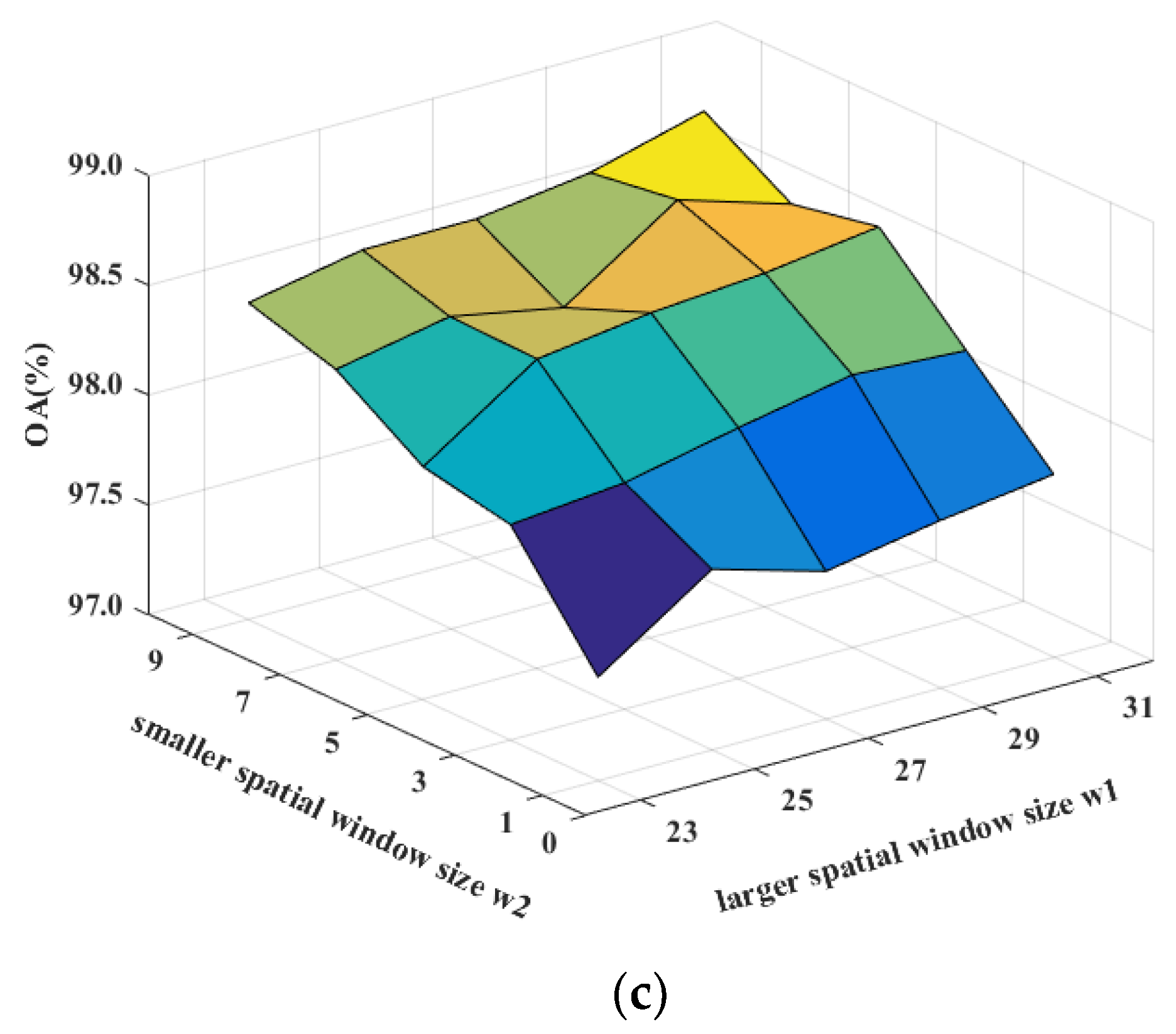
Figure 12.
Sensitivity analysis to the spatial window sizes w1 and w2 for DDCNN on (a) the Indian Pines, (b) the Pavia University, and (c) the Salinas datasets.
Figure 12.
Sensitivity analysis to the spatial window sizes w1 and w2 for DDCNN on (a) the Indian Pines, (b) the Pavia University, and (c) the Salinas datasets.
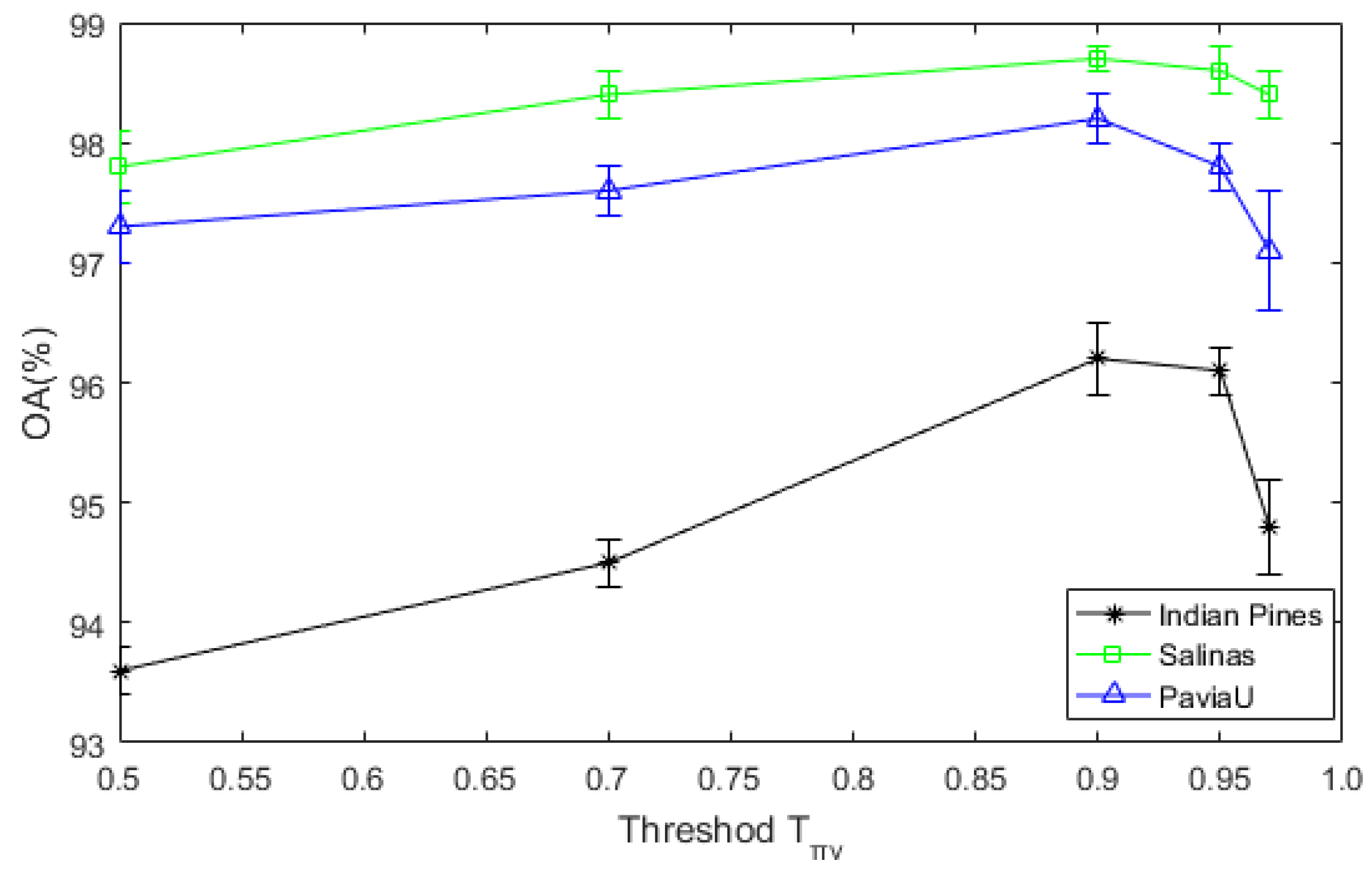
Figure 13.
The sensitivity analysis of DDCNN to the threshold .
Figure 13.
The sensitivity analysis of DDCNN to the threshold .
Table 1.
The procedure of the proposed DDCNN method.
Table 1.
The procedure of the proposed DDCNN method.
INPUT: The training samples and test samples from classes, the class labels of training samples, mini-batch size n, the number of training epochs E Begin Segment the whole HSI into superpixels The training samples are expanded to new training samples by (7) Training samples are divided into and , and test samples are divided into and by (6) initialize all the weight matrices and biases Input the training samples for every epoch for n training sample of every mini-batch compute the objective function by the cross-entropy loss function update the parameters of the multi-scale CNN by minimizing loss function end for end for Input the training samples for every epoch for n training sample of every mini-batch compute the objective function by the cross-entropy loss function update the parameters of the multi-scale CNN by minimizing loss function end for end for Count the labels by and END OUTPUT: the labels of the test samples classified by the trained DDCNN
|
Table 2.
The 16 Classes of the Indian Pines dataset and the numbers of training and test samples for each class.
Table 2.
The 16 Classes of the Indian Pines dataset and the numbers of training and test samples for each class.
| Class | Number of Samples |
|---|
| No | Name | Training | Test |
|---|
| 1 | Alfalfa | 2 | 42 |
| 2 | Corn-notill | 71 | 1286 |
| 3 | Corn-mintill | 42 | 746 |
| 4 | Corn | 12 | 213 |
| 5 | Grass-pasture | 24 | 435 |
| 6 | Grass-trees | 36 | 658 |
| 7 | Grass-pasture-mowed | 1 | 26 |
| 8 | Hay-windrowed | 24 | 430 |
| 9 | Oats | 1 | 18 |
| 10 | Soybean-notill | 49 | 874 |
| 11 | Soybean-mintill | 123 | 2209 |
| 12 | Soybean-clean | 30 | 533 |
| 13 | Wheat | 10 | 185 |
| 14 | Woods | 63 | 1139 |
| 15 | Buildings-Grass-Trees-Drives | 19 | 348 |
| 16 | Stone-Steel-Towers | 5 | 83 |
| Total | 512 | 9225 |
Table 3.
Classification results of RBF-SVM, SAE, DBN, CNN, PPF-CNN, 3DCNN, and DDCNN on the Indian Pines dataset.
Table 3.
Classification results of RBF-SVM, SAE, DBN, CNN, PPF-CNN, 3DCNN, and DDCNN on the Indian Pines dataset.
| Class | RBF-SVM | SAE | DBN | CNN | PPF-CNN | 3DCNN | DDCNN |
|---|
| 1 | 6.1±11.2 | 10.0±6.4 | 13.6±5.6 | 78.4±10.2 | 50.4±8.4 | 83.8±13.4 | 99.3±1.6 |
| 2 | 72.9±3.6 | 79.7±2.3 | 79.8±2.9 | 75.4±2.4 | 89.2±2.1 | 92.7±3.5 | 94.3±2.5 |
| 3 | 58.0±3.6 | 74.9±4.8 | 70.5±2.2 | 82.8±3.3 | 77.1±2.7 | 87.2±10.4 | 99.0±0.8 |
| 4 | 39.0±15.0 | 62.8±8.3 | 71.3±6.6 | 89.2±3.5 | 87.7±3.7 | 83.4±8.3 | 95.0±3.3 |
| 5 | 87.0±4.5 | 84.2±3.3 | 80.1±4.1 | 69.0±4.6 | 92.7±1.0 | 84.0±5.7 | 92.7±2.8 |
| 6 | 92.4±2.0 | 94.3±1.7 | 94.2±2.4 | 92.8±2.5 | 93.1±1.9 | 93.4±2.5 | 98.8±0.8 |
| 7 | 0±0 | 24.4±18.8 | 28.1±22.6 | 51.1±12.3 | 0±0 | 97.2±4.8 | 100.0±0.0 |
| 8 | 98.1±1.4 | 98.8±0.4 | 98.5±1.5 | 97.1±1.6 | 99.6±0.3 | 97.4±2.8 | 99.8±0.6 |
| 9 | 0±0 | 11.1±10.1 | 9.5±2.4 | 41.6±9.9 | 0±0 | 77.0±11.1 | 97.8±5.4 |
| 10 | 65.8±3.7 | 73.6±3.8 | 73.2±4.7 | 81.0±2.6 | 85.6±2.8 | 93.3±5.0 | 93.8±1.2 |
| 11 | 85.3±2.9 | 83.4±2.0 | 82.7±2.2 | 87.2±1.5 | 83.8±1.6 | 94.9±2.7 | 98.1±1.3 |
| 12 | 69.6±6.5 | 70.4±8.0 | 62.0±5.8 | 84.4±2.3 | 90.4±3.1 | 89.8±4.3 | 94.4±2.5 |
| 13 | 92.3±4.1 | 94.2±4.3 | 89.7±10.6 | 83.1±4.2 | 97.8±0.9 | 92.8±5.9 | 99.9±0.2 |
| 14 | 96.6±1.0 | 94.2±1.5 | 94.4±1.6 | 98.2±0.8 | 95.5±1.1 | 98.3±1.3 | 99.5±0.4 |
| 15 | 41.7±7.0 | 66.1±5.6 | 64.2±6.5 | 84.7±4.5 | 78.0±2.4 | 77.8±13.4 | 95.7±2.6 |
| 16 | 75.2±9.0 | 87.6±8.1 | 80.5±13.2 | 76.0±8.1 | 97.3±1.3 | 88.4±5.3 | 89.7±9.4 |
| OA (%) | 77.8±0.8 | 81.9±0.1 | 80.6±0.1 | 85.4±0.8 | 87.9±0.8 | 92.8±0.8 | 96.9±0.6 |
| AA (%) | 61.3±1.4 | 69.4±1.9 | 68.3±1.7 | 79.4±1.6 | 76.5±0.6 | 89.4±1.4 | 96.6±0.7 |
| Kappa (%) | 74.5±1.0 | 79.3±1.1 | 77.8±1.3 | 84.3±2.9 | 86.3±0.9 | 91.9±0.9 | 96.3±0.8 |
Table 4.
9 Classes of the Pavia University dataset and the numbers of training and test samples for each class.
Table 4.
9 Classes of the Pavia University dataset and the numbers of training and test samples for each class.
| Class | Number of Samples |
|---|
| No | Name | Training | Test |
|---|
| 1 | Asphalt | 199 | 6233 |
| 2 | Meadows | 559 | 17531 |
| 3 | Gravel | 63 | 1973 |
| 4 | Trees | 92 | 2880 |
| 5 | Painted metal sheets | 40 | 1265 |
| 6 | Bare Soil | 151 | 4727 |
| 7 | Bitumen | 40 | 1250 |
| 8 | Self-Blocking Bricks | 110 | 3462 |
| 9 | Shadows | 28 | 891 |
| Total | 1282 | 40212 |
Table 5.
Classification results of RBF-SVM, SAE, DBN, CNN, PPF-CNN, 3DCNN, and DDCNN on the Pavia University dataset.
Table 5.
Classification results of RBF-SVM, SAE, DBN, CNN, PPF-CNN, 3DCNN, and DDCNN on the Pavia University dataset.
| Class | RBF-SVM | SAE | DBN | CNN | PPF-CNN | 3DCNN | DDCNN |
|---|
| 1 | 90.7±1.1 | 92.3±1.1 | 91.6±0.8 | 93.1±1.4 | 98.0±0.1 | 95.5±1.2 | 97.8±1.1 |
| 2 | 96.8±0.7 | 97.6±0.3 | 97.4±0.4 | 97.6±0.9 | 99.2±0.2 | 99.4±0..3 | 99.5±0.1 |
| 3 | 60.2±5.4 | 72.1±3.5 | 69.7±6.0 | 77.9±4.5 | 84.9±1.8 | 92.6±5.4 | 98.4±0.9 |
| 4 | 90.8±2.0 | 90.9±1.4 | 91.2±1.4 | 86.4±3.6 | 95.8±0.8 | 75.2±4.9 | 95.9±1.1 |
| 5 | 98.8±0.4 | 98.7±0.4 | 98.6±0.6 | 98.5±1.4 | 99.8±0.1 | 95.4±4.3 | 99.4±0.5 |
| 6 | 79.5±4.9 | 86.9±1.9 | 85.6±2.2 | 91.0±2.8 | 96.4±0.3 | 99.4±0.6 | 99.7±0.3 |
| 7 | 74.3±5.1 | 78.1±4.9 | 74.8±4.8 | 81.2±2.9 | 89.2±0.8 | 91.5±3.4 | 99.6±0.4 |
| 8 | 88.8±2.2 | 87.8±1.4 | 88.2±1.3 | 92.5±2.2 | 93.7±1.2 | 94.8±1.4 | 97.8±1.3 |
| 9 | 99.8±0.1 | 99.5±0.3 | 99.6±0.1 | 79.0±4.1 | 98.5±0.7 | 77.4±2.8 | 87.9±2.5 |
| OA (%) | 90.3±0.6 | 92.4±0.3 | 91.9±0.3 | 93.0±0.6 | 96.9±0.2 | 95.2±0.7 | 98.5±0.2 |
| AA (%) | 86.6±0.9 | 89.3±0.7 | 88.5±0.8 | 88.6±0.8 | 95.1±0.2 | 91.2±1.1 | 97.3±0.4 |
| Kappa (%) | 87.1±0.8 | 89.9±0.4 | 89.2±0.4 | 90.7±0.7 | 96.0±0.2 | 93.8±0.9 | 98.1±0.2 |
Table 6.
The 16 Classes of the Salinas dataset and the numbers of training and test samples for each class.
Table 6.
The 16 Classes of the Salinas dataset and the numbers of training and test samples for each class.
| Category | Number of samples |
|---|
| No | Name | Training | Test |
|---|
| 1 | Brocoli_green_weeds_1 | 20 | 1969 |
| 2 | Brocoli_green_weeds_2 | 37 | 3652 |
| 3 | Fallow | 20 | 1936 |
| 4 | Fallow_rough_plow | 14 | 1366 |
| 5 | Fallow_smooth | 27 | 2624 |
| 6 | Stubble | 40 | 3879 |
| 7 | Celery | 36 | 3507 |
| 8 | Grapes_untrained | 113 | 11045 |
| 9 | Soil_vinyard_develop | 62 | 6079 |
| 10 | Corn_senesced_green | 33 | 3212 |
| 11 | Lettuce_romaine_4wk | 11 | 1046 |
| 12 | Lettuce_romaine_5wk | 19 | 1889 |
| 13 | Lettuce_romaine_6wk | 9 | 898 |
| 14 | Lettuce_romaine_7wk | 11 | 1048 |
| 15 | Vinyard_untrained | 73 | 7122 |
| 16 | Vinyard_vertical | 18 | 1771 |
| Total | 543 | 53043 |
Table 7.
Classification results of RBF-SVM, SAE, DBN, CNN, PPF-CNN, 3DCNN, and DDCNN on the Salinas dataset.
Table 7.
Classification results of RBF-SVM, SAE, DBN, CNN, PPF-CNN, 3DCNN, and DDCNN on the Salinas dataset.
| Class | RBF-SVM | SAE | DBN | CNN | PPF-CNN | 3DCNN | DDCNN |
|---|
| 1 | 97.4±1.5 | 97.9±0.5 | 98.5±0.8 | 93.3±8.7 | 98.5±0.5 | 88.6±3.5 | 100.0±0.0 |
| 2 | 99.7±0.2 | 99.1±0.5 | 98.9±0.2 | 97.4±1.2 | 99.7±0.2 | 94.5±2.9 | 99.8±0.2 |
| 3 | 93.7±1.5 | 95.3±0.6 | 97.5±0.1 | 86.4±4.1 | 99.8±0.1 | 91.4±4.7 | 99.7±0.4 |
| 4 | 97.8±1.3 | 99.5±0.6 | 99.0±0.3 | 98.2±1.8 | 99.7±0.2 | 96.8±2.1 | 98.3±0.8 |
| 5 | 97.5±1.1 | 98.5±0.4 | 97.5±0.2 | 98.1±1.0 | 96.8±0.2 | 96.7±2.7 | 99.3±0.5 |
| 6 | 99.5±0.3 | 99.9±0.1 | 99.3±0.1 | 99.9±0.2 | 99.8±0.3 | 98.5±1.2 | 99.9±0.2 |
| 7 | 99.3±0.2 | 99.2±0.1 | 99.0±0.3 | 99.0±0.9 | 99.5±0.2 | 98.0±1.3 | 99.9±0.1 |
| 8 | 88.9±2.9 | 82.7±0.7 | 83.0±1.4 | 88.4±2.8 | 89.9±0.9 | 92.3±1.1 | 99.4±0.3 |
| 9 | 99.2±0.3 | 99.2±0.1 | 99.0±0.1 | 95.1±0.7 | 99.8±0.2 | 98.9±0.4 | 99.9±0.1 |
| 10 | 88.8±1.9 | 88.9±0.9 | 92.8±0.1 | 93.6±2.4 | 88.3±2.7 | 99.1±0.8 | 95.3±1.2 |
| 11 | 87.5±4.6 | 93.6±7.0 | 91.7±0.1 | 97.6±1.0 | 93.4±2.9 | 97.6±2.1 | 99.8±0.2 |
| 12 | 98.0±2.3 | 98.6±1.0 | 99.0±0.1 | 98.9±1.1 | 99.7±0.7 | 96.6±2.7 | 98.6±0.9 |
| 13 | 98.0±0.8 | 99.2±0.7 | 99.3±0.2 | 94.7±2.4 | 98.6±0.7 | 90.9±0.7 | 99.7±0.2 |
| 14 | 89.6±2.6 | 94.8±0.2 | 92.0±7.4 | 92.5±3.9 | 92.3±1.7 | 98.2±1.0 | 93.8±1.8 |
| 15 | 53.9±7.6 | 75.9±2.4 | 69.5±0.2 | 80.1±5.3 | 72.9±2.5 | 98.6±0.8 | 96.6±0.5 |
| 16 | 90.8±5.0 | 96.1±1.9 | 96.1±2.5 | 93.6±2.6 | 95.7±1.8 | 96.3±3.0 | 98.0±1.0 |
| OA (%) | 89.3±0.7 | 91.5±0.1 | 90.8±0.6 | 92.3±1.2 | 92.8±0.4 | 95.9±0.2 | 98.8±0.2 |
| AA (%) | 92.5±0.6 | 94.9±0.2 | 94.5±0.8 | 94.2±0.9 | 95.5±0.7 | 95.8±0.2 | 98.6±0.2 |
| Kappa (%) | 88.0±0.8 | 90.6±0.4 | 89.7±0.7 | 91.4±1.4 | 91.9±0.4 | 95.5±0.2 | 98.6±0.2 |
Table 8.
Running time and Parameters of RBF-SVM, SAE, DBN, CNN, PPF-CNN, 3DCNN, and DDCNN on the Indian Pines dataset.
Table 8.
Running time and Parameters of RBF-SVM, SAE, DBN, CNN, PPF-CNN, 3DCNN, and DDCNN on the Indian Pines dataset.
| Dataset | Method | Training Time (s) | Test Time (s) | Parameters |
|---|
| Indian Pines | RBF-SVM | 0.4±0.1 | 1.2±0.1 | 200 |
| SAE | 76.3±8.4 | 0.2±0.1 | 26160 |
| DBN | 114.3±20.1 | 0.2±0.1 | 24060 |
| CNN | 220.7±27.9 | 0.5±0.1 | 81408 |
| PPF-CNN | 2056.0±36.7 | 5.3±0.3 | 61870 |
| 3DCNN | 2690.2±57.9 | 16.0±0.1 | 44961792 |
| DDCNN | 587.2±22.7 | 0.7±0.1 | 376932 |
Table 9.
Running time and Parameters of RBF-SVM, SAE, DBN, CNN, PPF-CNN, 3DCNN, and DDCNN on the Pavia University dataset.
Table 9.
Running time and Parameters of RBF-SVM, SAE, DBN, CNN, PPF-CNN, 3DCNN, and DDCNN on the Pavia University dataset.
| Dataset | Method | Training Time (s) | Test Time (s) | Parameters |
|---|
| Pavia University | RBF-SVM | 0.5±0.1 | 3.5±0.1 | 200 |
| SAE | 82.2±5.3 | 0.3±0.1 | 19920 |
| DBN | 147.0±10.6 | 0.4±0.2 | 21420 |
| CNN | 371.8±15.3 | 1.2±0.1 | 61249 |
| PPF-CNN | 4367.9±29.5 | 7.2±0.4 | 61310 |
| 3DCNN | 1979.0±12.6 | 31.4±5.5 | 5866224 |
| DDCNN | 682.1±10.6 | 2.3±0.1 | 375140 |
Table 10.
Running time and Parameters of RBF-SVM, SAE, DBN, CNN, PPF-CNN, 3DCNN, and DDCNN on the Salinas dataset.
Table 10.
Running time and Parameters of RBF-SVM, SAE, DBN, CNN, PPF-CNN, 3DCNN, and DDCNN on the Salinas dataset.
| Dataset | Method | Training Time (s) | Test Time (s) | Parameters |
|---|
| Salinas | RBF-SVM | 0.4±0.1 | 2.7±0.1 | 204 |
| SAE | 70.1±2.4 | 0.6±0.1 | 26160 |
| DBN | 102.6±9.1 | 0.5±0.2 | 24060 |
| CNN | 165.1±2.1 | 0.7±0.1 | 82216 |
| PPF-CNN | 1940.1±17.4 | 64.6±1.5 | 61870 |
| 3DCNN | 1157.7±25.7 | 28.1±0.4 | 5867520 |
| DDCNN | 657.2±20.6 | 4.7±0.2 | 376932 |
Table 11.
Classification results of CNN, RPCA-CNN, DCNN, and DDCNN on the Indian Pines, Pavia University, and Salinas Datasets.
Table 11.
Classification results of CNN, RPCA-CNN, DCNN, and DDCNN on the Indian Pines, Pavia University, and Salinas Datasets.
| Data set | Classification Index | CNN | RPCA-CNN | DCNN | DDCNN |
|---|
| Indian Pines Dataset | OA (%) | 85.4±0.8 | 88.6±0.6 | 93.4±0.5 | 96.9±0.6 |
| AA (%) | 79.4±1.6 | 82.6±2.3 | 89.5±1.7 | 96.6±0.7 |
| Kappa (%) | 84.3±2.9 | 86.1±0.7 | 92.5±0.5 | 96.3±0.8 |
| Pavia University Dataset | OA (%) | 93.0±0.6 | 94.2±0.2 | 95.7±0.8 | 98.5±0.2 |
| AA (%) | 88.6±0.8 | 91.6±0.2 | 95.3±0.8 | 97.3±0.4 |
| Kappa (%) | 90.7±0.7 | 92.4±0.5 | 95.2±0.9 | 98.1±0.2 |
| Salinas Dataset | OA (%) | 92.3±1.2 | 92.9±0.6 | 94.5±0.6 | 98.8±0.2 |
| AA (%) | 94.2±0.9 | 94.2±0.9 | 94.5±0.6 | 98.6±0.2 |
| Kappa (%) | 91.4±1.4 | 91.4±1.4 | 93.9±0.7 | 98.6±0.2 |
Table 12.
Classification results of DDCNN, MCNN, FCNN, and DDCNN-WDA on the Indian Pines, Pavia University, and Salinas Datasets.
Table 12.
Classification results of DDCNN, MCNN, FCNN, and DDCNN-WDA on the Indian Pines, Pavia University, and Salinas Datasets.
| Data set | Classification Index | DDCNN | FCNN | MCNN | DDCNN-WDA |
|---|
| Indian Pines Dataset | OA (%) | 96.9±0.6 | 93.3±0.7 | 95.8±0.5 | 95.9±0.7 |
| AA (%) | 96.6±0.7 | 90.6±2.1 | 92.6±1.9 | 93.2±2.0 |
| Kappa (%) | 96.3±0.8 | 92.4±0.8 | 95.3±0.6 | 95.3±0.8 |
| Pavia University Dataset | OA (%) | 98.5±0.2 | 97.4±0.2 | 97.8±0.4 | 97.7±0.9 |
| AA (%) | 97.3±0.4 | 95.9±0.5 | 95.5±1.1 | 95.9±0.9 |
| Kappa (%) | 98.1±0.2 | 96.6±0.3 | 97.1±0.5 | 96.9±1.3 |
| Salinas Dataset | OA (%) | 98.8±0.2 | 96.3±0.7 | 97.1±1.5 | 98.4±0.3 |
| AA (%) | 98.6±0.2 | 97.4±0.5 | 97.1±1.7 | 97.7±0.6 |
| Kappa (%) | 98.6±0.2 | 95.9±0.9 | 96.8±1.7 | 97.9±1.4 |
Table 13.
The sensitivity analysis of numbers of convolutional layers.
Table 13.
The sensitivity analysis of numbers of convolutional layers.
| Dataset | Classification Index | the Number of Convolutional Layers |
|---|
| 1 | 2 | 3 | 4 | 5 |
|---|
| Indian Pines Dataset | OA (%) | 93.6±0.4 | 95.5±0.4 | 96.0±0.1 | 96.9±0.6 | 96.4±0.3 |
| AA (%) | 91.6±1.1 | 94.5±0.3 | 95.5±0.3 | 96.6±0.7 | 95.3±0.7 |
| Kappa (%) | 92.8±0.4 | 94.9±0.4 | 95.4±0.1 | 96.3±0.8 | 95.8±0.4 |
| Pavia University Dataset | OA (%) | 95.8±0.1 | 97.4±0.2 | 98.7±0.1 | 98.5±0.2 | 98.4±0.1 |
| AA (%) | 95.1±0.4 | 96.7±0.3 | 98.3±0.1 | 97.3±0.4 | 98.2±0.2 |
| Kappa (%) | 94.5±0.1 | 96.6±0.3 | 98.4±0.2 | 98.1±0.2 | 97.8±0.1 |
| Salinas Dataset | OA (%) | 94.3±0.2 | 95.5±0.6 | 98.5±0.2 | 98.8±0.2 | 98.6±0.2 |
| AA (%) | 96.2±0.3 | 97.1±0.5 | 98.5±0.2 | 98.6±0.2 | 98.5±0.3 |
| Kappa (%) | 93.7±0.3 | 95.1±0.7 | 98.4±0.2 | 98.6±0.2 | 98.5±0.2 |
Table 14.
The sensitivity analysis of numbers of superpixels in DDCNN.
Table 14.
The sensitivity analysis of numbers of superpixels in DDCNN.
| Dataset | Classification Index | The Number of Superpixels |
|---|
| 50 | 100 | 500 | 1000 | 5000 |
|---|
| Indian Pines Dataset | OA (%) | 94.7±0.4 | 96.9±0.6 | 96.3±0.3 | 93.7±0.3 | 92.7±0.5 |
| AA (%) | 92.1±1.6 | 96.6±0.7 | 95.4±0.9 | 91.6±1.8 | 91.1±1.3 |
| Kappa (%) | 94.0±0.4 | 96.3±0.8 | 95.8±0.3 | 92.8±0.4 | 91.4±0.9 |
| Pavia University Dataset | OA (%) | 97.1±0.2 | 97.5±0.2 | 98.3±0.1 | 98.5±0.2 | 97.3±0.3 |
| AA (%) | 95.5±0.4 | 96.9±0.2 | 97.8±0.1 | 97.3±0.4 | 96.3±0.2 |
| Kappa (%) | 96.4±0.3 | 96.7±0.3 | 97.8±0.1 | 98.1±0.2 | 96.4±0.5 |
| Salinas Dataset | OA (%) | 97.2±0.4 | 98.8±0.2 | 97.3±0.4 | 95.9±0.9 | 94.9±0.5 |
| AA (%) | 96.5±1.0 | 98.6±0.2 | 96.7±0.4 | 94.5±1.6 | 92.9±0.8 |
| Kappa (%) | 96.9±0.5 | 98.6±0.2 | 97.0±0.4 | 95.5±0.9 | 94.9±0.5 |