Long-Term Satellite Monitoring of the Slumgullion Landslide Using Space-Borne Synthetic Aperture Radar Sub-Pixel Offset Tracking
Abstract
1. Introduction
2. Materials and Methods
2.1. Study area and available data
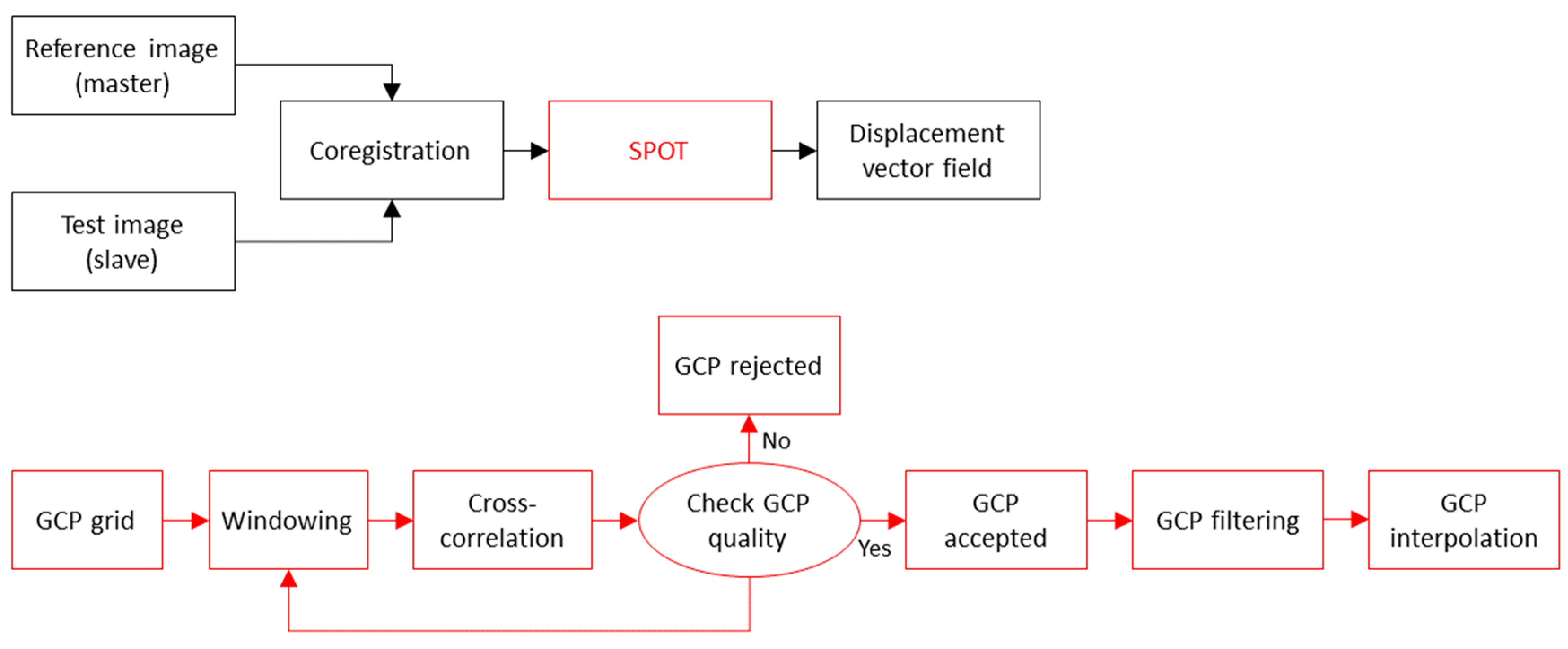
2.2. Implemented Sub-Pixel Offset Tracking (SPOT) technique
3. Results
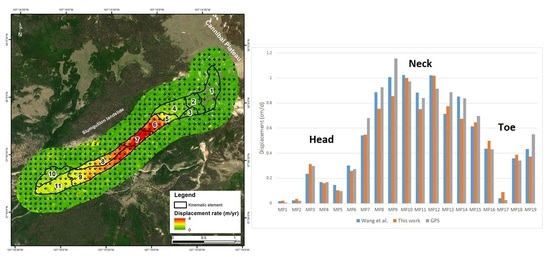
3.1. Validation
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Coe, J.A. Regional moisture balance control of landslide motion: Implications for landslide forecasting in a changing climate. Geology 2012, 40, 323–326. [Google Scholar] [CrossRef]
- Milillo, P.; Fielding, E.J.; Shulz, W.H.; Delbridge, B.; Burgmann, R. COSMO-SkyMed Spotlight Interferometry Over Rural Areas: The Slumgullion Landslide in Colorado, USA. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2919–2926. [Google Scholar] [CrossRef]
- Lanari, R.; Mora, O.; Manunta, M.; Mallorqui, J.J.; Berardino, P.; Sansosti, E. A small-baseline approach for investigating deformations on full-resolution differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1377–1386. [Google Scholar] [CrossRef]
- Di Martire, D.; Paci, M.; Confuorto, P.; Costabile, S.; Guastaferro, F.; Verta, A.; Calcaterra, D. A nation-wide system for landslide mapping and risk management in Italy: The second Not-ordinary Plan of Environmental Remote Sensing. Int. J. Appl. Earth Obs. Geoinf. 2017, 63, 143–157. [Google Scholar] [CrossRef]
- Tapete, D.; Cigna, F. InSAR data for geohazard assessment in UNESCO World Heritage sites: State-of-the-art and perspectives in the Copernicus era. Int. J. Appl. Earth Obs. Geoinf. 2017, 63, 24–32. [Google Scholar] [CrossRef]
- Di Martire, D.; Iglesias, R.; Monells, D.; Centolanza, G.; Sica, S.; Ramondini, M.; Pagano, L.; Mallorquí, J.J.; Calcaterra, D. Comparison between Differential SAR interferometry and ground measurements data in the displacement monitoring of the earth-dam of Conza della Campania (Italy). Remote Sens. Environ. 2014, 148, 58–69. [Google Scholar] [CrossRef]
- Colesanti, C.; Ferretti, A.; Novali, F.; Prati, C.; Rocca, F. Sar monitoring of progressive and seasonal ground deformation using the permanent scatterers technique. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1685–1701. [Google Scholar] [CrossRef]
- Fumagalli, A.; Novali, F.; Prati, C.; Ferretti, A.; Rocca, F.; Rucci, A. A New Algorithm for Processing Interferometric Data-Stacks: SqueeSAR. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3460–3470. [Google Scholar]
- C Prati, C.; Ferretti, A.; Perissin, D. Recent advances on surface ground deformation measurement by means of repeated space-borne SAR observations. J. Geodyn. 2010, 49, 161–170. [Google Scholar] [CrossRef]
- Hooper, A. A multi-temporal InSAR method incorporating both persistent scatterer and small baseline approaches. Geophys. Res. Lett. 2008, 35, 1–5. [Google Scholar] [CrossRef]
- Singleton, A.; Li, Z.; Hoey, T.; Muller, J.-P. Evaluating sub-pixel offset techniques as an alternative to D-InSAR for monitoring episodic landslide movements in vegetated terrain. Remote Sens. Environ. 2014, 147, 133–144. [Google Scholar] [CrossRef]
- Wasowski, J.; Bovenga, F. Investigating landslides and unstable slopes with satellite Multi Temporal Interferometry: Current issues and future perspectives. Eng. Geol. 2014, 174, 103–138. [Google Scholar] [CrossRef]
- Manconi, A.; Casu, F.; Ardizzone, F.; Bonano, M.; Cardinali, M.; De Luca, C.; Gueguen, E.; Marchesini, I.; Parise, M.; Vennari, C.; et al. Brief Communication: Rapid mapping of landslide events: The 3 December 2013 Montescaglioso landslide, Italy. Nat. Hazards Earth Syst. Sci. 2014, 14, 1835–1841. [Google Scholar] [CrossRef]
- Sun, L.; Muller, J.-P. Evaluation of the Use of Sub-Pixel Offset Tracking Techniques to Monitor Landslides in Densely Vegetated Steeply Sloped Areas. Remote Sens. 2016, 8, 695. [Google Scholar] [CrossRef]
- Lüttig, C.; Neckel, N.; Humbert, A. A Combined Approach for Filtering Ice Surface Velocity Fields Derived from Remote Sensing Methods. Remote Sens. 2017, 9, 1062. [Google Scholar] [CrossRef]
- Strozzi, T.; Luckman, A.; Murray, T.; Wegmuller, U.; Werner, C. Glacier motion estimation using SAR offset-tracking procedures. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2384–2391. [Google Scholar] [CrossRef]
- Riveros, N.; Euillades, L.; Euillades, P.; Moreiras, S.; Balbarani, S. Offset tracking procedure applied to high resolution SAR data on Viedma Glacier, Patagonian Andes, Argentina. Adv. Geosci. 2013, 35, 7–13. [Google Scholar] [CrossRef]
- Huang, J.; Deng, K.; Fan, H.; Yan, S. An improved pixel-tracking method for monitoring mining subsidence. Remote Sens. Lett. 2016, 7, 731–740. [Google Scholar] [CrossRef]
- Fan, H.; Gao, X.; Yang, J.; Deng, K.; Yü, Y. Monitoring Mining Subsidence Using A Combination of Phase-Stacking and Offset-Tracking Methods. Remote Sens. 2015, 7, 9166–9183. [Google Scholar] [CrossRef]
- Parise, M.; Guzzi, R. Volume and Shape of the Active and Inactive Parts of the Slumgullion Landslide, Hinsdale County, Colorado. Open-File Rep. 1992. Available online: https://pubs.er.usgs.gov/publication/ofr92216 (accessed on 11 February 2019).
- Crandell, D.R.; Varnes, D.J. Slumgullion earthflow and earth slide near Lake City, Colorado. Geol. Soc. Am. Bull. 1960, 71, 1846. [Google Scholar]
- Schulz, W.H.; Coe, J.A.; Ricci, P.P.; Smoczyk, G.M.; Shurtleff, B.L.; Panosky, J. Landslide kinematics and their potential controls from hourly to decadal timescales: Insights from integrating ground-based InSAR measurements with structural maps and long-term monitoring data. Geomorphology 2017, 285, 121–136. [Google Scholar] [CrossRef]
- Guzzi, R.; Parise, M. Surface Features and Kinematics of the Slumgullion Landslide, near Lake City, Colorado. US Geol. Surv. 1992; pp. 92–252. Available online: https://pubs.er.usgs.gov/publication/ofr92252 (accessed on 11 February 2019).
- Coe, J.; Godt, J.; Ellis, W.; Savage, W.; Savage, J.; Powers, P.; Varnes, D.; Tachker, P. Preliminary interpretation of seasonal movement of the Slumgullion landslide as determined from GPS observations, July 1998–July 1999; Open-File Report; U.S. Geological Survey: Reston, VA, USA, 2000. Available online: http://pubs.usgs.gov/of/2000/ofr-00-0102/ (accessed on 11 February 2019).
- Wang, C.; Mao, X.; Wang, Q. Landslide Displacement Monitoring by a Fully Polarimetric SAR Offset Tracking Method. Remote Sens. 2016, 8, 624. [Google Scholar] [CrossRef]
- Wang, C.; Cai, J.; Li, Z.; Mao, X.; Feng, G.; Wang, Q. Kinematic Parameter Inversion of the Slumgullion Landslide Using the Time Series Offset Tracking Method with UAVSAR Data. J. Geophys. Res. Solid Earth 2018, 123, 8110–8124. [Google Scholar] [CrossRef]
- Delbridge, B.G.; Fielding, E.; Hensley, S.; Schulz, W.H. Three-dimensional surface deformation derived from airborne interferometric UAVSAR: Application to the Slumgullion Landslide. J. Geophys. Res. Solid Earth 2016, 121, 3951–3977. [Google Scholar] [CrossRef]
- Tepel, R.E. Landslides: Investigation and Mitigation. Environ. Eng. Geosci. 1998, VI, 277–279. [Google Scholar] [CrossRef]
- Smith, W. Photogrammetric Determination of Movement on the Slumgullion Slide, Hinsdale County, Colorado 1985–1990; Open-File Report; U.S. Geological Survey: Reston, VA, USA, 1993. [CrossRef]
- Fleming, R.; Baum, R.L.; Giardino, M. Map and Description of the Active Part of the Slumgullion Landslide, Hinsdale County, Colorado; U.S. Geological Survey: Reston, VA, USA, 1999.
- Delbridge, B.; Burgmann, R.; Fielding, E.; Hensley, S. Kinematics of the slumgullion landslide from UAVSAR derived interferograms. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 3842–3845. [Google Scholar]
- Franceschetti, G.; Lanari, R.; Fidler, J. Synthetic Aperture Radar Processing; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Shapiro, L.; Stockman, G.C. Computer Vision; Prentice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Coe, J.A.; Godt, J.W.; Ellis, W.L.; Savage, W.Z.; Savage, J.E.; Powers, P.S.; Varnes, D.J.; Tachker, P. Seasonal Movement of the Slumgullion Landslide as Determined from GPS Observations, July 1998–July 1999; U.S. Geological Survey: Reston, VA, USA, 2000.
- Hensley, S.; Zebker, H.; Jones, C.; Michel, T.; Muellerschoen, R.; Chapman, B. First deformation results using the NASA/JPL UAVSAR instrument. In Proceedings of the 2009 2nd Asian-Pacific Conference on Synthetic Aperture Radar, Xi’an, China, 36–30 October 2009; pp. 1051–1055. [Google Scholar]
- Coe, J.A.; McKenna, J.P.; Godt, J.W.; Baum, R. Basal-topographic control of stationary ponds on a continuously moving landslide. Earth Surf. Process. Landforms 2009, 34, 264–279. [Google Scholar] [CrossRef]
- Sun, L.; Muller, J.-P.; Chen, J. Time Series Analysis of Very Slow Landslides in the Three Gorges Region through Small Baseline SAR Offset Tracking. Remote Sens. 2017, 9, 1314. [Google Scholar] [CrossRef]
- De Zan, F. Coherent Shift Estimation for Stacks of SAR Images. IEEE Geosci. Remote Sens. Lett. 2011, 8, 1095–1099. [Google Scholar] [CrossRef]
- Yonezawa, C.; Takeuchi, S. Decorrelation of SAR data by urban damages caused by the 1995 Hyogoken-nanbu earthquake. Int. J. Remote Sens. 2001, 22, 1585–1600. [Google Scholar] [CrossRef]
- Nitti, D.O.; Hanssen, R.F.; Refice, A.; Bovenga, F.; Nutricato, R. Impact of DEM-Assisted Coregistration on High-Resolution SAR Interferometry. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1127–1143. [Google Scholar] [CrossRef]
- Wempen, J.M.; McCarter, M.K. Comparison of L-band and X-band differential interferometric synthetic aperture radar for mine subsidence monitoring in central Utah. Int. J. Min. Sci. Technol. 2017, 27, 159–163. [Google Scholar] [CrossRef]
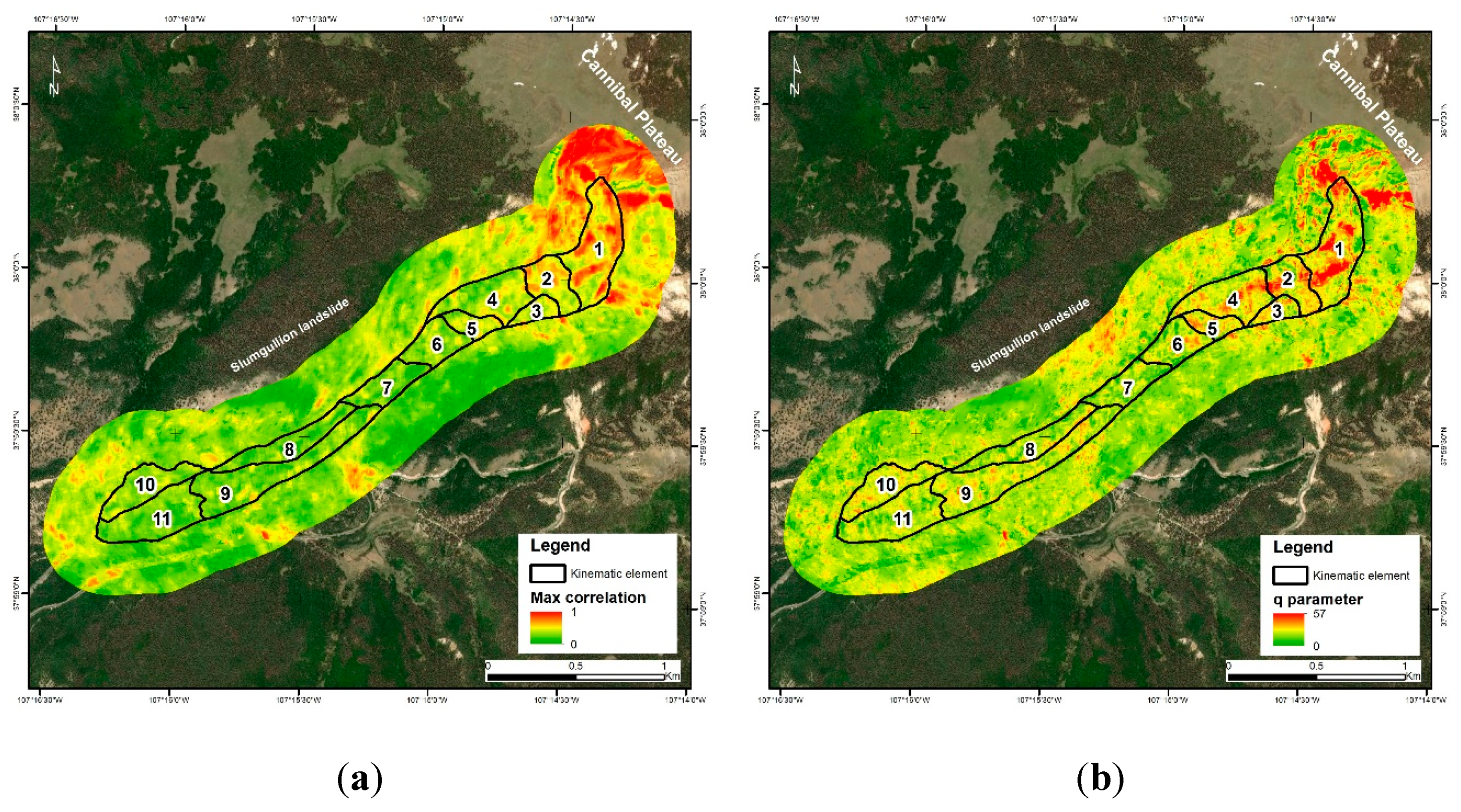
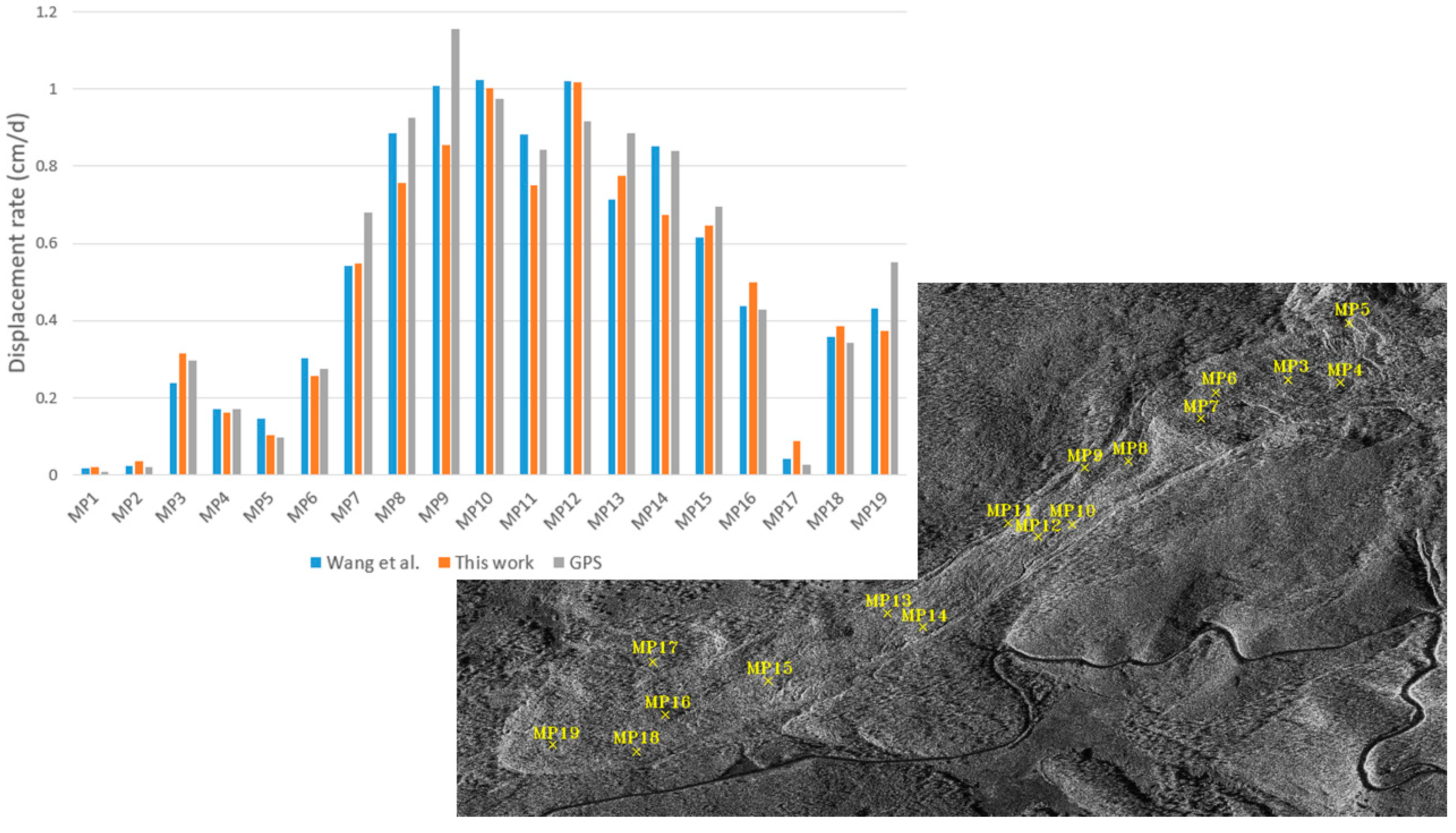
| Run 1 | Run 2 | Run 3 | |
|---|---|---|---|
| Parameter | Value | Value | Value |
| Master image | 2011/08/03 | 2012/08/06 | 2011/08/03 |
| Slave image | 2012/08/06 | 2013/08/08 | 2013/08/08 |
| Time span | 369 d | 367 d | 736 d |
| Pixel spacing azimuth | 0.70 m | 0.70 m | 0.70 m |
| Pixel spacing range | 0.38 m | 0.38 m | 0.38 m |
| x-grid spacing | 10 pixels | 10 pixels | 10 pixels |
| y-grid spacing | 10 pixels | 10 pixels | 10 pixels |
| Oversampling factor | 4 | 4 | 4 |
| Cross-correlation threshold | 0.1 | 0.1 | 0.1 |
| q threshold | 4 | 4 | 4 |
| Max displacement | 8 m | 8 m | 16 m |
| Computational time | ≈ 45 min | ≈ 45 min | ≈ 45 min |
| Region id | <V> 2011–2012 | std(V) 2011–2012 | <V> 2012–2013 | std(V) 2012–2013 | |CC| | std(CC) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| w = 64 | w = 128 | w = 64 | w = 128 | w = 64 | w = 128 | w = 64 | w = 128 | w = 64 | w = 128 | w = 64 | w = 128 | |
| Landslide | 1.03 | 1.03 | 0.79 | 0.80 | 0.81 | 0.86 | 0.72 | 0.73 | 0.01 | 0.02 | 0.42 | 0.42 |
| 1 | 0.11 | 0.06 | 0.09 | 0.07 | 0.13 | 0.14 | 0.08 | 0.06 | 0.07 | 0.04 | 0.14 | 0.10 |
| 2 | 0.26 | 0.24 | 0.13 | 0.11 | 0.16 | 0.19 | 0.09 | 0.09 | 0.00 | 0.00 | 0.15 | 0.09 |
| 3 | 0.33 | 0.31 | 0.13 | 0.16 | 0.24 | 0.27 | 0.10 | 0.10 | 0.03 | 0.01 | 0.19 | 0.17 |
| 4 | 0.54 | 0.56 | 0.18 | 0.34 | 0.38 | 0.45 | 0.16 | 0.15 | 0.08 | 0.03 | 0.19 | 0.13 |
| 5 | 1.11 | 1.11 | 0.29 | 0.25 | 0.91 | 0.98 | 0.29 | 0.34 | 0.12 | 0.07 | 0.23 | 0.28 |
| 6 | 2.00 | 2.05 | 0.49 | 0.43 | 1.80 | 1.89 | 0.42 | 0.37 | 0.09 | 0.24 | 0.63 | 0.74 |
| 7 | 2.40 | 2.44 | 0.67 | 0.58 | 2.14 | 2.25 | 0.55 | 0.44 | 0.07 | 0.05 | 0.89 | 1.04 |
| 8 | 1.56 | 1.54 | 0.47 | 0.46 | 1.24 | 1.29 | 0.45 | 0.42 | 0.05 | 0.05 | 0.50 | 0.54 |
| 9 | 1.63 | 1.64 | 0.47 | 0.47 | 1.34 | 1.39 | 0.59 | 0.51 | 0.09 | 0.05 | 0.52 | 0.36 |
| 10 | 0.58 | 0.54 | 0.23 | 0.19 | 0.36 | 0.30 | 0.16 | 0.10 | 0.09 | 0.06 | 0.30 | 0.15 |
| 11 | 1.00 | 1.01 | 0.17 | 0.11 | 0.52 | 0.59 | 0.18 | 0.14 | 0.05 | 0.00 | 0.26 | 0.15 |
| Region id | <Vf> 1985–1990 | std(Vf) 1985–1990 | <VGB> 2010 | std(VGB) 2010 |
|---|---|---|---|---|
| Landslide | 2.48 | 1.38 | 1.16 | 1.35 |
| 1 | 0.73 | 0.40 | 0.14 | 0.91 |
| 2 | 1.20 | 0.25 | 0.32 | 1.27 |
| 3 | 1.42 | 0.14 | 0.36 | 1.31 |
| 4 | 1.60 | 0.51 | 0.36 | 0.98 |
| 5 | 2.44 | 0.29 | 1.05 | 1.53 |
| 6 | 3.86 | 0.87 | 1.67 | 2.51 |
| 7 | 5.25 | 0.73 | 2.84 | 3.35 |
| 8 | 3.57 | 0.40 | 1.64 | 3.13 |
| 9 | 3.65 | 0.87 | 1.93 | 3.06 |
| 10 | 1.56 | 0.18 | 0.91 | 6.49 |
| 11 | 1.97 | 0.36 | 1.13 | 2.37 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amitrano, D.; Guida, R.; Dell’Aglio, D.; Di Martino, G.; Di Martire, D.; Iodice, A.; Costantini, M.; Malvarosa, F.; Minati, F. Long-Term Satellite Monitoring of the Slumgullion Landslide Using Space-Borne Synthetic Aperture Radar Sub-Pixel Offset Tracking. Remote Sens. 2019, 11, 369. https://doi.org/10.3390/rs11030369
Amitrano D, Guida R, Dell’Aglio D, Di Martino G, Di Martire D, Iodice A, Costantini M, Malvarosa F, Minati F. Long-Term Satellite Monitoring of the Slumgullion Landslide Using Space-Borne Synthetic Aperture Radar Sub-Pixel Offset Tracking. Remote Sensing. 2019; 11(3):369. https://doi.org/10.3390/rs11030369
Chicago/Turabian StyleAmitrano, Donato, Raffaella Guida, Domenico Dell’Aglio, Gerardo Di Martino, Diego Di Martire, Antonio Iodice, Mario Costantini, Fabio Malvarosa, and Federico Minati. 2019. "Long-Term Satellite Monitoring of the Slumgullion Landslide Using Space-Borne Synthetic Aperture Radar Sub-Pixel Offset Tracking" Remote Sensing 11, no. 3: 369. https://doi.org/10.3390/rs11030369
APA StyleAmitrano, D., Guida, R., Dell’Aglio, D., Di Martino, G., Di Martire, D., Iodice, A., Costantini, M., Malvarosa, F., & Minati, F. (2019). Long-Term Satellite Monitoring of the Slumgullion Landslide Using Space-Borne Synthetic Aperture Radar Sub-Pixel Offset Tracking. Remote Sensing, 11(3), 369. https://doi.org/10.3390/rs11030369