Abstract
The convolutional neural network (CNN) has shown great potential in many fields; however, transferring this potential to synthetic aperture radar (SAR) image interpretation is still a challenging task. The coherent imaging mechanism causes the SAR signal to present strong fluctuations, and this randomness property calls for many degrees of freedom (DoFs) for the SAR image description. In this paper, a statistics learning network (SLN) based on the quadratic form is presented. The statistical features are expected to be fitted in the SLN for SAR image representation. (i) Relying on the quadratic form in linear algebra theory, a quadratic primitive is developed to comprehensively learn the elementary statistical features. This primitive is an extension to the convolutional primitive that involves both nonlinear and linear transformations and provides more flexibility in feature extraction. (ii) With the aid of this quadratic primitive, the SLN is proposed for the classification task. In the SLN, different types of statistics of SAR images are automatically extracted for representation. Experimental results on three datasets show that the SLN outperforms a standard CNN and traditional texture-based methods and has potential for SAR image classification.
1. Introduction
Synthetic aperture radar (SAR) has significant research value and very broad application prospects because it can obtain ground information all day and during all weather [1], etc. SAR is widely used in land resources, disaster management, agroforestry, oceans and other fields [2,3,4]. Germany, Canada, Russia, China, and other countries have successfully developed SAR systems, such as TerraSAR-X [5], RADARSAT-2 [6], Sentinel-1 [7], and Gaofen-3 [8], etc. With the increasing abundance of SAR image data and the gradually increasing resolution of SAR images [9], the problem of automatically interpreting SAR images has received extensive attention, especially for classification purposes [10].
1.1. Related Work
Over recent years, many methods have been proposed for SAR image classification. These methods can be broadly categorized as statistical models, textural analysis, and deep networks.
Perhaps the most widely used approach is based on statistical analysis. The idea behind this approach is rooted in the statistical nature of SAR echoes. The coherent imaging mechanism causes SAR to exhibit strong fluctuations in echoes, which are known as speckle [11]. This distinctive characteristic allows a statistical model to be used as an effective tool for SAR image analysis. Numerous statistical models have been presented describing SAR images, e.g., Rayleigh [12], Gamma [13], [14], Log-normal [15], Weibull [16], Fisher [17], etc. These statistical models provide good approximations to the distributions of various types of SAR data; for example, the distribution is appropriate for describing heterogeneous regions [18] and the log-normal distribution shows more potential than Weibull, Gamma and in modeling high-resolution TerraSAR-X images [19]. However, accurately approximating the distributions of various SAR data by relying on a single statistical model is still challenging. To cope with this issue, mixture models, such as finite mixture models (FMM) [20] and Mellin transform-based approaches [21], have been used to improve the generalization capability. Moreover, the new generation of SAR systems with high-resolution images increases the challenge of describing the images with a statistical model. In high-resolution SAR, the number of elementary scatterers inside each resolution cell is reduced, which invalidates the central limit theorem and causes the emergence of heterogeneous regions. Consequently, how to precisely model high-resolution SAR data is still an open issue [22]. The idea of statistical analysis is strongly embraced in this paper, which extracts different types of statistics of SAR data for description.
The textural analysis category is another mainstream approach in SAR image classification. Fundamental works have been presented such as the gray-level co-occurrence matrix (GLCM) [23], Gaussian Markov random fields (GMRF) [24], Gabor filter [25], local binary pattern (LBP) [26], and others. In the context of texture analysis, a series of primitives or so-called textons are first explicitly extracted. These primitives capture the elementary patterns embedded in an image. Then, the histogram of these primitives is formed into a feature vector to represent the image. Finally, this feature vector is fed into a classifier such as a support vector machine (SVM) [27] to perform the classification task. For SAR images, different regions, such as vegetation and high-density residential and low-density residential areas, manifest with discriminative textures. Therefore, texture-based methods can be effectively used to capture the underlying patterns. However, the texture feature is a type of low-level or middle-level representation; therefore, the robustness of texture-based methods require improvement, especially for high-resolution SAR images that contain structural and geometrical information. In this paper, the presented method is a multilayer model that extracts a more abstract textural description, i.e., a high-level feature, for SAR image representation.
Deep networks [28] is the third category for SAR image classification, and significant efforts have been made to gradually shift to this paradigm [29,30,31,32,33]. In addition, the convolutional neural network (CNN) [34] can be interpreted as a multilayer mapping function that maps from the input data to the task-related output. Several studies have explored applying deep learning schemes to SAR image classification: (i) One typical work uses the probability distribution. Concretely, probabilistic graphical models such as the restricted Boltzmann machine (RBM) and the deep belief network (DBN) [35] are used to capture the underlying dependencies between the input and output. For example, Liu et al. presented a Wishart-Bernoulli RBM (WRBM) for polarimetric SAR (PolSAR) image classification [36], and both Wishart and Bernoulli distributions have been used to model the conditional probabilities of visible and hidden units. This idea was also adopted in [37]; in fact, the DBN has been tested on urban regions without considering the prior distribution of PolSAR data [38]. Zhao et al. proposed a generalized Gamma deep belief network (g-DBN) for SAR image statistical modeling and land-cover classification [39]. (ii) Other works have mainly focused on learning effective features for SAR images, where the discriminant function is generally not imposed by a probability distribution. In [40,41], handcrafted features (e.g., HOG, Gabor, GLCM, etc.) are integrated into an autoencoder for feature learning. Zhao et al. presented a discriminant deep belief network (DisDBN) for discriminant as well as high-level feature learning [42]. However, it is often difficult to collect massive amounts of training data. In this case, how to leverage the specific domain knowledge of the SAR mechanism to augment deep model learning is of great importance [43]. (iii) In addition, to make full use of the phase information contained in SAR data, several works have extended real-valued deep models to the complex-valued domain. For example, Ronny presented a complex-valued multilayer perceptron (CV-MLP) for SAR image classification [44], and Zhang et al. proposed a complex-valued CNN (CV-CNN) [45]. Indeed, phases in multiple channels are mutually coherent and thus carry useful information [16]. In this paper, the proposed statistics learning network (SLN) is a typical deep network, and the quadratic primitive used in the SLN is an extension to the convolutional primitive, involving both nonlinear and linear transforms.
1.2. Motivations
The coherent imaging mechanism causes SAR signals to present strong fluctuations. Exploiting this distinctive nature while investigating the potential of CNNs for SAR image interpretation is the motivation of this paper. To establish this goal, the existing challenges are as follows:
- The intrinsic randomness of SAR signal allows statistical models to be an effective tool for SAR image analysis. The parameters of a statistical model capture valuable information for describing the SAR image—for example, the mean and variance of a normal distribution . However, fitting these distribution parameters using CNNs is still a challenge, especially when insufficient training data is available. Consider the variance of as an example. This variable can be estimated bywhere n denotes the number of pixels, and is the i-th pixel value. It should be noted that both the quadratic terms and the cross terms are needed in Equation (1). However, in a typical CNN, both the quadratic and cross terms are discarded.
- The CNN has demonstrated a powerful ability to learn features, but that ability relies primarily on the availability of big data. However, collecting massive amounts of SAR data is difficult in practice. Moreover, the coherent imaging mechanism causes the SAR signals to present strong fluctuations. This distinctive nature calls for many degrees of freedom (DoFs) for SAR image description, which increases the difficulty of applying a CNN to SAR image interpretation.
1.3. Contributions
This paper concentrates on the statistical characteristics of SAR signals and presents a statistics learning network (SLN) based on the quadratic form for SAR image classification. The SLN seeks to automatically extract statistical features for that describe the SAR image. The main contributions of this study are summarized as follows.
- A quadratic primitive is designed to comprehensively learn elementary statistical features. The novel aspects of this primitive lie in an adaptation and extension of the standard convolutional primitive to cope with the SAR image. Concretely, the weighted combination of high-order components, including the quadratic and cross terms, are implemented in this primitive. As shown in Section 3.1, the motivation behind this primitive is derived from the finding that the quadratic and cross terms are often needed for elementary statistical parameter fitting.
- With the aid of the quadratic primitive, the SLN is presented for SAR image classification as depicted in Figure 3. The SLN is a type of deep model that seeks to automatically fit statistical features for SAR image representation.
The remainder of this paper is organized as follows. In Section 2, the statistics of the SAR image and the framework of deep learning are briefly reviewed. The quadratic primitive and SLN are detailed in Section 3. Section 4 presents the experiment and discussion. Finally, conclusions are given in Section 5.
2. Preliminaries
This section briefly reviews the statistical properties of a SAR image and the framework of deep learning.
2.1. SAR Image Statistics
SAR is an active remote sensing technology that radiates electromagnetic waves and receives the backscattered echoes. The signal received by SAR can be interpreted as a coherent sum of many elemental scatterers’ echoes within a resolution cell; thus, it can be expressed as follows:
where N is the number of scatterers, and and denote the amplitude and phase of the i-th backscattered echoes, respectively. Due to the randomness of and , the received signal presents strong pixel-to-pixel fluctuations between adjacent resolution cells, known as speckle [12].
In the fully developed case, the amplitude A follows a Rayleigh distribution, and the intensity has an exponential probability density function [12]. However, these statistical models hold only in modeling single-look SAR data backscattered from homogeneous regions. In many practical cases, many statistical models have been presented to fit the distributions of SAR data. These statistical models can be roughly divided into two categories, i.e., empirical distribution model and a priori hypothesis models, which are summarized in Table 1. For the empirical distribution model, e.g., the log-normal [15], Weibull [16], Fisher [17], etc. distributions are obtained primarily by analyzing SAR data. In contrast, the a priori hypothesis model, is derived from different a priori assumptions and mainly involves distributions such as Rayleigh [12], Gamma [13], [14].

Table 1.
Typical statistical models for SAR image analysis.
Despite the large numbers of statistical models that have been proposed for SAR image analysis, these models are valid only in certain circumstances. For example, the Gamma distribution is effective only when modeling multi-look intensity SAR data within homogeneous regions; however, high-resolution SAR images present both structural and geometrical information, resulting in heterogeneous regions. New statistical models have been presented for high-resolution SAR image, such as the generalized Gamma mixture model (GMM) [20]. However, when the resolution is improved, SAR signals follow heavy-tailed distributions, and modeling these distributions is a challenging task.
2.2. Deep Learning Framework
Deep learning is characterized by its multilayer architecture, in which linear transformation, probability theory and other types of machine learning algorithms are combined. Various types of deep models have appeared in the literature, e.g., CNN [34], DBN [35], and recurrent neural network (RNN) [46], etc. In particular, CNNs have shown great success in image processing, and many popular architectures have been presented, such as AlexNet [47], VGGNet [48], ResNet [49], GoogLeNet [50], and DenseNet [51]. In a typical CNN, an input undergoes a series of transformations, including convolution, activation, etc. Figure 1 shows an example illustrating the convolutional and tanh (tanh is a type of activation function expressed as .) layers. As shown in Figure 1b, the input is rotated, translated, and scaled by the convolutional layer. However, the relative spatial positions of the two curves remain unchanged, and they still cannot be separated by a straight line. The tanh layer performs nonlinear transformation, and the output of this layer can be linearly separated, as illustrated in Figure 1c.
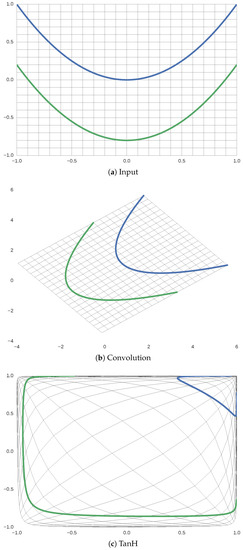
Figure 1.
Behavior of convolution and tanh layers. Here, two curves (a) that the curve above is blue and the curve below is green, cannot be linearly separated, and are fed into a standard CNN; the input undergoes various types of transformations in the convolution and tanh layers. Images (b,c) display the outputs of the convolution and TanH layers, respectively.
A deep model is composed of a recursive application of several elementary layers, e.g., convolution, activation, and pooling layers in CNN. Stacking multiple levels of these elementary layers increases the depth of the deep model, allowing it to approximate complex functionality similar to human visual perception in the brain. A deep model is typically composed of the following modules:
- Information extraction module: This module involves the convolutional primitive [34], autoencoder primitive [52], RBM [53], etc. The convolution primitive is used for linear transformation, the autoencoder is used for data compression, and the RBM is used for probability distribution modeling.
- Activation and pooling module: This module is mainly devoted to nonlinear transformation and dimensionality reduction, which are implemented by activation functions and pooling operations, respectively. Popular activation functions include the sigmoid, tanh and rectified linear unit (ReLU), etc. For the pooling operation, max and average pooling are widely used at present [54].
- Tricks module. Different types of optimization strategies are included in this module to speed up the training procedure and prevent the overfitting. Generally, preprocessing, data augmentation, dropout [55], shakeout [56], and batch-normalization [57] are included in this module.
Deep learning has achieved excellent results in optical image understanding, for example, ResNet-152 [49] shows 3.57% top-5 error on the ImageNet task [58] while SENet [59] shows only 2.30%, which are better than human error for this task at 5%. However, it is still a challenge to effectively apply deep learning for SAR image interpretation. The coherent imaging mechanism causes SAR images to present high fluctuations. This distinctive nature of SAR data is essentially different from optical images. Without considering this difference, the straightforward use of deep models for SAR image understanding cannot reach comparable performance levels to those obtained with optical images. Thus, how to exploit the power of deep learning as well as the mechanism of the SAR image is the starting point of this paper, and will be detailed in the following section.
3. Methodology
In this section, first, the quadratic primitive is presented; then, a comparison between the quadratic and convolutional primitives is provided; and finally, the proposed SLN is detailed.
3.1. Quadratic Primitive
The intrinsic randomness of SAR signals allows a statistical model to be an effective tool for SAR image analysis. A statistical model is generally defined by its parameters, and estimating these parameters is a significant topic in both probability theory and statistics. The method of moments (MoM) is one commonly used estimation approach. The MoM estimates for some typical statistical models are summarized in Table 2, where and denote the first- and second-order moments, respectively, and is the square of . These values are formulated as follows:
where n is the number of pixels, and denotes the i-th pixel value.

Table 2.
Parameter estimates for typical statistical models by MoM.
Table 2 indicates that and are the elementary components needed to fit the parameters of statistical models. The first-order moment, , is the linear weighted sum of and can be realized by a convolution layer in which all kernel weights are set to . In contrast, and cannot be fitted by a typical convolution layer because the quadratic terms and cross terms are needed. Nevertheless, they can be expressed in terms of the quadratic form in linear algebra theory. Generally, a quadratic form can be formulated as
where is a quadratic polynomial, namely, the quadratic form; denotes the coefficients of the quadratic terms , while represents the coefficients of the cross terms . The quadratic form can be used to fit and . Consider , for example, where only the quadratic terms are retained, and the associated coefficients are set to , which is a special case of the quadratic form.
The quadratic form in Equation (6) can be reformulated as the following matrix expression:
where is a weight matrix containing the coefficients for the quadratic and cross terms, , and denotes the transpose operation. Using this strategy, the parameter estimation can be concretely represented in terms of the matrix expression. For example, the variance estimate can be formulated as follows:
As shown in Equation (8), can be estimated by the weighted combination of the quadratic and cross terms, and the associated matrix expression for is
To avoid discarding the first terms , they are combined with the quadratic form by an additive neuron and thereby form the quadratic primitive, which is defined as
where , , , and denote the vectorization operation. In Equation (10), the quadratic primitive is an extension of the convolutional primitive. In the quadratic primitive, the quadratic and cross terms and the first terms are exploited for parameter fitting and are expected to be able to extract the effective features for describing SAR image. Inspired by the convolution primitive, the local connection and weight-sharing strategies are also adopted in the quadratic primitive.
3.2. Comparison between Quadratic and Convolutional Primitives
Inspired by Colah [60], the two curves, shown in Figure 2a, which cannot be linearly separated, are used as an example to compare the behavior of quadratic and convolutional primitives. In Figure 2b, the curves are rotated, scaled, and shifted by the convolutional primitive. However, the curves in Figure 2b are linearly transformed and still cannot be separated by a straight line. For the quadratic primitive, as shown in Figure 2c, the curves undergo nonlinear as well as linear transformations. Apparently, the relative spatial position of the curves in Figure 2c is changed, and the transformed curves can be linearly separated.
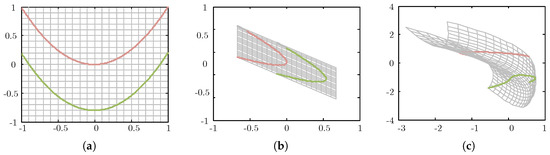
Figure 2.
Behavior of quadratic and convolutional primitives. The two curves in (a) cannot be linearly separated, the curve above is red and the curve below is green. The behaviors of convolutional and quadratic primitives are illustrated in (b,c), respectively. An apparent nonlinear transformation is presented in (c), where the curves can be linearly separated.
3.3. Statistics Learning Network
Figure 3 illustrates the framework of the statistics learning network (SLN) based on the quadratic primitive. An input is first fed into the quadratic module for elementary statistical parameter extraction. Then, further fitting is implemented in the CNN module, where the structural information is considered. Finally, the output is generated by the fully connected and SoftMax layers.
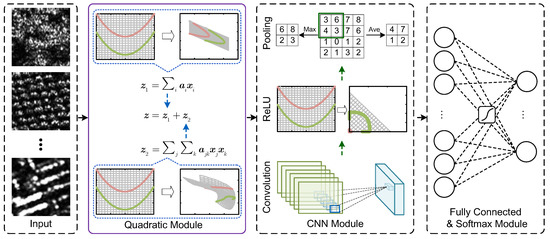
Figure 3.
Framework of statistics learning network based on the quadratic form. First, elementary statistical features are automatically extracted in the quadratic module. Then, further fitting is implemented by the CNN module, followed by the fully connected and SoftMax module.
3.3.1. Forward Pass
As shown in Figure 3, the first step of the SLN is learning the elementary statistics, which consists of two branches, i.e., the quadratic form and the convolutional operation. (i) The quadratic form is the weighted combination of the quadratic and cross terms; the associated output is in Figure 3. (ii) The convolutional operation is the weighted sum of the first terms, and the output is . Finally, and are summed to form z in Figure 3.
The second step of the SLN is implemented by the CNN module. The output of the quadratic module is denoted as which is input into the CNN module for further feature learning. The CNN module is composed of a recursive application of convolution, ReLU activation, and pooling layers. The convolutional layer preserves the spatial information in the input; the ReLU performs nonlinear feature mapping, as shown in Figure 3, and avoids problems with vanishing gradient and exploding gradient and simplifies the calculation process; and the pooling layer reduces the dimensionality of features with translation invariance. Formally, for a CNN with L layers, the forward pass can be expressed as follows:
where represents the output of the l-th layer, is an activation function, and and denote the weight and bias of the l-th layer, respectively.
3.3.2. Optimization
In the context of a classification task, the learning procedure of the SLN can be formulated as an optimization problem. Concretely, given a training set , this optimization problem is mathematically expressed as minimizing the following function:
where is the true label of the training sample , denotes the predicted label, and and are the parameters to be learned in l-th layer of the SLN. represents the cross-entropy [54] loss function, which is given by
where denotes the inner product, is the label vector of generated by the one-hot encoding, and represents the predicted output of the SoftMax layer. In this paper, the gradients of the loss function with respect to the parameter to be updated are estimated by every mini-batch of training samples. Thus, the parameter in the l-th layer is updated using the following strategy:
where represents the gradient of with respect to parameter , K is the number of training samples in a mini-batch, and is the learning rate.
For the quadratic primitive, the gradient of the loss function with respect to the associated parameter is derived as follows. As illustrated in Figure 4, the output of the quadratic primitive is , where , and ; and represent the weight vectors that need to be updated.
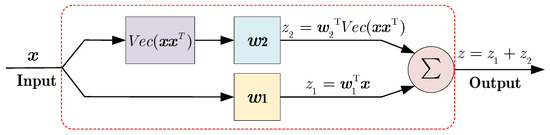
Figure 4.
Quadratic primitive.
Let denote the loss function, the gradient of with respect to is
where , and ; , . Therefore, can be given by
Please note that in Equation (16) can be obtained by the back-propagation algorithm [61]. Using the same strategy described above, the gradient of with respect to is
For the CNN module, fully connected and SoftMax modules of the SLN and the gradients of can be obtained straightforwardly by the back-propagation algorithm [61] with respect to the parameters. Then, the gradient descent algorithm, namely, Equation (14), can be used for optimization.
4. Experiments
In this section, experiments conducted on three data sets are presented, including both space- and airborne data. The performance of the SLN is quantitatively and qualitatively compared with the standard CNN and texture-based approaches, followed by a discussion and an analysis.
4.1. Datasets
The SLN is evaluated on three datasets, including both space- and airborne SAR data as described below.
Guangdong data: The first image, as shown in Figure 5, is multi-look and single polarized (VV channel) data acquired by TerraSAR-X in Guangdong Province, China. The image size is 7518 × 4656 pixels with 1.25 m × 1.25 m of spatial resolution. The dataset includes five classes: i.e., , , , , and .
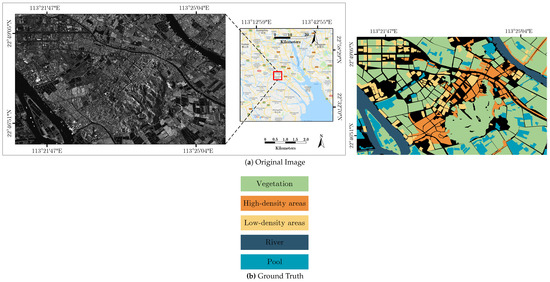
Figure 5.
TerraSAR-X image (VV) of Guangdong, China.
Orchard data: The second is a PolSAR image, as shown in Figure 6. These data were provided by the China Electronics Technology Group Corporation (CETC) 38 Institute [62] and were acquired by an X-band airborne sensor in Hainan Province, China. This image is in the format of a scattering matrix, including the HH, HV, VH, and VV channels; the SPAN image is used for experiments. The spatial resolution is approximately 0.5 m × 0.5 m, and the image size is 2200 × 2400 pixels. Seven classes are considered for the experiment: , , , , , , and .
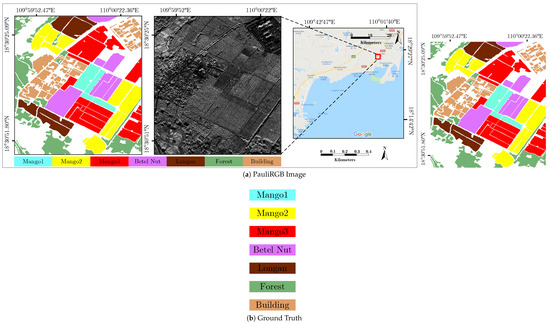
Figure 6.
PauliRGB image and ground truth of Orchard image acquired by fully polarimetric airborne sensor with X-band.
Rice data: The image in Figure 7 also consists of PolSAR data provided by the CETC 38 Institute. It has a pixel resolution of 2048 × 2048 pixels and a spatial resolution of approximately 0.5 m × 0.5 m. This dataset is composed of 7 categories: to and , where to represent rice at different growth stages. The SPAN image is used for the experiments.
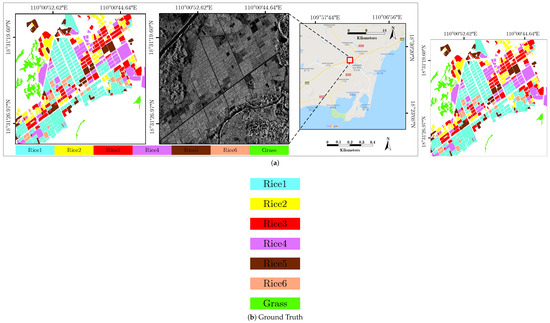
Figure 7.
PauliRGB image and ground truth of Rice data provided by CETC 38 Institute.
For each dataset, the ground truth images are generated by manual annotation according to the associated optical image which can be found in the Google Earth by the information provided in the metadata files. 64 × 64-pixel image patches were randomly collected according to the associated ground truth; the number of collected image patches for each dataset is given in Table 3. The collected image patches were then randomly divided into training, validation, and test sets, accounting for , , and of the total image patches, respectively. The effectiveness of the SLN is evaluated on the test set.

Table 3.
The number of collected image patches and data information in experimental datasets.
4.2. Experimental Setup
To assess the effectiveness of the proposed SLN, it is compared with the standard CNN and traditional texture-based methods, including GLCM, Gabor, and LBP. The architecture of the SLN is presented in Table 4. Here, take the parameter of “conv1”, for example, where “3 × 3, 1” denotes that the kernel size and stride are set to and 1, respectively. The setup for the other compared methods is described below.

Table 4.
SLN experimental architecture.
CNN: The structure of the CNN is similar to the SLN except for the second layer. The second layer in the CNN is a convolution layer, while it is a quadratic module in the SLN. It should be noted that the parameters associated with each layer in the CNN are identical to the ones in the SLN.
GLCM: The number of gray levels is set to 4, and the offsets for the row and column are set to 0 and 2, respectively. Four types of features are considered for GLCM, i.e., contrast, correlation, energy, and inverse different moment, resulting in a 4-D GLCM feature vector.
Gabor: Gabor filters are implemented on three linear scales (2, 3, 4) and eight orientations . The ratio of the mean and variance of each sub-band generates a Gabor feature vector with a dimension of 24.
LBP: The input image is first uniformly divided into subpatches; then, the uniform LBP feature is extracted from these subpatches. A -dimensional LBP feature vector is obtained for image representation.
For the texture-based methods, an SVM [27] is used for classification. The experiments were performed on a desktop PC with dual Intel Xeon E3-1200 v3 processors, a single Nvidia GTX Titan-X GPU, and 32-GB RAM, running Ubuntu 14.04 LTS with the CUDA 8 release.
4.3. Experiment Results
4.3.1. Classification Accuracy
Table 5, Table 6 and Table 7 show the classification accuracies on each class for the Guangdong, Orchard, and Rice datasets, respectively. The uncertainty is included in the study of CNN and SLN.

Table 5.
Classification accuracy (%) on the Guangdong dataset.

Table 6.
Classification accuracy (%) on the Orchard dataset.

Table 7.
Classification accuracy (%) on the Rice dataset.
On the Guangdong dataset, the SLN and CNN outperform the texture-based methods as shown in Table 5. Compared with the CNN, the SLN’s accuracy on the Pool and HD Area classes is improved by 1.60% and 9.20%, respectively. The SLN also slightly improves the average accuracy (AA) and Kappa coefficient. Please note that the CNN performs better at recognizing the LD area class, and it shows a performance comparable to the SLN for River classification.
Table 6 displays the classification accuracies on the Orchard dataset. The results indicate that the SLN performs better than do the CNN and texture-based methods. The AA and Kappa coefficient achieved by the SLN reach 88.28% and 0.86, respectively. Concretely, the SLN shows potential for effectively classifying Mango2, Betel Nut, Longan and Building—especially Longan and Building—for which the classification accuracies are improved by approximately 2.00% and 8.80%, respectively, compared with the CNN. Interestingly, the Gabor performs best at recognizing the Forest class.
The results for the Rice dataset are reported in Table 7. As expected, the SLN achieves the best performance, with an AA and Kappa coefficient of 89.28% and 0.87, respectively. The CNN shows comparable performance to the SLN in classifying Rice2 and Rice6; moreover, the CNN performs best for the Rice4 and Rice5 classes.
4.3.2. Confusion Matrix
To evaluate the discriminative capability of the SLN, the confusion matrix is investigated. Figure 8, Figure 9 and Figure 10 display the results on the Guangdong, Orchard, and Rice datasets. Here, because GLCM and LBP perform better than Gabor, they are selected as candidates for comparison.
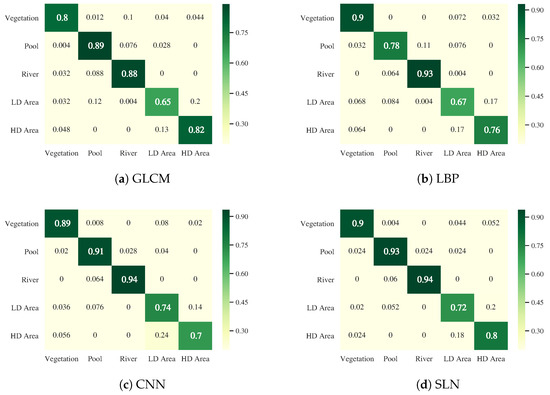
Figure 8.
Confusion matrices for Guangdong dataset.
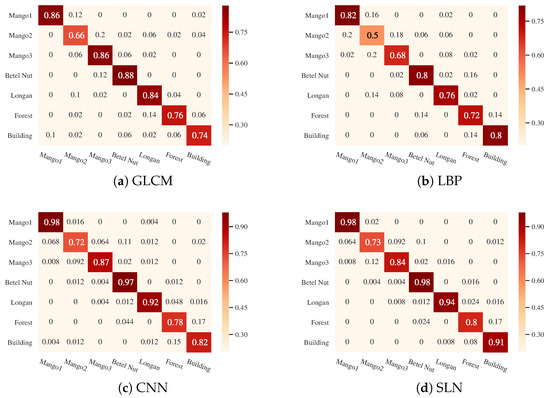
Figure 9.
Confusion matrices for Orchard dataset.

Figure 10.
Confusion matrices for Rice dataset.
Figure 8 shows the results of the Guangdong dataset. (i) The GLCM and LBP have apparent confusions between the HD and LD areas as shown in Figure 8a,b. (ii) The CNN and SLN significantly reduce misclassifications of Vegetation, Pool and River as shown in Figure 8c,d. More specifically, the SLN shows better discriminative capability than the CNN in discriminating between LD and HD areas. In fact, the interclass variations between the HD and LD areas are non-salient due to the similar and complex scattering; therefore, it is difficult to eliminate these confusions.
The confusion matrices for the Orchard dataset are displayed in Figure 9. Three classes: Mango1, Forest and Building, are selected for investigation. (i) For the Mango1 class, Figure 9a,b indicate that GLCM and LBP misclassify Mango1 as Mango2 at a high probability (16.00% and 20.00%, respectively). The CNN and SLN reduce this misclassification rate as shown in Figure 9c,d where the probabilities are 1.60% and 2.00%, respectively. (ii) For the Forest class, the CNN and SLN perform better. The confusions between Forest and Betel Nut by the SLN is 2.40% which is lower than CNN. (iii) For the Building class, the SLN performs best as shown in Figure 9d, and the Building class is misclassified only as Longan or Forest at a low probability (0.80% and 8.00%, respectively).
Figure 10 shows the results of the Rice dataset. Here, Rice1, Rice3 and Rice4 are selected for comparison. (i) For the Rice1 class, LBP’s performance is poor compared with the GLCM and CNN, while the SLN performs better than CNN. As shown in Figure 10d, Rice1 is misclassified only as Rice3 with a probability of 5.00%. (ii) For the Rice3 class, the SLN achieves a better result than the other methods; confusions occur only between Rice1 and Rice4 at probabilities of 5.00% and 7.50%, respectively. (iii) For the Rice4 class which is difficult to precisely recognize, this confusion is reduced by the CNN and SLN and the CNN performs slightly better. However, the SLN’s misclassification accuracy for Rice3 is lower compared to the CNN (17.00% vs. 20.00%). In summary, these results suggest that the SLN is more competitive.
4.3.3. Classification Map
To perform a quantitative comparison, the classification maps shown in Figure 11 and Figure 12 were evaluated. These classification maps were generated with a post-processing method based on conditional random fields [63] for a better visualization.
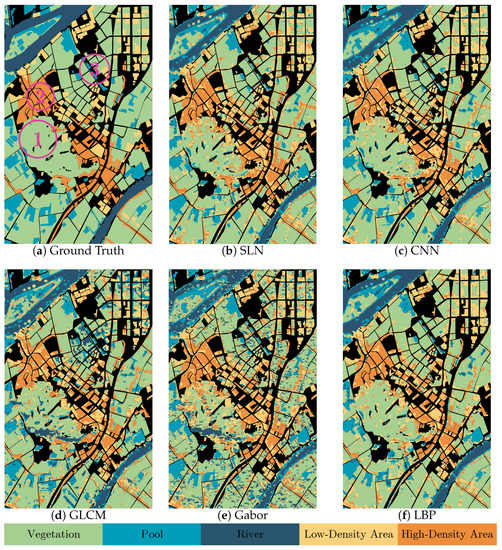
Figure 11.
Classification map overlaid with ground truth for Guangdong dataset. Three highlighted regions shown in (a) are selected for the convenience of comparison.

Figure 12.
Classification map overlaid with ground truth for Orchard dataset. Three regions are selected for the convenience of comparison.
Figure 11 displays the classification maps of the Guangdong dataset, and Figure 11a is the ground truth of this dataset. The three regions shown in Figure 11a were selected for convenience of comparison. Visually, the results by the SLN, CNN, and LBP in Figure 8b–d, respectively, are more consistent with the ground truth Figure 8a. (i) In the selected region 1, GLCM and Gabor show poor performance than the SLN, CNN, and LBP. (ii) In the highlighted regions 2 and 3, the SLN, CNN, and LBP achieve similar results but the GLCM and Gabor results are unsatisfactory. These results indicate that while the SLN works well, it does not achieve a remarkable improvement on this dataset.
The results of the Orchard dataset are shown in Figure 12. (i) In the highlighted region 1, the SLN and CNN provide more satisfactory performance, since they correctly recognize most parts of the Longans. (ii) In the region 2, the SLN and CNN results, as expected, are more consistent with the ground truth Figure 12a, while the texture-based methods misclassify a large portion of Mango3 as Mango2 and Betel Nut. (iii) For the region 3, the SLN and CNN provide almost identical results, and both are better than the GLCM, Gabor, and LBP. In summary, these results suggest that the SLN works best on this dataset, and further reduced the confusions between Mango3 and Betel Nut as compared to the CNN.
4.3.4. Average Accuracy vs. Training Samples
To further evaluate the effectiveness of the SLN, the average accuracies achieved with different training samples percentages are compared. Figure 13 shows the results for the Guangdong and Orchard datasets. (i) In Figure 13a,b, the traditional texture-based methods obtain better performance when the training data comprise less than 20%. This result occurs because of the data-driven natures of the SLN and CNN such that they are unable to learn a large number of parameters effectively with insufficient training data, thus having a dramatic impact on the performance of the SLN and CNN. (ii) As the amount of training data increases, the performance of all the compared methods improve. Moreover, when the percentage of training data exceeds 30%, the SLN and CNN outperform the texture-based methods. (iii) Compared with the CNN, the SLN achieves better performance when the amount of training data lies in the interval . In contrast, when the training data are sufficient (e.g., above 40% in Figure 13a), the SLN and CNN obtain almost the same level of performance.
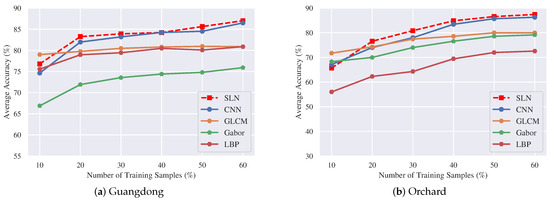
Figure 13.
Average accuracy obtained at different percentages of training data. When the training data comprise less than 20%, the texture-based methods such as GLCM and Gabor achieve better results than do the SLN and CNN. As the amount of training data increase, the SLN and CNN achieve superior performance.
4.4. Analysis and Discussion
The experimental results indicate that the proposed SLN performs better than do the compared methods. An analysis of this improvement is that the SLN exploits more of the information contained in the SAR images. The randomness of the SAR signal calls for many DoFs when creating the SAR image description. In the SLN, the first, quadratic and cross terms are combined with the quadratic primitive to fit the elementary statistical features. The quadratic primitive extends the feature space and provides more flexibility in feature representation. This characteristic of the quadratic primitive is expected to provide potential for feature extraction in SAR images.
As possible future research directions some discussion is provided as follows:
- Given a random vector , its linear transformation is still a random variable, because can be regarded as a statistic that is a function of some observable random variables. This fact implies that the strategy used for elementary statistical feature extraction can be extended to deeper layers of the SLN. Using such an extension is expected to be more effective in SAR image interpretation. However, this approach also increases the number of weights that must be learned. Therefore, a tradeoff should be considered, and the effectiveness of this extension is in need of investigation.
- The SLN is a patchwise approach; thus, when the SLN is used to process large images, it suffers from the same disadvantage as the patch-based methods [64,65]. For semantic labeling or segmentation, post-processing, e.g., smoothness constraints, or other end-to-end methods such as a fully convolutional network [66] should considered in further research.
5. Conclusions
The distinctive nature of SAR signals, such as high fluctuations, poses a large challenge to extending the potential of CNNs to understanding SAR images. In this paper, a statistics learning network(SLN) based on the quadratic form is presented for SAR image classification. The innovation of this approach lies in its capability to fit the statistical features for SAR image representation. By using the quadratic form in linear algebra theory, a quadratic primitive that features learnable capability is proposed for learning the elementary statistical features. The quadratic primitive extends the feature space by exploiting more of the information contained in the input, including the quadratic and cross terms. This primitive is an extension of the convolutional primitive, and it is expected to be an alternative to the convolutional primitive. The experiments conducted on three SAR images indicate that the SLN achieves better performance than do the standard CNN and texture-based methods. The scheme proposed in this paper has room for further improvement, and discussions on a general framework and semantic labeling based on this scheme are presented.
Author Contributions
C.H. and B.H. conceived and designed the experiments; X.L. and C.K. performed the experiments and analyzed the results; B.H. wrote the paper; and M.L. revised the paper.
Funding
This research was funded by the National Key Research and Development Program of China (No. 2016YFC0803000), the National Natural Science Foundation of China (No. 41371342 and No. 61331016), and the Hubei Innovation Group (2018CFA006).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| CNN | Convolutional Neural Network |
| SAR | Synthetic Aperture Radar |
| DoFs | Degrees of Freedom |
| SLN | Statistics Learning Network |
| FMM | Finite Mixture Models |
| GLCM | Gray-Level Co-occurrence Matrix |
| GMRF | Gaussian Markov Random Field |
| LBP | Local Binary Pattern |
| SVM | Support Vector Machine |
| DBN | Deep Belief Network |
| RBM | Restricted Boltzmann Machine |
| WRBM | Wishart-Bernoulli RBM |
| PolSAR | Polarimetric SAR |
| g-DBN | Generalized Gamma Deep Belief Network |
| GMM | Gamma Mixture Model |
| ReLU | Rectified Linear Unit |
| MoM | Method of Moments |
| CETC | China Electronics Technology Group Corporation |
| AA | Average Accuracy |
References
- Moreira, A.; Prats-Iraola, P.; Younis, M.; Krieger, G.; Hajnsek, I.; Papathanassiou, K.P. A tutorial on synthetic aperture radar. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–43. [Google Scholar] [CrossRef]
- Lee, I.K.; Shamsoddini, A.; Li, X.; Trinder, J.C.; Li, Z. Extracting hurricane eye morphology from spaceborne SAR images using morphological analysis. J. Photogramm. Remote Sens. 2016, 117, 115–125. [Google Scholar] [CrossRef]
- Ma, P.; Lin, H.; Lan, H.; Chen, F. Multi-dimensional SAR tomography for monitoring the deformation of newly built concrete buildings. J. Photogramm. Remote Sens. 2015, 106, 118–128. [Google Scholar] [CrossRef]
- Zhang, C.; Sargent, I.; Pan, X.; Li, H.; Gardiner, A.; Hare, J.; Atkinson, P.M. An object-based convolutional neural network (OCNN) for urban land use classification. Remote Sens. Environ. 2018, 216, 57–70. [Google Scholar] [CrossRef]
- Werninghaus, R.; Buckreuss, S. The TerraSAR-X mission and system design. IEEE Trans. Geosci. Remote Sens. 2010, 48, 606–614. [Google Scholar] [CrossRef]
- Seguin, G.; Srivastava, S.; Auger, D. Evolution of the RADARSAT Program. IEEE Geosci. Remote Sens. Mag. 2014, 2, 56–58. [Google Scholar] [CrossRef]
- Aschbacher, J.; Milagro-Pérez, M.P. The European Earth monitoring (GMES) programme: Status and perspectives. Remote Sens. Environ. 2012, 120, 3–8. [Google Scholar] [CrossRef]
- Gu, X.; Tong, X. Overview of China Earth Observation Satellite Programs [Space Agencies]. IEEE Geosci. Remote Sens. Mag. 2015, 3, 113–129. [Google Scholar]
- Mathieu, P.P.; Borgeaud, M.; Desnos, Y.L.; Rast, M.; Brockmann, C.; See, L.; Kapur, R.; Mahecha, M.; Benz, U.; Fritz, S. The ESA’s Earth Observation Open Science Program [Space Agencies]. IEEE Geosci. Remote Sens. Mag. 2017, 5, 86–96. [Google Scholar] [CrossRef]
- Mahdianpari, M.; Salehi, B.; Mohammadimanesh, F.; Motagh, M. Random forest wetland classification using ALOS-2 L-band, RADARSAT-2 C-band, and TerraSAR-X imagery. J. Photogramm. Remote Sens. 2017, 130, 13–31. [Google Scholar] [CrossRef]
- Deledalle, C.A.; Denis, L.; Tabti, S.; Tupin, F. MuLoG, or How to apply Gaussian denoisers to multi-channel SAR speckle reduction? IEEE Trans. Image Process. 2017, 26, 4389–4403. [Google Scholar] [CrossRef]
- Argenti, F.; Lapini, A.; Bianchi, T.; Alparone, L. A tutorial on speckle reduction in synthetic aperture radar images. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–35. [Google Scholar] [CrossRef]
- Li, H.C.; Hong, W.; Wu, Y.R.; Fan, P.Z. On the empirical-statistical modeling of SAR images with generalized gamma distribution. IEEE J. Sel. Top. Signal Process. 2011, 5, 386–397. [Google Scholar]
- Joughin, I.R.; Percival, D.B.; Winebrenner, D.P. Maximum likelihood estimation of K distribution parameters for SAR data. IEEE Trans. Geosci. Remote Sens. 1993, 31, 989–999. [Google Scholar] [CrossRef]
- Keinosuke, F. Introduction to Statistical Pattern Recognition, 2nd ed.; Academica Press: Washington, DC, USA, 1990; pp. 2133–2143. [Google Scholar]
- Oliver, C.; Quegan, S. Understanding Synthetic Aperture Radar Images; SciTech Publishing: Raleigh, NC, USA, 2004. [Google Scholar]
- Bombrun, L.; Beaulieu, J.M. Fisher distribution for texture modeling of polarimetric SAR data. IEEE Geosci. Remote Sens. Lett. 2008, 5, 512–516. [Google Scholar] [CrossRef]
- Gao, G. Statistical modeling of SAR images: A survey. Sensors 2010, 10, 775–795. [Google Scholar] [CrossRef] [PubMed]
- Liu, G.; Jia, H.; Rui, Z.; Zhang, H.; Jia, H.; Bing, Y.; Sang, M. Exploration of Subsidence Estimation by Persistent Scatterer InSAR on Time Series of High Resolution TerraSAR-X Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2011, 4, 159–170. [Google Scholar] [CrossRef]
- Li, H.; Krylov, V.A.; Fan, P.Z.; Zerubia, J.; Emery, W.J. Unsupervised Learning of Generalized Gamma Mixture Model With Application in Statistical Modeling of High-Resolution SAR Images. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2153–2170. [Google Scholar] [CrossRef]
- Nicolas, J.M.; Anfinsen, S.N. Introduction to second kind statistics: Application of log-moments and log-cumulants to the analysis of radar image distributions. Trait. Signal 2002, 19, 139–167. [Google Scholar]
- Deng, X.; López-Martínez, C.; Chen, J.; Han, P. Statistical Modeling of Polarimetric SAR Data: A Survey and Challenges. Remote Sens. 2017, 9, 348. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I. Textural Features for Image Classification. IEEE Trans. Syst. Man Cybern. 1973, 3, 610–621. [Google Scholar] [CrossRef]
- Datcu, M. Wavelet-based despeckling of SAR images using Gauss–Markov random fields. IEEE Trans. Geosci. Remote Sens. 2007, 45, 4127–4143. [Google Scholar]
- Lee, T.S. Image representation using 2D Gabor wavelet. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 18, 959–971. [Google Scholar]
- Ojala, T.; Pietikainen, M.; Maenpaa, T. Multiresolution gray-scale and rotation invariant texture classification with local binary patterns. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 971–987. [Google Scholar] [CrossRef]
- Maulik, U.; Chakraborty, D. Remote Sensing Image Classification: A survey of support-vector-machine-based advanced techniques. IEEE Geosci. Remote Sens. Mag. 2017, 5, 33–52. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Zhu, X.X.; Tuia, D.; Mou, L.; Xia, G.S.; Zhang, L.; Xu, F.; Fraundorfer, F. Deep Learning in Remote Sensing: A Comprehensive Review and List of Resources. IEEE Geosci. Remote Sens. Mag. 2018, 5, 8–36. [Google Scholar] [CrossRef]
- Han, W.; Feng, R.; Wang, L.; Cheng, Y. A semi-supervised generative framework with deep learning features for high-resolution remote sensing image scene classification. J. Photogramm. Remote Sens. 2018, 145, 23–43. [Google Scholar] [CrossRef]
- Paoletti, M.; Haut, J.; Plaza, J.; Plaza, A. A new deep convolutional neural network for fast hyperspectral image classification. J. Photogramm. Remote Sens. 2018, 145, 120–147. [Google Scholar] [CrossRef]
- Anwer, R.M.; Khan, F.S.; van de Weijer, J.; Molinier, M.; Laaksonen, J. Binary patterns encoded convolutional neural networks for texture recognition and remote sensing scene classification. J. Photogramm. Remote Sens. 2018, 138, 74–85. [Google Scholar] [CrossRef]
- Liu, X.; Jiao, L.; Tang, X.; Sun, Q.; Zhang, D. Polarimetric Convolutional Network for PolSAR Image Classification. IEEE Trans. Geosci. Remote Sens. 2018. [Google Scholar] [CrossRef]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Hinton, G.E.; Osindero, S.; Teh, Y.W. A fast learning algorithm for deep belief nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef] [PubMed]
- Liu, F.; Jiao, L.; Hou, B.; Yang, S. POL-SAR image classification based on Wishart DBN and local spatial information. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3292–3308. [Google Scholar] [CrossRef]
- Jiao, L.; Liu, F. Wishart deep stacking network for fast POLSAR image classification. IEEE Trans. Image Process. 2016, 25, 3273–3286. [Google Scholar] [CrossRef] [PubMed]
- Lv, Q.; Dou, Y.; Niu, X.; Xu, J.; Xu, J.; Xia, F. Urban land use and land cover classification using remotely sensed SAR data through deep belief networks. J. Sens. 2015, 2015, 538063. [Google Scholar] [CrossRef]
- Zhao, Z.; Guo, L.; Jia, M.; Wang, L. The Generalized Gamma-DBN for High-Resolution SAR Image Classification. Remote Sens. 2018, 10, 878. [Google Scholar] [CrossRef]
- Geng, J.; Wang, H.; Fan, J.; Ma, X. Deep supervised and contractive neural network for SAR image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2442–2459. [Google Scholar] [CrossRef]
- Geng, J.; Fan, J.; Wang, H.; Ma, X.; Li, B.; Chen, F. High-resolution SAR image classification via deep convolutional autoencoders. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2351–2355. [Google Scholar] [CrossRef]
- Zhao, Z.; Jiao, L.; Zhao, J.; Gu, J.; Zhao, J. Discriminant deep belief network for high-resolution SAR image classification. Pattern Recognit. 2017, 61, 686–701. [Google Scholar] [CrossRef]
- He, C.; Liu, X.; Han, G.; Kang, C.; Chen, Y. Fusion of statistical and learnt features for SAR images classification. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 5490–5493. [Google Scholar]
- Hänsch, R. Complex-Valued Multi-Layer Perceptrons—An Application to Polarimetric SAR Data. Photogramm. Eng. Remote Sens. 2010, 76, 1081–1088. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, H.; Xu, F.; Jin, Y.Q. Complex-valued convolutional neural network and its application in polarimetric SAR image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 7177–7188. [Google Scholar] [CrossRef]
- Graves, A.; Mohamed, A.R.; Hinton, G. Speech Recognition with Deep Recurrent Neural Networks. arXiv, 2013; arXiv:1303.5778. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. In Proceedings of the International Conference on Neural Information Processing Systems, Lake Tahoe, NV, USA, 2–8 December 2012; pp. 1097–1105. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv, 2014; arXiv:1409.1556. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas Valley, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going Deeper with Convolutions. arXiv, 2014; arXiv:1409.4842. [Google Scholar]
- Huang, G.; Liu, Z.; Weinberger, K.Q.; van der Maaten, L. Densely connected convolutional networks. arXiv, 2016; arXiv:1608.06993. [Google Scholar]
- Vincent, P.; Larochelle, H.; Lajoie, I.; Bengio, Y.; Manzagol, P.A. Stacked denoising autoencoders: Learning useful representations in a deep network with a local denoising criterion. J. Mach. Learn. Res. 2010, 11, 3371–3408. [Google Scholar]
- Fischer, A.; Igel, C. Training restricted Boltzmann machines: An introduction. Pattern Recognit. 2014, 47, 25–39. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A.; Bengio, Y. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Hinton, G.E.; Srivastava, N.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R.R. Improving neural networks by preventing co-adaptation of feature detectors. Comput. Sci. 2012, 3, 212–223. [Google Scholar]
- Kang, G.; Li, J.; Tao, D. Shakeout: A New Approach to Regularized Deep Neural Network Training. IEEE Trans. Pattern Anal. Mach. Intell. 2017. [Google Scholar] [CrossRef]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. arXiv, 2015; arXiv:1502.03167. [Google Scholar]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M. ImageNet Large Scale Visual Recognition Challenge. Int. J. Comput. Vis. 2015, 115, 211–252. [Google Scholar] [CrossRef]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 22 2018; pp. 7132–7141. [Google Scholar]
- Olah, C. Neural Networks, Manifolds, and Topology. Available online: https://colah.github.io/posts/2014-03-NN-Manifolds-Topology/ (accessed on 5 August 2018).
- Bottou, L.; Curtis, F.E.; Nocedal, J. Optimization methods for large-scale machine learning. arXiv, 2016; arXiv:1606.04838. [Google Scholar] [CrossRef]
- China Electronics Technology Group Corporation 38 Institute. Available online: http://www.cetc38.com.cn/ (accessed on 21 Augugust 2018).
- Fulkerson, B. Class segmentation and object localization with superpixel neighborhoods. ICCV 2009, 2009, 670–677. [Google Scholar]
- Sherrah, J. Fully Convolutional Networks for Dense Semantic Labelling of High-Resolution Aerial Imagery. arXiv, 2016; arXiv:1606.02585. [Google Scholar]
- Mnih, V. Machine Learning for Aerial Image Labeling. Ph.D. Thesis, University of Toronto, Toronto, ON, Canada, 2013. [Google Scholar]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 640–651. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).