Fast Reproducible Pansharpening Based on Instrument and Acquisition Modeling: AWLP Revisited
Abstract
1. Scenario and Motivations
- the projective model, which is derived from the Gram-Schmidt (GS) orthogonalization procedure, representing the basis of many state-of-the-art pansharpening approaches like the GS spectral sharpening [18], the context-based decision (CBD) [19], and the regression-based injection model [20]. This model can be either global, as for GS, or local [21], as for CBD [19];
- the multiplicative (or contrast-based) model. High-pass modulation (HPM), Brovey transform (BT) [1], smoothing filter-based intensity modulation (SFIM) [22], and the spectral distortion minimizing (SDM) injection model [23] are all based on this injection model. This model is inherently local since the injection gain changes pixel by pixel. Furthermore, it is at the basis of the raw data fusion of physically heterogeneous data, such as MS and synthetic aperture radar (SAR) images [24,25].
2. Instrument and Acquisition Modeling
2.1. Overview of Sensor Model
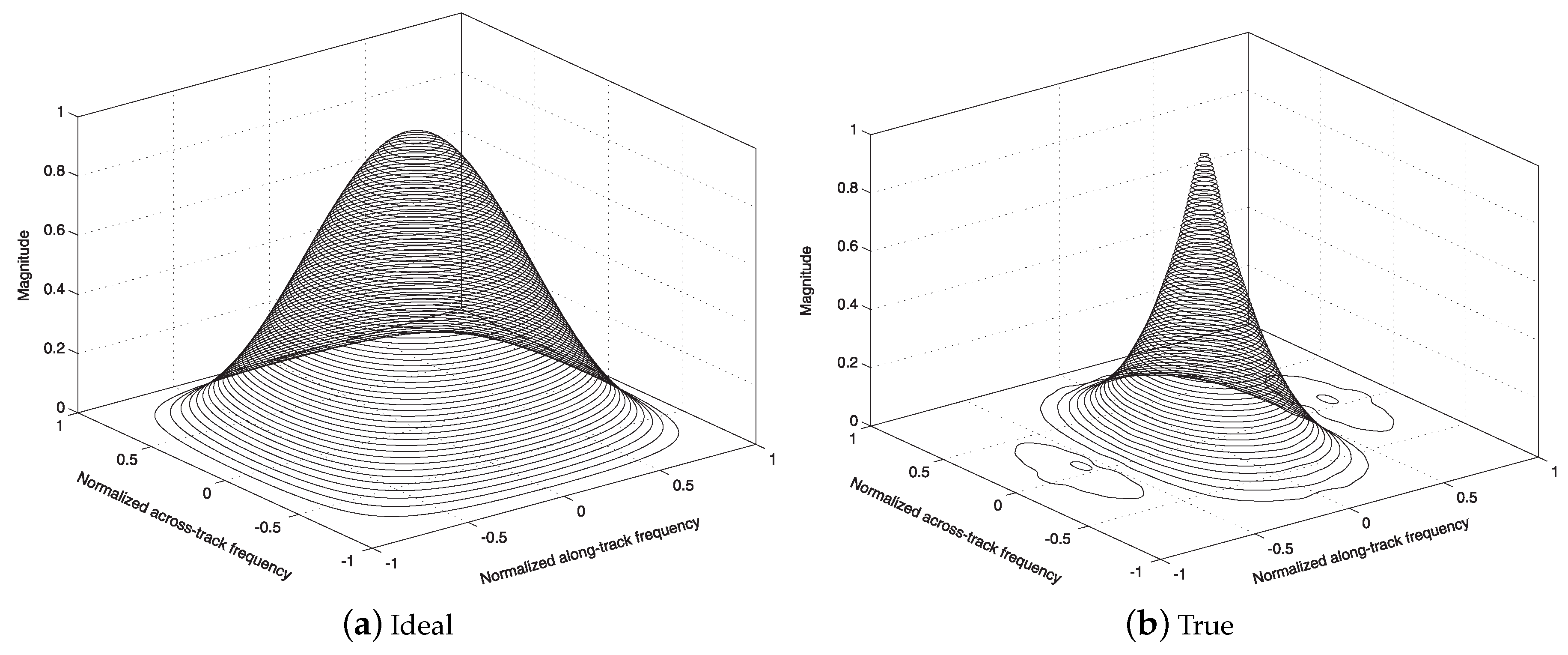
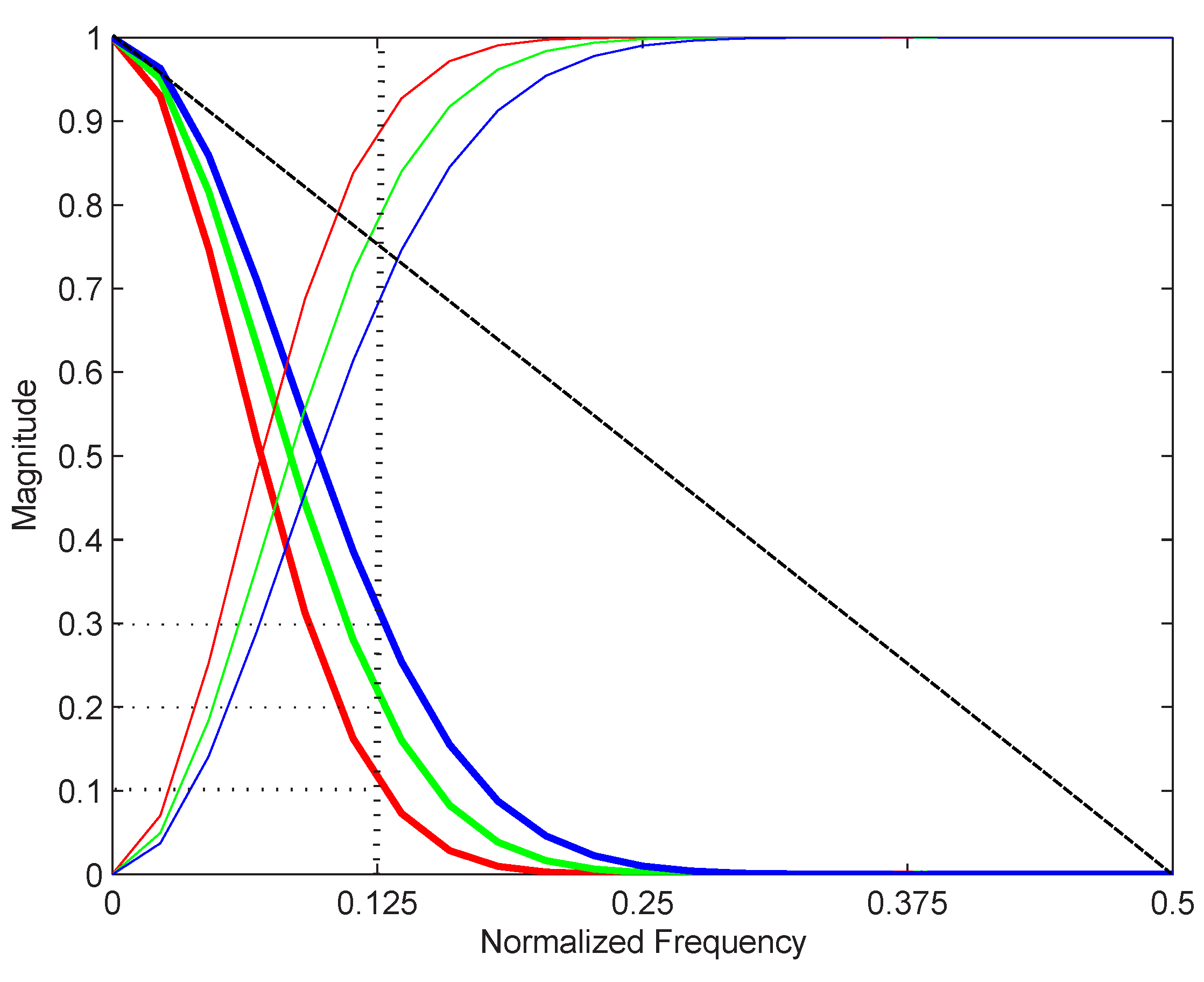
2.1.1. Spatial Response of Instrument
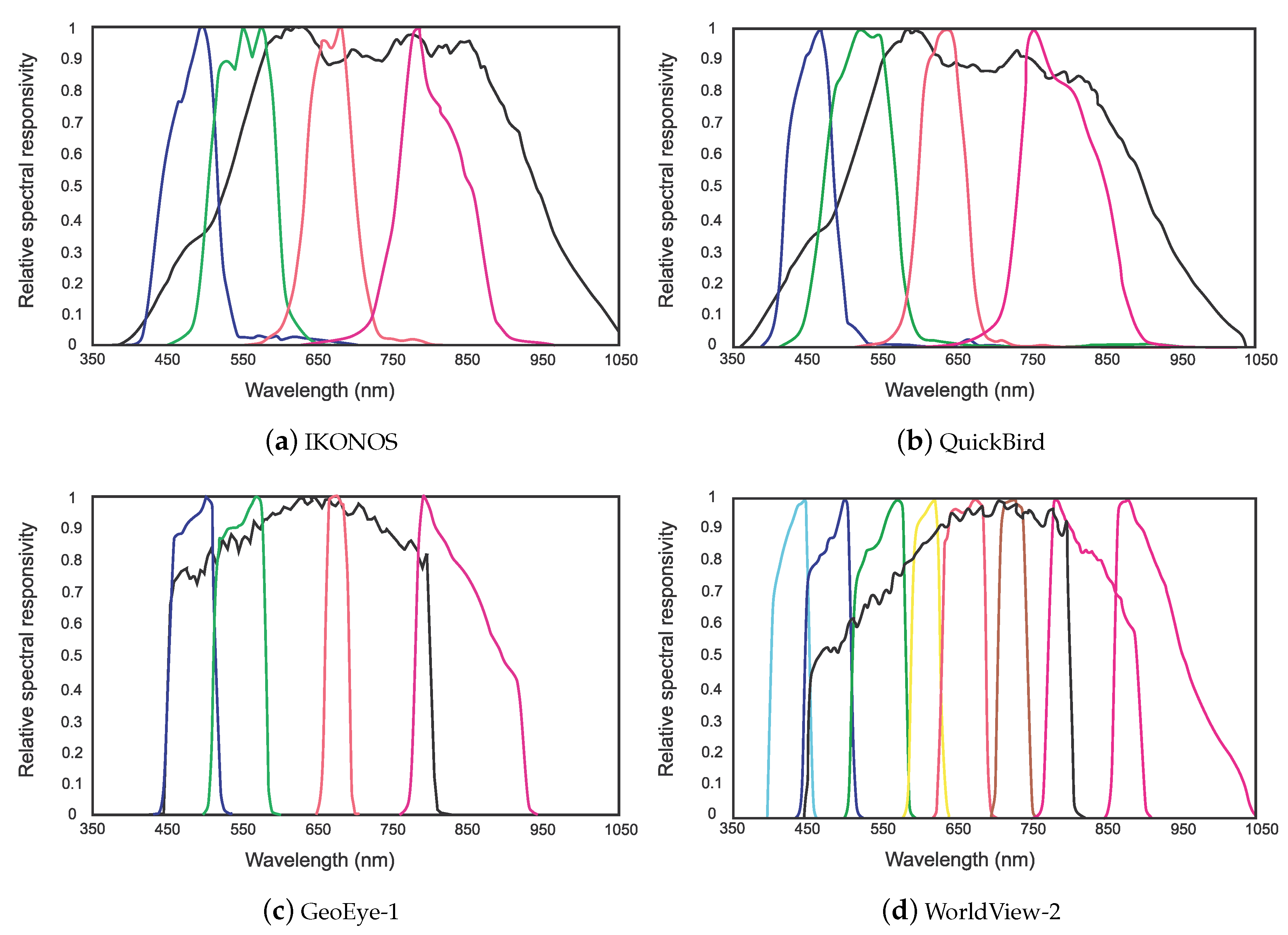
2.1.2. Spectral Response of Instrument
2.2. The Radiative Transfer Model and the Path Radiance
- the scene is small enough to consider the path radiance homogeneous; this assumption reasonably holds for an image of few squared Kilometers under a clear atmosphere, i.e. without precipitation and clouds;
- the scene is large enough to be a statistically consistent sample; in this case, the minimum number of pixels, not the size in squared Kilometers is crucial; in this sense VHR/EHR sensors having small pixels are favored to achieve a finer resolution;
- the scene contains shadowed pixels, in which the direct solar irradiance is masked by some obstacle; this assumption may not hold for ice-covered, desert, and rural regions and high sun elevation;
- the diffuse irradiance at the surface is negligible with respect to the direct solar irradiance; again, this assumption requires that the atmosphere is clear, with little aerosols and/or water vapor [37].
3. A Review of Pansharpening Methods
3.1. Notation
3.2. CS
3.3. MRA
3.4. Hybrid Methods
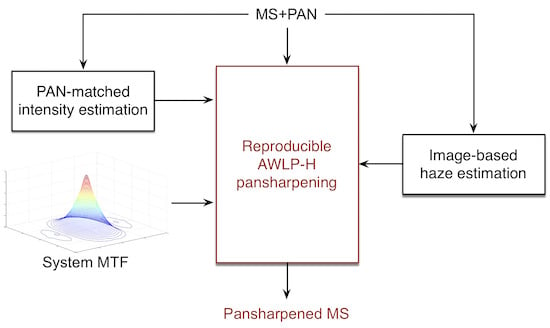
4. AWLP Pansharpening with Haze Correction
5. Assessment Protocols and Indices
6. Experimental Results
6.1. Datasets
- Toulouse dataset: An IKONOS image composed by 512×512 MS pixels and 2048×2048 panchromatic pixels has been acquired over the urban area of Toulouse, France, in June 2000. The MS sensor acquires four spectral bands in the visible and near-infrared (VNIR) spectrum range (i.e., blue, green, red, and near-infrared). The spatial sampling interval (SSI) is 4 m for the MS bands and 1 m for the Pan channel (the scale ratio R is equal to 4). The format of the data is spectral radiance rescaled to digital numbers (DNs) with 11-bits wordlength. A true color representation of the dataset is given in Figure 5l.
- Trento dataset: A QuickBird image composed by 256×256 MS pixels and 1024×1024 Pan pixels has been acquired over the outskirts of Trento, in Italy. The MS sensor acquires four spectral bands in the VNIR spectrum range (i.e., blue, green, red, and near-infrared). The SSI is m for MS and m for the Pan channel (). The data format is spectral radiance rescaled to DNs with 11-bits resolution. A true color representation of the dataset is given in Figure 6l.
- Rio dataset: A WorldView-2 image composed by 512×512 MS pixels and 2048×2048 Pan pixels has been acquired over the urban area of Rio De Janeiro, in Brazil. The MS instrument acquires eight spectral bands in the VNIR spectrum range (i.e., coastal, blue, green, yellow, red, red edge, NIR1 and NIR2). The SSI is 2 m for MS and m for the Pan channel (). The data format is spectral radiance rescaled to 11-bit DNs. A true color representation of the dataset is given in Figure 7l.
6.2. Methods
- EXP: the MS image interpolation using a polynomial kernel with 23 coefficients (EXP) [61];
- MTF-GLP-HPM-H: MRA-based method with MTF filters, GLP analysis, and contrast-based detail injection model with haze correction [29];
- AWLP-H: AWLP-Toolbox with haze correction (see Equation (16)).
6.3. Fusion Simulations
6.4. Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Alparone, L.; Aiazzi, B.; Baronti, S.; Garzelli, A. Remote Sensing Image Fusion; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Vivone, G.; Alparone, L.; Chanussot, J.; Dalla Mura, M.; Garzelli, A.; Licciardi, G.A.; Restaino, R.; Wald, L. A critical comparison among pansharpening algorithms. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2565–2586. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, H.K.; Roy, D.P.; Yan, L.; Huang, H.; Li, J. Landsat 15-m panchromatic-assisted downscaling (LPAD) of the 30-m reflective wavelength bands to Sentinel-2 20-m resolution. Remote Sens. 2017, 9, 755. [Google Scholar]
- Selva, M.; Aiazzi, B.; Butera, F.; Chiarantini, L.; Baronti, S. Hyper-sharpening: A first approach on SIM-GA data. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2015, 8, 3008–3024. [Google Scholar] [CrossRef]
- Selva, M.; Santurri, L.; Baronti, S. Improving hypersharpening for WorldView-3 data. IEEE Geosci. Remote Sens. Lett. 2019, 16, 987–991. [Google Scholar] [CrossRef]
- Yin, H. A joint sparse and low-rank decomposition for pansharpening of multispectral images. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3545–3557. [Google Scholar] [CrossRef]
- Garzelli, A. A review of image fusion algorithms based on the super-resolution paradigm. Remote Sens. 2016, 8, 797. [Google Scholar] [CrossRef]
- Meng, X.; Shen, H.; Li, H.; Zhang, L.; Fu, R. Review of the pansharpening methods for remote sensing images based on the idea of meta-analysis. Inform. Fusion 2019, 46, 102–113. [Google Scholar] [CrossRef]
- Zhu, X.X.; Grohnfeld, C.; Bamler, R. Exploiting joint sparsity for pan-sharpening: The J-sparseFI algorithm. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2664–2681. [Google Scholar] [CrossRef]
- Palsson, F.; Sveinsson, J.R.; Ulfarsson, M.O. A new pansharpening algorithm based on total variation. IEEE Geosci. Remote Sens. Lett. 2014, 11, 318–322. [Google Scholar] [CrossRef]
- Addesso, P.; Longo, M.; Restaino, R.; Vivone, G. Sequential Bayesian methods for resolution enhancement of TIR image sequences. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2015, 8, 233–243. [Google Scholar] [CrossRef]
- Scarpa, G.; Vitale, S.; Cozzolino, D. Target-adaptive CNN-based pansharpening. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5443–5457. [Google Scholar] [CrossRef]
- Chavez, P.S., Jr.; Sides, S.C.; Anderson, J.A. Comparison of three different methods to merge multiresolution and multispectral data: Landsat TM and SPOT panchromatic. Photogramm. Eng. Remote Sens. 1991, 57, 295–303. [Google Scholar]
- Alparone, L.; Aiazzi, B.; Baronti, S.; Garzelli, A. Spatial methods for multispectral pansharpening: Multiresolution analysis demystified. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2563–2576. [Google Scholar] [CrossRef]
- Alparone, L.; Garzelli, A.; Vivone, G. Intersensor statistical matching for pansharpening: Theoretical issues and practical solutions. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4682–4695. [Google Scholar] [CrossRef]
- Xie, B.; Zhang, H.K.; Huang, B. Revealing implicit assumptions of the component substitution pansharpening methods. Remote Sens. 2017, 9, 443. [Google Scholar] [CrossRef]
- Vivone, G.; Restaino, R.; Chanussot, J. A regression-based high-pass modulation pansharpening approach. IEEE Trans. Geosci. Remote Sens. 2018, 56, 984–996. [Google Scholar] [CrossRef]
- Aiazzi, B.; Baronti, S.; Selva, M. Improving component substitution pansharpening through multivariate regression of MS+Pan data. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3230–3239. [Google Scholar] [CrossRef]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Garzelli, A.; Selva, M. MTF-tailored multiscale fusion of high-resolution MS and Pan imagery. Photogramm. Eng. Remote Sens. 2006, 72, 591–596. [Google Scholar] [CrossRef]
- Vivone, G.; Restaino, R.; Chanussot, J. Full scale regression-based injection coefficients for panchromatic sharpening. IEEE Trans. Image Process. 2018, 27, 3418–3431. [Google Scholar] [CrossRef]
- Aiazzi, B.; Baronti, S.; Lotti, F.; Selva, M. A comparison between global and context-adaptive pansharpening of multispectral images. IEEE Geosci. Remote Sens. Lett. 2009, 6, 302–306. [Google Scholar] [CrossRef]
- Liu, J.G. Smoothing filter based intensity modulation: A spectral preserve image fusion technique for improving spatial details. Int. J. Remote Sens. 2000, 21, 3461–3472. [Google Scholar] [CrossRef]
- Alparone, L.; Aiazzi, B.; Baronti, S.; Garzelli, A. Sharpening of very high resolution images with spectral distortion minimization. Proc. IEEE Int. Geosci. Remote Sens. Symp. 2003, 1, 458–460. [Google Scholar]
- Garzelli, A. Wavelet-based fusion of optical and SAR image data over urban area. ISPRS Arch. 2002, 34, 59–62. [Google Scholar]
- Alparone, L.; Facheris, L.; Baronti, S.; Garzelli, A.; Nencini, F. Fusion of multispectral and SAR images by intensity modulation. In Proceedings of the 7th International Conference on Information Fusion, Stockholm, Sweden, 28 June–1 July 2004; Volume 2, pp. 637–643. [Google Scholar]
- Pacifici, F.; Longbotham, N.; Emery, W.J. The importance of physical quantities for the analysis of multitemporal and multiangular optical very high spatial resolution images. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6241–6256. [Google Scholar] [CrossRef]
- Schowengerdt, R.A. Remote Sensing: Models and Methods for Image Processing, 2nd ed.; Academic Press: Orlando, FL, USA, 1997. [Google Scholar]
- Li, H.; Jing, L. Improvement of a pansharpening method taking into account haze. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2017, 10, 5039–5055. [Google Scholar] [CrossRef]
- Lolli, S.; Alparone, L.; Garzelli, A.; Vivone, G. Haze correction for contrast-based multispectral pansharpening. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2255–2259. [Google Scholar] [CrossRef]
- Garzelli, A.; Aiazzi, B.; Alparone, L.; Lolli, S.; Vivone, G. Multispectral pansharpening with radiative transfer-based detail-injection modeling for preserving changes in vegetation cover. Remote Sens. 2018, 10, 1308. [Google Scholar] [CrossRef]
- Otazu, X.; González-Audícana, M.; Fors, O.; Núñez, J. Introduction of sensor spectral response into image fusion methods. Application to wavelet-based methods. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2376–2385. [Google Scholar] [CrossRef]
- Vivone, G.; Alparone, L.; Chanussot, J.; Dalla Mura, M.; Garzelli, A.; Licciardi, G.A.; Restaino, R.; Wald, L. A critical comparison of pansharpening algorithms. In Proceedings of the 2014 IEEE Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014; pp. 191–194. [Google Scholar]
- Coppo, P.; Chiarantini, L.; Alparone, L. End-to-end image simulator for optical imaging systems: Equations and simulation examples. Adv. Opt. Technol. 2013, 2013. [Google Scholar] [CrossRef]
- Thomas, C.; Ranchin, T.; Wald, L.; Chanussot, J. Synthesis of multispectral images to high spatial resolution: A critical review of fusion methods based on remote sensing physics. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1301–1312. [Google Scholar] [CrossRef]
- Chavez, P.S., Jr. An improved dark-object subtraction technique for atmospheric scattering correction of multispectral data. Remote Sens. Environ. 1988, 24, 459–479. [Google Scholar] [CrossRef]
- Chavez, P.S., Jr. Image-based atmospheric corrections–Revisited and improved. Photogramm. Eng. Remote Sens. 1996, 62, 1025–1036. [Google Scholar]
- Lolli, S.; Di Girolamo, P.; Demoz, B.; Li, X.; Welton, E. Rain evaporation rate estimates from dual-wavelength lidar measurements and intercomparison against a model analytical solution. J. Atmos. Ocean. Technol. 2017, 34, 829–839. [Google Scholar] [CrossRef]
- Alparone, L.; Selva, M.; Aiazzi, B.; Baronti, S.; Butera, F.; Chiarantini, L. Signal-dependent noise modelling and estimation of new-generation imaging spectrometers. In Proceedings of the 2009 First Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing, Grenoble, France, 26–28 August 2009. [Google Scholar]
- Lolli, S.; Delaval, A.; Loth, C.; Garnier, A.; Flamant, P. 0.355-micrometer direct detection wind lidar under testing during a field campaign in consideration of ESA’s ADM-Aeolus mission. Atmos. Meas. Tech. 2013, 6, 3349–3358. [Google Scholar] [CrossRef]
- Campbell, J.; Ge, C.; Wang, J.; Welton, E.; Bucholtz, A.; Hyer, E.; Reid, E.; Chew, B.; Liew, S.C.; Salinas, S.; et al. Applying advanced ground-based remote sensing in the Southeast Asian maritime continent to characterize regional proficiencies in smoke transport modeling. J. Appl. Meteorol. Climatol. 2016, 55, 3–22. [Google Scholar] [CrossRef]
- Lolli, S.; Campbell, J.; Lewis, J.; Gu, Y.; Marquis, J.; Chew, B.; Liew, S.C.; Salinas, S.; Welton, E. Daytime top-of-the-atmosphere cirrus cloud radiative forcing properties at Singapore. J. Appl. Meteorol. Climatol. 2017, 56, 1249–1257. [Google Scholar] [CrossRef]
- Lolli, S.; Madonna, F.; Rosoldi, M.; Campbell, J.R.; Welton, E.J.; Lewis, J.R.; Gu, Y.; Pappalardo, G. Impact of varying lidar measurement and data processing techniques in evaluating cirrus cloud and aerosol direct radiative effects. Atmos. Meas. Tech. 2018, 11, 1639–1651. [Google Scholar] [CrossRef]
- Fu, Q.; Liou, K.N. On the correlated k-distribution method for radiative transfer in nonhomogeneous atmospheres. J. Atmos. Sci. 1992, 49, 2139–2156. [Google Scholar] [CrossRef]
- Aiazzi, B.; Alparone, L.; Garzelli, A.; Santurri, L. Blind correction of local misalignments between multispectral and panchromatic images. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1625–1629. [Google Scholar] [CrossRef]
- Baronti, S.; Aiazzi, B.; Selva, M.; Garzelli, A.; Alparone, L. A theoretical analysis of the effects of aliasing and misregistration on pansharpened imagery. IEEE J. Sel. Top. Signal Process. 2011, 5, 446–453. [Google Scholar] [CrossRef]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Carlà, R.; Garzelli, A.; Santurri, L. Sensitivity of pansharpening methods to temporal and instrumental changes between multispectral and panchromatic data sets. IEEE Trans. Geosci. Remote Sens. 2017, 55, 308–319. [Google Scholar] [CrossRef]
- Shah, V.P.; Younan, N.H.; King, R.L. An efficient pan-sharpening method via a combined adaptive-PCA approach and contourlets. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1323–1335. [Google Scholar] [CrossRef]
- Licciardi, G.A.; Khan, M.M.; Chanussot, J. Fusion of hyperspectral and panchromatic images: A hybrid use of indusion and nonlinear PCA. In Proceedings of the 2012 19th IEEE International Conference on Image Processing, Orlando, FL, USA, 30 September–3 October 2012; pp. 2133–2136. [Google Scholar]
- Wald, L.; Ranchin, T.; Mangolini, M. Fusion of satellite images of different spatial resolutions: Assessing the quality of resulting images. Photogramm. Eng. Remote Sens. 1997, 63, 691–699. [Google Scholar]
- Alparone, L.; Baronti, S.; Garzelli, A.; Nencini, F. A global quality measurement of pan-sharpened multispectral imagery. IEEE Geosci. Remote Sens. Lett. 2004, 1, 313–317. [Google Scholar] [CrossRef]
- Garzelli, A.; Nencini, F. Hypercomplex quality assessment of multi-/hyper-spectral images. IEEE Geosci. Remote Sens. Lett. 2009, 6, 662–665. [Google Scholar] [CrossRef]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Carlà, R. Assessment of pyramid-based multisensor image data fusion. In Image and Signal Processing for Remote Sensing IV; Serpico, S.B., Ed.; International Society for Optics and Photonics: Barcelona, Spain, 1998; pp. 237–248. [Google Scholar]
- Aiazzi, B.; Alparone, L.; Argenti, F.; Baronti, S. Wavelet and pyramid techniques for multisensor data fusion: A performance comparison varying with scale ratios. In Image and Signal Processing for Remote Sensing V; Serpico, S.B., Ed.; International Society for Optics and Photonics: Florence, Italy, 1999; pp. 251–262. [Google Scholar]
- Du, Q.; Younan, N.H.; King, R.L.; Shah, V.P. On the performance evaluation of pan-sharpening techniques. IEEE Geosci. Remote Sens. Lett. 2007, 4, 518–522. [Google Scholar] [CrossRef]
- Carlà, R.; Santurri, L.; Aiazzi, B.; Baronti, S. Full-scale assessment of pansharpening through polynomial fitting of multiscale measurements. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6344–6355. [Google Scholar] [CrossRef]
- Vivone, G.; Restaino, R.; Chanussot, J. A Bayesian procedure for full resolution quality assessment of pansharpened products. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4820–4834. [Google Scholar] [CrossRef]
- Selva, M.; Santurri, L.; Baronti, S. On the use of the expanded image in quality assessment of pansharpened images. IEEE Geosci. Remote Sens. Lett. 2018, 15, 320–324. [Google Scholar] [CrossRef]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Carlà, R.; Garzelli, A.; Santurri, L. Full scale assessment of pansharpening methods and data products. In Image and Signal Processing for Remote Sensing XX; Bruzzone, L., Ed.; International Society for Optics and Photonics: Amsterdam, The Netherlands, 2014; p. 924402. [Google Scholar]
- Alparone, L.; Aiazzi, B.; Baronti, S.; Garzelli, A.; Nencini, F.; Selva, M. Multispectral and panchromatic data fusion assessment without reference. Photogramm. Eng. Remote Sens. 2008, 74, 193–200. [Google Scholar] [CrossRef]
- Khan, M.M.; Alparone, L.; Chanussot, J. Pansharpening quality assessment using the modulation transfer functions of instruments. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3880–3891. [Google Scholar] [CrossRef]
- Aiazzi, B.; Baronti, S.; Selva, M.; Alparone, L. Bi-cubic interpolation for shift-free pan-sharpening. ISPRS J. Photogramm. Remote Sens. 2013, 86, 65–76. [Google Scholar] [CrossRef]
- Laben, C.A.; Brower, B.V. Process for Enhancing the Spatial Resolution of Multispectral Imagery Using Pan-Sharpening, 2000. U.S. Patent #6,011,875, 4 January 2000. [Google Scholar]
- Garzelli, A.; Nencini, F.; Capobianco, L. Optimal MMSE Pan sharpening of very high resolution multispectral images. IEEE Trans. Geosci. Remote Sens. 2008, 46, 228–236. [Google Scholar] [CrossRef]
- Kwan, C.; Choi, J.; Chan, S.; Zhou, J.; Budavari, B. A super-resolution and fusion approach to enhancing hyperspectral images. Remote Sens. 2018, 10, 1416. [Google Scholar] [CrossRef]
- Alparone, L.; Selva, M.; Capobianco, L.; Moretti, S.; Chiarantini, L.; Butera, F. Quality assessment of data products from a new generation airborne imaging spectrometer. Proc. IGARSS 2009, IV, IV422–IV425. [Google Scholar]






| SAM | ERGAS | Q4 | |
|---|---|---|---|
| EXP | 4.8403 | 5.8793 | 0.5185 |
| GS | 4.2603 | 4.1908 | 0.8082 |
| GSA | 3.0211 | 2.5860 | 0.9324 |
| BDSD | 2.7998 | 2.4674 | 0.9307 |
| MTF-GLP-CBD | 3.0159 | 2.5660 | 0.9332 |
| AWLP-Otazu | 4.8403 | 3.2624 | 0.8970 |
| AWLP-Toolbox | 3.6653 | 2.8281 | 0.9320 |
| OBT-H | 2.7713 | 2.4578 | 0.9350 |
| MTF-GLP-HPM-H | 2.7428 | 2.3884 | 0.9380 |
| AWLP-H | 2.7556 | 2.4330 | 0.9360 |
| GT | 0 | 0 | 1 |
| SAM | ERGAS | Q4 | |
|---|---|---|---|
| EXP | 4.3152 | 4.6769 | 0.7600 |
| GS | 5.2356 | 4.1871 | 0.7994 |
| GSA | 4.6799 | 3.3997 | 0.8573 |
| BDSD | 4.3415 | 3.1802 | 0.8742 |
| MTF-GLP-CBD | 4.4858 | 3.1825 | 0.8690 |
| AWLP-Otazu | 4.3152 | 3.2195 | 0.8562 |
| AWLP-Toolbox | 3.9893 | 3.0819 | 0.8800 |
| OBT-H | 3.3547 | 2.8671 | 0.9086 |
| MTF-GLP-HPM-H | 3.3207 | 2.7351 | 0.9147 |
| AWLP-H | 3.3030 | 2.7162 | 0.9148 |
| GT | 0 | 0 | 1 |
| SAM | ERGAS | Q8 | |
|---|---|---|---|
| EXP | 5.0695 | 6.3837 | 0.7245 |
| GS | 5.0822 | 4.1997 | 0.8607 |
| GSA | 4.3747 | 3.3158 | 0.9153 |
| BDSD | 4.8990 | 3.6592 | 0.8974 |
| MTF-GLP-CBD | 4.3274 | 3.2779 | 0.9198 |
| AWLP-Otazu | 5.0695 | 3.4988 | 0.9059 |
| AWLP-Toolbox | 4.6716 | 3.5206 | 0.9154 |
| OBT-H | 4.0205 | 3.1933 | 0.9215 |
| MTF-GLP-HPM-H | 3.9895 | 3.1504 | 0.9241 |
| AWLP-H | 4.0022 | 3.1602 | 0.9243 |
| GT | 0 | 0 | 1 |
| Q | Q | Q | Q | Q | |
|---|---|---|---|---|---|
| EXP | 0.7883 | 0.7810 | 0.7906 | 0.7454 | 0.7764 |
| GS | 0.7836 | 0.8382 | 0.8235 | 0.8469 | 0.8231 |
| GSA | 0.8138 | 0.8652 | 0.8542 | 0.9077 | 0.8602 |
| BDSD | 0.8492 | 0.8864 | 0.8745 | 0.9211 | 0.8828 |
| MTF-GLP-CBD | 0.8296 | 0.8785 | 0.8649 | 0.9154 | 0.8721 |
| AWLP-Otazu | 0.7544 | 0.8832 | 0.9141 | 0.9334 | 0.8713 |
| AWLP-Toolbox | 0.8422 | 0.8654 | 0.9112 | 0.9318 | 0.8877 |
| OBT-H | 0.8982 | 0.9249 | 0.9184 | 0.9268 | 0.9171 |
| MTF-GLP-HPM-H | 0.9032 | 0.9305 | 0.9238 | 0.9352 | 0.9232 |
| AWLP-H | 0.9039 | 0.9308 | 0.9238 | 0.9349 | 0.9233 |
| GT | 1 | 1 | 1 | 1 | 1 |
| Method | Time [s] | Increment with Respect to GS |
|---|---|---|
| GS | 0.04 | 0% |
| GSA | 0.10 | 150% |
| BDSD | 0.11 | 175% |
| MTF-GLP-CBD | 0.09 | 125% |
| OBT-H | 0.04 | 0% |
| MTF-GLP-HPM-H | 0.18 | 350% |
| AWLP-Otazu | 0.23 | 475% |
| AWLP-Toolbox | 0.26 | 550% |
| AWLP-H | 0.11 | 175% |
| HQNR | |||
|---|---|---|---|
| EXP | 0.0316 | 0.1963 | 0.7783 |
| GS | 0.0638 | 0.0908 | 0.8512 |
| GSA | 0.0321 | 0.1113 | 0.8601 |
| BDSD | 0.0401 | 0.0584 | 0.9039 |
| MTF-GLP-CBD | 0.0134 | 0.0955 | 0.8924 |
| AWLP-Otazu | 0.0224 | 0.0943 | 0.8854 |
| AWLP-Toolbox | 0.0227 | 0.0898 | 0.8896 |
| OBT-H | 0.0323 | 0.0895 | 0.8811 |
| MTF-GLP-HPM-H | 0.0154 | 0.0750 | 0.9107 |
| AWLP-H | 0.0145 | 0.0744 | 0.9122 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vivone, G.; Alparone, L.; Garzelli, A.; Lolli, S. Fast Reproducible Pansharpening Based on Instrument and Acquisition Modeling: AWLP Revisited. Remote Sens. 2019, 11, 2315. https://doi.org/10.3390/rs11192315
Vivone G, Alparone L, Garzelli A, Lolli S. Fast Reproducible Pansharpening Based on Instrument and Acquisition Modeling: AWLP Revisited. Remote Sensing. 2019; 11(19):2315. https://doi.org/10.3390/rs11192315
Chicago/Turabian StyleVivone, Gemine, Luciano Alparone, Andrea Garzelli, and Simone Lolli. 2019. "Fast Reproducible Pansharpening Based on Instrument and Acquisition Modeling: AWLP Revisited" Remote Sensing 11, no. 19: 2315. https://doi.org/10.3390/rs11192315
APA StyleVivone, G., Alparone, L., Garzelli, A., & Lolli, S. (2019). Fast Reproducible Pansharpening Based on Instrument and Acquisition Modeling: AWLP Revisited. Remote Sensing, 11(19), 2315. https://doi.org/10.3390/rs11192315