2D Image-To-3D Model: Knowledge-Based 3D Building Reconstruction (3DBR) Using Single Aerial Images and Convolutional Neural Networks (CNNs)
Abstract
1. Introduction
- It proposes a novel procedure to extract latent and inherent information from a single 2D image contributing to understanding and interpreting the 3D scenes;
- An optimized multi-scale convolutional–deconvolutional network (MSCDN) is designed for height prediction as well as extraction of the linear elements of roofs from single aerial images;
- The building detection, building boundary extraction, and segmentation of roofs can be performed simultaneously using one network, trained by a manually generated training dataset;
- In the proposed framework, the prismatic and parametric models of the individual buildings are reconstructed from a single aerial image without the need for any additional data;
- A training dataset (https://github.com/loosgagnet/Roofline-Extraction) including linear elements of different roofs is created manually, which can be used for different applications such as 3D city modeling and CAD models.
2. Materials and Methods
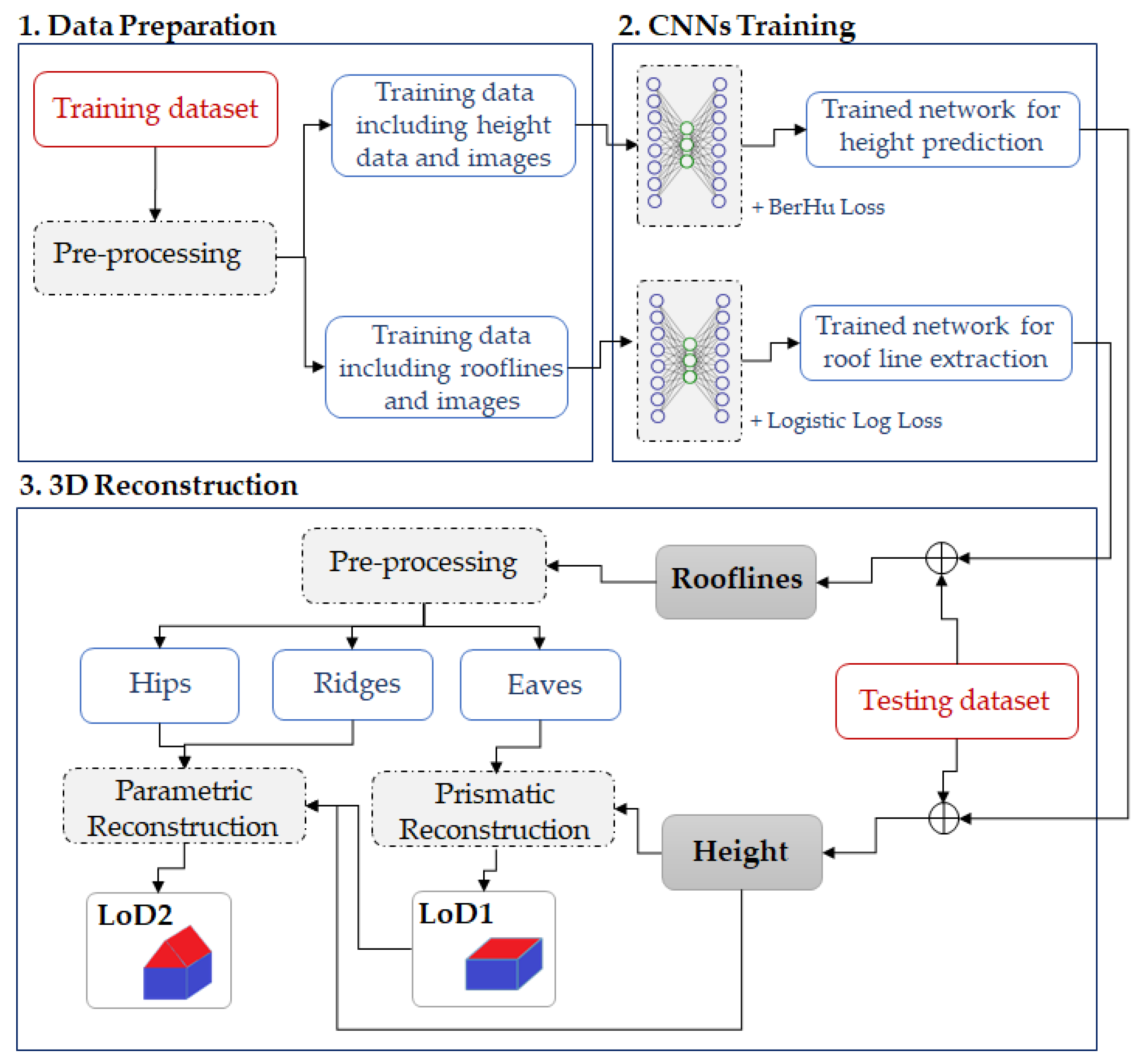
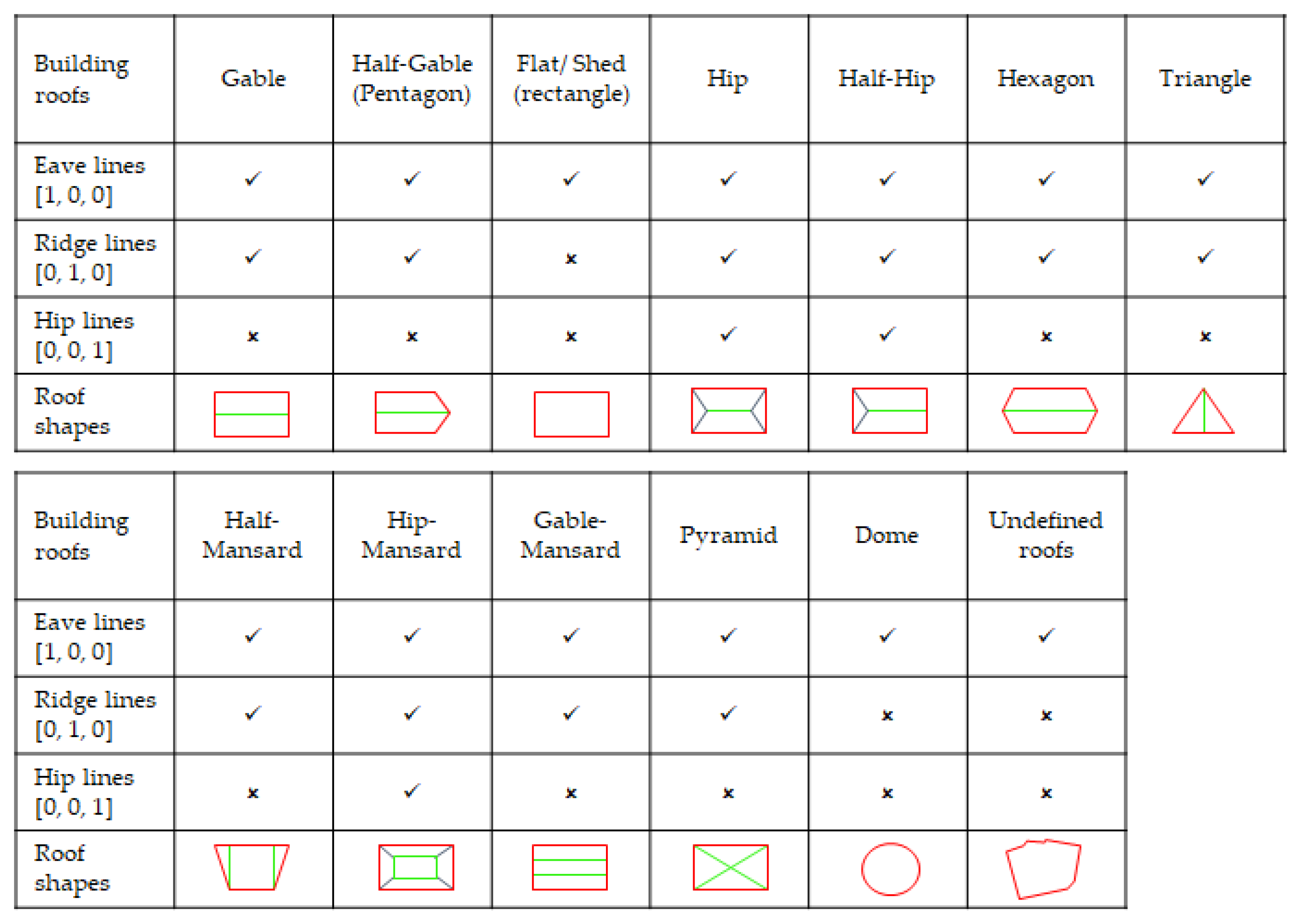
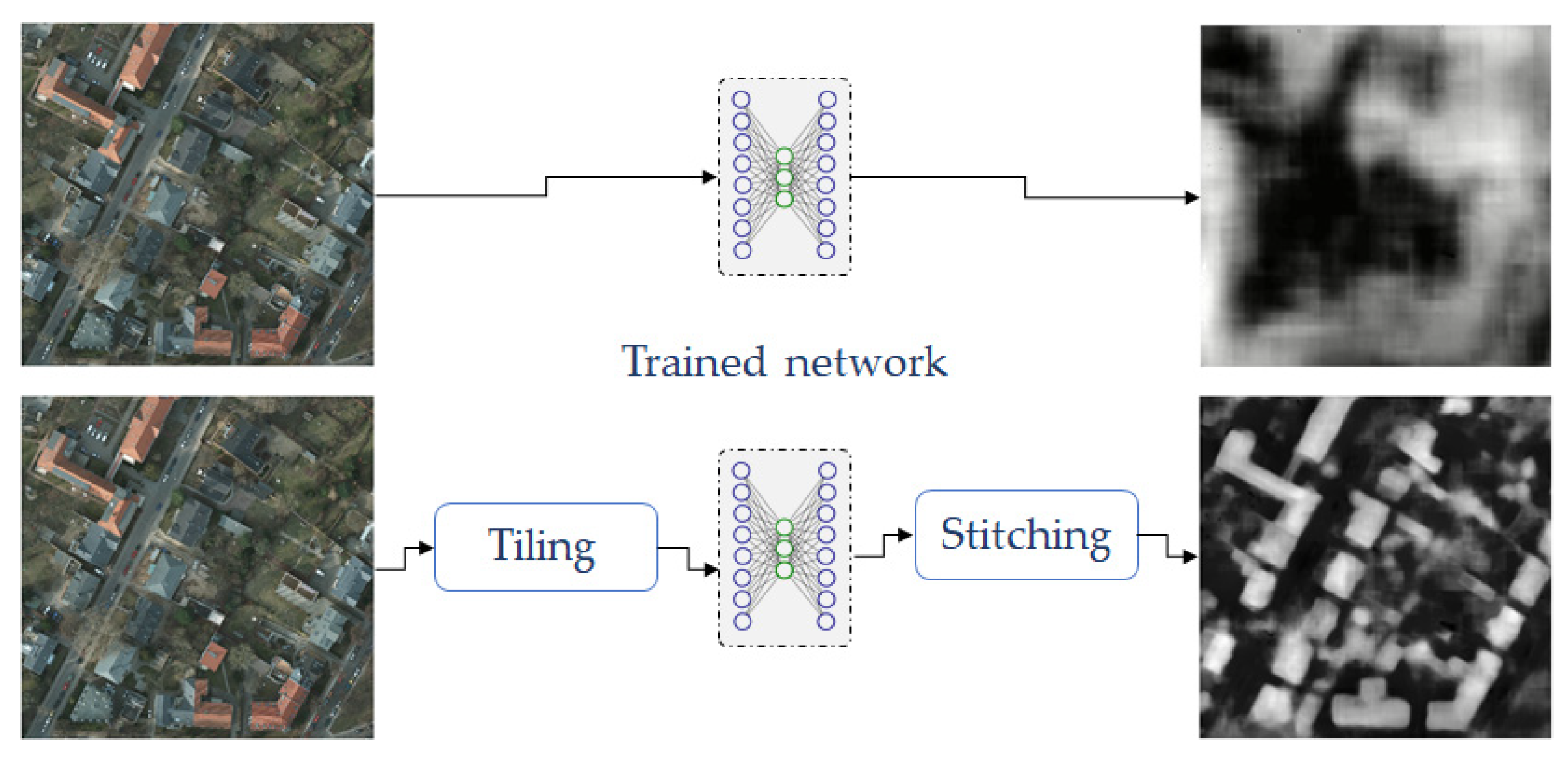
2.1. Data Preparation
- Scale: all image tiles are randomly scaled by s ∈ [1, 1.5];
- Rotation: all image tiles are randomly rotated by r ∈ [−5, 5] degrees;
- Color: ortho-photo tiles are multiplied globally by a random RGB value c ∈ [0.8, 1.2];
- Flips: all image tiles are horizontally and vertically flipped with a probability of 0.5.
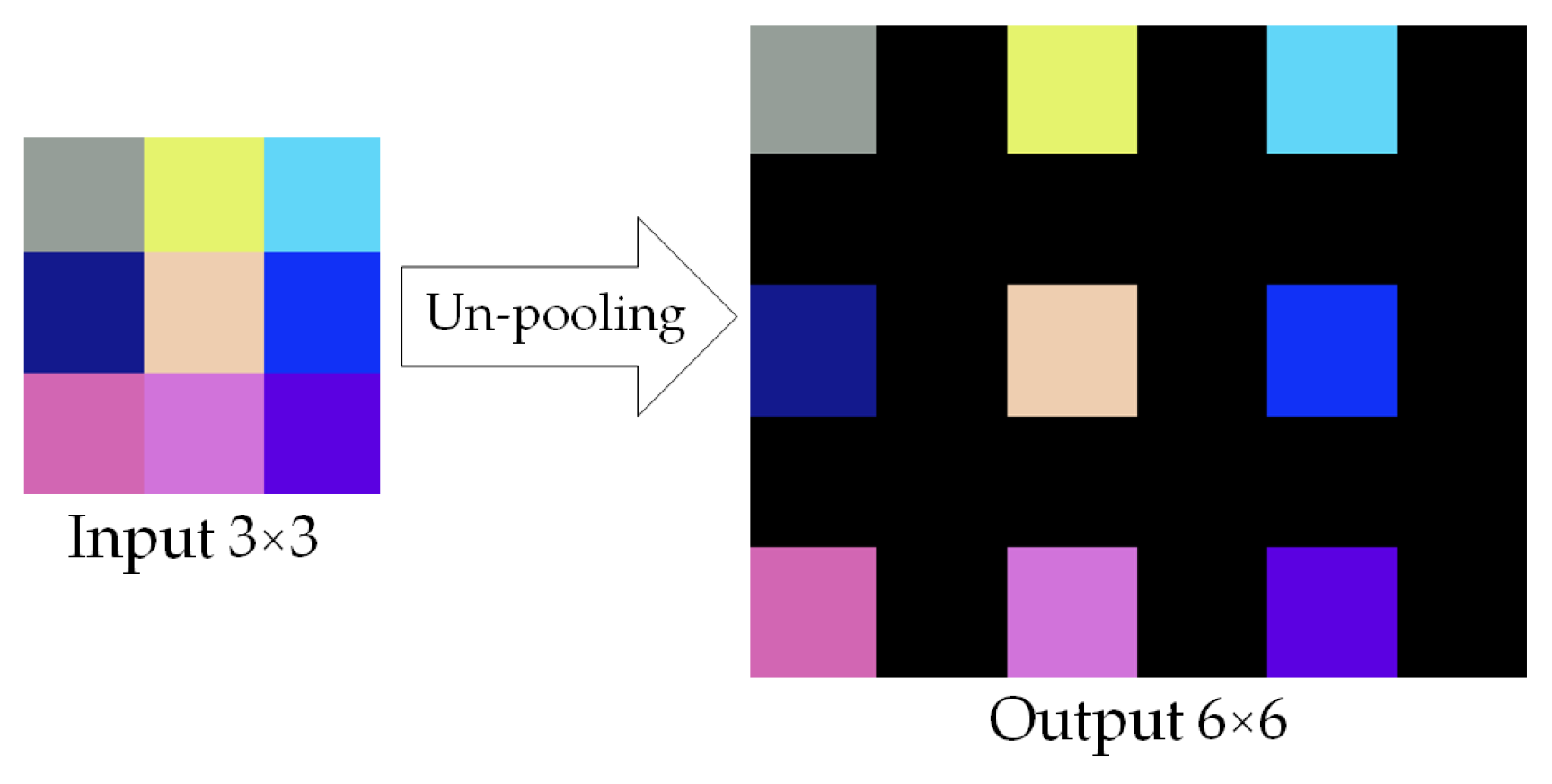
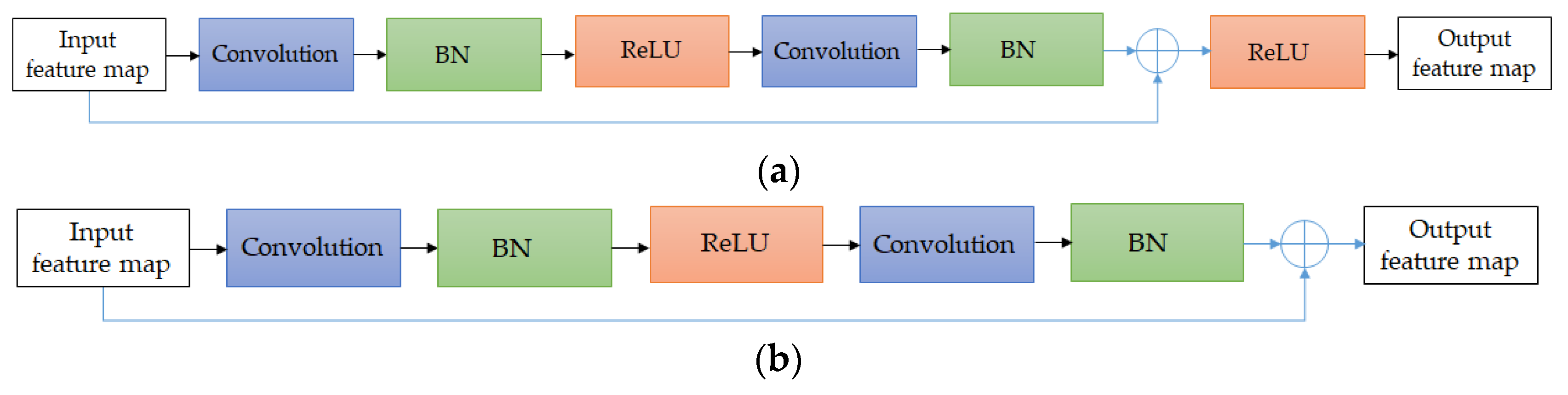
2.2. CNNs Training
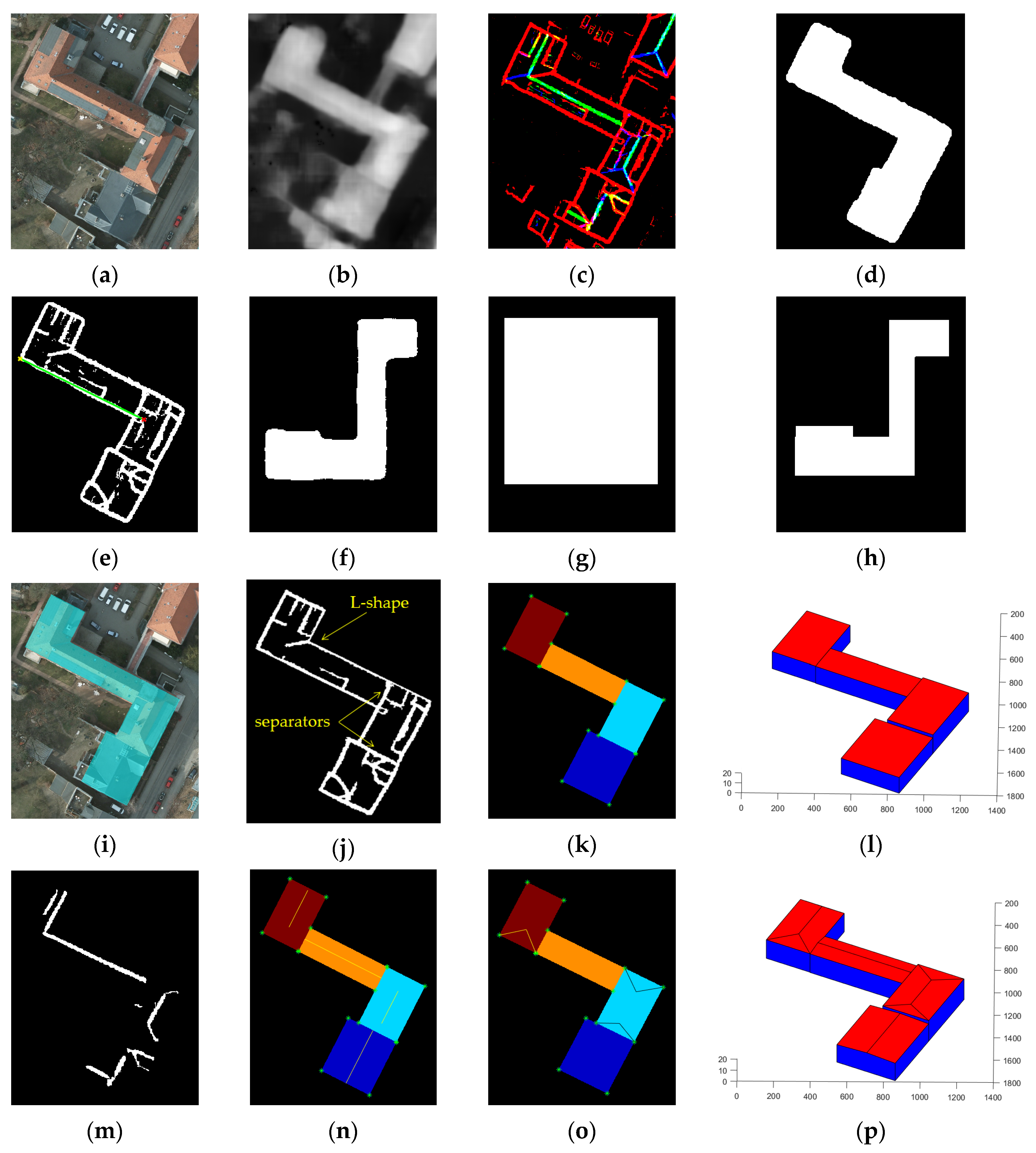
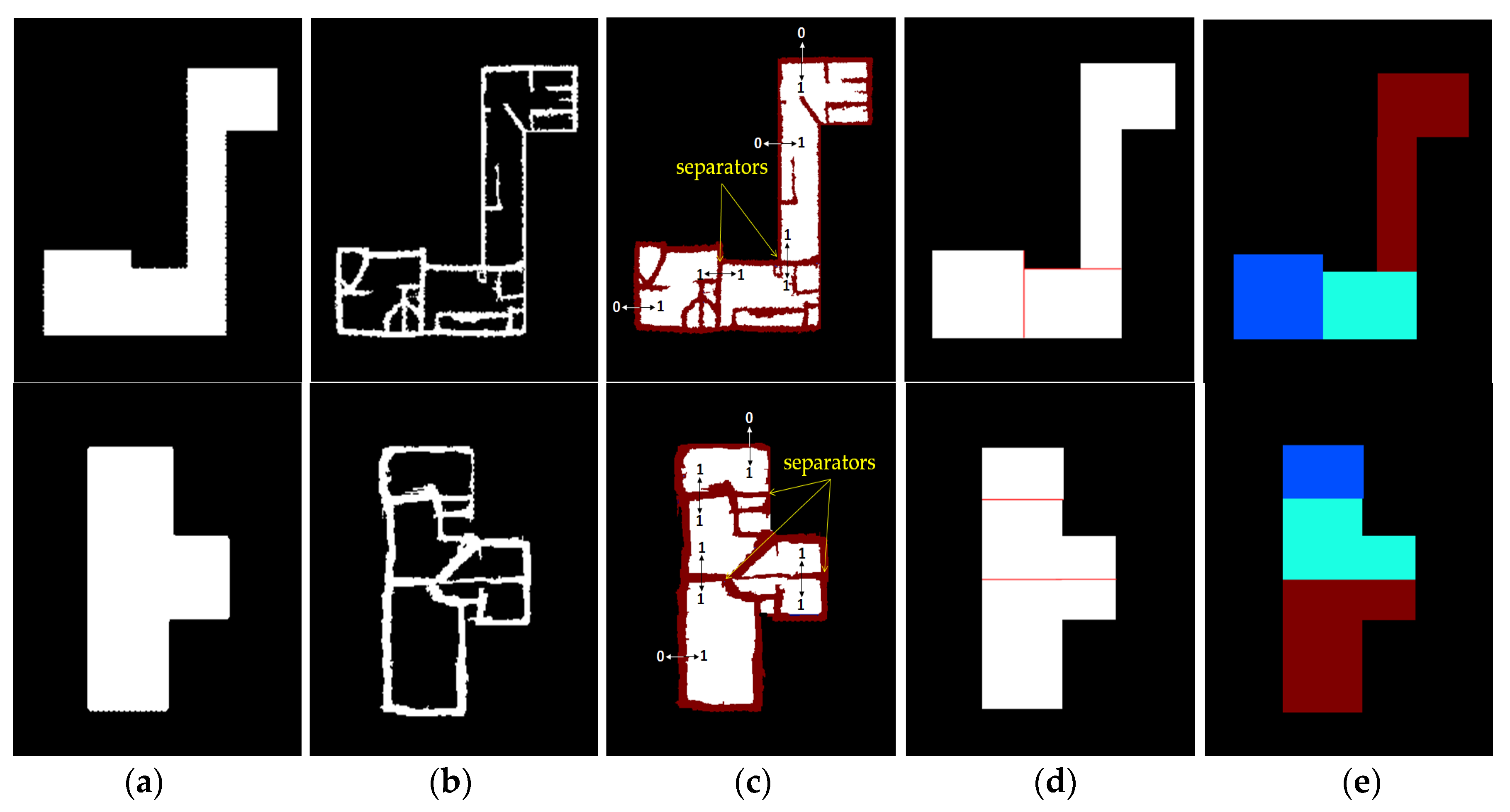
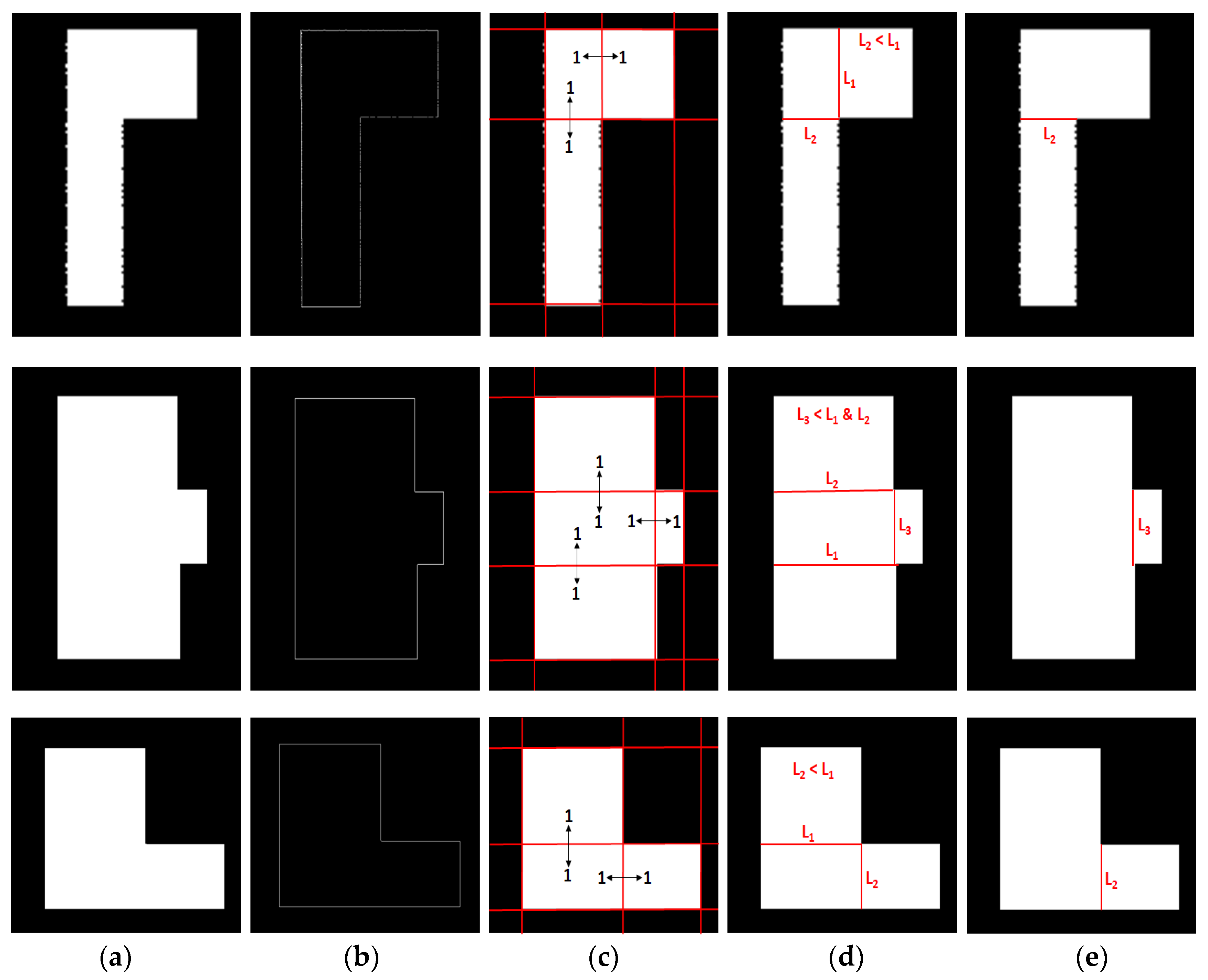
2.3. 3D Reconstruction
3. Results
4. Discussion
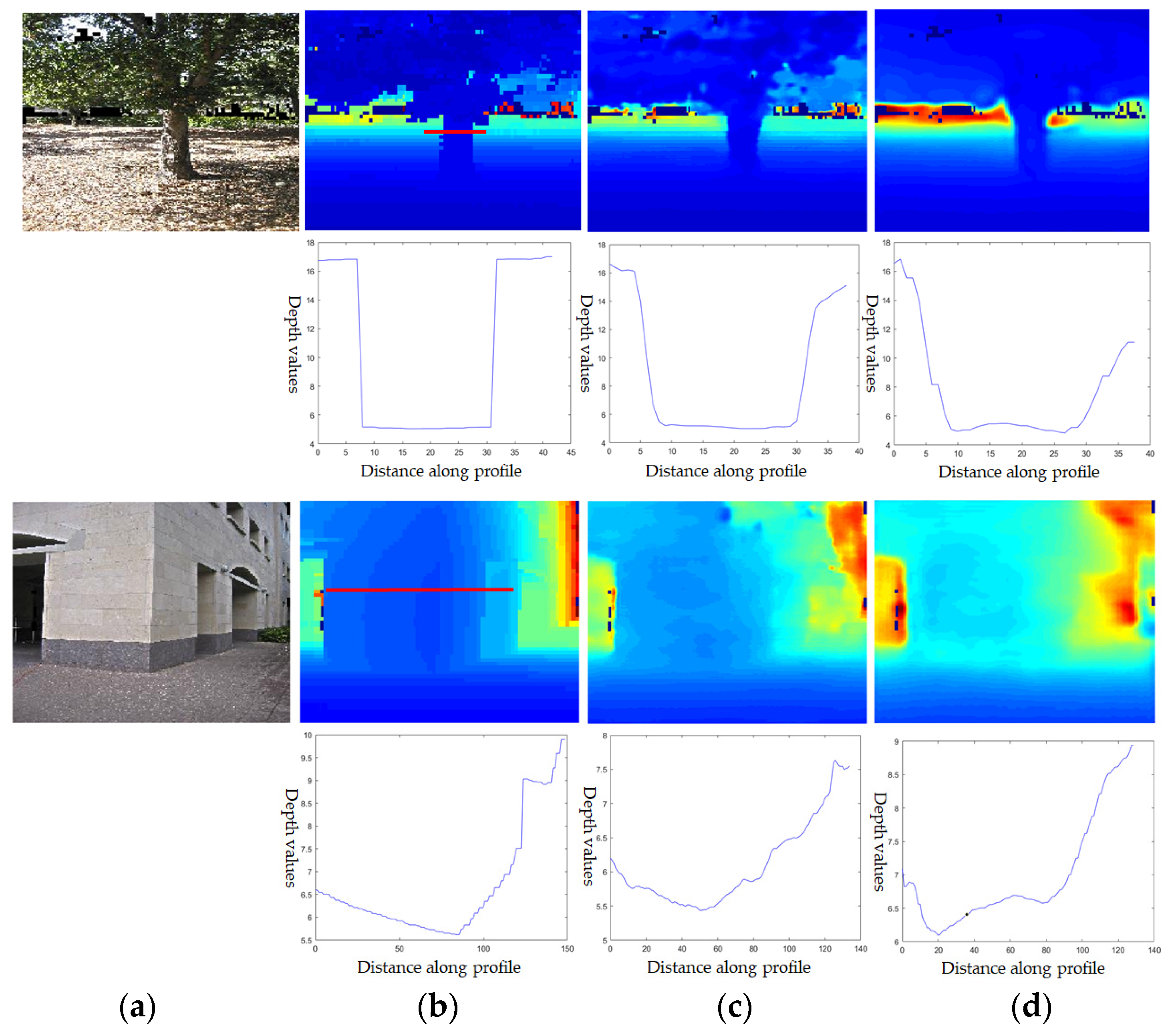
4.1. Quality Assessment of Depth Prediction
4.2. Quality Assessment of Roof Line Segmentation
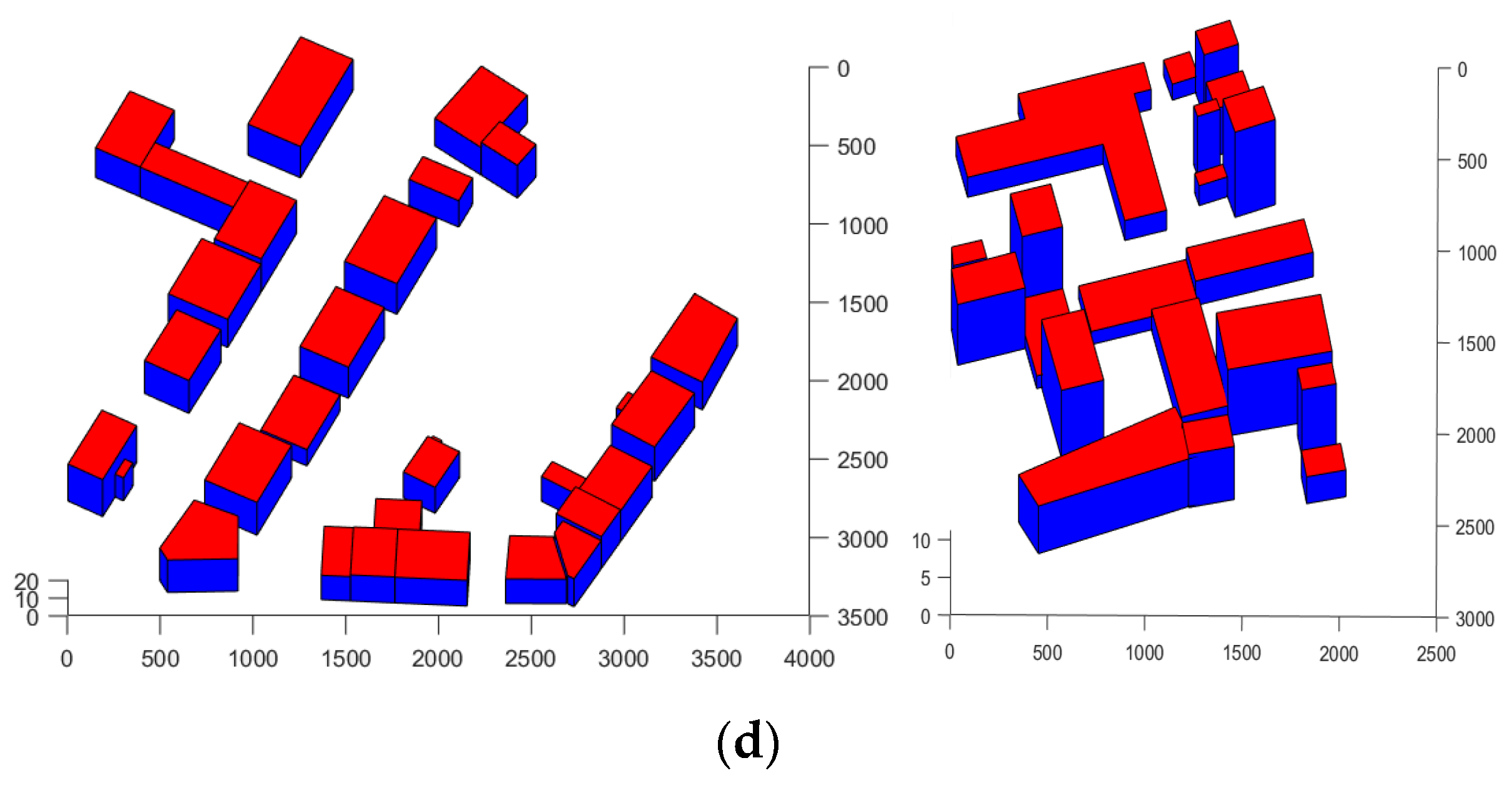
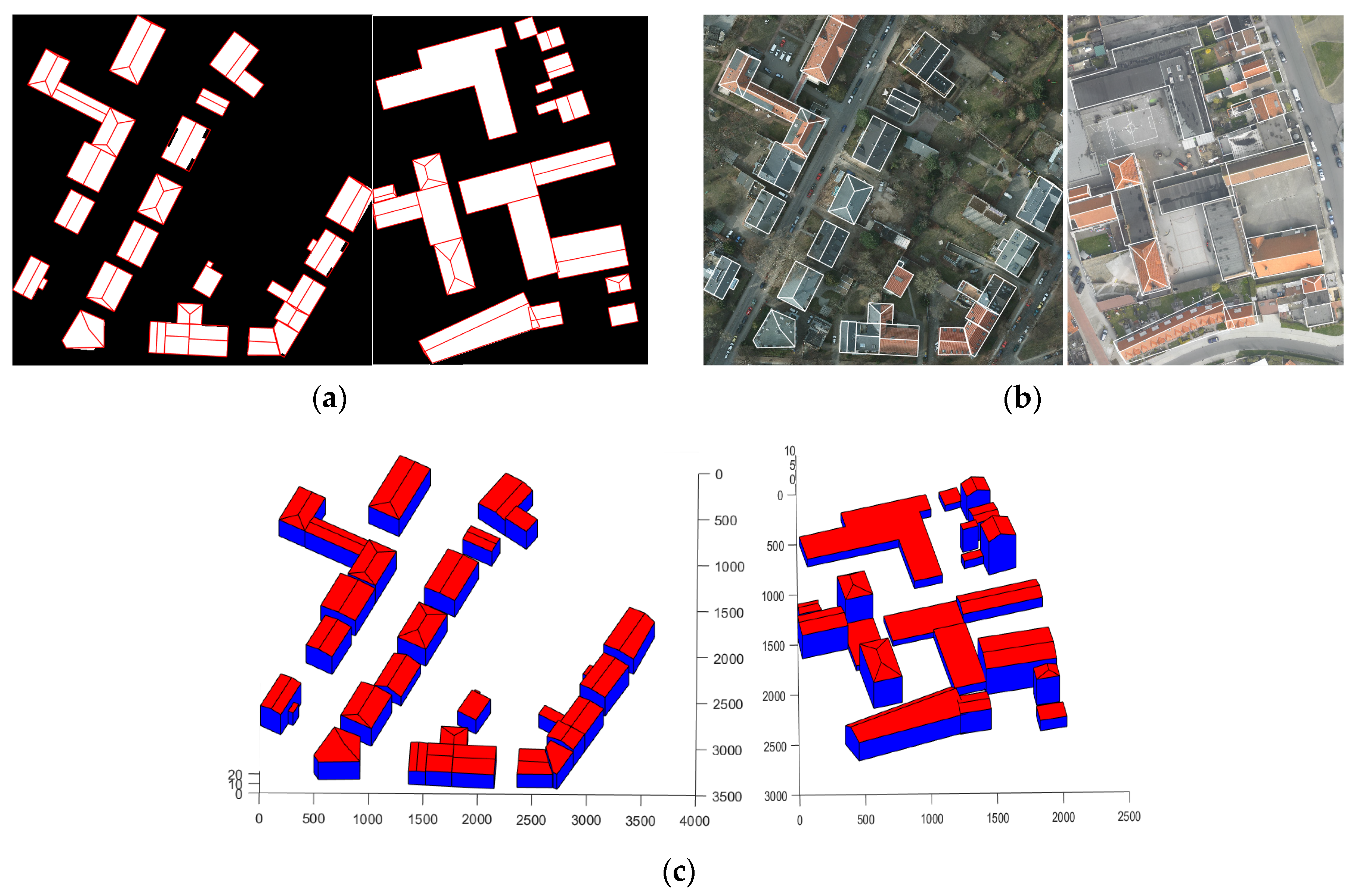
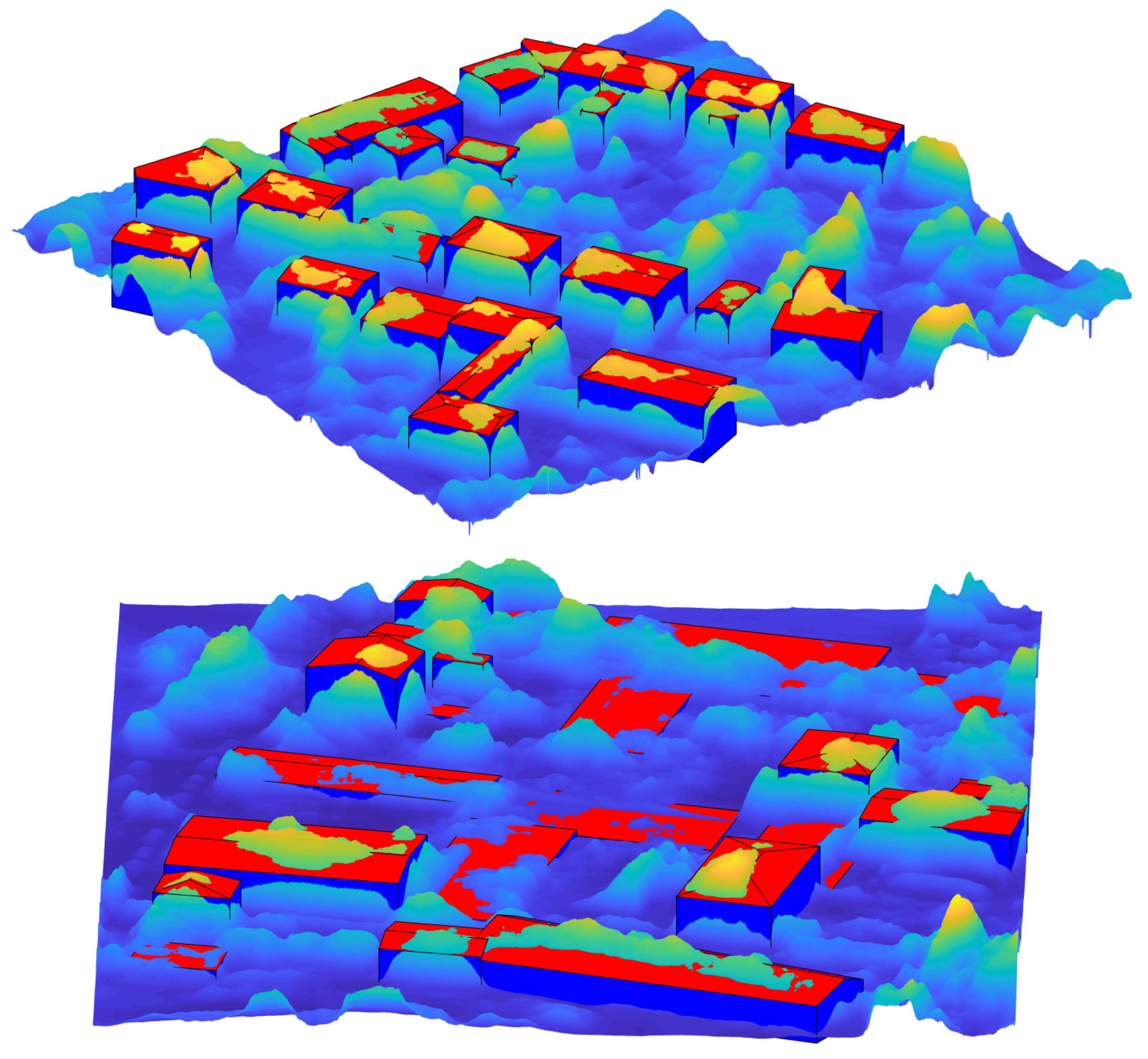
4.3. Quality Assessment of 3D Reconstruction
- Trees are one of the common error sources which decrease the accuracy of the predicted eave lines, significantly (Figure 22a);
- If the ridge lines are not extracted, the tilted roofs could be modeled as the flat roofs (Figure 22b).
- There are some classification errors between the eave and ridge lines (Figure 22c);
- If there are some errors in the predicted nDSM, the median values of the eave lines are not measured accurately (Figure 22d).
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kolbe, T.H.; Gröger, G.; Plümer, L. CityGML—Interoperable Access to 3D City Models. In Proceedings of the Int. Symposium on Geo-information for Disaster Management, Delft, The Netherlands, 21–23 March 2005. [Google Scholar]
- Tarsha-Kurdi, F.; Landes, T.; Grussenmeyer, P.; Koehl, M. Model-Driven and Data-Driven Approaches Using Lidar Data: Analysis and Comparison. In Proceedings of the International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, Munich, Germany, 19–21 September 2006; Volume 36, pp. 87–92. [Google Scholar]
- Wang, R.; Peethambaran, J.; Chen, D. LiDAR Point Clouds to 3D Urban Models: A Review. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 606–627. [Google Scholar] [CrossRef]
- Cheng, L.; Gong, J.; Li, M.; Liu, Y. 3D Building Model Reconstruction from Multi-view Aerial Imagery and Lidar Data. Photogramm. Eng. Remote Sens. 2011, 77, 125–139. [Google Scholar] [CrossRef]
- Kim, K.; Shan, J. Building roof modeling from airborne laser scanning data based on level set approach. ISPRS J. Photogramm. Remote Sens. 2011, 66, 484–497. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, H.; Cheng, L.; Li, M.; Wang, Y. Three-Dimensional Reconstruction of Building Roofs from Airborne LiDAR Data Based on a Layer Connection and Smoothness Strategy. Remote Sens. 2016, 8, 415. [Google Scholar] [CrossRef]
- Yan, Y.; Gao, F.; Deng, S.; Su, N. A Hierarchical Building Segmentation in Digital Surface Models for 3D Reconstruction. Sensors 2017, 17, 222. [Google Scholar] [CrossRef] [PubMed]
- Mccann, M.T.; Member, S.; Mixon, D.G.; Fickus, M.C.; Castro, C.A.; Ozolek, J.A.; Kovacevic, J. Images as Occlusions of Textures: A Framework for Segmentation. IEEE Trans. Image Process. 2014, 23, 2033–2046. [Google Scholar] [CrossRef] [PubMed]
- Awrangjeb, M.; Ali, S.; Gilani, N. An Effective Data-Driven Method for 3-D Building Roof Reconstruction and Robust Change Detection. Remote Sens. 2018, 10, 1512. [Google Scholar] [CrossRef]
- Lafarge, F.; Descombes, X.; Zerubia, J.; Pierrot-deseilligny, M. Structural Approach for Building Reconstruction from a Single DSM. J. Latex Cl. Files 2007, 6, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Huang, H.; Brenner, C.; Sester, M.; Hannover, D. 3D Building Roof Reconstruction from Point Clouds via Generative Models Categories and Subject Descriptors. In Proceedings of the 19th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, Chicago, IL, USA, 1–4 November 2004. [Google Scholar]
- Zhang, W.; Wang, H.; Chen, Y.; Yan, K.; Chen, M. 3D Building Roof Modeling by Optimizing Primitive’s Parameters Using Constraints from LiDAR Data and Aerial Imagery. Remote Sens. 2014, 6, 8107–8133. [Google Scholar] [CrossRef]
- Zheng, Y.; Weng, Q. Model-driven Reconstruction of 3D Buildings Using LiDAR Data. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1541–1545. [Google Scholar] [CrossRef]
- Zheng, Y.; Weng, Q.; Zheng, Y. A Hybrid Approach for Three-Dimensional Building Reconstruction in Indianapolis from LiDAR Data. Remote Sens. 2017, 9, 310. [Google Scholar] [CrossRef]
- Kaiser, P.; Wegner, J.D.; Aurélien, L.; Jaggi, M.; Hofmann, T.; Schindler, K. Learning Aerial Image Segmentation from Online Maps. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6054–6068. [Google Scholar] [CrossRef]
- Persello, C.; Stein, A. Deep Fully Convolutional Networks for the Detection of Informal Settlements in VHR Images. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2325–2329. [Google Scholar] [CrossRef]
- Wen, Q.; Jiang, K.; Wang, W.; Liu, Q.; Guo, Q.; Li, L.; Wang, P. Automatic building extraction from google earth images under complex backgrounds based on deep instance segmentation network. Sensors 2019, 19, 333. [Google Scholar] [CrossRef] [PubMed]
- Srivastava, S.; Volpi, M.; Tuia, D. Joint Height Estimation and Semantic Labeling of Monocular Aerial Images with CNNs. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017. [Google Scholar]
- Ghamisi, P.; Yokoya, N. IMG2DSM: Height Simulation from Single Imagery Using Conditional Generative Adversarial Net. IEEE Geosci. Remote Sens. Lett. 2018, 5, 794–798. [Google Scholar] [CrossRef]
- Mou, L.; Member, S.; Zhu, X.X.; Member, S. IM2HEIGHT: Height Estimation from Single Monocular Imagery via Fully Residual Convolutional-Deconvolutional Network. arXiv 2018, arXiv:1802.10249, 1–13. [Google Scholar]
- Amirkolaee, H.A.; Arefi, H. Height estimation from single aerial images using a deep convolutional encoder-decoder network. ISPRS J. Photogramm. Remote Sens. 2019, 149, 50–66. [Google Scholar] [CrossRef]
- Bittner, K.; D’Angelo, P.; Körner, M.; Reinartz, P. DSM-to-LoD2: Spaceborne Stereo Digital Surface Model Refinement. Remote Sens. 2018, 10, 1926. [Google Scholar] [CrossRef]
- Axelsson, P.E. DEM generation from laser scanner data using adaptive TIN models. In Proceedings of the International Archives of the Photogrammetry and Remote Sensing, Amsterdam, The Netherlands, 16–22 July 2000; pp. 110–117. [Google Scholar]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. SegNet: A Deep Convolutional Encoder-Decoder Architecture for Image Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef]
- Laina, I.; Rupprecht, C.; Belagiannis, V.; Tombari, F.; Navab, N. Deeper Depth Prediction with Fully Convolutional Residual Networks. In Proceedings of the IEEE International Conference on 3D Vision (3DV), Stanford, CA, USA, 25–28 October 2016. [Google Scholar]
- Eigen, D.; Fergus, R. Predicting Depth, Surface Normals and Semantic Labels with a Common Multi-Scale Convolutional Architecture. In Proceedings of the International Conference on Computer Vision (ICCV), Washington, DC, USA, 7–13 December 2015; pp. 2650–2658. [Google Scholar]
- Kaiming, H.; Xiangyu, Z.; Shaoqing, R.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 26 June–1 July 2016; pp. 1–9. [Google Scholar]
- Robbins, H.; Monro, S. A Stochastic Approximation Method. Ann. Math. Stat. 2007, 22, 400–407. [Google Scholar] [CrossRef]
- Kiefer, J.; Wolfowitz, J. Stochastic Estimation of the Maximum of a Regression Function. Ann. Math. Stat. 1952, 23, 462–466. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J.L. Adam: A Method for Stochastic Optimization. In Proceedings of the the 3rd International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015; pp. 1–15. [Google Scholar]
- Arefi, H.; Reinartz, P. Building Reconstruction Using DSM and Orthorectified Images. Remote Sens. 2013, 5, 1681–1703. [Google Scholar] [CrossRef]
- ISPRS 2D Semantic Labeling Contest-Potsdam. Available online: http://www2.isprs.org/commissions/comm3/wg4/2d-sem-label-potsdam.html. (accessed on 15 September 2019).
- 2015 IEEE GRSS Data Fusion Contest. Available online: http://www.grss-ieee.org/community/technical-committees/data-fusion. (accessed on 15 September 2019).
- Shepard, D. A two-dimensional interpolation function for irregularly-spaced data. In Proceedings of the the 1968 ACM National Conference, New York, NY, USA, 27–29 August 1968; pp. 517–524. [Google Scholar]
- Saxena, A.; Sun, M.; Ng, A.Y. Make3D: Learning 3D Scene Structure from a Single Still Image. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 12, 824–840. [Google Scholar] [CrossRef]
- Eigen, D.; Puhrsch, C.; Fergus, R. Depth Map Prediction from a Single Image using a Multi-Scale Deep Network. Int. Conf. Neural Inf. Process. Syst. 2014, 2, 2366–2374. [Google Scholar]
- Zhao, S.; Fu, H.; Gong, M.; Tao, D. Geometry-Aware Symmetric Domain Adaptation for Monocular Depth Estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 9788–9798. [Google Scholar]
- Liu, F.; Shen, C.; Lin, G. Deep Convolutional Neural Fields for Depth Estimation from a Single Image. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 5162–5170. [Google Scholar]
- Goldman, M.; Hassner, T.; Avidan, S. Learn Stereo, Infer Mono: Siamese Networks for Self-Supervised, Monocular, Depth Estimation. In Proceedings of the Computer Vision and Pattern Recognition Workshops (CVPRW), Long Beach, CA, USA, 16–20 June 2019. [Google Scholar]
- Li, B.; Shen, C.; Dai, Y.; Van Den Hengel, A.; He, M. Depth and surface normal estimation from monocular images using regression on deep features and hierarchical CRFs. In Proceedings of the Conf. Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 1119–1127. [Google Scholar]
- He, L.; Wang, G.; Hu, Z. Learning depth from single images with deep neural network embedding focal length. IEEE Trans. Image Process. 2018, 27, 4676–4689. [Google Scholar] [CrossRef]
- Li, Z.; Snavely, N. MegaDepth: Learning Single-View Depth Prediction from Internet Photos. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 2041–2050. [Google Scholar]
- McGlone, J.C.; Shufelt, J.A. Projective and object space geometry for monocular building extraction. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition CVPR-94, Seattle, WA, USA, 21–23 June 1994; IEEE Computer Society Press: Washington, DC, USA; pp. 54–61. [Google Scholar]
- McKeown, D.M.; Bulwinkle, T.; Cochran, S.; Harvey, W.; McGlone, C.; Shufelt, J.A. Performance evaluation for automatic feature extraction. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Amsterdam, The Netherlands, 16–22 July 2000; pp. 379–394. [Google Scholar]
- Rottensteiner, F.; Trinder, J.; Clode, S.; Kubik, K. Using the Dempster-Shafer method for the fusion of LIDAR data and multi-spectral images for building detection. Inf. Fusion 2005, 6, 283–300. [Google Scholar] [CrossRef]
- ISPRS. ISPRS Test Project on Urban Classification and 3D Building Reconstruction. Available online: http://www2.isprs.org/commissions/comm3/wg4/results/a3_recon.html (accessed on 15 September 2019).

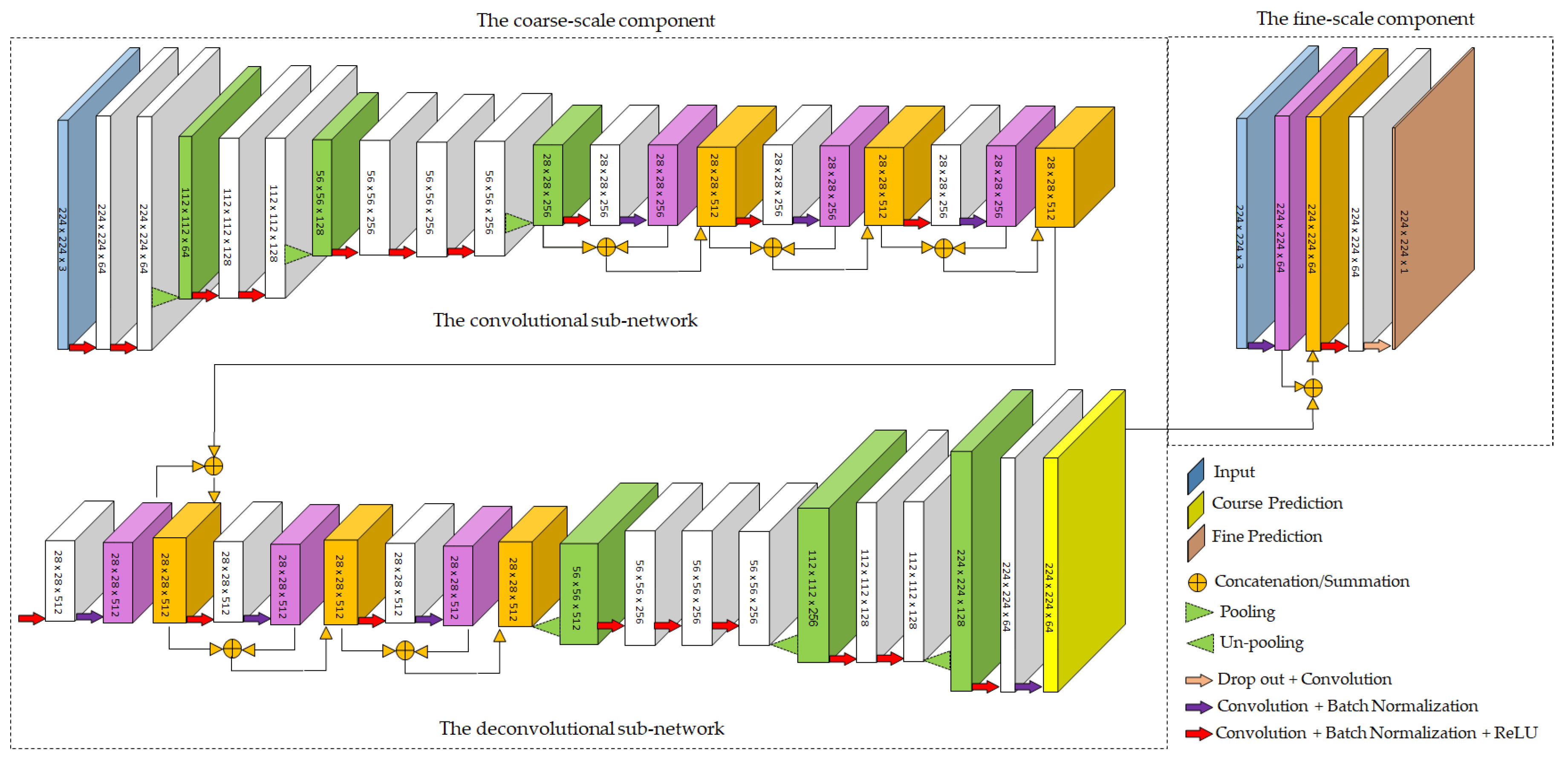








| Encoder | Act. | Output size | Param. | Decoder | Act. | Output size | Param. | Fine-scale | Act. | Output size | Param. |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Input image | - | 224 × 224 × 3 | - | Conv 3 × 3, s1 + BN | ReLU | 28 × 28 × 512 | 2.3 M | Input image | - | 224 × 224 × 3 | - |
| 2x {Conv 3 × 3, s1 + BN} | ReLU | 224 × 224 × 64 | 3.6 k | Conv 3 × 3, s1 + BN | - | 28 × 28 × 512 | 2.3 M | Conv 3 × 3, s1 + BN | - | 224 × 224 × 64 | 1.8 k |
| Pooling 2 × 2, s2 | - | 112 × 112 × 64 | - | Summation | - | 28 × 28 × 512 | - | Summation | - | 224 × 224 × 64 | - |
| 2x {Conv 3 × 3, s1 + BN} | ReLU | 112 × 112 × 64 | 73.8 k | Conv 3 × 3, s1 + BN | ReLU | 28 × 28 × 512 | 2.3 M | Conv 3 × 3, s1 + BN | ReLU | 224 × 224 × 64 | 36.9 k |
| Pooling 2 × 2, s2 | - | 56 × 56 × 64 | - | Conv 3 × 3, s1 + BN | - | 28 × 28 × 512 | 2.3 M | Conv 3 × 3, s1 | - | 224 × 224 × 1 | 577 |
| 3x {Conv 3 × 3, s1 + BN} | ReLU | 56 × 56 × 256 | 443.1 k | Summation | - | 28 × 28 × 512 | - | ||||
| Pooling 2 × 2, s2 | - | 28 × 28 × 256 | - | Conv 3 × 3, s1 + BN | ReLU | 28 × 28 × 512 | 2.3 M | ||||
| Conv 3 × 3, s1 + BN | ReLU | 28 × 28 × 256 | 590.1 k | Conv 3 × 3, s1 + BN | - | 28 × 28 × 512 | 2.3 M | ||||
| Conv 3 × 3, s1 + BN | - | 28 × 28 × 256 | 590.1 k | Summation | - | 28 × 28 × 512 | - | ||||
| Concatenation | - | 28 × 28 × 512 | - | Un-pooling 2 × 2 | - | 56 × 56 × 512 | - | ||||
| Conv 3 × 3, s1 + BN | ReLU | 28 × 28 × 256 | 1.2 M | 3x {Conv 3 × 3, s1 + BN} | ReLU | 56 × 56 × 256 | 3.5 M | ||||
| Conv 3 × 3, s1 + BN | - | 28 × 28 × 256 | 590.1 k | Un-pooling 2 × 2 | - | 112 × 112 × 256 | - | ||||
| Concatenation | - | 28 × 28 × 512 | - | 2x {Conv 3 × 3, s1 + BN} | ReLU | 112 × 112 × 256 | 1.2 M | ||||
| Conv 3 × 3, s1 + BN | ReLU | 28 × 28 × 256 | 1.2 M | Un-pooling 2 × 2 | - | 224 × 224 × 256 | - | ||||
| Conv 3 × 3, s1 + BN | - | 28 × 28 × 256 | 590.1 k | Conv 3 × 3, s1 + BN | ReLU | 224 × 224 × 64 | 147.5 k | ||||
| Concatenation | - | 28 × 28 × 512 | - | ||||||||
| Total Parameters: | 5.2 M | Total Parameters: | 19.0M | Total Parameters: | 39.3 k | ||||||
| Metrics | Descriptors | The Potsdam Test Data | The Zeebrugge Test Data |
|---|---|---|---|
| Standard | Mean Error | 1.69 m | 2.03 m |
| Standard Deviation (SD) | 1.31 m | 1.26 m | |
| Root Mean Square Error (RMSE) | 3.57 m | 3.30 m | |
| Relative Error (REL) | 0.4% | 0.9% | |
| Root Mean Squared Logarithmic Error (RMSLE) | 0.23 m | 1.19 m | |
| Robust | Median Error | 1.35 m | 1.68 m |
| Normalized Median Absolute Deviation (NMAD) | 1.32 m | 0.98 m | |
| Quantile 68.3% | 2.16 m | 2.27 m | |
| Quantile 95% | 4.31 m | 4.75 m |
| Dataset | Method | RMSE [m] | REL [%] | RMSLE [m] |
|---|---|---|---|---|
| Make3D | Zhao et al. [37] | 10.424 | 0.403 | - |
| Liu et al. [38] | 9.49 | 0.355 | 0.137 | |
| Goldman et al. [39] | 8.789 | 0.406 | 0.183 | |
| Li et al. [40] | 7.19 | 0.278 | 0.092 | |
| Eigen et al. [36] | 7.16 | 0.190 | 0.270 | |
| He et al. [41] | 6.801 | 0.208 | 0.087 | |
| Laina et al. [25] | 4.46 | 0.176 | 0.072 | |
| Li et al. [42] | 4.25 | 0.178 | 0.064 | |
| Proposed MSCDN | 4.31 | 0.184 | 0.074 | |
| Potsdam | Ghamisi et al. [19] | 3.89 | - | - |
| Amini et al. [21] | 3.468 | 0.571 | 0.259 | |
| Proposed MSCDN | 3.57 | 0.4 | 0.23 |
| Classes of Linear Elements | Pre._eave [1, 0, 0] | Pre._ridge [0, 1, 0] | Pre._hip [0, 0, 1] | Pre._black [0, 0, 0] | Quality Measures | [%] |
|---|---|---|---|---|---|---|
| Ref._eave [1, 0, 0] | 49,181 | 2873 | 3215 | 5653 | Comp. | 95.46 |
| Ref._ridge [0, 1, 0] | 5217 | 9332 | 5984 | 968 | Corr. | 95.46 |
| Ref._hip [0, 0, 1] | 956 | 1301 | 3258 | 803 | Qual. | 91.31 |
| Ref._black [0, 0, 0] | 1,300,905 | 210,002 | 187,722 | 36,224,481 | F1 score | 95.46 |
| Classes of Linear Elements | Pre._eave [1, 0, 0] | Pre._ridge [0, 1, 0] | Pre._hip [0, 0, 1] | Pre._black [0, 0, 0] | Quality Measures | [%] |
|---|---|---|---|---|---|---|
| Ref._eave [1, 0, 0] | 237,914 | 23,994 | 7161 | 292,100 | Comp. | 91.12 |
| Ref._ridge [0, 1, 0] | 11,203 | 32,590 | 13,540 | 11,093 | Corr. | 91.12 |
| Ref._hip [0, 0, 1] | 6804 | 1996 | 11,248 | 5627 | Qual. | 83.69 |
| Ref._black [0, 0, 0] | 968,694 | 121,216 | 75,591 | 15,514,881 | F1 score | 91.12 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alidoost, F.; Arefi, H.; Tombari, F. 2D Image-To-3D Model: Knowledge-Based 3D Building Reconstruction (3DBR) Using Single Aerial Images and Convolutional Neural Networks (CNNs). Remote Sens. 2019, 11, 2219. https://doi.org/10.3390/rs11192219
Alidoost F, Arefi H, Tombari F. 2D Image-To-3D Model: Knowledge-Based 3D Building Reconstruction (3DBR) Using Single Aerial Images and Convolutional Neural Networks (CNNs). Remote Sensing. 2019; 11(19):2219. https://doi.org/10.3390/rs11192219
Chicago/Turabian StyleAlidoost, Fatemeh, Hossein Arefi, and Federico Tombari. 2019. "2D Image-To-3D Model: Knowledge-Based 3D Building Reconstruction (3DBR) Using Single Aerial Images and Convolutional Neural Networks (CNNs)" Remote Sensing 11, no. 19: 2219. https://doi.org/10.3390/rs11192219
APA StyleAlidoost, F., Arefi, H., & Tombari, F. (2019). 2D Image-To-3D Model: Knowledge-Based 3D Building Reconstruction (3DBR) Using Single Aerial Images and Convolutional Neural Networks (CNNs). Remote Sensing, 11(19), 2219. https://doi.org/10.3390/rs11192219





