Automatic Extrinsic Self-Calibration of Mobile Mapping Systems Based on Geometric 3D Features
Abstract
:1. Introduction
1.1. Geometric Features
1.2. Contributions and Structure
2. Related Work
2.1. Extrinsic Calibration of Mobile Mapping Systems
2.2. Geometric Features
- A linear (1D) structure is given for , since the respective points in the local neighborhood are mainly spread along one principal axis.
- A planar (2D) structure is given for , since the considered points spread within a plane spanned by two principal axes.
- A volumetric (3D) structure is given for , since the considered points are similarly spread in all directions.
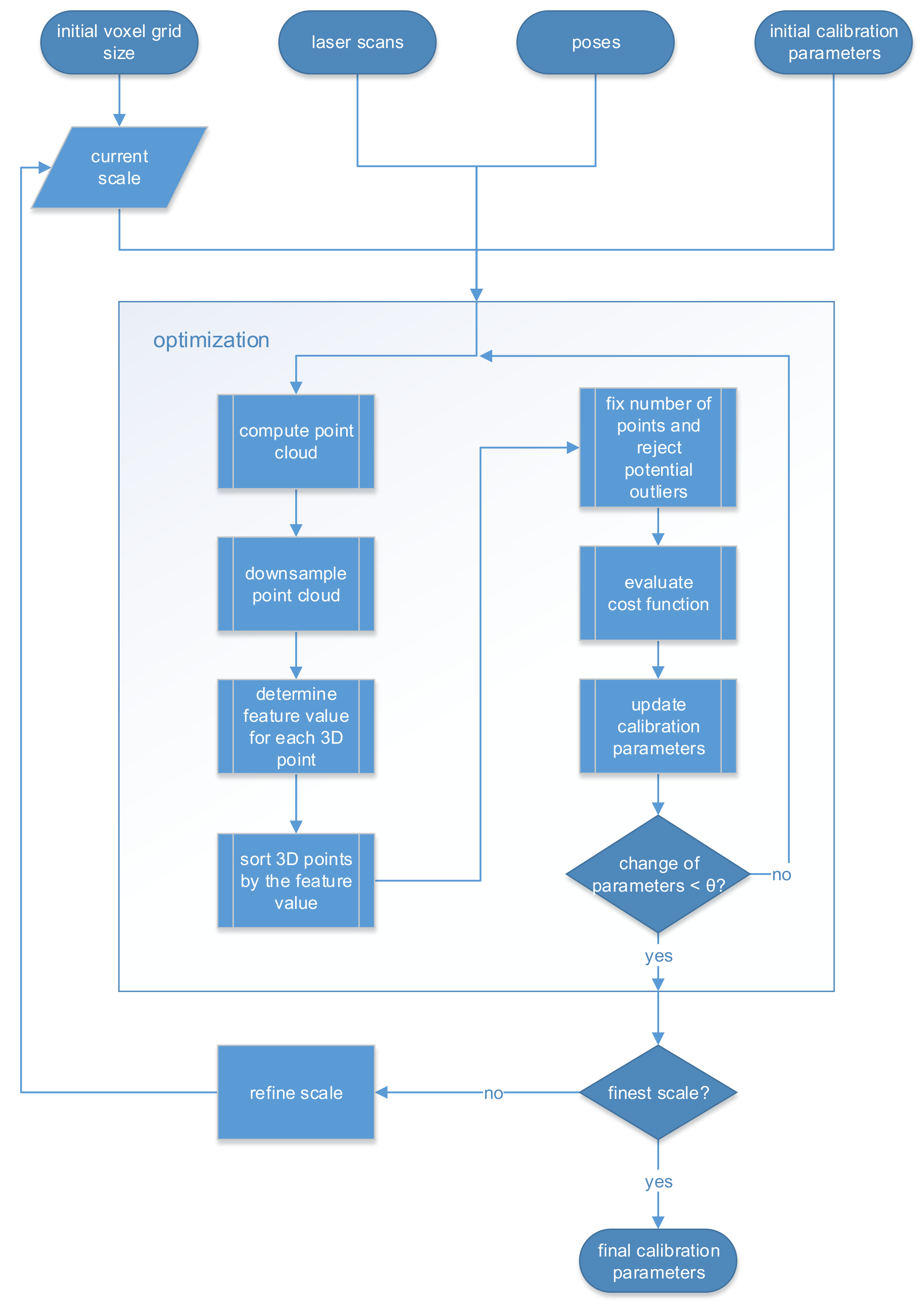
3. Methodology
3.1. Input and Output Parameters
- The first category consists of a single parameter that represents the initial size a of a voxel grid filter. The size is defined by the edge length of each voxel. Section 3.2.2 gives more details on the downsampling.
- The second category contains the measurements of the mapping sensor. For each timestep t the mapping sensor measures a point or a point set in the Cartesian mapping frame m. The set of point sets for each utilized time step is the input to the self-calibration.
- The third category contains the measurements of the pose estimation sensor, analogous to the second category. For each timestep t the pose estimation sensor provides a 6-DOF pose that is associated to a single point set. The 6-DOF pose represents the rigid transformation from the navigation frame n to the world frame w. For this simplified formal description, synchronized sensors and the interpolation of movements during the scanning are assumed.
- The fourth category consists of the six initial calibration parameters. The initial calibration matrix is a reparametrization of these parameters. In Section 4.1.2 we investigate how accurate the initial calibration parameters must be for the self-calibration to be applicable.
3.2. Optimization
3.2.1. Computation of the Point Cloud
3.2.2. Downsampling
3.2.3. Determination of the Geometric Feature
3.2.4. Computation of the Cost Function and Parameter Estimation
3.3. Multi-Scale Approach
4. Experiments
4.1. Synthetic Data
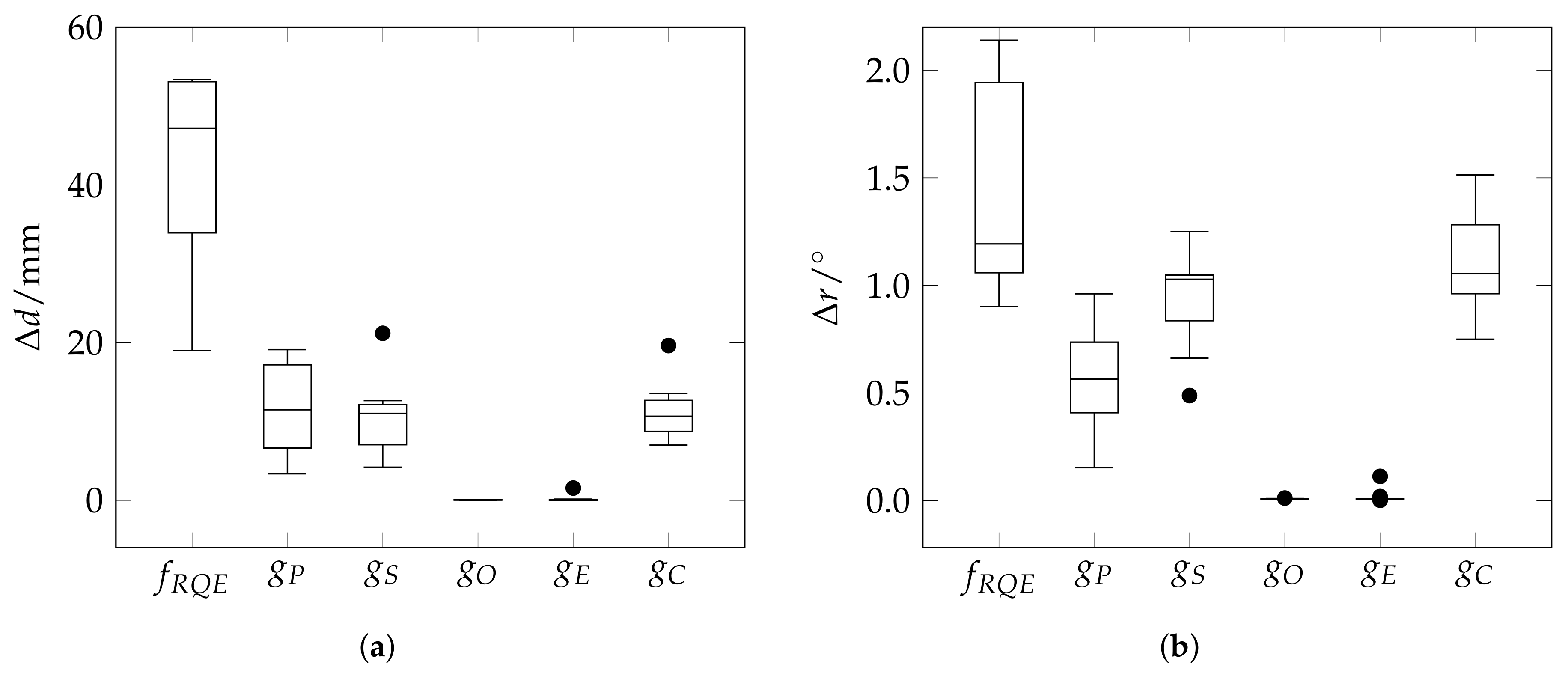
4.1.1. Suitability of the Cost Functions
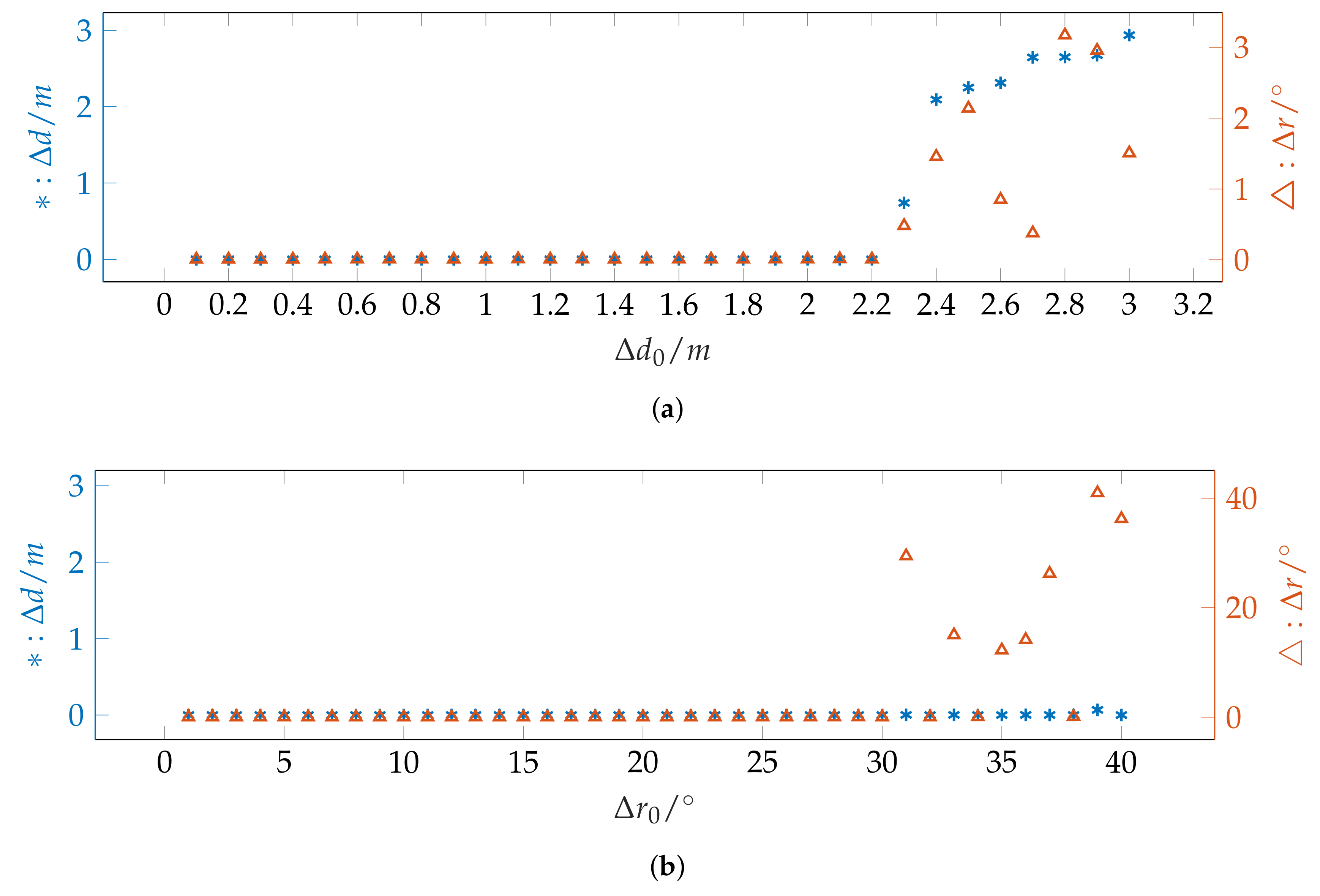
4.1.2. Radius of Convergence
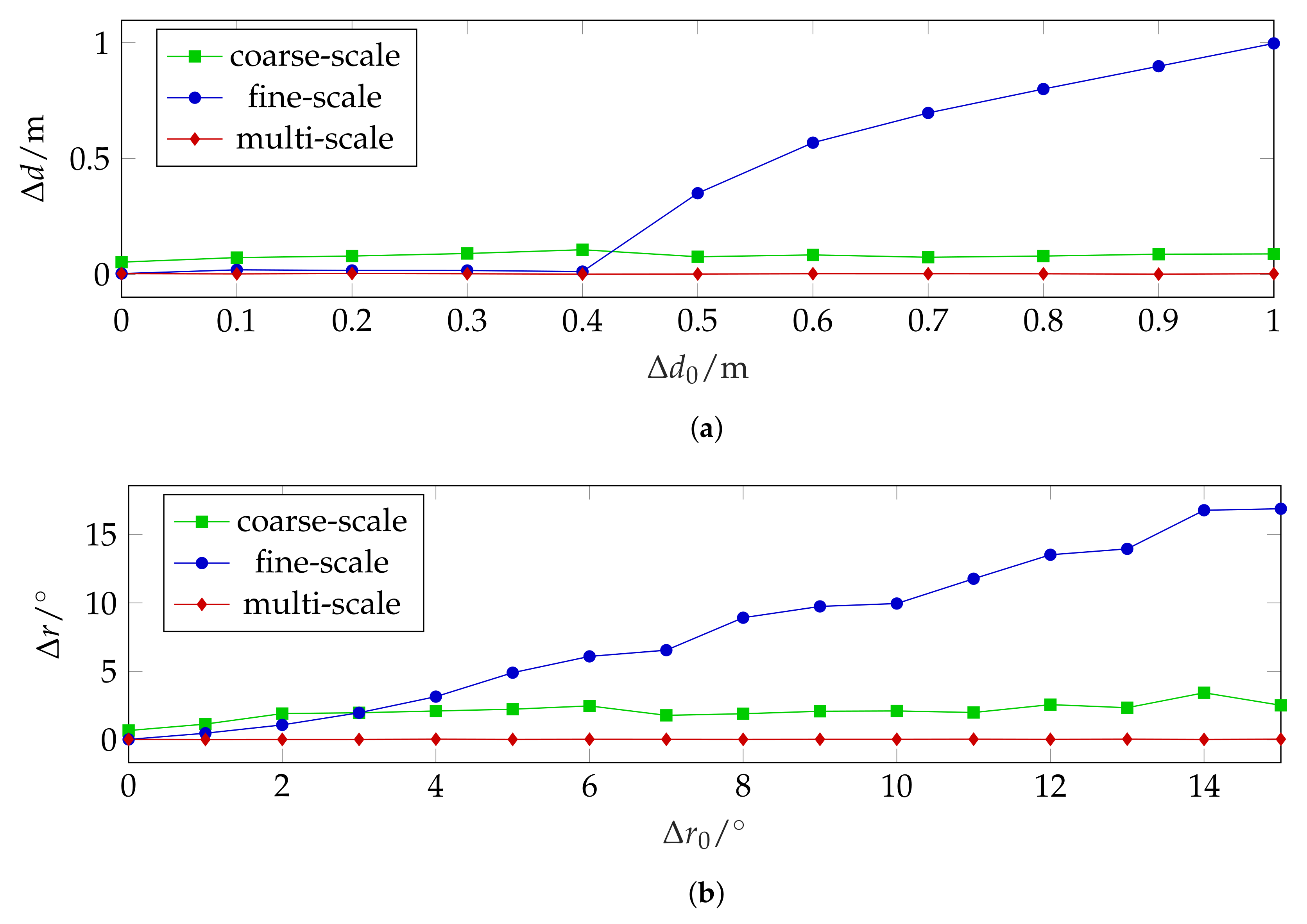
4.1.3. Single-Scale vs. Multi-Scale
4.2. Real Data
4.2.1. Small-Scale Indoor Dataset
4.2.2. Large-Scale Outdoor Dataset
5. Discussion
5.1. Suitability of the Cost Function
5.2. Radius of Convergence
5.3. Single-Scale vs. Multi-Scale
5.4. Real data
5.4.1. Small-Scale Indoor Dataset
5.4.2. Large-Scale Outdoor Dataset
6. Conclusions and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhang, Q.; Pless, R. Extrinsic Calibration of a Camera and Laser Range Finder (Improves Camera Calibration). In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Sendai, Japan, 28 September–2 October 2004; Volume 3, pp. 2301–2306. [Google Scholar]
- Kassir, A.; Peynot, T. Reliable automatic camera-laser calibration. In Proceedings of the 2010 Australasian Conference on Robotics and Automation (ARAA), Brisbane, Australia, 1–3 December 2010. [Google Scholar]
- Vasconcelos, F.; Barreto, J.P.; Nunes, U. A Minimal Solution for the Extrinsic Calibration of a Camera and a Laser-Rangefinder. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 2097–2107. [Google Scholar] [CrossRef] [PubMed]
- Weinmann, M.; Jutzi, B.; Hinz, S.; Mallet, C. Semantic point cloud interpretation based on optimal neighborhoods, relevant features and efficient classifiers. ISPRS J. Photogramm. Remote Sens. 2015, 105, 286–304. [Google Scholar] [CrossRef]
- Hackel, T.; Wegner, J.D.; Schindler, K. Fast semantic segmentation of 3D point clouds with strongly varying density. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 3, 177–184. [Google Scholar]
- Bueno, M.; Bosché, F.; González-Jorge, H.; Martínez-Sánchez, J.; Arias, P. 4-Plane congruent sets for automatic registration of as-is 3D point clouds with 3D BIM models. Autom. Constr. 2018, 89, 120–134. [Google Scholar] [CrossRef]
- Frome, A.; Huber, D.; Kolluri, R.; Bülow, T.; Malik, J. Recognizing objects in range data using regional point descriptors. In Proceedings of the European Conference on Computer Vision, Prague, Czech Republic, 11–14 May 2004; pp. III:224–III:237. [Google Scholar]
- Sheehan, M.; Harrison, A.; Newman, P. Self-calibration for a 3D laser. Int. J. Robot. Res. 2012, 31, 675–687. [Google Scholar] [CrossRef]
- Kong, J.; Yan, L.; Liu, J.; Huang, Q.; Ding, X. Improved Accurate Extrinsic Calibration Algorithm of Camera and Two-dimensional Laser Scanner. J. Multimed. 2013, 8-6, 777–783. [Google Scholar] [CrossRef]
- Yu, L.; Peng, M.; You, Z.; Guo, Z.; Tan, P.; Zhou, K. Separated Calibration of a Camera and a Laser Rangefinder for Robotic Heterogeneous Sensors. J. Adv. Robot. Syst. 2013, 10-10, 367–377. [Google Scholar] [CrossRef]
- Hu, Z.; Li, Y.; Li, N.; Zhao, B. Extrinsic Calibration of 2-D Laser Rangefinder and Camera From Single Shot Based on Minimal Solution. IEEE Trans. Instrum. Meas. 2016, 65, 915–929. [Google Scholar] [CrossRef]
- Sim, S.; Sock, J.; Kwak, K. Indirect Correspondence-Based Robust Extrinsic Calibration of LiDAR and Camera. Sensors 2016, 16, 933. [Google Scholar] [CrossRef]
- Dong, W.; Isler, V. A novel method for the extrinsic calibration of a 2-D laser-rangefinder & a camera. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 5104–5109. [Google Scholar]
- Li, N.; Hu, Z.; Zhao, B. Flexible extrinsic calibration of a camera and a two-dimensional laser rangefinder with a folding pattern. Appl. Opt. 2016, 55, 2270. [Google Scholar] [CrossRef]
- Chen, Z.; Yang, X.; Zhang, C.; Jiang, S. Extrinsic calibration of a laser range finder and a camera based on the automatic detection of line feature. In Proceedings of the 2016 9th International Congress on Image and Signal Processing, BioMedical Engineering and Informatics (CISP-BMEI), Datong, China, 15–17 October 2016; pp. 448–453. [Google Scholar]
- Zhou, L. A New Minimal Solution for the Extrinsic Calibration of a 2D LIDAR and a Camera Using Three Plane-Line Correspondences. IEEE Sens. J. 2014, 14, 442–454. [Google Scholar] [CrossRef]
- Tulsuk, P.; Srestasathiern, P.; Ruchanurucks, M.; Phatrapornnant, T.; Nagahashi, H. A novel method for extrinsic parameters estimation between a single-line scan LiDAR and a camera. In Proceedings of the 2014 IEEE Intelligent Vehicles Symposium, Dearborn, MI, USA, 8–11 June 2014; pp. 781–786. [Google Scholar]
- Hillemann, M.; Jutzi, B. UCalMiCeL–Unified intrinsic and extrinsic calibration of a Multi-Camera-System and a Laserscanner. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 4, 17–24. [Google Scholar] [CrossRef]
- Talaya, J.; Alamus, R.; Bosch, E.; Serra, A.; Kornus, W.; Baron, A. Integration of a terrestrial laser scanner with GPS/IMU orientation sensors. In Proceedings of the XXth ISPRS Congress, Istanbul, Turkey, 12–23 July 2004; Volume 35-B5, pp. 1049–1055. [Google Scholar]
- Gräfe, G. High precision kinematic surveying with laser scanners. J. Appl. Geod. 2007, 1-4, 185–199. [Google Scholar] [CrossRef]
- Heinz, E.; Eling, C.; Wieland, M.; Klingbeil, L.; Kuhlmann, H. Development, calibration and evaluation of a portable and direct georeferenced laser scanning system for kinematic 3D mapping. J. Appl. Geod. 2015, 9-4, 227–243. [Google Scholar] [CrossRef]
- Jung, J.; Kim, J.; Yoon, S.; Kim, S.; Cho, H.; Kim, C.; Heo, J. Bore-sight calibration of multiple laser range finders for kinematic 3D laser scanning systems. Sensors 2015, 15, 10292–10314. [Google Scholar] [CrossRef] [PubMed]
- Skaloud, J.; Lichti, D. Rigorous approach to bore-sight self-calibration in airborne laser scanning. ISPRS J. Photogramm. Remote Sens. 2006, 61, 47–59. [Google Scholar] [CrossRef]
- Habib, A.F.; Kersting, A.P.; Shaker, A.; Yan, W.Y. Geometric calibration and radiometric correction of LiDAR data and their impact on the quality of derived products. Sensors 2011, 11, 9069–9097. [Google Scholar] [CrossRef]
- Besl, P.; McKay, N.D. A method for registration of 3-D shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 239–256. [Google Scholar] [CrossRef]
- Chen, Y.; Medioni, G. Object modelling by registration of multiple range images. Image Vis. Comput. 1992, 10, 145–155. [Google Scholar] [CrossRef]
- Ravi, R.; Shamseldin, T.; Elbahnasawy, M.; Lin, Y.J.; Habib, A. Bias Impact Analysis and Calibration of UAV-Based Mobile LiDAR System with Spinning Multi-Beam Laser Scanner. Appl. Sci. 2018, 8, 297. [Google Scholar] [CrossRef]
- Maddern, W.; Harrison, A.; Newman, P. Lost in translation (and rotation): Rapid extrinsic calibration for 2D and 3D LIDARs. In Proceedings of the 2012 IEEE International Conference on Proceedings of the Robotics and Automation (ICRA), Saint Paul, MN, USA, 14–18 May 2012; pp. 3096–3102. [Google Scholar]
- Wang, F.; Syeda-Mahmood, T.; Vemuri, B.C.; Beymer, D.; Rangarajan, A. Closed-form Jensen-Renyi divergence for mixture of Gaussians and applications to group-wise shape registration. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, London, UK, 20–24 September 2009; pp. 648–655. [Google Scholar]
- Maddern, W.; Pascoe, G.; Linegar, C.; Newman, P. 1 year, 1000 km: The Oxford RobotCar dataset. Int. J. Robot. Res. 2017, 36, 3–15. [Google Scholar] [CrossRef]
- Jutzi, B.; Gross, H. Nearest neighbour classification on laser point clouds to gain object structures from buildings. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2009, 38, 4–7. [Google Scholar]
- West, K.F.; Webb, B.N.; Lersch, J.R.; Pothier, S.; Triscari, J.M.; Iverson, A.E. Context-driven automated target detection in 3-D data. In Automatic Target Recognition XIV; International Society for Optics and Photonics: Orlando, FL, USA, 2004; Volume 5426, pp. 133–143. [Google Scholar]
- Pauly, M.; Keiser, R.; Gross, M. Multi-scale feature extraction on point-sampled surfaces. Comput. Graph. Forum 2003, 22, 281–289. [Google Scholar] [CrossRef]
- Dittrich, A.; Weinmann, M.; Hinz, S. Analytical and numerical investigations on the accuracy and robustness of geometric features extracted from 3D point cloud data. ISPRS J. Photogramm. Remote Sens. 2017, 126, 195–208. [Google Scholar] [CrossRef]
- Munoz, D.; Bagnell, J.A.; Vandapel, N.; Hebert, M. Contextual classification with functional max-margin Markov networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 975–982. [Google Scholar]
- Waldhauser, C.; Hochreiter, R.; Otepka, J.; Pfeifer, N.; Ghuffar, S.; Korzeniowska, K.; Wagner, G. Automated classification of airborne laser scanning point clouds. Solving Computationally Expensive Engineering Problems: Methods and Applications; Koziel, S., Leifsson, L., Yang, X.-S., Eds.; Springer: Cham, Switzerland, 2014; pp. 269–292. [Google Scholar]
- Johnson, A.E.; Hebert, M. Using spin images for efficient object recognition in cluttered 3d scenes. IEEE Trans. Pattern Anal. Mach. Intell. 1999, 21, 433–449. [Google Scholar] [CrossRef]
- Tombari, F.; Salti, S.; Di Stefano, L. Unique signatures of histograms for local surface description. In Proceedings of the European Conference on Computer Vision, Heraklion, Greece, 5–11 September 2010; pp. III:356–III:369. [Google Scholar]
- Salti, S.; Tombari, F.; Di Stefano, L. SHOT: unique signatures of histograms for surface and texture description. Comput. Vis. Image Underst. 2014, 125, 251–264. [Google Scholar] [CrossRef]
- Osada, R.; Funkhouser, T.; Chazelle, B.; Dobkin, D. Shape distributions. ACM Trans. Graph. 2002, 21, 807–832. [Google Scholar] [CrossRef]
- Rusu, R.B.; Blodow, N.; Beetz, M. Fast point feature histograms (FPFH) for 3D registration. In Proceedings of the IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 3212–3217. [Google Scholar]
- Rusu, R.B. Semantic 3D object maps for everyday manipulation in human living environments. Künstl. Intell. (KI) 2010, 24, 345–348. [Google Scholar] [CrossRef]
- Huber, P.J. Robust statistics. In International Encyclopedia of Statistical Science; Springer: Cham, Switzerland, 2011; pp. 1248–1251. [Google Scholar]
- Geiger, A.; Lenz, P.; Urtasun, R. Are we ready for autonomous driving? The KITTI vision benchmark suite. In Proceedings of the 2012 IEEE Conference on Proceedings of the Computer Vision and Pattern Recognition (CVPR), Providence, RI, USA, 16–21 June 2012; pp. 3354–3361. [Google Scholar]
- Mur-Artal, R.; Tardós, J.D. ORB-SLAM2: An open-source SLAM system for monocular, stereo, and RGB-D cameras. IEEE Trans. Robot. 2017, 33, 1255–1262. [Google Scholar] [CrossRef]
- Geiger, A.; Lenz, P.; Stiller, C.; Urtasun, R. Visual Odometry/SLAM Evaluation 2012. Available online: http://www.cvlibs.net/datasets/kitti/eval_odometry.php (accessed on 23 July 2019).
- Geiger, A.; Moosmann, F.; Car, O.; Schuster, B. Automatic camera and range sensor calibration using a single shot. In Proceedings of the International Conference on Robotics and Automation (ICRA), Saint Paul, MN, USA, 14–18 May 2012; pp. 3936–3943. [Google Scholar]
- Gehrung, J.; Hebel, M.; Arens, M.; Stilla, U. An Approach to Extract Moving Objects from MLS Data Using a Volumetric Background Representation. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 4, 107–114. [Google Scholar] [CrossRef]


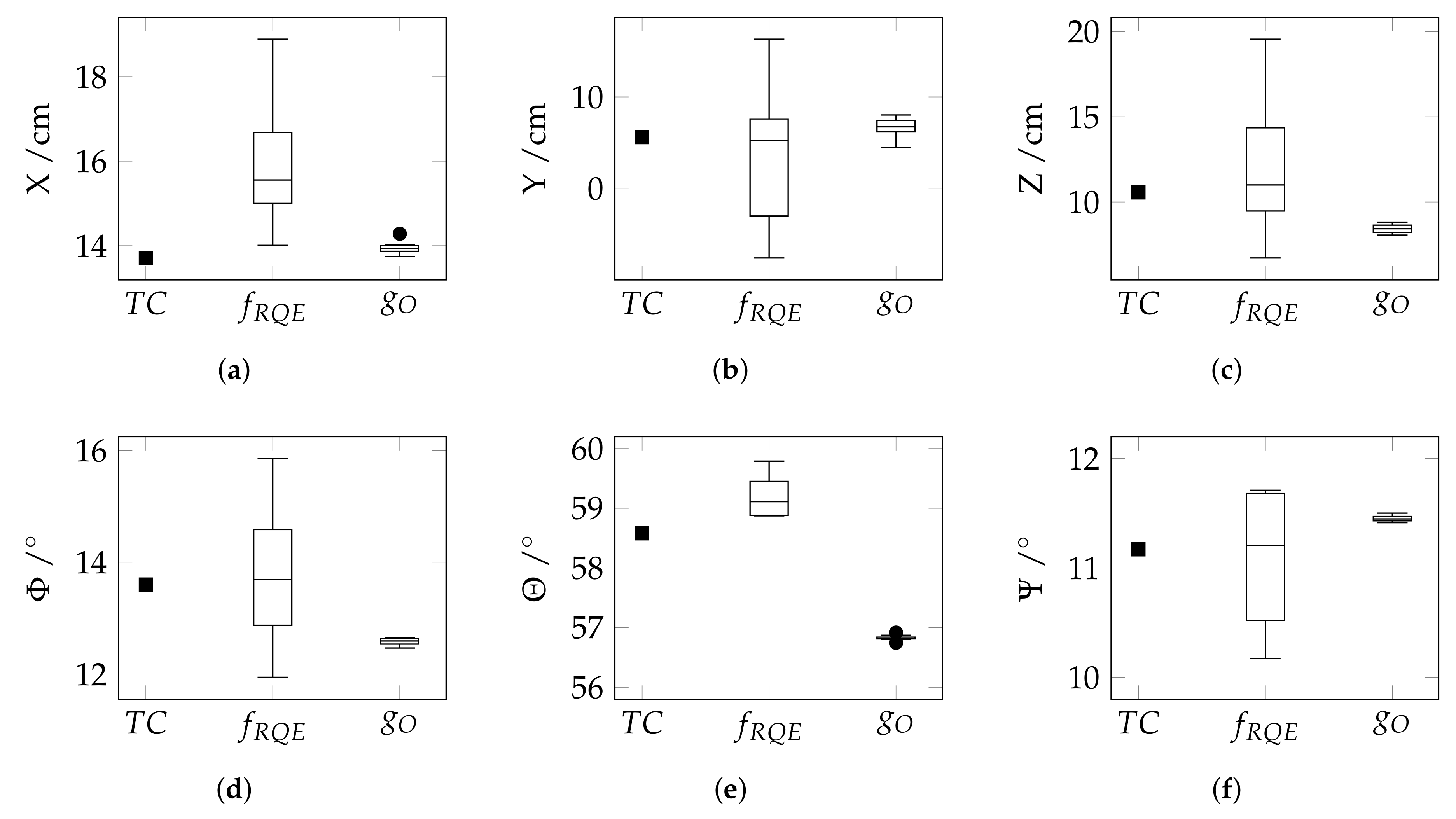

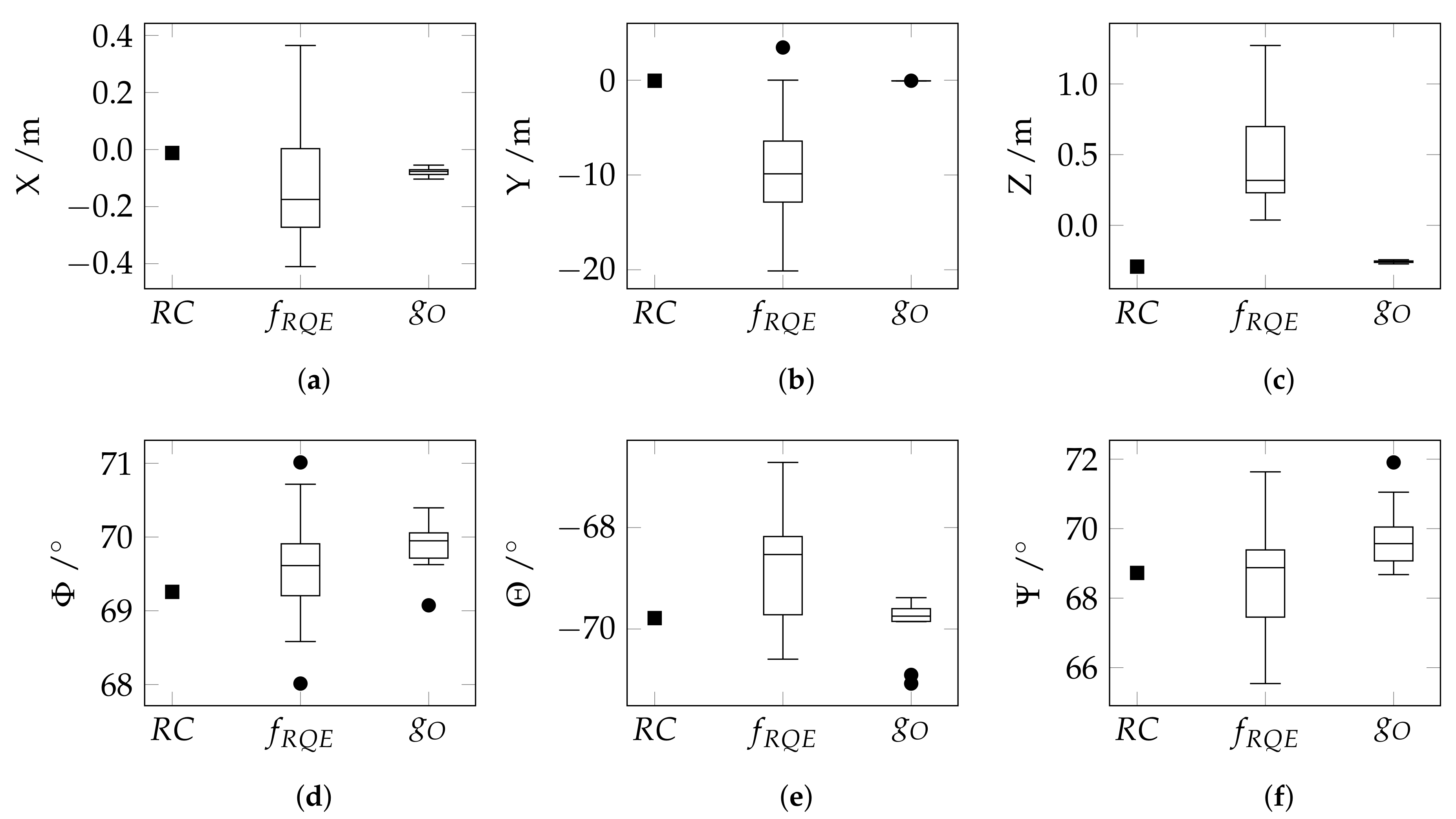
| Approach | med | med | med | med | med | med | med |
|---|---|---|---|---|---|---|---|
| TC | |||||||
| X | X | X | X | X | X | X | |
| X | X | X | X | X | X | X | |
| Approach | Plane 1 | Plane 2 | Plane 3 | Plane 4 | Plane 5 | Plane 6 |
|---|---|---|---|---|---|---|
| TC | ||||||
| X | X | X | X | X | X | |
| X | X | X | X | X | X | |
| Approach | Plane 1 | Plane 2 | Plane 3 | Plane 4 | Plane 5 | Plane 6 |
|---|---|---|---|---|---|---|
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hillemann, M.; Weinmann, M.; Mueller, M.S.; Jutzi, B. Automatic Extrinsic Self-Calibration of Mobile Mapping Systems Based on Geometric 3D Features. Remote Sens. 2019, 11, 1955. https://doi.org/10.3390/rs11161955
Hillemann M, Weinmann M, Mueller MS, Jutzi B. Automatic Extrinsic Self-Calibration of Mobile Mapping Systems Based on Geometric 3D Features. Remote Sensing. 2019; 11(16):1955. https://doi.org/10.3390/rs11161955
Chicago/Turabian StyleHillemann, Markus, Martin Weinmann, Markus S. Mueller, and Boris Jutzi. 2019. "Automatic Extrinsic Self-Calibration of Mobile Mapping Systems Based on Geometric 3D Features" Remote Sensing 11, no. 16: 1955. https://doi.org/10.3390/rs11161955
APA StyleHillemann, M., Weinmann, M., Mueller, M. S., & Jutzi, B. (2019). Automatic Extrinsic Self-Calibration of Mobile Mapping Systems Based on Geometric 3D Features. Remote Sensing, 11(16), 1955. https://doi.org/10.3390/rs11161955





