Abstract
Semantic segmentation in high-resolution remote-sensing (RS) images is a fundamental task for RS-based urban understanding and planning. However, various types of artificial objects in urban areas make this task quite challenging. Recently, the use of Deep Convolutional Neural Networks (DCNNs) with multiscale information fusion has demonstrated great potential in enhancing performance. Technically, however, existing fusions are usually implemented by summing or concatenating feature maps in a straightforward way. Seldom do works consider the spatial importance for global-to-local context-information aggregation. This paper proposes a Learnable-Gated CNN (L-GCNN) to address this issue. Methodologically, the Taylor expression of the information-entropy function is first parameterized to design the gate function, which is employed to generate pixelwise weights for coarse-to-fine refinement in the L-GCNN. Accordingly, a Parameterized Gate Module (PGM) was designed to achieve this goal. Then, the single PGM and its densely connected extension were embedded into different levels of the encoder in the L-GCNN to help identify the discriminative feature maps at different scales. With the above designs, the L-GCNN is finally organized as a self-cascaded end-to-end architecture that is able to sequentially aggregate context information for fine segmentation. The proposed model was evaluated on two public challenging benchmarks, the ISPRS 2Dsemantic segmentation challenge Potsdam dataset and the Massachusetts building dataset. The experiment results demonstrate that the proposed method exhibited significant improvement compared with several related segmentation networks, including the FCN, SegNet, RefineNet, PSPNet, DeepLab and GSN.For example, on the Potsdam dataset, our method achieved a 93.65% score and 88.06% score for the segmentation of tiny cars in high-resolution RS images. As a conclusion, the proposed model showed potential for object segmentation from the RS images of buildings, impervious surfaces, low vegetation, trees and cars in urban settings, which largely varies in size and have confusing appearances.
1. Introduction
With the rapid development of global observation technologies, a large number of remote-sensing (RS) images with high spatial resolution can be acquired every day. High-resolution RS images render rich ground details. Accordingly, extracting objects of interest in RS images with high quality has become an urgent need. Technically, efforts in semantic segmentation for RS images have surged in recent decades because it is a fundamental approach to analyze RS images, which has many important real-world applications [1,2,3,4], typically including plant-disease detection [5,6,7,8,9,10], land-cover planning [11], vegetation extraction [12], cloud detection [13,14], urban-change detection [15,16,17], vehicle detection [18], building extraction [19,20] and road extraction [21,22]. However, none of these applications reaches satisfactory segmentation quality. The main challenge lies in that, in the absence of prior knowledge about the image itself and the motivation behind segmentation for applications, there is no general way to instruct a computer on how to group visual patterns of colors, textures and other features. To this end, this paper mainly focuses on the fundamental task of semantic segmentation in high-resolution RS images obtained by airborne sensors.
The task of semantic segmentation is to partition an image into several semantically meaningful regions, such that pixels in each region have the same object category label. Specifically, given an image, the goal of semantic segmentation is to develop an agent that can infer a category label for pixels belonging to the same object. This task has been addressed in many ways in terms of pattern analysis [1,3,4]. In spite of great progress and many thoughtful attempts in the past decades, it still remains far from solved for various RS images. The main challenge lies in the following four aspects. First, objects in urban remote-sensing images often have different scales. For example, roofs usually appear in the form of large areas, while cars and trees take over small areas. Second, because remote-sensing images are usually taken in a vertical view, lots of confusing artificial objects are spatially distributed, for example, buildings, roads, vehicles and trees are scattered in every corner of the picture. Third, there exist objects with large variations in visual appearance and size belonging to the same category in RS images, which causes high intra-class diversity and low inter-class variance. Taking the roofs as an example, buildings are different from one another in RS images due to different architectural styles and materials, which causes intraclass diversity. However, some roofs closely resemble roads, which cause interclass similarity. Finally, recently the resolution of remote-sensing images has gradually improved, which improved visual perception but also caused issues, too as much detailed information came out that could not before be presented in low-resolution images. This further increases segmentation difficulty. The above four factors make RS imaging quite difficult. Thus, supervised segmentation via learning has been receiving growing attention to enhance segmentation techniques in recent years.
Recently, the usage of deep learning methods developed under the convolutional neural network [23] brings out the boost of the field of computer vision. The task of semantic segmentation for natural images has now been largely benefited from this development [24,25,26,27,28,29]. Technically, it is natural to apply those existing approaches for natural images to RS images. The efforts have been actually made by researchers with comparative studies [30,31,32,33]. Such practices have demonstrated the fact that directly using the existing approaches for natural images cannot guarantee to yield satisfactory segmentations for RS images. In other words, one needs to design new architectures of neural networks to gear to the above characteristics of RS images.
The main purpose of this study is to develop a deep-learning model for semantic segmentation in high-resolution RS images taken by airborne sensors. To this end, a Learnable Gated-Deep Convolutional Neural Network (L-GCNN) was developed by using multiscale information fusion to address challenging issues caused by various types of artificial objects with large variations in visual appearance and size. Specifically, a gate function with learnable parameters was first introduced to generate weights at different spatial positions. With this gate function, a Parameterized Gating Module (PGM) was constructed to perform weighted sum operations on two adjacent levels of convolutional layers. Then, the design of the single PGM and its densely connected counterpart were embedded, respectively, into multilevels of the encoder in the L-GCNN. In this way, discriminative features could be extracted at multiscales of receptive fields. Finally, the proposed L-GCNN was organized as a self-cascaded end-to-end architecture with explicit encoder–decoder modules to sequentially aggregate context information. That is, upon this architecture, pixelwise importance identified by the PGMs can be transferred from high- to low-level so as to achieve global to local refinement for the semantical segmentation of RS objects. Furthermore, the performance of the L-GCNN was examined with extensively comparative experiments on challenging public datasets, indicating the validity of the proposed approach.
The article is organized as follows: Section 1 describes the background information, the problem statement, the objective and the predictions of this study. Section 2 presents the related works of the semantic-segmentation algorithm and its improved applications in remote-sensing images. Section 3 addresses the details of the proposed method. In Section 4, results are reported and analyzed. Section 5 discusses the method, followed by the conclusions in Section 6.
2. Related Works
Advances on the semantic segmentation of RS images have been always associated with those for natural images. However, traditional methods based on manual features usually fail to produce satisfactory results and lack robustness to complex situations, with low accuracy performance. Thanks to the development of deep learning [34], CNNs [23] and its variants [24,25,26] demonstrate powerful capacity for semantic segmentation in natural images. In the literature, the Fully Convolutional Network (FCN) [24] is a seminal work for this task. Later, some sophisticated models were developed, typically including the Deconvolution Network [27], SegNet [26], U-Net [25], Pyramid Scene Parsing Network (PSPNet) [35], RefineNet [28] and DeepLab [29]. Beyond traditional methods with manual features, these methods can learn hierarchically abstract features from data that show good segmentation performance in natural images.
Technically, the boost of the deep models as well as the availability of large-scale RS images with high visual quality provide a chance to enhance the segmentation performance. Accordingly, the idea of deep learning has already been applied to semantic segmentation for RS images. In the literature, most researches focus on how to modify the FCN framework for this issue. Typically, Sherrah [36] combined the dilated convolution [29] into the FCN with no down-sampling operations for high-resolution RS images. Later, multiple FCN-based frameworks are constructed to segment buildings, vehicle and the informal settlements [37,38,39,40] in RS images. Wang et al. [30] proposed a Gated Segmentation Network (GSN) to select adaptive features when fusing feature maps at different levels. Liu et al. [31] constructed a cascaded network for partitioning confusing manmade objects. Chen et al. [38] proposed to use the shuffling CNN to segment aerial images. Yuan [41] considered to integrate the activations from multiple layers in FCN for pixel-wise prediction. These researches have largely enriched the methodology of semantic segmentation for RS images.
In summary, the key in most models [24,25,26,30] is to develop tricks to fuse the feature maps learned at different scales for fine segmentation. One popular way being used is to add them together. In this way, the contribution of all of the pixels are equally considered. However, it is well known that the segmentation errors often occur with higher probabilities at the pixels in edge regions between objects. This fact implies that the contributions to the above fusion should be different at different spatial positions. Based on this observation, a new semantic segmentation model will be developed in this paper to learn different weights at different pixels and a gate function with learnable parameters will be constructed to achieve this goal.
3. Method
This section describes the details of the proposed method. The fusion strategy for multiscale feature maps under the FCN framework is first introduced, which motivated us to design the parameterized gate module. Then, the architecture of the segmentation network is described in detail. Finally, the training algorithm and the inference approach are given for clarity.
3.1. Parameterized Gate Module
To achieve the goal of multi-scale feature fusion, a weighted fusion strategy is first introduced as follows:
where and record feature maps (tensors) obtained at high level and low level, respectively, is the fusion result, “” indicates the convolution operation, is the elementwise summation operation and “↑” performs spatial upsampling. In Equation (1), collects pixel weights and “⊗” stands for the entitywise product of two tensors. Note that, it is unnecessary to provide another weight matrix on the operation at the left side in Equation (2), as such two weight matrices can be shrunk to one for parameter reduction in deep-learning frameworks.
The fusion in Equation (1) has actually been considered in GSN proposed by Wang et al. [30], where the weights in are calculated with information entropy. Formally, information entropy is defined on the probabilities of pixel z belonging to all of the categories:
where is the predicted probability of pixel z belonging to the i-th category; and C is the number of categories. Information entropy acts as a feature selector by supplying different weights for different pixels. Thus, it can perform as a gate function to guide the fusion.
Note that in Equation (2) all the weights are computed in a pre-defined way. This indicates that the gate function is not a learnable one that cannot tune well to data. To remedy this drawback, we first consider the Taylor expression of information-entropy function. With a notation replacement from to and by considering the expression at point , it follows that
where , is the Peano residual term and n is the highest order of the expression. Here, , , can be viewed as the probability of a pixel belonging to the i-th category. Thus, each drops into the interval [0, 1]. Then, we parameterize the above expression in Equation (3) by taking its coefficients as variables.
Ignoring the Peano residual term, a gate function is then defined as follows:
where , and , are parameters to be learned from the data.
The proposed gate function is actually an extension of the single variable function “” in C-dimensional space with the primitive polynomial . As gives a single curve, the gate function in Reference [30] can only yield the weights in a predefined way. In contrast, the gate function in Equation (4) can generate flexible curves. With learnable parameters, it provides a weighting mechanism, adaptive to data.
Finally, we embedded the above gate function into the neural network to develop a Parameterized Gate Model (PGM). The task of the PGM is to integrate high-level contextual information and detailed low-level information together in a spatially weighting way. The structure of the PGM is demonstrated in the bottom-right dashed box in Figure 1. It takes high-level feature maps (already having performed 2×upsampling) and low-level feature maps as inputs. By denoting the output of PGM by , it follows that
where performs “” convolutions on thetensor and “⊗” and “⊕” stand for the entitywise product and sum of two tensors, respectively. There are C categories in total that need to be segmented from the RS images. Thus, the output of the convolution layer contains C channels. Feature maps in these channels are finally transformed by the softmax layer to be the probabilities of each pixel belonging to the C categories. This gears to the need that C inputs of gate function in Equation (4) should be dropped into the interval [0, 1].
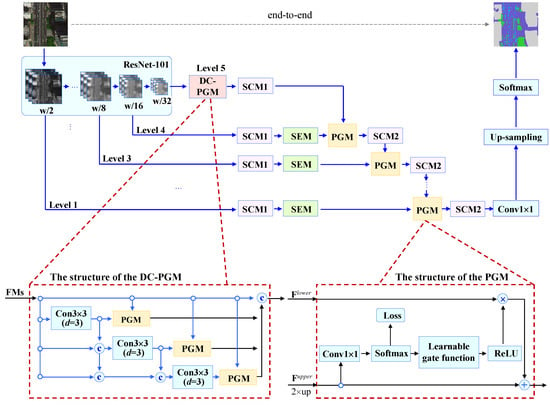
Figure 1.
Overview of the model Learnable Gated Convolutional Neural Network (L-GCNN) for remote-sensing (RS) image segmentation. In the encoder part, ResNet-101 is used as feature extractor. In the decoder part, the Parameterized Gate Module (PGM) and Densely Connected PGM (DC-PGM) are proposed for feature fusion. In addition, the Shortcut Convolution Module (SCM) and Squeeze-and-Excitation Module (SEM) were employed as basic processing units. Details of PGM and DC-PGM are shown in dashed boxes.
Note that, in Equation (4), there are no constraints on the parameters. Accordingly, the value of the function may be negative. Considering that the weight should be non-negative, the Rectified Linear Unit (ReLU) operation is employed to achieve this goal. That is, the output of the gate function in Equation (4) is supplied to a ReLU layer.
Technically, since the gate function in Equation (5) contains parameters to be learned, it will take part in the process of back-propagation during model training. To make the gate more discriminative, a loss function was embedded into the PGM, as shown in the bottom-right dashed box in Figure 1. Specifically, at the high level, the label matrix of the training RS image is first downsampled to be of a size equal to that of the channel and then standard cross-entropy is employed as the loss function at this level. Since label information is directly utilized on this level, minimizing loss function guides the convolution operation in the PGM to learn the semantic features. As a result, this treatment in turn helps enhance the goodness of the gate in PGM.
3.2. Densely Connected Pgm
High-resolution RS images contain confusing artificial objects and complex background. To further improve the segmentation performance, it is inadequate to consider only the local information for multiple-level (layer) feature fusion. It is well known that context information around objects is an important visual hint for object perception as it describes the dependency between the object and its surroundings. To this end, context information at the highest layer of the CNN is utilized since it has the largest receptive filewith high nonlinearity on the feature maps.
Technically, the proposed PGM and dilated convolution [29] are combined to utilize multiscale context information. The reason behind this combination can be explained as follows. On the one hand, the PGM provides a mechanism to provide the spatial importance of the feature maps. Intrinsically, it is a local operation between two adjacent levels in the decoder phase for image segmentation. On the other hand, dilated convolution can enlarge the receptive field. As a result, semantic information from a large spatial region can be captured in this way. Furthermore, with multiscale configurations of dilated convolution, multiscale contexts can easily be accumulated together for convolutional operations. Thus, the combination of the PGM and dilated convolution can be achieved by spatial context weighting.
Based on the above analyses, a Densely Connected PGM (DC-PGM) was designed that is performed at the highest layer of the CNN (namely, the ResNet101). The structure of DC-PGM is demonstrated in the bottom-left of Figure 1. Specifically, dilated convolution is performed in three context scales. Operation “Conv 3 × 3 (d = 3)”, for example, stands for dilated convolution with dilation rate d equal to 3 and pixel stride equal to 1. That is, d is set to be 3, 6 and 12, respectively. Then, the PGM and dilated convolution are combined to capture multiscale context information where PGM takes the output of one dilated convolution and the original Feature Maps (FMs) as its input to guide multiscale feature fusion. Symbol “∘” means feature-copy operation. Topologically, this yields a structure in which PGMs are densely connected. As a result, context information with three scales can be fully utilized to improve performance. Finally, with concatenation operation “©”, the output of ResNet101 at the highest level and the outputs of the PGMs at the three context scales are concatenated together. In this way, four scales of context information are actually fused together.
3.3. L-GCNN Neural Architecture
Based on the above PGM and DC-PGM designs, a Learnable Gated CNN (L-GCNN) was developed for RS image semantic segmentation. Figure 1 illustrates its architecture. In this model, the encoder part for feature learning was constructed on ResNet-101 [42]. ResNet-101 is a well-structured module and details can be found in Reference [42]. In addition, the architectures of the Shortcut Convolution Module (SCM) and Squeeze-and-Excitation Module (SEM) can be found in References [30,43], respectively.
As demonstrated in Figure 1, the L-GCNN consists of two parts. The first part is the encoder that is responsible for feature extraction from the input images. As ResNet is capable of developing a deeper network with high efficiency for training by shortcut connections, the 101-layer ResNet (named as ResNet101 [42]) was employed to fulfil this task.
The second part in the L-GCNN is the decoder for pixel-level classification to achieve the goal of semantic segmentation. It performs five-level information fusion, corresponding, respectively, to the size of “ , , , , ”, where w stands for the width of the image. At the highest level (Level 5 in Figure 1), it contains two modules: DC-PGM and SCM. All the remainder levels consist of the modules of SCM, SEM and PGM. Note that, at the lowest lever (Level 1 in Figure 1 ), operation “” was employed to map the output of the decoder for label inferring.
Table 1 gives the L-GCNN configuration. The ResNet101 with 99 convolution layers was employed to learn the feature maps at five levels. In Table 1, symbol “3×3, 64”, for example, indicates that 64 channels are output by convolutional operations with 3×3 kernel size on the feature-map channel. In SEM [43], for example, “GP-FC-4-FC” stands for the operation in the “global pooling layer, fully connected layer and fully connected layer” subnetwork, with four nodes between two fully connected layers. The configurations of the PGM and DC-PGM gear to structures shown in Figure 1. In addition, in ResNet101 and SCM, a ReLU layer is performed immediately after each group of convolutional operations in the bracket.

Table 1.
L-GCNN configuration. Here, C stands for number of objects to be segmented, “/2” indicates that strides for convolution are equal to 2 and “×” outside the bracket indicates that the convolution group in the bracket is repeated by the following numbers.
Finally, it is worth pointing out that, in Figure 1 the combination of the three modules of SCM, SEM and PGM is performed at levels 4, 3, 2 and 1, in order. This treatment renders a new characteristic for multilevel feature fusion in that both the spatial importance and channel importance of the feature maps are considered with adequate nonlinearity via the deeper network. As a result, in the decoder phase, abstract features could be filtered out well for semantic segmentation.
3.4. Training and Inference
In the learning stage, the original RS images and their segmented images are employed to train the model. All of them are previously repaired in the same size with , where w and h stand for the width and height of the image, respectively. As the segmentation task is essentially multicategory classification for pixels, normalized cross-entropy loss is used as the learning objective. For each image and its segmented (ground truth), the predicted segmentation is denoted by . Then, the loss for image is defined as follows:
where collects all parameters in the L-GCNN, C is the number of categories, is the truth function, is the i-th pixel in image , is the ground-truth label of and is the output of the softmax layer at the k-th channel for pixel .
Note that the above loss function is also used to define loss in the PGM. Correspondingly, ground truth Is downsampled to be fitting to the same size at the j-th level. For example, at the fourth level, the width and height of are equal to one quarter of those of the original image. Formally, it can be formulated as follows:
where superscript j indicates the j-th level and the meanings of the notations correspond to those in Equation (6) for understanding.
For one training image , loss function is in total constructed as follows:
where and are two regularization parameters and indicates the vector norm. Specifically, is used to balance PGM contributions, while is employed to avoid model overfitting after training. The formulation in Equation (8) considers all losses in PGMs, including those in DC-PGM in Figure 1, to automatically cotrain the model.
The function in Equation (8) calculates loss for one image. During training, the goal is to minimize all loss for all training samples. Due to the huge memory requirement, however, supplying all of the training images into the network in one batch mode is actually impractical. Alternatively, random minibatches are constructed to train the network by multiple iterations in an end-to-end manner. Technically, the L-GCNN is trained by the methodology of error back-propagation. Stochastic gradient descent (SGD) was employed to achieve this goal.
Algorithm 1 lists the steps of how to train the L-GCNN. Learning rate associates to the step of the gradient update when using the SGD strategy to train the model. Specifically, it is trained in minibatch mode. Thus, the main loss in Equation (8), as well as the update of the parameters, are averaged on all of the images in the minibatch used in the current iteration. In addition, as L-GCNN includes more than 100 convolution layers, batch normalization is performed after each group of convolution operations to guarantee convergence of learning. The convergence condition in Step 10 is set so that the loss of the network stays unchanged at two adjacent iterations.
In the inference stage, new RS image with size equal to that of the training images is supplied to the trained L-GCNN. In this stage, no loss in the PGMs is calculated. After obtaining the output of the final softmax layer, for pixel , probability of pixel belonging to the k-th category is picked out and its finally predicted class label is determined by the following inference formulation:
As for an RS image whose size is larger than the training images, it is first cropped into several patches. After each of these patches are finally segmented, the probabilities of the overlapped regions are averaged for final inference.
| Algorithm 1: Training algorithm for the proposed L-GCNN. |
| Input: Training samples composed of images and their corresponding segmented ground truth labels , regularization parameters and , learning rate and maximum number of iterations T. Output: Network parameters in of L-GCNN.
|
4. Experiments
4.1. Data Description
The proposed approach to semantic segmentation for RS images has been evaluated on two public benchmark datasets. Figure 2 demonstrates some examples of the images and their manually segmented ground truths. As can be seen from these examples, there are many artificial objects with different sizes and confusing appearance, which poses a challenge for achieving both consistent and accurate semantic segmentation. The details are described as follows:

Figure 2.
Example images and their manually segmented ground truths in he Potsdam dataset (six categories: impervious surface, building, low vegetation, tree, car and clutter) and the Massachusetts building dataset (two categories: building and nonbuilding).
Potsdam Dataset: This dataset is constructed for the ISPRS 2D Semantic labeling challenge in Potsdam [44], which shows a typical historical city with large building blocks, narrow streets and a dense settlement structure acquired by airborne sensors. It consists of 38 true orthophoto (TOP) tiles (images). Each tile has four bands, infrared, red, green and blue channels. Corresponding Digital Surface Model (DSM) and Normalized Digital Surface Model (NDSM) data were also provided. The size of each image was pixels. The ground-sampling distance (spatial resolution) of both the TOP and the DSM was 5 cm. Thus, they were taken with a very high resolution in the field of RS image processing. Before this dataset was released by ISPRS, dense image matching with Trimble INPHO 5.6 software was used to generate DSM data, while Trimble INPHO OrthoVista was employed to generate the TOP mosaic [44]. In order to avoid hole areas without data in the TOP and the DSM, patches were selected from the central part of the TOP mosaic and the very small remaining holes in the TOP and the DSM were interpolated [44]. In this work, only the bands of red, green and blue were employed.
All of these images have been manually segmented into six categories at pixel level, impervious surfaces (imp surf), building, low vegetation (low veg), tree, car and clutter. Background objects (e.g., containers, tennis courts, swimming pools), different from the above five class of objects of interest, were collected into the clutter class. It should be pointed out that, following treatment in previous works [30,31], the class of clutter in the Potsdam dataset was not considered in the experiments, as the background accounts for a very small ratio in total image pixels. Note again that the ground truth (class labels) of only 24 images was publicly available. Accordingly, the 24 images with ground truth available were randomly divided into a training subset of 16 images and a test subset of 8 images.
Massachusetts Building Dataset: This dataset was constructed by Mnih [45], which consists of 151 aerial color (red, green and blue) images taken in the Boston area. Each image has pixels with a ground-sampling distance (spatial resolution) of 1 m. The entire dataset covers roughly 340 square kilometers, mostly urban and suburban areas and buildings of all sizes. Target maps were obtained by rasterizing building footprints obtained from the OpenStreetMap project and data were selected to regions with average omission noise level of roughly 5% or less [45]. The data were split in advance into a training subset of 141 images and a test subset of 10 images. All of these images have been segmented into two categories at pixel level, building and nonbuilding. Thus, this dataset is associated with a task of binary-class classification.
Data preprocessing for training: In experiments, to reduce the problem of overfitting and train an effective model, the trick of data augmentation was employed to enlarge the training samples. Specifically, in the training stage, each training image is first processed by the following one or combined operations: mirrors horizontally and vertically, rotation between −10 and 10 degrees and resizing with a factor between 0.5 and 1.2 (multiscale). Then, 384 × 384 patches are randomly cropped from the processed images to construct the dataset. As a result, the Potsdam dataset is finally comprised of 9600 samples for training, among which 8000 samples were employed to build up the training subset and the remaining samples were used as test samples. The Massachusetts building dataset consisted of 14,700 samples, among which 13,700 samples were used for training and the remaining were employed for testing.
4.2. Evaluation Metrics
To give a comprehensive evaluation on the performance of the different networks compared in the experiments, two overall benchmark metrics were employed, the score of the classification and the score of the Intersection over Union (). The mean value of the obtained scores on all of the test samples is then reported. For clarity, the score of each image is calculated as follows:
where denotes the set of ground-truth pixels, stands for the set of prediction pixels and “∩” and “∪” indicate the intersection and union operations between two sets, respectively. Operation indicates the number of the elements in the set.
Note that, for classification tasks, precision recall (PR) is a useful measure of prediction success when categories are imbalanced. Accordingly, PR curves are drawn to render the tradeoff between Recall and Precision on each of the categories. Technically, to this end, score maps of each category predicted by the deep-learning model are first binarized with a series of thresholds changing from 0 to 1 and these binarized results are then compared with the ground truth to obtain the values of Precision and Recall at different thresholds. In this way, the PR curves are finally drawn by taking Recall as the horizontal axis and Precision as the vertical axis.
4.3. Compared Methods and Experiment Settings
The proposed L-GCNN was compared with the six classic models developed with deep learning for semantic segmentation, which demonstrate different strategies of multiscale feature fusion for fine segmentation. The main information about these models is summarized as follows:
- FCN: a seminal work proposed by Long et al. [24] for semantic segmentation. Currently, it is usually taken as the baseline for comparison. Three versions of FCN models, FCN-32s, FCN-16s and FCN-8s, are available for public use. From them, the FCN-8s model with fine edge segmentation preserving was employed for comparison.
- SegNet: This model was actually developed on the FCN framework by employing pooling indices recorded in the encoder to fulfil nonlinear upsampling in the decoder [26]. It is now taken as a fundamental structure for comparative evaluation on semantic segmentation.
- RefineNet: It is an approach for natural-image segmentation that takes ResNet as its encoder. The performance of RefineNet has been evaluated with multiple benchmarks of natural images. The distinct characteristic of RefineNet lies in the structure design of coarse-to-fine refinement for semantic segmentation. Thus, it was also employed for comparison.
- PSPNet: The encoder of PSPNet [35] is the classical CNN. Its decoder includes a pyramid parsing module, upsampling layer and convolution layer to form final feature representation and obtain final per-pixel prediction. The distinct characteristic lies in the pyramid parsing module that fuses together features under four different pyramid scales.
- DeepLab: In DeepLab [29], atrous spatial pyramid pooling is employed to capture multiscale representations at the decoder stage. In the experiments, the ResNet101 network was employed to design its encoder. Three-scale images with 0.5, 0.75 and 1 the size of the input image were supplied to three nets of ResNet101, respectively, which were finally fused for prediction.
- GSN: This model was developed under the SegNet framework of with multilevel information fusion [30]. At the decoder stage, a gate control module was designed to automatically select adaptive features when merging multilevel feature maps. The gate function is defined on , which does not contain parameters for learning.
In the experiments, all the six above models and the proposed L-GCNN were performed in the same experiment settings within the Pytorch framework, except the differences between initializations for the hyperparameters and the parameters of the models. Technically, the guidance given by the authors in their works is followed to initialize the hyperparameters. Specifically, when using the SGD strategy to train the L-GCNN, learning rate was initially set as , which was later dropped by a decay factor of every 20 epochs. As for the two regularization parameters and in Equation (8), they were set to be 0.2 and 0.0005, respectively, in our implementation. The maximum number of iterations in Algorithm 1 was set to be 30,000. Due to the limit of GPU memory, the size of each minibatch was taken as 4 for training.
In addition, all models were pretrained with the tricks of transfer learning that are commonly used for model training in the field of deep learning [46,47]. Intrinsically, it is a technique of fine-tuning. Specifically, except for the L-GCNN, all other models are trained on PASCAL VOC 2012 [48] with a semantic-segmentation task. For the L-GCNN, parameters in the encoder are inherited from those for the ResNet101 [42] and those in the encoder part are also initialized with the pretrained models in terms of transfer learning.
4.4. Experiment Results
The quantitative scores of and obtained by the seven models on all test images in the Potsdam dataset are listed in Table 2 and Table 3, respectively. Table 4 reports the quantitative scores obtained on all test images in the Massachusetts building dataset. In this experiment, the buildings were identified as the objects of interest and thus only the scores measured on the buildings are reported here. Due to class imbalance where the ratios of the total regions belonging to the objects were largely different from each other, the two metrics of and IoU were measured, respectively, on each of the five categories. As can be seen from the comparative results in these tables, L-GCNN largely outperformed the seminal FCN and SegNet models, which were initially developed for semantic image segmentation. In addition, it is also superior to the PSPNet, RefineNet and DeepLab models, which were all designed with the idea of multiscale information fusion in large receptive fields. In structure, the L-GCNN is similar to the GSN. Compared with the GSN, the key in the L-GCNN is the design of the gate function in Equation (4), which provides a mechanism to learn the spatial importance for multilevel information fusion. The quantitative scores on the two datasets indicate the distinct improvement of the L-GCNN over the GSN, demonstrating the effectiveness of our design for RS image segmentation.

Table 2.
scores (%) obtained on Potsdam dataset. “imp surf”: “impervious surfaces”; “low veg”: “low vegetation”.

Table 3.
scores (%) obtained on Potsdam dataset.

Table 4.
Metric scores (%) obtained on Massachusetts Building Dataset. They were measured on the foreground object (the building) for comparison since there were only two categories in this task.
To give a comprehensive comparison between the models, Table 2 and Table 3 also list the mean scores of the averaged segmentations on all of the five categories in the Potsdam dataset, which were calculated from the test images. As can be seen from the comparisons, the performance of the L-GCNN outperformed other advanced models by a considerable margin on the categories, especially on the score, which is an important metric for semantic segmentation. This fact can be clearly witnessed from the tiny objects, including the car and the tree in the scenes.
Furthermore, Figure 3 shows PR curves obtained from each of the categories. To give a compact arrangement on these curves, the first five subfigures in Figure 3 were calculated on the Potsdam dataset, including the categories of impervious surfaces (imp surf), building, low vegetation (low veg), tree and car. The last subfigure was calculated on the Massachusetts building dataset, where only the curves on the building category were needed to illustrate for comparison. It is seen that PR curves obtained by the L-GCNN are always located at the top positions on all the given categories, which indicates the effectiveness of the design of the network.
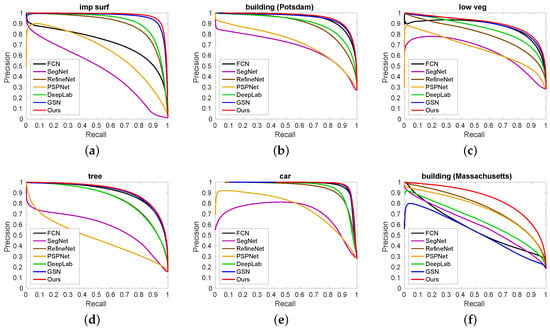
Figure 3.
Precision-recall (PR) curves obtained by all seven compared models. First five subfigures were calculated on the Potsdam dataset and the last subfigure was calculated on the Massachusetts building dataset. (a): imp surf; (b): building (Potsdam); (c): low veg; (d): tree; (e): car; and (f): building (Massachusetts).
Figure 4 and Figure 5 demonstrate segmentations of a few images obtained by the seven models, FCN, SegNet, RefineNet, PSPNet, DeepLab, GSN and the L-GCNN. For clarity, segmentation quality at different scales is demonstrated. As can be seen from these figures, the FCN, SegNet and PSPNet models had difficulty in segmenting confusing size-variable buildings in the Potsdam dataset. The obtained results by these three models rendered segmentations with low accuracy. RefineNet and DeepLab improved the quality of segmentation but clear false negatives can also be perceived from the segmentation results. Typically, they lack enough robustness to preserve the fine edges of artificial objects. In contrast, the GSN and the L-GCNN performed better. Compared with the GSN, the L-GCNN improved performance with satisfactory edge preserving. This fact can be witnessed from results with coherent segmentations on both confusing and fine-structured buildings and the tiny cars.

Figure 4.
Visual comparisons between L-GCNN (ours) and other related methods on the Potsdam dataset. Label includes six categories: impervious surface (white), building (blue), low vegetation (cyan), tree (green), car (yellow) and clutter/background (red). Here, backgrounds are directly shown as they were considered as masks when training the models.

Figure 5.
Visual comparisons between L-GCNN (ours) and other related methods on the Massachusetts building dataset. Label includes two categories: building (red) and nonbuilding (black).
In summary, the extensive comparisons above show that the L-GCNN can segment confusing artificial objects in high-resolution RS images. In addition, it is quite robust to size-changeable objects with satisfactory edge preserving. Furthermore, no poster-processing methods like conditional random field or graph cut were employed to polish the final segmentation. This fact implies that the L-GCNN can generate smooth results on complex visual regions of artificial objects. In addition, the available information of the corresponding Digital Surface Model (DSM) and Normalized DSM (NDSM) data in the Potsdam dataset was not employed to help segmentation. The above observations indicate the validity of L-GCNN refinement for RS image segmentation.
5. Discussion
5.1. Result Analysis
In order to improve the prediction accuracy of boundaries and tiny objects, each of the six classical models (FCN, SegNet, RefineNet, PSPNet, DeepLab and GSN) has its own advantages in different aspects, such as optimizations on convolutions and feature fusion. By contrast, the proposed L-GCNN mainly focuses on multiscale feature fusion.
Technically, summation and concatenation of feature maps are the most popular operations for feature fusion. Beyond the direct concatenation operation, where additional 3D convolutions should be performed on fused feature blocks, the summation operation in the L-GCNN was employed as there were a relatively small number of parameters to be learned. Considering different situations for each of the pixels can actually guarantee to yield satisfactory segmentation results. This motivated us to design the L-GCNN, that is, the L-GCNN utilizes pixel category probability at multiscales obtained from the current iteration during training and thus increases model-parameter effectiveness. This treatment not only prevents possible training overfitting but also enhances the representation capability of the model.
From a qualitative point of view, our L-GCNN kept the advantage of the GSN, namely, the gated mechanism to generate weights on different pixels in feature fusion. But from a quantitative view, associated weights with low-level features should not be limited to [0, 1]. In other words, they can be adaptively larger or smaller so as to improve segmentation accuracy. By contrast to the GSN, the feature fusion in the L-GCNN is not a fixed formula that realizes the authentic data driven in feature fusion. The main technical characteristics in the L-GCNN can be highlighted as follows:
- A gate function is proposed for multiscale feature fusion. The most distinct characteristic of our gate function lies in that it is a parameterized formulation of the Taylor expression of the information-entropy function. Beyond the entropy function with no parameters, our gate function has learnable parameters that can be learned from data. This helps increase the representation capability of our proposed L-GCNN.
- The design of a single PGM and its densely connected counterpart were embedded, respectively, into multilevels of the encoder in the L-GCNN. This strategy yields a multitask learning framework for gating multiscale information fusion, from which discriminative features can be extracted at multiscales of receptive fields.
- Topologically, our L-GCNN is a self-cascaded end-to-end architecture that is able to sequentially aggregate context information. Upon this architecture, pixelwise importance identified by the PGMs can be transferred from high to low level, achieving global-to-local refinement for the semantical segmentation of remote-sensing objects.
5.2. Parameter Sensitivity
As can be seen from previous sections, the performance of the L-GCNN is associated with the learnable gate function, the design of the PGMs and the training strategy of the model. Therefore, this subsection mainly discusses the above issues in light of the above aspects in order to better analyze their effects on semantic segmentation. As the Potsdam dataset is a public benchmark containing multiple categories in this work, the investigation was made experimentally with this dataset.
First, the power of the gate function in Equation (4) was analyzed. Note that it is formulated as a polynomial. When training the L-GCNN, the highest order of the polynomial should be given in advance. Let n denote the highest order. Table 5 lists the performance of the gate function with n equal to 2, 3, 4, 5 and 6, respectively, where the two scores of the segmentation accuracy and the are measured on all five object categories in the test images in the Potsdam dataset. Other experiment settings are the same as those used in Section 4.4. For simplicity, scores here were obtained on the models trained without the help of the augmented multiscale samples. It can be seen that, when n is larger than 3, performance is not largely improved. Thus, it is recommended to set n to 5 in usage.

Table 5.
Performance of the gate function with different polynomial orders in the L-GCNN. Here, segmentation accuracy and IoU scores (%) reported for comparison. None of the augmented multiscale samples was employed for training.
Second, the effects of the training strategy were investigated with different values of the important parameters, including regularization parameters and in the objective function in Equation (8) and learning rate when employing the GSD strategy to train the model. Parameter acts as a tradeoff between the designs of PGMs and non-PGMS, while is a factor of weight decay that is related to avoiding network overfitting. Learning rate is associated with quality of convergence. To this end, the performance of these parameters within a large range was investigated. Specifically, the value set for was taken as , the set for is taken as and that for was in order. Figure 6 demonstrates their effect on segmentation in terms of segmentation accuracy and score on the Potsdam dataset. Besides the parameter currently evaluated, other experiment settings were the same as those used in Section 4.4. It is seen that all of these parameters could yield better performance in a large region but it may degreethe performance with a small or a large value. Thus, it is recommended to have the values of , and as , and , respectively, in usage.
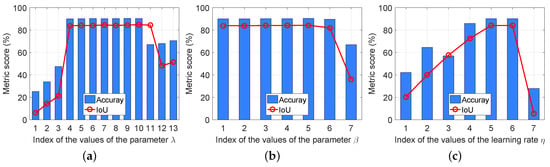
Figure 6.
Effects of regularization parameters and in the objective function in Equation (8) and learning rate when employing GSD strategy to train the model. Scores were obtained on the Potsdam dataset. Metric scores of (a): parameter ; (b) parameter ; and (c): parameter .
Finally, the effect of the PGMs in Section 3.1 was analyzed. To this end, all modules of the PGMs and the DC-PGM are removed in this process. This treatment yielded a reduced model that was evaluated along with original model L-GCNN in the same experiment settings. The highest polynomial order of the gate function was set to be 5 in the experiments. Table 6 reports the metric scores of the segmentations on the Potsdam dataset. Compared with the reduced model, it is seen that the L-GCNN with gate function largely improved performance by a considerable margin on each category, typically on the easily confusing category of “impervious surfaces” and the tiny objects of cars. This fact indicates the validity of our design.

Table 6.
Comparisons between reduced model and L-GCNN with segmentation accuracy and IoU scores (%). Note that here none of the augmented multiscale samples were employed for training.
5.3. Model Complexity
This subsection analyzes the computational complexity of the L-GCNN. For comprehensive analysis, it is compared with the related six networks, FCN, SegNet, RefineNet, PSPNet, DeepLab and GSN. Table 7 outlines factors related to computational complexity, including total number of the FLoating-point OPerations (FLOPs) in terms of Giga Multiplier ACcumulators (GMACs) and the number of network parameters.

Table 7.
Computational complexity, including total number of the FLoating-point OPerations (FLOPs), number of network parameters and average test time for each image of pixels on a TITAN Xp GPU with 12G RAM.
For comparison, averaged test time is also reported in Table 7. It was evaluated on images of pixels, which was fulfilled on a TITAN Xp GPU with 12G RAM. As can be seen, computation scale in the L-GCNN was largely reduced to a certain degree compared with FCN, SegNet, RefineNet, PSPNet and DeepLab. It was slightly larger than that of the GSN. However, the total number of parameters in the L-GCNN stands at the median level. Accordingly, average test time was also at the same level among the models.
5.4. Implications and Limitations
The main function of the gated mechanism in PGM module is to improve segmentation accuracy on the details of RS images. In our L-GCNN, multiple PGMs were embedded, respectively, into multilevels of the encoder that could automatically recognize objects with different sizes. In recent years, with the continuous development of remote-sensing satellite sensors, many details that have been overlooked in low-resolution images surface today. Therefore, improving the segmentation accuracy of tiny objects is an urgent problem to be solved in the future. In addition, there are many objects with various scales in RS images due to top-view imagery. Obviously, recognition of multiscale objects is also a difficulty in semantic segmentation.
Beyond that, however, traditionally fixed weighting computation for information fusion has been reconsidered as one that can be learned from data. To this end, the Taylor expression of a nonlinear function was employed to achieve this goal, which was further formulated as a polynomial with parameters and embedded into the network architecture. Such a formulation may render a trick of commonly used generalization from nonlinear function with no parameters to that with learnable parameters. This helps increase the representation capability of the network. Therefore, one can reconsider many similar tasks in the fields of RS image processing, where explicate nonlinearity governs the processes, by transforming them to be neural networks for learning from data.
Methodologically, however, the proposed L-GCNN model was developed on a classical convolutional neural network for semantical segmentation. It has several limitations, as follows:
- As reported in Table 7, the L-GCNN has more than 54 million network parameters. Such a huge model requires to be trained with high-performance computing resources (like a computing server with GPUs), which limits its usage in real-time semantical segmentation, embedded systems and other situations with limited computational resource like those on orbiting satellites. This drawback could be overcome by using the technique of model compression and more effective topology with neural architecture search.
- The L-GCNN should be trained with a large number of samples. For example, on the Potsdam dataset, there were 8000 samples in total, well-labeled for training. That is, good performance may not be guaranteed due to the small size of sample sets. However, in the field of RS image processing, public samples with truthful ground truth are very limited. One way to overcome this point is to embed prior knowledge related to the task of semantic segmentation into the network. Another way is to employ a generative adversarial network to yield more samples.
- The L-GCNN has no capability to treat new situations with different sample distributions and unseen categories. Its performance could largely be reduced on unseen or adversarial samples. In the future, its generalization power could be overcome by introducing a mechanism in the network to allow online learning in terms of domain adaption, deep transfer learning and deep reinforcement learning.
6. Conclusions
In this work, an L-GCNN has been proposed for semantic segmentation in high-resolution RS images. The proposed L-GCNN is an end-to-end learning system that can achieve excellent performance with the following three characteristics. First, a PGM was developed to integrate multilevel feature maps together in way of pixelwise weighting. The distinct merit in the PGM design lies in that the gate function has parameterized formulation for learning to select feature maps on spatial positions. Second, the design of the single PGM and its densely connected extension was embedded into multilevels of the encoder in the L-GCNN to help identify the discriminative features at different scales. Third, as a whole, the L-GCNN is a self-cascaded architecture to sequentially aggregate context information for the segmentation of artificial objects with large variations in visual appearance and size. With these well-motivated topological designs, the L-GCNN can effectively implement semantic segmentation in a manner of global-to-local and coarse-to-fine refinement.
Extensive comparative experiments demonstrated the advantages of the proposed L-GCNN, in that it can achieve more accurate segmentation performance on both quantitative measurement and visual evaluation compared with the related models. In the future, we aim to employ the design of PGM to solve other tasks in the field of RS image processing, including fine-object localization, change detection and object recognition in hyperspectral and SAR images. Furthermore, we aim to study the limitations addressed in this work for related real-world applications.
Author Contributions
S.G., Q.J. and H.W. designed the deep learning model and performed the experiments; S.G. and S.X. wrote the paper. X.W. guided the design of the network and checked the experiments; Y.W. reviewed the paper.
Funding
This work was supported in part by the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDA19020103), the National Key Research and Development Project (Grant No. 2017YFB0202202) and the National Natural Science Foundation of China (Grant No. 91646207).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bruzzone, L.; Demir, B. A review of modern approaches to classification of remote sensing data. In Land Use and Land Cover Mapping in Europe; Springer: Berlin/Heidelberg, Germany, 2014; pp. 127–143. [Google Scholar]
- Ghamisi, P.; Dalla Mura, M.; Benediktsson, J.A. A survey on spectral–spatial classification techniques based on attribute profiles. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2335–2353. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, L.; Du, B. Deep learning for remote sensing data: A technical tutorial on the state of the art. IEEE Geosci. Remote Sens. Mag. 2016, 4, 22–40. [Google Scholar] [CrossRef]
- Cheng, G.; Han, J.; Lu, X. Remote Sensing Image Scene Classification: Benchmark and State of the Art. arXiv 2017, arXiv:1703.00121. [Google Scholar] [CrossRef]
- Sladojevic, S.; Arsenovic, M.; Anderla, A.; Culibrk, D.; Stefanovic, D. Deep Neural Networks Based Recognition of Plant Diseases by Leaf Image Classification. Comput. Intell. Neurosci. 2016, 2016, 3289801. [Google Scholar] [CrossRef] [PubMed]
- Singh, V.; Misra, A. Detection of plant leaf diseases using image segmentation and soft computing techniques. Inf. Process. Agric. 2017, 4, 41–49. [Google Scholar] [CrossRef]
- Lu, J.; Hu, J.; Zhao, G.; Mei, F.; Zhang, C. An in-field automatic wheat disease diagnosis system. Comput. Electron. Agric. 2017, 142, 369–379. [Google Scholar] [CrossRef]
- Golhani, K.; Balasundram, S.K.; Vadamalai, G.; Pradhan, B. A review of neural networks in plant disease detection using hyperspectral data. Inf. Proc. Agric. 2018, 5, 354–371. [Google Scholar] [CrossRef]
- Al-Saddik, H.; Laybros, A.; Billiot, B.; Cointault, F. Using Image Texture and Spectral Reflectance Analysis to Detect Yellowness and Esca in Grapevines at Leaf-Level. Remote Sens. 2018, 10, 618. [Google Scholar] [CrossRef]
- Dang, L.M.; Hassan, S.I.; Suhyeon, I.; Sangaiah, A.K.; Mehmood, I.; Rho, S.; Seo, S.; Moon, H. UAV based wilt detection system via convolutional neural networks. Sustain. Comput. Inf. Syst. 2019. [Google Scholar] [CrossRef]
- Matikainen, L.; Karila, K. Segment-based land cover mapping of a suburban area-comparison of high-resolution remotely sensed datasets using classification trees and test field points. Remote Sens. 2011, 3, 1777–1804. [Google Scholar] [CrossRef]
- Wen, D.; Huang, X.; Liu, H.; Liao, W.; Zhang, L. Semantic Classification of Urban Trees Using Very High Resolution Satellite Imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 1413–1424. [Google Scholar] [CrossRef]
- Xie, F.; Shi, M.; Shi, Z.; Yin, J.; Zhao, D. Multilevel Cloud Detection in Remote Sensing Images Based on Deep Learning. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3631–3640. [Google Scholar] [CrossRef]
- Liu, C.C.; Zhang, Y.C.; Chen, P.Y.; Lai, C.C.; Chen, Y.H.; Cheng, J.H.; Ko, M.H. Clouds Classification from Sentinel-2 Imagery with Deep Residual Learning and Semantic Image Segmentation. Remote Sens. 2019, 11, 119. [Google Scholar] [CrossRef]
- Zhang, P.; Gong, M.; Su, L.; Liu, J.; Li, Z. Change detection based on deep feature representation and mapping transformation for multi-spatial-resolution remote sensing images. ISPRS J. Photogramm. Remote Sens. 2016, 116, 24–41. [Google Scholar] [CrossRef]
- Lu, X.; Yuan, Y.; Zheng, X. Joint Dictionary Learning for Multispectral Change Detection. IEEE Trans. Cybern. 2017, 47, 884–897. [Google Scholar] [CrossRef]
- Tang, Y.; Zhang, L. Urban change analysis with multi-sensor multispectral imagery. Remote Sens. 2017, 9, 252. [Google Scholar] [CrossRef]
- Audebert, N.; Saux, B.L.; Lefevre, S. Segment-before-Detect: Vehicle Detection and Classification through Semantic Segmentation of Aerial Images. Remote Sens. 2017, 9, 368. [Google Scholar] [CrossRef]
- Li, E.; Femiani, J.; Xu, S.; Zhang, X.; Wonka, P. Robust Rooftop Extraction From Visible Band Images Using Higher Order CRF. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4483–4495. [Google Scholar] [CrossRef]
- Xu, S.; Pan, X.; Li, E.; Wu, B.; Bu, S.; Dong, W.; Xiang, S.; Zhang, X. Automatic Building Rooftop Extraction From Aerial Images via Hierarchical RGB-D Priors. IEEE Trans. Geosci. Remote Sens. 2018, 56, 7369–7387. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, Q.; Wang, Y. Road Extraction by Deep Residual U-Net. IEEE Geosci. Remote Sens. Lett. 2018, 15, 749–753. [Google Scholar] [CrossRef]
- Xu, Y.; Xie, Z.; Feng, Y.; Chen, Z. Road Extraction from High-Resolution Remote Sensing Imagery Using Deep Learning. Remote Sens. 2018, 10, 1416. [Google Scholar] [CrossRef]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-Based Learning Applied to Document Recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 79, 1337–1342. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. Segnet: A deep convolutional encoder-decoder architecture for image segmentation. arXiv 2015, arXiv:1511.00561. [Google Scholar] [CrossRef] [PubMed]
- Noh, H.; Hong, S.; Han, B. Learning Deconvolution Network for Semantic Segmentation. In Proceedings of the IEEE International Conference on Computer Vision, Las Condes, Chile, 11–18 December 2015; pp. 1520–1528. [Google Scholar]
- Lin, G.; Milan, A.; Shen, C.; Reid, I.D. RefineNet: Multi-Path Refinement Networks for High-Resolution Semantic Segmentation. arXiv 2016, arXiv:1611.06612. [Google Scholar]
- Chen, L.C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. Deeplab: Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected crfs. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 834–848. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Wang, Y.; Zhang, Q.; Xiang, S.; Pan, C. Gated Convolutional Neural Network for Semantic Segmentation in High-Resolution Images. Remote Sens. 2017, 9, 446. [Google Scholar] [CrossRef]
- Liu, Y.; Fan, B.; Wanga, L.; Bai, J.; Xiang, S.; Pan, C. Semantic Labeling in very High Resolution Images via A Self-cascaded Convolutional Neural Network. ISPRS J. Photogramm. Remote Sens. 2018, 145, 78–95. [Google Scholar] [CrossRef]
- Li, L.; Yao, J.; Liu, Y.; Yuan, W.; Shi, S.; Yuan, S. Optimal Seamline Detection for Orthoimage Mosaicking by Combining Deep Convolutional Neural Network and Graph Cuts. Remote Sens. 2017, 9, 701. [Google Scholar] [CrossRef]
- Panboonyuen, T.; Jitkajornwanich, K.; Lawawirojwong, S.; Srestasathiern, P.; Vateekul, P. Semantic Segmentation on Remotely Sensed Images Using an Enhanced Global Convolutional Network with Channel Attention and Domain Specific Transfer Learning. Remote Sens. 2019, 11, 83. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Zhao, H.; Shi, J.; Qi, X.; Wang, X.; Jia, J. Pyramid Scene Parsing Network. arXiv 2016, arXiv:1612.01105. [Google Scholar]
- Sherrah, J. Fully convolutional networks for dense semantic labelling of highresolution aerial imagery. arXiv 2016, arXiv:1606.02585. [Google Scholar]
- Alshehhi, R.; Marpu, P.R.; Woon, W.L.; Mura, M.D. Simultaneous extraction of roads and buildings in remote sensing imagery with convolutional neural networks. ISPRS J. Photogramm. Remote Sens. 2017, 130, 139–149. [Google Scholar] [CrossRef]
- Chen, K.; Fu, K.; Yan, M.; Gao, X.; Sun, X.; Wei, X. Semantic Segmentation of Aerial Images With Shuffling Convolutional Neural Networks. IEEE Geosci. Remote Sens. Lett. 2018, 15, 173–177. [Google Scholar] [CrossRef]
- Chen, G.; Zhang, X.; Wang, Q.; Dai, F.; Gong, Y.; Zhu, K. Symmetrical Dense-Shortcut Deep Fully Convolutional Networks for Semantic Segmentation of Very-High-Resolution Remote Sensing Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1633–1644. [Google Scholar] [CrossRef]
- Persello, C.; Stein, A. Deep Fully Convolutional Networks for the Detection of Informal Settlements in VHR Images. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2325–2329. [Google Scholar] [CrossRef]
- Yuan, J. Learning Building Extraction in Aerial Scenes with Convolutional Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 2793–2798. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-Excitation Networks. In Proceedings of the IEEE International Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 7132–7141. [Google Scholar]
- ISPRS. 2D Semantic Labeling Challenge by International Society for Photogrammetry and Remote Sensing. Available online: http://www2.isprs.org/commissions/comm3/wg4/semantic-labeling.html (accessed on 16 August 2019).
- Mnih, V. Machine Learning for Aerial Image Labeling. Ph.D. Thesis, University of Toronto, Toronto, ON, Canada, 2013. [Google Scholar]
- Yosinski, J.; Clune, J.; Bengio, Y.; Lipson, H. How Transferable are Features in Deep Neural Networks. In Neural Information Processing Systems; Mit Press: Cambridge, MA, USA, 2014; pp. 3320–3328. [Google Scholar]
- Penatti, O.A.; Nogueira, K.; dos Santos, J.A. Do deep features generalize from everyday objects to remote sensing and aerial scenes domains. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshop, Boston, MA, USA, 7–12 June 2015; pp. 44–51. [Google Scholar]
- Everingham, M.; Eslami, S.M.A.; Gool, L.J.V.; Williams, C.K.I.; Winn, J.M.; Zisserman, A. The Pascal Visual Object Classes Challenge: A Retrospective. Int. J. Comput. Vis. 2015, 111, 98–136. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).