Application of Laplace Domain Waveform Inversion to Cross-Hole Radar Data
Abstract
1. Introduction
2. Methods
2.1. Laplace-Transformed Wavefield
2.2. Forward Problem
2.3. Inversion Problem
3. Results
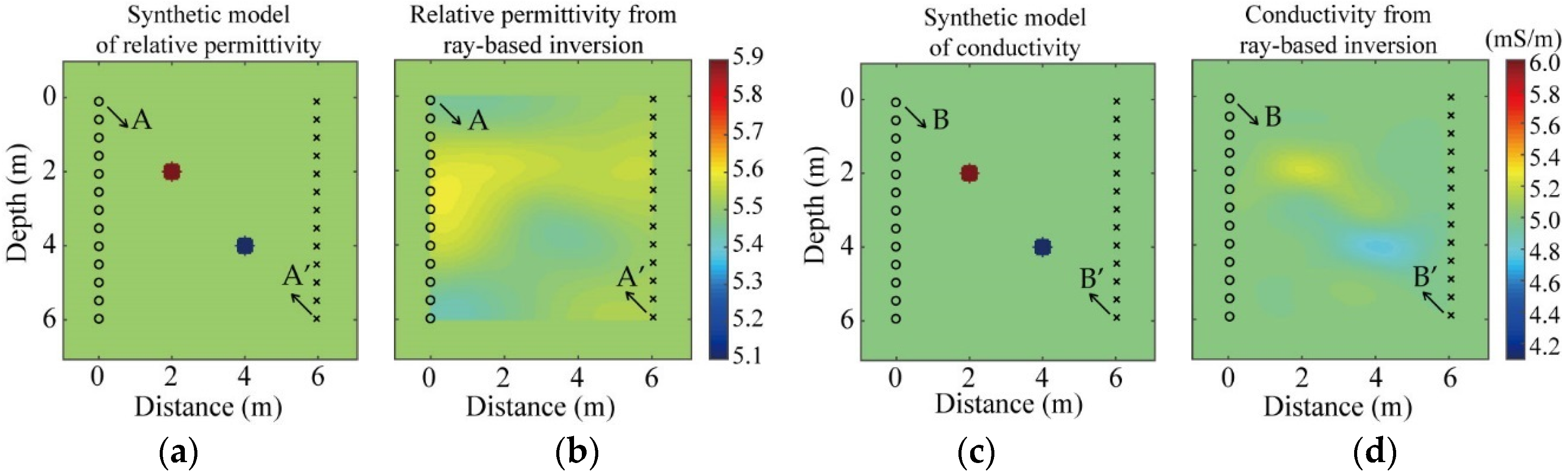
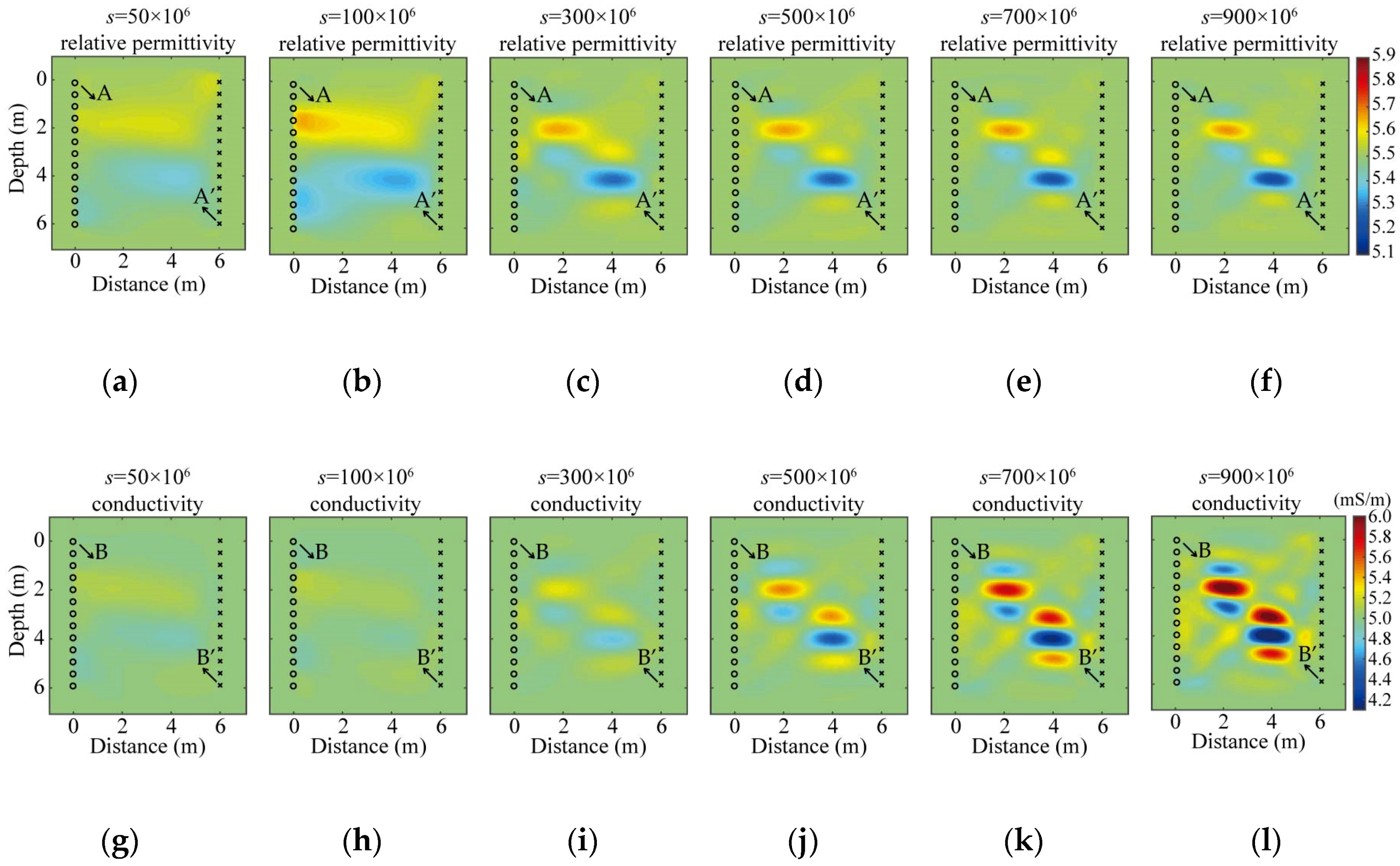
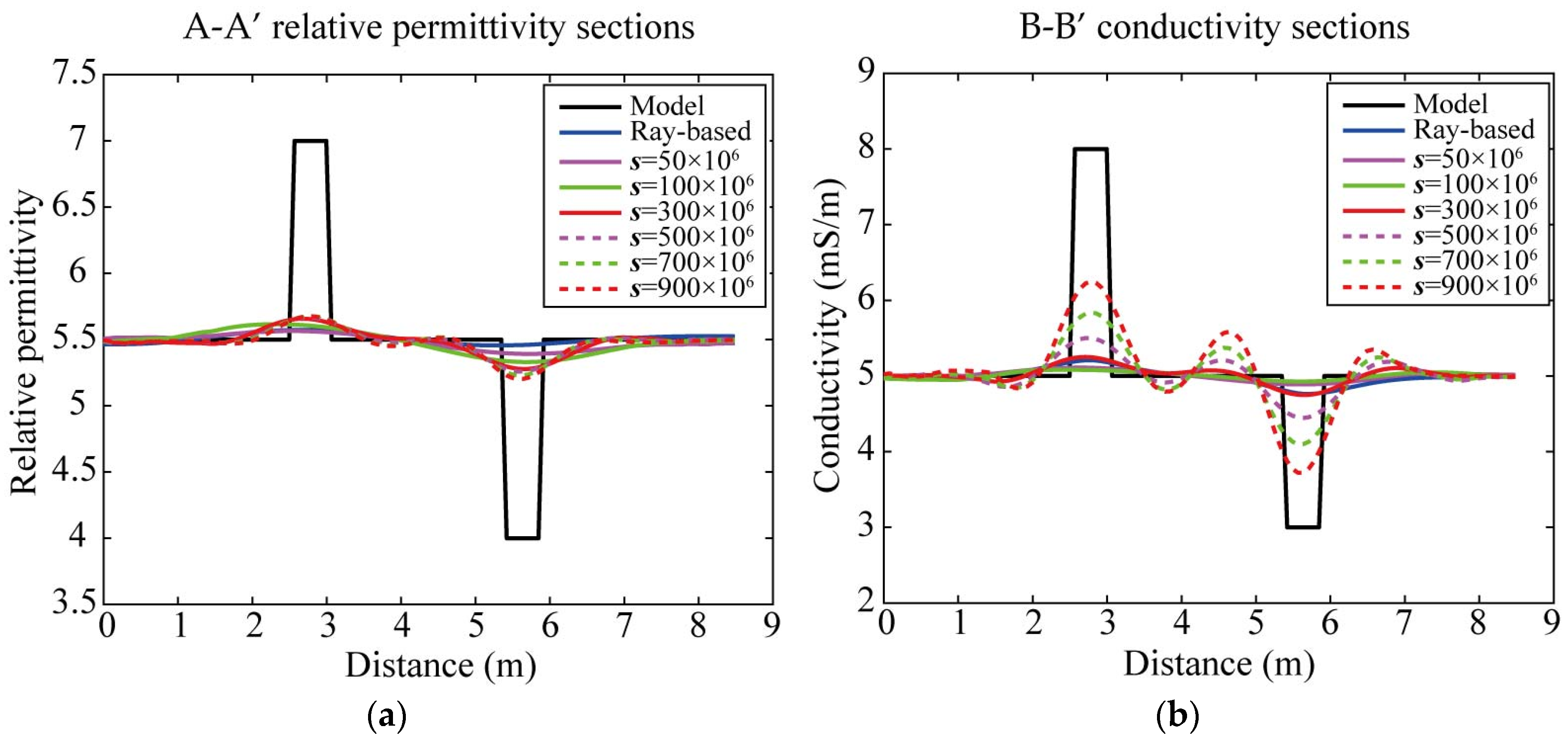
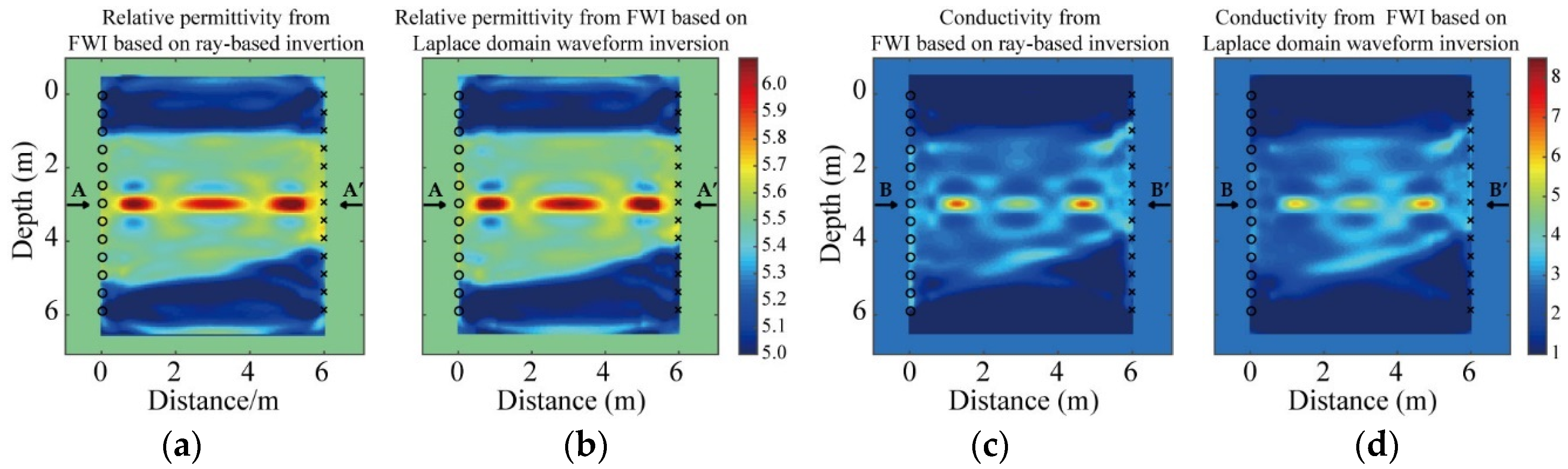
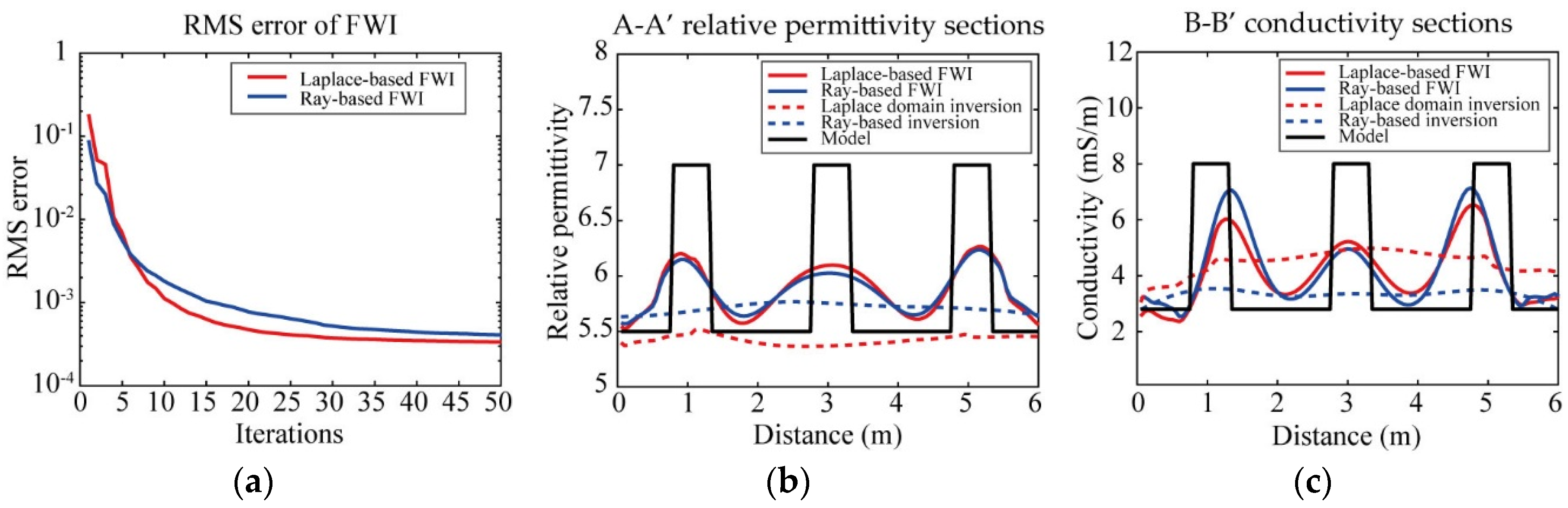
3.1. Synthetic Data 1: A Simple Model
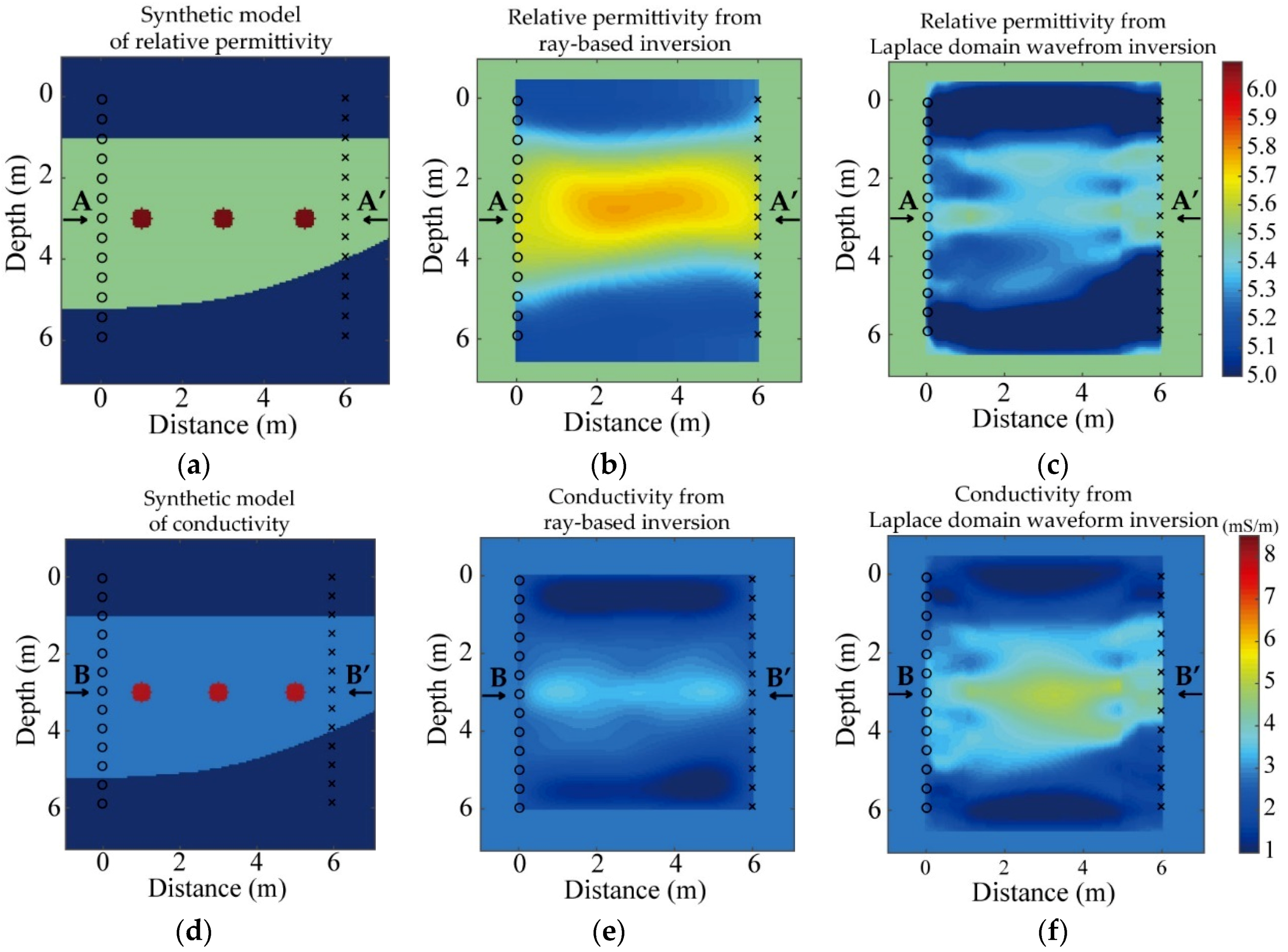
3.2. Synthetic Data 2: A Complex Model
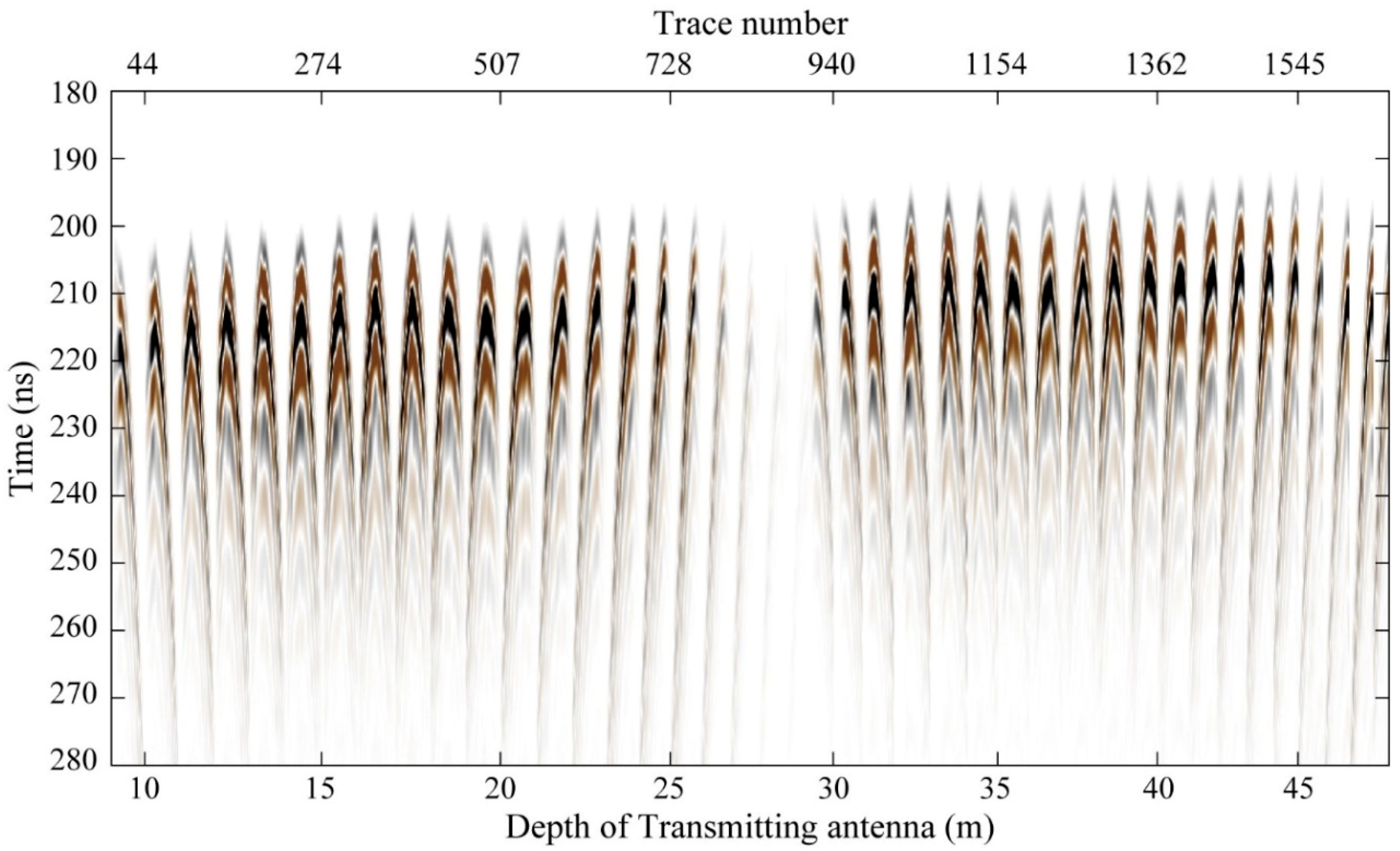
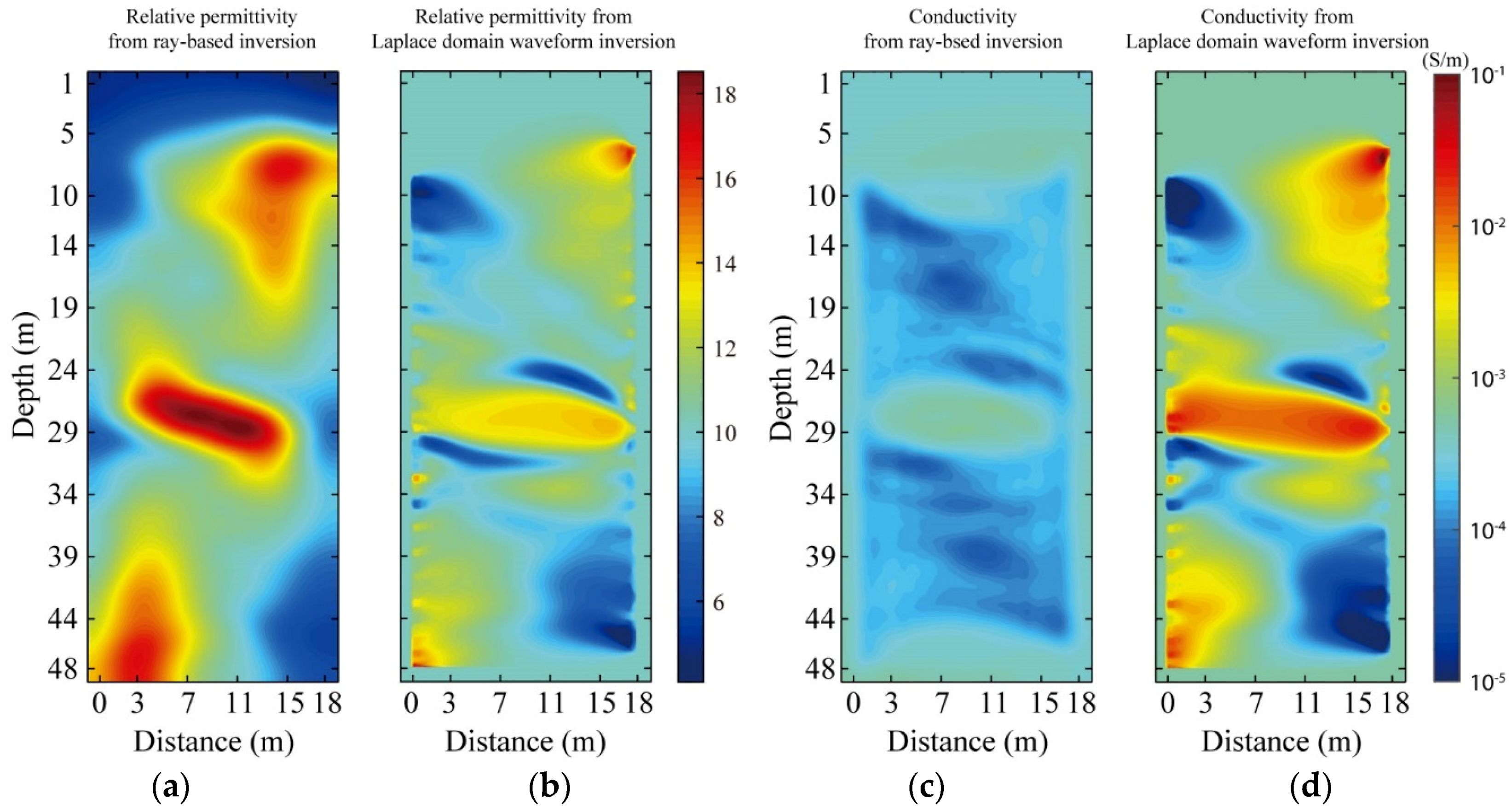
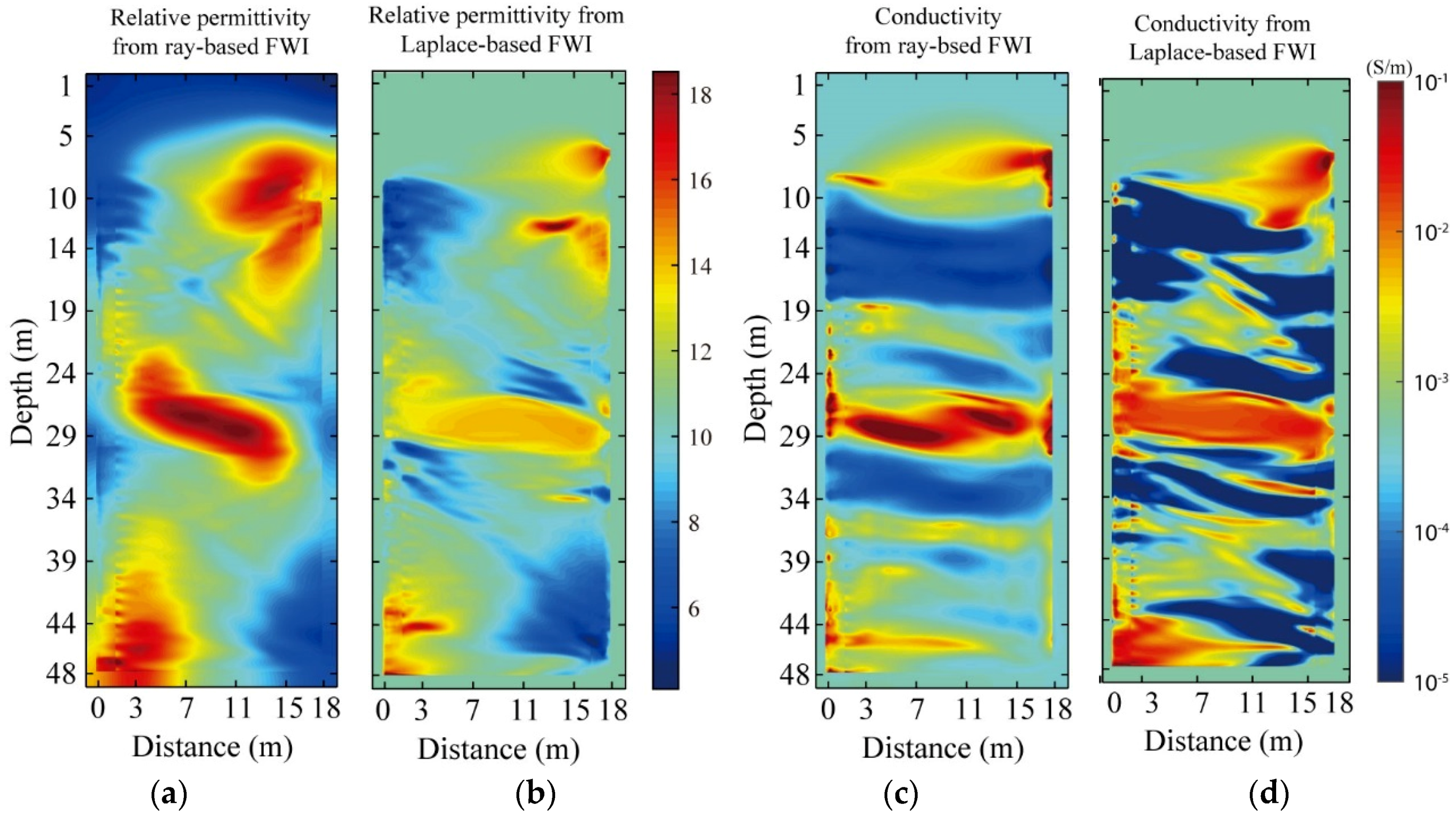
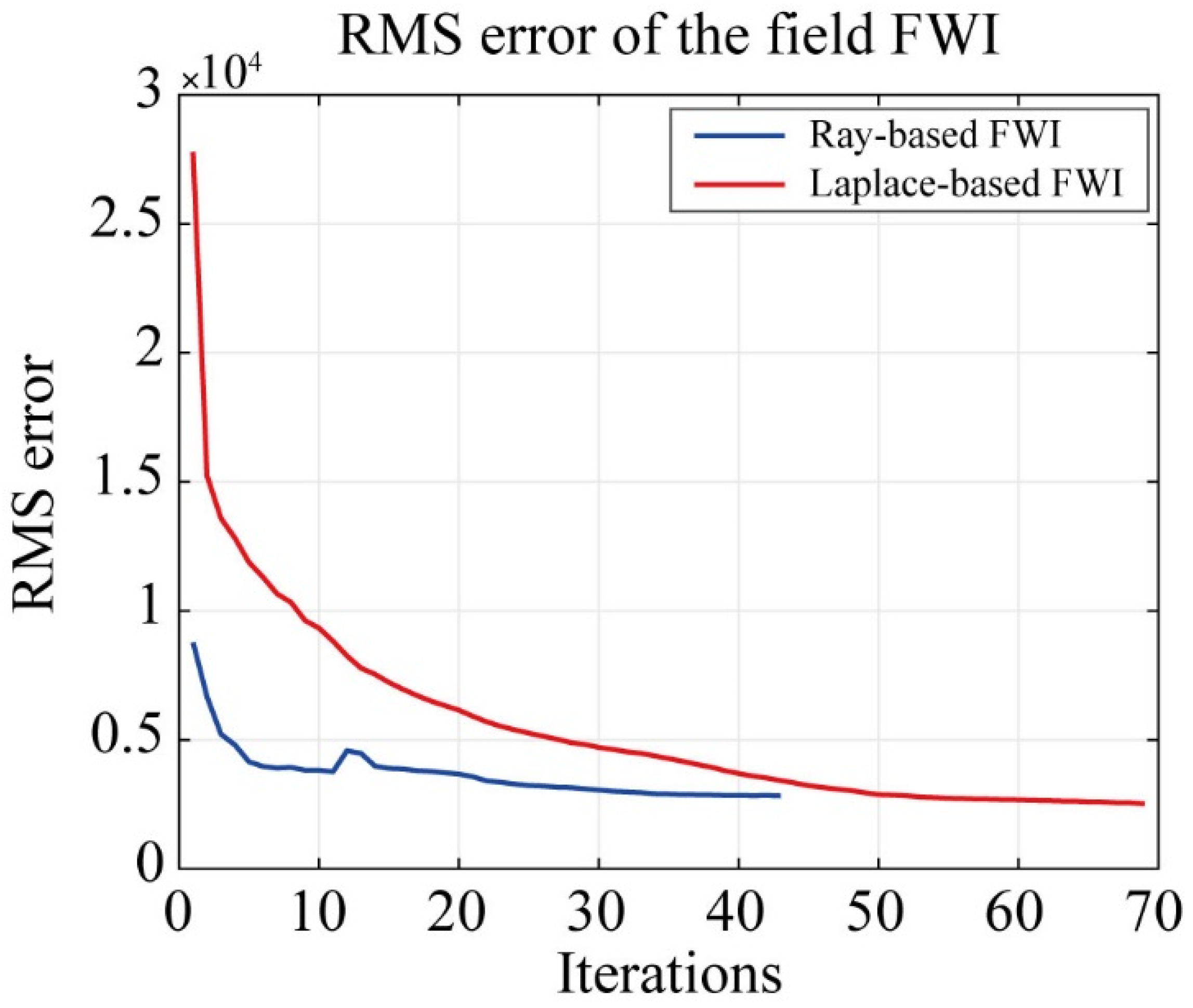
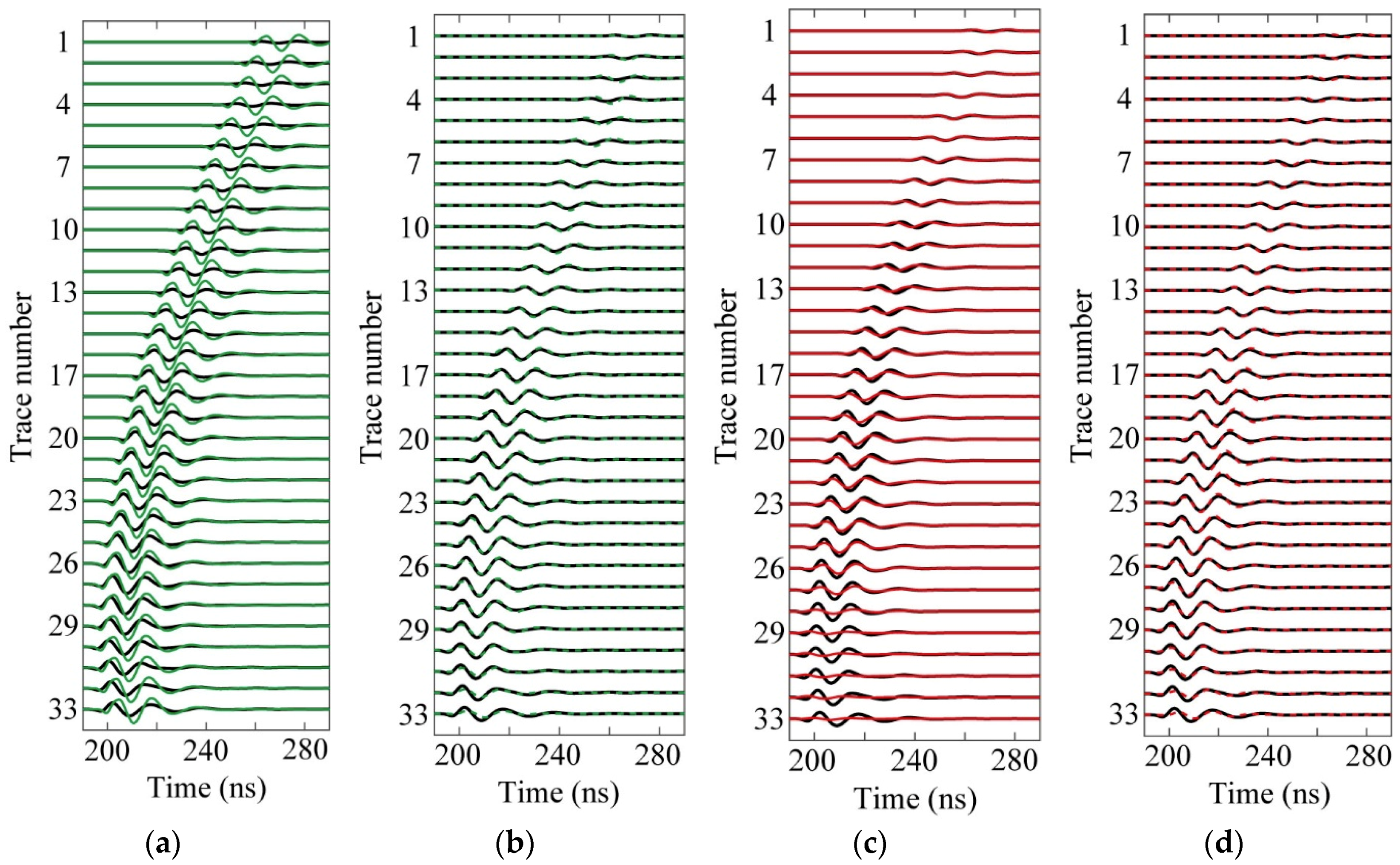
3.3. Field Data Measured at Guizhou
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Source Index | Source Position (m) | Traces Number | First Receiver Position (m) | Final Receiver Position (m) |
|---|---|---|---|---|
| 1 | 9 | 43 | 8 | 29 |
| 2 | 10 | 45 | 7.5 | 29.5 |
| 3 | 11 | 46 | 7 | 29.5 |
| 4 | 12 | 45 | 7 | 29 |
| 5 | 13 | 46 | 6.5 | 29 |
| 6 | 14 | 48 | 6.5 | 30 |
| 7 | 15 | 47 | 6.5 | 29.5 |
| 8 | 16 | 46 | 7 | 29.5 |
| 9 | 17 | 47 | 6.5 | 29.5 |
| 10 | 18 | 46 | 7 | 29.5 |
| 11 | 19 | 47 | 7 | 30 |
| 12 | 20 | 47 | 7 | 30 |
| 13 | 21 | 46 | 7.5 | 30 |
| 14 | 22 | 44 | 8.5 | 30 |
| 15 | 23 | 43 | 8 | 29 |
| 16 | 24 | 41 | 9 | 29 |
| 17 | 25 | 39 | 10 | 29 |
| 18 | 26 | 38 | 10.5 | 29 |
| 19 | 27 | 38 | 12 | 30.5 |
| 20 | 28 | 36 | 13 | 30.5 |
| 21 | 29 | 61 | 14 | 44 |
| 22 | 30 | 37 | 26 | 44 |
| 23 | 31 | 41 | 26.5 | 46.5 |
| 24 | 32 | 47 | 23.5 | 46.5 |
| 25 | 33 | 49 | 23 | 47 |
| 26 | 34 | 40 | 27 | 46.5 |
| 27 | 35 | 40 | 27 | 46.5 |
| 28 | 36 | 42 | 25.5 | 46 |
| 29 | 37 | 43 | 25.5 | 46.5 |
| 30 | 38 | 40 | 27 | 46.5 |
| 31 | 39 | 43 | 25 | 46 |
| 32 | 40 | 38 | 27.5 | 46 |
| 33 | 41 | 39 | 27 | 46 |
| 34 | 42 | 36 | 29 | 46.5 |
| 35 | 43 | 37 | 28.5 | 46.5 |
| 36 | 44 | 33 | 30.5 | 46.5 |
| 37 | 45 | 33 | 30.5 | 46.5 |
| 38 | 46 | 33 | 30.5 | 46.5 |
| 39 | 47 | 31 | 31.5 | 46.5 |
| 40 | 48 | 22 | 36 | 46.5 |
References
- Daniels, D.J. Ground Penetrating Radar, 2nd ed.; The Institution of Engineering and Technology: London, UK, 2004. [Google Scholar]
- Olsson, O.; Falk, L.; Forslund, O.; Lundmark, L. Borehole radar applied to the characterization of hydraulically conductivity fracture-zones in crystalline rock. Geophys. Prospect. 1992, 40, 109–142. [Google Scholar] [CrossRef]
- Fullagar, P.K.; Livelybrooks, D.W.; Zhang, P.; Calvert, A.J.; Wu, Y. Radio tomography and borehole radar delineation of the McConnell nickel sulfide deposit, Sudbury, Ontario, Canada. Geophysics 2000, 65, 1920–1930. [Google Scholar] [CrossRef]
- Irving, J.D.; Knight, R.J. Effect of antennas on velocity estimates obtained from crosshole GPR data. Geophysics 2005, 70, K39–K42. [Google Scholar] [CrossRef]
- Wang, F.; Liu, S.X.; Qu, X.X. Crosshole radar traveltime tomographic inversion using the fast marching method and the iteratively linearized scheme. J. Environ. Eng. Geophys. 2014, 19, 229–237. [Google Scholar] [CrossRef]
- Zhang, J.; Toksoz, M.N. Nonlinear refraction traveltime tomography. Geophysics 1998, 63, 1496–1823. [Google Scholar] [CrossRef]
- Liu, L.; Lane, J.W.; Quan, Y. Radar attenuation tomography using the centroid frequency downshift method. J. Appl. Geophys. 1998, 40, 105–116. [Google Scholar] [CrossRef]
- Williamson, P.R. A guide to the limits of resolution imposed by scattering in ray tomography. Geophysics 1991, 56, 202–207. [Google Scholar] [CrossRef]
- Williamson, P.R.; Worthington, M.H. Resolution limits in ray tomography due to wave behavior—Numerical experiments. Geophysics 1993, 58, 727–735. [Google Scholar] [CrossRef]
- Tarantola, A.; Valette, B. Generalized no-linear inverse problems solved using the least-squares criterion. Rev. Geophys. 1982, 20, 219–232. [Google Scholar] [CrossRef]
- Devaney, A.J. Geophysical diffraction tomography. IEEE Trans. Geosci. Remote Sens. 1984, GE-22, 3–13. [Google Scholar] [CrossRef]
- Reiter, D.T.; Rodi, W. Nonlinear waveform tomography applied to crosshole seismic data. Geophysics 1996, 61, 902–913. [Google Scholar] [CrossRef]
- Kuroda, S.; Takeuchi, M.; Kim, H.J. Full waveform inversion algorithm for interpreting cross-borehole GPR data. In Proceedings of the 2005 SEG Annual Meeting, Houston, TX, USA, 6–11 November 2005; pp. 1176–1179. [Google Scholar]
- Ernst, J.R.; Green, A.G.; Maurer, H.; Holliger, K. Application of a new 2D time-domain full-waveform inversion scheme to crosshole radar data. Geophysics 2007, 72, J53–J64. [Google Scholar] [CrossRef]
- Ernst, J.R.; Maurer, H.; Green, A.G.; Holliger, K. Full-waveform inversion of crosshole radar data based on 2-D finite-difference time-domain solutions of Maxwell’s equations. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2807–2828. [Google Scholar] [CrossRef]
- Meles, G.A.; Kruk, J.V.D.; van der Kruk, J.; Greenhalgh, S.A.; Ernst, J.R.; Maurer, H.; Green, A.G. A new vector waveform inversion algorithm for simultaneous updating of conductivity and permittivity parameters from combination crosshole/borehole-to-surface GPR data. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3391–3407. [Google Scholar] [CrossRef]
- Belina, F.A.; Irving, J.; Ernst, J.R.; Holliger, K. Waveform inversion of crosshole georadar data: Influence of source wavelet variability and the suitability of a single wavelet assumption. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4610–4625. [Google Scholar] [CrossRef]
- Liu, S.; Liu, X.; Meng, X.; Fu, L.; Lu, Q.; Deng, L. Application of time-domain full waveform inversion to cross-hole radar data measured at Xiuyan Jade Mine, China. Sensors 2018, 18, 3114. [Google Scholar] [CrossRef] [PubMed]
- Virieux, J.; Operto, S. An overview of full-waveform inversion in exploration geophysics. Geophysics 2009, 74, WCC127–WCC152. [Google Scholar] [CrossRef]
- Shin, C.; Cha, Y.H. Waveform inversion in the Laplace domain. Geophys. J. Int. 2008, 173, 922–931. [Google Scholar] [CrossRef]
- Ha, W.; Shin, C. Why do Laplace-domain waveform inversions yield long-wavelength results? Geophysics 2013, 78, R167–R173. [Google Scholar] [CrossRef]
- Shin, C.; Ha, W. A comparison between the behavior of objective functions for waveform inversion in the frequency and Laplace domains. Geophysics 2008, 73, VE119–VE133. [Google Scholar] [CrossRef]
- Shin, C.; Cha, Y. Waveform inversion in the Laplace-Fourier domain. Geophys. J. Int. 2009, 177, 1067–1079. [Google Scholar] [CrossRef]
- Ha, W.; Shin, C. Laplace-domain full-waveform inversion of seismic data lacking low-frequency information. Geophysics 2012, 77, R199–R206. [Google Scholar] [CrossRef]
- Park, E.; Ha, W.; Chung, W.; Shin, C.; Min, D.-J. 2D Laplace-domain waveform inversion of field data using a power objective function. Pure Appl. Geophys. 2013, 170, 2075–2085. [Google Scholar] [CrossRef]
- Yoon, B.J.; Ha, W.; Son, W.; Shin, C.; Calandra, H. 3D acoustic modelling and waveform inversion in the Laplace domain for an irregular sea floor using the Gaussian quadrature integration method. J. Appl. Geophys. 2012, 87, 107–117. [Google Scholar] [CrossRef]
- Kim, Y.; Shin, C.; Calandra, H.; Min, D.-J. An algorithm for 3D acoustic time-Laplace-Fourier-domain hybrid full waveform inversion. Geophysics 2013, 78, R151–R166. [Google Scholar] [CrossRef]
- Shin, J.; Ha, W.; Jun, H.; Min, D.-J.; Shin, C. 3D Laplace-domain full waveform inversion using a single GPU card. Comput. Geosci. 2014, 67, 1–13. [Google Scholar] [CrossRef]
- Ha, W.; Kang, S.-G.; Shin, C. 3D Laplace-domain waveform inversion using a low-frequency time-domain modeling algorithm. Geophysics 2015, 80, R1–R13. [Google Scholar] [CrossRef]
- Son, W.; Pyun, S.; Shin, C.; Kim, H.-J. Laplace-domain wave-equation modeling and full waveform inversion in 3D isotropic elastic media. J. Appl. Geophys. 2014, 105, 120–132. [Google Scholar] [CrossRef]
- Roden, J.A.; Gedney, S.D. Convolution PML (CPML): An efficient FDTD implementation of the CFS-PML for arbitrary media. Microw. Opt. Technol. Lett. 2000, 27, 334–339. [Google Scholar] [CrossRef]
- Shin, C.; Min, D.-J. Waveform inversion using a logarithmic wavefield. Geophysics 2006, 71, R31–R42. [Google Scholar] [CrossRef]
- Pica, A.; Diet, J.P.; Tarantola, A. Nonlinear inversion of seismic reflection data in a laterally invariant medium. Geophysics 1990, 55, 284–292. [Google Scholar] [CrossRef]
- Kryzhniy, V.V. Numerical inversion of the Laplace transform: Analysis via regularized analytic continuation. Inverse Probl. 2006, 22, 579–597. [Google Scholar] [CrossRef]
- Tukey, J.W. Exploratory Data Analysis; Addison Wesley: Massachusetts, MA, USA, 1977. [Google Scholar]
- Tarantola, A. Inverse Problem Theory and Methods for Model Parameter Estimation; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2005. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, X.; Liu, S.; Xu, Y.; Fu, L. Application of Laplace Domain Waveform Inversion to Cross-Hole Radar Data. Remote Sens. 2019, 11, 1839. https://doi.org/10.3390/rs11161839
Meng X, Liu S, Xu Y, Fu L. Application of Laplace Domain Waveform Inversion to Cross-Hole Radar Data. Remote Sensing. 2019; 11(16):1839. https://doi.org/10.3390/rs11161839
Chicago/Turabian StyleMeng, Xu, Sixin Liu, Yi Xu, and Lei Fu. 2019. "Application of Laplace Domain Waveform Inversion to Cross-Hole Radar Data" Remote Sensing 11, no. 16: 1839. https://doi.org/10.3390/rs11161839
APA StyleMeng, X., Liu, S., Xu, Y., & Fu, L. (2019). Application of Laplace Domain Waveform Inversion to Cross-Hole Radar Data. Remote Sensing, 11(16), 1839. https://doi.org/10.3390/rs11161839






