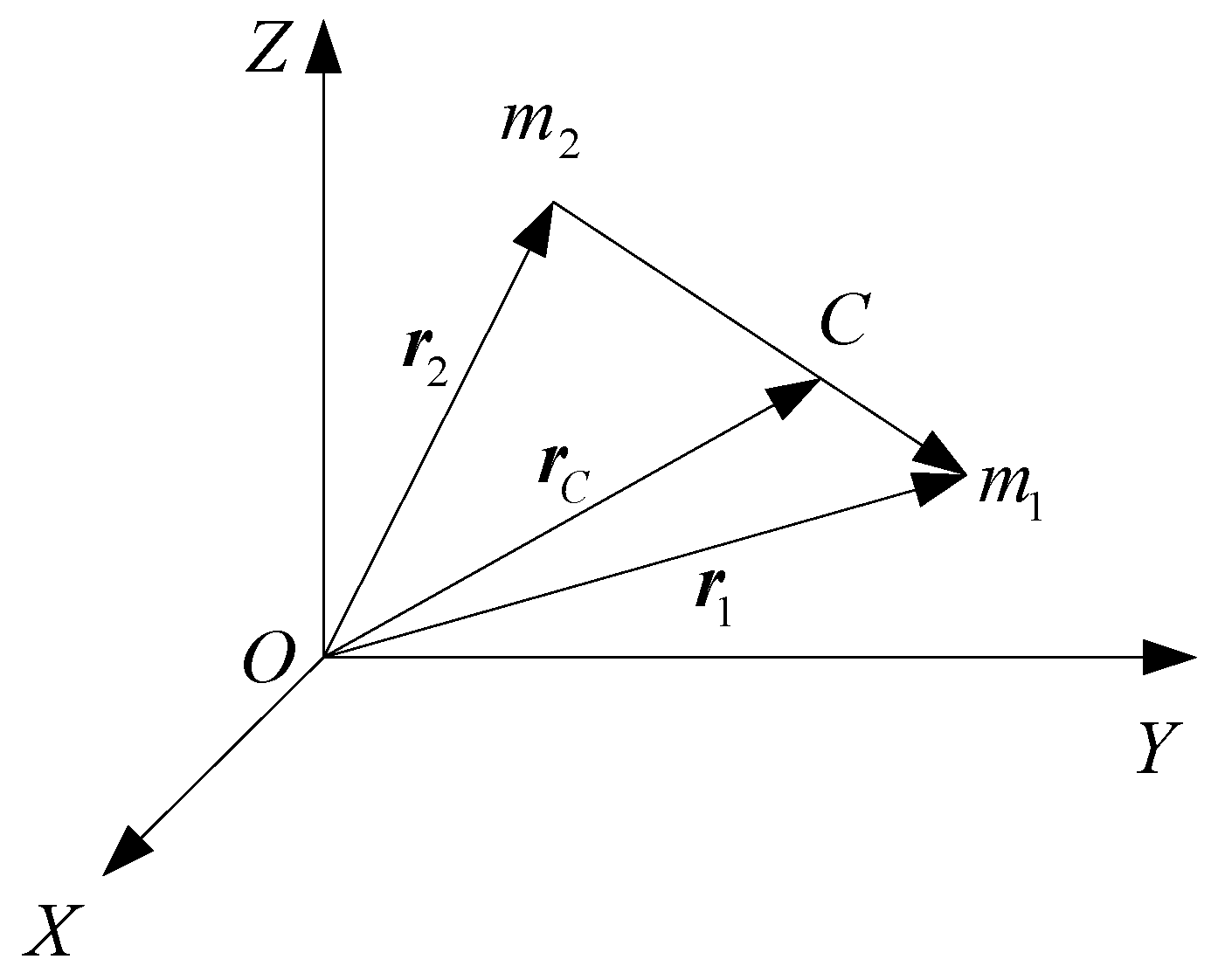
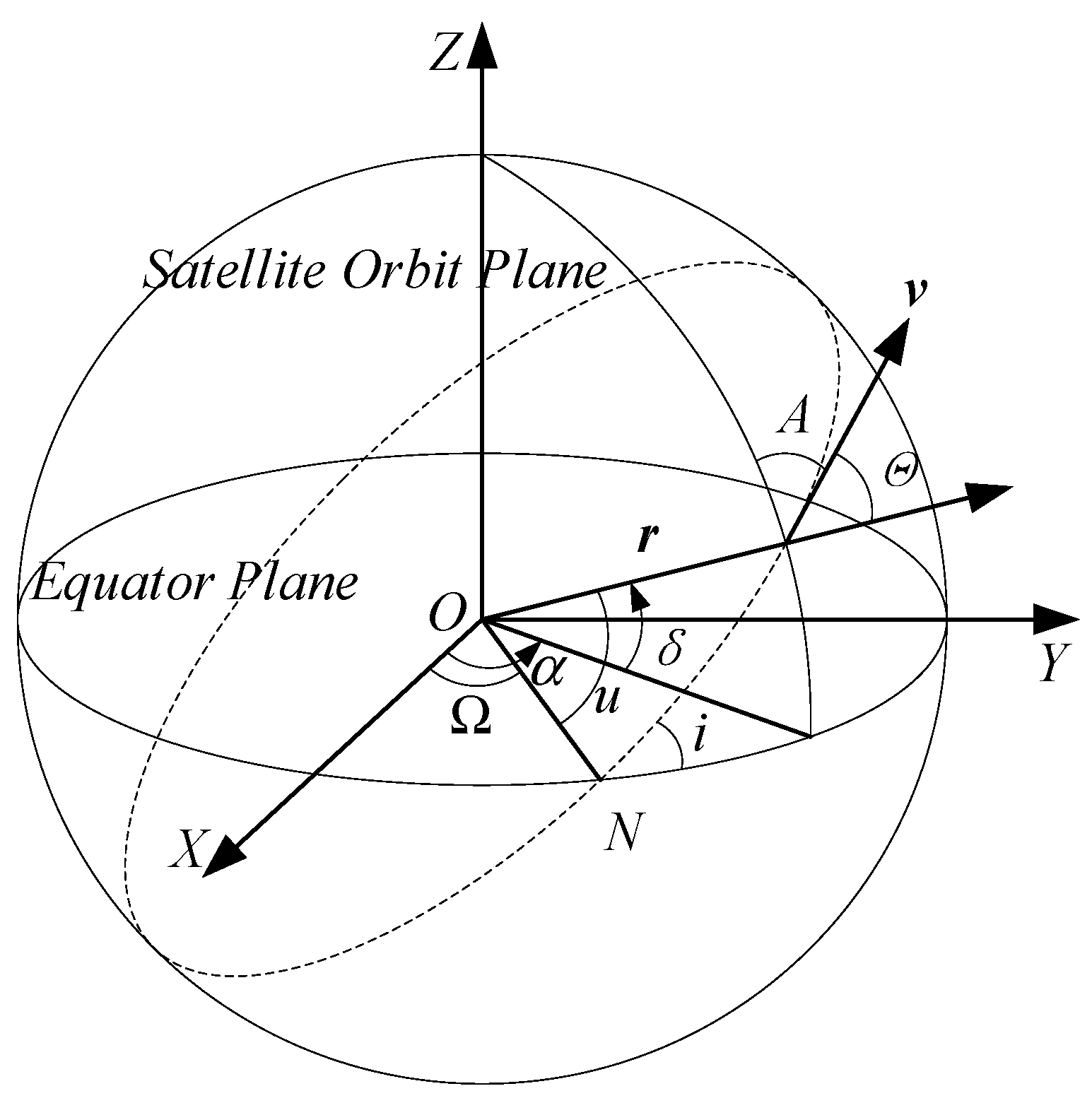
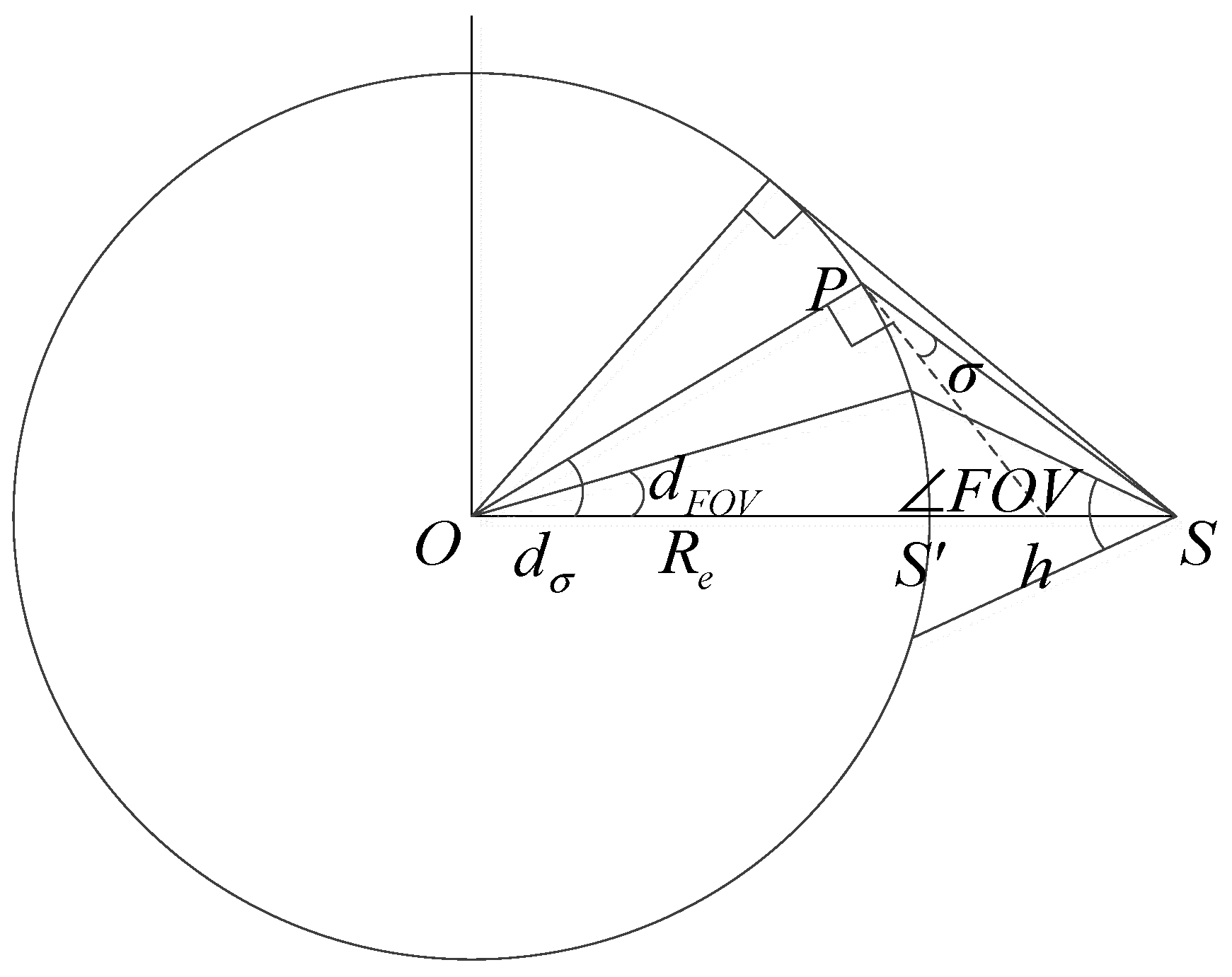
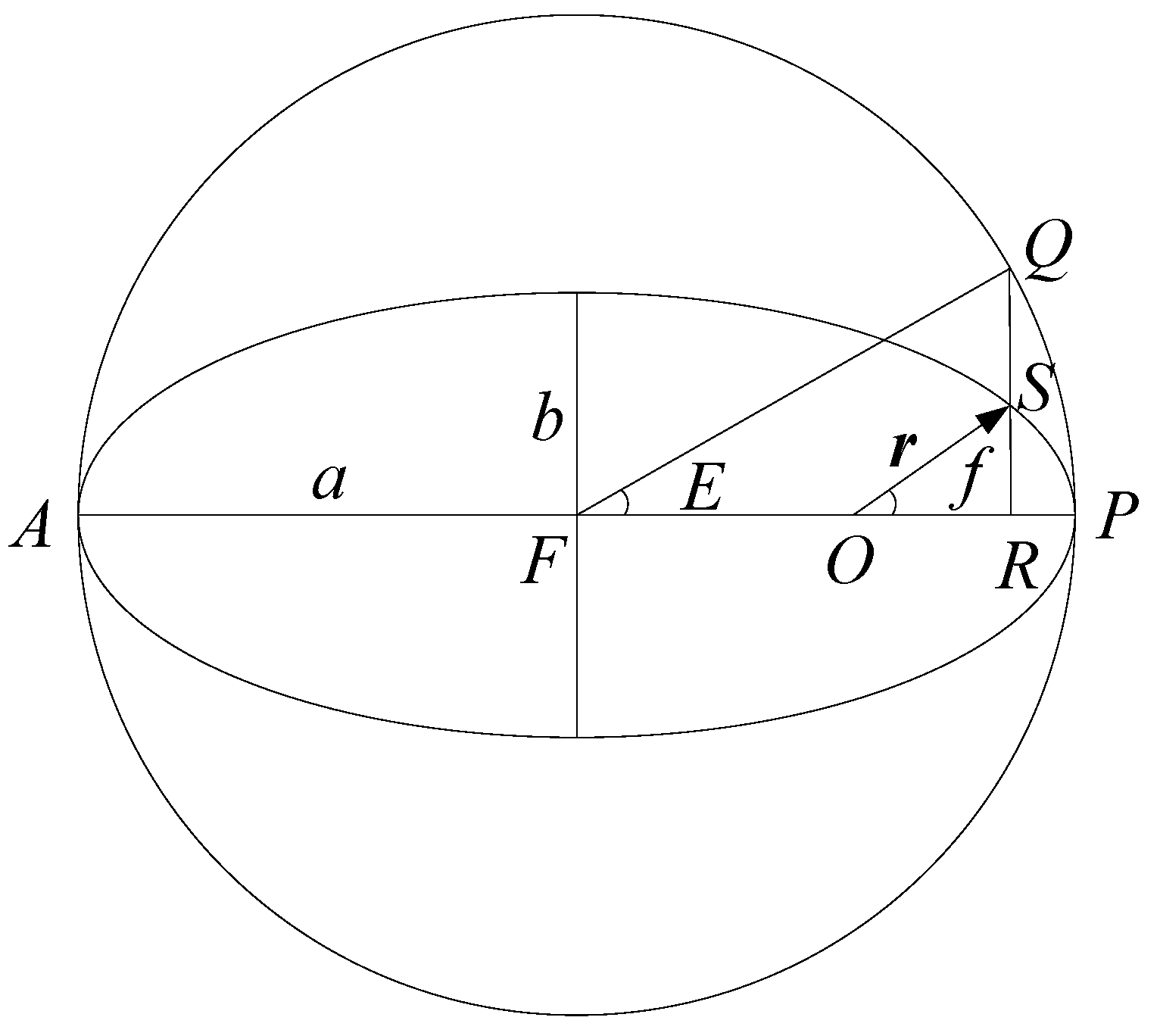1. Introduction
Earth observation satellites (EOSs) use Earth-observing sensors to detect the Earth’s surface and lower atmosphere to obtain information [
1]. By using many kinds of remote sensing systems, such satellites can measure a wide range of spatial, spectral, and temporal parameters [
2]. Consequently, Earth observation satellites have been recognized as valuable tools for viewing, analyzing, characterizing, and making decisions about our environment. Spectral measurements from satellite remote sensors have been applied in many fields, including national defense construction, economic development, national security, environmental protection, disaster assessment, and land resource surveys [
3,
4]. According to the satellite database of the Union of Concerned Scientists [
5], as of 30 November 2018, a total of 1957 active satellites were orbiting the Earth, 65% of which were owned by three nations, i.e., the United States (849), Russia (152), and China (284). The total number of satellites has been growing sharply in recent years; in 6.5 years from 2012 to 2019, the number increased from 1000 to nearly 2000, while in the previous 6.5 years (from 2005 to 2012) the number had only increased from 800 to 1000 [
6]. Among the satellites active on 30 November 2018, 1232 of them (63%) were low Earth orbit (LEO) satellites, i.e., those orbiting at an altitude of less than 2000 km above the Earth’s surface. Since LEO satellites have the property of low propagation delay, they are very suitable for use in multimedia technology, as they should be able to deliver a large amount of information such as image and video signals at a higher data rate, as well as audio signals at a relatively low data rate [
7,
8].
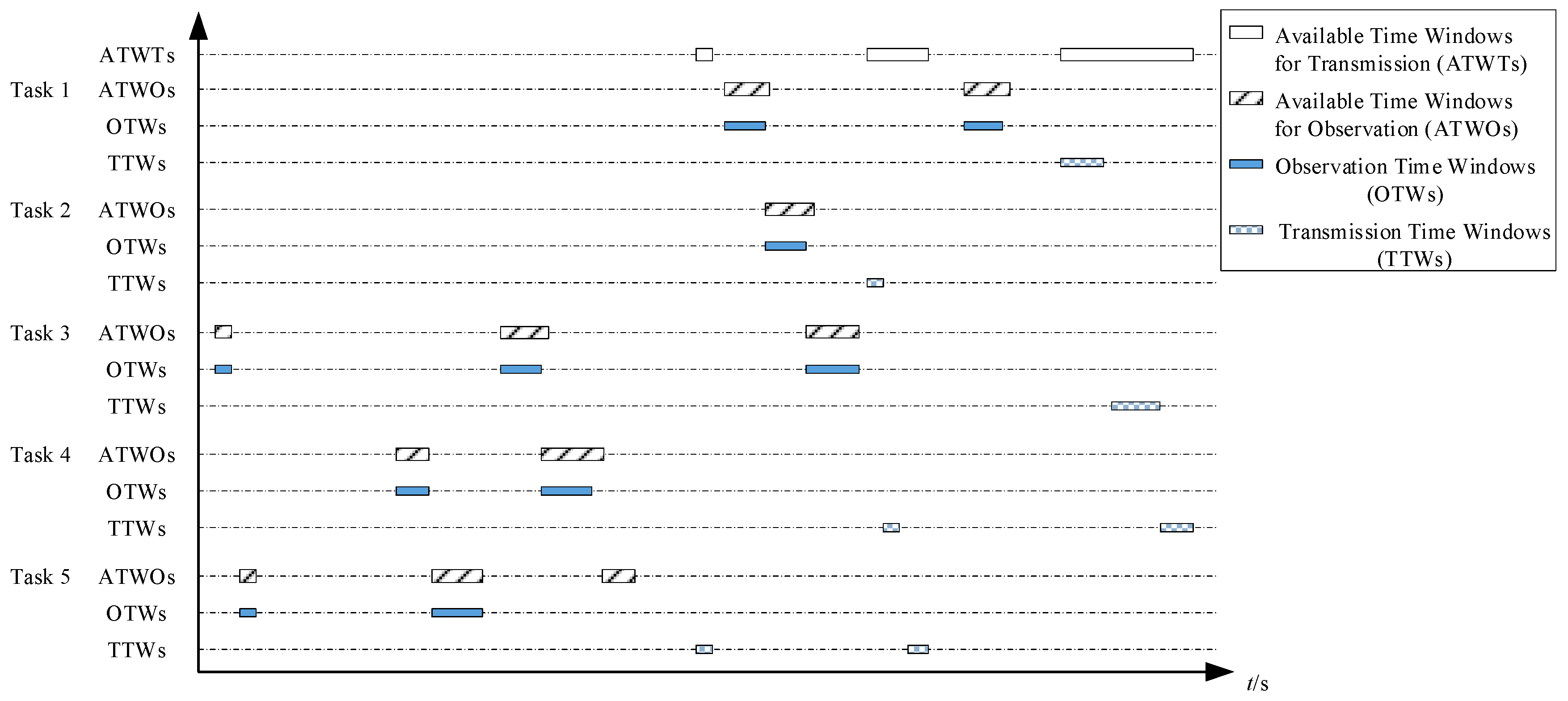
LEO satellites can execute observation tasks only when passing above the target area, and their success rates are often influenced by local weather conditions, illumination conditions (sunlight angles), seasonal factors, etc. A large amount of image/video data is produced after observation and should be transmitted to ground receiver stations when the satellite passes over them. Therefore, LEO satellites can only execute tasks at certain times [
9], which are defined as available time windows (ATWs) in this paper. Only after the acquired data has been transmitted to a ground receiver station can an observation task be considered as completely successful. Some observations can only be made when the footprint of the satellite is illuminated by sunlight [
10]. Additionally, the quality of satellite observation missions may also be affected by weather conditions. Moreover, observation missions may fail even within the observable time windows, since the quality of the images may not meet the requirements of accuracy and clarity. Therefore, satellite resources are very limited and are much more costly than terrestrial observation resources (i.e., satellites are power- and bandwidth-constrained) [
11]. When observing dynamic targets and regional targets, multiple satellites may be used to conduct joint observation missions, which present more complex multi-type task scheduling problems [
1,
12,
13,
14,
15]. Thus, developing an effectiveness evaluation method for task scheduling for LEO satellites is important to allow decision-makers to evaluate the effectiveness of planned observation tasks. Increasing the effectiveness of observation tasks increases the number of acquisitions that can be made, and therefore ultimately benefits multitemporal analysis. In fact, in this field, the availability of a substantial number of acquisitions is a determinant of the success of observation missions. Therefore, from this perspective, the availability of images can be considered as a key factor of the quality of satellite observations.
System effectiveness is defined as the ability of a system to meet given quantitative characteristics and service requirements under specified conditions. Effectiveness evaluation involves estimating the overall availabilities, efficiencies, success rates, and commercial returns of a system based on their comprehensive performances in order to support the optimization and improvement of task planning [
16]. Effectiveness evaluation models have been studied in a wide variety of applications for many years. Many researchers examined the effectiveness of systems by using various methods, including simulations, analytical calculations, computational workflows, and various factors-based and model-assisted approaches, with the goal of validating the systems’ economic advantages in practice. Kabban et al. (2018) proposed a simulation model by using a time- and cost-efficient method to determine sensitive factors of a structural health monitoring (SHM) system in order to enable SHM validation [
17]. Madni et al. (2019) proposed a methodological framework for analyzing investments in and potential gains from satellites, considering system complexity, environmental complexity and regulatory constraints, and system lifespan [
18]. Liu et al. (2019) used computational workflows for evaluations of the design of complex system solutions, which were also able to support co-simulations as part of larger workflows including additional auxiliary computational tasks [
19]. The Availability–Dependability–Capability (ADC) model, Data Envelopment Analysis (DEA), Analytic Hierarchy Process (AHP), Bayesian network, fuzzy evaluation, etc., are all applicable to effectiveness evaluation. The ADC model is based on the availability model of the Weapons System Effectiveness Industry Advisory Committee (WSEIAC), which is improved and applied in this paper. In the model, system effectiveness is defined as the performance metrics of a system that satisfy the specific requirement of varied missions, and it is a function of availability, dependability, and capability [
20]. Xiao et al. (2015) first defined the efficiency of family farms, then used Farrell’s production efficiency measurements to investigate the premise assumptions and the realization condition, and then constructed a model to evaluate the effectiveness of family farms based on a nonparametric DEA method [
21]. Wu et al. (2016) adopted AHP to determine the weight of all the evaluation indexes and established an assessment model for campus emergency management capability using the fuzzy comprehensive evaluation method [
22]. Kabir et al. (2018) developed a Bayesian belief network (BBN) model to evaluate the performance of an employee considering the dependencies and correlations between performance criteria which is also capable of assessing the credibility of multiple experts and ranking employees for different purposes such as reward, improvement, training, promotion, termination, and compensation [
23].
Studies of satellite effectiveness evaluation (SEE) in the literature are relatively limited. Li et al. (2018) focused on the assessment of the coverage effectiveness of remote sensing satellites and proposed a multi-index evaluation method based on index weight using an entropy weight method and AHP [
24]. In the mentioned papers [
17,
18,
19,
20,
21,
22,
23,
24], commercial profit is not within the index system, which means the authors cannot measure the economic value of the task scheduling for satellites. Additionally, the effects of weather uncertainties on different observation targets were not considered. In the present study, we firstly describe the motion of a LEO satellite in an Earth-centered inertial (ECI) coordinate frame and then provide a method for generating the ATWs considering sunlight angles, elevation angles, and sensor types. Systems Tool Kit (STK, formerly Satellite Tool Kit) is a mature software tool that can achieve this functionality, however the product is subject to the International Traffic in Arms Regulations (ITAR), administered by the U.S. Department of State, and the Export Administration Regulations (EAR), administered by the U.S. Department of Commerce [
25], which means that STK cannot be used in some cases. We propose this method and attempt to provide an alternative reference for others who engage in relevant research. Secondly, we develop an effectiveness evaluation model for satellite observation and data-downlink scheduling (SODS) based on the Availability–Capacity–Profitability (ACP) framework from the perspectives of satellites’ time availability, the success rates of the planned tasks, and the return rate of task profits, which is a comprehensive model to estimate the overall performance of the satellite task system. Furthermore, we consider the effects of weather uncertainties in the SEE model such that different observation tasks are allowed to have different success rates under different weather conditions. Thirdly, we a case study is provided to verify the proposed models and the result is analyzed.
The rest of this paper is organized as follows: In
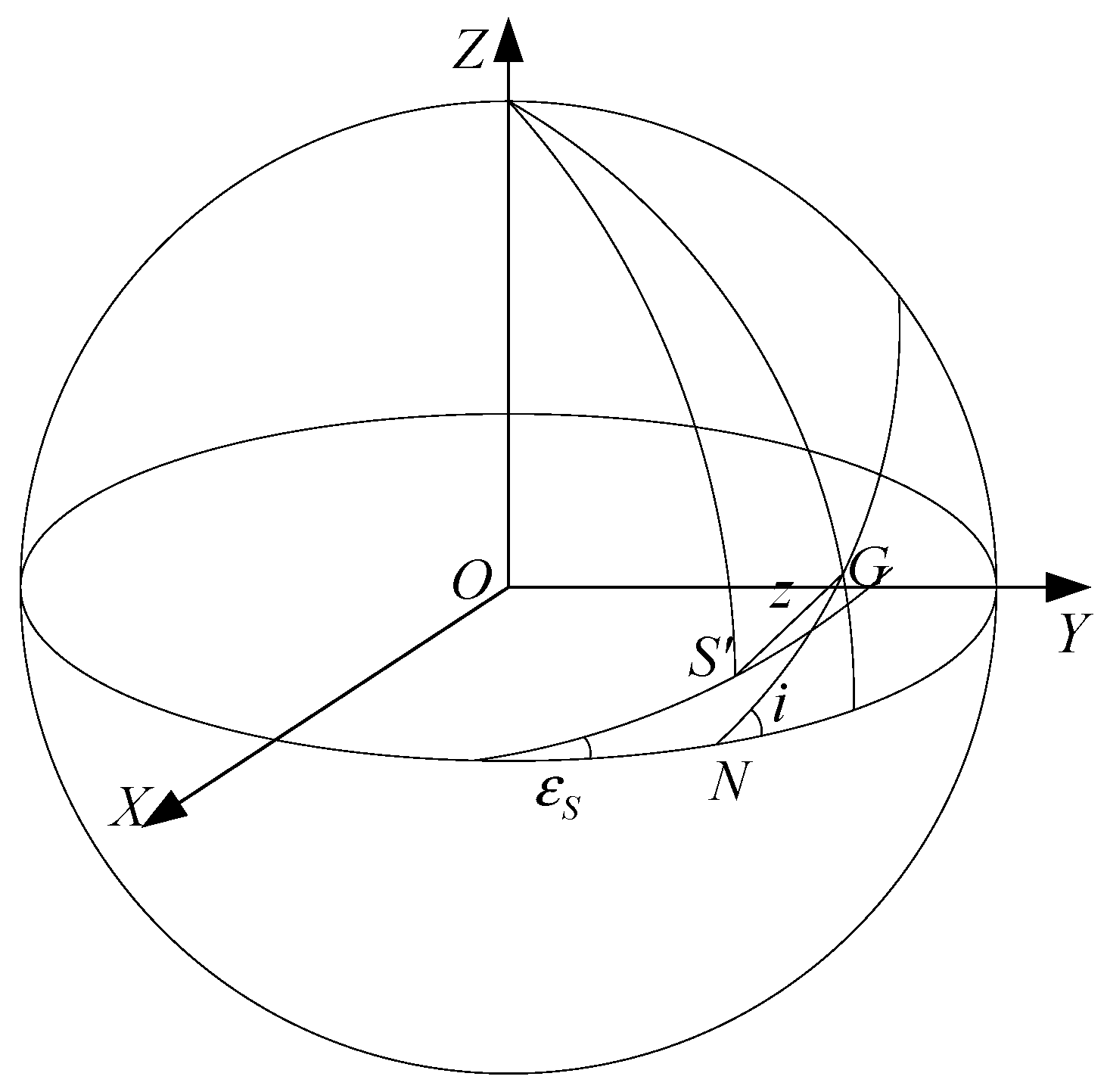
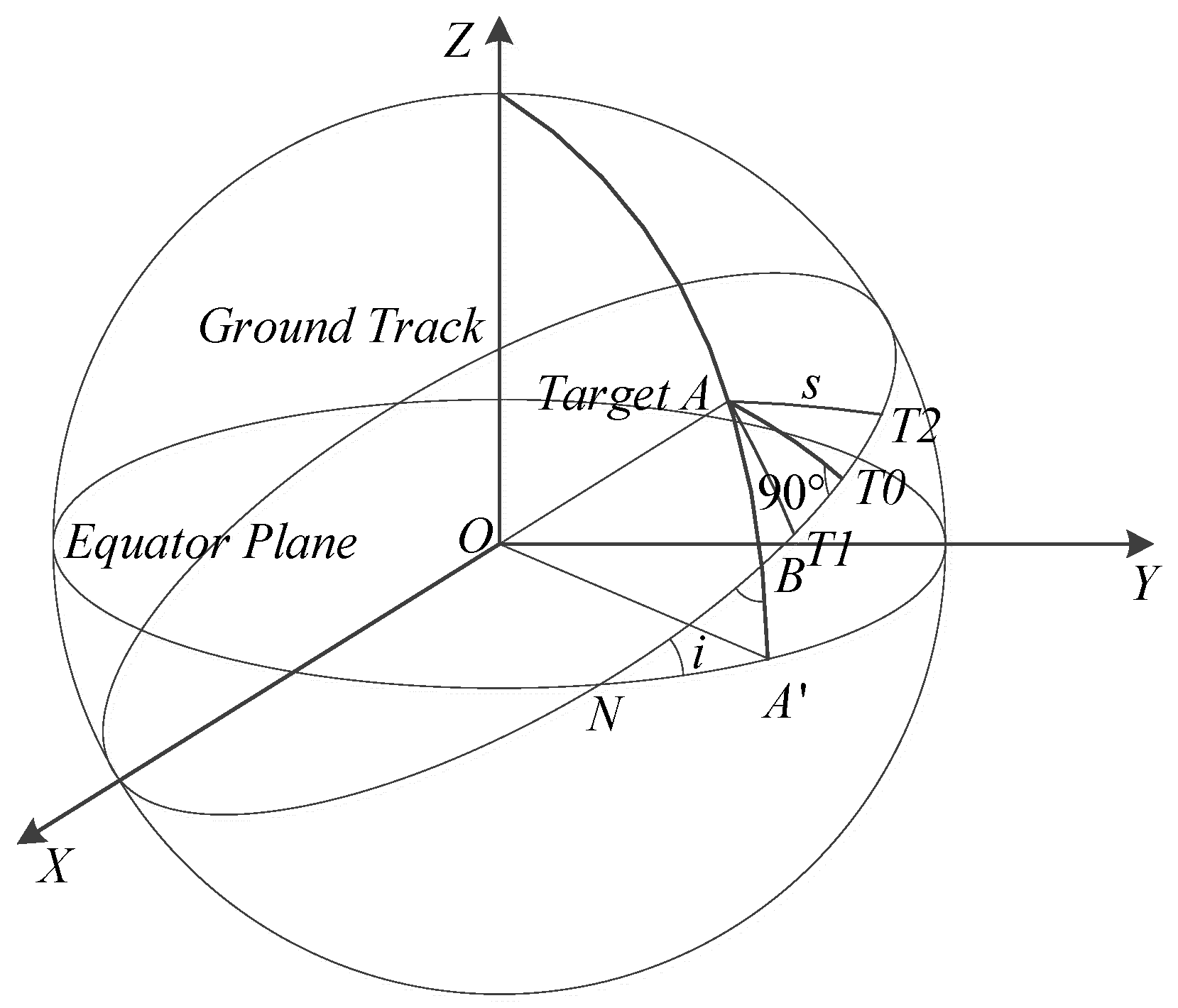
Section 2, we briefly illustrate the two-body motion model and propose a procedure for obtaining ATWs considering some necessary constraints. In
Section 3, a formal description of the SEE model for SODS considering weather uncertainties is provided. In this model, the time availability, success rate of observation, rate of return, and mission effectiveness are determined. In
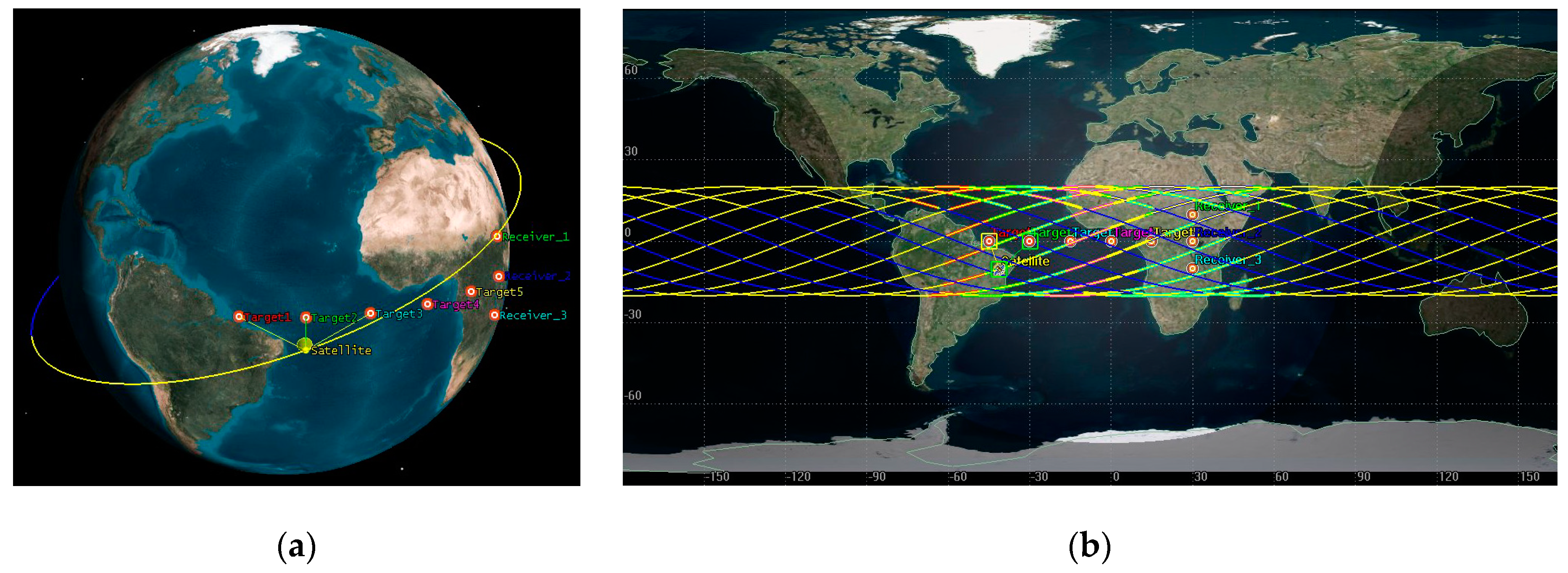
Section 4, a case study is presented to demonstrate the effectiveness of the method for obtaining ATWs and the ACP-based SEE model. Finally, in
Section 5, we conclude the paper.